Periodic Orbits Close to That of the Moon in Hill's Problem

In the framework of the restricted, circular, 3-dimensional 3-body problem Sun-Earth-Moon, Valsecchi et al. (1993) found a set of 8 periodic orbits, with duration equal to that of the Saros cycle, and differing only for the initial phases, in which the motion of the massless Moon follows closely that of the real Moon. Of these, only 4 are actually independent, the other 4 being obtainable by symmetry about the plane of the ecliptic. In this paper the problem is treated in the framework of the 3-dimensional Hill's problem. It is shown that also in this problem there are 8 periodic orbits of duration equal to that of the Saros cycle, and that in these periodic orbits the motion of the Moon is very close to that of the real Moon. Moreover, as a consequence of the additional symmetry of Hill's problem about the y-axis, only 2 of the 8 periodic orbits are independent, the other ones being obtainable by exploiting the symmetries of the problem.

1. Introduction

Roy (1973) was apparently the first to notice and discuss the occurrence of near Mirror Configurations in the main lunar prolem. In a system of n gravitating point-masses, a Mirror Configuration (MC; Roy and Ovenden, 1955) occurs when each radius vector from the centre of mass of the system happens to be perpendicular to every velocity vector. The importance of MCs for such systems is due to the following property: if, during its evolution, a system of n gravitating point-masses passes through an MC, then the Mirror Theorem (Roy and Ovenden, 1955) states that the time evolution of the system afterwards is the mirror image of the evolution before the occurrence of the MC; moreover, a corollary of the Mirror Theorem states that, if a system passes through two MCs, then each of its point-masses is on a periodic orbit.

The latter property was exploited, in the framework of the circular, restricted, 3-dimensional 3-body problem (CR3D3BP) Sun-Earth-Moon, to show the existence of periodic orbits with duration equal to that of the Saros (Valsecchi et al., 1993), an eclipse cycle known since more than two millennia, in which the mutual configurations of Sun, Earth and Moon nearly repeat, to considerable accuracy, after 223 synodic months (Roy, 1973; Perozzi et al., 1991).

In this paper, the issue is revisited in the framework of the 3-dimensional Hill's problem (3DHP), proceeding as in Valsecchi et al. (1993), and it is shown that 8 periodic orbits with duration equal to that of the Saros exist also in this case, but only 2 of them are actually independent, while the other ones can be obtained considering the symmetries of the problem.

2. Mirror Configurations

According to Roy and Ovenden (1955), there are two types of MCs: colinear MCs, in which all the bodies are located along a straight line, with their velocity vectors orthogonal to the straight line, and coplanar MCs, in which all the bodies are located on a plane, with the velocity vectors orthogonal to that plane.

2.1. MCs in the CR3D3BP

In Valsecchi et al. (1993) the two types of MCs are discussed in the framework of the CR3D3BP Sun-Earth-Moon. Given that in this problem the Earth moves on a circular orbit about the Sun, a colinear MC is achieved if the massless Moon is at perigee or apogee, at the ascending or at the descending node of its geocentric orbit, and perfectly aligned with the Sun and the Earth (i.e., in solar or lunar eclipse configuration).

In terms of the geocentric orbital elements of the Moon, these conditions imply that the Moon must be at mean anomaly M equal to either 0° or 180°, argument of mean latitude θ = ω+M equal to either 0° or 180°, and difference of mean longitude Δλ = λ − λ′ between the mean longitude of the Moon λ and that of the Sun λ′ again equal to either 0° or 180°.

For a coplanar MC to occur, the constraints on M and Δλ are the same, while that on the argument of mean latitude becomes θ equal to either 90° or 270°. Given that anyway M must be either 0° or 180°, the constraint on the argument of latitude implies ω = 0° or ω = 180° for a colinear MC, and ω = 90° or ω = 270° for a coplanar MC.

Table 1 summarizes the situation; in it the MCs are coded as in Valsecchi et al. (1993), with a three-digit code representing ω, M and Δλ as multiples of 90°. Note that MCs differing by 180° in ω are grouped together in the same row, due to the symmetry of the problem about the plane in which the Sun and the Earth move.

TABLE 1

Table 1. The 16 possible MC's of the CR3D3BP.

2.2. MCs in the 3DHP

In the 3DHP the possible MCs are again 16, and their coding is exactly the same as in the CR3D3BP. In this case, however, there is an important difference, due to the additional symmetry present in this problem, namely, the one about the y-axis; as a consequence, two MCs differing only because in one of them Δλ = 0° and in the other Δλ = 180° are equivalent. Taking this into account, in the case of the 3DHP we rearrange the MCs of Table 1 as shown in Table 2.

TABLE 2

Table 2. The 16 possible MC's of the 3DHP.

3. The Saros Cycle and the Associated Periodic Orbits

There is a vast literature concerning lunar cycles (see, e.g., Steves, 1997) and the Saros is perhaps the most interesting one among them. In fact, at variance from most of the other lunar eclipse-predicting cycles, it involves not only the synodic and the nodical months, but also the anomalistic one. Let us consider the mean durations of the synodic (T_Δλ), anomalistic (T_M) and nodical month (T_θ), given by:

$\begin{array}{l}{\text{T}}_{\Delta \lambda }=29.530589\text{ d}\\ {\text{T}}_M=27.554551\text{ d}\\ {\text{T}}_{\theta }=27.212220\text{ d};\end{array}$

then, one easily sees that:

$223T_{\Delta \lambda }=\mathrm{6\; 585}.32\simeq 239T_M=\mathrm{6\; 585}.54\simeq 242T_{\theta }=\mathrm{6\; 585}.36.$

In the rest of this paper, the duration of the Saros will be taken to be that of 223 synodic months, i.e., 6 585.321 347 d.

During a Saros, the argument of perigee ω of the lunar orbit makes 3 full revolutions; this happens because the argument of latitude makes 242 revolutions (the 242 nodical months), and the mean anomaly M makes 239 revolutions (the 239 anomalistic months): the difference is due to the 3 revolutions of ω. If the Moon is started from, say, the MC coded 000, in which ω = 0°, M = 0°, Δλ = 0°, after a half Saros each of these angles will have made a half-integer number of revolutions; thus, the MC occurring at that time will be 222, in which ω = 180°, M = 180°, Δλ = 180°. In this way it is possible to establish the pairs of MCs that occur during the periodic orbits of duration equal to that of the Saros (Valsecchi et al., 1993).

3.1. Periodic Orbits in the CR3D3BP

As shown in Valsecchi et al. (1993), there exist 8 such periodic orbits in the CR3D3BP, in which the 16 MCs are combined in pairs as discussed above. To find these orbits, Valsecchi et al. (1993) used a 3-dimensional Newton-Raphson root finder and Everhart's integrator RADAU (Everhart, 1985) at 15th order. In these computations, the ratio of the mass of the Earth to that of the Sun was set to

$m_{\oplus }=\frac{1}{328900.53},$

corresponding to that of the real Earth-Moon system.

The Moon was placed in one of the 8 colinear MCs, say 000, by specifying the appropriate values for ω, M and Δλ from Table 1, assigning tentative values for the starting geocentric orbital elements a, e and i, and then looking for the occurrence of the paired MC (in this case 222) at the end of a numerical integration for half of a Saros. The Newton-Raphson root finder was used to converge to the values of a, e and i that led to the occurrence of the paired MC. In this way, all the 8 periodic orbits were found; they are summarized in Table 3.

TABLE 3

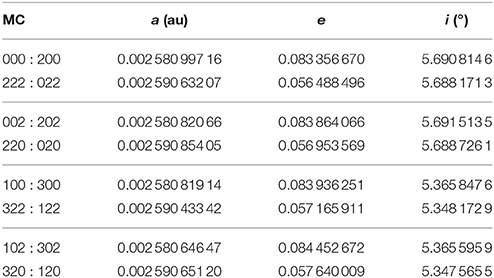
Table 3. The osculating elements a, e and i of the massless Moon, in the periodic orbits associated to the Saros, when at the 16 possible MCs of the CR3D3BP (from Valsecchi et al., 1993).

3.2. Periodic Orbits in the 3DHP

The procedure followed to find the periodic orbits associated to the Saros in Hill's problem has been the same as in Valsecchi et al. (1993), the only difference being in the equations of motion; those used in the present work are the ones of Hill's problem, in the form given in Schmidt (1979):

$\begin{array}{l}ẍ=-\frac{\mu }{r^3}x+2n\prime ẏ+3{n\prime }^{2}x\\ ý=-\frac{\mu }{r^3}y-2n\prime ẋ\\ \ddot{z}=-\frac{\mu }{r^3}z-{n\prime }^{2}z,\end{array}$

where:

$\begin{array}{l}k=0.01720209895\\ \mu =k^2{m}_{\oplus }\\ n\prime =\frac{k}{\sqrt{1+m_{\oplus }}}\\ r=\sqrt{x^2+y^2+z^2}.\end{array}$

In this way, distances are in astronomical units, and time is in days.

The resulting periodic orbits are given in Table 4; comparing the values of a, e, i with those of the corresponding MCs in Table 3, one sees that the differences are rather small.

TABLE 4

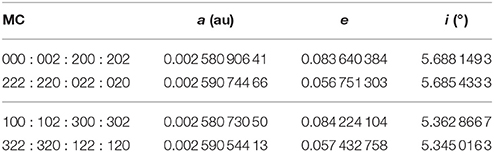
Table 4. The osculating elements a, e and i of the Moon, in the periodic orbits associated to the Saros, when at the 16 possible MCs of the 3DHP.

The time behaviour of the geocentric orbital elements of the Moon in these periodic orbits is quite close to that of the real Moon, just as found by Valsecchi et al. (1993); a similar comparison is repeated here.

A good approximation to a MC 200 was realized by the real Moon on JD 2 371846.872 (17.372 October 1781, Valsecchi et al., 1993); according to the JPL ephemeris DE406, the orbit of the Moon had, at that time, ω = 179°.0, M = 0°.0 and Δλ = 0°.0.

The four panels of Figure 1 show the time evolution of, from top to bottom, a, e, i, ω of the real Moon, taken from JPL DE406, in red, and the corresponding quantities for the periodic orbit passing through MCs 200 and 022, in green. The behaviour of a and ω of the periodic orbit match very closely that of the real Moon. For e and i there is a systematic difference, but the short-period terms affecting these two elements appear to be the same as those of the real orbit.

FIGURE 1

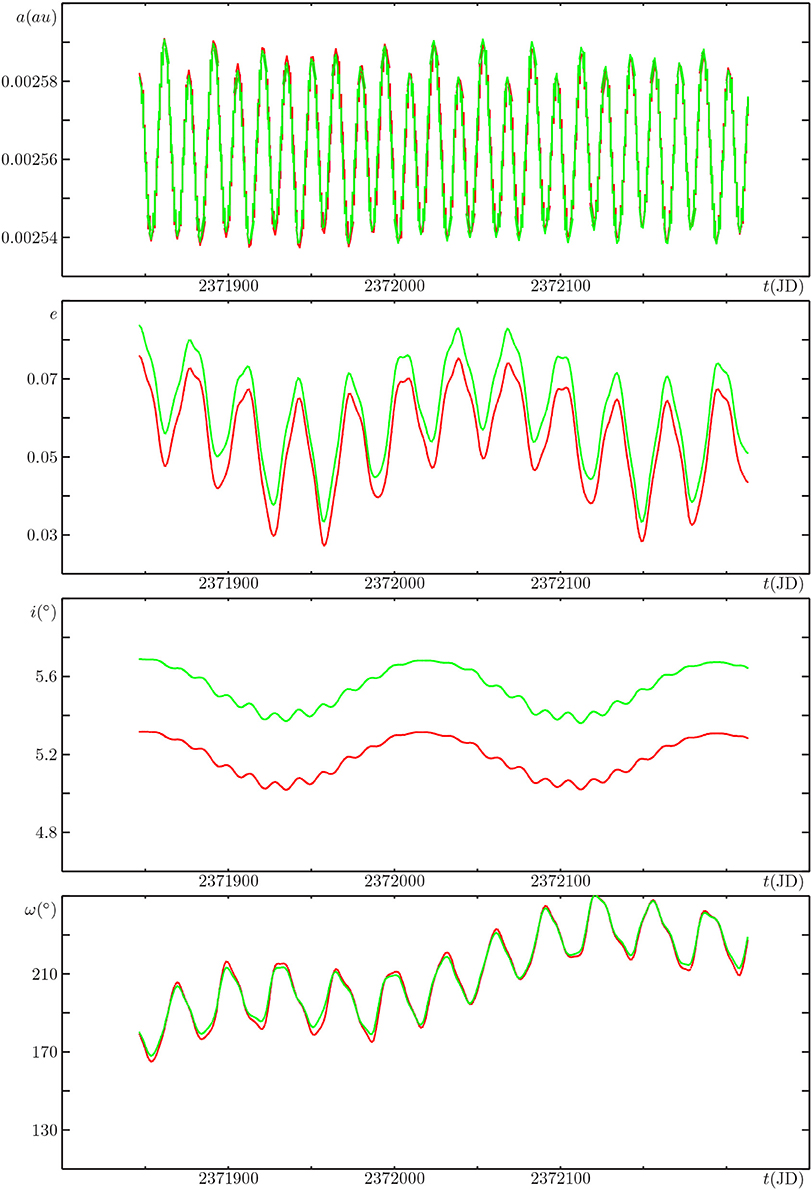
Figure 1. Time evolution of the elements of the Moon taken from JPL DE406 (in red) and for the periodic orbit passing through MCs 200 and 022 (in green); top to bottom: semimajor axis a, eccentricity e, inclination i, argument of perigee ω; the time span covered is one year, starting from 17.372 October 1781.

Figure 2 contains the last year of the Saros, and shows that the close matching is preserved for the entire cycle.

FIGURE 2

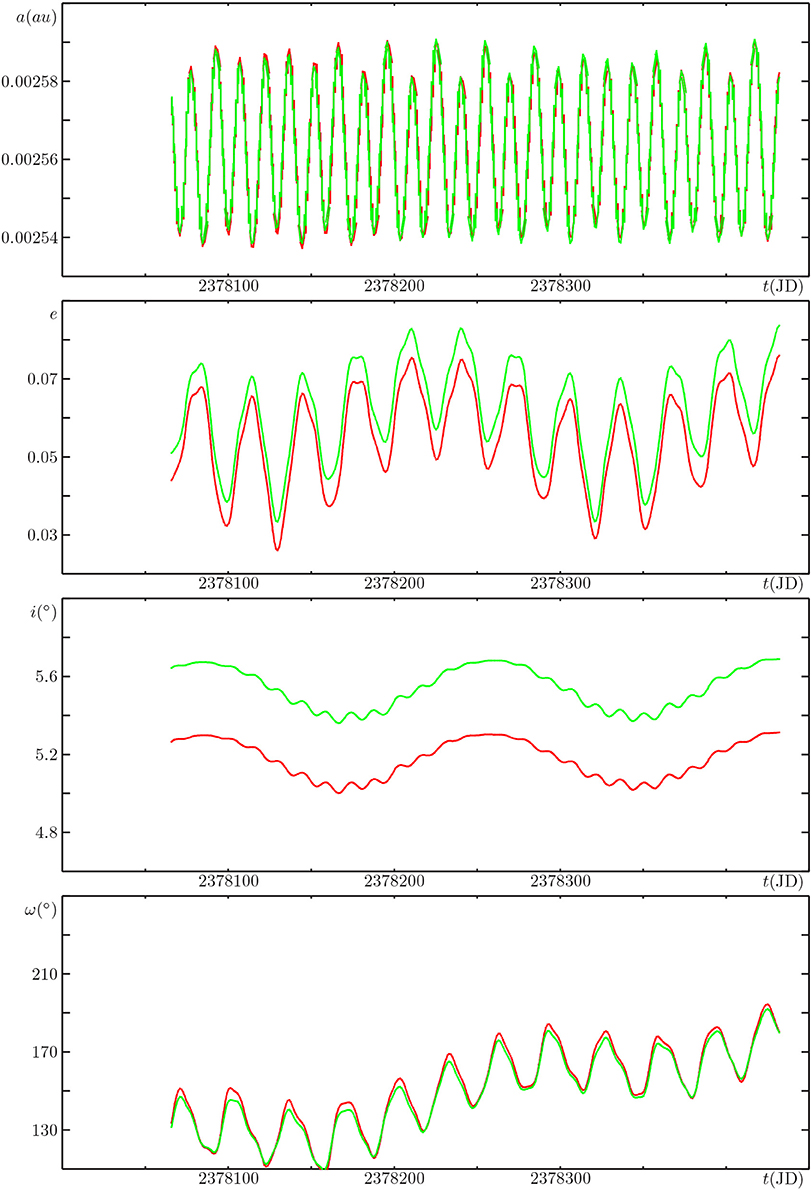
Figure 2. Same as Figure 1, but for the time span of one year, ending one Saros later, on 28.693 October 1799.

4. Discussion

The periodic orbits found in the 3DHP, besides mimicking closely the real lunar orbit, are also very similar to those found in Valsecchi et al. (1993) in the CR3D3BP, as also shown by the closeness of the values of the geocentric orbital elements reported by Tables 3, 4. In fact, the principal lunar short-period terms (Brouwer and Clemence, 1961) are contained in the periodic orbits in both problems:

• the variation, a term depending on 2Δλ, an angle that makes 446 revolutions in the periodic orbits associated to the Saros;

• the parallactic inequality, depending on Δλ, that makes 223 revolutions;

• the evection, to which are due a perturbation in e and ω, depending on $2{\lambda }^{\prime }-2\tilde{\omega }$, that makes 32 revolutions, and another perturbation in λ, depending on $\lambda -2\lambda \prime +\tilde{\omega }$, that makes 207 revolutions;

• the principal perturbation in latitude, depending on λ − 2λ′+Ω, that makes 204 revolutions.

On the other hand, these orbits differ substantially from Hill's periodic orbit (Hill, 1878). Hill's periodic orbit lasts for exactly one synodic month, is planar, and in it all the crossings of the x and y-axes take place at right angles.

Actually, using the same periodic-orbit-finder software used to find the orbits of Table 4, we can compute Hill's orbit. The MCs in this orbit are of the colinear type (coplanar MCs, in spite of their name, cannot take place if the motion is planar), and correspond to the two crossings of the x-axis. At these crossings, the geocentric distance of the Moon has two identical minima, and the orbital elements are:

$\begin{array}{l}a=0.00258607180\text{ au}\\ e=0.013517273,\end{array}$

while at the two crossings of the y-axis, where the geocentric distance has two identical maxima, the orbital elements are:

$\begin{array}{l}a=0.00254002084\text{ au}\\ e=0.018894762.\end{array}$

It is notheworthy that in Hill's orbit there are two perigee passages of the Moon, at the crossings of the x-axis, and two apogee passages, at the crossings of the y-axis; this means that during the single synodic month corresponding to its duration, there are two full anomalistic months. Moreover, the osculating geocentric eccentricity never exceeds 0.02, a value much lower than the mean eccentricity of the real lunar orbit.

Therefore, the time evolution of the elements of the periodic orbits described in this paper follows the behaviour of the osculating geocentric elements of the real Moon much more closely than in the case of Hill's orbit; on the other hand, the latter is succesfully used as intermediate orbit in the Hill-Brown lunar theory (Brown, 1896). Whether these new, longer periodic orbits are suitable for such a task will be the subject of future research.

A natural question to ask is whether periodic orbits similar to those described here do exist, in Hill's problem, for different values of the geocentric distance of the Moon, i.e., for different values of the ratio of the mean motion of Sun and Moon; in Valsecchi et al. (1993) an example of such an orbit of the CR3D3BP was given, corresponding to the probable lunar orbit of the late Precambrian. On the other hand, the Saros-associated periodic orbits in the two problems are so close to each other, as can be seen comparing the numbers in Tables 3, 4, that very likely the same orbits should exist in Hill's problem; also this issue will be the subject of future research.

5. Conclusions

Building on the results of Valsecchi et al. (1993) for the CR3D3BP, it has been shown that also in Hill's problem it is possible to find 8 periodic orbits of duration one Saros, in which the orbital evolution of the Moon closely resembles that of the real Moon. An important difference from the previous case is that, at variance from the periodic orbits found in the CR3D3BP, in Hill's case only 2 orbits are independent, the others being obtainable by considering the symmetries of the problem.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Fruitful discussions with Ettore Perozzi, Bonnie Steves and the late Archie Roy on the subject of this paper are gratefully acknowledged.

References

Brouwer, D., and Clemence, G. M. (1961). Methods of Celestial Mechanics. New York, NY: Academic Press.

Google Scholar

Brown, E. W. (1896). An Introductory Treatise on the Lunar Theory. Cambridge, The University Press.

Everhart, E. (1985). “An efficient integrator that uses Gauss-Radau spacings,” in Dynamics of Comets: Their Origin and Evolution, eds A. Carusi, and G. B. Valsecchi (Dordrecht: D. Reidel), 185.

Google Scholar

Hill, G. W. (1878). Researches in the Lunar Theory. Am. J. Math. 1, 5–26. doi: 10.2307/2369430

CrossRef Full Text | Google Scholar

Perozzi, E., Roy, A. E., Steves, B. A., and Valsecchi, G. B. (1991). Significant high number commensurabilities in the main lunar problem. I - The Saros as a near-periodicity of the Moon's orbit. Celest. Mech. Dynam. Astron. 52:241. doi: 10.1007/BF00048486

CrossRef Full Text | Google Scholar

Roy, A. E. (1973). The use of the saros in lunar dynamical studies. Moon 7:6. doi: 10.1007/BF00578803

CrossRef Full Text | Google Scholar

Roy, A. E., and Ovenden, M. W. (1955). On the occurrence of commensurable mean motions in the solar system. The mirror theorem. Mon. Not. R. Astron. Soc. 115:296. doi: 10.1093/mnras/115.3.296

CrossRef Full Text | Google Scholar

Schmidt, D. S. (1979). Literal solution for Hill's lunar problem. Celest. Mech. 19:279. doi: 10.1007/BF01230219

CrossRef Full Text | Google Scholar

Steves, B. A. (1997). The cycles of Selene. Vistas Astron. 41:543. doi: 10.1016/S0083-6656(98)00004-X

CrossRef Full Text | Google Scholar

Valsecchi, G. B., Perozzi, E., Roy, A. E., and Steves, B. A. (1993). Periodic orbits close to that of the Moon. Astron. Astrophys. 271:308.

Google Scholar