- 1Institute of Nuclear Physics PAN, Kraków, Poland
- 2Max Planck Institute for Nuclear Physics, Heidelberg, Germany
- 3Institute of Nuclear Physics PAN, Kraków, Poland
The TeV diffuse emission from the Galactic plane is produced by multi TeV electrons and nuclei interacting with radiation fields and ambient gas, respectively. Measurements of the TeV diffuse emission help constrain CR origin and transport properties. We present a preliminary analysis of HAWC diffuse emission data from the inner Galaxy. The HAWC measurements will be used to constrain particle transport properties close to the Galaxy center correlating the HAWC maps with predictions of the DRAGON code.
1. Introduction
Cosmic rays (CRs) are the highly energetic nuclei and protons which carry, at least close to the Solar System, an energy density of about 1 eV/cm3. This is comparable to the Galactic magnetic fields, energy density of the radiation fields, and turbulent motions of the interstellar gas. Thus CRs are an energetically important component of the interstellar medium (ISM). They play an important role in the dynamical balance of our Galaxy, and have an important effect on interstellar chemistry through the heating and ionization of the ISM, particularly in its denser regions. Being charged particles, CRs are also strongly coupled to the magnetic fields by Lorentz forces and by strong scattering off field irregularities (MHD waves).
CRs up to at least 1015 eV are believed to be accelerated through diffusive shock acceleration (DSA) in young supernova remnants (SNRs). In the shells of SNRs suprathermal particles would be injected into the acceleration process at the shock propagating into the ISM where collisionless processes transfer to them the kinetic energy of the magnetohydrodynamic shocks Krymskii (1977); Axford (1981); Blandford and Eichler (1987); Bell and Lucek (2001); Malkov (2001). The SNR paradigm for the CR origin is based upon energetic considerations. At least one supernovae explosion event is expected in every 30 years, and considering that, the non thermal energy release at each supernovae event should be 1050 ergs, (which is almost ten percent of total energy release at each SN explosion event), in order to explain the energy density of cosmic ray (which is about 1 ev/cm3) Ginzburg and Syrovatskii (1964) in the Galaxy. This is in good agreement with the typical amount of energy predicted to be created during the acceleration of relativistic particles in supernovae remnant shocks within a DSA scenario Voelk and Biermann (1988); Drury et al. (1989).
Cosmic rays runaway the acceleration sites and finally propagate into the galactic magnetic field, so it is impossible to observe cosmic rays from the candidate injection sites directly.
The information on the cosmic ray spectra at the acceleration sites cannot be traced back, because of the unknown propagation mechanisms of cosmic ray spectra. Secondary CR data suggest that cosmic ray protons and nuclei diffuse in the magnetic fields for times of the order of years, E being the particle energy, before escaping the Galaxy. During this time the particles accelerated by individual sources diffuse into the Galaxy, mix together, get isotropized by the galactic magnetic fields and contribute to the bulk of Galactic cosmic rays known as cosmic ray background or cosmic ray sea, the information on the CR source and CR energy distribution at the source is lost.
However, while cosmic rays scape injection sources and diffuse in the Galaxy, they interact inelastically with ambient molecules and atoms of the interstellar gas and create gamma rays by decay of neutral pions. Electrons produce gamma-rays through inverse Compton scattering and also by bremsstrahlung processes. In contrast to CRs, the gamma rays produced by these accelerated particles, are neutral and travel in straight lines from the site where they were produced to the detector. The gamma ray energy flux from the different directions on the sky provides thus direct information about the parental cosmic ray flux in different locations in the Galaxy. This emission, extending from GeV to hundreds of TeV, is thus the most powerful tool to probe the origin and propagation mechanisms of CRs in the Galaxy and to investigate the extreme astrophysical environments in which these particles are accelerated.
Observational evidences show that the cosmic ray energy density varies strongly in different locations of the Galaxy, in particularly in leactive regions of the Galaxy, such as the MCs (Molecular clouds) close to young and middle aged SNRs and in active star forming regions. These regions, where the CR spectrum is also expected to be harder than the background CR spectrum, are the candidate sites for CR acceleration, which we will investigate deeply in our analysis.
2. HAWC
HAWC (High Altitude Water-Cherenkov) Telescope is well-designed to study cosmic rays and TeV gamma rays between 100 GeV and 100 TeV by observing the air-shower particles created by the primary particles in the high atmosphere which get in the detector. HAWC is placed on the side of the Sierra Negra volcano near Puebla, Mexico at an altitude of 4,100 meters.
Thanks to its wide field-of-view, with an instantaneous field of view which covers fifteen percent of the sky, within each 24 h period, HAWC observes two-third of the sky. Applying the HAWC observatory, we are performing a high-sensitivity synoptic survey of the gamma rays from the Northern Hemisphere. The detector contains 300 similar water Cherenkov detectors (WCDs) with 7.32 m diameter, 5 m high. Each tank comprises 190,000 L of purified water. Four skyward facing photomultiplier tubes (PMTs) are mounted at the base of each tank, a 10” Hamamatsu PMT located at the center and three 8” Hamamatsu PMTs which are located halfway between the tank center and rim. A trigger is produced when a big enough number of PMTs record a hit in a 150 Nanosecond time interval (see Figure 1).
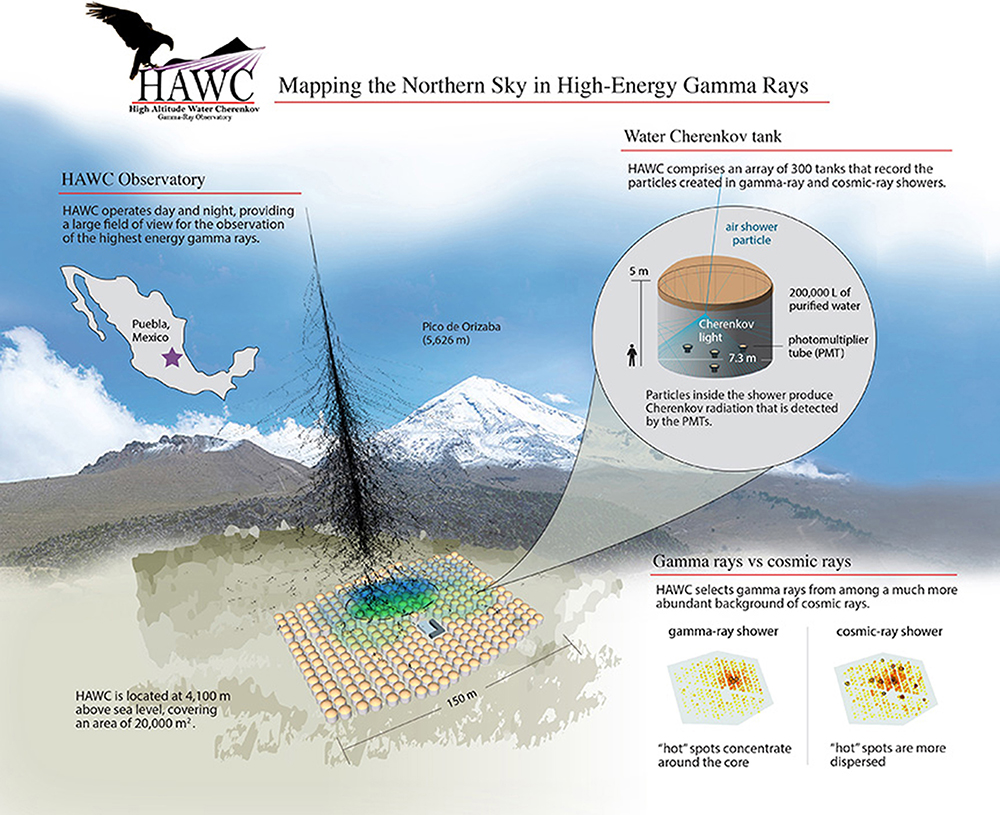
Figure 1. The HAWC Observatory is a next-generation gamma-ray detector placed at an altitude of 4,100 m on the slope of the dormant volcano Pico de Orizaba in Mexico1.
Parameters of the air shower, such as, the direction, the size, and some gamma/hadron separation variables (for each triggered event), are calculated from the recorded hit times and amplitudes, using a shower model developed through the study of Monte Carlo simulations and calibrated using observations of the Crab Nebula.
HAWC is an ideal tool to study Galactic gamma-ray sources. In the following we will review the HAWC map of the sky at 10s TeV after collecting one year of data.
3. Data and Analysis
The analysis presented here is based on a dataset which contains 275 ± 1 source transits of the inner Galaxy taken between August 2, 2013, and July 9, 2014, While the HAWC array was partially constructed. Since the sensitivity of HAWC is related to the source declination, for the sources which transit via the detector vertex, the best sensitivity is gained. For the analysis presented here a zenith angle cut of 45° and declination between −26° and +64° is applied. The background rejection, energy and angular resolution of the detected gamma rays are associated with the shower size detected in the array, So the data are categorized into 10 bins corresponding to the ratio h of PMTs triggered out of the sum of the active PMTs.
In order to detach the cosmic-ray background from the gamma-ray signal, we apply cuts to three parameters (the fraction of the chi-square and reduced chi-square of the fit and a topological cut according to the compactness of the charge distribution) in each h bin Abeysekara et al. (2015a):
4. Sky Maps and Maximum Likelihood Method
The air shower simulation program CORSIKA Heck (1998) and the detector simulation package GEANT4 Agostinelli et al. (2003) generate the detector response file which describes the PSF (Point Source Function) and energy distribution as a function of source declination and fraction of hit h bins. In order to simulate flux from the gamma ray, we use a simulation model which turns the detector response to source of gamma rays.
Constructing a source model determined by spectrum and position of the source is the preliminary step of the maximum likelihood fit. The source spectrum in the following analysis is assumed to obey a power law:
where Γ is the spectral index. It has been assumed here a fixed index of 2.3 because of the limited sensitivity in this data set. The index of 2.3 is indicative of observed values for known Galactic objects, and I0 is the differential flux normalization, E0 is the pivot energy which is picked where the differential flux normalization is least dependent on the spectral index. Right ascension (R.A.) α and Declination (Dec.) δ are used to describe the source position.
The region of interest (ROI) which is applied for a likelihood fit should contain most photons from a given source so it must be wider than the angular resolution of the detector, and because of the high possibility of source confusion in the Galactic plane data, it is not usually easy to find an ROI which contains only photons from one single source.
Thus, the source model likely should contain more than one source, and in this case, the expected count is:
where γijk and βij are the expected number of gamma rays and the background events respectively, in the jth pixel of ith h bin, correlated to the kth source. The event entwine with detector response.
since the detected event counts distribution obeys Poisson distribution in each pixel, one can assumes the probability of measuring N number of events given an expected count λ of the source model be:
The product the likelihood in each h bin and of each pixel (in an ROI) is the likelihood in the source model (given parameter set θ = (α, δ, I0))
Where Nij is detected and λij is expected event counts in the jth pixel of the ith h bin. The logarithm of the likelihood is applied for ease of calculation:
Using the MINUIT package Brun and Rademakers (1997), The log likelihood became maximized with respect to the parameter set θ in the source model. Since Nij is not dependent of the parameters in the source model, it is discarded from Equation (5).
In order to determine how many sources are required to properly model an ROI a likelihood ratio test is performed.
In choose the preferred model over the background-only model first we calculate the log likelihood of the background-only model ln . Afterward we compute the log likelihood ln of the one-source model. The test statistic (TS) defined by:
the test statistics is applied to compare the advantage of the fit between the two models. In order to to compare between two models with N and N+1 sources, similar method of likelihood ratio test is used, in an iterative process; one source with three free parameters ( α, δ, I0 ) is added to the model step by step with the amplitude and position of the current sources free to change in respect to the new source. Finally the TS and differential flux of each source are calculated by fitting one source and considering other sources as a part of the background while parameters are fixed(differential fluxes and positions).
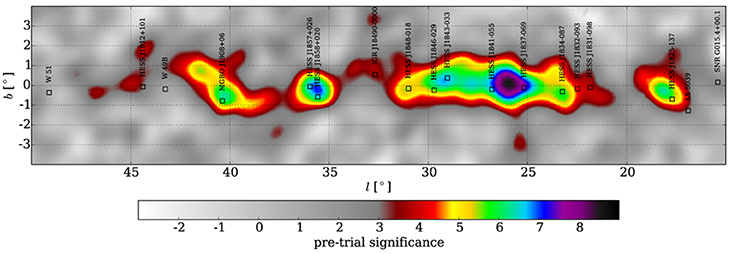
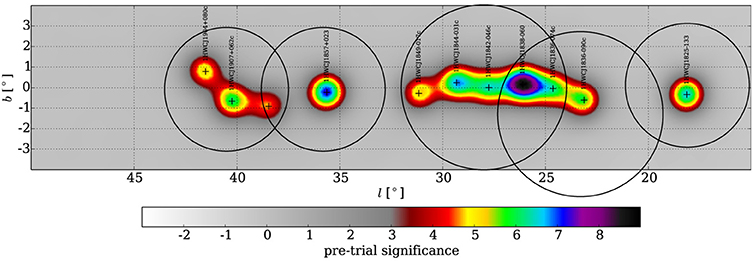
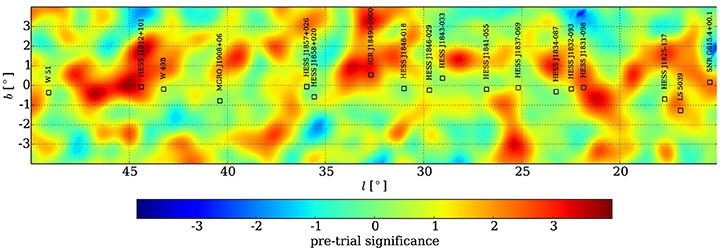
Figures 2–4 present the significance map of the inner Galaxy region investigated here. The map is made by moving a supposed point like source through each pixel, presenting a maximum likelihood fit of differential flux normalization with the fixed spectral index at 2.3. As it is shown in Figure 2.
There are multiple >σ hot spots in the studied region. The area is divided into five region of interests. The method explained above is used to simultaneously account for the flux contributions of neighboring sources in each of divided region.
5. Dragon
DRAGON is a code to solve the equation of CR transport in the Galaxy, it is implemented to simulate all the related processes relevant to Galactic CR propagation, in particular: diffusion, re-acceleration,cooling convection, (due to bremsstrahlung, synchrotron, Coulomb, inverse-Compton, and ionization), catastrophic losses (annihilation), and spallation). The code numerically solves the interstellar CR transport equation, including inhomogeneous and anisotropic diffusion emission. Evoli et al. (2008).
After solving the equation, the code provides the cosmic ray spectra in all regions of the Galaxy. With such information the code derives the gamma ray spectra. The DRAGON predicted gamma ray spectra from the Galactic plane will be compared to the observed spectra, measured by HAWC. In this way the CR transport propagation will be fine-tuned.
6. Forthcoming Research and Conclusions
We showed a preliminary analysis of gamma-ray diffuse emission from the inner galaxy using data from HAWC detector. This analysis will serve to calibrate the dragon code. We will use the results to constrain particle transport properties in that region using the Dragon code in order to understand whether particle transport there proceeds through isotropic diffusion, anisotropic diffusion or maybe through advection.
Author Contributions
AN student, Has written this manuscript and also has presented it in Quasars at all cosmic epochs 2017, all the results have been gotten under supervision FS as a member of the group and also under the supervision of SC as a supervisor and head of the group.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge the support from: the US Department of Energy Office of High-Energy Physics; the US National Science Foundation (NSF); the Laboratory Directed Research and Development (LDRD) program of Los Alamos National Laboratory; L'OREAL Fellowship for Women in Science 2014; the University of Wisconsin Alumni Research Foundation; Red HAWC, México; DGAPA-UNAM (grants IG100317, IN111315, IN111716-3, IA102715, 109916, IA102917); VIEP-BUAP; PIFI 2012, 2013, PROFOCIE 2014, 2015; the Institute of Geophysics, Planetary Physics, and Signatures at Los Alamos National Laboratory; AN, SC, and FS acknowledge the Polish Science Centre under grant DEC-2014/13/B/ST9/945; Coordinación de la Investigación Científica de la Universidad Michoacana. Consejo Nacional de Ciencia y Tecnología (CONACyT), México (grants 271051, 232656, 260378, 179588, 239762, 254964, 271737, 258865, 243290, 132197), Laboratorio Nacional HAWC de rayos gamma; Thanks to Luciano Díaz and Eduardo Murrieta for technical support.
Footnotes
1. ^The High-Altitude Water Cherenkov Observatory (HAWC). HAWC Collaboration. Available online at: http://www.hawc-observatory.org/
References
Abeysekara, A. U., Alfaro, R., Alvarez, C., Álvarez, J. D., Arceo, R., Arteaga-Velázquez, J. C., et al. (2015a). HAWC Contributions to the 34th International Cosmic Ray Conference (ICRC2015). (The Hague).
Agostinelli, S., Allison, J., Amako, K., Apostolakis, J., Araujo, H., Arce, P., et al. (2003). GEANT4—a simulation tool kit. Nucl. Instrum. Methods A506, 250–303. doi: 10.1016/S0168-9002(03)01368-8
Bell, A. R., and Lucek, S. G. (2001). Cosmic ray acceleration to very high energy through the non-linear amplification by cosmic rays of the seed magnetic field. MNRAS 321, 433B.
Brun, R., and Rademakers, F. (1997). ROOT—an object oriented data analysis framework, in proceedings AIHENP'96 workshop. Nucl. Inst. & Meth. Phys. Res. A389, 81–86. Available online at: http://root.cern.ch
Blandford, R., and Eichler, D. (1987). Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154:1.
Drury, L. O'. C., and Markiewicz, W. J. Voelk, H. J. (1989). Simplified models for the evolution of supernova remnants including particle acceleration. Astron. Astrophys. 225:179D
Evoli, C., Gaggero, D., Grasso, D., and Maccione, L. (2008). Cosmic-ray nuclei, antiprotons and gamma-rays in the galaxy: a new diffusion model. JCAP arXiv:0807.4730 [astro-ph]. doi: 10.1088/1475-7516/2008/10/018
Heck, D., Schatz, G., Thouw, T., Knap, J., and Capdevielle, J. N. (1998). CORSIKA: a monte carlo code to simulate extensive air showers. Tech. Rep. FZKA-6019:95.
Krymskii, G. F. (1977). A regular mechanism for the acceleration of charged particles on the front of a shock wave. Akademiia Nauk SSSR. 234, 1306–1308.
Malkov, M. A., and Drury, L. O'. C. (2001). Nonlinear theory of diffusive acceleration of particles by shock waves. Rept. Prog. Phys. 64, 429–481.
Keywords: high energy astrophysics, inner galaxy, gamma rays, diffuse emission, cosmic rays, interstellar medium
Citation: Nayerhoda A, Salesa Greus F and Casanova S (2018) TeV Diffuse Emission From the Inner Galaxy. Front. Astron. Space Sci. 5:8. doi: 10.3389/fspas.2018.00008
Received: 10 September 2017; Accepted: 28 February 2018;
Published: 23 April 2018.
Edited by:
Mauro D'Onofrio, Università degli Studi di Padova, ItalyReviewed by:
Aldo Morselli, Istituto Nazionale di Fisica Nucleare (INFN), ItalyMilan S. Dimitrijevic, Astronomical Observatory, Serbia
Copyright © 2018 Nayerhoda, Salesa Greus and Casanova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amid Nayerhoda, YW1pZC5uYXllcmhvZGFAZ21haWwuY29t
 Amid Nayerhoda
Amid Nayerhoda Francisco Salesa Greus2
Francisco Salesa Greus2 Sabrina Casanova
Sabrina Casanova