- 1Computer Science Department, University of Texas at Dallas, Dallas, TX, United States
- 2Georgia Tech Research Institute, Georgia Institute of Technology, Atlanta, GA, United States
- 3Amazon, Seattle, WA, United States
- 4Department of Computer Science, Hessian Center for AI (hessian.AI), Technical University of Darmstadt, Darmstadt, Germany
We consider the problem of learning with sensitive features under the privileged information setting where the goal is to learn a classifier that uses features not available (or too sensitive to collect) at test/deployment time to learn a better model at training time. We focus on tree-based learners, specifically gradient-boosted decision trees for learning with privileged information. Our methods use privileged features as knowledge to guide the algorithm when learning from fully observed (usable) features. We derive the theory, empirically validate the effectiveness of our algorithms, and verify them on standard fairness metrics.
1. Introduction
Machine learning methods that consider learning from sources beyond just a single set of labeled data have long been explored under several paradigms—learning with advice (Towell and Shavlik, 1994; Fung et al., 2002; Maclin et al., 2005; Kunapuli et al., 2013; Das et al., 2021), learning from preferences (Boutilier, 2002; Drummond and Boutilier, 2014; Pang et al., 2018), learning from qualitative constraints (Altendorf et al., 2005; Yang et al., 2013; Kokel et al., 2020), active learning (Settles, 2012), transductive learning (Joachims, 1999), and as knowledge injection inside deep learning (Ding et al., 2018; Wang and Pan, 2020; Bu and Cho, 2021).
We view the problem of learning with sensitive information using the lens of privileged information. For instance, in a clinical study for improving adverse pregnancy outcomes, it is natural to solicit information about race or sexual orientation. While race can potentially affect the prior chances of an outcome (e.g., gestational diabetes or pre-term birth), the treatment plan in the clinic should not discriminate based on this feature. Similarly, while age/zipcode could be important to obtain a prior about the capacity to repay a loan, it should not be used as a feature (due to its sensitive nature) during deployment of the system. Chouldechova et al. (2018) consider these sensitive information as non-discriminatory for fair machine learning. Kilbertus et al. (2018) encrypt sensitive attributes, and Williamson and Menon (2019) measure the fairness risk on sensitive features.
In a different direction, Vapnik and Vashist (2009) introduced the problem of learning from privileged information where more information in the form of features is provided during training but is not available during testing/deployment. These privileged features could be sensitive features (race/age/sexual orientation) or features that are simply too expensive to collect during deployment (expensive sensors or FMRIs—functional magnetic resonance imaging, in a small clinic). Hence, the classifier cannot use these privileged features during deployment but may still be able to use them to improve the quality of the model.
Our key idea is to use the privileged features as an “inductive bias” or as knowledge constraints. To this effect, we develop two versions of the gradient boosting algorithm—in the first approach, a prior model is learned on the privileged/sensitive features. This prior model is then used to constrain the model learned from the fully observable features. Since this is inspired from the knowledge-based learning literature, we refer to this as KbPIB (knowledge-based privileged information boosting). In the second approach, the models over the privileged/sensitive features and the observed features are learned in a joint stage-wise manner. At each iteration, first a small tree is learned on the privileged features, the set of which is used as constraints for the observed feature model and the process is repeated. Since these are learned jointly, we refer to this as JPIB (joint privileged information boosting). The intuition is that while the privileged features provide extra information, they are not fully relied on when building the model. The resulting model, in essence, is a trade-off between the privileged information and the fully observed features—as is typically done in advice-based methods where the data and the expert knowledge are explicitly considered when learning.
We make a few key contributions: First, inspired by Quadrianto and Sharmanska (2017), we pose the problem of fair machine learning with sensitive data using the framework of privileged information. Second, we present algorithms for learning trees via functional-gradient boosting and show the gradient updates. Specifically, we derive two different types of boosted algorithms that can effectively exploit the sensitive/privileged features. Finally, we perform exhaustive empirical evaluation that demonstrates the effectiveness of the proposed approaches on different types of test beds—standard benchmark data sets, fairness data sets with sensitive information, and real-world medical data sets where the goals are to predict gestational diabetes, nephrotic syndrome, and rare disease occurrences. The results across data sets and evaluation metrics (including fairness metrics) clearly show the effectiveness of the algorithms.
2. Background
2.1. Learning with privileged information
Learning with privileged information is inspired by richer forms of interactions between human teachers and students (Vapnik and Vashist, 2009). Particular (labeled) examples are given to the student along with explanations and intuitions that are able to speed up the comprehension of novel concepts. More formally, learning with privileged information assumes that more information is known about the training examples. However, as the expert is not available for testing, this additional information is not available at test time. Thus, training examples have the form while testing examples have the form . CF refers to the classifier/normal features available during testing and PF refers to the privileged features.
Learning algorithms for privileged information have previously focused on SVMs (Vapnik and Vashist, 2009; Sharmanska et al., 2013). The original formulation—SVM+ (Vapnik and Vashist, 2009)—learned the difficulty of each training example. The key idea was to learn an SVM in the privileged space (using ) and find the margin with respect to this SVM for each training example. Training examples closer to the margin are considered “more difficult” as they are closer to the decision boundary while examples farther from the margin are considered “less difficult.” Since the introduction of the new learning paradigm and the corresponding SVM+ approach, there is a growing body of work on learning with privileged information. Pechyony and Vapnik (2010) developed a theoretical justification of the learning setting. Liang et al. (2009) established links between the SVM+ and the multi-task learning. Hernández-Lobato et al. (2014) showed that the privileged information can naturally be treated as noise in the latent function of a Gaussian process classifier (GPC). In contrast to the standard GPC setting, the latent function becomes a natural measure of confidence about the training data by modulating the slope of the GPC sigmoid likelihood function.
Most closely related to our study, Chen et al. (2012) extend the setting to AdaBoost, and Lapin et al. (2014) relate privileged information to importance weighting within SVMs. Decision tree learners, however, have not been explored in this context yet. Instead of giving more importance to certain examples, we establish a novel connection to knowledge-based machine learning that relies on existing knowledge (Section 3.2). We show that the knowledge we have beforehand, which can be described with privileged features, can also be represented using labels assigned to each training example. These labels help guide the learning process. Moreover, we improve the learning process by introducing a regularization term into the log-likelihood for boosting method. This regularization term is calculated as the KL divergence between the distribution using classifier features and the distribution using privileged features, which are available only at training time and not during testing.
While our setting is similar to the generalized distillation (Lopez-Paz et al., 2016), the fundamental principles are different. We focus on two sets of features—privileged features and normal features. Our goal is to build a model (teacher model) on privileged features that guides the learning of a model (student model) on normal features to improve performance. While our strategy at a high-level appears similar to knowledge distillation by Hinton et al. (2015), there are notable and important differences as follows: (1) the teacher function and student function are learned sequentially, and (2) predictions of teacher model are included as soft labels for the student model.
Our study is also related to knowledge injection in deep networks. Ding et al. (2018) use mean images as (color) knowledge to produce class weight and object occurrence frequencies as scene knowledge to determine scene weight; Wang and Pan (2020) integrate logical knowledge in the form of first-order logic as knowledge regularization into deep learning system; Bu and Cho (2021) perform neuro-symbolic integration using domain knowledge as first-order logic rules.
2.2. Functional gradient boosting
Many probabilistic learning methods learn the conditional distribution P(yi|xi; ψ) using standard techniques such as gradient-descent that is usually performed on the log-likelihood w.r.t. parameters to find the best set of parameters that model the training data. Functional Gradient Boosting methods (GB; Friedman, 2001; Dietterich et al., 2008; Natarajan et al., 2012, 2015), on the other hand, represent the likelihood in a functional form (typically using the sigmoid function) where ψ is a regression function defined over the examples. Given this representation, GB methods obtain the gradient of the log-likelihood w.r.t. ψ(yi = 1, xi) for each training example, xi as: Δ(yi) = I(yi = 1)−P(yi = 1|xi; ψ), where I is an indicator function which returns 1 for positive examples and 0 for negative examples in a binary classification task. The GB approach starts with an initial regression function, ψ0 = 0 to compute the probabilities of the training examples and thereby the gradients Δ1. A regression function (typically a tree), , is fit on the training examples with the gradients as the target regression values. This learned function is now added to ψ0, and the process is repeated with . Given that the stage-wise growth of trees resembles boosting, and that the process involves computing gradients of functions, this method is called Gradient Boosting (GB).
2.3. Sensitive features in fairness
Several studies within fairness in ML treat the sensitive information (e.g., race, gender, or financial status) as non-discriminatory (Žliobaitė, 2017; Chouldechova et al., 2018). Several approaches have been proposed to avoid the use of sensitive features, including by utilizing encrypted sensitive attributes (Choudhuri et al., 2017; Kilbertus et al., 2018) or utilizing sensitive features to measure the fairness risk by proposing a new definition of fairness to include categorical or real-valued sensitive groups beyond binary sensitive features (Angwin et al., 2016; Williamson and Menon, 2019). Krasanakis et al. (2018) reweigh training samples on trade-offs between accuracy and disparate impact. Kamishima et al. (2012) regularize on prejudice (a statistical dependence between sensitive features and other information) to achieve fairness. Quadrianto and Sharmanska (2017) enforce fairness constraints through privileged learning. They consider the setting from the study by Vapnik and Vashist (2009) to build a privileged model on all features, optimizing the prediction boundary of a privileged model and adapting the boundary of the normal model. On the other hand, we use a boosted model as the privileged model relying only on the privileged features and incorporate constraints from the privileged model into the objective of the model constructed on non-privileged features. Wang et al. (2021) approach fairness by putting strict restraints on the ability to infer sensitive features from the available features. Their approach focuses on improving fairness while maintaining performance. Alternatively, our approach aims to leverage the sensitive information to improve performance. Empirically, we demonstrate that our approach maintains fairness.
3. Boosting with privileged sensitive information
Motivating real-world task: The Nulliparous Pregnancy Outcomes Study (NuMoM2b) monitors expectant mothers with the goal of predicting adverse pregnancy outcomes (Haas et al., 2015). The data set includes clinical tests (e.g., BMI, METs) and demographic information. Our goal is to use this data to predict gestational diabetes. While the prevalence of gestational diabetes varies significantly across ethnic groups, it may not be appropriate to use the sensitive demographic information to make the diagnoses. Thus, we may utilize this privileged information during training but want to withhold it from our diagnostic models. A similar consideration is in our rare disease data where certain demographic information, such as age, gender, and marital status, is considered privileged and cannot be used during deployment. While we focus on four specific medical tasks, one could imagine such situations in other high social impact problems including, but not limited to, credit card/home/auto/education loan approvals, hiring decisions, clinical study recruitment, or allocation of resources, where some sensitive information could be used while training to better understand the problem but cannot be used during deployment.
3.1. Problem formulation
Recalling that our goal is to learn robust models that do not include sensitive/privileged information but still leverage them to improve training. Our problem is formally defined as follows:
GIVEN: A set of training examples and a set of test examples , where
TO DO: Learn a classifier that employs only the classifier features CF for classifying the test data and can utilize the privileged features PF effectively in learning a better model.
F is the set of all features, CF is the set of features that are available at both training and testing time (and we call them classifier features), PF are the privileged features that are accessible only during training and not during testing, yi is the label of the ith example and xi is the feature of that example. We use {} to denote sets. For example, the input to the algorithm is the set of all examples . We first consider a knowledge-based approach to leverage with privileged features. Then, we extend this approach to joint training over the classifier and the privileged features. While we use tree-based classifiers, our approach can easily be extended to other clustering/classification techniques.
3.2. Knowledge-based privileged information boosting
Inspired by knowledge-based machine learning methods, Fung et al. (2002), for example, reformulated SVM classifier that uses previous knowledge in the form of multiple polyhedral sets; Kunapuli et al. (2013) incorporate expert advice in states and actions by stating preferences; Towell and Shavlik (1994) map domain theories in propositional logic into neural networks, which leverage external knowledge via human input to guide the learning process; we consider privileged information as a source of high-quality knowledge. We introduce two models: a model learned over the classifier features and a privileged model that is learned over the privileged features in Algorithm 1. By attempting to guide the predictions of the classifier model with the privileged model, we can potentially find a way to insert informed priors to the labels based on both the privileged and classifier features. We first train a model over privileged features at line 2 in Algorithm 1. Then, from lines 3 to 9, we learn a model over the classifier features while reducing the margin with the privileged model. An overview of our KbPIB approach is shown in Figure 1.
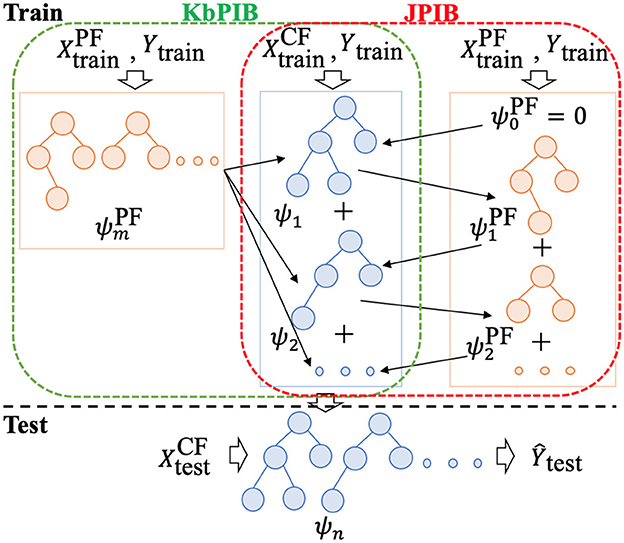
Figure 1. Overview of proposed approaches KbPIB and JPIB [Both approaches train a model on CF, while KbPIB trains a model on PF once and uses it as a bias for the classifier, JPIB learns models on CF and PF in an iterative manner (in a manner loosely similar to co-training); models on PF data are dropped after training to avoid consideration during testing/deployment].
In Vapnik's SVM+ model, the PF features were used to define an oracle function that can predict the slack on each example. In our probabilistic framework, we use the PF features to build an oracle model that can predict a close approximation to the true distribution of each example which is not captured by the discrete class labels. Instead of modeling the error (distance between the labels and the underlying distribution), we directly model the distribution of labels using privileged features during training. We use P(y|xPF; ψ′) to indicate this true label distribution learned over privileged features and P(y|xCF; ψ) for the distribution learned over classifier features. Similar to SVM+, we can now use the privileged features to model this difference between the true distribution and the label distribution. Since the training labels are completely observed, the privileged features can be directly used to model the distribution of the examples. Thus, we learn a model that minimizes the error of the model over the training labels and the margin between the distribution P(y|xPF; ψ′) and P(y|xCF; ψ),
NLL denotes the negative log-likelihood of the training data that models the error while KL denotes the KL divergence between P(*;ψ′) and P(*;ψ) and is equal to . We use α to model the trade-off between fitting to the labeled data versus fitting to the distribution learned over the privileged features. We can now use gradient boosting with respect to to minimize this objective function.
Notably, in our formulation, the model ψ′ could be provided by the domain expert on the privileged features (for instance, a Bayesian network or a neural network that is used in the literature on these privileged features). We do not assume any specific form for ψ′, and the goal is to use this privileged knowledge. In our experiments, we learn ψ′ from data. If the model of ψ′ is provided, one could treat that as a regularizer (similar to knowledge-based learning).
The first term of our objective function is the standard log-likelihood function which has the gradient as follows1:
For the second term, we derive the gradients below:
We combine the gradient terms to get the final gradient for each example as follows2:
Intuitively, if the learned distribution has a higher probability of an example belonging to the positive class compared with the distribution, would be positive and the gradient would be pushed lower. Hence, the additional term would push the gradient (weighted by α) toward the distribution as predicted by our privileged features.
The parameter α controls the influence of the privileged data on the learned distribution. When α = 0, privileged features are ignored resulting in the standard functional gradient. As α is increased, the gradient is pushed lower, for example, where predicted probability is higher than true probability (w.r.t. privileged model) and vice versa.
3.3. Joint privileged information boosting
While the previous approach used the privileged information to influence final model learned over CF at each step in gradient boosting, it did not leverage this learned model to further tune the privileged tree labels. By attempting to reduce the margin by jointly training the two models, we can potentially find more consistent predictions based on both the privileged and classifier features. Similar to Equation (2), the gradients can be computed for learning the true distribution using the privileged features with P(*;ψ) and P(*;ψ′) switched around.
Given these gradients, we can now describe our approach called JPIB to perform gradient boosting jointly over the classifier features and the privileged information. We iteratively learn regression functions (trees in our case) to fit to these gradients. However, the key difference from KbPIB is that we perform co-ordinate gradient descent, i.e., we alternate between taking a gradient step along ψ and ψ′. From lines 2 to 11 in Algorithm 2, we learn one regression tree using the gradients based on the classifier features (lines 2–5), compute the gradients for the privileged features, learn a tree for the privileged features (lines 8–10), and repeat this at most N times to generate at most N trees of the boosting model. The early-stop mechanism at line 7 helps return the best performing model on validation data (line 6).
3.4. Sensitive attributes and fairness constraints
Notably, since our algorithms drop the privileged information after learning, one could argue that they do not discriminate between the different groups at deployment time. However, one could go even deeper and establish a strong connection between the learning framework and the fairness constraints. Given the above definitions of the objective function, several fairness constraints can be easily captured by our model. For instance, to handle metric fairness, the privileged model could simply be a constraint of the form
that can be used inside the second term of Equations (2) and (3), where the second term is the probability of the constraint satisfied by the model (computed by counting). Weakly meritocratic fairness can be handled by the form
while group fairness can be handled by
and group parity can be handled by using precision and recall. Similar to the metric constraints, all these constraints can be included in the second term of the model. Essentially one could drop the privileged tree model and use these constraints. Another way is to include these constraints along with the privileged model. However, as we show in our experiments, with treating the sensitive attributes as privileged features, the algorithm performs significantly better in terms of the fairness criteria compared with the boosting baseline.
4. Experiments
Our experimental evaluations aim to answer the following questions:
Q1: How effective is incorporating privileged information into gradient boosting?
Q2: Can jointly updating the privileged model with the classifier improve performance?
Q3: How is model fairness affected by withholding sensitive information from the classifier?
We present empirical evaluations of our proposed approaches—(KbPIB) and (JPIB). We evaluate the approaches in two ways. To evaluate the effect of privileged information, we compare against learning a gradient-boosted model over only the classifier/normal features, NF. To evaluate fairness, our approaches are compared with All, which is learned over both CF and imputed PF based on mode. Notably, though we explicitly evaluate against the SVM-based approach and fairness approach, the key question in our study is whether the notion of privileged information can help gradient boosting and whether the sensitive features are handled appropriately. We adopt 10-fold cross-validation for all datasets: 8-folds of training, 1-fold of validation, and 1-fold of test. Due to the data size and very few negative instances in the dataset Nephrotic Syndrome, we use 5-fold cross-validation: 3-folds of training, 1-fold of validation, and 1-fold of test. The value of α and thresholds of precision and recall are selected based on the validation data. More details are presented in Supplementary material. The experiments are conducted on the machine with CentOS Linux 7, CPU of Intel Xeon E5-2630 with 2.40 GHz and 16 cores, and 512 GB RAM. The source code (details of dependency) of our methods and prepared data can be downloaded.3
4.1. Datasets
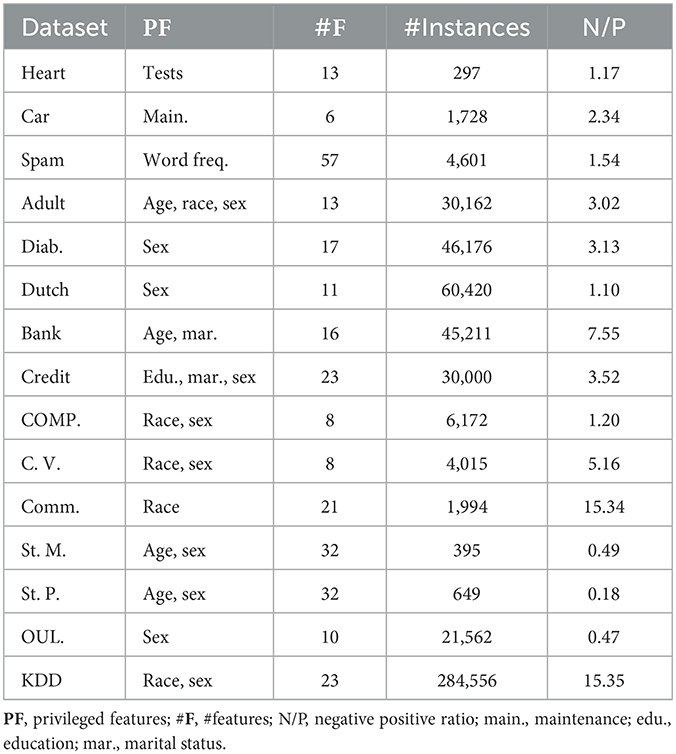
We employ three types of datasets: standard benchmarks, medical datasets, and fairness benchmarks. The standard benchmarks consist of three datasets from UCI ML repository (Dheeru and Taniskidou, 2017). The fairness benchmarks include 12 datasets from 10 data sources: Adult (Kohavi, 1996), Diabetes (Diab.) (Strack et al., 2014), Dutch Census (Dutch) (Van der Laan, 2000), Bank Marketing (Bank) (Moro et al., 2014), Credit Card Clients (Credit) (Yeh and Lien, 2009), COMPAS (COMP.) and COMPAS Violence (C. V.) (Angwin et al., 2016), Student–Mathematics (St. M.) and Student–Portuguese (St. P.) (Cortez and Silva, 2008), OULAD (OUL.) (Kuzilek et al., 2017), Communities and Crime (Comm.), and KDD Census Income (KDD) (Dheeru and Taniskidou, 2017). While we describe the medical datasets in more detail, the properties of standard and fairness benchmarks are presented in Table 1.
4.2. Real-world medical datasets
4.2.1. NuMoM2b_a
Polygenic risk scores (PRS) for type 2 diabetes (T2D) can improve risk prediction for gestational diabetes (GD) (Haas et al., 2015). We use PRS as the privileged feature. Demographic information and clinical history serve as normal features: body mass index (BMI), exercise levels or metabolic equivalents of time (METs), age, diabetes history (DM_Hist), polycystic ovary syndrome (PCOS), and high blood pressure (HiBP). The classification task is to predict GD. There are 3,657 instances with Neg/Pos ratio of 25.89.
4.2.2. NuMoM2b_b
We use the attribute race as privileged feature, which often is not usable during test or deployment for privacy concern (Haas et al., 2015). The normal features and classification task are same as NuMoM2b_a. There are 6,164 instances with the Neg/Pos ratio of 23.76.
4.2.3. Nephrotic syndrome
A novel dataset of symptoms that indicates kidney damage is sourced from Dr Lal PathLabs, India.4 This consists of 50 clinical reports with patient history information. The privileged features are age and gender. History of other diseases, Edema duration, urine test, and blood reports are used as normal features. The classification task is to predict Nephrotic Syndrome. The Neg/Pos ratio is 0.14.
4.2.4. Rare disease
This dataset is collected to identify rare diseases from behavioral data (MacLeod et al., 2016). We consider age, gender, and marital status as privileged features. The survey questions are used as normal features and include demographic information, disease information, technology use, and health care professional inputs. The boolean classification task is to predict the presence of rare diseases. There are 284 instances with the Neg/Pos ratio of 2.69 and 69 features.
4.3. Results
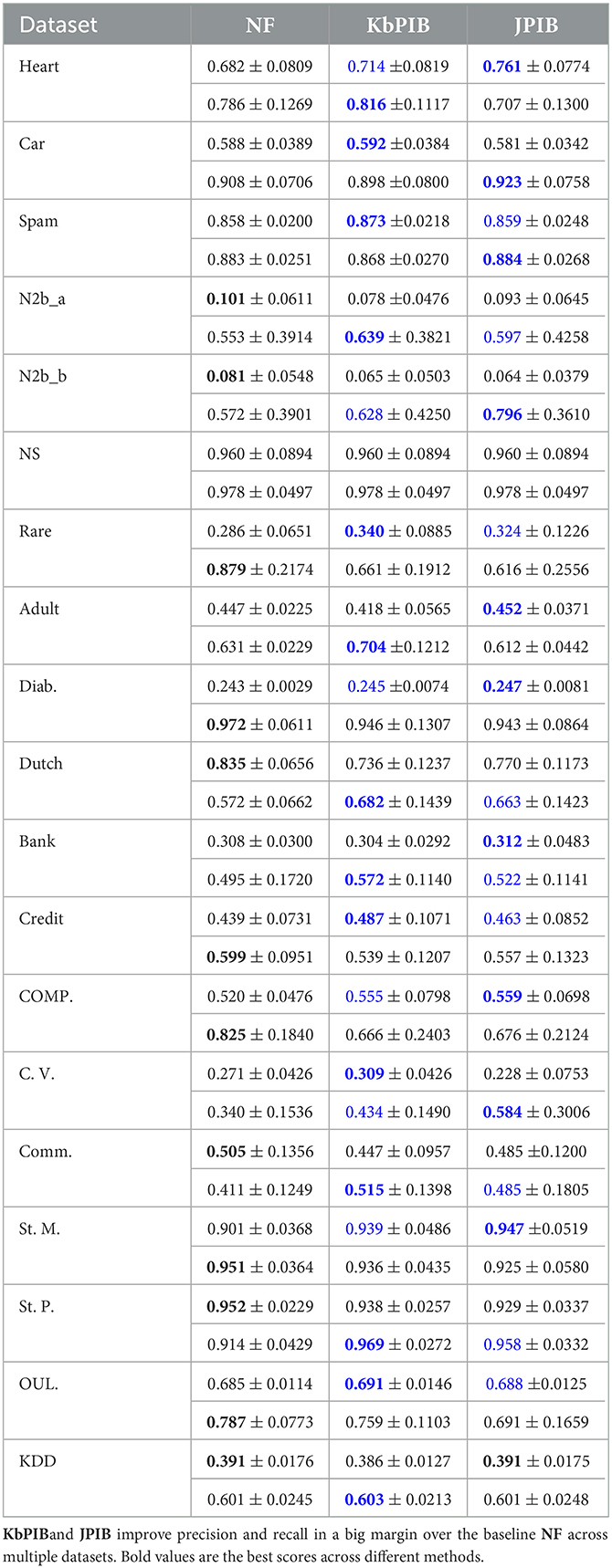
We first compare our KbPIB and JPIB approaches to the baseline NF that does not use privileged information during training. We evaluate the approaches based on the AUC ROC, as shown in Table 2, due to class imbalance. Blue denotes when either of our approaches outperform the baseline. The best performance is bolded. Overall, our approaches outperform the baseline, showing improvement in 18 out of 19 datasets. Both of our methods perform at least as well as the baseline across the rest of the datasets. Notably, both KbPIB (2 out of 4) and JPIB (3 out of 4) outperform the baseline in real-world medical tasks, where sensitive information includes demographic information. The NS dataset, on the other hand, has a large number of positives to negatives (but a small number of examples over all), and the base model that uses the urine tests gets nearly perfect example. It is an example of a situation where privileged information does not quite helpful, and it is natural that in many domains, the data might be sufficient to learn a good predictive model and extra information may not be helpful. We present this result to show the absence of improvement and acknowledge this case. KbPIB performs slightly worse than the baseline NF on three domains. In future, we can attempt different classifiers on privileged features and normal features.
We also evaluate the approaches based on precision and recall in Table 3 due to class imbalance. In 6 out of 19 datasets, our approaches yield both higher precision and recall. Our approaches achieve higher precision and higher recall in 12 datasets. Collectively, our approaches that incorporate privileged information are able to achieve better performance across several metrics (Q1).
Comparing AUC ROC in Table 2, JPIB outperforms KbPIB in 10 and achieves at least the same performance in 14 out of 19 datasets. Comparing precision and recall in Table 3, precision of JPIB outperforms KbPIB in 10 and achieves at least the same performance in 11 datasets; recall of JPIB outperforms KbPIB in 6 datasets and achieves at least the same performance in 7 datasets. Overall, JPIB outperforms KbPIB, suggesting that updating the privileged model with the classifier improves gradient boosting with sensitive information (Q2).
Intuitively, we expect the gains from our approach to be relative to the quality of the privileged information. When privileged information is highly discriminative, we expect greater gains from our approach and vice versa. For the standard benchmark and medical datasets (ref. Table 2), there is a correlation between the quality of the privileged information and the performance. We compare the performance only using the privileged features with KbPIB and JPIB, respectively. The Pearson correlation values of the AUC ROC are 0.237 (KbPIB) and 0.306 (JPIB). This helps explain the reason that JPIB outperforms KbPIB overall (Q2).
4.3.1. Prior framework for privileged information
To compare with previous study of using privileged information with SVM, we run SVM+ on our data splits and include results, as shown in Table 2. The major drawback of the previous study with SVM is that it lacks interpretability and cannot handle large datasets well. SVM+ runs slowly on large datasets (~20 k instances) and fails to train on datasets with ~30+k instances (6 datasets) due to out-of-memory error. As the performance difference between our method JPIB and SVM+, as shown in Figure 2, our method can outperform SVM+ (Q1). For some domains, our method JPIB gets lower AUC ROC compared with SVM+. This shows that SVM is still a very competitive base classifier. Applying our methods to a more powerful base classifier is a prospective future study to further improve the performance on more domains.
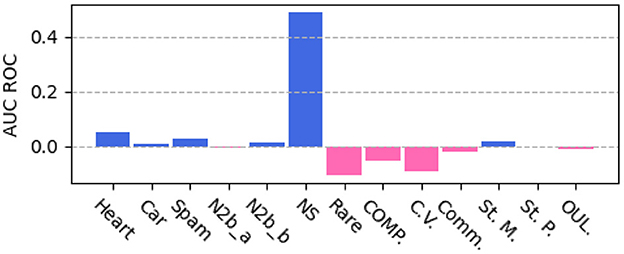
Figure 2. Performance comparison between JPIB and SVM+ (positive value if JPIB performs better; SVM+ fails to train on six large datasets).
4.3.2. Privileged information and fairness
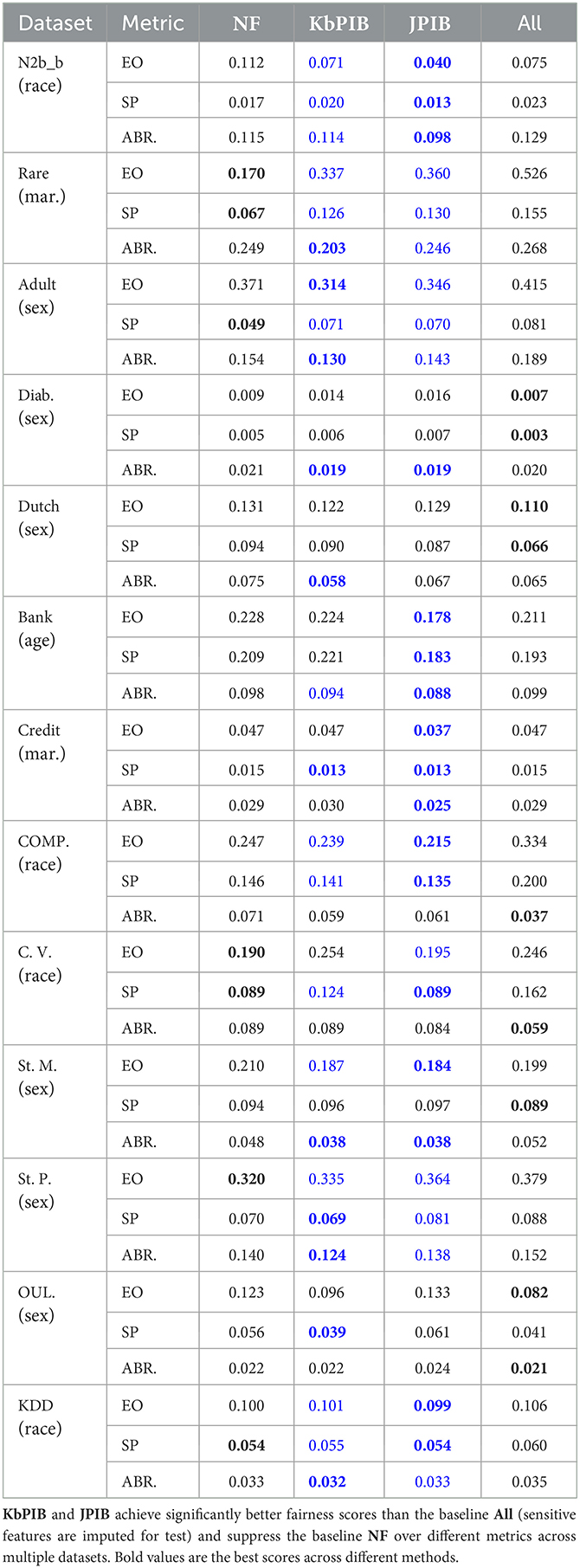
We evaluate fairness on the fairness benchmark datasets (Table 4) and the real-world medical datasets. We compare against several fairness metrics: Statistical Parity (SP; Dwork et al., 2012), Equalized Odds (EO; Hardt et al., 2016), and Absolute Between-ROC Area (ABROCA; Gardner et al., 2019). SP measures the bias of predicting positive for different groups. We use SP to measure the overall fairness in predictive accuracy of our methods. EO measures the bias of predicting positive between different groups conditioned on the label. We take EO to further examine the fairness in predictive accuracy of our methods, specifically given different labels. ABROCA measures the divergence of ROC curves between different groups. ABROCA is adopted to quantify the fairness of our methods over all possible thresholds.
In addition to the previous baseline, we also compare against All, which learns a model that contains (imputed) privileged and classifier features. However, at test time, it estimates the privileged features based on the most common training value. Blue denotes when our approach outperforms All and bold denotes the best performance. As shown in Table 4, our approach achieves better fairness metrics than All in 10 (EO), 10 (SP), and 10 (ABROCA) datsests. Our approaches also perform at least as well as NF in 9 (EO), 9 (SP), and 13 (ABROCA) datasets. When considering the privacy or fairness of the resulting predictions, imputing the privileged information by treating them as missing has a clear negative impact on the resulting fairness (see “All” in Table 4). Collectively, our approaches are able to improve performance by leveraging sensitive privileged information while maintaining fairness (Q3).
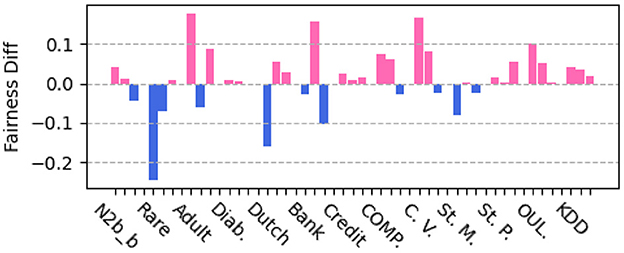
To further verify the fairness benefit of our approach, we compare with MFC (Zafar et al., 2017). MFC learns fair classifiers by leveraging measurement of decision boundary (un)fairness, gaining fine-grained control on fairness with small cost of accuracy. As compared with MFC, our methods improve the prediction accuracy over the boosting baseline, and we would like to confirm that our methods enhance fairness. We apply MFC to our data splits and generate fairness scores on the same datasets of Table 4. Figure 3 shows the difference of scores of three fairness metrics between our approach JPIB and the baseline MFC on each dataset. We can observe that our approach JPIB achieves comparable fairness scores to MFC.
5. Conclusion
We considered the problem of learning with privileged and sensitive information using gradient boosting and proposed two algorithms that learned using these information. The extensive experiments in standard, medical, and fairness datasets demonstrated the ability of our algorithms to learn robust yet fair models. More extensive evaluation on large data sets, integration of other forms of domain knowledge into our framework, understanding the relationship with other fairness models, and considering more expressive models such as deep networks remain interesting future directions.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The aim of our study is to use the sensitive features as privileged ones to avoid any discriminative social bias in our study. While we do not foresee many ethical issues with our study, it is conceivable that some sensitive features might be grouped under normal feature set. The risk for ethical issues when the privileged information is identified and flagged appropriately is low. The identification of sensitive features is the most important task and could potentially affect the results of the deployment of the algorithm. The code will be released publicly and maintained by the authors in GitHub.
Author contributions
SY: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—review & editing. PO: Investigation, Methodology, Writing—original draft, Writing—review & editing. RP: Conceptualization, Investigation, Writing—original draft. KK: Conceptualization, Investigation, Writing—original draft. SN: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing—original draft, Writing—review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. SY and SN gratefully acknowledge AFOSR Minerva award FA9550-19-1-039. KK gratefully acknowledges the Hessian Ministry of Higher Education, Research, Science and the Arts (HMWK) cluster project The Third Wave of AI as well as the project safeFBDC—Financial Big Data Cluster (FKZ: 01MK21002K), funded by the German Federal Ministry for Economics Affairs and Energy as part of the GAIA-x initiative.
Acknowledgments
The authors acknowledge the support of members of STARLING lab for the discussions. The authors also thank the reviewers for their insightful comments and in significantly improving the study.
Conflict of interest
RP was employed by Amazon.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Author disclaimer
Any opinions, findings, and conclusion or recommendations expressed in this material are those of the authors and do not necessarily reflect the view of the AFOSR or the US government.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frai.2023.1260583/full#supplementary-material
Footnotes
1. ^We use to denote the probability mass of being positive given the classifier features.
2. ^More details of derivation in Supplementary material.
References
Altendorf, E., Restificar, A., and Dietterich, T. (2005). “Learning from sparse data by exploiting monotonicity constraints,” in UAI'05: Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence (Edinburgh: AUAI Press), 18–26.
Angwin, J., Larson, J., Mattu, S., and Kirchner, L. (2016). “Machine bias,” in Ethics of Data and Analytics (Auerbach Publications), 254–264.
Boutilier, C. (2002). “A POMDP formulation of preference elicitation problems,” in Proceedings of the Eighteenth National Conference on Artificial Intelligence and Fourteenth Conference on Innovative Applications of Artificial Intelligence, eds R. Dechter, M. J. Kearns, and R. S. Sutton (Edmonton, AB: AAAI Press; The MIT Press), 239–246. Available online at: http://www.aaai.org/Library/AAAI/2002/aaai02-037.php
Bu, S., and Cho, S. (2021). “Integrating deep learning with first-order logic programmed constraints for zero-day phishing attack detection,” in IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP (Toronto, ON: IEEE), 2685–2689. doi: 10.1109/ICASSP39728.2021.9414850
Chen, J., Liu, X., and Lyu, S. (2012). “Boosting with side information,” in 11th Asian Conference on Computer Vision, eds K. M. Lee, Y. Matsushita, J. M. Rehg, and Z. Hu (Daejeon: Springer), 563–577. doi: 10.1007/978-3-642-37331-2_43
Choudhuri, A., Green, M., Jain, A., Kaptchuk, G., and Miers, I. (2017). “Fairness in an unfair world: fair multiparty computation from public bulletin boards,” in Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, eds B. Thuraisingham, D. Evans, T. Malkin, and D. Xu (Dallas, TX: ACM), 719–728. doi: 10.1145/3133956.3134092
Chouldechova, A., Benavides-Prado, D., Fialko, O., and Vaithianathan, R. (2018). “A case study of algorithm-assisted decision making in child maltreatment hotline screening decisions,” in Conference on Fairness, Accountability and Transparency, FAT 2018, eds S. A. Friedler, and C. Wilson (New York, NY: PMLR), 134–148.
Cortez, P., and Silva, A. (2008). Using Data Mining to Predict Secondary School Student Performance. EUROSIS-ETI.
Das, M., Dhami, D., Yu, Y., Kunapuli, G., and Natarajan, S. (2021). “Human-guided learning of column networks: knowledge injection for relational deep learning,” in CODS-COMAD '21: Proceedings of the 3rd ACM India Joint International Conference on Data Science & Management of Data (8th ACM IKDD CODS & 26th COMAD), eds J. R. Haritsa, S. Roy, M. Gupta, S. Mehrotra, B. V. Srinivasan, and Y. Simmhan (ACM: Bengaluru), 110–118. doi: 10.1145/3430984.3431018
Dheeru, D., and Taniskidou, E. (2017). The UCI Machine Learning Repository. Available online at: https://archive.ics.uci.edu
Dietterich, T., Hao, G., and Ashenfelter, A. (2008). Gradient tree boosting for training conditional random fields. J. Mach. Learn. Res. 9.
Ding, X., Luo, Y., Li, Q., Cheng, Y., Cai, G., Munnoch, R., et al. (2018). Prior knowledge-based deep learning method for indoor object recognition and application. Syst. Sci. Control 6, 249–251. doi: 10.1080/21642583.2018.1482477
Drummond, J., and Boutilier, C. (2014). “Preference elicitation and interview minimization in stable matchings,” in Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, eds C. E. Brodley, and P. Stone (Québec City: AAAI Press), 645–653. doi: 10.1609/aaai.v28i1.8829
Dwork, C., Hardt, M., Pitassi, T., Reingold, O., and Zemel, R. (2012). “Fairness through awareness,” in Innovations in Theoretical Computer Science 2012, ed S. Goldwasser (Cambridge, MA: ACM), 214–226. doi: 10.1145/2090236.2090255
Friedman, J. (2001). Greedy function approximation: a gradient boosting machine. Ann. Stat. 29, 1189–1232. doi: 10.1214/aos/1013203451
Fung, G., Mangasarian, O., and Shavlik, J. (2002). “Knowledge-Based support vector machine classifiers,” in Advances in Neural Information Processing Systems 15 (NIPS 2002), eds S. Becker, S. Thrun, and K. Obermayer (Vancouver, BC: MIT Press), 521–528.
Gardner, J., Brooks, C., and Baker, R. (2019). “Evaluating the fairness of predictive student models through slicing analysis,” in LAK19: Proceedings of the 9th International Conference on Learning Analytics & Knowledge (Tempe, AZ: ACM), 225–234. doi: 10.1145/3303772.3303791
Haas, D., Parker, C., Wing, D., Parry, S., Grobman, W., Mercer, B., et al. (2015). A description of the methods of the nulliparous pregnancy outcomes study: monitoring mothers-to-be (numom2b). Am. J. Obstet. Gynecol. 212, 539.e1–539.e24. doi: 10.1016/j.ajog.2015.01.019
Hardt, M., Price, E., and Srebro, N. (2016). “Equality of opportunity in supervised learning,” in Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, eds D. D. Lee, M. Sugiyama, U. von Luxburg, I. Guyon, and R. Garnett (Barcelona), 3315–3323.
Hernández-Lobato, D., Sharmanska, V., Kersting, K., Lampert, C., and Quadrianto, N. (2014). “Mind the nuisance: Gaussian process classification using privileged noise,” in Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, eds Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger (Montreal, QC), 837–845.
Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling the knowledge in a neural network. arXiv:1503.02531. doi: 10.48550/arXiv.1503.02531
Joachims, T. (1999). “Transductive inference for text classification using support vector machines,” in Proceedings of the Sixteenth International Conference on Machine Learning (ICML 1999), eds I. Bratko and S. Dzeroski (Bled: Morgan Kaufmann), 200–209.
Kamishima, T., Akaho, S., Asoh, H., and Sakuma, J. (2012). “Fairness-aware classifier with prejudice remover regularizer,” in Machine Learning and Knowledge Discovery in Databases - European Conference, ECML PKDD 2012, eds P. A. Flach, T. De Bie, and N. Cristianini (Bristol: Springer), 35–50. doi: 10.1007/978-3-642-33486-3_3
Kilbertus, N., Gascón, A., Kusner, M., Veale, M., Gummadi, K., and Weller, A. (2018). “Blind justice: fairness with encrypted sensitive attributes,” in Proceedings of the 35th International Conference on Machine Learning, ICML 2018, eds J. G. Dy and A. Krause (Stockholm: PMLR), 2635–2644.
Kohavi, R. (1996). “Scaling up the accuracy of naive-Bayes classifiers: a decision-tree hybrid,” in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), eds E. Simoudis, J. Han, and U. M. Fayyad (Portland, OR: AAAI Press), 202–207. Available online at: http://www.aaai.org/Library/KDD/1996/kdd96-033.php
Kokel, H., Odom, P., Yang, S., and Natarajan, S. (2020). A unified framework for knowledge intensive gradient boosting: leveraging human experts for noisy sparse domains. Proc. AAAI Conf. Artif. Intell. 34, 4460–4468. doi: 10.1609/aaai.v34i04.5873
Krasanakis, E., Spyromitros-Xioufis, E., Papadopoulos, S., and Kompatsiaris, Y. (2018). “Adaptive sensitive reweighting to mitigate bias in fairness-aware classification,” in WWW '18: Proceedings of the 2018 World Wide Web Conference, eds P.-A. Champin, F. Gandon, M. Lalmas, and P. G. Ipeirotis (Lyon: ACM), 853–862. doi: 10.1145/3178876.3186133
Kunapuli, G., Odom, P., Shavlik, J., and Natarajan, S. (2013). “Guiding autonomous agents to better behaviors through human advice,” in 2013 IEEE 13th International Conference on Data Mining, eds H. Xiong, G. Karypis, B. Thuraisingham, D. J. Cook, and X. Wu (Dallas, TX: IEEE Computer Society), 409–418. doi: 10.1109/ICDM.2013.79
Kuzilek, J., Hlosta, M., and Zdrahal, Z. (2017). Open university learning analytics dataset. Sci. Data. 4, 170171. doi: 10.1038/sdata.2017.171
Lapin, M., Hein, M., and Schiele, B. (2014). Learning using privileged information: SV M+ and weighted SVM. Neural Netw. 53, 95–108. doi: 10.1016/j.neunet.2014.02.002
Liang, L., Cai, F., and Cherkassky, V. (2009). Predictive learning with structured (grouped) data. Neural Netw. 22, 766–773. doi: 10.1016/j.neunet.2009.06.030
Lopez-Paz, D., Bottou, L., Schölkopf, B., and Vapnik, V. (2016). “Unifying distillation and privileged information,” in 4th International Conference on Learning Representations, ICLR 2016, eds Y. Bengio and Y. LeCun (San Juan, PR). Available online at: http://arxiv.org/abs/1511.03643
MacLeod, H., Yang, S., Oakes, K., Connelly, K., and Natarajan, S. (2016). “Identifying rare diseases from behavioural data: a machine learning approach,” in Proceedings of the First IEEE International Conference on Connected Health: Applications, Systems and Engineering Technologies, CHASE, 2016 (Washington, DC: IEEE Computer Society), 130–139. doi: 10.1109/CHASE.2016.7
Maclin, R., Shavlik, J., Torrey, L., Walker, T., and Wild, E. (2005). “Giving advice about preferred actions to reinforcement learners via knowledge-based kernel regression,” in Proceedings, the Twentieth National Conference on Artificial Intelligence and the Seventeenth Innovative Applications of Artificial Intelligence Conference, eds M. M. Veloso and S. Kambhampati (Pittsburgh, PA: AAAI Press/The MIT Press), 819–824. Available online at: http://www.aaai.org/Library/AAAI/2005/aaai05-129.php
Moro, S., Cortez, P., and Rita, P. (2014). A data-driven approach to predict the success of bank telemarketing. Decis. Support Syst. 62, 22–31. doi: 10.1016/j.dss.2014.03.001
Natarajan, S., Kersting, K., Khot, T., and Shavlik, J. (2015). Boosted Statistical Relational Learners: From Benchmarks to Data-Driven Medicine. Springer. doi: 10.1007/978-3-319-13644-8
Natarajan, S., Khot, T., Kersting, K., Gutmann, B., and Shavlik, J. (2012). Gradient-based boosting for statistical relational learning: the relational dependency network case. Mach. Learn. 86, 25–56. doi: 10.1007/s10994-011-5244-9
Pang, S., Orgun, M., and Yu, Z. (2018). A novel biomedical image indexing and retrieval system via deep preference learning. Comput. Methods Prog. Biomed. 158, 53–69. doi: 10.1016/j.cmpb.2018.02.003
Pechyony, D., and Vapnik, V. (2010). “On the theory of learning with privileged information,” in Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems 2010, eds J. D. Lafferty, C. K. I. Williams, J. Shawe-Taylor, R. S. Zemel, and A. Culotta (Vancouver, BC: Curran Associates, Inc.), 1894–1902.
Quadrianto, N., and Sharmanska, V. (2017). “Recycling privileged learning and distribution matching for fairness,” in Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, eds I. Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S. V. N. Vishwanathan, and R. Garnett (Long Beach, CA), 677–688.
Settles, B. (2012). Active Learning. Synthesis Lectures on Artificial Intelligence and Machine Learning. Morgan & Claypool. doi: 10.1007/978-3-031-01560-1
Sharmanska, V., Quadrianto, N., and Lampert, C. (2013). “Learning to rank using privileged information,” in CVPR. doi: 10.1109/ICCV.2013.107
Strack, B., DeShazo, J. P., Gennings, C., Olmo, J. L., Ventura, S., Cios, K. J., et al. (2014). Impact of hba1c measurement on hospital readmission rates: analysis of 70,000 clinical database patient records. BioMed Res. Int. 2014. doi: 10.1155/2014/781670
Towell G. and Shavlik, J. (1994). Knowledge-based artificial neural networks. Artif. Intell. 70, 119–165. doi: 10.1016/0004-3702(94)90105-8
Van der Laan, P. (2000). “The 2001 census in the Netherlands,” in Conference the Census of Population.
Vapnik, V., and Vashist, A. (2009). A new learning paradigm: learning using privileged information. Neural Netw. 22, 544–557. doi: 10.1016/j.neunet.2009.06.042
Wang, H., Zhang, H., Wang, Y., and Gao, J. (2021). “Fair classification under strict unawareness,” in Proceedings of the 2021 SIAM International Conference on Data Mining, SDM 2021, eds C. Demeniconi and I. Davidson (SIAM), 199–207. doi: 10.1137/1.9781611976700.23
Wang, W., and Pan, S. (2020). “Integrating deep learning with logic fusion for information extraction,” in The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020 (New York, NY: AAAI Press), 9225–9232. doi: 10.1609/aaai.v34i05.6460
Williamson, R., and Menon, A. (2019). “Fairness risk measures,” in Proceedings of the 36th International Conference on Machine Learning, ICML 2019, eds K. Chaudhuri and R. Salakhutdinov (Long Beach, CA: PMLR), 6786–6797.
Yang, S., Khot, T., Kersting, K., and Natarajan, S. (2013). “Knowledge intensive learning: combining qualitative constraints with causal independence for parameter learning in probabilistic models,” in Machine Learning and Knowledge Discovery in Databases - European Conference, ECML PKDD 2013, eds H. Blockeel, K. Kersting, S. Nijssen, and F. Zelezný (Prague: Springer), 580–595. doi: 10.1007/978-3-642-40991-2_37
Yeh, I., and Lien, C. (2009). The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients. Expert Syst. Appl. 36, 2473–2480. doi: 10.1016/j.eswa.2007.12.020
Zafar, M., Valera, I., Rodriguez, M., and Gummadi, K. (2017). “Fairness constraints: mechanisms for fair classification,” in Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, AISTATS 2017, eds A. Singh and X. Zhu (Fort Lauderdale, FL: PMLR), 962–970.
Keywords: privileged information, fairness, gradient boosting, knowledge-based learning, sensitive features
Citation: Yan S, Odom P, Pasunuri R, Kersting K and Natarajan S (2023) Learning with privileged and sensitive information: a gradient-boosting approach. Front. Artif. Intell. 6:1260583. doi: 10.3389/frai.2023.1260583
Received: 18 July 2023; Accepted: 20 October 2023;
Published: 13 November 2023.
Edited by:
Thommen Karimpanal George, Deakin University, AustraliaReviewed by:
Shahram Rahimi, Mississippi State University, United StatesManas Gaur, University of Maryland, Baltimore County, United States
Copyright © 2023 Yan, Odom, Pasunuri, Kersting and Natarajan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Siwen Yan, c2l3ZW4ueWFuQHV0ZGFsbGFzLmVkdQ==
 Siwen Yan
Siwen Yan Phillip Odom2
Phillip Odom2 Rahul Pasunuri
Rahul Pasunuri Kristian Kersting
Kristian Kersting Sriraam Natarajan
Sriraam Natarajan