Analysis of casson nanofluid transport rates near a vertical stretching sheet with dissipation and slip effects

Practical applications: Analysis of Casson nanofluid transport rates near a vertical stretching sheet with dissipation and slip effects will provide relevant information for practitioners to make informed decisions in handling real flow systems. Hence, the present study will contribute in not only supplementing the theoretical gaps for the scientific community but also improving the working efficiency of practical flow systems in manufacturing industries and the quality of their products.

Purpose: This study mainly focused on examining the rates of hydromagnetic transport phenomena of Casson nanofluid near a vertical surface in the presence of slip, dissipation, and cross-diffusion effects. Based on the underlying conservation laws in physical sciences and significant model assumptions, a more comprehensive mathematical model is taken into account. Efforts are made to analyze variations in the rates of heat, mass, and momentum transfer against the continuous change of the variables.

Methodology: The solutions for the resulting model equations are explored with the help of the optimal homotopy analysis method.

Findings: Among the results of the study, it is determined that the rate of heat transfer between the solid surface and the surrounding fluid is enhanced by increasing the effect of magnetic field (B > 3.5), thermal radiation (R_d > 2.5), or concentration buoyancy force (G_c > 5). On the other hand, the mass transfer near the solid surface can be assisted by increasing the effect of thermal diffusion (Sr > 0), heat generation (Q > 2), thermal radiation (R_d > 2.5), and concentration buoyancy force (G_c > 3). Furthermore, the rate of momentum transfer of the fluid flow near the solid surface can be facilitated by increasing the effect of flow unsteadiness (A > 2.5) or heat sink (Q < −4).

Originality: Most of the available studies on the physical quantities of practical interest were made based on presenting their variations at only some selected values of the parameters. Such analysis cannot give full information about the complete behavior of the quantities in response to the governing parameters. Thus, in this study a considerable attention is given to how the fluid transport rates vary with the relevant factors in a continuous domain of the parameters. Furthermore, the study considers a more comprehensive mathematical model in the area under consideration and the resulting equations are solved by an efficient optimal homotopy analysis method.

1 Introduction

Experimental investigations are the most realistic ways of analyzing fluid flow phenomena. Unfortunately, such investigations are so expensive to apply in fluid flow problems and other related scientific investigations. Consequently, it is common to carryout mathematical model analysis to understand flow behaviors, instead of doing physical experiments. Still, exact modeling of fluid flow phenomena is quite difficult, several investigators are considering over-simplified model assumptions. For instance, a number of studies in fluid dynamics have been reported without considering slip effects in their flow considerations [1, 2]. However, flows such as food processing undergo velocity slip phenomena [3]. In addition, in some manufacturing industries where there is high concentration and temperature difference between the boundary surface and the ambient fluid, heat can be transferred due to concentration difference, called Dufour effect, and conversely, mass flux can be produced due to temperature gradient, called Soret effect [4]. Flows such as those that start suddenly from rest or come to rest usually depend on time. This time-dependent flow system is called an unsteady flow. In boundary layer flows induced by stretching of solid surfaces, the effect of flow unsteadiness is an important tool to stabilize a flow system by adjusting the velocity of the stretching surface. However, due to the complex nature of the governing equations and their difficulty to solve, several studies [5–9] are focusing on steady flow problems rather than unsteady flow problems.

On the other hand, improving the thermal conductivity of certain fluids becomes an important area of investigation in processes such as effective cooling of vehicles, machinery, transformers, electronics, and other technological appliances. In particular, analysis of Casson nanofluid transport rates near a vertical stretching sheet with dissipation and slip effects has attracted significant attention in recent years due to its wide range of applications in various fields, such as geothermal energy extraction, nuclear reactor cooling, and electromagnetic filtration. Ighoroje et al. [10] presented an MHD fluid flow past a moving vertical surface in a velocity slip flow by applying modified homotopy perturbation method. They showed that the increase in the Schmidt number increases the fluid concentration and velocity and the increase in the magnetic field parameter decreases the fluid velocity. Awad et al. [11] presented a mathematical description of a two-dimensional unsteady magneto-hydrodynamics slow flow with thermoelectric properties on an infinite vertical partially hot porous plate. The Laplace–Fourier transform technique was applied to obtain exact expressions for the temperature and stream function in the case of steady-state heat transfer. More recently, Awad [12] utilized Couette formulation describing a pressure-driven flow of a viscous thick liquid-metal layer bounded by two similar metallic plates. In this study, a numerical technique based on Fourier series approximation was employed and found that the retarded crossover of low thermal conduction shows “ultraslow” temperature propagation within the thick layer. As traditional fluids such as air, water, and engine oils are naturally poor conductors of heat [13]. Many theoretical and experimental investigations revealed that dispersion of nanosized solid particles into conventional fluids increases the thermal conductivity of the hosting fluids [14, 15]. The extraordinary thermophysical properties of nanofluids were explained by Buongiorno [16]. Currently, these innovative fluids are widely used in advanced thermal management systems, metal cutting, drug targeting, cancer treatment, and many other industrial and medical applications [17]. Manjunatha et al. [18] presented a new theoretical nanofluid model for enhancing heat transfer. They observed that the trihybrid nanofluid has a better thermal conductivity than the hybrid nanofluid. Adnan et al. [19] analyzed the heat transmission ability of a nanofluid inside a squeezing channel. The results revealed that high viscosity parameter, porous absorber walls, and strong surface–surface interaction due to aggregation of nanoparticles significantly control the fluid movement. In addition, Bani-Fwaz et al. [20] studied nanofluid heat transfer applications inside a channel formed by expanding/contracting walls. They introduced a new heat transport model by adding the effects of walls permeability, thermal radiations, nanoparticles, and molecular diameters. For expanding and contracting walls, the velocity is maximum in the channel center. Furthermore, contracting walls and temperature ratio number reduced the temperature.

Fluids in which the shear rate is not proportional to the applied shear stress are termed non-Newtonian fluids. Many of the fluids processed in industries and our body system including lubricants, paints, paper pulp, polymer solution, honey, apple sauce, blood, and other biological fluids are non-Newtonian. Due to the complex nature of non-Newtonian fluids, the well-known Navier–Stokes equations becomes inadequate to fully describe these essential fluids and this introduces interesting challenges to researchers. Motivated by the significance applications of non-Newtonian nanofluids, several researchers have been interested in introducing notable results in the area of fluid mechanics. Ramesh et al. [21] investigated the effect of transverse magnetic field, thermophoresis, and Brownian motion of nanoparticles on a non-Newtonian tangent hyperbolic fluid passing via a porous medium. In this report, it was found that the increase in radiation parameter leads to a decrease in temperature profile and the rise in Brownian motion effect corresponds to greater nanoparticle volume fraction. Alqsair et al. [22] also studied the convective heat transfer phenomena of a non-Newtonian micropolar nanofluid. They reported that as the values of the viscoelastic parameter increase, both the temperature of the micropolar fluid and the wall shear stress grow. Akbar et al. [23] investigated the impact of Deborah's number and significance of linear and quadratic convection on a steady boundary layer flow of Maxwell fluid past a linearly stretched sheet. They employed the bvp4c approach to handle the mathematical analysis. The study reported that the linear convection model provides more heat transfer than the quadratic convection model. Patil et al. [24] applied the quasi-linearization and implicit finite difference methods to analyze the impacts of periodic magnetic field and multiple diffusions effects in a non-Newtonian Eyring–Powell fluid flow past a spinning cone. It was reported that increasing values of bioconvective Rayleigh number correspond to the decreasing fluid velocity and the friction between the cone surface and the surrounding fluid. In addition, Patil et al. [25] provided a characterization of the impacts of activation energy, time and diffusions of liquid hydrogen, and ammonia in a multidiffusive nanofluid flow over a sphere. They revealed that the mass transport strength of liquid ammonia is big enough to dwarf liquid hydrogen and the entropy generation can be minimized by enhancing the values of temperature difference and Brownian diffusion parameter.

In order to estimate the heat transfer rate at the fluid–solid interfaces, an expression called the Nusselt number, which is a quantity that depends on temperature gradient is used. In addition, the ratio of the convective mass transfer to mass diffusion is given by Sherwood number. It is used to quantify the rate of mass flux based on the concentration gradient near the solid surface. The third important quantity is the rate of momentum transfer that is commonly measured in terms of the skin friction coefficient, which depends on the velocity gradient, is used to analyze the surface drag force between the solid and the fluid molecules. Here, the coefficient is used to predict the amount of force needed to withdraw materials in extrusion processes. On the other hand, fluids with reduced skin friction coefficient can be used as good lubricants in mechanical and industrial activities.

It is important to note that understanding the rates at which fluid transport takes place in a flow system will help practitioners improve the quality of final products and their cost of production. To this end, a number of investigators have been reporting on how these quantities vary with the diversified nature of thermophysical parameters. For instance, Khan et al. [26] analyzed a boundary layer flow of a nanofluid flow with non-linear thermal radiation past a moving needle. They reported that the rate of heat transfer increases for greater values of the Eckert number, whereas it slows down for magnetic field parameters. Das et al. [27] reported a numerical investigation on micropolar nanofluid flow toward a linearly stretching sheet. They found that near the stretching surface, the rate of heat transfer decreases for larger values of thermophoresis and Brownian parameters while the mass transfer rate is facilitated with these constraints.

However, most of the available studies on the physical quantities of practical interest were made based on presenting their variations at only some selected values of the parameters. Such analysis cannot give full information about the complete behavior of the quantities in response to the governing parameters. Thus, in this study a considerable attention is given on how the fluid transport rates in a hydromagnetic nanofluid flow phenomena vary with the relevant factors in a continuous domain of the parameters. Furthermore, the study considers a more comprehensive mathematical model in the area under consideration and the resulting equations are solved by an efficient optimal homotopy analysis method. Hence, the present study will contribute in not only supplementing the theoretical gaps for the scientific community but also improving the efficiency of practical flow systems in manufacturing industries.

2 Model considerations and mathematical descriptions

In fluid dynamics, the study of fluid flows over vertically stretching surfaces plays decisive roles in the extraction of polymer sheets and metallic plates, drawing of plastic films, paper and glass fiber productions, food processing, material insulation, geothermal energy extraction, and in many other industrial and biomedical applications. In this study, the hydromagnetic nanofluid transport phenomena over a permeable vertical solid surface are considered. It is assumed that the vertical surface placed in a stationary fluid is stretched suddenly along the vertical and this causes a time-dependent boundary layer flow as outlined in Figure 1. In addition, the constant values of velocity (u = 0), temperature (T = T_∞), and concentration (C = C_∞) outside the boundary layer region are considered. Furthermore, a uniform external magnetic field normal to the vertical surface is applied to influence the flow system integrated into a porous medium.

Figure 1

Figure 1. Sketch of the flow problem.

Here, for non-Newtonian fluids such as printing inks, lubricants, liquid detergents, cosmetics, fruit juices, tomato sauce, and so on, Casson fluid model defined as in Casson [28] is considered.

$\begin{array}{ll}{\tau }_{i,j}=\{\begin{array}{l}\left({\mu }_b+\frac{{\tau }_0}{\sqrt{2\pi }}\right)2e_{i,j},\pi >{\pi }_c\\ \left({\mu }_b+\frac{{\tau }_0}{\sqrt{2{\pi }_c}}\right)2e_{i,j},\pi <{\pi }_c\end{array}& (1)\end{array}$

where τ_i,j are components of the stress tensor, τ₀ is a finite value of Casson yield stress, μ_b is the coefficient for plastic dynamic viscosity, $e_{i,j}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$ is the rate of strain tensor with u_i denoting the components of fluid velocity, π = e_i,je_i,j is the self-product of fluid deformation rate e_i,j, and π_c is the critical value of π. In addition, the kinematic viscosity υ for Casson fluid is defined as:

$\begin{array}{ll}\upsilon =\frac{{\mu }_b}{\rho }\left(1+\frac{1}{\beta }\right),& (2)\end{array}$

where ρ is the fluid density and $\beta =\frac{{\mu }_b\sqrt{2{\pi }_c}}{{\tau }_0}$ is the Casson parameter. Furthermore, for π > π_c, the shear stress can be expressed as:

$\begin{array}{ll}{\tau }_{i,j}={\mu }_b\left(1+\frac{1}{\beta }\right)\left(2e_{i,j}\right)={\mu }_b\left(1+\frac{1}{\beta }\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right).& (3)\end{array}$

With the aforementioned assumptions and constitutive equation, the flow situation is described mathematically by using non-linear coupled differential equations that are steamed from the underlying principles of physical sciences along with the Maxwell laws of electromagnetism. In addition, by using the boundary layer approximation principle, small variations in the flow profiles are neglected so that two-dimensional sets of differential equations are obtained in the Cartesian coordinate system. As a non-compressible flow is considered under the study, the continuity equation for the conservation of mass takes the form

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0& (4)\end{array}$

where u and v are the x and y dimensions of the fluid velocity.

As the fluid is taken to be electrically conducting due to the addition of nanoparticles, the flow system can be managed by implementing a uniform magnetic force B perpendicular to the flow direction. Considering the theory of Boussinesq's approximation [29], the density variation which induces the buoyancy force is taken into account. In addition, by assuming the porosity of the medium, the linear momentum equation is formulated as

$\begin{array}{r}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\upsilon \left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}u}{\partial y^2}-\left(\frac{\sigma B_0^2}{\rho }+\frac{\upsilon }{K_0}\right)u\\ +g\left[{\beta }_T\left(T-T_{\infty }\right)+{\beta }_c\left(C-C_{\infty }\right)\right],& (5)\end{array}$

where t is the time variable for the unsteady flow; g is the magnitude for the force of gravity; the terms σ, υ, and ρ denote electric conductivity, kinematic viscosity, and density of the fluid, respectively; K₀ is coefficient of medium porosity; β_c and β_T are coefficients of volumetric concentration and thermal expansion quantities; the pair of expressions (T, T_∞) and (C, C_∞) represent the temperature and concentration of nanoparticles in the boundary layer and inviscid regions, respectively.

Considering the Rosseland approximation [30] for thermal radiation and taking the impacts of Brownian and thermophrosis effects of nanoparticles, heat transfer due to concentration gradient, heat source, and heat lost by dissipation, the energy equation for the problem is given as follows:

$\begin{array}{l}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\tau \left[D_B\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right]\\ +\frac{\upsilon }{C_p}\left(1+\frac{1}{\beta }\right){\left(\frac{\partial u}{\partial y}\right)}^2+\frac{\sigma B_0^2}{{\left(\rho C_p\right)}_f}{u}^2+\frac{D_m{K}_T}{C_s{C}_p}\frac{{\partial }^{2}C}{\partial y^2}\\ +{\alpha }_f\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}}\right)\frac{{\partial }^{2}T}{\partial y^2}+\frac{Q_0}{\rho C_p}\left(T-T_{\infty }\right),& (6)\end{array}$

where D_B, C_s, D_m, D_T, σ^*, k, k^*, K_T, and Q₀ stands correspondingly for Brownian diffusion, concentration susceptibility, species diffusivity, thermophoresis diffusion coefficient, Stefan–Boltzmann constant, thermal conductivity of the fluid, mean thermal absorption coefficient, thermal diffusion ratio, and coefficient of heat source, respectively. The symbols $\tau =\frac{{\left(\rho c_p\right)}_p}{{\left(\rho c_p\right)}_f}$ represent the ratio of heat capacities of nanoparticle to that of the base fluid where c_p is the specific heat capacity of nanoparticles at constant pressure. The term ${\alpha }_f=\frac{k}{{\left(\rho C_p\right)}_f}$ stands for the coefficient of thermal diffusivity of the fluid.

Taking the impacts of chemical reaction and mass transfer due to temperature difference, the conservation of nanoparticle volume fraction is governed by the following equation:

$\begin{array}{ll}\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}+\frac{D_m{K}_T}{T_m}\frac{{\partial }^{2}T}{\partial y^2}-K_r\left(C-C_{\infty }\right),& (7)\end{array}$

where T_m and K_r stand for the mean temperature and coefficient of chemical reaction.

To get a convergent unique solution for each of the unknown quantities of interest, the following significant boundary conditions are considered in the flow situation. Suppose the solid surface is stretched with a velocity $U_w=\frac{ax}{1-ct}$, where a and c are constant numbers such that 1 − ct > 0. The heat exchange between the solid and the surface involves a convective mechanism and the concentration of nanoparticles is assumed to be constant at the interface between the solid surface and the fluid [31–33].

$\begin{array}{ll}u=U_w\left(x,t\right)+U_{slip},v=V_w,T=T_w\left(x,t\right)+T_{slip},C=C_w\left(x,t\right)+C_{slip},& (8)\end{array}$

where $V_w=-\frac{V_0}{\sqrt{1-ct}}$ is the fluid velocity through the permeable surface. The quantities $T_w\left(x,t\right)=T_{\infty }+\frac{T_{0}ax}{2\upsilon {\left(1-ct\right)}^2}$ and $C_w\left(x,t\right)=C_{\infty }+\frac{C_{0}ax}{2\upsilon {\left(1-ct\right)}^2}$ denote estimates of wall temperature and concentration. In addition, the slip terms are described as $U_{slip}=N_1\upsilon \frac{\partial u}{\partial y}$, $T_{slip}=D_1\frac{\partial T}{\partial y}$, and $C_{slip}=D_2\frac{\partial C}{\partial y}$; with the coefficients N₁, D₁, and D₂ representing hydrolic, thermal, and concentration slip factors.

In the ambient region, the following constant values of velocity, temperature, and nanoparticle concentration are considered as y → ∞.

$\begin{array}{ll}u\to 0,T\to T_{\infty },C\to C_{\infty }.& (9)\end{array}$

The efficiency of many industrial and technological activities that involve fluid flow phenomena is determined by the rates of fluid transport near the solid–fluid interface. These quantities include local Nusselt number Nu_x, Sherwood number Sh_x, and wall friction coefficient C_f given as:

$\begin{array}{ll}N{u}_x=\frac{x{q}_w}{\kappa \left(T_f-T_{\infty }\right)},S{h}_x=\frac{x{q}_m}{D_m\left(C_w-C_{\infty }\right)}and{C}_f=\frac{{\tau }_w}{{\rho }_f{U}_w^2},& (10)\end{array}$

where

$\begin{array}{l}{q}_w=-\left(\kappa +\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}\right){\left[\frac{\partial T}{\partial y}\right]}_{y=0},q_m=-D_m{\left[\frac{\partial C}{\partial y}\right]}_{y=0}and\\ {\tau }_w=-\left(1+\frac{1}{\beta }\right){\left[\frac{\partial u}{\partial y}\right]}_{y=0}& (11)\end{array}$

are the heat flux, mass flux, and shear stress at the surface of the solid, respectively.

Currently, in order to simplify the equations governing the flow profiles, boundary conditions, and quantities of interest Equations 4–11, the following transformation variable is introduced:

$\begin{array}{ll}\eta =y\sqrt{\frac{U_w}{\upsilon x}}.& (12)\end{array}$

Again defining the Stoke's function ψ as

$\begin{array}{ll}\psi (x,y)=\sqrt{U_w\upsilon x}f(\eta ,& (13)\end{array}$

where f is the dimensionless stream function and the velocity components are satisfying the conditions

$\begin{array}{ll}u=\frac{\partial \psi }{\partial y}andv=-\frac{\partial \psi }{\partial x}& (14)\end{array}$

Furthermore, the temperature and concentration profiles are non-dimensionlized by defining new dimensionless functions as follows:

$\begin{array}{ll}\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}& (15)\end{array}$

and

$\begin{array}{ll}\phi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }}.& (16)\end{array}$

Currently, determining the necessary partial derivatives of the unknown functions, substituting the results, and simplifying the expressions, one can easily verify that the continuity equation in Equation 4 is satisfied identically.

However, the momentum expression in Equation 5 is reduced to the form

$\begin{array}{ll}\left(1+\frac{1}{\beta }\right)f^{‴}+f{f}^{″}-{f^{\prime }}^2-(Kp+M)f^{\prime }-A\left(f^{\prime }+\frac{\eta }{2}{f}^{″}\right)+Gr\theta +Gc\phi =0.& (17)\end{array}$

Here, the symbol ' stands for differentiation in the variable η. The terms $Kp=\frac{\upsilon x}{K_0{U}_w}$, $M=\frac{\sigma B_0^2}{a\rho }$ and $A=\frac{t}{a}$ represent the parameters for medium porosity, magnetic field, and flow unsteadiness, respectively. The expressions $Gr=\frac{g{T}_0}{2a\upsilon }{\beta }_T$ and $Gc=\frac{g{C}_0}{2a\upsilon }{\beta }_c$ are Grashof numbers for thermal and concentration distributions.

Again simplifying the energy equation in Equation 6, it is possible to obtain the following expression

$\begin{array}{l}\left(1+\frac{4}{3}Rd\right){\theta }^{″}+Pr[f{\theta }^{\prime }-f^{\prime }\theta -A\left(\frac{\eta }{2}{\theta }^{\prime }+2\theta \right)+\left(1+\frac{1}{\beta }\right)Ec{f^{″}}^2\\ +M{E}_c{f^{\prime }}^2+N_b{\theta }^{\prime }{\phi }^{\prime }+N_t{{\theta }^{\prime }}^2+D_f{\phi }^{″}+Q\theta ]=0,& (18)\end{array}$

where the parameters $P_r=\frac{\upsilon }{\alpha }$, $Rd=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k{k}^{*}}$, $Ec=\frac{U_w^2}{{\left(C_p\right)}_f(T_w-T_{\infty }}$,

$N_b=\frac{\tau D_m\left(C_w-C_{\infty }\right)}{\upsilon }$, $N_t=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{\upsilon T_{\infty }}$, $D_f=\frac{D_m{K}_T}{\upsilon C_s{C}_p}\frac{C_w-C_{\infty }}{T_w-T_{\infty }}$ and $Q=\frac{Q_0}{a\left(\rho C_p\right)}$ Define, respectively, for the Prandtl number, thermal radiation, Eckert number, Brownian motion, thermophoresis, Dufour number, and heat source.

In addition, the conservation of nanoparticle volume fraction stated in Equation 7 is reduced to the expression

$\begin{array}{ll}{\phi }^{″}+Sc\left[f{\phi }^{\prime }-f^{\prime }\phi -A\left(\frac{\eta }{2}{\phi }^{\prime }+2\phi \right)-\gamma \phi +S_r{\theta }^{″}\right]+\frac{N_t}{N_b}{\theta }^{″}=0,& (19)\end{array}$

where $Sc=\frac{\upsilon }{D_m}$ is the Schmidt number, $\gamma =\frac{K_{r}x}{U_w}$ is the chemical reaction parameter and $S_r=\frac{D_m{K}_T}{T_m\upsilon }\frac{T_w-T_{\infty }}{C_w-C_{\infty }}$ is the Soret number.

Similarly, by simplifying the boundary conditions in Equations 8, 9, it is possible to get the following reduced forms:

$\begin{array}{l}f\left(\eta \right)=S,f^{\prime }\left(\eta \right)=1+N_f{f}^{″}\left(0\right),\theta \left(\eta \right)=1\\ +N_{\theta }{\theta }^{\prime }\left(\eta \right),\phi \left(\eta \right)=1+N_{\phi }{\phi }^{\prime }\left(0\right)at\eta =0,& (20)\end{array}$

and

$\begin{array}{ll}{f}^{\prime }\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0,\phi \left(\eta \right)\to 0as\eta \to \infty ,& (21)\end{array}$

where $S=-\frac{V_0}{\sqrt{\frac{1-ct}{a\upsilon }}}$ is the permeability parameter for which the values S > 0, S = 0, and S < 0 corresponds to fluid suction and injection. The coefficients given by $N_f=N_1\upsilon R{e}^{1/2}{x}^{-1/4}$, $N_{\theta }=D_{1}R{e}^{1/4}{x}^{-1/4}$ and $N_{\phi }=D_{2}R{e}^{1/4}{x}^{-1/4}$ represent the slip parameters for momentum, thermal, and concentration profiles with $Re=\frac{U_{w}x}{\upsilon }$ defining the Reynolds number.

Furthermore, the local skin friction coefficient, Nusselt number and Sherwood number in Equation 10 are simplified and reduced to the form:

$\begin{array}{c}R{e}_x^{1/2}{C}_f=f^{″}\left(0\right),N{u}_x=-R{e}_x^{1/2}\left(1+\frac{4}{3}Rd\right){\theta }^{\prime }\left(0\right),and\\ S{h}_x=-R{e}_x^{1/2}{\phi }^{\prime }\left(0\right).& (22)\end{array}$

Hence, the boundary derivatives f″(0), θ′(0), and φ′(0) are proportional to the estimates for rate of change of momentum, heat, and concentration diffusion near the solid surface.

3 Method of analysis

Determining exact solutions to non-linear governing equations is not an easy task for researchers. Accordingly, various analytic and numerical methods have been proposed each with its own limitation. In this study, the efficient optimal homotopy analysis method, designed by Liao, has been implemented successfully with the help of mathematical computational software. This method provides a more accurate analytic approximation to the unknown functions in the non-linear models evaluated at the continuous domain of the parameters. This method is preferred due to its effectiveness as the method has obtained the combined advantages of numerical and analytical methods. One can refer to the books cited in Liao [34] and Zhao and Liao [35] for more information about the concept and implementation procedures of the method.

In order to obtain the solutions for the unknown functions in Equations 17–19, the following initial approximations for the dimensionless velocity, temperature, and concentration profiles are identified based on the boundary conditions under consideration.

$\begin{array}{ll}{f}_0\left(\eta \right)=S+\frac{1-e^{-\eta }}{1+N_f},{\theta }_0\left(\eta \right)=\frac{1}{1+N_{\theta }}{e}^{-\eta },{\phi }_0\left(\eta \right)=\frac{1}{1+N_{\phi }}{e}^{-\eta }.& (23)\end{array}$

The homotopy analysis method involves the construction of continuous mappings of initial approximations to the exact solutions. To this end, the following linear differential operators are chosen.

$\begin{array}{ll}{L}_f\left(f\right)=f^{‴}+f^{″},L_{\theta }\left(\theta \right)={\theta }^{″}+\theta ,L_{\phi }\left(\phi \right)={\phi }^{″}+\phi & (24)\end{array}$

It is also essential to define auxiliary functions of the form

$\begin{array}{ll}{H}_f\left(\eta \right)=H_{\theta }\left(\eta \right)=H_{\phi }\left(\eta \right)=e^{-\eta }.& (25)\end{array}$

Using the so-called convergence control parameters (ℏ_i), it is possible to ensure convergence of the series solution. The optimal values of these parameters are obtained from reducing the residual errors defined as:

$\begin{array}{ll}{\epsilon }_k^i\left({\hslash }_i\right)\approx \frac{1}{N+1}{\displaystyle \sum _{j=0}^N}{\left\{{\aleph }_i\left[{\displaystyle \sum _{n=0}^k}{\varphi }_n^i\left(\eta \right)\right]\right\}}^2& (26)\end{array}$

where ℵ_i and ϕⁱ are the non-linear operators and homotopy approximations for the unknown functions.

Currently, all the required computations in the study are carried out with the help of a Mathematica-based BVPh 2.0 package, which was designed by Zhao and Liao [35]. The package is successfully implemented for the study to generate the required tabular and graphical results. To this end, the following values of the involved parameters are considered, unless otherwise stated: A = Gr = Gc = Rd = 0.2, β = 10, Sr = 0.03, Df = 0.02, M = Kp = Nt = γ = Ec = Q = 0.1, S = Pr = Sc = N_f = 1, N_θ = N_ϕ = Nb = 0.3. Thus, the optimal values for the parameters are as follows: ℏ_f ≈ −0.52, ℏ_θ ≈ −0.65 and ℏ_φ ≈ −1.01. for which the residual errors ε_f, ε_θ, and ε_φ against the order of homotopy approximations are outlined as indicated in the right columns of Table 1.

Table 1

Table 1. Convergence of some solutions with the order of HAM approximations.

It is shown in Table 1 that the individual errors for each profile are decreasing rapidly with the increase in order of homotopy approximations. Furthermore, the values of derivatives −f″(0), −θ′(0), and −φ′(0) for the dimensionless velocity, temperature, and concentration profiles at the solid boundary are computed. It is found in Table 1 that the values of each derivative converge with the increase in the order of HAM approximations. So as to give a better insight about the residual errors, the total average squared residual error is determined and plotted as depicted in Figure 2. Figure 2 displays that the total residual error is declining very fast after the first few iterations and less variation is observed for higher orders of iteration.

Figure 2

Figure 2. Total residual errors in relation to the HAM approximations.

These observations on the declining errors in both the residual errors and solution errors confirm that the optimal homotopy analysis method converges for the considered non-linear equations. On the other hand, to ensure the accuracy of the method a comparative analysis is made; that is, some important results of the present study are compared against certain previous studies under common parameters values. Here, the values of −f″(0) for selected values of the unsteadiness parameter are computed and compared as presented in Table 2.

Table 2

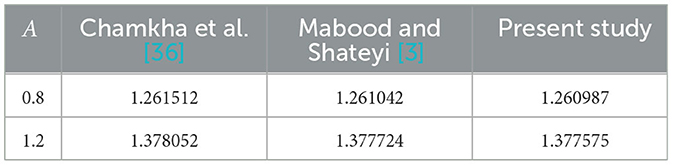
Table 2. Values of −f″(0) for Pr = Sc = 1, N_b → 0, β → ∞, M = Kp = N_t = N_f = N_θ = N_ϕ = S = Gr = Gc = S_r = D_f = γ = Q = 0 against some values of A.

Table 2 reveals that the values of −f″(0) obtained from the present problem agree well with that of the previous reports. This verifies the plausibility of the proposed model and the implemented method of analysis. Consequently, the major findings of the study on the influences of the emerging parameters on the rates of fluid transport phenomena near the solid surface are presented in the following section.

4 Results and discussions

The influences of relevant parameters on the rate of mass, heat, and momentum transfer are analyzed in terms of the derivatives of the dimensionless profiles near the solid surface. In order to give a better understanding about the variations of relevant quantities in response to the involved thermophysical variables, a graphical method of presentation is used and a brief discussion is made on the physical realities behind the observed outcomes.

4.1 Magnetic field effects

As the fluid is considered to be electrically conducting, the effects of the magnetic field on the rates of fluid transport profiles near the solid surface are examined and presented in Figure 3. It can be revealed from Figure 3 that the variation of the boundary derivatives is insignificant until the value of M is approximately 2, and then as the values of the parameter increase, the rate of momentum transfer and concentration diffusion decline while the rate of heat transfer is upgraded near the solid surface.

Figure 3

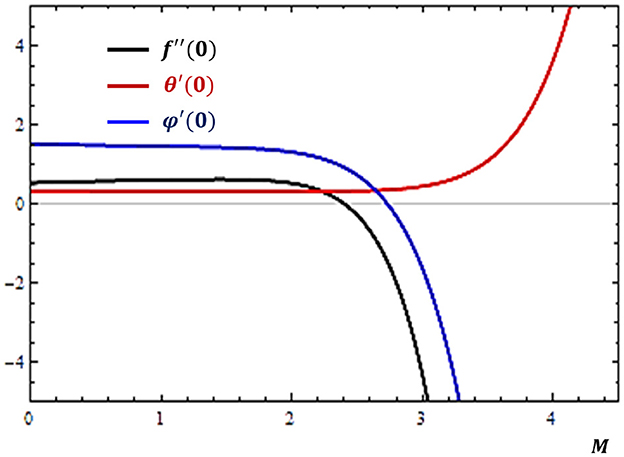
Figure 3. Effects of magnetic field (M) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

This is due to the induced electromagnetic force produced by the interaction between the motion of electrically conducting fluid and the external magnetic field. In particular, as the magnetic field is applied normally to the direction of flow, the induced force acts opposite to the direction of the flow, which tends to retard the velocity of the fluid and the rate of momentum transfer. On the other hand, the work done by the fluid molecules against the electromagnetic force allows the transfer of more heat energy in the flow system. This role of magnetic field can be used to manage flow systems in material processing and various biomedical applications.

4.2 Unsteadiness effects

As a flow system that starts from rest is considered, it is expected that its flow profiles and related quantities may depend on the time variable. The rates of variations of flow profiles with time are measured by the unsteadiness parameter. The impacts of the unsteadiness effect on the rates of relevant profiles are shown in Figure 4. It can be revealed from the results in Figure 4 that as the flow system becomes more unsteady, less amount of heat and mass diffusion occurs while the momentum transfer is facilitated with the increase in the unsteadiness parameter.

Figure 4

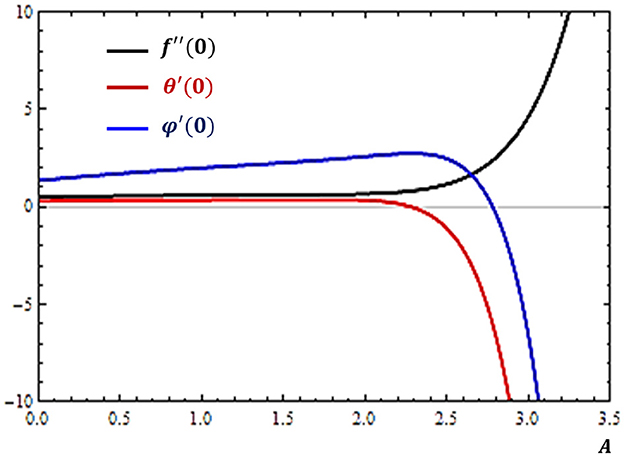
Figure 4. Effects of unsteadiness (A) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

4.3 Medium porosity effects

Fluid flows across media such as soil, beach sand, cement, crushed rock, or other materials with pores are practically useful in filtration, separation, and other similar activities. It is therefore essential to examine the impacts of medium porosity on fluid transport rates. The results of the present study are displayed in Figure 5.

Figure 5

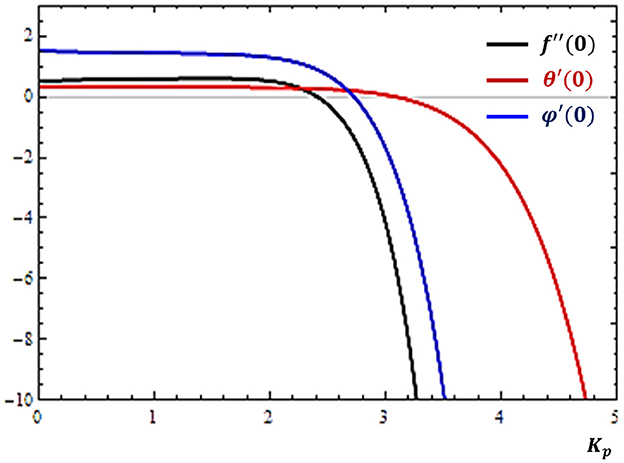
Figure 5. Effects of medium porosity (K_p) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

Figure 5 displays that the boundary derivatives are declining as the values of K_p increase. This agrees with the fact that a medium with large values of porosity parameter has a smaller permeability to fluid flow. This limited permeability has a tendency to inhibit fluid transport rates.

4.4 Buoyancy effects

The presence of a gravitational field with variations in concentration and temperature distributions develops body forces, known as the concentration and thermal buoyancy forces. These forces are quantified, respectively, as mass and thermal Grashof numbers. The impacts of these numbers on the boundary derivatives are depicted in Figures 6, 7, respectively.

Figure 6

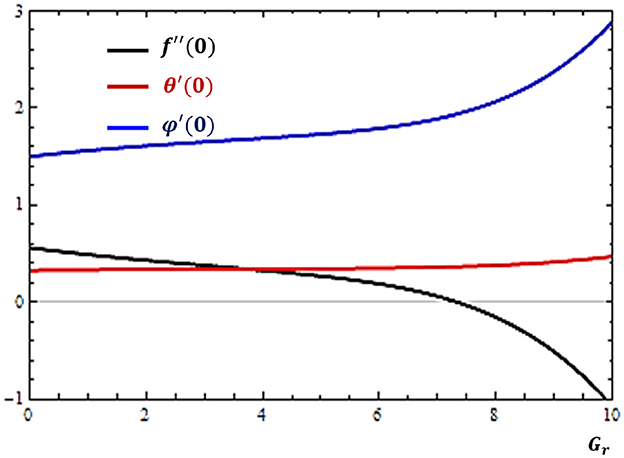
Figure 6. Effects of thermal Grashof number (G_r) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

Figure 7

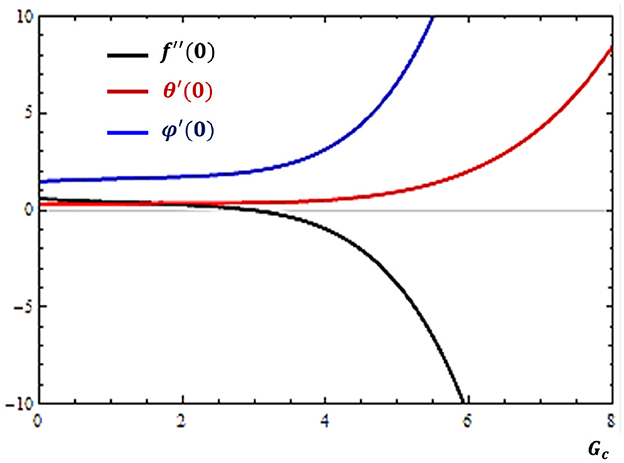
Figure 7. Effects of mass Grashof number (G_c) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

It is possible to note from Figures 6, 7 that as the buoyancy forces due to temperature and concentration differences increase, the rate of mass diffusion is facilitated while the rate of momentum transfer is restricted. On the other hand, it is found that the rate of heat transfer is less affected by thermal buoyancy force while it is facilitated as the mass buoyancy force increases.

4.5 Cross diffusion effects

The cross contributions of mass and temperature gradients to the heat and mass transfer rates are studied in terms of the Dufour and Soret numbers, respectively. The influences of these parameters on the boundary derivatives are depicted in Figures 8, 9.

Figure 8

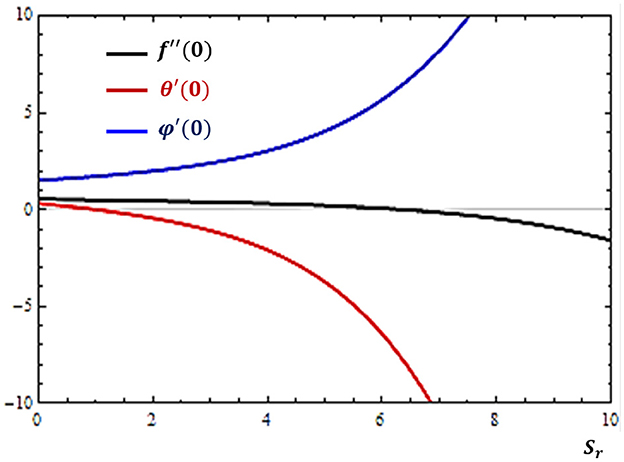
Figure 8. Effects of Soret number (S_r) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

Figure 9

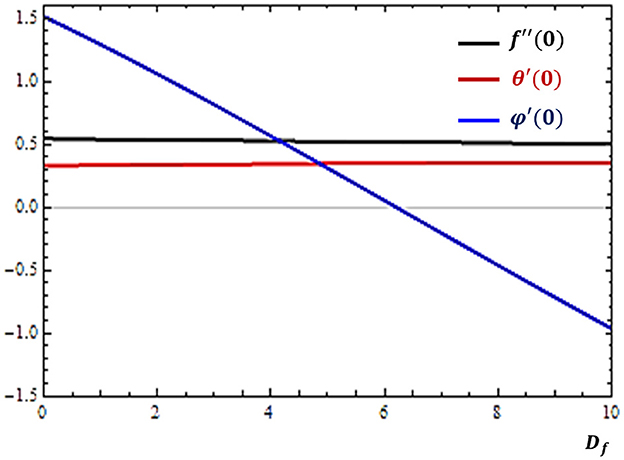
Figure 9. Effects of Dufour number (D_f) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

It is shown in Figure 8 that as the Soret number increases, the rate of mass transfer is encouraged while the rate of heat transfer is inhibited. On the other hand, the increase in Dufour number causes the reduction in mass transfer rate as indicated in Figure 9. These results also follow from the facts that the Soret effect is responsible for generating mass flux while the Dufour effect contributes to energy flux.

4.6 Thermal radiation effects

The study of thermal radiation (Rd) in fluid flow systems is significant for high-temperature environments. The results of the present study on the impacts of Rd is plotted in Figure 10.

Figure 10

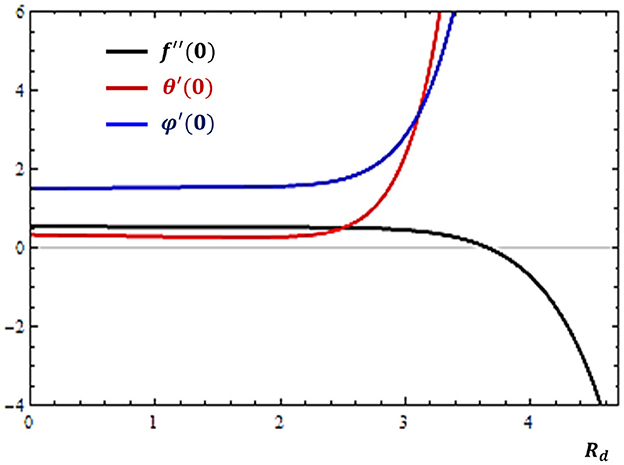
Figure 10. Effects of thermal radiation (Rd) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

One can notice from Figure 10 that the thermal radiation parameter has the tendency to rise both the mass and heat transfer rates while it retards the momentum transfer rate.

4.7 Heat source effects

Fluid flows may occur in conditions where the addition or removal of heat energy is significant. The rates at which the mass, heat, and momentum transfer varies in relation to the changing trends of heat sink (Q < 0) and heat source (Q > 0) are determined as shown in Figure 11. It is revealed in Figure 11 that the rate of heat transfer can be inhibited by increasing either the heat sink or increasing heat source effects. However, opposite behaviors are noticed by the rates of momentum and mass diffusion.

Figure 11

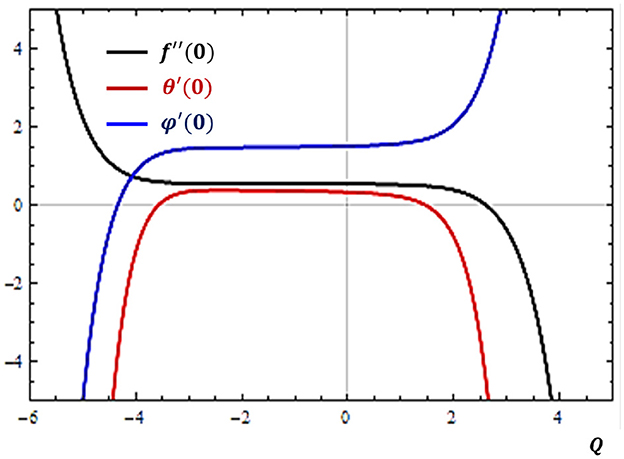
Figure 11. Effects of heat sink (Q < 0) and heat source (Q > 0) on the rates of velocity (f″), concentration (ϕ′), and temperature (θ′) profiles near the solid surface (atη = 0).

5 Conclusion

In this study, special attention is given to analyze the rates of mass, heat, and momentum transfer in a magnetic Casson nanofluid flow with dissipation and slip and cross-diffusion effects near a solid surface. The governing principles of fluid dynamics and heat transfer together with tangible boundary conditions are represented mathematically by using systems of differential equations. An efficient optimal homotopy analysis method is implemented to obtain analytic approximations for the momentum, heat, and mass transfer rates of unknown functions in response to the continuous variations of relevant parameters. Attempts are also made to ensure the validity, accuracy, and convergence of the results. Based on the results of the present study, it is possible to make the following conclusions:

• The heat transfer between the solid surface and the surrounding fluid can be enhanced by increasing the values of thermal radiation (R_d), magnetic field (B), or concentration buoyancy force (G_c). It can also be enhanced by decreasing the effect of thermal diffusion (Sr), porosity of the medium (Kp), flow unsteadiness (A), and heat source (Q) effects.

• The mass transfer near the solid surface can be assisted by increasing the effect of thermal diffusion (Sr), heat generation (Q > 0), thermal radiation (R_d), and concentration buoyancy force (G_c). It can also be assisted by decreasing the effect of diffusion thermo (Df), heat sink (Q < 0), medium porosity (Kp), magnetic field (B), or flow unsteadiness (A) parameters.

• The rate of momentum transfer of the fluid flow near the solid surface can be facilitated by increasing the effect of flow unsteadiness (A) or heat sink (Q < 0). This can also be facilitated by decreasing the effect of medium porosity (Kp), heat generation (Q > 0), magnetic field (B), thermal radiation (R_d), and concentration buoyancy force (G_c).

Among other things, the analysis of Casson nanofluid transport rates near a vertical stretching sheet with dissipation and slip effects over a continuous domain of parameters will provide relevant information for practitioners to make informed decisions in handling real flow systems. Hence, the present study will contribute in not only supplementing the theoretical gaps for the scientific community but also improving the working efficiency of practical flow systems in manufacturing industries and the quality of industrial products. This study can be further extended in many directions for more complicated real applications. This may include analyzing various fluid behaviors over different flow geometries in the presence of other relevant flow parameters and by implementing other efficient mathematical methods.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TW: Conceptualization, Formal analysis, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

A, Unsteady parameter; B, Magnetic field strength (N.m.A⁻¹); C, Concentration in boundary layer; Cf_x, Local Skin friction coefficient; C_p, Specific heat capacity at constant pressure (J.Kg⁻¹.K⁻¹); C_s, Concentration susceptibility; C_w, Wall nanoparticle concentration; C_∞, Concentration in ambient flow; D_m, Molecular diffusivity coefficient (m².s⁻¹); D_f, Dufour number; D_T, Thermophoretic diffusion coefficient; f, Dimensionless stream function; g, Gravitational acceleration; G_c, Mass Grashof number; G_r, Thermal Grashof number; J_w, Mass flux at the surface; K₀, Permeability of porous medium; K_P, Porosity parameter; K_T, Thermal diffusion ratio; K_r, Rate of chemical reaction; k^*, Thermal absorption coefficient; M, Magnetic field parameter; N_b, Brownian motion parameter; N_f, Momentum slip parameter; N_t, Thermophoresis parameter; Nu_x, Nusselt number; N_θ, Thermal slip parameter; N_φ, Concentration slip parameter; Pr, Prandtl number; Q, Heat generation/absorption parameter; Q₀, Coefficient of heat source; q_m, Mass flux of the nanofluid (Kg.m²s); q_w, Surface heat flux (W.m⁻²); Rd, Radiation parameter; Re_x, Local Reynolds number; S, Injection/suction parameter; Sh_x, Sherwood number; S_c, Schmidt number; S_r, Soret number; T, Temperature (K); T_m, Mean temperature (K); T_w, Wall temperature (K); T_∞, Ambient fluid temperature (K); U_w, Velocity of surface (m.s⁻¹); V_w, Velocity of mass through the wall (m.s⁻¹); (u, v), Velocity components (m.s⁻¹); α_f, Thermal diffusivity of the nanofluid (m².s⁻¹); β_c, Concentration expansion coefficient; β_T, Thermal expansion coefficient; γ, Chemical reaction parameter; η, Similarity variable; θ, Dimensionless temperature; κ, Thermal conductivity coefficient (W.m⁻¹.K⁻¹); μ, Dynamic viscosity (Kg/(m.s)); ρ_f, Density of fluid (Kg.m⁻³); ρ_p, Density of nanoparticles (Kg.m⁻³); (ρc)_f, Heat capacity of the fluid; (ρc)_p, Heat capacity of the nanoparticles; σ, Electric conductivity; σ^*, Stefan–Boltzmann constant; τ, Ratio of heat capacities; τ_w, Wall shear stress (Pa); υ, Kinematic viscosity (m²/s); φ, Dimensionless concentration function; ϕ, Homotopy approximation; ψ, Stokes stream function; ℏ, Convergence-control parameter.

References

1. Walelign T, Kebede T, Haile E, Walelgn A. Analytical study of heat and mass transfer in unsteady MHD radiant flow of Williamson nanofluid over stretching sheet with heat generation and chemical reaction. Heat Transfer. (2020) 48:4246–4263. doi: 10.1002/htj.21825

Crossref Full Text | Google Scholar

2. Kebede T, Haile E, Awgichew G, Walelign T. Heat and mass transfer in unsteady boundary layer flow of Williamson nanofluids. J Appl Mathem. (2020) 18:972. doi: 10.1155/2020/1890972

Crossref Full Text | Google Scholar

3. Mabood F, Shateyi S. Multiple slip effects on MHD unsteady flow heat and mass transfer impinging on permeable stretching sheet with radiation. Modell Simul Eng. (2019) 30:1–11. doi: 10.1155/2019/3052790

Crossref Full Text | Google Scholar

4. Haroun H, Mondal S, Sibanda P. Effects of thermal radiation on mixed convection in a MHD nanofluid flow over a stretching sheet using a spectral relaxation method. Int J Mathem Comput Phys Electr Comput Eng. (2017) 11:52–61. Available online at: https://zenodo.org/records/1339868/files/10006276.pdf

Google Scholar

5. Kejela SB, Firdi MD. Analytical analysis of effects of buoyancy, internal heat generation, magnetic field, and thermal radiation on a boundary layer over a vertical plate with a convective surface boundary condition. Int J Differ Equat. (2020) 88:510. doi: 10.1155/2020/8890510

Crossref Full Text | Google Scholar

6. Walelign T, Haile E, Kebede T, Awgichew G. Heat and mass transfer in stagnation point flow of maxwell nanofluid towards a vertical stretching sheet with effect of induced magnetic field. Mathem Problems Eng. (2021) 2021:1–15. doi: 10.1155/2021/6610099

Crossref Full Text | Google Scholar

7. Manvi BK, Kerur SB, Tawade JV, Nieto JJ, Sankeshwari SN, Ahmad H, et al. Casson nanofluid boundary layer flow in presence of radiation and non-uniform heat source/sink. Math Model Control. (2023) 3:152–67. doi: 10.3934/mmc.2023014

Crossref Full Text | Google Scholar

8. Suresh Kumar Y, Hussain S, Raghunath K, Ali F, Guedri K, Eldin SM, et al. Numerical analysis of magnetohydrodynamics Casson nanofluid flow with activation energy, Hall current and thermal radiation. Sci Rep. (2023) 13:4021. doi: 10.1038/s41598-023-28379-5

PubMed Abstract | Crossref Full Text | Google Scholar

9. Mahabaleshwar US, Maranna T, Mishra M, Hatami M, Sunden B. Radiation effect on stagnation point flow of Casson nanofluid past a stretching plate/cylinder. Sci Rep. (2024) 14:1387. doi: 10.1038/s41598-024-51963-2

PubMed Abstract | Crossref Full Text | Google Scholar

10. Okuyade WA, Abbey TM. Transient MHD fluid flow past a moving vertical surface in a velocity slip flow regime. Wseas Trans Fluid Mech. (2024) 19:99–112. doi: 10.37394/232013.2024.19.10

Crossref Full Text | Google Scholar

11. Awad E, Abo-Dahab SM, Abdou MA. Exact solutions for a two-dimensional thermoelectric MHD flow with steady-state heat transfer on a vertical plate with two instantaneous infinite hot suction lines. arXiv:2212.01665. (2022).

Google Scholar

12. Awad E. Modeling of anomalous thermal conduction in thermoelectric magnetohydrodynamics: Couette formulation with a multiphase pressure gradient. Phys Fluids. (2024) 36:033608. doi: 10.1063/5.0190970

Crossref Full Text | Google Scholar

13. Vasu V, Rama Krishna K, Kumar ACS. Application of nanofluids in thermal design of compact heat exchanger. Int J Nanotechnol Appl. (2008) 2:75–87. doi: 10.1504/IJNM.2008.018949

PubMed Abstract | Crossref Full Text | Google Scholar

14. Choi US, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. In: 1995 International Mechanical Engineering Congress and Exhibition. San Francisco, CA (United States) (1995).

Google Scholar

15. Qiu L, Zhu N, Feng Y, Michaelides EE, Zyła G, Jing D, et al. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys Rep. (2020) 843:1–81. doi: 10.1016/j.physrep.2019.12.001

Crossref Full Text | Google Scholar

16. Buongiorno J. Convective transport in nanofluids. ASME J Heat Transfer. (2006) 128:240–50. doi: 10.1115/1.2150834

Crossref Full Text | Google Scholar

17. Kumar S, Kumar A. A comprehensive review on the heat transfer and nanofluid flow characteristics in different shaped channels. Int J Ambient Energy. (2021) 42:345–61. doi: 10.1080/01430750.2018.1530139

Crossref Full Text | Google Scholar

18. Manjunatha S, Puneeth V, Gireesha BJ, Chamkha A. Theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. J Appl Comput Mech. (2022) 8:1279–86. doi: 10.22055/JACM.2021.37698.3067

Crossref Full Text | Google Scholar

19. Adnan, Alharbi KAM, Bani-Fwaz MZ, Eldin SM, Yassen MF. Numerical heat performance of TiO2/Glycerin under nanoparticles aggregation and nonlinear radiative heat flux in dilating/squeezing channel. Case Stud Thermal Eng. (2023) 41:102568. doi: 10.1016/j.csite.2022.102568

Crossref Full Text | Google Scholar

20. Bani-Fwaz MZ, Mahmood Z, Bilal M, Ei-Zahhar AA, Khan I, Niazai S. Computational investigation of thermal process in radiated nanofluid modulation influenced by nanoparticles (Al2O3) and molecular (H2O) diameters. J Comput Des Eng. (2024) 11:22–36. doi: 10.1093/jcde/qwae011

Crossref Full Text | Google Scholar

21. Ramesh K, Patel A, Rawal M. Electroosmosis transverse magnetic effects on radiative tangent hyperbolic nanofluid flow through porous medium. Int J Ambient Energy. (2020) 2020:1–8. doi: 10.1080/01430750.2020.1862912

Crossref Full Text | Google Scholar

22. Li YX, Alqsair UF, Ramesh K, Khan SU, Khan MI. Nonlinear heat source/sink and activation energy assessment in double diffusion flow of micropolar (non-Newtonian) nanofluid with convective conditions. Arabian J Sci Eng. (2021) 47:859–66. doi: 10.1007/s13369-021-05692-7

Crossref Full Text | Google Scholar

23. Akbar AA, Awan AU, Bani-Fwaz MZ, Tag-ElDin EM, Guedri K, Yassen MF, et al. Linear and quadratic convection significance on the dynamics of MHD Maxwell fluid subject to stretched surface. Front Phys. (2022) 10:974681. doi: 10.3389/fphy.2022.974681

Crossref Full Text | Google Scholar

24. Patil PM, Goudar B, Patil M, Momoniat E. Bioconvective periodic MHD Eyring-Powell fluid flow around a rotating cone: influence of multiple diffusions and oxytactic microorganisms. Alexandria Eng J. (2023) 81:636–55. doi: 10.1016/j.aej.2023.09.056

Crossref Full Text | Google Scholar

25. Patil PM, Goudar B. Multidiffusive nanofluid flow over a sphere with time-reliant nonlinear convective regime: impact of activation energy. Numer Heat Transfer, Part A. (2024) 85:2197–219. doi: 10.1080/10407782.2023.2219835

Crossref Full Text | Google Scholar

26. Khan Z, Srivastava HM, Mohammed PO, Jawad M, Jan R, Nonlaopon K. Thermal boundary layer analysis of MHD nanofluids across a thin needle using non-linear thermal radiation. Mathem Biosci. Eng. (2022) 19:14116–41. doi: 10.3934/mbe.2022658

PubMed Abstract | Crossref Full Text | Google Scholar

27. Das K, Acharya N, Kundu PK, Duari PR. Magneto chemically reacting micropolar nanofluid flow in existence of heat source/sink. J Nanofluids. (2022) 11:528–536. doi: 10.1166/jon.2022.1862

Crossref Full Text | Google Scholar

28. Casson N. A flow equation for pigment-oil suspensions of the printing ink type. In: Mill CC., editor. Rheology Disperse Systems. Oxford, UK: Pergamon Press (1959). p. 84–104.

Google Scholar

29. Shah NA, Khan I. Heat transfer analysis in a second grade fluid over oscilating vertical plate using fractional caputo-fabrizio derivatives. Eur J C. (2016) 76:1–11. doi: 10.1140/epjc/s10052-016-4209-3

PubMed Abstract | Crossref Full Text | Google Scholar

30. Mondal S, Haroun NA, Sibanda P. The effects of thermal radiation on an unsteady MHD axisymmetric stagnation-point flow over a shrinking sheet in presence of temperature dependent thermal conductivity with Navier slip. PLoS ONE. (2015) 10:e0138355. doi: 10.1371/journal.pone.0138355

PubMed Abstract | Crossref Full Text | Google Scholar

31. Ramana RM, Raju KV, Kumar JG. Multiple slips and chemical reaction effects on unsteady MHD heat and mass transfer flow over a permeable stretching sheet with radiation. Turkish J Comput Mathem Educ. (2021) 12:4489–98. Available online at: https://turcomat.org/index.php/turkbilmat/article/view/8435/6615

Google Scholar

32. Kebede T, Haile E, Awgichew G, Walelign T. Heat mass transfer analysis in unsteady flow of tangent hyperbolic nanofluid over a moving wedge with buoyancy and dissipation effects. Heliyon. (2020) 6:e03776. doi: 10.1016/j.heliyon.2020.e03776

PubMed Abstract | Crossref Full Text | Google Scholar

33. Ibrahim W, Zemedu C. Numerical solution of micropolar nanofluids with Soret, Dufor effects and multiple slip conditions. J Phys Commun. (2020) 4:015016. doi: 10.1088/2399-6528/ab5260

Crossref Full Text | Google Scholar

34. Liao S. Beyond Perturbation: Introduction to the Homotopy Analysis Method. Boca Raton: Hall/CRC Press. (2003).

Google Scholar

35. Zhao Y, Liao SJ. Advances in the Homotopy Analysis Method. Singapore: World Scientific Publishing Co. Pte. Ltd. (2013). p. 361.

Google Scholar

36. Chamkha AJ, Aly AM, Mansour MA. Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects. Chem Eng Commun. (2010) 197:846–58. doi: 10.1080/00986440903359087

Crossref Full Text | Google Scholar