1 Introduction
The old Babylonian algorithm, a remarkable mathematical artifact from ancient Mesopotamia (around 1800–1600 BC), has long been a subject of fascination to scholars. This ancient algorithm not only demonstrates the advanced intellectual capabilities of the Babylonians but also holds significant relevance in modern times. It is particularly known for its ingenious method of approximating square roots [1].
In recent research, an exciting transformation has occurred. The traditional old Babylonian algorithm has been ingeniously modified to solve differential equations, breathing new life into this ancient technique [1]. In this study, we aimed to explore how this remarkable revival has played a significant role in the complex and captivating field of non-linear vibration theory, thereby bridging the gap between ancient and modern mathematics and demonstrating the timeless nature of mathematical concepts.
Non-linear vibration analysis presents several specific challenges. Strong non-linear oscillators, such as the one considered in this study (as shown in Equation 1), are characterized by the presence of higher-order non-linear terms. These non-linearities can lead to complex dynamic behaviors that are difficult to analyze using traditional methods [3–5]. For instance, the homotopy perturbation method, while widely used, attempts to convert the original non-linear problem into a sequence of linear sub-problems through the introduction of a homotopy parameter. However, it may still encounter difficulties in accurately handling highly non-linear systems [2–4]. The variational iteration method, another commonly employed approach, also has its limitations in addressing the complexities of non-linear vibrations [5]. Its frequency formulation, originating from an ancient Chinese algorithm, offers a relatively simple and effective way to analyze non-linear vibration systems and has proven to be valuable in the field of non-linear dynamics due to its straightforward and efficient nature [6–8]. However, the modified old Babylonian algorithm proposed in He [1] provides a novel perspective and potentially a more efficient solution to the strongly non-linear oscillator problem compared to these traditional methods. It combines the ancient wisdom of the Babylonian algorithm with modern adaptations to better suit the context of non-linear dynamics analysis.
By exploring the application of the modified old Babylonian algorithm in non-linear vibrations, we aim to contribute to a deeper understanding of both the ancient mathematical heritage and its practical implications in contemporary scientific research. This study not only sheds light on the historical significance of the old Babylonian algorithm but also paves the way for further advancements in the field of non-linear dynamics.
2 Modified old Babylonian algorithm
We considered a strongly non-linear oscillator in the form:
This oscillator is characterized by the presence of high-order non-linear terms, where a and b are constants. The initial conditions are set as u(0) = A and u′(0) = 0, where A is the amplitude.
Traditionally, numerous methods have been employed to solve non-linear oscillator problems. The homotopy perturbation method has widespread application. This method aims to convert the original non-linear problem into a series of linear sub-problems by introducing a homotopy parameter [2–4]. The variational iteration method is also a commonly used approach [5]. Moreover, its frequency formulation [6–8], which originates from an ancient Chinese algorithm, offers a simple yet effective means to analyze non-linear vibration systems. It has demonstrated to be valuable in the field of non-linear dynamics with its straightforward and efficient characteristics [9–13].
However, in this research, we applied the modified old Babylonian algorithm proposed in He [1]:
where is a weighting factor. This modified algorithm [1] offers a novel viewpoint and potentially a more efficient solution to the strongly non-linear oscillator problem in contrast to traditional methods. To better understand the derivation of this modified algorithm, let us consider the following step-by-step explanation.
Suppose the initial solution is:
where ω is the frequency. Utilizing the modified old Babylonian algorithm, we obtain
By setting ωt = 31° and and considering cos31° = 0.8572, we have
Figure 1 provides an elaborate and in-depth comparison of the approximate solution and the exact one for a wide range of values of parameters a and b. This comparison is of great significance as it vividly showcases the remarkable performance of the modified old Babylonian algorithm within the context of this complex problem domain. The excellent agreement between the approximate and exact solutions effectively validates the effectiveness of the modified algorithm. It provides strong evidence that the modified old Babylonian algorithm is not only theoretically sound but also practically applicable.
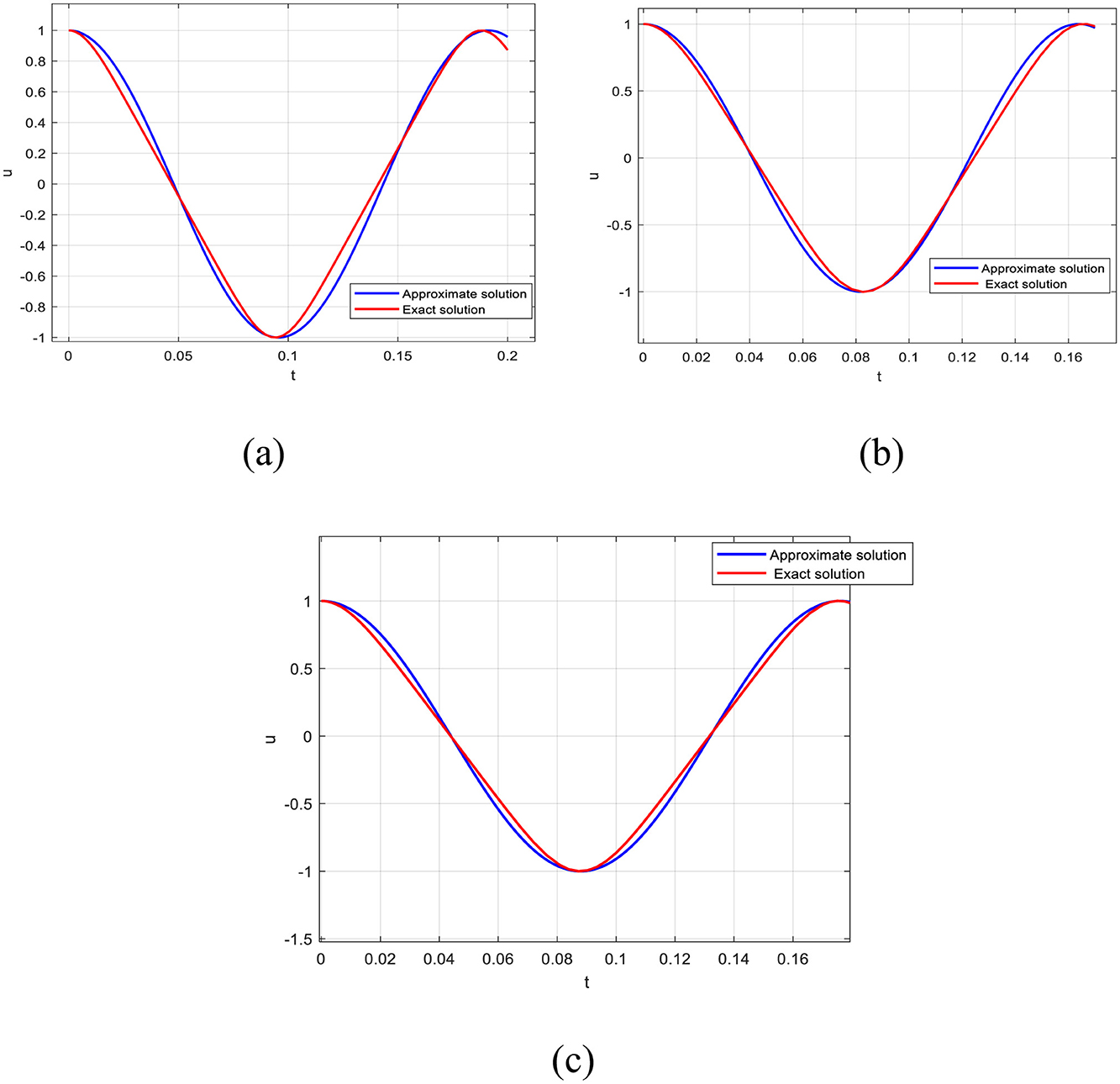
Figure 1. Comparative analysis of the approximate and exact analytical solutions for different parameter cases (A) A = 1, a = 2000, b = 0; (B) A = 1, a = 0, b = 2, 000; (C) A = 1, a = 1000, b = 1, 000.
3 Conclusion
In conclusion, the modified old Babylonian algorithm has emerged as a highly promising approach in the analysis of strongly non-linear oscillators. Through its unique combination of ancient mathematical wisdom and modern adaptations, it offers an alternative and efficient solution method to traditional techniques.
The successful application of this algorithm in the context of non-linear vibrations not only validates its theoretical soundness but also showcases its practical applicability. The excellent agreement between the approximate and exact solutions, as demonstrated in the comparison presented in this study, provides compelling evidence of its effectiveness.
Looking ahead, the findings of this research have significant implications for future studies and applications. In the field of Micro-Electro-Mechanical Systems (MEMS), for instance, the algorithm could potentially be employed to enhance the understanding and optimization of the dynamic behavior of MEMS devices. By accurately modeling and analyzing the non-linear vibrations in these miniature systems, it may be possible to improve their performance, reliability, and lifespan.
Furthermore, this research paves the way for further exploration of the algorithm's capabilities. Future investigations could focus on extending its application to more complex non-linear systems, such as those with time-varying parameters or multiple degrees of freedom. In addition, there is potential for integrating the modified old Babylonian algorithm with other advanced computational and analytical tools, such as machine learning algorithms, for more efficient parameter identification and system optimization.
Overall, the resurgence of the old Babylonian algorithm in the modern context of non-linear dynamics holds great promise for advancing our understanding and ability to handle complex non-linear systems, opening up new avenues for research and innovation across various scientific and engineering disciplines.
Author contributions
LZ: Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. He J-H. An old Babylonian algorithm and its modern applications. Symmetry. (2024) 16:1467. doi: 10.3390/sym16111467
2. He CH, El-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low Freq Noise Vib Act Control. (2022) 41:572–603. doi: 10.1177/14613484211059264
3. He CH, Tian D, Moatimid GM, Salman HF, Zekry MH. Hybrid rayleigh-van der pol-duffing oscillator: stability analysis and controller. J Low Freq Noise Vib Act Control. (2022) 41:244–68. doi: 10.1177/14613484211026407
4. He J-H, He C-H, Alsolami A. A good initial guess for approximating nonlinear oscillators by the homotopy perturbation method. Facta Univ Ser: Mech Eng. (2023) 21:21–9. doi: 10.22190/FUME230108006H
5. Tang W, Anjum N, He JH. Variational iteration method for the nanobeams-based N/mems system. MethodsX. (2023) 11:102465. doi: 10.1016/j.mex.2023.102465
6. He JH. The simpler, the better: analytical methods for nonlinear oscillators and fractional oscillators. J Low Freq Noise Vib Act Control. (2019) 38:1252–60. doi: 10.1177/1461348419844145
7. He JH. The simplest approach to nonlinear oscillators. Results Phys. (2019) 15:102546. doi: 10.1016/j.rinp.2019.102546
8. He JH. Frequency formulation for nonlinear oscillators (part 1). Sound Vib. (2024) 59:1687. doi: 10.59400/sv1687
9. He CH, Liu C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals. (2022) 30:2250046. doi: 10.1142/S0218348X22500463
10. Tian Y, Shao Y. Mini-review on periodic properties of mems oscillators. Front Phys. (2024) 12:1498185. doi: 10.3389/fphy.2024.1498185
11. Zhang J-G, Song Q-R, Zhang J-Q, Wang F. Application of He's frequency formula to nonlinear oscillators with generalized initial conditions. Facta Univ Ser: Mech Eng. (2023) 21:701–12. doi: 10.22190/FUME230909047Z
12. He J-H. Periodic solution of a micro-electromechanical system. Facta Univ Ser: Mech Eng. (2024) 22:187–98. doi: 10.22190/FUME240603034H
Keywords: ancient mathematics, nonlinear vibration system, frequency-amplitude relationship, nonlinear differential equation, MEMS
Citation: Zhang L (2025) The old Babylonian algorithm: reborn with a bang and its application in non-linear vibration. Front. Appl. Math. Stat. 10:1530024. doi: 10.3389/fams.2024.1530024
Received: 20 November 2024; Accepted: 16 December 2024;
Published: 15 January 2025.
Edited by:
Igor Kondrashuk, University of Bío-Bío, ChileReviewed by:
Ahmad Qazza, Zarqa University, JordanCopyright © 2025 Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liangyuan Zhang, bGlhbmd5dWFuX3poYW5nQDE2My5jb20=
 Liangyuan Zhang
Liangyuan Zhang