- 1Mathematics Department, College of Natural Science, Arba Minch University, Arba Minch, Ethiopia
- 2Mathematics Department, Faculty of Sciences, Badji Mokhtar Annaba University, Annaba, Algeria
In this research study, two new types of fractional derivatives, the Caputo-Fabrizio derivative that does not involve a singular kernel (like the Riemann–Liouville derivative), which helps in eliminating some drawbacks, such as non-locality, and the Atangana–Baleanu–Caputo () derivative that uses a non-singular and non-local kernel, offering different characteristics from other fractional derivatives and often leading to more accurate models in certain physical systems, are used. The primary goal of the research is to analyze a non-linear fractional differential equation involving the fractional derivatives of Caputo–Fabrizio and admit at least one solution. Fixed point theory is a fundamental tool in mathematical analysis used to prove the existence of solutions to various equations. Hence, in this study, to achieve the desired results, we employ a novel fixed point theory known as the -contraction type. The study also includes required conditions and inequalities that need to be satisfied to ensure that a solution exists. One of these conditions is based on the Lipschitz hypothesis. Therefore, we provide the required conditions and inequalities, based on the Lipschitz hypothesis, to show that solutions to our problem exist. Furthermore, we provide two illustrative examples to support our primary findings.
1 Introduction
Since Leibniz and L'Hospital's 1695 introduction to the theory of calculus of integrals and derivatives of any arbitrary order, eminent mathematicians have made substantial contributions to the field. Mathematicians like Hadamard, Caputo, Grunwald–Letnikov, Riemann–Liouville, and others have contributed significantly throughout the years to the definition of fractional integrals and derivatives within the framework of fractional calculus [1]. These mathematicians provided valuable information and mathematical formulations that improved our understanding of fractional calculus and its applications. Their contributions paved the way for the development of various techniques and methodologies to tackle problems involving fractional derivatives and integrals, enabling the exploration of fractional calculus in various fields of science, engineering, and mathematics. In recent years, two new types of fractional operators have been introduced: the Caputo–Fabrizio fractional derivative and the Atangana–Baleanu–Caputo () fractional derivative. The Caputo–Fabrizio derivative [2], proposed in 2015 by Caputo and Fabrizio, doesn't rely on the Gamma function and has a nonsingular kernel. Similarly, the fractional derivative [3], suggested in 2016 and based on the Mittag-Lefler function, also features a nonsingular kernel. The use of ABC and Caputo–Fabrizio fractional derivatives in non-linear fractional differential equations offers significant potential for practical applications in fields ranging from physics and engineering to bioengineering and geophysics. The incorporation of and Caputo–Fabrizio derivatives into non-linear fractional differential equations (FDEs) are used to model complex physical and engineering systems that are not well described by classical integer-order models by providing more flexibility in capturing real-world phenomena. The Atangana-Baleanu derivative is gaining attention in fields where memory, relaxation, and hereditary properties are critical, such as viscoelastic materials, biological tissues, and complex fluids. The Caputo–Fabrizio derivative avoids the singularities of the traditional Caputo derivative, which can be useful in many engineering contexts. Therefore, in recent years numerous researchers have been concentrating on modeling real-world situations with different types of fractional derivatives. A novel, thorough investigation of using residual neural networks to approximate Erdélyi–Kober fractional derivatives is presented in the publication [4], which also provides an upper constraint on the parameters for these networks. In the research study [5], a brand-new iteration scheme called was developed. Its rate of convergence is faster than that of practically all previous iteration schemes, allowing it to find solutions with the fewest steps possible, and this new iteration scheme is applied to solve a specific delay differential equation. In the article [6], the existence and uniqueness of a solution by using the Picard iterative technique for a non-linear functional Volterra integral equation, which belongs to the Urysohn type class of non-linear integral equations, was demonstrated. The research studies [5, 7, 8] discussed how to solve weakly singular Volterra and Fredholm integral equations and second-kind non-linear Volterra–Fredholm–Hammerstein integral equations numerically using the modified Lagrange polynomial interpolation technique in conjunction with the biconjugate gradient stabilized method and the discretization technique, and these equations are used to model problems like heat conduction in engineering and the electrostatic potential theory. They have used fixed-point theory to examine and solve these mathematical models. Fixed-point theorems have a crucial component in studying the solutions of non-linear problems involving ordinary, partial, and fractional differential equations. By utilizing the Krasnoselskii fixed-point theorem, scholars have demonstrated the existence of solutions for many different types of equations. For example, they have investigated the existence of solutions for non-linear fractional oscillator equations, sequential fractional integro-differential equations, and Euler–Bernoulli Beam equations. The application of fixed point theory, combined with other mathematical techniques like natural transform and Adomian decomposition, has facilitated advancements in understanding and solving complex problems in diverse fields [9–13].
Different fixed-point theorems have recently been devised by researchers to analyze non-linear fractional differential equation (FDE) solutions. The existence and uniqueness of solutions for fractional differential equations with the Atangana–Baleanu fractional derivative were examined in a paper [14] using fixed-point techniques. Atangana–Baleanu–Caputo fractional differential equations' Hyers–Ulam stability was anayzed in the research study [15], which used the Wright function and the Laplace transform technique. The solution analysis for a specific type of implicit fractional differential equation of a non-local initial value problem were examined in [16], and in this research study, the Banach contraction principle and Krasnoselskii's fixed-point theorem were applied. In Ref. [17], fractional differential equations with instantaneous impulses involving the Caputo-Fabrizio fractional derivative were examined and found that the equation admits one solution by using fixed point theorems such as Schauder and Monch along with the measure of non-compactness approach. The estimation of the Atangana–Baleanu–Caputo () fractional derivative at extreme points was investigated in a paper [18]. The work showed how to use Peano's existence theorem to investigate non-linear fractional differential equation solutions. Furthermore, in another study [19], a fractional derivative containing the Caputo–Fabrizio alcoholism model was developed. To show that this model admits at least one solution and that the solution is unique, the researchers used the fixed-point theorem. In [20], the authors utilized the Picard–Lindel of technique and fixed point theory to examine the existence of a unique solution for a fractional model related to the human liver. The model involved the Caputo–Fabrizio derivative containing an exponential kernel. Similarly, in the study [21], the researchers applied the Banach fixed point theorem to investigate the existence and uniqueness of the semi-analytical solution for the Pine Wilt Disease (PWD) model involving Caputo–Fabrizio fractional derivative. In the paper [22], a fixed point approach was used to investigate the existence and uniqueness of the solution for a weakly singular non-linear functional Volterra integral equations of Urysohn type involving Riemann–Liouville operator. In the paper [23], the existence, uniqueness, and stability of solutions to the non-linear Volterra–Fredholm integral equations involving the Erdlyi–Kober fractional integral operator were examined using the Leray-Schauder alternative, Banach's fixed point theorem, and the Hyers–Ulam and Hyers–Ulam–Rassias stability. Various research studies indicate that most of the non-linear problems containing different types of fractional derivatives are analyzed by employing Schauder's theorem and Krasnoselskii's theorem. However, Schauder's theorem is very general but relies heavily on the compactness of the operator, which may not hold in many non-linear FDEs, and Krasnoselskii's theorem is effective when the operator can be decomposed into a compact and a contraction part, but it imposes restrictive conditions. -contraction fixed-point theory offers a more flexible and generalized framework that accommodates the specific challenges posed by non-linear fractional differential equations. It does so by relaxing the strict conditions imposed by classical theorems and introducing a broader class of contraction mappings suitable for analyzing the existence and uniqueness of solutions to such equations. Hence, -contraction theory is often preferred for its versatility, less restrictive conditions, and wider applicability, especially in the context of non-linear FDEs. Some fixed-point theorems in b-dislocated metric space were established in the article [24], and the application of the fixed point technique was used to solve non-linear fractional differential equations of the Caputo type as well as to solve a non-linear integral equation. The studies, [25, 26] presented new classes of cyclic contractions of the Hardy–Rogers type and the concept of a cyclic compatible contraction and established the relevant fixed point theorems for these types of contractions in the generating space of a b-dislocated metric and b-quasi-metric family. In the studies, [27, 28], the concept of -contraction was examined from the perspective of d-metric spaces, as well as the topological features of a d-neighborhood system derived from dislocated metric space and the uniqueness of fixed points and coincidence points of such mappings. Additionally, it used different cyclic contractions in weaker forms of generating spaces to prove a few fixed point theorems. In 2020, Afshari and Baleanu conducted a study that focused on the existence of solutions for Atangana–Baleanu fractional differential equations in the Caputo sense. They employed several fixed point theorems for contractive mappings, including α−γ-Geraghty type, α-type -contraction, and other contractions in an -complete -metric space [29]. The stability analysis, existence, and uniqueness of the solution for a system of non-linear fractional differential equations containing Caputo–Fabrizio fractional derivatives of order α ∈ (0, 1) were investigated in the study [30]. This study examines these qualities using several mathematical techniques, such as the Ulam–Hyers stability theorem, Schauder's fixed point theorem, Krasnoselskii's fixed point theorem, and the Banach contraction principle. The research work [41] showed the existence and stability of solutions for a system of non-linear time-delayed fractional differential equations involving fractional derivatives, represented by a six-compartment model, by utilizing a coordinate transformation and linearizing the system through a matrix coefficient.
The aforementioned study publications mentioned above as inspiration; this study is highly innovative; the methods used to investigate the solution of the proposed problems are highly innovative studies that take the form of a non-linear fractional differential equation that have never been used before to solve problems involving the two new operators, the Caputo–Fabrizio and Atangana–Baleanu–Caputo () fractional derivatives. Therefore, the aim of this study is to investigate the solutions for an initial value problem involving non-linear fractional differential equations (FDE). The equations under investigation are equipped with two types of fractional derivatives: the Caputo–Fabrizio fractional derivative of order ν ∈ (0, 1) and the Atangana–Baleanu–Caputo () fractional derivative of order ν ∈ (0, 1). Non-linear differential equations are already difficult to solve. When non-linearities are combined with fractional derivatives, the difficulty increases, and the effects of introducing fractional derivatives interact with the non-linear terms, leading to highly complex behaviors that are not easy to find classical solution. Because of these challenges, researchers often turn to tackle the solution analysis for non-linear fractional differential equations with Caputo–Fabrizio and Atangana–Baleanu–Caputo derivatives by employing fixed point theory. This research work focuses on examining the existence of solutions for non-linear equations described in Equations 1, 2, respectively, by using a novel fixed point theory known as the -contraction type. This method has proven to be effective in analyzing solutions to non-linear fractional differential equations.
and
This research study is organized into several sections. In Section 2, the basic definitions of the Caputo–Fabrizio and Atangana–Baleanu–Caputo fractional derivatives are provided. The section also includes the presentation of fixed point theorems of the -contraction type. These theorems serve as crucial tools for analyzing the solutions of non-linear fractional differential equations. Section 3 focuses on the main results of the study. It delves into the examination of the existence of solutions for various types of non-linear fractional differential equations and systems of non-linear differential equations. Specifically, Equations 1, 2 mentioned in the introduction are thoroughly analyzed in this section. The goal is to establish the conditions under which solutions exist for these equations. Some illustrative example are presented in Section 4.
2 Preliminaries
In this section, we begin by introducing some fundamental definitions and stating theorems related to -contraction type fixed point theorems. We also provide the definitions of Caputo-Fabrizio and Atangana-Baleanu-Caputo fractional derivatives. Additionally, we describe some relevant lemmas that play a significant role in the analysis of the solutions.
Definition 2.1. [31] If for every u, v, w ∈ E satisfy the following three requirements, and a constant λ≥1, the mapping d:E × E → [0, +∞) on a nonempty set E is said to be b− metric-like space on E.
(d1) d(u, v) = 0 ⇔ u = v,
(d2) d(u, v) = d(v, u),
(d3) d(u, w) ≤ λ[d(u, v) + d(v, w)].
Then, (E, d, λ) is referred to as b−metric-like space.
In 2012, Wardowski [32] suggested a novel type contraction type known as -contraction and proposed a novel fixed point theorem associated with it. The well-known Banach contraction principle is extended by this theorem.
Definition 2.2. [32] If is a mapping of the interval (0, +∞) into the set of real numbers, which satisfies the following three properties:
() For all γ, δ ∈ ℝ+, whenever 0 < γ < δ;
() If {βn}⊂(0, +∞) then if and only if
() as β → 0+ for some p ∈ (0, 1).
If there is a positive number τ such that the mapping T:E→E of the metric space is said to be contraction for any u, v ∈ E. Then,
F stands for the set of all functions that satisfy the definition given by D.Wardowski above.
Remark 2.1. [32] Let . Then, is in 𝔽.
Theorem 2.1. [39, 40] Assume that (E, d) is a complete metric space and T:E→E is contraction and for every u ∈ E, if the sequence converges to u*,then T possesses a distinct fixed point u* ∈ E.
Definition 2.3. [33] Assume that the sequence {un} exists in the b-metric-like space (E, d, λ).
(i) If , the sequence {un} is said to converge to u.
(ii) Suppose (E, d, λ) is a b−metric-like space, the sequence {un} is b−Cauchy in (E, d, λ) if exists and is finite, then there exists . If , the {un} sequence is known as the 0−b−Cauchy sequence.
(iii) A b-metric-like space (E, d, λ) is said to be b− complete (resp. 0−b−complete) if for every b−Cauchy (resp. 0−b− Cauchy) sequence {un} there exists u ∈ E such that .
(iv) A mapping T:(E, d, λ) → (E, d, λ) is said to be b−continuous if the sequence {Tun} tends to Tu whenever the sequence {un}⊂E converges to u as n → +∞, that is, if as a result .
Definition 2.4. [34] Let T be a self-mapping on a space that resembles the b−metric-like space (E, d, λ). If there is strictly increasing , the mapping T is said to be generalized (λ, p)−Jaggi contraction-type and τ > 0 so that for any u, v ∈ E:
for all u, v ∈ E, where with β + γ + 2δλ < 1 and p > 1. Where d(u, v) > 0.
Theorem 2.2. [35] Let (E, d, λ) be 0−b−complete and T:E→E be a generalized (λ, p)−Jaggi- contraction-type mapping. Then, T possesses a distinct fixed point u* ∈ E, if it is b−continuous and , for every u ∈ E.
Definition 2.5. The space H1(a, b) = {f:f ∈ L2(a, b) and f′ ∈ L2(a, b)}. Where L2(a, b) is the space of square integrable functions on the interval (a, b).
Definition 2.6. [2] Suppose f ∈ H1(a, b) and ν ∈ (0, 1). Then the Caputo-Fabrizio fractional derivative is defined as;
If the normalization function has the property that . As stated in definition (2.6), the kernel does not have singularity for t = s, even though the is zero when u(t) is constant.
Definition 2.7. [36] Later, Losada and Nieto modified the Caputo-Fabrizio fractional derivative and the fractional integral that corresponds to its derivative for 0 < ν < 1, as shown in Equations 6, 7 below.
Lemma 2.1. ([37]) The initial value problem
has a solution in terms of the integral given by:
Definition 2.8. [3] The derivative of an absolutely continuous function f and 0 < ν ≤ 1 is given by:
where is a normalizing function that makes and is a special Mittag-Leffler function.
Lemma 2.2. [38] The solution to
is given by:
3 Main result
Let and d:E×E → ℝ+ is a continuous function endowed with the b-metric-like defined by:
where
In order to establish the existence of solutions for Equations 1, 2, we will utilize the -contraction type approach. We introduce the following assumptions:
(H1) be a continuous function.
(H2) There exist a constants κ ∈ (0, 1), such that:
3.1 Existence of solution for (FDE) with Caputo–Fabrizio fractional derivative
The solution to the initial value problem of Equation 1 of a non-linear fractional differential equation with Caputo–Fabrizio fractional derivatives is examined in this subsection. Utilizing Lemma 2.1 and the initial value given in Equation 1, χ0 = 0, we obtain the integral solution for Equation 1 as follows:
Define for all t ∈ [0, T], the mapping as:
Theorem 3.1. Consider Equation 1, where is a given mapping and the hypotheses (H1) and (H2) are satisfied. We further assume that the following claims hold:
Let χ, ω ∈ E. If d(Tχ, Tω) > 0 and d(χ, ω) > 0, then there exists τ > 0 such that the following inequality yields,
for all t ∈ [0, T]. Where 𝔇(χ, ω) is defined as given in definition 2.4.
ii) If υ(χ(t), ω(t))≥0 for all t ∈ [0, T], then υ(Tχ(t), Tω(t)) ≥ 0.
iii) If the following inequality holds,
Then Equation 1 has a solution.
Proof
Our aim is to establish the existence of an element χ* ∈ E that serves as a fixed point for the mapping T. Let χ, ω ∈ E such that υ(χ(t), ω(t))≥0 for all t ∈ [0, T]. Based on condition (ii), we can deduce that υ(Tχ, Tω)≥0. Furthermore, according to hypothesis (i), the following inequalities hold.
By taking the supremum of both sides, we obtain:
Using Equation 17, we get:
Hence
If we take for all χ > 0 and since , we have:
That is;
This is equivalent to
where β, γ, δ ≥ 0 with β + γ + 2δλ < 1 and p > 1. Therefore, based on the satisfaction of the assumption in Theorem 2.2, we can conclude that the mapping T possesses a fixed point. This fixed point represents a solution to Equation 1.
3.2 Existence of solution for (FDE) with fractional derivative
In this subsection, we apply Lemma 2.2 to derive an integral solution for Equation 2 and from the given initial value ω0 = 0, as shown below.
Furthermore, we can utilize Theorem 2.2 to establish the existence of a solution for Equation 2.
Define the mapping as:
Theorem 3.2. Consider Equation 2 with fractional derivative. Let be a given mapping and be a continuous function. Assume that the following claims are satisfied:.
i) There exists τ > 0 such that if d(Tω, Tϖ) > 0 and d(ω, ϖ) > 0 for all ω, ϖ ∈ E, then
for all t ∈ [0, T]. Where 𝔇(ω, ϖ) is as given in definition 2.4.
ii) For all t ∈ [0, T], if υ(ω(t), ϖ(t))≥0, then υ(Tω(t), Tϖ(t))≥0.
iii) If the inequality
holds. Then, there exists at least one solution for Equation 2.
Proof
Let ω, ϖ ∈ E, such that υ(ω(t), ϖ(t)) ≥ 0 for all t ∈ [0, T]. By (ii) we have υ(Tω, Tϖ) ≥ 0. Consequently, based on assumption (i), the following inequality exists.
Taking the supremum of both sides, we get:
From Equation 26, we obtain:
Which gives us:
Since , then for all ω > 0. Thus Equation 29 becomes:
Thus
Equivalently written as:
where β, γ, δ ≥ 0 with β + γ + 2δλ < 1 and p > 1. Therefore, by applying Theorem 2.2, we can conclude that T has a fixed point. Therefore, Equation 2 has at least one solution.
4 Illustrative examples
In this section, we provide examples to demonstrate the application and effectiveness of Theorems 3.1 and 3.2. These examples serve to illustrate the theoretical results.
Example 4.1. Consider the following fractional differential equation (FDE) involving the Caputo–Fabrizio fractional derivative:
For u, v ∈ E and t ∈ [0, 1] we have:
where
Moreover we get:
Hence
It remains to show that the condition (iii) of Theorem 3.1 is satisfied:
It follows from Theorem 3.1 that the problem (32) has at least one solution.
Figure 1 shows the plots for the illustrative example containing Caputo–Fabrizio fractional derivatives given in Equation 32 for different values of the fractional orders ν = 0.1, 0.5, 0.7, 0.8, 0.9, respectively. As shown in Figure 1, we can observe from these plots that the curves for different values of ν have the same trend when ν is changed, and the solution is bounded in (0, 1). Therefore, we again conclude that there is a solution for Equation 32.

Figure 1. Plots for the solution of illustrative example (Equation 32).
Example 4.2. Consider the following non-linear initial value problem involving fractional derivative:
Set
Let v, w ∈ E and t ∈ [0, 1]. Then
For all t ∈ [0, 1], we have:
since sin(t) and cos(t) are continuous positive functions ∀t ∈ [0, 1], we have and . Then:
Hence
We check that condition (iii) of Theorem 3.2 is satisfied. We have
Thus, by Theorem 3.2 we conclude that the problem (Equation 33) has at least one solution.
Plots for the numerical example involving Atangana-Baleanu-Caputo fractional derivatives, which given in Equation 33 for varying fractional orders ν = 0.1, 0.2, 0.3, 0.5, 0.7, 0.8, 0.9, are displayed in Figure 2. These plots, as illustrated in Figure 2, demonstrate that the solution is bounded in (0, 1) and that the curves for various values of ν have the same trend as ν is changed. As a result, we draw the conclusion that Equation 33 has a solution.
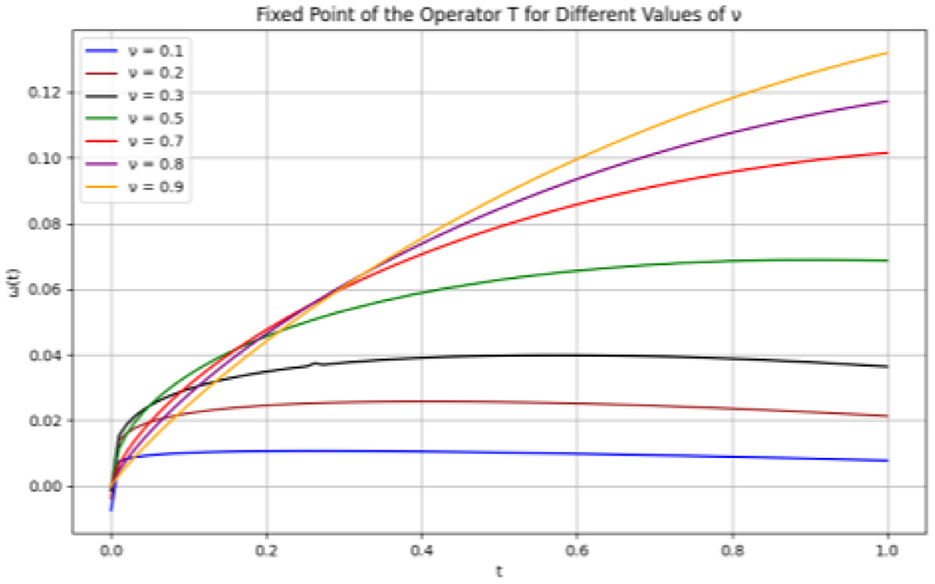
Figure 2. Plots for the solution of (Equation 33).
Conclusions
In this research study, we successfully explored the existence of solutions to non-linear fractional differential equations involving the Atangana–Baleanu–Caputo and Caputo–Fabrizio fractional derivatives admit at least one solution. We have investigated whether the Equations 1, 2 under consideration have a solution through our research. We have developed necessary conditions and inequalities based on Lipschitz assumptions, and our analysis was based on a novel approach using -contraction-type fixed point theorems and b-metric-like spaces. The use of the Atangana–Baleanu–Caputo and Caputo–Fabrizio fractional derivatives represents a significant advancement in the field of fractional calculus, as these derivatives provide better modeling capabilities for various real-world phenomena that exhibit memory and hereditary properties. The fractional derivative incorporates a non-singular kernel, while the Caputo–Fabrizio derivative is defined through an exponential kernel, making them highly suitable for describing complex systems such as viscoelasticity, diffusion processes, and control theory applications. Our application of -contraction theory allowed us to overcome some of the complexities associated with non-linear fractional differential equations. This theory, which generalizes classical contraction mappings, was instrumental in showing the existence of at least one solution. By constructing appropriate conditions and assumptions on the non-linear terms involved, we ensured the applicability of -contraction, proving the existence of fixed points corresponding to the solutions of the differential equations. Furthermore, we have presented relevant examples to show how successful the findings. Future work could extend these findings by investigating uniqueness and stability solutions under various boundary and initial conditions.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
SK: Formal analysis, Investigation, Writing – original draft. AG: Methodology, Project administration, Writing – review & editing. HY: Project administration, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations (Vol. 204). Elsevier (2006).
2. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Different Appl. (2015) 1:73–85. doi: 10.12785/pfda/010201
3. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv preprint arXiv:1602.03408. (2016). doi: 10.2298/TSCI160111018A
4. Agarwal S, Mishra LN. Attributes of residual neural networks for modeling fractional differential equations. Heliyon. (2024) 2024:e38332. doi: 10.1016/j.heliyon.2024.e38332
5. Sharma N, Mishra LN, Mishra VN, Pandey S. Solution of delay differential equation via iteration algorithm. Eur J Pure Appl Math. (2020) 13:1110–30. doi: 10.29020/nybg.ejpam.v13i5.3756
6. Bhat IA, Mishra LN. A comparative study of discretization techniques for augmented Urysohn type nonlinear functional Volterra integral equations and their convergence analysis. Appl Math Comput. (2024) 470:128555. doi: 10.1016/j.amc.2024.128555
7. Bhat IA, Mishra LN, Mishra VN, Tunc C, Tunc O. Precision and efficiency of an interpolation approach to weakly singular integral equations. International J Numer Methods Heat Fluid Flow. (2024) 34:1479–99. doi: 10.1108/HFF-09-2023-0553
8. Bhat IA, Mishra LN, Mishra VN, Tunc, C. Analysis of efficient discretization technique for nonlinear integral equations of Hammerstein type. Int J Numer Methods Heat Fluid Flow. (2024) 2024:459. doi: 10.1108/HFF-06-2024-0459
9. Assia GL, Adem, K. On resonant mixed Caputo fractional differential equations. Bound Val Probl. (2020) 2020:7. doi: 10.1186/s13661-020-01465-7
10. Khaldi R, Guezane-Lakoud A. On generalized nonlinear Euler-Bernoulli Beam type equations. Acta Universitatis Sapientiae Mathematica. (2018) 10:90–100. doi: 10.2478/ausm-2018-0008
11. Guezane-Lakoud A, Rodr-guez-Lpez R. On a fractional boundary value problem in a weighted space. SeMA J. (2018) 75:435–43. doi: 10.1007/s40324-017-0142-0
12. Khaldi R, Guezane-Lakoud A. Upper and lower solutions method for higher order boundary value problems. Progr Fract Differ Appl. (2017) 3:53–7. doi: 10.18576/pfda/030105
13. Guezane-Lakoud A, Khaldi R, Torres DF. On a fractional oscillator equation with natural boundary conditions. arXiv preprint arXiv:1701.08962. (2017). doi: 10.18576/pfda/030302
14. Ravichandran C, Logeswari K, Jarad F. New results on existence in the framework of Atangana-Baleanu derivative for fractional integro-differential equations. Chaos Solitons Fractals. (2019) 125:194–200. doi: 10.1016/j.chaos.2019.05.014
15. Mu J, Nan J, Zhou Y. Existence and stability of square-mean S-asymptotically periodic solutions to a fractional stochastic diffusion equation with fractional Brownian Motion. Complexity. (2020) 2020:1–15. doi: 10.1155/2020/1045760
16. Sitthiwirattham T, Gul R, Shah K, Mahariq I, Soontharanon J, Ansari KJ. Study of implicit-impulsive differential equations involving Caputo-Fabrizio fractional derivative. AIMS Math. (2022) 7:4017–37. doi: 10.3934/math.2022222
17. Abbas S, Benchohra M, Nieto JJ. Caputo-Fabrizio fractional differential equations with instantaneous impulses. AIMS Math. (2021) 6:2932–46. doi: 10.3934/math.2021177
18. Kucche KD, Sutar ST. Analysis of nonlinear fractional differential equations involving Atangana-Baleanu-Caputo derivative. Chaos Solitons Fractals. (2021) 143:110556. doi: 10.1016/j.chaos.2020.110556
19. Dokuyucu MA. A fractional order alcoholism model via Caputo-Fabrizio derivative. Aims Math. (2020) 5:781–97. doi: 10.3934/math.2020053
20. Baleanu D, Jajarmi A, Mohammadi H, Rezapour S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals. (2020) 134:109705. doi: 10.1016/j.chaos.2020.109705
21. Shah K, Alqudah MA, Jarad F, Abdeljawad T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo-Febrizio fractional order derivative. Chaos Solitons Fractals. (2020) 135:109754. doi: 10.1016/j.chaos.2020.109754
22. Bhat IA, Mishra LN, Mishra VN, Abdel-Aty M, Qasymeh M. A comprehensive analysis for weakly singular nonlinear functional Volterra integral equations using discretization techniques. Alexandr Eng J. (2024) 104:564-75. doi: 10.1016/j.aej.2024.08.017
23. Paul SK, Mishra LN, Mishra VN, Baleanu D. Analysis of mixed type nonlinear Volterra-Fredholm integral equations involving the Erdelyi-Kober fractional operator. J King Saud Univ Sci. (2023) 35:102949. doi: 10.1016/j.jksus.2023.102949
24. Kumari S, Alqahtani O, Karapinar E. Some fixed-point theorems in b-dislocated metric space and applications. Symmetry. (2018) 10:691. doi: 10.3390/sym10120691
25. Kumari S, Panthi D. Connecting various types of cyclic contractions and contractive self-mappings with Hardy-Rogers self-mappings. Fixed Point Theor Appl. (2016) 2016:1–19. doi: 10.1186/s13663-016-0498-3
26. Kumari S, Panthi D. Cyclic compatible contraction and related fixed point theorems. Fixed Point Theor Appl. (2016) 2016:1–18. doi: 10.1186/s13663-016-0521-8
27. Kumari S, Panthi D. Cyclic contractions and fixed point theorems on various generating spaces. Fixed Point Theor Appl. (2015) 2015:1–17. doi: 10.1186/s13663-015-0403-5
28. Kumari S, Zoto K, Panthi D. d-Neighborhood system and generalized F-contraction in dislocated metric space. Springerplus. (2015) 4:1–10. doi: 10.1186/s40064-015-1095-3
29. Afshari H, Baleanu D. Applications of some fixed point theorems for fractional differential equations with Mittag-Leffler kernel. Adv Differ Equat. (2020) 2020:1–11. doi: 10.1186/s13662-020-02592-2
30. Kebede SG, Lakoud AG. Analysis of mathematical model involving nonlinear systems of Caputo-Fabrizio fractional differential equation. Bound Val Probl. (2023) 2023:44. doi: 10.1186/s13661-023-01730-5
31. Alghamdi MA, Hussain N, Salimi A. Fixed point and coupled fixed point theorems on b-metric-like spaces. J Inequal. Appl. (2013) 2013:1–25. doi: 10.1186/1029-242X-2013-402
32. Wardowski D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theor Appl. (2012) 2012:1–6. doi: 10.1186/1687-1812-2012-94
33. Kadelburg Z, Radenovic S. Notes on some recent papers concerning F-contractions in b-metric spaces. Construct. Math. Anal. (2018) 1:108–12. doi: 10.33205/cma.468813
34. Hammad HA, De la Sen, M. (2020). Fixed-point results for a generalized almost (s, q)-jaggi F-Contraction-Type on b-metric-like spaces. Mathematics 8:63. doi: 10.3390/math8010063
35. Guran L, Mitrovic ZD, Reddy G, Belhenniche A, Radenovic S. Applications of a fixed point result for solving nonlinear fractional and integral differential equations. Fractal Fractional. (2021) 5:211. doi: 10.3390/fractalfract5040211
36. Losada J, Nieto JJ. Properties of a new fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:87-92. doi: 10.12785/pfda/010202
37. Shaikh A, Tassaddiq A, Nisar KS, Baleanu D. Analysis of differential equations involving Caputo-Fabrizio fractional operator and its applications to reaction-diffusion equations. Adv Differ Equat. (2019) 2019:1–14. doi: 10.1186/s13662-019-2115-3
38. Din A, Khan A, Zeb A, Sidi Ammi MR, Tilioua M, Torres DF. Hybrid method for simulation of a fractional COVID-19 model with real case application. Axioms. (2021) 10:290. doi: 10.3390/axioms10040290
39. Hussain A, Kanwal T, Adeel M, Radenovic S. Best proximity point results in b-metric space and application to nonlinear fractional differential equation. Mathematics. (2018) 6:221. doi: 10.3390/math6110221
40. Moustafa SI. New fixed point results in extended b-metric-like spaces via simulation functions with applications. Afrika Matematika. (2022) 33:80. doi: 10.1007/s13370-022-01017-5
Keywords: F-contraction type, existence of solution, Caputo-Fabrizio derivative, Atangana-Baleanu-Caputo derivative, non-linear fractional derivative
Citation: Kebede SG, Guezane Lakoud A and Yesuf HE (2024) Solution analysis for non-linear fractional differential equations. Front. Appl. Math. Stat. 10:1499179. doi: 10.3389/fams.2024.1499179
Received: 20 September 2024; Accepted: 28 October 2024;
Published: 20 November 2024.
Edited by:
Firdous A. Shah, University of Kashmir, IndiaReviewed by:
Sumati Kumari Panda, GMR Institute of Technology, IndiaLakshmi Narayan Mishra, VIT University, India
Copyright © 2024 Kebede, Guezane Lakoud and Yesuf. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shiferaw Geremew Kebede, Z2VyZW1ld3NoaWZlcmF3MTRAeWFob28uY29t
 Shiferaw Geremew Kebede
Shiferaw Geremew Kebede Assia Guezane Lakoud2
Assia Guezane Lakoud2 Haider Ebrahim Yesuf
Haider Ebrahim Yesuf