- 1Istituto di calcolo e reti ad alte prestazioni (ICAR), National Research Council (CNR), Palermo, Italy
- 2Institute of Physics and Astronomy, Universität Potsdam, Potsdam, Germany
- 3Research Department of Complexity Science, Potsdam Institute for Climate Impact Research (PIK), Leibniz Association, Potsdam, Germany
- 4Dipartimento di Scienze Molecolari e Nanosistemi (DSMN), Università Ca' Foscari di Venezia, Venice, Italy
- 5Department of Telecommunications, VSB - Technical University of Ostrava, Ostrava, Czechia
- 6Institute of Geosciences Potsdam, University of Potsdam, Potsdam, Germany
The onset and progression of a neurological disease can often be explained in terms of brain-network alteration. They can be formalized as the action of an operator representing the disease, the so-called K-operator, acting on the network. The healing process can thus be seen as the inverse of the disease mechanism. However, perfect healing is often impossible to achieve. Here, we formalize the ideal healing in terms of perturbative variation of the possible partial healing. The modeling and analytical strategy is based on techniques from theoretical physics, with the language of matrix operators. In addition, using the language of category theory, we also formalize the progressive abstraction from the reality of diseased patients to the definition of a disease and the comparison between different diseases as a natural transformation between colimits. This theoretical presentation can provide a new, interdisciplinary perspective on neurological investigation and possibly foster new theoretical-experimental developments.
1 Introduction
A system of stations and highways, with signals transmitted throughout agglomerates of stations and communicating with far-away areas: this is a way to visualize the complexity of the brain network regulating the processes inside our minds and brains, from the cortex to the deepest areas (Figure 1). As accidents can occur on highways and traffic can be altered, also the brain network can suffer from anatomic or functional alterations. Nowadays, several neurological pathologies are experimentally investigated in terms of network alteration [1, 2], exploiting concepts and methods from network theory in physics [3, 4]. However, a general mathematical model for the neurological disease, whose specific pathologies can be particular cases, is missing [5]. Recently, a multi-layer network structure of the human brain has been proposed [23] also jointly with modeling a generic neurological disease as an operator acting on it [6]. Let us indicate with the functional brain network of a healthy individual, where stands for Gehirn, German for brain, and with the brain network of a person affected by a disease. The so-called K-operator, from Krankheit, German for disease, is defined as [6]:
Knowing both and , K can be computed through a matrix inversion:
K can be computed via an element-wise product. In this way, its elements will be multiplicative factors that modify the elements of the brain matrix one by one, allowing a direct interpretation of the results [7, 8]. Alternatively, K could be computed via a classical row-by-column product, becoming interpretable through a diagonalization.
A formal analysis of neurological disease features can also help distinguish the neurodegenerative processes occurring in normal aging from the abnormalities occurring in diseases.
Here, we develop the idea of K, focusing on two crucial aspects. First, we develop the formal relationship between a person affected by a disease, which is real, and the concept of disease itself, which is an abstraction. To this aim, we use the language of category theory [9], a branch of mathematics born to model structures and analogies between different areas of mathematics, being inspired by and its generalization power, and its application to different areas of science [10].
Second, we develop the idea of the healing process as the inverse of K-operator [6]. In ideal conditions, with complete reversibility, the matrix depiction of healing is the exact inverse of the disease operator. In real conditions, the healing is often only partial, if possible at all, given the general condition of irreversibility [11]. Here, we start from a “partial healing” of some brain regions, due to medications or surgery, proposing its progressive improvement through perturbative variations in the style of theoretical physics.
The article is organized as follows. In Section 2, we present the methodological approach; then, we formalize the abstraction process from patients to diseases and the comparison between diseases (Section 3.1) and explore the “vice versa” (Section 3.2). Section 4 summarizes open questions and lists possible further research developments.
2 On disease and abstraction: methods
Disease onset and development can be formalized as a transformational process [6]. The definition of a “disease” is an abstraction; the “reality” is given by real patients affected by the disease. The description of a new disease after a collection of particular cases is an inductive process; the diagnosis of a patient's condition is a deductive process, from the abstraction of the disease to the reality of the specific condition. Each patient is different and may present a unique situation and eventual comorbidities; the common features of a group of patients provide hints on the key elements of a disease and its interaction with other diseases. The comparison between illnesses can be formalized as a high-abstraction process. For all these reasons, to navigate the different layers of abstraction, we will recur here to the language of categories, initially developed to formalize the idea of transformations of transformations [9]. Categories are being more and more applied to different branches of science [10].
To start our analysis, let us first roughly schematize the brain activity. We can start from neurons, formalize the activity of neural masses, and then move up toward the overall brain organization. First, one can distinguish between excitatory and inhibitory neurons [12, 13]. The first can only produce excitatory synapses and the second only inhibitory ones. Focusing only on one type of population, for instance, excitatory [6], we can describe the dendritic potential of the i-th neuron as [12]:
where f(xj) is the activation function, and wij is the weight of the coupling with the j-th neuron. We can see neurons as nodes in a network and the synapses between them as their links. Moving up one level along the brain architecture, we can consider an overall population of neurons as a node and the connections/information exchange between populations as their links [6]. The potential of a neural agglomerate is obtained from Equation 3 by summing up all its excitatory neurons [12]:
In this research, we consider the neural masses as big as to make them coincide with the so-called regions of interest (ROIs) into which the human brain can be divided. Thus, the potential of a lobe will be determined by the overall potential of the ROIs that belong to it. Thus, according to Mannone et al. [6], the potential of the l-th lobe is:
where is the weight of the z-th node in the l-th lobe, and El is the potential of the l-th lobe:
We can draw a connection between the data extracted from functional magnetic resonance imaging (fMRI) and the connectivity matrices containing information exchange between pairs of ROIs. Because there are different numbers, dimensions, and distributions of ROIs according to the medical atlas choice (due to the different parcellation of the brain) that highlight different aspects, connectivity matrices can also change. However, the proposed formalism is general enough to not require a specific choice or indication; it can be adapted to specific atlas choices in experimental setups.
A generic element of the connectivity matrix of the l-th lobe can be denoted as (i.e., a weight), indicating the connection between the z-th and z′-th ROI in the l-th lobe. Thus, we indicate the connectivity matrix for the l-th lobe as . We can relate the weights , of nodes z, z′ of lobe l to the link z, z′, whose weight is an element of the connectivity matrix, that is, .
Then, starting from the diagonal block-matrix characterization of the brain areas proposed by Mannone et al. [6], to define the whole connectivity matrix, in this study, we consider not only all the brain areas but also their connections, thus including the non-diagonal blocks. Then, the brain structure can be formalized by the connectivity matrix (i.e., all n lobes) defined according to the following block matrix:
Moreover, making the name of the lobes and inter-lobe areas explicit, the same matrix can be represented as follows:
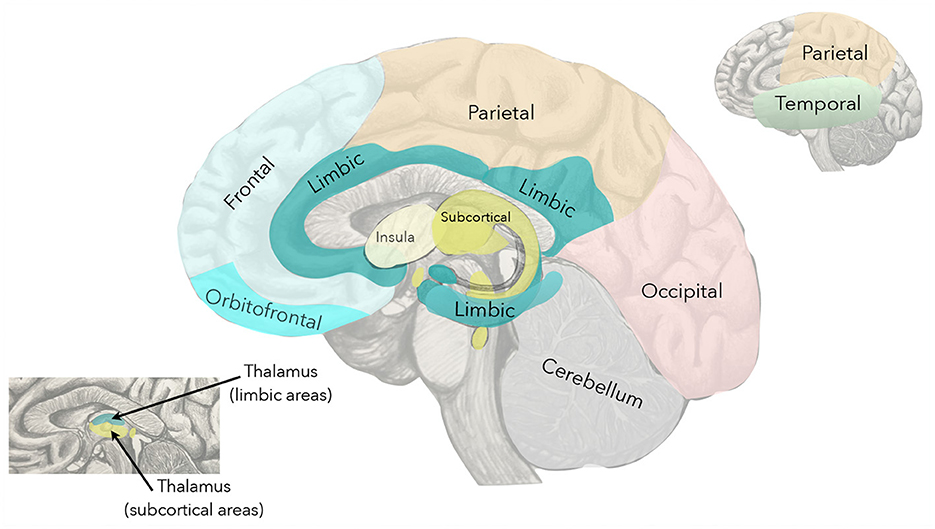
where F indicates the frontal lobe, T the temporal lobe, P the parietal lobe, O the occipital lobe, S the subcortical, L the limbic system, I the insula, and C the cerebellum (see Figure 2). The double letters indicate the inter-lobe exchanges. It is worth noting that the size of the blocks depends upon the number of neuronal agglomerates in each lobe that we identify with the ROIs. The number of ROIs differs for each lobe in brain atlases such as MSDL [14], Oxford-Harvard [15], and AAL3 [16]. A customized choice of atlas would allow one to have the same number of ROIs in each lobe.
With a compact notation based on tensor products, can be written as:
where ⊗ is the tensor product, I is the identity matrix, F stands for the frontal lobe, T for the temporal lobe, and mix indicates the inter-lobe connections.
The K-operator acts on as a tensor Kδ, δ = 1, 2…, with the labels indicating the different diseases.
In Section 3, we will be using the language of category theory [9] to lift up in abstraction our analysis. The advantage of categories is mainly formal, allowing a general view of relationships and structure in a considered phenomenon or problem. The idea of function, which can be thought of as a mapping between points, is generalized as a mapping between points and arrows (morphisms) between them. Thus, a structure can be mapped into another one. The comparison of structures is a powerful conceptual also computational tool [17]. A detailed or tutorial discussion of categories is out of the scope of this article. However, a basic yet complete introduction to the topic is provided by Fong and Spivak [10]. In our study, categories help us formalize the comparisons between patients' features and the process of abstraction from patients to diseases, as well as the inverse process of disease development, that is, healing. We will first provide some basic categorical definitions, using them to shape our model.
Before moving to Section 3, we show here a basic example of categorical thinking. Let us denote as A, B two patients with similar symptoms, which can be related to the same disease α. Let be the brain network of the first patient at the baseline and at the first follow-up. The disease progress can be described as:
The disease progress of patient B will be thus:
And the comparison between the disease progresses will be thus an arrow between and , that is, an arrow between arrows (a natural transformation), here denoted as ζ:
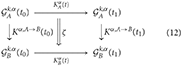
and the arrows Kα, A→B denote the comparison of symptoms between the first and the second patient, at the same time point.
3 Results
3.1 A more abstract view
We can discuss the proposed idea in a more general way, using language and structures from an abstract branch of mathematics, that is, category theory.
A category is constituted by objects (points) and morphisms between them (arrows), satisfying compositionality, associativity, and the existence of the identity [9].
In our brain model, the first layer is constituted by neurons as nodes, and synapses between them as links. However, they do not constitute a category, as there is no proper mathematical composition between synapses. Thus, we move to the second layer of brain organization: the layer of neural agglomerates as nodes, and pathways and signal transmissions/links as arrows between them. We can think of neural agglomerates and their weighted connections as categories. Let us consider the functor, a categorical extension of the concept of function, acting both on objects and morphisms, preserving their structure [9]. We can think of the disease Kδ as a functor mapping neural agglomerates and connections at t into neural agglomerates (and connections) at t+1, changing the weights. Given the underlying structure of graph, and the weight assigned to each link, we recall the structure of Petri nets [18], simple conceptualizations of a neural network, with nested structures. Thus, they are suitable for neural-agglomerate modeling. Moving up along the layers, we reach the overall brain. Let us define Kδ as acting element-wise on each element of the connectivity matrix:
In general, supposing of having fixed δ = 1, the action of the K-operator on a healthy brain gives the diseased brain [6]:
The action of K on an already-diseased brain at the baseline gives the follow-up, that is, provides a segment of the time evolution:
Using a diagrammatic representation, we can schematize the action of the K-operator for a disease δ from a healthy brain to a diseased brain as follows:
Let δ and ϵ label be two different diseases. We can schematize the transition δ to ϵ as a commutative diagram:
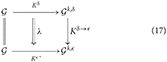
where, on the left, there is a vertical equal sign indicating that the healthy, initial brain is the same, and the double arrow λ is a transformation of transformations, which is called natural transformation in category theory [9]:
This would represent the passage from a matrix Kδ to another one (Kϵ), as a “navigation” inside the K-tensor, and an ideal transformation from a disease to another one. The transformation Kδ → ϵ denotes the changes occurring between the functional brain network of a brain affected by δ to a brain affected by ϵ.
In category theory, the attention is shifted from objects to the transformations between them. In this sense, the focus on K implies a shift from a specific, or a collection of, diseased brains to the mechanism of the disease. The idea itself of disease is an abstraction. Higher levels of abstraction find also an analogous in medical applications; for instance, the arrow Kδ⇒Kϵ represents the comparison between the two diseases δ and ϵ.
Diseased people are real, and diseases are abstractions. The “disease” in a person is the embodiment of the idea of disease. Such an idea can be thought of in terms of a categorical structure, the colimit. A colimit is a “universal object” formalizing the intuition of the most general way to connect elements, generalizing the notion of direct sum or union [9]. We can sketch the categorical structure of the colimit for a single disease, let it be α. Treating the transformations K as points themselves, we can write:
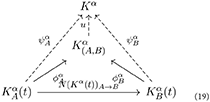
where:
• A and B are two patients affected by α;
• is a natural transformation representing the transition from an instance of the K-operator for the α disease and patient A, to an instance of K for the same disease on patient B;
• is the partial abstraction obtained by considering two or more patients;
• Kα is the “absolute abstraction” defining the disease α: here, it is the colimit;
• the dashed arrow u represents the passage from the first idea of the disease sketched upon multiple cases () and the general idea of the disease (Kα);
• and are part of the inductive process from specific features of disease process in diseased people to the first abstraction of the disease;
• and represent the connection between the disease process in diseased individuals and the disease as an abstraction. For this reason, the corresponding arrows are also dashed, to indicate the movement toward the same final degree of abstraction reached by u. By definition of colimit, there is one and only one transformation u such that:
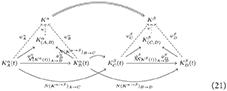
In , we focus on the common brain damage between A and B; thus, we refer to a non-empty intersection. In general, damage for another patient C could present also differences with respect to patient A or another patient D affected by the same disease. The meaning of this step is collecting the commonalities. The meaning of and is the correct diagnosis from the set of displayed damage and symptoms. In fact, moving up through the diagram, we proceed in the path toward abstraction. Overlaps between diseases are possible, and they are often cause of concerns among physicians and patients, and errors in diagnoses. The idea of natural transformations between diseases also includes the presence of virtual “intermediate states” between diseases, which could correspond to existing, yet-to-discover diseases, or situations of co-morbidity. With this refined framework, where each disease is a colimit, comparing diseases becomes a natural transformation between colimits.
Let α and β be again two diseases, and C and D be two patients affected by disease β. The diagram in Equation (19) thus becomes:
3.2 Healing and perturbative approximation
One of the key ideas of category theory is duality of structures, that is, the form of symmetry between some structures and other structures obtained by reversing all arrows. For instance, reversing the arrows of a colimit, we obtain a limit [9]. The conceptual inversion of arrows also plays a fundamental role in medicine. From the point of view of neurological disease represented by the K-operator, reversing the arrows means going from a diseased brain to a healthy brain . Thus, the dual action of the K-operator can be represented by the H-operator, the Healing (German Heilung) process. For a disease δ, the healing process is represented by reversing the arrows with respect to the action of Kδ:
where Hδ = (Kδ)−1. In diagrammatic terms:
Mirroring the previous diagrams, we can go from the specific, particular healing of single patients to the generalized healing process for a specific disease.
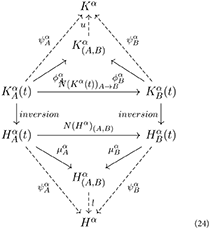
As one can notice similarities between diseases, it is also possible to notice similarities between healing processes. We indicate the process of perfect, ideal healing as the inverse of the K-operator. Fixed a disease δ = 1, relating global to local action, we have:
The action of Hδ can be performed due to a specific medication or set of medications, pharmacological treatments, or surgery. The local action, expressed on the right side in Equation 25, refers to the elements . All these elements are time-dependent.
However, such a healing mechanism, as a perfect inversion of all arrows, is ideal. In general, perfect healing may not be possible due to the irreversibility of some disease progression [11]. If the perfect, ideal healing process is the inverse of the disease operator, real healing is only partial. We argue that perfect healing can be schematized as a sequence of perturbations on partial healing.
Let us characterize with HP the global action (on the whole brain network) of partial healing. The elements of HP are all zero except those corresponding to the ROIs where the “treatment” acts.
As said, HP≠H, the total healing we set here equals K−1. Then, we can approximate the complete healing H via a perturbative approach:
where n stands for the number of approximating terms σ1, …, σn > 0, is the starting therapy, and are all the other existing and future approaches.
Neglecting the terms of higher order, we get:
where we can focus on , the “missing therapy” for a good approximation of the healing. Thus, we obtain:
where, fixed a disease, we consider the restriction of the inverse K concerning specific ROIs. Thus, the missing therapy can be approximated as the difference between the matrix elements of the inverse K-operator, equivalent to the perfect, ideal healing, and the matrix elements of the starting therapy. The consequence of found HP would allow one to find which ROIs need more attention to improve the therapeutic strategy. This may suggest, for instance, a joint use of medications, those belonging to the “existing” therapy for the partial healing (), and other ones chosen, or developed, for their action on the other ROIs indicated by HP. This could lead to tests in vitro and in silico on platforms such as the brains-on-a-chip [19].
4 Discussion and conclusion
The present study explores the potential application of concepts and methods theoretical physics and category theory to neurology. The recent conjecture of a mathematical operator (K) to describe the onset and progression of a general neurological disease in terms of brain-network alterations [6] is the starting point of our analysis. In this article, we developed the initial insights with the connection of patients (real) and disease (abstract) levels, the discussion of the inverse process, and patients' particular healing process (real) and general healing process from a disease (abstract). Finally, we sketched a perturbative approach to relate the perfect and ideal healing (i.e., the inverse of the disease operator) with the possible partial healing (i.e., existing medications or surgery). We used the language of category theory [9] to treat our topics in a formal and general way.
Some first applications of the K-operator concepts dealt with Parkinson's datasets (PPMI) and Alzheimer-Perusini's datasets (ADNI) and were based on the element-wise computation of K-operator [7, 8]. An in-progress investigation is directed to explore a row-by-column computation of K, its diagonalization, and interpretation [21].
To validate the model, the required data can be obtained through a long-term monitoring and regular fMRI examinations, for instance, choosing a number of patients affected by the same disease, and performing fMRI examination with the same machines, for the same time of exposition (duration of the image collection inside the MRI machine), at regular time intervals (e.g., each 6 months for some years). The same approach should be adopted for healthy controls comparable to the diseased patients (considering sex and age range). Such an experimental study could help estimate the time evolution of the functional brain network in healthy controls and, through a crossed comparison with diseased brains over time, estimate the impact of the considered disease, approximating a shape for K. Adding one layer of complexity, the same strategy allows one to compute K for different diseases, highlighting, through the comparison, the disease-specific features of the operator. Specific data can be derived from the DICOM images of fMRI. From fMRI, after a brain parcellation according to specific brain atlases, one can extract time series for each region and compute the connectivity matrices, to be used as (if the brain is healthy) or (if the brain is diseased). Or, as for the diseased brain at different time points. In Figure 3, we show an example of the K-operator for a Parkinson's female patient [20], showing a sparsity correspondence. An analysis of eigenvalues and eigenvector similarities of these matrices is in progress [21] and deserves further investigation. Next research will also focus on EEG and recursive plots. A fine-tuning study of K may also address the comparison between different forms of Alzheimer-Perusini's disease [22].
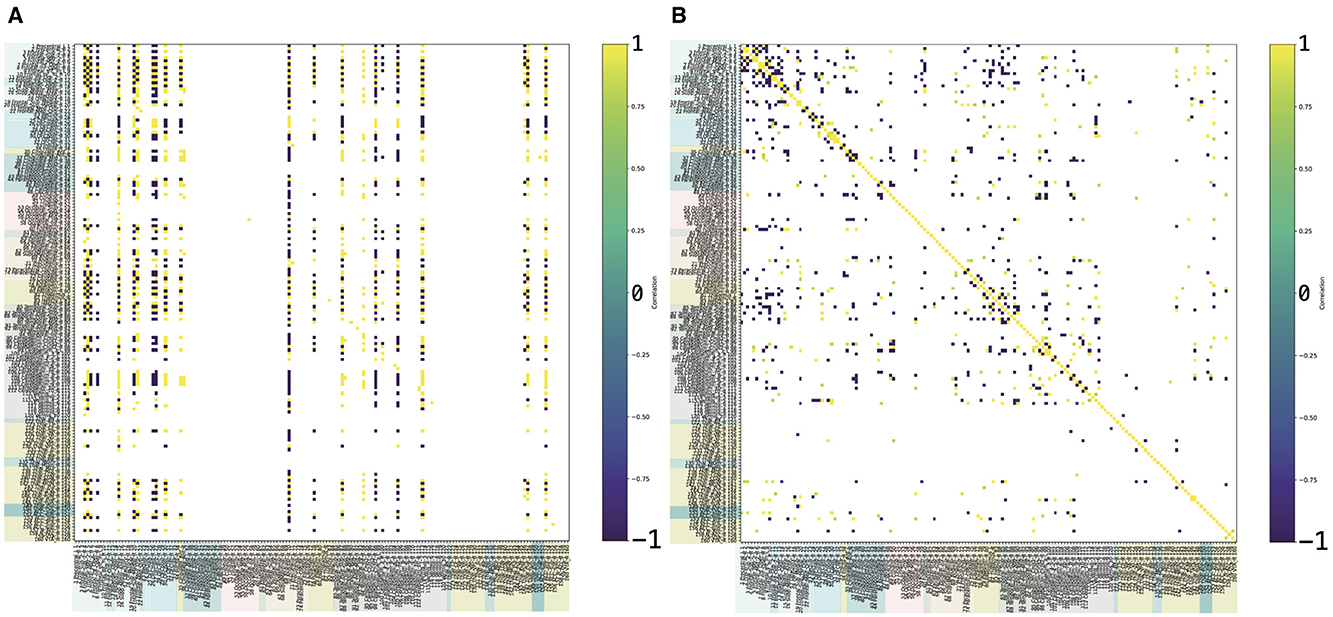
Figure 3. Example of K-operator computed from the connectivity matrices of a Parkinson's disease female patient (atlas AAL3), with row-by-column (left) and element-wise product (right), from Mannone et al. [7]. In (A), the elements above 12 are shown; in (B), above 0.8. The color code is the same of Figure 2.
Moreover, future research will focus on the experimental definition of HP. In particular, a novel research endeavor may aim to investigate the anomalies observed in the substantia nigra and the therapeutic effects of dopamine-based pharmaceutical interventions by approximating the needed action to improve the degree of healing, comparing pathologies with similar underlying mechanisms, such as Parkinson's disease and schizophrenia.
Such a double study, for one side contextualized in the proposed formalism, and for the other side, strictly related to a data-based approach, can help foster new insights for knowledge and concretely help the real, suffering patients.
Abstract thinking can provide insights for scientific development and help guide data comparison in complex networks, not only for brain studies. K-operator can in general describe the accidents occurring in stations and pathways, while the healing operator represents how to resolve them.
Data availability statement
The original contributions presented in the study are included in the article. The analyzed data derived from the Parkinson's Progression Markers Initiative (PPMI) dataset, not available to the public, with the following licenses and restrictions: Investigators seeking access to PPMI data must sign the Data Use Agreement, submit an Online Application and comply with the study Publications Policy. Requests to access these datasets should be directed to PPMI, https://ida.loni.usc.edu/collaboration/access/appLicense.jsp.
Author contributions
MM: Conceptualization, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing. PF: Conceptualization, Supervision, Writing – review & editing. PR: Conceptualization, Funding acquisition, Methodology, Supervision, Writing – review & editing. NM: Conceptualization, Formal analysis, Funding acquisition, Methodology, Supervision, Validation, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research by MM and PR is supported by the Next Generation EU “Age-It—Ageing well in an ageing society” project (PE0000015), National Recovery and Resilience Plan (NRRP)—PE8—Mission 4, C2, Intervention 1.3. The research by PF, leading to a part of the published results, was supported by the European Union within the REFRESH project—Research Excellence For Region Sustainability and High-tech Industries ID No. CZ.10.03.01/00/22 003/0000048 of the European Just Transition Fund.
Acknowledgments
The authors thank the mathematician Giuseppe Metere for his comments on categories.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. van den Heuvel MP, Mandl RC, Stam CJ, Kahn RS, Pol HEH. Aberrant frontal and temporal complex network structure in schizophrenia: a graph theoretical analysis. J Neurosci. (2010) 30:15915–26. doi: 10.1523/JNEUROSCI.2874-10.2010
2. Bartolomei F, Guye M, Wendling F. Abnormal binding and disruption in large scale networks involved in human partial seizures. EPJ Nonl Biomed Phys. (2013) 1:1–16. doi: 10.1140/epjnbp11
3. Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, et al. Networks beyond pairwise interactions: structure and dynamics. Phys Rep. (2020) 874:1–192. doi: 10.1016/j.physrep.2020.05.004
4. Newman MEJ. The structure and function of complex networks. SIAM Rev. (2003) 45:167–256. doi: 10.1137/S003614450342480
5. Seeley WW. Mapping neurodegenerative disease onset and progression. Cold Spring Harb Perspect Biol. (2017) 9:1–18. doi: 10.1101/cshperspect.a023622
6. Mannone M, Fazio P, Marwan N. Modeling a neurological disorder as the result of an operator acting on the brain: a first sketch based on network channel modeling. Chaos. (2024) 34:053133. doi: 10.1063/5.0199988
7. Mannone M, Fazio P, Ribino P, Marwan N. A Brain network operator for modeling disease: a first data-based application for Parkinson's disease. Eur Phys J Special Topics. (2024) (under review).
8. Mannone M, Fazio P, Marwan N, Ribino P. K-operator as a predictor for Alzheimer-Perusini's disease. In: Proceedings of HCist. (2024).
9. Mac Lane S. Categories for the working mathematician. New York: Springer. (1978). doi: 10.1007/978-1-4757-4721-8
10. Fong B, Spivak D. Seven sketches in compositionality: an invitation to applied category theory. arXiv preprint arXiv:1803.05316. (2019).
11. Chen L, Liu R, Liu ZP Li M, Aihara K. Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers. Sci Rep. (2012) 2:342. doi: 10.1038/srep00342
12. beim Graben P, Kurths J, Liebscher T. Neural and cognitive modeling with networks of leaky integrator units. In:beim Graben P, Zhou C, Thiel M, Kurths J, , editors Understanding Complex Systems. Lectures in Supercomputational Neuroscience: Dynamics in Complex Brain Networks. Berlin: Springer (2008). doi: 10.1007/978-3-540-73159-7
13. Dale H. Pharmacology and nerve-endings (Walter Ernest Dixon memorial lecture): (section of therapeutics and pharmacology). Proc R Soc Med. (1934) 28:319–32.
14. Varoquaux G, Gramfort A, Pedregosa F, Michel V, Thirion B. Multisubject dictionary learning to segment an atlas of brain spontaneous activity. In: Information Processing in Medical Imaging: 22nd International Conference, IPMI 2011, Kloster Irsee, Germany, July 3-8, 2011. Berlin Heidelberg: Springer (2011). p. 562–73. doi: 10.1007/978-3-642-22092-0_46
15. Kennedy D, Haselgrove C, Breeze J, Frazier J, Seidman L, Goldstein J. Harvard Oxford cort maxprob thr25 2 mm. (2023). Available at: https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Atlases
16. Rolls ET, Huang CC, Lin CP, Feng J, Joliot M. Automated anatomical labelling atlas. Neuroimage. (2020) 206:116189. doi: 10.1016/j.neuroimage.2019.116189
18. Baez JC, Master J. Open petri nets. Mathem Struct Comput Sci. (2020) 30:314–41. doi: 10.1017/S0960129520000043
19. Amirifar L, Shamloo A, Nasiri R, de Barros NR, Wang ZZ, Unluturk BD, et al. Brain-on-a-chip: Recent advances in design and techniques for microfluidic models of the brain in health and disease. Biomaterials. (2022) 285:121531. doi: 10.1016/j.biomaterials.2022.121531
20. Bergamino M, Keeling EG, Ray NJ, Macerollo A, Silverdale M, Stokes AM. Structural connectivity and brain network analyses in Parkinson's disease: a cross-sectional and longitudinal study. Front Neurol. (2023) 14:1137780. doi: 10.3389/fneur.2023.1137780
21. Fazio S, Ribino P, Gasparini F, Marwan N, Fazio P, Gherardi M, et al. A physics-based view of brain-network alteration in neurological disease. (2024). Submitted.
22. Donato L, Mordà D, Scimone C, Alibrandi S, D'Angelo R, Sidoti A. How many Alzheimer-Perusini's atypical forms do we still have to discover. Biomedicines. (2023) 11:2035. doi: 10.3390/biomedicines11072035
Keywords: complex networks, neurodegenerative diseases, Alzheimer, Parkinson, operator algebra
Citation: Mannone M, Fazio P, Ribino P and Marwan N (2024) On disease and healing: a theoretical sketch. Front. Appl. Math. Stat. 10:1468556. doi: 10.3389/fams.2024.1468556
Received: 22 July 2024; Accepted: 27 August 2024;
Published: 19 September 2024.
Edited by:
Christian Uhl, Ansbach University of Applied Sciences, GermanyReviewed by:
Angelyn Lao, De La Salle University, PhilippinesMarek Lampart, IT4Innovations, VSB-Technical University of Ostrava, Czechia
Copyright © 2024 Mannone, Fazio, Ribino and Marwan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maria Mannone, bWFyaWEubWFubm9uZUBpY2FyLmNuci5pdA==; bWFyaWEubWFubm9uZUB1bmktcG90c2RhbS5kZQ==
 Maria Mannone
Maria Mannone Peppino Fazio
Peppino Fazio Patrizia Ribino
Patrizia Ribino Norbert Marwan
Norbert Marwan