Optimal control and cost-effectiveness analysis for bacterial meningitis disease

In this study, we developed an optimal control deterministic model for the dynamics of bacterial meningitis disease. The objective was to investigate the efficiency and cost-effectiveness of the three controls (prevention, treatment, and screening) in curtailing the spread of bacterial meningitis. To accomplish this, we applied Pontryagin's maximum principle to derive the optimality system. We examined different combination strategies to investigate the effect of the interventions on the spread of bacterial meningitis. We used an incremental cost-effectiveness ratio (ICER) to examine which control technique was the most successful. The simulation results show that combining prevention and screening is the most cost-effective strategy. The objective function and the incremental cost-effectiveness ratio further support this result, indicating that maximum utilization of prevention and screening is required for the entire period.

1 Introduction

Meningitis is an infection of the membranes surrounding the brain and spinal cord. It can be caused by viruses, bacteria, parasites, protozoa, or fungi. Bacterial meningitis is particularly serious if not diagnosed and treated early [1, 2]. Neisseria meningitidis (meningococcal meningitis), Streptococcus pneumoniae (pneumococcal meningitis), Haemophilus influenzae (haemophilus meningitis), Group B Streptococcu, Listeria monocytogenes, Escherichia coli, and Myobacterium tuberculosis (Tuberculous meningitis) are the principal pathogens that can cause bacterial meningitis. It transmits from one person to another through coughing, sneezing, or close contact with an individual carrying the bacterium [3]. Even though bacterial meningitis is widespread worldwide, the majority of cases occur in sub-Saharan Africa. In this region, known as the meningitis belt, 1.2 million people contract the disease annually, 135,000 of which result in death. In wealthy nations, the case death rate can range from 3 to 10%. However, it can reach 20% in countries located in the African meningitis belt, and up to 20% of survivors develop neurological sequelae [4, 5].

Mathematical models are essential tools for comprehending the dynamics of disease spread and deciding on intervention measures for disease control. In addition, they can be used to predict how diseases will affect populations, explain key aspects of the disease transmission cycle, and assess the severity and potential scope of an epidemic [6]. Several mathematical models have been investigated to study the dynamics of bacterial meningitis using different control strategies. In light of this, a non-linear SCIRS mathematical model for transmission of bacterial meningitis, incorporating vaccine and therapy control, was studied by Asamoah et al. [7]. The study's simulations revealed that the most effective approach for controlling bacterial meningitis infection was to combine vaccination and therapy. Workineh and Kassa [8] formulated an optimal control model for the spread of bacterial meningitis, taking into account behavioral changes in society and information-dependent vaccination to study the interactions of bacterial meningitis spread and the cost-effectiveness of control measures. The model employs three time-dependent controls: education, vaccination, and treatment. The authors found that combining education and vaccination is the most cost-effective strategy. Agusto and Leite [9] used optimal control to study a mathematical model of bacterial meningitis outbreaks in Nigeria, with personal protection measures (such as using facial masks and vaccination) as control strategies. Their simulation results showed that combining both control measures is the most cost-saving. The research by Asamoah et al. [10] examined a deterministic mathematical model of bacterial meningitis that included vaccination as a control measure. According to their simulation results, focusing on vaccination or supplying hospital beds was less effective than delivering successful antibiotics for treatment by effectively providing hospital beds and a vaccine to treat bacterial meningitis in an endemic setting. Yano et al. [11] formulated and analyzed an optimal control analysis of meningococcal meningitis with a variable population. Their simulation analysis demonstrated that the most effective control strategy for eliminating meningitis is to combine prevention and treatment efforts. Other researchers, such as Yusuf [12], Veronica et al. [13], Afolabi et al. [14], Blyuss [15], Crankson [16], Elmojtaba and Adam [17], Musa et al. [18], and Koutangni et al. [19], have also studied the dynamics of bacterial meningitis. Belay et al. [20] formulated and analyzed a mathematical model to study the transmission dynamics of bacterial meningitis, including a drug-resistant class. They provided a comprehensive stability analysis of the steady states of their model, both qualitatively and quantitatively. In addition, they demonstrated the effects of model parameters on disease dynamics and conducted numerical experiments to validate their theoretical findings. This study did not consider cost-effectiveness analysis and optimal control theory. Therefore, in this study, we are interested in studying an optimal control model with a cost-effectiveness analysis of bacterial meningitis disease, proposed by Belay et al. [20]. The study begins by formulating a non-autonomous system for the system formulated by Belay et al. [20]. In this study, the proposed time-dependent controls are prevention (wearing a face mask), denoted by u₁(t); treatment applied to the infected individuals, denoted by u₂(t); and screening the carriers through test diagnosis, denoted by u₃(t).

This study is arranged as follows: In Section 2, the formulation and description of the bacterial meningitis model with time-dependent control measures are presented. Section 3 contains a numerical simulation of the optimal control problem with various control strategies and incremental cost-effectiveness. We generalized in Section 4 with conclusion.

2 Model formulation

The bacterial meningitis epidemic model formulated by Belay et al. [20] included a drug-resistant class and was proposed and analyzed without control measures. The total population, N(t), is divided into six categories: individuals susceptible to bacteria meningitis S(t), carrier C(t), infected I(t), vaccinated V(t), drug resistance D_r(t), and recovered R(t) individuals. Thus, the total population is defined as follows:

$\begin{array}{ll}N(t)=S(t)+C(t)+V(t)+I(t)+D_r(t)+R(t).& (2.1)\end{array}$

The model assumes that a portion of the population was vaccinated at a rate of κΠ before the disease outbreak, leaving the remaining (1−κ)Π individuals susceptible. In this study, Π represents the recruitment rate, and κ is the proportion of those vaccinated. The susceptible population is exposed to infection by carriers, infected individuals, or those with drug resistance, with the force of infection denoted by λ = β(q₁C + q₂I + q₃D_r). In this equation, 0 < q₁ < 1, 0 < q₃ < 1, and 0 < q₂ ≤ 1 are the modification parameters for C, D_r, and I, respectively, and β is the effective transmission probability per contact. Infected individuals can recover at a per capita rate of η, with a proportion α moving to the recovered class through proper treatment, while the remaining (1−α) join the drug-resistant class. Since the vaccine does not confer complete immunity, vaccinated individuals can still become infected at a reduced rate compared to unvaccinated individuals, with a force of infection ελ, where ε represents vaccine inefficacy and 0 < ε < 1. The rates of recovery for carrier and drug-resistant individuals are represented by ω and θ, respectively. The parameters μ and σ represent the natural and disease mortality rates, respectively. Furthermore, we denote the vaccine waning and uptake rates by γ₁ and γ₂, respectively.

The following system of non-linear differential Equations 2.2 models the transmission dynamics of bacterial meningitis disease without control, as presented by Belay et al. [20].

$\begin{array}{ll}\{\begin{array}{l}\frac{dS}{dt}=\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V-(\lambda +\mu +{\gamma }_2)S\\ \frac{dV}{dt}=\text{Π}\kappa +{\gamma }_{2}S-(\mu +\epsilon \lambda +{\gamma }_1)V\\ \frac{dC}{dt}=\lambda S+\epsilon \lambda V-(\delta +\omega +\mu )C\\ \frac{dI}{dt}=\delta C-(\eta +\sigma +\mu )I\\ \frac{d{D}_r}{dt}=(1-\alpha )\eta I-(\theta +\mu )D_r\\ \frac{dR}{dt}=\omega C+\alpha \eta I+\theta D_r-(\vartheta +\mu )R\end{array}& (2.2)\end{array}$

with the initial conditions,

S(0) = S₀ ≥ 0 , C(0) = C₀ ≥ 0 , I(0) = I₀ ≥ 0 , V(0) = V₀ ≥ 0 , D_r(0) = D_{r, 0} ≥ 0 , and R(0) = R₀ ≥ 0.

Theorem 2.1. ${\text{Ω}}_m(0)=(S(0),V(0),C(0),I(0),D_r(0),R(0))\in R_{+}^6$ be the initial conditions for the Model 2.2, then, the set of solutions {S(t), V(t), C(t), I(t), D_r(t), R(t)} of the model Equation 2.2 is non-negative for all t > 0.

Proof: To prove this, let us define, t₁ = sup{t > 0:S(t₀) > 0, V(t₀) > 0, C(t₀) > 0, I(t₀) > 0, D_r(t₀) > 0, R(t₀) > 0, ∀t₀ in [0, t]}. Since, S₀ > 0, V₀ > 0, C₀ > 0, I₀ > 0, D_r0 > 0 and R₀ > 0, consequently, t₁ > 0. If t₁ < ∞, then necessarily one of the state variables is equal to zero at t₁. By using the variation of the constant formula to the first equation of Model 2.2 at t₁ given by

$\begin{array}{ll}\frac{dS}{dt}+(\lambda (t)+\mu +{\gamma }_2)S& =\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V,\end{array}$

which can be rewritten as,

$\begin{array}{l}\frac{d}{dt}\left[S(t)e^{(\mu +{\gamma }_2)t+{\displaystyle {\int }_0^t}\lambda (m)dm}\right]=\\ (\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V)e^{(\mu +{\gamma }_2)t+{\displaystyle {\int }_0^t}\lambda (m)dm}.\end{array}$

hence,

$\begin{array}{l}S(t_1)e^{(\mu +{\gamma }_2)t_1+{\displaystyle {\int }_0^{t_1}}\lambda (m)dm}-S(0)=\\ {\displaystyle {\int }_0^{t_1}}(\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V)\left[e^{(\mu +{\gamma }_2)z+{\displaystyle {\int }_0^z}\lambda (m)dm}\right]dz.\end{array}$

Solving for S(t₁), yields,

$\begin{array}{l}S(t_1)=S(0)e^{(-\mu -{\gamma }_2)t_1-{\displaystyle {\int }_0^{t_1}}\lambda (m)dm}+\\ \left[e^{(-\mu -{\gamma }_2)t_1-{\displaystyle {\int }_0^{t_1}}\lambda (m)dm}\right]\times \\ {\displaystyle {\int }_0^{t_1}}(\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V)\left[e^{(\mu +{\gamma }_2)z+{\displaystyle {\int }_0^z}\lambda (m)dm}\right]dz>0,\end{array}$

Taking the second equation from 2.2,

$\begin{array}{ll}\frac{dV}{dt}+({\gamma }_1+\epsilon \lambda +\mu )V& =\text{Π}\kappa +{\gamma }_{2}S,\end{array}$

then rewrite it as

$\begin{array}{l}\frac{d}{dt}\left[V(t)e^{(\mu +{\gamma }_1)t+{\displaystyle {\int }_0^t}\epsilon \lambda (m)dm}\right]=\\ (\text{Π}\kappa +{\gamma }_{2}S(t))e^{(\mu +{\gamma }_1)t+{\displaystyle {\int }_0^t}\epsilon \lambda (m)dm}.\end{array}$

Thus,

$\begin{array}{l}V(t_1)e^{(\mu +{\gamma }_1)t_1+{\displaystyle {\int }_0^{t_1}}\epsilon \lambda (m)dm}-V(0)=\\ {\displaystyle {\int }_0^{t_1}}(\text{Π}\kappa +{\gamma }_{2}S(z))\left[e^{(\mu +{\gamma }_1)z+{\displaystyle {\int }_0^z}\epsilon \lambda (m)dm}\right]dz.\end{array}$

Therefore,

$\begin{array}{l}V(t_1)=V(0)e^{(-\mu -{\gamma }_1)t_1-{\displaystyle {\int }_0^{t_1}}\epsilon \lambda (m)dm}+\\ \hspace{1em}\hspace{1em}\left[e^{(-\mu -{\gamma }_1)t_1-{\displaystyle {\int }_0^{t_1}}\epsilon \lambda (m)dm}\right]\times \\ \hspace{1em}\hspace{1em}{\displaystyle {\int }_0^{t_1}}(\text{Π}\kappa +{\gamma }_{2}S(z))\left[e^{(\mu +{\gamma }_1)z+{\displaystyle {\int }_0^z}\epsilon \lambda (m)dm}\right]dz>0.\end{array}$

Take the third equation from Model 2.2

$\begin{array}{l}\frac{dC}{dt}=\lambda S+\epsilon \lambda V-(\delta +\omega +\mu )C,\\ \frac{dC}{dt}\ge -(\mu +\delta +\omega )C,\end{array}$

using separation of variable approach

$\begin{array}{c}\frac{dC}{C}\ge -(\mu +\delta +\omega )dt,\\ ln\mid C\mid \ge -(\mu +\delta +\omega )t+m_3,\\ C\ge A_3{e}^{-(\mu +\delta +\omega )t},\end{array}$

then, applying the initial condition to obtained the value A₃,

$\begin{array}{l}C\ge C(0)e^{-(\mu +\delta +\omega )t}>0.\end{array}$

Take the fourth equation from Model 2.2,

$\begin{array}{l}\frac{dI}{dt}=\delta C-(\eta +\sigma +\mu )I,\\ \frac{dI}{dt}\ge -(\eta +\sigma +\mu )I,\end{array}$

by the help of separation of variable method

$\begin{array}{c}\frac{dI}{I}\ge -(\eta +\sigma +\mu )dt,\\ ln\mid I\mid \ge -(\eta +\sigma +\mu )t+m_4,\\ I\ge A_4{e}^{(-(\eta +\sigma +\mu )t)},\end{array}$

applying the initial condition to find the value of A₄,

$\begin{array}{l}I\ge I(0)e^{-(\eta +\sigma +\mu )t}>0.\end{array}$

Using the fifth equation of the System 2.2

$\begin{array}{l}\frac{d{D}_r}{dt}=(1-\alpha )\eta I-(\theta +\mu )D_r,\\ \frac{d{D}_r}{dt}\ge -(\theta +\mu )D_r,\end{array}$

by the help of separation of variable,

$\begin{array}{c}\frac{d{D}_r}{D_r}\ge -(\theta +\mu )dt,\\ ln\mid D_r\mid \ge -(\theta +\mu )t+m_5,\\ D_r\ge A_5{e}^{(-(\theta +\mu )t},\end{array}$

apply the initial condition to obtain A₅

$\begin{array}{l}{D}_r\ge D_r(0)e^{-(\theta +\mu )t}>0.\end{array}$

Using the last equation of Model 2.2

$\begin{array}{l}\frac{dR}{dt}=\omega C+\alpha \eta I+\theta D_r-(\vartheta +\mu )R,\\ \frac{dR}{dt}\ge -(\vartheta +\mu )R,\end{array}$

using separation of variable,

$\begin{array}{c}\frac{dR}{R}\ge -(\vartheta +\mu )dt,\\ ln\mid R\mid -(\vartheta +\mu )t+m_6,\\ R\ge A_6{e}^{-(\vartheta +\mu )t},\end{array}$

apply the initial condition which gives,

$\begin{array}{l}R\ge R(0)e^{-(\vartheta +\mu )t}>0.\end{array}$

Therefore, from the above verifications, all solutions of the state variables are positive for all non-negative initial conditions. Thus, Model 2.2 is epidemiologically and mathematically well-posed.

Controlling infectious disease epidemics is a formidable problem for health policymakers. Adapting the proper control measures to eliminate or reduce infection within a society is not easy. The optimal control analysis provides insights into selecting an efficient approach for reducing the disease's transmission. In this study, three time-dependent controls on Model 2.2 are incorporated based on the results obtained from the sensitivity analysis and numerical results studied by Belay et al. [20]. The first control, u₁(t), stands for an appropriate personal preventive measure (wearing a face mask, avoiding close contact with people who are sick, and good hand washing), which protects susceptible and vaccinated individuals from contacting the disease by reducing the rates β and modification parameters q₁, q₂, and q₃. A fraction of the susceptible and vaccinated populations are becoming infectious at a rate of (1−u₁)λ, while the rest remain susceptible and vaccinated. The second measure, u₂(t), represents treatment to infected individuals to reduce their number. A fraction of infected individuals who are not taking the treatment according to prescriptions properly are joining the drug resistance class at a rate of (1−α)(1−u₂)η and the remaining going to the recovered class. The third control measure, u₃(t), denotes screening applied to carriers individuals to detect bacterial meningitis disease in populations who do not have symptoms of the disease. The control model of System 2.2, by the incorporation of the above three control measures, is developed as follows:

$\begin{array}{ll}\{\begin{array}{l} \frac{dS}{dt}=\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V-\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)S\\ \hspace{1em}-(\mu +{\gamma }_2)S\\ \frac{dV}{dt}=\text{Π}\kappa +{\gamma }_{2}S-\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)V\\ \hspace{1em}-(\mu +{\gamma }_1)V\\ \frac{dC}{dt}=\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)S\\ \hspace{1em}+\epsilon \beta (1-u_1)(q_{1}C\\ \hspace{1em}+q_{2}I+q_3{D}_r)V-(u_3+\delta )C-(\omega +\mu )C\\ \frac{dI}{dt}=(\delta +u_3)C-(\eta +u_2)I-(\sigma +\mu )I\\ \frac{d{D}_r}{dt}=(1-\alpha )(1-u_2)\eta I-(\theta +\mu )D_r\\ \frac{dR}{dt}=\omega C+(u_2+\alpha \eta )I+\theta D_r-(\vartheta +\mu )R\end{array}& (2.3)\end{array}$

The aim is to minimize the number of infected individuals and the cost of control within the allocated period. To achieve this, the objective functional (2.4) is proposed:

$\begin{array}{l}J={\displaystyle \underset{U}{\text{Min}}}{\displaystyle \underset{0}{\overset{t_f}{\int }}}[k_{1}C+k_{2}I+k_3{D}_r+\frac{1}{2}(w_1{u}_1^2(t)+w_2{u}_2^2(t)\\ \hspace{1em}+w_3{u}_3^2(t))]dt& (2.4)\end{array}$

where k₁, k₂, k₃, w₁, w₂, and w₃ are positive constants. The expressions $\frac{1}{2}{w}_1{u}_1^2(t),\frac{1}{2}{w}_2{u}_2^2(t)$, and $\frac{1}{2}{w}_3{u}_3^2(t)$ represent costs which are associated with the controls u₁(t), u₂(t), and u₃(t), respectively. Based on the presumption that the cost follows a non-linear form Alemneh et al. [21], we apply a non-linear cost to the controls. The aim is to minimize the number of carriers, infectives, drug resistance, and overall costs. Thus, we seek to find an optimal triple controls $(u_1^{*},u_2^{*},u_3^{*})$ such that: $J(u_1^{*},u_2^{*},u_3^{*})=$ minJ(u₁(t), u₂(t), u₃(t)) : u_i(t) ∈ U, where U = {(u₁(t), u₂(t), u₃(t)) such that u_i(t) is Lebesgue measurable function on 0 ≤ u_i(t) ≤ 1 for 0 ≤ t ≤ t_f, i = 1, 2, 3}.

2.1 Existence of an optimal control

Theorem 2.2. Given J(u) subject to System 2.3 with (S₀, V₀, C₀, I₀, D_r0, R₀) ≥ (0, 0, 0, 0, 0, 0), then there exists an optimal control $(u_1^{*},u_2^{*},u_3^{*})$ and corresponding state variables $(S^{*},V^{*},C^{*},I^{*},D_r^{*},R^{*})$ that minimizes J(u) over U that means

$\begin{array}{l}J(u_1^{*},u_2^{*},u_3^{*})=min\left\{J(u_1,u_2,u_3)/(u_1,u_2,u_3)\in U\right\}\end{array}$

Proof: The proof relies on the following assumptions outlined by Fleming and Rishel [22]:

1. The set of controls and their corresponding state variables are not empty.

2. The measurable control set is convex and closed.

3. Each right-hand side of the state system is continuous, bounded above by a sum of the bounded control and the state, and can be written as a linear function of u with coefficients depending on time and the state.

4. The integrand f(x, u) of the objective functional is convex on U.

5. There exist constants d₁, d₂ > 0, and β^* > 1 such that the integrand of the objective functional satisfies

$\begin{array}{l}f\ge d_1{(|u_1{|}^2+|u_2{|}^2+|u_3{|}^2)}^{\frac{{\beta }^{*}}{2}}-d_2.\end{array}$

Proof.

1. U is a non-empty set of measurable functions on 0 ≤ t_f with values in real numbers R. System 2.3 has bounded coefficients, and hence, any solutions are bounded on [0, t_f]. So, the corresponding solutions for the System 2.3 exist [23].

2. It is enough to write U = U₁ × U₂ × U₃. Therefore, U = U₁ × U₂ × U₃ is bounded and convex ∀t ∈ [0, t_f].

3. By definition, each right-hand side of System 2.3 is continuous. The interval [0, t_f] bounds all variables S, V, C, I, R, D_r, R, and U. To demonstrate the bounded nature, we use the method of Burden et al. [24]. To this end, we use the fact that the super solutions of System Equation 2.3 given by System Equation 2.5 are bounded within a finite time interval.

$\begin{array}{l}\frac{dŜ}{dt}=\text{Π}+\vartheta \widehat{R}+{\gamma }_1\widehat{V}\\ \frac{d\widehat{V}}{dt}=\pi \kappa +{\gamma }_2Ŝ\\ \frac{dĈ}{dt}=\beta (q_1+q_2+q_3)Ŝ+\epsilon \beta (q_1+q_2+q_3)\widehat{V}\\ \frac{dÎ}{dt}=(\delta +u_3)Ĉ\\ \frac{d\widehat{D_r}}{dt}=(\eta +\alpha u_2\eta )Î\\ \frac{d\widehat{R}}{dt}=\omega Ĉ+(u_2+\alpha \eta )Î+\theta \widehat{D_r}& (2.5)\end{array}$

System 2.5 can be described as

$\begin{array}{l}x=\left[\begin{array}{c}\frac{dS}{dt}\\ \frac{dV}{dt}\\ \frac{dC}{dt}\\ \frac{dI}{dt}\\ \frac{d{D}_r}{dt}\\ \frac{dR}{dt}\end{array}\right]\\ =\left[\begin{array}{cccccc}0& {\gamma }_1& 0& 0& 0& \vartheta \\ {\gamma }_2& 0& 0& 0& 0& 0\\ \beta (q_1+q_2+q_3)& \epsilon \beta (q_1+q_2+q_3)& 0& 0& 0& 0\\ 0& 0& \delta +u_3& 0& 0& 0\\ 0& 0& \eta +\alpha u_2\eta & 0& 0& 0\\ 0& 0& \omega & u_2+\alpha \eta & \theta & 0\end{array}\right]\\ \left[\begin{array}{c}Ŝ\\ \widehat{V}\\ Ĉ\\ Î\\ \widehat{D_r}\\ \widehat{R}\end{array}\right]+\left[\begin{array}{c}\text{Π}\\ \text{Π}\kappa \\ 0\\ 0\\ 0\\ 0\end{array}\right].\end{array}$

The system is linear in finite time with bounded coefficients, and therefore, the super solutions $Ŝ,\widehat{V},Ĉ,Î,\widehat{D_r}$ and $\widehat{R}$ are uniformly bounded. Since the solution to each state equation is bounded, we see that,

$\begin{array}{l}\left|f(t,x,u)\right|\le \\ |\left[\begin{array}{cccccc}0& {\gamma }_1& 0& 0& 0& \vartheta \\ {\gamma }_2& 0& 0& 0& 0& 0\\ \beta (q_1+q_2+q_3)& \epsilon \beta (q_1+q_2+q_3)& 0& 0& 0& 0\\ 0& 0& \delta +u_3& 0& 0& 0\\ 0& 0& \eta +\alpha u_2\eta & 0& 0& 0\\ 0& 0& \omega & u_2+\alpha \eta & \theta & 0\end{array}\right]\\ \left[\begin{array}{c}Ŝ\\ \widehat{V}\\ Ĉ\\ Î\\ \widehat{D_r}\\ \widehat{R}\end{array}\right]|+|I\left[\begin{array}{c}0\\ 0\\ 0\\ u_3\\ 0\\ 0\end{array}\right]+\left|I\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ \alpha \eta u_2\\ u_2\end{array}\right]\right|\\ +\left|\left[\begin{array}{c}\text{Π}\\ \text{Π}\kappa \\ 0\\ 0\\ 0\\ 0\end{array}\right]\right|\le M_1\left|x\right|+I(\left|u_3\right|+M_2\left|u_2\right|)+M_3\end{array}$

where M₁, M₂, and M₃ are depend on the coefficients of the system. Thus, the assumption holds.

4. The integrand f(x, u) of the goal function is given by

$\begin{array}{l}f(x,u)=k_{1}C+k_{2}I+k_3{D}_r+\frac{1}{2}(w_1{u}_1^2+w_2{u}_2^2+w_3{u}_3^2)\end{array}$

Let t ∈ [0, 1], θ = (θ₁, θ₂, θ₃) and p = (p₁, p₂, p₃) ∈ U, and tθ+(1−t)p =(tθ₁+(1−t)p₁, tθ₂+(1−t)p₂, tθ₃+(1−t)p₃).

Then, we have

$\begin{array}{l}f(x,t\theta +(1-t)p)-(tf(x,\theta )+(1-t)f(x,p))\\ =\frac{w_1}{2}(t^2{\theta }_1^2+2t(1-t){\theta }_1{p}_1+{(1-t)}^2{p}_1^2)\\ +\frac{w_2}{2}(t^2{\theta }_2^2+2t(1-t){\theta }_2{p}_2+{(1-t)}^2{p}_2^2)\\ +\frac{w_3}{2}(t^2{\theta }_3^2+2t(1-t){\theta }_3{p}_3+{(1-t)}^2{p}_3^2)\\ -t(\frac{w_1}{2}{\theta }_1^2+\frac{w_2}{2}{\theta }_2^2+\frac{w_3}{2}{\theta }_3^2)\\ -(1-t)(\frac{w_1}{2}{p}_1^2+\frac{w_2}{2}{p}_2^2+\frac{w_3}{2}{p}_3^2)\\ =(t^2-t)(\frac{w_1}{2}{(p_1-{\theta }_1)}^2+\frac{w_2}{2}{(p_2-{\theta }_2)}^2\\ +\frac{w_3}{2}{(p_3-{\theta }_3)}^2)\\ =\frac{(t^2-t)}{2}{\displaystyle \sum _{i=1}^3}{w}_i{(p_i-{\theta }_i)}^2\le 0.\end{array}$

Hence, f(x, tθ + (1−t)p) ≤ tf(x, θ) + (1−t)f(x, p). Thus, this supposition is validated.

5. There exist constants d₁ and d₂ > 0 and β^* > 1 so that the integrand f(x, u) of the goal function

$\begin{array}{l}f(x,u)=k_{1}C+k_{2}I+k_3{D}_r+\frac{1}{2}(w_1{u}_1^2+w_2{u}_2^2+w_3{u}_3^2)\\ \hspace{1em}\hspace{1em}\ge \frac{d_1}{2}(u_1^2+u_2^2+u_3^2)-d_2.\end{array}$

where d₁ = min{w₁, w₂, w₃}; ${\beta }^{*}=2,d_2>0$. Thus, this supposition is validated. Therefore, the optimal control u exists.

2.2 The Hamiltonian and optimality system

To derive the essential conditions for optimizing the objective functional, we applied Pontryagin's [25]. Hence, using this principle, System 2.3 and the objective functional Equation 2.4 are transformed into a pointwise Hamiltonian (H), regarding to u₁, u₂, and u₃. Thus,

$\begin{array}{l}H(S,V,C,I,D_r,R)=k_{1}C+k_{2}I+k_3{D}_r\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}(w_1{u}_1^2+w_2{u}_2^2+w_3{u}_3^2)+{\lambda }_1\frac{dS}{dt}+{\lambda }_2\frac{dV}{dt}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\lambda }_3\frac{dC}{dt}+{\lambda }_4\frac{dI}{dt}+{\lambda }_5\frac{d{D}_r}{dt}+{\lambda }_6\frac{dR}{dt}.\end{array}$

where, λ_i, i = 1, 2, 3, 4, 5, and 6 are the adjoint variables associated with S, V, C, I, D_r, and R and to be determined.

Theorem 2.3. For a given optimal controls $(u_1,u_2,u_3)=(u_1^{*},u_2^{*},u_3^{*})$ and corresponding state variables of Model 2.3 that minimize J over U, there are adjoint variables λ₁...λ₆ such that:

$\begin{array}{ll}\{\begin{array}{l}\frac{d{\lambda }_1}{dt}=(\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)+{\gamma }_2+\mu ){\lambda }_1-{\gamma }_2{\lambda }_2\\ \hspace{1em}-\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_2}{dt}=-{\gamma }_1{\lambda }_1+(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)+\mu +{\gamma }_1){\lambda }_2\\ \hspace{1em}-(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_3}{dt}=\beta (1-u_1)q_{1}S{\lambda }_1+\epsilon \beta (1-u_1)q_{1}V{\lambda }_2\\ \hspace{1em}-\beta q_1(1-u_1)(S+\epsilon V){\lambda }_3+(u_3+\delta +\omega +\mu ){\lambda }_3\\ \hspace{1em}-(\delta +u_3){\lambda }_4-\omega {\lambda }_6-k_1\\ \frac{d{\lambda }_4}{dt}=\beta q_2(1-u_1)S{\lambda }_1+\epsilon \beta (1-u_1)q_{2}V{\lambda }_2\\ \hspace{1em}-\beta q_2(1-u_1)(S+\epsilon V){\lambda }_3+(\eta +u_2+\sigma +\mu ){\lambda }_4\\ \hspace{1em}-(1-\alpha )(1-u_2)\eta {\lambda }_5-(u_2+\alpha \eta ){\lambda }_6-k_2\\ \frac{d{\lambda }_5}{dt}=\beta (1-u_1)q_{3}S{\lambda }_1+\epsilon \beta (1-u_1)q_{3}V{\lambda }_2\\ \hspace{1em}-\beta q_3(1-u_1)(S+\epsilon V){\lambda }_3+(\theta +\mu ){\lambda }_5-\theta {\lambda }_6-k_3\\ \frac{d{\lambda }_6}{dt}=-\vartheta {\lambda }_1+(\vartheta +\mu ){\lambda }_6\end{array}& (2.6)\end{array}$

with transversality conditions λ_i(t_f) = 0, i = 1, ..., 6. In addition, we acquire the control set $(u_1^{*},u_2^{*},u_3^{*})$ satisfying the optimality conditions by

$\begin{array}{l}{u}_1^{*}(t)=\text{max}\left\{0,min(1,{\psi }_1)\right\}\\ u_2^{*}(t)=\text{max}\left\{0,min(1,{\psi }_2)\right\}\\ u_3^{*}(t)=\text{max}\left\{0,min(1,{\psi }_3)\right\}\end{array}$

where

$\begin{array}{l}{\psi }_1=\frac{\beta (q_{1}C+q_{2}I+q_3{D}_r)((S+\epsilon V){\lambda }_3-{\lambda }_{1}S-\epsilon V{\lambda }_2)}{w_1}\\ {\psi }_2=\frac{I{\lambda }_4+(1-\alpha )\eta I{\lambda }_5-I{\lambda }_6}{w_2}\\ {\psi }_3=\frac{C({\lambda }_3-{\lambda }_4)}{w_3}\end{array}$

Proof. Differentiating partially the Hamiltonian equation with respect to the state variables, S, V, C, I, D_r, and R, respectively, and then formulate the adjoint system as follows:

$\begin{array}{l}\frac{d{\lambda }_1}{dt}=-\frac{\partial H}{\partial S}=(\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)+{\gamma }_2+\mu ){\lambda }_1\\ \hspace{1em}-{\gamma }_2{\lambda }_2-\beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_2}{dt}=-\frac{\partial H}{\partial V}=-{\gamma }_1{\lambda }_1+(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)+\mu \\ \hspace{1em}+{\gamma }_1){\lambda }_2-(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_3}{dt}=-\frac{\partial H}{\partial C}=\beta (1-u_1)q_{1}S{\lambda }_1+\epsilon \beta (1-u_1)q_{1}V{\lambda }_2\\ \hspace{1em}-\beta q_1(1-u_1)(S+\epsilon V){\lambda }_3+(u_3+\delta +\omega +\mu ){\lambda }_3\\ \hspace{1em}-(\delta +u_3){\lambda }_4-\omega {\lambda }_6-k_1\\ \frac{d{\lambda }_4}{dt}=-\frac{\partial H}{\partial I}=\beta q_2(1-u_1)S{\lambda }_1+\epsilon \beta (1-u_1)q_{2}V{\lambda }_2\\ \hspace{1em}-\beta q_2(1-u_1)(S+\epsilon V){\lambda }_3+(\eta +u_2+\sigma +\mu ){\lambda }_4\\ \hspace{1em}-(1-\alpha )(1-u_2)\eta {\lambda }_5-(u_2+\alpha \eta ){\lambda }_6-k_2\\ \frac{d{\lambda }_5}{dt}=-\frac{\partial H}{\partial D_r}=\beta (1-u_1)q_{3}S{\lambda }_1+\epsilon \beta (1-u_1)q_{3}V{\lambda }_2\\ \hspace{1em}-\beta q_3(1-u_1)(S+\epsilon V){\lambda }_3+(\theta +\mu ){\lambda }_5-\theta {\lambda }_6-k_3\\ \frac{d{\lambda }_6}{dt}=-\frac{\partial H}{\partial R}=-\vartheta {\lambda }_1+(\vartheta +\mu ){\lambda }_6\end{array}$

In a similar manner following Pontryagin's maximum principle to get the controls. Hence, we solved the equation $\frac{\partial H}{\partial u_i}=0$ at $u_i^{*}$ for i = 1, 2, 3 and obtained

$\begin{array}{l}{u}_1^{*}=\frac{\beta (q_{1}C+q_{2}I+q_3{D}_r)((S+\epsilon V){\lambda }_3-{\lambda }_{1}S-\epsilon V{\lambda }_2)}{w_1},\\ u_2^{*}=\frac{I{\lambda }_4+(1-\alpha )\eta I{\lambda }_5-I{\lambda }_6}{w_2},\\ u_3^{*}=\frac{C({\lambda }_3-{\lambda }_4)}{w_3}.\end{array}$

When we express using conventional control arguments concerning the constraints on the controls, we conclude

$\begin{array}{ll}{u}_1^{*}=\{\begin{array}{ll}{\psi }_1,& \text{if }0<{\psi }_1<1\text{;}\\ 0,& \text{if }{\text{Ψ}}_1\le 0\text{;}\\ 1,& \text{if }{\psi }_1\ge 1\end{array},& u_2^{*}=\{\begin{array}{ll}{\psi }_2,& \text{if }0<{\psi }_2<1\text{;}\\ 0,& \text{if }{\text{Ψ}}_2\le 0\text{;}\\ 1,& \text{if }{\psi }_2\ge 1\end{array},\\ u_3^{*}=\{\begin{array}{ll}{\psi }_3,& \text{if }0<{\psi }_3<1\text{;}\\ 0,& \text{if }{\text{Ψ}}_3\le 0\text{;}\\ 1,& \text{if }{\psi }_3\ge 1\end{array}.\end{array}$

Alternately, in compact form, each optimal control can be expressed as

$\begin{array}{l}{u}_1^{*}(t)=\text{max}\left\{0,min(1,{\psi }_1)\right\}\\ u_2^{*}(t)=\text{max}\left\{0,min(1,{\psi }_2)\right\}\\ u_3^{*}(t)=\text{max}\left\{0,min(1,{\psi }_3)\right\}\end{array}$

where

$\begin{array}{l}{\psi }_1=\frac{\beta (q_{1}C+q_{2}I+q_3{D}_r)((S+\epsilon V){\lambda }_3-{\lambda }_{1}S-\epsilon V{\lambda }_2)}{w_1}\\ {\psi }_2=\frac{I{\lambda }_4+(1-\alpha )\eta I{\lambda }_5-I{\lambda }_6}{w_2}\\ {\psi }_3=\frac{C({\lambda }_3-{\lambda }_4)}{w_3}\end{array}$

Thus, the optimal equations are developed from the non-autonomous System 2.3 and the adjoint Equations 2.6, with the defined control set, initial and transversal conditions as

$\begin{array}{ll}\{\begin{array}{l}\frac{dS}{dt}=\text{Π}(1-\kappa )+\vartheta R+{\gamma }_{1}V\\ \hspace{1em}-\beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r)S-(\mu +{\gamma }_2)S\\ \frac{dV}{dt}=\text{Π}\kappa +{\gamma }_{2}S-\epsilon \beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r)V\\ \hspace{1em}-(\mu +{\gamma }_1)V\\ \frac{dC}{dt}=\beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r)S\\ \hspace{1em}+\epsilon \beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r)V-(u_3^{*}+\delta )C\\ \hspace{1em}-(\omega +\mu )C\\ \frac{dI}{dt}=(\delta +u_3^{*})C-(\eta +u_2)I-(\sigma +\mu )I\\ \frac{d{D}_r}{dt}=(1-\alpha )(1-u_2^{*})\eta I-(\theta +\mu )D_r\\ \frac{dR}{dt}=\omega C+(u_2^{*}+\alpha \eta )I+\theta D_r-(\vartheta +\mu )R\\ \frac{d{\lambda }_1}{dt}=(\beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r)+{\gamma }_2+\mu ){\lambda }_1-{\gamma }_2{\lambda }_2\\ \hspace{1em}-\beta (1-u_1^{*})(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_2}{dt}=-{\gamma }_1{\lambda }_1+(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r)+\mu \\ \hspace{1em}+{\gamma }_1){\lambda }_2-(\epsilon \beta (1-u_1)(q_{1}C+q_{2}I+q_3{D}_r){\lambda }_3\\ \frac{d{\lambda }_3}{dt}=\beta (1-u_1^{*})q_{1}S{\lambda }_1+\epsilon \beta (1-u_1^{*})q_{1}V{\lambda }_2\\ \hspace{1em}-\beta q_1(1-u_1^{*})(S+\epsilon V){\lambda }_3+(u_3^{*}+\delta +\omega +\mu ){\lambda }_3\\ \hspace{1em}-(\delta +u_3^{*}){\lambda }_4-\omega {\lambda }_6-k_1\\ \frac{d{\lambda }_4}{dt}=\beta q_2(1-u_1^{*})S{\lambda }_1+\epsilon \beta (1-u_1^{*})q_{2}V{\lambda }_2\\ \hspace{1em}-\beta q_2(1-u_1^{*})(S+\epsilon V){\lambda }_3+(\eta +u_2^{*}+\sigma +\mu ){\lambda }_4\\ \hspace{1em}-(1-\alpha )(1-u_2^{*})\eta {\lambda }_5-(u_2^{*}+\alpha \eta ){\lambda }_6-k_2\\ \frac{d{\lambda }_5}{dt}=\beta (1-u_1^{*})q_{3}S{\lambda }_1+\epsilon \beta (1-u_1^{*})q_{3}V{\lambda }_2\\ \hspace{1em}-\beta q_3(1-u_1^{*})(S+\epsilon V){\lambda }_3+(\theta +\mu ){\lambda }_5-\theta {\lambda }_6-k_3\\ \frac{d{\lambda }_6}{dt}=-\vartheta {\lambda }_1+(\vartheta +\mu ){\lambda }_6\\ u_1^{*}(t)=\text{max}\left\{0,min\left(1,\frac{\begin{array}{c}\beta (q_{1}C+q_{2}I+q_3{D}_r)\\ ((S+\epsilon V){\lambda }_3-{\lambda }_{1}S-\epsilon V{\lambda }_2)\end{array}}{w_1}\right)\right\}\\ u_2^{*}(t)=\text{max}\left\{0,min\left(1,\frac{I{\lambda }_4+(1-\alpha )\eta I{\lambda }_5-I{\lambda }_6}{w_2}\right)\right\}\\ u_3^{*}(t)=\text{max}\left\{0,min\left(1,\frac{C({\lambda }_3-{\lambda }_4)}{w_3}\right)\right\}\end{array}& (2.7)\end{array}$

$\begin{array}{l}{\lambda }_i(t_f)=0,i=1,...,6,S(0)=S_0,V(0)=V_0,C(0)=C_0,I(0)\\ \hspace{1em}\hspace{1em}=I_0,D_r(0)=D_{r0},R(0)=R_0.\end{array}$

3 Simulations of the optimal system

This section discusses the numerical results of Model 2.3 to demonstrate the impact of various control measures, such as prevention, treatment, and screening of carrier individuals, on the transmission of bacterial meningitis. Using the forward-backward sweep method, we solved System 2.7 by addressing the state and adjoint variables. The first step involves solving the state equations by initializing the controls over the simulation period, utilizing the forward fourth-order Runge–Kutta scheme. The second step is to solve the adjoint equations using the backward fourth-order Runge–Kutta scheme based on the solutions from the current iteration of the state equations and the transversality conditions. The controls are then updated based on the intervention results and the characteristics and outcomes of the state and adjoint systems. Lenhart and Workman [26] stated that this process repeats until consecutive iterations converge within a sufficiently small tolerance.

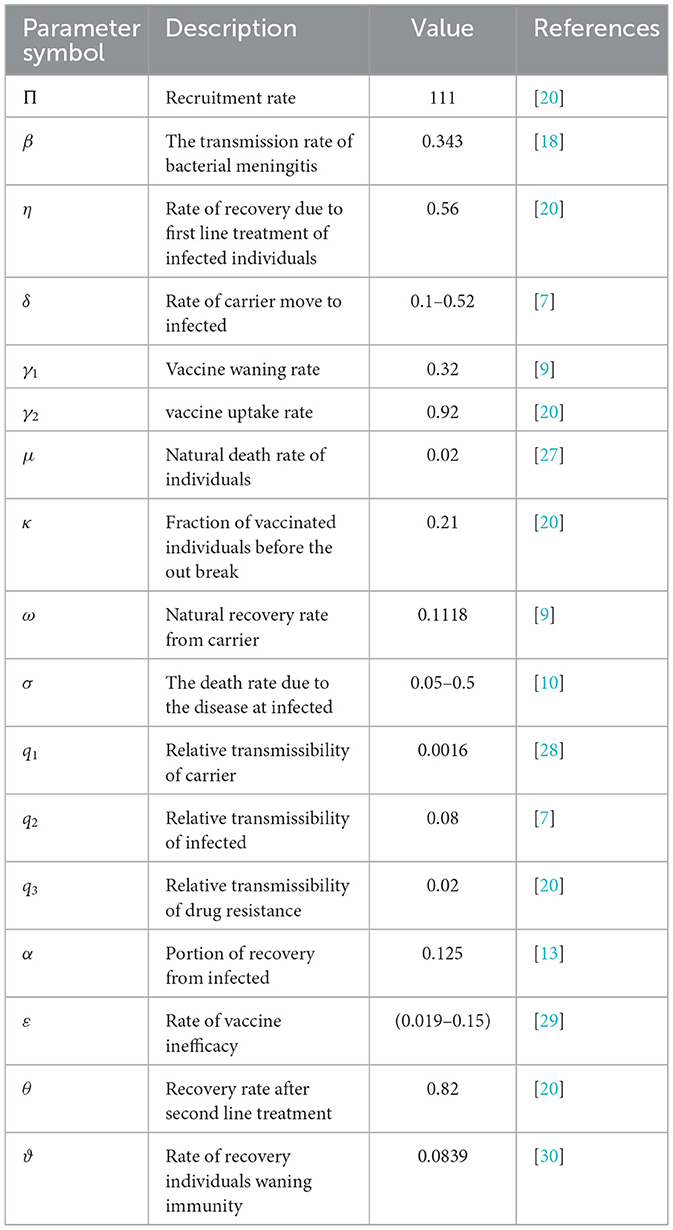
Here, the assumption is w₂ > w₃ > w₁ based on the fact that the cost associated with treatment for bacterial meningitis is higher than the costs of screening carrier individuals and preventing susceptible populations, while the cost of prevention is the lowest. To demonstrate the impact of different combinations of control strategies on the transmission of bacterial meningitis in a population, we use the initial conditions (S₀, V₀, C₀, I₀, D_r0, R₀) = (5, 550, 4, 100, 1, 620, 210, 180, 350), along with parameters k₁ = 30, k₂ = 10, k₃ = 8, w₁ = 20, w₂ = 90, w₃ = 50, and u_1max = u_2max = u_3max = 1, and values given in Table 1 for simulation of System 2.7.

Table 1

Table 1. Parameter values used for the simulations of control bacterial meningitis model.

The simulation of the optimal control model is divided into four strategies, incorporating more than control once, as we ordered below.

Strategy one: Combination of u₂(t) and u₃(t),

Strategy two: Combination of u₁(t) and u₃(t),

Strategy three: Combination of u₁(t) and u₂(t),

Strategy four: Combination of u₁(t), u₂(t), and u₃(t).

3.1 Strategy one: implementing treatment (u₂) and screening (u₃) only

Figure 1 illustrates the effect of the first strategy on bacterial meningitis dynamics. Using this strategy, the number of C(t), I(t), and D_r(t) individuals decreases significantly compared to the scenario without control. For ~0.25 months, the number of carrier individuals with control matches those without control, as illustrated in Figure 1A. However, after ~0.25 months, the number of individuals in this class with control decreases due to the implementation of the screening measure. The results in Figure 1B indicate that the infected class receives more individuals from the carriers due to screening. Hence, for ~1.5 months, the optimal control curve for the infected class lies above the curve for the scenario without control measures. Figure 1C shows that, with this strategy, the number of drug-resistant individuals decreases rapidly compared to those without the strategy. Consequently, implementing treatment and screening measures is effective in reducing drug-resistant individuals. The controls are implemented at a maximum rate for the entire period, as demonstrated in Figure 1D.

Figure 1

Figure 1. Impact of combined application of the control variables u₂ and u₃ on bacterial meningitis dynamics; (A) Carrier; (B) Infected; (C) Durgresist; (D) Control profile of u₂ and u₃.

3.2 Strategy two: implementing prevention (u₁) and screening (u₃) only

In this study, by setting the treatment intervention to zero and considering the prevention associated with screening intervention, the aim is to illustrate the interactions of bacterial meningitis infection. The impact of prevention and screening interventions on various population compartments is depicted graphically in Figure 2. The numbers of C(t) individuals in Figure 2A and I(t) individuals in Figure 2B decline more rapidly than in strategy one, but the numbers of drug-resistant populations in Figure 2C decrease more slowly than in strategy one. The control profile u₁ in Figure 2D is executed at a maximum level almost for the whole time, while the control u₃ is at upper bound for 3 months and then drop down after month 3.

Figure 2

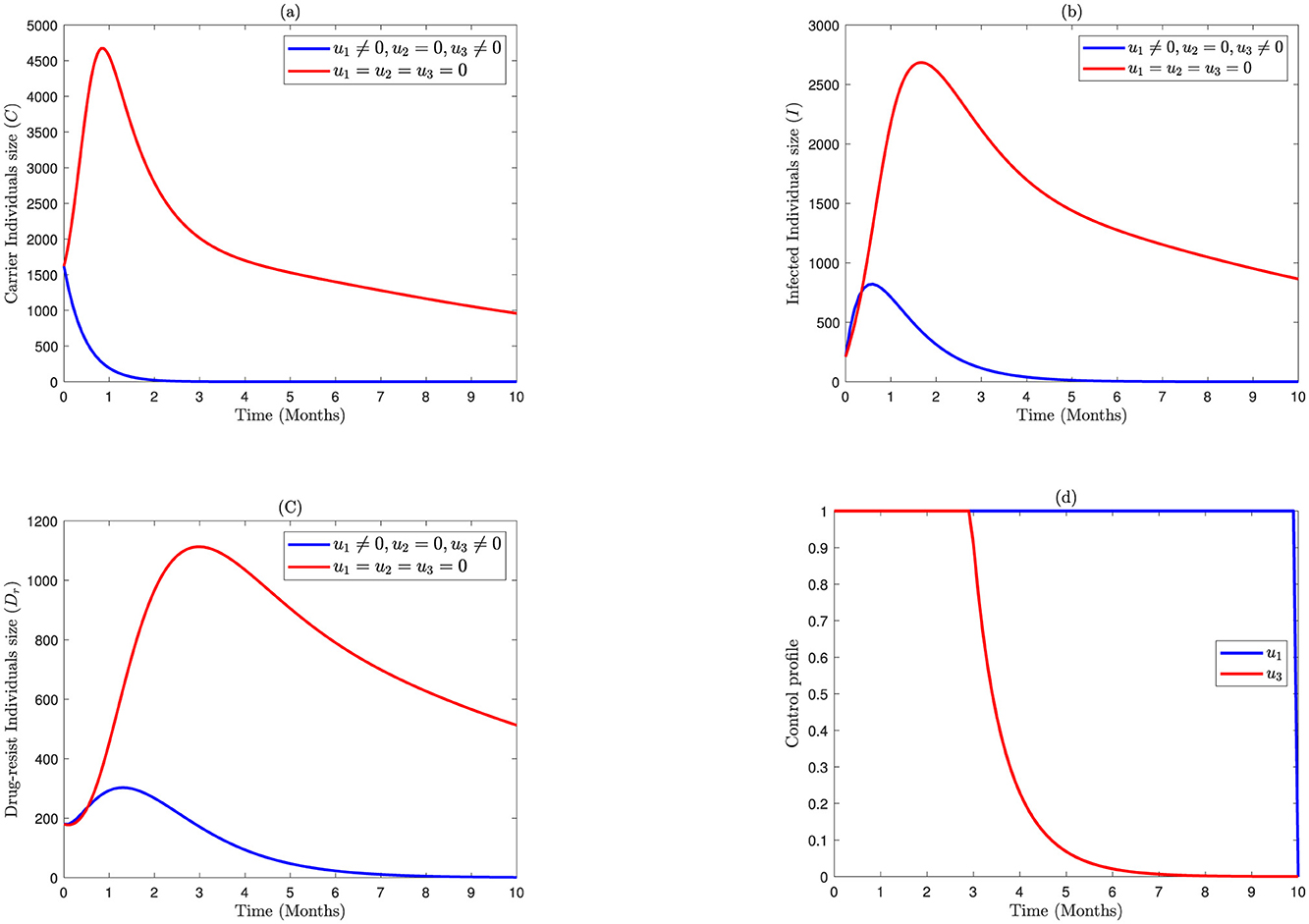
Figure 2. Impact of combined application of the control variables u₁ and u₃ on bacterial meningitis dynamics; (A) Carrier; (B) Infected; (C) Durgresist; (D) Control profile of u₁ and u₃.

3.3 Strategy three: implementing prevention (u₁) and treatment (u₂) only

In this strategy, we set the screening control to zero and consider the prevention associated with the treatment control to explain the interactions of bacterial meningitis infection. Compared to the previous strategies, the numbers of carrier populations in Figure 3A are decreasing slower than the numbers of carrier individuals in strategy two but faster than in strategy one. Similarly, the numbers of infected individuals in Figure 3B diminish faster as assessed to strategy one but the same as strategy two. Moreover, the numbers of drug-resistance populations in Figure 3C decrease faster than those in strategy two but the same as strategy one. In this study, the control profile u₁ in Figure 3D is implemented at a maximum capacity up to 9.8 months, while the control (u₂) is at upper bound for 4.5 months and then drop down after month 4.5.

Figure 3

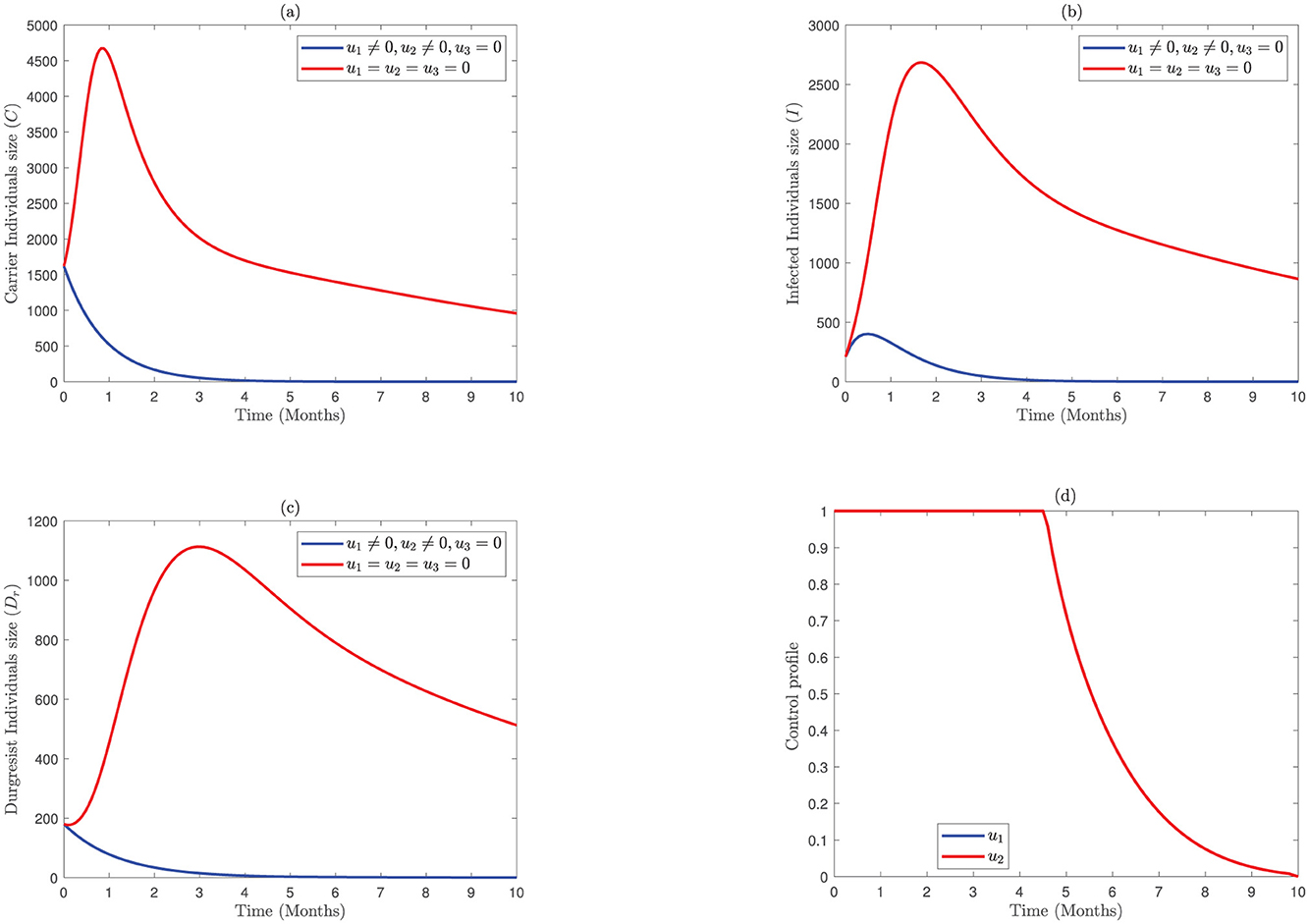
Figure 3. Impact of combined application of the control variables u₁ and u₂ on bacterial meningitis dynamics; (A) Carrier; (B) Infected; (C) Durgresist; (D) Control profile of u₁ and u₂.

3.4 Strategy four: implementing prevention (u₁), treatment (u₂), and screening (u₃) measures

Figure 4 demonstrates the implementation of all three interventions in Model 2.3. It shows that, as illustrated in Figure 4A, carriers are eliminated within 2 months. Similarly, the numbers of I(t) in Figure 4B and the numbers of drug resistance individuals in Figure 4C are eradicated approximately within 3 months. To attain these results, the control profile u₁ is executed at a maximum level for 9.3 months, while the controls u₃ and u₂ are at higher limits only for 3 and 3.4 months and then drop down after months 3 and 3.4, respectively. Thus, the optimal control trajectories from the simulation indicate that the proper combination of the intervention strategies may lead to a preferable intervention of bacterial meningitis.

Figure 4

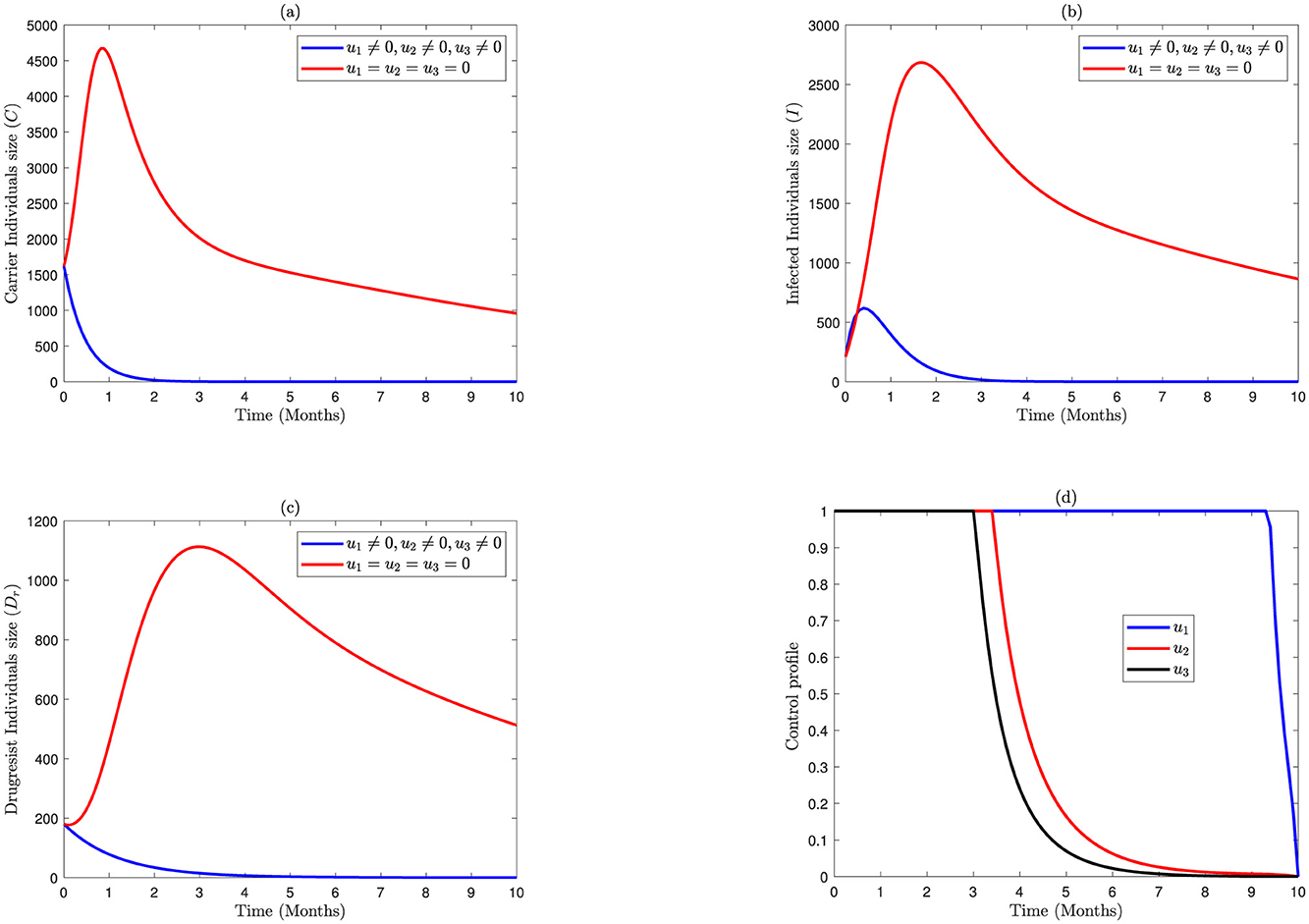
Figure 4. Impact of combined application of the control variables of u₁, u₂, and u₃ on bacterial meningitis dynamics; (A) Carrier; (B) Infected; (C) Durgresist; (D) Control profile of u₁, u₂, and u₃.

3.5 Cost-effectiveness analysis

We can compare the cost benefits of implementing the control intervention through cost-effectiveness analysis. Consequently, we adopted the methodology employed in numerous earlier investigations [9, 31, 32] to calculate the incremental cost-effectiveness ratio (ICER) and identify the less costly but more effective intervention among the listed strategies considered in this study. Most frequently, ICER is used to compare the costs and health advantages of any two alternative control intervention techniques i and j, competing for the same scarce resources. The ICER is defined mathematically as

$\begin{array}{ll}\text{ICER}=\frac{\begin{array}{c}\text{Difference in the total cost produced by strategies}\\ \text{i and j}\end{array}}{\begin{array}{c}\text{Difference in the total number infectious averted in}\\ \text{strategies i and j}\end{array}}& (3.1)\end{array}$

where the total infectious averted (Ta) is the difference between the total number of infectious without controls and with controls during the infectious period [9, 31, 32]. It is defined mathematically as follows:

$\begin{array}{ll}\text{Ta}={\displaystyle \underset{0}{\overset{t_f}{\int }}}(C(t)+I(t)+D_r(t))dt-{\displaystyle \underset{0}{\overset{t_f}{\int }}}(\bar{C}(t)+Ī(t)+\overline{D_r}(t))dt& (3.2)\end{array}$

where $\underset{0}{\overset{t_f}{\int }}(C(t)+I(t)+D_r(t))dt$ denotes the total number of infectious individuals without control over a given period of time, while $\underset{0}{\overset{t_f}{\int }}(\bar{C}(t)+Ī(t)+\overline{D_r}(t))dt$ denotes the total number of infectious individuals with control over a given period of time. The total cost (Tc) implemented during the period is also given by

$\begin{array}{ll}\text{Tc}=\frac{1}{2}{\displaystyle \underset{0}{\overset{t_f}{\int }}}[(w_1{u}_1^2(t)+w_2{u}_2^2(t)+w_3{u}_3^2(t)]dt.& (3.3)\end{array}$

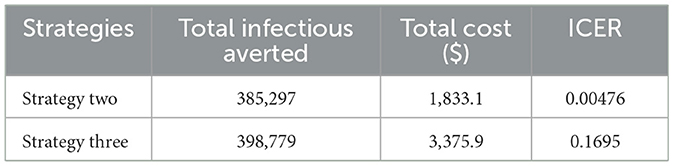
We separated the control strategies into double and triple scenarios to use ICER to analyze their cost efficiency. Therefore, as shown in Table 2, to examine the cost-effectiveness for the double scenario, the control strategies are primarily ranked in increasing order of the aggregated count of infectious averted.

$\begin{array}{l}\text{ICER(one)}=\frac{6,999.8}{209,417}=0.0334,\\ \text{ICER(two)}=\frac{1,833.1-6,999.8}{385,297-209,417}=-0.0294,\\ \text{ICER(three)}=\frac{3375.9-1,833.1}{394,401-385,297}=0.1695.\end{array}$

Table 2

Table 2. Incremental cost-effective ratio for double scenario.

From Table 2, we observed that the values of ICER (one) are more significant than ICER(two). This implies that strategy one is more costly and less effective than strategy two. For this reason, strategy one is eliminated from the list of alternative control interventions. Then, by recomputing ICER for strategies two and three, we obtained Table 3.

Table 3

Table 3. Incremental cost-effective ratio for double scenario.

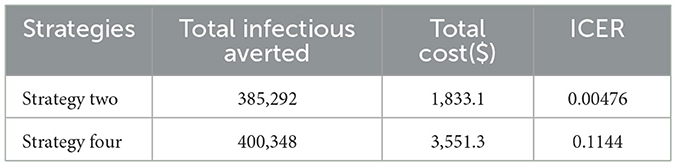
Table 3 shows that the ICER (three) is higher than the ICER (two). This makes strategy three strongly dominant, more costly, and less effective than strategy two. Therefore, we eliminate strategy three from the list of control interventions, and strategy two (integrating the use of prevention (u₁) and screening (u₃)) is the most cost-effective strategy from the double scenario. Next, we calculate an ICER for the triple scenario, as shown in Table 4.

$\begin{array}{c}\text{ICER(four)}=\frac{3,551.3}{400,348}=0.00887\end{array}$

Table 4

Table 4. Incremental cost-effective ratio for triple scenario.

Finally, we compare the most cost-saving strategy obtained from the double and triple scenarios and calculate the ICER, as show n in Table 5.

$\begin{array}{l}\text{ICER (two)}=\frac{1,833.1}{385,297}=0.00476\\ \text{ICER (four)}=\frac{3,551.3-1,833.1}{400,348-385,297}=0.1144\end{array}$

Table 5

Table 5. Incremental cost-effectiveness ratio for the most effective strategies.

Table 5 clearly shows that strategy two has the lowest ICER value. Thus, out of all the control measures mentioned in this study, strategy two (the combined use of prevention and screening) is the most cost-saving and effective control intervention.

4 Conclusion

In this study, we applied an optimal control theory to a bacterial meningitis model developed by Belay et al. [20]. We used Pontryagin's maximum principle to derive the Hamiltonian equation, adjoint variables, characterizations of the controls, and the optimality system. In addition, the existence of the optimal control model was proven. To control the spread of bacteria meningitis disease, we introduced three time-dependent control variables, such as prevention u₁(t), treatment u₂(t), and screening u₃(t), into Model 2.2 and investigated the associated benefits of different control strategies using cost-effectiveness analysis. To do this, we calculated the incremental cost-effectiveness ratio (ICER). The numerical results indicate that all implemented control strategies significantly reduce bacterial meningitis infections in the population, with the combined use of all protective and control interventions proving the most effective. Even though our result of cost-effectiveness analysis indicates that strategy two (the combined use of prevention and screening) is the most cost-saving and effective strategy to eradicate the bacteria meningitis disease, in terms of the infection averted, we saw that strategy three (the combined use of prevention and treatment) and strategy four (the use of all controls) were more significant than strategy two (the combined use of prevention and screening).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by Gondar University Hospital, Gondar, Ethiopia. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin. Written informed consent was obtained from the individual(s), and minor(s)' legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.

Author contributions

MB: Formal analysis, Writing – original draft. JA: Supervision, Writing – review & editing. HA: Supervision, Writing – review & editing. HE: Writing – review & editing, Methodology. MF: Conceptualization, Writing – review & editing. SD: Project administration, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to thank Pan African University Institute of Basic Sciences Technology and Innovation (PAUSTI) for providing the necessary support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bloch KC, Tang YW. Molecular approaches to the diagnosis of meningitis and encephalitis. In:Persing DH, Tenover FC, Hayden RT, Ieven M, Miller MB, Nolte FS, et al., , editors. Molecular Microbiology: Diagnostic Principles and Practice. Washington, DC: ASM Press (2016), p. 285–305.

Google Scholar

2. Oordt-Speets AM, Bolijn R, van Hoorn RC, Bhavsar A, Kyaw MH. Global etiology of bacterial meningitis: a systematic review and meta-analysis. PLoS ONE. (2018) 13:e0198772. doi: 10.1371/journal.pone.0198772

PubMed Abstract | Crossref Full Text | Google Scholar

3. Ali SA, Taj MK, Ali SH. Antimicrobial resistance pattern of bacterial meningitis among patients in Quetta, Pakistan. Infect Drug Resist. (2021) 14:5107. doi: 10.2147/IDR.S339231

PubMed Abstract | Crossref Full Text | Google Scholar

4. Mazamay S, Guégan JF, Diallo N, Bompangue D, Bokabo E, Muyembe JJ, et al. An overview of bacterial meningitis epidemics in Africa from 1928 to 2018 with a focus on epidemics “outside-the-belt”. BMC Infect Dis. (2021) 21:1-13. doi: 10.1186/s12879-021-06724-1

PubMed Abstract | Crossref Full Text | Google Scholar

5. Martcheva M. Crispino-O'Connell G. The transmission of meningococcal infection: a mathematical study. J Math Anal Appl. (2003) 283:251–75. doi: 10.1016/S0022-247X(03)00289-0

Crossref Full Text | Google Scholar

6. Li MY. Important concepts in mathematical modeling of infectious diseases. In:Li MY, , editor. An Introduction to Mathematical Modeling of Infectious Diseases. Cham: Springer (2018), p. 1–33. doi: 10.1007/978-3-319-72122-4_1

Crossref Full Text | Google Scholar

7. Asamoah JKK, Nyabadza F, Seidu B, Chand M, Dutta H. Mathematical modelling of bacterial meningitis transmission dynamics with control measures. Comput Math Methods Med. (2018) 2018:2657461. doi: 10.1155/2018/2657461

PubMed Abstract | Crossref Full Text | Google Scholar

8. Workineh YH, Kassa SM. Optimal control of the spread of meningitis: in the presence of behaviour change of the society and information dependent vaccination. Commun Math Biol Neurosci. (2021) 2021:29. doi: 10.28919/cmbn/5575

Crossref Full Text | Google Scholar

9. Agusto F, Leite M. Optimal control and cost-effective analysis of the 2017 meningitis outbreak in Nigeria. Infect Dis Modell. (2019) 4:161–87. doi: 10.1016/j.idm.2019.05.003

PubMed Abstract | Crossref Full Text | Google Scholar

10. Asamoah JKK, Nyabadza F, Jin Z, Bonyah E, Khan MA, Li MY, et al. Backward bifurcation and sensitivity analysis for bacterial meningitis transmission dynamics with a nonlinear recovery rate. Chaos Solit Fractals. (2020) 140:110237. doi: 10.1016/j.chaos.2020.110237

Crossref Full Text | Google Scholar

11. Yano TK, Bitok J, Jerop R. Optimal control analysis of meningococcal meningitis disease with varying population size. Appl Comput Math. (2022) 11:140–9. doi: 10.11648/j.acm.20221105.14

Crossref Full Text | Google Scholar

12. Yusuf T. Mathematical modelling and simulation of meningococcal meningitis transmission dynamics, FUTA J. Res Sci. (2018) 14:94–104.

Google Scholar

13. Veronica CM, Olusegun O, Newton A, Sunday AA. Mathematical modeling and stability analyses on the transmission dynamics of bacterial meningitis. J Math Comput Sci. (2021) 11:7384–413. doi: 10.28919/jmcs/6513

Crossref Full Text | Google Scholar

14. Afolabi M, Adewoye KS, Folorunso AI, Omoloye MA. A mathematical model on transmission dynamics of meningococcal meningitis. IRE J. (2021) 4:59–66.

Google Scholar

15. Blyuss KB. Mathematical modelling of the dynamics of meningococcal meningitis in Africa. In:PJ Aston, AJ Mulholland, KMM Tant, , editors. UK Success Stories in Industrial Mathematics. Cham: Springer (2016), p. 221–6. doi: 10.1007/978-3-319-25454-8_28

Crossref Full Text | Google Scholar

16. Crankson MV. Mathematical Modeling and Optimal Control of the Transmission Dynamics of Bacterial Meningitis Population in Ghana. Tarkwa: University of Mines and Technology (2021).

PubMed Abstract | Google Scholar

17. Elmojtaba IM, Adam S. A mathematical model for meningitis disease. Red Sea Univ J Basic Appl Sci. (2017) 2:467–72.

Google Scholar

18. Musa SS, Zhao S, Hussaini N, Habib AG, He D. Mathematical modeling and analysis of meningococcal meningitis transmission dynamics. Int J. Biomath. (2020) 13:2050006. doi: 10.1142/S1793524520500060

Crossref Full Text | Google Scholar

19. Koutangni T, Crepey P, Woringer M, Porgho S, Bicaba B, Tall H, et al. Compartmental models for seasonal hyperendemic bacterial meningitis in the African meningitis belt. Epidemiol Infect. (2019) 147:e14. doi: 10.1017/S0950268818002625

PubMed Abstract | Crossref Full Text | Google Scholar

20. Belay MA, Abonyo OJ, Theuri DM. Mathematical model analysis for the transmission dynamics of bacterial meningitis disease incorporating drug-resistance class. Commun Math Biol Neurosci. (2022) 2022:121. doi: 10.28919/cmbn/7774

Crossref Full Text | Google Scholar

21. Alemneh HT, Kassa AS, Godana AA. An optimal control model with cost effectiveness analysis of Maize streak virus disease in maize plant. Infect Dis Model. (2021) 6:169–82. doi: 10.1016/j.idm.2020.12.001

PubMed Abstract | Crossref Full Text | Google Scholar

22. Fleming WH, Rishel RW. Deterministic and stochastic optimal control. Bull New Ser Am Math Soc. (1976) 82:869–70. doi: 10.1090/S0002-9904-1976-14186-9

PubMed Abstract | Crossref Full Text | Google Scholar

23. Lukes DL. Differential Equations: Classical to Controlled, Vol 162. New York, NY: Academic press (1982).

Google Scholar

24. Burden T, Ernstberger J, Fister KR. Optimal control applied to immunotherapy. Discrete Continuous Dyn Syst B. (2004) 4:135. doi: 10.3934/dcdsb.2004.4.135

Crossref Full Text | Google Scholar

25. Pontryagin LS. Mathematical Theory of Optimal Processes. Boca Raton, FL: CRC press (1987).

Google Scholar

26. Lenhart S, Workman JT. Optimal Control Applied to Biological Models. Boca Raton, FL: Chapman and Hall/CRC. (2007). doi: 10.1201/9781420011418

Crossref Full Text | Google Scholar

27. Irving T, Blyuss K, Colijn C, Trotter C. Modelling meningococcal meningitis in the African meningitis belt. Epidemiol Infect. (2012) 140:897–905. doi: 10.1017/S0950268811001385

PubMed Abstract | Crossref Full Text | Google Scholar

28. Baba IA, Olamilekan LI, Yusuf A, Baleanu D. Analysis of meningitis model: A case study of northern Nigeria. AIMS Bioeng. (2020) 7:179–93. doi: 10.3934/bioeng.2020016

Crossref Full Text | Google Scholar

29. Ojo MM. Mathematical modeling of Neisseria meningitidis: a case study of Nigeria. Lawrence: University of Kansas (2019).

Google Scholar

30. Karachaliou A, Conlan AJ, Preziosi MP, Trotter CL. Modeling long-term vaccination strategies with MenAfriVac in the African meningitis belt. Clin Infect Dis. (2015) 61(suppl_5):S594–600. doi: 10.1093/cid/civ508

PubMed Abstract | Crossref Full Text | Google Scholar

31. Makinde OD, Okosun KO. Impact of chemo-therapy on optimal control of malaria disease with infected immigrants. Biosystems. (2011) 104:32–41. doi: 10.1016/j.biosystems.2010.12.010

PubMed Abstract | Crossref Full Text | Google Scholar

32. Berhe HW, Makinde OD, Theuri DM. Co-dynamics of measles and dysentery diarrhea diseases with optimal control and cost-effectiveness analysis. Appl Math Comput. (2019) 347:903–21. doi: 10.1016/j.amc.2018.11.049

Crossref Full Text | Google Scholar