- 1Department of Philosophy, Al-Farabi Kazakh National University, Almaty, Kazakhstan
- 2Department of Psychology, Sevastopol State University, Sevastopol, Russia
- 3Department of General Psychology, V.I. Vernadsky Crimean Federal University, Sevastopol Economic and Humanitarian Institute, Sevastopol, Russia
- 4National Scientific Laboratory for Collective use of Information and Space Technologies, Satbayev University, Almaty, Kazakhstan
It is shown that the problem of the adequacy of psychological testing methods, which are varieties of “projective techniques”, is far from being universally recognized. To solve this problem, we used an empirical method based on collecting of statistics of respondents’ answers, as well as a method of analyzing this statistics by means of representing permutations through functions taking values in Galois fields. Based on experimental data, it is shown that the distribution of respondents’ answers to a test in which they are asked to rank pictures in accordance with their own preferences is not homogeneous. Experimental data show that there are answer options that are statistically most common. An interpretation of testing is proposed in which passing the test is considered as “connecting” an external additional layer to the neural network formed by the respondent’s brain. In accordance with this interpretation, the most frequently occurring answer options can be considered as the basis for the formation of classification characteristics. It is shown that during using tests of this type it is advisable to take into account the code distances between the answer of a particular respondent and the codes corresponding to the most frequently occurring sequences. The possibilities of generating psychological tests directly based on experimental data and images generated by neural networks are discussed.
1 Introduction
Currently, the issue of diagnosing the psychological state of various social groups is becoming increasingly urgent (1–3), which is associated, among other things, with the need to determine the reaction of society to various stimuli of both a subjective and objective nature (4, 5). Moreover, the issue of creating valid tools for diagnosing psychophysiological state that could be used on a massive scale is becoming more and more important, and Big Data is actively used here (6, 7). One of the possible options here is associated with the use of aromatherapy methods (8, 9), which are becoming increasingly popular, including due to the growing interest in ancient Eastern practices such as Feng Shui (10, 11). One of the options for using aromatherapy for this purpose was considered in our reports (12, 13).
Carrying out mass psychological and psychophysiological diagnostics of society is obviously significantly simplified through the use of modern digital technologies (14, 15). Psychological testing can be carried out online, and its results are processed automatically (16, 17), and a wide variety of source material can be used here (18, 19).
These facts are well known, but they can be looked at from a slightly different point of view.
Namely, the creation of a psychological test was and is an act of creativity of a professional psychologist. As a rule, it is based on some concept, put forward from a hypothesis. Next, the test itself is created, the use of which in practice is ensured by an appropriate verification procedure, which makes it possible to verify, among other things, reliability and representativeness of the test.
The current level of use of digital resources allows, however, to pose the question differently.
There is a set of certain data that can potentially carry information about the psychological state of users. There is no need to prove that all information (photos, texts, etc.) posted by users of online social networks in the public domain contains information about the identity of the author, which, with the proper approach, can be decrypted and used, including for diagnostics of society.
This approach is actually used in practice for various purposes (20, 21).
This paper proves that digital technologies make it possible to significantly transform the methodology for constructing psychological tests, and for this purpose a variety of objects that carry information reflecting the personality of the respondent (in particular, images) can be used.
Specifically, we demonstrate that it is possible to implement a testing methodology even when the rules for interpreting the results obtained are not known in advance. We argue that they can be obtained directly as a result of processing the correspondent set of experimental data.
2 Methods
2.1 Experimental procedure
A set of images (visual stimuli) presented in Table 1 is used in this report. The images were obtained using a tool (23) (neural network), which is publicly available. The table also shows Jung’s archetypes that correspond to these visual stimuli.
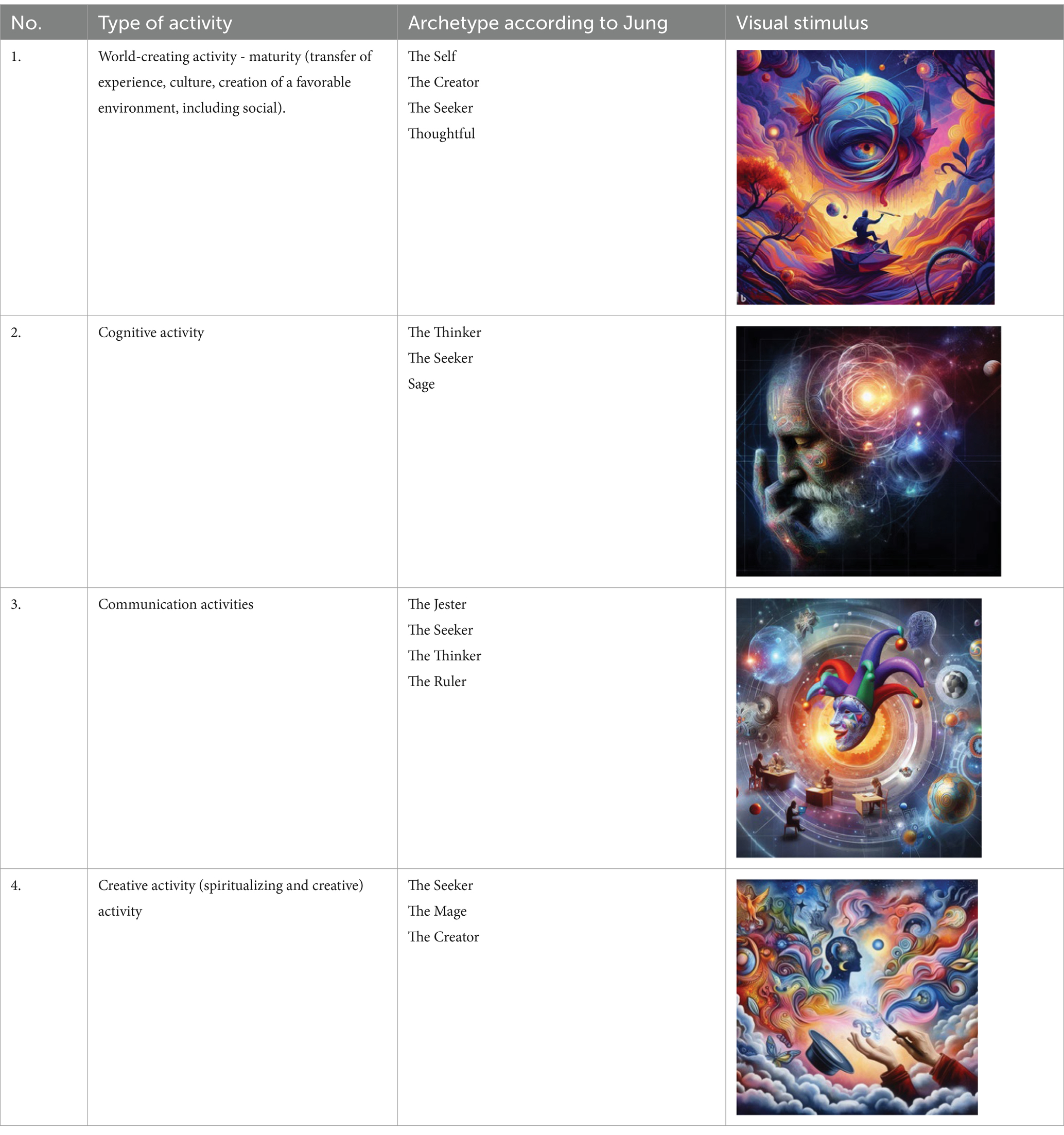
Table 1. Visual stimuli corresponding to different types of activities (experimental example of a test that meets “projective techniques,” built using images generated by a neural network «GitHub Copilot» 22).
Respondents were asked to rank these images according to their individual preferences. This approach corresponds to the methodology for constructing many classical psychological tests, in particular, the Luscher test (24), the Szondi test (25), as well as the psychogeometric test by Susan Dellinger (26).
Specifically, respondents were given the following instructions: arrange the pictures in the following sequence:
Picture 1 is the most attractive for you.
Picture 2 is the most unattractive for you.
Picture 3 is less attractive to you.
Picture 4 is less unattractive for you.
The respondents were 106 students studying in the following areas of training: “Psychology,” “Psychology of professional activity” (60%) and “Nuclear power plants: design, operation and engineering” (40%). Of these, 71 respondents are girls (67%), 35 respondents are boys (33%). The set is representative.
Further, the results obtained were subjected to statistical processing using the theory of group representations based on abstract algebra methods.
2.2 Methodology for statistical processing of experimental data
This technique is based on the representation of symmetric groups through functions that take values in Galois fields.
The choice of this particular methodology is conditioned by the following considerations. We proceed from the assumption that the classification of answers to any tests should provide for the possibility of small deviations from the sequence that can be regarded as “reference,” i.e., knowingly belonging to a certain classification feature. Such deviations can be most easily observed when considering a test, the answers to which correspond to the binary logic (yes or no). In this case, a set of answers to a test can be put in correspondence to a sequence of binary symbols. For such sequences, a coding distance (Hemming distance) is defined: the coding distance between two sequences is equal to the number of mismatched binary symbols.
Sequences of this kind can also be used as images recognized by neural networks of the most common types. Neural networks, as it is known, interpret sequences, the coded distance between which is less than a given one, as identical. This principle of pattern recognition corresponds to the approach used: close (in the sense of coding distance) sequences are interpreted as corresponding to the same result. It is convenient to characterize quantitatively the number of images that are interpreted as reference images (more precisely, corresponding to a certain classification feature) using the analogy between neural networks and error-correcting codes.
One of the best known codes of this type is the Hemming code (7,4). It contains 7 binary symbols, 3 of which are additional (allowing to correct an error). Correction of one error means that the set containing 27 = 128 sequences is projected to the set containing 24 = 16 variants.
It can be seen that the consideration of close (in the sense of coding distance) variants really allows us to identify sequences that meet the classification features, without using any hypotheses.
However, the notion of coding distance, which is quite natural for the case of sequences of binary symbols, requires a significant clarification when we move to the use of permutation tests. In this case, two test results should be interpreted as close when they differ by a given number of transpositions (permutations of set elements).
In order to quantitatively identify the test results that meet the above proximity criterion, it is reasonable to use Galois fields, which can be used to represent symmetric groups—groups of permutations of a set containing a finite number of elements.
The next methods of representing elements of symmetric groups are most common: representation through cycles, as well as representation through matrices (27, 28). In particular, the symmetric group , which corresponds to the permutations of the images presented in Figure 1, also corresponds to the symmetry group of the tetrahedron, which is represented by 3 by 3 matrices (28). This circumstance is a reflection of the general provisions of the theory of algebras. In particular, it is known that the group can be represented using a system of four vectors whose sum is equal to zero.
However, for the purposes of this work the most convenient method is representation of symmetric groups through functions whose arguments and values are elements of Galois fields.
Indeed, let us consider the next form of permutation
Where , is a prime number.
For such a case, each integer can be assigned to some non-zero element of the Galois field .
The mutual correspondence between Equations 1, 2 is as follows. Each number m standing in a certain place of the first or second line in Equation 1 is assigned an element , standing in the same place in table (Equation 2). Due to this, instead of tracking the displacements of numbers 1,…, N, we can track the displacements of the degrees of the primitive element . The advantages of this approach are that together permutations of the classical type (Equation 1) can be considered as a function of one variable whose arguments and values lie in the Galois field under consideration. This function of one variable is exhaustively defined by table (Equation 2). Thus, the description of permutations is reduced to the analysis of functions taking values in Galois fields.
We emphasize that the degrees of the primitive element exhaust all non-zero elements of the field , since the next expression is valid for such a field
where is an arbitrary non-zero element of the field .
The function of one variable specified by table (Equation 2) can be represented in explicit form using the results of Equations 29 and 30. Following these works (Equation 3), we define a logical -function as
By virtue of Equation 4, for this function we have
Using logical -functions (Equation 5), a function of one variable specified by table (Equation 2), can be represented as an explicit algebraic expression.
Where , and the values are specified by the truth table (Equation 2).
Formula Equation 7 allows us to represent permutations that are elements of the symmetric group by polynomial functions of a variable taking values in the field .
Indeed, for the field
This formula follows from the fact that all intermediate binomial coefficients in the formula during calculations in the field are equal to zero, since they contain the multiplier , and in this field for any .
Besides,
From Equations 7, 8 it follows that (30).
Substituting Equation 9 into Equation 4 and further into Equation 6, we obtain
Where
Thus, permutations of the type under consideration can be represented by polynomials over Galois fields, concrete examples of which are given by relations (Equations 10 and 11).
Next, in the Galois field one can construct the following orthogonal sequences (31, 32).
Where
Respectively, the -th element of the -th sequence is expressed by the formula
Sequences (Equation 12) are orthogonal in the following sense
Property (Equation 14) can be proven using expression (Equation 13) as follows. Let us consider the sum of the products of elements of two sequences and at each other.
If the condition is met
then
This Expression (Equation 17) uses the formula for geometric progression. If condition (Equation 16) is not satisfied, then Equation 15 sums up units, which proves Equation 14.
From Equation 15 it follows that the coefficients represents the components of the Fourier-Galois spectrum of functions (31, 32).
where is the number of the sequence from the set (Equation 12) conjugated to the sequence with number m, and the conjugation is understood in the sense of Equation 14, i.e., .
It is important that the specific type of functions , corresponding to the permutations, leads to equality
(The sum of all non-zero elements of the Galois field is equal to zero.)
Thus, the elements of any group can be represented by polynomials over the Galois field . The advantage of this representation over the matrix one is its compact form, and the advantage over the representation of permutations through cycles is its ease of use.
The representation of the group which is used in this work for statistical processing of the results of testing is formed according to the method described above, in particular, using formulas (Equations 18 and 19).
3 Results
3.1 Experimental results
Figure 1 shows a histogram reflecting the results of the experiment. Specifically, it shows the probability of the respondent’s answer with number . The value is obtained as the ratio of the frequency of occurrence of an answer with a number to the total number of answers. Each of the respondents arranged the pictures presented in Figure 1 in a sequence that corresponded to his own preferences. This choice can be put in correspondence with a certain permutation, i.e., a certain element of the symmetric group . The elements of this group are numbered in accordance with methodology discussed in Section 3.2.
Figure 2 shows a histogram of the distribution of test results taking into account the gender factor. The probabilities , where index 1 corresponds to men and index 2 to women, were defined as the ratio of the frequency of occurrence of an answer with a number to the total number of answers provided by male and female respondents, respectively.
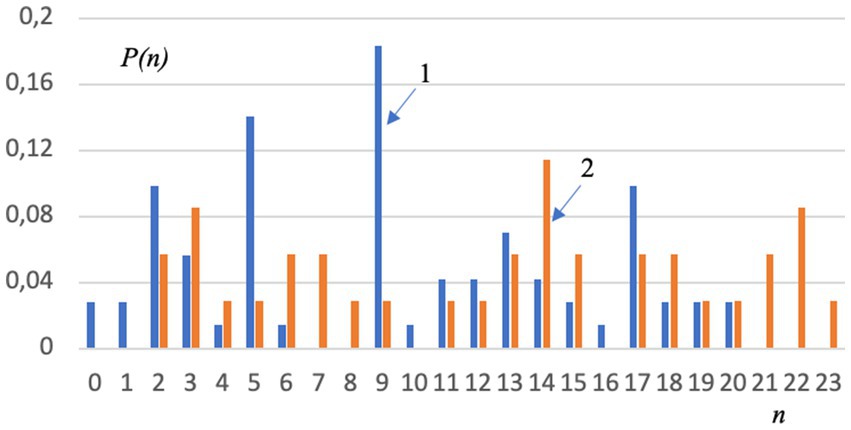
Figure 2. Distribution of test results by sequence numbers, taking into account gender; 1—boys, 2—girls.
It can be seen that the distribution of answers by number differs significantly from homogeneous. There are pronounced peak values. The interpretation of this result below is given on the basis of Jung’s theory of archetypes.
Figure 3 shows a distribution similar to that shown in Figure 1, but with taking into account an error factor.

Figure 3. Distribution of test results by sequence numbers, taking into account the single error factor.
Namely, by analogy with the Hamming distance, widely used in noise-correcting coding (33, 34), it is also possible to introduce a “distance” between the answer on the test used in this work.
Indeed, any of the choices made by the respondent can be represented as a permutation (1) or, since the top line is fixed, in the form of a sequence of numbers from 1 to 4, where none of the numbers is repeated.
The distance between two such sequences can be defined as the number of transpositions (two numbers and change places) required for passing of one sequence into another.
Figure 3 shows the distribution obtained as follows. Each respondent’s answer was associated not only with the sequence that corresponded to his answer, but also with sequences spaced from it by a unit code distance (one transposition).
Figure 4 shows a distribution similar to that shown in Figure 3, but taken into account the gender factor.
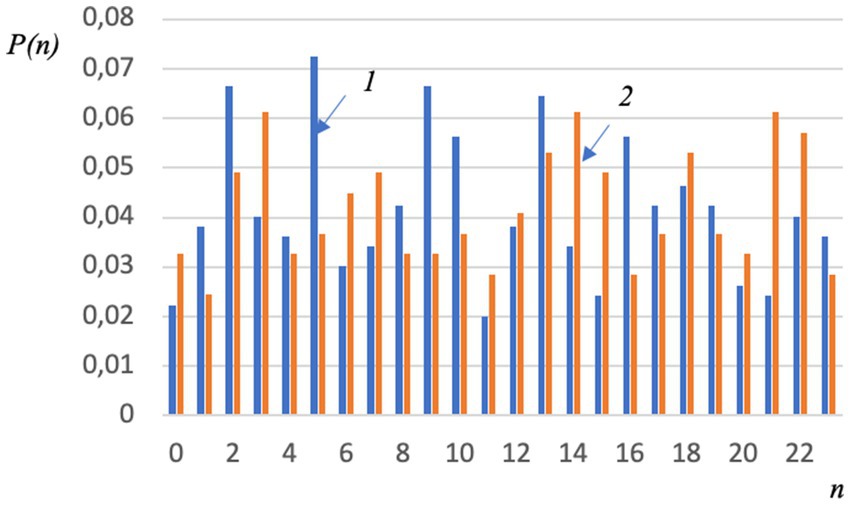
Figure 4. Distribution of test results by sequence numbers, taking into account the single error factor and gender factor; 1—boys, 2—girls.
It can be seen that the maximum values in Figures 1, 3 correspond to the same numbers; such similarity can be seen for Figures 2, 4 too.
Note that the problem of numbering of elements of a group is nontrivial. Let us consider how it can be solved using functions of one variable that take values in Galois field. Looking ahead somewhat, we also note that this approach not only allows for the numbering of substitutions, but also creates the prerequisites for further improvement of the methodology proposed in this work.
3.2 Numbering of elements of group S4 using the representation through functions in Galois field GF(5)
Let us consider, using the methodology presented in Section 2.2, a specific type of polynomials corresponding to the elements of the group . In accordance with this methodology, this group corresponds to the field . Elements of this field can be selected as follows: .
A primitive element can be selected as follows: . Then the original sequence, which includes powers of the primitive element, takes the form
Note that a similar correspondence can be established for other fields, e.g., . However, the use of such fields leads to very cumbersome computations. In addition, in order to achieve the goals outlined in the introduction (mass coverage of the population by testing), it makes sense to concentrate on using tests that use a relatively small number of pictures (the simplicity of the test provides an opportunity for its wider dissemination). Accordingly, it makes sense to make the test as simple as possible for the user. From this point of view, the choice of the GF(5) field seems justified, including because the degrees of a primitive element are represented in a very simple form (Equation 20).
Orthogonal sequences (Equation 12) for the case under consideration take the form
In accordance with Equation 14, the conjugate sequence of is a sequence (and vice versa). Sequences and are self-adjoint.
Applying formulas for orthogonal sequences (Equations 21–24), we find that permutations from the group under consideration can be represented by polynomials of the following form over the field
Where
The spectral component is equal to zero due to Equation 19.
Let us show that the values of the coefficients , expressions for which are given by formulas (Equations 26–28), satisfied to quite certain restrictions.
Let us consider the case of two sequential permutations, each of which is represented by a polynomial (Equation 25). One should substitute polynomial (Equation 25) corresponding to first permutation into the similar polynomial
corresponding to the second permutation in order to obtain a polynomial corresponding to the resulting one.
Substituting (Equation 25) into (Equation 29), we have
The multiplier (right side of this formula) can be represented as
where it is taken into account that for the case under consideration
Further, since the polynomial (Equation 30) must be reduced to the form (Equation 25) for any values of , the next condition must be satisfied
Table 2 shows all possible 24 combinations of values that correspond to 4! possible substitutions. The values of, as well as the values of and , are also presented in the table. One can see that these quantities are either both equal to zero or have the same sign. In the latter case, and . Taking into account relation , one can see that Equation 32 is satisfied for all possible combinations.
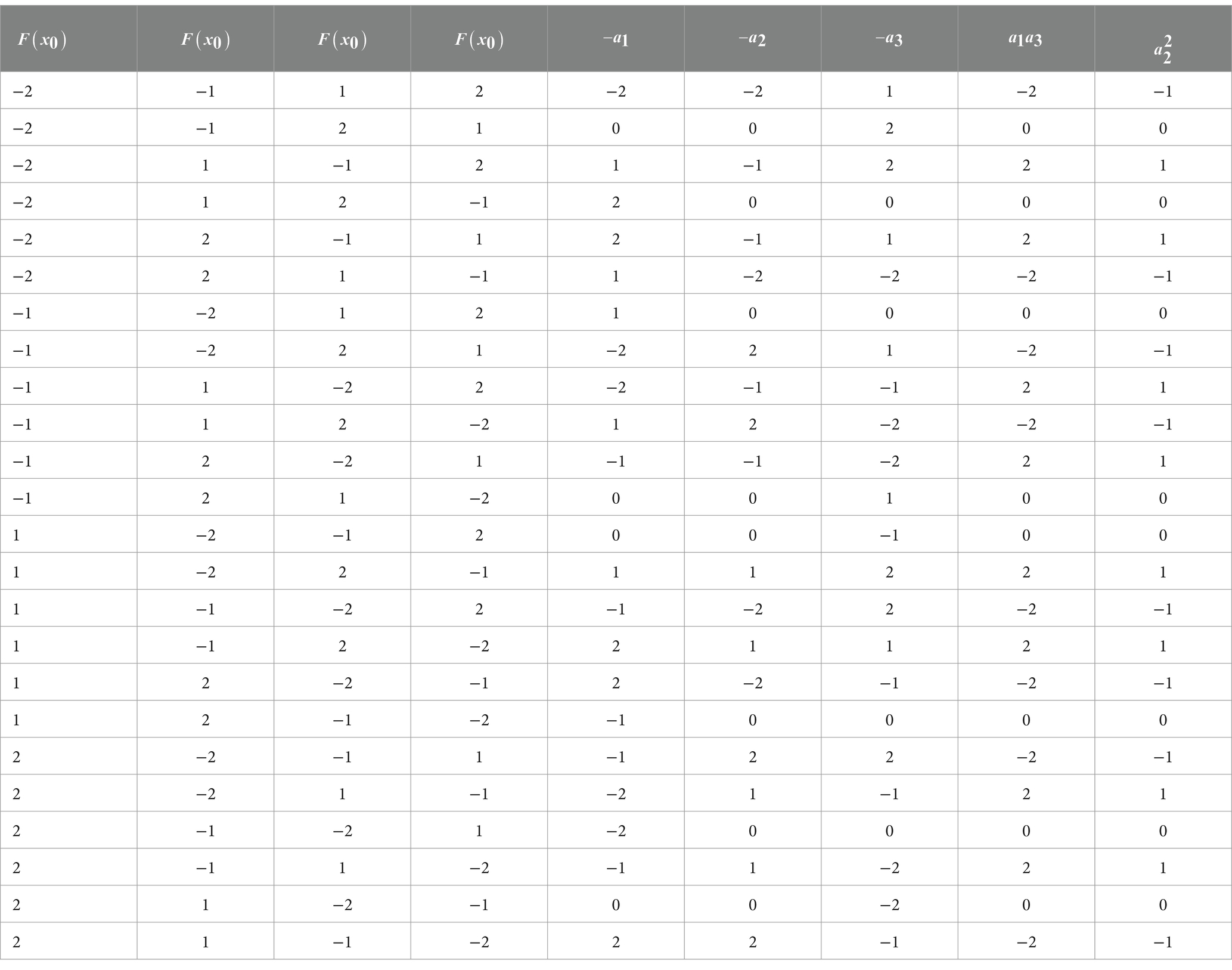
Table 2. On the classification of representations of elements of group S4 by polynomials over the field GF(5).
Moreover, the combinations of values presented in Table 2 exhaust the entire set of situations when Equation 32 is satisfied. Indeed, for anyone in the field . Therefore, in this case should be , as Table 2 shows.
Therefore, combinations of values are classified as follows.
First subset: , and there are 8 options in this case. Four of them correspond to the case , and in this case takes four possible values, and another four correspond to the reverse situation ( takes four possible values).
Second subset: In this case , and can take four arbitrary values that uniquely determine the values . Each of these options corresponds to two solutions to the equation , i.e., there are also 8 options here.
The third subset also corresponds to 8 options given by the relation and two solutions to the equation .
Thus, Equation 32 really exhausts all possible combinations of and gives rise to their classification from the point of view of representing the elements of the group under consideration over the field .
Next, let us consider the expression
This expression was obtained taking into account Equations 31, 32. One can see that the coefficient of the zero degree in this expression is given by the following formula.
Direct verification can verify that this coefficient is also zero. It can be seen that formulas (Equations 33 and 34) show that additional constraints are indeed imposed on the coefficients .
Consequently, substitutions of the form (Equation 30) leave unchanged the form of representation (Equation 25), in which the coefficient at the zero degree of variable is equal to zero.
The advantage of the classification under consideration is that each element of the group can be characterized by a code combination of the following form
Where
Variables are assigned values according to the following algorithm.
Equality is checking. If , then the variable is assigned the value 0. For this case, the equality is checked on next step.
If , then the variable is assigned the value 0, and the variables and are assigned values corresponding to the values of the number in binary representation and subjected to the following transformation.
If , then the variable is assigned the value 1, and the variables and are assigned values corresponding to the value of and also subjected to transformation (Equation 36). Those, in both of these cases, the values of the variables and correspond to one of the numbers from 0 to 3 in binary representation.
If , the sign of the product is checked. If , then the variable is assigned the value 1. If , then the variable is assigned the value 2.
Next, the sign is checked. If , then the variable is assigned the value 1. If , then the variable is assigned the value 0.
Variables and are assigned values corresponding to the values in binary encoding and subjected to transformation (Equation 36).
This allows you to calculate answer numbers using simple software tools.
Note that a similar code sequence arises, for example, in the following representation of the elements of the group under consideration
Where
Representation Equation 37 corresponds to the compositional series possessed by the group ; this series includes the alternating group and the quaternary Klein group (Equation 35); it also corresponds to the number of values that the variables in formula (Equation 36) can take.
The transition to the decimal number system from entry (Equation 1) is carried out according to the formula
The numbers given by Equation 38 were used to construct Figures 1–3.
4 Discussion
The most important empirical result of the study is the very fact of a sharply heterogeneous distribution of respondents’ answers by number.
This means that there are certain types of structure of personal preferences, and, consequently, some psychological types that can be interpreted as dominant (at least as the most frequently occurring).
Specifically, from Figure 1 it follows that the most common answer is number 9 (combination 4,132). The archetypes closest to these respondents are the Seeker, the Creator, the Jester and the Thinker (the sequence is important).
We can conclude that in the personality structure of such respondents, a creative orientation prevails, the motive of self-actualization, the motive of creating something new, original, non-standard through self-development, personal growth, self-search, personal and professional self-determination dominates.
Personal maturity, as well as communicative and cognitive activities for such respondents are obviously in the second place. There is every reason to assert that such people still occupy an infantile position regarding themselves and their place in society.
It follows from Figure 2 that this answer option is most often found among young people; for girls it remains at the second level.
Answer No. 5 (combination 4,123) is closest to such archetypes as “The Creator” (his calling and greatest joy in life is creativity in all its manifestations, and the need to spend most of his time on routine matters turns into a tragedy for him) and “The Self,” then is the main archetype, the archetype of the psychological structure and integrity of the individual, reflecting the unity of the conscious and unconscious, the unity of all parts.
Respondents who choose this sequence of pictures are characterized, first of all, by the following features: focus on creation, creativity, inspiration, avoidance of stereotyping and materiality (personal development, self-understanding, acceptance of oneself, mental and physical unity). In this combination, the creativity of the respondents is inversely related to the need for affiliation (to be accepted by society): creativity is not an external structure, but is internal in nature.
The frequency of occurrence of this answer option reaches one of its peak values only among boys; for girls it remains at a background level. This, however, does not mean that men are more creative. In this case, Jung’s archetypal structures “anima / animus” are highlighted, where the internal image of a woman in a man and vice versa are embodied in all spheres of life in the context of productive / reproductive life.
Answer choice No. 2 (combination 1,432) suggests that such respondents are characterized by the following features. The archetype “The Self” dominates (as something that we feel, think, sense, intuitively predict, something that is learned from experience and creative activity). That is, the respondents see their self-realization through creativity, spontaneity, insight, and intuition. The sphere of contacts and cognition as such are less significant.
This answer option is statistically the most significant for boys (the third most common value), but for girls it noticeably exceeds the background values.
The choice of answer No. 17 (combination 1,342) suggests that such respondents have an expressed process of individuation - conscious interaction with their inner center (mental core) or The Self. This is the only one of the most common answers for which the process of individualization is associated with communication and interaction. Creativity and knowledge fade into the background. The closest archetypes to this answer are the Self, the Jester, the Seeker, the Thinker, and the Ruler.
This answer option is statistically the most significant for boys (the third most common value), but for girls it noticeably exceeds the background values.
For girls, the most common answer options are No. 3.
This option corresponds to the archetypes of the Jester, the Seeker, the Thinker and the Ruler. This indicates that girls are more focused on interaction and communication, i.e., they are focused on the external plane, and the importance of external stimuli for self-realization is manifested.
It is noteworthy that option No. 22, which is often found in girls, is not found at all in boys, i.e., for this case, gender differences become most pronounced.
This option corresponds to cognitive archetypes (the Thinker, the Seeker, the Sage), which form the cognitive sphere of the individual. At an unconscious level, girls are dominated by a gnostic orientation, that is, towards the process of acquiring knowledge. Contrary to the existing stereotype that women live by emotions, we see a completely opposite picture, where reflection and cognitive abilities come to the fore.
Thus, the most common answer options make it possible to identify two opposite tendencies among students. The first of them is a focus on creativity and self-development, the second tendency is the desire for oneself, one’s self. Moreover, only for options No. 9 and No. 5, communication and cognitive activity become psychological conditions for the achievement of personally significant needs.
Of course, the interpretation presented above, in which archetypes are used, is debatable, especially if we take into account that such tests as the Luscher test and its analogues (24–26) have often been criticized in the literature (36). We emphasize that such tests based on ranking images are used quite actively (36), and in the psychological literature they are united by the common term “projective techniques.”
It is appropriate to emphasize that the article cited above (36) was written based on discussions held as part of a special organized conferences “Conditions of using projection methods in psychological diagnosis for court purposes,” which was held on 16–17 November 2012 in Lublin. As emphasized in (Equation 36), the Conference was prompted by an initiative launched by the polish Sceptics Society under the slogan “psychology is science, not witchcraft” to protest against the use of projective techniques, which it saw as harmful and anachronistic, and this the discussion spilled out onto the pages of Polish media in 2012.
Moreover, the authors of (36) claim that tests of the type under consideration are, strictly speaking, not projective techniques. In their opinion, these tests are not based on the Frank’s projective hypothesis (22, 37), but on the belief—which cannot be explained rationally—that there is a set of interdependencies between a person’s particular preferences and the general characteristics of his personality.
The edge of this kind of criticism is also largely directed at the fact that the development “projective techniques” is based on intuitive considerations, and does not have a consistent methodological justification.
Based on the results obtained in present report, difficulties of this kind, in our opinion, can be overcome in the following way.
Experiments on ranking pictures based on preferences can be represented by the following equivalent circuit (Figure 5). The neural network formed by brain cells in such experiments is de facto connected to another external additional layer of neurons. In the case of four pictures, this layer, as follows from formula (35), contains three binary neurons, and one neuron having three possible output states.
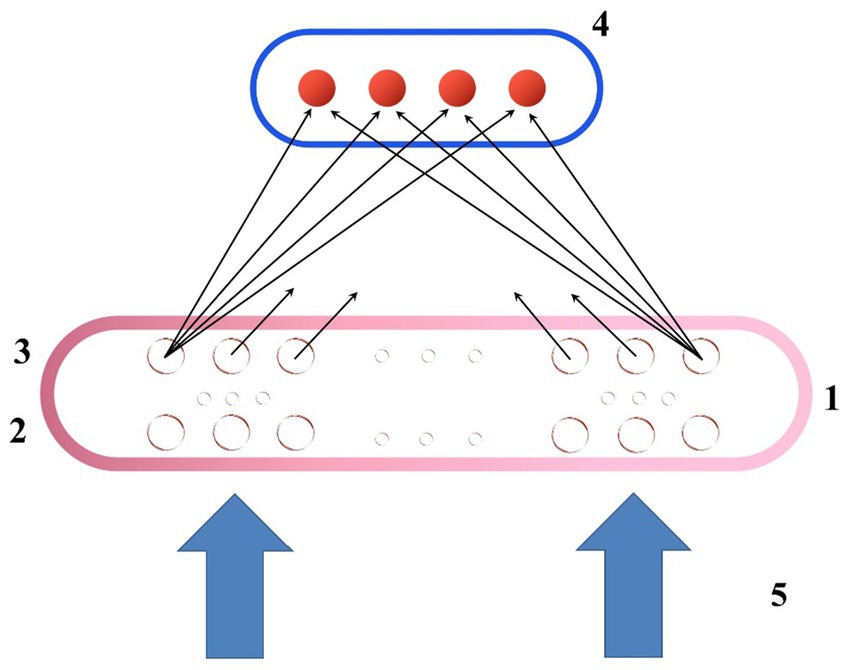
Figure 5. Equivalent diagram of the test procedure using “projective techniques”; 1—neural network formed by the brain, 2 and 3—its separate layers, 4—equivalent output layer responsible for testing, 5—external stimuli.
Let us recall that the “image” in the theory of neural networks is often understood as a set of binary (or other) variables that is formed at the inputs of the neurons of the first layer of the network (as well as at the outputs of its last layer).
Accordingly, according to the scheme in Figure 5, those complex images that are formed in the base neural network (the respondent’s brain) are actually projected onto the last (external) layer.
The most significant thing here is that the test result should also be interpreted as an “image.” In particular, this means that not any combination of variables in formula (35) makes sense, but only those that dominate in obtained statistics.
This removes many of the objections reflected in publications such as (36). Not every sequence of pictures (not every choice of the respondent) is meaningful. This is a projection of a complex image onto an extremely simplified one, and such a projection may also contain “errors.” Nevertheless, they can be interpreted as permissible deviations from the basic ones, i.e., from those that are statistically most common. The adequacy of this approach follows, among other things, from a comparison of Figures 1, 3 and Figures 2, 4, the maxima in which in most cases correspond to the same numbers.
In particular, in relation to the result shown in Figure 1, the number of base images is 4. The number of images related to the neighborhood of the base (one transposition) is 7 (six possible transpositions + the base image itself). Therefore, the total number of images that can be correlated with the base ones is 28, which covers the set of possible combinations, 4! = 24.
Consequently, tests of the type under consideration can be interpreted, first of all, as classification ones. However, the choice of images used is largely arbitrary.
To summarize, we can propose the following approach to constructing tests related to “projective techniques.”
For intuitive or heuristic reasons, a set of pictures similar to those presented in table is formed 1. Next, diagrams similar to those shown in Figures 1, 2 are constructed. Provided that the result shows the presence of pronounced maxima, then they are interpreted (possibly using additional testing methods).
Testing is carried out using the correlation of a specific result with basic images that correspond to the maxima on empirically constructed diagrams.
At the end of this section, we emphasize that within the framework of this work, the authors did not set themselves the task of proving the adequacy of using this particular test in full (in any case, this task was by no means the main one). We saw our task in developing new tools for analyzing the statistics of respondents’ answers to questions that demonstrate the identification of certain classification features that allow for further interpretation. The pictures used were constructed from heuristic considerations. Strictly speaking, other sets could have been used for the task at hand.
However, in order to demonstrate the adequacy of the choice made (which also serves as an additional confirmation of the results obtained), calculations were performed using an additional technique. Specifically, correlation coefficients were calculated between the numbers of answers on the i-th and j-th positions in the respondents’ ranking list. The corresponding data are presented in Table 3 (critical values for 100 or more respondents r = 0.195, at p ≥ 0.05).

Table 3. Calculation of correlation coefficients between the number of answers at the i-th and j-th positions in the ranked list of respondents.
It can be seen that the choice of archetypal images of respondents is in inverse relation to each other, i.e., there is an inverse internal consistency, which serves to confirm the adequacy of the choice of pictures used for the proposed test.
5 Conclusion
Thus, the results of our experiments show that the distribution of respondents’ answers to a test in which they are asked to rank pictures according to the nature of their personal preferences is clearly heterogeneous.
In this case, for quantitative processing of the results of experimental measurements, it is convenient to use a technique based on representing permutations by polynomials defined over a Galois field. Specifically, for a test containing 4 pictures it is convenient to use the GF(5) field.
The results obtained and our proposed interpretation make it possible to remove at least some of the objections to the use of “projective techniques” in psychological testing. Our interpretation is based on considering the test result as an additional (external) layer of the neural network, formed when the test is “connected” to the neural network formed by the human brain. In this case, the test result is considered as a projection image, possibly containing “errors,” i.e., deviations from basic projection images that correspond to the results most often encountered in experiments.
The results obtained also allow us to propose the following methodology for creating psychological tests based on experimental data.
It is based on the selection of sequences (permutations) that are most often encountered in experiments. They are interpreted as basic projection images used as classification features.
The correlation of the result of a specific test with the base images is carried out according to the principle of the minimum code distance (minimum number of transpositions) from a certain base image.
Calculating code distances between different permutations can also be done by representing the permutations as polynomials over the corresponding Galois field. In particular, when using a test that includes six pictures, the Galois field GF(7) should be used.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The studies involving humans were approved by Ethics committee Al-Farabi Kazakh National University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
IS: Funding acquisition, Writing – original draft, Writing – review & editing. MK: Conceptualization, Methodology, Resources, Writing – original draft, Writing – review & editing. AG: Conceptualization, Formal analysis, Methodology, Resources, Writing – original draft, Writing – review & editing. DM: Formal analysis, Funding acquisition, Software, Validation, Visualization, Writing – review & editing. YV: Data curation, Funding acquisition, Investigation, Project administration, Supervision, Visualization, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research has been funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP14870416).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Lee, M, Kim, Y, and Kim, Y-K. Generating psychological analysis tables for children's drawings using deep learning. Data Knowl Eng. (2024) 149:102266. doi: 10.1016/j.datak.2023.102266
2. Webber, TA, Collins, RL, Sullivan, KL, Chen, DK, and Grabyan, JM. Clinical identification of psychogenic nonepileptic events using combinations of psychological tests in a veteran sample. Epilepsy Behav. (2021) 115:107631. doi: 10.1016/j.yebeh.2020.107631
3. Bakirov, AS, Vitulyova, YS, Zotkin, AA, and Suleimenov, IE. Internet users' behavior from the standpoint of the neural network theory of society: prerequisites for the meta-education concept formation. Int Arch Photogramm Remote Sens Spatial Inf Sci. (2021) XLVI-4/W5-2021:83–90. doi: 10.5194/isprs-archives-XLVI-4-W5-2021-83-2021
4. Sarah, M, Hutchison, OD-JG, Watts, A, Oberle, E, Gadermann, A, Goldfarb, DM, et al. Anxiety symptoms, psychological distress, and optimism in school staff: testing associations with stressors and coping during the second year of the COVID−19 pandemic. J Affect Disord Rep. (2023) 14:100662. doi: 10.1016/j.jadr.2023.100662
5. Bianchi, D, Morelli, M, Baiocco, R, and Chirumbolo, A. Sexting as the mirror on the wall: body-esteem attribution, media models, and objectified-body consciousness. J Adolesc. (2017) 61:164–72. doi: 10.1016/j.adolescence.2017.10.006
6. Matz, SC, and Netzer, O. Using big data as a window into consumers’ psychology. Curr Opin Behav Sci. (2017) 18:7–12. doi: 10.1016/j.cobeha.2017.05.009
7. Dyriv, A., Andrunyk, V., Burov, Y., Karpov, I., and Chyrun, L. The user's psychological state identification based on big data analysis for person's electronic diary. In 2021 IEEE 16th international conference on computer sciences and information technologies (CSIT) (Vol. 1, pp. 101–112). IEEE; (2021).
8. Reis, D, and Jones, T. Aromatherapy: using essential oils as a supportive therapy. Clin J Oncol Nurs. (2017) 21:16–9. doi: 10.1188/17.CJON.16-19
9. Vitulyova, YS, Kadyrzhan, KN, Kabdushev, SB, Bakirov, AS, Kostsova, MV, Grishina, AV, et al. Aromatherapeutic correction of psychoemotional state as a means of promoting an ecological worldview In: A Beskopylny, M Shamtsyan, and V Artiukh, editors. XV international scientific conference INTERAGROMASH 2022. INTERAGROMASH 2022. Lecture notes in networks and systems, vol 574. Cham: Springer (2023)
10. Matthews, MR. Feng Shui in science programs. Sci Educ. (2021) 30:1319–32. doi: 10.1007/s11191-021-00281-4
11. Suleimenov, IE, and Gabrielyan, OA. Bakirov AS neural network approach to the interpretation of ancient Chinese geomancy Feng Shui practices. Eur J Sci Theol. (2023) 19:39–51.
12. Kabdushev, S., Kadyrzhan, K., Vitulyova, Y., Bakirov, A., Yevstifeyev, V., and Suleimenov, I., "Means of aromatherapy of mass use as a tool for correcting the psychophysiological state of society,"2022 2nd international conference on robotics, automation and artificial intelligence (RAAI), Singapore, Singapore (2022), 152–156, doi: 10.1109/RAAI56146.2022.10092984
13. Saidakhmet, AT, Vitulyova, YS, Bakirov, AS, Kabdushev, SB, Baipakbayeva, ST, and Kostcova, MV, … Sileimenov, IE. Principles and technical means of implementing the methods of group correction of the Psychoemotional state in the online format. In International scientific conference on agricultural machinery industry Interagromash (1126–1136). Cham: Springer International Publishing; (2022), doi: 10.1007/978-3-031-21432-5_120
14. Björngrim, S, van den Hurk, W, Betancort, M, Machado, A, and Lindau, M. Comparing traditional and digitized cognitive tests used in standard clinical evaluation–a study of the digital application minnemera. Front Psychol. (2019) 10. doi: 10.3389/fpsyg.2019.02327
15. Montag, C, and Rumpf, H-J. The potential of digital phenotyping and Mobile sensing for psycho-diagnostics of internet use disorders. Curr Addict Rep. (2021) 8:422–30. doi: 10.1007/s40429-021-00376-6
16. Wang, C. Application of MPP database and artificial intelligence system in online evaluation of college students' mental health. Prev Med. (2023) 173:107580. doi: 10.1016/j.ypmed.2023.107580
17. Shafiq, M, Zhang, Q, Akbar, MA, Khan, AA, Hussain, S, Amin, FE, et al. Effect of project management in requirements engineering and requirements change management processes for global software development. IEEE Access. (2018) 6:25747–63. doi: 10.1109/ACCESS.2018.2834473
18. Salah, M, Al Halbousi, H, and Abdelfattah, F. May the force of text data analysis be with you: unleashing the power of generative AI for social psychology research. Comput Human Behav Artif Humans. (2023) 1:100006. doi: 10.1016/j.chbah.2023.100006
19. Pellert, M., Lechner, C. M., Wagner, C., Rammstedt, B., and Strohmaier, M.. AI Psychometrics: Assessing the Psychological Profiles of Large Language Models Through Psychometric Inventories. Perspect Psychol Sci. (2024) 19:808–826. doi: 10.1177/17456916231214460
20. Frank, E-S, Olli, Y-H, and Matthias, D. Utilizing social media data for psychoanalysis to study human personality. Front Psychol. (2019) 10. doi: 10.3389/fpsyg.2019.02596
21. Ruiz-Mafe, C, Chatzipanagiotou, K, and Curras-Perez, R. The role of emotions and conflicting online reviews on consumers' purchase intentions. J Bus Res. (2018) 89:336–44. doi: 10.1016/j.jbusres.2018.01.027
23. Stanzani Maserati, M, Mitolo, M, Medici, F, D'Onofrio, R, Oppi, F, Poda, R, et al. Color choice preference in cognitively impaired patients: a look inside Alzheimer's disease through the use of Lüscher color diagnostic. Front Psychol. (2019) 10:1951. doi: 10.3389/fpsyg.2019.01951
24. Thiry, B, and Parete, S. Predictive validity of the Szondi test in the assessment of psychopathy [Validité prédictive du test de Szondi dans l'évaluation de la psychopathie]. Ann Med-Psychol. (2016) 174:456–60. doi: 10.1016/j.amp.2014.12.016
25. Sityaeva, SM, Yaremtchuk, SV, and Tarasenko, VV. The position in the family relations system as a predictor of young men extremist attitudes In: D Solovev, editor. Smart technologies and innovations in Design for Control of technological processes and objects: Economy and production. FarEastСon 2018. Smart innovation, systems and technologies, 139. Cham: Springer (2019)
26. Webb, P. A course in finite group representation theory (vol. 161). Cambridge: Cambridge University Press (2016).
28. Suleimenov, IE, Vitulyova, YS, Kabdushev, SB, and Bakirov, AS. Improving the efficiency of using multivalued logic tools. Sci Rep. (2023) 13:1108. doi: 10.1038/s41598-023-28272-1
29. Suleimenov, IE, Vitulyova, YS, Kabdushev, SB, and Bakirov, AS. Improving the efficiency of using multivalued logic tools: application of algebraic rings. Sci Rep. (2023) 13:22021. doi: 10.1038/s41598-023-49593-1
30. Moldakhan, I, Matrassulova, DK, Shaltykova, DB, and Suleimenov, IE. Some advantages of non-binary Galois fields for digital signal processing. Indones J Electr Eng Comput Sci. (2021) 23:871–7. doi: 10.11591/ijeecs.v23.i2
31. Vitulyova, ES, Matrassulova, DK, and Suleimenov, IE. Application of non-binary Galois fields Fourier transform for digital signal processing: to the digital convolution theorem. Indones J Electr Eng Comput Sci. (2021) 23:1718–26. doi: 10.11591/ijeecs.v23.i3.pp1718-1726
32. Sun, X, Zhang, T, Cheng, C, Yan, X, Cai, Y, Yang, Y, et al. A memristor-based in-memory computing network for hamming code error correction. IEEE Electron Device Lett. (2019) 40:1080–3. doi: 10.1109/LED.2019.2917944
33. Bakirov, AS, and Suleimenov, IE. On the possibility of implementing artificial intelligence systems based on error-correcting code algorithms. J Theor Appl Inf Technol. (2021) 99:83–99.
34. Kobayashi, M. Hopfield neural networks using Klein four-group. Neurocomputing. (2020) 387:123–8. doi: 10.1016/j.neucom.2019.12.127
35. Paluchowski, WJ, and Stemplewska-Żakowicz, K. The reliability of projective techniques as tools of psychological assessment. Part 1: why it is unjustified to describe some of them as projective. Prob Forensic Sci. (2013) 93:421–30.
36. Jain, M, Singh, A, Kar, SK, Weiner, IB, and Kuehnle, K. Projective assessment of children and adolescents In: The Curated Reference Collection in Neuroscience and Biobehavioral Psychology (2016) 431–58.
Keywords: psychological testing, symmetric groups, Jungian philosophy, Galois fields, archetypes, projective technique
Citation: Suleimenov I, Kostsova M, Grishina A, Matrassulova D and Vitulyova Y (2024) Empirical validation of the use of projective techniques in psychological testing using Galois fields. Front. Appl. Math. Stat. 10:1455500. doi: 10.3389/fams.2024.1455500
Edited by:
Lorentz Jäntschi, Technical University of Cluj-Napoca, RomaniaReviewed by:
Adam Miranowicz, Adam Mickiewicz University, PolandMunish Kansal, Thapar Institute of Engineering & Technology, India
Mihaela Aurelia Tomescu, Universitatea Din Petrosani, Romania
Copyright © 2024 Suleimenov, Kostsova, Grishina, Matrassulova and Vitulyova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yelizaveta Vitulyova, bGl6YXZpdGFAbGlzdC5ydQ==
 Ibragim Suleimenov1
Ibragim Suleimenov1 Yelizaveta Vitulyova
Yelizaveta Vitulyova