- 1Department of Mathematics and Statistics, College of Science, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
- 2Information and Communication Technology Research Group, Scientific Research Center, Al-Ayen University, Thi-Qar, Iraq
In this effort, we present a new definition of the Steiner symmetrization by using special analytic functions in a complex domain (the open unit disk) with respect to the origin. This definition will be used to optimize the class of univalent analytic functions. Our method is based on the concept of differential subordination and the Carathéodory theory. Examples are illustrated in the sequel involving the modified Libera–Livingston–Bernardi integral operator over the open unit disk. The result gives that this integral satisfies the definition of bounded turning function (univalent analytic function).
1 Introduction
In convex geometry, the process of “Steiner symmetrization” is used to change an existing convex body into a symmetric one when compared with a particular axis or plane. Steiner symmetrization takes a convex body and replaces every point with the midpoint of the line segment that goes from that point to its reflection across the selected axis or plane. Because the resultant symmetric body and the original body share some geometric features, analysis of the half plane becomes simpler. This transformation may streamline computations and provide insightful findings in specific situations, such as geometric inequalities and optimization issues affecting convex bodies. The definition of Steiner symmetrization in a complex domain admits many formulas. Smith et al. [1] suggested some Poincare domains Ω to define Steiner symmetrization, which are as follows:
Peretz [2] considered the formula in the open unit disk Ω: = {ζ ∈ ℂ:|ζ| < 1} as follows:
The above definitions can sometimes yield loss in information when symmetrizing a shape or function. This situation might not be desired, especially if the original shape or function's features or properties are crucial for analysis or interpretation. Depending on the original form or function being symmetrical, Steiner symmetrization may or may not be successful. The application of this type of approach may be limited by some geometries or functions that are not well suited for symmetrization using this method. Moreover, the computational cost of Steiner symmetrization can be high, particularly for intricate forms or functions. For some applications, especially those that call for real-time or very real-time analysis, this computing expense can render it unfeasible. Therefore, we aim to enhance the above definitions using special functions.
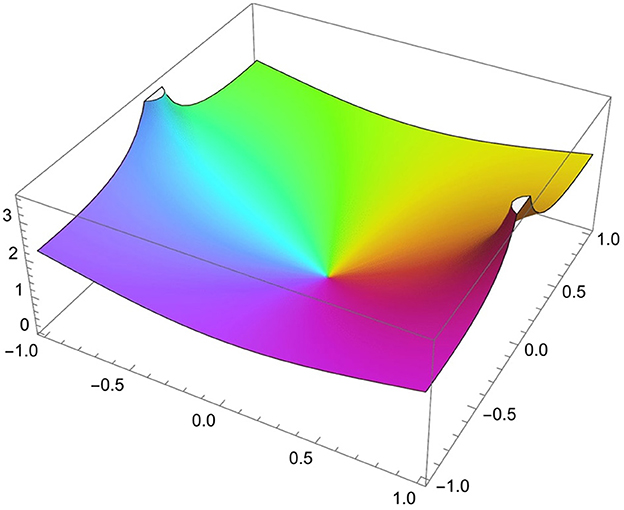
In this study, we consider the function (see Figure 1) as follows:
This function maps Ω conformally onto the horizontal strip Π = {ζ:|ℑζ| < π/2}. Moreover, this function maps the hyperbolic geodesic (−1, 1) onto the real axis, and it maps the curves equidistant from (−1, 1) onto the horizontal lines Π. To define the Steiner symmetrization, we need the following function:
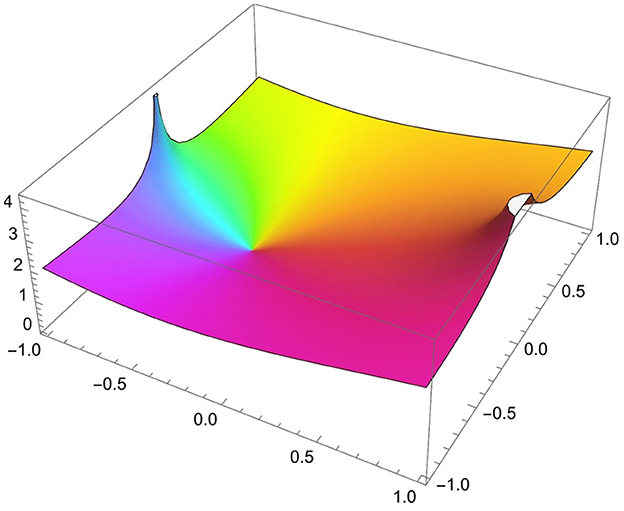
where S(0) = 1 (see Figure 2). Then, the Steiner symmetrization becomes
where φ is analytic function in , where is the class of analytic function with the power series
such that φ(0) = 1. A good example of this function (or the extreme function of this class) is the Janowski function [3], which will be investigated in the next section.
Our goal is to maximize the class of analytic functions that are univalent. The Carathéodory theory and the idea of differential subordination serve as the foundation for our approach. In the sequel, illustrations are given. The study is organized as follows: Section 2 deals with preliminaries and Section 3 involves the main results.
2 Methods
For two analytic functions, f1(ζ) and f2(ζ) in Ω are called subordinated denoting by f1(ζ) ≺ f2(ζ) if they satisfy f1(0) = f2(0) and the inclusion property f1(Ω) ⊂ f2(Ω) (see [4]). As an application, Ma-Minda formula for some special classes
for starlike functions, and
for convex functions, where ρ has a positive real part in Ω, ρ(0) = 1 and the normalized class of analytic functions in Ω with f(0) = 0 and f′(0) = 1. Thus, f admits the power series
In fact, the function f is starlike whenever , and it is convex when
The function is starlike whenever −1 < ℜ(ζ) < 0 or 0 < ℜ(ζ) < 1. Moreover, it is convex whenever, −1 < ℜ(ζ) < 1 and
This function is considered for symmetrization in the study mentioned in Betsakos et al. [5]. While for the function is starlike and convex when −1 < ℜ(ζ) < 0 or 0 < ℜ(ζ) < 1. Note that is an extreme Janowski function.
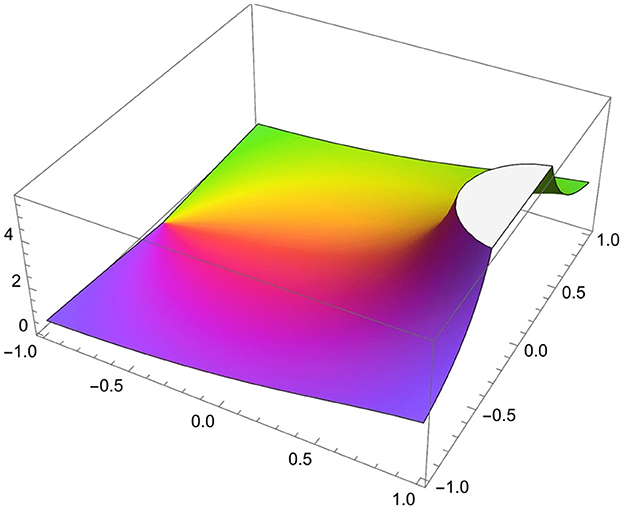
In our investigation, we concern about the Carathéodory function (a function that maps Ω onto the right half plane), φ(ζ), which is involved in the inequalities (see Figure 3):
where φ(0) = 1 and ℜ(φ) > 0.
Our aim is to determine the upper bound of the parameter σ, where the function ϱ ∈ Ω is analytic such that ϱ(0) = 1 and ℜ(ϱ(ζ)) > 0. Note that the condition of where φ(0) = 1, ℜ(φ) > 0 is equivalent to achieve the inequality:
where the function is a Carathéodory function. Moreover, the function has a root and two branch points at ζ = ±1, with the power series at ζ = −1
and at ζ = 1 when
The notion of the Carathéodory function, often referred to as the Carathéodory kernel function, is principally used in the theory of univalent functions, which are complex functions that are holomorphic (analytic) and injective (one-to-one).
3 Results
In this part, we illustrate the main results.
Theorem 3.1. Assume that the function φ ∈ Ω is analytic such that φ(0) = 1 and ℜ(φ(ζ)) > 0. If
then
where
Proof: Case 1.
Let k = 0. Then, by Equation 1, we get:
Define a function Φσ0:Ω → ℂ as follows:
Clearly, Φσ0(ζ) is analytic in Ω such that Φσ0(0) = 1, and it is a solution of the first order differential equation
Burt is starlike in Ω, and then according to Miller-Mocanu Lemma in Miller and Mocanu [4] -P132, the subordination
yields
Now, we aim to show that
Obviously, Φσ0(ζ) achieves the inequality
Since satisfies the following inequality
this function has two branch points ζ = ±1, and then, we get
where and
As a consequence, we obtain the inequality subordination
Thus, inequality (Equation 2) is valid.
Case 2
Let k = 1. From Equation 1, we have:
Define a function Φσ1: Ω → ℂ as follows:
Obviously, Φσ1(ζ) is analytic in Ω with Φσ1(0) = 1. Moreover, it is indicated a solution of the differential equation
Then Miller-Mocanu Lemma implies that the subordination
gives
A computation yields
By using Equation 3, we obtain the inequality:
where
As a consequence, we obtain the inequality subordination:
Thus, inequality (Equation 2) is valid.
Case 3
Let k = 2. From Equation 1, we have:
Define a function Φσ2: Ω → ℂ as follows:
Obviously, Φσ2(ζ) is analytic in Ω with Φσ2(0) = 1. Moreover, it is indicated as a solution of the differential equation:
Then Miller-Mocanu Lemma implies that the subordination
gives
A computation yields
and
which means that
By using Equation 3, the inequality
has a maximum solution when
As a consequence, we obtain the inequality subordination:
Thus, inequality (Equation 2) is valid.
Example 3.2. One of the important applications in this direction is the modified Libera–Livingston–Bernardi integral operator over Ω, which has the following structure:
For the integral satisfies
where Bζ[, ] indicates the Beta function. Moreover, for the integral satisfies
Hence, the integral is preserved the normalization f(0) = f′(0)−1 = 0. Let
with ℜ(φ(ζ)) > 0. Then, a computation yields
We have the following result:
Proposition 3.3. Consider f(ζ) is a normalized analytic function in Ω such that f(0) = f′(0)−1 = 0 and for with ℜ(φ(ζ)) > 0. If
then
where
Proposition 3.3 indicates that F(f(ζ)) is bounded turning function. A bounded turning function is a type of mathematical function made up of straight line segments connected linked at predetermined locations, each segment having a bounded slope (or derivative). It is sometimes referred to as a piecewise linear function or zigzag function. Numerous applications, including as robotics, computer graphics, and signal processing, frequently make advantage of these features. Moreover, bounded turning describes the restriction that the rate of change (slope or derivative) of the function is restricted within a given range. This indicates that the graph of the function shows moderate shifts in orientation within predetermined bounds rather than abrupt or unbounded alterations.
4 Conclusion and discussion
The above investigation concerned about a new definition of the Steiner symmetrization using a special function The main result was about using the suggested definition to optimize a class of analytic functions. This optimization showed the geometric symmetrization of the class. In our research, we utilized the differential subordination based on Miller–Mocanu Lemma. The effort is satellited in the open unit disk, where the symmetrization can be recognized. Moreover, our result yielded the type of analytic functions that the set can be contained. This type was the Carathéodory function. Because it offers a quantitative assessment of how these functions behave closely to a certain point, the Carathèodory function is significant in the theory of univalent functions, like the function . It is useful in gaining an understanding of conformal mappings and geometric function theory among other fields of complex analysis.
Moreover, among polygons, Steiner symmetrization is a potent approach for maximizing the Laplace operator's initial eigenvalue with Dirichlet boundary conditions. It can use the characteristics of symmetric domains to minimize the eigenvalue by reshaping the polygon into a more symmetrical form. Nevertheless, careful numerical implementation and consideration of the particular qualities of the initial polygonal domain are necessary for the actual application of the technique. Depending on the domain's geometry, such as its volume and eigenvalue index, Polya's theorem gives a lower bound on the Laplace operator's eigenvalues. This facilitates the comprehension of the relationship between the eigenvalues and the domain's size and form. According to Hirsch's theorem, a domain's initial eigenvalue does not rise when it is symmetric. This is helpful in optimization issues when the goal is to change the domain into a more symmetric shape in order to reduce the first eigenvalue.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
IA: Resources, Writing – review & editing. RI: Formal analysis, Methodology, Writing – original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Smith W, Stanoyevitch A, Stegenga DA. Planar poincar domains: geometry and Steiner symmetrization. J Anal Mathm. (1995) 66:137–83. doi: 10.1007/BF02788821
2. Peretz R. Applications of Steiner symmetrization to some extremal problems in geometric function theory. arXiv preprint arXiv:1607.01674. (2016).
3. Janowski W. Some extremal problems for certain families of analytic functions I. In: Annales Polonici Mathematici. (1973). p. 297–326. doi: 10.4064/ap-28-3-297-326
4. Miller SS, Mocanu PT. Differential Subordinations: Theory and Applications. London: CRC Press. (2000). doi: 10.1201/9781482289817
Keywords: analytic function, univalent function, Steiner symmetrization, subordination and superordination, open unit disk
Citation: Alazman I and Ibrahim RW (2024) A new Steiner symmetrization defined by a subclass of analytic function in a complex domain. Front. Appl. Math. Stat. 10:1385590. doi: 10.3389/fams.2024.1385590
Received: 18 March 2024; Accepted: 11 July 2024;
Published: 13 August 2024.
Edited by:
Xiaodong Luo, Norwegian Research Institute (NORCE), NorwayReviewed by:
Yuchen Wang, Tianjin Normal University, ChinaSeck Diaraf, Cheikh Anta Diop University, Senegal
Copyright © 2024 Alazman and Ibrahim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rabha W. Ibrahim, cmFiaGFAYWxheWVuLmVkdS5pcQ==; cmFiaGFpYnJhaGltQHlhaG9vLmNvbQ==
 Ibtehal Alazman
Ibtehal Alazman Rabha W. Ibrahim
Rabha W. Ibrahim