Optimal control problem for mathematical modeling of Zika virus transmission using fractional order derivatives

This study delves into the dynamics of Zika virus transmission by employing a mathematical model to explain virus spread with fractional order derivatives. The population is divided into two groups: the human group and the ticks group to accurately explain the transmission routes of the virus. The objective of this research is to protect susceptible individuals from infection and curb the spread of this endemic disease. To achieve this, we have included two control measures: the first is a sensibilization program, and the second is treatment. We investigate the use of optimal control strategies and fractional derivative techniques under the Caputo method to reduce the number of exposed and infected individuals. By employing the Pontryagin maximum principle to analyze and characterize the optimal controls, the proposed method is further validated through numerical simulations. The outcome of this study highlights the importance of containing the rate of dynamic dissemination in preventing the Zika epidemic.

1 Introduction

Zika virus infection is a disease caused by a viral infection that spreads primarily through the bites of infected mosquitoes. While some person may not experience any noticeable symptoms, others may develop fever, rash, joint pain, or conjunctivitis (known as pink eye). The consequences of Zika virus infection can be particularly devastating for pregnant women, as it can lead to severe birth defects such as microcephaly, where a baby is born with an abnormally small head, as well as eye abnormalities. Apart from mosquito bites, the virus can also be transmitted through sexual contact, blood transfusion, and from a pregnant woman to her fetus before or during birth.¹ Although symptoms, if any, are generally mild, healthcare professionals often consider a person's symptoms and recent history to suspect Zika virus infection. Vis–vis to confirm the diagnosis, blood or urine tests are usually performed.²

Zika virus infection can be effectively prevented by taking certain precautions. First, it is important to avoid mosquito bites completely. Although there is currently no specific treatment for Zika virus infection, there are measures that can help relieve symptoms.³ Adequate rest, drinking plenty of fluids, and using acetaminophen can help reduce fever and relieve pain. Zika virus spreads in a similar way to other arthropod-borne viruses such as dengue, yellow fever, and chikungunya. It is transmitted primarily by certain types of mosquitoes called Aedes mosquitoes, which lay their eggs in areas with stagnant water. These mosquitoes are particularly active during the day, both indoors and in shaded areas outdoors [1].

The Zika virus was first identified in the Zika Forest of Uganda in 1947. It remained relatively unknown until 2007 when significant outbreaks began occurring in the South Pacific islands. The situation escalated in May 2015 when cases of local transmission were reported in South America, followed by Central America and the Caribbean. Eventually, the virus reached Mexico in late November 2015. Local transmission refers to the transmission of the virus through mosquito bites in areas where people live or work, rather than contracting it during their travels. During the initial week of infection, the Zika virus can be detected in the bloodstream. When an infected person is bitten by a mosquito, the mosquito ingests the virus by feeding on the infected blood. The virus then multiplies within the mosquito's body, allowing it to transmit the virus to another person when it bites again after a few days. Consequently, individuals who have traveled to regions with a high prevalence of Zika virus infection may carry the virus in their bloodstream upon returning home, potentially leading to local transmission of the Zika virus [2].

Zika virus can be spread through various means, including sexual contact, mother-to-child transmission, blood transfusion or organ transplantation, and accidental exposure in laboratories. Understanding these modes of transmission is essential for implementing effective preventive measures against Zika virus [3].

To prevent Zika virus infection, it is important to take precautions and use acetaminophen to treat fever and relieve pain. Zika virus is spread by Aedes mosquitoes, similar to dengue, yellow fever, and chikungunya. These mosquitoes are most active during the day, especially a few hours after sunrise and before sunset. They can also sting at night. Zika virus was first identified in the Zika Forest, Uganda, in 1947, but gained more attention after a large outbreak in the South Pacific islands in 2007. It subsequently spread to South America, Central America, and the Pacific Rim, Caribbean, and Mexico. Local transmission occurs when infected mosquitoes bite people in their living or work areas. While cases have been reported in certain parts of the United States, as of December 2019, no new cases of local transmission have been recorded. However, Zika virus infections have been reported among travelers returning from affected countries. The Centers for Disease Control and Prevention (CDC) permanent diagnosis for travelers is essential [4–7].

The Zika virus has received significant attention because of its potential impact on public health. While many individuals infected with Zika virus do not experience any symptoms, others may develop a range of mild symptoms such as fever, conjunctivitis, joint and muscle pain, headache, and rash. In rare cases, the virus has been linked to the Guillain-Barr syndrome, a neurological disorder characterized by muscle weakness and sensory abnormalities. One of the most troubling aspects of Zika virus infection is its potential to cause serious complications in pregnant women and their unborn babies. In addition, children infected with the virus before birth may face various developmental challenges, including delayed speech and motor skills, intellectual disabilities, seizures, and movement difficulties [8, 9].

A number of contributions have been published in related topics. Tesla et al. [10] studied temperature drives Zika virus transmission: evidence from empirical and mathematical models. Agusto et al. [11] considered a mathematical model for Zika virus dynamics with sexual transmission route. Khan et al. [9] studied a dynamical model of asymptomatic carrier Zika virus with optimal control strategies. By replacing the ordinary normal equation with a fractional derivative equation, the fractional derivatives approach achieves an important goal of controlling the fact that the system dynamics are affected by memory. Ahmed et al. [12] studied equilibrium points, stability, and numerical solutions of fractional-order predator–prey and rabies models. Zeb et al. [13] studied the optimal campaign strategies in fractional-order smoking dynamics. Sardar et al. [14] proposed a mathematical model of dengue transmission with memory. Kouidere et al. [15] studied the analysis and optimal control of a mathematical modeling of the spread of African swine fever virus with a case study of South Korea and cost-effectiveness. Raza et al. studied and proposed the number model in Zika virus and the epedmic model related in it [16–20]. And papers related it [21–33].

Considering the above, they did not take into account the ability of the memory to contain the spreading of the Zika virus, as well as the transmission of the Zika virus model to the fractional derivative.

Among the models used for epidemic analysis of Zika virus, the majority was formulated using ODE's, while others were based on fractional calculus. Recall that the fractional calculus is applied in different directions of physics, mathematical biology, fluid mechanics, electrochemistry, signal processing, viscoelasticity, finance, and many others. Fractional derivatives were used in the literature to monitor the effect of memory on the system dynamics by replacing the normal derivative arrangement with a fractional derivative arrangement. In epidemic modeling, fractional derivatives and fractional integrals are important aspects, because the effect of memory plays an important role in the spread of the disease. The presence of memory effects on past events will affect the spread of the disease in the future so that the disease can be controlled in the future, and the distance of the memory effect indicates the date of the disease spread. Thus, the effects of memory on the spread of infectious diseases can be verified using fractional derivatives. The fractional calculus adds an extra dimension in the study of dynamics of epidemiological models, especially for COVID-19 pandemic. Therefore, the fractional version of many epidemic models has been investigated as in Ahmed et al. [12] and Khan and Atangana [34].

This article is organized using the following methodology: in the first section, we present some basic characteristics and definitions of the integral and fractional derivatives. Because of its applicability to the initial conditions of differential equations, we will apply Caputo's definition to fractional order differentiation. In Section 2, we describe the problem of optimal command on the basis of the suggested model, and we also characterize the terms of optimal command by utilizing the principle of Pontryagin's maximum. In Section 4, we performed some computational simulations. Finally, in Section 5, the article is terminated.

2 Methods

2.1 Mathematical model

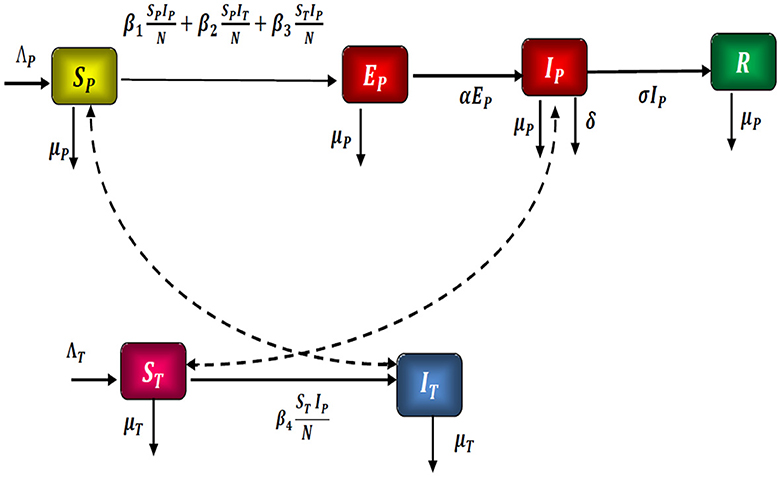
A mathematical model S_PE_PI_PR_PS_MI_M is considered, which represents the spread of the Zika virus through a population. As a result, we divided the N population into six compartments: To begin, the people susceptible S_P, the people exposed E_P, the people infected I_P, the people recovered R_P, the ticks susceptible S_M, and the ticks infected I_M.

In Figure 1, the considered model is graphically represented.

Figure 1

Figure 1. Figure population compartments model.

As a result, we present the fractional optimal command mathematical model of the Zika virus, which is governed by the system of differential equations shown below Equation 1:

$\begin{array}{ll}\{\begin{array}{l}{D}^{\alpha }{S}_P(t)={\xi }_P-{\mu }_P{S}_P(t)-{\beta }_1\frac{S_P(t)E_P(t)}{N}-{\beta }_2\frac{S_P(t)I_P(t)}{N}-{\beta }_3\frac{S_P(t)I_T(t)}{N}\hfill \\ D^{\alpha }{E}_P(t)={\beta }_1\frac{S_P(t)E_P(t)}{N}+{\beta }_2\frac{S_P(t)I_P(t)}{N}+{\beta }_3\frac{S_P(t)I_T(t)}{N}-({\mu }_P+\alpha )E_P(t)\hfill \\ D^{\alpha }{I}_P(t)=\alpha E_P(t)-({\mu }_P+\sigma +\delta )I_P(t)\hfill \\ D^{\alpha }{R}_P(t)=\sigma I_P(t)-{\mu }_P{R}_P(t)\hfill \\ D^{\alpha }{S}_T(t)={\xi }_T-{\mu }_M{S}_T(t)-{\beta }_4\frac{S_T(t)I_T(t)}{N}\hfill \\ D^{\alpha }{I}_T(t)={\beta }_3\frac{S_T(t)I_T(t)}{N}-{\mu }_M{I}_T(t)\hfill \end{array}& (1)\end{array}$

where S_P(0) ≥ 0, E_P(0) ≥ 0, I_P(0) ≥ 0, R_P(0) ≥ 0, S_T(0) ≥ 0 and I_T(0) ≥ 0 are the initial state.

With

- ξ_P : recruitment rate of people susceptible.

- ξ_T : ratio of susceptible Zika being recruited.

- μ_P : death ratio in the population from natural causes.

- μ_T : death ratio in Zika due to natural causes.

- β₁: infection ratio among people through contact with exposed people.

- β₂: contamination ratio among people through contact with infected individuals.

- β₃: infection ratio among people through contact with infected Zika.

- β₄: infection rate among Zika through contact with infected individuals.

- α: the ratio of exposed becoming infected with the virus.

- σ: the ratio of infected become recovered from the virus.

- δ: death ratio caused by complications.

3 Optimal command problem with fractional derivation

3.1 Application of optimal command

Our strategy for managing the Zika virus focuses on reducing its spread among the population. The aims is to minimize both the number of individuals exposed to the virus and the number of those who become infected. To accomplish this, we developed a program that employs two distinct controls, denoted as w₁(t) and w₂(t), for a time period of tinlbrack [0, T]. The control w₁(t) represents an awareness campaign launched at a specific time t, whereas the control w₂(t) represents treatment options available at the same time t.

$\begin{array}{ll}\{\begin{array}{l}{D}^{\alpha }{S}_P(t)={\xi }_P-{\mu }_P{S}_P(t)-{\beta }_1(1-w_1(t))\frac{S_P(t)E_P(t)}{N}-\hfill \\ {\beta }_2(1-w_1(t))\frac{S_P(t)I_P(t)}{N}-{\beta }_3(1-w_1(t))\frac{S_P(t)I_T(t)}{N}\hfill \\ D^{\alpha }{E}_P(t)={\beta }_1(1-w_1(t))\frac{S_P(t)E_P(t)}{N}+\hfill \\ {\beta }_2(1-w_1(t))\frac{S_P(t)I_P(t)}{N}+{\beta }_3(1-w_1(t))\frac{S_P(t)I_T(t)}{N}-({\mu }_P+\alpha )E_P(t)\hfill \\ D^{\alpha }{I}_P(t)=\alpha E_P(t)-\sigma (1-w_2(t))I_P-({\mu }_P+\delta )I_P(t)\hfill \\ D^{\alpha }{R}_P(t)=\sigma (1-w_2(t))I_P(t)-{\mu }_P{R}_P(t)\hfill \\ D^{\alpha }{S}_T(t)={\xi }_T-{\mu }_T{S}_T(t)-{\beta }_3\frac{S_T(t)I_T(t)}{N}\hfill \\ D^{\alpha }{I}_T(t)={\beta }_3\frac{S_T(t)I_T(t)}{N}-{\mu }_T{\text{I}}_{\text{T}}(\text{t})\hfill \end{array}& (2)\end{array}$

with S_P(0) ≥ 0, E_P(0) ≥ 0, I_P(0) ≥ 0, R_P(0) ≥ 0, S_T(0) ≥ 0 and I_T(0) ≥ 0 are the initial state (Equation 3).

$\begin{array}{ll}J(w_1,w_2)={\displaystyle \underset{0}{\overset{T}{\int }}}\left[E_P(t)+I_P(t)+\frac{A}{2}{w}_1^2(t)+\frac{B}{2}{w}_2^2(t)\right]dt& (3)\end{array}$

In this equation, we assign relative weights to the cost of implementing the awareness program and treatment controls using parameters A and B, where A and B are positive numbers. These weights assist us in determining the relative significance of the controls w₁(t) and w₂(t) at a given time t. To capture the non-linear interactions that arise from high levels of implementation, we use a quadratic cost function for the controls. This cost function includes the financial resources required for the treatment and implementation of an awareness campaign. The final time period in the implementation of the controls is represented by T.

To put it differently, we aim to find the optimal controls $w_1^{*}$ and $w_2^{*}$ that would minimize the cost function and meet the objectives of controlling the spread of the Zika virus.

To put it another way, we want to find the optimal controls $w_1^{*}$ and $w_2^{*}$ that minimize the cost function (Equation 4), while also controlling the spread of the Zika virus.

$\begin{array}{ll}J(w_1^{*},w_2^{*})={\displaystyle \underset{(w_1,w_2)\in U}{min}}J(w_1,w_2)& (4)\end{array}$

Where U is the set of admissible commands defined by U = {(w₁, w₂)/0 ≤ w_1min ≤ w_1i(t) ≤ w_1max ≤ 1, 0 ≤ w_2min ≤ w_2i(t) ≤ w_2max ≤ 1, /t ∈ [0, T]}.

The primary objective in FOCPs is to determine the optimal command pair (w₁, w₂) by minimizing the objective function:

$\begin{array}{ll}J(w_1,w_2)={\displaystyle \underset{0}{\overset{T}{\int }}}\left[E_P(t)+I_P(t)+\frac{A}{2}{w}_1^2(t)+\frac{B}{2}{w}_2^2(t)\right]dt& (5)\end{array}$

Subject to the constraint

$D^{\alpha }{S}_P(t)=f_1(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

$D^{\alpha }{E}_P(t)=f_2(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

$D^{\alpha }{I}_P(t)=f_3(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

$D^{\alpha }{R}_P(t)=f_4(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

$D^{\alpha }{S}_T(t)=f_4(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

$D^{\alpha }{I}_T(t)=f_5(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2)$

The following expression defines a modified objective function (Equation 6):

$\begin{array}{c}\widehat{ȷ}(w_1,w_2)={\displaystyle \underset{0}{\overset{T}{\int }}}\left[H^{*}(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)\right]dt-{\displaystyle \underset{0}{\overset{T}{\int }}}\\ \left[{\displaystyle \sum _{i=1}^6}{\xi }_i(t)f_i(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)\right]dt& (6)\end{array}$

where H(S_P, E_P, I_P, R_P, S_T, I_T, w₁, w₂, t)

$\begin{array}{c}H(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)=E_P(t)+I_P(t)+\\ \frac{A}{2}{w}_1^2(t)+\frac{B}{2}{w}_2^2(t)+{\displaystyle \sum _{i=1}^6}{\xi }_i(t)f_i(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)& (7)\end{array}$

From Equations (5, 7), we can derive the following

$\begin{array}{ll}\begin{array}{cc}{D}^{\alpha }{S}_P(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_1}(t)& D^{\alpha }{E}_P(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_2}(t)\\ D^{\alpha }{I}_P(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_3}(t)& D^{\alpha }{R}_P(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_4}(t)\\ D^{\alpha }{S}_T(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_5}(t)& D^{\alpha }{I}_T(t)=-\frac{\partial H^{*}(t)}{\partial {\xi }_6}(t)\end{array}& (8)\end{array}$

With the transversality conditions at time T :

$\begin{array}{c}{\xi }_1(T)=0,{\xi }_2(T)=0,{\xi }_3(T)=0,{\xi }_4(T)=0,{\xi }_5(T)=0\\ \text{ and }{\xi }_6(T)=0& (9)\end{array}$

Equations (8, 9) outline the required conditions for the previously defined FOCP in terms of a Hamiltonian.

These conditions generate a series of fractional differential equations defined by the state variables S_P, E_P, I_P, R_P, S_T, I_T and commands w₁, w₂, and solving for the Lagrange multiplier ξ_i can be accomplished through analytical, numerical, or a blended approach.

3.2 Characterization of optimal command

The Pontryagain's principle [35] to solve the optimal commands problem is given below. This method converted this into a problem of minimizing a Hamiltonian H(t) at time t (Equation 10), which is defined by

$\begin{array}{c}H(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)=E_P(t)+I_P(t)+\frac{A}{2}{w}_1^2(t)+\\ \frac{B}{2}{w}_2^2(t)+{\displaystyle \sum _{i=1}^6}{\xi }_i(t)f_i(S_P,E_P,I_P,R_P,S_T,I_T,w_1,w_2,t)& (10)\end{array}$

That f_i is the right side of the differential equation of the i^th state variable of the system at time t.

Theorem 1. The optimals commands $(w_1^{*},w_2^{*})$ and the solutions $S_P^{*}$, $E_P^{*}$, $I_P^{*}$, $R_P^{*}$, $S_T^{*}$ and $I_T^{*}$ of the corresponding co-state system (Equation 2) are given, the adjoint variables ξ₁(t), λ₂(t), ξ₃(t), ξ₄(t), ξ₅(t), and ξ₆(t)satisfying:

$\begin{array}{c}{D}^{\alpha }{\xi }_1(t)=-{\xi }_1(t)[-{\mu }_P-{\beta }_1(1-w_1(t))\frac{E_P(t)}{N}-\\ {\beta }_2\frac{I_P(t)}{N}-{\beta }_3\frac{I_T(t)}{N}]-{\xi }_2(t)\left({\beta }_1(1-w_1(t))\frac{E_P(t)}{N}-{\beta }_2\frac{I_P(t)}{N}-{\beta }_3\frac{I_T(t)}{N}\right)\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_2(t)=-{\xi }_1(t)\left[-{\beta }_1(1-w_1(t))\frac{S_P(t)}{N}\right]-\\ {\xi }_2(t)\left[{\beta }_1(1-w_1(t))\frac{S_P(t)}{N}-({\mu }_P+\alpha )\right]\\ -{\xi }_3(t)\alpha +{\xi }_4(t){\beta }_3\frac{S_T(t)}{N}-{\xi }_5(t){\beta }_3\frac{S_T(t)}{N}\end{array}$

$\begin{array}{c}{D}^{\alpha }{\xi }_3(t)=-{\xi }_1(t)\left[-{\beta }_2(1-w_1(t))\frac{S_P(t)}{N}\right]-\\ {\xi }_2(t)[{\beta }_2(1-w_1(t))\frac{S_P(t)}{N}-({\mu }_P+\alpha ])\\ -{\xi }_3(t)\left[({\mu }_P-(1-w_2(t))\sigma )-{\xi }_4(t)((1-w_2(t))\sigma )\right]\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_4(t)={\xi }_4(t){\mu }_P\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_5(t)={\xi }_5(t)({\mu }_M{I}_T(t)+{\beta }_4\frac{E_P(t)}{N})-{\xi }_6(t)({\beta }_4\frac{I_T(t)}{N})\end{array}$

$\begin{array}{r}{D}^{\alpha }{\xi }_6(t)={\xi }_1(t)({\beta }_3\frac{S_P(t)}{N})\\ -{\xi }_2(t)({\beta }_3\frac{S_P(t)}{N})+{\xi }_5(t)(S_T(t)+{\beta }_4\frac{E_P(t)}{N})-{\xi }_6(t)({\mu }_M\\ \text{+}{\beta }_4\frac{S_T(t)}{N})\end{array}$

We find the transversality conditions at time T: ξ₁(T) = 0, λ₂(T) = −1, ξ₃(T) = −1, ξ₄(T) = 0; ξ₅(T) = 0 and ξ₆(T) = 0.

Furthermore, for t ∈ [0, T], the optimal controls $w_1^{*}$ and $w_2^{*}$ are given by

$\begin{array}{c}{w}_1^{\ast }=\min (w_{1\max },\max (w_{1\min },\frac{({\lambda }_1(t)-{\xi }_2(t))}{A}\times \\ {\beta }_1\frac{S_P^{\ast }(t)E_P^{\ast }(t)}{N}+{\beta }_2\frac{S_P^{\ast }(t)I_P^{\ast }(t)}{N}+{\beta }_3\frac{S_P^{\ast }(t)I_T^{\ast }(t)}{N}))& (11)\end{array}$

$\begin{array}{ll}{w}_2^{\ast }=\min \left(w_{2\max },\max \left(w_{2\min },\frac{{\lambda }_3(t)-{\xi }_4(t))}{B}\times I_P^{\ast }(t)\right)\right)& (12)\end{array}$

Proof. Here, we applied the Pontryagain's principle [35] to solve the optimal command problem given below.

So, we defined the Hamiltonian H by Equation 13:

$\begin{array}{l}{H}^{\ast }(t)=E_P(T)+I_P(T)+\frac{A}{2}{w}_1^2(t)+\frac{B}{2}{w}_2^2(t)\\ +{\xi }_1(t)[{\xi }_P-{\mu }_P{S}_P(t)-{\beta }_1(1-w_1(t))\frac{S_P(t)E_P(t)}{N}-\\ {\beta }_2(1-w_1(t))\frac{S_P(t)I_P(t)}{N}-{\beta }_3(1-w_1(t))\frac{S_P(t)I_T(t)}{N}]\\ +{\xi }_2(t)[{\beta }_1(1-w_1(t))\frac{S_P(t)E_P(t)}{N}+\\ {\beta }_2(1-w_1(t))\frac{S_P(t)I_P(t)}{N}+{\beta }_3(1-w_1(t))\frac{S_P(t)I_T(t)}{N}-\\ ({\mu }_P+\alpha )E_P(t)]\\ +{\xi }_3(t)\left[\alpha E_P(t)-\sigma (1-w_2(t))I_P-({\mu }_P+\delta )I_P(t)\right]\\ +{\xi }_4(t)[\sigma (1-w_2(t))I_P(t)-\\ {\mu }_P{R}_P(t)]\\ +{\xi }_5(t)\left[{\xi }_T-{\mu }_T{S}_T(t)-{\beta }_3\frac{S_T(t)I_T(t)}{N}\right]\\ +{\xi }_6(t)\left[{\beta }_3\frac{S_T(t)I_T(t)}{N}-{\mu }_T{I}_T(t)\right]\end{array}(13)$

For t ∈ [0, T], the adjoint equations and transversality conditions can be obtained by using the Pontryagin's maximum principle [35–38] such that

$\begin{array}{l}{D}^{\alpha }{\xi }_1(t)=-\frac{\partial H(t)}{\partial S_P(t)}=-{\xi }_1(t)[-{\mu }_P-{\beta }_1(1-w_1(t))\frac{E_P(t)}{N}-\\ {\beta }_2\frac{I_P(t)}{N}-{\beta }_3\frac{I_T(t)}{N}]\\ -{\xi }_2(t)({\beta }_1(1-w_1(t))\frac{E_P(t)}{N}-\\ {\beta }_2\frac{I_P(t)}{N}-{\beta }_3\frac{I_T(t)}{N})\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_2(t)=-\frac{\partial H(t)}{\partial E_P^{}(t)}=-{\xi }_1(t)\left[-{\beta }_1(1-w_1(t))\frac{S_P(t)}{N}\right]-\\ {\xi }_2(t)\left[{\beta }_1(1-w_1(t))\frac{S_P(t)}{N}-({\mu }_P+\alpha )\right]\\ -{\xi }_3(t)\alpha +{\xi }_4(t){\beta }_3\frac{S_T(t)}{N}-{\xi }_5(t){\beta }_3\frac{S_T(t)}{N}\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_3(t)=-\frac{\partial H(t)}{\partial I_P^{}(t)}=-{\xi }_1(t)\left[-{\beta }_2(1-w_1(t))\frac{S_P(t)}{N}\right]-\\ {\xi }_2(t)[{\beta }_2(1-w_1(t))\frac{S_P(t)}{N}-({\mu }_P+\alpha ])\\ -{\xi }_3(t)\left[({\mu }_P-(1-w_2(t))\sigma )-{\xi }_4(t)((1-w_2(t))\sigma )\right]\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_4(t)=-\frac{\partial H(t)}{\partial R_P^{}(t)}={\xi }_4(t){\mu }_P\end{array}$

$\begin{array}{l}{D}^{\alpha }{\xi }_5(t)=-\frac{\partial H(t)}{\partial S_T^{}(t)}={\xi }_5(t)({\mu }_M{I}_T(t)+{\beta }_4\frac{E_P(t)}{N})-{\xi }_6(t)({\beta }_4\frac{I_T(t)}{N})\end{array}$

$\begin{array}{c}{D}^{\alpha }{\xi }_6(t)=-\frac{\partial H(t)}{\partial I_T^{}(t)}={\xi }_1(t)({\beta }_3\frac{S_P(t)}{N})-\\ {\xi }_2(t)({\beta }_3\frac{S_P(t)}{N})+{\xi }_5(t)(S_T(t)+{\beta }_4\frac{E_P(t)}{N})-{\xi }_6(t)({\mu }_M+{\beta }_4\frac{S_T(t)}{N})\end{array}$

With the transversality conditions at time T: ξ₁(T) = 0, λ₂(T) = −1, ξ₃(T) = −1, ξ₄(T) = 0; ξ₅(T) = 0 and ξ₆(T) = 0.

For, t ∈ [0, T] the optimal commands w₁ and w₂ can be solved from the optimality condition

$\begin{array}{l}-\frac{\partial H(t)}{\partial w_1(t)}=0 \Rightarrow -A{w}_1(t)-({\xi }_2(t)-{\xi }_1(t)){\beta }_1\frac{S_P^{\ast }(t)E_P^{\ast }(t)}{N})+\\ {\beta }_2\frac{S_P^{\ast }(t)I_P^{\ast }(t)}{N})+{\beta }_3\frac{S_P^{\ast }(t)I_T^{\ast }(t)}{N}=0\\ -\frac{\partial H(t)}{\partial w_2(t)}=0\Rightarrow -B{w}_2(t)-({\xi }_4(t)-{\xi }_3(t))I_P(t)=0\end{array}$

We have

$w_1(t)=\frac{({\xi }_1(t)-{\xi }_2(t))}{A}\times {\beta }_1\frac{S_P(t)E_P(t)}{N})+{\beta }_2\frac{S_P(t)I_P(t)}{N})+{\beta }_3\frac{S_P(t)I_T(t)}{N}$

$w_2(t)=\frac{{\lambda }_3(t)-{\xi }_4(t))}{B}\times I_P(t)$

By the bounds in U of the commands, it is easy to obtain $w_1^{*}$ and $w_2^{*}$, which are given by Equations (11, 12) in the form of system (Equation 8).

4 Discussion

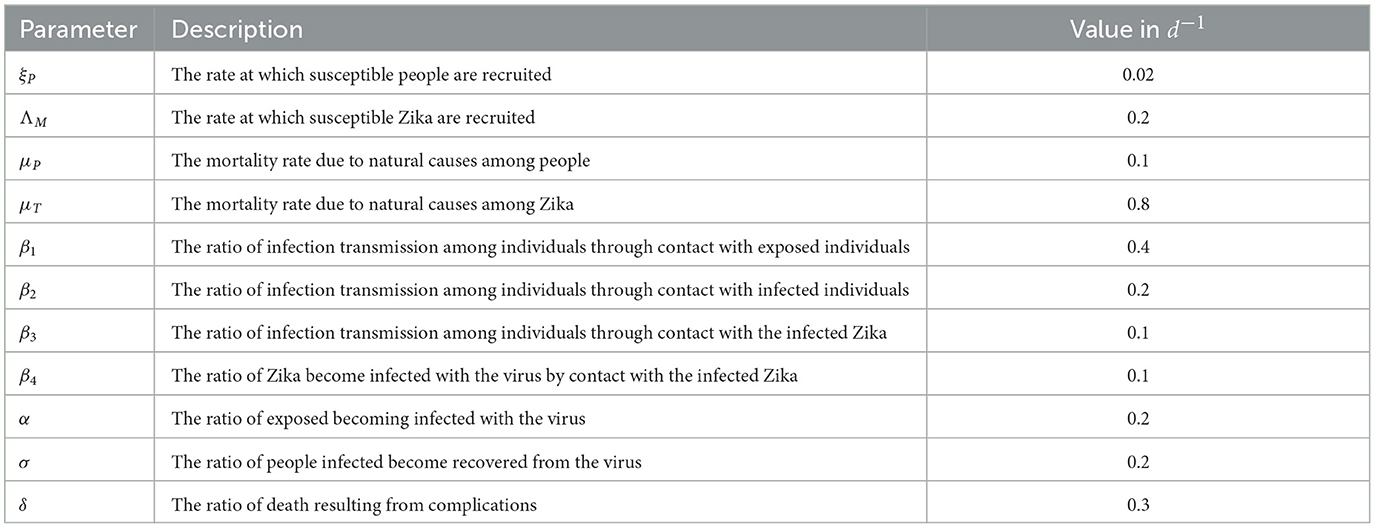
This section delves into the outcomes obtained through the numerical resolution of the optimality system. In our problem of control, the state variables have initial conditions and the adjoint conditions have terminal conditions. In other words, the optimality system is a boundary problem with two points and distinct boundary conditions for the time steps i = t₀ and i = t_f. The optimality problem is resolved iteratively, in which the state system is progressed forward and the adjoint system is progressed backward. We initially estimate the controls during the first iteration and subsequently update them using characterization before the next iteration commences. We proceed until we reach the convergence of the successive iterations. An optimality program is compiled and written in MATLAB according to the data below.

As the control and state functions have different magnitudes, the weight constant is set to the following values: A = 100 and B = 100.

4.1 Scenario without control

In this scenario, we use any control.

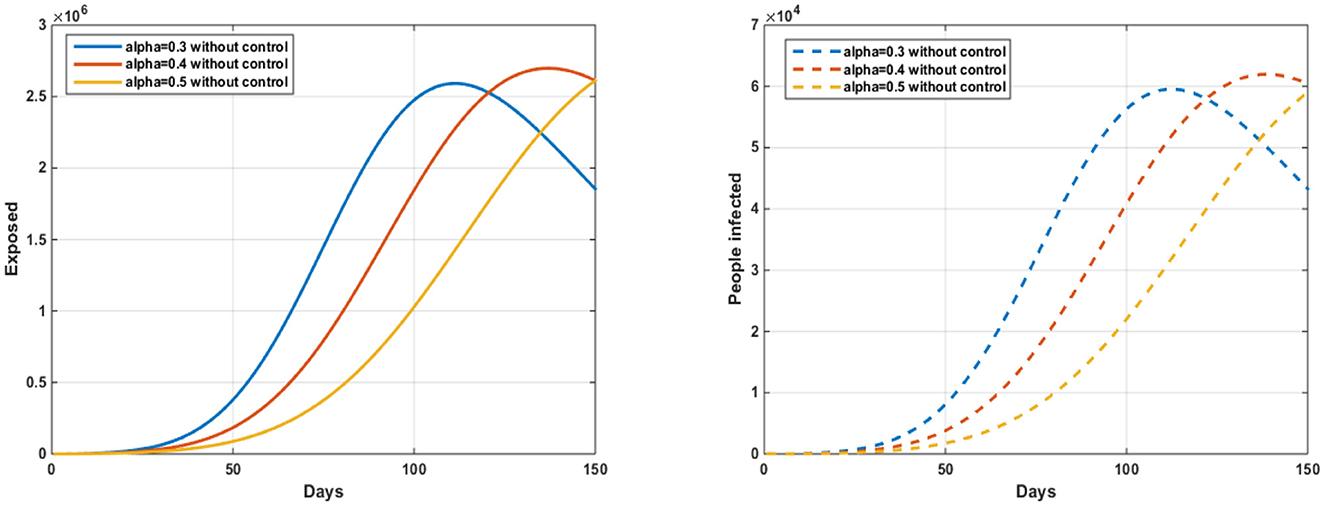
Based on Figure 2 and the parameter values in Table 1, we noted an increase in the number of exposed and infected people with the Zika virus, which leads to an increase in the number of deaths due to the lack of any strategy to contain the disease and prevent its spread.

Figure 2

Figure 2. The evolution of the number of exposed and infected people without control.

Table 1

Table 1. The values of the parameters used in the numerical simulation.

4.2 Scenario 1: awareness program: education

In this scenario, we use only the optimal control w₁(t).

The number of people exposed to and infected with the Zika virus has decreased, as shown in Figure 2. Due to the implementation of the strategy, sensitization campaigns will be conducted for people who are likely to be infected. Moreover, due to the risks of mixing with people infected with the virus, this biological strategy aims to prevent the spread of the disease. The number of people exposed without control ranges from 150 (alpha = 0.3) to 3.03105 (alpha = 0.6) and from 150 (alpha = 0.4) to 3.42106 (alpha = 0.4) with control. The number of people infected without treatment ranges from 50* (alpha = 0.6) to 9.06, 104 (alpha = 0.3) with treatment, and from 50 (alpha = 0.4) to 8.14, 104 (alpha = 0.4) without treatment.

On the other hand, the fractional derivatives have a significant influence on the description of memory effects in dynamic systems. Memory's effects diminish as alpha approaches 1. Furthermore, in ordinary differential equations, the derivative order fractional alpha acts as a time delay. Figure 3 shows that the memory effect of the system increases when the order of the derivative alpha is equal to 1, and as a result, the number of infected people decreases over time.

Figure 3

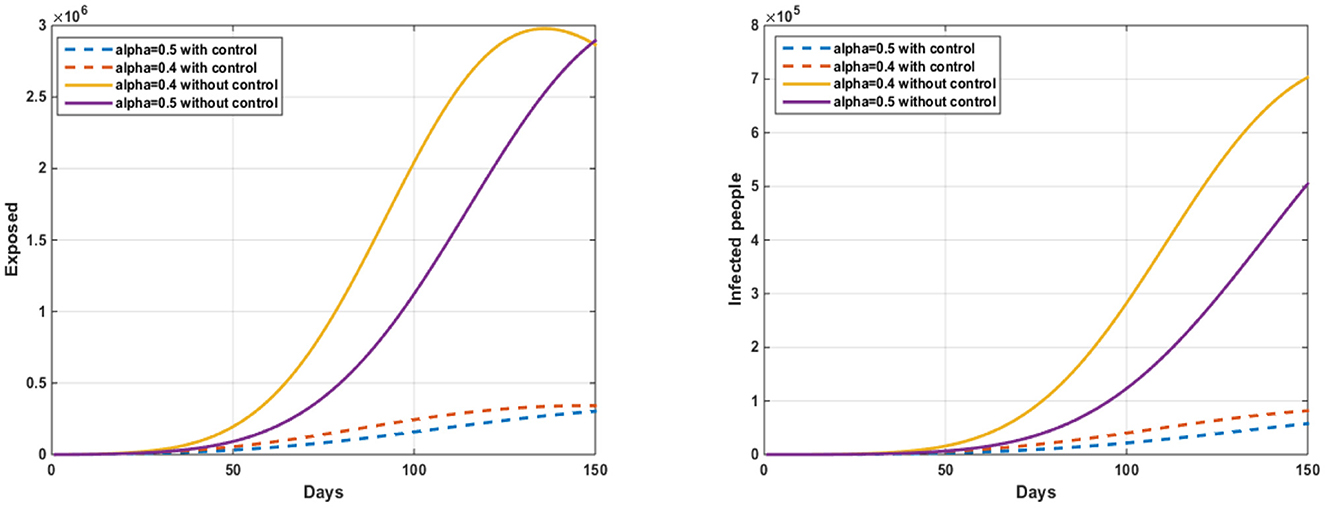
Figure 3. The evolution of the number of exposed and infected people without and with control w₁(t).

4.3 Scenario 2: education and treatment

In this scenario, we use only the optimal control w₂(t).

In Figure 4, we notice an important decrease in the number of people infected with a virus, that after 150 days, the number of exposed without control is 150 (α = 0.3) to 1.85.10⁶ (α = 0.6) and 150 (α = 0.4) to 2.61.10⁶ (α = 0.4) with control. The number of infected without control is 50 (α = 0.6) to 4.32.10⁴ (α = 0.3) and 50 (α = 0.4) to 6, 04.10⁴ (α = 0.4) with control. After applying this strategy of treatment as a vaccine and other treatments and quarantines, which will have important results in limiting the spread of the virus, the results were positive.

Figure 4

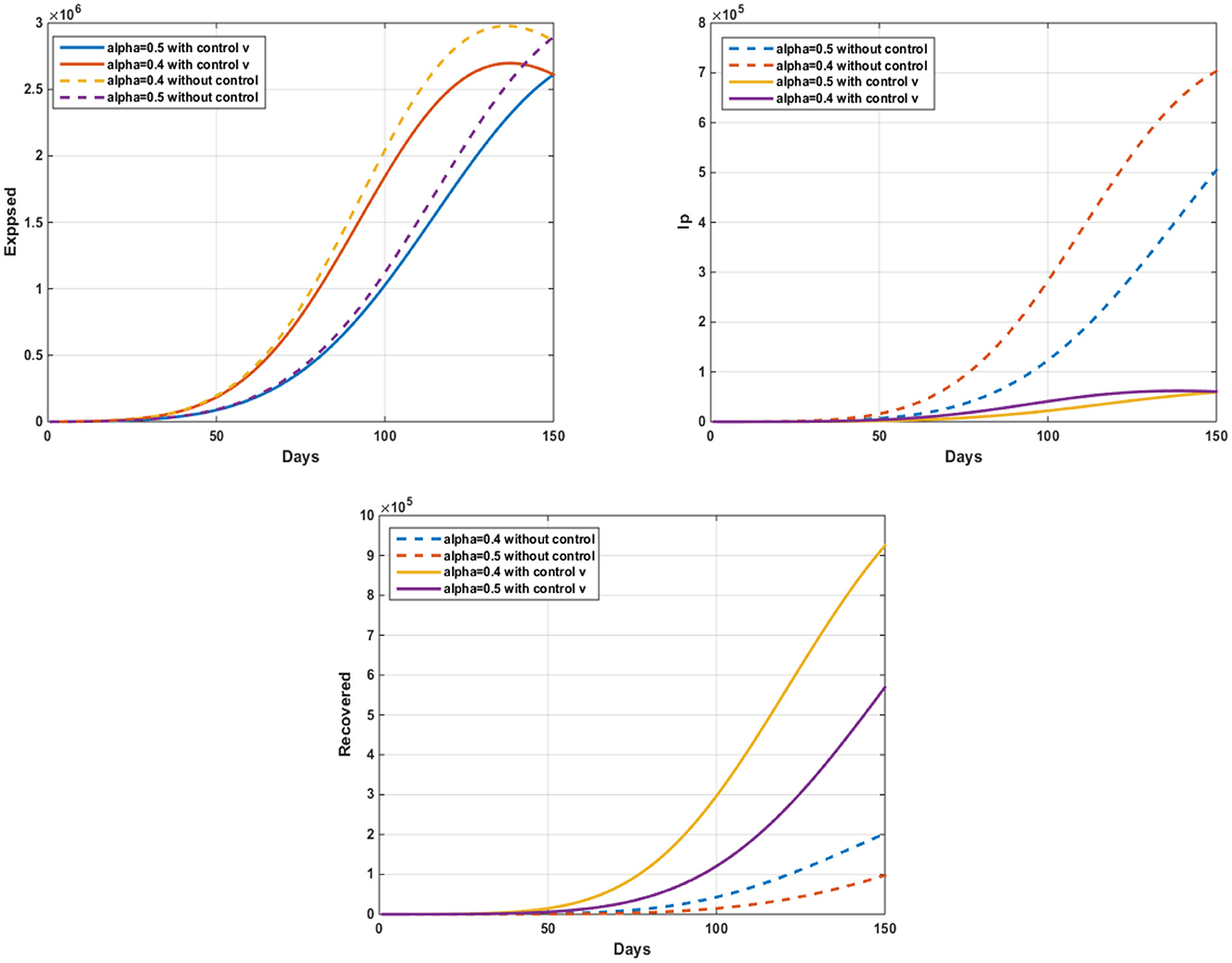
Figure 4. The evolution of the number of infected pigs and ticks susceptible to infection with and without controls w₂(t).

5 Conclusion

Our study has successfully employed fractal derivatives to establish a theoretical and computational analysis for a mathematical model of Zika transmission through a population. The model is a fractional mathematical model called S_PE_PI_PR_PS_TI_T, and it depicts the spread of the Zika virus throughout the population, which contained two controls. Our study has effectively integrated two control measures, an awareness program and a treatment, into the mathematical model of Zika transmission.

We have also conducted a thorough investigation of the optimal control strategy, which aims to minimize the spread of the virus by reducing the number of exposed and infected individuals. Utilizing the principles of control theory, we were able to derive the characterization of optimal control. The numerical simulations of our results have confirmed the effectiveness of the proposed containment strategies. Our research has conclusively shown that controlling the rate of dynamic dissemination is critical in containing the Zika epidemic.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AK: Data curation, Methodology, Validation, Writing – original draft, Writing – review & editing. AE: Writing – original draft, Writing – review & editing. IM: Writing – original draft, Writing – review & editing. OB: Writing – original draft, Writing – review & editing. KA: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://www.who.int/news-room/fact-sheets/detail/zika-virus?gclid=Cj0KCQjwuLShBhC_ARIsAFod4fKV2P6U3A_KwDudnmZawXdqhB7fwGDuSd412P5HnQHhJKP9_dh_gP8aAsMPEALw_wcB

2. ^https://www.who.int/westernpacific/health-topics/zika-virus-disease

3. ^https://www.who.int/news-room/feature-stories/detail/the-history-of-zika-virus

References

1. Yun S-I, Lee Y-M. Zika virus: an emerging flavivirus. J Microbiol. (2017) 55:204–19. doi: 10.1007/s12275-017-7063-6

PubMed Abstract | Crossref Full Text | Google Scholar

2. Rezapour S, Mohammadi H, Jajarmi A. A new mathematical model for Zika virus transmission. Adv Diff Equ. (2020) 2020:1–15. doi: 10.1186/s13662-020-03044-7

Crossref Full Text | Google Scholar

3. Bjornstad ON, Shea K, Krzywinski M, Altman N. The SEIRS model for infectious disease dynamics. Nat Methods. (2020) 17:557–8. doi: 10.1038/s41592-020-0856-2

Crossref Full Text | Google Scholar

4. Iqbal S, Baleanu D, Javaid Ali HM, Younas M, Riaz B. Fractional analysis of dynamical novel COVID-19 by semi-analytical technique. Comput Model Eng Sci. (2021) 29:705–27. doi: 10.32604/cmes.2021.015375

Crossref Full Text | Google Scholar

5. Akbari N, Asheghi R. Optimal control of an HIV infection model with logistic growth, celluar and homural immune response, cure rate and cell-to-cell spread. Bound Value Probl. (2022) 2022:5. doi: 10.1186/s13661-022-01586-1

Crossref Full Text | Google Scholar

6. Gonzlez-Parra G, Daz-Rodrguez M, Arenas AJ. Optimization of the controls against the spread of Zika virus in populations. Computation. (2020) 8:76. doi: 10.3390/computation8030076

Crossref Full Text | Google Scholar

7. John Hodgkiss H, Man SH. Stock density and mortality assessment of Sarotherodon mossambicus (Cichlidae) in Plover Cove Reservoir, Hong Kong. Environ Biol Fishes. (1977) 1:171–80. doi: 10.1007/BF00000408

Crossref Full Text | Google Scholar

8. Elhia M, Rachik M, Benlahmar E. Optimal control of an SIR model with delay in state and control variables. ISRN Biomath. (2013) 2013:403549. doi: 10.1155/2013/403549

Crossref Full Text | Google Scholar

9. Khan MA, Wasim Shah A, Ullah S, Gmez-Aguilar JF. A dynamical model of asymptomatic carrier Zika virus with optimal control strategies. Nonlinear Anal Real World Appl. (2019) 50:144–70. doi: 10.1016/j.nonrwa.2019.04.006

Crossref Full Text | Google Scholar

10. Tesla B, Demakovsky LR, Mordecai EA, Ryan SJ, Bonds MH, Ngonghala CN, et al. Temperature drives Zika virus transmission: evidence from empirical and mathematical models. Proc R Soc B. (2018) 285:20180795. doi: 10.1098/rspb.2018.0795

PubMed Abstract | Crossref Full Text | Google Scholar

11. Agusto FB, Bewick S, Fagan WF. Mathematical model for Zika virus dynamics with sexual transmission route. Ecol Complex. (2017) 29:61–81. doi: 10.1016/j.ecocom.2016.12.007

Crossref Full Text | Google Scholar

12. Ahmed E, El-Sayed A, El-Saka HA. Equilibrium points stability and numerical solutions of fractional-order predator–prey and rabies models. J Math Anal Appl. (2007) 325:542–53. doi: 10.1016/j.jmaa.2006.01.087

Crossref Full Text | Google Scholar

13. Zeb A, Zaman G, Jung IH, Khan M. Optimal campaign strategies in fractional-order smoking dynamics. Z Naturforschung A. (2014) 69:225–31. doi: 10.5560/zna.2014-0020

Crossref Full Text | Google Scholar

14. Sardar T, Rana S, Chattopadhyay J. A mathematical model of dengue transmission with memory. Commun Nonlinear Sci Numer Simul. (2015) 22:511–25. doi: 10.1016/j.cnsns.2014.08.009

Crossref Full Text | Google Scholar

15. Kouidere A, Balatif O, Rachik M. Analysis and optimal control of a mathematical modeling of the spread of African swine fever virus with a case study of South Korea and cost-effectiveness. Chaos, Solitons & Fractals. (2021) 146:110867. doi: 10.1016/j.chaos.2021.110867

Crossref Full Text | Google Scholar

16. Alfwzan WF, Raza A, Martin-VaqueroJ, Baleanu D, Rafiq M, Ahmed N, et al. Modeling and transmission dynamics of Zika virus through efficient numerical method. AIP Advan. (2023) 13:095221. doi: 10.1063/5.0168945

Crossref Full Text | Google Scholar

17. Raza A. Mathematical modelling of rotavirus disease through efficient methods. Comput Mater Contin. (2022) 72:4727–40. doi: 10.32604/cmc.2022.027044

Crossref Full Text | Google Scholar

18. Raza A, Arif MS, Rafiq MA. reliable numerical analysis for stochastic dengue epidemic model with incubation period of virus. Adv Differ Equ. (2019) 2019:1–19. doi: 10.1186/s13662-019-1958-y

Crossref Full Text | Google Scholar

19. Raza A, Rafiq M, Awrejcewicz J, Ahmed N, Mohsin M. Dynamical analysis of coronavirus disease with crowding effect, and vaccination: a study of third strain. Nonlinear Dyn. (2022) 107:3963–82. doi: 10.1007/s11071-021-07108-5

PubMed Abstract | Crossref Full Text | Google Scholar

20. Raza A, Awrejcewicz J, Rafiq M, Ahmed N, Mohsin M. Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods. Mathematics. (2022) 10:368. doi: 10.3390/math10030368

Crossref Full Text | Google Scholar

21. Boyce WE, DiPrima RC. Elementary Differential Equations and Boundary Value Problems. New York, NY: John Wiley & Sons. (2009).

Google Scholar

22. Birkhoff G, Rota GC. Ordinary Differential Equations, 4th edition. New York, NY: John Wiley & Sons (1989).

Google Scholar

23. Beltrán-Alcrudo D, Arias M, Gallardo C, Kramer S, Penrith ML. African Swine Fever: Detection and Diagnosis – A Manual for Veterinarians. FAO Animal Production and Health Manual No. 19. Rome. Food and Agriculture Organization of the United Nations (2017). p. 88.

Google Scholar

24. Bani-Yaghoub M, Gautam R, Shuai Z, van den Driessche P, Ivanek R. Reproduction numbers for infections with free-living pathogens growing in the environment. J Biol Dyn. (2012) 6:923–40. doi: 10.1080/17513758.2012.693206

PubMed Abstract | Crossref Full Text | Google Scholar

25. Driessche PV, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. (2002) 180:29–48. doi: 10.1016/S0025-5564(02)00108-6

PubMed Abstract | Crossref Full Text | Google Scholar

26. LaSalle JP. The stability of dynamical systems. In: Regional Conference Series in Applied Mathematics, Vol. 25. Philadelphia, PA: SIAM (1976).

Google Scholar

27. Gumel AB, Shivakumar PN, Sahai BMA. mathematical model for the dynamics of HIV-1 during the typical course of infection. Nonlinear Anal. (2001) 47:17731783. doi: 10.1016/S0362-546X(01)00309-1

Crossref Full Text | Google Scholar

28. Karrakchou J, Rachik M, Gourari S. Optimal control and infectiology: application to an HIV/AIDS model. Appl Math Comput. (2006) 177:807818. doi: 10.1016/j.amc.2005.11.092

Crossref Full Text | Google Scholar

29. Agrawal OP. Formulation of Euler–Lagrange equations for fractional variational problems. J Math Anal Appl. (2002) 272:368–79. doi: 10.1016/S0022-247X(02)00180-4

Crossref Full Text | Google Scholar

30. Podlubny I. Fractional Differential Equations, Vol. 198 of Mathematics in Science and Engineering. San Diego, CA: Academic Press (1999).

Google Scholar

31. Miller S, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. Hoboken, NJ: Wiley (1993). p. 480.

Google Scholar

32. Fang B. Topics in Machine Learning Optimization. Evanston, IL : Northwestern University (2022).

Google Scholar

33. Fleming WH, Rishel RW. Deterministic and Stochastic Optimal Control. New York, NY: Springer (1975). doi: 10.1007/978-1-4612-6380-7

Crossref Full Text | Google Scholar

34. Khan MA, Atangana A. Modeling the dynamics of novel coronavirus (2019-nCoV) with fractional derivative. Alexandria Eng J. (2020) 599:2379–89. doi: 10.1016/j.aej.2020.02.033

Crossref Full Text | Google Scholar

35. Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF. The Mathematical Theory of Optimal Processes. New York, NY: Wiley (1962).

Google Scholar

36. Kouidere A, Balatif O, Ferjouchia H, Boutayeb A, Rachik M. Optimal control strategy for a discrete time to the dynamics of a population of diabetics with highlighting the impact of living environment. Discrete Dyn Nat Soc. (2019) 2019:5949303. doi: 10.1155/2019/6342169

Crossref Full Text | Google Scholar

37. Kada D, Kouidere A, Balatif O, Rachik M, Labriji EH. Mathematical modeling of the spread of COVID-19 among different age groups in Morocco: optimal control approach for intervention strategies. Chaos Solit Fractals. (2020) 141:110437. doi: 10.1016/j.chaos.2020.110437

PubMed Abstract | Crossref Full Text | Google Scholar

38. Kouidere A, Kada D, Balatif O, Rachik M, Naim M. Optimal control approach of a mathematical modeling with multiple delays of the negative impact of delays in applying preventive precautions against the spread of the COVID-19 pandemic with a case study of Brazil and cost-effectiveness. Chaos Solit Fractals. (2020) 142:110438. doi: 10.1016/j.chaos.2020.110438

PubMed Abstract | Crossref Full Text | Google Scholar