Khalouta transform and applications to Caputo-fractional differential equations

Abstract

The paper aims to utilize an integral transform, specifically the Khalouta transform, an abstraction of various integral transforms, to address fractional differential equations using both Riemann-Liouville and Caputo fractional derivative. We discuss some results and the existence of this integral transform. In addition, we also discuss the duality between Shehu transform and Khalouta transform. The numerical examples are provided to confirm the applicability and correctness of the proposed method for solving fractional differential equations.

2010 Mathematics Classification:

Primary 92B05, 92C60; Secondary 26A33.

1 Introduction

Fractional calculus extends the traditional calculus operation of differentiation and integral to non- integer orders. Although the concept finds its roots in the works of Euler, Laplace and Fourier in the 18th and 19th centuries, it has gained significant attention in recent years for its applications in diverse scientific and engineering fields. Solving fractional differential can be more challenging than solving traditional differential equations, and various numerical and analytical method [1–5] have been developed for this purpose. An integral transform is an operation that takes a function and maps it to another function through integration. It is often used to simplify and solve complex problems in various fields. The basic idea behind an integral transform is to express a function in terms of a different set of functions, making it easier to analyze and manipulate. One of the most well-known integral transforms is the Laplace transform [6, 7], which is widely used in control theory and signal processing. Another common integral transform is the Fourier transform, used in fields like signal analysis and image processing. These transforms have applications in solving differential equations, analyzing signals, and studying the frequency components of functions. Now days many integral transforms can be used to convert differential equations into algebraic equations, making them easier to solve such as Sumudu transform method, Natural transform method, Kamal transform method, Mohand transform method, Aboodh transform method, Shehu transform method [4], and Complex integral transform method etc. [8–32]. Integral transform are employed to solve partial differential equations governing heat transfer and fluid flow problems in engineering, such as in solving the heat conduction equation. The Fourier and wavelet transforms are used in image processing to analyze and enhance images, as well as to extract features and perform image compression [33–40]. The Khalouta integral transform is employed in this article to drive explanatory solutions for fractional differential equations utilizing both the both the Riemann-Liouville integral and caputo fractional derivative. The approach aims to provide a comprehensive understanding of the solutions within the context of these specific fractional calculus operators. Khalouta transform method for Atangana-Baleanu or other derivatives can also be adapted since Sumudu transform, Shehu transform and various other transforms exists for these derivatives and relationship of Khalouta transform exists with all these transforms. Applying Khalouta transform methods to highly nonlinear fractional differential equations can pose several challenges like analytical solutions complexity, convergence issues and others. Khalouta transform rely on the convergence of series or integrals. For highly nonlinear problems, convergence may be slow.

2 Pre-requisites

We present few fundamental definition and properties related to the fractional calculus. These definitions and properties form the basis for understanding and applying fractional calculus in various scientific and engineering disciplines. For detailed explanations, please refer to the cited sources [41, 42].

Definition 1 The Riemann Liouville fractional integral operator of order β for a function f:(0, ∞) → R for all β ∈ R⁺ is defined as,

Where Γ(.) is the widely known pseudo gamma function. It is an abstraction of factorial function,

Definition 2 The Riemann-Liouville fractional derivative operator of order β for a function f:(0, ∞) → R for all β ∈ R⁺ is defined as,

where n − 1 < β ≤ n  n ∈ N.

Definition 3 The Caputo fractional derivative of function f:(0, ∞) → R for all β ∈ R⁺ is defined as,

where n − 1 < β ≤ n   n ∈ N.

Definition 4 The Mittag-Leffler function is abstraction of exponential function E_β (k) which is defined as,

here δ, γ ∈ R⁺and k ∈ c An abstraction of Mittag-Leffler function of is introduced by Prabhaker as given [43, 44]:

here δ, γ, ε ∈ R⁺and k ∈ c

3 Khalouta transform

The function f:u ∈ [0, ∞[→ R of exponential order β > 0, then Khalouta transform, over the set of function is defined as [45]

by the following integral

We can also define it as,

or

where s, λ, η > 0 are the Khalouta transform variables. β is a real number and the integral is taken along the limit u = ϕ. Equations (1–10) give the basic details of fractional operators and of Khalouta transform.

Since the Khalouta transform is very recently discovered so there might be some general queries about the efficiency and reliability of the transform but one can trust this transform as it has fair connections with other established transforms as well. Extending the Khalouta transform method to handle systems of fractional differential equations (FDEs) for improved efficiency and accuracy involves several considerations. Efficiency and accuracy depend on the specific characteristics of the system and the problem at hand. Khalouta transform possesses certain mathematical properties that make it suitable for solving problems related to Caputo fractional derivatives like, linearity, exponential behavior, derivatives property, initial value problem and semi group property. It can also be used to derive approximate solutions for fractional differential equations when exact solutions are challenging to obtain. Dealing with fractional orders involves performing computations related to fractional calculus. These computations can be more complex and computationally intensive than traditional integer-order calculus. Efficient algorithms and numerical methods may be needed. Fractional calculus problems may benefit from adaptive algorithms, such as adaptive time-stepping methods. These algorithms adjust the step size dynamically, which can impact the overall computation requirements. It's a complex area with challenges, and not all deep learning frameworks readily support fractional derivatives. we may need specialized tools or libraries designed for fractional calculus to address such multi-dimensional problem.

Khalouta transform methods can be applied to multidimensional problems involving partial derivatives with fractional orders in some scientific and engineering fields. Here are few examples: fractional heat equations, fractional wave equations and fractional diffusion equation. There are many examples from science and engineering where Khalouta transform has been successfully applied to solve real-world problems involving fractional calculus [1, 2]. The convergence properties of the transform method in solving fractional differential equations depend on the nature of the given problem. Generally, Khalouta transforms, can exhibit good convergence for well-behaved functions and problems with appropriate initial or boundary conditions. The convergence may be influenced by the smoothness of the solution, the decay properties of the involved functions, In some cases, careful consideration of the choice of fractional derivative definition (e.g., Caputo or Riemann-Liouville) is crucial for convergence analysis. This transform can also be extended to handle fractional integro differential equations like the first order volterra integro- differential equation with the initial condition and the second order volterra differential equations with the initial condition. When dealing with singularities or irregularities in fractional differential equations, specialized numerical techniques like the Caputo or Riemann-Liouville fractional differ-integration methods can be employed. These methods are designed to handle fractional calculus operations and may provide better performance in capturing the behavior of systems with singularities. Additionally, techniques such as fractional Adams-Bashforth or Adams-Moulton methods can be useful for solving fractional differential equations numerically. This transform may not be directly applicable to problems with variable order derivatives. These methods are most effective for problems with constant order derivatives. For variable order derivatives, you might need to explore specialized techniques like fractional calculus or other advanced mathematical tools, depending on the specific characteristics of our problem.

This transform method, often used for solving fractional differential equations (FDEs). The theoretical underpinning involves extending classical calculus to include fractional derivatives and integrals, allowing the analysis of systems with non-integer order derivatives. Mathematically, fractional derivatives are defined through integral operators, such as the Riemann-Liouville or Caputo operators. Transforming FDEs into the frequency or Laplace domain simplifies the equations, making them amenable to solution using standard techniques. This approach leverages the well-established properties of Khalouta transforms, enabling the application of existing mathematical tools to fractional calculus. There are some basic properties where Khalouta transform method fails to provide accurate solution like sudden changes or discontinuities in a function can lead to inaccuracies in transform solutions, Khalouta transforms may not converge for certain functions, leading to divergent or nonsensical results and incorrect or poorly defined boundary conditions can affect the accuracy of transform. Khalouta transform method can be generalized to address mixed fractional differential equations involving both Caputo and Riemann-Liouville fractional derivatives for future point of view. Till now no such study has been conducted. The choice of initial conditions and boundary conditions significantly influences the applicability and success of Khalouta transform method in solving fractional differential equations. Selecting appropriate conditions ensures the compatibility of the method with the problem at hand, enhancing convergence and accuracy. Incorrect choices may lead to divergence or inaccurate solutions, emphasizing the importance of a careful match between the problem's characteristics and the chosen conditions for a successful application of transform methods. Till now, there is no practical guidelines or best practices for researchers and practitioners when applying the Khalouta transform method to complex problems in fractional calculus. Integrating machine learning and AI techniques with the transform method holds potential for enhancing solutions to challenging fractional calculus problems. These technologies can improve accuracy, efficiency, and adaptability in handling complex mathematical operations, offering innovative approaches to problem-solving in this domain. If we clearly compare this transform with other transforms then we can say that this is another tool we have got to address the scientific and technical problems. The efficiency of the Khalouta transform method compare to other numerical methods commonly used in fractional calculus, such as the finite difference method or the Laplace transform method is not done till now but it can be a new vertical for the future studies as well. Since this is the newly introduced transform so till now not much work has been done with this so the classes of problems where Khalouta transform outperforms other existing techniques, is not defined till now. This was the some basic and important information about the Khalouta transform which can help the researchers to think in some new vertical of the solutions.

3.1 Khalouta—Shehu duality

Let k(s, λ, η) be the Khalouta transform of the function f(u) ∈ ς. If we take η = 1 then equation become,

where Sh(s, λ) denotes the Shehu transform of the function f(u) ∈ ς.

Corollary Shehu transform of Mittag–Leffler function [46],

exists and is given as

if we take ω = −1 and ε = −1 Equation (12) becomes

or,

Using relation (Equation 11), we can find Khalouta transform of Mittag- Leffler function as

3.2 Some basic properties of Khalouta transform

Now we are going to discuss some properties of Khalouta transform.

a. Linear property of the Khalouta transform If λ and μ are non- zero arbitrary constants and f(u) and g(u) are functions defined over the set ς, then (λf(u) + μg(u)) ∈ ς, and (Equation 14)

b. Khalouta transform of derivatives of the functions Let f(u) be the function, then n^th derivative of the function is defined as fⁿ(u) ∈ ς with respect to u. For n = 1, 2, 3, …… and its Khalouta transform is specified,

Here we also define the Khalouta transform of n^th partial derivative. Let v = v(x, t) and both defined in the set ς. And suppose k(x, s, λ, η,) be the Khalouta transform of v(x, t) and is the n^th derivative of the function v(x, t) with respect to x. Then

where n = 1, 2, 3, …

c. Khalouta transform of the convolution of two functions Suppose k₁(s, λ, η)and k₂(s, λ, η) are the Khalouta transforms of f(u) and g(u), respectively, both defined in the set ς. Then the Khalouta transform of their convolution is given by (Equation 17),

where (f * g) is convolution of two functions defined as,

d. Khalouta transform for some functions Below are the Khalouta transforms of some standard functions:

e. Khalouta transform of some fractional derivatives

3.2.1 Theorem 1

Suppose that k(s, λ, η) be the Khalouta integral transform of the function f(u), which satisfy n ∈ Z⁺ and n − 1 < β ≤ n, then the Khalouta integral transform of the Riemann-Liouville fractional integral of f(u) of order β > 0, is

Proof For the function f(u) , the Riemann Liouville fractional integral can be expressed as the convolution by Now, by applying the Khalouta transform of the convolution of two function (property c), we have

now using property (d) we get

or,

Hence Proved.

3.2.2 Theorem 2

Suppose that k(s, λ, η) be the Khalouta integral transform of the function f(u), which satisfy n ∈ Z⁺ and n − 1 < β ≤ n , then the Khalouta integral transform of the Riemann-Liouville fractional derivative of f(u) of order β > 0, is

Proof Let us consider the function

Now, applying Khalouta transform of Equation (19) and using Equation (18), we have

then, from the definition of Riemann-Liouville fractional derivative (2), we have

Applying the Khalouta transform on Equation (21) both the sides,

Now we use property (b), we have

this equation can also be written as

Using Equation (20) and definition (2), we have

Hence Proved.

3.2.3 Theorem 3

Suppose that k(s, λ, η) be the Khalouta integral transform of the function f(u), which satisfy n ∈ Z⁺ and n − 1 < β ≤ n , then the Khalouta integral transform of Caputo fractional derivative of f(u) of order β > 0, is

Proof By definition (3) of the Caputo fractional derivative of function, we have,

by applying the Khalouta transform on both sides of Equation (23) and using theorem 1, as a result,

where G(s, λ, η) is the Khalouta integral transform of the function g(u). Now, applying Khalouta transform and using the property (b), we obtain

Therefore, the Equation (24) becomes

where n − 1 < β ≤ n

which gives Equation (22), hence from Equation (25), we get our result.

This article is divided into five parts. Part one is consisting of origination of the article. Section 2 is dealing with pre-requisites related to the paper. Khalouta transform and some properties are discussed in segment 3 while Section 4 is having application part. Paper is concluded in Section 5. List of references is attached at the end to acknowledge the researchers and mathematicians.

4 Applications

In this segment, we are going to discuss some particular applications of Khalouta transform in solving the fractional differential equations. Using fractional order, here we take a linear ordinary differential equation [46].

with initial conditions

we take Khalouta transform of Equation (26), and we secure

now by the linearity property of Khalouta transform, we have

Using theorem 3 and property (b), we obtain

or by using Equation (27), we have,

By using inverse Khalouta transform on of Equation (28), and we secure result of Equation (26) as,

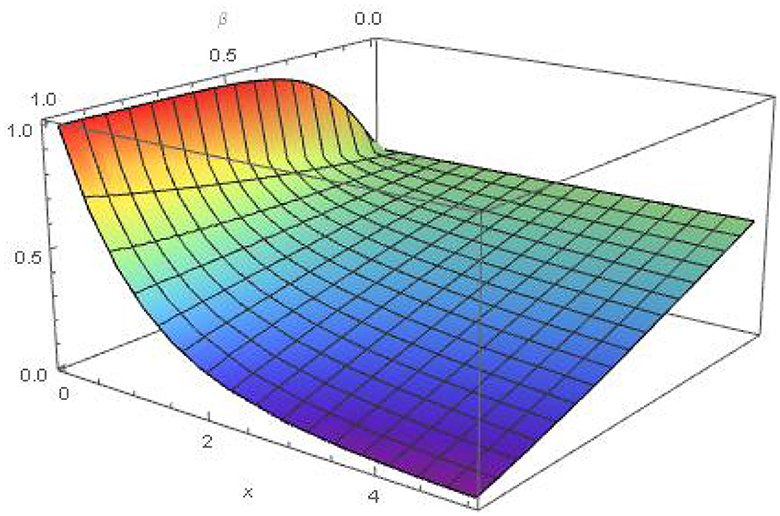
4.1 Example 1

When n = 1, b₀ = −1, b₁ = g(u) = 0 we secure [47],

with initial condition y(0) = 1

Solution Substituting n, b₀, b₁, and g in Equation (29), we get

or,

or

Thus, by Khalouta transform of Mittag-Leffler function of Equation (13), we have

We get absolute result of Equation (30) as (Figure 1),

Figure 1

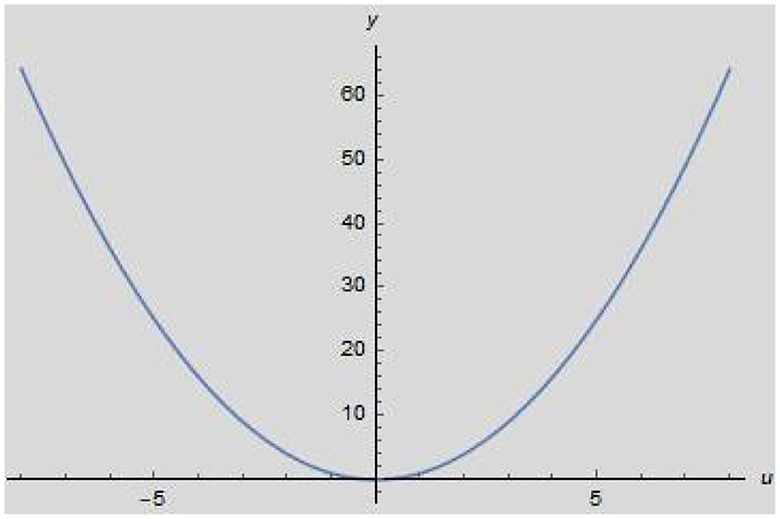
4.2 Example 2

Let we take homogeneous ordinary differential equation with fractional order [48].

with initial condition y(0) = 0.

Solution Now we have to find absolute result of Equation (31), so we take Equation (29), for n = 1, b₀ = −1, b₁ = 0 and , we get

or,

or,

or,

or, finally we get (Figure 2)

Figure 2

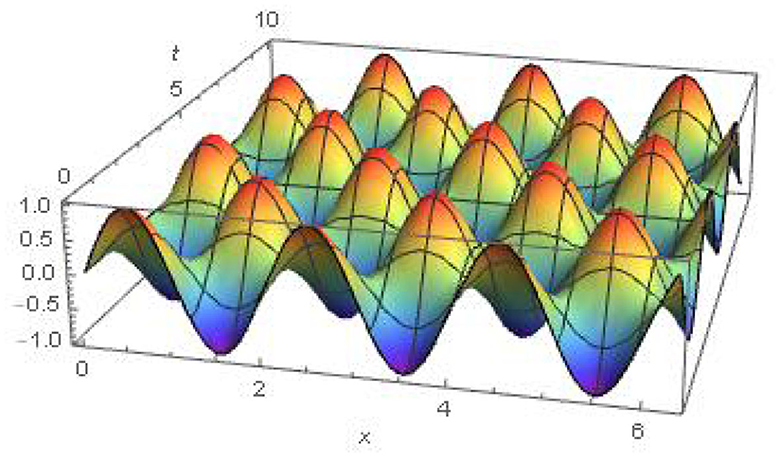
4.3 Example 3

Consider the wave equation [49].

with initial conditions

Solution Taking the Khalouta transform of Equation (32) and using Equations (15, 16) of Property (b), we obtain

Using initial conditions (Equation 33) and simplifying the Equation (34), we obtain

or,

Which is linear ordinary differential equation with second order, so that the overall result of Equation (35) can be put down,

or,

by using the inverse Khalouta transform of above, the absolute result of Equation (32) (Figure 3) is

Figure 3

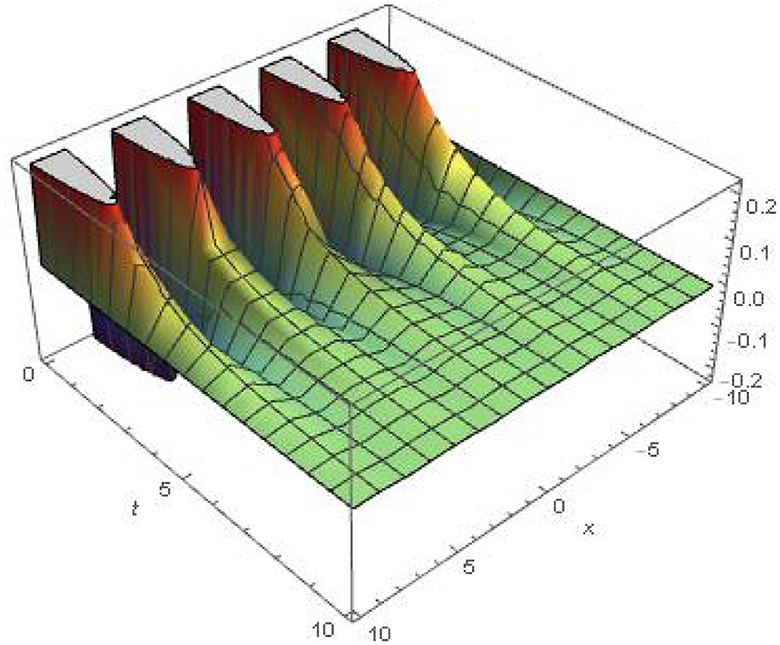
4.4 Example 4

Let we take the homogeneous heat equation [49].

with initial condition

Solution Applying the Khalouta transform on Equation (36), we have

Using Equations (15, 16) of property (b), and we obtain,

Using the initial conditions (Equation 37) and simplifying the Equation (38), we obtain

which is linear ordinary differential equation with second order. The overall result of Equation (39) can be put down

or,

by using the inverse Khalouta transform of the above, the absolute result of Equation (36) (Figure 4) is reported by

Figure 4

5 Conclusion

The Khalouta transform method appears to be a valuable approach for addressing Riemann-Liouville fractional derivatives and integrals, as well as Caputo fractional derivatives. The successful application of this mehod in resolving examples suggests its efficacy and efficiency in obtaining exact solutions for fractional differential equations involving Caputo derivatives and partial derivatives. This could contribute to advancements in solving complex mathematical problems in the realm of fractional calculus.

References

• 1.

  KhaloutaAKademA. A new method to solve fractional differential equations: inverse fractional Shehu transform method. Appl Appl Math. (2019) 14:19. 10.17512/jamcm.2020.3.04

  • CrossRef
  • Google Scholar

• 2.

  KhaloutaA. A new general integral transform for solving Caputo fractional-order differential equations. Int J Nonlinear Anal Appl. (2023) 14:67–78.

  • Google Scholar

• 3.

  ThangeTGGadeAR. On Aboodh transform for fractional differential operator. Malaya J Mathematik. (2020) 8:225–9. 10.26637/MJM0801/0038

  • CrossRef
  • Google Scholar

• 4.

  MaitamaSZhaoW. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv [preprint]. (2019). 10.48550/arXiv.1904.11370

  • CrossRef
  • Google Scholar

• 5.

  AhmadiSAPHosseinzadehHCheratiAY. A new integral transform for solving higher order linear ordinary Laguerre and Hermite differential equations. Int J Appl Comp Math. (2019) 5:1–7. 10.1007/s40819-019-0712-1

  • CrossRef
  • Google Scholar

• 6.

  DebnathLDebnathL. Nonlinear Partial Differential Equations for Scientists and Engineers. Boston, MA: Birkhäuser (2005). p. 528–9.

  • Google Scholar

• 7.

  PatilD. Application of integral transform (Laplace and Shehu) in chemical sciences. Aayushi Int Interdiscip Res J. (2022). 10.2139/ssrn.4006213

  • CrossRef
  • Google Scholar

• 8.

  RezapourSEtemadSAsamoahJKKAhmadHNonlaoponK. A mathematical approach for studying the fractal-fractional hybrid Mittag-Leffler model of malaria under some control factors. AIMS Math. (2023) 8:3120–62. 10.3934/math.2023161

  • CrossRef
  • Google Scholar

• 9.

  AlqahtaniAMShuklaA. Computational analysis of multi-layered Navier—Stokes system by Atangana—Baleanu derivative. Appl Math Sci Eng. (2024) 32:2290723. 10.1080/27690911.2023.2290723

  • CrossRef
  • Google Scholar

• 10.

  DubeyRSBaleanuDMishraMGoswamiP. Solution of modified Bergman's minimal blood glucose insulin model using caputo-fabrizio fractional derivative. CMES. (2021) 128:1247–63. 10.32604/cmes.2021.015224

  • CrossRef
  • Google Scholar

• 11.

  KhanMAUllahSKumarS. A robust study on 2019-nCOV outbreaks through non-singular derivative. Eur Phys J Plus. (2021) 136:1–20. 10.1140/epjp/s13360-021-01159-8

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 12.

  DubeyRSMishraMNGoswamiP. Effect of Covid-19 in India-A prediction through mathematical modeling using Atangana Baleanu fractional derivative. J Interdiscip Math. (2022) 1–4. 10.1080/09720502.2021.1978682

  • CrossRef
  • Google Scholar

• 13.

  OwolabiKMAtanganaA. Mathematical modelling and analysis of fractional epidemic models using derivative with exponential kernel. In: Fractional Calculus in Medical and Health Science. CRC Press (2020). p. 109–28.

  • Google Scholar

• 14.

  NisarKSFarmanMAbdel-AtyMCaoJ. A review on epidemic models in sight of fractional calculus. Alexandria Eng J. (2023) 75:81–113. 10.1016/j.aej.2023.05.071

  • CrossRef
  • Google Scholar

• 15.

  DjennadiSShawagfehNOsmanMSGómez-AguilarJFArqubOA. The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique. Phys Scripta. (2021) 96:094006. 10.1088/1402-4896/ac0867

  • CrossRef
  • Google Scholar

• 16.

  AlzahraniEOKhanMA. Comparison of numerical techniques for the solution of a fractional epidemic model. Eur Phys J Plus. (2020) 135:110. 10.1140/epjp/s13360-020-00183-4

  • CrossRef
  • Google Scholar

• 17.

  DhandapaniPBJayakumarTDumitruBVinothS. On a novel fuzzy fractional retarded delay epidemic model. AIMS Math. (2022) 7:10122–42. 10.3934/math.2022563

  • CrossRef
  • Google Scholar

• 18.

  GeorgeRMohammadiKMohammadiHGhorbanianRRezpourSDucA. The study of cholera transmission using an SIRZ fractional order mathematical model. Fractals. (2023). 10.1142/S0218348X23400534

  • CrossRef
  • Google Scholar

• 19.

  TaghvaeiAGeorgiouTTNortonLTannenbaumA. Fractional SIR epidemiological models. Sci Rep. (2020) 10:20882. 10.1038/s41598-020-77849-7

  • CrossRef
  • Google Scholar

• 20.

  AngstmannCNHenryBIMcGannAV. A fractional-order infectivity and recovery SIR model. Fract Fract. (2017) 1:11. 10.3390/fractalfract1010011

  • CrossRef
  • Google Scholar

• 21.

  AlòsEMancinoMEMerinoRSanfeliciS. A fractional model for the COVID-19 pandemic: application to Italian data. Stochast Anal Appl. (2021) 39:842–60. 10.1080/07362994.2020.1846563

  • CrossRef
  • Google Scholar

• 22.

  AlbalawiKSMishraMNGoswamiP. Analysis of the multi-dimensional navier—stokes equation by caputo fractional operator. Fract Fract. (2022) 6:743. 10.3390/fractalfract6120743

  • CrossRef
  • Google Scholar

• 23.

  AngstmannCNHenryBIMcGannAV. A fractional-order infectivity SIR model. Phys A Stat Mech Appl. (2016) 452:86–93. 10.1016/j.physa.2016.02.029

  • CrossRef
  • Google Scholar

• 24.

  MishraMNAljohaniAF. Mathematical modelling of growth of tumour cells with chemotherapeutic cells by using Yang—Abdel—Cattani fractional derivative operator. J Taibah Univ Sci. (2022) 16:1133–41. 10.1080/16583655.2022.2146572

  • CrossRef
  • Google Scholar

• 25.

  SinghAKMehraMGulyaniS. A modified variable-order fractional SIR model to predict the spread of COVID-19 in India. Math Methods Appl Sci. (2023) 46:8208–22. 10.1002/mma.7655

  • CrossRef
  • Google Scholar

• 26.

  AlqahtaniAMMishraMN. Mathematical analysis of Streptococcus suis infection in pig- human population by Riemann-Liouville fractional operator. Progr Fract Diff Appl. (2024) 10:119–35. 10.18576/pfda/100112

  • CrossRef
  • Google Scholar

• 27.

  RazaARafiqMAwrejcewiczJAhmedNMohsinM. Dynamical analysis of coronavirus disease with crowding effect, vaccination: a study of third strain. Nonlinear Dyn. (2022) 107:3963–82. 10.1007/s11071-021-07108-5

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 28.

  AhmedNElsonbatyARazaARafiqMAdelW. Numerical simulation and stability analysis of a novel reaction—diffusion COVID-19 model. Nonlinear Dyn. (2021) 106:1293–310. 10.1007/s11071-021-06623-9

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 29.

  RazaAAwrejcewiczJRafiqMMohsinM. Breakdown of a nonlinear stochastic nipah virus epidemic models through efficient numerical methods. Entropy. (2021) 23:1588. 10.3390/e23121588

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 30.

  RazaAArifMSRafiqM. A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect. Int J Biomath. (2019) 12:1950072. 10.1142/S1793524519500724

  • CrossRef
  • Google Scholar

• 31.

  HamamHRazaAAlqarniMMAwrejcewiczJRafiqMAhmedNet al. Stochastic modelling of Lassa fever epidemic disease. Mathematics. (2022) 10:2919. 10.3390/math10162919

  • CrossRef
  • Google Scholar

• 32.

  RazaAAwrejcewiczJRafiqMAhmedNMohsinM. Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods. Mathematics. (2022) 10:368. 10.3390/math10030368

  • CrossRef
  • Google Scholar

• 33.

  PhaijooGRGurungDB. Sensitivity analysis of SEIR-SEI model of dengue disease. GAMS J Math Math Biosci. (2018) 6:41–50.

  • Google Scholar

• 34.

  KoziołKStanisławskiRBialicG. Fractional-order sir epidemic model for transmission prediction of covid-19 disease. Appl Sci. (2020) 10:8316. 10.3390/app10238316

  • CrossRef
  • Google Scholar

• 35.

  BaleanuDMohammadiHRezapourS. Analysis of the model of HIV-1 infection of CD4+ CD4⁺ T-cell with a new approach of fractional derivative. Adv Diff Eq. (2020) 1–17. 10.1186/s13662-020-02544-w

  • CrossRef
  • Google Scholar

• 36.

  BahloulMAChahidALaleg-KiratiTM. Fractional-order SEIQRDP model for simulating the dynamics of COVID-19 epidemic. IEEE Open J Eng Med Biol. (2020) 1:249–56. 10.1109/OJEMB.2020.3019758

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 37.

  LiuXur RahmamnMAhmadSBaleanuDNadeem AnjamY. A new fractional infectious disease model under the non-singular Mittag—Leffler derivative. Waves Random Comp Media. (2022) 1–27. 10.1080/17455030.2022.2036386

  • CrossRef
  • Google Scholar

• 38.

  SeneN. Fractional SIRI model with delay in context of the generalized Liouville—Caputo fractional derivative. Math Model Soft Comp Epidemiol. (2020) 107–25. 10.1201/9781003038399-6

  • CrossRef
  • Google Scholar

• 39.

  YangXJBaleanuDSrivastavaHM. Local Fractional Integral Transforms and Their Applications. Academic Press (2015).

  • Google Scholar

• 40.

  SeneN. SIR epidemic model with Mittag—Leffler fractional derivative. Chaos Solit Fract. (2020) 137:109833. 10.1016/j.chaos.2020.109833

  • CrossRef
  • Google Scholar

• 41.

  PodlubnyI. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier (1998).

  • Google Scholar

• 42.

  KilbasAASrivastavaHMTrujilloJJ. Theory and Applications of Fractional Differential Equations. Vol. 204. Elsevier (2006).

  • Google Scholar

• 43.

  GarraRGarrappaR. The Prabhakar or three parameter Mittag—Leffler function: theory and application. Commun Nonlinear Sci Numer Simul. (2018) 56:314–29. 10.1016/j.cnsns.2017.08.018

  • CrossRef
  • Google Scholar

• 44.

  AyM. A new generalization of beta function with three parameters Mittag-Leffler function. arXiv [preprint]. (2018). 10.48550/arXiv.1803.03122

  • CrossRef
  • Google Scholar

• 45.

  KhaloutaA. A New Exponential Type Kernel Integral Transform: Khalouta Transform and Its Application. Vol. LVII (2023).

  • Google Scholar

• 46.

  BelgacemRBaleanuDBokhariA. Shehu Transform and Applications to Caputo-Fractional Differential Equations. (2019).

  • Google Scholar

• 47.

  OdibatZMMomaniS. An algorithm for the numerical solution of differential equations of fractional order. J Appl Math Informat. (2008) 26:15–27.

  • Google Scholar

• 48.

  BulutHBaskonusHMBelgacemFBM. The analytical solution of some fractional ordinary differential equations by the Sumudu transform method. In: Abstract and Applied Analysis. Vol. 2013. Hindawi (2013).

  • Google Scholar

• 49.

  AboodhKS. Application of new transform “Aboodh Transform” to partial differential equations. Global J Pure Appl Math. (2014) 10:249–54.

  • Google Scholar