- 1Department of Mathematics and Statistics, College of Science, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
- 2Department of Mathematics, Amity School of Applied Sciences, Amity University Rajasthan, Jaipur, Rajasthan, India
- 3Department of Mathematics, College of Science, King Saud University, Riyadh, Saudi Arabia
This study aims to address the difficulties in solving coupled generalized non-linear Burger equations using local fractional calculus as a framework. The methodology used in this work, particularly in the area of local fractional calculus, combines the Elzaki transform with the Adomian decomposition method. This combination has proven to be a highly effective strategy for addressing non-linear partial differential equations within the local fractional context, which finds numerous practical applications. The proposed method offers a systematic and easily understandable procedure for tackling both linear and non-linear partial differential equations (PDEs). It provides an easy-to-follow path to solve these problems. We offer a real-world example that exhibits the method's successful use in resolving issues to corroborate its efficacy. The obtained solution is visually represented to illustrate the practical utility of this approach.
2010 Mathematics Subject Classification: 34A34, 65M06, 26A33.
1 Introduction
The main aspiration of fractional calculus is to extend differentiation integration to fractional order, which has been around since the seventeenth century, thanks to the groundbreaking work of Leibnitz, Euler, Lagrange, Abel, Liouville, and many others [1–3]. A growing area of mathematics called fractional calculus (FC) has diverse applications in all connected sectors of science and problems of engineering. Some of the findings were published in books or related review articles [4–11]. It is interesting to note that these derivatives and integrals are not just mathematical oddities, these models are increasingly being employed in fields such as engineering fields, electrical circuits, digital control systems, fluid movement, and many more [12–14]. Fractional differential equations have seen a lot of use in physics and engineering over the last few decades. Thousands of efforts have been put into developing reliable and consistent numerical and analytical methodologies to solve these fractional equations over the past decade or more [15–25]. To find precise and approximative analytical solutions, certain potent techniques have been developed, few of them are Yang-Laplace decomposition approach [26], Sumudu decomposition in local fractional [27], the method of variational iteration [28, 29], the method of homotopy analysis [30, 31], and the method of fractional difference [32]. For fractional differential equations, the method of Adomian decomposition and the method of variational iteration stand out among the rest because they offer approximations of the issues under consideration without the use of linearization or discretization.
Burger [33] developed Burger's equations, which were derived by qualitatively approximating Navier Stoke's equation. To comprehend non-linear diffusion and dissipation phenomena, such as those pertaining to shock waves, unsaturated oil, soil dynamics in water, cosmology, approximation theory of flow, and non-linear kinematics wave of debris flows, Burger's equation is an essential tool.
Here, we investigated an equation of one of the most important coupled non-linear Burgers [34]. Recent years have seen the application of coupled partial differential equations in several practical scientific and engineering fields. Burgers' coupled-form equations, also known as coupled partial differential equations, provide an approximation for the flow theory that arises when a shock wave travels through a viscous fluid. The novel aspect of this paper is that it will investigate the generalized non-linear coupled Burger equations listed below:
Many authors have used different techniques to solve coupled Burgers equations. For example, Rashid and Ismail solved one-dimensional coupled Burgers equations using the Fourier pseudo-dospectral method. Mesh-free interpolation was accomplished using the methods developed by Rashid and Ismail [35], Islam et al. [36], and Alqahtani and Prasad [37], who also invented the RBF collocation method to numerically treat coupled Burger equations and other non-linear PDEs. The generalized non-linear coupled Burger equation within the framework of local fractional calculus is difficult to solve, as the equation has generalized form in terms of non-linearity. Researchers have solved many non-linear coupled equations so far but, generalized form of that equation is more advanced form and direct methods are not available.
For the numerical evaluation of coupled equations, Kumar and Pandit [38] adopted a composite numerical technique that was built using finite difference and Haar wavelets. For an analytical solution represented by Burger equations, Mohammadi and Mokhtari [39] used a reproducing Kernal approach. Bak et al. [40] created a new strategy in 2019 called a semi-Lagrangian strategy to numerically solve coupled Burger equations. To show how our suggested approach might be utilized to address issues that arise in applied science and engineering, we compare our findings with those of [40]. In this investigation, we employ the Elzaki transform decomposition method within the framework of local fractional calculus. This approach is constructed through the utilization of the Adomian decomposition method and the Elzaki transform in local fractional form [41]. The objective is to address the challenges posed by solving generalized non-linear coupled Burgers Equation (1). The Elzaki transform decomposition technique has an advantage in its applicability, speed of convergence, and accuracy, unlike other numerical methods. Applying the Elzaki transform decomposition technique yields the series solution. The Elzaki transform decomposition technique is a very effective tool in finding the solution of the generalized non-linear coupled Burger equation. It can also be applied to several other more complex ordinary differential equations (both linear and non-linear). This technique does not require linearization and initial guess points.
This research advocates the adoption of the proposed method for addressing real-life problems in various domains of applied mathematics. Tarig and Elzaki [42] introduced a modified version of the Sumudu transform, known as the Elzaki transform and applied it to solve a wide range of partial differential equations and ordinary differential equations that emerge in the realms of physics, engineering, and biology.
The Elzaki-Adomian composition method is an effective and powerful tool that can be used to solve differential equations that cannot be solved by Sumudu Transform [42]. The method can be used to solve the non-linear Klein-Gordon equation. Klein -Gordon mathematical model [43] is regarded as one of the most essential models in quantum mechanics. The method can also be used to solve the non-linear Sine Gordon equation [41], this equation plays a major role in the propagation of fluxons in Josephson junctions between two superconductors. Furthermore, it is applicable in non-linear optics, solid-state physics, and stability of fluid motions.
Not every kind of non-linear equation will exhibit convergence of ADM. The features of the equation being solved determine whether the approach will converge, and there are situations in which convergence might be challenging. ADM was created especially to solve non-linear issues. While it is applicable to linear problems, other numerical techniques' like the finite element or finite difference methods' are frequently more effective when dealing with linear equations. Certain parameter choices may have an impact on the procedure, and it can occasionally be difficult to identify the best values for the parameters. Depending on the type of problem and how many terms are in the series solution, the accuracy of ADM can change. Sometimes, a lot of terms are needed to get a reasonable level of precision. When working with equations that need a lot of terms in the series expansion, the procedure could be very computationally expensive. It is crucial to remember that, despite its drawbacks, ADM has been effectively used to solve a variety of non-linear issues in a variety of domains. The particulars of the topic at hand determine which numerical approach is best, and researchers frequently combine several approaches to handle different facets of a given problem. The other segments of the study are composed along the below lines:
Section 2: Preliminaries.
Section 3: Existence and oneness of solution.
Section 4: Elzaki transform decomposition method in local fractional.
Section 5: Applications.
Section 6: Conclusions.
Section 7: Conflict of interest.
Section 8: Funding.
Section 9: Acknowledgments.
2 Preliminaries
Throughout this endeavor, basic definitions and introductory concepts of Elzaki transform in local fractional and calculus of fractional domain are provided. In the beginning, the local fractal derivative is described using the [41–46],
Definition 1. Let R is a real-valued function [45, 46], such as
the fractal derivative at t = t0 in local sense, is defined as
where
Definition 2. If Ω(ℓ) in fractal space has order ω(0, 1), then the LF integral of Ω(ℓ) is defined in the interval (α, λ) as follows.
where Δθj = θj+1−θj, Δθ = max{Δθ1, Δθ2, Δθ3, ….} and [θj, θj+1], j = 0, …, I−1, θ0 = s, θM = t, is a division of (α, λ) ([45, 46]).
Theorem 1. We have the Laplace transform of local fractional derivative defined as
Definition 3. The Elzaki transform in local fractional [42] of function ψ(p) of order ω is defined by
integral convergence occurs and τω∈ω The inverse of Elzaki transform in local fractional of function [42] ψ(p) is elucidate by
Theorem 2. Let and . Then, we have
Theorem 3. Let and . Then, we get
Theorem 4. Let . Then, we get
3 Existence and oneness of solution
We have the generalized fractional coupled Burger equations as:
with
System (Equations 2, 3) can be written as
where and
Theorem 1: Let ρ[I(κ, o)] defined by Equation (4) is local fractional continuous and satisfies Lipschitz condition i.e.,
Then the system
Has a distinctive solution in Cω[l, p], where Cω is the domain of a function of continuous and having derivative with fractal order ω.
Proof. Assume the map Θ:Cω[l, p] → Cω[l, p] be defined by
First, we establish by induction that
For r = 1, one can get
This implies that
Assume the equality holds for r = j
For r = j+1, consider
Further it can be written as,
Therefore,
So it validates our presumptions.
Now, we have
as r → ∞.
Similarly for Equation (3) one can write
as r → ∞.
Therefore system presents a unique solution.
4 Elzaki transform (local fractional) decomposition method
We use the Elzaki transform decomposition method on general local fractional non-linear coupled equations:
where shows the linear derivative operator in local fractional, of order ω, 0 < ω ≤ 1 along with the initial conditions, Qω, 1(I, N) and Qω, 2(I, N) are the linear operators in local fractional, Pω, 1(I, N) and Pω, 2(I, N) are the local fractional operators with non-linearity and Π(κ, o), Λ(κ, o) are two unidentified functions. The following steps will obtain an analytical solution for this system.
If both sides of the Equation (5) are subjected to the Elzaki transform in local fractional
If the Elzaki transform's differential property is used, we have
After applying inverse LFET to both sides of Equation (7).
Now according to the Adomian decomposition method, M and N can be replaced by infinite series.
And the non-linear terms can be written as,
where Ai and Bi are Adomian Polynomials. If Equations (9–11) are substituted in Equation (8), we get
When the two sides of Equation (12) are compared, we get
and
and
as well as
and so on. In the same manner
and
as well as
and so on.
The system Equations (5, 6)'s analytical solution for (I, N) comes out as
5 Applications
As an example, consider Burger equations in the context of a generalized coupled non-linear system
0 < ω ≤ 1 along with the initial conditions.
If both parts of Equations (13, 14) in the system are applied with the LFET,
Each equation in Equation (15) is solved by using the inverse LFET on both sides
To replace each function of the solution, use the Adomian decomposition technique, (M, N) is written as an infinite series
and the non-linear term can be decomposed as,
Substitute Equations (17–19) in Equation (16), then we have
Now when we compare both sides of Equation (20), we get
and
as well as
and
By using the same approach, other terms can be obtained. Also,
and
as well as
and
and so on. The first few components of Ar(M), Br(M, N) and Cr(N) polynomials (Equation 16) are obtained as
and
and
as well as
and
as well as
and so on. According to Equations (21–30).
The first terms of solutions of Equation (13) are as follows:
and
as well as
and so on. Same the manner
and
also
and so forth.
As a result, the local fractional series solution of M(m, τ) and N(m, τ).
Particular case: If we consider n = 1 in our defined model given in Equations (13, 14). The model reduces to a well-known model. And our obtained results reduce to known results:
We plot the numerical outcomes of Equations (13) and (14) for different values ω = 0.8 and 1.0, see Figures 1–4.
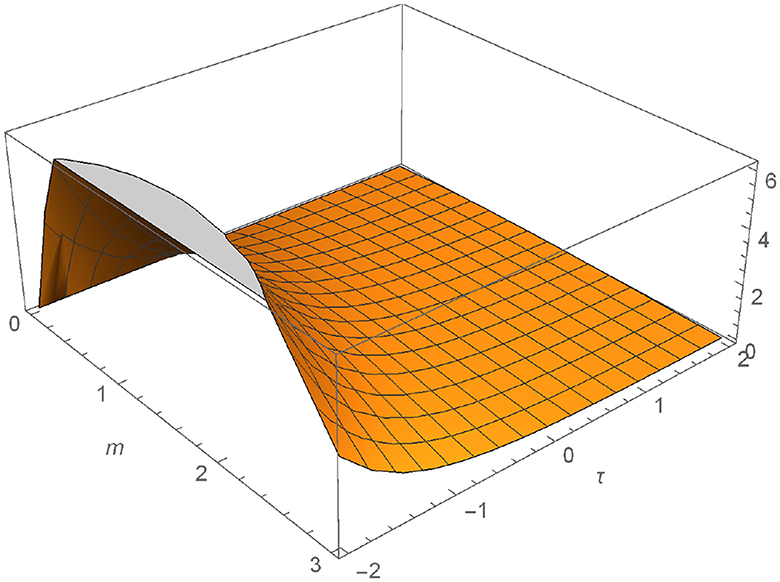
Figure 1. Graphical representation of M defined in Equation (13) for ω = 0.8.
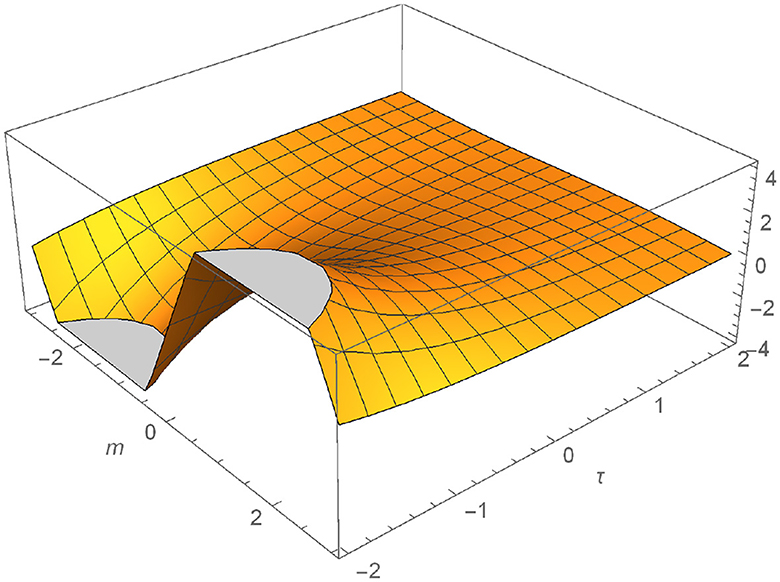
Figure 2. Graphical representation of M defined in Equation (13) for ω = 1.
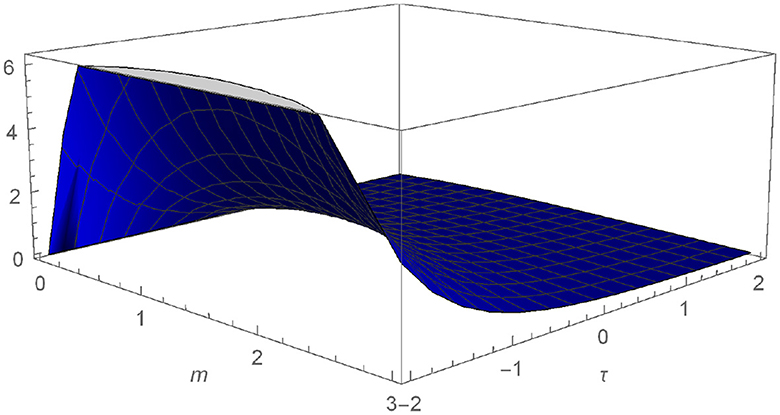
Figure 3. Graphical representation of N defined in Equation (14) for ω = 0.8.
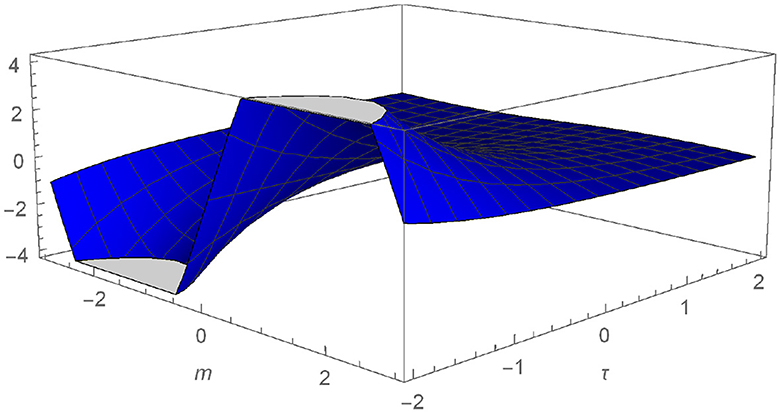
Figure 4. Graphical representation of N defined in Equation (14) for ω = 1.
6 Conclusions
In this study, a strategy that combines the Elzaki-transform and Adomian-decomposition approaches is used. We made an effort to show the effectiveness of the recommended strategy. The objective of this study is to resolve the coupled Burger equation. The illustration depicts the proposed method's applicability. Visual representations of the solution show how the method applies to generalized non-linear equations. Plots with various values of ω are used to illustrate the solutions that were found during the inquiry. Elzaki decomposition is a powerful, quick, and effective approach to solving the local fractional non-linear coupled Burger equation, as we have discovered.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
GA: Funding acquisition, Resources, Visualization, Writing—review & editing. JP: Conceptualization, Investigation, Methodology, Writing—original draft. BA: Data curation, Formal analysis, Project administration, Writing—review & editing. RD: Software, Supervision, Validation, Writing—original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU; grant number: IMSIU-RP23066).
Acknowledgments
We would like to express our sincere thanks to the editor and reviewers for their valuable comments and suggestions. The authors thank the Dean of Scientific Research at Imam Mohammad Ibn Saud Islamic University for their support.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Oldham KB, Spanier J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order, Vol. 11 of Mathematics in Science and Engineering. New York, NY: Academic Press (1974).
2. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. A Wiley-Interscience Publication. New York, NY: John Wiley and Sons (1993).
3. Podlubny I. Fractional Differential Equations. Vol. 198 of Mathematics in Science and Engineering. San Diego, CA: Academic Press (1999).
4. Srivastava HM, Owa S. Univalent functions, Fractional Calculus and Their Applications. New York, NY: Halsted Press/Wiley (1989).
5. Singh H, Srivastava HM, Hammouch, Z, Nisar KS. Numerical simulation and stability analysis for the fractional-order dynamics of COVID-19. Result Phys. (2021) 20:103722. doi: 10.1016/j.rinp.2020.103722
6. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, 204. Amsterdam: Elsevier Science B.V. (2006).
7. Gdawiec K, Qureshi, IK, Qureshi, S, Soomro, A. An optimal homotopy continuation method: convergence and visual analysis. J Comput Sci. (2023) 74:102166. doi: 10.1016/j.jocs.2023.102166
8. Abdulganiy R, Ramos H, Adekunle OJ, Okunga SA. A functionally-fitted block hybrid Falkner method for Kepler equations and related problems. Comput Appl Math. (2023) 42:327. doi: 10.1007/s40314-023-02463-y
9. Onder I, Esen H, Secer A, Ozisik M. Stochastic optical solitons of the perturbed nonlinear Schrodinger equation with Kerr law via lto calculus. Eur Phys J Plus. (2023) 138:1–12. doi: 10.1140/epjp/s13360-023-04497-x
10. Zafar ZUA, Yusuf A, Musa SS, Qureshi S, Alshomrani AS, Balenau D. Impact of public health awareness programs on COVID-19 dynamics: a fractional modeling approach. Fractals. (2022) 2022:S0218348X23400054. doi: 10.1142/S0218348X23400054
11. Sharma S, Goswami, P, Baleanu D, Dubey RS. Comprehending the model of omicron variant using fractional derivatives. Appl Math Sci Eng. (2022) 31:2159027. doi: 10.1080/27690911.2022.2159027
12. Barbosa RS, Machado JAT, Ferreira IM. PID controller tuning using fractional calculus concepts. Fract Calc Appl Anal. (2004) 7:119–34. doi: 10.1115/DETC2003/VIB-48375
13. Saadeh R, Ahmed SA, Qazza A, Elzaki TM. Adapting partial differential equations via the modified double ARA-Sumudu decomposition method. Part Diff Eq Appl Math. (2023) 8:100539. doi: 10.1016/j.padiff.2023.100539
14. Machado JAT. Analysis and design of fractional-order digital control systems. Syst Anal Model Simul. (1997) 27:107–22.
15. Momani S. Analytical approximate solution for fractional heat-like and wave-like equations with variable coefficients using the decomposition method. Appl. Math. Comput. (2005) 165:459–72. doi: 10.1016/j.amc.2004.06.025
16. Althobaiti S, Dubey RS, Prasad JG. Solution of local fractional generalized Fokker-Planck equation using local fractional mohand adomian decomposition method. Fractals. (2021) 30:1–9. doi: 10.1142/S0218348X2240028X
17. Saadeh R, Qazza A, Burqan A, Al-Omari S. On time fractional partial differential equations and their solution by certain formable transform decomposition method. Comput Model Eng Sci. (2023) 136:3121–39. doi: 10.32604/cmes.2023.026313
18. Albalawia, KS, Shokhandab R, Goswami P. On the solution of generalized time-fractional telegraphic equation. Appl Math Sci Eng. (2023) 31:1. doi: 10.1080/27690911.2023.2169685
19. Momani S, Odibat Z. Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl Math Comput. (2006) 177:488–94. doi: 10.1016/j.amc.2005.11.025
20. Jafari H, Prasad JG, Goswami P, Dubey RS. Solution of the local fractional generalized KDV equation using homotopy analysis method. Fractal. (2021) 29:5. doi: 10.1142/S0218348X21400144
21. Alquran M, Ali M, Gharaibeh F, Qureshi S. Novel investigation of dual-wave solutions to the Kadomtsev-Petviashvili model involving second-order temporal and spatial-temporal dispersion terms. Part Diff Eq Appl Math. (2023) 8:100543. doi: 10.1016/j.padiff.2023.100543
22. Qureshi S, Akanbi MA, Shaikh AA, Wusu AS, Ogunlaran OM, Mahmoud W, et al. A new adaptive nonlinear numerical method for singular and stiff differential problems. Alexand Eng J. (2023) 74:585–97. doi: 10.1016/j.aej.2023.05.055
23. Ilhan Ö, Sahin G. A numerical approach for an epidemic SIR model via Morgan-Voyce series. Int J Math Comput Eng. (2024) 2:123–38. doi: 10.2478/ijmce-2024-0010
24. Erdogan F. A second order numerical method for singularly perturbed Volterra integro differential equations with delay. Int J Math Comput Eng. (2024) 2:85–96. doi: 10.2478/ijmce-2024-0007
25. Nasir M, Jabeen S, Afzal F, Zafar A. Solving the generalized equal width wave equation via sextic B-spline collocation technique. Int J Math Comput Eng. (2023) 1:229–42. doi: 10.2478/ijmce-2023-0019
26. Ziane D. Cherif MH, Cattani C, Belghaba K. Yang-Laplace decomposition method for nonlinear system of local fractional partial differential equations. Appl Math Nonlin Sci. (2019) 4:489–502. doi: 10.2478/AMNS.2019.2.00046
27. Ziane D, Baleanu D, Belghaba K, Cherif MH. Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. J King Saud Univ Sci. (2019) 31:83–8. doi: 10.1016/j.jksus.2017.05.002
28. He JH, Wu GC, Austin F. The variational iteration method which should be followed. Nonlin Sci Lett A. (2010) 1:1–30. doi: 10.4236/oalib.1106601
29. Momani S, Odibat Z, Alawneh A. Variational iteration method for solving the space and time-fractional KdV equation. Numer Methods Part Diff Eq. (2008) 24:262–71. doi: 10.1002/num.20247
30. Maitama S, Zhao W. Local fractional homotopy analysis method for solving non-differentiable problems on Cantor sets. Adv Diff Eq. (2019) 127:22. doi: 10.1186/s13662-019-2068-6
31. Liao SJ. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, (Ph.D. thesis), Shanghai Jiao Tong University, Shanghai, China (1992).
32. Zhao Z, Li C. Fractional difference/finite element approximations for the time-space fractional telegraph equation. Appl Math Comput. (2012) 219:2975–88. doi: 10.1016/j.amc.2012.09.022
33. Burgers JM. A mathematical model illustrating the theory of turbulence. Adv Appl Mech. (1948) 1:171–99.
34. Esipov SE. Coupled Burgers' equations: a model of polydispersive sedimentation. Phys Rev E. (1995) 52:3711–8.
35. Rashid A, Ismail AIBM. A fourier pseudospectral method for solving coupled viscous Burgers equations. Comput Methods Appl Math. (2009) 9:412–20. doi: 10.2478/cmam-2009-0026
36. Islam SU, Haq S, Uddin M. A meshfree interpolation method for the numerical solution of the coupled nonlinear partial differential equations. Eng Anal Bound Elem. (2009) 33:399–409. doi: 10.1016/j.enganabound.2008.06.005
37. Alqahtani AM, Prasad JG. Solution of local fractional generalized coupled Korteweg–de vries (cKdV) equation using local fractional homotopy analysis method and Adomian decomposition method. Appl Math Sci Eng. (2024) 32:1. doi: 10.1080/27690911.2023.2297028
38. Kumar M, Pandit S. A composite numerical scheme for the numerical simulation of coupled Burgers' equation. Comput Phys Commun. (2014) 185:809–17. doi: 10.1016/j.cpc.2013.11.012
39. Mohammadi M, Mokhtari R. A reproducing kernel method for solving a class of nonlinear systems of pdes. Math Model Anal. (2014) 19:180–98. doi: 10.3846/13926292.2014.909897
40. Bak S, Kim P, Kim D. A semi-Lagrangian approach for numerical simulation of coupled Burgers' equations. Commun Nonlin Sci Numer Simul. (2019) 69:31–44. doi: 10.1016/j.cnsns.2018.09.007
41. Anac H. A local fractional elzaki transform decomposition method for the nonlinear system of local fractional partial differential equations. Fractal Fraction. (2022) 6:167. doi: 10.3390/fractalfract6030167
42. Tarig E, Elzaki SM. Application of new transform “Elzaki Transform” to partial differential equations. Glob J Pure Appl Math. (2011) 7:65–70. doi: 10.3390/fractalfract6030167
43. Dubey RS, Goswami P, Gomati AT. A new analytical method to solve Klein-Gordon equations by using homotopy perturbation Mohand transform method. Malaya J Matematik. (2022) 10:1. doi: 10.26637/mjm1001/001
44. Ige OE, Oderinu RA, Elzaki TM. Adomian polynomial and Elzaki transform method for solving Sine-Gordon equations. IAENG Int J Appl Math. (2019) 49:344–50. doi: 10.12732/ijam.v32i3.7
45. Yang XJ. Local Fractional Calculus and Its Applications. New York, NY: World Science Publisher (2012).
Keywords: local fractional Coupled Burger equations, Elzaki transform, Adomian transform, local fractional Coupled differential equations, non-linear fractional differential equations
Citation: Alhamzi G, Prasad JG, Alkahtani BST and Dubey RS (2024) Unveiling new insights: taming complex local fractional Burger equations with the local fractional Elzaki transform decomposition method. Front. Appl. Math. Stat. 10:1323759. doi: 10.3389/fams.2024.1323759
Received: 20 October 2023; Accepted: 16 February 2024;
Published: 08 March 2024.
Edited by:
Snezhana I. Abarzhi, University of Western Australia, AustraliaReviewed by:
Sania Qureshi, Mehran University of Engineering and Technology, PakistanHaci Mehmet Baskonus, Harran University, Türkiye
Pranay Goswami, Ambedkar University Delhi, India
Rania Saadeh, Zarqa University, Jordan
Copyright © 2024 Alhamzi, Prasad, Alkahtani and Dubey. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: R. S. Dubey, cmF2aW1hdGgxM0BnbWFpbC5jb20=
 Ghaliah Alhamzi1
Ghaliah Alhamzi1 R. S. Dubey
R. S. Dubey