Mathematical model of physicochemical regulation of precipitation of bone hydroxyapatite

Introduction: Formation of hydroxyapatite in bone, dentin, and enamel occurs at restricted molecular sites of specific extracellular matrix proteins and is controlled by multiple mineralization inhibitors. However, the role of physicochemical factors, such as the availability of required ions and the saturation status of the aqueous environment in biological mineralization, is not fully understood. The goal of this study was to use mathematical modeling to describe the complex physicochemical environment permissive to the precipitation of biological hydroxyapatite.

Methods: We simulated the processes occurring in the bone interstitial fluid (ISF) defined as an aqueous environment containing seven chemical components (calcium, phosphate, carbonate, sodium, potassium, magnesium, and chloride) that form 30 chemical species. We simulated reversible equilibrium reactions among these chemical species, and calculated supersaturation for hydroxyapatite and its precipitation rate using kinetic theory.

Results and Discussion: The simulated ISF was of correct ionic strength and predicted the equilibrium component concentrations that were consistent with the experimental findings. Supersaturation of physiological ISF was ~15, which is consistent with prior findings that mineralization inhibitors are required to prevent spontaneous mineral precipitation. Only total calcium, total phosphate and to a lesser degree total carbonate affected ion availability, solution supersaturation and hydroxyapatite precipitation rate. Both calcium and phosphate levels directly affected hydroxyapatite precipitation, and phosphate was affected by pH, which additionally influenced hydroxyapatite precipitation. Integrating mathematical models capturing the physiochemical and biological factors regulating bone mineralization will allow in silico studies of complex clinical scenarios associated with alterations in ISF ion composition, such as rickets, hypophosphatemia, and chronic kidney disease.

1 Introduction

Bone is a biological composite material including three different phases, a mineral phase, an organic phase, and water [1]. The mature bone mineral phase is made up of nanosized crystalline hydroxyapatite (HAP) with chemical formula of Ca₁₀(PO₄)₆(OH)₂ [1]. The mineral phase of bone provides a strong structure for the mechanical resistance for the tissue [2], and an abundant number of ions (particularly calcium and phosphate) for whole body homeostasis [3]. The organic phase of the bone consists of almost 90% type I collagen, 5% non-collagenous proteins (NCPs), and 2% lipids by weight [1]. Finally, the aqueous phase is responsible for cell and matrix nutrition, mediating interactions between collagen fibrils and minerals, and controlling ion flux [3]. Bone formation starts with deposition of organic matrix by osteoblasts, which happens at a much faster rate than bone mineralization [4]. The unmineralized bone matrix, osteoid, is mineralized through physicochemical processes regulated by the presence of nucleation centers that can be provided by matrix vesicles [5] and can arise with the maturation of extracellular matrix [6], and the concentrations of mineralization inhibitors produced by osteoblasts or present in the circulation. Thus, complex biological and physicochemical phenomena are involved in regulating hydroxyapatite mineralization.

Mathematical models provide a deeper understanding of how different components interact and influence each other in complex environments [7]. We have previously modeled the role of biological factors in bone mineralization [8], and have examined a simplified model of pH regulation in bone microenvironment [9]. Building on the concept of simulated interstitial fluid (ISF) introduced in the previous work [9], in the current study, we aimed to develop a mathematical model describing the complex physicochemical environment permissive to the precipitation of biological hydroxyapatite. The aqueous environment of ISF was defined to contain seven commonly reported chemical components (calcium, phosphate, carbonate, sodium, potassium, magnesium, and chloride) that form 30 chemical species. Computing the outcomes of reversible equilibrium reactions among these chemical species allowed us to calculate solution supersaturation for HAP and assess HAP precipitation rate using kinetic theory.

2 Model development and simulations

2.1 Model assumptions

In this study, we have simulated the processes occurring in the interstitial fluid (ISF) in the bone vicinity. It is assumed that the environment is homogenous, and ions are immediately distributed evenly in the environment. The following assumptions regarding the biological components of the system were made: [1] the effects of biological factors on equilibrium reactions in ISF are minimal; [2] the presence of biological inhibitors of mineralization increases the precipitation threshold [10]; [3] the nucleation of biological mineral is controlled by biological processes [11], and physicochemical aspects are involved in crystal growth. Efforts have been made to keep the model working with the minimum number of components and complexity while ensuring the predictions are reliable and close enough to the actual processes happening in the body.

Figure 1 provides a map of the model, its different compartments, and the flow of data in the model. A detailed description of how the model is constructed is provided in the following sections.

FIGURE 1

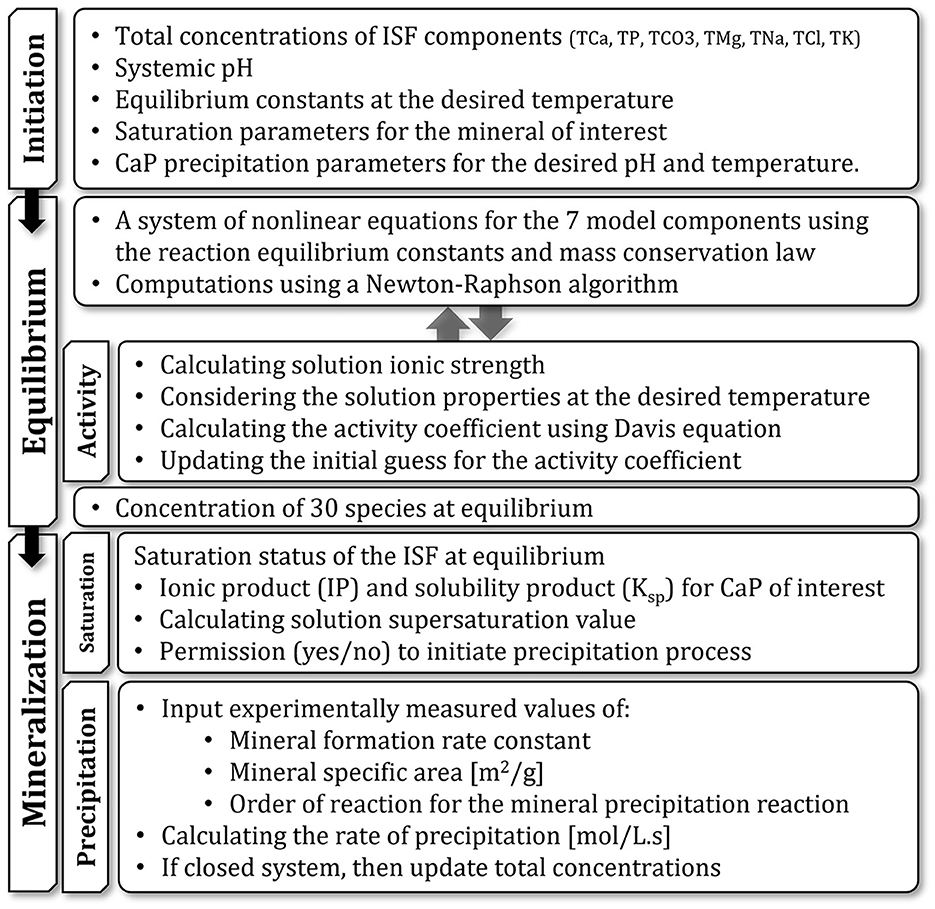
Figure 1. Schematic representation of the model and its different compartments and their functions. Arrows show the flow of data between compartments.

2.2 Simulated ISF

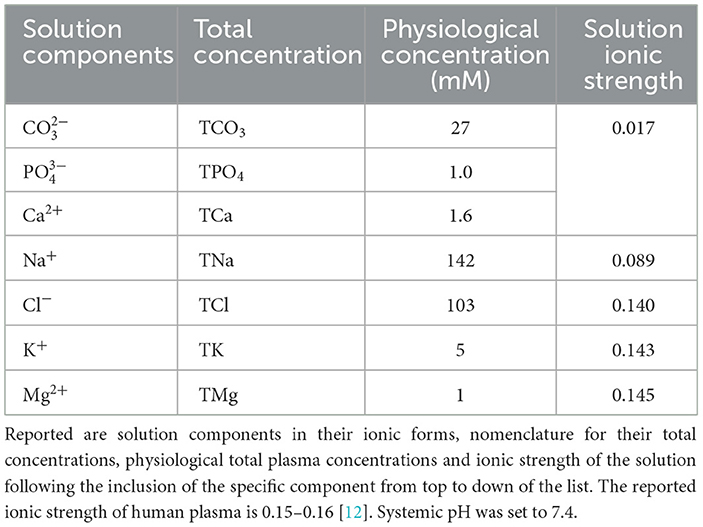
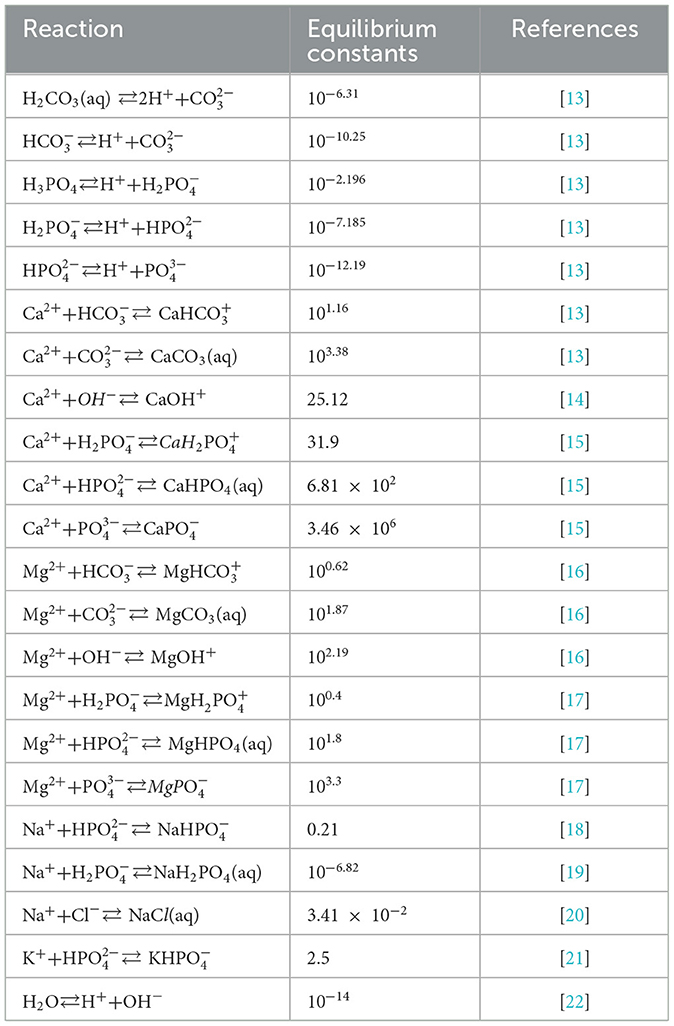
Previously, we developed the model of the ISF reactions that focused on four components involved in pH regulation, calcium (Ca²⁺), phosphate (${\text{PO}}_4^{3-}$), carbonate (${\text{CO}}_3^{2-}$), and hydrogen(H⁺) [9]. However, the ionic strength of the solution containing four components is 0.017, which is notably lower than 0.15–0.16 reported experimentally [12]. Since ionic strength directly affects the calculation of activity coefficients and thus the equilibrium concentrations, to improve model precision, we included the additional chemical components and examined how their inclusion affected the ionic strength of the ISF (Table 1). The resulting ISF was defined as a solution containing seven major components: calcium (Ca²⁺), phosphate ($P{O}_4^{3-}$), carbonate ($C{O}_3^{2-}$), sodium (Na⁺), chloride (Cl⁻), magnesium (Mg²⁺), and potassium (K⁺) (Table 1). These components interact through reversible reactions forming 22 different chemical species listed here: H₃PO₄, ${H_{2}PO}_4^{-}$, $HP{O}_4^{2-}$, H₂CO₃(aq), $HC{O}_3^{-}$, $CaHC{O}_3^{+}$, CaCO₃(aq), CaOH⁺, ${Ca{H}_{2}PO}_4^{+}$, CaHPO₄(aq), $CaP{O}_4^{-}$, $NaHP{O}_4^{-}$, Na_H2PO4(aq), $MgHC{O}_3^{+}$, MgCO₃(aq), MgOH⁺, ${Mg{H}_{2}PO}_4^{+}$, MgHPO₄(aq), $MgP{O}_4^{-}$, NaCl, $KHP{O}_4^{-}$, OH⁻. The equilibrium constants for the 22 reactions were obtained from experimental studies; where reported, we used the value at the body temperature of 37 °C (Table 2). Seven equations for the principle of mass conservation for total amounts of calcium (TCa), phosphate (TPO₄), carbonate (TCO₃), magnesium (TMg), sodium (TNa), potassium (TK), and chloride (TCl) in addition to pH value completed the description of ISF (Table 2). The total amounts of these components were matched to those reported in human plasma [12](Table 1). The ISF is an ionic solution which requires the inclusion of activity coefficients in calculating its equilibrium concentrations. Ionic strength of a solution is defined as:

$\begin{array}{ll}I=\frac{1}{2}{\displaystyle \sum _{i=1}^n}{c}_i.{z_i}^2& (1)\end{array}$

where c_i is the molar concentration of ion i, z_i is its valence, and n is the number of different ions in the solution. The activity coefficients were calculated as follows:

$\begin{array}{ll}log{\gamma }_i=-A{z}_i^2\left(\frac{\sqrt{I}}{\left(1+\sqrt{I}\right)}-0.3I\right)& (2)\end{array}$

γ_i is the activity coefficient of ion i, which depends on ionic strength I of the solution, ion valence z_i, and temperature and the dielectric constant of the solvent expressed in parameter A. This parameter was previously approximated [23] for a solution with water as the solvent as:

$\begin{array}{ll}A=0.486+6.07\times 10^{-4}{T}_C+6.43\times 10^{-6}{T}_C^2& (3)\end{array}$

where T_C is temperature in Celsius (37 °C in this study). Equation 2 is only valid for I ≤ 0.5 M [18], which is applicable in this case (Table 1). Finally, equilibrium concentrations are calculated as:

$\begin{array}{ll}{Q}_i=c_i.{\gamma }_i& (4)\end{array}$

where Q_i, the corrected concentration is a product of nominal concentration c_i of each ion and its activity coefficient γ_i.

TABLE 1

Table 1. Model components and their effect on the ionic strength of the solution.

TABLE 2

Table 2. ISF Reactions and their equilibrium constants.

For the calculation of the equilibrium concentrations a system of non-linear equation had to be formed and solved. Using the reaction rate law and equilibrium constants for the 22 reactions (Table 2), one equation from pH definition, in addition of 7 equations derived from mass conservation law for total concentration of calcium (TCa), phosphate (TPO₄), carbonate (TCO₃), magnesium (TMg), sodium (TNa), potassium (TK), and chloride (TCl), a system of 30 equations was formed. Using the definition of equilibrium constants, the system was later simplified to a system of 7 non-linear equations with 7 variables (the components in Table 1). The system of equation was solved for these 7 variables and the rest of chemical species were later calculated by reversing the simplifying step using equilibrium constants.

2.3 Saturation

The simulated ISF includes the possibility of mineral formation. Physicochemically speaking, mineral formation requires the solution to be at a supersaturated state, meaning that there must be more solute available than the amount that can be dissolved in the solvent at a defined physical condition (temperature and pressure). To investigate the state of saturation, the minerals of interest must be known. Although there have been many studies on the formation of intermediate calcium phosphate precipitates prior to or simultaneous with the formation of hydroxyapatite [24], in the current model we did not take into account the intermediate precipitates and their gradual transition into the stable hydroxyapatite form. In this study we assumed that hydroxyapatite with the chemical formula of Ca₁₀(PO₄)₆(OH)₂ is the only form of mineral that could be formed. With that, to investigate the state of saturation we calculated supersaturation using the following equation:

$\begin{array}{ll}S={(\frac{IP}{K_{SP}})}^{1/9}& (5)\end{array}$

S in Equation 5 is the solution supersaturation which depends on the ionic product and the solubility product of hydroxyapatite. Ionic product is calculated as:

$\begin{array}{ll}IP={(C_{Ca}\times {\gamma }_{Ca})}^5{(C_{P{O}_4}\times {\gamma }_{P{O}_4})}^3{(C_{OH}\times {\gamma }_{OH})}^1& (6)\end{array}$

where C and γ stand for the equilibrium concentration and the activity coefficient for each ion in the mineral structure. Solubility product, K_SP, is the equilibrium constant for a chemical reaction in which a solid ionic compound dissolves to yield its ions and is measured experimentally. K_SP for hydroxyapatite at 37°C is reported $2.03\times 10^{-59}\frac{mo{l}^9}{L^9}$ [12]. For other precipitates, we used the following K_SP: brushite (DCPD) 10⁻⁷ [25], octacalcium phosphate (OCP) 1.05 × 10⁻⁴⁷ [26], β-tricalcium phosphate (TCP) 2.83 × 10⁻³⁰ [27], and calcium carbonate (CaCO₃) 3.36 × 10⁻⁹ [28]. Supersaturation, S, >1 in a solution indicates a supersaturated state where mineral precipitation occurs until S = 1 (or IP = K_SP) and the system rests at equilibrium. In a biological system like the human body, availability of mineralization inhibitors can affect this behavior. For example, this threshold at human urine is estimated at ~10 [29], while for human plasma it is calculated in the range of 1.5 to 13 [12, 18]. The difference in the reported values comes also from the fact that different studies considered different values for plasma concentrations and did the calculations with different levels of simplification. In the current study, supersaturation S was calculated at 14.9 for the concentrations introduced at Table 1.

It is worth noting here that different studies report the saturation state of the solution using slightly different methods, although they are all addressing the same phenomenon. Some studies use solution supersaturation defined as ${(\frac{IP}{K_{SP}})}^{\frac{1}{\vartheta }}$, where ϑ is the sum of stochiometric coefficients of cations and anions involved in the mineral, some other use the saturation index defined as $log(\frac{IP}{K_{SP}})$, and in some cases, they just looked at the saturation ratio defined by $\frac{IP}{K_{SP}}$. It is obvious that the interpretation of the values calculated differs depending on the method used, for example while solution supersaturation of 1 means the solution is in equilibrium, the saturation index of value of 0 means the same state. In this study we used the solution supersaturation method.

2.4 Mineral precipitation

A supersaturated solution proceeds with mineral precipitation. Calcium phosphates and among them biologically important ones like hydroxyapatite have been studied over the years and different theoretical and experimental studies tried to address their rate of precipitation [30, 31]. In the current study, we relied on experimental study of hydroxyapatite precipitation rate at a solution with pH 7.4 to 8.4 [30] considering human physiology. The precipitation rate equation was reported as:

$\begin{array}{ll}R=k_{f}s{\gamma }_2{\gamma }_3\left[C{a}^{2+}\right]\left[P{O}_4^{3-}\right]& (7)\end{array}$

where R is rate of hydroxyapatite precipitation (mol HAP L⁻¹s⁻¹), k_f is the rate constant (L²mol¹m⁻²s⁻¹), s is surface area (m²L⁻¹), γ₂ and γ₃ are the divalent and trivalent activity coefficients, and brackets are the concentrations of Ca²⁺ and $P{O}_4^{3-}$ (mol L^{− 1}).

2.5 Model simulation and analysis (numerical solution)

Due to the high level of non-linearity and large number of variables, the Newton-Raphson (NR) method was used to solve the system of equations.

To avoid divergence in the NR solver, as proposed by Morel and Morgan [32], in cases that ${\left[X_j\right]}^n+\Delta {X_j}^n<0$, the next iteration would be calculated using ${\left[X_j\right]}^{n+1}=\frac{{\left[X_j\right]}^n}{10}$. The initial guess of equal concentrations and equal activity coefficients of 0.5 was made to initiate solving the system. During an iterative process, the calculated concentrations and coefficients of each iteration were used to initiate the next iteration of calculations. This iterative process was repeated to the point where the maximum difference between the last two iterative values of activity coefficients were smaller than an arbitrary value of ${\epsilon }_{act}=10^{-8}$. At this point, the equilibrium concentrations of all chemical species in the solution were calculated.

3 Results

We investigated how the changes in total concentrations of 7 model components, TCa, TPO₄, TCO₃, TMg, TNa, TK, TCl (Table 1), affect ISF composition, hydroxyapatite saturation and hydroxyapatite precipitation. We explored the range of changes corresponding to physiologically reported mild and severe decreases and increases in individual components (Table 3). In addition, we studied the effect of physiological variation in systemic pH from pH7.3 to pH7.55 [37] on ions distribution.

TABLE 3

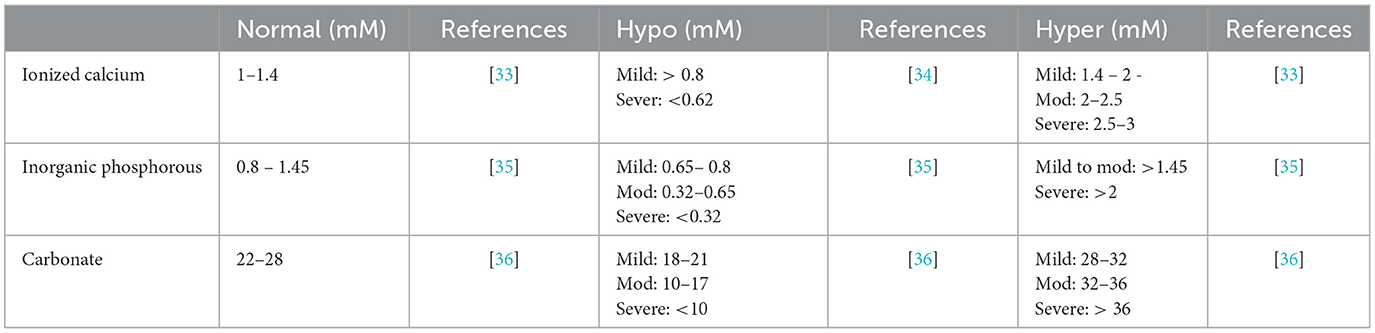
Table 3. Physiological and pathophysiological levels of total calcium, total phosphate, total carbonate.

3.1 Distribution of ions

We focused on the effect of total concentrations of individual components on the concentrations of ions relevant to hydroxyapatite precipitation, i.e., Ca²⁺ and $P{O}_4^{3-}$ (Figure 2). Changes in TCa positively correlated with ionized calcium concentration (Figure 2A) and negatively correlated with ionized phosphate level (Figure 2B), although the effect of TCa on $P{O}_4^{3-}$ was less prominent than on Ca²⁺. The TPO₄ positively correlated with ionized phosphate concentration and negatively correlated with ionized calcium and had a stronger effect on ionized phosphate (Figures 2C, D). Changes in total concentrations of other components in the model had minimal effect on ionized calcium and phosphate with the exception of carbonate that demonstrated negative association with ionized calcium and no association with ionized phosphate (Figures 2E, F). The effect of systemic pH was negligible for the ionized calcium, while ionized phosphate level was considerably influenced by pH level (Figure 2).

FIGURE 2

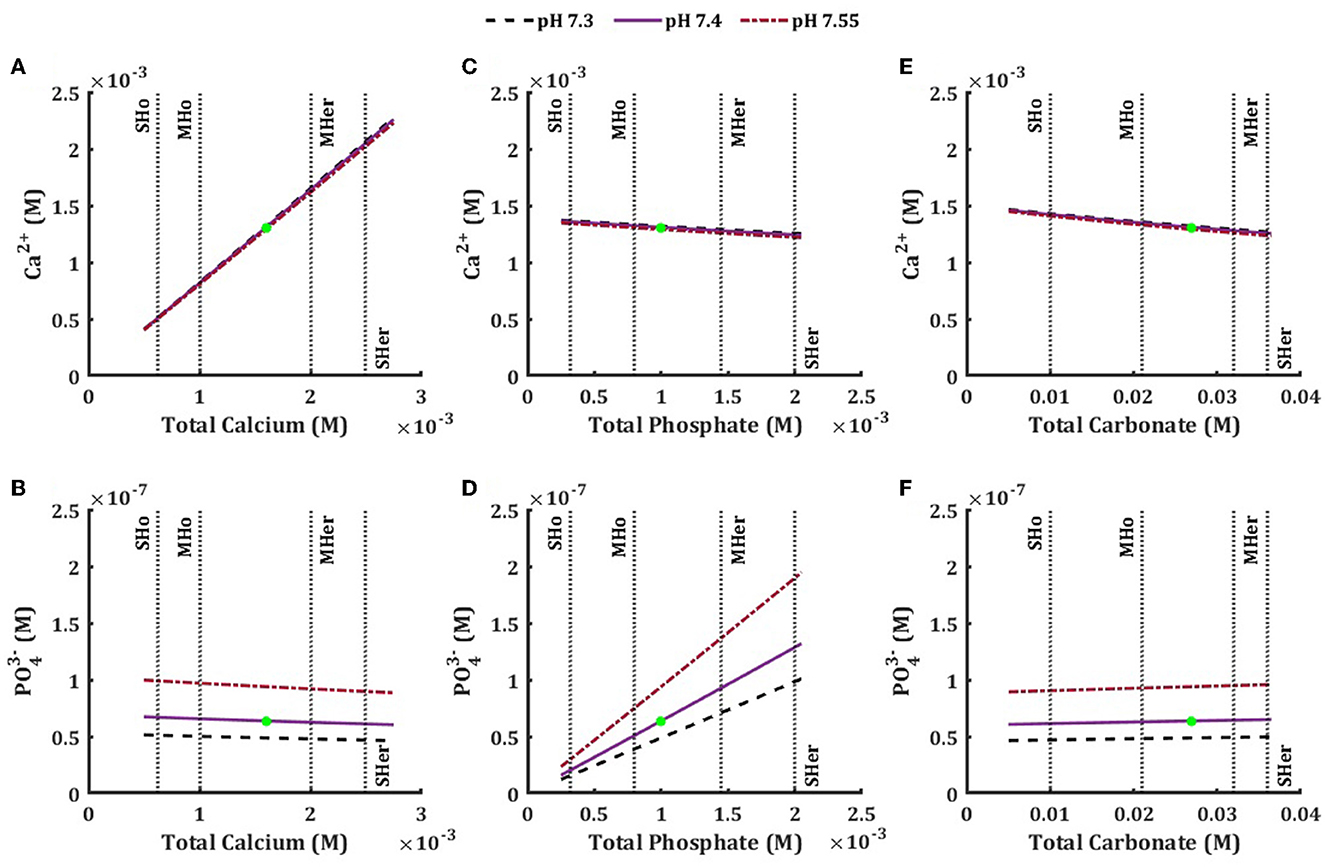
Figure 2. Effect of physiological and pathophysiological total concentration of calcium (A, B), phosphate (B, D), and carbonate (E, F) on the equilibrium concentration of ionized calcium (A, C, E), and ionized phosphate (B, D, E) at physiological pH7.4 (solid line), low pH 7.3 (dashed line) and high pH 7.55 (dished-dotted line). The vertical lines are the mild and severe levels for low and high total concentrations (Table 3).

3.2 Saturation

We next examined how total concentrations of individual components affect hydroxyapatite solution supersaturation (Equation 5). Solution supersaturation for HAP at the physiological levels of ions was 14.9, which is consistent with previously reported values [12, 38] and demonstrates that the action of mineralization inhibitors is critical for preventing precipitation in biological fluids [6]. The HAP solution supersaturation was positively associated with the levels of total calcium (Figure 3A) and total phosphate (Figure 3B). It was also mildly affected by total carbonate (negative association) (Figure 3C), but not by any other model components. Mild and severe hypercalcemia and hyperphosphatemia showed a similar effect in increasing the HAP solution supersaturation. Mild and severe hypocalcemia and hypophosphatemia lead to a decrease in HAP solution supersaturation, with total calcium having a more prominent effect (Table 4). We also considered the solution supersaturation for other mineral species, including DCPD, OCP, TCP and CaCO3 (Figures 3D–F). For all these components the level of solution supersaturation was lower than that of HAP, and for DCPD specifically, it was below 1 in the physiological ranges of total calcium, phosphate, and carbonate.

FIGURE 3

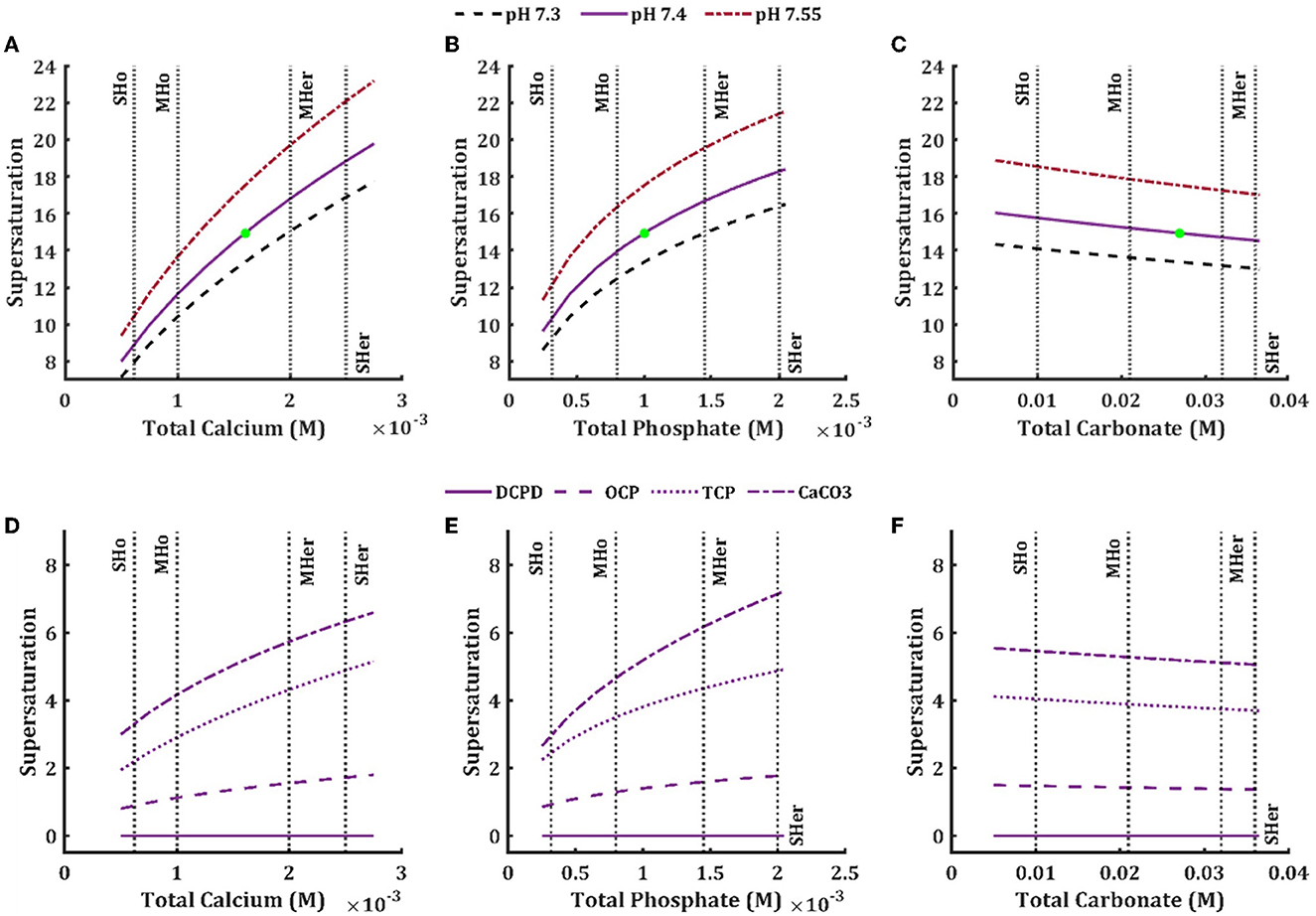
Figure 3. Effect of physiological and pathophysiological total concentration of calcium (A, D), phosphate (B, E), and carbonate (C, F) on the solution supersaturation (Equation 5) of hydroxyapatite (A–C) in the ISF at physiological pH 7.4 (solid line), low pH 7.3 (dashed line) and high pH 7.55 (dash-dotted line), and brushite (D–F, solid line), octacalcium phosphate (D–F, dashed line), tricalcium phosphate (D–F, dotted line), and calcium carbonate (D–F, dash-dotted line) in the ISF at physiological pH 7.4. The vertical lines are the mild and severe levels for low and high total concentrations (Table 3).

TABLE 4

Table 4. Percentage of saturation ratio changes in hypo/hyper levels of blood calcium, phosphate, and carbonate compared to normal concentrations at physiological pH (7.4).

3.3 Precipitation

Precipitation starts with nucleation and proceeds with crystal growth [39]. In the biological context of bone mineralization, the nucleation step is mostly controlled biologically by the extracellular matrix proteins including collagens [11], while the physicochemical processes are involved in the growth phase. Thus, we assumed that the number of nucleators were not limiting and examined how hydroxyapatite precipitation rate was affected by change in the ISF total concentrations of different components (Figure 4). Increase in total calcium (Figure 4A) and total phosphate (Figure 4B) concentrations led to higher hydroxyapatite precipitation rate and this increase was considerably influenced by the pH of the ISF. A more basic environment favored higher precipitation rate, while an acidic environment decreased the precipitation rate, although the lower physiological pH limit caused less change in the rate compared to the higher physiological limit. While both hypercalcemia and hyperphosphatemia caused the precipitation rate to increase, hyperphosphatemia (both mild and severe) led to an almost two-fold higher increase in the rate compared to hypercalcemia (Table 5). Hypocalcemia and hypophosphatemia led to decrease of the precipitation rate (Table 5). Changes in total concentrations of other model components did not affect the hydroxyapatite precipitation rate, except for total carbonate (Figure 4C, Table 5) which showed a mild negative association with the precipitation rate.

FIGURE 4

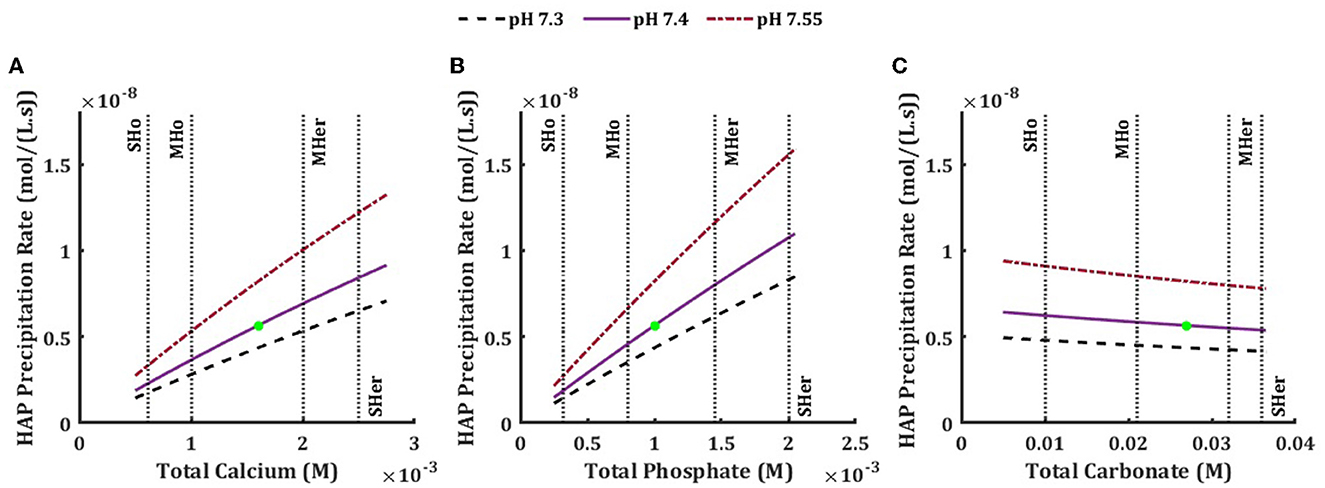
Figure 4. Effect of physiological and pathophysiological total concentration of calcium (A), phosphate (B), and carbonate (C) on the precipitation rate of hydroxyapatite in the ISF, at physiological pH7.4 (solid line), low pH 7.3 (dashed line) and high pH 7.55 (dished-dotted line). The vertical lines are the mild and severe levels for low and high total concentrations (Table 3).

TABLE 5

Table 5. Percentage of hydroxyapatite precipitation rate change in hypo/hyper levels of blood calcium, phosphate, and carbonate compared to normal concentrations at physiological pH (7.4).

Since from seven model components, only two, total calcium and total phosphate, considerably influenced the hydroxyapatite precipitation in ISF, we examined how simultaneous changes in these two components affect hydroxyapatite supersaturation and precipitation rate. The simultaneous changes of TCa and TPO₄ had non-linear effect on both hydroxyapatite supersaturation and especially on the hydroxyapatite precipitation rate, which increased synergistically when both TCa and TPO₄ increased, but was only mildly affected when both TCa and TPO₄ decreased (Figure 5).

FIGURE 5

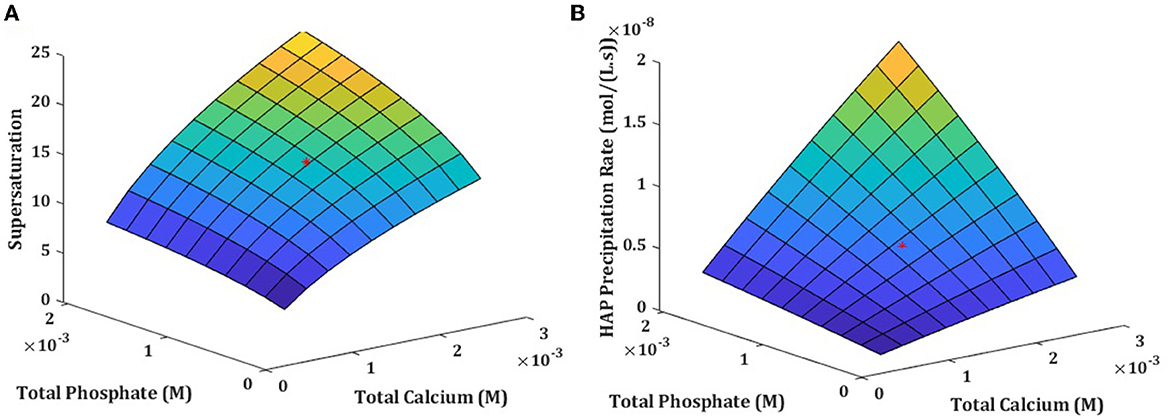
Figure 5. Solution supersaturation (A) and precipitation rate (B) influenced by simultaneous changes in total calcium and total phosphate concentration in physiologically relevant cncentrations at normal 7.4 pH.

3.4 The case of isolated ISF

So far in this study, we investigated the behavior of the system under the assumption that ISF is in constant contact with the blood circulation, and the ions involved in the mineral formation will be immediately replenished. This assumption is supported by the fact that the rate of precipitation is much slower than the rate of ion delivery to the ISF. Nonetheless, many experimental studies are performed in a closed environment, where there is no continuous delivery of ions consumed in mineral formation. Thus, we adapted the model to simulate such scenarios by employing the following modifications. We assumed that an ISF unit has the volume of 1 μm³ and the smallest time step to measure changes in the ISF was equal to 1 s. Given the initial total concentrations of model components, we calculated the equilibrium concentrations, supersaturation, and precipitation rate (Equations 4, 5, and 7). Then, the amounts of ions that would have been removed by precipitation in the defined time step (1 s) were calculated and subtracted from the initial total concentrations of model components to produce the updated total concentrations of model components for the next iteration. This process was repeated to investigate the model behavior for a desired time length. This modified model was used to examine the temporal dynamics of hydroxyapatite precipitation in the closed system under different pH levels and initial component concentrations (Figure 6). Initial precipitation rate in closed system strongly depended on pH, resulting in more hydroxyapatite precipitation at alkaline pH, which is similar to experimental observations [40].

FIGURE 6

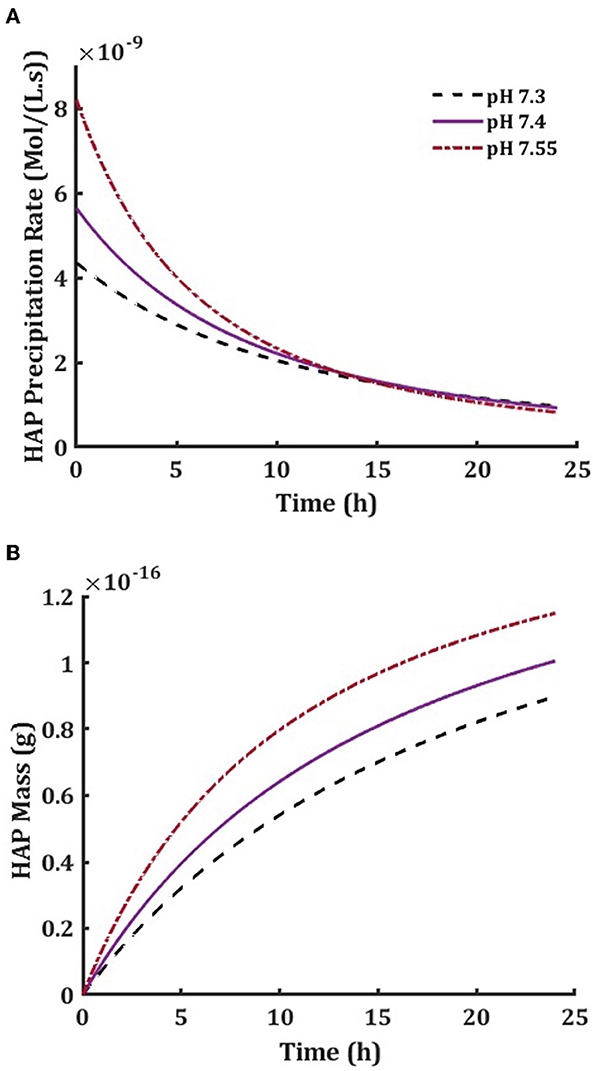
Figure 6. Hydroxyapatite precipitation rate in a 24-h precipitation period of the isolated ISF (A) and the accumulated mass of hydroxyapatite in a cube of 1 μm³ volume (B) at physiological pH7.4 (solid line), low pH 7.3 (dashed line) and high pH 7.55 (dished-dotted line).

Next, we compared our model predictions to previously published experimental data. First, we modeled the dependence of ionized calcium on pH reported by Miyajima et al. [41]. We used in the model the reported values of component concentrations and pH for the experimental study and calculated the concentration of Ca²⁺ as a function of pH (Figure 7A). Our model agreed well with the experimental values at pH 7.4–7.8 but deviated at higher pH levels. Next, we modeled the pH dependence of ion distributions reported by Boistelle et al. [42]. We have similarly used the experimental values reported in the paper and calculated the resulting ionic concentrations of model species (Figure 7B), and the solution supersaturation for hydroxyapatite (Figure 7C). Our findings were consistent with reported experimentally for pH 5–8 and deviated from reported values at higher pH. Thus, our model predictions were consistent with experimental findings for pH values in the physiological range.

FIGURE 7

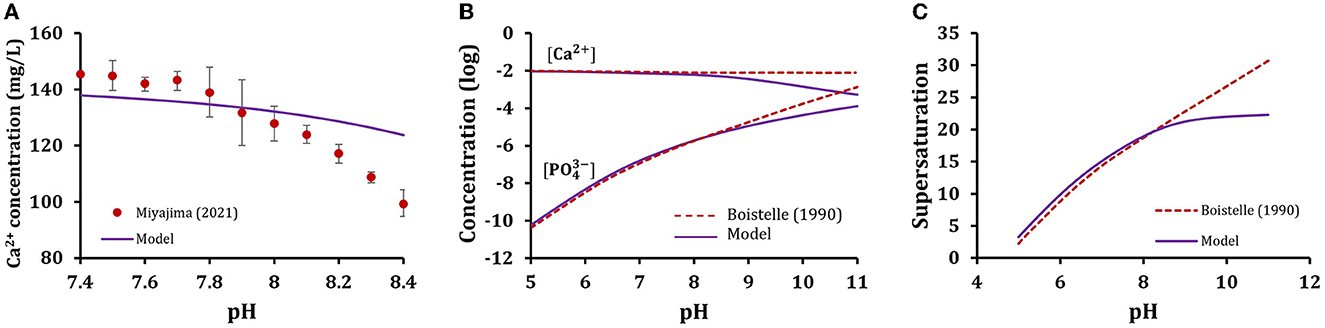
Figure 7. Model validation with prior experimental data. Simulations were performed with experimental data reported by (A) Miyajima et al. [41] or (B) Boistelle et al. [42]. Model predictions are plotted as solid line and published data (circles with experimental errors for A and dashed lines for B, C) were extracted from the published papers and replotted with permission.

4 Discussion

The goal of this study was to investigate the role of physicochemical factors in the precipitation of bone hydroxyapatite in an environment that resembles bone interstitial fluid. We demonstrate that of the 7 components taken into consideration, only total calcium, total phosphate and to a lesser degree total carbonate affected ion availability, solution supersaturation and hydroxyapatite precipitation rate. Strong effect of systemic pH on solution supersaturation and hydroxyapatite precipitation was due to its effect on ionized phosphate level since ionized calcium was not affected by pH. Hydroxyapatite precipitation was more strongly affected by availability of phosphate than availability of calcium within physiological range of changes in these components. Simultaneous change in total calcium and phosphate had synergetic effect on hydroxyapatite precipitation rate. Thus, while both calcium and phosphate levels affected hydroxyapatite precipitation directly, phosphate also demonstrated susceptibility to changes in pH, which additionally influenced hydroxyapatite precipitation.

Building a chemically sound model of interactions among different chemical species present in the ISF allowed us to investigate their effect on ionized calcium and phosphate, which are critical for hydroxyapatite formation. While it was challenging to find experimental or computational works that had the exact same solution parameters as the ones implemented in the model, using values from similar experimental studies, we were able to reproduce experimentally observed ion distribution for physiological levels of pH [41, 42]. The negative association between total phosphate and pH with ionized calcium observed previously [43], was also confirmed by the model. Our study suggests that only levels of total calcium and phosphate and to a lesser degree total carbonate affect availability of ionized calcium and phosphate relevant for hydroxyapatite precipitation. However, the chemical complexity of ISF should still be taken into account to obtain correct predictions of the ionic strength and interactions in the solution.

The distribution of ions matters not only because they define the properties of the ISF, but also as they can affect the precipitation behavior by modifying the solution saturation status. Building on previous findings that total calcium, phosphate and carbonate influence the ionized calcium and phosphate availability, we investigated their consequent effect on saturation state of the ISF. At physiological levels of model components, the model predicted the solution supersaturation of 14.9, which is close to reported experimental values [12]. While the model confirmed the state of supersaturation normally observed in human plasma [44], it also provided a broader understanding of how this supersaturation state could be influenced when total concentration of model components (i.e., their plasma or ISF levels) change. Moreover, the model predicts and explains the previously reported [40, 45] relationship of increased supersaturation values when pH increases at constant calcium and phosphate levels. In the future, the model predictions can be improved by a more precise incorporation of different parameters, such as accounting for the variability in K_SP due to pH, temperature, and solution composition [46]. Investigating the effect of ion distribution and saturation status on hydroxyapatite precipitation behavior demonstrated that precipitation rate is driven by the values of ionized calcium and phosphate, which in turn depend on pH. Model predictions were consistent with previous findings that an increase in ionized phosphate at high pH levels increases the deposition rate of hydroxyapatite and that decrease in phosphate availability interferes with hydroxyapatite precipitation [47]. Thus, our findings are consistent with the well-recognized role of phosphate in regulating bone mineralization in physiological condition and in hypophosphatemic osteomalacia.

While many simplifications are implemented in constructing this model, the fact that its findings are in line with experimental works and current understanding of human physiology reassure us that the findings are reliable and that the model is suitable further developed. Combining this model with models of bone mineralization that account for biological factors such as collagen maturation [48] and bone cells-derived regulators [49] will provide a powerful tool in studying the formation of bone hydroxyapatite or other biological mineralized tissues. Another field of modeling that could potentially benefit from the combined physicochemical and biological model is the whole-body calcium and phosphate homeostasis models. Bone is a major component of calcium and phosphate homeostasis, and its behavior is regulated by hormonal regulation by PTH, vitamin D, FGF23, calcitonin which directly or indirectly affect calcium and phosphate concentration in the body [50].

Taken together, we developed a mathematical model that captures the physiochemical factors involved in hydroxyapatite precipitation. We demonstrated how factors such as availability of ions in the environment and their distribution of these ions, as well as pH levels affect hydroxyapatite precipitation. Integrating this model with biological models of bone mineralization will allow in silico studies of complex clinical scenarios associated with alterations in ISF ion composition, such as osteomalacia, osteogenesis imperfecta, rickets, hypophosphatemia, and chronic kidney disease. Moreover, with minor adaptations, it could be used to understand mineralization in other physiological tissues, such as dentin and enamel, and in pathological conditions such as kidney stones and atherosclerotic plaques [51].

5 Additional resources

Implementation of current bone physicochemical model in MATLAB is available on GitHub: https://github.com/Hosseinpoorhemati/bone_physicochemical_regulation.git.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

HP: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—review & editing. SVK: Conceptualization, Funding acquisition, Methodology, Project administration, Writing—review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the operating grant from the Natural Sciences and Engineering Research Council of Canada (NSERC, RGPIN-288253).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Boskey AL. Bone composition: relationship to bone fragility and antiosteoporotic drug effects. BoneKEy Rep. (2013) 2:181. doi: 10.1038/bonekey.2013.181

CrossRef Full Text | Google Scholar

2. Willie BM, Zimmermann EA, Vitienes I, Main RP, Komarova SV. Bone adaptation: Safety factors and load predictability in shaping skeletal form. Bone. (2020) 131:115114. doi: 10.1016/j.bone.2019.115114

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Boskey AL, Robey PG. The composition of bone. Primer Metab Bone Dis Disord Miner Metab. (2013) 15:49–58. doi: 10.1002/9781118453926.ch6

CrossRef Full Text | Google Scholar

4. Vassiliou V, Chow E, Kardamakis D. Bone Metastases: A Translational and Clinical Approach. Cham: Springer Science & Business Media (2013).

Google Scholar

5. Ambre AH, Katti DR, Katti KS. Biomineralized hydroxyapatite nanoclay composite scaffolds with polycaprolactone for stem cell-based bone tissue engineering. J Biomed Mater Res A. (2015) 103:2077–101. doi: 10.1002/jbm.a.35342

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Murshed M. Mechanism of Bone Mineralization. Cold Spring Harb Perspect Med. (2018) 8:12. doi: 10.1101/cshperspect.a031229

CrossRef Full Text | Google Scholar

7. Collin CB, Gebhardt T, Golebiewski M, Karaderi T, Hillemanns M, Khan FM, et al. Computational models for clinical applications in personalized medicine—guidelines and recommendations for data integration and model validation. J Pers Med. (2022) 12:166. doi: 10.3390/jpm12020166

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Komarova SV, Safranek L, Gopalakrishnan J, Ou MJ, McKee MD, Murshed M, et al. Mathematical model for bone mineralization. Front Cell Dev Biol. (2015) 3:51. doi: 10.3389/fcell.2015.00051

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Poorhemati H, Komarova SV. Mathematical modeling of the role of bone turnover in pH regulation in bone interstitial fluid. Comput Biol Chem. (2021) 94:107564. doi: 10.1016/j.compbiolchem.2021.107564

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hunter GK, Kyle CL, Goldberg HA. Modulation of crystal formation by bone phosphoproteins: structural specificity of the osteopontin-mediated inhibition of hydroxyapatite formation. Biochem J. (1994) 300:723–8. doi: 10.1042/bj3000723

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Olszta MJ, Cheng X, Jee SS, Kumar R, Kim Y-Y, Kaufman MJ, et al. Bone structure and formation: a new perspective. Mat Sci Eng R Rep. (2007) 58:77–116. doi: 10.1016/j.mser.2007.05.001

CrossRef Full Text | Google Scholar

12. Söhnel O, Grases F. Supersaturation of body fluids, plasma and urine, with respect to biological hydroxyapatite. Urol Res. (2011) 39:429–36. doi: 10.1007/s00240-011-0387-5

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Oyane A, Kim HM, Furuya T, Kokubo T, Miyazaki T, Nakamura T. Preparation and assessment of revised simulated body fluids. J Biomed Mater Res A. (2003) 65:188–95. doi: 10.1002/jbm.a.10482

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Koutsoukos P, Nancollas G. Crystal growth of calcium phosphates-epitaxial considerations. J Cryst Growth. (1981) 53:10–9. doi: 10.1016/0022-0248(81)90051-8

CrossRef Full Text | Google Scholar

15. Chughtai AR, Marshall R, Nancollas GH. Complexes in calcium phosphate solutions. J Phys Chem. (1968) 72:208–11. doi: 10.1021/j100847a039

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Butler JN. Ionic Equilibrium: Solubility and pH Calculations. London: John Wiley & Sons (1998).

Google Scholar

17. Childs C. Potentiometric study of equilibriums in aqueous divalent metal orthophosphate solutions. Inorg Chem. (1970) 9:2465–9. doi: 10.1021/ic50093a017

CrossRef Full Text | Google Scholar

18. Granjon D, Bonny O, Edwards A. Coupling between phosphate and calcium homeostasis: a mathematical model. Am J Physiol Renal Physiol. (2017) 313:F1181–F99. doi: 10.1152/ajprenal.00271.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Salaun F, Mietton B, Gaucheron F. Influence of mineral environment on the buffering capacity of casein micelles. Milchwissenschaft Milk Sci Int. (2007) 62:20–3.

Google Scholar

20. Crundwell FK. Path from reaction control to equilibrium constraint for dissolution reactions. ACS Omega. (2017) 2:4845–58. doi: 10.1021/acsomega.7b00344

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Guynn RW. Equilibrium constants under physiological conditions for the reactions of choline kinase and the hydrolysis of phosphorylcholine to choline and inorganic phosphate. J Biol Chem. (1976) 251:7162–7. doi: 10.1016/S0021-9258(17)32957-5

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Silverstein TP, Heller ST. pK_a values in the undergraduate curriculum: What is the real pK_a of water? J Chem Educ. (2017) 94:690–5. doi: 10.1021/acs.jchemed.6b00623

CrossRef Full Text | Google Scholar

23. Drake F, Pierce G, Dow M. Measurement of the dielectric constant and index of refraction of water and aqueous solutions of KCl at high frequencies. Phys Rev. (1930) 35:613. doi: 10.1103/PhysRev.35.613

CrossRef Full Text | Google Scholar

24. Castro F, Ferreira A, Rocha F, Vicente A, Teixeira JA. Characterization of intermediate stages in the precipitation of hydroxyapatite at 37 C. Chem Eng Sci. (2012) 77:150–6. doi: 10.1016/j.ces.2012.01.058

CrossRef Full Text | Google Scholar

25. Nancollas G, Tomazic B. Growth of calcium phosphate on hydroxyapatite crystals. Effect of supersaturation and ionic medium. J Phys Chem. (1974) 78:2218–25. doi: 10.1021/j100615a007

CrossRef Full Text | Google Scholar

26. Moreno EC, Brown WE, Osborn G. Stability of dicalcium phosphate dihydrate in aqueous solutions and solubility of octocalcium phosphate. Soil Sci Soc Am J. (1960) 24:99–102. doi: 10.2136/sssaj1960.03615995002400020010x

CrossRef Full Text | Google Scholar

27. Gregory T, Moreno E, Patel J, Brown W. Solubility of β-Ca3 (PO4) 2 in the System Ca (OH) 2-H3PO4-H2O at 5, 15, 25, and 37° C. J Res Nat Bureau Standards Sec A Phys Chem. (1974) 78:667. doi: 10.6028/jres.078A.042

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gal J-Y, Bollinger J-C, Tolosa H, Gache N. Calcium carbonate solubility: a reappraisal of scale formation and inhibition. Talanta. (1996) 43:1497–509. doi: 10.1016/0039-9140(96)01925-X

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Herbert FK, Miller H, Richardson G. Chronic renal disease, secondary parathyroid hyperplasia, decalcification of bone and metastatic calcification. J Pathol Bacteriol. (1941) 53:161–82. doi: 10.1002/path.1700530202

CrossRef Full Text | Google Scholar

30. Inskeep WP, Silvertooth JC. Kinetics of hydroxyapatite precipitation at pH 7. 4 to 84. Geochimica et Cosmochimica Acta. (1988) 52:1883–93. doi: 10.1016/0016-7037(88)90012-9

CrossRef Full Text | Google Scholar

31. Yun J, Holmes B, Fok A, Wang Y, A. kinetic model for hydroxyapatite precipitation in mineralizing solutions. Cryst Growth Des. (2018) 18:2717–25. doi: 10.1021/acs.cgd.7b01330

CrossRef Full Text | Google Scholar

32. Morel F, Morgan J. A numerical method for computing equilibria in aqueous chemical systems. Environ Sci Technol. (1972) 21:1–14. doi: 10.1021/es60060a006

CrossRef Full Text | Google Scholar

33. Carroll MF, Schade DS. A practical approach to hypercalcemia. Am Fam Physician. (2003) 67:1959–66.

Google Scholar

34. Pepe J, Colangelo L, Biamonte F, Sonato C, Danese VC, Cecchetti V, et al. Diagnosis and management of hypocalcemia. Endocrine. (2020) 69:485–95. doi: 10.1007/s12020-020-02324-2

CrossRef Full Text | Google Scholar

35. Koumakis E, Cormier C, Roux C, Briot K. The causes of hypo-and hyperphosphatemia in humans. Calcified Tissue Int. (2021) 108:41–73. doi: 10.1007/s00223-020-00664-9

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Narins RG, Emmett M. Simple and mixed acid-base disorders: a practical approach. Medicine. (1980) 59:161–82. doi: 10.1097/00005792-198005000-00001

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Mehta AN, Emmett M. Approach to Acid-Base Disorders. National Kidney Foundation Primer on Kidney Diseases. Amsterdam: Elsevier (2018), 120–9.

Google Scholar

38. Aleš H, Lenka J, Ludvík Š. The influence of simulated body fluid composition on carbonated hydroxyapatite formation. Ceram-Silik. (2002) 46:9–14.

Google Scholar

39. Eanes ED. Dynamics of calcium phosphate precipitation. Calcif Biol Syst. (2020) 21:1–17. doi: 10.1201/9781003068396-2

CrossRef Full Text | Google Scholar

40. Lei Y, Song B, van der Weijden RD, Saakes M, Buisman CJ. Electrochemical induced calcium phosphate precipitation: importance of local pH. Environ Sci Technol. (2017) 51:11156–64. doi: 10.1021/acs.est.7b03909

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Miyajima H, Touji H, Iijima K. Hydroxyapatite particles from simulated body fluids with different pH and their effects on mesenchymal stem cells. Nanomaterials. (2021) 11:2517. doi: 10.3390/nano11102517

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Boistelle R, Lopez-Valero I. Growth units and nucleation: the case of calcium phosphates. J Cryst Growth. (1990) 102:609–17. doi: 10.1016/0022-0248(90)90420-P

CrossRef Full Text | Google Scholar

43. Lehmann M, Mimouni F. Serum phosphate concentration. Effect on serum ionized calcium concentration in vitro. Am J Dis Child. (1989) 143:1340–1. doi: 10.1001/archpedi.1989.02150230098031

CrossRef Full Text | Google Scholar

44. Zhu P, Masuda Y, Yonezawa T, Koumoto K. Investigation of apatite deposition onto charged surfaces in aqueous solutions using a quartz-crystal microbalance. J Am Ceram Soc. (2003) 86:782–90. doi: 10.1111/j.1151-2916.2003.tb03375.x

CrossRef Full Text | Google Scholar

45. Nancollas GH, Zhang J. Formation and Dissolution Mechanisms of Calcium Phosphates in Aqueous Systems. Hydroxyapatite and Related Materials. London: CRC Press (2017), 73–81.

Google Scholar

46. Ito A, Maekawa K, Tsutsumi S, Ikazaki F, Tateishi T. Solubility product of OH-carbonated hydroxyapatite. J Biomed Mat Res Biomat. (1997) 36:522–8. doi: 10.1002/(SICI)1097-4636(19970915)36:4<522::AID-JBM10>3.0.CO;2-C

CrossRef Full Text | Google Scholar

47. Bhadada SK, Rao SD. Role of phosphate in biomineralization. Calcified Tissue Int. (2021) 108:32–40. doi: 10.1007/s00223-020-00729-9

CrossRef Full Text | Google Scholar

48. Oosterlaken BM, Vena MP, de With G. In vitro mineralization of collagen. Adv Mat. (2021) 33:2004418. doi: 10.1002/adma.202004418

CrossRef Full Text | Google Scholar

49. Staines KA, Zhu D, Farquharson C, MacRae VE. Identification of novel regulators of osteoblast matrix mineralization by time series transcriptional profiling. J Bone Miner Metab. (2014) 32:240–51. doi: 10.1007/s00774-013-0493-2

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Case RM, Eisner D, Gurney A, Jones O, Muallem S, Verkhratsky A. Evolution of calcium homeostasis: from birth of the first cell to an omnipresent signalling system. Cell Calcium. (2007) 42:345–50. doi: 10.1016/j.ceca.2007.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Hinterdobler J, Schott, Simin, Jin H, Meesmann A, Steinsiek A-L, Zimmermann A-S, et al. Acute mental stress drives vascular inflammation and promotes plaque destabilization in mouse atherosclerosis. Eur Heart J. (2021) 42:4077–88. doi: 10.1093/eurheartj/ehab371

CrossRef Full Text | Google Scholar