Optimized repetitive sampling X-bar control chart: performance evaluation and comparison with Shewhart control chart

When initial sample information falls short of enabling industrial engineers to confidently make decisions about lot quality assessment, repetitive sampling emerges as a solution. In this study, we present an optimized repetitive sampling control chart for X-bar values. Through meticulous analysis, we determined the optimal control chart coefficients. Additionally, we established the control chart parameters for scenarios where the sample size equals the average sample number, encompassing both in-control and out-of-control processes. To underscore the effectiveness of our proposed chart compared to the traditional Shewhart control chart, we provide comprehensive tables across various sample sizes. By meticulously examining these tables alongside the corresponding control charts, the chart's efficacy in relation to the Shewhart alternative becomes evident.

1 Introduction

Control charts have been widely used in the industry for monitoring the process. These charts are powerful tools used to minimize non-conforming products. The control charts are designed to increase the quality of the product. In industry, when the process is out of control, control charts provide a signal so that the processes can be controlled. Due to the simplicity of the Shewhart control, it has been widely used in industry for the monitoring of manufacturing processes. The operational procedure of the Shewhart control chart relies on three control limits, namely, the lower control limit (LCL), the central limit (CL), and the upper control limit (UCL). The process is deemed out of control if the plotting statistic is beyond LCL or UCL. The applications of the Shewhart control chart can be observed in Lee and Jun [1], Fu et al. [2], Oprime and Mendes [3], Hanandeh and Al-Nasser [4], Shafqat et al. [5], Vasconcelos et al. [6], and Park et al. [7].

Typically, Shewhart control charts are constructed using single sampling, where the determination of whether a process is in control or out of control relies on a single sample. However, real-world scenarios may not always permit such conclusive decisions with a single sample. One alternative to single sampling is repetitive sampling (RS). When there is uncertainty regarding the status of the production process, a random sample is taken, and the process is repeated until the in-control or out-of-control status of the production process is determined. At its core, RS, introduced by Sherman [8], involves the repeated collection of small samples from a production process at regular intervals. This technique allows for a continuous and real-time assessment of a process's performance. Unlike traditional single-sample approaches, RS enables a more thorough understanding of process variability over time, making it a valuable tool in quality control [8].

Aslam et al. [9] introduced the RS in the area of control charts, which considered the same values of control limit coefficients for various control limit shifts. Conventional Shewhart control charts were primarily designed for processes with large sample sizes taken at infrequent intervals but may struggle to detect subtle shifts or trends in processes where samples are collected frequently in smaller quantities. This limitation can lead to delayed responses to deviations, potentially resulting in higher defect rates and increased production costs. As outlined by Ahmad et al. [10], the development of this chart stemmed from the need to effectively monitor processes characterized by continuous, high-frequency production. The X-bar control chart with RS effectively addresses a critical limitation of conventional Shewhart control charts, which may struggle to detect subtle shifts or trends in processes with frequent but smaller sample sizes [9]. These limitations can lead to delayed responses to deviations, potentially resulting in higher defect rates and increased production costs. By utilizing RS, the X-bar control chart offers enhanced sensitivity, ensuring even minor variations are promptly identified and addressed.

One of the key advantages of RS is its ability to provide a continuous evaluation of the performance of a process. This allows for prompt corrective actions when deviations from quality standards occur. Additionally, RS is particularly effective in situations where a conclusive decision cannot be made based on a single sample. It offers enhanced sensitivity to small and intermediate process changes, addressing a limitation of conventional Shewhart control charts designed for processes with large sample sizes taken at infrequent intervals [8, 9].

RS has extensive applications in industries with continuous, high-frequency production processes. It is especially valuable in scenarios where immediate detection and response to deviations are crucial for maintaining product quality. RS has been employed in various sectors, including manufacturing, healthcare, and telecommunications, to monitor and control processes effectively. Aslam et al. [11] proposed Shewhart control charts using RS and Ahmad et al. [12] designed a process capability control chart using RS. Further details on control charts using RS can also be seen in Mughal et al. [13], Adeoti and Olaomi [14], Enami and Torabi [15], Al-Nasser et al. [16], Nezhad and Nesaee [17], and Adeoti and Rao [18].

In a recent study by Saleh et al. [19], an intriguing finding emerged. Increasing the sample size could enhance the effectiveness of the Shewhart control chart compared to utilizing repetitive sampling in control chart analysis. Furthermore, their research proposed the utilization of control charts with repetitive sampling specifically for count data. When Aslam et al. [9] introduced attribute and variable control charts using repetitive sampling, they overlooked the optimization aspect where the fixed sample size aligned with or was less than the average sample number (ASN). As emphasized by Saleh et al. [19], it is crucial for the fixed sample size to match the ASN for both in-control and shifted processes.

The objective of this study is to outline the design of the X-bar control chart using RS, adhering to the optimization principles outlined in De Araújo Rodrigues et al. [20]. We aim to demonstrate that when the optimal sample size and ASN are less than or equal to the fixed sample size, the control chart using repetitive sampling outperforms the Shewhart control chart in terms of average run length. Our findings will illustrate that the optimized repetitive sampling (RS) chart consistently demands smaller sample sizes compared to the corresponding fixed sample sizes of the Shewhart control chart. Furthermore, we aim to provide evidence that the optimized RS chart consistently functions with reduced sample sizes, indicating a more resource-efficient approach to process monitoring. Our findings are presented through simulations and a real-world example.

2 X-bar control chart using RS

The X-bar control chart using RS is outlined in this section. The operational process and control limits are taken from Aslam et al. [9] and stated as follows:

Step 1: Compute $\overline{X}$ from the sample size of n from the production process.

Step 2: The process is in-control if $\text{LC}{\text{L}}_2<\overline{\text{X}}<\text{UC}{\text{L}}_2$ and out-of-control if $\overline{\text{X}}>\text{UC}{\text{L}}_1$ or $\overline{\text{X}}<\text{LC}{\text{L}}_1$. In case of indecision, go to Step 1.

The inner control limits of $\overline{\text{X}}$ chart are given by

$\begin{array}{ll}{\text{UCL}}_1=\text{m}+{\text{k}}_1\sigma /\sqrt{\text{n}}& (1)\end{array}$

$\begin{array}{ll}{\text{LCL}}_1=\text{m}-{\text{k}}_1\sigma /\sqrt{\text{n}}& (2)\end{array}$

The upper control limits of $\overline{\text{X}}$ chart are given by

$\begin{array}{ll}{\text{UCL}}_2=\text{m}+{\text{k}}_2\sigma /\sqrt{\text{n}}& (3)\end{array}$

$\begin{array}{ll}{\text{LCL}}_2=\text{m}-{\text{k}}_2\sigma /\sqrt{\text{n}},& (4)\end{array}$

where m and σ are the mean and standard deviation of the averages, n is the sample size in each subgroup, and k₁ and k₂ are the control chart coefficients, which will be determined using an optimization model. Let $P_{in}^{RS}$ be the probability of the in-control state:

$\begin{array}{ll}{\text{P}}_{\text{in}}^{\text{RS}}=\frac{\text{P}({\text{LCL}}_2<\overline{\text{X}}<{\text{ UCL}}_2)}{1-{\text{P}}_{\text{rep}}},& (5)\end{array}$

where ${\text{P}}_{\text{rep}}=\text{P}({\text{LCL}}_1<\overline{\text{X}}<{\text{LCL}}_2)+\text{P}({\text{UCL}}_2<\overline{\text{X}}<{\text{UCL}}_1)$

The simplified form of ${\text{P}}_{\text{in}}^{\text{RS}}$ is given by

$\begin{array}{ll}{\text{P}}_{\text{in}}^{\text{RS}}=\frac{2\Phi ({\text{k}}_2)-1}{1-2\left[\Phi ({\text{k}}_1)-\Phi ({\text{k}}_2)\right]}& (6)\end{array}$

Suppose that μ = m + cσ is the shifted mean, where c is ≥ 0 and it is a shift constant. Let $P_1^{RS}$ be the probability of in-control at μ, and it is defined by

$\begin{array}{r}{\text{P}}_1^{\text{RS}}=\\ \frac{\Phi ({\text{k}}_2-\text{c}\sqrt{\text{n}})+\Phi ({\text{k}}_2+\text{c}\sqrt{n})-1}{\Phi ({\text{k}}_2+\text{c}\sqrt{\text{n}})-\Phi ({\text{k}}_1+\text{c}\sqrt{\text{n}})-\Phi ({\text{k}}_1-\text{c}\sqrt{\text{n}})+\Phi ({\text{k}}_2-\text{c}\sqrt{\text{n}})+1}& (7)\end{array}$

The average run length (ARL) for the in-control process is given by

$\begin{array}{ll}{\text{ARL}}_0=\frac{1}{1-{\text{P}}_{\text{in}}^{\text{RS}}}& (8)\end{array}$

The ARL for the shifted process is given by

$\begin{array}{ll}{\text{ARL}}_1=\frac{1}{1-{\text{P}}_1^{\text{RS}}}& (9)\end{array}$

The average sample number (ASN) is given by

$\begin{array}{ll}\text{ASN}=\frac{\text{n}}{1-{\text{P}}_{\text{rep}}}& (10)\end{array}$

3 Optimization model

The parameters of the proposed control chart are determined using the following optimization model:

$\begin{array}{l}{\text{minimize ARL}}_1\\ {\text{decision variables}:\text{ k}}_1,{\text{k}}_2,\text{ n}\\ \text{restrictions }:\\ 5<\text{n}<2({\text{n}}_0)\\ \text{ASN}<{\text{n}}_0\\ {\text{ARL}}_0>{\text{r}}_0\\ {\text{k}}_2<{\text{k}}_1\end{array}$

For the above model, r₀ sets a predefined lower limit for the average number of samples between false alarms. Concurrently, configuring n₀ compels the algorithm to seek a setup, ensuring that, while the process is in control, the sampling load does not surpass the equivalent of scrutinizing n₀ units per sample used in the classical Shewhart chart, i.e., the ASN value is limited by the fixed sample n₀ of the classical Shewhart chart.

Aslam et al. [9] used a similar optimization model but considered k₁ and k₂ as decision variables only, and these were constant for any shift value (c). Here, we considered different k₁, k₂, and n values in each shift, and we also set limits for n. A lower limit is useful so that the chart does not choose a value close to 1 when the change in the mean is close to zero or zero. An upper limit prevents the chart from taking very large values for n. De Araújo Rodrigues et al. [20] established an optimization model for double sampling np control chart where 0.5n ≤ n₁ ≤ 0.8n and n₁ ≤ n₂ ≤ 5n₁. In this study, we set n to < 2(n₀). This was because, after several runs, it was concluded that the model does not yield solutions beyond this limit. Further, we had taken into consideration a considerable maximum value twice the sample size used by the Shewhart control chart.

The r₀ and n₀ are user-set constants, which indicate the ARL₀ value and sample size, respectively, pertaining to the Shewhart control chart.

4 Comparison between the Shewhart and optimized RS control chart

This section shows the performance of Shewhart and optimized RS control charts through the ARL₁ values under multiple scenarios. Tables 1–6 present the ARL₁ value for the Shewhart control chart and k₁, k₂, n, ASN, ARL₀, and ARL₁ values for the optimized RS control chart. Tables 1, 2 show the comparison for n = 20, Tables 3, 4 for n = 30, and Tables 5, 6 show it for n = 40. All the tables contain r₀ values of 300 and 370.

TABLE 1

Table 1. ARL₁ values for Shewhart and optimized RS when n₀ = 20 and r₀ = 300.

TABLE 2

Table 2. ARL₁ values for Shewhart and optimized RS when n₀ = 20 and r₀ = 370.

TABLE 3

Table 3. ARL₁ values for Shewhart and optimized RS when n₀ = 30 and r₀ = 300.

TABLE 4

Table 4. ARL₁ values for Shewhart and optimized RS when n₀ = 30 and r₀ = 370.

TABLE 5

Table 5. ARL₁ values for Shewhart and optimized RS when n₀ = 40 and r₀ = 300.

TABLE 6

Table 6. ARL₁ values for Shewhart and optimized RS when n₀ = 40 and r₀ = 370.

From Tables 1–6, it is possible to conclude the following:

• In general, for small and moderate changes in the mean in control (c = [0.2 − 0.7]), the proposed RS control chart has small values in the ARL₁ metric compared to the Shewhart control chart while maintaining a lower ASN. This could be beneficial in scenarios where small and moderate shifts are important while maintaining the false alarm rate.

• The optimized RS chart consistently requires sample sizes (n) that are lower than the corresponding values of n₀ from the Shewhart control chart. The fact that the optimized RS chart consistently operates with smaller sample sizes suggests a more efficient use of resources in process monitoring.

• For all cases, when there is no change in the mean of the process (c = 0), the optimized control chart takes the lowest value of n allowed in the optimization model, i.e., it is not necessary to use large sample sizes since the process has not had a change in its mean.

• For any value of n₀, the optimized RS chart shows, on average, a greater difference in ARL₁ values with respect to the Shewhart chart as r₀ increases. This implies that when the process is consistently in the control state (higher ARL₀), the optimized RS chart tends to be more effective at detecting out-of-control conditions compared to the Shewhart chart.

• For any value of r₀, the optimized RS chart shows a lower difference in ARL₁ values with respect to the Shewhart chart as n₀ increases. This implies that, when a larger sample size is required to effectively monitor the process, the performance gap in detecting out-of-control conditions between the optimized RS chart and the Shewhart chart diminishes.

• For any value of n₀, the ARL₁ values in the Shewhart and optimized RS control charts are larger as r₀ increases. In practical terms, this means that when the process is consistently in control for extended periods (higher ARL₀), both the Shewhart and optimized RS control charts will, on average, take longer to signal an out-of-control condition.

• For any value of r₀, the ARL₁ values in the Shewhart and optimized RS control charts decrease as n₀ increases. This is consistent because the larger the sample size, the easier it is to detect a change in the state of the process while maintaining the desired level of ARL₀ rate. However, increasing the sample size is only a partially good method because it incurs higher costs.

• For larger shifts (c = [0.8 − 3.00]), both charts have ARL₁ values close to 1, indicating that they are effective in quickly detecting larger shifts in the process. This result is logical and consistent since it is expected that the larger the change in the state of the process, the sooner any control chart is able to detect it, with the minimum value being 1.

5 Experiment through simulated data

We then tested the performance of the optimized RS chart compared to the performance of the Shewhart chart through two scenarios with simulated data. This section details the two simulations.

For the first case, we simulated 15 subgroups in control under the following arbitrarily chosen conditions: m = 15, σ = 3, n₀ = 20, c = 0.3, and r₀ = 300. Having n₀ and r₀, from Table 2, it can be observed that k₁ = 2.9866, k₂ = 1.4348, and n = 17. Therefore, the control limits are UCL₁ = 17.17, LCL₁ = 12.83, UCL₂ = 16.04, and LCL₂ = 13.96. On the other hand, for the Shewhart control chart, we have k = 2.9352, UCL = 16.97, and LCL = 13.03. From subgroup 16, simulated data are generated with the change in the process mean: u = 15+0.3^*3 = 15.9.

For the second case, we simulated 15 subgroups in control also under the following arbitrarily chosen conditions: m = 10, σ = 2, n₀ = 30, c = 0.25 and r₀ = 370. Having n₀ and r₀, from Table 6, it can be observed that k₁ = 3.0316, k₂ = 1.6346, and n = 27. Therefore, the control limits are UCL₁ = 11.17, LCL₁ = 8.83, UCL₂ = 10.63, and LCL₂ = 9.37. On the other hand, for the Shewhart control chart, we have k = 2.9997, UCL = 11.09, and LCL = 8.90.

Each case of simulation has two replications. Figures 1A–C show the schemes for the Shewhart and optimized RS control charts, respectively, in these conditions. Furthermore, from subgroup 16, simulated data are generated with the change in the process mean: u = 10+0.25^*2 = 10.5. Figures 2A–C show the schemes for the Shewhart and optimized RS control charts. The red dots in all the figures show the subgroup where each chart detects the change in the mean.

FIGURE 1

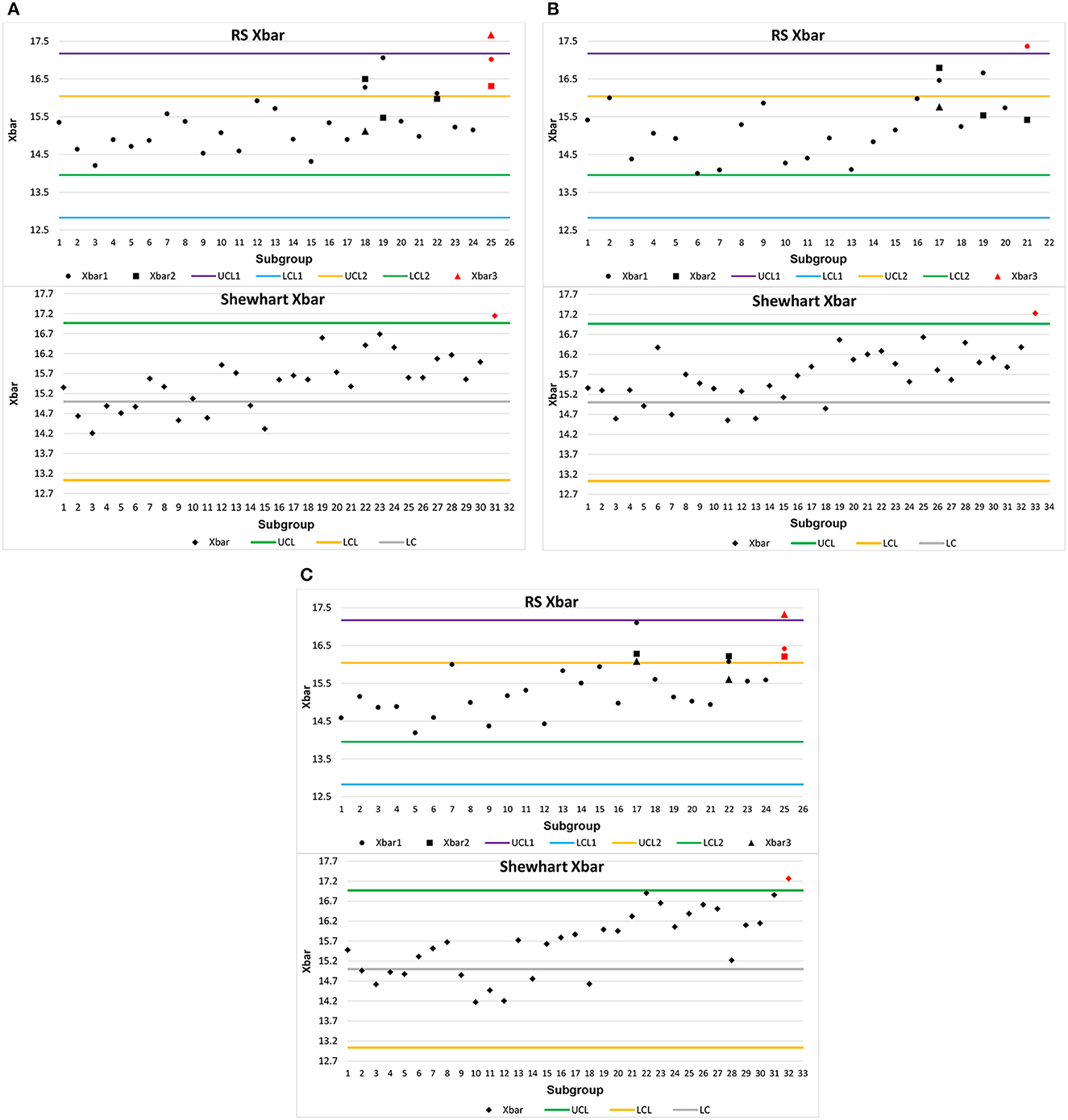
Figure 1. (A) Schemes for optimized RS and Shewhart charts with simulated data when m = 15, σ = 3, n₀ = 20, c = 0.3, and r₀ = 300. (B) Replication 1 of schemes for RS and Shewhart charts with simulated data when m = 15, σ = 3, n₀ = 20, c = 0.3, and r₀ = 300. (C) Replication 2 of schemes for RS and Shewhart charts with simulated data when m = 15, σ = 3, n₀ = 20, c = 0.3, and r₀ = 300.

FIGURE 2

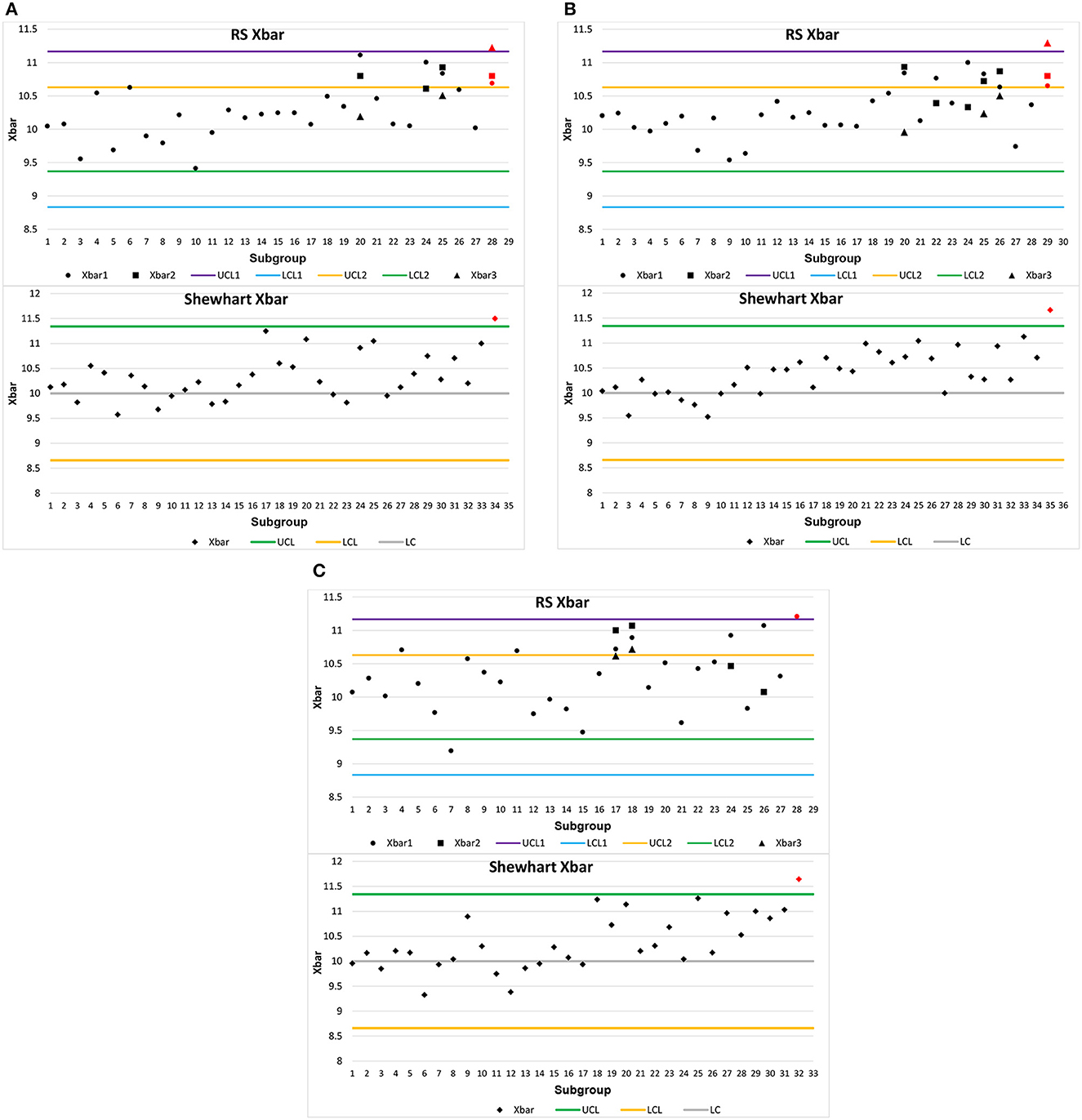
Figure 2. (A) Schemes for optimized RS and Shewhart charts with simulated data when m = 10, σ = 2, n₀ = 30, c = 0.25, and r₀ = 370. (B) Replication 1 of schemes for optimized RS and Shewhart charts with simulated data when m = 10, σ = 2, n₀ = 30, c = 0.25, and r₀ = 370. (C) Replication 2 of schemes for optimized RS and Shewhart charts with simulated data when m = 10, σ = 2, n₀ = 30, c = 0.25, and r₀ = 370.

By analyzing Figures 1A–C, it is evident that the RS chart identifies process shifts ahead of the Shewhart control chart. In these illustrations, the RS control chart detects shifts at sample #25, sample #21, and sample #25. Conversely, the Shewhart control chart only detects these shifts at sample #31, sample #33, and sample #32. Figures 1A–C unequivocally demonstrate that the RS chart outperforms the Shewhart control chart in terms of ARL₁. Similarly, in Figures 2A–C, we observe a similar trend—the RS chart detects process shifts before the Shewhart control chart does. In these instances, the RS control chart identifies shifts at sample #28, sample #29, and sample #28, while the Shewhart control chart registers them at sample #34, sample #35, and sample #32. Figures 2A–C provide compelling evidence that the RS chart surpasses the Shewhart control chart in terms of ARL₁ performance. Based on these simulations, it is evident that the optimized RS control chart consistently delivers superior ARL₁ performance while maintaining a lower ASN value.

6 Application of Shewhart and RS schemes using real data

In this section, we detail the use of actual data taken from Montgomery [21]. The data shown here are taken with a size n = 10 and 15 subgroups. These data concern soft drink bottle fill volume and are presented at a nominal level of 0. For graphical purposes, we have taken a nominal level of 10.

Because these data pertain to a process under control, from Table 2, we took the RS and Shewhart chart conditions for c = 0. When the RS chart takes sample sizes n = 6, set size n₀ = 20 should be taken for the Shewhart chart. Since the real data are taken with n = 10, we need to simulate 10 more variables by gathering their mean and standard deviation in order to obtain the Shewhart chart averages. For the RS chart, we arbitrarily took the last 6 variables to plot the averages. Figure 3 shows the graph of the averages of these actual data.

FIGURE 3

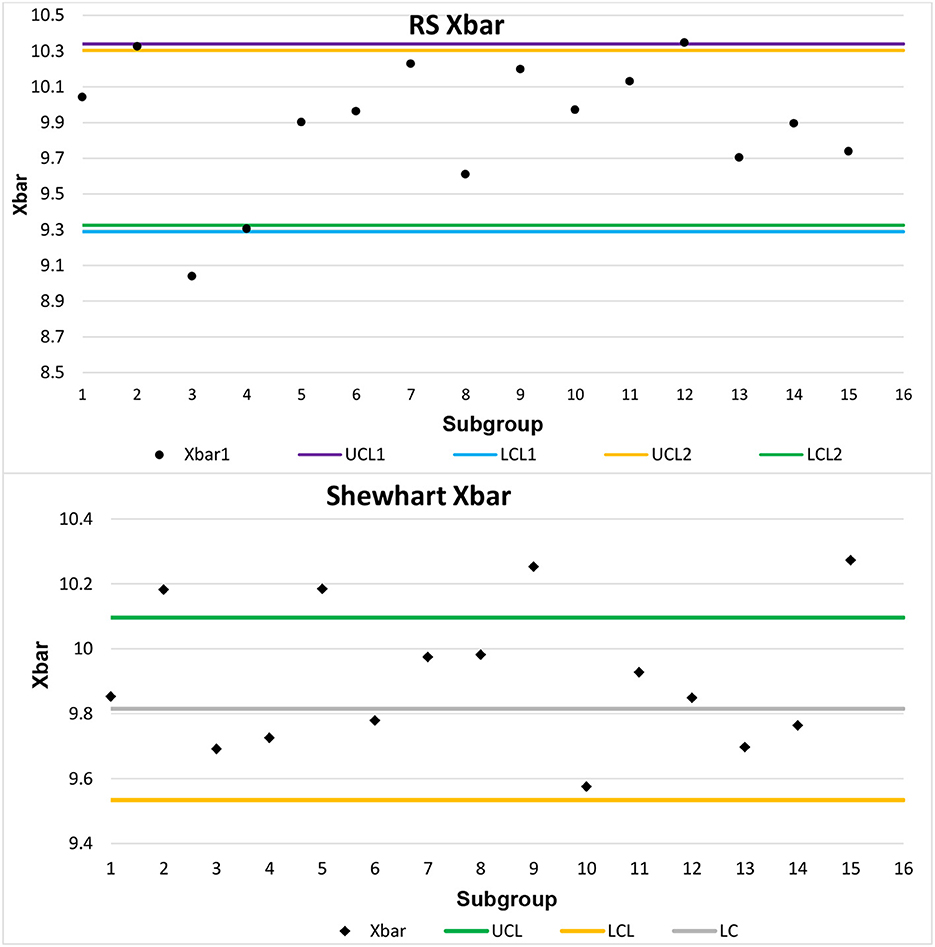
Figure 3. Application of Shewhart and RS schemes using real data from Montgomery [21].

Figure 3 shows that the RS chart shows a process mean output in two subgroups (subgroups 3 and 12), while the Shewhart chart shows a process mean output in four subgroups (subgroups 2, 5, 9, and 15). This reflects the ability of the RS chart to maintain the desired level of ARL₀ and being efficient with ARL₁ compared to the Shewhart chart. Furthermore, it is worth mentioning that the RS chart highlights subgroups 2 and 4 as being in a state of indecision. Conversely, the Shewhart control chart does not offer insights into data points within repetitive areas.

7 Concluding remarks

The X-bar control chart using the RS procedure is discussed in this study. The parameters of the X-bar control chart using RS were determined using an optimized model. To explain the X-bar control chart using RS, simulated studies and extensive tables were provided. The study showed that the X-bar control chart using RS provided smaller values of ARL₁ compared to the Shewhart control chart. Based on this discussion, it is concluded that the X-bar control chart using RS outperforms the Shewhart control chart. The X-bar control chart using RS can be applied in the industry for monitoring the process. The variance control chart using RS and the optimized model can be studied in future research. The efficiency of the X-bar control chart using RS using a cost model can be extended in future research.

Author contributions

MA: Writing—review & editing. JM: Writing—original draft. MC: Writing—review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors are deeply thankful to the editor and reviewers for their valuable suggestions to improve the quality and presentation of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lee S-H, Jun C-H. A new control scheme always better than X-bar chart. Commun Stat Theory Methods. (2010) 39:3492–503. doi: 10.1080/03610920903243744

CrossRef Full Text | Google Scholar

2. Fu X, Wang R-F, Dong Z-Y. Application of a Shewhart control chart to monitor clean ash during coal preparation. Int J Min Process. (2017) 158:45–54. doi: 10.1016/j.minpro.2016.11.019

CrossRef Full Text | Google Scholar

3. Oprime PC, Mendes GHDS. The X-bar control chart with restriction of the capability indices. Int J Qual Reliab Manag. (2017) 34:38–52. doi: 10.1108/IJQRM-08-2014-0103

CrossRef Full Text | Google Scholar

4. Hanandeh AA, Al-Nasser AD. Improved Shewhart control chart using minimax ranked set sampling. Investigación Operacional. (2020) 41:923–34.

Google Scholar

5. Shafqat A, Huang Z, Aslam M. Design of X-bar control chart based on inverse rayleigh distribution under repetitive group sampling. Ain Shams Eng J. (2021) 12:943–53. doi: 10.1016/j.asej.2020.06.001

CrossRef Full Text | Google Scholar

6. Vasconcelos RM, Quinino RC, Ho LL, Cruz FR. About Shewhart control charts to monitor the Weibull mean based on a Gamma distribution. Qual Reliabil Eng Int. (2022) 38:4210–22. doi: 10.1002/qre.3200

CrossRef Full Text | Google Scholar

7. Park C, Ouyang L, Wang M. Development of Robust X-bar Charts With Unequal Sample Sizes. (2022). arXiv preprint arXiv:2212.10731.

Google Scholar

8. Sherman RE. Design and evaluation of a repetitive group sampling plan. Technometrics, (1965). 7:11–21. doi: 10.2307/1266124

CrossRef Full Text | Google Scholar

9. Aslam M, Azam M, Jun C-H. New attributes and variables control charts under repetitive sampling. Industr Eng Manage Syst. (2014) 13:101–6. doi: 10.7232/iems.2014.13.1.101

CrossRef Full Text | Google Scholar

10. Ahmad L, Aslam M, Jun C-H. Designing of X-bar control charts based on process capability index using repetitive sampling. Trans Inst Meas Control. (2014) 36:367–74. doi: 10.1177/01423312135020

CrossRef Full Text | Google Scholar

11. Aslam M, Arif OH, Jun C-H. An attribute control chart based On the birnbaum-saunders distribution using repetitive sampling. IEEE Access. (2016) 5:9350–60. doi: 10.1109/ACCESS.2016.2643692

CrossRef Full Text | Google Scholar

12. Ahmad L, Aslam M, Jun C-H. The design of a new repetitive sampling control chart based on process capability index. Transact Instit Measur Control. (2016) 38:971–80. doi: 10.1177/0142331215571120

CrossRef Full Text | Google Scholar

13. Mughal MA, Azam M, Aslam M. Restricted repetitive sampling in designing of control charts. Pakistan J Stat Oper Res. (2017) 1:297–312. doi: 10.18187/pjsor.v13i2.1571

CrossRef Full Text | Google Scholar

14. Adeoti OA, Olaomi JO. Capability index-based control chart for monitoring process mean using repetitive sampling. Commun Stat Theory Meth. (2018) 47:493–507. doi: 10.1080/03610926.2017.1307401

CrossRef Full Text | Google Scholar

15. Enami S, Torabi H. A repetitive sampling-based control chart for multivariate weighted poisson distribution with two different indices?. J Statistic Res Iran JSRI. (2019) 16:245–54. doi: 10.52547/jsri.16.1.245

CrossRef Full Text | Google Scholar

16. Al-Nasser AD, Ciavolino E, Al-Omari A. Extreme ranked repetitive sampling control charts. Pesquisa Operacional. (2020) 40:26135. doi: 10.1590/0101-7438.2020.040.00226135

CrossRef Full Text | Google Scholar

17. Nezhad F, Nesaee M. Development of a new variable repetitive group sampling plan based on EWMA yield index. Scientia Iranica. (2021) 28:2457–76.

Google Scholar

18. Adeoti OA, Rao GS. Attribute control chart for rayleigh distribution using repetitive sampling under truncated life test. J Probabil Stat. (2022) 22:3091. doi: 10.1155/2022/8763091

CrossRef Full Text | Google Scholar

19. Saleh NA, Mahmoud MA, Woodall WH. A re-evaluation of repetitive sampling techniques in statistical process monitoring. Qual Technol Quant Manage. (2023) 23:1–19. doi: 10.1080/16843703.2023.2246770

CrossRef Full Text | Google Scholar

20. De Araújo Rodrigues AA, Epprecht EK, De Magalhães MS. Double-sampling control charts for attributes. J Appl Stat. (2011) 38:87–112. doi: 10.1080/02664760903266007

CrossRef Full Text | Google Scholar

21. Montgomery DC. Introduction to Statistical Quality Control. New York, NY: John Wiley and Sons (2020).

Google Scholar