Real block-circulant matrices and DCT-DST algorithm for transformer neural network

In the encoding and decoding process of transformer neural networks, a weight matrix-vector multiplication occurs in each multihead attention and feed forward sublayer. Assigning the appropriate weight matrix and algorithm can improve transformer performance, especially for machine translation tasks. In this study, we investigate the use of the real block-circulant matrices and an alternative to the commonly used fast Fourier transform (FFT) algorithm, namely, the discrete cosine transform–discrete sine transform (DCT-DST) algorithm, to be implemented in a transformer. We explore three transformer models that combine the use of real block-circulant matrices with different algorithms. We start from generating two orthogonal matrices, U and Q. The matrix U is spanned by the combination of the reals and imaginary parts of eigenvectors of the real block-circulant matrix, whereas Q is defined such that the matrix multiplication QU can be represented in the shape of a DCT-DST matrix. The final step is defining the Schur form of the real block-circulant matrix. We find that the matrix-vector multiplication using the DCT-DST algorithm can be defined by assigning the Kronecker product between the DCT-DST matrix and an orthogonal matrix in the same order as the dimension of the circulant matrix that spanned the real block circulant. According to the experiment's findings, the dense-real block circulant DCT-DST model with largest matrix dimension was able to reduce the number of model parameters up to 41%. The same model of 128 matrix dimension gained 26.47 of BLEU score, higher compared to the other two models on the same matrix dimensions.

1 Introduction

A matrix is deemed structured if it can be exploited to create effective algorithms [1] and has a small displacement rank [2]. Kissel and Diepold [3] have explored four main matrix structure classes, namely, semiseparable matrices, matrices of low displacement rank, hierarchical matrices and products of sparse matrices, and their applications in neural network. Toeplitz, Hankel, Vandermonde, Cauchy, and Circulant matrices are among the possibly most well-known matrix structures that are all included in the class of matrices with Low Displacement Rank (LDR) in [4].

Circulant matrices are structured matrices that have several features, including identical rows, but are shifted one step to the right [5]. It can be decomposed unitarily into a diagonal matrix whose diagonal entries come from its eigenvalues [6]. The eigenvalues of such matrices are derived in terms of the eigenvalues of matrices of decreased dimension, and linear equation systems involving these matrices are easily solved using fast Fourier transforms [7]. A block circulant matrix is formed by a circulant matrix containing circulant matrix entries. The block-circulant matrices, as circulant matrices, have some unique properties. They have Schur decomposition [8] that can be related to some algorithm of its multiplication [9].

The use of structured matrices as a neural network weight matrices has been demonstrated in a number of earlier research as one method of reducing memory, particularly for memory models and optimizers. The most well-known example is the sparse Toeplitz matrix-based convolutional neural network (CNN) architecture [10]. Convolutional neural networks are currently the top choice for machine learning tasks involving images due to their effectiveness and prediction accuracy [11–13]. The connections between the neurons in CNNs often encode the structure in an implicit manner. There are other intriguing strategies for enhancing conventional CNNs. When performing operations on images represented in the quaternion domain, for instance, Quaternion CNNs [14–16] outperform conventional real-valued CNNs on a number of benchmark tasks. In addition, Cheng et al. [17] substituted circulant projections for the linear ones in fully connected neural networks, while Liao and Yuan [18] proposed using matrices with a circulant structure in convolutional neural networks. Block Toeplitz matrices used in discrete convolutions were merged with the effective weight representation used in neuromorphic hardware by Appuswamy et al. [19], resulting in a family of naturally hardware efficient convolution kernels. The use of generic matrices with low displacement rank in place of weight matrices in neural networks has also been suggested. Toeplitz-like weight matrices, such as circulant matrices and Toeplitz matrices and their inverses, are used, as in the study by Sindhwani et al. [20]. Additionally, Thomas et al. [21] presented a class of low displacement rank matrices for which they trained the operators and low-rank components of the neural network. The theoretical characteristics of neural networks with low displacement rank weight matrices are the subject of several studies. The universal approximation theorem holds for these networks, as demonstrated, for instance, by Zhao et al. [22]. Using Toeplitz or Hankel weight matrices, Liu et al. [23] provide yet another demonstration that the universal approximation theorem remains true for neural networks.

The transformer is one of the well-known neural network models for machine translation that was first presented by Vaswani et al. [24]. This model has been developed up to this point for a variety of uses, such as text summarization [25], video text and images [26], chat bots [27], and speech recognition [28]. One of the improvements is the swapping out of the transformer weight matrices with a structured matrices. Li et al. [29] proposed an efficient acceleration framework, Ftrans, for transformer-based large-scale language representations. Their framework includes an improved block-circulant matrix (BCM)-based weight representation, which allows for model compression on large-scale language representations at the algorithm level with little accuracy. The results of their experiments show that their model significantly reduces the size of NLP models by up to 16 times. Their FPGA design improves performance and energy efficiency by 27.07 and 81 times, respectively, when compared to the CPU and 8.80 times when compared to GPU degradation, with an acceleration design at the architecture level. Moreover, Liao et al. [30] also applied block-circulant matrices for DNNs (deep neural networks), which enabled the network to achieve up to 3.5 TOPS computation performance and 3.69 TOPS/W energy efficiency while saving 108× and 116× memory with negligible accuracy degradation.

Structured weight matrix multiplication often entails the use of an algorithm. It is typical to utilize the FFT algorithm when dealing with a structured matrix that is a circulant matrix. In Multi30k Task 1 German to English with 100x compression, Reid [31] demonstrated that the use of a block-circulant matrix in the feed forward transformer layer in conjunction with the FFT algorithm is able to enhance the performance of transformers. The DCT-DST algorithm, which may be used in place of the FFT approach in circulant matrix multiplication with a vector, has been introduced by Liu et al. [9]. In previous studies, the DCT-DST was generally used for image processing and video/image coding [32–34].

In neural networks, particularly transformer models, the DCT-DST algorithm has not been used for weight matrix-vector multiplication. This study investigates the application of the real block-circulant matrix-DCT-DST method in layers of transformer. In summary, the main contribution of this study is 2-fold. First, we explored the eigenstructures of the real block-circulant matrices. They are then used to verify the Schur decomposition that applied in the DCT-DST algorithm. Second, we formulate the orthogonal matrices which are used to decompose the real block-circulant matrices. The multiplication of these orthogonal matrices will then be used in the DCT-DST algorithm. In particular, when compared to the original transformer approach, using the dense matrices on the multihead attention transformer and the real block-circulant matrices with DCT-DST on the feed forward layer takes less number of model parameters.

After this introduction section, we organize the remainder of this study as follows: We outline the fundamental theory related to the real block-circulant matrices and DCT-DST matrices in Section 2. Using these theories, we explored the eigenstructures of the real block-circulant matrices and formulas of the Kronecker product for orthogonal matrices in Section 3. In the same section, we formulate the Schur form for the real block-circulant matrices. In Section 4, we explain the experiment of the real block-circulant transformer in conjunction with the DCT-DST algorithm.

2 Theoritical foundation

Definition 2.1. A n × n circulant matrix is formed by cyclically permuting its entries of the n-vector c₀, c₁, .., c_n−1, and is of the form $\left[\begin{array}{cccc}{c}_0& c_1& \cdots & c_{n-1}\\ c_{n-1}& c_0& \cdots & c_{n-2}\\ ⋮& ⋮& \ddots & ⋮\\ c_1& c_2& \cdots & c_0\end{array}\right].$ The set of all such matrices with real entries of order n is denoted by B_n, whereas a nm × nm block-circulant matrix is generated from the ordered set C₁, C₂, …, C_n, and is of the form $\left[\begin{array}{cccc}{C}_1& C_2& \cdots & C_n\\ C_n& C_1& \cdots & C_{n-1}\\ ⋮& ⋮& \ddots & ⋮\\ C_2& C_3& \cdots & C_1\\ \end{array}\right]$ with C_i an m × m circulant matrix for each i = 1, 2, …, n. If C is a real block-circulant matrix, the set of all such matrices of order nm × nm is denoted by BC_nm.

Definition 2.2. The discrete Fourier transform (DFT) matrix F = F_n is defined by

$\begin{array}{ll}{F}_n=\frac{1}{\sqrt{n}}{\omega }^{-jk},j,k=0,1,\cdots ,n-1& (1)\end{array}$

with $\omega =e^{\frac{2\pi }{n}i},i=\sqrt{-1}$.

Any circulant matrix A has a Schur canonical form A = F^*ΛF with F^* is a conjugate transpose of F and Λ is a diagonal matrix, holding the eigenvalues of A. The eigenvalues of a real circulant matrix C can be arranged in the following order

$\begin{array}{ll}\lambda =\{\begin{array}{ll}[{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{h-1},{\lambda }_h,{\overline{\lambda }}_{h-1},\cdots ,{\overline{\lambda }}_1],\hfill & \text{if }n=2h\hfill \\ \hfill & \hfill \\ [{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_h,{\overline{\lambda }}_h,\cdots ,{\overline{\lambda }}_1],\hfill & \text{if }n=2h+1\hfill \end{array}& (2)\end{array}$

Partitioning $F^{*}=\left[f_0,,\cdots ,f_{n-1}\right]$ with f_k = t_k + js_k we have $f_{n-k}={\overline{f}}_k$, where ${\overline{f}}_k$ is a conjugate of f_k. For any eigenvalue λ_k, Cf_k = λ_kf_k means $C({\text{f}}_k+{\overline{f}}_k)={\lambda }_k{\text{f}}_k+{\lambda }_k{\overline{f}}_k$ and $C({\text{f}}_k-{\overline{f}}_k)={\lambda }_k{\text{f}}_k-{\lambda }_k{\overline{f}}_k$. Like circulant matrices over complex numbers, the real circulant matrix C also posses a real Schur canonical form $\Omega =U_n^{T}C{U}_n$ where U_n is an orthogonal matrix

$\begin{array}{ll}{U}_n=\{\begin{array}{ll}\left[t_0,\sqrt{2}{t}_1,\cdots ,\sqrt{2}{t}_{h-1},t_h,\sqrt{2}{s}_{h-1},\cdots ,\sqrt{2}{s}_1\right],\hfill & \text{if }n=2h\hfill \\ \left[t_0,\sqrt{2}{t}_1,\cdots ,\sqrt{2}{t}_h,\sqrt{2}{s}_h,\cdots ,\sqrt{2}{s}_1\right],\hfill & \text{if }n= 2h+1\hfill \end{array}& (3)\end{array}$

where t_k and s_k are real and imaginary parts of f_k, k = 0, .., h. The matrix Ω is real and has the form

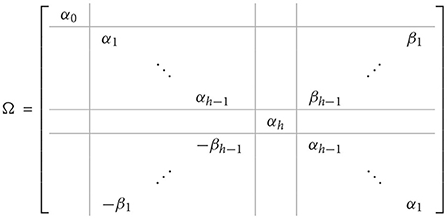
and

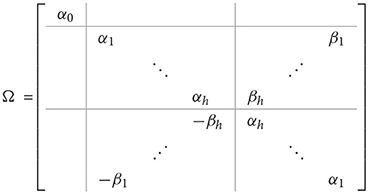
where α_k and β_k are, respectively, a real and imaginary part of eigenvalues of C, k = 0, …, h.

In working with real block-circulant matrices, we will involve a fundamental operation, namely, Kronecker product. This operation will be applied to diagonalize and represent matrix U_bc and the DCT-DST algorithm for a real block-circulant matrix. The diagonalization of the real block-circulant matrices, their eigenvalues, and vectors will be discussed in the next three theorems.

Theorem 2.3. Olson et al. [8] Let C ∈ BC_nm and generated by C₁, C₂, ⋯ , C_n ∈ B_m. If F_n is a Fourier matrix of dimension n × n and I_m is an identity matrix of order m, then

$\begin{array}{ll}(F_n^{*}\otimes I_m)C(F_n\otimes I_m)=diag({\wedge }_1,{\wedge }_2,\cdots ,{\wedge }_n)& (4)\end{array}$

is a diagonal block matrix of dimension nm x nm with

$\begin{array}{ll}{\wedge }_i=\rho ({\omega }_n^{l-1},C_k)={\displaystyle \sum _{k=1}^n}{C}_k{\omega }_n^{(k-1)(l-1)}& (5)\end{array}$

$F_n^{*}$ is the conjugate transpose of F_n, ω_n is the nth primitive root of unity, and $\rho (t,\tau )=\sum _{k=1}^n{t}^{(k-1)}\otimes \tau$ with t and τ are any square matrices.

Theorem 2.4. Olson et al. [8] Let C ∈ BC_nm has generating elements C₁, C₂, ⋯ , C_n ∈ B_m. If $c_i^{(1)},c_i^{(2)},\cdots ,c_i^{(m)}$ are generating elements of C_i, then

$\begin{array}{l}(F_n^{*}\otimes F_m^{*})C(F_n\otimes F_m)=dia{g}_{i=1,\cdots ,n}\left[\begin{array}{cccc}{\lambda }_i^{(1)}& 0& \cdots & 0\\ 0& {\lambda }_i^2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_i^m\end{array}\right]\end{array}$

is a diagonal matrix of dimension nm x nm with

$\begin{array}{c}{\lambda }_i^{(p)}={\displaystyle {\sum }_{k=1}^n}{\displaystyle {\sum }_{l=1}^m}{c}_k^l{\omega }_{p-1}^{l-1}{\omega }_{i-1}^{k-1},\text{with }i=1,2,\cdots ,n\text{and }\\ p=1,2,\cdots ,m.\end{array}$

Theorem 2.5. Olson et al. [8] Let C ∈ BC_nm, $u_i^{(p)}$ denotes the eigenvectors of Λ_i and e_i be the i-th column of the DFT matrix. The eigenvectors of C are

$f_i^{(p)}=e_i\otimes u_i^{(p)}$

with i = 1, ⋯ , n and p = 1, ⋯ , m.

The eigenvalues and eigenvectors from the preceding theorems will be used later to construct a real Schur canonical form of a real block-circulant matrix and will be used in conjunction with DCT-DST matrices to define multiplication of a real block-circulant matrix with any vector. The discrete trigonometric transform family consists of eight DCT and eight DST versions. Two versions of them are used in this study.

Definition 2.6. The DCT-I and DCT-V matrices are defined as follows:

$\begin{array}{ll}{\mathcal{C}}_{n+1}^I=\sqrt{\frac{2}{n}}{\left[{\tau }_j{\tau }_{k}cos\frac{jk\pi }{n}\right]}_{j,k=0}^n& (6)\end{array}$

$\begin{array}{ll}{\mathcal{C}}_n^V=\frac{2}{\sqrt{2n-1}}{\left[{\tau }_j{\tau }_{k}cos\frac{2jk\pi }{2n-1}\right]}_{j,k=0}^{n-1}& (7)\end{array}$

with ${\tau }_{l(l=j,k)}=\{\begin{array}{ll}\frac{1}{\sqrt{2}},\hfill & \text{if }l=0\text{or}l=n\hfill \\ 1,\hfill & \text{if }l\text{otherwise}\hfill \end{array}$

${\iota }_k=\{\begin{array}{ll}\frac{1}{\sqrt{2}},\hfill & \text{if }k=n-1\hfill \\ 1,\hfill & \text{if }k\text{otherwise}\hfill \end{array}$

Definition 2.7. The DST-I and DST-V matrices are defined as follows:

$\begin{array}{ll}{\mathcal{S}}_{n-1}^I=\sqrt{\frac{2}{n}}{\left[sin\frac{jk\pi }{n}\right]}_{j,k=1}^{n-1}& (8)\end{array}$

$\begin{array}{ll}{\mathcal{S}}_{n-1}^V=\frac{2}{\sqrt{2n-1}}{\left[sin\frac{2jk\pi }{2n-1}\right]}_{j,k=1}^{n-1}& (9)\end{array}$

Note that all those transformation matrices are orthogonal. In the following theorem, we will see that the matrix U_n as defined in Equation (3) can be partitioned into a matrix that is generated by the DCT and DST matrices.

Theorem 2.8. Liu et al. [9] Let U_n be the matrix stated in Equation (3). Then, U_n can be partitioned into the following form:

$\begin{array}{ll}{U}_n=\{\begin{array}{ll}\left[\begin{array}{cc}{\sigma }_1{q}_{h+1}^T& 0\\ \mathcal{C}& -\frac{1}{2}\sqrt{2}{\mathcal{S}}_{h-1}^I{J}_{h-1}\\ {\sigma }_1{v}_{h+1}^T& 0\\ J_{h-1}\mathcal{C}& \frac{1}{2}\sqrt{2}{J}_{h-1}{\mathcal{S}}_{h-1}^I{J}_{h-1}\end{array}\right],\hfill & \text{if }n=2h\hfill \\ \hfill & \hfill \\ \left[\begin{array}{cc}{\sigma }_1{p}_{h+1}^T& 0\\ \mathcal{C}& -\frac{1}{2}\sqrt{2}{\mathcal{S}}_h^V{J}_h\\ J_h\mathcal{C}& \frac{1}{2}\sqrt{2}{J}_h{\mathcal{S}}_h^V{J}_h\end{array}\right],\hfill & \text{if }n=2h+1\hfill \end{array}& (10)\end{array}$

Define

$\begin{array}{ll}{Q}_n=\{\begin{array}{ll}\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}\sqrt{2}& 0& 0& \\ 0& I_{h-1}& 0& J_{h-1}\\ 0& 0& \sqrt{2}& 0\\ 0& -J_{h-1}& 0& I_{h-1}\end{array}\right],\hfill & \text{if }n=2h\hfill \\ \hfill & \hfill \\ \frac{1}{\sqrt{2}}\left[\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& I_h& J_h\\ 0& -J_h& I_h\end{array}\right],\hfill & \text{if }n=2h+1\hfill \end{array}& (11)\end{array}$

with ${\sigma }_1=\sqrt{\frac{2}{n}},{\sigma }_2=\frac{1}{\sqrt{2}},p_{h+1}=(\frac{1}{\sqrt{2}},1,\cdots ,1),q_{h+1}={(\frac{1}{\sqrt{2}},1,\cdots ,1,\frac{1}{\sqrt{2}})}^T,$

$v_{h+1}={(\frac{1}{\sqrt{2}},-1,\cdots ,{(-1)}^{h-1},\frac{{(-1)}^h}{\sqrt{2}})}^T$,

and

$\mathcal{C}=\{\begin{array}{l}\begin{array}{cc}{\sigma }_2{P}_{1,h}{\mathcal{C}}_{h+1}^I\in {ℝ}^{(h-1)x(h+1)},& \text{if }n=2h\\ & \\ {\sigma }_2{P}_{1,h+1}{\mathcal{C}}_{h+1}^V\in {ℝ}^{(h)x(h+1)},& \text{if }n=2h+1\end{array}\hfill \end{array}$

where $P_{a,b}{(x_j)}_{j=0}^{n-1}={(x_j)}_{j=a}^{b-1},b\ge a$. Then, the multiplication of Q_n and U_n will be

$Q_n{U}_n=\{\begin{array}{ll}\left[\begin{array}{cc}{C}_{h+1}^I& 0\\ 0& J_{h-1}{S}_{h-1}^I{J}_{h-1}\end{array}\right],\hfill & \text{if }n=2h\hfill \\ \hfill & \hfill \\ \left[\begin{array}{cc}{C}_{h+1}^V& 0\\ 0& J_h{S}_h^V{J}_h\end{array}\right],\hfill & \text{if }n=2h+1\hfill \end{array}$

By using this rule, the multiplication of the circulant matrix with any vector only involves (h+1)-vectors of 1 DCT-I and (h−1)-vectors of 1 DST-I if n = 2h, and (h+1)-vectors of 1 DCT-V and h-vectors of 1 DST-V if n = 2h+1 [9].

3 The DCT-DST algorithm for real block-circulant matrix-vector multiplication

In this section, we will define the matrix-vector multiplication algorithm for the real block-circulant matrices. For this reason, the DCT-DST algorithm will be adapted from Liu et al. [9] by first defining the orthogonal matrices U_bc, Q_bc, multiplication Q_bcU_bc, and the real Schur form Ω_bc. In defining those orthogonal matrices, we leverage a Kronecker product operation as introduced in Olson et al. [8]. In the following theorem, we will see what U_bc, Q_bc, and Q_bcU_bc look like.

Theorem 3.1. Let C be a real block-circulant matrix of dimension nm × nm, U_n, U_m, and Q_n are orthogonal matrices as denoted in Equations (12) and (13). The matrices U_bc and Q_bc that assosiated with C can be defined as

$\begin{array}{ll}{U}_{bc}=U_n\otimes U_m& (12)\end{array}$

and

$\begin{array}{ll}{Q}_{bc}=Q_n\otimes U_m& (13)\end{array}$

The multipication between Q_bc and U_bc will have the form

$\begin{array}{l}{Q}_{bc}{U}_{bc}=Q_n{U}_n\otimes U_m^2\\ =\{\begin{array}{cc}\left[\begin{array}{cc}{\mathcal{C}}_{h+1}^I& 0\\ 0& J_{h-1}{\mathcal{S}}_{h-1}^I{J}_{h-1}\end{array}\right]\otimes U_m^2,& \text{if}n=2h\\ \left[\begin{array}{cc}{\mathcal{C}}_{h+1}^V& 0\\ 0& J_h{\mathcal{S}}_h^V{J}_h\end{array}\right]\otimes U_m^2,& \text{if}n=2h+1\end{array}\end{array}(14)$

The last theorem shows that the multiplication of Q_bcU_bc can be calculated by applying the multiplication of Q_nU_n with an orthogonal matrix U at dimension m. This multiplication gives a fast way to solve the multiplication between a real block-circulant matrix with any vector by using 1 DCT-I for (h+1)-vector and 1 DST-I for (h−1)-vector, if n = 2h and 1 DCT-V for (h + 1)-vector and 1 DST-V for h-vector if n = 2h + 1.

Furthermore, the two theorems below give the structure of the eigenvalues and the real Schur form of block circulant matrices. The eigenvalue structure of the real block-circulant matrices is fundamental like those of a circulant matrices. The knowledge of it is needed to recognize the real Schur form of the real block circulant matrices. The following theorems describe how their structures are.

Theorem 3.2. Let C ∈ BC_nm and ${\lambda }_i^{(p)}$ denotes the pth eigenvalue on the ith block of matrix C, i = 1, ..., n and p = 1, ..., m. If n = 2h, the eigen structure of C is

$\begin{array}{ll}{\lambda }_i^{(p)}=\left[{\lambda }_1^{(p)},{\lambda }_2^{(p)},\cdots ,{\lambda }_h^{(p)},{\lambda }_{h+1}^{(p)},\overline{{\lambda }_h^{(p)}},\cdots ,\overline{{\lambda }_2^{(p)}}\right]& (15)\end{array}$

with ${\lambda }_1^{(p)}\ne {\lambda }_{h+1}^{(p)}$ and ${\lambda }_{n+2-s}^{(m+2-r)}=\overline{{\lambda }_s^{(r)}}$, and for n = 2h+1 we have

$\begin{array}{ll}{\lambda }_i^{(p)}=\left[{\lambda }_1^{(p)},{\lambda }_2^{(p)},\cdots ,{\lambda }_h^{(p)},{\lambda }_{h+1}^{(p)},\overline{{\lambda }_{h+1}^{(p)}},\overline{{\lambda }_h^{(p)}},\cdots ,\overline{{\lambda }_2^{(p)}}\right]& (16)\end{array}$

with ${\lambda }_1^{(p)}\ne {\lambda }_j^{(p)}$ for j ≠ 1 and ${\lambda }_{n+2-s}^{(m+2-r)}=\overline{{\lambda }_s^{(r)}}$.

Proof. The eigenvalue of C can be written as

$\begin{array}{ll}\begin{array}{cc}{\lambda }_i^{(p)}\hfill & ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l{\omega }_{p-1}^{l-1}{\omega }_{i-1}^{k-1}\hfill \\ \hfill & ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi \left[\frac{(l-1)(p-1)}{m}+\frac{(k-1)(i-1)}{n}\right]+\hfill \\ \hfill & j sin 2\pi \left[\frac{(l-1)(p-1)}{m}+\frac{(k-1)(i-1)}{n}]\right)\hfill \end{array}& (17)\end{array}$

It is clear by tedious straightforward calculation that ${\lambda }_1^{(p)}\ne {\lambda }_{h+1}^{(p)}$. We will show that ${\lambda }_{n+2-s}^{(m+2-r)}=\overline{{\lambda }_s^{(r)}},p=1,\cdots ,m$.

$\begin{array}{l}\overline{{\lambda }_s^{(r)}}={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi \left[\frac{(l-1)(r-1)}{m}+\frac{(k-1)(s-1)}{n}\right]\\ -j sin 2\pi \left[\frac{(l-1)(r-1)}{m}+\frac{(k-1)(s-1)}{n}\right])\\ {\lambda }_{n+2-s}^{(m+2-r)}={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi [\frac{(l-1)(m+2-r-1)}{m}\\ +\frac{(k-1)(n+2-s-1)}{n}]\\ +j sin 2\pi \left[\frac{(l-1)(m+2-r-1)}{m}+\frac{(k-1)(n+2-s-1)}{n}\right])\\ ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi \left[\frac{(l-1)(m-r+1)}{m}+\frac{(k-1)(n-s+1)}{n}\right]\\ +j sin 2\pi \left[\frac{(l-1)(m-r+1)}{m}+\frac{(k-1)(n-s+1)}{n}\right])\\ ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi [\frac{(l-1)(-r+1)}{m}+\frac{(k-1)(-s+1)}{n}\\ +(l+k-2)]\\ + j sin 2\pi \left[\frac{(l-1)(-r+1)}{m}+\frac{(k-1)(-s+1)}{n}+(l+k-2)\right])\\ ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi \left[\frac{(l-1)(-r+1)}{m}+\frac{(k-1)(-s+1)}{n}\right]\\ +j sin 2\pi \left[\frac{(l-1)(-r+1)}{m}+\frac{(k-1)(-s+1)}{n}\right])\\ ={\displaystyle \sum _{k=1}^n{\displaystyle \sum _{l=1}^m}}{c}_k^l(cos 2\pi \left[\frac{(l-1)(r-1)}{m}+\frac{(k-1)(s-1)}{n}\right]\\ -j sin 2\pi \left[\frac{(l-1)(r-1)}{m}+\frac{(k-1)(s-1)}{n}\right])\end{array}$

Theorem 3.3. Let C = circ(C₁, C₂, ⋯ , C_n) be a real block-circulant matrix of dimension nm × nm with $C_k\in {ℝ}^{m\times m}$ and U_bc as defined in Equation (14). Define

$\begin{array}{ll}C={\displaystyle \sum _{k=1}^n}{\sigma }_n^k\otimes C_k& (18)\end{array}$

with ${\sigma }_n^1=circ(1,0,0,...,0,0),{\sigma }_n^2=circ(0,1,0,...,0,0),...,{\sigma }_n^n=circ(0,0,0,...,0,1)$ and ${\sigma }_n^{n+1}={\sigma }_n^1=circ(1,0,0,...,0,0)$. Let t_k = a_k + jb_k and λ_k = α_k + j β_k are the eigenvalues of ${\sigma }_n^k$ and C_k, respectively. Then, $U_{bc}^{T}C{U}_{bc}={\Omega }_{bc}$ is real and for n = 2h it has the form

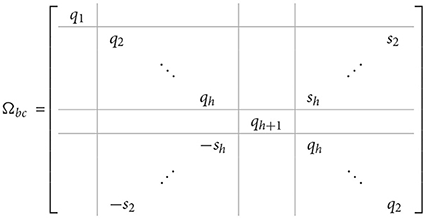
and for n = 2h + 1 it will be

with

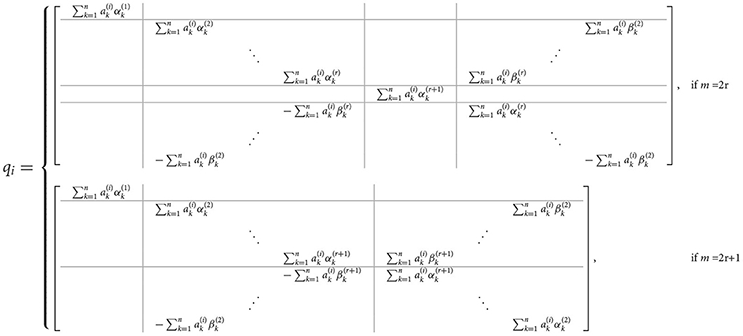
and

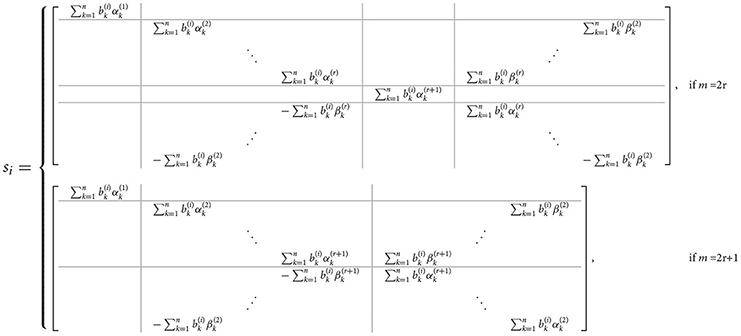
We will use the above theorems to define a real block-circulant matrix multiplication algorithm with any vector below.

Algorithm 3.4 The Multiplication of Cx

1. Compute v = Q_bcc₁ directly, c₁ = Ce₁, $e_1={(1,0,0,\cdots ,0)}^T$

2. Compute $\widehat{v}={(Q_{bc}{U}_{bc})}^{T}v$ by DCT and DST

3. Form Ω_bc

4. Compute y₁ = Q_bcx directly

5. Compute $y_2={(Q_{bc}{U}_{bc})}^T{y}_1$ by DCT and DST

6. Compute y₃ = Ω_bcy₂ directly

7. Compute y₄ = (Q_bcU_bc)y₃ by DCT and DST

8. Compute $Q_{bc}^T{y}_4$, i.e., Cx

The following is an example of implementing the above algorithm. Let C be a real block-circulant matrix with n = 4 and m = 3,

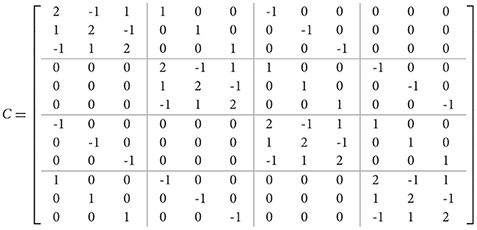
The eigenvalues of C are as follows:

${\lambda }_1^{(1)}=2{\lambda }_2^{(1)}=3-i$

${\lambda }_3^{(1)}=0{\lambda }_4^{(1)}=3+i$

${\lambda }_1^{(2)}=2+\frac{1}{2}\sqrt{3}i{\lambda }_2^{(2)}=3+0.732i$

${\lambda }_3^{(2)}=\frac{1}{2}\sqrt{3}i{\lambda }_4^{(2)}=3+2.732i$

${\lambda }_1^{(3)}=2+\frac{1}{2}\sqrt{3}i{\lambda }_2^{(3)}=3-2.732i$

${\lambda }_3^{(3)}=-\frac{1}{2}\sqrt{3}i{\lambda }_4^{(3)}=3-0.732i$

and the eigenvectors are

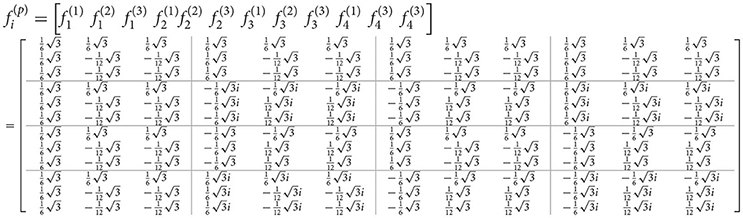
U_bc matrix will be in the form

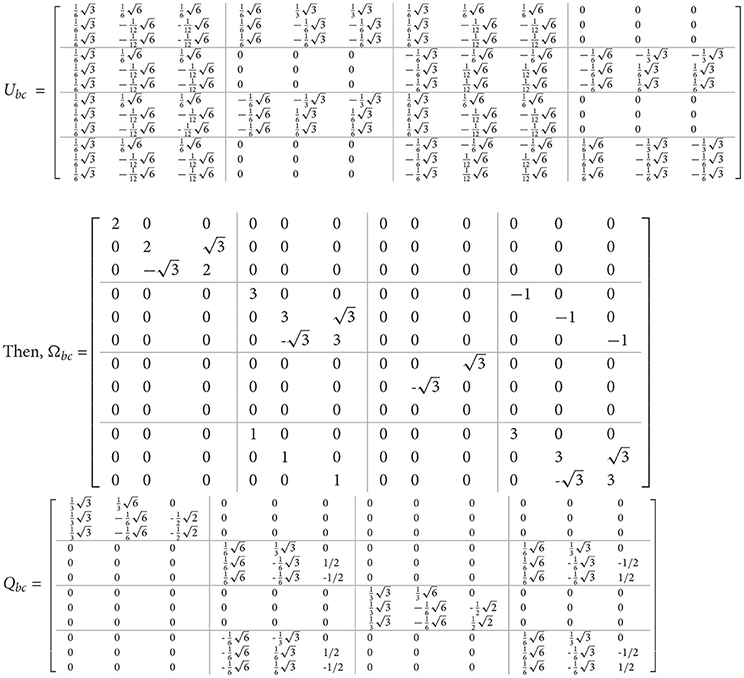
By following the above DCT-DST algorithm, if x = [1 2 3 4 5 6 7 8 9 10 11 12]^T, then $Cx=Q_{bs}^T{y}_4={\left[0-146510242328181722\right]}^T$.

4 Experiment of real block-circulant transformer

4.1 Data

In this experiment, data from D Talks Open Translation Project's Portuguese-English was used as the dataset, and Tensorflow Datasets was then used to load the data. This dataset contains ~52,000 training examples, 1,200 validation examples, and 1,800 test examples. The dataset was then tokenized using tokenization as used by Vaswani et al. [24].

4.2 Evaluation

On a held-out set of 500 samples, we evaluated performance using the corpus Bilingual Evaluation Understudy (BLEU) score. The corpus BLEU score employed the English sentence as its single reference and the top English sentence output of beam search as the hypothesis for each pair of Portuguese and English sentences in the evaluation set. The corpus BLEU was obtained by aggregating references and hypotheses across all pairings.

4.3 Experiment detail

We used the code from the tensorflow.org tutorial neural machine translation with a Transformer and Keras. We utilized various set ups that were slightly different by dense-dense transformer model [24]. Each model applied four layers, eight attention heads, and a dropout rate of 0.1. We set a batch size of 64, while the number of epoch is 20. The model has various matrix dimensions, depending on the size of the weight matrices being tested. The size of the tested matrices is the combinations of n and m values such that a block-circulant matrix of nm × nm size was obtained, namely, 16 × 16, 32 × 32, 64 × 64, 128 × 128, 256 × 256, and 512 × 512. Our feed forward dimensions are four times of the model dimension. Like Vaswani et al., we used an Adam optimizer with β₁ = 0.9; β₂ = 0.98, and ϵ = 10⁻⁹. Actually we used two types of matrices (dense and real block-circulant matrices) and two algorithms (FFT and DCT-DST algorithm). The model's name depicts to the type of matrices and algorithms that are applied in the multihead attention and feed forward, respectively, for instance, the dense - real block circulant DCT-DST transformer model. It means that we applied the dense matrix in the multihead attention and the feed forward sublayer used the real block-circulant matrix with DCT-DST algorithm. In this experiment, we trained 3 (three) transformer models with various matrices dimension. The three models were chosen based on the findings by Reid [31], which demonstrated that the block-circulant weight matrix was only appropriate for the feed forward sublayer. The following are the models tested (Table 1).

TABLE 1

Table 1. Tested transformer model.

4.4 Result and discussion

The performance measured from model experiments consists of accuracy, model memory size, and BLEU score. Accuracy is the percentage of correctly predicted tokens. The model memory is simply the memory used to store the model parameters, i.e., the weights and biases of each layer in the network [35]. BLEU (BiLingual Evaluation Understudy) is a metric for automatically evaluating machine-translated text.

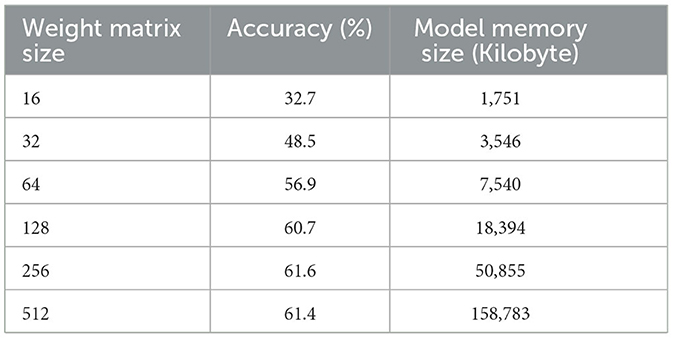
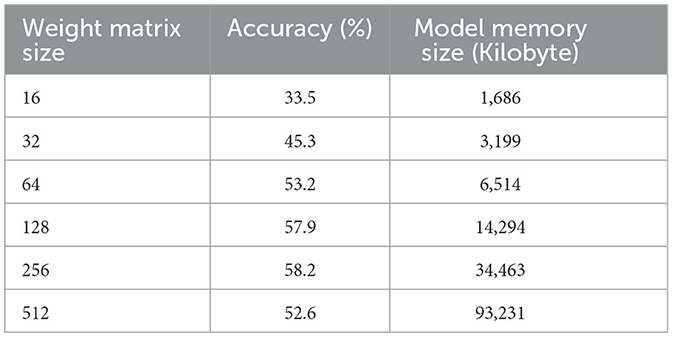
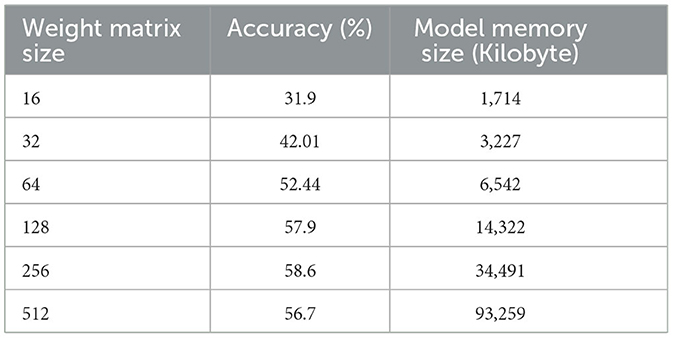
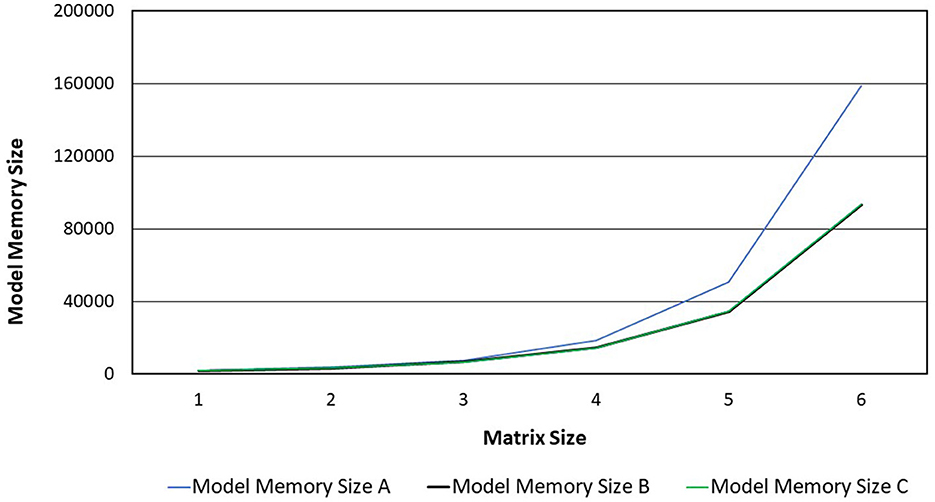
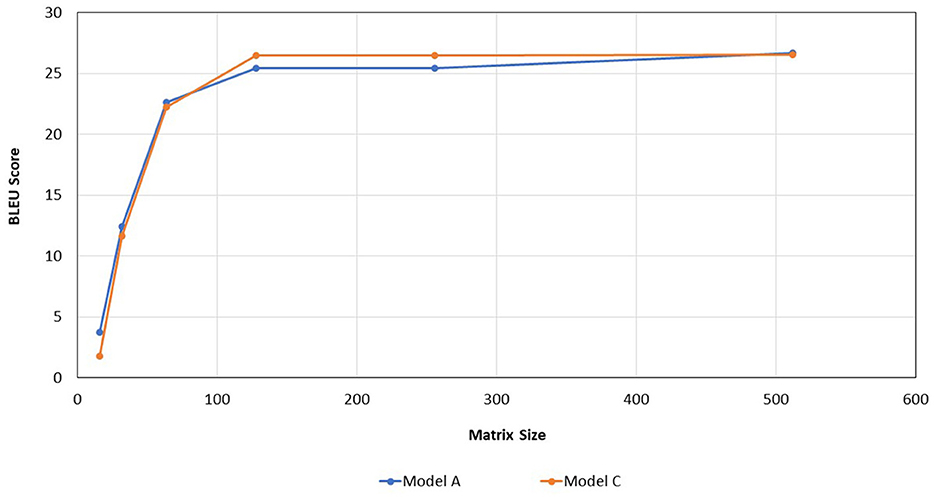
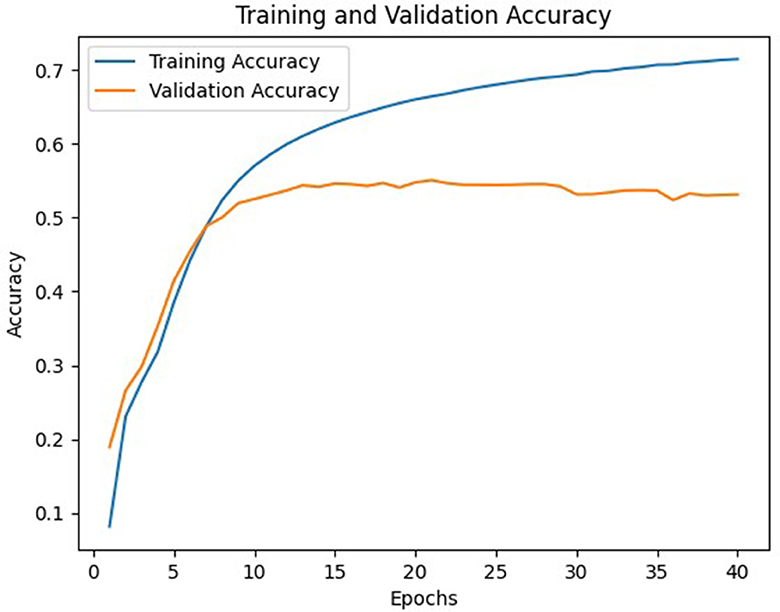
The experimental results on Tables 2–4 show that, for the three transformer models trained, the size of the weight matrix tends to be directly proportional to the accuracy values. Especially on B and C models, up to the weight matrix size of 256, the accuracy reaches a value that keeps rising; at 512, it starts to decline. Additionally, model C tends to have smaller memory sizes than model A, despite being marginally less efficient than model B in this regard. The disparity in model memory size reaches almost 41% when utilizing a 512-dimensional weight matrix (Figure 1). The use of the C model will provide significant advantages when used to perform translation tasks in at least two language pairs. For example, if we are going to translate four language pairs, then model A will require 643,778 KB of storage, while model C will require 510,597 KB. This means that there is a storage savings of around 20%. Furthermore, we can see that model C outperforms the model A in terms of BLEU score. With a 128 × 128 weight matrix, model C achieves 26.47 on the BLEU score (Figure 2).

TABLE 2

Table 2. Experiment result of dense-dense transformer model (A).

TABLE 3

Table 3. Experiment result of dense-block-circulant FFT transformer model (B).

TABLE 4

Table 4. Experiment result of dense-block-circulant DCT-DST transformer model (C).

FIGURE 1

Figure 1. Model memory size of the three transformer models.

FIGURE 2

Figure 2. Comparation of BLEU score of models A and C.

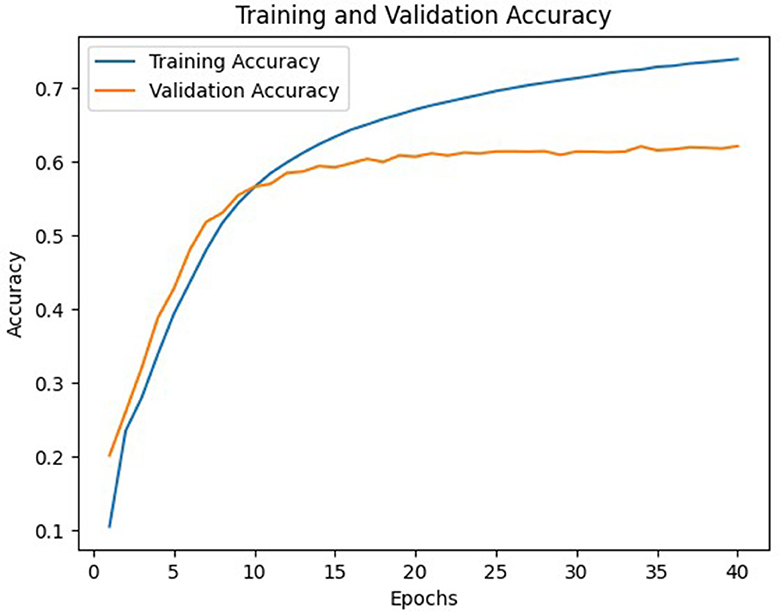
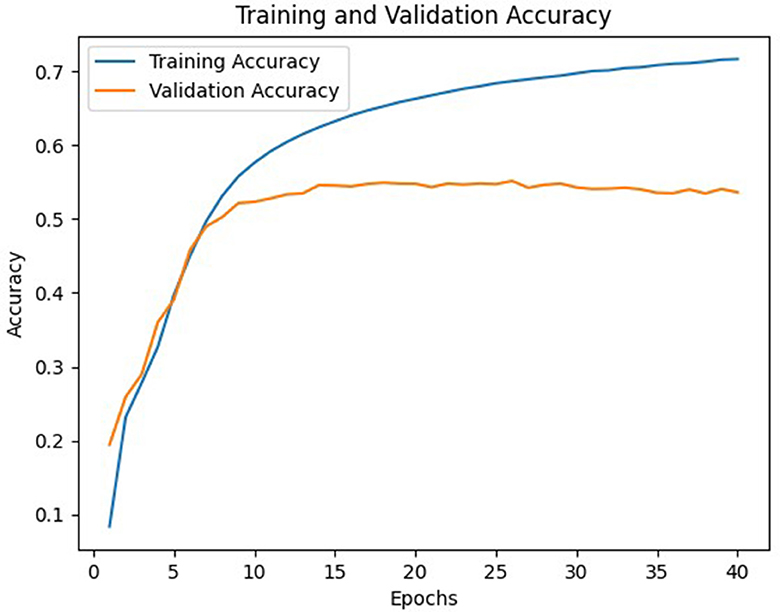
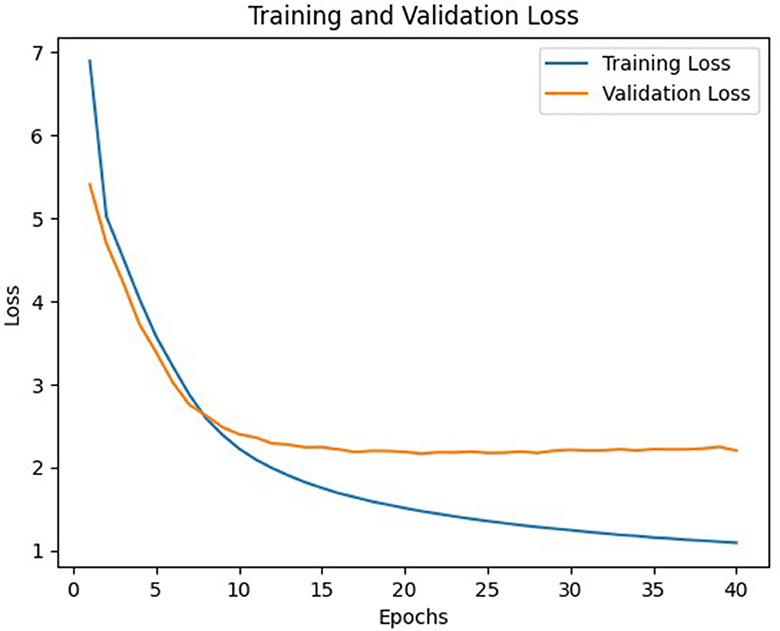
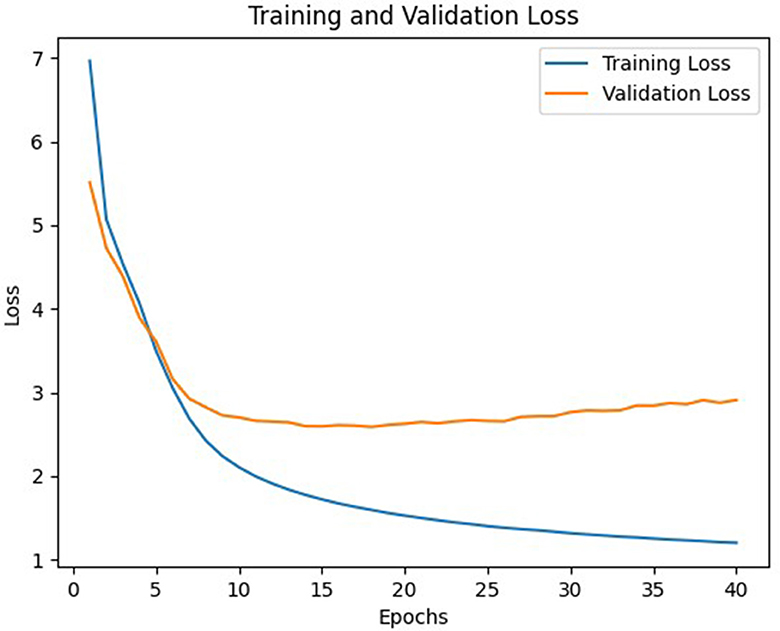
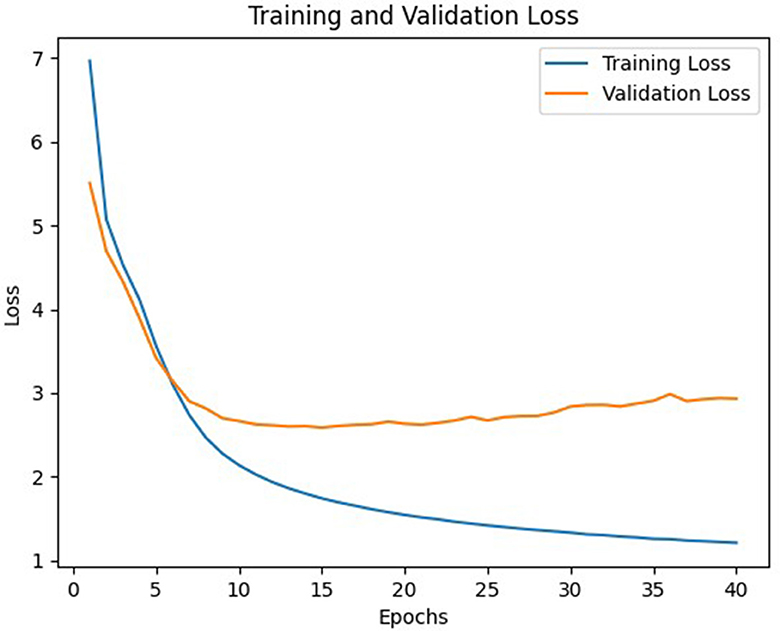
In general, model C with a weight matrix dimension of 128 provides relatively better performance compared to other models. Even though the accuracy value is slightly smaller than a larger matrix size, this matrix can still save storage usage and achieve a higher BLEU score. The accuracy and loss values from the training and validation process of the three models using a 128 × x128 matrix can be seen in Figures 3–8.

FIGURE 3

Figure 3. Accuracy of A model.

FIGURE 4

Figure 4. Accuracy of B model.

FIGURE 5

Figure 5. Accuracy of C model.

FIGURE 6

Figure 6. Loss of A model.

FIGURE 7

Figure 7. Loss of B model.

FIGURE 8

Figure 8. Loss of C model.

The results of this research are in line with the results obtained by Reid [31] that in general the use of the real block-circulant model in the feed forward transformer sublayer is able to compress the number of parameters at significant rate. At the same time, it ignores the accuracy value as found in Li et al. [29], Liao et al. [30], Ding et al. [36], and Qin et al. [37]. The fewer parameters in the C model allegedly are caused by the use of the real block-circulant matrices. Based on Kissel and Diepold [3], circulant matrix is one of the matrices in the class of low displacement rank matrices. These belong to the class of structured matrices which are identical to the data sparse matrices. Data sparsing means that the representation of n × n matrix requires <O(n²) parameters because there is a relationship between the matrix entries. In the use of data sparse matrices, we can find an efficient algorithm, in this case DCT-DST algorithm, so that in computing matrix-vector multiplication we have computation complexity with <$\mathcal{O}(n^2)$, even we only need O(nlog(n)) operations. Furthermore, in the process of generating the DCT-DST algorithm, not all generated matrices are computed. For example, the Schur form matrix, Ω_bc. This matrix was not computed directly but is created by arranging the entries that have been saved before, as shown in Liu et al. [9]. This is supposed to cut down on the amount of parameters and thus reducing the computation complexity of the model.

5 Conclusion

The use of the real block-circulant matrices as a transformer weight matrix combined with the DCT-DST algorithm for multiplication with any vector provides advantages in saving model memory and increasing the BLEU score. In general, based on this study, it was found that the real block-circulant matrix of dimension 128 provides relatively better performance compared to others. However, it needs to be studied further, whether a larger weight matrix size can provide better performance or not.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

EA: Data curation, Formal analysis, Investigation, Software, Visualization, Writing—original draft, Writing—review & editing. IM-A: Conceptualization, Funding acquisition, Methodology, Resources, Supervision, Validation, Writing—review & editing. AP: Data curation, Resources, Software, Supervision, Validation, Writing—review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by RISET UNGGULAN ITB 2022, grant number 293/IT1.B07.1/TA.00/2022.

Acknowledgments

The authors are grateful to Mikhael Martin who helped to conceive the programming language.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang G, Wei Y, Qiao S, Lin P, Chen Y. Generalized Inverses: Theory and Computations. Vol 53. New York, NY: Springer (2018).

Google Scholar

2. Comon P, Golub G, Lim LH, Mourrain B. Symmetric tensors and symmetric tensor rank. SIAM J Matrix Anal Appl. (2008) 30:1254–79. doi: 10.1137/060661569

CrossRef Full Text | Google Scholar

3. Kissel M, Diepold K. Structured Matrices and Their Application in Neural Networks: A Survey. New Generation Computing. New York, NY: Springer (2023). p. 1–26.

Google Scholar

4. Pan V. Structured Matrices and Polynomials: Unified Superfast Algorithms. Birkhäuser: Springer Science & Business Media (2001).

Google Scholar

5. Davis PJ. Circulant Matrices. New York, NY: Wiley (1979).

Google Scholar

6. Karner H, Schneid J, Ueberhuber CW. Spectral decomposition of real circulant matrices. Linear Algebra Appl. (2003) 367:301–11. doi: 10.1016/S0024-3795(02)00664-X

CrossRef Full Text | Google Scholar

7. Rjasanow S. Effective algorithms with circulant-block matrices. Linear Algebra Appl. (1994) 202:55–69. doi: 10.1016/0024-3795(94)90184-8

CrossRef Full Text | Google Scholar

8. Olson BJ, Shaw SW, Shi C, Pierre C, Parker RG. Circulant matrices and their application to vibration analysis. Appl Mech Rev. (2014) 66:040803. doi: 10.1115/1.4027722

CrossRef Full Text | Google Scholar

9. Liu Z, Chen S, Xu W, Zhang Y. The eigen-structures of real (skew) circulant matrices with some applications. Comp Appl Math. (2019) 38:1–13. doi: 10.1007/s40314-019-0971-9

CrossRef Full Text | Google Scholar

10. O'Shea K, Nash R. An introduction to convolutional neural networks. arXiv [preprint] (2015). doi: 10.48550/arXiv.1511.08458

CrossRef Full Text | Google Scholar

11. He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. In: Proceedings of the IEEE Conference on Computer. New York, NY: IEEE (2016). p. 770–8.

Google Scholar

12. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In:Bartlett P, Pereira FCN, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems. New York, NY: Neural Information Processing Systems Foundation, Inc. (NeurIPS) (2012). p. 25.

Google Scholar

13. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv [preprint] (2014). doi: 10.48550/arXiv.1409.1556

CrossRef Full Text | Google Scholar

14. Gaudet CJ, Maida AS. Deep quaternion networks. In: International Joint Conference on Neural Networks (IJCNN). New York, NY: IEEE (2018). p. 1–8.

Google Scholar

15. Parcollet T, Morchid M, Linarès G. Quaternion convolutional neural networks for heterogeneous image processing. In: ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New York, NY: IEEE (2019). p. 8514–18.

Google Scholar

16. Zhu X, Xu Y, Xu H, Chen C. Quaternion Convolutional Neural Networks. In: Proceedings of the European Conference on Computer Vision (ECCV). Cham: Springer (2018). p. 631–47.

Google Scholar

17. Cheng Y, Yu FX, Feris RS, Kumar S, Choudhary AN, Chang S. Fast neural networks with circulant projections. arXiv [preprint] (2015) 2. Available online at: https://arxiv.org/pdf/1502.03436.pdf

Google Scholar

18. Liao S, Yuan B. Circconv: a structured convolution with low complexity. arXiv. (2019) 33:4287–94. doi: 10.1609/aaai.v33i01.33014287

CrossRef Full Text | Google Scholar

19. Appuswamy R, Nayak T, Arthur J, Esser S, Merolla P, Mckinstry J, et al. Structured convolution matrices for energy-efficient deep learning. arXiv [preprint] (2016). doi: 10.48550/arXiv.1606.02407

CrossRef Full Text | Google Scholar

20. Sindhwani V, Sainath T, Kumar S. Structured transforms for small-footprint deep learning. In:In: Cortes C, Lawrence N, Lee D, Sugiyama M, Garnett R, editors. Advances in Neural Information Processing Systems. New York, NY: Neural Information Processing Systems Foundation, Inc. (NeurIPS) (2015). p. 28.

Google Scholar

21. Thomas A, Gu A, Dao T, Rudra A, Ré C. Learning compressed transforms with low displacement rank. In:Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R, editors. Advances in Neural Information Processing Systems. New York, NY: Neural Information Processing Systems Foundation, Inc. (2018). p. 31.

PubMed Abstract | Google Scholar

22. Zhao L, Liao S, Wang Y, Li Z, Tang J, Yuan B. Theoretical properties for neural networks with weight matrices of low displacement rank. In: Proceedings of International Conference on Machine Learning. Mlr.press (2017). p. 4082–90.

Google Scholar

23. Liu Y, Jiao S, Lim LH. LU decomposition and Toeplitz decomposition of a neural network. arXiv [preprint] (2022). doi: 10.2139/ssrn.4300402

CrossRef Full Text | Google Scholar

24. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In:Guyon I, Von Luxburg U, Bengio S, Wallach H, Fergus R, Vishwanathan S, Garnett R, editors. Advances in Neural Information Processing Systems. New York, NY: Neural Information Processing Systems Foundation, Inc. (2017). p. 30.

Google Scholar

25. Khandelwal U, Clark K, Jurafsky D, Kaiser L. Sample efficient text summarization using a single pre-trained transformer. arXiv [preprint] (2019). doi: 10.48550/arXiv.1905.08836

CrossRef Full Text | Google Scholar

26. Xiong Y, Du B, Yan P. Reinforced transformer for medical image captioning. In: Machine Learning in Medical Imaging: 10th International Workshop, MLMI 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, October 13, 2019. Cham: Springer (2019). p. 673–80.

Google Scholar

27. Peng Z, Ma X. A survey on construction and enhancement methods in service chatbots design. CCF Transact Pervas Comp Interact. (2019) 1:204–23. doi: 10.1007/s42486-019-00012-3

CrossRef Full Text | Google Scholar

28. Dong L, Xu S, Xu B. Speech-transformer: a no-recurrence sequence-to-sequence model for speech recognition. In: 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New York, NY: IEEE (2018). p. 5884–8.

Google Scholar

29. Li B, Pandey S, Fang H, Lyv Y, Li J, Chen J, et al. Ftrans: energy-efficient acceleration of transformers using fpga. In: Proceedings of the ACM/IEEE International Symposium on Low Power Electronics and Design. New York, NY (2020). p. 175–80.

Google Scholar

30. Liao S, Li Z, Lin X, Qiu Q, Wang Y, Yuan B. Energy-efficient, high-performance, highly-compressed deep neural network design using block-circulant matrices. In: 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD). New York, NY: IEEE (2017). p. 458–65.

Google Scholar

31. Reid S. Fast Fourier Transformed Transformers: Circulant Weight Matrices for NMT Compression. (2019). Available online at: https://api.semanticscholar.org/CorpusID:204747960

Google Scholar

32. Saxena A, Fernandes FC. DCT/DST-based transform coding for intra prediction in image/video coding. IEEE Transact Image Process. (2013) 22:3974–81. doi: 10.1109/TIP.2013.2265882

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Rose K, Heiman A, Dinstein IH. DCT/DST alternate-transform image coding. IEEE Transact Commun. (1990) 38:94–101. doi: 10.1109/26.46533

CrossRef Full Text | Google Scholar

34. Park W, Lee B, Kim M. Fast computation of integer DCT-V, DCT-VIII, and DST-VII for video coding. IEEE Transact Image Process. (2019) 28:5839–51. doi: 10.1109/TIP.2019.2900653

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sohoni NS, Aberger CR, Leszczynski M, Zhang J, Ré C. Low-memory neural network training: a technical report. arXiv [preprint] (2019). doi: 10.48550/arXiv.1904.10631

CrossRef Full Text | Google Scholar

36. Ding C, Liao S, Wang Y, Li Z, Liu N, Zhuo Y, et al. Circnn: accelerating and compressing deep neural networks using block-circulant weight matrices. In: Proceedings of the 50th Annual IEEE/ACM International Symposium on Microarchitecture. New York, NY (2017). p. 395–408.

Google Scholar

37. Qin Z, Zhu D, Zhu X, Chen X, Shi Y, Gao Y, et al. Accelerating deep neural networks by combining block-circulant matrices and low-precision weights. Electronics. (2019) 8:78. doi: 10.3390/electronics8010078

CrossRef Full Text | Google Scholar