The Lagrangian numerical relativity code SPHINCS_BSSN_v1.0

We present version 1.0 of our Lagrangian numerical relativity code SPHINCS_BSSN. This code evolves the full set of Einstein equations, but contrary to other numerical relativity codes, it evolves the matter fluid via Lagrangian particles in the framework of a high-accuracy version of smooth particle hydrodynamics (SPH). The major new elements introduced here are: (i) a new method to map the stress–energy tensor (known at the particles) to the spacetime mesh, based on a local regression estimate; (ii) additional measures that ensure the robust evolution of a neutron star through its collapse to a black hole; and (iii) further refinements in how we place the SPH particles for our initial data. The latter are implemented in our code SPHINCS_ID which now, in addition to LORENE, can also couple to initial data produced by the initial data library FUKA. We discuss several simulations of neutron star mergers performed with SPHINCS_BSSN_v1.0, including irrotational cases with and without prompt collapse and a system where only one of the stars has a large spin (χ = 0.5).

1. Introduction

The first neutron star merger event, GW170817, opened the era of gravitational wave-based multi-messenger astrophysics with a bang. The inspiral stages were recorded in the detectors for ~1 min [1], and subsequently, a firework was observed all across the electromagnetic spectrum [2]. Starting with a (special) short gamma-ray burst (sGRB) detected 1.7 s after the peak gravitational wave (GW) emission [3, 4], followed by an initially blue and subsequently rapidly reddening kilonova [5–7]. The event also displayed a rising X-ray flux starting 9 days after merger [8], peaking after 160 days, which then started to decline steeply afterward [9–12]. This was interpreted as the imprints of a structured jet observed at an angle of ~25° from the jet core [13–16]. Several years later, broad-band synchroton afterglow was detected [17, 18] that was interpreted as a “kilonova afterglow” due to a mildly relativistic ejection component interacting with the interstellar medium [16, 19, 20].

These observations allowed for a number of remarkable conclusions to be drawn. For example, the pre-merger gravitational wave signal placed constraints on the neutron star tidal deformability and, therefore, on the nuclear matter equation of state [1]. The time delay between the GW peak and the sGRB showed that GWs propagate at the speed of light to an enormous precision [21]. The event also allowed for a determination of the Hubble parameter [22] completely independent of previous approaches. The bolometric light curve evolution of the kilonova was remarkably consistent with a broad range of decaying r-process elements [23–25], thereby confirming the long-held suspicion that neutron star mergers are major sources of r-process elements in the cosmos [26–30]. While one would naively expect a red kilonova due to the extreme neutron-richness of the original neutron star material and the related large opacities [31], the early blue kilonova emission underlined that about 0.01 M_⊙ of the ejecta contained light (nucleon numbers A < 130) r-process material, which is also consistent with the identification of strontium lines [32]. While underlining that a broad range of heavy elements has been produced, these observations also stress the importance of weak interactions that have transformed a substantial fraction of the neutrons into protons to produce the light r-process material. The “kilonova afterglow” in turn, hints at a broad velocity distribution within the ejecta, extending to at least mildly relativistic velocities (≳ 0.6c).

The phenomena described above illustrates the richness of the properties of the ejected material, and they stress the importance of understanding the detailed properties of this ~1% of the total neutron star binary mass. Numerical simulations play an integral part in understanding and interpreting multi-messenger observations of compact binary systems. The initial generations of simulation models had a strong focus on the strong-field spacetime dynamics, the motion of the neutron star fluid in it, and the resulting gravitational wave emission, often with highly idealized microphysics. Today's frontiers, however, have shifted more toward a complex multi-physics modeling in which general relativity/strong-field gravity is only one ingredient out of many. Apart from including more physical processes such as magnetic field evolution or neutrino transport, the now observationally established connection with the electromagnetic emission also places higher demands on the length and time scales that need to be modeled in a neutron star merger event.

The vast majority of today's numerical relativity codes makes use of Eulerian hydrodynamics. While these codes have produced a multitude of important results, a larger methodological variety would be desirable, for independent checks of results but also to potentially address problems where established methods struggle, as, for example, in the long-term evolution of merger ejecta. The SPHINCS_BSSN code is the first Lagrangian hydrodynamics code that solves the full set of Einstein equations. The first results, restricted to standard relativistic hydrodynamics tests and oscillating and collapsing neutron stars, were presented in Rosswog and Diener [33]. In Diener et al. [34], the scope was extended to neutron star mergers, and at that stage, using simple polytropic equations of state and LORENE-based initial conditions [35–37] produced with an extension of the “artificial pressure method,” originally proposed in Rosswog [38], to the case of neutron star binaries. Subsequently, further technical improvements were introduced [39] and nuclear matter properties were approximated in terms of piecewise polytropic equations of state [40]. We have further improved our simulation technology, and in this study, we describe the ingredients of what we have tagged as “version 1.0” of our code, SPHINCS_BSSN_v1.0. We emphasize the latest improvements while still giving a broad overview of the complete methodology. The new elements include a further refined method to map the particle properties (specifically their stress–energy tensor) to the spacetime mesh and additional measures to ensure that we can robustly evolve a neutron star through its collapse to a black hole. We also describe further refinements in the particle setup of our initial data, produced with the code SPHINCS_ID [41].

Our article is structured as follows. In Section 2, we describe the methodology, with Section 2.1 focusing on the hydrodynamics, Section 2.2 on the equation of state, Section 2.3 on the spacetime evolution, and Section 2.4 on how spacetime and matter evolution are coupled. In Section 2.5, we describe measures to robustly evolve the collapse of a neutron star to a black hole, and in Section 3, we summarize our latest improvements in constructing SPH initial conditions in full general relativity. In Section 4, we discuss several examples of neutron star mergers, and we summarize our results in Section 5.

2. Methodology of SPHINCS_BSSN_v1.0

Here, we describe the methodological elements of the code SPHINCS_BSSN_v1.0. We only concisely summarize those parts that have been laid out already elsewhere in the literature, but we describe in detail the elements that are presented here for the first time. These are in particular: (a) a more sophisticated coupling between the spacetime and the fluid (via a local polynomial regression estimate), (b) specific measures (enhancement of grid resolution and the potential transformation of fluid into “dust” particles) that enable us to robustly simulate the formation of black holes.

2.1. Hydrodynamics

The hydrodynamic evolution equations in SPHINCS_BSSN are modeled via a high-accuracy version of smooth particle hydrodynamics (SPH), see [42–46] for reviews of the method. The basics of the relativistic SPH equations have been derived very explicitly in Section 4.2 of Rosswog [43], and we will only present the final equations here. Several accuracy-enhancing elements such as kernels, gradient estimators, and dissipation-steering strategies (for either Newtonian or relativistic cases) have been explored in a recent series of studies [38, 47, 48] and most of them are also implemented in SPHINCS_BSSN_v1.0.

We use units in which G = c = 1, and masses are measured in solar units. These “code units” approximately correspond in physical units to 1.47663 km for lengths to 4.92549 × 10⁻⁶ s for time and to 6.17797 × 10¹⁷ gcm⁻³ for densities. We further use the metric signature (-,+,+,+), and we measure all energies in units of $m_0{c}^2$, where m₀ is the average baryon mass¹. Greek indices run from 0 to 3 and Latin indices from 1 to 3. Contravariant spatial indices of a vector quantity $\overrightarrow{w}$ at particle a are denoted as $w_a^i$, while covariant ones will be written as (w_i)_a.

To discretize our fluid equations, we choose a “computing frame” in which the computations are performed. Quantities in this frame usually differ from those calculated in the local fluid rest frame. The line element in a 3 + 1 split of spacetime reads (e.g., [49]):

$\begin{array}{ll}d{s}^2=-{\alpha }^{2}d{t}^2+{\gamma }_{ij}\left(d{x}^i+{\beta }^{i}dt\right)\left(d{x}^j+{\beta }^{j}dt\right),& (1)\end{array}$

where α is the lapse function, βⁱ the shift vector, and γ_ij the spatial 3-metric. We use a generalized Lorentz factor

$\begin{array}{ll}\Theta \equiv \frac{1}{\sqrt{-g_{\mu \nu }{v}^{\mu }{v}^{\nu }}}\text{ with }{v}^{\alpha }=\frac{d{x}^{\alpha }}{dt}.& (2)\end{array}$

The coordinate velocities v^α are related to the four-velocities, normalized as $U_{\alpha }{U}^{\alpha }=-1$, by

$\begin{array}{ll}{v}^{\alpha }=\frac{d{x}^{\alpha }}{dt}=\frac{U^{\alpha }}{\Theta }=\frac{U^{\alpha }}{U^0}.& (3)\end{array}$

We choose the computing frame baryon number density N as density variable, which is related to the baryon number density as measured in the local fluid rest frame, n, by

$\begin{array}{ll}N=\sqrt{-g}\Theta n.& (4)\end{array}$

Here, g is the determinant of the spacetime metric. Note that this density variable is very similar to what is used in Eulerian approaches [49–52]. We keep the baryon number of each SPH particle, ν_a, constant so that exact numerical baryon number conservation is hard-wired. At every (Runge–Kutta sub-)step, the computing frame baryon number density at the position of a particle a is calculated via a weighted sum (actually very similar to Newtonian SPH):

$\begin{array}{ll}{N}_a={\displaystyle \sum _b}{\nu }_{b}W\left(|\overrightarrow{r_a}-{\overrightarrow{r}}_b|,h_a\right),& (5)\end{array}$

where the smoothing length h_a characterizes the support size of the SPH smoothing kernel W, see below. As numerical momentum variable, we choose the canonical momentum per baryon:

$\begin{array}{ll}{\left(S_i\right)}_a={\left(\Theta \mathcal{E}{v}_i\right)}_a,& (6)\end{array}$

where $\mathcal{E}=1+u+P/n$ is the relativistic enthalpy per baryon with u being the internal energy per baryon and P the gas pressure. The quantity S_i evolves according to

$\begin{array}{ll}\frac{d{\left(S_i\right)}_a}{dt}={\left(\frac{d{\left(S_i\right)}_a}{dt}\right)}_{\text{hyd}}+{\left(\frac{d{\left(S_i\right)}_a}{dt}\right)}_{\text{met}},& (7)\end{array}$

where the hydrodynamic part is given by

$\begin{array}{ll}{\left(\frac{d{\left(S_i\right)}_a}{dt}\right)}_{\text{hyd}}=-{\displaystyle \sum _b}{\nu }_b\left\{\frac{P_a}{N_a^2}{D}_i^a+\frac{P_b}{N_b^2}{D}_i^b\right\}& (8)\end{array}$

and the gravitational part by

$\begin{array}{ll}{\left(\frac{d{\left(S_i\right)}_a}{dt}\right)}_{\text{met}}={\left(\frac{\sqrt{-g}}{2N}{T}^{\mu \nu }\frac{\partial g_{\mu \nu }}{\partial x^i}\right)}_a.& (9)\end{array}$

Here, we have used the abbreviations

$\begin{array}{ll}{D}_i^a\equiv \sqrt{-g_a}\frac{\partial W_{ab}\left(h_a\right)}{\partial x_a^i}\text{ and }{D}_i^b\equiv \sqrt{-g_b}\frac{\partial W_{ab}\left(h_b\right)}{\partial x_a^i}& (10)\end{array}$

and W_ab(h_k) is a shorthand for $W\left(|{\overrightarrow{r}}_a-{\overrightarrow{r}}_b|/h_k\right)$. As a numerical energy variable, we use the canonical energy per baryon

$\begin{array}{ll}{e}_a={\left(S_i{v}^i+\frac{1+u}{\Theta }\right)}_a={\left(\Theta \mathcal{E}{v}_i{v}^i+\frac{1+u}{\Theta }\right)}_a,& (11)\end{array}$

which is evolved according to

$\begin{array}{ll}\frac{d{e}_a}{dt}={\left(\frac{d{e}_a}{dt}\right)}_{\text{hyd}}+{\left(\frac{d{e}_a}{dt}\right)}_{\text{met}},& (12)\end{array}$

with

$\begin{array}{ll}{\left(\frac{d{e}_a}{dt}\right)}_{\text{hyd}}=-{\displaystyle \sum _b}{\nu }_b\left\{\frac{P_a}{N_a^2}{v}_b^i{D}_i^a+\frac{P_b}{N_b^2}{v}_a^i{D}_i^b\right\}& (13)\end{array}$

and

$\begin{array}{ll}{\left(\frac{d{e}_a}{dt}\right)}_{\text{met}}=-{\left(\frac{\sqrt{-g}}{2N}{T}^{\mu \nu }\frac{\partial g_{\mu \nu }}{\partial t}\right)}_a.& (14)\end{array}$

It is instructive to make the connection between our numerical momentum variable S_i, Equation (6), and the Arnowitt–Deser–Misner (ADM) momentum of the fluid. Given a spatial vector field ξⁱ which tends to a Cartesian basis vector at spatial infinity, the ADM linear momentum along the direction of ξⁱ is defined as [53, Equation (8.40)] (see also [54, Sec. II])

$\begin{array}{ll}{P}_{\xi }^{\text{ADM}}≔\frac{1}{8\pi }{\displaystyle {\int }_{\partial \Sigma }\text{d}}{\sigma }_j\left(K^j{}_i-{\delta }^j{}_{i}K\right){\xi }^i,& (15)\end{array}$

where ∂Σ is the boundary of a spacelike hypersurface Σ that extends up to spatial infinity, dσ_j is its surface element, K^j_i is the extrinsic curvature, and K = Kⁱ_i its trace. Using Gauss' theorem, the momentum constraint, and some geometry, the integral in Equation (15) can be written as (see Appendix B):

$\begin{array}{ll}{P}_{\xi }^{\text{ADM}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }\left[{\xi }^i{s}_i+\frac{1}{16\pi }\left(K^{ij}-{\gamma }^{ij}K\right){\mathcal{L}}_{\xi }{\gamma }_{ij}\right],& (16)\end{array}$

where γ_ij is the spatial metric, s_i is the spatial part of the momentum density measured by the Eulerian observer $s_{\rho }≔-n^{\mu }{T}_{\mu \nu }{\gamma }^{\nu }{}_{\rho }$, and $\mathcal{L}$_ξ is the Lie derivative along ξⁱ. The two terms in the integrand of Equation (16) are the parts of the ADM linear momentum determined by the fluid and the spacetime, respectively. The expression in Equation (16) allows us to write the ADM momentum of the fluid in terms of the SPH canonical momentum S_i, after we relate the latter with the Eulerian spatial momentum density s_i. We do this explicitly in Appendix B. Here, we show the final result and its SPH approximation:

$\begin{array}{ll}{P}_{\xi }^{\text{ADM},\text{fluid}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }{\xi }^i{s}_i={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}xN{\xi }^i{S}_i\simeq {\displaystyle \sum _b}{\nu }_b{\left({\xi }^i{S}_i\right)}_b& (17)\end{array}$

with the index b running over all the particles, ν_b being the baryon number of particle b, N defined in Equation (4), s_i = ΘnαS_i, α is the lapse function, and $\sqrt{-g}=\alpha \sqrt{\gamma }$ [49, Equation (2.124)]. The rightmost formula in Equation (17) can be used to compute an estimate of the ADM momentum of the fluid using only SPH fields. Such an estimate can then be compared with another one computed using Equation (15); this comparison tells us about the error on the ADM momentum of the fluid introduced when we model the fluid with SPH particles. We make this comparison at the level of the initial data (ID) in Section 3.4.

For the kernel function that is needed for the SPH approximation, we have implemented a large variety of choices. We have performed many numerical experiments similar to the one shown in Figure 1, some of which are documented in detail in Rosswog [47]. Here, we only provide the details of our preferred kernels. The first of these favorites is the Wendland C6-smooth kernel [55]:

$\begin{array}{ll}W\left(q\right)=W^{WC6}\left(q\right)=\frac{\sigma }{h^3}{\left(1-q\right)}_{+}^8\left(32q^3+25q^2+8q+1\right),& (18)\end{array}$

where we use exactly 300 constributing neighbor particles. The normalization constant is σ = 1, 365/(64π) in 3D, and the symbol (.)₊ denotes the cutoff function max(., 0). Other favorites include (some) members of the family of the harmonic-like kernels [56]:

$\begin{array}{ll}W\left(q\right)=W_n^{\text{H}}\left(q\right)=\frac{{\sigma }_n}{h^3}\{\begin{array}{cc}1,\hfill & q=0,\\ {\left(\frac{sin\left[\frac{\pi }{2}q\right]}{\frac{\pi }{2}q}\right)}^n\hfill & 0<q<2,\\ 0,\hfill & \text{else},\end{array}\hfill & (19)\end{array}$

namely, those with n = 7 and 8. Out of this family, we chose, after ample experiments, the kernel with n = 8 for which we use exactly 220 contributing neighbor particles. For this kernel, the normalization constant is σ₈ = 1.17851074088357 in 3D. Contrary to Wendland kernels [55], this kernel is not immune against the (benign) pairing instability, but it provides an excellent density estimate. We show in Figure 1 the result of a density measurement experiment. Particles are placed on a cubic lattice, and masses are assigned so that the mass density is exactly unity. We then use several kernel functions, the commonly used cubic spline kernel [57], the Wendland C2, C4, and C6 kernels (see [58] for the explicit expressions) and the $W_8^{\text{H}}$ kernel, Equation (19).

FIGURE 1

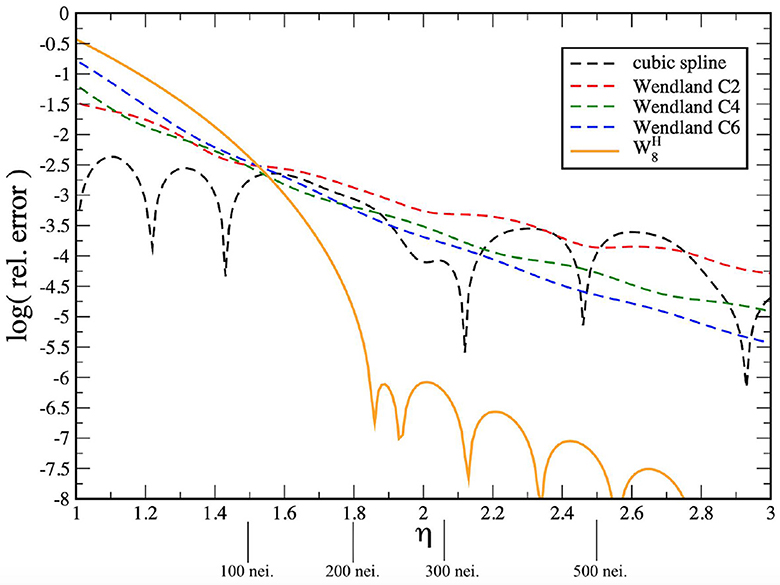
Figure 1. Error on the density estimate for different kernels as a function of support size for particles arranged on a cubic lattice. The parameter η determines the smoothing length h as a multiple of the typical particle spacing via h = η(ν/N)^1/3, the support radius of all kernels is 2h. We have also indicated the corresponding number of neighbor particles.

The smoothing lengths h in this experiment are set as multiples of the typical particle separation (ν/N)^1/3, h = η(ν/N)^1/3, and each of the kernels has a support radius of 2h. We have also indicated some approximate numbers of contributing particles (“neighbors”) for our cubic lattice. For neighbor numbers just beyond 200, the density accuracy in this experiment is about three orders of magnitude better for $W_8^{\text{H}}$ compared to the Wendland C6 kernel. While it is a priori not entirely clear how to weigh the excellent performance in this idealized experiment against the desirable property of the Wendland kernels to maintain a very regular particle distribution during dynamical evolution [47], we choose in this study, the $W_8^{\text{H}}$-kernel, and we found very satisfactory results. On inspecting the simulations presented here, we do not see any significant pairing among the particles and the density distributions appear noise-free while exhibiting sharp features.

To keep the numerical noise at a minimum, we choose at each time step the smoothing length of each particle a, h_a, so that there are exactly 220 contributing neighbor particles within the support radius 2h_a. In other words, at each time step, the smoothing length of particle a, h_a, is set so that 2h_a equals the distance to the 221-th closest SPH particle. This particle sits by definition at the radius where the kernel becomes zero so that exactly 220 particles have a non-zero contribution. This approach ensures a very smooth and subtle evolution of the smoothing length and avoids the introduction of noise through the update of the smoothing length. In practice, this is achieved by using our fast RCB-tree [59], for more details on the exact procedure, we refer to the MAGMA2 code study [38] where the same approach was used. A large number of experiments confirms that we get very similar results when using W^WC6 and $W_8^H$.

To robustly handle relativistic shocks, our momentum and energy equations are augmented with dissipative terms. These terms consist of an artificial dissipation and an artificial conductivity part. In both of these terms, we apply a slope-limited reconstruction to the mid-point of each particle pair, and this reconstruction approach has been shown to massively reduce unwanted dissipative effects [38]. In order to further reduce dissipation where it is not needed, we make our dissipation parameters time-dependent; they are increased when a shock or numerical noise is detected, but otherwise they decay exponentially to a small value (here chosen as α₀ = 0.1). Since no changes compared to our previous study have been made, we refer the interested reader for the equations, implementation details and tests to Rosswog et al. [39].

The quantities that we evolve numerically, S_i and e, together with the density N, see Equation (5), are numerically very convenient, but they are not the physical quantities that we are interested in. We, therefore, have to recover the physical quantities n, u, vⁱ, P from N, S_i, e at every integration (sub-)step. This “recovery” step is done in a very similar way as in Eulerian approaches. For polytropic equations of state, our strategy is described in detail in Section 2.2.4 of Rosswog and Diener [33], and the modifications needed for piecewise polytropic equations of states (EOSs) are laid out explicitly in Appendix A of Rosswog et al. [39].

2.2. Equations of state

To close the system of hydrodynamic equations, we need an equation of state. Currently, we are using piecewise polytropic approximations to cold nuclear matter equations of state [40], that are enhanced with an ideal gas-type thermal contribution to both pressure and specific internal energy, a common approach in numerical relativity simulations. For explicit expressions, please see Appendix A of Rosswog et al. [39]. To date, we have implemented 14 piecewise polytropic equations of state, but since the effects coming from different EOSs are not the topic of this code study, we restrict ourselves to results obtained for the APR3 EOS [60] only. This EOS allows for a maximum mass of $M_{\text{TOV}}^{\text{max}}=2.39$ M_⊙ and a 1.4 M_⊙ neutron star has a dimensionless tidal deformability of Λ_1.4 = 390. Indirect arguments and the statistics of the radio pulsar/X-ray neutron star distribution point to values in the range of ~ 2.2 − 2.4 M_⊙ [61–67] for the “best educated guess” of the maximum neutron star mass and a recent Bayesian study [68] suggests a maximum TOV mass of 2.52${}_{-0.29}^{+0.33}$ M_⊙, all broadly consistent with our choice of the APR3 EOS. More sophisticated treatments of high-density nuclear matter physics will be addressed in future.

2.3. Spacetime evolution

We evolve the spacetime according to the (“Φ-version” of the) BSSN equations [69, 70]. We have written wrappers around code extracted from the well tested McLachlan thorn of the Einstein Toolkit [71, 72]. The dynamical variables used in this method are related to the Arnowitt–Deser–Misner (ADM) variables γ_ij (3-metric), K_ij (extrinsic curvature), α (lapse function) and βⁱ (shift vector) and they read

$\begin{array}{ll}\varphi =\frac{1}{12}log\left(\gamma \right),& (20)\end{array}$

$\begin{array}{ll}{\tilde{\gamma }}_{ij}=e^{-4\varphi }{\gamma }_{ij},& (21)\end{array}$

$\begin{array}{ll}K={\gamma }^{ij}{K}_{ij},& (22)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}^i={\tilde{\gamma }}^{jk}{\tilde{\Gamma }}_{jk}^i,& (23)\end{array}$

$\begin{array}{ll}{Ã}_{ij}=e^{-4\varphi }\left(K_{ij}-\frac{1}{3}{\gamma }_{ij}K\right),& (24)\end{array}$

where γ = det(γ_ij), ${\tilde{\Gamma }}_{jk}^i$ are the Christoffel symbols related to the conformal metric ${\tilde{\gamma }}_{ij}$ and Ã_ij is the conformally rescaled, traceless part of the extrinsic curvature. The corresponding evolution equations read

$\begin{array}{ll}{\partial }_t\varphi =-\frac{1}{6}\left(\alpha K-{\partial }_i{i}^{\beta }\right)+{\beta }^i{\bar{\partial }}_i\varphi ,& (25)\end{array}$

$\begin{array}{ll}{\partial }_t{\tilde{\gamma }}_{ij}=-2\alpha {Ã}_{ij}+{\tilde{\gamma }}_{ik}{\partial }_j{\beta }^k+{\tilde{\gamma }}_{jk}{\partial }_i{\beta }^k-\frac{2}{3}{\tilde{\gamma }}_{ij}{\partial }_k{\beta }^k+{\beta }^k{\bar{\partial }}_k{\tilde{\gamma }}_{ij},& (26)\end{array}$

$\begin{array}{l}{\partial }_{t}K=-e^{-4\varphi }\left({\tilde{\gamma }}^{ij}\left[{\partial }_i{\partial }_j\alpha +2{\partial }_i\varphi {\partial }_j\alpha \right]-{{\tilde{\Gamma }}_{\left(\text{n}\right)}}^i{\partial }_i\alpha \right)\\ +\alpha \left({Ã}_j^i{Ã}_i^j+\frac{1}{3}{K}^2\right)+{\beta }^i{\bar{\partial }}_{i}K+4\pi \alpha \left(\rho +s\right),& (27)\end{array}$

$\begin{array}{l}{\partial }_t{\tilde{\Gamma }}^i=-2{Ã}^{ij}{\partial }_j\alpha +2\alpha \left({\tilde{\Gamma }}_{jk}^i{Ã}^{jk}-\frac{2}{3}{\tilde{\gamma }}^{ij}{\partial }_{j}K+6{Ã}^{ij}{\partial }_j\varphi \right)\\ +{\tilde{\gamma }}^{jk}{\partial }_j{\partial }_k{\beta }^i+\frac{1}{3}{\tilde{\gamma }}^{ij}{\partial }_j{\partial }_k{\beta }^k-{{\tilde{\Gamma }}_{\left(\text{n}\right)}}^j{\partial }_j{\beta }^i+\frac{2}{3}{{\tilde{\Gamma }}_{\left(\text{n}\right)}}^i{\partial }_j{\beta }^j& (28)\end{array}$

$\begin{array}{l}+{\beta }^j{\bar{\partial }}_j{\tilde{\Gamma }}^i-16\pi \alpha {\tilde{\gamma }}^{ij}{s}_j,\\ {\partial }_t{Ã}_{ij}=e^{-4\varphi }{\left[-{\partial }_i{\partial }_j\alpha +{\tilde{\Gamma }}_{ij}^k{\partial }_k\alpha +2\left({\partial }_i\alpha {\partial }_j\varphi +{\partial }_j\alpha {\partial }_i\varphi \right)+\alpha R_{ij}\right]}^{\text{TF}}\\ +\alpha \left(K{Ã}_{ij}-2{Ã}_{ik}{Ã}_j^k\right)\\ +{Ã}_{ik}{\partial }_j{\beta }^k+{Ã}_{jk}{\partial }_i{\beta }^k-\frac{2}{3}{Ã}_{ij}{\partial }_k{\beta }^k\\ +{\beta }^k{\bar{\partial }}_k{Ã}_{ij}-e^{-4\varphi }\alpha 8\pi \left(T_{ij}-\frac{1}{3}{\gamma }_{ij}s\right),& (29)\end{array}$

where

$\begin{array}{ll}\rho =\frac{1}{{\alpha }^2}\left(T_{00}-2{\beta }^i{T}_{0i}+{\beta }^i{\beta }^j{T}_{ij}\right),& (30)\end{array}$

$\begin{array}{ll}s={\gamma }^{ij}{T}_{ij},& (31)\end{array}$

$\begin{array}{ll}{s}_i=-\frac{1}{\alpha }\left(T_{0i}-{\beta }^j{T}_{ij}\right),& (32)\end{array}$

and ${\beta }^i{\bar{\partial }}_i$ denote partial derivatives that are upwinded based on the shift vector. The superscript “TF” in the evolution equation of Ã_ij denotes the trace-free part of the bracketed term. Finally, $R_{ij}={\tilde{R}}_{ij}+R_{ij}^{\varphi }$, where

$\begin{array}{ll}{\tilde{\Gamma }}_{ijk}=\frac{1}{2}\left({\partial }_k{\tilde{\gamma }}_{ij}+{\partial }_j{\tilde{\gamma }}_{ik}-{\partial }_i{\tilde{\gamma }}_{jk}\right),& (33)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_{ij}^k={\tilde{\gamma }}^{kl}{\tilde{\Gamma }}_{ijl},& (34)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_{jk}^i={\tilde{\gamma }}^{il}{\tilde{\Gamma }}_{ljk},& (35)\end{array}$

$\begin{array}{ll}{{\tilde{\Gamma }}_{\left(\text{n}\right)}}^i={\tilde{\gamma }}^{jk}{\tilde{\Gamma }}_{jk}^i,& (36)\end{array}$

$\begin{array}{l}{\tilde{R}}_{ij}=-\frac{1}{2}{\tilde{\gamma }}^{kl}{\partial }_k{\partial }_l{\tilde{\gamma }}_{ij}+{\tilde{\gamma }}_{k(i}{\partial }_j{}_{)}{\tilde{\Gamma }}^k+{\tilde{\Gamma }}_{(n)}^k{\tilde{\Gamma }}_{(ij)k}\\ +{\tilde{\Gamma }}_{il}^k{\tilde{\Gamma }}_{jk}{}^l+{\tilde{\Gamma }}_{jl}^k{\tilde{\Gamma }}_{ik}{}^l+{\tilde{\Gamma }}_{il}^k{\tilde{\Gamma }}_{kj}{}^l,& (37)\end{array}$

$\begin{array}{l}{R}_{ij}^{\varphi }=-2\left({\partial }_i{\partial }_j\varphi -{\tilde{\Gamma }}_{ij}^k{\partial }_k\varphi \right)-2{\tilde{\gamma }}_{ij}{\tilde{\gamma }}^{kl}\\ \left({\partial }_k{\partial }_l\varphi -{\tilde{\Gamma }}_{kl}^m{\partial }_m\varphi \right)+4{\partial }_i\varphi {\partial }_j\varphi \\ -4{\tilde{\gamma }}_{ij}{\tilde{\gamma }}^{kl}{\partial }_k\varphi {\partial }_l\varphi .& (38)\end{array}$

The derivatives on the right-hand side of the BSSN equations are evaluated via standard finite differencing techniques and, unless mentioned otherwise, we use the sixth order differencing as a default. We have recently implemented a fixed mesh refinement for the spacetime evolution, which is described in detail in Diener et al. [34], to which we refer the interested reader. For the gage choices, we use a variant of “1+log-slicing,” where the lapse is evolved according to

$\begin{array}{ll}{\partial }_t\alpha =-2\alpha K& (39)\end{array}$

and a variant of the “Γ-driver” shift condition with

$\begin{array}{ll}{\partial }_t{\beta }^i=\frac{3}{4}\left({\tilde{\Gamma }}^i-\eta {\beta }^i\right),& (40)\end{array}$

where η is the “β-driver” parameter.

2.4. Coupling between spacetime and matter

The SPHINCS_BSSN approach of evolving the spacetime on a mesh and the matter fluid via particles requires a continuous information exchange: the gravity part of the particle evolution is driven by derivatives of the metric, see Eqs (9) and (14), which are known on the mesh, while the stress–energy tensor, needed in Equation (25)–(32), is known on the particles. This bidirectional information exchange is needed at every Runge–Kutta substep; in our case, with an optimal third order Runge–Kutta algorithm [73], three times per numerical time step.

The mesh-to-particle mapping step is performed via fifth order Hermite interpolation, that we developed [33] extending the work of Timmes and Swesty [74]. Contrary to a standard Lagrange polynomial interpolation, the Hermite interpolation guarantees that the metric remains twice differentiable as particles pass from one grid cell to another and therefore avoids the introduction of additional noise. Our approach is explained in detail in Section 2.4 of Rosswog and Diener [33] to which we refer the interested reader.

Here, we provide a further improvement to the more challenging of the two steps, the particle-to-mesh mapping. As in our previous work [34, 39], we follow a “multi-dimensional optimal order detection” (MOOD) strategy. The mapping is performed simultaneously with different orders, and the most accurate solution is selected out of the possible results (according to some error measure, see below), provided that the solution meets additional physical admissibility conditions.

This is somewhat similar in spirit to ENO reconstruction schemes in mesh-based hydrodynamics, see Zhang and Shu [75] for a concise summary of ENO and WENO schemes, in the sense that one does not pretend to know a priori which reconstruction order (or here: interpolation order) is “good enough.” Instead one tries a variety of options and selects the best one. Our scheme is similar to ENO methods where one tries different stencils and selects the smoothest one according to a suitable criterion (WENO actually goes one step further by using a weighted sum of the different options to combine them into potentially higher order).

In Rosswog et al. [39], we used kernel functions of different orders borrowed from vortex methods [76, 77], we determine here the best fit to the particle properties at a grid point by using the local polynomial regression estimate that we describe in the next section.

2.4.1. Local regression estimate

The task is to find the function that best fits the values of the particles surrounding the grid point ${\overrightarrow{r}}^{\text{G}}$ (see Figure 2). If we assume that the values at the particle positions {f^p} are described by a function $f\left(\overrightarrow{r}\right)$, we can Taylor-expand this function around the desired grid point ${\overrightarrow{r}}^{\text{G}}$:

$\begin{array}{l}f(\overrightarrow{r})=f({\overrightarrow{r}}^{\text{G}})+{({\partial }_{i}f)}_{{\overrightarrow{r}}^{\text{G}}}{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^i+\frac{1}{2!}{({\partial }_{ij}f)}_{{\overrightarrow{r}}^{\text{G}}}{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^i{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^j\\ +\frac{1}{3!}{({\partial }_{ijk}f)}_{{\overrightarrow{r}}^{\text{G}}}{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^i{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^j{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^k\\ +\frac{1}{4!}{({\partial }_{ijkl}f)}_{{\overrightarrow{r}}^{\text{G}}}{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^i{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^j{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^k{(\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}})}^l\\ +\text{higher order terms}.& (41)\end{array}$

This Taylor expansion can be interpreted as a polynomial approximation of a given order where the basis functions have been shifted to the point of interest ${\overrightarrow{r}}^{\text{G}}$. The local approximation $\tilde{f}\left(\overrightarrow{r}\right)$ of $f\left(\overrightarrow{r}\right)$ around the point ${\overrightarrow{r}}^{\text{G}}$ then reads

$\begin{array}{ll}{\tilde{f}}^G\left(\overrightarrow{r}\right)={\overrightarrow{\beta }}^G·{\overrightarrow{P}}^G\left(\overrightarrow{r}\right),& (42)\end{array}$

where the coefficient vector reads

$\begin{array}{l}{\overrightarrow{\beta }}^G=[f\left({\overrightarrow{r}}^{\text{G}}\right),{\left({\partial }_{x}f\right)}_{{\overrightarrow{r}}^{\text{G}}},{\left({\partial }_{y}f\right)}_{{\overrightarrow{r}}^{\text{G}}},{\left({\partial }_{z}f\right)}_{{\overrightarrow{r}}^{\text{G}}},\\ \frac{1}{2}{\left({\partial }_{xx}f\right)}_{{\overrightarrow{r}}^{\text{G}}},{\left({\partial }_{xy}f\right)}_{{\overrightarrow{r}}^{\text{G}}},{\left({\partial }_{xz}f\right)}_{{\overrightarrow{r}}^{\text{G}}},\frac{1}{2}{\left({\partial }_{yy}f\right)}_{{\overrightarrow{r}}^{\text{G}}},{\left({\partial }_{yz}f\right)}_{{\overrightarrow{r}}^{\text{G}}},\\ \frac{1}{2}{\left({\partial }_{zz}f\right)}_{{\overrightarrow{r}}^{\text{G}}},\cdots ],& (43)\end{array}$

and the “shifted basis functions” read

$\begin{array}{ll}{\overrightarrow{P}}^G\left(\overrightarrow{r}\right)=[1,{\Delta }^{G}x,{\Delta }^{G}y,{\Delta }^{G}z,& (44)\end{array}$

$\begin{array}{l}{\Delta }^{G}x{\Delta }^{G}x,{\Delta }^{G}x{\Delta }^{G}y,{\Delta }^{G}x{\Delta }^{G}z,{\Delta }^{G}y{\Delta }^{G}y,{\Delta }^{G}y{\Delta }^{G}z,\\ {\Delta }^{G}z{\Delta }^{G}z,\cdots {]}^T,& (45)\end{array}$

where ${\Delta }^G\overrightarrow{r}=\overrightarrow{r}-{\overrightarrow{r}}^{\text{G}}={\left[{\Delta }^{G}x,{\Delta }^{G}y,{\Delta }^{G}z\right]}^T$ and Δ^Gx = x − x^G (similarly for the other components). The degrees of freedom (DoF) for a given number of dimensions d and a maximum polynomial order of the basis m are given by

$\begin{array}{ll}\text{DoF}=\frac{\left(d+m\right)!}{d!m!},& (46)\end{array}$

that is, in 3D, we have 1, 4, 10, 20, and 35 DoF for constant, linear, quadratic, cubic, and quartic polynomials.

FIGURE 2

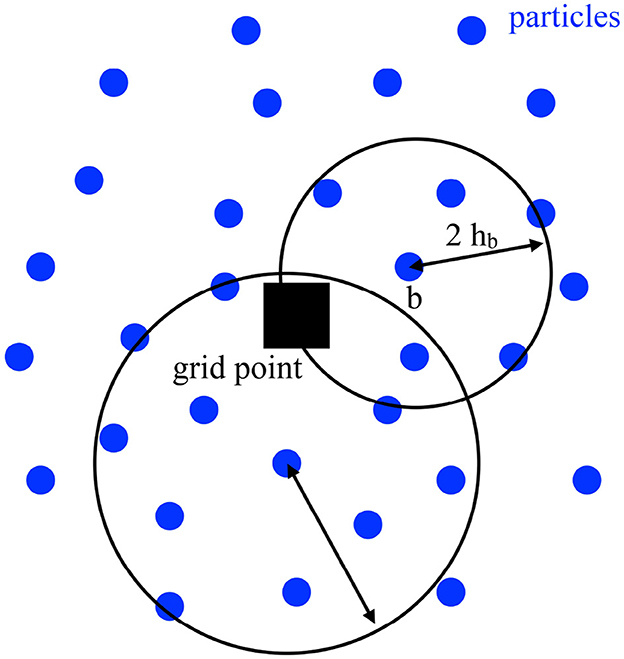
Figure 2. Geometry of the particle-to-mesh mapping: function values that are known at particle positions (blue circles) are to be mapped to a grid point (black square).

The optimal coefficients at ${\overrightarrow{r}}^G$, ${\overrightarrow{\beta }}^G$, are found by minimizing the error functional:

$\begin{array}{ll}{ϵ}^G\equiv {\displaystyle \sum _p}{\left[f_p-{\tilde{f}}^G\left({\overrightarrow{r}}_p\right)\right]}^2{W}_{pG}={\displaystyle \sum _p}{\left[f_p-{\displaystyle \sum _{i=1}^{\text{DoF}}}{\beta }_i^G{P}_i^G\left({\overrightarrow{r}}_p\right)\right]}^2{W}_{pG},& (47)\end{array}$

where $W_{pG}=W\left({\overrightarrow{r}}^p-{\overrightarrow{r}}^G,l_p\right)$ is a smooth weighting function that ensures that particles further away from the grid point are weighted less in the error functional, and the p-sum runs over all contributing particles. The kernel width is set by $l_p={\left({\nu }_p/N_p\right)}^{1/3}$. One could choose, for example, compactly supported SPH kernels for this weighting function; we choose simple tensor products of 1D M₄-kernels. The exact form of the weight function does not have a strong influence on the resulting error measure.

The optimal coefficients that minimize the error at ${\overrightarrow{r}}^G$ are determined via

$\begin{array}{ll}{\left(\frac{\partial {ϵ}^G}{\partial {\beta }_i^G}\right)}_{{\overrightarrow{r}}^{\text{G}}}\stackrel{!}{=}0,& (48)\end{array}$

and, with a few steps of algebra, one finds

$\begin{array}{ll}{\beta }_i^G={\left(M_{ik}\right)}^{-1}{B}_k,& (49)\end{array}$

where

$\begin{array}{ll}{M}_{ik}={\displaystyle \sum _p}{P}_i^G\left({\overrightarrow{r}}_p\right)P_k^G\left({\overrightarrow{r}}_p\right)W_{pG}& (50)\end{array}$

is the “moment matrix” and

$\begin{array}{ll}{B}_k={\displaystyle \sum _p}{f}_p{P}_k^G\left({\overrightarrow{r}}_p\right)W_{pG}& (51)\end{array}$

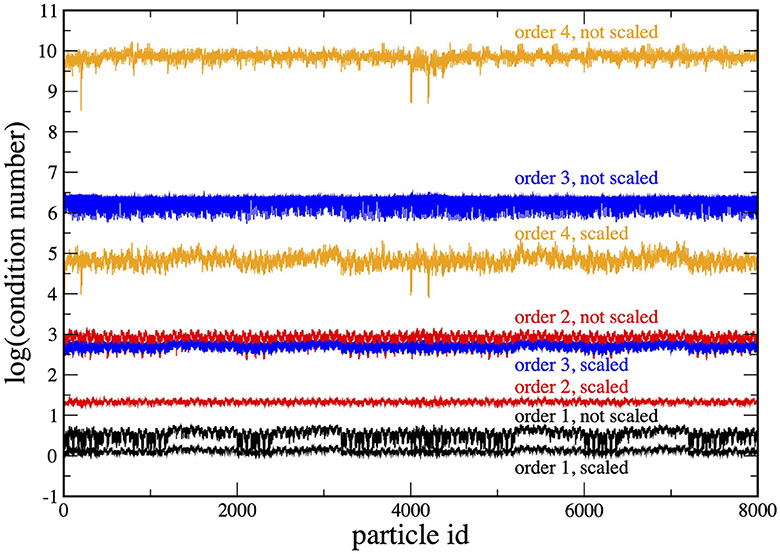
is a vector depending on the function values at the particles. Since the moment matrix does not depend on the function values themselves (only on the relative positions), it can be used for several function vectors (here one for each T_μν component). With increasing polynomial order, the condition number of the moment matrix $\mathcal{C}\equiv \Vert M{M}^{-1}\Vert$, a measure for how close a matrix is to being singular, can become very large; therefore, we use the singular value decomposition [78] to solve the system in Equation (49). The condition numbers, however, can be massively reduced by using remore details can be found-scaled basis functions which we illustrate in Appendix D and Figure A2. In practice, we use re-scaled basis functions.

The function value estimate at the grid point [see Equation (43)], $\tilde{f}({\overrightarrow{r}}^G)$ is the first component of β^G, the derivatives ${\partial }_x\tilde{f}({\overrightarrow{r}}^G),{\partial }_y\tilde{f}({\overrightarrow{r}}^G)$, ${\partial }_z\tilde{f}({\overrightarrow{r}}^G)$ are the components two to four, and so on. For the case, where we only allow the lowest polynomial order (i.e., a constant polynomial), the moment matrix has only one element

$\begin{array}{ll}M={\displaystyle \sum _p}{W}_{pG}\Rightarrow M^{-1}=\frac{1}{{\displaystyle {\sum }_p}{W}_{pG}},& (52)\end{array}$

and the function vector becomes

$\begin{array}{ll}B={\displaystyle \sum _p}{f}_p{W}_{pG}.& (53)\end{array}$

In this case the function value at the grid point is estimated as

$\begin{array}{ll}{\tilde{f}}^G=\frac{{\displaystyle {\sum }_p}{f}_p{W}_{pG}}{{\displaystyle {\sum }_p}{W}_{pG}}.& (54)\end{array}$

In other words, this is just the straightforward kernel-weighted average of the values at the contributing particles (with an exact partition of unity enforced). We show an example of the local regression estimate (LRE) function approximation in Appendix D.

2.4.2. An LRE-based MOOD approach

While in a well-sampled region, as for example the stellar interior, a high-order LRE approximation likely provides the most accurate function estimate, and this is not necessarily true near the stellar surface. There, due to the Gibbs phenomenon, spurious oscillations may occur. Therefore, we calculate T_μν estimates for different polynomial orders m, ${\tilde{T}}_{\mu \nu }^{\text{G},m}$, and then select the “optimal order” that best represents the particle values and is physically admissible. We use the following error measure:

$\begin{array}{l}{E}^{\text{G},m}\equiv {\displaystyle {\sum }_p}{W}_{pG}\left[{\displaystyle {\sum }_{\mu ,\nu }}{\left\{{\tilde{T}}_{\mu \nu }^{\text{G},m}\left({\overrightarrow{r}}_p\right)-T_{\mu \nu ,p}\right\}}^2\right]\\ ={\displaystyle {\sum }_p}{W}_{pG}\left[{\displaystyle {\sum }_{\mu ,\nu }}{\left\{\left({\overrightarrow{\beta }}_{\mu ,\nu }^{G,m}·P^G\left({\overrightarrow{r}}_p\right)\right)-T_{\mu \nu ,p}\right\}}^2\right].& (55)\end{array}$

In other words, based on the optimal coefficients at the grid point, we estimate the function values at each particle position that contributes and calculate the weighted quadratic deviation as error measure. This approach differs from our earlier one [39] by not using pre-defined kernel functions, but instead applying the LRE-approximation, and by considering all T_μν components in the error measure rather than just T₀₀ as before.

The most straightforward MOOD estimate would be to calculate estimates for different polynomial orders m and to select the solution with the smallest value of E^G,m. Unfortunately, this only works in nearly all cases. In very few cases, where a grid point lies outside the neutron star surface, but the finite-size SPH particles still contribute to this point, we found that the approximation with the smallest error may deliver values much larger than those at the contributing particles, or even unphysical values such as a negative T₀₀ (energy density). For these reasons, additional measures need to be taken near the stellar surface. However, the question to be answered is: how does an SPH particle know that it is near the surface?

2.4.3. Detecting not well-embedded grid points

Here, we use a simple, yet, as it turns out, very robust method to detect whether a grid point is well engulfed by particles or not. In a first step, at each particle position, we numerically calculate an estimate for an expression that has an analytically known result and where the deviation from the exact result can be used to identify surface particles. For this purpose, we chose $\nabla ·\overrightarrow{r}=3$ and the numerical estimate given by

$\begin{array}{ll}{\left(\nabla ·\overrightarrow{r}\right)}_a={\displaystyle \sum _b}\frac{{\nu }_b}{N_b}\left({\overrightarrow{r}}_b-{\overrightarrow{r}}_a\right)·{\nabla }_a{W}_{ab}\left(h_a\right).& (56)\end{array}$

This expression is one of the standard SPH discretizations (similar to the commonly used expression for $\nabla ·\overrightarrow{v}$, see Equation (31) in Rosswog [43]). To avoid another neighbor-loop over all particles, expression (56) can be conveniently calculated alongside the SPH derivatives. This means that the update of $\nabla ·\overrightarrow{r}$ is lagging behind by one-third of a time step. The property of being at the surface changes on a much longer time scale and only averages of the deviations are used, see below, so that using a value of $\nabla ·\overrightarrow{r}$ calculated a third of a time step earlier is well suited for our purposes. In deriving SPH expressions, surface terms are usually neglected, and therefore, the expression Equation (56) only yields an accurate approximation to the exact value of 3 if it is embedded from all sides with particles. If instead the expression is evaluated near a surface, contributing particles are missing on one side, and therefore, the numerical estimate is substantially smaller than the theoretical value. From the relative error

$\begin{array}{ll}{\delta }_a\equiv \frac{|{\left(\nabla ·\overrightarrow{r}\right)}_a-3|}{3}& (57)\end{array}$

we calculate the average deviation ${\langle \delta \rangle }_G=\left(\sum _{b=1}^n{\delta }_b\right)/n$ over the particles that contribute to the error measure Equation (55). If 〈δ〉_G is above a given threshold, the corresponding grid point is identified as being outside the particle surface. We show an example from the inspiral of two neutron stars in Figure 3. In the stellar interior, the values of 〈δ〉_G are ≈ 0.005, while those at the surface reach ~ 0.1. After some experimentation, we have chosen a threshold of 0.05 for 〈δ〉_G; for grid points at which 〈δ〉_G exceed this threshold, we only use the lowest order mapping, m = 0, see below. This approach robustly avoids all “outlier points” in the mapping, and the mapped values of T_μν accurately reflect the matter distribution.

FIGURE 3

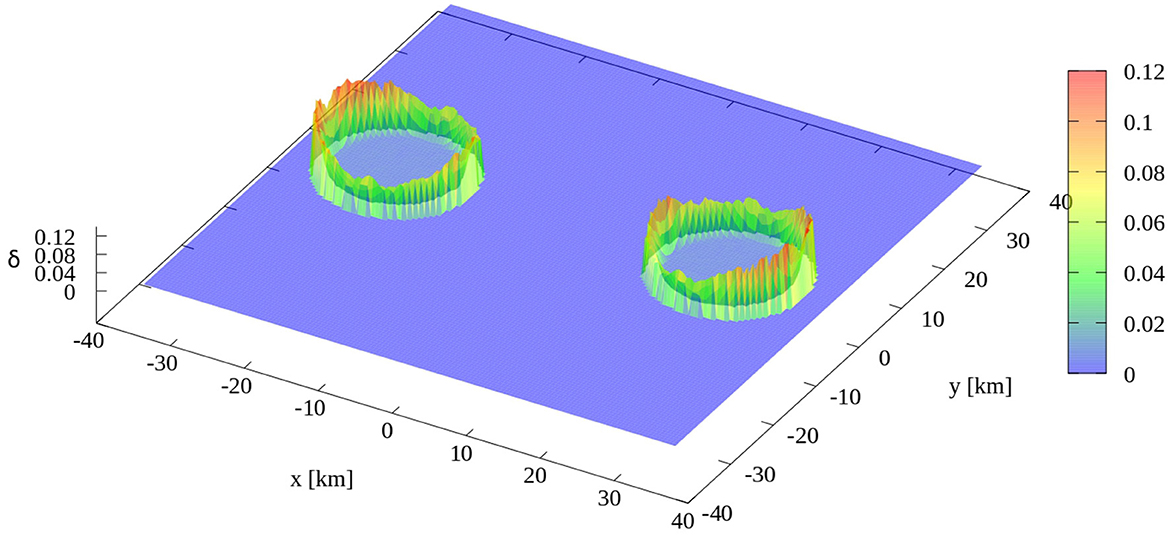
Figure 3. Average value of 〈δ〉_G for all the particles that contribute to the mapping of the stress–energy tensor at grid points in the xy-plane. For grid points inside the stars, the value is typically δ ≈ 0.005.

2.4.4. Summary of the particle-to-mesh mapping algorithm

The first step in the algorithm consists in identifying the particles that contribute to a given grid point G. This list of particles is identified via a hash-grid as described in detail in Section 2.1.3 of Diener et al. [34]. Subsequently, we perform the following steps:

• Calculate the LRE estimates ${\tilde{T}}_{\mu \nu }^{\text{G},m}$ for the polynomial orders m = 0, 1, 2, 3 using Equation (42).

• If 〈δ〉_G > 0.05, choose ${\tilde{T}}_{\mu \nu }^{\text{G},m=0}$ since this is a grid point outside the particle surface.

• If more than 40 particles (= twice the number of degrees of freedom for cubic polynomials) contribute and the error E^{G, 3} is smallest and ${\tilde{T}}_{00}^{\text{G},m=3}>0$, choose ${\tilde{T}}_{\mu \nu }^{\text{G},m=3}$.

• If more than 20 particles (= twice the number of degrees of freedom for quadratic polynomials) contribute and the error E^{G, 2} is smallest and ${\tilde{T}}_{00}^{\text{G},m=2}>0$, choose ${\tilde{T}}_{\mu \nu }^{\text{G},m=2}$.

• If more than 8 particles (= twice the number of degrees of freedom for linear polynomials) contribute and the error E^{G, 1} is smallest and ${\tilde{T}}_{00}^{\text{G},m=1}>0$, choose ${\tilde{T}}_{\mu \nu }^{\text{G},m=1}$.

• In all remaining cases choose the robust “parachute method,” that is, polynomial order 0 and ${\tilde{T}}_{\mu \nu }^{\text{G},m=0}$.

The additional conditions on the number of contributing particles have been introduced to avoid the inversion of poorly conditioned matrices. In Figure 4 we illustrate how well this procedure works. The top plot shows a cut of the density of particles at t = 2.95 ms for the case of an equal mass binary system with two 1.5 M_⊙ neutron stars with the APR3 equation of state. The bottom plot shows the resulting mapped tt-component of the stress energy tensor in the xy-plane of the grid. As can be seen, all the features, that are visible in the particle density profile, are clearly reproduced in the mapped stress-energy tensor.

FIGURE 4

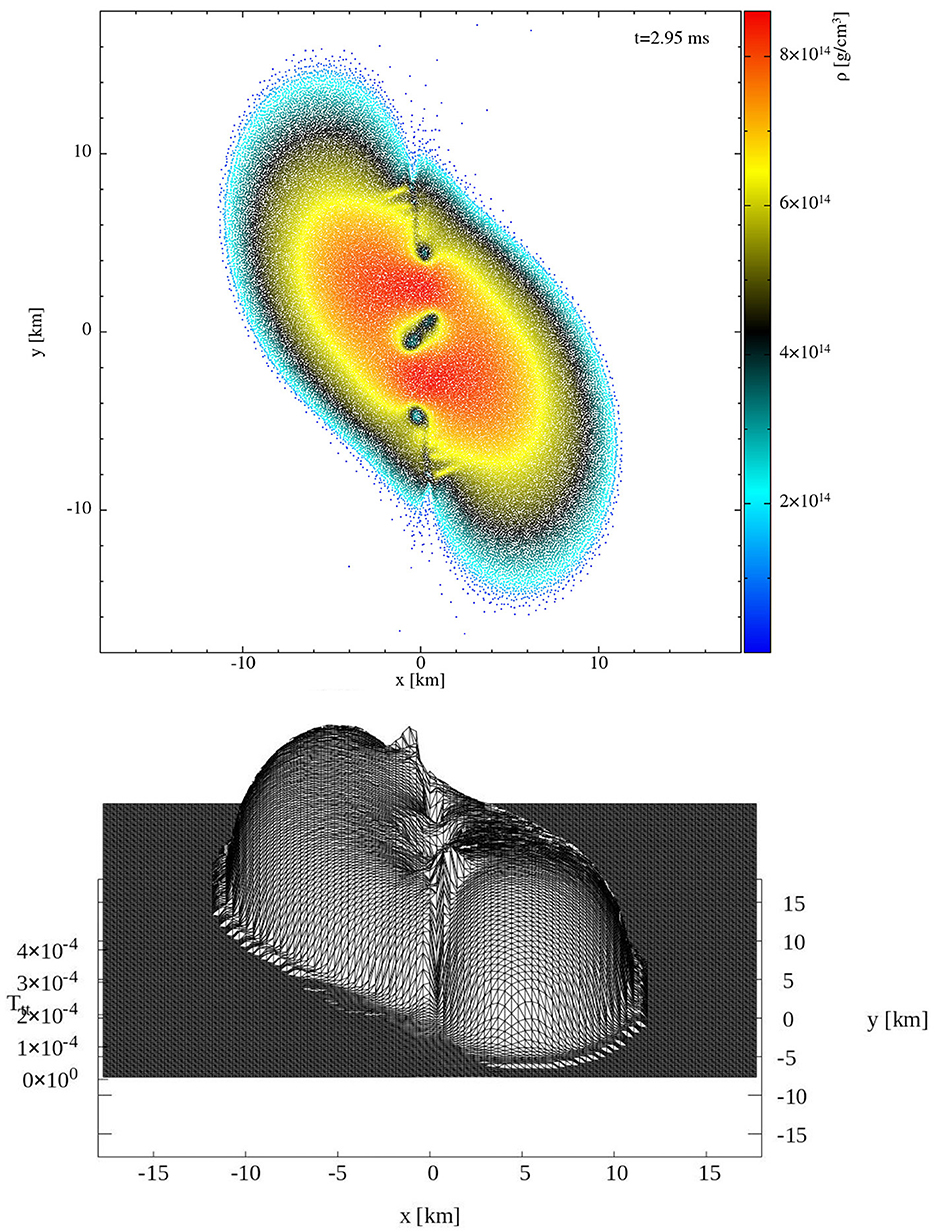
Figure 4. At the top, we show a cut of the density at t = 2.95 ms for the case of a equal mass binary system with 2 1.5 M_⊙ neutron stars with the APR3 equation of state. At the bottom, we show the corresponding mapping of the tt-component of the stress–energy tensor onto the grid.

2.5. Stably simulating the formation of black holes

The remnant of a binary NS merger can, depending on the EOS, the total mass and spin (and further processes which are not modeled here), undergo a collapse to a black hole (BH). This can happen either “promptly” on the dynamical timescale of the remnant (typically ~1 ms), or it can be “delayed” for several dynamical timescales, or for binaries at the low-mass end, it may not occur at all. If a BH does form, extra care is required in order to avoid numerical problems.

The first potential problem we noticed when we initially attempted to simulate a collapse was simply that at some point in time, the particles become packed so close together, that the grid resolution is insufficient to evolve the metric accurately enough to maintain a physically valid solution. This can result in failures in the recovery of the primitive variables.

To cure this problem, we allow for the addition of more refinement levels. After some experiments, we decided to use the ratio of the hydrodynamic and the BSSN time step as an indicator of when it is time to add another refinement level. As the particles move closer together, their Courant time step, Δt_SPH = ξ_SPH(h/c_s), decreases (here c_s is the speed of sound), whereas the Courant time step for the mesh, Δt_BSSN = ξ_G(Δx/c), stays constant. Note that we have omitted particle and grid labels for readability, and for clarity, we have written the expression using the speed of light c explicitly. Δx is the resolution on the finest grid. For the dimensionless pre-factors, our default values are ξ_SPH = 0.2 and ξ_G = 0.35. Whenever the ratio of the two time steps grows beyond a threshold,

$\begin{array}{ll}\frac{\Delta t_{\text{BSSN}}}{\Delta t_{\text{SPH}}}>C_{\text{refine}}& (58)\end{array}$

we add a refinement level. In numerical experiments, we found that C_refine = 2.5 works well.

Our current mesh refinement hierarchy is very simple: our finer grids are always half the size of the next coarser grid, and they are centered at the origin. We follow this strategy also when we create a new refinement level: the new level has the same number of points and half the size of the previously finest grid, and it is again centered at the origin. The data on the new grid are calculated from the data on the previously finest grid using the same interpolation operators that we use in the prolongation operators to fill the ghost cells of the refinement levels, i.e., via cubic Lagrange interpolation.

After adding a new refinement level, Δt_BSSN is half its previous value and the time step ratio will again be less than C_refine. As the collapse proceeds, Δt_SPH will continue to decrease and may eventually trigger the addition of another refinement level. This can in principle continue indefinitely but would eventually slow the simulation to a halt due to very small time steps. Therefore, at some point in time, we start to remove particles in the innermost, collapsing core.

The best criterion would of course be to remove particles when they are deep enough inside the forming black hole. Since we have not yet implemented an apparent horizon finder, we do not know precisely when and where the black hole forms at run time. Instead, we rely on the value of the lapse, α, at the location of the particles as a proxy. With the slicing and shift conditions used in the code, it is observed that the value of α at the horizon of a single static black hole, evolved to numerical stationarity, is ~0.3, see e.g., Figures 14 and 16 in Rosswog and Diener [33]. The value of α at the actual horizon during the dynamical phase of the collapse will of course vary slightly but will not differ too much from the value of 0.3. Thus, we remove particles when they enter regions that have a substantially lower lapse than this threshold value.

Based on the turduckening idea of Brown et a. [79], we should be able to safely change the interior of a black hole as long as it is done sufficiently deep inside. In particular, removing the source (the particles) of the stress energy tensor should not affect how the continuing collapse is seen from the outside. To be safe, we want to wait as long as possible before starting to remove particles, but as the particles pile up inside the black hole the Courant time step decreases dramatically, potentially making the collapse process very computationally expensive. However, we are saved by the observation that particles are essentially in free fall when they are that deep inside a black hole. Hence, the energy momentum tensor is completely dominated by the rest mass and velocity with the pressure and internal energy only providing negligible small corrections. Therefore, we can convert particles into “dust” by setting their pressure and internal energy to zero once the lapse at their position is less than α_dust = 0.05.

The dust particles will no longer affect the evolution of their neighbors and will no longer contribute to Δt_SPH. They will simply evolve along geodesics until the lapse at their positions falls below α_cut = 0.02 at which point we simply remove them completely from the simulation. With this two-stage process, converting particles first to dust and then later removing them, we manage to have the particles contribute to the stress energy tensor for significantly longer without adversely affecting the time step. We found that removing particles as soon as the lapse dropped below α = 0.05 could lead to a delay in the collapse of the lapse in the center of the black hole.

Post-processing our data using the apparent horizon finder from the Einstein Toolkit [71] showed that this delay in the lapse did not significantly affect the horizon properties, but we still prefer to avoid it.

It turns out that even with extra refinement levels, once we start converting particles to dust and later removing particles, it is still possible to eventually get failures in the recovery of primitive variables. However, this only happens when the particles are essentially in free fall and the solution is to convert them to dust before they reach α_dust. This is only necessary in very few cases, if at all.

Once particles have been converted to dust, we still have to recover the primitive variables from the evolved variables, but this is very simple. The relations between the evolved and primitive variables, Equations (4), (6) and (11), for a dust particle with vanishing u and P reduce to (omitting for simplicity the particle label)

$\begin{array}{ll}N=\sqrt{-g}\Theta n,& (59)\end{array}$

$\begin{array}{ll}{S}_i=\Theta v_i,& (60)\end{array}$

$\begin{array}{ll}e=\Theta v_i{v}^i+\frac{1}{\Theta }.& (61)\end{array}$

That is, S_i reduces to the spatial part of the covariant 4-velocity, U_μ. Therefore, we can find U₀ so that the 4-velocity is properly normalized, $U_{\mu }{U}^{\mu }=-1$. Raising the index on the covariant 4-velocity, we can simply read off Θ = U⁰ and then find n. In case a fluid particle is transformed to dust, we also adjust e so that it is consistent with the values of vⁱ and Θ. In summary, the recovery of primitive from evolved variables is always possible for dust particles in a straightforward way, and the particles can keep evolving, contributing to the stress–energy tensor but do not affect any of their neighbor particles in any negative way until they can be safely removed once their lapse value has dropped below the removal threshold.

3. Improvements to the initial data setup

In this section, we describe recent improvements in setting up the SPH particles in the initial data (ID) code SPHINCS_ID [41]. It can now also be linked to our fork of FUKA [80, 81]—extended to comply with our needs—to produce BSSN and SPH ID for neutron star binaries. The FUKA codes are built on an extended version of the KADATH library [82]. In this section, we refer generically to LORENE [35–37] and FUKA with the term “ID solver” when the discussion applies to both solvers.

3.1. Modeling neutron stars with the artificial pressure method

As described in Diener et al. [34, Sec. 2.2.2], the initial neutron stars are modeled by placing the SPH particles according to the “artificial pressure method” (APM) which uses the solutions found by the ID solver. We briefly summarize the original method below, and refer the reader to Rosswog [38], Rosswog and Diener [33], and Diener et al. [34, Sec. 2.2.2] for more details, before we describe an additional improvement.

First, particles are placed according to a freely specified geometry (lattice, spherical surfaces, etc.), and then each particle a is assigned the same baryon number ν₀ = ν_tot/N_part, where ν_tot is the total baryon number for the star and N_part is the number of SPH particles used to model it. Subsequently an “artificial pressure” is defined as

$\begin{array}{ll}{\pi }_a=\text{max}\left(1+\frac{N_a-N_{\text{ID}}\left({\overrightarrow{r}}_a\right)}{N_{\text{ID}}\left({\overrightarrow{r}}_a\right)},0.1\right).& (62)\end{array}$

Here, N_a is the SPH estimate of the density variable defined in Equation (4) on particle a and $N_{\text{ID}}\left({\overrightarrow{r}}_a\right)$ is the result from the ID solver. The lower bound of 0.1 is imposed to avoid negative values. The major goal of the original APM is to minimize the difference between N_a and $N_{\text{ID}}\left({\overrightarrow{r}}_a\right)$ while using SPH particles of the same baryon number². Therefore, at each iteration of the APM, the particle positions are updated in order to achieve vanishing (artificial) pressure gradients. The corresponding position update reads:

$\begin{array}{ll}{\delta {\overrightarrow{r}}_a}^{\text{APM}}=-\frac{1}{2}{h}_a^2{\nu }_a{\displaystyle \sum _b}\frac{{\pi }_a+{\pi }_b}{N_b}{\nabla }_a{W}_{ab}\left(h_a\right),& (63)\end{array}$

see Section 2.1 for the meaning of the involved quantities. The iteration stops when the differences between N_a and $N_{\text{ID}}\left({\overrightarrow{r}}_a\right)$ do not change significantly anymore³.

While we want to construct initial conditions with densities N_a as close as possible to $N_{\text{ID}}\left({\overrightarrow{r}}_a\right)$, it is in the end the (physical) pressure gradients that, apart from gravity, drive the physical fluid motion. Therefore, it may be advantageous to construct the artificial pressure, π_a, from the physical pressures rather than the densities as in Equation (62), For a short motivation as to why to use the pressure, we will briefly switch to a Newtonian description (the GR case with our conventions follows in a straight-forward way) and we define, for a general EOS, the quantity

$\begin{array}{ll}\bar{\gamma }\equiv {\left(\frac{\partial P}{\partial \rho }\right)}_s\frac{\rho }{P},& (64)\end{array}$

which, for the special case of a polytropic EOS, simply reduces to the polytropic exponent γ. If we assume that we have found a numerical solution for the density, that is ρ = ρ₀ + δρ, where ρ₀ is the true solution, the resulting pressure is

$\begin{array}{ll}P\left({\rho }_0+\delta \rho \right)\approx P\left({\rho }_0\right)+{\left(\frac{\partial P}{\partial \rho }\right)}_s\delta \rho .& (65)\end{array}$

With P₀ = P(ρ₀), the relative error ϵ_P in the pressure reads

$\begin{array}{ll}{ϵ}_P=\frac{P\left({\rho }_0+\delta \rho \right)-P_0}{P_0}=\frac{{\left(\partial P/\partial \rho \right)}_s\delta \rho }{P_0}=\bar{\gamma }\frac{\delta \rho }{\rho }=\bar{\gamma }{ϵ}_{\rho }.& (66)\end{array}$

Neutron star equations of state can be approximated by piecewise polytropes [40], which even at the lowest density piece (as is the case for all other equations of state that we are aware of) have a polytropic exponent value of γ > 1.3. The higher density pieces have substantially larger values, often larger than 3. Thus, we expect that for all physically relevant EOSs (not just polytropes), the relative error in P will be larger than in ρ. This motivates us to change the definition of the artificial pressure from Equation (62) to

$\begin{array}{ll}{\pi }_a=\text{max}\left(1+\frac{p\left({\rho }_a\right)-p\left({\rho }_{\text{ID}}\left({\overrightarrow{r}}_a\right)\right)}{p\left({\rho }_{\text{ID}}\left({\overrightarrow{r}}_a\right)\right)},0.1\right),& (67)\end{array}$

so the APM iteration minimizes the error on the pressure directly. In Figure 5, we see a comparison between the errors on the pressure when using the definitions (62) and (67). With definitions (67), the errors decrease in the inner 93% of stellar radius but do not improve significantly in the outermost layers. This is the case because at finite numerical resolution, the extremely steep (physical) gradients in the stellar surface cannot be resolved. However, these outer layers only constitute a very small fraction of the baryonic mass of the star, ~0.01% for the star in Figure 5, and are therefore not a matter of concern here.

FIGURE 5

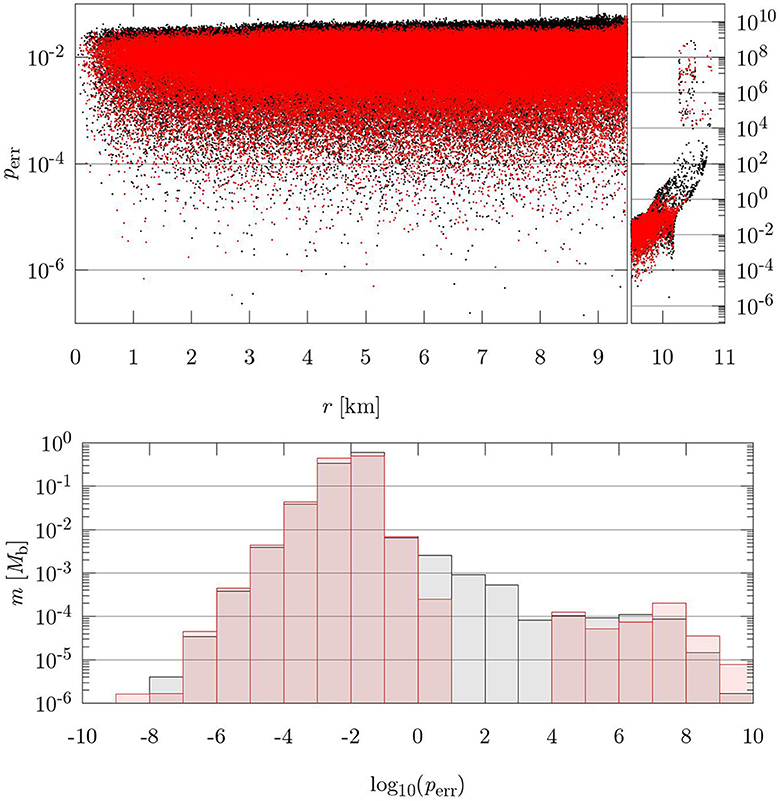
Figure 5. Relative errors on the pressure $p_{\text{err}}≔|p\left({\rho }_a\right)-p\left({\rho }_{\text{ID}}\left({\overrightarrow{r}}_a\right)\right)|/p\left({\rho }_{\text{ID}}\left({\overrightarrow{r}}_a\right)\right)$ at the end of an APM iteration that uses definition (62) (black) and another APM iteration that uses definition (67) (red). The errors are evaluated on 2.5 × 10⁶ particles modeling the same neutron star, which belongs to a 1.9M_⊙ equal-mass, 47.5 km separation, MS1b, irrotational BNS produced with LORENE. (Top) p_err(r), with r radial coordinate of each particle measured from the barycenter of the star. The left panel shows the data for r ∈ [0, 9.5] km; the right panel for r ∈ [9.5, 11] km. (Bottom) p_err binned in log scale; each bin is one order of magnitude wide. m is the sum of the baryonic masses of the particles in each bin, in units of the baryonic mass of the star M_b = 2.016M_⊙. Except for the outermost particles with r ≳ 10 km ≃ 93%R (R being the larger radius of the star), whose errors do not decrease, the errors for the particles in the bulk of the star decrease using definition (67). For example, ~10% of the baryonic mass of the star improves the error by roughly one order of magnitude, moving from bin [10⁻², 10⁻¹] to bin [10⁻³, 10⁻²].

In summary, the errors do not reduce very significantly, but the change in the definition of the artificial pressure is nevertheless a welcome enhancement that complements the other improvements to SPHINCS_ID and SPHINCS_BSSN_v1.0. The SPHINCS_ID code lets the user choose which definition to use, (62) or (67). The ID used for the runs described in this study were produced using (67).

3.2. The initial particle distribution on surface-conforming ovals

Until recently, we have prepared the initial condition for the APM on each star by placing particles on spherical surfaces with radii in the interval (0, R), with R being the larger radius of the star, see Diener et al. [34, Sec. 2.2.2]. This algorithm places close-to-equal-mass particles on each spherical surface, taking into account the mass of the spherical shell bounded by a spherical surface and the next. Therefore, some information on the density profile of the star is considered already at the level of the initial condition for the APM iteration. We have improved our algorithm by placing the initial particles on ovals that conform to the (scaled) surface of the star; otherwise, we follow the same steps as described in Diener et al. [34, Appendix B.1], more details can be found in Appendix A. A comparison between particle distributions, produced using ovals and ellipsoids, is shown in Figure 6 for a star whose geometry deviates significantly from spherical. The placement of particles on ovals improves the accuracy of the particle model of the outer layers of the star. This is because the APM starts with initial conditions having a smoother particle distribution on the outer layers compared to the distributions obtained using spheres or ellipsoids. The latter include cuts on the outer layers when the spheres or ellipsoids cut through the surface of the star. This improvement is even more important for rotationally flattened stars.

FIGURE 6

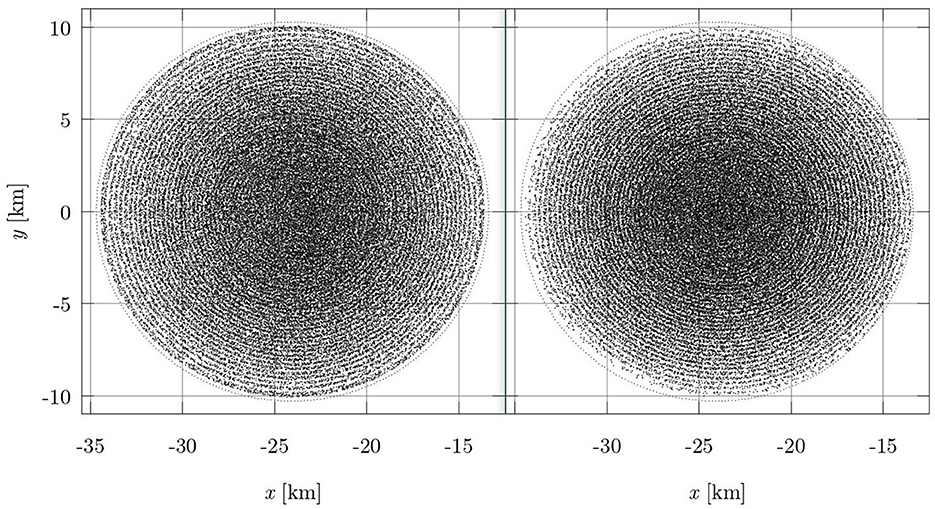
Figure 6. Cuts along the xy plane, with |z| < ~0.89 km, of particle distributions with 10⁶ particles modeling the same star. The left panel shows particles placed on surface-conforming ovals; the right panel shows particles placed on ellipsoids. In both cases, a small random displacement is applied, since it leads to a better initial condition for the APM iteration, as already noted in Diener et al. [34]. The star belongs to a 1.9 M_⊙ equal-mass, 47.5 km separation, MS1b, irrotational BNS produced with LORENE. The blue points have |z| < ~0.16 km and trace the surface of the star (for more details, see Appendix A). The particles placed on surface-conforming ovals model very accurately the shape of the star and produce a smooth surface, thus providing a more accurate initial condition for the APM.

3.3. The boundary particles used during the APM

The APM iteration uses “ghost” or “boundary” particles outside the star that prevent the particles modeling the star from being pushed outside the stellar surface, see Diener et al. [34, Sec. 2.2.2] and [34, Appendix B.2]. At each step of the iteration, the boundary particles are assigned an artificial pressure that increases linearly with their distance from the center of the star. The boundary particles closest to the star are assigned an artificial pressure equal to 3π_max, those farthest away with a value of 30π_max and for those in between, the artificial pressure varies linearly between these bounds, where π_max be the maximum artificial pressure of the real particles. For these bounds, we empirically found the best APM results. This artificial pressure gradient makes the real particles feel a stronger repulsive force, the closer they approach the stellar surface. Previously [34], we placed the boundary particles on a lattice, between two ellipsoidal surfaces, and now, we place them on a lattice between two surface-conforming ovals instead. This, analogously to the initial placement of real particles on surface-conforming ovals described in Section 3.2, makes it easier for the APM iteration to model the outer layers and the overall geometry of the star.

In Diener et al. [34, Appendix B.2], the parameter δ was introduced, which is the distance between the surface of the star and the boundary particle closest to it, along the direction of the star's largest radius. The modeling of the outer layers turns out to somewhat depend on the value of δ, and it would be desirable to remove this dependence. If δ is too small, the real particles cannot approach the surface of the star; if δ is too large, the particle distribution on the outer layers can become non-smooth, leaving a few isolated particles outside the otherwise smooth stellar surface. In order to reduce the dependence on δ, we set a small value of δ initially, and then let the boundary particles move outwards (effectively increasing δ) very slowly until the condition |r_av − R| < h_av/3 is met, where r_av and h_av are the average values of radius and smoothing lengths of the particles in the outer layers and R is the largest radius of the star. The particles modeling the outer layers are defined as those having a radial coordinate (measured from the center of the star) larger than 99.5% of R. In case, these should be <10 particles, this fraction is reduced in steps of 0.5% until this number is exceeded. This algorithm starts out producing a smooth particle distribution on the outer layers since δ is initially small and preserves the smoothness when it gently allows the real particles to move toward the surface. In addition, it reduces the dependence on the initial value of δ since the latter is increased during the iteration.

A comparison between a particle distribution obtained using the latest methods described in this section and in Section 3.2, and a particle distribution obtained with older methods, is shown in Figure 7. Note how the model of the geometry of the star and its outer layers have improved with the new methods.

FIGURE 7

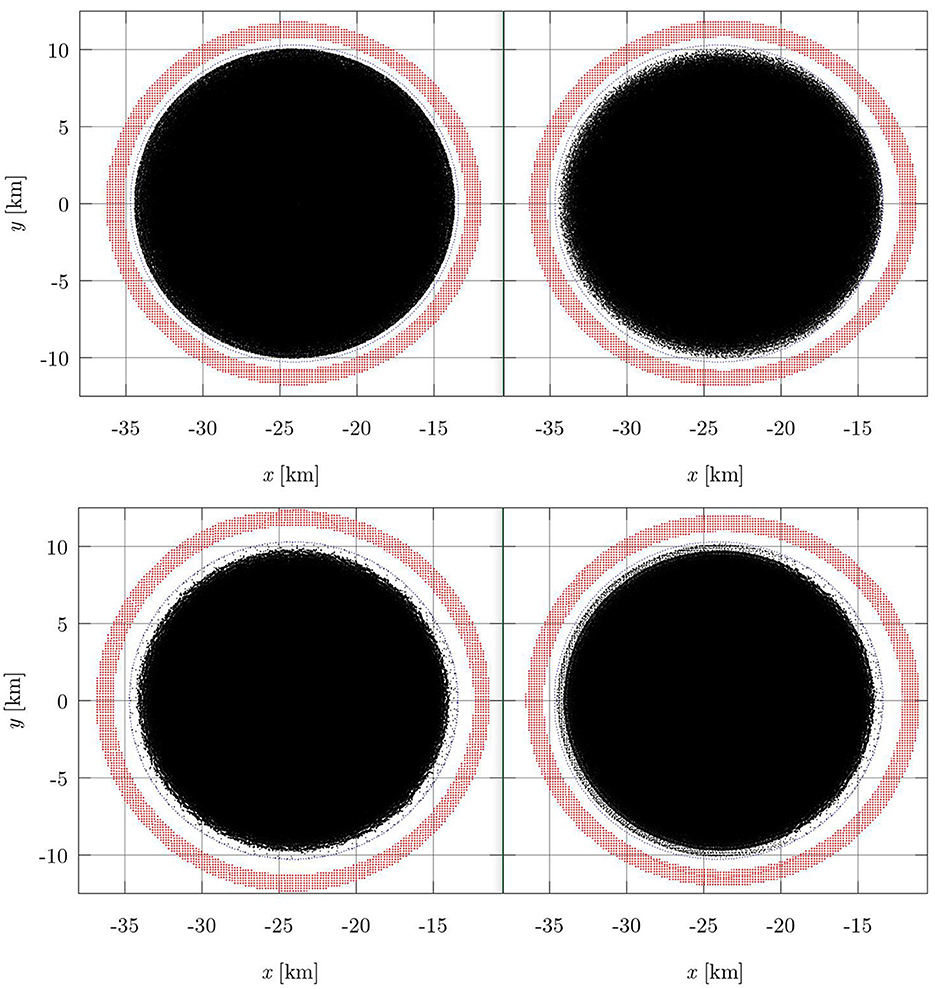
Figure 7. Projections of particle distributions with 2.5 × 10⁶ particles modeling the same neutron star. Real particles are in black, boundary particles with |z| < ~0.74 km are in red, and the points lying on the surface of the star with |z| < ~0.16 km are in blue. The star belongs to a 1.9M_⊙ equal-mass, 47.5 km separation, MS1b, irrotational BNS produced with LORENE. (Top-left) The real and boundary particles are placed on surface-conforming ovals, see Section 3.2 and Section 3.3. (Top-right) The real and boundary particles are placed on ellipsoids. (Bottom-left) Particles placed with our latest APM algorithm, with the particles in the top-left panel as the initial condition. (Bottom-right) Particles placed with our older APM algorithm, with the particles in the top-right panel as the initial condition. See main text for details. The particles in the bottom-left panel better model the outer layers and the geometry of the star compared to those in the bottom-right panel.

3.4. The ADM linear momentum for the initial data

When considering ID produced with LORENE and FUKA, we can simplify the SPH estimate of the ADM momentum of the fluid, Equation (17). The ID solvers assume asymptotic flatness, conformal flatness, and maximal slicing on the initial spacelike hypersurface [36, 80]. In coorbiting coordinates of Cartesian type, the conformal flatness condition can be written as Gourgoulhon et al. [36, Sec. IV.A], Papenfort et al. [80, Equation (6)]:

$\begin{array}{ll}{\gamma }_{ij}=A^2{\delta }_{ij},& (68)\end{array}$

with A being the conformal factor and δ_ij = diag(1, 1, 1) the Euclidean metric. Hence, a global, orthogonal, non-orthonormal frame $e_{\left(j\right)}^i$ = δⁱ_j exists on the initial spacelike hypersurface. This frame also becomes orthonormal, hence Cartesian, at spatial infinity where A → 1 due to the asymptotic flatness condition. Therefore, we can set ${\xi }^i=e_{\left(j\right)}^i$ in Equation (16) to compute the j^th Cartesian component of the ADM linear momentum. Doing so, and imposing the maximal slicing condition, the part of the ADM linear momentum determined by the spacetime—i.e., the second term in the squared parenthesis in Equation (16)—is zero. We show this explicitly in Appendix C.

Hence, for the ID, the total ADM linear momentum is equal to the ADM momentum of the fluid, which can be estimated with (17) for the LORENE and FUKA ID. In addition, we can compare this estimate with the one obtained using (15). It is possible to compute the linear ADM momentum within LORENE as a surface integral at infinity⁴. LORENE can easily handle this computation thanks to its compactified coordinates. FUKA also provides an estimate of the ADM momentum. Hence, for each ID, we have two independent estimates of the ADM linear momentum: one computed by the ID solver as a surface integral using (15), and the other computed by SPHINCS_ID as an SPH estimate of a volume integral using (17). For the irrotational, equal-mass 1.3M_⊙ LORENE ID with 2 million SPH particles, see Section (4.1), the two estimates are as follows:

$\begin{array}{ll}\text{ LORENE}:P_i^{\text{ADM}}\simeq (<10^{-15},6.336\times 10^{-11},<10^{-15}),& (69\text{a})\end{array}$

$\begin{array}{ll}\text{SPHINCS\_ID}:P_i^{\text{ADM}}\simeq (-1.393\times 10^{-7},6.318\times 10^{-11},<10^{-15}).& (69\text{b})\end{array}$

Only the x component is affected by a substantial error after the particles are placed, but it stays very small nonetheless. We obtain similar results for the other equal-mass, non-spinning systems we consider in Section 4.2. For the equal-mass 1.3M_⊙FUKA ID used in the simulation described in Section 4.3, where one star is spinning with χ ≃ 0.5, the estimates are as follows:

$\begin{array}{ll}\text{ FUKA}:P_i^{\text{ADM}}\simeq (-2.804\times 10^{-13},1.683\times 10^{-10},<10^{-15}),& (70\text{a})\end{array}$

$\begin{array}{ll}\text{SPHINCS\_ID}:P_i^{\text{ADM}}\simeq (6.030\times 10^{-6},2.809\times 10^{-4},<10^{-15}).& (70\text{b})\end{array}$

It makes sense that the SPH estimate is much better for the non-spinning systems since the particles modeling the second star are placed mirroring those modeling the first star, with respect to the yz plane [34, Sec. 2.2]. Triggered by questions from the referee, we realized that it would be even better to reflect the particle positions of star one through the origin to set up star two. In this case, particles would be placed with complete symmetry for all components of the coordinates (including x) and the helical symmetry present in the initial data would guarantee that the velocity of a particle in star two is exactly opposite the corresponding particle in star one. There would then be exact cancelation (to roundoff error) of their contribution to the momentum, allowing us to reduce the small initial value for the x-component of the ADM momentum for irrotational, equal mass systems. This procedure will be used in future particle setups. In the system with a spinning star, however, neither mirror nor reflection symmetry can be enforced, and the terms in the sum (17) do not compensate to the same degree.

4. Numerical results for neutron star mergers

Here, we show astrophysical examples of neutron star mergers with SPHINCS_BSSN_v1.0. Standard hydrodynamics tests such as shock tube tests are not impacted by any of the new elements introduced here; therefore, we refer the interested reader to our previous studies [33, 39]. In Section 4.1, we show a binary neutron star merger where a remnant survives (for at least several dynamical time scales), Section 4.2 shows an example where the merger remnant promptly collapses to form a black hole, and Section 4.3 shows results for a binary system where only one of the neutron stars has a large spin, whereas the other has none. All systems are of equal mass, the simulations start from an initial separation of 45 km and are performed with slightly more than 2 million SPH particles (except for the case where collapse to a black hole happens promptly; here 1 million SPH particles are used), the APR3 EOS, initially seven mesh refinement levels out to ≈2268 km in each coordinate direction and a minimum initial grid spacing of Δx = 369 m. Keep in mind that new refinement levels are added dynamically when the criterion described in Section 2.5 is met. In the run presented in Section 4.2, where there is a collapse to a black hole, the number of refinement levels dynamically increases up to 11.

4.1. Neutron star merger with surviving remnant

We show here the merger of two 1.3 M_⊙ neutron stars, with initial conditions produced by LORENE. After a few orbits of inspiral, the stars merge and remain initially close to perfect symmetry, see panel 1 in Figure 8. The strong shear at the interface between the stars is Kelvin–Helmholtz unstable and as matter from this region is sprayed out, deviations from perfect symmetries emerge (panel 2), as also frequently seen in Eulerian neutron star merger simulations. A few milliseconds later, the remnant settles into what seems a stationary state with a bar-like central object shedding mass via a spiral-wave into the surrounding torus. This spiral wave ejection channel might have played an important role in the early blue kilonova signal after the first observed neutron star merger GW170817 [84], see [85] for a review.

FIGURE 8

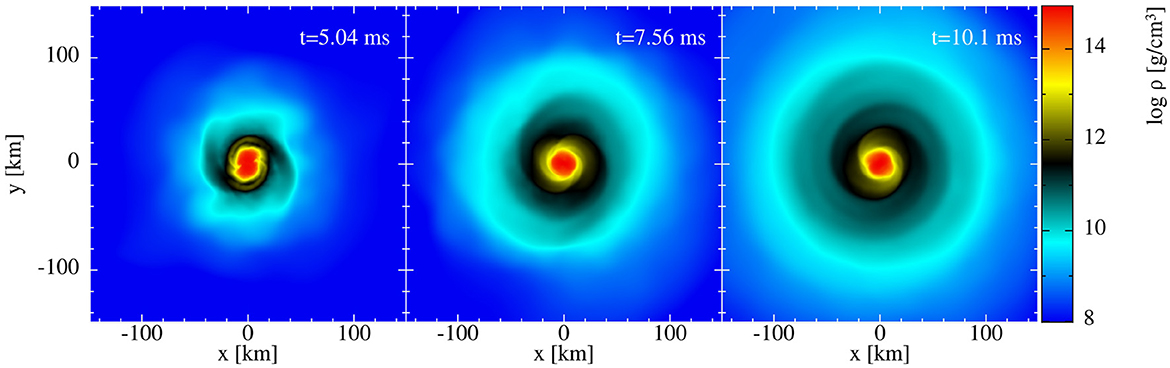
Figure 8. Density distribution in the orbital plane of an irrotational binary system with 2 × 1.3 M_⊙ with the APR3 EOS.

In the left panel of Figure 9, we show the evolution of the maximum density (red curve, right axis) together with the minimum lapse function value (black curve, left axis). In an initial very deep compression, the density reaches a value close to 9.4 × 10¹⁴ g cm⁻³, then the remnant bounces back and, after several more oscillations, the peak density settles near a value of 9.5 × 10¹⁴ g cm⁻³. As expected, the lapse is the lowest, where the density is the highest and vice versa. The right panel shows the value of the maximum GW amplitude times the distance to the observer as calculated via the quadrupole approximation (orange) and as extracted from the spacetime via the Weyl scalar ψ₄ (black), and how these are calculated in detail can be found in Appendix A of Diener et al. [34]. All Ψ₄-based GW waveforms were analyzed using kuibit [86]. Again, we find a rather good agreement of the quadrupole result with the more sophisticated ψ₄ method. The radiated energy (red curve, left axis) and angular momentum (black curve, right axis) are plotted as a percentage of the initial ADM values in the left panel of Figure 16. More than 2% of the initial ADM mass and more than 20% of the initial ADM angular momentum are radiated.

FIGURE 9

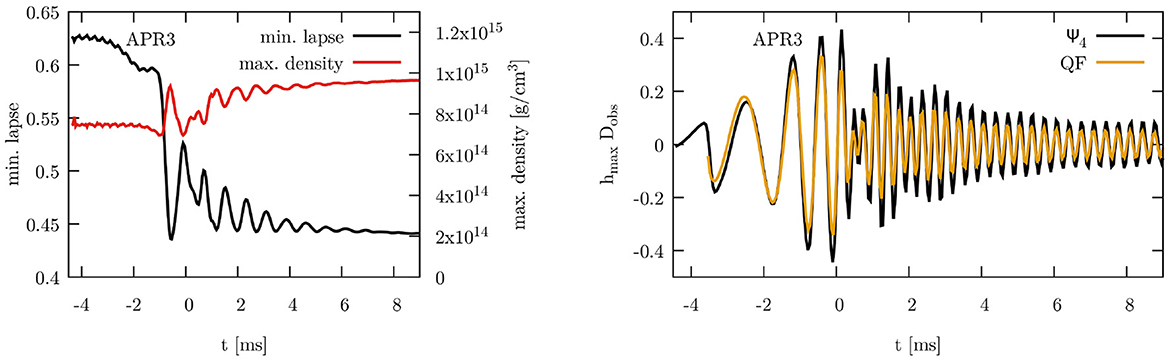
Figure 9. (Left) Maximum mass density (red curve, right axis) together with the minimum value of the lapse function α (black curve, left axis). (Right) Maximum gravitational wave amplitude extracted via the Weyl scalar Ψ₄ (black curve) and the quadrupole formula (yellow curve). Both panels refer to the simulation of an irrotational 2 × 1.3 M_⊙ neutron star binary shown in Figure 8. For convenience with comparison with other plots, t = 0 correspond to the time of the maximum amplitude in the gravitational waveform.

4.2. Neutron star merger with black hole formation

We also show the merger of two 1.5 M_⊙ neutron stars, with initial conditions produced by LORENE. Only 1 million particles are used here (runs with higher resolution become very slow due to the timestep requirements) with a corresponding initial grid spacing of Δx = 499 m. In this case, the merged object is massive enough that it undergoes a prompt collapse. During the collapse additional grid, refinement levels are added when needed, and at the end, we have a total of 11 refinement levels with a finest grid resolution of Δx = 32 m.

In Figure 10, we show three snapshots of the equatorial density. The first, at t = 3.28 ms, is from well before particles start to be removed and the density is still increasing. At t = 4.29 ms, ~90% of the particles have already been removed, but the maximum density of the remaining particles is still close to the initial central density of the stars. At 5.29 ms, matter has been drained down to 4 × 10⁻³ M_⊙. Only ~6 × 10⁻⁴ M_⊙ of this material is unbound from the black hole.

FIGURE 10

Figure 10. Density distribution in the orbital plane of an irrotational binary system with 2 × 1.5 M_⊙ with the APR3 EOS.

In the left panel of Figure 11, we show the evolution of the maximal density (red curve, right axis) and the minimum lapse (black curve, left axis). In this plot, particles that have been converted to dust do not count toward the maximum density and minimum lapse. The rapid drop in the maximum density is completely due to the conversion of particles to dust and their eventual removal at lapse values is below 0.02.

FIGURE 11

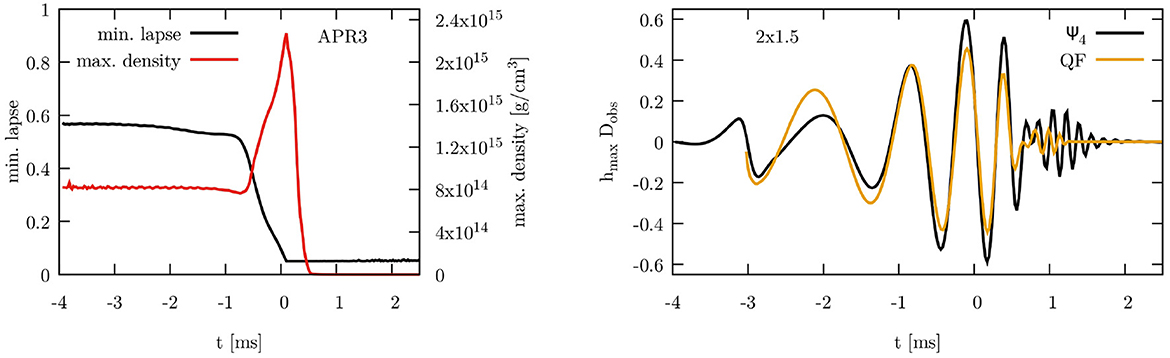
Figure 11. (Left) Maximum mass density (red curve, right axis) together with the minimum value of the lapse function α (black curve, left axis). (Right) Maximum gravitational wave amplitude extracted via the Weyl scalar Ψ₄ (black curve) and the quadrupole formula (yellow curve). Both panels refer to the simulation of an irrotational 2 × 1.5 M_⊙ neutron star binary. For convenience with comparison with other plots, t = 0 correspond to the time of the maximum amplitude in the gravitational waveform.

In the right panel of Figure 11, we show a comparison between the maximum GW amplitude times at the distance to the observer as extracted from the quadrupole formula and from Ψ₄. As expected, the quadrupole waveform shuts off too early as it is sourced by the matter motion and does not know about the quasinormal ringdown of the spacetime itself. In this simulation, ~3.8 × 10⁻² M_⊙ of energy and 1.18 M_⊙² of angular momentum is radiated away by GWs. By analyzing the properties of the final horizon using the tools from the Einstein Toolkit[87], we find that the black hole that formed has a dimensionless spin parameter of a/M ≈ 0.8, consistent with earlier findings that binary neutron star mergers leads to faster spinning black holes than binary black hole mergers (see e.g.,[88]). These last numbers should be taken by a grain of salt as the finite resolution may still have an impact. A more detailed analysis is left for future study.

4.3. Neutron star merger with a single spinning star

Most commonly, irrotational binary systems are studied, and they are considered as most realistic since dissipative effects cannot spin up neutron stars to substantial spin values [89, 90] and, at merger, any residual stellar spin is likely small compared to the huge orbital angular momentum. Nature, however, likely can produce neutron star binary systems in several ways [91] and, likely at smaller rates, more extreme systems may be produced. As one such example, we study here a binary system where only one of the two neutron stars is rapidly spinning, while the other is irrotational. Such systems have hardly been explored before, we are only aware of one such study by Papenfort et al. [92], where authors study extreme mass ratio and spin spin configurations.

We evolve a binary system with 2 × 1.3 M_⊙ stars, where one of the stars is spinning. The chosen value of the spin parameter, χ = 0.5, corresponds to a spin period of 1.2 ms. Since LORENE cannot construct such a case, we use the FUKA library instead. As can be seen from Figure 12, this initial data produces a matter distribution that is substantially different from the case shown in Section 4.1. During merger, a massive tidal tail forms and our evolution here is, qualitatively, similar to panel 1 in figure 1 of Papenfort et al. [92]. (Note however that their system has a different spin value, a different EOS, and a different mass.) In panels two and three of Figure 12, one sees how the rapidly spinning central remnant is punching shock waves into the remnant. This strong shock compression in the torus drives polar outflows at ~40° from the polar axis, see the volume rendering in the left panel of Figure 13, with velocities up to ~0.4 c (right panel same figure). The density compression at merger is much milder, see left panel of Figure 14, and the post-merger gravitational wave amplitudes (right panel) are substantially lower than in the non-spinning case. This effect is also reflected in the Fourier power spectra shown in Figure 15. Here, the non-spinning case (with higher power) is shown in blue and the spinning case in orange. It can also be seen that the frequency of the main peak after merger shifts to lower frequency in the spinning case compared to the non-spinning case, consistent with the less compact remnant.

FIGURE 12

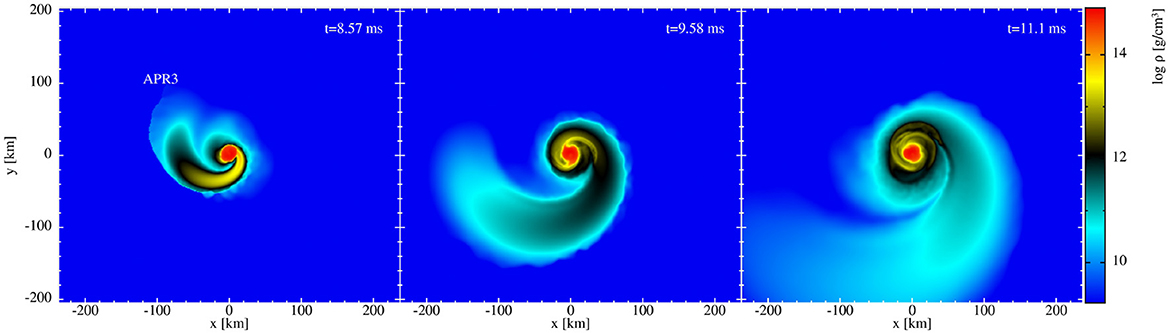
Figure 12. Density distribution in the orbital plane of a 2 × 1.3 M_⊙ binary with the APR3 EOS. One of the stars no spin, while the other has χ ≃ 0.5.

FIGURE 13

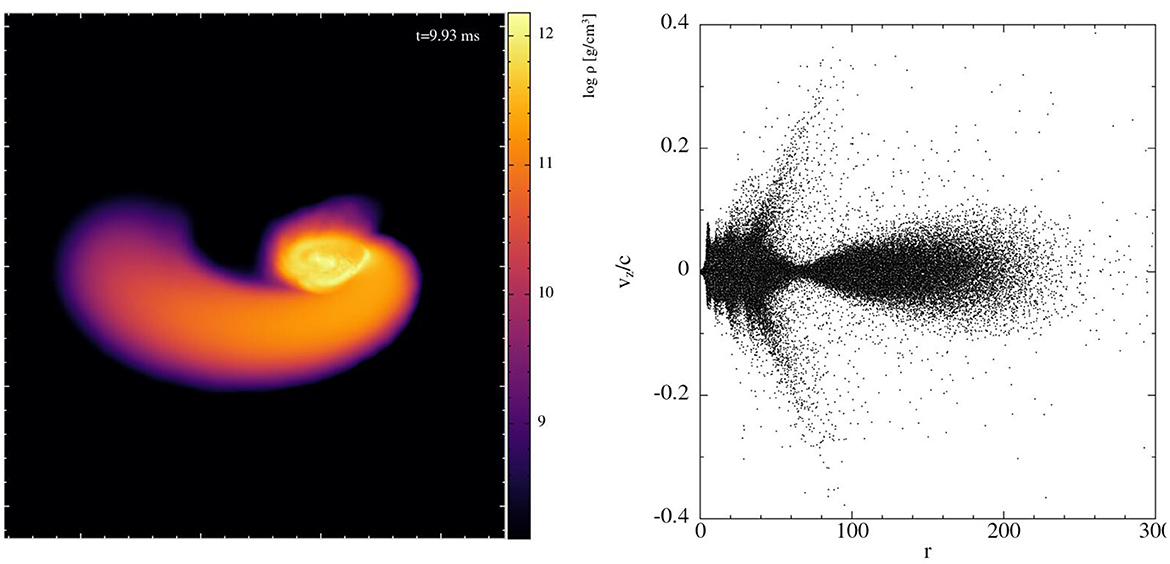
Figure 13. (Left) Volume rendering of the density distribution at t = 9.93 ms of the 2 × 1.3 M_⊙ merger with a single spinning star. The rapidly spinning central object compresses the torus by shock waves which results in polar bulk outflows with velocities reaching ~0.4c (Right).

FIGURE 14

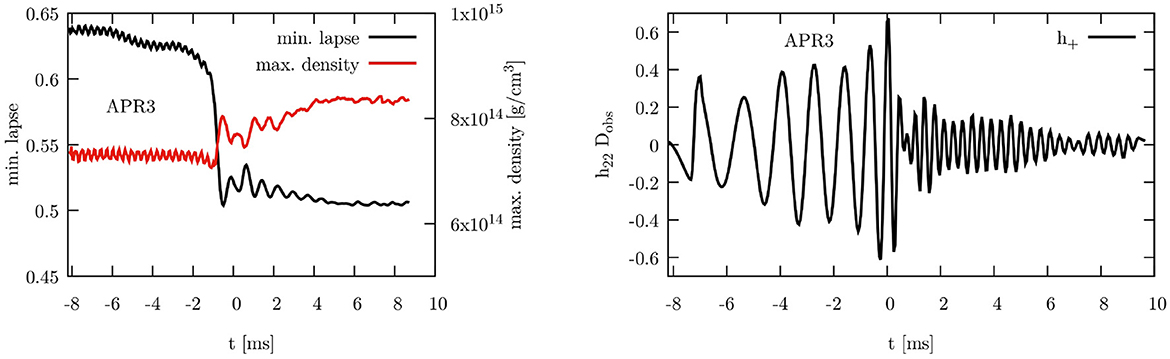
Figure 14. (Left) Maximum mass density (red curce, right axis) together with the minimum value of the lapse function α (black curve, left axis. (Right) ℓ = 2, m = 2 mode of the h₊ polarization of the gravitational wave strain extracted from the Weyl scalar Ψ₄. Both panels refer to the simulation of a 2 × 1.3 M_⊙ neutron star binary where one star has a spin of χ ≃ 0.5. For convenience with comparison with other plots t = 0 correspond to the time of the maximum amplitude in the gravitational waveform.

FIGURE 15

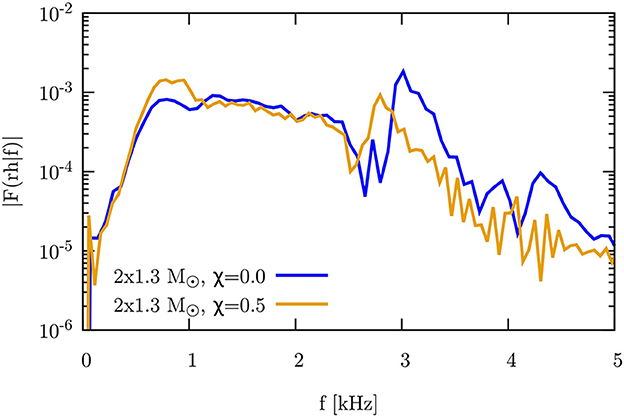
Figure 15. Spectra of the ℓ = 2, m = 2 gravitational waveforms for the non-spinning case (blue curve) and the case with one spinning star (orange curve).

As a quick test, we can compare the peak frequency with the prediction of the empirical quasi-universal relation given by Equation (4) in Vretinaris et al. [93]. This relation is

$\begin{array}{l}{f}_{\text{peak}}/M_{\text{chirp}}=13.822-0.576M_{\text{chirp}}-1.375R_{1.6}\\ +0.479M_{\text{chirp}}^2-0.073R_{1.6}{M}_{\text{chirp}}+0.044R_{1.6}^2,& (71)\end{array}$

where R_1.6 is the circumferential radius of a 1.6M_⊙ star with the given EOS and $M_{\text{chirp}}={\left(m_1{m}_2\right)}^{3/5}/{\left(m_1+m_2\right)}^{1/5}$ is the chirp mass of the binary. Using LORENE, we can calculate R_1.6 for a star with the APR3 equation of state to be R_1.6 = 11.75 km. With m₁ = m₂ = 1.3 M_⊙, we find a chirp mass of M_chirp = 1.13 M_⊙. Inserting these numbers into Equation (71), we find that the relation predicts a value of f_peak = 3.09 kHz in excellent agreement with the location of the peak of the spectrum for the non-spinning case (blue curve). Finally, in Figure 16, we compare the radiated energy (red curve, left axis) and angular momentum (black curve, right axis) for the non-spinning (left panel) and spinning (right panel) case. In both cases, the values are given as a percentage of the initial ADM value and the solid line only includes the contribution form ℓ = 2, whereas the dashed line includes the contribution from all modes up to ℓ = 4. The non-spinning case radiates about twice as much energy as the spinning case and does it predominantly in the ℓ = 2 modes. The spinning case does show a bit more contribution from the higher ℓ modes, consistent with a more asymmetric merger.

FIGURE 16

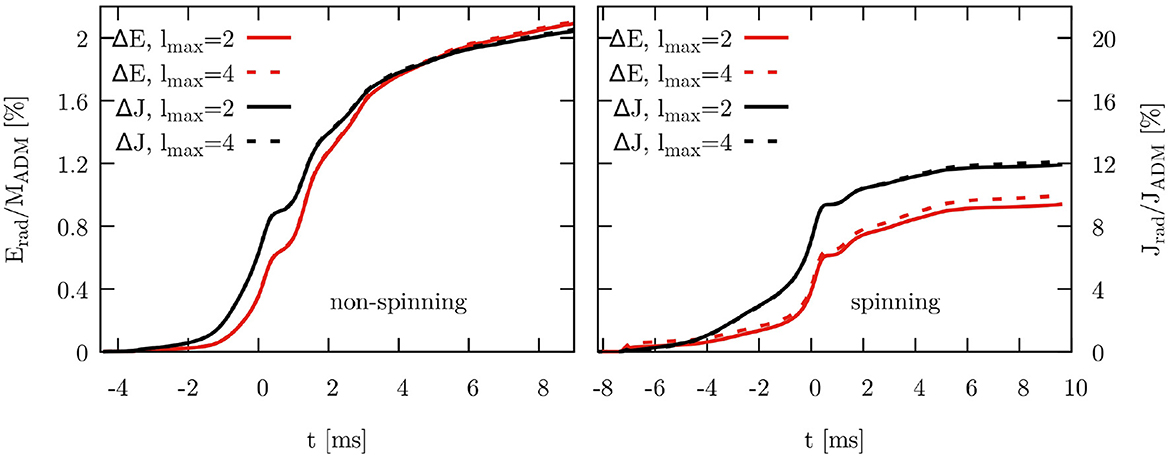
Figure 16. The radiated energy (red curves) and angular momentum (black curves) as function of time with t = 0 corresponding to the peak amplitude of the gravitational waveform. Both are shown as percentages of the initial ADM values. The left axis is for energy and the right axis for angular momentum. The solid lines only includes the contribution from the ℓ = 2 modes, while the dashed lines includes all modes up to ℓ = 4. The plot on the left is for the non-spinning case, while the plot on the right is for the case with one spinning star.

Since our main aim here is to demonstrate that challenging astrophysical problems can be robustly addressed by SPHINCS_BSSN_v1.0, we leave a further discussion of the astrophysical implications of such problems to future publications.

5. Summary

In this study, we have presented version 1.0 of our Lagrangian numerical relativity code SPHINCS_BSSN. Some of the methodological elements have been published before [33, 34, 39], and others are introduced here for the first time.

First, a new way to map the stress–energy tensor T_μν (known at the particle positions) to our spacetime mesh is introduced. The new method sets up a polynomial bases of a given order at each grid point and then computes expansion coefficients that are optimal (for the given order) in the sense that they minimize an error functional. We do this for polynomial orders from 0 to 3, and out of those possibilities, we select the one that best represents the surrounding particle values and meets some admissibility criteria. Our procedure is described in detail in Section 2.4, and we show an instructive example of the method in Appendix D.

Second, we have introduced measures that make the simulation of a collapse to a black hole more robust. We realized that in some cases, our originally chosen spacetime evolution was not resolved well enough, and we now add additional refinement levels when the hydrodynamically allowed time step drops substantially below the time step that is admissible for the space time evolution. Once the lapse value at a particle position has dropped to a very small value (here α_cut = 0.02), we remove the particle to avoid the time step shrinking toward zero. The lapse value α_cut is well below the value, where an apparent horizon forms (~0.3). While evolving toward this very low lapse value, the recovery of the physical variables from the numerical ones can fail. While this happens well inside the horizon and thus should not affect the spacetime outside of it, we nevertheless need to keep the particle evolution going until the threshold lapse for removal is reached. To avoid this problem, we transform the corresponding fluid particle into “dust” with vanishing pressure and internal energy when the lapse at a particle drops below a_dust. This allows for a simple and robust recovery of the physical variables, and the particle's contribution to the stress–energy tensor is counted until it is finally removed. For more details on the procedure, see Section 2.5.

The third improvement concerns the placement of the SPH particles modeling the fluid at the level of the initial data and is implemented in the code SPHINCS_ID. This code can now use initial data produced with the FUKA library in addition to those produced with the LORENE library. In the latest version of the code, the particles—both physical particles modeling the stars, and boundary particles used in the “artificial pressure method”—are placed so that they model the geometry of the stars more accurately than before. This allows for a better approximation of hydrodynamical equilibrium with SPH particles. After their initial placement, the particles are iterated into optimal positions according to a variant of the artificial pressure method. In the original version of this method, the relative error between the density provided by the ID solver and the SPH estimate was used to define an “artificial pressure.” The latter's gradient pushes the particles in positions where they reduce the error on the density. In the latest version of this method, we instead use the relative error of the physical pressure (rather than the density) to compute the artificial pressure. This minimizes the error on the physical pressure directly and leads (with everything else being the same) to lower errors in the physical pressure and thus to more accurate initial data.

To illustrate the working and robustness of SPHINCS_BSSN_v1.0, we have performed three simulations: one irrotational binary merger (2 × 1.3 M_⊙) that remains stable on the simulation timescale, one irrotational system (2 × 1.5 M_⊙) that collapses “promptly” (i.e., without any bounce) and one extreme binary system where only one of the stars has a (large) spin, χ = 0.5. All these simulations use the APR3 equation of state, the first two simulations are produced using LORENE, the latter using FUKA.

Not too surprisingly, for the stable irrotational case, we find an anti-correlation between the maximum density and the minimum lapse value (see Figure 9, left panel). Concerning the GW emission, we have rather good agreement between the quadrupole waveform (for more details see Rosswog et al. [39]) and the waveform extracted from the Weyl scalar ψ₄ (see Figure 9, right panel), right panel. We show the agreement for the first two cases only, but it is similarly good for the third case. Again expected, we find that the GW emission is strongly dominated by the l = 2, m = 2 mode. We find that GWs carry away ~2% of the initial ADM mass and 20% of the initial ADM angular momentum.

For the collapsing system, we find that very little mass < 6 × 10⁻⁴M_⊙ escapes the fate of falling into the BH and that the final BH is spinning fairly fast. The dimensionless spin parameter of a/M ≈ 0.8 is significantly larger than the end result of an irrotational binary BH merger where a/M ≈ 0.68.

Last, but not least, we performed a simulation of an extreme case with only one rapidly spinning star that has been produced using the FUKA library. We find that the neutron star spin has a very large impact on the merger morphology. Similar to cases with extreme mass ratios, a single puffed up tidal tail forms. Overall, the collision is less violent in the sense that the high-density regions become not as much compressed as in the equal mass case and the minimum lapse values remain larger. We also observe that less energy and angular momentum are radiated by GWs in the post-merger phase likely because the central regions are less perturbed in the less violent collision and thus deviate less from rotational symmetry.

Clearly, SPHINCS_BSSN_v1.0 would benefit from the inclusion of more microphysics, and its computational performance needs to be further improved. These issues will be addressed in future studies.

Data availability statement

The data underlying this article will be shared on reasonable request to the corresponding author.

Author contributions

SR has developed the methods in and coded the fluid part of SPHINCS_BSSN v1.0, and designed various versions of mapping particle properties to the mesh, the latest of which is described here in Section 2.4 and exemplified in Appendix D. All of this has happened in close coordination with PD. SR has further written the first draft of this study. FT developed SPHINCS_ID, produced the initial data used in the simulations using LORENE, FUKA, and SPHINCS_ID, performed the computation of the ADM momentum of the fluid in SPH, and wrote the part of Section 2.1 describing the SPH estimate of the ADM momentum, Section 3, and Appendices A–C. PD has developed the methods necessary for grid structures (including refinement), coded the interface to the needed routines from McLachlan from the Einstein Toolkit and implemented them in SPHINCS_BSSN v1.0, derived and implemented the Hermite polynomial routines used for mapping metric information from the grid to the particles, and worked closely with SR on developing and testing the methods to map the stress energy tensor from the particles to the grid. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

SR has been supported by the Swedish Research Council (VR) under grant number 2020-05044, by the research environment grant Gravitational Radiation and Electromagnetic Astrophysical Transients (GREAT) funded by the Swedish Research Council (VR) under Dnr 2016-06012, by which also FT has been supported, and by the Knut and Alice Wallenberg Foundation under grant Dnr. KAW 2019.0112, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy—EXC 2121 Quantum Universe—390833306 and by the European Research Council (ERC) Advanced Grant INSPIRATION under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 101053985). SR's calculations were performed on the facilities of the North-German Supercomputing Alliance (HLRN) on the resources provided by the Swedish National Infrastructure for Computing (SNIC) in Linköping, partially funded by the Swedish Research Council through Grant Agreement no. 2016-07213, and at the SUNRISE HPC facility supported by the Technical Division at the Department of Physics, Stockholm University.

Acknowledgments

We thank Ian Hawke for insightful comments on our LRE method, and we are very grateful to Sam Tootle for his help with the FUKA library. We also thank the referees for insightful and useful comments. Special thanks go to Holger Motzkau and Mikica Kocic for their excellent support in upgrading and maintaining SUNRISE.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^This quantity depends on the actual nuclear composition, but simply using the atomic mass unit m_u gives a precision of better than 1%. We therefore use the approximation m₀ ≈ m_u in the following. A more detailed discussion can be found in Section 2.1.1 of Diener et al. [34].

2. ^Another goal of the APM is to produce a locally isotropic particle distribution [38], that is, a distribution such that for every particle, there exist a small enough neighborhood around it such that the particle distribution inside such neighborhood is isotropic.

3. ^Currently, we exit the APM iteration if the baryon number ratio ν_max/ν_min does not change more than 0.25% for 300 iterations. The maximum and minimum are taken over all the particles.

4. ^We added this feature to our fork of LORENE, since we could not find a function that does it in the original fork. However, a function that computes the Bowen–York angular momentum as described in Gourgoulhon et al. [36, Sec. IIID], was included in the original fork [83], and we used it as a template.

References

1. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Multi-messenger observations of a binary neutron star merger. Astrophys J Lett. (2017) 848:L12. doi: 10.3847/2041-8213/aa91c9

CrossRef Full Text | Google Scholar

3. Goldstein A, Veres P, Burns E, Briggs MS, Hamburg R, Kocevski D, et al. An ordinary short gamma-ray burst with extraordinary implications: fermi-GBM detection of GRB 170817A. Astrophys J Lett. (2017) 848:L14. doi: 10.3847/2041-8213/aa8f41

CrossRef Full Text | Google Scholar

4. Savchenko V, Ferrigno C, Kuulkers E, Bazzano A, Bozzo E, Brandt S, et al. Integral detection of the first prompt gamma-ray signal coincident with the gravitational-wave event GW170817. Astrophys J Lett. (2017) 848:L15. doi: 10.3847/2041-8213/aa8f94

CrossRef Full Text | Google Scholar

5. Arcavi I, Hosseinzadeh G, Howell DA, McCully C, Poznanski D, Kasen D, et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature. (2017) 551:64–6. doi: 10.1038/nature24291

CrossRef Full Text | Google Scholar

6. Evans PA, Cenko SB, Kennea JA, Emery SWK, Kuin NPM, Korobkin O, et al. Swift and NuSTAR observations of GW170817: detection of a blue kilonova. Science. (2017) 358:1565–70. doi: 10.1126/science.aap9580

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Cowperthwaite PS, Berger E, Villar VA, Metzger BD. The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. Astrophys J Lett. (2017) 848:L17.

Google Scholar

8. Troja E, Piro L, van Eerten H, Wollaeger RT, Im M, Fox OD, et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature. (2017) 551:71–4. doi: 10.1038/nature24290

CrossRef Full Text | Google Scholar

9. Hallinan G, Corsi A, Mooley KP, Hotokezaka K, Nakar E, Kasliwal MM, et al. A radio counterpart to a neutron star merger. Science. (2017) 358:1579–83. doi: 10.1126/science.aap9855

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Margutti R, Berger E, Fong W, Guidorzi C, Alexander KD, Metzger BD, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. V. Rising X-ray emission from an off-axis jet. Astrophys J Lett. (2017) 848:L20. doi: 10.3847/2041-8213/aa9057

CrossRef Full Text | Google Scholar

11. Lyman JD, Lamb GP, Levan AJ, Mandel I, Tanvir NR, Kobayashi S, et al. The optical afterglow of the short gamma-ray burst associated with GW170817. Nat Astron. (2018) 2:751–4. doi: 10.1038/s41550-018-0511-3

CrossRef Full Text | Google Scholar

12. Troja E, Piro L, Ryan G, van Eerten H, Ricci R, Wieringa MH, et al. The outflow structure of GW170817 from late-time broad-band observations. Mon Not R Astron Soc Lett. (2018) 478:L18–23. doi: 10.1093/mnrasl/sly061

CrossRef Full Text | Google Scholar

13. Lamb GP, Kobayashi S. Electromagnetic counterparts to structured jets from gravitational wave detected mergers. Mon Not R Astron Soc Lett. (2017) 472:4953–64. doi: 10.1093/mnras/stx2345

CrossRef Full Text | Google Scholar

14. Fong W, Berger E, Blanchard PK, Margutti R, Cowperthwaite PS, Chornock R, et al. The electromagnetic counterpart of the binary neutron star merger LIGO/virgo GW170817. VIII. A comparison to cosmological short-duration gamma-ray bursts. Astrophys J Lett. (2017) 848:L23. doi: 10.3847/2041-8213/aa9018

CrossRef Full Text | Google Scholar

15. Lamb GP, Kobayashi S, GRB. 170817A as a jet counterpart to gravitational wave triggerGW 170817. Mon Not R Astron Soc Lett. (2018) 478:733–40. doi: 10.1093/mnras/sty1108

CrossRef Full Text | Google Scholar

16. Hotokezaka K, Kiuchi K, Shibata M, Nakar E, Piran T. synchrotron radiation from the fast tail of dynamical ejecta of neutron star mergers. Astrophys J. (2018) 867:95. doi: 10.3847/1538-4357/aadf92

CrossRef Full Text | Google Scholar

17. Hajela A, Margutti R, Bright JS, Alexander KD, Metzger BD, Nedora V, et al. Evidence for X-Ray emission in excess to the jet-afterglow decay 3.5 yr after the binary neutron star merger GW 170817: a new emission component. Astrophys J Lett. (2022) 927:L17. doi: 10.3847/2041-8213/ac504a

CrossRef Full Text | Google Scholar

18. Troja E, van Eerten H, Zhang B, Ryan G, Piro L, Ricci R, et al. A thousand days after the merger: continued X-ray emission from GW170817. Mon Not R Astron Soc Lett. (2020) 498:5643–51. doi: 10.1093/mnras/staa2626

CrossRef Full Text | Google Scholar

19. Nakar E, Piran T. Detectable radio flares following gravitational waves from mergers of binary neutron stars. Nature. (2011) 478:82–4. doi: 10.1038/nature10365

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hotokezaka K, Piran T, Paul M. Short-lived ²44Pu points to compact binary mergers as sites for heavy r-process nucleosynthesis. Nat Phys. (2015) 11:1042. doi: 10.1038/nphys3574

CrossRef Full Text | Google Scholar

21. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys J Lett. (2017) 848:L13. doi: 10.3847/2041-8213/aa920c

CrossRef Full Text | Google Scholar

22. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature. (2017) 551:85–8. doi: 10.1038/nature24471

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Metzger BD, Martinez-Pinedo G, Darbha S, Quataert E, Arcones A, Kasen D, et al. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of R-process nuclei. Mon Not R Astron Soc Lett. (2010) 406:2650–62. doi: 10.1111/j.1365-2966.2010.16864.x

CrossRef Full Text | Google Scholar

24. Kasen D, Metzger B, Barnes J, Quataert E, Ramirez-Ruiz E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature. (2017) 551:80–4. doi: 10.1038/nature24453

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Rosswog S, Sollerman J, Feindt U, Goobar A, Korobkin O, Wollaeger R, et al. The first direct double neutron star merger detection: implications for cosmic nucleosynthesis. Astron Astrophys. (2018) 615:A132. doi: 10.1051/0004-6361/201732117

CrossRef Full Text | Google Scholar

26. Lattimer JM, Schramm DN. Black-hole-neutron-star collisions. Astrophys J. (1974) 192:L145. doi: 10.1086/181612

CrossRef Full Text | Google Scholar

27. Symbalisty E, Schramm DN. Neutron star collisions and the R-process. Astrophys Lett. (1982) 22:143.

Google Scholar

28. Eichler D, Livio M, Piran T, Schramm DN. Nucleosynthesis, neutrino bursts and γ-Ray from coalescing neutron stars. Nature. (1989) 340:126. doi: 10.1038/340126a0

CrossRef Full Text | Google Scholar

29. Rosswog S. Liebendörfer M, Thielemann FK, Davies MB, Benz W, Piran T. Mass ejection in neutron star mergers. Astron Astrophys. (1999) 341:499–526.

Google Scholar

30. Freiburghaus C, Rosswog S, Thielemann FK. R-Process in neutron star mergers. Astrophys J. (1999) 525:L121. doi: 10.1086/312343

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kasen D, Badnell NR, Barnes J. Opacities and spectra of the R-process ejecta from neutron star mergers. Astrophys J. (2013) 774:25. doi: 10.1088/0004-637X/774/1/25

CrossRef Full Text | Google Scholar

32. Watson D, Hansen CJ, Selsing J, Koch A, Malesani DB, Andersen AC, et al. Identification of strontium in the merger of two neutron stars. Nature. (2019) 574:497–500. doi: 10.1038/s41586-019-1676-3

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Rosswog S, Diener P. SPHINCS_BSSN: a general relativistic smooth particle hydrodynamics code for dynamical spacetimes. Class Quantum Gravity. (2021) 38:115002. doi: 10.1088/1361-6382/abee65

CrossRef Full Text | Google Scholar

34. Diener P, Rosswog S, Torsello F. Simulating neutron star mergers with the Lagrangian numerical relativity code SPHINCS_BSSN. Eur Phys J A. (2022) 58:74. doi: 10.1140/epja/s10050-022-00725-7

CrossRef Full Text | Google Scholar

35. Grandclément P, Bonazzola S, Gourgoulhon E, Marck JA. A Multidomain spectral method for scalar and vectorial poisson equations with noncompact sources. J Comput Phys. (2001) 170:231–60. doi: 10.1006/jcph.2001.6734

CrossRef Full Text | Google Scholar

36. Gourgoulhon E, Grandclément P, Taniguchi K, Marck JA, Bonazzola S. Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity: method and tests. Phys Rev D. (2001) 63:064029. doi: 10.1103/PhysRevD.63.064029

CrossRef Full Text | Google Scholar

37. LORENE. (2023). Available online at: http://lorene.obspm.fr (accessed April 28, 2023).

Google Scholar

38. Rosswog S. The Lagrangian hydrodynamics code MAGMA2. Mon Not R Astron Soc Lett. (2020) 498:4230–55. doi: 10.1093/mnras/staa2591

CrossRef Full Text | Google Scholar

39. Rosswog S, Diener P, Torsello F. Thinking outside the box: numerical relativity with particles. Symmetry. (2022) 14:1280. doi: 10.3390/sym14061280

CrossRef Full Text | Google Scholar

40. Read JS, Lackey BD, Owen BJ, Friedman JL. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys Rev D. (2009) 79:124032. doi: 10.1103/PhysRevD.79.124032

CrossRef Full Text | Google Scholar

41. SPHINCS_ID. (2023). Available online at: https://sphincsid.bitbucket.io (accessed April, 28, 2023).

Google Scholar

42. Monaghan JJ. Smoothed particle hydrodynamics. Rep Prog Phys. (2005) 68:1703–59. doi: 10.1088/0034-4885/68/8/R01

CrossRef Full Text | Google Scholar

43. Rosswog S. Astrophysical smooth particle hydrodynamics. New Astron Rev. (2009) 53:78–104. doi: 10.1016/j.newar.2009.08.007

CrossRef Full Text | Google Scholar

44. Springel V. Smoothed particle hydrodynamics in astrophysics. Ann Rev Astron Astrophys. (2010) 48:391–430. doi: 10.1146/annurev-astro-081309-130914

CrossRef Full Text | Google Scholar

45. Price DJ. Smoothed particle hydrodynamics and magnetohydrodynamics. J Comput Phys. (2012) 231:759–94. doi: 10.1016/j.jcp.2010.12.011

CrossRef Full Text | Google Scholar

46. Rosswog S. SPH methods in the modelling of compact objects. Living Rev Comput Astrophys. (2015) 1. doi: 10.1007/lrca-2015-1

CrossRef Full Text | Google Scholar

47. Rosswog S. Boosting the accuracy of SPH techniques: Newtonian and special-relativistic tests. Mon Not R Astron Soc Lett. (2015) 448:3628–64. doi: 10.1093/mnras/stv225

CrossRef Full Text | Google Scholar

48. Rosswog S. A simple, entropy-based dissipation trigger for SPH. Astrophys J. (2020) 898:60. doi: 10.3847/1538-4357/ab9a2e

CrossRef Full Text | Google Scholar

49. Baumgarte TW, Shapiro SL. Numerical Relativity: Solving Einstein's Equations on the Computer. Cambridge: Cambridge University Press (2010). doi: 10.1017/CBO9781139193344

CrossRef Full Text | Google Scholar

50. Alcubierre M. Introduction to 3+1 Numerical Relativity. Oxford: Oxford University Press (2008). doi: 10.1093/acprof:oso/9780199205677.001.0001

CrossRef Full Text | Google Scholar

51. Rezzolla L, Zanotti O. Relativistic Hydrodynamics. Oxford: Oxford University Press (2013). doi: 10.1093/acprof:oso/9780198528906.001.0001

CrossRef Full Text | Google Scholar

52. Shibata M. Numerical Relativity. Singapore: World Scientific (2016). doi: 10.1142/9692

CrossRef Full Text | Google Scholar

53. Gourgoulhon É. 3+1 Formalism in General Relativity: Bases of Numerical Relativity. Lecture Notes in Physics. Berlin: Springer Berlin Heidelberg (2012). doi: 10.1007/978-3-642-24525-1

CrossRef Full Text | Google Scholar

54. Krishnan B, Lousto CO, Zlochower Y. Quasi-local linear momentum in black-hole binaries. Phys Rev D. (2007) 76:081501. doi: 10.1103/PhysRevD.76.081501

CrossRef Full Text | Google Scholar

55. Wendland H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv Comput Math. (1995) 4:389–296. doi: 10.1007/BF02123482

CrossRef Full Text | Google Scholar

56. Cabezon RM, Garcia-Senz D, Relano A. A one-parameter family of interpolating kernels for smoothed particle hydrodynamics studies. J Comput Phys. (2008) 227:8523–40. doi: 10.1016/j.jcp.2008.06.014

CrossRef Full Text | Google Scholar

57. Monaghan JJ. Smoothed particle hydrodynamics. Ann Rev Astron Astrophys. (1992) 30:543. doi: 10.1146/annurev.aa.30.090192.002551

CrossRef Full Text | Google Scholar

58. Dehnen W, Aly H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon Not R Astron Soc Lett. (2012) 425:1068–82. doi: 10.1111/j.1365-2966.2012.21439.x

CrossRef Full Text | Google Scholar

59. Gafton E, Rosswog S. A fast recursive coordinate bisection tree for neighbour search and gravity. Mon Not R Astron Soc Lett. (2011) 418:770–81. doi: 10.1111/j.1365-2966.2011.19528.x

CrossRef Full Text | Google Scholar

60. Akmal A, Pandharipande VR, Ravenhall DG. Equation of state of nucleon matter and neutron star structure. Phys Rev C. (1998) 58:1804–28. doi: 10.1103/PhysRevC.58.1804

CrossRef Full Text | Google Scholar

61. Fryer CL, Belczynski K, Ramirez-Ruiz E, Rosswog S, Shen G, Steiner AW. The fate of the compact remnant in neutron star mergers. Astrophys J. (2015) 812:24. doi: 10.1088/0004-637X/812/1/24

CrossRef Full Text | Google Scholar

62. Antoniadis J, Tauris TM, Ozel F, Barr E, Champion DJ, Freire PCC. The millisecond pulsar mass distribution: evidence for bimodality and constraints on the maximum neutron star mass. arXiv. (2016) [preprint]. doi: 10.48550/arXiv.1605.01665

CrossRef Full Text | Google Scholar

63. Margalit B, Metzger BD. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys J Lett. (2017) 850:L19. doi: 10.3847/2041-8213/aa991c

CrossRef Full Text | Google Scholar

64. Bauswein A, Just O, Janka HT, Stergioulas N. Neutron-star radius constraints from GW170817 and future detections. Astrophys J Lett. (2017) 850:L34. doi: 10.3847/2041-8213/aa9994

CrossRef Full Text | Google Scholar

65. Shibata M, Fujibayashi S, Hotokezaka K, Kiuchi K, Kyutoku K, Sekiguchi Y, et al. Modeling GW170817 based on numerical relativity and its implications. Phys Rev D. (2017) 96:123012. doi: 10.1103/PhysRevD.96.123012

CrossRef Full Text | Google Scholar

66. Rezzolla L, Most ER, Weih LR. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys J Lett. (2018) 852:L25. doi: 10.3847/2041-8213/aaa401

CrossRef Full Text | Google Scholar

67. Alsing J, Silva HO, Berti E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon Not R Astron Soc Lett. (2018) 478:1377–91. doi: 10.1093/mnras/sty1065

CrossRef Full Text | Google Scholar

68. Biswas B, Datta S. Constraining neutron star properties with a new equation of state insensitive approach. arXiv. (2021) [preprint]. doi: 10.48550/arXiv.2112.10824

CrossRef Full Text | Google Scholar

69. Shibata M, Nakamura T. Evolution of three-dimensional gravitational waves: harmonic slicing case. Phys Rev D. (1995) 52:5428–44. doi: 10.1103/PhysRevD.52.5428

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Baumgarte TW, Shapiro SL. Numerical integration of Einstein's field equations. Phys Rev D. (1999) 59:024007. doi: 10.1103/PhysRevD.59.024007

CrossRef Full Text | Google Scholar

71. Löffler F, Faber J, Bentivegna E, Bode T, Diener P, Haas R, et al. The Einstein Toolkit: a community computational infrastructure for relativistic astrophysics. Class Quantum Gravity. (2012) 29:115001. doi: 10.1088/0264-9381/29/11/115001

CrossRef Full Text | Google Scholar

72. Einstein Toolkit Web Page. (2020). Available online at: https://einsteintoolkit.org/ (accessed December 9, 2020).

Google Scholar

73. Gottlieb S, Shu CW. Total variation diminishing Runge-Kutta schemes. Math Comput. (1998) 67:73–85. doi: 10.1090/S0025-5718-98-00913-2

CrossRef Full Text | Google Scholar

74. Timmes FX, Swesty FD. The accuracy, consistency, and speed of an electron-positron equation of state based on table interpolation of the Helmholtz Free Energy. Astrophys J Suppl Ser. (2000) 126:501–16. doi: 10.1086/313304

CrossRef Full Text | Google Scholar

75. Zhang YT, Shu WC. ENO and WENO Schemes. Handbook of Numerical Ananlysis. (2016). Amsterdam: Elsevier. doi: 10.1016/bs.hna.2016.09.009

CrossRef Full Text | Google Scholar

76. Cottet GH, Koumoutsakos PD. Vortex Methods. Cambridge: Cambridge University Press (2000). doi: 10.1017/CBO9780511526442

CrossRef Full Text | Google Scholar

77. Cottet GH, Etancelin JM, Perignon F, Picard C. High order semi-Lagrangian particle methods for transport equations. Esaim Math Model Numer Anal. (2014) 48:1029–60. doi: 10.1051/m2an/2014009

CrossRef Full Text | Google Scholar

78. Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes. New York, NY: Cambridge University Press (1992).

Google Scholar

79. Brown JD, Diener P, Sarbach O, Schnetter E, Tiglio M. Turduckening black holes: an analytical and computational study. Phys Rev D. (2009) 79:044023. doi: 10.1103/PhysRevD.79.044023

CrossRef Full Text | Google Scholar

80. Papenfort LJ, Tootle SD, Grandclément P, Most ER, Rezzolla L. New public code for initial data of unequal-mass, spinning compact-object binaries. Phys Rev D. (2021) 104:024057. doi: 10.1103/PhysRevD.104.024057

CrossRef Full Text | Google Scholar

81. Frankfurt University/Kadath Initial Data Solver. (2023). Available online at: https://kadath.obspm.fr/ (accessed April 06, 2023).

Google Scholar

82. Grandclement P. KADATH: a spectral solver for theoretical physics. J Comput Phys. (2010) 229:3334–57. doi: 10.1016/j.jcp.2010.01.005

CrossRef Full Text | Google Scholar

83. LORENE Reference Guide Definition of Lorene::Binaire::angu_mom. (2023). Available online at: https://lorene.obspm.fr/Refguide/classLorene_1_1Binaire.html#a3e33ff8bbf0552580707577de0937ba4 (accessed April 06, 2023).

Google Scholar

84. Nedora V, Bernuzzi S, Radice D, Perego A, Endrizzi A, Ortiz N. Spiral-wave Wind for the Blue Kilonova. Astrophys J Lett. (2019) 886:2200306. doi: 10.3847/2041-8213/ab5794 Available online at: https://onlinelibrary.wiley.com/toc/15213889/0/0

CrossRef Full Text | Google Scholar

85. Rosswog S, Korobkin O. Heavy elements and electromagnetic transients from neutron star mergers. Ann Phys. (2022). doi: 10.1002/andp.202200306

CrossRef Full Text | Google Scholar

86. Bozzola G. kuibit: analyzing Einstein toolkit simulations with python. J Open Source Softw. (2021) 6:3099. doi: 10.21105/joss.03099

CrossRef Full Text | Google Scholar

87. Löffler F, Faber J, Bentivegna E, Bode T, Diener P, Haas R, et al. The Einstein toolkit: a community computational infrastructure for relativistic astrophysics. Class Quantum Grav. (2012) 29:115001.

Google Scholar

88. Baiotti L, Giacomazzo B, Rezzolla L. Accurate evolutions of inspiralling neutron-star binaries: prompt and delayed collapse to a black hole. Phys Rev D. (2008) 78:084033. doi: 10.1103/PhysRevD.78.084033

CrossRef Full Text | Google Scholar

89. Bildsten L, Cutler C. Tidal interactions of inspiraling compact binaries. Astrophys J. (1992) 400:175–80. doi: 10.1086/171983

CrossRef Full Text | Google Scholar

90. Kochanek CS. Coalescing binary neutron stars. Astrophys J. (1992) 398:234–47. doi: 10.1086/171851

CrossRef Full Text | Google Scholar

91. Tauris TM, van den Heuvel EPJ. Physics of Binary Star Evolution. From Stars to X-ray Binaries and Gravitational Wave Sources New Jersey, NJ: Princeton University Press. (2023).

Google Scholar

92. Papenfort LJ, Most ER, Tootle S, Rezzolla L. Impact of extreme spins and mass ratios on the post-merger observables of high-mass binary neutron stars. Mon Not R Astron Soc Lett. (2022) 513:3646–62. doi: 10.1093/mnras/stac964

CrossRef Full Text | Google Scholar

93. Vretinaris S, Stergioulas N, Bauswein A. Empirical relations for gravitational-wave asteroseismology of binary neutron star mergers. Phys Rev D. (2020) 101:084039. doi: 10.1103/PhysRevD.101.084039

CrossRef Full Text | Google Scholar

Appendix

A. Surface-conforming ovals

In order to use the surface-conforming ovals as discussed in Sec. 3.2, we first need to find the surface of the star. We do this in SPHINCS_ID in the following way.

1. Choose a threshold density that marks the end of the star. Currently, this value is ${\rho }_{\text{thres}}=10^{-12}\mathrm{\text{code units}}\simeq 6.2\times 10^5\text{g}/\text{c}{\text{m}}^3$ (see the beginning of Sec. 2.1 for the definition of our code units). Also, choose a tolerance value tol = 10⁻⁶ (code units), the choices of these values are motivated in step 3.

2. Select a direction (θ, ϕ) centered at the center of the star, and choose two points lying on it, one inside and one outside the star. Read the density provided by the ID solver at these points.

3. Apply the bisection algorithm around ρ_thres until the distance between the two points is equal to or lower than tol Then, the innermost of the two points is declared to be the radius r along the considered (θ, ϕ) direction. Arguably, the values of ρ_thres and tol are somewhat arbitrary. We determined them by comparing the resulting values for the 4 radii along the positive and negative x direction, and along the y and z direction, with the values provided by LORENE.

4. Repeat steps 2 and 3 for the desired number of directions, to find a set of points {θ, ϕ, r} that lie on the surface of the star. Currently, we sample the surface every degree in both θ and ϕ; we thus have 180 × 360 points.

Once the sample {θ, ϕ, r} lying on the surface is found, the value of r(θ, ϕ) for any (θ, ϕ) ∈ [0, π) × [0, 2π) is found with bilinear interpolation.

B. The SPH estimate of the ADM linear momentum of the fluid

Here we explicitly compute the ADM linear momentum of the fluid in terms of the SPH canonical momentum, as mentioned in Sec. 3.4. The integral in (15) can be written as an integral over the spacelike hypersurface Σ using Gauss' theorem,

$\begin{array}{l}{P}_{\xi }^{\text{ADM}}≔\frac{1}{8\pi }{\displaystyle {\int }_{\partial \sigma }\text{d}}{S}_j\left(K^j{}_i-{\delta }^j{}_{i}K\right){\xi }^i\\ =\frac{1}{8\pi }{\displaystyle {\int }_{\Sigma }{\text{d}}^3}x\sqrt{\gamma }\left[{\xi }^i{D}_j\left(K^j{}_i-{\delta }^j{}_{i}K\right)+\left(K^j{}_i-{\delta }^j{}_{i}K\right)D_j{\xi }^i\right],& (\text{A}1)\end{array}$

with γ determinant of the spatial metric γ_ij, and D_j covariant derivative compatible with γ_ij. The second term in the square parenthesis can be rewritten as

$\begin{array}{l}\left(K^j{}_i-{\delta }^j{}_{i}K\right)D_j{\xi }^i=\left(K^{ij}-{\gamma }^{ij}K\right)D_j{\xi }_i\\ =\left(K^{ij}-{\gamma }^{ij}K\right)\frac{D_j{\xi }_i+D_i{\xi }_j}{2}\\ =\left(K^{ij}-{\gamma }^{ij}K\right)\frac{{ℒ}_{\xi }{\gamma }_{ij}}{2},& (\text{A}2)\end{array}$

where the first equality uses the compatibility between γ_ij and D_j, the second equality uses the symmetry of K^ij and γ^ij in their indices, and the last equality uses the definition of the Lie derivative $\mathcal{L}$_ξγ_ij. The first term in the square parenthesis in (A1) can be rewritten using the momentum constraint [49, eq.(2.126)],

$\begin{array}{ll}{D}_j\left(K^j{}_i-{\delta }^j{}_{i}K\right)=8\pi s_i,& (\text{A}3)\end{array}$

where s_i is the spatial part of the momentum density measured by the Eulerian observer $s_{\rho }≔-n^{\mu }{T}_{\mu \nu }{\gamma }^{\nu }{}_{\rho }$, with T_μν being the stress–energy tensor, n^μ = (1, −βⁱ)/α vector normal to Σ (and 4-velocity of the Eulerian observer), α lapse function, βⁱ shift vector, and ${\gamma }^{\mu }{}_{\nu }={\delta }^{\mu }{}_{\nu }+n^{\mu }{n}_{\nu }$ projector onto Σ. Hence, the ADM linear momentum in (A1) can be rewritten as

$\begin{array}{ll}{P}_{\xi }^{\text{ADM}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }\left[{\xi }^i{s}_i+\frac{1}{16\pi }\left(K^{ij}-{\gamma }^{ij}K\right){\mathcal{L}}_{\xi }{\gamma }_{ij}\right].& (\text{A}4)\end{array}$

Now we use the definition of s_μ to write

$\begin{array}{ll}{s}_{\mu }≔-n^{\rho }{T}_{\rho \nu }{\gamma }^{\nu }{}_{\mu }=-n^{\rho }{T}_{\rho \mu }-\left(n^{\rho }{T}_{\rho \nu }{n}^{\nu }\right)n_{\mu }.& (\text{A}5)\end{array}$

The spatial part of s_μ is (see Eq. (32))

$\begin{array}{ll}{s}_i=-n^{\nu }{T}_{\nu i}-\left(n^{\nu }{T}_{\nu \rho }{n}^{\rho }\right)n_i=-n^{\nu }{T}_{\nu i}=\frac{{\beta }^j{T}_{ji}-T_{0i}}{\alpha }& (\text{A}6)\end{array}$

where we used n_μ = (−α, 0, 0, 0) and the expression for the components of n^μ, given above.

The SPH canonical momentum per baryon, for a perfect fluid, is defined as (see, e.g., [43, eq. 198])

$\begin{array}{ll}{S}_i≔\Theta \left(1+u+\frac{P}{n}\right)g_{i\mu }{v}^{\mu },& (\text{A}7)\end{array}$

where v^μ = U^μ/U⁰ is the fluid velocity in the SPH computing frame, U^μ = dx^μ/dτ is the 4-velocity of the fluid, τ is the proper time of the fluid, Θ is the generalized Lorentz factor $\Theta ≔{\left(-g_{\mu \nu }{v}^{\mu }{v}^{\nu }\right)}^{-1/2}=U^0$, with g_μν spacetime metric constructed from γ_ij, α and βⁱ; u is the specific internal energy, P the pressure, and n the baryon density of the fluid. The last three hydrodynamical quantities are measured in the local rest frame of the fluid. It holds:

$\begin{array}{l}{U}_i=g_{i\mu }{U}^{\mu }=g_{i0}{U}^0+g_{ij}{U}^j=U^0{\beta }_i+{\gamma }_{ij}{U}^j\Rightarrow {\gamma }_{ij}{U}^j\\ =U_i-U^0{\beta }_i,\\ g_{i\mu }{v}^{\mu }=g_{i\mu }\frac{U^{\mu }}{U^0}=\frac{g_{i0}{U}^0+g_{ij}{U}^j}{U^0}=g_{i0}+\frac{{\gamma }_{ij}{U}^j}{U^0}\\ ={\beta }_i+\frac{U_i-U^0{\beta }_i}{U^0}=\frac{U_i}{U^0}.& (\text{A}8)\end{array}$

Using (A8) in (A7),

$\begin{array}{ll}{S}_i=\left(1+u+\frac{P}{n}\right)U_i.& (\text{A}9)\end{array}$

Since the SPH canonical momentum is a momentum per baryon, we can try to build it from the stress–energy tensor in the following way:

$\begin{array}{ll}{q}_i≔\frac{T_{0i}}{N},& (\text{A}10)\end{array}$

where $N≔\sqrt{-g}\Theta n$ is the baryon number density in the computing frame, with g determinant of g_μν. Dimensionally, q_i is a momentum per baryon. The expression (A7) holds for a perfect fluid, hence we now specialize to the stress–energy tensor of a perfect fluid,

$\begin{array}{ll}{q}_i=\frac{\left(e+P\right)U_0{U}_i+P{g}_{0i}}{N},& (\text{A}11)\end{array}$

with e = n(1 + u) energy density of the fluid measured in its local rest frame. We use

$\begin{array}{l}{U}_0=g_{0\mu }{U}^{\mu }=g_{00}{U}^0+g_{0i}{U}^i=g_{00}\Theta +g_{0i}\Theta v^i\\ =\Theta \left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right),& (\text{A}12)\end{array}$

in expanding (A11),

$\begin{array}{ll}{q}_i=\frac{e+P}{\sqrt{-g}\Theta n}\Theta \left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)U_i+\frac{P}{\sqrt{-g}\Theta n}{\beta }_i.& (\text{A}13)\end{array}$

We substitute e = n(1 + u) into (A13),

$\begin{array}{l}{q}_i=\frac{1}{\sqrt{-g}}\left[\left(1+u+\frac{P}{n}\right)U_i\right]\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\sqrt{-g}\Theta n}{\beta }_i\\ =\frac{1}{\sqrt{-g}}\left[S_i\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\Theta n}{\beta }_i\right].& (\text{A}14)\end{array}$

Using (A10), the expression in (A14) becomes

$\begin{array}{l}{T}_{0i}=\frac{N}{\sqrt{-g}}\left[S_i\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\Theta n}{\beta }_i\right]\\ =\Theta n\left[S_i\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\Theta n}{\beta }_i\right],& (\text{A}15)\end{array}$

that is, we related the SPH momentum per baryon S_i with the T_0i components of the perfect fluid stress–energy tensor. Note that, if the expression for the SPH momentum per baryon was known in general, the same computation could in principle be generalized to any type of fluid.

We can now insert (A15) into (A6), and obtain the relation between the Eulerian momentum density s_i and the SPH momentum per baryon S_i,

$\begin{array}{l}{s}_i=\frac{{\beta }^j{T}_{ji}-T_{0i}}{\alpha }\\ =\frac{{\beta }^j{T}_{ji}}{\alpha }-\frac{\Theta n}{\alpha }\left[S_i\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\Theta n}{\beta }_i\right]\\ =\frac{{\beta }^j}{\alpha }\left[n\left(1+u+\frac{P}{n}\right)U_i{U}_j+P{\gamma }_{ij}\right]-\frac{\Theta n}{\alpha }\\ \left[S_i\left(-{\alpha }^2+{\beta }^j{\beta }_j+{\beta }_j{v}^j\right)+\frac{P}{\Theta n}{\beta }_i\right]\\ =\frac{{\beta }^j{U}_{j}n}{\alpha }{S}_i-\frac{\Theta n}{\alpha }{S}_i{\beta }_j{v}^j+\frac{P{\beta }_i}{\alpha }-\frac{P{\beta }_i}{\alpha }-\frac{\Theta n}{\alpha }\left(-{\alpha }^2+{\beta }^j{\beta }_j\right)S_i\\ =\frac{S_{i}n}{\alpha }\left({\beta }^j{U}_j+\Theta {\alpha }^2-\Theta {\beta }^j{\beta }_j-\Theta {\beta }_j{v}^j\right).& (\text{A}16)\end{array}$

Using (A8), we rewrite

$\begin{array}{ll}{\beta }^j{U}_j={\beta }^j\Theta g_{j\mu }{v}^{\mu }=\Theta \left({\beta }^j{g}_{j0}{v}^0+{\beta }^j{g}_{jk}{v}^k\right)=\Theta \left({\beta }^j{\beta }_j+{\beta }_k{v}^k\right),& (\text{A}17)\end{array}$

where we used v⁰ = U⁰/U⁰ = 1. Substituting (A17) into (A16),

$\begin{array}{ll}{s}_i=\frac{S_i\Theta n}{\alpha }\left({\beta }^j{\beta }_j+{\beta }_k{v}^k+{\alpha }^2-{\beta }^j{\beta }_j-{\beta }_j{v}^j\right)=\Theta n\alpha S_i.& (\text{A}18)\end{array}$

Using (A18), the expre/ssion for the ADM momentum determined by the fluid becomes [see (16)]

$\begin{array}{l}{P}_{\xi }^{\text{ADM},\text{fluid}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }{\xi }^i{S}_i={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\left(\sqrt{\gamma }\Theta n\alpha \right){\xi }^i{S}_i\\ ={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}xN{\xi }^i{S}_i.& (\text{A}19)\end{array}$

where we used $\sqrt{-g}=\alpha \sqrt{\gamma }$ and $N≔\sqrt{-g}\Theta n$.

The integral in (A19) is over the entire spacelike hypersurface Σ, but it has support only where S_i (or N) is nonzero, that is, where the fluid is. Therefore, we can approximate the integral with an SPH summation over the particles, to obtain an estimate of the ADM linear momentum of the fluid,

$\begin{array}{ll}{P}_{\xi }^{\text{ADM},\text{fluid}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}xN{\xi }^i{S}_i\simeq {\displaystyle \sum _a}{\nu }_a{\left({\xi }^i{S}_i\right)}_a,& (\text{A}20)\end{array}$

with the index a running over all the particles, ν_a being the baryon number of particle a.

C. Computation of the ADM linear momentum for the ID

Both LORENE and FUKA assume a spacetime free of gravitational waves which implies that the whole momentum should be carried by the fluid alone. We briefly show this here explicitly.

As discussed in (3.4), on the initial spacelike hypersurface and with the assumptions of asymptotic flatness, conformal flatness and maximal slicing, used by LORENE and FUKA to solve for the ID, $e_{\left(j\right)}^i$ = δⁱ_j is an orthogonal frame which becomes orthonormal, hence Cartesian, at spatial infinity. We can then set ${\xi }^i=e_{\left(j\right)}^i$ in (16), and obtain a formula for the Cartesian components of the ADM linear momentum at t = 0:

$\begin{array}{ll}{P}_j^{\text{ADM}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }\left[e_{\left(j\right)}^i{s}_i+\frac{1}{16\pi }\left(K^{mi}-{\gamma }^{mi}K\right){\mathcal{L}}_{e_{\left(j\right)}}{\gamma }_{mi}\right].& (\text{A}21)\end{array}$

We now use (68) to note that

$\begin{array}{l}{\mathcal{L}}_{e_{\left(j\right)}}{\gamma }_{mi}={\mathcal{L}}_{e_{\left(j\right)}}\left(A^2{\delta }_{mi}\right)={\delta }_{mi}{\mathcal{L}}_{e_{\left(j\right)}}{A}^2+A^2{\mathcal{L}}_{e_{\left(j\right)}}{\delta }_{mi}\\ ={\delta }_{mi}{e}_{\left(j\right)}^k{\partial }_k{A}^2+A^2(e_{\left(j\right)}^k{\partial }_k{\delta }_{mi}+{\delta }_{ik}{\partial }_m{e}_{\left(j\right)}^k+{\delta }_{mk}{\partial }_i{e}_{\left(j\right)}^k)\\ ={\delta }_{mi}{e}_{\left(j\right)}^k{\partial }_k{A}^2,& (\text{A}22)\end{array}$

were the last equality follows from δ_mi and $e_{\left(j\right)}^k$ having constant components. Inserting (A22) into (A21),

$\begin{array}{ll}{P}_j^{\text{ADM}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }\left[e_{\left(j\right)}^i{s}_i+\frac{1}{16\pi }\left(K^{mi}-{\gamma }^{mi}K\right){\delta }_{mi}{e}_{\left(j\right)}^k{\partial }_k{A}^2\right].& (\text{A}23)\end{array}$

Finally, using the maximal slicing condition $K=K^i{}_i=K^{mi}{\gamma }_{mi}=A^2{K}^{mi}{\delta }_{mi}=0$, which implies $K^{mi}{\delta }_{mi}=0$ because A ≠ 0,

$\begin{array}{ll}{P}_j^{\text{ADM}}={\displaystyle {\int }_{\Sigma }}{\text{d}}^{3}x\sqrt{\gamma }{e}_{\left(j\right)}^i{s}_i={\displaystyle {\int }_{\text{stars}}}{\text{d}}^{3}x\sqrt{\gamma }{s}_j.& (\text{A}24)\end{array}$

Hence, for the LORENE and FUKA binary neutron star ID, it suffices to integrate (A24) over a compact domain (the stars), to obtain the total linear ADM momentum.

D. An example of function approximation via a Local Regression Estimate (LRE)

To illustrate the function approximation via LRE, we place a set of “grid points” on a Cartesian mesh in [−0.5:0.5]³ with a spacing of Δ_g = 0.07. Our “particles” are originally placed on a Cartesian grid between [−0.9:0.9] × [−0.9:0.9] × [−0.9:0.9] with a spacing of Δ_p = 0.1, but then slightly randomized by adding to each particle position component a random number in [−0.01, 0.01]. This regular but not perfect distribution is meant to mimmick an SPH particle distribution. Each of the particles is assigned a smoothing length of h = 0.1 and a function value according to

$\begin{array}{ll}f\left(x,y,z\right)=10-\sqrt{x^2+y^2+z^2}.& (\text{A}25)\end{array}$

We then calculate the LRE approximations of a specified polynomial order at each grid point and we measure at the grid points the relative error of the LRE estimate compared with the original function f, see Figure A1, left panel.

FIGURE A1

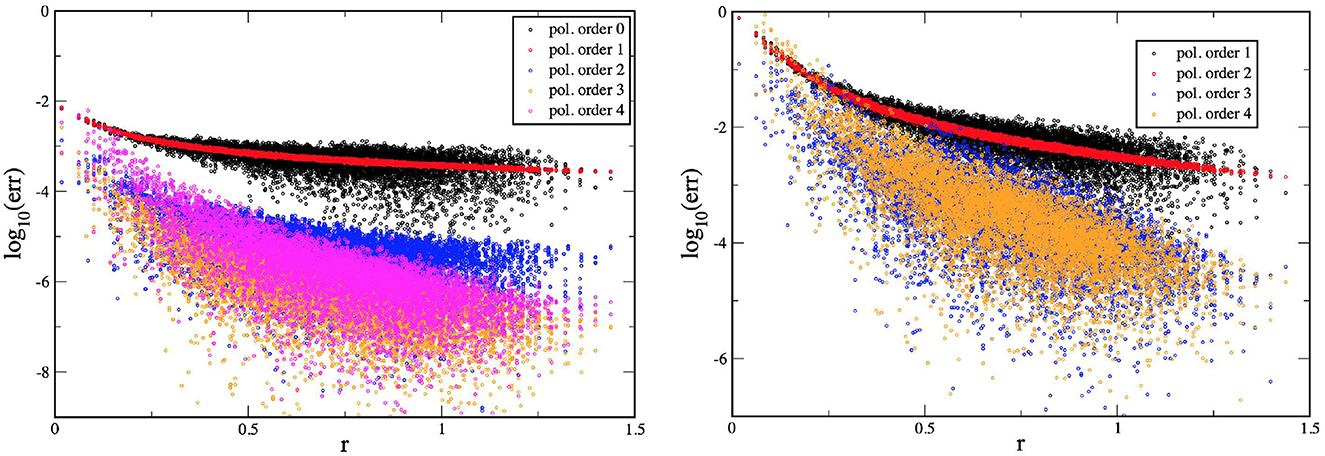
Figure A1. Relative errors of the function approximation (left) and the gradient of the function approximation (right) as function of radius of the grid points.

The lowest polynomial order already provides estimates below 1% error (black), but with a large spread of accuracies, while the linear order provides estimates of the same order, but with substantially less noise (red). The transition from linear to quadratic polynomials (blue) provides a serious enhancement of the accuracy, while cubic (orange) and quartic polynomials (magenta) only marginally improve the results further.

The situation is similar for the gradient estimates, where we use

$\begin{array}{ll}\text{err}\equiv \frac{\Vert {\left(\nabla f\right)}_{\text{num}}|-|{\left(\nabla f\right)}_{\text{theo}}\Vert }{\left|{\left(\nabla f\right)}_{\text{theo}}\right|}.& (\text{A}26)\end{array}$

as error measure and (∇f)_num is the numerically calculated gradient estimate while (∇f)_theo is the exact result. Also here, the overall scale between the lowest (linear) and next-to-lowest order (quadratic) is similar, but the quadratic results are much less noisy. Again we find a substantial improvement going to the next order (cubic), but no more substantial gain when further increasing the polynomial order.

We also want to briefly illustrate the effect of re-scaling the moment matrix with appropriate powers of the length $l_p={\left({\nu }_p/N_p\right)}^{1/3}$ to ensure that all matrix elements have the same dimension. In practice, this is achieved by de-dimensionalizing the shifted basis functions, e.g. ${\Delta }^{\text{G}}x\to {\Delta }^{\text{G}}x/l_p$, ${\Delta }^{\text{G}}x{\Delta }^{\text{G}}y\to {\Delta }^{\text{G}}x{\Delta }^{\text{G}}y/l_p^2$ etc. We show in Figure A2 the condition numbers, $\mathcal{C}\equiv \Vert M{M}^{-1}\Vert$, a measure for how close a matrix is to being singular, for the above experiment, once for the straight forward and once for the re-scaled version. The condition numbers in the re-scaled case improve dramatically, e.g. by five orders of magnitude in the case of quartic basis functions (orange curves in Figure A2. We do, however, not see any noteworthy improvement of the accuracy which we interpret as a success of the well-working Singular Value Decomposition. Nevertheless, since the re-scaling is essentially free of computational cost, we always use re-scaled basis functions.

FIGURE A2

Figure A2. Condition number for (not) re-scaled basis functions for polynomial orders from one to four. Note that for order four the re-scaling improves the condition number by as much as five orders of magnitude.