- 1Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge, United Kingdom
- 2Faculty of Science and Engineering, School of Mathematical Sciences, Queen Mary University of London, London, United Kingdom
- 3The Alan Turing Institute, London, United Kingdom
We propose a novel framework for the regularized inversion of deep neural networks. The framework is based on the authors' recent work on training feed-forward neural networks without the differentiation of activation functions. The framework lifts the parameter space into a higher dimensional space by introducing auxiliary variables, and penalizes these variables with tailored Bregman distances. We propose a family of variational regularizations based on these Bregman distances, present theoretical results and support their practical application with numerical examples. In particular, we present the first convergence result (to the best of our knowledge) for the regularized inversion of a single-layer perceptron that only assumes that the solution of the inverse problem is in the range of the regularization operator, and that shows that the regularized inverse provably converges to the true inverse if measurement errors converge to zero.
1. Introduction
Neural networks are computing systems that have revolutionized a wide range of research domains over the past decade and outperformed many traditional machine learning approaches [cf. [1, 2]]. This performance often comes at the cost of interpretability (or rather a lack thereof) of the outputs that a neural network produces for given inputs. As a consequence, a lot of research has focused on understanding representations of neural networks and on developing strategies to interpret these representations, predominantly with saliency maps [3–6]. An alternative approach focuses on understanding deep image representations by inverting them [7]. The authors propose a total-variation-based variational optimization method that aims to infer the network input from the network output with regularized inversion.
While the concept of inverting neural networks is certainly not new [cf. [8–11]], there has been increasing interest in recent years largely due to developments in nonlinear dimensionality reduction and generative modeling that include (but are not limited to) (variational) Autoencoders [12], Normalizing Flows [13, 14], Cycle-Consistent Generative Adversarial Networks [15], and Probabilistic Diffusion Models [16, 17].
While several approaches for the inversion of neural networks have been proposed especially in the context of generative modeling [see for example [18, 19] in the context of normalizing flows, [20] in the context of generative adversarial networks, and [21] in the context of probabilistic diffusion models] an important aspect, which is often overlooked, is that invertible operations alone are not automatically stable with respect to small variations in the data. For example, computing the solution of the heat equation after a fixed termination time is stable with respect to variations in the initial condition, but estimating the initial condition from the terminal condition of the heat equation is not stable with respect to perturbations in the terminal condition. This issue cannot be resolved without approximation of the inverse with a family of continuous operators, also known as regularization. The research field of Inverse and Ill-posed Problems and its branch Regularization Theory focus strongly on the stable approximation of ill-posed and ill-conditioned inverses via regularizations [22] and so-called variational regularizations [23, 24] that are a special class of (nonlinear) regularizations. The optimization model proposed in [7] can be considered as a variational regularization method with total variation regularization; however, the work in Mahendran and Vedaldi [7] is purely empirical, and to the best of our knowledge no works exist that rigorously prove that the proposed approach is a variational regularization.
In this work, we propose a novel regularization framework based on lifting with tailored Bregman distances and prove that the proposed framework is a convergent variational regularization for the inverse problem of estimating the inputs from single-layer perceptrons or the inverse problem of estimating hidden variables in a multi-layer perceptron sequentially. While there has been substantial work in previous years that focuses on utilizing neural networks as nonlinear operators in variational regularization methods [25–29], this is the first work that provides theoretical guarantees for the stable, model-based inversion of neural networks to the best of our knowledge.
Our contributions are three-fold. (1) We propose a novel framework for the regularized inversion of multi-layer perceptrons, respectively feed-forward neural networks, that is based on the lifted Bregman framework recently proposed by the authors in [30]. (2) We show that for the single-layer perceptron case, the proposed variational regularization approach is a provably convergent regularization under very mild assumptions. To our knowledge, this is the first time that an inversion method has been proposed that does not just allow to perform inversion empirically, but for which we can prove that the proposed method is a convergent regularization method without overly restrictive assumptions such as differentiability of the activation function and the presence of a tangential cone condition. (3) We propose a proximal first-order optimization strategy to solve the proposed variational regularization method and present several numerical examples that support the effectiveness of the proposed model-based regularization approach.
The paper is structured as follows. In Section 2, we introduce the lifted Bregman formulation for the model-based inversion of feed-forward neural networks. In Section 3, we prove that for the single-layer perceptron case the proposed model is a convergent variational regularization method and provide general error estimates as well as error estimates for a concrete example of a perceptron with ReLU activation function. In Section 4, we discuss how to implement the proposed variational regularization computationally for both the single-layer and multi-layer perceptron setting with a generalization of the primal-dual hybrid gradient method and coordinate descent. Subsequently, we present numerical results that demonstrate empirically that the proposed approach is a model-based regularization in Section 5, before we conclude this work with a brief section on conclusions and outlook in Section 6.
2. Model-based inversion of feed-forward networks
Suppose we are given an L-layer feed-forward neural network of the form
for input data x ∈ ℝn and pre-trained parameters . Here, denotes the collection of nonlinear activation functions and f denotes a generic function parameterized by parameters . For ease of notation, we use Θ to refer to all parameters . For a given network output y ∈ ℝm, our goal is to solve the inverse problem
for the unknown input x ∈ ℝn. The problem (2) is usually ill-posed in the sense that a solution may not exist (especially if n ≪ m) or is not unique (especially if m ≪ n, or if information is lost through application of nonlinear activation functions). Moreover, even for a network with identity activation functions σl and affine linear transformation f, solving (2) is often ill-conditioned in the sense that errors in y get heavily amplified when solving for x. We therefore, propose to approximate the inverse of this nonlinear, potentially ill-posed inverse problem via the minimization of a lifted Bregman formulation of the form
where we assume x0 = x and for simplicity of notation. The data yδ is a perturbed version of y, for which we assume , for some constant δ ≥ 0 and . Please note that this approach is referred to as “lifted” because the solution space is lifted to a higher dimensional space that also includes auxiliary variables for all intermediate layers. The functions BΨl for l = 1, …, L are defined as
for a proper, convex, and lower semi-continuous function . The notation refers to the convex or Fenchel conjugate of , i.e., . Last but not least, the function R:ℝn → ℝ∪{∞} is a proper, convex, and lower semi-continuous function that enables us to incorporate a-priori information into the inversion process. The impact of this is controlled by the parameter α > 0.
Please note that the functions BΨl are directly connected to the chosen activation functions . Following [30], we observe
where is the proximal map with respect to Ψl, i.e.
for all l ∈ {1, …, L}. This means that we will solely focus on feed-forward neural networks with nonlinear activation functions that are proximal maps.
The advantage of using functions BΨl over more conventional functions such as the squared Euclidean norm of the difference of the network output and the measured output, i.e., , is that the functions BΨl are continuously differentiable with respect to their second argument [along with several other useful properties, cf. [30], Theorem 10]. If we define , we observe
Please note that the family of objective functions BΨl satisfies several other interesting properties; we refer the interested reader to [30], Theorem 10.
For the remainder of this work, we assume that the parameterized functions f are affine-linear in the first argument, with parameters Θl. A concrete example is the affine-linear transformation f(x, Θl) = Wlx + bl, for a (weight) matrix , a (bias) vector and the collection of parameters Θl = (Wl, bl).
In the next section, we show that (3) is a variational regularization method for L = 1 and prove a convergence rate with which the solution of (3) converges toward the true input of a perceptron when δ converges to zero.
3. Convergence analysis and error estimates
In this section, we show that the proposed model (3) is a convergent variational regularization for the specific choice L = 1 and the assumption f(x, Θ) = Wx + b for Θ = (W, b), which reduces (3) to a variational regularization model for the perceptron case studied in Wang and Benning [31]. In contrast to Wang and Benning [31] we are not interested in estimating the perceptron parameters W and b but assume that these are fixed, and that we study the regularization operator
where dom(Ψ) is defined as dom(Ψ): = {y ∈ ℝm|Ψ(y) < ∞}. We first want to establish under which assumptions (6) is well-defined for all yδ.
3.1. Well-definedness
For simplicity, we focus on the finite-dimensional setting with network inputs in ℝn and outputs in dom(Ψ). However, the following analysis also extends to more general Banach space settings with additional assumptions on the operator W, see for instance [24], Section 5.1. Following [24], we assume that R is non-negative and the polar of a proper function, i.e., R = H* for a proper function H:ℝn → ℝ∪{∞}. Note that this automatically implies convexity of R. Moreover, we assume that Ψ is a proper, non-negative and convex function that is continuous on dom(Ψ), which implies that BΨ is proper, non-negative, convex in its second argument and continuous in its first argument for every yδ ∈ dom(Ψ). Then, for every g ∈ dom(Ψ) there exists x with
Last but not least, we assume that R and Ψ are chosen such that for each g ∈ dom(Ψ) and α > 0 we have
for constants a, d, and a constant c that depends monotonically non-decreasing on all arguments. With these assumptions, we can then verify the following lemma.
Theorem 1. Let the assumptions outlined in the previous paragraph be satisfied.
1. Then, for every the selection operator
is well-defined.
2. The regularization operator as defined in (3) is well-defined in the sense that for every y ∈ dom(Ψ) there exists with . Moreover, the set is a convex set.
3. For every sequence yn→y ∈ dom(Ψ) there exists a subsequence converging to an element .
Proof. The results follow directly from [24], Lemma 5.5, Theorem 5.6, and Theorem 5.7. The latter statement originally only implies convergence in the weak-star topology; however, since we are in a finite-dimensional Hilbert space, this automatically implies strong convergence here.
3.2. Error estimates
Having established that (3) is a regularization operator, we now want to prove that it is also a convergent regularization operator in the sense of the estimate
such that
Here, the term DR denotes the (generalized) Bregman distance [or divergence, [cf. [32, 33]] with respect to R, i.e.,
for two arguments and a subgradient . The vector xα is a solution of (3) with data yδ for which we assume , and C ≥ 0 is a constant. The vector x† is an element of the selection operator as specified in Lemma 1. 1, i.e., for y ∈ dom(Ψ). Note that is equivalent to x† being a R-minimizing vector amongst all vectors that satisfy 0 = W*(σ(Wx† + b) − y), where σ denotes the proximal map with respect to Ψ. This is due to the fact that is equivalent to . Assuming that σ(Wx† + b) − y does not lie in the nullspace of W*, this further implies y = σ(Wx† + b).
In order to be able to derive error estimates of the form (7), we restrict ourselves to solutions x† that are in the range of . This means that there exists y† such that . Considering the optimality condition of (3) for y†, this implies
which for v†: = (y† − σ(Wx† + b))/α = (y† − y)/α is equivalent to the existence of a source condition element v† that satisfies the source condition [cf. [22, 24]].
In the following, we verify that the symmetric Bregman distance with respect to R between a solution of the regularization operator and the solution of the inverse problem is converging to zero if the error in the data is converging to zero. The symmetric Bregman distance or Jeffreys distance between two vectors x and simply is the sum of two Bregman distances with interchanged arguments, i.e.,
for q ∈ ∂R(x) and ; hence, an error estimate in the symmetric Bregman distance also implies an error estimate in the classical Bregman distance.
Before we begin our analysis, we recall the concept of the Jensen-Shannon divergence [34], which for general proper, convex and lower semi-continuous functions F:ℝn → ℝ∪{∞} generalizes to so-called Burbea-Rao divergences [35–37] and are defined as follows.
Definition 1 (Burbea-Rao divergence). Suppose F:ℝn → ℝ∪{∞} is a proper, convex and lower semi-continuous function. The corresponding Burbea-Rao divergence is defined as
for all .
Another important concept that we need in order to establish error estimates is that of Fenchel conjugates [cf. [38]].
Definition 2 (Fenchel conjugate). The Fenchel (or convex) conjugate F*:ℝn → ℝ∪{−∞, ∞} of a function F:ℝn → ℝ∪{−∞, +∞} is defined as
The Fenchel conjugate that is of particular interest to us is the conjugate of the function BΨ(y, z) with respect to the second argument, which we characterize with the following lemma.
Lemma 1. The Fenchel conjugate of Fy(z): = BΨ(y, z) with respect to the second argument z reads
Proof. From the definition of the Fenchel conjugate we observe
which concludes the proof.
Having defined the Burbea-Rao divergence and having established the Fenchel conjugate of BΨ(y, z) with respect to the second argument z for fixed y, we can now present and verify our main result that is motivated by [39].
Theorem 2. Suppose R and Ψ satisfy the assumptions outlined in Section 3.1. Then, for data yδ and x† that satisfy with δ ≥ 0, a solution of the variational regularization problem (3), and a solution x† of the perceptron problem y = σ(Wx†+b) that satisfies and (8), we observe the error estimate
for a constant c ∈ (0, 1].
Proof. Every solution xα that satisfies can equivalently be characterized by the optimality condition
for any subgradient pα ∈ ∂R(xα). Subtracting p† ∈ ∂R(x†) from both sides of the equation and taking a dual product with then yields
We easily verify
hence, we can replace with in (10) to obtain
We know due to the convexity of , and we also know that (SC) enables us to choose p† = W*v†. Hence, we can estimate
Next, we introduce the constant c ∈ (0, 1] to split the loss functions and into and , respectively. This means we estimate
Next, we make use of Lemma 1 to estimate
and
Adding both estimates together yields
which together with the error bound concludes the proof.
Remark 1. We want to emphasize that for continuous Ψ and c > 0 we automatically observe
in which case the important question from an error estimate point-of-view is if the term converges quicker to zero than α, as we would need to guarantee in order to guarantee that the symmetric Bregman distance in (9) converges to zero for α → 0.
Example 1 (ReLU perceptron). Let us consider a concrete example to demonstrate that (6) is a convergent regularization with respect to the symmetric Bregman distance of R. We know that for σ(z) = proxΨ(z) = max(0, z) to hold true we have to choose . This means that for to be well-defined for any z we require for all i ∈ {1, …, m}. In order for the Burbea-Rao divergence to be well-defined, we further require
for all i ∈ {1, …, m}, or in more compact notation. If is guaranteed, we observe . Hence, we can simplify the estimate (9) to
where we have also divided by α on both sides of the inequality. If we choose , we obtain the estimate
as long as we can ensure
Together with we have established an estimate of the form (7), with constant . Hence, we have verified that the variational regularization method (3) is not only a regularization method but even a convergent regularization method in this specific example.
We want to briefly comment on the extension of the convergence analysis to the general case L > 1 with the following remark.
Remark 2. The presented convergence analysis easily extends to a sequential, layer-wise inversion approach. Suppose we have L layers and begin with the final layer, then we can formulate the variational problem
which is also of the form of (6), but where R has been replaced with ΨL−1. Alternatively, one can also replace ΨL−1 with another function RL−1 if good prior knowledge for the auxiliary variable xL−1 exists. Once we have estimated , we can recursively estimate
for l = L−1, …, 2 and subsequently compute xα as a solution of (3) but with data instead of yδ.
The advantage of such a sequential approach is that every individual regularization problem is convex and the previously presented theorems and guarantees still apply. The disadvantage is that for this approach to work in theory, we require bounds for every auxiliary variable of the form , which is a rather unrealistic assumption. Moreover, it is also not realistic to assume that good prior knowledge for the auxiliary variables exist.
Please note that showing that the simultaneous approach (3) is a (convergent) variational regularization is beyond the scope of this work as it is harder and potentially requires additional assumptions for the following reason. The overall objective function in (3) is no longer guaranteed to be convex with respect to all variables simultaneously, which means that we cannot simply carry over the analysis of the single-layer to the multi-layer perceptron case.
Remark 3 (Infinite-dimensional setting). Please note that almost all theoretical results presented in this section also apply to neural networks that map functions between Banach spaces instead of finite-dimensional vectors. The only result that changes is Theorem 1, Item 3, where the statement in an infinite-dimensional setting only implies convergence in the weak-star topology.
This concludes the theoretical analysis of the perceptron inversion model. In the following section, we focus on how to implement (6) and its more general counterpart (3).
4. Implementation
In this section, we describe how to computationally implement the proposed variational regularization for both the single-layer and the multi-layer perceptron setting. More specifically, we show that the proposed variational regularization can be efficiently solved via a generalized primal-dual hybrid gradient method and a coordinate descent approach.
4.1. Inverting perceptrons
To begin with, we first consider the example of inverting a (single-layer) perceptron. For L = 1, Problem (3) reduces to (6), which for a composite regularization function R°K reads
Here K is a matrix and αR(Kx) denotes the regularization function acting on the argument x. The above Problem (11) can be reformulated to the saddle-point problem
where R* denotes the convex conjugate of R. Computationally, we can then solve the saddle-point problem with a generalized version [40] of the popular primal-dual hybrid gradient (PDHG) method [41–45]:
where we alternate between a descent step in the x variable and an ascent step in the dual variable z. Since (11) is a convex minimization problem, (13) is guaranteed to converge globally for arbitrary starting point, given that τx and τz are chosen such that and such that (13a) is contractive [check [40], Theorem 5.1 for details].
In this work, we will focus on the discrete total variation ||∇x||p, 1, [46, 47], as our regularization function R(Kx), but other choices are certainly possible. If we consider a two-dimensional scalar-valued image x ∈ ℝH×W, we can define a finite forward difference discretization of the gradient operator ∇:ℝH×W → ℝH×W×2 as
The discrete total variation is defined as the ℓ1 norm of the p-norm of the pixel-wise image gradients, i.e.
For our numerical results we consider the isotropic total variation and consequently choose p = 2. Hence for a perceptron with affine-linear transformation f(x, Θ) = Wx+b, and with σ = proxΨ denoting the activation function, the PDHG approach (13) of solving the perceptron inversion problem (6) can be summarized as
Please note that we define the discrete approximation of the divergence div such that it satisfies div = −∇⊤ in order to be the negative transpose of the discretized finite difference approximation of the gradient in analogy to the continuous case, which is why the sign in (14a) is flipped in comparison to (13a). The proximal map with regards to the convex conjugate of is simply the argument itself if the maximum of the Euclidean vector-norm per pixel is bounded by one or the projection onto this unit ball.
4.2. Inverting multi-layer perceptrons
We now discuss the implementation of the inversion of multi-layer perceptrons with L layers as described in (3). Note that in this case in order to minimize for x, we also need to optimize with respect to the auxiliary variables x1, …, xL−1.
For the minimization of (3) we consider an alternating minimization approach, also known as coordinate descent [48–50]. In this approach we minimize the objective with respect to one variable at a time. In particular, we focus on a semi-explicit coordinate descent algorithm, where we linearize with respect to the smooth functions of the overall objective function. This breaks down the overall minimization problem into L sub-problems, where for x0 and each xl variable for l ∈ {1, …, L−1}, we have individual minimization problems of the following form:
Note that one advantage for adopting this approach is that we exploit that the overall objective function is convex in each individual variable when all other variables are kept fixed. In the following, we will discuss different strategies to computationally solve each sub-problem.
When optimizing with respect to the input variable x0, the structure of sub-problem (15a) is identical to the perceptron inversion problem that we have discussed in Section 4.1. Hence, we can approximate with (12), but now with respect to instead of yδ, which yields the iteration
For each auxiliary variable xl with l ∈ {1, …, L−1}, the sub-problem associated with (15b) amounts to solving a proximal gradient step with suitable step-size τxl, which we can rewrite to
This concludes the discussion on the implementation of the regularized single-layer and multi-layer perceptron inversion. In the next section, we present some numerical results to demonstrate the effectiveness of the proposed approaches empirically.
5. Numerical results
In this section, we present numerical results for the perceptron inversion problem implemented with the PDHG algorithm as outlined in (14), and for the multi-layer perceptron inversion problem implemented with the coordinate descent approach as described in (16) and (17). In the following, we first demonstrate that we can invert a perceptron with random weights and bias terms and ReLU activation function via (11) with total variation regularization and the algorithm described in (14). We then proceed to a more realistic example of inverting the code of a simple autoencoder with perceptron encoder, before we extend the results to the total variation-based inversion of encodings from multi-layer convolutional autoencoders. All results have been computed using PyTorch 3.7 on an Intel Xeon CPU E5-2630 v4.
5.1. The perceptron
We present results for two experiments: the first one is the perceptron inversion of the image of a circle from the noisy output of the perceptron, where we compare the Landweber regularization and the total-variation-based variational regularization (6). For the second experiment, we perform perceptron inversion for samples from the MNIST dataset [51], where we compare the performance of the proposed inversion strategy with the performance of linear and nonlinear decoders on the collection of (approximately) piecewise constant images of hand-written digits.
5.1.1. Circle
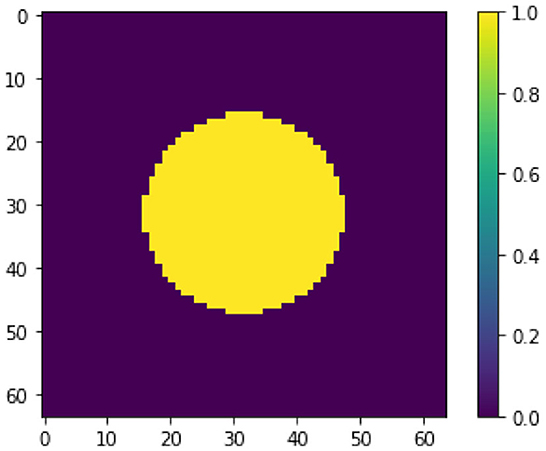
We begin with the toy example of recovering the image of a circle from noisy measurements of a ReLU perceptron. To prepare the experiment, we generate a circle image x† ∈ ℝ64 × 64, as shown in Figure 1. We construct a perceptron with ReLU activation function using random weights and biases where W ∈ ℝ512 × 4, 096, b ∈ ℝ512 × 1. The weights operates on the column-vector representation of x, where x ∈ ℝ4, 096 × 1. The noise-free data is generated via the forward operation of the model, i.e., y = σ(Wx†+b). We generate noisy data yδ by adding Gaussian noise with mean 0 and standard deviation 0.005. Note that we clip all the negative values of yδ to ensure yδ ∈ dom(Ψ).
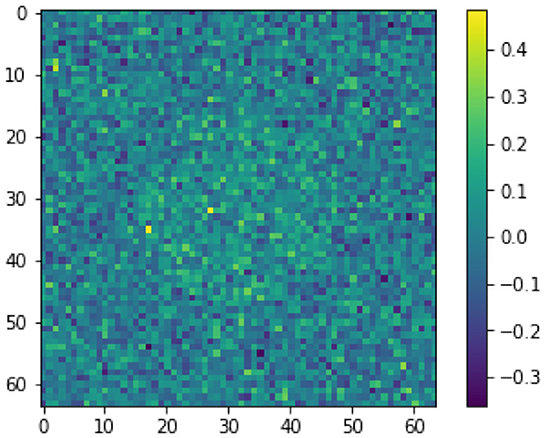
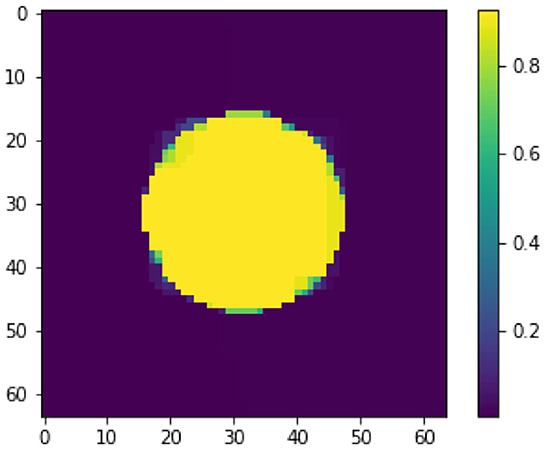
A first attempt to solve this ill-posed perceptron inversion problem is via Landweber regularization [52]. In Figure 2, we see the reconstructed image obtained with Landweber regularization in combination with early stopping following Morozov's discrepancy principle [22, 53]. Even though the Landweber regularized reconstruction matches the data up to the discrepancy value ||σ(WxK + b) − yδ||, the recovered image does not resemble the image x†. We will discuss shortly the reason for this visually poor inversion. In comparison, we see a regularized inversion via the total variation regularization approach following (14) in Figure 3. The regularization parameter for this reconstruction is chosen as α = 1.5 × 10−2. Both x0 and z are initialized with zero vectors. The stepsize-parameters are chosen as and τz = 1/(8α), see [54]. We stop the iterations when changes in x0 and z in norm are less than a threshold of 10−5 or when we reach the maximum number of iterations, which we set to 10, 000. As shown in Figure 3, the TV-regularization approach is capable of finding a (visually) more meaningful solution.
To explain why the Landweber iteration performs worse compared to the total variation regularization for this specific example, we compare the ℓ2 norms of each two solutions and the groundtruth image x†. The ℓ2 norm of the Landweber solution in Figure 2 measures 6.58 while the TV-regularized solution as in Figure 3 and the groundtruth image x† measure 25.69 and 28.07, respectively. This is not surprising, as the Landweber iteration is known to converge to a minimal Euclidean norm solution if the noise level converges to zero. On the other hand, when we compare the TV semi-norm of each solution, the groundtruth image in measures 128.0, while the Landweber solution in Figure 2 and TV-regularized solution in Figure 3 measure 707.02 and 114.93, respectively, suggesting that the TV-semi-norm is a more suitable regularization function for the inversion of cartoon-like images such as x†.
5.1.2. MNIST
In this second example, we perform perceptron inversion on the MNIST dataset [51]. In particular, we consider the following experimental setup. We first train an autoencoder , where and denotes the decoder and the encoder, parameterized by parameters and , respectively. We pre-train the autoencoder , compute the code and assign it to the noise-free data variable y, and solve the inverse problem for the input x from the perturbed code yδ
To be more precise, we first train a two-layer fully connected autoencoder using the vanilla stochastic gradient method (SGM) by minimizing the mean squared error (MSE) on the MNIST training dataset. We set the code dimension to 100 and use ReLU as the activation function. Hence where and .
We then invert the code via (11) with Equation (14). All MNIST images are centered as a means of pre-processing. The stepsize-parameters are chosen at and τz = 1/(8α). We choose the regularization parameter α in the range [10−4, 10−2] and set to 5 × 10−3 for all sample images from the training set, and to α = 5 × 10−2 for all sample images from the validation set. These choices work well with regards to the visual quality of the inverted images.
In Figure 4, we show visualizations of five sample images from the training set, and from the validation set respectively. In comparison, we have also visualized the decoder output. As can be seen, using the code that contains the same compressed information, the inverted images show more clearly defined edges and better visual quality than the decoded outputs. This is to be expected as we compare a nonlinear regularized inversion method with a linear decoder.

Figure 4. Groundtruth input images from the MNIST training dataset (Left) and validation dataset (Right), together with the corresponding autoencoder output images and inversions xα of the encoding via (11).
5.2. Multi-layer perceptrons
In this section, we present numerical results for inverting multi-layer perceptrons. In particular, we consider feedforward neural networks with convolutional layers (CNN), where in the network architecture two-dimensional convolution operations are used to represent the linear operations in the affine-linear functions f(x, Θ). Similar to the experimental design described in Section 5.1, we consider a multi-layer neural network inversion problem where we infer input image x from a noise perturbed code yδ.
More specifically, we first train a six-layer convolutional autoencoder on the MNIST training dataset via stochastic gradient method to minimize the MSE. The encoder consists of two convolutional layers, both with 4 × 4 convolutions with stride 2, each followed by the application of a ReLU activation function. As image spatial dimension reduces by half, we double the number of feature channels from 8 to 16. We use a fully-connected layer with weights and bias to generate the code. The decoder network first expands the code with an affine-linear transformation with weights and bias . This is followed by two layers of transpose convolutions with kernel size 4 × 4, where each is followed by a ReLU activation function. The number of feature channels halves each time as we double the spatial dimension.
Following the implementation details outlined in Section 4.2, we iteratively compute the update steps (16) and (17) to recover x from . For the PDHG method, we choose the stepsize-parameters as and τz = 1/(8α). The initial values x0 and z are both zero. The update steps stop either after reaching the maximum iterations of 1, 500 or when the improvements on x0 and z are < 10−5 in norm. For the coordinate descent algorithm, the stepsize-parameters are set to for each layer, where ||·|| denotes the spectral norm.
In Figure 5, we visualize the inverted images, the decoder output images, along with the groundtruth images, from the training dataset and validation dataset, respectively. For each image, α is chosen in the range [10−4, 10−2] and set at 9 × 10−3 for both training sample images and validation sample images for best visual inversion quality.

Figure 5. Groundtruth input images from the MNIST training dataset (Left) and validation dataset (Right), together with the corresponding CNN autoencoder output images and inversions xα of the encoding via (3).
In Figure 6, we further compare how total variation regularization and decoder respond to different levels of data noise. The noisy data is produced by adding Gaussian noise to perturb the code of each image. We start with zero mean Gaussian noise with standard deviation 0.33 and gradually reduce the noise level, this translates to decreasing δ2 from 6.80 down to 0.00.
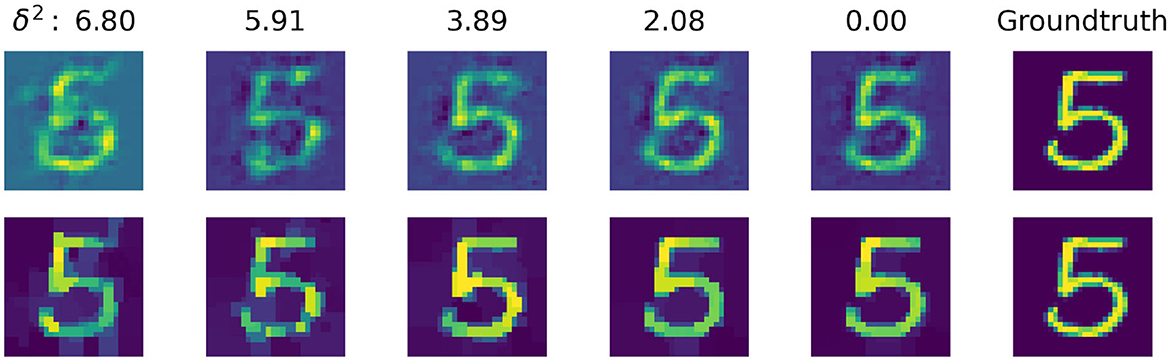
Figure 6. Visualization of the comparison between inverted image and decoded image against various levels of noise. (Top) Decoded output image from the trained convolutional autoencoder. (Bottom) Inverted input image from the CNN with total variation regularization.
Please note that for each noise level the regularization factor α is manually selected in the range [10−4, 10−2] for the best PSNR value. As we can see, for the noise level with standard deviation 0.33 where δ2 is at 6.80, the decoder is only capable of producing a blurry distorted output, while the inverted image shows the structure of the digit more clearly. When we decrease the noise level down to 0.00, the inverted image becomes more clean-cut while the decoded image is still less sharply defined.
Figure 7 plots the PSNR value of the decoded and inverted image against decreasing noise level. We want to emphasize that it would be more rigorous to compute and compare as suggested in the error estimate bound in (9), but empirically the PSNR value does also support the notion of a convergent regularization.
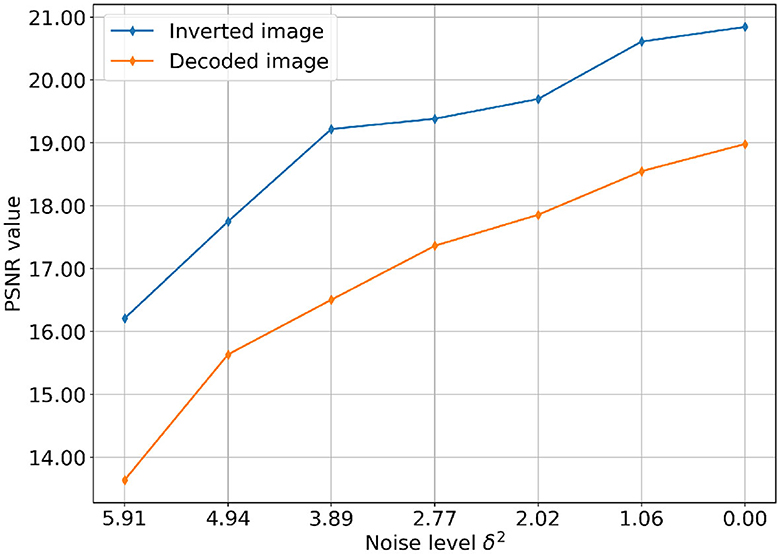
Figure 7. Comparison of PSNR values of total variation-based reconstruction and decoder output per noise level. Each curve reports the change of PSNR value over gradually decreasing levels of Gaussian noise, with δ2 ranging from 0.00 to 6.80.
6. Conclusions and outlook
We have introduced a novel variational regularization framework based on a lifted Bregman formulation for the stable inversion of feed-forward neural networks (also known as multi-layer perceptrons). We have proven that the proposed framework is a convergent regularization for the single-layer perceptron case under the mild assumption that the inverse problem solution has to be in the range of the regularization operator. We have derived a general error estimate as well as a specific error estimate for the case that the activation function is the ReLU activation function. We have also addressed the extension of the theory to the multi-layer perceptron case, which can be carried out sequentially, albeit under unrealistic assumptions. We have discussed implementation strategies to solve the proposed scheme computationally, and presented numerical results for the regularized inversion of the image of a circle and piecewise constant images of hand-written digits from single- and multi-layer perceptron outputs with total variation regularization.
Despite all the positive achievements presented in this work, the proposed framework also has some limitations. The framework is currently restricted to feed-forward architectures with affine-linear transformations and proximal activation functions. While it is straight-forward to extend the framework to other architectures such as ResNets [55] or U-Nets [56], it is not straight-forward to include nonlinear operations that cannot be expressed as proximal maps of convex functions, such as max-pooling. However, for many examples there exist remedies, such as using average pooling instead of max-pooling in the previous example.
An open question is how a convergence theory without restrictive, unrealistic assumptions can be established for the multi-layer case. One issue is the non-convexity of the proposed formulation. A remedy could be the use of different architectures that lead to lifted Bregman formulations that are jointly convex in all auxiliary variables.
And last but not least, one would also like to consider other forms of regularization, such as iterative regularization, data-driven regularizations [57], or even combinations of both [58]. However, a convergence analysis for such approaches is currently an open problem.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found at: http://yann.lecun.com/exdb/mnist/. The programming code for this study can be found in the University of Cambridge data repository at https://doi.org/10.17863/CAM.94404.
Author contributions
XW has programmed and contributed all numerical results as well as Sections 4 and 5. MB has contributed the introduction (Section 1) as well as the theoretical results (Section 3). XW and MB have contributed equally to Sections 2 and 6. Both authors contributed to the article and approved the submitted version.
Funding
The authors acknowledge support from the Cantab Capital Institute for the Mathematics of Information, the Cambridge Centre for Analysis (CCA), and the Alan Turing Institute (ATI).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
3. Simonyan K, Vedaldi A, Zisserman A. Deep inside convolutional networks: Visualising image classification models and saliency maps. In: Proceedings of the International Conference on Learning Representations (2014). p. 1–8.
4. Fong RC, Vedaldi A. Interpretable explanations of black boxes by meaningful perturbation. In: Proceedings of the IEEE International Conference on Computer Vision. (2017). p. 3429–37. doi: 10.1109/ICCV.2017.371
5. Chang CH, Creager E, Goldenberg A, Duvenaud D. Explaining image classifiers by counterfactual generation. arXiv [Preprint]. (2019). arXiv: 1807.08024. Available online at: https://arxiv.org/pdf/1807.08024.pdf
6. Fong R, Patrick M, Vedaldi A. Understanding deep networks via extremal perturbations and smooth masks. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. (2019). p. 2950–8. doi: 10.1109/ICCV.2019.00304
7. Mahendran A, Vedaldi A. Understanding deep image representations by inverting them. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2015). p. 5188–96. doi: 10.1109/CVPR.2015.7299155
8. Linden A, Kindermann J. Inversion of multilayer nets. In: Proceedings of International Joint Conference on Neural Networks. Vol. 2 (1989). p. 425–30. doi: 10.1109/IJCNN.1989.118277
9. Kindermann J, Linden A. Inversion of neural networks by gradient descent. Parallel Comput. (1990) 14:277–86. doi: 10.1016/0167-8191(90)90081-J
10. Jensen CA, Reed RD, Marks RJ, El-Sharkawi MA, Jung JB, Miyamoto RT, et al. Inversion of feedforward neural networks: algorithms and applications. Proc IEEE. (1999) 87:1536–49. doi: 10.1109/5.784232
11. Lu BL, Kita H, Nishikawa Y. Inverting feedforward neural networks using linear and nonlinear programming. IEEE Trans Neural Netw. (1999) 10:1271–90. doi: 10.1109/72.809074
13. Rezende D, Mohamed S. Variational inference with normalizing flows. In: International Conference on Machine Learning. (2015). p. 1530–8.
14. Dinh L, Krueger D, Bengio Y. Nice: Non-linear independent components estimation. In: International Conference on Learning Representations (2015).
15. Zhu JY, Park T, Isola P, Efros AA. Unpaired image-to-image translation using cycle-consistent adversarial networks. In: Proceedings of the IEEE International Conference on Computer Vision. (2017). p. 2223–32. doi: 10.1109/ICCV.2017.244
16. Sohl-Dickstein J, Weiss E, Maheswaranathan N, Ganguli S. Deep unsupervised learning using nonequilibrium thermodynamics. In: International Conference on Machine Learning. (2015). p. 2256–65.
17. Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models. Adv Neural Inform Process Syst. (2020) 33:6840–51.
18. Behrmann J, Grathwohl W, Chen RT, Duvenaud D, Jacobsen JH. Invertible residual networks. In: International Conference on Machine Learning. (2019). p. 573–82.
19. Behrmann J, Vicol P, Wang KC, Grosse R, Jacobsen JH. Understanding and mitigating exploding inverses in invertible neural networks. In: International Conference on Artificial Intelligence and Statistics. (2021). p. 1792–800.
20. Xia W, Zhang Y, Yang Y, Xue JH, Zhou B, Yang MH. GAN inversion: a survey. IEEE Trans Pattern Anal Mach Intell. (2022) 45:3121–38. doi: 10.1109/TPAMI.2022.3181070
21. Gal R, Alaluf Y, Atzmon Y, Patashnik O, Bermano AH, Chechik G, et al. An image is worth one word: Personalizing text-to-image generation using textual inversion. arXiv preprint arXiv:220801618. (2022).
22. Engl HW, Hanke M, Neubauer A. Regularization of Inverse Problems. Vol. 375. Springer Science & Business Media (1996). doi: 10.1007/978-94-009-1740-8
23. Scherzer O, Grasmair M, Grossauer H, Haltmeier M, Lenzen F. Variational Methods in Imaging. (2009). doi: 10.1007/978-0-387-69277-7
24. Benning M, Burger M. Modern regularization methods for inverse problems. Acta Numer. (2018) 27:1–111. doi: 10.1017/S0962492918000016
25. Lunz S, Öktem O, Schönlieb CB. Adversarial regularizers in inverse problems. In: Advances in Neural Information Processing Systems. (2018). p. 31.
26. Arridge S, Maass P, Öktem O, Schönlieb CB. Solving inverse problems using data-driven models. Acta Numer. (2019) 28:1–174. doi: 10.1017/S0962492919000059
27. Schwab J, Antholzer S, Haltmeier M. Deep null space learning for inverse problems: convergence analysis and rates. Inverse Probl. (2019) 35:025008. doi: 10.1088/1361-6420/aaf14a
28. Li H, Schwab J, Antholzer S, Haltmeier M. NETT: Solving inverse problems with deep neural networks. Inverse Probl. (2020) 36:065005. doi: 10.1088/1361-6420/ab6d57
29. Mukherjee S, Dittmer S, Shumaylov Z, Lunz S, Öktem O, Schönlieb CB. Learned convex regularizers for inverse problems. arXiv preprint arXiv:200802839v2. (2021).
30. Wang X, Benning M. Lifted Bregman training of neural networks. arXiv preprint arXiv:220808772. (2022).
31. Wang X, Benning M. Generalised perceptron learning. In: 12th Annual Workshop on Optimization for Machine Learning. (2020). Available online at: https://opt-ml.org/papers/2020/paper_68.pdf
32. Bregman LM. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput Math Math Phys. (1967) 7:200–17. doi: 10.1016/0041-5553(67)90040-7
33. Kiwiel KC. Proximal minimization methods with generalized Bregman functions. SIAM J Control Optim. (1997) 35:1142–68. doi: 10.1137/S0363012995281742
34. Lin J. Divergence measures based on the Shannon entropy. IEEE Trans Inform Theory. (1991) 37:145–51. doi: 10.1109/18.61115
35. Burbea J, Rao C. On the convexity of higher order Jensen differences based on entropy functions (Corresp.). IEEE Trans Inform Theory. (1982) 28:961–3. doi: 10.1109/TIT.1982.1056573
36. Burbea J, Rao C. On the convexity of some divergence measures based on entropy functions. IEEE Trans Inform Theory. (1982) 28:489–95. doi: 10.1109/TIT.1982.1056497
37. Nielsen F, Boltz S. The burbea-rao and bhattacharyya centroids. IEEE Trans Inform Theory. (2011) 57:5455–66. doi: 10.1109/TIT.2011.2159046
39. Benning M, Burger M. Error estimates for general fidelities. Electron Trans Numer Anal. (2011) 38:77.
40. Chambolle A, Pock T. An introduction to continuous optimization for imaging. Acta Numer. (2016) 25:161–319. doi: 10.1017/S096249291600009X
41. Zhu M, Chan T. An efficient primal-dual hybrid gradient algorithm for total variation image restoration. Ucla Cam Rep. (2008) 34:8–34.
42. Pock T, Cremers D, Bischof H, Chambolle A. An algorithm for minimizing the Mumford-Shah functional. In: 2009 IEEE 12th International Conference on Computer Vision. (2009). p. 1133–40. doi: 10.1109/ICCV.2009.5459348
43. Esser E, Zhang X, Chan TF. A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science. SIAM J Imaging Sci. (2010) 3:1015–46. doi: 10.1137/09076934X
44. Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imaging Vis. (2011) 40:120–45. doi: 10.1007/s10851-010-0251-1
45. Benning M, Riis ES. Bregman methods for large-scale optimization with applications in imaging. In: Chen K, Schönlieb CB, Tai XC, Younces L, editors. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging. Cham: Springer (2023). doi: 10.1007/978-3-030-03009-4_62-2
46. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Phys D. (1992) 60:259–68. doi: 10.1016/0167-2789(92)90242-F
47. Chambolle A, Lions PL. Image recovery via total variation minimization and related problems. Numer Math. (1997) 76:167–88. doi: 10.1007/s002110050258
48. Beck A, Tetruashvili L. On the convergence of block coordinate descent type methods. SIAM J Optim. (2013) 23:2037–60. doi: 10.1137/120887679
49. Wright SJ. Coordinate descent algorithms. Math Programm. (2015) 151:3–34. doi: 10.1007/s10107-015-0892-3
50. Wright SJ, Recht B. Optimization for Data Analysis. Cambridge University Press (2022). doi: 10.1017/9781009004282
51. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. (1998) 86:2278–324. doi: 10.1109/5.726791
52. Landweber L. An iteration formula for Fredholm integral equations of the first kind. Am J Math. (1951) 73:615–24. doi: 10.2307/2372313
53. Morozov VA. Methods for Solving Incorrectly Posed Problems. Springer Science & Business Media (2012).
54. Chambolle A. An algorithm for total variation minimization and applications. J Math Imaging Vis. (2004) 20:89–97. doi: 10.1023/B:JMIV.0000011321.19549.88
55. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2016). p. 770–8. doi: 10.1109/CVPR.2016.90
56. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015: 18th International Conference. Munich: Springer (2015). p. 234–41. doi: 10.1007/978-3-319-24574-4_28
57. Kabri S, Auras A, Riccio D, Bauermeister H, Benning M, Moeller M, et al. Convergent data-driven regularizations for CT reconstruction. arXiv [Preprint]. (2022). arXiv: 2212.07786. Available online at: https://arxiv.org/pdf/2212.07786.pdf
Keywords: inverse problems, regularization theory, lifted network training, Bregman distance, perceptron, multi-layer perceptron, variational regularization, total variation regularization
Citation: Wang X and Benning M (2023) A lifted Bregman formulation for the inversion of deep neural networks. Front. Appl. Math. Stat. 9:1176850. doi: 10.3389/fams.2023.1176850
Received: 01 March 2023; Accepted: 08 May 2023;
Published: 13 June 2023.
Edited by:
Housen Li, University of Göttingen, GermanyReviewed by:
Laura Antonelli, National Research Council (CNR), ItalyMarkus Haltmeier, University of Innsbruck, Austria
Copyright © 2023 Wang and Benning. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Benning, bS5iZW5uaW5nQHFtdWwuYWMudWs=
 Xiaoyu Wang1
Xiaoyu Wang1 Martin Benning
Martin Benning