Optimal vaccination control for COVID-19 in a metapopulation model: a case of the Philippines

We investigate a contextual problem of how to distribute a limited supply of vaccines over a period of time in a country where different regions have its own vaccination capacities. Considering that daily vaccination will affect future disease progression, we aim to find a distribution strategy over time that can minimize the total infection and implementation costs. Lagrangian and Eulerian migrations connect our multi-patch COVID-19 model, and vaccination is added as a control measure. An optimal control problem with an isoperimetric constraint is formulated and solved using the Adapted Forward–Backward Sweep Method. In distributing 5 million vaccines in 50 days, simulations showed that the optimal control strategy could lead to a difference of reducing two hundred thousand infections in just one region.

1. Introduction

The rapid development of COVID-19 vaccines, which began less than a year after the emergence of the SARS-CoV-2 virus, has made vaccination arguably the most effective method for preventing the spread of COVID-19 [1–3]. Despite the numerous problems with the COVID-19 vaccine, global communities applauded its introduction and accelerated mass vaccination. The Philippines have administered 166,138,040 vaccinations as of 8 December 2022 since vaccinations began in March 2021. It includes the first and second doses (71 million and 73 million, respectively) and more than 21 million booster doses administered to frontline workers, senior citizens, and the immunocompromised ¹. In the second quarter of 2020–2021, the government's gross domestic product (GDP) increased by 12.1% due to the expansion of economic activities made possible by vaccination mandates and the strengthening of minimum health protocols. This is in stark contrast to the −16.6% GDP recorded at the height of the pandemic [4]. In addition, the unemployment rate decreased from 8.8 percent in 2021 to 6.4 percent in 2022.

By the end of 2022, however, approximately 36 percent of the country's population still remained not fully vaccinated. In some areas of the region, vaccination participation is low. Vaccine hesitancy is endemic in every nation. In the Philippines, the decision to vaccinate can be influenced by differing factors, including individuals (i.e., perceptions of vaccine effectiveness and also inefficiency and inflexibility of the system), the community (i.e., vaccine hesitancy for religious reasons and social networks), and the health system (politics and policy) [5]. On a global level, countries with large vaccine industries reserve their own supplies for their own populations. Moreover, global manufacturing capabilities remain far below what is required, which leads to vaccine politics or global competition over a limited supply. The longer the vaccinations are delayed, the greater the likelihood that new virus strains will emerge and undermine the efficiency of vaccines.

Since the early stages of the pandemic, mathematical modeling has assisted the Philippines in its response, and a number of studies [6–8], including regional ones [9, 10], have been published. In addition, it has been used extensively in many countries to evaluate pandemic control strategies such as lockdown, social distancing, testing, face mask use, and public awareness [11–21].

With the introduction of COVID-19 vaccines, numerous modeling studies on vaccine allocation are available worldwide, based on age or risk group [22–25], space [26], and dose timing [27, 28]. However, there are few mathematical modeling studies on the optimal control of vaccine prioritization against COVID-19 at the regional level. Molla et al. [29] introduced an SEIR-type compartmental model with vaccination that accounts for heterogeneity across age groups and mobility across geographic regions. To optimize the allocation of vaccines in Italy, Lemaitre et al. [30] evaluated a second spatially explicit COVID-19 epidemiological model of the SEIR type, which proposes prioritizing precise targeting over delivery speed to increase the number of doses distributed in provinces where the impact of vaccines is anticipated to be greater.

In light of the fact that the Philippines is an archipelagic nation with vaccine supply and distribution issues, an effective spatial vaccination prioritization strategy must be developed to optimize the use of the limited vaccine supply. Thus, the objective of this paper is to use optimal control theory to determine time-dependent optimal vaccine allocation strategies that could minimize infections with associated intervention costs under various epidemiological scenarios, including mobility, supply level, infected individuals, and vaccination capacity. See our problem setup below.

In support of the “last mile” program of the Philippines, [31], we hope that the findings of this paper will help improve COVID-19 vaccine uptake and reach.

2. Problem setup

There are 17 regions in the Philippines. The nation's vaccine supply arrived in large quantities, and it should be distributed to the regions over a period of time. Since there is definitely a very limited supply, a methodical approach to distributing it over time to the various regions is required. The distribution of the vaccines should minimize both the implementation expenditure and the country's overall risk of infection. Each region has a daily cap on the number of people it can immunize, which restricts the distribution. Additionally, it is conceivable that each day that vaccines are administered will impact the disease's progression in the following days. One may consider using a linear program right at the beginning of the distribution. This, however, will not be able to take the effects of vaccination over time into account. One option is to use a dynamic linear program to solve it every day while also resolving how the disease develops in relation to the impact of vaccinations from the day before. This is technically feasible but very computationally demanding. Here, we demonstrate how to use optimal control theory to address these constraints and resolve the distribution problem, with an emphasis on the Philippines.

We do not intend to evaluate the vaccination policy choices made by the Philippine government in this article. With the constraints and goal discussed above, this study aims to demonstrate the viability of using mathematical optimization, more specifically optimal control theory, to resolve the distribution problem.

3. Mathematical model

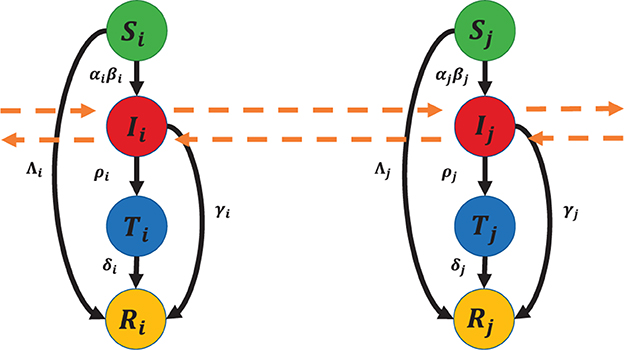
In [32], a modeling concept of the progression of COVID-19 disease was presented. This modeling concept serves as the basis for the base model, which represents a single region. The structure of the model makes it possible to estimate the hidden untested infection figure, which is also sometimes referred to as the dark figure of the pandemic. This estimate can be obtained by using the model. Instead of having a separate compartment for the vaccinated people in this study, we incorporate the effect of vaccination by the flow from the susceptible to the removed compartment. This allows us to account for the full scope of the phenomenon. During the process of applying the base model to every region of the country, we take into account the possibility that some infected individuals may travel between regions, which has the effect of influencing the transmission rate of the regions.

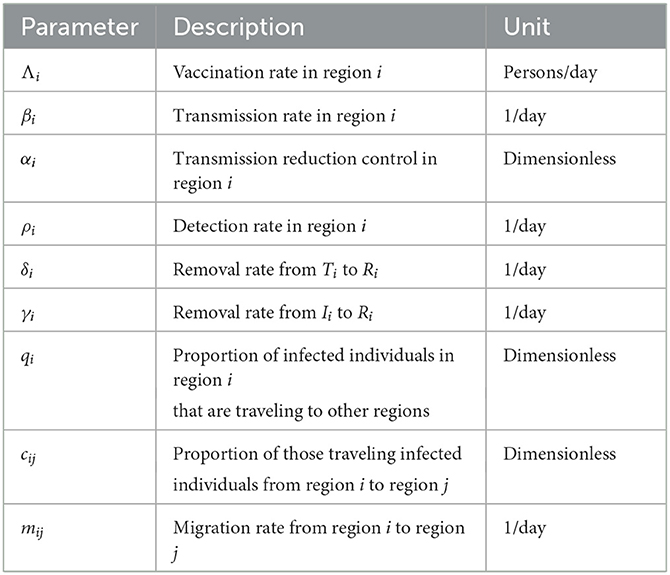
The population in region i is divided into four compartments: Susceptible (S_i), Infected (I_i), Tested positive (T_i), and Removed (R_i). The natural birth and death rates, as well as the effect of reinfection, are not accounted for in the model because the simulations used in this study are conducted over a relatively short period of time. We denote by N_0i the total population in region i. The flowchart of the model is given in Figure 1.

FIGURE 1

Figure 1. Dynamics within and between patches.

The model is governed by the following system of 4n ordinary differential equations:

For i = 1, 2, ..., n,

$\frac{d{S}_i}{dt}=-{\alpha }_i{\beta }_{0i}{S}_i(I_i+{\displaystyle \sum _{j\ne i}{c}_{ji}}{q}_j{I}_j)-{\Lambda }_i,(1)$

$\frac{d{I}_i}{dt}={\alpha }_i{\beta }_{0i}{S}_i(I_i+{\displaystyle \sum _{j\ne i}{c}_{ji}}{q}_j{I}_j)-{\displaystyle \sum _{j\ne i}{m}_{ij}}{I}_i+{\displaystyle \sum _{j\ne i}{m}_{ji}}{I}_j-({\gamma }_i+{\rho }_i)I_i,(2)$

$\begin{array}{lll}\frac{d{T}_i}{dt}& ={\rho }_i{I}_i-{\delta }_i{T}_i,& (3)\end{array}$

$\begin{array}{lll}\frac{d{R}_i}{dt}& ={\gamma }_i{I}_i+{\delta }_i{T}_i+{\Lambda }_i,& (4)\end{array}$

where j ∈ {1, 2, ..., n}, β_0i = β_i/N_0i, and ${\displaystyle \sum _{j=1}^n}{c}_{ij}=1$. The time domain is only up to time t_f, where Λ_i < S_i(t_f), for all i = 1, 2, ..., n. The description of the parameters is given in Table 1.

TABLE 1

Table 1. Parameters of the model.

4. Parameter values

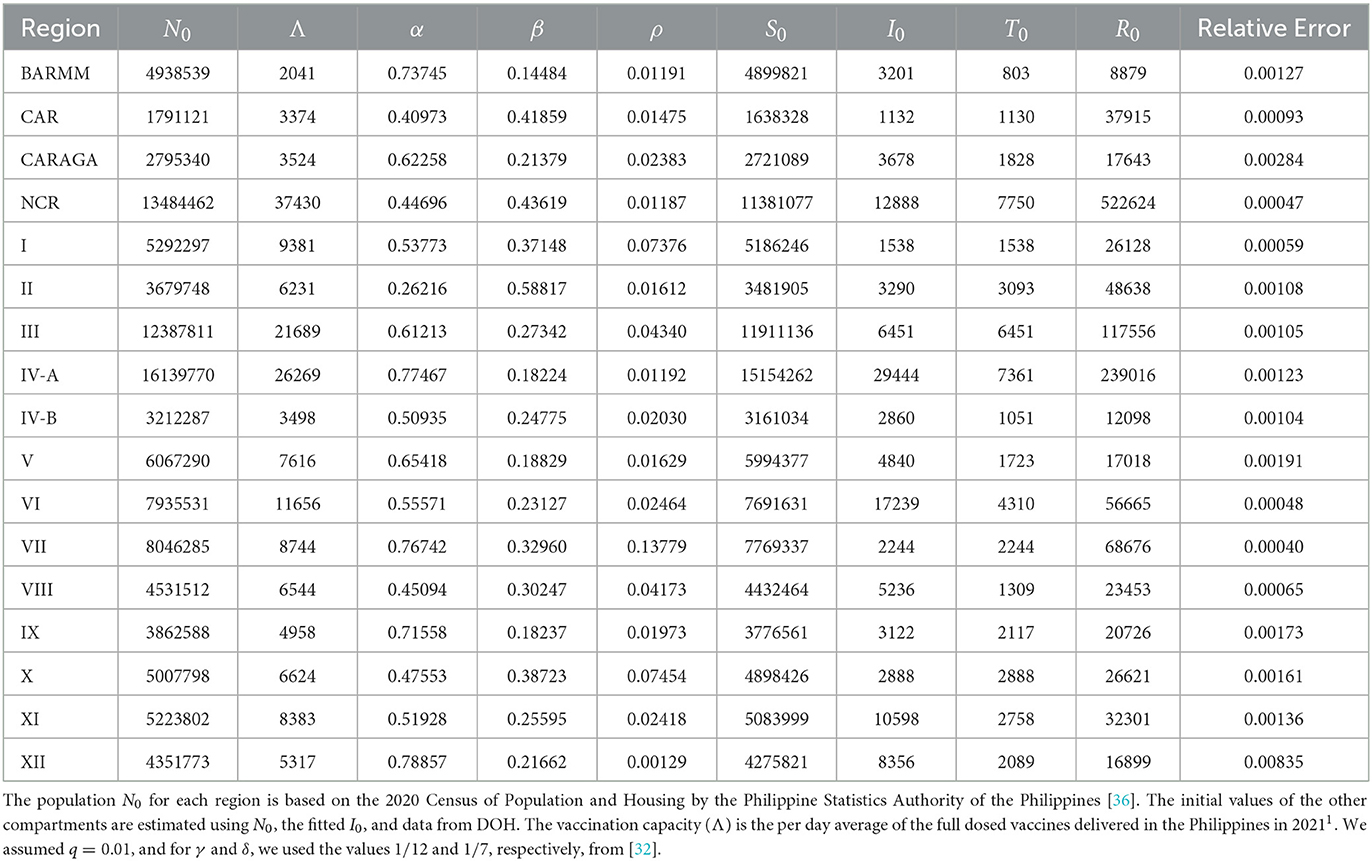
The Philippines' Department of Health (DOH) has made data on confirmed cases available to the public², so ethical approval is unnecessary. The parameter calibration was set up with the help of such information. The data spans the period of 1 June 2021 to 31 October 2021. We chose this time frame for our simulations since it represents the Philippines' first notable peak, the vaccination campaign has just recently started to gain traction, and there is a dearth of vaccines. To determine the fitted values for the parameters β, α, ρ, and I₀, we minimized a non-linear least squares function that is given by the sum of the squares of the differences between the output of the model and the data. To solve the optimization problem, the Levenberg-Marquardt algorithm and approximate Bayesian computation are used [33–35]. This was done for every region. The results are presented in Table 2, where the last column displays the relative error of the fitting technique for each region.

TABLE 2

Table 2. Parameter values.

5. Optimal control problem

In this study, we consider the vaccination controls ν_i for each region i, where 0 ≤ ν_i ≤ 1. The system with the regions' vaccination controls is given by:

For i = 1, 2, ..., n,

$\frac{d{S}_i}{dt}=-{\alpha }_i{\beta }_{0i}{S}_i(I_i+{\displaystyle \sum _{j\ne i}{c}_{ji}}{q}_j{I}_j)-{\nu }_i(t){\Lambda }_i,(5)$

$\frac{d{I}_i}{dt}={\alpha }_i{\beta }_{0i}{S}_i(I_i+{\displaystyle \sum _{j\ne i}{c}_{ji}}{q}_j{I}_j)-{\displaystyle \sum _{j\ne i}{m}_{ij}}{I}_i+{\displaystyle \sum _{j\ne i}{m}_{ji}}{I}_j-({\gamma }_i+{\rho }_i)I_i,(6)$

$\begin{array}{lll}\frac{d{T}_i}{dt}& ={\rho }_i{I}_i-{\delta }_i{T}_i,& (7)\end{array}$

$\begin{array}{lll}\frac{d{R}_i}{dt}& ={\gamma }_i{I}_i+{\delta }_i{T}_i+{\nu }_i(t){\Lambda }_i,& (8)\end{array}$

where j ∈ {1, 2, ..., n}, β_0i = β_i/N_0i, and ${\displaystyle \sum _{j=1}^n}{c}_{ij}=1$. Our time domain is only up to time t_f such that Λ_i < S_i(t_f), for all i = 1, 2, ..., n.

Our objective is to determine the vaccine distribution to the regions over time so that the total number of infections for a given period and the associated cost are minimized. We take note of the fact that our options are constrained by the vaccines that are on hand and the daily vaccination capacity of each region.

Letting B be the total number of available vaccines, the objective functional to be minimized is given by

$J({\nu }_1,{\nu }_2,\mathrm{...},{\nu }_n)={\displaystyle {\int }_{t_0}^{t_f}{\displaystyle \sum _{i=1}^n(}}{I}_i(t)+\frac{A_i}{2}{\nu }_i^2(t))dt(9)$

such that

$\begin{array}{ll}{\displaystyle {\int }_{t_0}^{t_f}}{\displaystyle \sum _{i=1}^n}{\nu }_i(t){\Lambda }_{i}dt=B.& (10)\end{array}$

Equation (10) is an isoperimetric constraint, and we will do the trick discussed in [37]. We let Z(t) be an additional state variable such that

$\begin{array}{ll}{Z}^{\prime }(t)={\displaystyle \sum _{i=1}^n}{\nu }_i(t){\Lambda }_i,& (11)\end{array}$

where Z(t₀) = 0 and Z(t_f) = B. Note that then we will have satisfied (10).

The Hamiltonian H is then given by

$H={\displaystyle \sum _{i=1}^n(}{I}_i(t)+\frac{A_i}{2}{\nu }_i^2(t)+{\lambda }_{Si}{G}_{Si}+{\lambda }_{Ii}{G}_{Ii}+{\lambda }_{Ti}{G}_{Ti}+{\lambda }_{Ri}{G}_{Ri})+{\lambda }_Z{G}_Z,$

where G_Si, G_Ii, G_Ti, G_Ri, and G_Z are the right hand sides of Equations (5), (6), (7), (8), and (11), respectively, for i = 1, 2, ..., n. Applying Pontryagin's maximum principle, there exist adjoint variables λ_Si, λ_Ii, λ_Ti, λ_Ri, λ_Z, i = 1, 2, ..., n, which satisfy the following system of ordinary differential equations: for i = 1, …, n,

$\begin{array}{l}\frac{\partial {\lambda }_{Si}}{\partial t}=({\lambda }_{Si}-{\lambda }_{Ii}){\alpha }_i{\beta }_{0i}(I_i+{\displaystyle \sum _{j\ne i}}{c}_{ji}{q}_j{I}_j),\\ \frac{\partial {\lambda }_{Ii}}{\partial t}=-1+({\lambda }_{Si}-{\lambda }_{Ii}){\alpha }_i{\beta }_{0i}{S}_i+({\lambda }_{Ii}-{\lambda }_{Ri}){\gamma }_i+({\lambda }_{Ii}-{\lambda }_{Ti}){\rho }_i{\tau }_i,\\ +{\displaystyle \sum _{j\ne i}}\left[({\lambda }_{Ii}-{\lambda }_{Ij})m_{ij}+({\lambda }_{Sj}-{\lambda }_{Ij})c_{ij}{q}_i{\alpha }_j{\beta }_{0j}{S}_j\right],\\ \frac{\partial {\lambda }_{Ti}}{\partial t}=({\lambda }_{Ti}-{\lambda }_{Ri}){\delta }_i,\\ \frac{\partial {\lambda }_{Ri}}{\partial t}=0,\\ \frac{\partial {\lambda }_Z}{\partial t}=0,\end{array}$

with transversality conditions λ_Si(t_f) = λ_Ii(t_f) = λ_Ti(t_f) = λ_Ri(t_f) = 0, for i = 1, 2, ..., n.

For i = 1, …, n, optimal controls ν_i(t) are derived by the following optimality conditions:

$\begin{array}{ll}\frac{\partial H}{\partial {\nu }_i}={\nu }_i(t)A_i-({\lambda }_{Si}-{\lambda }_{Ri}-{\lambda }_Z){\Lambda }_i=0.& (12)\end{array}$

We thus have the following theorem.

Theorem 5.1. Problem (9)-(10) has a solution and the optimal control variables are given by, for i = 1, …, n

${\nu }_i(t)=max\left(0,min\left(\frac{({\lambda }_{Si}-{\lambda }_{Ri}-{\lambda }_Z){\Lambda }_i}{A_i},1\right)\right).$

6. Simulations

Using the adapted forward-backward sweep method, which is used to solve isoperimetric problems [37], we numerically solved the optimization problem. This is a combination of the forward-backward sweep method and the shooting method, which is a variation of Newton's method for finding zeros. In the simulations, we consider distributing 5 million vaccines over a period of 50 days, subject to the limitations described in Section 2. Thus, we anticipated the arrival of the next batch of vaccines in 50 days.

6.1. Intuition vs. optimal control

Table 2 lists the daily vaccination capacity for each region. Our intuition would lead us to recommend administering each region's full daily allotment of vaccines until they are all consumed. This suggests that all 5 million vaccine doses will be consumed in just 28 days. Figures 2A, B show this strategy. Figure 2A displays the control values for all regions, which are 100% for 28 days, and Figure 2B displays the number of vaccines each region uses based on their daily vaccination capacity.

FIGURE 2

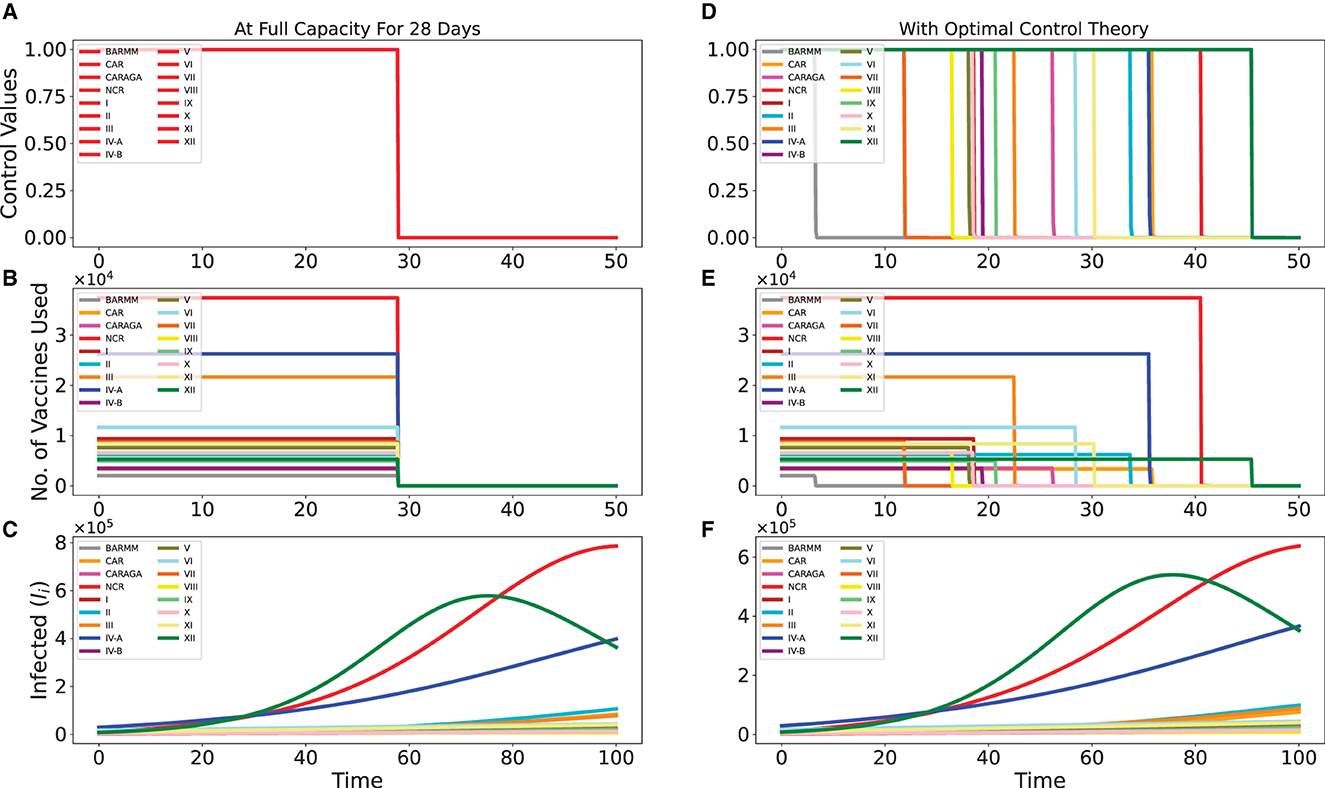
Figure 2. Intuitive vaccination strategy of distributing the vaccines by the full capacity of each region for 28 days vs. distribution strategy via optimal control theory. Here, we only have 5 million vaccines to be distributed in 50 days. In (A, D), we have the control values, while in (B, E) we have the no. of vaccines used, for both strategies. In (C, F), we extend the simulation time up to 100 to better see the effect of the vaccination strategies.

The Philippines has implemented lockdowns and border control between regions during the simulation's time frame (1 June 2021 to 31 October 2021). We assume these precautions are sufficient to prevent infected people from traveling between different regions. The impact of infected people moving between regions is not included in this simulation. During this time, every region urgently needs vaccination; therefore, implementation costs are not a concern. Therefore, the implementation cost for each region in this simulation is set at the same value. However, these values can be modified easily if necessary.

Figure 2C illustrates how this intuitive strategy affected the disease progression in each region. This is compared to the distribution strategy derived from optimal control theory shown in Figures 2D, E, with the effect on disease progression given in Figure 2F. One can observe that it did not advocate using all of each region's resources for 28 days. The NCR, III, and IV-A regions received higher priority under the strategy. Since infection rates were much higher in these areas, especially in the three regions XII, NCR, and IV-A, which could be seen clearly in Figures 2C, F, this strategy can be explained by the need to control the progression of the disease there.

Even though the progression of the disease looks the same for both strategies, the optimal control strategy is better at stopping infections than the other one. This is evident when comparing the y-axes of Figures 2C, F, which compare the two strategies. As an illustration, for NCR, the infected reached approximately 8 × 10⁵ using the intuitive strategy but only approximately 6 × 10⁵ using the optimal control strategy.

Information about the overall infection can be found in Figure 3. According to the intuitive strategy shown in the left figure, all 5 million vaccines were used up by Day 28, compared to that to the non-linear, more gradual approach of the optimal control strategy. The total number of infected people over time in each of the 17 regions is shown in the right figure. The simulation is carried out through Day 100 to clearly demonstrate how the sums vary (with no additional vaccination after Day 50).

FIGURE 3

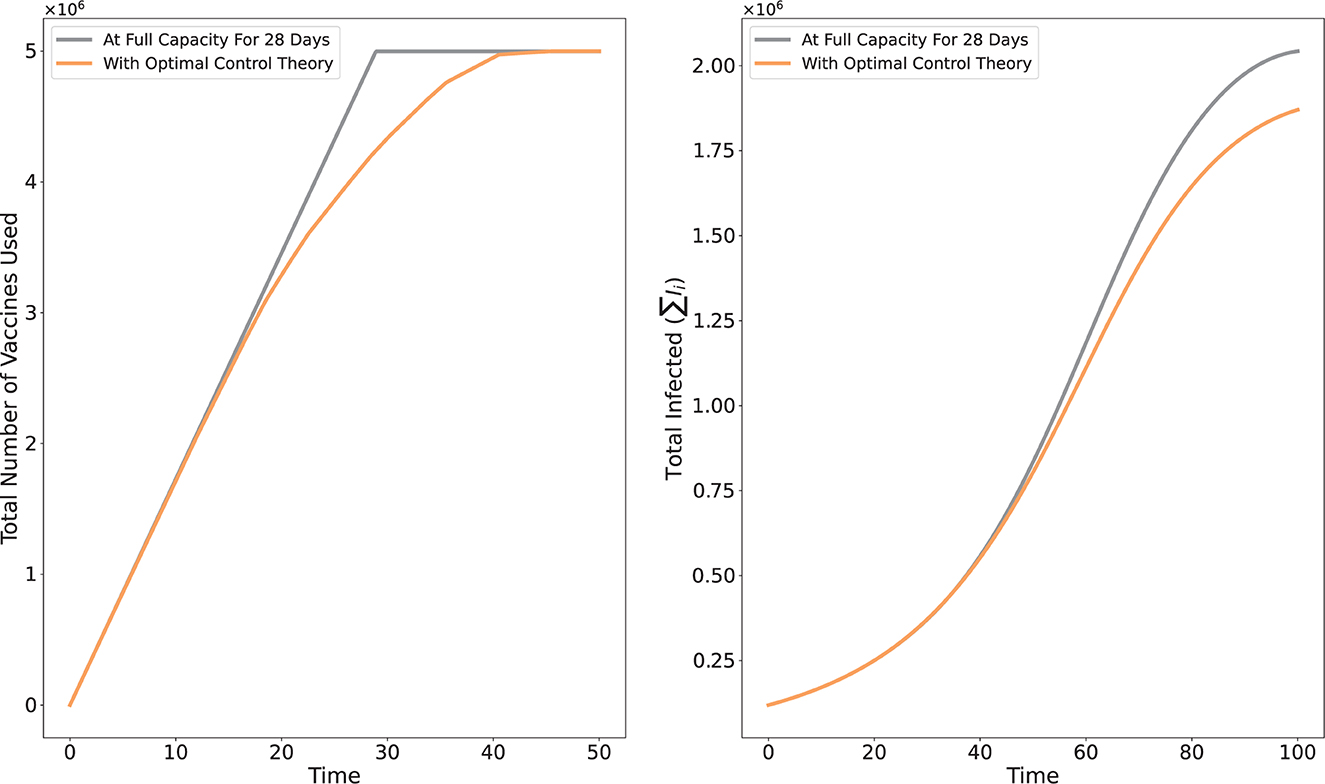
Figure 3. Comparison of the intuitive vaccination strategy of distributing the vaccines by the full capacity of each region for 28 days vs. distribution strategy via optimal control theory.

6.2. Limited vs. unlimited vaccines

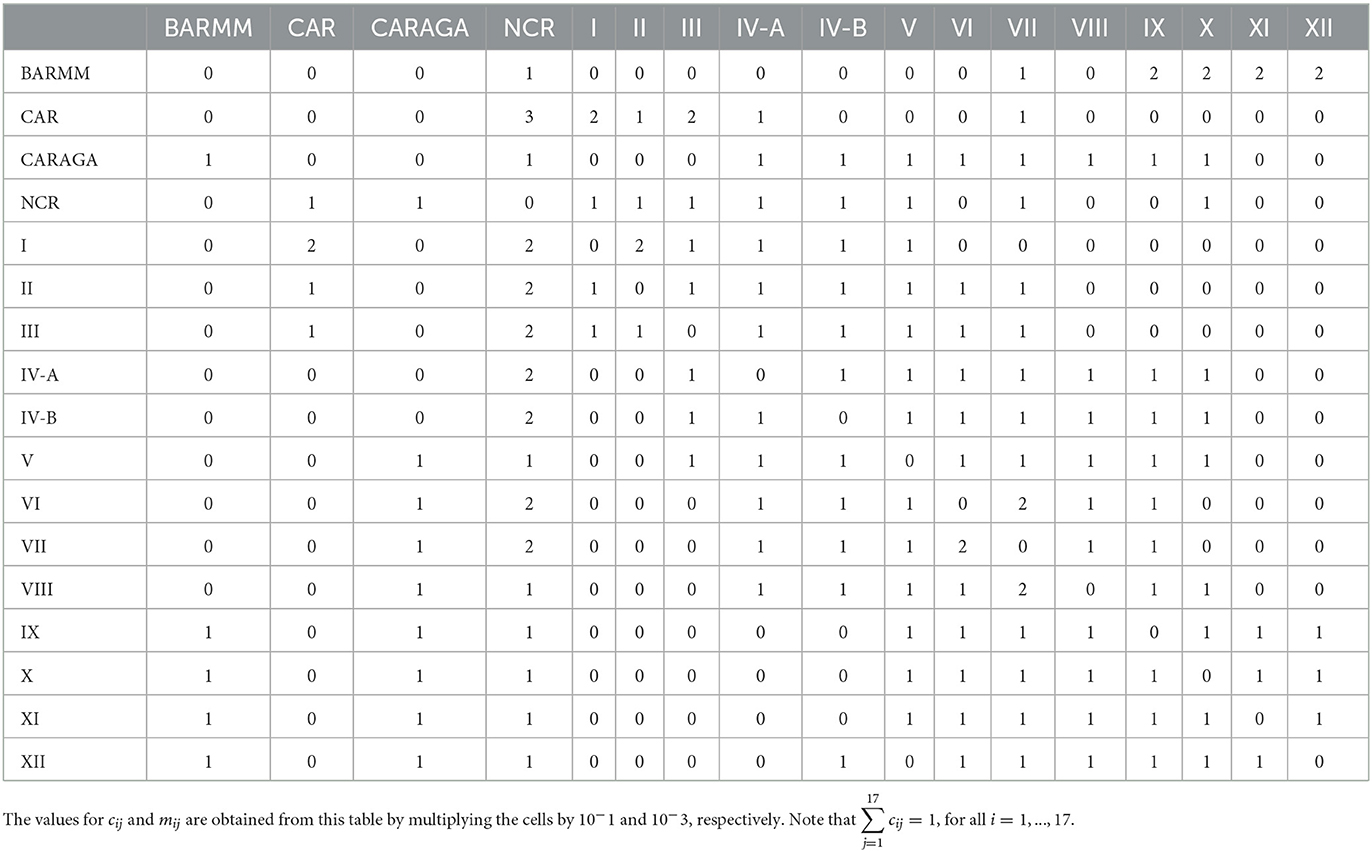
In this simulation, we assume that lockdowns and border controls are not working that well, and so there is mobility of infected individuals between regions. There are no publicly available statistics on interregional movement, particularly for infected people. Based on our knowledge of the regions of the Philippines and their relationships with one another, we estimate the values of the mobility parameters q_i, c_ij, and m_ij for the purpose of demonstration. The used values are listed in Table 3.

TABLE 3

Table 3. Mobility values used.

This situation is comparable to the later stages of the pandemic when lockdowns are not used, and only lax border controls are in place. We contrast the scenario where vaccine supply is limited, just like in the preceding simulation (Section 6.1), and the scenario where vaccine supply is seemingly unlimited, or where there is always enough vaccine to meet each region's vaccination capacity over the course of the simulation.

Figures 4A, B depict the simulation for the scenario where vaccine supply is limited. In contrast, Figures 4C, D depict the simulation for the scenario where vaccine supply is presumptively limitless. In the unlimited case, optimal control theory also recommends providing all the regions with their full vaccination capacity, as is intuitively expected. Figure 4E depicts the variation in the overall number of vaccines used, while Figure 4F depicts the anticipated variation in the overall infections (sum of the infected in the 17 regions), for both cases.

FIGURE 4

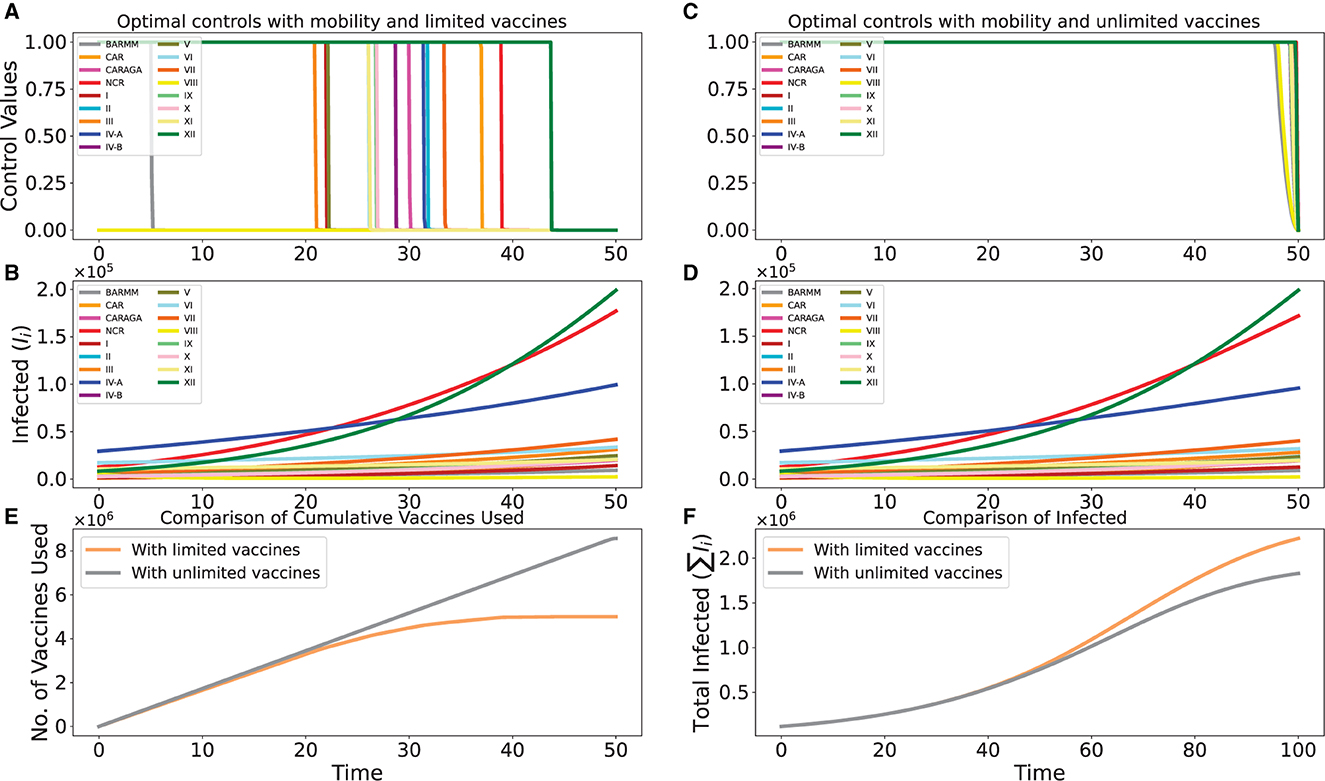
Figure 4. Optimal controls for the cases with limited and unlimited vaccines. In (A, B, E), we have the limited case, while in (C, D, F), we have the unlimited case.

7. Discussion and conclusion

Our simulations showed how important it is to use optimal control theory to figure out how to give out a limited amount of vaccine over a certain amount of time in a country with different regions and a daily vaccination limit for each region. The advantage of this approach is that it seeks to determine the most efficient distribution plan while accounting for the influence that daily vaccination rates have on the progression of the disease in the days that follow in each region. In Section 6.1, we clearly saw that the optimal control formulation's solution minimizes the overall infection in the country better than the intuitive approach of simply distributing the supply to all the regions based on their vaccination capacity. We also demonstrated the effectiveness of our method even when individual mobility between infected regions is considered.

We could also point out some drawbacks though. For instance, we did not take political and social factors into account. Due to lower reported cases or higher infection rates in other regions that needed to be prioritized, an optimal control strategy might, for instance, recommend against administering vaccines to a specific region. Although we can be mathematically confident that the strategy will reduce the overall infection of the country more effectively, it could be easily interpreted as simple discrimination. These things can also be taken into account when developing our formulation. As an illustration, we could stipulate that the lower limit for the controls ν_i must be 30%.

We note here that the method presented in this study can be easily extended or adapted to consider more divisions of the country. For instance, instead of the 17 regions, we could also consider more than 7,000 islands of the country. However, this would entail a much higher computational cost. Alternatively, we could zoom in on one city and consider the distribution problem for its barangays, which are the smallest administrative divisions in the country.

As stated in Section 2, we do not intend to assess the government's distribution initiative here. Instead, we propose a different strategy for administering the vaccines that we have mathematically demonstrated to be more effective with regard to our goal of reducing the overall infection rate in the country.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RC-a and JA contributed to the conception and design of the study and wrote the first draft of the manuscript. JMM and MR provided mathematical analysis and calculation. JD handled data collection and processing. JGM provided biological expertise. RC-a carried out the numerical simulations. All authors discussed the results and implications, and reviewed and approved the final version of the manuscript.

Funding

The authors would like to thank DOST through PCHRD and ASTHRDP, MSU-IIT's OVCRE through PRISM, and CSU's MSCRC for the funding support.

Acknowledgments

The authors would like to thank W. Bock for a fruitful discussion.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^National COVID-19 Vaccination Dashboard | Department of Health Website. Available online at: https://doh.gov.ph/covid19-vaccination-dashboard.

2. ^Department of Health Website (2022). Available online at: https://doh.gov.ph/vaccines.

References

1. Harris RJ, Hall JA, Zaidi A, Andrews NJ, Dunbar JK, Dabrera G. Effect of vaccination on household transmission of SARS-CoV-2 in England. N Engl J Med. (2021) 385:759–60. doi: 10.1056/NEJMc2107717

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Katella K. Comparing the COVID-19 Vaccines: How Are They Different? (2023). Available online at: https://www.yalemedicine.org/news/covid-19-vaccine-comparison (accessed January 29, 2023).

3. Geddes L. How Effective Are COVID-19 Vaccines in the Real-World? | Gavi, the Vaccine Alliance (2021). Available online at: https://www.gavi.org/vaccineswork/how-effective-are-covid-19-vaccines-real-world (accessed January 29, 2023).

4. PSA. GDP Expands by 7.6 Percent in the Third Quarter of 2022 | Philippine Statistics Authority (2022). Available online at: https://psa.gov.ph/content/gdp-expands-76-percent-third-quarter-2022 (accessed January 29, 2023).

Google Scholar

5. Amit AML, Pepito VCF, Sumpaico-Tanchanco L, Dayrit MM. COVID-19 vaccine brand hesitancy and other challenges to vaccination in the Philippines. PLoS Global Public Health. (2022) 2:e0000165. doi: 10.1371/journal.pgph.0000165

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Arcede JP, Caga-anan RL, Mentuda CQ, Mammeri Y. Accounting for symptomatic and asymptomatic in a SEIR-type model of COVID-19. Math Modell Nat Phenomena. (2020) 15:34. doi: 10.1051/mmnp/2020021

CrossRef Full Text | Google Scholar

7. Dy LF, Rabajante JF. A COVID-19 infection risk model for frontline health care workers. In: Network Modeling Analysis in Health Informatics and Bioinformatics. Vienna: Springer (2020). p. 1–13.

PubMed Abstract | Google Scholar

8. Caldwell JM, Lara-Tuprio ED, Teng TR, Estuar MRJE, Sarmiento RFR, Abayawardana M, et al. Understanding COVID-19 dynamics and the effects of interventions in the Philippines: a mathematical modelling study. Lancet Reg Health West Pac. (2021) 14:100211. doi: 10.1016/j.lanwpc.2021.100211

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Arcede J, Caga-anan RL, Mammeri Y, Namoco R, Gonzales IC, Lachica ZP, et al. A modeling strategy for novel pandemics using monitoring data: the case of early COVID-19 pandemic in Northern Mindanao, Philippines. SCIENGGJ. (2022) 15:35–46.

Google Scholar

10. Bock W, Bornales JB, Burgard JP, Babiera JE, Caga-anan RL, Carmen DJS, et al. Testing, social distancing and age specific quarantine for COVID-19: Case studies in Iligan City and Cagayan de Oro City, Philippines. AIP Conf Proc. (2020) 2286:030002. doi: 10.1063/5.0029818

CrossRef Full Text | Google Scholar

11. Macalisang JM, Caay ML, Arcede JP, Caga-anan RL. Optimal control for a COVID-19 model accounting for symptomatic and asymptomatic. Comput Math Biophys. (2020) 8:168–79. doi: 10.1515/cmb-2020-0109

CrossRef Full Text | Google Scholar

12. Lazebnik T, Blumrosen G. Advanced multi-mutation with intervention policies pandemic model. IEEE Access. (2022) 10:22769–81. doi: 10.1109/ACCESS.2022.3149956

CrossRef Full Text | Google Scholar

13. Lazebnik T, Bunimovich-Mendrazitsky S, Shami L. Pandemic management by a spatio–temporal mathematical model. Int J Nonlinear Sci Num Simul. (2021). doi: 10.1515/ijnsns-2021-0063

CrossRef Full Text | Google Scholar

14. Di Domenico L, Pullano G, Sabbatini CE, Boëlle PY, Colizza V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Med. (2020) 18:240. doi: 10.1186/s12916-020-01698-4

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bhadauria AS, Pathak R, Chaudhary M. A SIQ mathematical model on COVID-19 investigating the lockdown effect. Infect Dis Modell. (2021) 6:244–57. doi: 10.1016/j.idm.2020.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Agarwal M, Bhadauria AS. Modeling spread of polio with the role of vaccination. Appl Appl Math Int J. (2011) 6:11.

Google Scholar

17. Tiwari PK, Rai RK, Khajanchi S, Gupta RK, Misra AK. Dynamics of coronavirus pandemic: effects of community awareness and global information campaigns. Eur Phys J Plus. (2021) 136:994. doi: 10.1140/epjp/s13360-021-01997-6

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Rai RK, Khajanchi S, Tiwari PK, Venturino E, Misra AK. Impact of social media advertisements on the transmission dynamics of COVID-19 pandemic in India. J Appl Math Comput. (2022) 68:19–44. doi: 10.1007/s12190-021-01507-y

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Srivastav AK, Tiwari PK, Srivastava PK, Ghosh M, Kang Y. A mathematical model for the impacts of face mask, hospitalization and quarantine on the dynamics of COVID-19 in India: deterministic vs. stochastic. Math Biosci Eng. (2020) 18:182–213. doi: 10.3934/mbe.2021010

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Majumder M, Tiwari PK, Pal S. Impact of saturated treatments on HIV-TB dual epidemic as a consequence of COVID-19: optimal control with awareness and treatment. Nonlinear Dyn. (2022) 109:143–76. doi: 10.1007/s11071-022-07395-6

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Naik PA, Zu J, Ghori MB, ud-din Naik M. Modeling the effects of the contaminated environments on COVID-19 transmission in India. Results Phys. (2021) 29:104774. doi: 10.1016/j.rinp.2021.104774

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hogan AB, Winskill P, Watson OJ, Walker PGT, Whittaker C, Baguelin M, et al. Within-country age-based prioritisation, global allocation, and public health impact of a vaccine against SARS-CoV-2: a mathematical modelling analysis. Vaccine. (2021) 39:2995–3006. doi: 10.1016/j.vaccine.2021.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Fitzpatrick MC, Galvani AP. Optimizing age-specific vaccination. Science. (2021) 371:890–1. doi: 10.1126/science.abg2334

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bubar KM, Reinholt K, Kissler SM, Lipsitch M, Cobey S, Grad YH, et al. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science. (2021) 371:916–21. doi: 10.1126/science.abe6959

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Rasambainarivo F, Ramiadantsoa T, Raherinandrasana A, Randrianarisoa S, Rice BL, Evans MV, et al. Prioritizing COVID-19 vaccination efforts and dose allocation within Madagascar. BMC Public Health. (2022) 22:724. doi: 10.1186/s12889-022-13150-8

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhou S, Zhou S, Zheng Z, Lu J. Optimizing spatial allocation of COVID-19 vaccine by agent-based spatiotemporal simulations. Geohealth. (2021) 5:e2021GH000427. doi: 10.1029/2021GH000427

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Saad-Roy CM, Morris SE, Metcalf CJE, Mina MJ, Baker RE, Farrar J, et al. Epidemiological and evolutionary considerations of SARS-CoV-2 vaccine dosing regimes. Science. (2021) 372:363–70. doi: 10.1126/science.abg8663

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kadire SR, Wachter RM, Lurie N. Delayed second dose versus standard regimen for Covid-19 vaccination. N Engl J Med. (2021) 384:e28. doi: 10.1056/NEJMclde2101987

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Molla J, Chavez APL, Hiraoka T, Ala-Nissila T, Kivela M, Leskela L. Adaptive and optimized COVID-19 vaccination strategies across geographical regions and age groups. PLoS Comput Biol. (2022) 18:e1009974. doi: 10.1371/journal.pcbi.1009974

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Lemaitre JC, Pasetto D, Zanon M, Bertuzzo E, Mari L, Miccoli S, et al. Optimal control of the spatial allocation of COVID-19 vaccines: Italy as a case study. PLoS Comput Biol. (2022) 18:e1010237. doi: 10.1371/journal.pcbi.1010237

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Domingo RW. Japan Gives Philippines' COVID-19 Vax Program ‘Last Mile' Boost (2022). Available online at: https://business.inquirer.net/375094/japan-gives-philippines-covid-19-vax-program-last-mile-boost (accessed January 29, 2023).

Google Scholar

32. Caga-anan RL, Raza MN, Labrador GSG, Metillo EB, del Castillo P, Mammeri Y. Effect of vaccination to COVID-19 disease progression and herd immunity. Comput Math Biophys. (2021) 9:262–72. doi: 10.1515/cmb-2020-0127

CrossRef Full Text | Google Scholar

33. Csilléry BMGGOE K, Francois O. Approximate Bayesian computation (ABC) in practice. Trends Ecol Evol. (2010) 25:410–8. doi: 10.1016/j.tree.2010.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Levenberg K. A method for the solution of certain non-linear problems in least squares. Q Appl Math. (1944) 2:164–8. doi: 10.1090/qam/10666

CrossRef Full Text | Google Scholar

35. Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. J Soc Indus Appl Math. (1963) 11:431–41.

Google Scholar

36. Philippine Statistics Authority. 2020 Census of Population Housing (2020 CPH) Population Counts Declared Official by the President (2021). Available online at: https://psa.gov.ph/content/2020-census-population-and-housing-2020-cph-population-counts-declared-official-president (accessed January 29, 2023).

Google Scholar

37. Lenhart S, Workman JT. Optimal Control Applied to Biological Models Suzanne Lenhart, John T. Workman. Hoboken, NJ: CRC Press (2007).

Google Scholar