- 1Department of Mathematics and Applied Mathematics, University of the Western Cape, Bellville, South Africa
- 2DSI-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS), Johannesburg, South Africa
- 3Department of Mathematics and Applied Mathematics, University of Johannesburg, Johannesburg, South Africa
- 4Department of Mathematics and Computer Science, Alabama State University, Montgomery, AL, United States
The co-infection of visceral leishmaniasis (VL) and tuberculosis (TB) patients pose a major public health challenge. In this study, we develop a mathematical model to study the transmission dynamics of VL and TB co-infection by first analyzing the VL and TB sub-models separately. The dynamics of these sub-models and the full co-infection model are determined based on the reproduction number. When the associated reproduction number () for the TB-only model and () for the VL-only are less than unity, the model exhibits backward bifurcation. If , then the TB-VL co-infection model exhibits backward bifurcation for values of . Furthermore, if , and by choosing the transmission probability, βL as the bifurcation parameter, then the phenomenon of backward bifurcation occurs for values of . Consequently, the full model, whose associated reproduction number is , also exhibits backward bifurcation when . The equilibrium points and their stability for the models are determined and analyzed based on the magnitude of the respective reproduction numbers. Finally, some numerical simulations are presented to show the reliability of our theoretical results.
1. Introduction
Leishmaniasis is a neglected tropical disease (NTD) that is transmitted by infected sandflies and is caused by obligate intracellular protozoans of the genus Leishmania [1]. There are more than 20 Leishmania species with three main forms of the disease: cutaneous leishmaniasis, mucocutaneous leishmaniasis, and visceral leishmaniasis, also known as kala-azar. Cutaneous leishmaniasis (CL) is the most common form of leishmaniasis and causes skin lesions, mainly ulcers, on exposed parts of the body, leaving life-long scars and serious disability or stigma. Mucocutaneous leishmaniasis (MCL) is the most disabling form of the disease, and it affects mostly the mucous membranes of the nose and mouth. Visceral leishmaniasis (VL) is the most fatal disease, causing enlargement of the spleen and liver [2]. It may cause epidemic outbreaks with a high mortality rate. A varying proportion of visceral cases may evolve into a cutaneous form known as post-kala-azar dermal leishmaniasis (PKDL), which requires lengthy and costly treatment [3, 4]. VL is responsible for nearly 48,000 deaths worldwide with 2,00,000–4,00,000 new cases annually [5]. If the disease is not treated, the fatality rate in developing countries can be as high as 100% within 2 years. Most cases are seen in six countries—Bangladesh, Brazil, Ethiopia, India, South Sudan, and Sudan [5]. There are no vaccines available, and all the current drug treatments have serious limitations such as prolonged administration, high cost, drug resistance, and toxicity [6]. Treatment efficacy is further compromised in the case of co-infection with tuberculosis (TB).
Co-infection of visceral leishmaniasis and TB is very common, increasing public health problems in tropical and subtropical areas [7–9]. TB is caused by the bacterium Mycobacterium tuberculosis and is spread through the air. It is a leading cause of death worldwide, especially among people with compromised immune systems. It is also an immuno-suppressive condition that helps latent leishmaniasis progress to clinical leishmaniasis [10]. Similarly, visceral leishmaniasis can reactivate latent tuberculosis. However, there has been growing interest in repurposing existing drugs used to treat tuberculosis and leishmaniasis. When compared to developing new drugs from scratch, this approach has several advantages, including the availability of well-characterized drugs with established safety profiles, shorter development timelines, and lower costs [6, 11]. It is also worth noting that, while some TB drugs may have anti-Leishmania parasite activity, they are not a universal cure for both TB and leishmaniasis. Treatment for each disease should be tailored to the individual patient's needs, and co-infected people may require a combination of drugs to effectively treat both diseases. When considering co-infection of leishmaniasis and TB, research has shown that co-infected individuals tend to have more severe disease and poorer treatment outcomes than those infected with only one of the diseases. This underscores the need for a co-infection model to better understand the interactions between the two diseases and develop effective treatment strategies. Hence, we develop a new mathematical model of VL and TB co-infection.
Mathematical models are now a critical component in developing control and mitigation strategies for any potential infectious disease epidemic. Mathematical models are frequently used to capture the dynamics of disease at different phases in order to understand the spread of diseases within a population and build both short- and long-term management strategies. We can evaluate a variety of different control tactics in computer simulations before applying them in real life using well-parameterized mathematical models [12, 13]. Many mathematical models have been developed to successfully explain real-life situations and played a key role in public health efforts. Driessche and Watmough [14] provided a precise definition of the basic reproduction number for a general compartmental disease model based on a system of ordinary differential equations. Castillo-Chavez and Song [15] provided a comprehensive review of the dynamics and control of tuberculosis. Standard disease transmission and control models in which the majority of the population steadily grows over time are presented in [16, 17]. Establishing the stability properties of a dynamic system is a difficult problem in general. Hence, the direct Lyapunov method is a used approach to establish the local and global stabilities of these models. Korobeinikov [18, 19] presented a family of Lyapunov functions for three-compartment epidemiological models that appear to be useful for more complex models. Furthermore, mathematical models have been used to understand the dynamic transmission of diseases such as malaria [17, 20], hepatitis [21], tuberculosis [22], dengue [23], and COVID-19 [24], and to understand the underlying dynamics of the target-mediated drug disposition [25–27]. Co-infections by multiple pathogens are common and theory predicts co-infections to have major consequences for both within- and between-host disease dynamics [17, 28]. The treatment of the co-infection of these diseases must be initiated in a systemic manner because their drugs do not always work well together. While some co-infection mathematical models have been developed and analyzed to understand the transmission dynamics of various diseases [3, 29, 30], such efforts for a mathematical model to understand the visceral leishmaniasis (VL) and tuberculosis (TB) co-infection have not taken place yet (to the best of our knowledge). Therefore, in this study, we develop and analyze a mathematical model designed to understand the dynamics of VL and TB co-infection.
The manuscript is organized as follows: Section 2 presents a development of the co-infection model. Section 3 presents the TB sub-model while Section 4 presents the VL sub-model. The full co-infection model with its analysis is provided in Section 5. Section 6 discusses the numerical results to validate the theoretical findings. Finally, Section 7 concludes key results found in the present study.
2. Model formulation
The formulation of this co-infection closely follows the epidemiological dynamics of the two diseases. The model analysis and methods are related to study carried out by Mwamtobe et al. [17] and Mtisi et al. [31]. Although similar to their study, the general approach herein is unique in its own right.
2.1. Basic framework
The model assumes that the human population is divided into, susceptible individuals (S), who are those exposed to TB-only (ET), those who are infected with TB (IT), those who recover from TB infection with temporal immunity (RT), those infected with visceral leishmaniasis (IL), those who develop PKDL after the treatment of visceral (PL), visceral leishmaniasis infected individuals having TB symptoms (ITL), and then those who are recovered having permanent immunity to visceral leishmaniasis (RL). The total population size N(t) is given by
Similarly, the sandfly population is divided into two categories, susceptible sandflies SV(t) and visceral leishmaniasis parasite-infected sandflies IV(t) and hence,
The force of infection associated with TB infection in humans is
where βT is the TB transmission probability and cT is per capital contact rate. Similarly, the force of infection associated with visceral leishmaniasis infection in humans is
where cL is the per capita biting rate of sandflies on humans, m is a modification parameter accounting for the relative risk of infectiousness of VL infected vector, and βL is the transmission probability of VL per bite per human. Susceptible sandflies are recruited at a constant rate ΛV and acquire leishmaniasis infection at an average rate of
following contact with leishmaniasis-infected humans. βV is the transmission probability for sandfly infection, and sandflies have a per capita natural mortality rate μV.
We assume that susceptible individuals are recruited into the population at per capita rate Λ and there is a per capita natural mortality rate μ in all the population classes. Susceptible individuals with TB enter the latency stage at rate λT and then progress to active TB at rate κ. Individuals latently infected with TB also progress to active TB as a result of re-infection at rate ψλT with ψ ∈ (0, 1) since primary infection confers some degree of immunity. Individuals with TB suffer disease-induced death at rate dT and recover at rate p. A fraction of individuals who recover from TB could be infected with TB at rate q(1 − f) or latently infected at rate qf. Individuals infected with VL-only are generated following infection at a rate λL. Infected individuals die due to VL at an average rate dL or get treatment at an average rate α1. A fraction σ of those who get treated recover and acquire permanent immunity, while the other fraction (1 − σ) develops PKDL. Those individuals with PKDL get treated at an average rate α2 or recover naturally at an average rate θ and acquire permanent immunity in both cases. Individuals infected with TB can be infected with VL at rate λL, while individuals infected with VL can be infected with TB at rate λT.
2.2. The model
Putting the above formulations and assumptions together gives the following system of differential equations:
The model diagram is shown in Figure 1 and the model has initial conditions given by
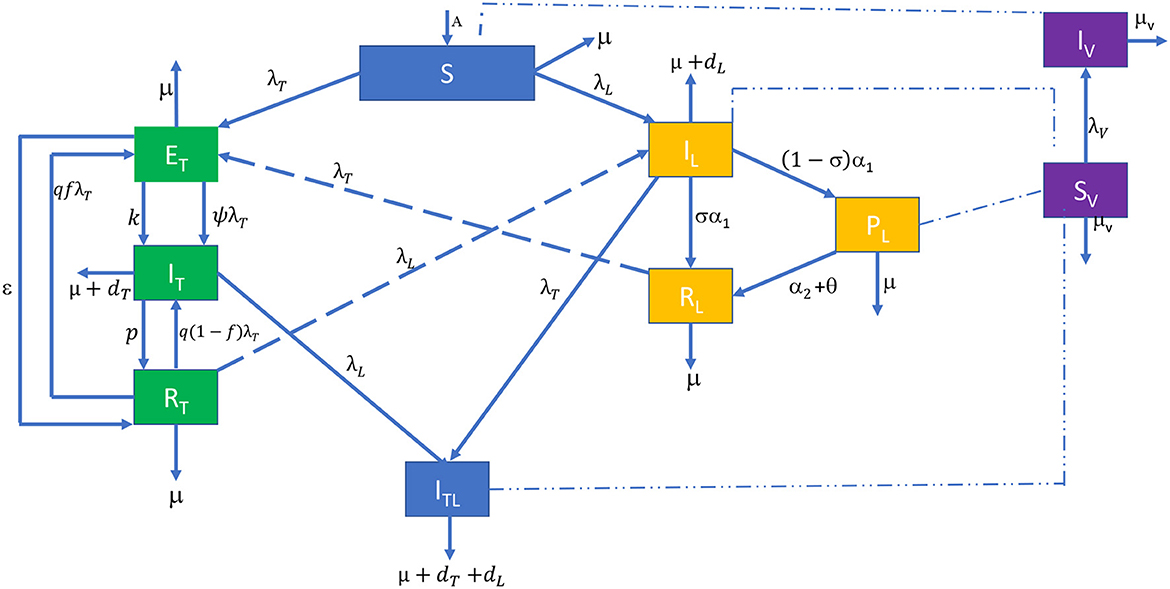
Figure 1. Compartment diagram of visceral leishmaniasis and tuberculosis co-infection. The dashed lines show that the infected sandflies (IV) infect susceptible individuals (S). Individuals infected with VL (IL), those who develop PKDL after the treatment of VL (PL) and VL infected individuals having TB symptoms (ITL) infect susceptible sandflies (SV).
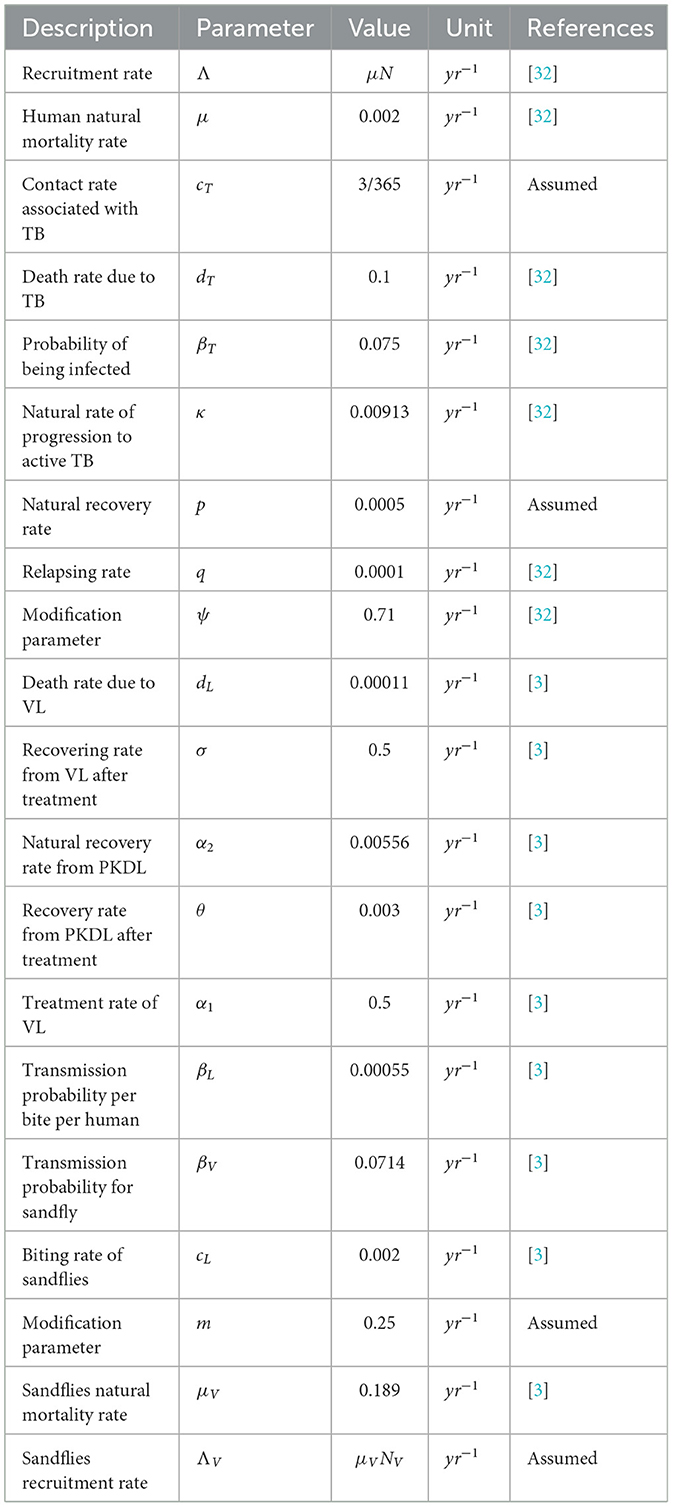
The parameters and their values of the model are summarized in Table 1.
2.3. Invariant region and positivity of solutions
The basic dynamical features of the co-infection model (6) are summarized in the following Lemma.
Lemma 1. Let (S, ET, IT, RT, IL, PL, RL, ITL, SV, IV) be the solution of the co-infection model (6) with initial conditions (7). The closed set
where
is positively invariant and attracting for the co-infection model (6).
Proof. Adding the first eight equations in system (6), we have
The comparison theorem [33] can be used to show that
Thus, as t → ∞, . This implies that ΩH is an attracting set with respect to the model (6). Similarly, adding the last two equations in system (6), we have
Similarly, it can be shown that as t → ∞, implying that ΩV is an attracting set with respect to model (6).
Thus, it follows that all possible solutions of the model (6) will enter the region
□
Lemma 2. Let the initial data be as given in 7. Then, the solution set {S, ET, IT, RT, IL, PL, RL, ITL, SV, IV} of system (6) is positive for all t > 0.
Proof. From the first equation of system (6), we have
Simple integration techniques yields
Similarly, it can be shown that the remaining variables are also positive for all t > 0. □
These lemmas verify that every solution of the co-infection model (6) with initial conditions in Ω remains there for t > 0. Furthermore, in Ω, the usual existence, uniqueness, and continuation results hold for the system so that the model system (6) is well posed mathematically and epidemiological. Thus, it is sufficient to consider the dynamics of the co-infection model (6) in Ω.
Next, we consider the dynamics of the two sub-models, namely, TB-only and VL-only models. This will help to lay down the foundation for the qualitative analysis of the full co-infection model.
3. TB sub-model
The TB sub-model is given by
with initial conditions (IC)
Here, the total human population is NT = S + ET + IT + RT. The parameters of the TB sub-model are as described in Table 1. The basic dynamical features of the TB sub-model model (9) are summarized in the following Lemma.
Lemma 3. Let the solution of system (9) be (S, ET, IT, RT) with initial conditions (10). The closed set
is positively invariant and attracting under the flow governed by model system (9).
Proof. Adding all the equations in the system (9), we obtain
The comparison theorem can be used to show that
Thus, as t → ∞, . This implies that is an attracting set with respect to model (9). □
3.1. TB sub-model disease-free equilibrium
The disease-free equilibrium (DFE) for the TB sub-model (9) is given by
According to the next-generation matrix approach in van den Driessche and Watmough [14], to compute the basic reproduction of the TB sub-model, we set and rewrite the model (9) in the matrix form
where
At the equilibrium point E0, the Jacobian matrices of and are
It follows that the TB sub-model reproduction number is given by
A value of less than one indicates that TB will be eliminated while a value greater than one indicates that a TB infection will continue to spread within the susceptible hosts.
Theorem 1. The disease-free equilibrium point of the TB-only sub-model (9) is locally asymptotically stable if and unstable otherwise.
Proof. The Jacobian matrix of model (9) at the disease-free equilibrium E0 is
The characteristic equation of matrix J0 is
where the eigenvalues can be obtained using the approach in [34]. Two eigenvalues of matrix J0 are −μ (twice) and are both negative. The remaining two eigenvalues can be found by finding the eigenvalues of the sub-matrix
By definition, the eigenvalues of matrix A are real and negative if tr(A) < 0 and det(A) > 0 (Routh-Hurwitz criterion). Thus, the trace and determinant of matrix A are
respectively. Since all model parameters are assumed to be non-negative, it follows that tr(A) < 0 regardless of the value of . We also have that det(A) > 0 if and only if .
Therefore, we conclude that if , then tr(A) < 0 and det(A) > 0, implying that all the eigenvalues of matrix J0 have a negative real part. The disease-free equilibrium is locally asymptotically stable. If , then det(A) ≤ 0, which proves the instability of E0. □
3.2. Existence of the endemic equilibrium
The endemic equilibrium is the equilibrium (EE) of model (9) in which the infected component of the system is non-zero. The endemic equilibrium E1 = (S*, ET*, IT*, RT*) in terms of the force of infection is given by
where
Substituting E1 into Equation (20) and simplifying yields the cubic equation
where
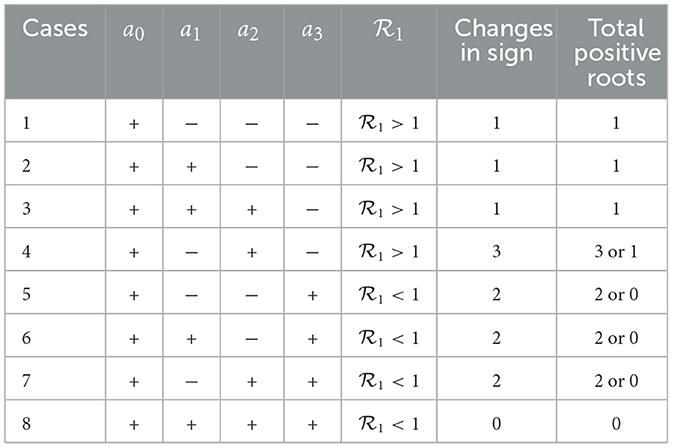
Thus, the endemic equilibrium E1 of the TB sub-model is obtained by solving Equation (21) for positive and substituting back into the equations in E1. The number of possible positive real roots of the cubic polynomial Equation (21) depends on the signs of a0, a1, a2, and a3. We investigate this by using the Descartes rule of signs. The rule asserts that the number of positive roots is at most the number of sign changes in the sequence of polynomial coefficients. The possibilities are illustrated in Table 2.
The outcomes are established in the following theorem.
Theorem 2. The TB sub-model (9) has the following features:
1. A unique endemic equilibrium when and cases 1–3 hold.
2. One or more endemic equilibrium when and case 4 holds, as well as when and cases 5-7 hold.
3. No endemic equilibrium when and case 8 holds. This is the case when all coefficients are positive.
3.3. Backward bifurcation
For model (9), the existence of multiple TB persistence equilibria E1 for suggests the possibility of the backward bifurcation phenomenon. Epidemiologically, it suggests that may not be sufficient to decide whether or not TB would persist in the population. Instead, it depends on the initial population size of the individuals when . We investigate and set a threshold for the presence of backward bifurcation in system (9).
From Theorem 1 and 2, we see that if we consider as a bifurcation parameter, then there is an exchange of stability properties between equilibrium E0 and E1 at . We investigate the nature of bifurcation involving E0 at based on the use of the center manifold theory [15]. First, consider the case when and solve for βT to obtain
The is chosen as the bifurcation parameter. Furthermore, the Jacobian of system (9) evaluated at E0 with is given by
The has only one eigenvalue with zero real part. This then implies that the model (9) with has at least one non-hyperbolic equilibrium point. We then use the center manifold approach to further analyze the dynamics of model (9). Corresponding to the zero eigenvalue, the Jacobian has a right eigenvector given by , where
and a left eigenvector given by , where
We then follow the analysis as carried out by [16, 17]. Compute the coefficients and defined in theorem 4.1 by Castillo-Chavez and Song [15].
Computation of and
The and are given by
We use the center manifold approach on the model system (9). Let S = x1, E = x2, I = x3, and R = x4. Then N = x1 + x2 + x3 + x4 so that
The associated non-zero partial derivatives of at E0 are given by
Using the above expressions, the coefficients is given by
For the sign of , we chose βT as the bifurcation parameter and it can be shown that the associated non-zero partial derivatives of fi at E0 are given by
so that
It is seen that is always positive, while can either be positive or negative. Depending on the signs of and , we establish the following lemmas
Lemma 4. If < 0 and , then the TB sub-model model (9) undergoes forward bifurcation which occurs at .
Lemma 5. If > 0 and , then the TB sub-model model (9) undergoes backward bifurcation which occurs at .
Hence, the positivity of offers the threshold circumstance for the phenomenon of backward bifurcation.
4. Visceral leishmaniasis sub-model
The visceral leishmaniasis (VL) sub-model is given by
The force of VL infection in humans is . Susceptible individuals are infected with visceral leishmaniasis following contact with infected sandflies at a per capita rate . Here, we have that the total human population is NL = S + IL + PL + RL. The total human population dynamics for the VL sub-model are given by
Given that the initial conditions are non-negative, i.e., NL(0) ≥ 0, the total human population is positive and bounded for all finite time t > 0. The dynamics of the sandflies population are given by
We conclude that all feasible solutions for the human population enter the region
while feasible solutions for the sandflies population entering the region,
4.1. The disease-free equilibrium
The disease-free equilibrium (DFE) for the VL-only model is given by
According to the next-generation matrix approach, to compute the basic reproduction of the VL sub-model we set and rewrite the model (22) in the matrix form
where
At the equilibrium point , the Jacobian matrices of and are
As such, the VL sub-model reproduction number is given by
Theorem 3. The disease-free equilibrium point of the VL-only sub-model (22) is locally asymptotically stable if and unstable when .
Proof. The Jacobian of model (22) at the disease-free equilibrium is
The matrix J1 has three negative eigenvalues −μ (twice) and μV. The remaining eigenvalues are found by finding the eigenvalues of
The characteristic polynomial of B is
where
The Routh-Hurwitz criteria reveals that the roots of polynomial (32) have negative real parts if
We observe that a2 > 0 always and a0 > 0 if . With a simple expansion, we can show that a2a1 > a0 (i.e., a2a1 − a0 > 0) if . Therefore, the disease-free equilibrium is locally stable when . □
4.2. Existence of the endemic equilibrium
The endemic equilibrium of model (22) is given by as functions of the forces of infection and
where
Substituting E2 into Equation (33) and simplifying yields the quadratic equation
where
Therefore, the endemic equilibrium E2 of the VL sub-model (22) is obtained by solving Equation (34) for positive λ* and substituting back into the equations in E2. To find the solutions of Equation (34), we make the following observations: a is always positive, while b and c may be positive or negative depending on the signs of , i.e., we have
From Equation (38), five cases in determining the solution/roots of Equation (34) arise:
(i) Case 1: If , then c > 0 and so Equation (34) has two positive roots when b < 0.
(ii) Case 2: If , then c > 0 and so Equation (34) has no positive roots (two negative roots) when b < 0.
(iii) Case 3: If , then c < 0 and so Equation (34) has one positive root when b > 0.
(iv) Case 4: If , then c < 0 and so Equation (34) also has one positive root when b < 0.
(v) Case 5: When , Equation (34) reduces to , at which (corresponding to the disease-free equilibrium ) and is a positive root when b < 0 and negative root (biologically meaningless) when b > 0.
Furthermore, the critical value of denoted by in the case when is found by setting the discriminant Δ = b2 − 4ac to be zero. This yields
Thus, the following connections hold
• .
• .
• .
It can be shown that backward bifurcation occurs for values of such that . The existence of the endemic equilibrium of model (22) is summarized as follows:
Theorem 4. The VL sub-model (22) has those as follows:
1. a unique endemic equilibrium if ;
2. two endemic equilibria exists, one of which is locally stable, if b < 0 and ;
3. otherwise, the DFE is the only unique attractor if .
From Theorems 3 and 4, model (22) has the usual bifurcation at . If we consider as the bifurcation parameter, then by definition, there is a switch in stability properties between equilibrium point and E2 at . Under certain conditions, model (22) exhibits a backward bifurcation, in which the endemic equilibrium exists for . Setting and solving for βL yields
and is chosen as the bifurcation parameter.
Determining the conditions for the nature of bifurcation using center manifold theory follows as outlined in the sections above. The Jacobian of the system (22) evaluated at E1 with is given by
The Jacobian has a right eigenvector given by , where
and a left eigenvector given by , where,
Computation of and
The and are given by
We use the center manifold approach on the model system (22). Let S = x1, IL = x2, PL = x3, RL = x4, SV = x5, and IV = x6. Then N = x1 + x2 + x3 + x4 and NV = x5 + x6 so that
The associated non-zero partial derivatives of at E1 are given by
Using the above expressions, the coefficients is given by
For the sign of , we chose βL as the bifurcation parameter. The associated non-zero partial derivatives of fi at E1 are given by
so that
It is seen that is always positive, while can either be positive or negative. Depending on the signs of and , we establish the following lemmas:
Lemma 6. If < 0 and , then the VL sub-model model (22) undergoes forward bifurcation which occurs at .
Lemma 7. If > 0 and , then the VL sub-model model (22) undergoes backward bifurcation which occurs at .
Hence, the positivity of offers the threshold circumstance for the phenomenon of backward bifurcation.
5. The full visceral leishmaniasis and tuberculosis co-infection model
In this section, we investigate the dynamical properties of the model (6). For convenience, we introduce the following new parameters:
5.1. The disease-free equilibrium
The disease-free equilibrium (EE) of the full model (6) is given as
We now use the next-generation matrix approach to compute the basic reproduction of the model (6). For this purpose, we set and rewrite the model (6) in the matrix form
where
We carry out the remainder of the calculations as before. The dominant eigenvalues of FV−1 are
and these correspond to the reproduction numbers for the TB transmission model and the leishmaniasis transmission model, respectively. Thus, the basic reproduction number, , for the full model (6) is given by
Theorem 5. The disease-free equilibrium point EF1 of the full model (6) is locally asymptotically stable if and unstable when .
5.2. Bifurcation parameters
The TB and VL-only sub-models are shown to exhibit the phenomenon of backward bifurcation and consequently, the full co-infection model will exhibit the same feature. Below, we derive the bifurcation parameters for the full co-infection model (6). Let S = x1, ET = x2, IT = x3, RT = x4, IL = x5, PL = x6, RL = x7, ITL = x8, SV = x9, and IV = x10. Hence,
Letting , the full co-infection model (6) can be written in the form , where F = (f1, f2, …, f10), as
and
The Jacobian matrix of the system above at the DFE point EF1 is given by
By computing the eigenvalues of the Jacobian JF1, it can be shown that , where and are as previously defined. , hence, there is no competitive exclusion and the two diseases amplify each other. Thus, when and , there is always co-existence no matter which of the reproduction numbers is greater. Although does not combine the two reproduction numbers, by only studying the two diseases in isolation, we would miss the dual TB-visceral leishmaniasis co-infection, which has different dynamics to that of TB-only and visceral leishmaniasis only sub-models. Some additional insights are derived from studying the interaction of the two diseases, hence the full model. If , then, from Theorem 2, the TB-VL co-infection model exhibits backward bifurcation for values of such that Lemma 5 holds.
On the contrary, if , and choosing βL as the bifurcation parameter, then, the phenomenon of backward bifurcation occurs for values of such that Lemma 7 holds. Consequently, the full model will also exhibit the phenomenon of backward bifurcation when .
5.3. Endemic equilibrium
The endemic equilibrium E4 of the full model system (6) is given by
Solving for ET2 in
The forces of infection at E4 are given by,
6. Simulations and results
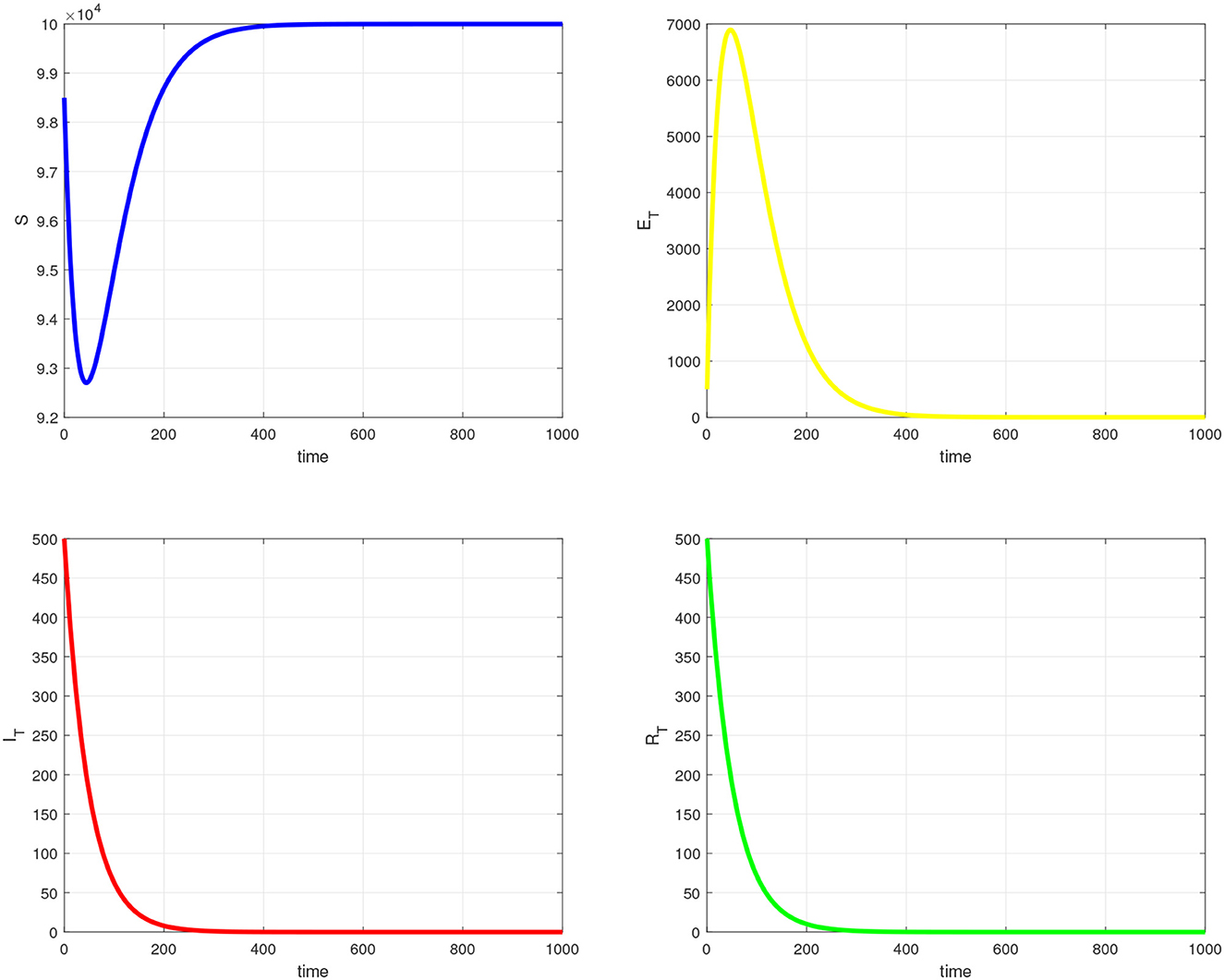
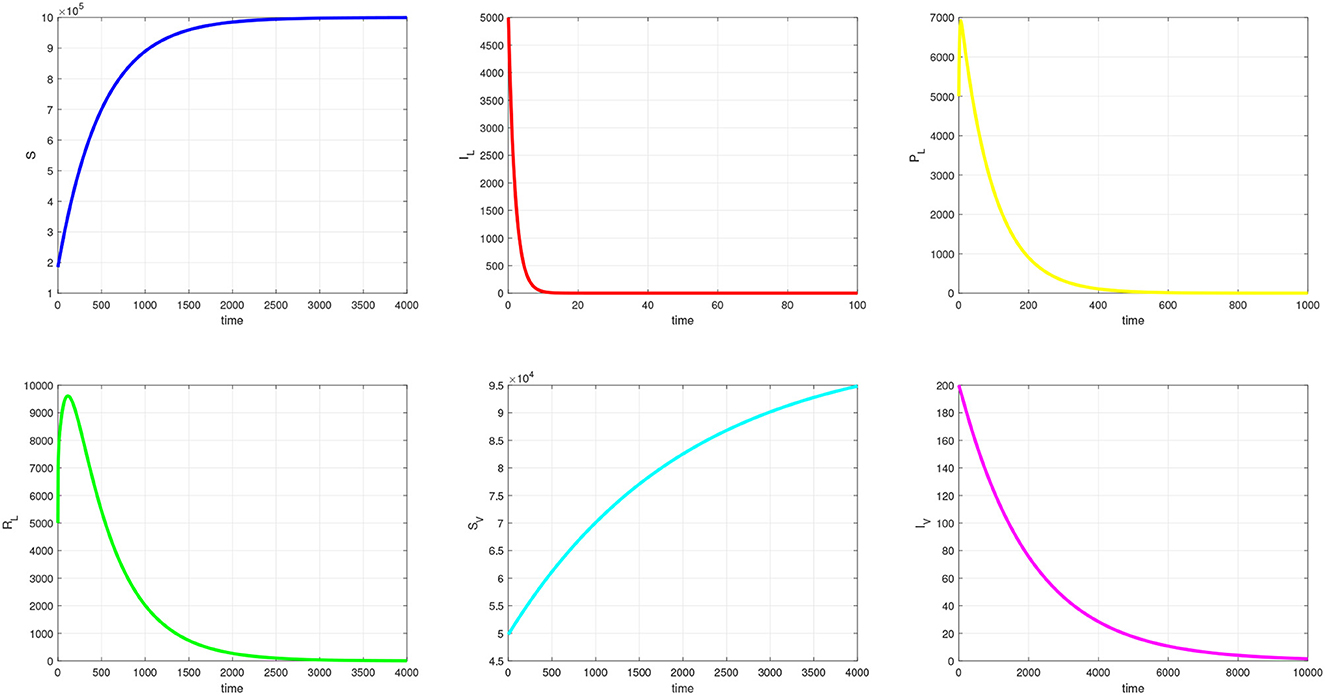
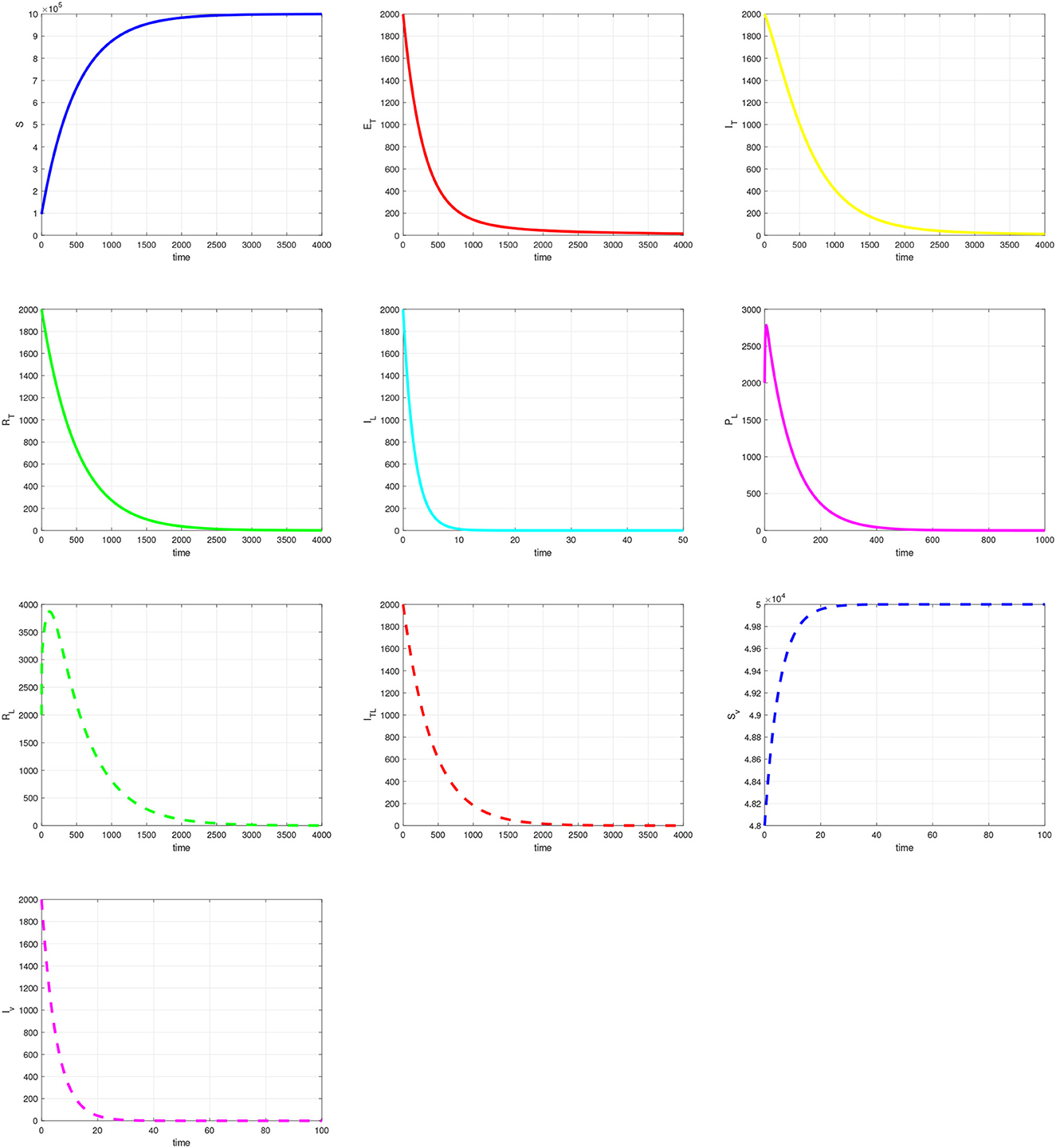
In this section, we provide simulation results for the TB-only model in Figure 2, the VL-only model in Figure 3, and the full VL-TB co-infection model in Figure 4. We performed the simulations using the in-built function ODE45 in MATLAB (MathWorks, Natick, MA, USA) [35], with the aim of understanding the long-term dynamics of the models and checking if it is consistent with the theoretical results. For this purpose, we used the parameter values given in Table 1. We observe from Figures 2–4 that the DFE points are locally asymptotically stable for each model. For the TB-only model, and hence, the DFE point is locally asymptotically stable. This implies that the epidemic will be eradicated. The solutions of the model 9 are depicted in Figure 2. Similarly, the VL-only model DFE point is locally asymptotically stable. This implies that the epidemic will be eradicated as depicted in 1. Therefore, Figures 2–4 are consistent with theoretical results obtained for each case, and these results imply that the disease will be eliminated.
6.1. Bifurcation analysis
6.1.1. TB-only model
The combined effect of βT and dT on the values of are explored next to determine the threshold conditions of these parameters at which the TB-only model exhibits backwards and forward bifurcations. The contours, see Figure 5, show an increase in as βT and dT increase.
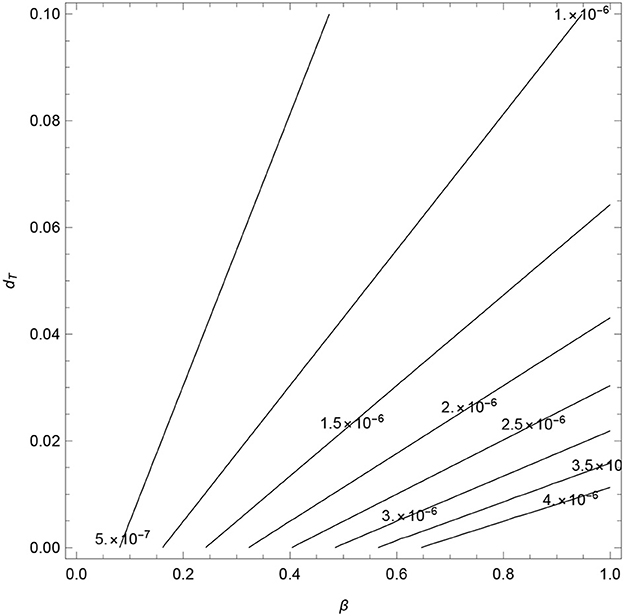
Figure 5. Contour plots of as a function of transmission rate (βT) and disease-induced death rate (dT).
6.1.2. VL-only model
The combined effect of βL, dL, σ, α1, and α2 on the values of are explored next to determine the threshold conditions of these parameters at which the VL-only model exhibits backward and forward bifurcations.
The contours, see Figure 6, show an increase in as βL increases and dL decreases. In Figure 7, we observe that decrease as σ1, α1, and α2 increase. All the contours are less than unity, which signifies that these values of σ1, α1, and α2 (and other fixed parameters) will lead to the elimination of VL from the community (in line with Theorem 3). However, the analysis verifies that the parameters σ1, α1, and α2 are the cause of occurring backward bifurcation in the VL model whenever as guaranteed by Lemma 6-7.
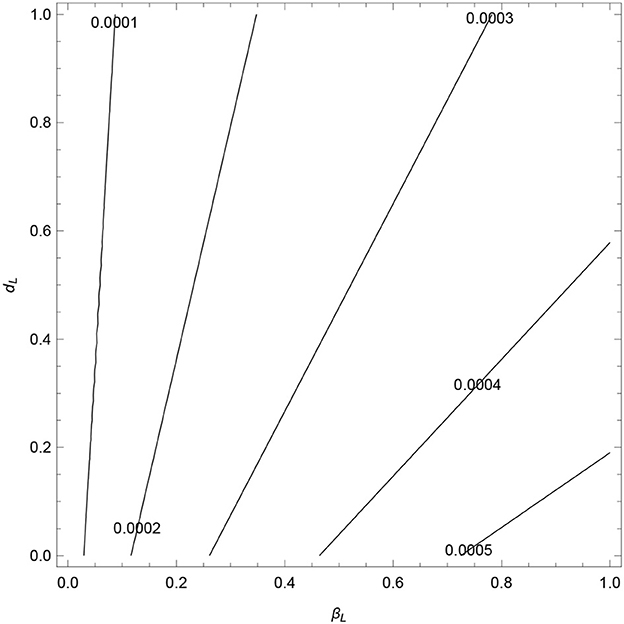
Figure 6. Contour plots of as a function of transmission rate (βL) and disease-induced death rate (dL).
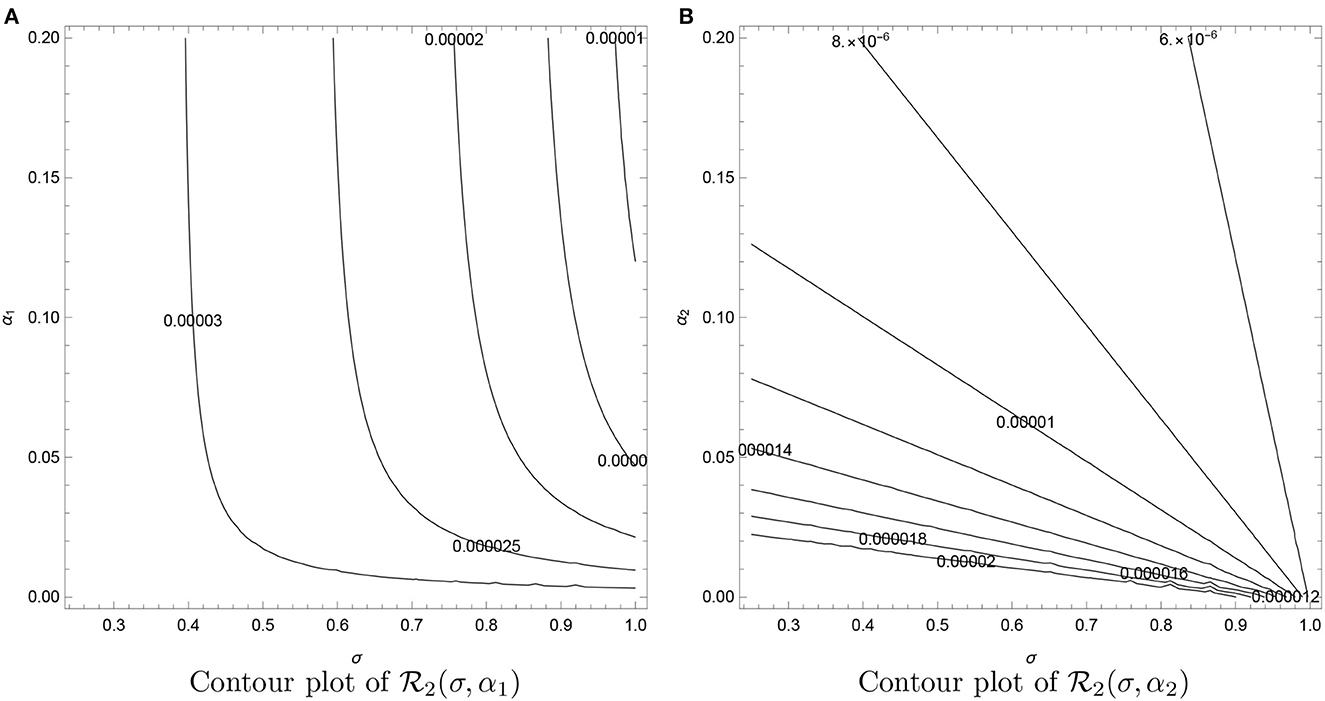
Figure 7. Contour plots of as functions of recovery rate after treatment (σ), treatment rate (α1), and recovery rate from PKDL (α2). (A) Contour plot of . (B) Contour plot of .
7. Conclusion
In developing nations, visceral leishmaniasis (VL) and tuberculosis (TB) co-infection is becoming a growing public health concern. Leishmaniasis infection alters the protective immunologic response to Bacillus Calmette-Guerin (BCG) vaccine against tuberculosis [36]. Tuberculosis is an immuno-suppressive disease that causes latent leishmaniasis to proceed to clinical leishmaniasis, and VL can provoke latent TB infection to TB disease [36]. In this study, we developed and analyzed a model that describes transmission dynamics of visceral leishmaniasis and tuberculosis co-infection. Firstly, we analyzed the VL and TB sub-models separately. The reproduction number for each sub-model was calculated by the next-generation matrix approach. The local stability properties of the sub-models were studied. We observed that when the associated reproduction numbers () for the TB-only model and () for the VL-only are less than unity, respectively, the model exhibits bifurcation. We observed that , hence, there is no competitive exclusion and the two diseases amplify each other. Thus, when and , there is always co-existence no matter which of the reproduction numbers is greater. If , then the TB-VL co-infection model exhibits backward bifurcation at which . Furthermore, if , and choosing the transmission probability βL as the bifurcation parameter, then the phenomenon of backward bifurcation occurs at . Consequently, the full model also exhibits the phenomenon of backward bifurcation when . The implication of this is that a stable endemic equilibrium coexists with a stable disease-free equilibrium whenever the fundamental reproduction number is less than unity. This study makes the argument that lowering the fundamental reproduction rate alone is insufficient to eradicate tuberculosis, leishmaniasis, and/or visceral leishmaniasis and tuberculosis co-infection models. The thresholds and equilibrium quantities for the models are determined, and their stability is analyzed. Finally, some numerical simulations are carried out to illustrate some of our theoretical results. The proposed model is not exhaustive and can be extended in various ways. As a future work, we intend to expand this study to construct a VL-TB co-infection model with a reservoir host population which considers antiviral therapy for VL infection. We will also expand it to consider treatment for both latent and active TB.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
OE: methodology, investigation, resources, formal analysis, simulations, and writing-original draft. JM: methodology, investigation, supervision, and writing-review and editing. SS: methodology, investigation, formal analysis, simulations, and writing-original draft. PD: methodology and simulations. FO: investigation, resources, and writing-review and editing. All authors contributed to the article and approved the submitted version.
Acknowledgments
OE acknowledge support from the DSI-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS), South Africa. Opinions expressed and conclusions arrived at are those of the authors and are not necessarily to be attributed to the CoE-MaSS. OE was particularly grateful to Raphael Taiwo Aruleba (University of Cape Town) for the useful discussion that led to this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Zou L, Chen J, Ruan S. Modeling and analyzing the transmission dynamics of visceral leishmaniasis. Math Biosci Eng. (2017) 14:1585–604. doi: 10.3934/mbe.2017082
2. Agyingi E, Wiandt T. Analysis of a model of leishmaniasis with multiple time lags in all populations. Math Comput Appl. (2019) 24:63. doi: 10.3390/mca24020063
3. ELmojtaba IM. Mathematical model for the dynamics of visceral leishmaniasis-malaria co-infection. Math Methods Appl Sci. (2016) 39:4334–53. doi: 10.1002/mma.3864
4. ELmojtaba IM, Mugisha JYT, Hashim MHA. Mathematical analysis of the dynamics of visceral leishmaniasis in the Sudan. Appl Math Comput. (2010) 217:2567–78. doi: 10.1016/j.amc.2010.07.069
5. Biswas S. Mathematical modeling of Visceral Leishmaniasis and control strategies. Chaos Solitons Fractals. (2017) 104:546–56. doi: 10.1016/j.chaos.2017.09.005
6. Patterson S, Wyllie S, Norval S, Stojanovski L, Simeons FRC, Auer JL, et al. The anti-tubercular drug delamanid as a potential oral treatment for visceral leishmaniasis. eLife. (2016) 5:e09744. doi: 10.7554/eLife.0974
7. van Griensven J, Mohammed R, Ritmeijer K, Burza S, Diro E. Tuberculosis in visceral leishmaniasis-human immunodeficiency virus coinfection: an evidence gap in improving patient outcomes? Open Forum Infect Dis. 5:ofy059. doi: 10.1093/ofid/ofy059
8. Li XX, Zhou XN. Co-infection of tuberculosis and parasitic diseases in humans: a systematic review. Parasit Vectors. (2013) 6:79. doi: 10.1186/1756-3305-6-79
9. Shweta SB, Gupta AK, Murti K, Pandey K. Co-infection of visceral leishmaniasis and pulmonary tuberculosis: a case study. Asian Pac J Trop Dis. (2014) 4:57–60. doi: 10.1016/S2222-1808(14)60315-7
10. Croft SL, Coombs GH. Leishmaniasis–current chemotherapy and recent advances in the search for novel drugs. Trends Parasitol. (2003) 19:502–8. doi: 10.1016/j.pt.2003.09.008
11. Egbelowo O, Sarathy JP, Gausi K, Zimmerman MD, Wang H, Wijnant G-J, et al. Pharmacokinetics and target attainment of SQ109 in plasma and human-like tuberculosis lesions in rabbits. Antimicrob Agents Chemother. (2021) 65:e00024-21. doi: 10.1128/AAC.00024-21
12. Keeling MJ, Danon L. Mathematical modelling of infectious diseases. Br Med Bull. (2009) 92:33–42. doi: 10.1093/bmb/ldp038
13. Grassly N, Fraser C. Mathematical models of infectious disease transmission. Nat Rev Microbiol. (2008) 6:477–87. doi: 10.1038/nrmicro1845
14. van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. (2002) 180:29–48. doi: 10.1016/s0025-5564(02)00108-6
15. Castillo-Chavez C, Song B. Dynamical models of Tuberculosis and their applications. Math Biosci Eng. (2004) 1:361–404. doi: 10.3934/mbe.2004.1.361
16. Nudee K, Chinviriyasit S, Chinviriyasit W. The effect of backward bifurcation in controlling measles transmission by vaccination. Chaos Solitons Fractals. (2019) 123:400–12. doi: 10.1016/j.chaos.2019.04.026
17. Mwamtobe PM, Simelane SM, Abelman S, Tchuenche JM. Optimal control of intervention strategies in malaria-tubercolosis co-infection with relapse. Int J Biomath. (2018) 11:1850017. doi: 10.1142/S1793524518500171
18. Korobeinikov A. Lyapunov functions and global properties for SEIR and SEIS epidemic models. Math Med Biol. (2004) 21:75–83. doi: 10.1093/imammb/21.2.75
19. Korobeiniikov A. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl Math Lett. (2002) 15:955–60. doi: 10.1016/S0893-9659(02)00069-1
20. Roop-O P, Chinviriyasit W, Chinviriyasit S. The effect of incidence function in backward bifurcation for malaria model with temporary immunity. Math Biosci. (2015) 265:47–64. doi: 10.1016/j.mbs.2015.04.008
21. Hoang MT, Egbelowo OF. On the global asymptotic stability of a hepatitis B epidemic model and its solutions by nonstandard numerical schemes. Bol Soc Math Mex. (2020) 26:1113–34. doi: 10.1007/s40590-020-00275-2
22. Rahman MU, Arfan M, Shah Z, Kumam P, Shutaywi M. Nonlinear fractional mathematical model of tuberculosis (TB) disease with incomplete treatment under Atangana-Baleanu derivative. Alex Eng J. (2021) 60:2845–56. doi: 10.1016/j.aej.2021.01.015
23. Tang TQ, Jan R, Bonyah E, Shah Z, Alzahrani E. Qualitative analysis of the transmission dynamics of dengue with the effect of memory, reinfection, and vaccination. Comput Math Methods Med. (2022) 2022:7893570. doi: 10.1155/2022/7893570
24. Zhang Z, Zeb A, Egbelowo OF, Erturk VS. Dynamics of a fractional order mathematical model for COVID-19 epidemic. Adv Differ Equat. (2020) 2020:420. doi: 10.1186/s13662-020-02873-w
25. Egbelowo OF, Hoang MT. Global dynamics of target-mediated drug disposition models and their solutions by nonstandard finite difference method. J Appl Math Comput. (2021) 66:621–43. doi: 10.1007/s12190-020-01452-2
26. Tang TQ, Shah Z, Jan R, Ebraheem A. Modeling the dynamics of tumor immune cells interactions via fractional calculus. Eur Phys J Plus. (2022) 137:367. doi: 10.1140/epjp/s13360-022-02591-0
27. Shah Z, Jan R, Kumam P, Deebani W, Shutaywi M. Fractional dynamics of HIV with source term for the supply of new CD4+ T-cells depending on the viral load via caputo-fabrizio derivative. Molecules. (2021) 26:1806. doi: 10.3390/molecules26061806
28. Susi H, Barres B, Pedro FV, Laine AL. Co-infection alters population dynamics of infectious disease. Nat Commun. (2015) 6:5975. doi: 10.1038/ncomms6975
29. Roeger LI, Feng Z, Castillo-Chavez C. Modeling TB and HIV co-infections. Math Biosci Eng. (2009) 6:815–37. doi: 10.3934/mbe.2009.6.815
30. Melese ZT, Alemneh HT. Enhancing reservoir control in the co-dynamics of HIV-VL: from mathematical modeling perspective. Adv Differ Equat. (2021) 2021:429. doi: 10.1186/s13662-021-03584-6
31. Mtisi E, Rwezaura H, Tchuenche JM. A mathematical analysis of malaria tuberculosis co-dynamics. Discr Contin Dyn Syst Ser B. (2009) 12:827–64. doi: 10.3934/dcdsb.2009.12.827
32. Bhunu CP, Garira W, Mukandavire Z. Modeling HIV/AIDS and tuberculosis coinfection. Bull Math Biol. (2009) 71:1745–80. doi: 10.1007/s11538-009-9423-9
33. Lakshmikantham V, Leela S, Martynyuk AA. Stability Analysis of Nonlinear Systems. New York, NY; Basel: Marcel Dekker Inc. (1989).
34. Winter PA, Jessop CL, Adewusi FJ. The complete graph: eigenvalues, trigonometrical unit-equations with associated t-complete-eigen sequences, ratios, sums and diagrams. Asian J Math Sci Res. (2015) 9:92–107.
Keywords: visceral leishmaniasis, tuberculosis, Routh-Hurwitz criterion, backward bifurcation, stability analysis
Citation: Egbelowo OF, Munyakazi JB, Dlamini PG, Osaye FJ and Simelane SM (2023) Modeling visceral leishmaniasis and tuberculosis co-infection dynamics. Front. Appl. Math. Stat. 9:1153666. doi: 10.3389/fams.2023.1153666
Received: 29 January 2023; Accepted: 14 April 2023;
Published: 15 May 2023.
Edited by:
Samson Olaniyi, Ladoke Akintola University of Technology, NigeriaReviewed by:
Ebenezer Bonyah, University of Education, Winneba, GhanaLijun Pei, Zhengzhou University, China
Afeez Abidemi, Federal University of Technology, Nigeria
Copyright © 2023 Egbelowo, Munyakazi, Dlamini, Osaye and Simelane. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Oluwaseun F. Egbelowo, b2x1d2FzZXVuQGFpbXMuZWR1Lmdo
 Oluwaseun F. Egbelowo
Oluwaseun F. Egbelowo Justin B. Munyakazi
Justin B. Munyakazi Phumlani G. Dlamini3
Phumlani G. Dlamini3