
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
PERSPECTIVE article
Front. Appl. Math. Stat., 28 February 2023
Sec. Dynamical Systems
Volume 9 - 2023 | https://doi.org/10.3389/fams.2023.1128224
This article is part of the Research TopicInsights in Dynamical Systems 2022View all 7 articles
Low-dimensional neural mass models are often invoked to model the coarse-grained activity of large populations of neurons and synapses and have been used to help understand the coordination of large scale brain rhythms. However, they are phenomenological in nature and, although motivated by neurobiological considerations, the absence of a direct link to an underlying biophysical reality is a weakness that means they may not be best suited to capturing some of the rich behaviors seen in real neuronal tissue. In this perspective article I discuss a simple spiking neuron network model that has recently been shown to admit to an exact mean-field description for synaptic interactions. This has many of the features of a neural mass model coupled to an additional dynamical equation that describes the evolution of population synchrony. This next generation neural mass model is ideally suited to understanding the patterns of brain activity that are ubiquitously seen in neuroimaging recordings. Here I review the mean-field equations, the way in which population synchrony, firing rate, and average voltage are intertwined, together with their application in large scale brain modeling. As well as natural extensions of this new approach to modeling the dynamics of neuronal populations I discuss some of the open mathematical challenges in developing a statistical neurodynamics that can generalize the one discussed here.
Neural mass and field models generate brain rhythms using the notion of population firing rates, and in some sense can be thought of as sitting above more detailed networks of interacting conductance-based spiking neuron models. The latter are hard to analyze in the raw, given that they are both high-dimensional and nonlinear, and are typically studied with tools from computational neuroscience, as exemplified by the work of the Human Brain Project [1]. In contrast neural mass and field models are much more amenable to mathematical analysis, as reviewed in Coombes et al. [2] and Cook et al. [3], and although these low-dimensional models are typically not derived from any underlying microscopic spiking dynamics they can be motivated by a number of phenomenological arguments for the evolution of coarse-grained neuronal variables. Nonetheless, they are only expected to provide appropriate levels of description for many thousands of near identical interconnected neurons with a preference to operate coherently. As such, they are not ideally suited to studying phenomenon that are known to be associated with changes of synchrony, such as the post stimulus response ubiquitously seen in human neuroimaging studies, see e.g., Mullinger et al. [4]. However, a new type of neural mass model has recently been developed that is able to capture the phenomenon of event-related synchronization/desynchronization (ERS/ERD) that is believed to underlie the changes in power seen in brain spectrograms, or more specifically for that seen in magneto-encephalography (MEG) data showing post-movement beta rebound [5]. Importantly, this new mean-field model is an exact description of a globally coupled network of heterogeneous θ-neuron models in the thermodynamic limit. The θ-neuron, or Ermentrout–Kopell canonical model, is the normal form for the saddle-node on a limit cycle bifurcation, and for constant stimulation can generate low firing rates typical of those seen in real cortical neurons [6]. Interestingly, the resulting mean-field model has a population firing rate that depends on the degree of population synchrony, and has a richer dynamical repertoire than standard neural mass models. Moreover, it can incorporate realistic models of synaptic currents (both chemical and electrical) and the mass model is easily incorporated into network studies (both discrete and continuous). In this perspective article I review some of the main features of this new neural population model, its application to neuroimaging studies, extensions of the model to incorporate further biologically important components, and some mathematical challenges for developing similar mean-field reductions for other spiking models.
The θ-neuron describes a single neuron using a phase θ ∈ [0, 2π) such that a spike is generated whenever θ passes through π from below. For a stimulus I it evolves according to the ordinary differential equation
The θ-neuron is formally equivalent to a quadratic integrate-and-fire (QIF) model for voltage dynamics [7] under the transformation v = tan(θ/2), and here we note that this can also be written as a Möbius transformation v = iM(eiθ; −1, 1, 1, 1), where
A network of θ-neurons can be described with the introduction of an index n = 1, …, N and the replacement I → μn + In, where In describes the synaptic input current to neuron n and μn is a constant drive. For a globally coupled network, the current arising from a chemical synapse can be written in the form In = g(t)(vsyn − vn) for some global conductance g, synaptic reversal potential vsyn, and local voltage vn. In the voltage representation this leads to the network equations
Where the voltage is reset to vr → −∞ whenever vth → ∞. Here, μn is a random variable drawn from a Lorentzian distribution with center μ0 and width at half maximum Δ. For a treatment of the model with a Gaussian and q-Gaussian distribution of drives, see Klinshov et al. [8] and Pyragas and Pyragas [9], respectivley. We will work in the thermodynamic limit (N → ∞), and choose a model of conductance change that is driven by delta–Dirac spikes in the form:
Where k is a strength of coupling, R is the population firing rate, and denotes the mth time that neuron n spikes. Here Q is a linear differential operator whose Green's function is chosen to capture the post-synaptic response to the arrival of a spike. A common choice is the α-function η(t) = α2te−αtH(t), where H is a Heaviside step function. The Q for this choice is the second order operator Q = (1 + α−1d/dt)2. For a schematic of the spiking network described below, see Figure 1.
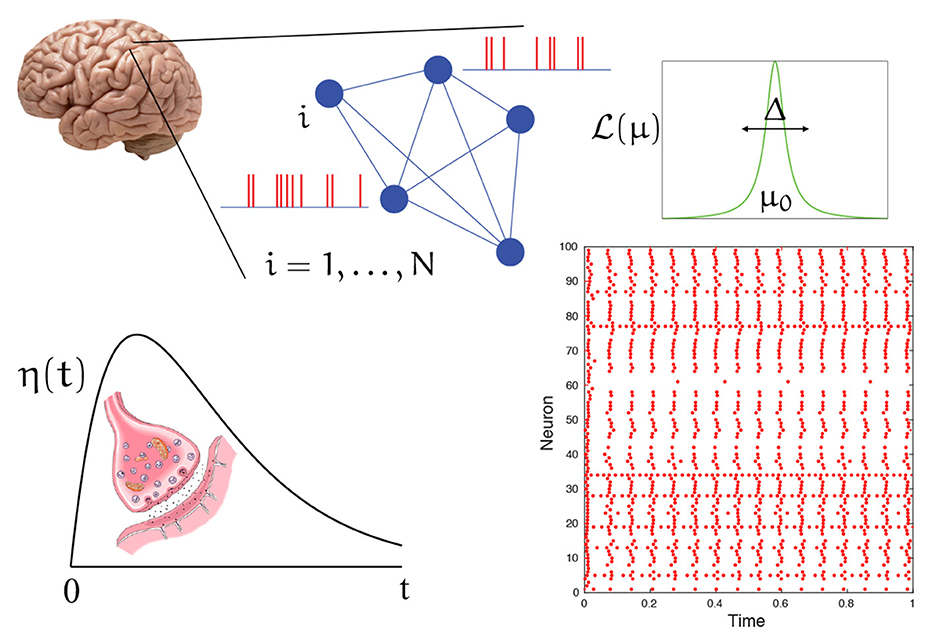
Figure 1. A schematic of the spiking network described by Equation (3) in the voltage representation. A patch of cortical tissue is modeled as a globally coupled network of heterogeneous quadratic integrate-and-fire neurons. Each neuron has a background drive drawn from a Lorentzian distribution . Interactions are mediated by chemical synapses that generate post synaptic conductance changes in response to the arrival of a spike (action potential) with a temporal shape described by η(t). A typical raster plot of firing times (red dots) for a (finite size) network shows a pattern with a clear degree of synchrony.
To date two independent approaches have been developed for obtaining mean-field equations for the spiking network model described above (with N → ∞), both finding exact solutions to the continuity equation describing the distribution of states. The first approach, due to Luke et al. [10], considers the θ-neuron representation and makes use of the Ott–Antonsen (OA) ansatz [11]. Here a Fourier series representation for the distribution of phases with all Fourier coefficients restricted to be powers of a function a(μ, t) ∈ ℂ is shown to be an exact solution provided that a(μ, t) satisfies a certain differential equation. Moreover, the average of a(μ, t) over the distribution of drives, denoted 〈a(μ, t)〉μ, has a physical interpretation as the Kuramoto order parameter for synchrony . Recent work of Cestnik and Pikovsky generalizes this approach to describe relaxation to the stable OA manifold in an exact manner [12]. The second approach due to Montbrió et al. [13], considers the QIF representation and shows that a Lorentzian choice for the distribution of voltages, with center y(μ, t) and width at half maximum x(μ, t), is also a solution provided that the pair (x, y) obey a set of coupled differential equations. Moreover, after averaging over the distribution of drives, this pair can also be related to physical variables. Introducing the average voltage then . Thus, in both approaches an evolution equation for physically meaningful macroscopic variables is generated. Introducing the complex number W(t) = πR(t) + iV(t) then this evolution equation from the approach of Montbrió et al. can be written succinctly as the complex Ricatti equation
It is noteworthy that the distribution of phases arising from the OA approach can be written as a Lorentzian distribution in eiθ. Thus, exploiting a result of McCullagh [14] that if the random variable X has a Lorentzian distribution with complex parameter ζ, then the random variable Y = M(X; a, b, c, d) has a Lorentzian distribution with parameter M(ζ; a, b, c, d), and remembering that the phase and voltage representations are related by a Möbius transformation, it can be shown that Z(t) and W(t) are related by the conformal map Z = M−1(W*; −1, 1, 1, 1), or more specifically:
Thus, the dynamical equation for Z(t) can either be obtained directly following the approach of Luke et al. or by applying (Equations 6–5). Either way, this gives the complex Ricatti equation for the evolution of synchrony as
A method for analyzing periodic solutions to complex Ricatti equations of the form given by Equations (5), (7) (in the self-consistent case that g(t) is periodic) has recently been proposed in Omel'chenko [15], exploiting the fact that every periodic solution corresponds to a fixed point of a Möbius transformation. For a numerical bifurcation analysis of Equation (7), see Coombes and Byrne [16] where the basic mechanism for generating oscillations at the single population level is shown to be a Hopf bifurcation (though note that oscillations can also emerge out of the blue along a branch of isolas in models with two interacting populations). The mean-field model can also exhibit canards and bursting solutions under slow periodic forcing [17], as well as chaos for moderately fast periodic forcing [18].
In contrast to more traditional phenomenological neural mass models, as exemplified by that of Wilson and Cowan [19], the population firing rate is a derived quantity that takes the form R(t) = π−1Re W(t) = π−1Re ((1 − Z*)/(1 + Z*)). Thus, the firing rate is determined by the degree of spike synchrony within a population (measured by the Kuramoto order parameter), rather than just keeping track of the fraction of active neurons in a given interval of time (as in the original heuristic derivation of the Wilson–Cowan equations). In cases where spike synchrony is not important, then the Wilson-Cowan equations would still be expected do a good job of qualitatively describing network dynamics. The main difference between the heuristic Wilson–Cowan model and next generation neural mass model is that the latter explicitly includes a dynamic component for describing spike synchrony within a population. Moreover, the next generation neural mass equations are closed in slightly different way in that R only depends indirectly on g through the dynamical evolution of W or Z [20]. Thus, we may select from one of the two equivalent perspectives depending on context. For example, when modeling MEG studies that highlight ERS/ERD it is convenient to use the Z representation for the Kuramoto order parameter. In contrast, for studies involving voltage sensitive dyes it is more natural to use the W representation and extract the average voltage from V = Im W. For a detailed derivation of the mean-field equations described above, see Coombes and Wedgwood [21, Chapter 8].
With the inclusion of an external time-dependent input, the mean-field equations described above have previously been shown to generate behavior consistent with neuroimaging experiments exhibiting so-called beta rebound [5]. Modulations in the beta power of human brain rhythms are known to occur during and after movement. A sharp decrease in neural oscillatory power is observed during movement followed by an increase above baseline on movement cessation. Both are captured in the response of the mean field model to simple square wave forcing, as illustrated in Figure 2.
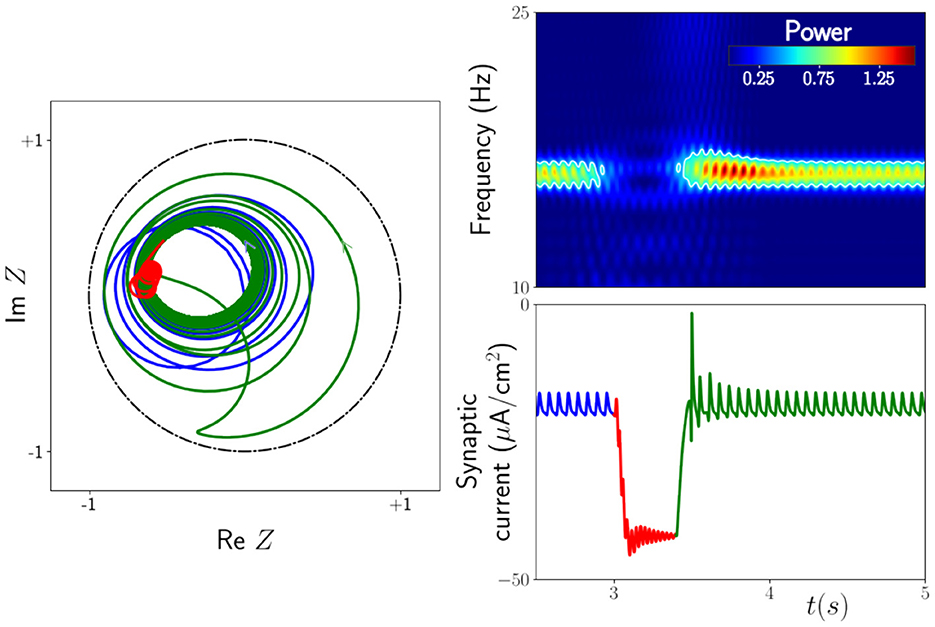
Figure 2. Response of the next generation neural mass model to an external drive A(t). This is modeled under the replacement μ0 → μ0 + A where (namely, a smoothed rectangular pulse). Note that the 0.4s pulse is not applied until time t = 3s after transients have dropped off. Right: Power spectrogram and time series of the synaptic current demonstrating the rebound of the system, i.e., an increase in amplitude (and hence power) after the drive is switched off. The white contour line in the spectrogram is the level set with value 0.5, highlighting that the power in the beta band ≃15 Hz drops off significantly during the drive and comes back stronger at the termination of the drive. Left: The corresponding trajectory of the Kuramoto order parameter Z. As the system relaxes back to its original oscillatory behavior the trajectory loops close to the border |Z| = 1. It is this enhanced synchrony that causes the rebound. Lines in blue indicate pre-stimulus activity, lines in red are for the response during stimulation, and lines in green are post-stimulus. The parameters are μ0 = 21.5, Δ = 0.5, vsyn = −10 mV, k = 3.2, α−1 = 33 ms, ms, τ = 400 ms, and Ω0 = 30. Figure adapted from Byrne et al. [5].
The extension of the mean-field equations to describe interacting excitatory and inhibitory sub-populations, with both reciprocal and self connections, is straightforward [16, 22–26], as is the further extension to whole brain models utilizing (connectivity and delay) data from the Human Connectome Project [27], and the corresponding limit of spatially continuous neural fields [28, 29]. Moreover, for certain forms of noise in the microscopic equations the mean-field reduction can also be generalized [30–36]. A variation on the Lorentzian ansatz (in the voltage representation) combined with a moment closure approach has also been shown to be useful for approximating networks of Izhikevich neurons [37, 38], namely QIF neurons with a form of adaptation [39].
The mean-field reduction remains viable with the inclusion of electrical synapses. These are electrically conductive links between two adjacent nerve cells at a so-called gap junction (modeled as a passive ohmic resistance). The synaptic delay for a chemical synapse is typically in the range 1 − 100 ms, while the synaptic delay for an electrical synapse may be only about 0.2 ms. Little is known about the functional aspects of gap junctions, but they are thought to be involved in the synchronization of neurons, see e.g., Bennet and Zukin [40]. For their inclusion in the next generation framework, see Laing [41], Pietras et al. [42], Montbrió and Pazó [43], Byrne et al. [44], and Clusella et al. [45]. Recent work has shown that they can have a strong effect on network excitability and that gap junction coupling strength can play a key role in generating empirically-observed patterns of large scale spatio-temporal brain activity [46].
In recent years there has been a growing use of the next generation population modeling framework in a variety of different neuroscience contexts, including abnormal beta rebound in schizophrenia [47], beta bursts seen in single trial data [48], the generation of gamma oscillations [49] and theta-nested gamma oscillations [50], syllable segregation in speech comprehension [51], the generation of functional connectivity in whole brain networks [48, 52], seizure propagation [53], cross-frequnecy coupling [54] and communication through coherence [55], working memory (with the inclusion of short-term synaptic plasticity) [56], non-invasive transcranial brain stimulation [57], and neurodegeneration [58].
The mean-field reduction discussed here leads to low dimensional equations that are in the spirit of previous neural mass and field equations, albeit with a direct link to an underlying microscopic spiking dynamics [59]. They have proven to have very rich dynamics, at the node [13, 16, 60], network [46, 48, 52], and continuum level [28, 29, 41, 44]. Nonetheless, their pattern forming properties remain relatively unexplored, providing an open challenge to the applied mathematics community. However, it is worth bearing in mind the caveats of heterogeneity, global coupling, and the thermodynamic limit in the reduction. For identical neurons one could instead turn to the Watanabe–Strogatz ansatz (instead of OA) as considered by Laing [61]. Moving away from global coupling is difficult without some form of approximation, and here the techniques developed by Thibeault et al. [62] might be useful for modular networks, and those of Restrepo and Ott for assortative networks [63] as considered in Chandra et al. [64] and Laing and Bläsche [65]. Moving away from the thermodynamic limit, to address finite size effects, may be possible with a perturbative approach (around the asynchronous state), such as the Bogolyubov–Born–Green–Kirkwood–Yvon hierarchy with an appropriate moment-closure approximation [66], or a path-integral formalism to determine the evolution of system covariances [67]. Interestingly, it has recently been shown that finite size effects can be captured with the inclusion of stochastic forcing by shot noise into the mean-field equations [68].
In essence the mean-field reduction discussed here is well suited to describing systems which dynamically evolve between an incoherent state and a partially synchronized state, which is often the case in phase oscillator networks with interactions that are prescribed by sinusoidal functions (and the large global network generates a unimodal distribution of phases). In systems with higher harmonics in their interactions, it is possible for cluster states to emerge, and the OA ansatz breaks down (as it cannot describe distributions with more than one peak). Thus, there is an interest in either generalizing the OA approach or developing an alternative. As a generalization it might be worth considering whether there are other models like the QIF that can be described by a multi-peak circular distribution [69] of network phases ρ(θ) (after integrating over the distribution of drives) of the form
Where are the Kuramoto–Daido order parameters. This choice effectively recovers the OA ansatz when M = 1. However, this would again only cover a special case of a particular choice of idealized single neuron model. Xiao et al. [70] have recently developed a data-informed mean-field approach that couples to the average network voltage (and note that the next generation approach also has a coupling to the average voltage), and it may be that this is a more promising line of attack for describing networks of biophysically realistic neurons.
Finally, it is important from a modeling perspective to realize that the brain consists of more than just the cortex and that for many sub-cortical structures intrinsic nonlinear ionic currents can dominate the firing rate response. It remains an open challenge to develop mean-field models that can incorporate such important features, though for slow intrinsic currents some progress has been possible, see e.g., Modhara et al. [71] for a mean-field model of the thalamus (sensory gateway to the cortex). Similarly, it is important to recognize that there is more to brain tissue than neurons, and that for many clinical applications, some form of coupling to the extracellular space is beneficial; a case in point being epilepsy, and the important role that extracellular K+ has in the genesis and propagation of seizure states [72].
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
SC is the single author of this article and contributed to the article and approved the submitted version.
This work was supported by the Engineering and Physical Sciences Research Council (grant number EP/V04866X/1).
I would like to thank Áine Byrne for many interesting discussions about the work described in this article.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Amunts K, Knoll AC, Lippert T, Pennartz CMA, Ryvlin P, Destexhe A, et al. The human brain project–synergy between neuroscience, computing, informatics, and brain-inspired technologies. PLoS Biol. (2019) 17:e3000344. doi: 10.1371/journal.pbio.3000344
2. Coombes S, Beim Graben PP, Potthast R, Wright J. Neural Fields: Theory and Applications. Berlin: Springer (2014).
3. Cook BJ, Peterson ADH, Woldman W, Terry JR. Neural field models: a mathematical overview and unifying framework. Math Neurosci Appl. (2022) 2:7284. doi: 10.46298/mna.7284
4. Mullinger KJ, Cherukara MT, Buxton RB, Francis ST, Mayhew SD. Post-stimulus fMRI and EEG responses: evidence for a neuronal origin hypothesised to be inhibitory. NeuroImage. (2017) 157:388–99. doi: 10.1016/j.neuroimage.2017.06.020
5. Byrne A, Brookes MJ, Coombes S. A mean field model for movement induced changes in the beta rhythm. J Comput Neurosci. (2017) 43:143–58. doi: 10.1007/s10827-017-0655-7
6. Ermentrout GB, Kopell N. Parabolic bursting in an excitable system coupled with a slow oscillation. SIAM J Appl Math. (1986) 46:233–53. doi: 10.1137/0146017
7. Latham PE, Richmond BJ, Nelson PG, Nirenberg S. Intrinsic dynamics in neuronal networks. I. Theory. J Neurophysiol. (2000) 83:808–27. doi: 10.1152/jn.2000.83.2.808
8. Klinshov V, Kirillov S, Nekorkin V. Reduction of the collective dynamics of neural populations with realistic forms of heterogeneity. Phys Rev E. (2021) 103:L040302. doi: 10.1103/PhysRevE.103.L040302
9. Pyragas V, Pyragas K. Mean-field equations for neural populations with q-Gaussian heterogeneities. Phys Rev E. (2022) 105:044402. doi: 10.1103/PhysRevE.105.044402
10. Luke TB, Barreto E, So P. Complete classification of the macroscopic behaviour of a heterogeneous network of theta neurons. Neural Computat. (2013) 25:3207–3234. doi: 10.1162/NECO_a_00525
11. Ott E, Antonsen TM. Low dimensional behavior of large systems of globally coupled oscillators. Chaos. (2008) 18:037113. doi: 10.1063/1.2930766
12. Cestnik R, Pikovsky A. Hierarchy of exact low-dimensional reductions for populations of coupled oscillators. Phys Rev Lett. (2022) 128:054101. doi: 10.1103/PhysRevLett.128.054101
13. Montbrió E, Pazó D, Roxin A. Macroscopic description for networks of spiking neurons. Phys Rev X. (2015) 5:021028. doi: 10.1103/PhysRevX.5.021028
14. McCullagh P. Conditional inference and Cauchy models. Biometrika. (1992) 79:247–59. doi: 10.1093/biomet/79.2.247
15. Omel'chenko O. Periodic orbits in the Ott-Antonsen manifold. arXiv:220601481. (2022) doi: 10.1088/1361-6544/aca94c
16. Coombes S, Byrne A. Next generation neural mass models. In: Torcini A, Corinto F, editors. Lecture Notes in Nonlinear Dynamics in Computational Neuroscience: From Physics Biology to ICT. Switzerland: Springer (2019). p. 1–16.
17. Avitabile D, Desroches M, Ermentrout GB. Cross-scale excitability in networks of quadratic integrate-and-fire neurons. PLoS Comput Biol. (2022) 18:e1010569. doi: 10.1371/journal.pcbi.1010569
18. So P, Luke TB, Barreto E. Networks of theta neurons with time-varying excitability: macroscopic chaos, multistability, and final-state uncertainty. Physica D. (2014) 267:16–26. doi: 10.1016/j.physd.2013.04.009
19. Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. (1972) 12:1–24. doi: 10.1016/S0006-3495(72)86068-5
20. Devalle F, Roxin A, Montbrió E. Firing rate equations require a spike synchrony mechanism to correctly describe fast oscillations in inhibitory networks. PLoS Computat Biol. (2017) 13:e1005881. doi: 10.1371/journal.pcbi.1005881
21. Coombes S, Wedgwood KCA. Neurodynamics: An Applied Mathematics Perspective. Vol. 75 of Texts in Applied Mathematics. Switzerland: Springer (2023).
22. Luke TB, Barreto E, So P. Macroscopic complexity from an autonomous network of networks of theta neurons. Front Comput Neurosci. (2014) 8:145. doi: 10.3389/fncom.2014.00145
23. Dumont G, Ermentrout GB, Gutkin B. Macroscopic phase-resetting curves for spiking neural networks. Phys Rev E. (2017) 96:042311. doi: 10.1103/PhysRevE.96.042311
24. Ratas I, Pyragas K. Symmetry breaking in two interacting populations of quadratic integrate-and-fire neurons. Phys Rev E. (2017) 96:042212. doi: 10.1103/PhysRevE.96.042212
25. Dumont G, Gutkin B. Macroscopic phase resetting-curves determine oscillatory coherence and signal transfer in inter-coupled neural circuits. PLoS Computat Biol. (2019) 15:e1007019. doi: 10.1371/journal.pcbi.1007019
26. Pyragas K, Fedaravičius AP, Pyragienẽ T. Suppression of synchronous spiking in two interacting populations of excitatory and inhibitory quadratic integrate-and-fire neurons. Phys Rev E. (2021) 104:014203. doi: 10.1103/PhysRevE.104.014203
27. Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, et al. The WU-Minn human connectome project: an overview. Neuroimage. (2013) 80:62–79. doi: 10.1016/j.neuroimage.2013.05.041
28. Laing CR. Derivation of a neural field model from a network of theta neurons. Phys Rev E. (2014) 90:010901(R). doi: 10.1103/PhysRevE.90.010901
29. Byrne A, Avitabile D, Coombes S. A next generation neural field model: the evolution of synchrony within patterns and waves. Phys Rev E. (2019) 99:012313. doi: 10.1103/PhysRevE.99.012313
30. Lai YM, Porter MA. Noise-induced synchronization, desynchronization, and clustering in globally coupled nonidentical oscillators. Phys Rev E. (2013) 88:012905. doi: 10.1103/PhysRevE.88.012905
31. Tyulkina IV, Goldobin DS, Klimenko LS, Pikovsky A. Dynamics of noisy oscillator populations beyond the ott-antonsen ansatz. Phys Rev Lett. (2018) 120:264101. doi: 10.1103/PhysRevLett.120.264101
32. Ratas I, Pyragas K. Noise-induced macroscopic oscillations in a network of synaptically coupled quadratic integrate-and-fire neurons. Phys Rev E. (2019) 100:052211. doi: 10.1103/PhysRevE.100.052211
33. Tönjes R, Pikovsky A. Low-dimensional description for ensembles of identical phase oscillators subject to Cauchy noise. Phys Rev E. (2020) 102:052315. doi: 10.1103/PhysRevE.102.052315
34. Goldobin DS, di Volo M, Torcini A. Reduction methodology for fluctuation driven population dynamics. Phys Rev Lett. (2021) 127:038301. doi: 10.1103/PhysRevLett.127.038301
35. Cestnik R, Pikovsky A. Exact finite-dimensional reduction for a population of noisy oscillators and its link to Ott-Antonsen and Watanabe-Strogatz theories. Chaos. (2022) 32:113126. doi: 10.1063/5.0106171
36. di Volo M, Segneri M, Goldobin DS, Politi A, Torcini A. Coherent oscillations in balanced neural networks driven by endogenous fluctuations. Chaos. (2022) 32:023120. doi: 10.1063/5.0075751
37. Chen L, Campbell SA. Exact mean-field models for spiking neural networks with adaptation. J Comput Neurosci. (2022) 50:445–69. doi: 10.1007/s10827-022-00825-9
38. Gast R, Solla SA, Kennedy A. Macroscopic dynamics of neural networks with heterogeneous spiking thresholds. arXiv:220903501. (2022). doi: 10.48550/arXiv.2209.03501
39. Ferrara A, Angulo-Garcia D, Torcini A, Olmi S. Population spiking and bursting in next generation neural masses with spike-frequency adaptation. bioRxiv:20221011511692. (2022) doi: 10.1101/2022.10.11.511692
40. Bennet MVL, Zukin RS. Electrical coupling and neuronal synchronization in the mammalian brain. Neuron. (2004) 41:495–511. doi: 10.1016/S0896-6273(04)00043-1
41. Laing CR. Exact neural fields incorporating gap junctions. SIAM J Appl Dyn Syst. (2015) 14:1899–929. doi: 10.1137/15M1011287
42. Pietras B, Devalle F, Roxin A, Daffertshofer A, Montbrió E. Exact firing rate model reveals the differential effects of chemical versus electrical synapses in spiking networks. Phys Rev E. (2019) 100:042412. doi: 10.1103/PhysRevE.100.042412
43. Montbrió E, Pazó D. Exact mean-field theory explains the dual role of electrical synapses in collective synchronization. Phys Rev Lett. (2020) 125:248101. doi: 10.1103/PhysRevLett.125.248101
44. Byrne A, Ross J, Nicks R, Coombes S. Mean-field models for EEG/MEG: from oscillations to waves. Brain Topography. (2022) 35:36–53. doi: 10.1007/s10548-021-00842-4
45. Clusella P, Pietras B, Montbrió E. Kuramoto model for populations of quadratic integrate-and-fire neurons with chemical and electrical coupling. Chaos. (2022) 32:013105. doi: 10.1063/5.0075285
46. Forrester M, Petros S, Lai YM, O'Dea RD, Sotiropoulos S, Coombes S. Whole brain functional connectivity: insights from next generation neural mass modelling incorporating electrical synapses. [Preprint]. (2023).
47. Byrne A, Coombes S, Liddle PF. A neural mass model for abnormal beta-rebound in schizophrenia. In: Cutsuridis V, editor. Handbook of Multi-Scale Models of Brain Disorders. Switzerland: Springer (2019).
48. Byrne A, Dea RO, Forrester M, Ross J, Coombes S. Next generation neural mass and field modelling. J Neurophysiol. (2020) 123:726–42. doi: 10.1152/jn.00406.2019
49. Keeley S, Byrne A, Fenton A, Rinzel J. Firing rate models for gamma oscillations. J Neurophysiol. (2019) 121:2181–90. doi: 10.1152/jn.00741.2018
50. Segneri M, Bi H, Olmi S, Torcini A. Theta-nested gamma oscillations in next generation neural mass models. Front Comput Neurosci. (2020) 14:47. doi: 10.3389/fncom.2020.00047
51. Toland M, Cucu MO, Homer M, Houghton C. Modelling neural entrainment to syllable-initial phonemes. Front Neurosci. (2023) 16:826105. doi: 10.3389/fnins.2022.826105
52. Rabuffo G, Fousek J, Bernard C, Jirsa V. Neuronal cascades shape whole-brain functional dynamics at rest. eNeuro. (2021) 8:ENEURO.0283-21.2021. doi: 10.1523/ENEURO.0283-21.2021
53. Gerster M, Taher H, Škoch A, Hlinka J, Guye M, Bartolomei F, et al. Patient-specific network connectivity combined with a next generation neural mass model to test clinical hypothesis of seizure propagation. Front Syst Neurosci. (2021) 15:675272. doi: 10.3389/fnsys.2021.675272
54. Ceni A, Olmi S, Torcini A, Angulo-Garcia D. Cross frequency coupling in next generation inhibitory neural mass models. Chaos. (2020) 30:053121. doi: 10.1063/1.5125216
55. Reyner-Parra D, Huguet G. Phase-locking patterns underlying effective communication in exact firing rate models of neural networks. PLoS Comput Biol. (2022) 18:e1009342. doi: 10.1371/journal.pcbi.1009342
56. Taher H, Torcini A, Olmi S. Exact neural mass model for synaptic-based working memory. PLoS Comput Biol. (2020) 16:e1008533. doi: 10.1371/journal.pcbi.1008533
57. Clusella P, Köksal-Ersöz E, Garcia-Ojalvo J, Ruffini G. Comparison between an exact and a heuristic neural mass model with second-order synapses. arXiv:220607521. (2022) doi: 10.1101/2022.06.15.496262
58. Reyes RG, Martinez Montes E. Modeling neural activity in neurodegenerative diseases through a neural field model with variable density of neurons. bioRxiv:20220823504980. (2022) doi: 10.1101/2022.08.23.504980
59. Bick C, Goodfellow M, Laing CR, Martens EA. Understanding the dynamics of biological and neural oscillator networks through exact mean-field reductions: a review. J Math Neurosci. (2020) 10:9. doi: 10.1186/s13408-020-00086-9
60. Ratas I, Pyragas K. Macroscopic oscillations of a quadratic integrate-and-fire neuron network with global distributed-delay coupling. Phys Rev E. (2018) 98:052224. doi: 10.1103/PhysRevE.98.052224
61. Laing CR. The dynamics of networks of identical theta neurons. J Math Neurosci. (2018) 8:4. doi: 10.1186/s13408-018-0059-7
62. Thibeault V, St-Onge G, Dubé LJ, Desrosiers P. Threefold way to the dimension reduction of dynamics on networks: an application to synchronization. Phys Rev Res. (2020) 2:043215. doi: 10.1103/PhysRevResearch.2.043215
63. Restrepo JG, Ott E. Mean-field theory of assortative networks of phase oscillators. Europhys Lett. (2014) 107:60006. doi: 10.1209/0295-5075/107/60006
64. Chandra S, Hathcock D, Crain K, Antonsen TM, Girvan M, Ott E. Modeling the network dynamics of pulse-coupled neurons. Chaos. (2017) 27:033102. doi: 10.1063/1.4977514
65. Laing CR, Bläsche C. The effects of within-neuron degree correlations in networks of spiking neurons. Biol Cybern. (2020) 114:337–47. doi: 10.1007/s00422-020-00822-0
66. Hildebrand EJ, Buice MA, Chow CC. Kinetic theory of coupled oscillators. Phys Rev Lett. (2007) 98:054101. doi: 10.1103/PhysRevLett.98.054101
67. Qiu SW, Chow CC. Finite-size effects for spiking neural networks with spatially dependent coupling. Phys Rev E. (2018) 98:062414. doi: 10.1103/PhysRevE.98.062414
68. Klinshov VV, Kirillov SY. Shot noise in next-generation neural mass models for finite-size networks. Phys Rev E. (2022) 106:L062302. doi: 10.1103/PhysRevE.106.L062302
69. Kato S, Jones MC. An extended family of circular distributions related to wrapped Cauchy distributions via Brownian motion. Bernoulli. (2013) 19:154–171. doi: 10.3150/11-BEJ397
70. Xiao ZC, Lin KK, Young LS. A data-informed mean-field approach to mapping of cortical parameter landscapes. PLoS Computat Biol. (2021) 17:e1009718. doi: 10.1371/journal.pcbi.1009718
71. Modhara S, Lai YM, Thul R, Coombes S. Neural fields with rebound currents: novel routes to patterning. SIAM J Appl Dyn Syst. (2021) 20:1596–620. doi: 10.1137/20M1364710
Keywords: theta neuron, Kuramoto order parameter, Ott-Antonsen ansatz, neural mass, neuronal synchrony, mean field reduction
Citation: Coombes S (2023) Next generation neural population models. Front. Appl. Math. Stat. 9:1128224. doi: 10.3389/fams.2023.1128224
Received: 20 December 2022; Accepted: 10 February 2023;
Published: 28 February 2023.
Edited by:
Axel Hutt, Inria Nancy-Grand-Est Research Centre, FranceReviewed by:
Alex Roxin, Universitat Autònoma de Barcelona, SpainCopyright © 2023 Coombes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stephen Coombes,  c3RlcGhlbi5jb29tYmVzQG5vdHRpbmdoYW0uYWMudWs=
c3RlcGhlbi5jb29tYmVzQG5vdHRpbmdoYW0uYWMudWs=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.