- Graduate School of Business Sciences, Humanities and Social Sciences, University of Tsukuba, Tokyo, Japan
This study aims to analyze the structure of the emergence and maintenance of the cartel mechanism as an informal organization and the measures to deter bid-rigging. We propose an agent-based bid-rigging norms model and validate it with a mathematical model. We clarify that the auction system primarily used in public procurements has a structure inducing bid-rigging in which meta-norms are unnecessary. We also show that punishment for deviation from bid-rigging plays a critical role in establishing and maintaining it. In addition, we explore the authorities' actions to deter bid-rigging by examining three measures: the flexible setting of reserve prices, the administrative surcharge and leniency system under the Antimonopoly Law, and applying the bid-rigging offense under the Criminal Law. As a result, the study reveals that the administrative surcharge and the leniency system are insufficient to deter bid-rigging, and the adequate measures are the flexible setting of reserve prices and applying the bid-rigging offense. Furthermore, the simultaneous implementation of these three measures more effectively enables deterring bid-rigging.
1. Introduction
The mechanism and structure of social cooperation have long been a critical issue in game theory, sociology, social psychology, biology, and other fields. This issue has been discussed concerning the n-person prisoners' dilemma problem.
This study focuses on bid-rigging in public procurements as a social problem because bid-rigging is a state of cooperation even though the bidding system does not assume cooperative behavior. First, we clarify factors that cause and maintain bid-rigging.
We require a bottom-up approach instead of the top-down one required when analyzing a formal organization because we should consider that the cartel mechanism is an informal organization and that the actions of individual agents establish collusion. Agent-based modeling (ABM) is a bottom-up approach, and Axelrod [1] is a typical example. In addition, it is noteworthy that we introduce the existence of punishment explicitly in the model.
This study aims to analyze the structure of the emergence and maintenance of the cartel mechanism as an informal organization and the measures to deter bid-rigging. There are three reasons for this.
First, although the problem of bid-rigging is a social problem, there is a lack of previous studies analyzing its structure due to the nature of the problem; this is because it is challenging to conduct empirical research on data. We need to establish and verify a certain specific hypothesis by constructing a model to overcome this difficulty. In this way, it can serve as the groundwork for better mechanism design.
Second, we can think that the cartel mechanism resolves social dilemmas in an aspect; thus, we want to provide academic contributions to social dilemmas problems that have been academically challenging.
Finally, we should demonstrate other practical solutions where the criminalization of bid-rigging poses various problems.
Therefore, relying on the model of Axelrod [1], we hypothesize that “bid-rigging norms” are established in the cartel mechanism, and we construct and simulate the model.
2. Related works
This section provides an overview of studies on bid-rigging issues.
2.1. Theoretical studies
2.1.1. Auction theory
We cite two representative studies on the problem of collusion in auction theory: McAfee and McMillan [2] and Graham and Marshall [3]. The former studies collusion in first-price sealed bid auctions, while the latter studies collusion in second-price English auctions.
McAfee and McMillan [2] characterized cooperative bidding strategies in two cases. One case is Weak Cartels, where payoff redistribution is not possible. The other case is Strong Cartels, where payoff redistribution is possible, and members can eliminate new entrants and redistribute payoff. In Strong Cartels, the cartel mechanism wherein bidders report their evaluation of an object in an auction; this mechanism determines the winner using a preliminary first-price sealed-bid auction.
In this cartel mechanism, bidders always have incentives to defect, even though they can earn high profits by cooperating in collusion; because bidders can make large profits by bidding slightly above (or below in public procurement) the price reported to the cartel mechanism. However, defection leads to competitive bidding and bidders can only minimize profits. Thus, we can see that this situation is the n-person-iterated prisoners' dilemma (n-IPD), which has long been considered in game theory.
McAfee and McMillan [2] followed the results of previous studies on enforcement to maintain the cartel mechanism; they listed the two enforcements: a grim-trigger strategy under game theory and the existence of punishing agents. Concerning the grim-trigger strategy, Fudenberg [4] proved the Folk Theorem that a set of agent behaviors achieved Nash equilibrium through the grim-trigger strategy, but notably under the assumption that the discount rate was sufficiently high.
Following McAfee and McMillan [2], Aoyagi [5, 6] showed theoretically that the bid rotation could be established in repeated sealed-bid auctions. To derive the equilibrium, he introduced two schemes to his theories: bid rotation, which adjusted bidders' payoffs, and direct adjustment of payoffs. The former states that a “center” as a communication device of bidders, equivalent to the cartel mechanism, compensates the loss of a loser by changing the winning permutation. The latter is equivalent to side payments of the strong cartels. These studies showed that efficient establishment of bid-rigging required equalizing profits between bidders.
Therefore, we focus on Strong Cartels in this study. Meanwhile, the auction theory assumes that bid-rigging is established and discusses how to prevent deviation through the grim-trigger strategy but does not clarify the factors inducing bid-rigging; therefore, we should investigate how bid-rigging emerges.
At the same time, Thomas [7] investigated the discount factor to sustain two bid-rigging strategies (Strong and Weak Cartels) of McAfee and McMillan [2] through the grim-trigger strategy. As a result, he revealed that to deter bid-rigging, the buyer must select the lowest reserve price for the lowest discount factor to ascend. Conversely, Section 6 shows that bid-rigging is deterred by allowing flexible setting of reserve prices, i.e., by ascending reserve prices.
2.1.2. Leniency system
To detect and deter bid-rigging, leniency systems, which reduce sanctions against cartel members that self-report to the authorities, have been introduced in many countries since the US first adopted it in 1978 and revised it in 1993. In line with this introduction, the effectiveness of leniency systems has been theoretically investigated in many studies.
Brisset and Thomas [12] theoretically investigated the effectiveness of the leniency system in the EU concerning bid-rigging in first-price sealed-bid procurement auctions. Their study focused on incentives of members in the cartel mechanism to report to the authorities. It revealed that the leniency system in the EU had no effect if investigation by the authorities was underway. At the same time, it clarified that introducing rewards for reporting members was effective even before the authorities began an investigation.
As representative studies regarding the leniency system in a standard Bertrand oligopoly, we refer to the studies of Motta and Polo [8], Spagnolo [9], Harrington [10], and Chen and Rey [11]. Their common aim was to investigate how to prevent firms in a Bertrand oligopoly from exploiting the leniency system, i.e., how to deter taking the strategy to collude and reveal in turn, and to specify an optimal leniency policy, e.g., optimal reduction rates.
Although their studies are in line with the game theory and auction theory of McAfee and McMillan [2], the model settings and the derived results differ in some points. We summarize these differences in Table 1, including the models of Brisset and Thomas [12] and our model.
Concerning the models, there are three characteristic differences: “Application of leniency before/after the authorities' investigation,” “Prosecution success probability,” and “Punishment.” The first indicates whether applying leniency under the authorities' investigation is within the scope of the study, the second indicates whether the probability of the authorities' prosecution success by receiving evidence of collusion is set in the model, measures to punish defecting firms from collusion : grim-trigger and material punishment; and the third shows the two punishments: the grim-trigger strategy, and a material punishment. “The material punishment” here means the punishment with cost in contrast to the grim-trigger strategy that means to defect forever.
Concerning the results of investigations, there are two characteristic differences: “Leniency system has effect before the authorities' investigation” and “Necessity of reward”. The first concerns whether leniency has effect before the authorities' investigation is underway, and the second concerns whether a reward is required in addition to leniency for deterring collusion.
Based on these differences, to analyze the effectiveness of the leniency system, we demonstrate the direction of building our model shown in Section 7.1, which is built by applying the model presented in Section 3, according to the following five points:
1. We set no leniency in our model in the case in which the authorities' investigation is underway because the leniency systems in Japan and the EU have strict limitations for reduction rates after the authorities' investigation. Notably, Motta and Polo [8] and Brisset and Thomas [12] denied the effectiveness of leniency before the authorities' investigation.
2. We do not set “Prosecution success probability,” which weakens the effectiveness of leniency and decreases the simplicity of analysis because we focus on balancing “carrot” and “stick” following Spagnolo [9].
3. We focus on material punishment concerning “Punishment,” as discussed in Section 2.4. Notably, Spagnolo [9] modeled the punishment including material one.
4. Although four related studies derived the result that leniency had to be limited to the first reporter, our model allows all reporters to receive full leniency because the leniency system of Japan allows for reporters to add the reduction rate of up to 40% to the normal reduction rate if the second and subsequent reporters submit enough evidence to the authorities. In addition, Spagnolo [9] commented that despite treating leniency only for the first reporter as optimal, if a second reporter's evidence would increase the probability of conviction, granting more leniency to a second reporter would become optimal in his model. Therefore, considering that our model omits the “Prosecution success probability,” we assume that all reporters submit enough evidence, receive full leniency, and the authorities can prosecute entirely.
5. We should focus on the studies of Spagnolo [9] and Brisset and Thomas [12], which insisted that a reward for the first reporter was required to efficiently deter collusion. At the same time, our model has a reward equivalent to the flexible setting of reserve prices, which we introduce as a “carrot” in Section 6.
2.1.3. Cryptography
Electronic bidding is promoted in public procurement. Abe and Suzuki [13] pointed out the risk of bid-rigging in electronic sealed-bid auctions and proposed a receipt-free sealed-bid auction scheme. At the same time, Howlader et al. [14, 15] mentioned that receipt-free mechanisms proposed in previous studies were based on strict assumptions, one of which was that the authorities were honest and not included in collusion. They proposed a receipt-free sealed-bid auction mechanism that could withstand colluded authorities.
2.2. Empirical studies
Suzuki [16] reviewed the 167 decisions on bid-rigging of the Japan Fair Trade Commission (JFTC) from 1947 to 2000. At the same time, Asker [17] analyzed the cartel mechanism, which he said was the internal organization of stamp dealers in the 1990s, which used knock-out auctions. In these studies, most of the bid-rigging cases involved pre-auction meetings of ring members designed to determine the winner, as modeled by McAfee and McMillan [2].
The study of Wachs and Kertsz [18] pointed out that the cartel in the 1980s Ohio school milk bidding market had high cohesion and exclusivity by presenting a network-based framework. The study of Maxime Reeves-Latour and Carlo Morselli [19], also using a network-based framework and a dataset compiled from more than 7,000 public construction tenders in Canada, noted the existence of the core participants in bid-rigging.
In game theory, we can interpret high cohesion, exclusivity, and the existence of the core participants as corresponding with n-IPD, which assumes no player change.
Andrighetto et al. [20] showed that the interaction of norms communication and material punishment in public goods games led to higher and more stable cooperation at a lower cost to the group than when used separately. Furthermore, they showed that norms communication enhanced cooperation, and material punishment helped to maintain it.
Porter and Zona [21, 22], Pesendorfer [23], Abrantes-Metz [24], and Ishii [25, 26] analyzed the problem of bid-rigging using data on cases uncovered by bid-rigging regulators. On the other hand, they also point out that the limited data on bid-rigging made the analysis difficult.
On the other hand, not relying on numerical data, Bajari [27] applied Bayesian statistical methods and developed a structural estimation model of competition and collusion models, focusing on the US seal coat industry and estimating prior distributions under findings from “experts.” Furthermore, Asker [17] employed structural analysis, applying the nonparametric estimation to recover the distribution of the valuation of bidders from limited numerical data and contributed to estimating the ring benefit and non-ring bidders' damage.
2.3. Legal studies
Competition Law has regulated bid-rigging [28, 29].
In recent years, the criminalization of bid-rigging and collusion has accelerated. The US is the pioneer in criminalizing bid-rigging and collusion. The US Department of Justice (DOJ) and US Federal Trade Commission (USFTC) have imposed criminal penalties under the traditional approach since the Sherman Act. Under the US Antimonopoly Law, bid-rigging is “illegal par se,” meaning that the mere act of engaging in bid-rigging constitutes a crime [28–30]. It has been noted that this concept extends to the EU, Japan, South America, and other countries through legal reforms [29].
Although EU law does not have criminal penalties, the size of the penalties is evaluated as going beyond the scope of administrative penalties and becoming de facto criminal penalties. In Germany, a member country of the EU, Section 298 of the Criminal Code was established in 1996, making bid-rigging a criminal offense. The law is actively used to detect bid-rigging [31].
In Japan, the 2005 amendment to the Antimonopoly Law made criminal penalties statutory in Article 89. This article also states that “attempted crimes shall be punished,” which means that a crime is committed by the bid-rigging act [29, 32]. In addition, Article 96-5 of the Penal Code was enacted in 2011. As clearly stated in this article, bid-rigging is a mere act that constitutes a crime, and it is not a requirement that bid-rigging be established.
In competition law enforcement, there is the administrative model with adjudicatory authority and a prosecutorial model with adjudicatory authority held by the courts. The advantage being that the former is efficient and the latter accurate. At the same time, the former has a disadvantage in accuracy, while the latter has a disadvantage in time and administrative costs [33].
In enforcement and effectiveness of criminal penalties, similar to the prosecutorial model above, while costly regarding time and administrative effort, they can inflict significant damage on the offender, including not only monetary penalties but also social stigma and disapproval. At the same time, there are doubts regarding the moral grounds for criminalizing cartels, including bid-rigging, and how they should be placed within the criminal legal system [33–35].
The criminalization of bid-rigging is indeed a worldwide trend. However, its enforcement requires a balance between the legal systems in each country and social and cultural consensus; thus, the criminalization of bid-rigging is not without difficulties [28, 29, 36].
2.4. The n-IPD
In this study, we focus on punishing agents, which McAfee and McMillan [2] did not make the main subject and have the potential to change the structure of the n-IPD.
2.4.1. Social theory
We can think of bid-rigging as collective action. Olson [37] developed his theory of collective or organizational behavior; rational, self-interested individuals will act to achieve the common good or the group's interests in two cases. One is that the number of individuals comprising the group is minimal, and the other is that coercion or some other device makes the individuals act in the common interest.
From this point of view, Yamagishi [38] proposed the “Structural/Goal Expectation Theory,” which was a modification of Pruitt and Kimmel [39]'s theory. The basic idea of Yamagishi [38] is that the only way to achieve agent cooperation is to change the structure such that cooperation is more profitable for the agents than defecting and that a subgroup of agents engages in establishing cooperation by punishing other agents.
2.4.2. Social physics-based studies
The works of Nowak et al. [40], Santos et al. [41], and Kojima et al. [42] showed that introducing some structures, lattices, and networks achieved cooperation in the n-IPD.
The works of Masuda [43] showed that introducing zealots who kept offering cooperation enhanced cooperation in the n-IPD theoretically; conversely, Matsuzawa et al. [44] showed that introducing zealots could not achieve cooperation in a spatial structure by simulations with a large number of agents in the order of n = 104.
Although it does not directly address the n-IPD, Ishii et al. [45] analyzed the hit phenomenon using the mathematical model established in a social physics-based study. Their study showed the mathematical model was consistent with actual big data.
2.4.3. The norms game
Although it does not directly address collusion in auctions or the bidding system, the norms game model of Axelrod [1] is a study that showed that punishment played a critical role in norms maintenance.
At the same time, the cartel mechanism is an informal organization. Considering that the actions of individual agents establish the cartel mechanism, bottom-up approaches are required rather than top-down ones when analyzing official organizations. The investigation by Axelrod [1] is an example of ABM, a bottom-up approach.
Axelrod [1]'s norms game model is as follows: An agent's strategy has two dimensions. One is boldness (bi), which determines when the agent will defect. The agent will defect whenever the chance of being seen by someone is less than the agent's boldness, which is represented by S<bi. The other is vengefulness (vi), which is the probability of punishing defecting agents. The greater an agent's vengefulness, the more likely they are to punish defecting agents.
Axelrod [1] demonstrated that meta-norms were necessary to maintain norms by modeling from an evolutionary approach and simulating over 100 generations.
Conversely, Galán and Izquierdo [46] demonstrated that norms were not onsistently maintained, even with meta-norms, expanding Axelrod's norms game model to a mathematical model and running simulations with increasing generations.
Similarly, Yamamoto and Okada [47, 48] showed that meta-norms maintained norms when there were defective agents in society. They called types kinds of agents “social vaccines.”
3. Bid-rigging norms model
In this study, we apply the norms game model of Axelrod [1] to the bid-rigging norms model.
Axelrod [1] defined a norm in his study as follows:
Definition 1. A Norm
A norm exists in a given social setting to the extent that individuals usually act in a certain way and are often punished when seen not to be acting in this way.
We follow this definition in this study.
We explore whether bid-rigging norms emerge and are maintained by replacing the meta-norms in Axelrod [1]'s norms game model with the basic structure of the bidding system, where only one of the participants can be the winner and take payoff in a single game.
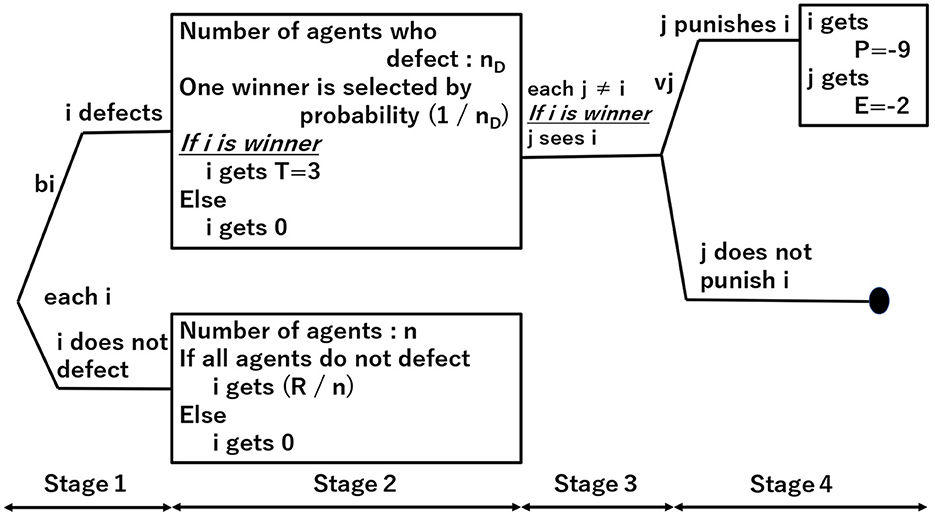
Figure 1 depicts the bid-rigging norms model.
Each agent has a strategy with two dimensions: boldness (bi) and vengefulness (vi), and a strategy assumes random variables ranging from to as discrete values, following Axelrod [1]. First, each agent decides whether to defect or cooperate with the cartel mechanism according to its boldness bi. If all n-participating agents cooperate, the cartel mechanism redistributes the winner's payoff R among all ().
If more than one agent defects, the defecting agents will compete. A winner who gets a payoff T is selected with a probability , where the number of defecting agents is nD. The other agents then punish only the winner with the probability of vengefulness (vi), giving P. The agent that punishes bears the punishment cost E.
The differences from the norms game model comprise the following four points:
1. Only one defecting agent can get T because one winner is selected in the bidding system or auctions (Figure 1, upper part of Stage 2). By contrast, in the norms game model, all defecting agents can get T by exploiting public goods.
2. We do not consider Hurt(H) (Figure 1, upper part of Stage 2); we cannot impose “hurt” on other agents by defecting in the bid-rigging norms model, whereas “hurt” makes sense in the norms game model. After all, we can consider the norms game model as one of the social models for public goods.
3. This model introduces reward (R, Figure 1, lower part of Stage 2). In the norms game model, cooperative agents will get R = 0.
4. It is the defecting winner whom all agents punish, whereas it is all defecting agents in the norms game model. Furthermore, we do not consider S, representing the probability of being observed or seen (Figure 1, upper part of Stage 3). Because the bidding system only discloses the winner and the winning bid amount, the defecting winner is always observed or seen by the other agents, and defecting agents who are not the winner are never observed or seen. McAfee and McMillan [2] also assumed that this information is made available, by law, in government procurement auctions and pointed out that this information is necessary to implement an enforcement strategy in bid-rigging.
We follow the parameter values used in the norms game model listed in Table 2.
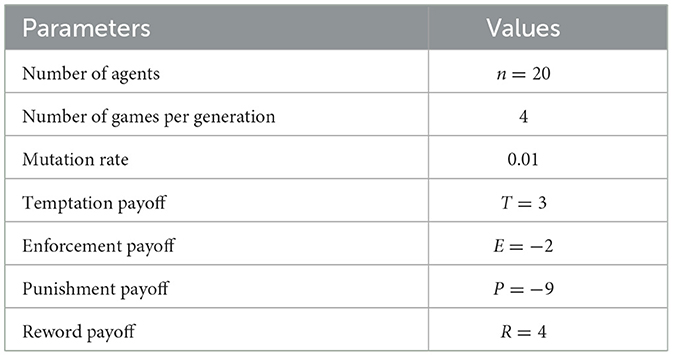
Table 2. Parameter value used by Axelrod [1].
Here, we assume that the value of R, which is not utilized in the model of Axelrod [1], is greater than T = 3 and set 4 in the simulation run because the incentive for following the cartel mechanism is due to the bid-rigging payoff being greater than the competition payoff.
4. Simulation
We use simulation to explore the bid-rigging model's behavior following Axelrod [1] and Galán and Izquierdo [46].
4.1. Simulation environment and source code
We use NetLogo. The source code of this simulation is available at openABM.
One generation comprises four steps: “initialization,” “execution,” “calculate standard deviation,” and “evolution” (selection by payoff and evaluation strategy), where we repeat “execution” four times, which we refer to as “game.”
The source code of “evolution.” is demonstrated in Appendix A. In “evolution,” we implement an evolutionary approach to the bid-rigging norms model in Figure 1. The evolutionary approach is as follows. First, we calculate the standard deviation of the payoffs obtained in each generation, consisting of four games. Second, we replace the strategies of agents whose payoffs are less than the standard deviation with those whose payoffs are greater than the standard deviation.
Axelrod's model adjusts the number of offspring so that the population size n does not change between generations but does not demonstrate the method. Thus, we use Yamamoto and Okada [47]'s Adjustment 2, a method of randomly moving individuals from the group within the standard deviation to the smaller group out of the two groups above and below the standard deviation.
The strategy is then mutated with a 1% probability. The mutation can vary between and .
4.2. Simulation result
Figure 2A depicts the average values of strategies (boldness and vengefulness) for each generation of 50 trials, following Yamamoto and Okada [47], up to the 1,000th generation. The vertical axis indicates the average values of the strategies (boldness and vengefulness), and the horizontal axis indicates the number of generations. After the 500th generation, boldness drops to almost zero, and the vengefulness converges to approximately 0.5; boldness does not drop to zero entirely since mutations constantly arise in each trial, leading to an average value of zero over 50 trials.
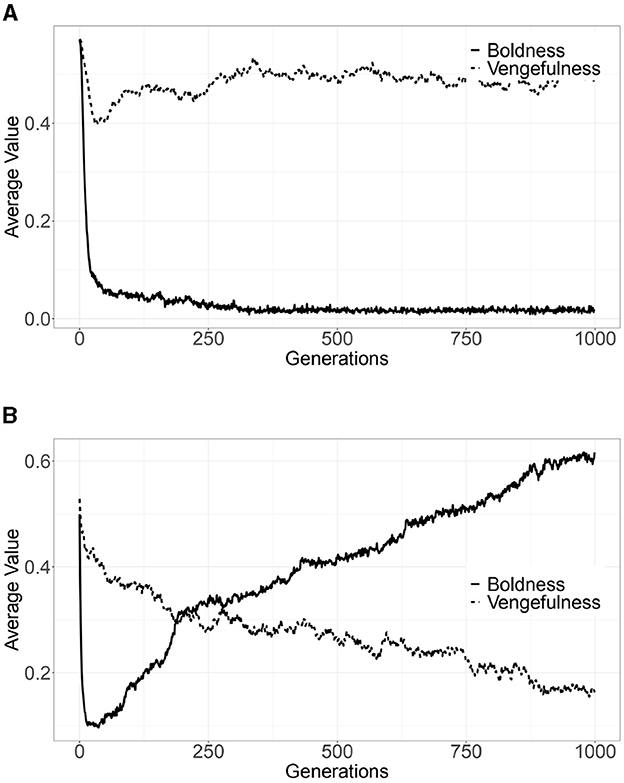
Figure 2. Simulation results (average of strategies per generation for 50 trials) (A) bid-rigging norms game model. (B) Norms game model.
For comparison, Figure 2B depicts the average values of the strategies (boldness and vengefulness) for each generation of 50 trials in the norms game model without considering the damage (H) caused to other agents by defecting (hereafter, we call this model the “norms game model”). Boldness decreases in the early generations but gradually increases; vengefulness decreases gradually from the early generations.
The results confirm that bid-rigging norms are quickly established in the bid-rigging norms model, while the norms collapse in the norms game model.
4.3. Number of agents with boldness of zero or one (average number of 50 trials)
To examine the strategy transition in detail, we focus on the number of agents whose boldness is zero or one.
Figure 3A depicts one result of 50 simulation trials of the bid-rigging norms model. The vertical axis indicates the average number of agents with a boldness of zero or one for each generation of 50 trials up to the 1,000th generation, and the horizontal axis indicates the number of generations. For comparison, Figure 3B depicts one result of 50 simulation trials of the norms game model.
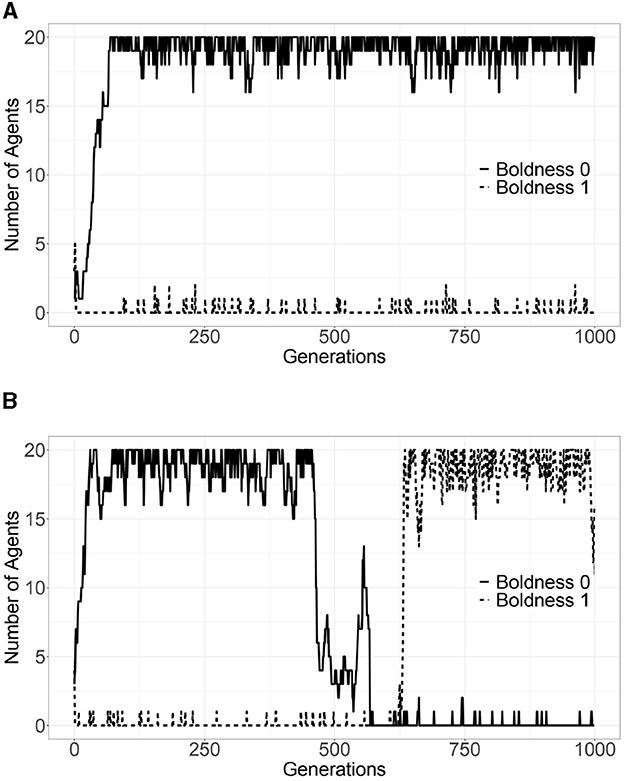
Figure 3. Number of agents with a boldness of zero or one (one example of 50 trials) (A) bid-rigging norms game model. (B) Norms game model.
By comparing Figure 3A with Figure 3B, we can see that the common feature is that the number of agents with a boldness of zero in the initial generation becomes 20 agents. In the bid-rigging norms model, this state becomes stable; by contrast, in the norms game model, a phase transition occurs where the number of agents with a boldness of one becomes 20 after the number of agents with a boldness of zero decreases. The slight fluctuation after the number of agents reaches zero or 20 is due to mutation.
This difference is because agents' boldness decreases faster than agents' vengefulness; this phenomenon brings the number of agents with a boldness of zero up to 20 in the initial generations of both models. The bid-rigging norms model does not change from this state; however, boldness increases again in the norms game model, and a phase transition occurs where the defect becomes dominant. Figure 2B shows that the timing of phase transitions varies across trials.
5. Validation
Galán [46] re-examined the simulation results of Axelrod [1] using a mathematical model and showed that meta-norms do not always establish norms.
Following Galán [46], we use the mathematical model to verify why the simulation results in the previous section differ between the bid-rigging norms model and the norms game model.
5.1. Mathematical model of bid-rigging norms
We formulate the Payoff equation in the bid-rigging norms model as
where T, E, and P follow Axelrod's parameter values listed in Table 2; the second term indicates that R is given equally to n rigging agents.
The variable βiT is one if agent i defects and wins the bidding and zero if agent i cooperates or defects and loses the bidding. Therefore, the probability of being one is defined as bi divided by the summation of all agents' bi because only one of all defecting agents can get T. Thus, βiT is calculated as
The variable βiR is one if agent i cooperates and zero if agent i defects. Therefore, the probability of being one is defined as the production of all agents' (1−bi) because agent i can get if all agents cooperate. Thus, βiR is calculated as
The variable υij follows those in Galn and Izquierdo [46]; however, (), which represents S, is omitted because the defecting agent should be observed, as mentioned earlier. υij can be described as
Consequently, the expected payoff of agent i in one round can be calculated as
5.2. Evolutionary stable state
We define the concept of a stability point, namely an Evolutionary Stable State (ESS), following Smith [49], Weibull [50], and Galn and Izquierdo [46].
Definition 2. ESS
An ESS is a state (determined by every agent's boldness and vengefulness) where:
a) Every agent in group Θ receives the same expected payoff (such that evolutionary selection pressures will not lead the system away from the state):
b) Any single (mutant) agent m who changes its strategy (let bm be its new boldness and vm its new vengefulness) gets a strictly lower expected payoff than any of the other agents in the incumbent group I≡Θ−m (such that if a single mutation occurs, the mutant agent will not be able to invade the group):
c) After any single (mutant) agent m has changed its strategy, all the other agents in the incumbent group I get the same expected payoff (such that a single mutant cannot distort the composition of the group except potentially by random drift):
Let m be an arbitrary mutant agent in a given population of agents Θ, and let bm be its boldness and vm its vengefulness. Let I be the set of incumbent agents in the population Θ, excluding m. If we assume continuity of agents' properties, we can formulate a necessary condition for ESS as
and
5.3. Necessary and sufficient conditions for ESS
We can derive the following lemma. We demonstrate the proofs in Appendix B.
Lemma 1. A necessary condition for an ESS is that every agent follows the same strategy:
We can derive the following propositions using Definition 2 and Equations (6) and (7). We demonstrate the proofs in Appendix C.
Proposition 1. The necessary and sufficient condition for an ESS subject to B≠0 is as
5.4. Comparison of two models: bid-rigging norms model and norms game model
We think that the simulation results shown in Figure 3A satisfy the necessary condition that every agent follows the same strategy in Lemma 1 since mutations that cause fluctuations of strategies in Figure 3A do not lead to a strategy's drift that other agents follow. Thus, we can say that the mathematical model confirms the validity of the simulation.
Conversely, Proposition 1 states that bid-rigging norms collapse except in the case of B≠0, which seems inconsistent with the simulation results in Figure 2A. By contrast, Galán and Izquierdo [46] showed that the mathematical norms game model is consistent with the simulation results in Figure 2B.
However, it is in the case of B≠0 that Proposition 1 holds; thus, we can assume that the state of B = 0 is also the ESS state. Therefore, we can assume that Figures 2A, 3A demonstrate the ESS state in the case of B = 0. At the same time, Proposition 1 does not demonstrate the process leading to B = 0, whereas Figures 2A, B demonstrate the process leading to B = 0, which is the same for the bid-rigging norms and norms game models.
Thus, we can assume no contradiction between the mathematical model and simulation results. In this respect, the mathematical model can confirm the simulation's validity. Furthermore, the simulation results demonstrate the process of arriving at the mathematical model results.
Proposition 1 has the condition B≠0 because the denominator, in the partial derivative of the expected payoff due to the boldness of the mutating agent, has B (see Appendix C). In other words, it is because the bidding system, which the bid-rigging model characterizes, has a structure wherein “only one agent can be the winner and get a payoff in a single game” (see the first term on the right-hand side of Equation (5)).
Consequently, we can assume that the bidding system has a structure that induces bid-rigging if the cartel mechanism uses punishment.
6. First measure to deter bid-rigging—Flexible setting of reserve prices
In the previous sections, we modeled the role of punishment in the cartel mechanism in establishing bid-rigging norms and verified it through simulation. In this section, we examine the measure to increase the bidder's defect payoff T by the flexible setting of reserve prices, i.e., by providing incentives to defect, as one measure to deter bid-rigging. Proposition 1 of the mathematical model holds even when the bidder's defecting payoff T increases. From this, we verify the actual behavior in the simulation.
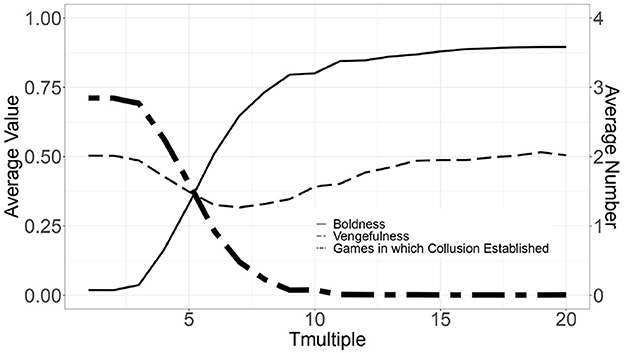
Since punishment P plays a critical role in establishing bid-rigging norms, we set the payoff for defecting T to be a multiple of the absolute value of P (we call this multiple as “Tmultiple”) and varied Tmultiple from 1 (T = 9) to 20 (T = 180), implementing simulations of 50 trials over 1000 generations.
Figure 4 depicts the simulation results. The left side of the vertical axis indicates the average values of the strategies (boldness and vengefulness) of 50 trials over the 200 - 1000th generations, and the horizontal axis indicates the number of Tmultiple. The solid line indicates the average value of boldness, and the dashed line indicates the average value of vengefulness. At the same time, the right side of the vertical axis indicates the number of games per generation where all 20 agents cooperate. The thick dashed line indicates the average number of games in which all players cooperate, i.e., the average number of games in which bid-rigging is established. Note that we calculate the average values from the data over the 200th generation because it is at this point that the strategies and bid-rigging are stable.
The flexible setting of reserve prices is a measure to promote boldness. Hence, increasing Tmultiple increases the average value of boldness. For example, when Tmultiple reaches 10 (T = 90), the number of games under which bid-rigging is established is less than 0.1 out of 4 games, and when it reaches 11 (T = 99) or more, the number of games is almost 0. Note that there is no significant variation in vengefulness.
The simulation results confirm that the measure of the flexible setting of reserve prices effectively deters bid-rigging. However, whether the operation that guarantees a payoff of nearly 100 is socially acceptable is questionable.
In the next section, we will examine the effectiveness of two systems in actual operation to deter bid-rigging.
7. Second and third measures—Comparative study of the effectiveness of existing systems to deter bid-rigging
The simulation analysis and mathematical modeling show that deterring bid-rigging requires a mechanism to favor boldness.
Existing mechanisms are the administrative surcharge and leniency system under the Antimonopoly Law, which we denote as Hal, and applying the bid-rigging offense under the Criminal Law, whose pecuniary loss we denote as Hcl. We model these two existing systems and examine their effectiveness through simulations.
7.1. Administrative surcharge and leniency system under the Antimonopoly Law
In this section, we introduce the administrative surcharge and leniency system under the Antimonopoly Law to the bid-rigging model shown in Figure 1 and implement the simulation to verify its anti-bid-rigging effect. The practical application of the administrative surcharge and leniency system is complex; therefore, we focus on those necessary for comparison when applying the bid-rigging offense under Criminal Law.
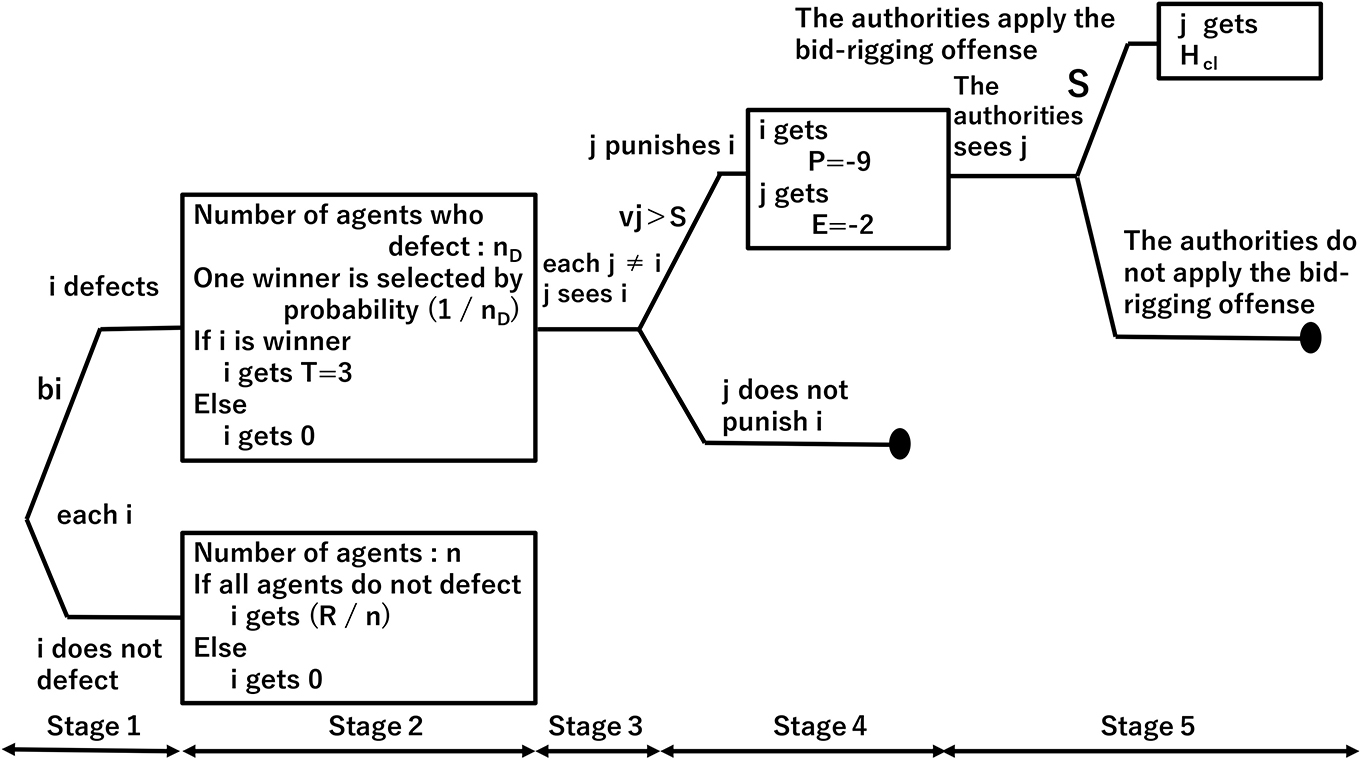
Figure 5 depicts the bid-rigging norms model introducing the administrative surcharge and the leniency system under the Antimonopoly law. Here, we model the leniency system under the Antimonopoly Law in Japan.
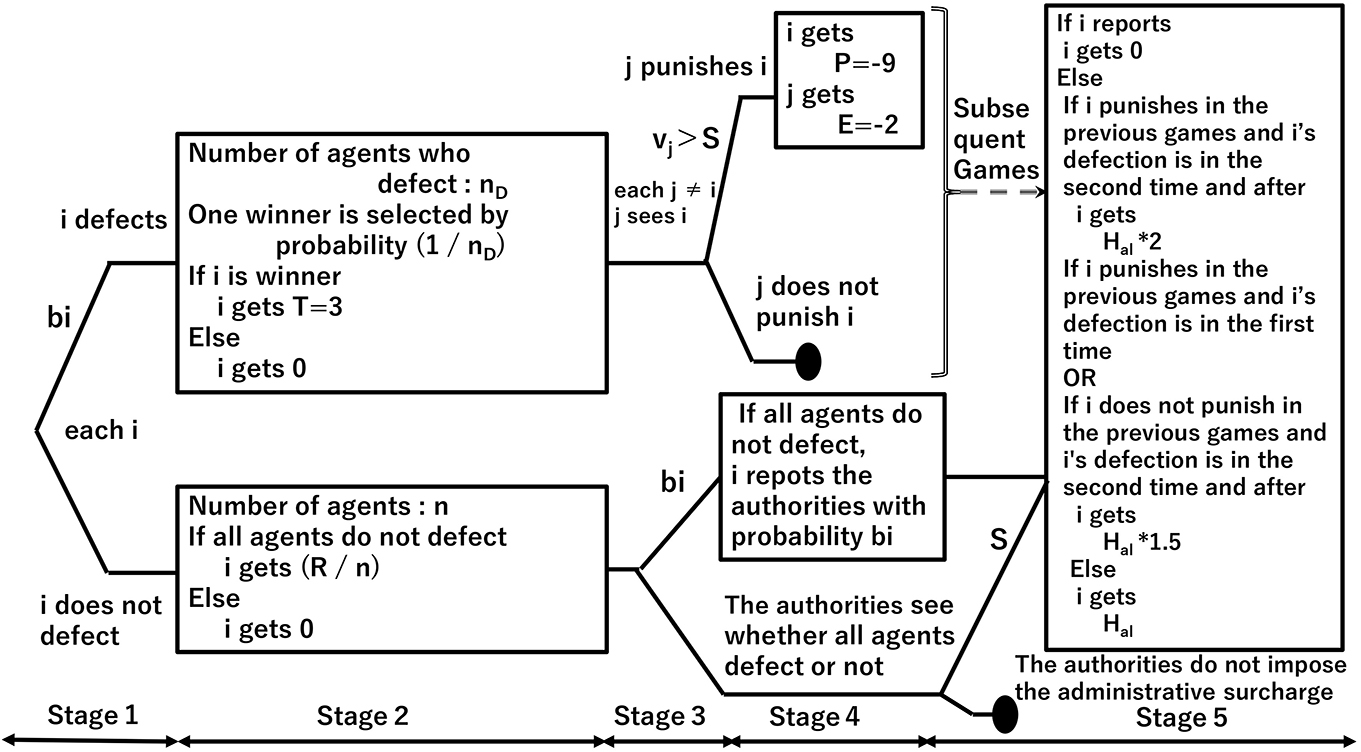
Figure 5. Model for introducing the administrative surcharge and leniency system under the Antimonopoly Law.
We add the following elements:
1. The authorities impose the administrative surcharge under the Antimonopoly Law only when bid-rigging is established, whereas the authorities apply the bid-rigging offense under Criminal Law even for attempting bid-rigging,
2. Following the norms game model, one generation consists of four games; the flow of one game is the same up to Stage 2 in Figure 1,
3. If bid-rigging is established (Figure 5, lower part of Stage 2), each agent decides whether or not to report to the authorities through the leniency system with probability bi (Figure 5, lower part of Stage 3 and 4),
4. The authorities exempt all agents who report under the leniency system from the administrative surcharge (Figure 5, upper part of Stage 5),
5. Based on the report, the authorities impose the administrative surcharge Hal on the agents who have not reported, double surcharge the agents who have led bid-rigging, i.e., have punished the defecting agent in earlier games in the current generation, and 1.5 times surcharge the agents who have been caught for over the second time in the current generation (Figure 5, Stage 5),
6. If no report is made (Figure 5, lower part of Stage 4), the authorities begin investigations (Figure 5, lower part of Stage 5),
7. The authorities observe bid-rigging with probability S and impose a surcharge Hal. The condition for increasing the surcharge is the same as in 5,
8. The agents punish the defecting agents if vi>S, considering the probability of being observed by the authorities S (Figure 5, upper part of Stage 4).
We implement this model in simulation by varying Hal from 0 to -100 for 1000 generations over 50 trials.
Figure 6 depicts the simulation results; the horizontal axis indicates the same as in Figure 4, the vertical axis indicates the Hal value from 0 to -100, and the three lines indicate the same as in Figures 4, 6A depicts the result of the model with the administrative surcharge and leniency system, and Figure 6B depicts the result of the model with only the administrative surcharge (without leniency system) for reference.
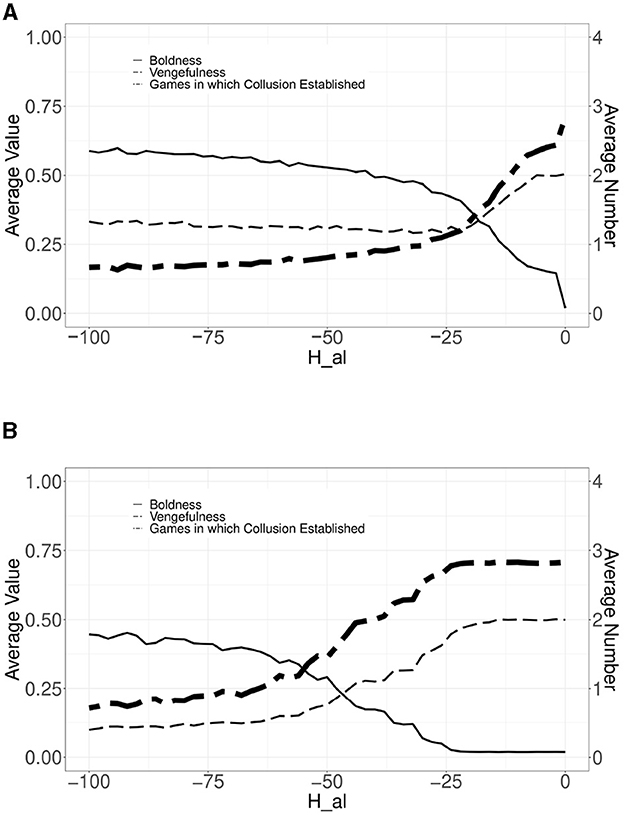
Figure 6. Simulation results of the model for introducing the administrative surcharge and (or without) leniency system under the Antimonopoly Law—Effect of Hal. (A) The administrative surcharge and leniency system. (B) The administrative surcharge without leniency system.
Concerning Figure 6A, even if Hal is set to –100, the number of games under which bid-rigging is established cannot drop to zero out of four games. However, we can see that the leniency system has the effect of deterring bid-rigging, compared with Figure 6B, especially in the area where Hal are large numbers (small absolute numbers). We should note the following difference: bordering –24 in concert with Hal decreasing (increasing absolute); in Figure 6A, the average value of vengefulness stop falling; and in Figure 6B, the average value of boldness begins increasing in concert with decreasing of vengefulness. This difference is caused as follows: bidders who exploit the leniency system, as pointed out in Section 2.1.2, avoid social punishment and preserve their strategies, including the vengefulness dimension; however, if the leniency system does not exist, only social punishment is effective, so selection diminishes vengefulness. Therefore, it is the leniency system that affects this difference.
Meanwhile, in Figure 6, the average value of boldness does not increase enough, and the average number in which bid-rigging is established does not fall enough compared with Figure 4. This difference is caused by two factors: the requirement for imposing the surcharge under the Antimonopoly Law, which is only the case in which bid-rigging is established, and the leniency system itself. Concerning the first factor, this requirement leads all 20 agents participating in the cartel mechanism to be surcharged basically, with no payoff difference or evolution. Figure 5 shows that there are differences in surcharge between agents who have punished other agents or have been caught in previous games and those that have not. However, Figure 6B shows that the surcharge is insufficient to lead to the evolution of decreasing vengefulness and increasing boldness. Concerning the second factor, as mentioned earlier, in Figure 6A, the average value of vengefulness does not decrease by the leniency system, which curtails the increase of boldness. By contrast, the flexible setting of reserve prices makes the defecting winner's payoff bigger than that of the other agents, leading to sufficient evolution to decrease vengefulness and increase boldness.
From this simulation result, we can consider that the administrative surcharge and leniency system under the Antimonopoly Law has a limited effect in deterring bid-rigging.
Next, we examine the effects of applying the bid-rigging offense under the Criminal Law.
7.2. Applying the bid-rigging offense under the Criminal Law
It is unique because the surcharge and leniency system requirement in the Antimonopoly Law is that “bid-rigging must be established.” By contrast, the requirement for applying the bid-rigging offense under the Criminal Law is that “bidders attempt to conduct collusion” is sufficient. We model this requirement as applying the bid-rigging offense toward the agents who lead bid-rigging, i.e., the agents who punish other agents in the bid-rigging norms model, because punishment has a critical role in establishing bid-rigging norms. Applying the bid-rigging offense under the Criminal Law is a mechanism to control the vengefulness level.
Figure 7 depicts the model for introducing the bid-rigging offense under the Criminal Law.
We add to Figure 1 the following elements:
1. Following the norms game model, one generation consists of four games; the flow of one game is the same up to Stage 2 in Figure 1.
2. The agents punish the defecting agents if vi>S, considering the probability of being observed by the authorities S (Figure 7, upper part of Stage 3).
3. The authorities observe agents who lead bid-rigging, i.e., have punished the defecting agent, with probability S and apply the bid-rigging offense Hcl (Figure 7, Stage 5).
We implement this model in simulation with Hcl varied from 0 to -100 for 1000 generations over 50 trials.
Figure 8 depicts the simulation result; the horizontal axis indicates the same as Figure 4, the vertical axis indicates the Hcl value from 0 to -100, and the three lines indicate the same as in Figure 4.
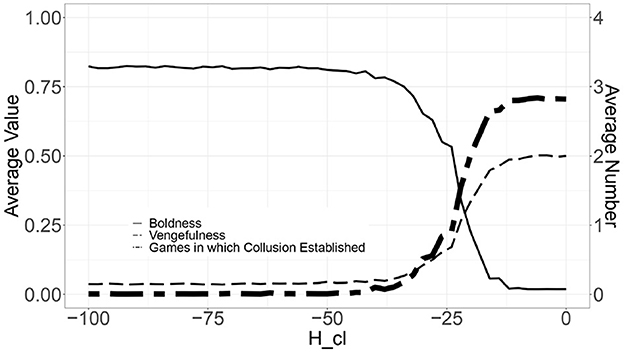
Figure 8. Simulation results of model for introducing the bid-rigging offense under the Criminal Law—Effect of Hcl.
As a result, if Hcl is set to less than -40, the number of games under which bid-rigging is established drops to zero out of four games. At the same time, comparing Figure 8 with Figure 6, as Hcl decreases, the average value of boldness decreases, and the average value of vengefulness increases.
This difference is because the requirement for applying the bid-rigging offense under the Criminal Law is sufficient (that is, “bidders attempt to conduct collusion”). In other words, the authorities can apply the bid-rigging offense under the Criminal Law as soon as observing the agents who punish other agents; this feature leads to a decrease in vengefulness through evolution, which leads to a increase in boldness. Thus, the number of games under which bid-rigging is established drops to zero.
This simulation result confirms that applying the bid-rigging offense under the Criminal Law effectively deters bid-rigging.
However, considering that the criminalization of bid-rigging has difficulties in balancing with the legal system in each country and the necessity of social and cultural consensus compared to the administrative penalty, actively applying the bid-rigging offense has a higher social cost.
In the next section, we examine measures to increase the effectiveness of the administrative surcharge and leniency system under the Antimonopoly law.
8. Combination of three measures to increase the effectiveness of the administrative surcharge and leniency system under the Antimonopoly Law
We consider adding two measures to the administrative surcharges and leniency system under the Antimonopoly Law in Section 7.1: the flexible setting of reserve prices in Section 6 and the application of the administrative penalty, similar to the bid-rigging offense under the Criminal Law in Section 7.2.
We cannot allow too great payoffs to the winner. Instead, we must search for a socially acceptable level of payoff. In addition, we should reduce the bid-rigging offense under the Criminal Law, which can effectively punish bid-rigging leaders but involves social stigma and disapproval, to the level of the administrative penalty deterring bid-rigging less costly and making administering more simple.
The issues here are the following two points:
1. We should make Tmultiple as small as possible from the minimum value of 10 that can deter bid-rigging, as shown in the simulation results in Section 6 as the benchmark value.
2. We should make the administrative penalty as small as possible from the minimum value of –40 of the bid-rigging offense under the Criminal law that can deter bid-rigging, as shown in the simulation results in Section 7.2 as the benchmark value.
Here, we set the benchmark value for deterring bid-rigging as 0.1 of the number of games out of 4 games, which is the number in the case of setting Tmultiple as 10 (T = 90) in Figure 4.
We implement the previous three models of Figures 1, 5, 7 simultaneously in simulation with Hal varied from –20 to 0, Tmultiple varied from 0 (T = 0) to 10 (T = 90), and Hcl as administrative penalty varied from –10 to 0, for 1,000 generations over 50 trials. Note that bid-rigging has been established for these values of Hal, Tmultiple, and Hcl, as demonstrated in the simulation results of previous sections.
Figure 9 depicts the scatter plot matrix created by extracting the data where the average number of games per generation in which collusion has been established is less than 0.1.
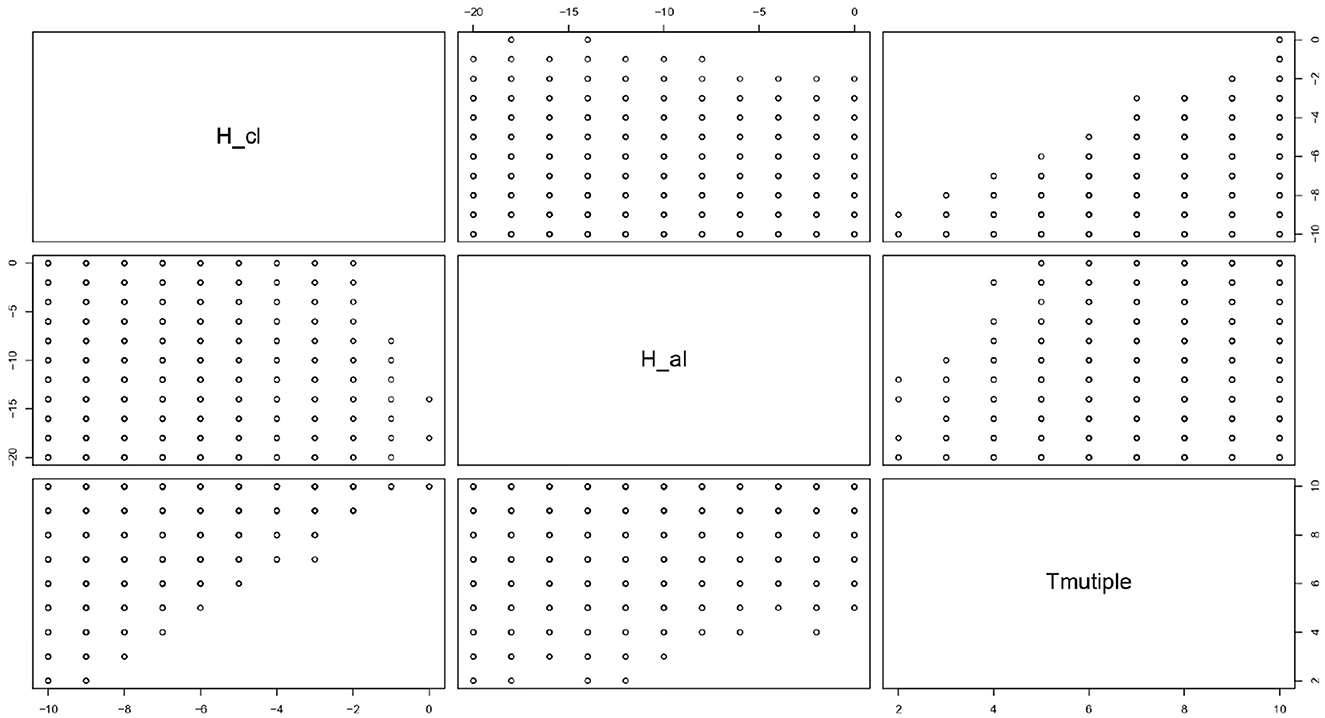
Figure 9. Scatterplot matrix with data created by extracting the data where the average number of games per generation in which collusion has been established is less than 0.1 games.
Since there are no data for which Tmultiple are 0 and 1, it is necessary to set Tmultiple as two or more, i.e., to set reserve prices that guarantee at least twice the absolute payoff of P. In the case Tmultiple is two, to make the average value of each generation under which bid-rigging is established lower than 0.1, we should set administrative surcharges Hal under the Antimonopoly Law to -12 or less. We note a missing value in the case where Hal is -16; therefore, we must set Hal to -18 or less to avoid this missing value. At the same time, we should set administrative penalties Hcl to -9 or less.
Therefore, to increase the effectiveness of the surcharge and leniency system under the Antimonopoly Law, we should set the surcharge from 1.5 times to 2.0 times P, the administrative penalty to the same amount as P, and the reserve price to twice as much as the absolute value of P.
9. Discussion and conclusion
In this study, from the aspect of enforcement to the cartel mechanism, which was not the subject of McAfee and McMillan [2], we modeled bid-rigging norms following the model of Axelrod [1]. We implemented this model under simulation to analyze the critical factors that led to the evolution of punishment. The results revealed that the structure of the bidding system or auctions, i.e., only one agent between agents who participate in the bidding system or auctions can take a payoff, is the critical factor.
Furthermore, we compared the simulation results and mathematical model of the bid-rigging norms model and the norms model; as a result, we confirmed no contradiction between the results of the simulation and the results of the mathematical model, as well as the validity of the simulation.
At the same time, using this bid-rigging norms model and simulations, we investigated the measures to deter bid-rigging. We examined three measures: the flexible setting of reserve prices, the administrative surcharge and leniency system under the Antimonopoly Law, and applying the bid-rigging offense under the Criminal Law. As a result, we clarified that the administrative surcharge and leniency system under the Antimonopoly Law is insufficient to deter bid-rigging and that the flexible setting of reserve prices and applying the bid-rigging offense under the Criminal Law are effective.
Finally, we implemented these three measures simultaneously. We investigated the lower limits of the three measures: reserve price, the administrative surcharge under the Antimonopoly Law, and the administrative penalty similar to applying the bid-rigging offense under the Criminal Law. As a result, we could reduce the bid-rigging offense under the Criminal Law to one-fourth, which we consider to be at the same level as the administrative penalty, and reduce the administrative surcharge under the Antimonopoly Law up to a maximum of twice the punishment, i.e., –18. Note that by setting the reserve price over twice the absolute values of punishment used in the cartel mechanism, we had to allow a payoff over 18 to defecting agents. With this, we could deter bid-rigging effectively.
The individual anti-bid-rigging measures presented in this study are already well-known or used. The contribution of this study is to clarify that using these measures separately is insufficient to deter bid-rigging and that their combination is effective.
The limitation of this study is that the number of agents is only 20, following Axelrod [1]. However, it is appropriate to conduct simulations with a small number of agents due to the nature of bid-rigging, which means that the cartel mechanism is not composed of a large number of agents as implemented in simulations in social physics-based studies. As shown in Section 2.4.2, in social physics-based studies, theoretical results are verified by simulations, which are conducted with a large number of agents or by big data [43–45]; at the same time, simulations can implement rich structures that mathematical models cannot represent. In this study, we implemented a mathematical model by simulations to change parameter values or implement actual structures and attempted to elucidate more complex phenomena. So, we are following the style of social physics-based studies in verifying theoretical results with simulations.
A future issue is the practical applicability of the measures presented to deter bid-rigging. As the first step, we should verify the measurability of the magnitude of the punishments (which are not necessarily measurable in monetary value) that are practiced in the cartel mechanism. In the second step, even if the punishments are measurable, we should verify the feasibility of the existing system, especially regarding the flexible setting of reserve prices and the administrative penalty similar to the bid-rigging offense under the Criminal Law.
Furthermore, we should explore how to deter bid-rigging that authorities initiate; as Howlader et al. [14, 15] pointed out, this is a critical case.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
HM: substantial contributions to the conception or design of the work, or the acquisition and analysis, or interpretation of data for the work, and drafting the work or revising it critically for important intellectual content. SK: substantial contributions to the conception or design of the work and providing approval for publication of the content. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by JSPS KAKENHI Grant Number JP19H04165.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2023.1045108/full#supplementary-material
References
1. Axelrod R. The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration: Agent-Based Models of Competition and Collaboration. Princeton, NJ: Princeton University Press. (1997). doi: 10.1515/9781400822300
3. Graham D, Marshall R. Collusive behavior at single-object second-price and English auctions. J Polit Econ. (1987) 95:1217–39. doi: 10.1086/261512
4. Fudenberg D, Maskin E. The folk theorem in repeated games with discounting or with incomplete information. Econometrica. (1986) 54:533–54. doi: 10.2307/1911307
5. Aoyagi M. Bid rotation and collusion in repeated auctions. J Econ Theory. (2003) 112:79–105. doi: 10.1016/S0022-0531(03)00071-1
6. Aoyagi M. Efficient collusion in repeated auctions with communication. J Econ Theory. (2007) 134:61–92. doi: 10.1016/j.jet.2005.07.016
7. Thomas CJ. Using reserve prices to deter collusion in procurement competition. J Ind Econ. (2005) 53:301–26. doi: 10.1111/j.1467-6427.2005.00257.x
8. Motta M, Polo M. Leniency programs and cartel prosecution. Int J Ind Organ. (2003) 21:347–79. doi: 10.1016/S0167-7187(02)00057-7
9. Spagnolo G. Divide et Impera: Optimal Leniency Programmes. C.E.P.R. Discussion Papers. (2004). Available online at: https://EconPapers.repec.org/RePEc:cpr:ceprdp:4840 (Retrieved July 30, 2023).
10. Harrington JE. Optimal corporate leniency programs. J Ind Econ. (2008) 56:215–46. doi: 10.1111/j.1467-6451.2008.00339.x
11. Chen Z, Rey P. On the design of leniency programs. J Law Econ. (2013) 56:917–57. doi: 10.1086/674011
12. Brisset K, Thomas L. Leniency program: a new tool in competition policy to deter cartel activity in procurement auctions. Eur J Law Econ. (2004) 17:5–19.
13. Abe M, Suzuki K. Receipt-free sealed-bid auction. In:Chan AH, Gligor V, , editors. Information Security. Berlin, Heidelberg: Springer Berlin Heidelberg (2002). p. 191–9. doi: 10.1007/3-540-45811-5_14
14. Howlader J, Roy SK, Mal AK. Practical receipt-free sealed-bid auction in the coercive environment. In:Lee HS, Han DG, , editors. Information Security and Cryptology-ICISC 2013. Cham: Springer International Publishing (2014). p. 418–34. doi: 10.1007/978-3-319-12160-4_25
15. Howlader J, Mal AK. Sealed-bid auction: a cryptographic solution to bid-rigging attack in the collusive environment. Secur Commun Netw. (2015) 8:3415–40. doi: 10.1002/sec.1268
16. Suzuki M. A Study of Bid Rigging (Nyusatsu dango no kenkyu) 2nd edition. Tokyo: Shinzan-Sha (2004) (in Japanese).
17. Asker J. A study of the internal organization of a bidding cartel. Am Econ Rev. (2010) 100:724–62. doi: 10.1257/aer.100.3.724
18. Wachs J, Kertész J. A network approach to cartel detection in public auction markets. Scient Rep. (2019) 9:10818. doi: 10.1038/s41598-019-47198-1
19. Reeves-Latour M, Morselli C. Bid-rigging networks and state-corporate crime in the construction industry. Soc Netw. (2017) 51:158–170. doi: 10.1016/j.socnet.2016.10.003
20. Andrighetto G, Brandts J, Conte R, Sabater-Mir J, Solaz H, Villatoro D. Punish and voice: punishment enhances cooperation when combined with norm-signalling. PLoS ONE. (2013) 8:e64941. doi: 10.1371/journal.pone.0064941
21. Porter RH, Zona JD. Detection of bid rigging in procurement auctions. J Polit Econ. (1993) 101:518–38. doi: 10.1086/261885
22. Porter RH, Zona JD. Ohio school milk markets: an analysis of bidding. Rand J Econ. (1999) 30:263–88. doi: 10.2307/2556080
23. Pesendorfer M. A study of collusion in first-price auctions. Rev Econ Stud. (2000) 67:381–411. doi: 10.1111/1467-937X.00136
24. Abrantes-Metz RM, Froeb LM, Geweke J, Taylor CT. A variance screen for collusion. Int J Ind Organ. (2006) 24:467–86. doi: 10.1016/j.ijindorg.2005.10.003
25. Ishii R. Favor exchange in collusion: Empirical study of repeated procurement auctions in Japan. Int J Ind Organ. (2009) 27:137–44. doi: 10.1016/j.ijindorg.2008.05.006
26. Ishii R. Bid roundness under collusion in Japanese procurement auctions. Rev Ind Organiz. (2014) 44:241–54. doi: 10.1007/s11151-013-9408-6
27. Bajari P, Ye L. Deciding between competition and collusion. Rev Econ Stat. (2003) 85:971–89. doi: 10.1162/003465303772815871
28. Godinho IF, Marques NC. Competition criminal law: an international and global trend? SHS Web Confer. (2021) 92:10. doi: 10.1051/shsconf/20219203011
29. Shaffer GC, Nesbitt NH, Waller SW. Criminalizing cartels: a global trend? In:Arlen Duke JD, Sweeney B, , editors. Comparative Competition Law (Research Handbooks in Comparative Law). Cheltenham: Edgar Elgar (2015). p. 301–344. doi: 10.4337/9781785362576.00019
30. Baker DI. Punishment for cartel participants in the united states: a special model? In:Beaton-Wells C, Ezrachi A, , editors. Criminalising Cartels: Critical Studies of an International Regulatory Movement. Oxford: Hart Pub Ltd. (2011). p. 27–44.
31. von Papp FW. What if all bid riggers went to prison and nobody noticed? Criminal antitrust law enforcement in Germany. In:Beaton-Wells C, Ezrachi A, , editors. Criminalising Cartels: Critical Studies of an International Regulatory Movement. Oxford: Hart Pub Ltd. (2011). p. 157–182.
32. Walle SV, Shiraishi T. Competition law in Japan. In:Arlen Duke JD, Sweeney B, , editors. Comparative Competition Law (Research Handbooks in Comparative Law). Cheltenham: Edgar Elgar (2015). p. 415–442.
33. Duke A. Public enforcement. In:Arlen Duke JD, Sweeney B, , editors. Comparative Competition Law (Research Handbooks in Comparative Law). Cheltenham: Edgar Elgar; 2015. p. 271–300. doi: 10.4337/9781785362576.00018
34. Wilks S. Cartel criminisation as juridification: political and regulatory danger. In:Beaton-Wells C, Ezrachi A, , editors. Criminalising Cartels: Critical Studies of an International Regulatory Movement. Oxford: Hart Pub Ltd. (2011). p. 341–358.
35. Williams R. Cartels in the criminal law landscape. In:Beaton-Wells C, Ezrachi A, , editors. Criminalising Cartels: Critical Studies of an International Regulatory Movement. Oxford: Hart Pub Ltd. (2011). p. 289–312.
36. Beaton-Wells C, Ezrachi A. Criminalising Cartels: Why Critical Studies? In:Beaton-Wells C, Ezrachi A, , editors. Criminalising Cartels : Critical Studies of an International Regulatory Movement. Oxford: Hart Pub Ltd. (2011). p. 3–24.
37. Olson M. The Logic of Collective Action: Public Goods and the Theory of Groups. London: Harvard Economic Studies Harvard University Press. (1965).
38. Yamagishi T. The structural goal/expectation theory of cooperation in social dilemmas. Adv Group Process. (1986) 3:52–87.
39. Pruitt DG, Kimmel MJ. Twenty years of experimental gaming: critique, synthesis, and suggestions for the future. Annu Rev Psychol. (1977) 28:363–92. doi: 10.1146/annurev.ps.28.020177.002051
40. Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. (1992) 359:826–9. doi: 10.1038/359826a0
41. Santos F, Pacheco J. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett. (2005) 95:098–104. doi: 10.1103/PhysRevLett.95.098104
42. Kojima T, Suzuki R, Arita T. Effects of ecological inheritance on coevolution of cooperative behaviors and physically niche constructing behaviors. J Adv Comput Intell Intell Inform. (2014) 18:391–400. doi: 10.20965/jaciii.2014.p0391
43. Masuda N. Evolution of cooperation driven by zealots. Scient Rep. (2012) 2:464. doi: 10.1038/srep00646
44. Matsuzawa R, Tanimoto J, Fukuda E. Spatial prisoner's dilemma games with zealous cooperators. Phys Rev E. (2016) 94:022114. doi: 10.1103/PhysRevE.94.022114
45. Ishii A, Kawahata Y. Sociophysics Analysis of the dynamics of peoples' interests in society. Frontiers in Physics. (2018) 10:89. doi: 10.3389/fphy.2018.00089
46. Galán JM, Izquierdo L. Appearances can be deceiving: lessons learned re-implementing axelrod's 'evolutionary approach to norms'. J Artif Societ Soc Simul. (2005) 8:1–2.
47. Yamamoto H, Okada I. Evolution of cooperation by a social vaccine. IEICE Trans Inform Syst. (2011) 94:1836–46 (in Japanese).
48. Yamamoto H, Okada I. How to keep punishment to maintain cooperation: Introducing social vaccine. Physica A. (2016) 443:526–36. doi: 10.1016/j.physa.2015.08.053
49. Smith JM, Price GR. The logic of animal conflict. Nature. (1973) 246:15–8. doi: 10.1038/246015a0
Keywords: bid-rigging, collusion, auction, prisoners' dilemma, norms, agent-based simulation
Citation: Morofuji H and Kurahashi S (2023) Carrot or stick? A study on “bid-rigging norms” by simulation: inducing factors and deterring measures. Front. Appl. Math. Stat. 9:1045108. doi: 10.3389/fams.2023.1045108
Received: 15 September 2022; Accepted: 03 August 2023;
Published: 24 August 2023.
Edited by:
Axel Hutt, Inria Nancy - Grand-Est Research Centre, FranceReviewed by:
Bedri Tas, Sultan Qaboos University, OmanJaydeep Howlader, National Institute of Technology, Durgapur, India
Copyright © 2023 Morofuji and Kurahashi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hideyuki Morofuji, czE5NDUwMTFAdS50c3VrdWJhLmFjLmpw
 Hideyuki Morofuji
Hideyuki Morofuji Setsuya Kurahashi
Setsuya Kurahashi