Corrigendum: A scalar poincaré map for anti-phase bursting in coupled inhibitory neurons with synaptic depression

A corrigendum on
A scalar poincaré map for anti-phase bursting in coupled inhibitory neurons with synaptic depression

by Olenik M, and Houghton C. (2022). Front. Appl. Math. Stat. 8:822782. doi: 10.3389/fams.2022.822782

In the published article, there was an error in Figure 10 as published. The analytically derived graph was plotted orange, and the numerically computed graph was plotted blue. In the correct version the analytically computed graph is blue, and the numerically computed graph is orange. The corrected Figure 10 and its caption appear below.

FIGURE 10

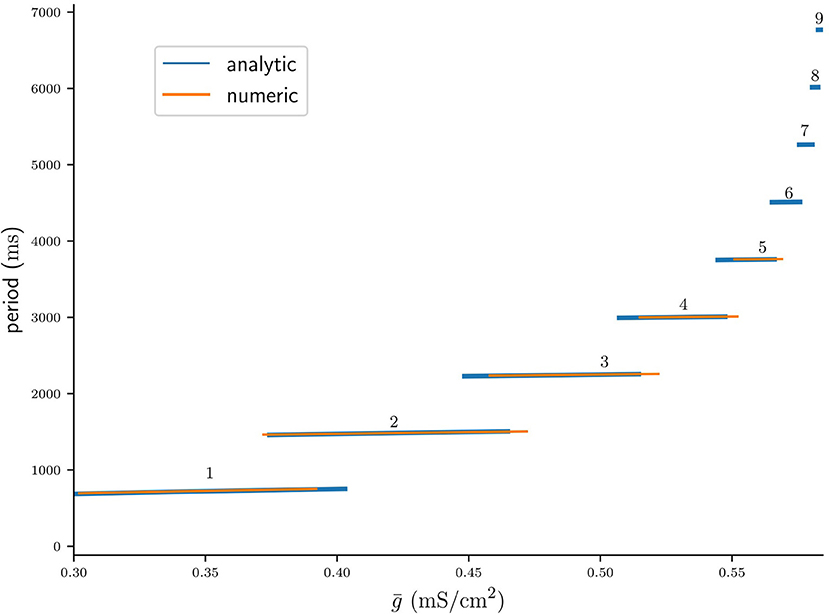
Figure 10. Bifurcation diagram of the period of stable n:n solutions computed analytically from fixed points of Π_n, plotted on the respective intervals of $\overline{g}\in [{\overline{g}}_{{L}}(n),{\overline{g}}_{{R}}(n)]$ (blue), and computed from numerical integrations of the ODEs (orange).

In the published article there is a typo in section 1, paragraph 5, where the singular form “parameter” was used, instead of the correct plural “parameters”. The last sentence of the paragraph previously stated:

“Because our map is fully explicit, it lays the framework for studying the effects of other model parameter on network dynamics without the need to run expensive numerical integrations of the ODEs.”

The corrected sentence appears below:

“Because our map is fully explicit, it lays the framework for studying the effects of other model parameters on network dynamics without the need to run expensive numerical integrations of the ODEs.”

A correction has been made to section 1.

In the original article, Equations 31 and 32 miss the differential in the denominator. A correction has been made to Results, “Construction of the Scalar Poincaré Map,” Equations 31, 32:

$\begin{array}{ll}\frac{d{\Pi }_n}{d\overline{g}}>0,& (31)\end{array}$

$\begin{array}{ll}\frac{d{\Pi }_n}{d{d}^{\star }}>0,& (32)\end{array}$

Moreover, in the published article Equation 36 misses the differential symbol in the denominator. A correction has been made to Results, “Existence and Stability of Fixed Points,” Equation 36:

$\begin{array}{ll}\frac{d}{d{d}^{\star }}{\Pi }_n({d^{\star }}_b,{\overline{g}}_b)=1.& (36)\end{array}$

In the published article in Equation 47, the symbol δ_n in the denominator is written incorrectly, the n should be a subscript. The correct Equation 47 is:

$\begin{array}{ll}\frac{\partial F_n}{\partial d_f^{\star }}={\tau }_{\kappa }\frac{{(\lambda \rho )}^{n-1}}{{\delta }_n(d_f^{\star })}>0.& (47)\end{array}$

A correction has been made to section 3.5.

In the published article in Equations 41 and 42, the “smaller than” and “greater than” signs appear in the wrong order. The correct Equations 41 and 42 are:

$\begin{array}{ll}\frac{d{G}_n}{d{d}_f^{\star }}>0,\text{ for }{d}_f^{\star }>d_b^{\star }(n)\text{ stable},& (41)\end{array}$

$\begin{array}{ll}\frac{d{G}_n}{d{d}_f^{\star }}<0,\text{ for }{d}_f^{\star }<d_b^{\star }(n)\text{ unstable},& (42)\end{array}$

In the published article in the Equations 51-54 some symbols have incorrect subscripts. The correct Equations 51-54 are:

$\begin{array}{ll}{\overline{g}}_{{L}}(n)<{\overline{g}}_{{R}}(n)& (51)\end{array}$

$\begin{array}{ll}{\overline{g}}_{{L}}(n)<{\overline{g}}_{{L}}(n+1)\text{ and }{\overline{g}}_{{R}}(n)<{\overline{g}}_{{R}}(n+1)& (52)\end{array}$

$\begin{array}{ll}{\overline{g}}_{{L}}(n+1)<{\overline{g}}_{{R}}(n)& (53)\end{array}$

$\begin{array}{ll}{\overline{g}}_{{R}}(n+1)-{\overline{g}}_{{L}}(n+1)<{\overline{g}}_{{R}}(n)-{\overline{g}}_{{L}}(n)& (54)\end{array}$

A correction has been made to section 3.6.

Finally, in the published article in Results, “Stable Solution Branch Borders,” paragraph 4, Equation 58 was quoted instead of Equation 54. The corrected sentence is:

Here $g_{{L}}(n)$ and ${\overline{g}}_{{R}}(n)$ were computed from Equations (56) and (54), respectively.

In the published article in the last sentence of section 4, paragraph 2, a wrong type of citation format was used. The original sentence previously stated “Our results are also in line with [7] rhythmogenesis hypothesis, namely that synaptic depression of inhibition is a mechanism by which anti-phase bursting may arise.”

The corrected sentence appears below:

“Our results are also in line with Brown's [7] rhythmogenesis hypothesis, namely that synaptic depression of inhibition is a mechanism by which anti-phase bursting may arise.”

In the published article there was a typo in the acknowledgments. The first sentence previously stated: “MO thank the Wellcome Trust for financial support of his Ph.D. study.”

The corrected sentence appears below: “MO thanks the Wellcome Trust for financial support of his Ph.D. study.”

The authors apologize for these errors and state that this does not change the scientific conclusions of the article in any way. The original article has been updated.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.