On Two Localized Particle Filter Methods for Lorenz 1963 and 1996 Models

Nonlinear data assimilation methods like particle filters aim to improve the numerical weather prediction (NWP) in non-Gaussian setting. In this manuscript, two recent versions of particle filters, namely the Localized Adaptive Particle Filter (LAPF) and the Localized Mixture Coefficient Particle Filter (LMCPF) are studied in comparison with the Ensemble Kalman Filter when applied to the popular Lorenz 1963 and 1996 models. As these particle filters showed mixed results in the global NWP system at the German meteorological service (DWD), the goal of this work is to show that the LMCPF is able to outperform the LETKF within an experimental design reflecting a standard NWP setup and standard NWP scores. We focus on the root-mean-square-error (RMSE) of truth minus background, respectively, analysis ensemble mean to measure the filter performance. To simulate a standard NWP setup, the methods are studied in the realistic situation where the numerical model is different from the true model or the nature run, respectively. In this study, an improved version of the LMCPF with exact Gaussian mixture particle weights instead of approximate weights is derived and used for the comparison to the Localized Ensemble Transform Kalman Filter (LETKF). The advantages of the LMCPF with exact weights are discovered and the two versions are compared. As in complex NWP systems the individual steps of data assimilation methods are overlaid by a multitude of other processes, the ingredients of the LMCPF are illustrated in a single assimilation step with respect to the three-dimensional Lorenz 1963 model.

1. Introduction

Data assimilation methods combine numerical models and observations to generate an improved state estimate. Besides optimization approaches, ensemble methods use an ensemble of states to approximate underlying probability distributions. For example the ensemble Kalman filter presented in Evensen [1] (see also [2, 3]) carries out Bayesian state estimation and samples from Gaussian distributions which equals a linearity assumption of the underlying system. However, the local ensemble transform Kalman filter (LETKF; [4]) is widely used in high dimensional environments. For example, the LETKF is successfully used as ensemble data assimilation method in the numerical weather prediction (NWP) system at the German meteorological service (DWD). Nevertheless, there is the aim to develop more general ensemble methods to account for the increasing complexity of numerical models.

Particle filter methods are based on Monte Carlo schemes and aim to solve the nonlinear filtering problem without any further assumptions on the distributions. Since Monte Carlo methods suffer the curse of dimensionality, the application of classical or bootstrap particle filters to high- dimensional problems results in filter divergence or filter collapse (see [5–7]). After first attempts to carry out nonlinear Bayesian state estimation approximately by Gordon et al. [8], further particle filters are developed, which are able to overcome filter collapse. For an overview of particle filters we refer to van Leeuwen [5] and van Leeuwen et al. [9].

One idea to prevent filter collapse is to develop hybrid methods between particle filters and ensemble Kalman filters. Examples for hybrid filters are the adaptive Gaussian mixture filters [10], the ensemble Kalman particle filter [11], which is further developed in Robert and Künsch [12] and Robert et al. [13], the merging particle filter [14] and the nonlinear ensemble transform filter (e.g., [15, 16]) which resembles the ensemble transform Kalman filter [17]. Transportation particle filters follow the approach to use transformations to transport particles in a deterministic way. A one-step transportation is carried out in Reich [18] and tempering of the likelihood, which leads to a multi-step transportation, is presented in, e.g., Neal [19], Del Moral et al. [20], Emerick and Reynolds [21], and Beskos et al. [22]. The guided particle filter described in van Leeuwen et al. [23] and van Leeuwen [5] tempers in the time domain, which means that background particles at each time step between two observations are used. The transportation of particle filters can also be described by differential equations. In Reich [24] and Reich and Cotter [25], the differential equation is simulated using more and more tempering steps. Approximations to the differential equation can also be derived by Markov-Chain Monte Carlo methods [25–27]. Localization is another approach in particle filter methods to overcome filter collapse. Localization schemes based on resampling are used in e.g., the local particle filter [28] which is applied for mesoscale weather prediction [29]. Additionally, the local particle filter (LPF) [30], the localized adaptive particle filter (LAPF; [31]) and the localized mixture coefficients particle filter (LMCPF; [32]) are based on localization schemes.

Moreover, the localized mixture coefficients particle filter (LMCPF) is based on Gaussian mixture distributions. In 1972, Alspach and Sorenson already introduced an approach to nonlinear Bayesian estimation using Gaussian sum approximations combined with linearization ideas [33]. Anderson and Anderson first presented a Monte Carlo approach with prior approximation by Gaussian or sum of Gaussian kernels in geophysical literature [34]. They proposed to extend the presented kernel filter by the transformation of the equations to a subspace spanned by the ensemble members to apply the filter in high-dimensional systems. The LMCPF is based on this kind of transformation. The first attempts were followed from various approaches to filtering with the usage of Gaussian mixture distributions (e.g., [35–38]). Some of the particle filters mentioned above are based on Gaussian mixture distributions as well (e.g., [10, 11, 24]).

The localized particle filter methods LPF [30], LAPF and LMCPF are structured in a way that a consistent implementation in existing LETKF code is possible. In Kotsuki et al. [39], the LPF and its Gaussian mixture extension, which resembles the LMCPF, are tested in an intermediate AGCM (SPEEDY model). Moreover, LAPF and LMCPF are applied in the global NWP system at DWD (see [31, 32]). The comparison of the LMCPF to the LETKF for the global ICON model [40] yields mixed results. In this study, we investigate if the LMCPF can outperform the LETKF with respect to a standard NWP setup and standard NWP score in the dynamical systems Lorenz 1963 and Lorenz 1996. We will see later that the answer is indeed positive and that the LMCPF yields far better results than the LAPF. To this end, a model error is introduced by applying different model parameters for the true run and in the forecast step. Furthermore, we focus on the root-mean-square-error of truth minus background, respectively, analysis ensemble mean, which is an important score in NWP, rather than looking at an entire collection of measures. In this study, we present and apply a revised version of the LMCPF. We derive the exact Gaussian particle weights, which are then used in the resampling step instead of approximate weights. This promising completion of the method was also recently introduced in Kotsuki et al. [39] and tested for an intermediate AGCM model. We will see that the revised method leads to the survival of a larger selection of background particles and as a consequence thereof to a higher filter stability concerning the spread control parameters.

In addition, the individual ingredients of the LMCPF method are portrayed in one assimilation step with respect to the Lorenz 1963 model. Background and analysis ensemble as well as the true state and observation vector can be easily displayed for this three dimensional model. With this part, we want to illustrate the advantage of LMCPF compared to LAPF in the case that the observation is far away from the ensemble. Furthermore, the difference between the approximate and exact particle weights are discussed and the improvement of LMCPF over LETKF for a bimodal background distribution is shown.

The manuscript is structured as follows. Section 2 covers the experimental setup based on the dynamical systems Lorenz 1963 and Lorenz 1996. The three localized ensemble data assimilation methods LMCPF, LAPF and LETKF are mathematically described in Section 3, which includes the derivation of the exact particle weights for the LMCPF. In Section 4, the LMCPF is studied for one assimilation step with respect to the Lorenz 1963 model. Finally, LMCPF is compared to LETKF and LAPF for Lorenz 1963 and Lorenz 1996 in Section 5 and the conclusion follows in Section 6.

2. Experimental Setup: Lorenz Models

The mathematician Edward Lorenz first presented the chaotic dynamical systems Lorenz 1963 and 1996. These are frequently used to develop and test data assimilation methods in a well understood and controllable environment. This section aims to state the experimental setup.

2.1. Lorenz 1963 Model

In Lorenz [41], Edward Lorenz introduced a nonlinear dynamical model, which is denoted as Lorenz 1963. Due to its chaotic behavior, the system has become a popular toy model to investigate and compare data assimilation methods (e.g., [34, 38, 42]).

The dynamics of Lorenz 1963 represent a simplified version of thermal convection. The three coupled nonlinear differential equations are given by

$\begin{array}{ll}\frac{d{x}_1}{dt}=\sigma (x_2-x_1)& (1)\end{array}$

$\begin{array}{ll}\frac{d{x}_2}{dt}=\rho x_1-x_2-x_1{x}_3& (2)\end{array}$

$\begin{array}{ll}\frac{d{x}_3}{dt}=x_1{x}_2-\beta x_3& (3)\end{array}$

where x₁(t), x₂(t), and x₃(t) are the prognostic variables and σ, ρ, and β denote the parameters of the model. In terms of the physical interpretation, σ is the Prandtl number, ρ a normalized Rayleigh number and β a non-dimensional wave number (see [43]). In this work, we follow Lorenz' suggestion to set σ = 10, ρ = 28 and β = 8/3, for which the system shows chaotic behavior [41]. In case of this parameter setting, the popular butterfly attractor is obtained (see Figure 5). Furthermore, x₁ describes the intensity of the convective motion, x₂ the temperature difference between the ascending and descending currents and the last variable x₃ denotes the distortion of the vertical temperature profile from linearity [41].

2.2. Lorenz 1996 Model

Since the introduction of the Lorenz 1996 model in Lorenz [44], the dynamical system is used as popular test bed for data assimilation methods (e.g., [28, 36, 45]). Not only different adaptions of the ensemble Kalman filter but also particle filter schemes or hybrid methods combining particle filter and EnKF schemes are tested in the high-dimensional and chaotic environment given by Lorenz 1996 with specific parameter settings (e.g., [30, 46, 47]). In contrast to Lorenz 1963, localization is an important component of the investigation of data assimilation methods and the later Lorenz 1996 model invites to test localization schemes (e.g., [48]).

The model considers n ∈ ℕ coupled time-dependent variables, whose dynamics are described by a system of n ordinary differential equations. We consider the state variable as x(t) = (x⁽¹⁾(t), …, x⁽ⁿ⁾(t)) ∈ ℝⁿ for t ∈ ℝ₊. The dynamics of the N-th component are governed by the ordinary differential equation

$\begin{array}{ll}\frac{\text{d}{x}^{(N)}}{\text{d}t}=-x^{(N-2)}{x}^{(N-1)}+x^{(N-1)}{x}^{(N+1)}-x^{(N)}+F& (4)\end{array}$

where the constant F is independent of N and describes a forcing term. Furthermore, we define

$\begin{array}{lll}{x}^{(N-n)}& :=x^{(N)}& (5)\end{array}$

$\begin{array}{lll}{x}^{(N+n)}& :=x^{(N)}& (6)\end{array}$

so that Equation (4) is valid for any N = 1, …, n. In addition to the external forcing term, the linear terms describe internal dissipation whereas the nonlinear, respectively, quadratic terms simulate advection. In this study, we use F = 8 as forcing term for the true run and choose differing values for the model propagation step.

In a meteorological context, each variable represents an atmospheric quantity, e.g., temperature, at one longitude on a latitude circle. The equidistant distribution of the nodes on a latitude circle for n = 40 variables is illustrated in Figure 1.

FIGURE 1

Figure 1. Set-up for Lorenz 1996 model with n = 40 variables.

2.3. Data Assimilation Setup

To test data assimilation methods with the Lorenz models, observations are produced at equidistant distributed measurement times. The system of differential equations of Lorenz 1963 model, respectively, Lorenz 1996 model is solved by a fourth-order Runge-Kutta scheme using a time-step of 0.05. The integration over a certain time is stored as truth, from which observations are generated with a distance of Δ_t time units. The true run is performed with model parameters σ^true = 10, ρ = 28 and β = 8/3 for Lorenz 1963 and with the forcing term F^true = 8 for the 40-dimensional Lorenz 1996 model. The integration of the ensemble of states is accomplished for different model parameters σ for Lorenz 1963 and F for Lorenz 1996 in order to simulate model error. Furthermore, the observation operator H ∈ ℝ^m×n is chosen linear for both dynamical systems. The observation vector y_k at the k−th measurement at time t_k is defined by

$\begin{array}{ll}{y}_k=H·x_k^{\text{true}}+\eta \in {ℝ}^m& (7)\end{array}$

whereas the entries of η ∈ ℝ^m are randomly drawn from a Gaussian distribution with zero expectation and standard deviation σ_obs. Additionally, the observation error covariance matrix is represented by

$\begin{array}{ll}R={\sigma }_{\text{obs}}^2·I_m\in {ℝ}^{m\times m}& (8)\end{array}$

with the m × m-identity matrix I_m. The ensemble is initialized by random draws from a uniform distribution around the true starting point $x_0^{\text{true}}$.

3. Localized Ensemble Data Assimilation Methods

Data assimilation methods aim to estimate some state vector. Methods based on an ensemble of states can additionally estimate the uncertainty of the state and provide an idea for the associated distribution. This section covers three localized ensemble data assimilation methods, which are compared against each other later in this paper. The localized adaptive particle filter (LAPF; [31]) describes a particle filter method which is applicable to real-size numerical weather prediction and implemented in the system of the German meteorological service (DWD). To improve the method and approximate the scores, the LAPF was further developed, which resulted in the localized mixture coefficients particle filter (LMCPF). The LMCPF combines a resampling step following the Monte Carlo approach with a shift of the particles toward the observation. The shift results from the application of Gaussian (mixture) distributions and exists in the localized ensemble transform Kalman filter (LETKF) [4] in the form that the ensemble mean is shifted. The LETKF is widely used in the data assimilation community and therefore already improved. Due to similarities between LETKF and the particle filter methods LAPF and LMCPF, the ensemble Kalman filter represents a good method to compare the newer methods LAPF and LMCPF with.

All of these ensemble methods fulfill Bayes' theorem in approximation. With the aid of Bayes' formula, a given prior or background distribution can be combined with the so-called likelihood distribution to obtain a posterior or analysis distribution. In terms of probability density functions, the theorem yields

$\begin{array}{ll}{p}^{(a)}(x)=c_{a}p(y|x)p^{(b)}(x),x\in {ℝ}^n,y\in {ℝ}^m& (9)\end{array}$

for the prior probability density function (pdf) p^(b) : ℝⁿ → [0, ∞), the likelihood pdf p(·|x) : ℝ^m → [0, ∞) for x ∈ ℝⁿ and the resulting posterior pdf p^(a) : ℝⁿ → [0, ∞) with n, m ∈ ℕ. In realistic NWP, the model space dimension n ∈ ℕ is in general larger than the dimension of the observation space described by m ∈ ℕ. Furthermore, the constant c_a ∈ ℝ in Equation (9) ensures that the resulting function is again a pdf. Due to the normalization constant, the likelihood function does not necessarily have to be a pdf to satisfy Bayes' formula. This form of Bayes' theorem is derived from the formula of the density function of a conditional probability function which is proven in Section 4-4 of Papoulis and Pillai [49].

In data assimilation, the likelihood is given by the observation error pdf as function of x ∈ ℝⁿ for given observation vector y ∈ ℝ^m. We assume a Gaussian distributed observation error for all presented filters, i.e.,

$\begin{array}{ll}p(y|x)=\frac{1}{\sqrt{{(2\pi )}^{m}det(R)}}·exp\left(-\frac{1}{2}{(y-Hx)}^T{R}^{-1}(y-Hx)\right),& (10)\end{array}$

for x ∈ ℝⁿ, some observation vector y ∈ ℝ^m, the linear observation operator H : ℝⁿ → ℝ^m and the observation error covariance matrix R ∈ ℝ^m×m. The derivations of the following methods are carried out for a time-constant linear observation operator H. The assumption on the prior distribution differs for the filters. In the LAPF, the prior pdf is approximated by a sum of delta functions following the idea of the classical particle filter. The LMCPF assumes a sum of Gaussian kernels while the LETKF approximates the prior pdf by a Gaussian pdf.

All of the following methods are based on localization so that the steps are carried out locally at a series of analysis points. Furthermore, the observations are weighted depending on the distance to the current location. As Lorenz 1963 is only built on three variables, localization is not implemented for this model. For the Lorenz 1996 model, the implementation is based on the smallest distance between two variables along the circle (e.g., [50]), which is plotted in Figure 1. The distances are weighted by the fifth-order polynomial localization Gaspari-Cohn function described in Gaspari and Cohn [51]. Moreover, the function depends from the localization radius r_loc > 0. The resulting weight matrix is applied by the Schur-product to the observation error covariance matrix R, which is then used to derive the analysis ensemble by one of the following methods.

In addition, the equations of the following localized methods are carried out in ensemble space to reduce the dimension. The ensemble space is spanned by the columns of

$\begin{array}{ll}X:=\left(x^{(b,1)}-{\stackrel{-}{x}}^{(b)},x^{(b,2)}-{\stackrel{-}{x}}^{(b)},\dots ,x^{(b,L)}-{\stackrel{-}{x}}^{(b)}\right)\in {ℝ}^{n\times L}& (11)\end{array}$

with ensemble size L ∈ ℕ_>1, respectively

$\begin{array}{ll}Y:=\left(y^{(b,1)}-{ȳ}^{(b)},y^{(b,2)}-{ȳ}^{(b)},\dots ,y^{(b,L)}-{ȳ}^{(b)}\right)\in {ℝ}^{m\times L}& (12)\end{array}$

where ${\stackrel{-}{x}}^{(b)}$ and ȳ^(b) denote the mean of the background ensemble ${(x^{(b,l)})}_{l=1,\dots ,L}$, i.e.,

$\begin{array}{ll}{\stackrel{-}{x}}^{(b)}=\frac{1}{L}{\displaystyle \sum _{l=1}^L}{x}^{(b,l)}& (13)\end{array}$

respectively the mean of the ensemble in observation space

$\begin{array}{ll}{ȳ}^{(b)}=\frac{1}{L}{\displaystyle \sum _{l=1}^L}{y}^{(b,l)}.& (14)\end{array}$

The ensemble in observation space is obtained by the application of the observation operator H to the background ensemble, i.e.,

$\begin{array}{ll}{y}^{(b,l)}:=H{x}^{(b,l)},l=1,\dots ,L.& (15)\end{array}$

The orthogonal projection P onto the ensemble space span(Y) weighted by R⁻¹ is defined as

$\begin{array}{ll}P:=Y{(Y^{*}Y)}^{-1}{Y}^{*}=Y{(Y^T{R}^{-1}Y)}^{-1}{Y}^T{R}^{-1}& (16)\end{array}$

whereas

$\begin{array}{ll}{Y}^{*}=Y^T{R}^{-1}& (17)\end{array}$

denotes the adjoint of Y with respect to the weighted scalar product $<·,·{>}_{R^{-1}}$ on ℝ^m and the standard scalar product on ℝ^L. To ensure the invertibility of Y^*Y, the formulas are restricted to ${C}(Y^{*})$ – the column space or range of Y^* – which is a subset of N(Y)^⊥⊂ℝ^L (see Lemma 3.2.1 and Lemma 3.2.3 in Nakamura and Potthast [52]). Additionally, the matrix Y^*Y is denoted as

$\begin{array}{ll}A:=Y^{*}Y=Y^T{R}^{-1}Y.& (18)\end{array}$

3.1. Localized Adaptive Particle Filter

The LAPF, introduced in Potthast et al. [31], is based on the idea for classical particle filters (e.g., the Sequential Importance Resampling Filter by Gordon et al. [8]) to approximate the background distribution by a sum of delta distributions. Let x^(b,l) for l = 1, …, L be an ensemble of background particles with ensemble size L ∈ ℕ_>1. The background pdf is described by

$\begin{array}{ll}{p}^{(b)}(x):=\frac{1}{L}{\displaystyle \sum _{l=1}^L}\delta (x-x^{(b,l)}).& (19)\end{array}$

With Bayes' Theorem for pdfs in Equation (9) and the observation error pdf p(y|x), the posterior pdf results in

$\begin{array}{ll}{p}^{(a)}(x)=c^{(a)}{\displaystyle \sum _{l=1}^L}p(y|x)\delta (x-x^{(b,l)})& (20)\end{array}$

with the normalization factor $c^{(a)}\in {ℝ}_{>0}$. Following Anderson and Anderson [34], the relative probability p_l that a sample should be taken from the l-th summand of p^(a) in the resampling step, is derived by

$\begin{array}{ll}{p}_l=\frac{\int c^{(a)}p(y|x)\delta (x-x^{(b,l)})\text{ d}x}{\int p^{(a)}(x)\text{ d}x}=\frac{p(y|x^{(b,l)})}{{\sum }_{l=1}^{L}p(y|x^{(b,l)})},& (21)\end{array}$

for l = 1, …, L. With the choice of a normal distributed observation error (Equation 10) this leads to

$\begin{array}{ll}{p}_l=\frac{e^{-\frac{1}{2}{(y-H{x}^{(b,l)})}^T{R}^{-1}(y-H{x}^{(b,l)})}}{{\sum }_{l=1}^L{e}^{-\frac{1}{2}{(y-H{x}^{(b,l)})}^T{R}^{-1}(y-H{x}^{(b,l)})}}& (22)\end{array}$

as the normalization factor in Equation (10) does not depend on l and can be canceled. To resample from the posterior distribution, stratified resampling is performed in ensemble space. To this end, the weights

$\begin{array}{ll}{\tilde{w}}^{(l)}:=e^{\frac{1}{2}{(y-H{x}^{(b,l)})}^T{R}^{-1}(y-H{x}^{(b,l)})},l=1,\dots ,L& (23)\end{array}$

are transformed to ensemble space with the help of the orthogonal projection P defined in Equation (16). With an analogous approach as in Section 3.2.1, the weights in ensemble space yield

$\begin{array}{ll}{\tilde{w}}_{\text{ens}}^{(l)}=e^{-\frac{1}{2}{(C-e_l)}^{T}A(C-e_l)}& (24)\end{array}$

for l = 1, …, L with A = Y^TR⁻¹Y and the projected observation vector

$\begin{array}{ll}C=A^{-1}{Y}^T{R}^{-1}(y-{ȳ}^{(b)}).& (25)\end{array}$

A detailed derivation of the weights in ensemble space is given in Potthast et al. [31]. These weights are normalized to obtain the relative weights

$\begin{array}{ll}{\tilde{w}}^{(a,l)}=L·\frac{{\tilde{w}}_{\text{ens}}^{(l)}}{{\sum }_{l=1}^L{\tilde{w}}_{\text{ens}}^{(l)}},l=1,\dots ,L& (26)\end{array}$

which sum up to L. As next step, stratified resampling [53] is performed based on the ensemble weights. To this end, accumulated weights are calculated. For l = 1, …, L, the accumulated weights are defined by

$\begin{array}{ll}{w}_{a{c}_0}=0,w_{a{c}_l}=w_{a{c}_{l-1}}+{\tilde{w}}^{(a,l)}.& (27)\end{array}$

Additionally, L on the interval [0, 1] uniformly distributed random numbers r_l are generated to introduce the variable R_l = l − 1 + r_l for l = 1, …, L. Then, the stratified resampling approach yields a matrix $\stackrel{⌣}{W}\in {\left\{0,1\right\}}^{L\times L}$ with entries

$\begin{array}{ll}\stackrel{⌣}{W}=\{\begin{array}{ll}1,& R_l\in (w_{a{c}_{i-1}},w_{a{c}_i}]\\ 0,& \text{else}\end{array}& (28)\end{array}$

where the number of ones in the i-th row indicates how often the i-th particle is chosen.

The particles chosen in the stratified resampling step build an ensemble of the background particles, which can be contained multiple times. To increase the ensemble variation, new particles are drawn from a Gaussian mixture distribution. Let each chosen particle represent the expectation of a Gaussian distribution with covariance $\sigma {(\rho )}^2/(L-1)·I_L\in {ℝ}^{L\times L}$. Under allowance of the frequency, new particles are drawn from the Gaussian distribution. The covariance matrix equals the estimated background covariance matrix in ensemble space $B_{\text{ens}}=1/(L-1)·I_L\in {ℝ}^{L\times L}$ multiplied with an inflation factor σ(ρ). The inflation factor is a rescaled version of the adaptive inflation factor ρ which is used in the LETKF (see [4]). The parameter ρ is defined by Equations (86) and (87). The dependence of σ(ρ) on ρ is given by Equation (88). The detailed description is given in Potthast et al. [31] and in Section 3.2.3.

All in all, the steps can be combined in a matrix W_LAPF. Let Z ∈ ℝ^L×L be a matrix whose entries originate from a standard normal distribution. Together with the resampling matrix $\stackrel{⌣}{W}$, the matrix W_LAPF is defined by

$\begin{array}{ll}{W}_{\text{LAPF}}=\stackrel{⌣}{W}+\frac{\sigma (\rho )}{\sqrt{L-1}}·Z.& (29)\end{array}$

The full analysis ensemble is calculated by multiplication of the background ensemble with the matrix W_LAPF, i.e.,

$\begin{array}{ll}{(x^{(a,l)})}_{l=1,\dots ,L}={\stackrel{-}{x}}^{(b)}·𝟙+X·W_{\text{LAPF}}& (30)\end{array}$

where X describes the ensemble pertubation matrix defined in Equation (11) and 𝟙 ∈ ℝ^1×L denotes a row vector with ones as entries. The multiplication of background mean with 𝟙 results in a matrix of size n × L with the mean vector replicated in each of the L columns.

3.2. Localized Mixture Coefficients Particle Filter

The LMCPF, presented in Walter et al. [32], builds on the LAPF but differs in the assumption on the background distribution. In difference to the ansatz of classical particle filters, the background particles are interpreted as the mean of Gaussian distributions. The background pdf is described as the sum of these Gaussians where each distribution has the same covariance matrix, i.e.,

$\begin{array}{ll}{p}^{(b)}(x):=c^{(b)}{\displaystyle \sum _{l=1}^L}{e}^{-\frac{1}{2}{(x-x^{(b,l)})}^T{B}^{-1}(x-x^{(b,l)})}& (31)\end{array}$

with ensemble size L ∈ ℕ_>1 and the normalization factor

$\begin{array}{ll}{c}^{(b)}:=\frac{1}{L·\sqrt{{(2\pi )}^{n}det(B)}}.& (32)\end{array}$

The covariance matrix is estimated by the background particles, i.e.,

$\begin{array}{ll}B:=\gamma X{X}^T& (33)\end{array}$

with the ensemble pertubation matrix X defined in Equation (11) and the parameter

$\begin{array}{ll}\gamma =\frac{\kappa }{L-1}\in {ℝ}_{+}.& (34)\end{array}$

With the parameter κ, the background uncertainty can be controlled. The general covariance estimator is given for κ = 1. To ensure the invertibility of B, the formulas are restricted to ${C}(X)$ – the range of X. From definition (Equation 33) the covariance matrix in ensemble space is derived by

$\begin{array}{ll}{B}_{\text{ens}}=\gamma I_L\in {ℝ}^{L\times L}& (35)\end{array}$

with the identity matrix $I_L\in {ℝ}^{L\times L}$. Following Bayes' Theorem, the analysis pdf is given by

$\begin{array}{ll}{p}^{(a)}(x):=p(y|x)·p^{(b)}(x)={\tilde{c}}^{(a)}{\displaystyle \sum _{l=1}^L}p(y|x)·p^{(b,l)}(x)& (36)\end{array}$

where p^(b,l)(x) denotes the l-th summand of the background pdf in Equation (31). The likelihood p(y|x) is chosen as Gaussian (see Equation 10). Following Theorem 4.1 in Anderson and Moore [54], the analysis pdf can be explicitly calculated. The result is again a Gaussian mixture pdf, i.e.,

$\begin{array}{ll}{p}^{(a)}(x)=c^{(a)}{\displaystyle \sum _{l=1}^L}{w}^{(l)}·e^{\left(-\frac{1}{2}{(x-x^{(a,l)})}^T{(B^{(a)})}^{-1}(x-x^{(a,l)})\right)}& (37)\end{array}$

with

$\begin{array}{ll}{B}^{(a)}:={(B^{-1}+H^T{R}^{-1}H)}^{-1}& (38)\end{array}$

$\begin{array}{ll}{x}^{(a,l)}:=x^{(b,l)}+B^{(a)}{H}^T{R}^{-1}(y-H{x}^{(b,l)})& (39)\end{array}$

$\begin{array}{ll}{w}^{(l)}:=e^{\left(-\frac{1}{2}{(y-H{x}^{(b,l)})}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}(y-H{x}^{(b,l)})\right)}& (40)\end{array}$

and a normalization factor c^(a) such that the integral of p^(a)(x) over the range of X denoted by ${C}(X)$ yields one. The weights w^(l) are important to obtain a sample from the posterior distribution. The relative probability that a sample from the l-th summand of p^(a) should be taken is described in Anderson and Anderson [34] by

$\begin{array}{ll}{p}_l=\frac{\int c^{(a)}{w}^{(l)}·e^{\left(-\frac{1}{2}{(x-x^{(a,l)})}^T{(B^{(a)})}^{-1}(x-x^{(a,l)})\right)}\text{ d}x}{\int p^{(a)}(x)\text{ d}x}=\frac{w^{(l)}}{{\sum }_{l=1}^L{w}^{(l)}}.& (41)\end{array}$

With the following steps, a posterior ensemble is generated as a sample of the posterior distribution in Equation (37).

3.2.1. Stratified Resampling

In the original version of the LMCPF described in Walter et al. [32], the particle weights are approximated by those of the LAPF defined in Equation (23). In this work, the exact Gaussian mixture weights are derived and applied in the resampling step. Furthermore, the effect on the filter performance is discovered. In Kotsuki et al. [39], the exact weights are applied to the Gaussian mixture extension of the LPF [30] and an improvement of the stability of the method is detected with respect to the inflation parameters within an intermediate AGCM.

To reduce the dimensionality, the weights in Equation (40) are transformed and projected in ensemble space. To this end, the sum of the projection P defined in Equation (16) and I−P with the identity matrix I is applied to the exponent of Equation (40). The weights are transformed to

$\begin{array}{ll}{w}^{(l)}=e^{\left(-\frac{1}{2}{(\left[P+(I-P)\right](y-H{x}^{(b,l)}))}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}\left[P+(I-P)\right](y-H{x}^{(b,l)})\right)}& (42)\end{array}$

$\begin{array}{ll}=c_{I-P}·e^{\left(-\frac{1}{2}{(y-H{x}^{(b,l)})}^T{P}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}P(y-H{x}^{(b,l)})\right)}& (43)\end{array}$

whereas c_I−P is defined by

$\begin{array}{ll}{c}_{I-P}:=e^{\left(-\frac{1}{2}{(y-H{x}^{(b,l)})}^T{(I-P)}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}(I-P)(y-H{x}^{(b,l)})\right)}.& (44)\end{array}$

First, the observation minus first guess vector can be reshaped to

$\begin{array}{ll}y-H{x}^{(b,l)}=(y-{ȳ}^{(b)})+({ȳ}^{(b)}-H{x}^{(b,l)})=y-{ȳ}^{(b)}-Y{e}_l& (45)\end{array}$

with the l-th unit vector $e_l\in {ℝ}^L$. The application of the projection matrix to Equation (45) leads to

$\begin{array}{ll}P(y-H{x}^{(b,l)})=Y{A}^{-1}{Y}^T{R}^{-1}\left[(y-{ȳ}^{(b)})-Y{e}_l\right]=Y(C-e_l)& (46)\end{array}$

whereas C denotes the projected observation vector in ensemble space

$\begin{array}{ll}C:=A^{-1}{Y}^T{R}^{-1}(y-{ȳ}^{(b)}).& (47)\end{array}$

With the aid of Equation (45), the application of I − P to observation minus first guess vector yields

$\begin{array}{ll}(I-P)(y-H{x}^{(b,l)})=(I-P)(y-{ȳ}^{(b)})-(I-P)Y{e}_l& (48)\end{array}$

$\begin{array}{l}=(y-{ȳ}^{(b)})-Y{A}^{-1}{Y}^T{R}^{-1}(y-{ȳ}^{(b)})\\ -Y{e}_l+Y{A}^{-1}{Y}^T{R}^{-1}Y{e}_l& (49)\end{array}$

$\begin{array}{ll}=(y-{ȳ}^{(b)})-YC.& (50)\end{array}$

This expression do not depend on l so that c_I−P of Equation (44) is constant and has no impact on the relative weights of the particles [see Equation (43)]. To derive the transformation, the equality

$\begin{array}{ll}{Y}^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}={({\gamma }^{-1}I+Y^T{R}^{-1}Y)}^{-1}{Y}^T{R}^{-1}& (51)\end{array}$

is used. Equation (51) is shown by multiplying

$\begin{array}{ll}({\gamma }^{-1}I+Y^T{R}^{-1}Y)Y^T=Y^T{R}^{-1}({\gamma }^{-1}R+Y{Y}^T)& (52)\end{array}$

from the left with the inverse

$\begin{array}{ll}{({\gamma }^{-1}I+Y^T{R}^{-1}Y)}^{-1}& (53)\end{array}$

and from the right with the inverse matrix

$\begin{array}{ll}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}=R^{-1}{({\gamma }^{-1}I+Y{Y}^T{R}^{-1})}^{-1}.& (54)\end{array}$

The invertibility of γ⁻¹I + Y^*Y and γ⁻¹I + YY^* on N(Y)^⊥, respectively, ${C}(Y)$ follows from Theorem 3.1.8 in Nakamura and Potthast [52]. Y^* denotes the adjoint matrix defined in Equation (17). The first mixed term

$\begin{array}{ll}{(P(y-H{x}^{(b,l)}))}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}(I-P)(y-H{x}^{(b,l)})& (55)\end{array}$

$\begin{array}{ll}={(y-H{x}^{(b,l)})}^T{P}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}(y-H{x}^{(b,l)})& (56)\end{array}$

$\begin{array}{ll}-{(y-H{x}^{(b,l)})}^T{P}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}P(y-H{x}^{(b,l)})& (57)\end{array}$

reduce to zero if the equality

$\begin{array}{ll}{P}^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}=P^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}P& (58)\end{array}$

holds. Starting with the right hand side of the equation, we obtain

$\begin{array}{l}{P}^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}P=R^{-1}Y{A}^{-1}({\gamma }^{-1}I\\ +Y^T{R}^{-1}Y{)}^{-1}{Y}^T{R}^{-1}Y{A}^{-1}{Y}^T{R}^{-1}& (59)\end{array}$

$\begin{array}{ll}=R^{-1}Y{A}^{-1}{({\gamma }^{-1}I+Y^T{R}^{-1}Y)}^{-1}{Y}^T{R}^{-1}& (60)\end{array}$

$\begin{array}{ll}=P^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}& (61)\end{array}$

with the application of equality [Equation (51)] in the first and last step and the definition of A in Equation (18) in the second step. The reduction of the second mixed term to zero can be proven following an analog approach. The combination of the formulation in Equation (46) with Equation (51) leads to the exponent

$\begin{array}{ll}{(P(y-H{x}^{(b,l)}))}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}P(y-H{x}^{(b,l)})& (62)\end{array}$

$\begin{array}{ll}={(C-e_l)}^T{Y}^T{\gamma }^{-1}{({\gamma }^{-1}R+Y{Y}^T)}^{-1}Y(C-e_l)& (63)\end{array}$

$\begin{array}{ll}={(C-e_l)}^T{\gamma }^{-1}{({\gamma }^{-1}I+Y^T{R}^{-1}Y)}^{-1}{Y}^T{R}^{-1}Y(C-e_l)& (64)\end{array}$

Finally, the particle weights in ensemble space yield

$\begin{array}{ll}{w}_{\text{ens}}^{(l)}=e^{-\frac{1}{2}{(C-e_l)}^T{\gamma }^{-1}{({\gamma }^{-1}I+A)}^{-1}A(C-e_l)},l=1,\dots ,L.& (65)\end{array}$

with the relation $w_{\text{ens}}^{(l)}=c_{I-P}·w^{(l)}$ to the weights in model space with c_I−P defined in Equation (44). In the following, the normalized weights

$\begin{array}{ll}{w}^{(a,l)}=L·\frac{w_{\text{ens}}^{(l)}}{{\sum }_{l=1}^L{w}_{\text{ens}}^{(l)}},l=1,\dots ,L& (66)\end{array}$

are used which sum up to L.

Following the approach of stratified resampling [53], uniformly distributed random numbers are used to calculate the frequency of each particle with the aid of the respective accumulated weights. For l = 1, …, L, the accumulated weights are defined by

$\begin{array}{ll}{w}_{a{c}_0}=0,w_{a{c}_l}=w_{a{c}_{l-1}}+w^{(a,l)}.& (67)\end{array}$

Then, L on the interval [0, 1] uniformly distributed random numbers r_l are generated to introduce the variable R_l = l − 1 + r_l for l = 1, …, L. The approach of stratified resampling then leads to the matrix $\stackrel{⌣}{W}\in {\left\{0,1\right\}}^{L\times L}$ with entries

$\begin{array}{ll}\stackrel{⌣}{W}=\{\begin{array}{ll}1,& R_l\in (w_{a{c}_{i-1}},w_{a{c}_i}]\\ 0,& \text{else}\end{array}& (68)\end{array}$

where the number of ones in the i-th row indicates how often the i-th particle is chosen.

3.2.2. Shift of Particles

Compared to the LAPF, the Gaussian mixture representation leads to a shift of the particles toward the observation. The shift resembles the shift of the mean of all particles toward the observation in ensemble space in the LETKF (see [4]). The new location of the particles is described by the expectation vectors in Equation (39) of the kernels of the posterior Gaussian mixture distribution. To carry out the particle shift, the transformed formula of Equation (39) is derived. First, the representation of the analysis covariance matrix B^(a) defined in Equation (38) is derived. To this end, the analysis covariance matrix is reshaped to the known representation

$\begin{array}{ll}{B}^{(a)}={(I-B{H}^T(R+HB{H}^T))}^{-1}B.& (69)\end{array}$

The equivalence of both formulas is proven in Lemma 5.4.2 in Nakamura and Potthast [52] for example. With the help of the definition of B in Equation (33), the representation can further reformulated to

$\begin{array}{ll}{B}^{(a)}=(I-\gamma X{X}^T{H}^T{(R+H\gamma X{X}^T{H}^T)}^{-1}H)\gamma X{X}^T& (70)\end{array}$

$\begin{array}{ll}=\gamma X(I-\gamma Y^T{(R+\gamma Y{Y}^T)}^{-1}Y)X^T& (71)\end{array}$

$\begin{array}{ll}=\gamma X(I-Y^T{({\gamma }^{-1}R+Y{Y}^T)}^{-1}Y)X^T.& (72)\end{array}$

The application of equality Equation (51) in Equation (72) in combination with the definition of A (Equation (18)) leads to

$\begin{array}{ll}{B}^{(a)}=\gamma X(I-{({\gamma }^{-1}I+A)}^{-1}A)X^T& (73)\end{array}$

$\begin{array}{ll}=\gamma X({({\gamma }^{-1}I+A)}^{-1}({\gamma }^{-1}I+A-A))X^T& (74)\end{array}$

$\begin{array}{ll}=X{({\gamma }^{-1}I+A)}^{-1}{X}^T.& (75)\end{array}$

so that the analysis covariance matrix in ensemble space is given by

$\begin{array}{ll}{B}_{\text{ens}}^{(a)}:={({\gamma }^{-1}I+A)}^{-1}.& (76)\end{array}$

The insertion of Equation (75) in the definition of x^(a,l) in Equation (39) yields

$\begin{array}{ll}{x}^{(a,l)}=x^{(b,l)}+X{({\gamma }^{-1}I+A)}^{-1}{X}^T{H}^T{R}^{-1}(y-H{x}^{(b,l)})& (77)\end{array}$

$\begin{array}{ll}={\stackrel{-}{x}}^{(b)}+x^{(b,l)}-{\stackrel{-}{x}}^{(b)}X{({\gamma }^{-1}I+A)}^{-1}{Y}^T{R}^{-1}(y-{ȳ}^{(b)}-Y{e}_l).& (78)\end{array}$

The second step results from the application of Equation (45). The equation can be further reshaped with the equality $x^{(b,l)}-{\stackrel{-}{x}}^{(b)}=X{e}_l$ and the multiplication of I = AA⁻¹, i.e.,

$\begin{array}{ll}{x}^{(a,l)}={\stackrel{-}{x}}^{(b)}+X(e_l+{({\gamma }^{-1}I+A)}^{-1}A{A}^{-1}{Y}^T{R}^{-1}(y-{ȳ}^{(b)}-Y{e}_l))& (79)\end{array}$

$\begin{array}{ll}={\stackrel{-}{x}}^{(b)}+X(e_l+{({\gamma }^{-1}I+A)}^{-1}A(C-e_l)).& (80)\end{array}$

The last formulation results from the definition of the projected observation vector C given in Equation (47) and the definition of A in Equation (18). The ensemble representation of the analysis expectation is then given by

$\begin{array}{ll}{\beta }^{(a,l)}:=e_l+{({\gamma }^{-1}I+A)}^{-1}A(C-e_l)\in {ℝ}^L.& (81)\end{array}$

Since the l-th unit vector $e_l\in {ℝ}^L$ denotes the l-th background particle in ensemble space, the second summand denotes the shift vectors, i.e.,

$\begin{array}{ll}{\beta }^{(\text{shift},l)}:={({\gamma }^{-1}I+A)}^{-1}A(C-e_l)\in {ℝ}^L.& (82)\end{array}$

All shift vectors are taken together in the matrix

$\begin{array}{ll}{W}^{(\text{shift})}:=\left({\beta }^{(\text{shift},1)},\dots ,{\beta }^{(\text{shift},L)}\right)\in {ℝ}^{L\times L}.& (83)\end{array}$

3.2.3. Draw Particles From Gaussian Mixture Distribution

In the last part of the LMCPF method the analysis ensemble is perturbed to increase the variability. To this end, new particles are drawn from a Gaussian distribution around each shifted particle which was previously selected. If a particle is selected multiple times, the same amount of particles is drawn from the respective Gaussian distribution. This approach equals the generation of L particles following the Gaussian mixture distribution in ensemble space, i.e.,

$\begin{array}{r}{p}_{\text{ens}}^{(a)}(\beta ):=c_{\text{ens}}^{(a)}{\displaystyle \sum _{l=1}^L}{e}^{-\frac{1}{2}{(\beta -{\beta }^{(a,l)})}^T{(\sigma {(\rho )}^2{B}_{\text{ens}}^{(a)})}^{-1}(\beta -{\beta }^{(a,l)})},\\ \beta \in {ℝ}^L.& (84)\end{array}$

The covariance matrix of each Gaussian is inflated by the factor σ(ρ) ∈ ℝ_>0 to control the ensemble spread. The variable ρ denotes the inflation factor implemented in the LETKF method (see [4]), which follows an ansatz introduced by Desroziers et al. [55] and Li et al. [45]. Based on statistics of observations minus background

$\begin{array}{ll}{d}^{o-b}=y-H{\stackrel{-}{x}}^{(b)}& (85)\end{array}$

an adaptive inflation factor is calculated (see [55] or section e on page 352f. of Potthast et al. [31]), i.e.,

$\begin{array}{ll}\tilde{\rho }=\frac{{(d^{o-b})}^T{d}^{o-b}-\text{trace}(R)}{\text{trace}(HB{H}^T)}.& (86)\end{array}$

To smooth the factor over time, the formula

$\begin{array}{ll}\rho =\alpha \tilde{\rho }+(1-\alpha ){\rho }_{\text{old}}& (87)\end{array}$

is applied for some α ∈ [0, 1] and the inflation factor ρ_old of the previous time step. In the LMCPF method as well as the LAPF method, the inflation factor ρ of the LETKF method is scaled. The factor σ(ρ) is derived by

$\begin{array}{ll}\sigma (\rho ):=\{\begin{array}{ll}{c}_0,& \rho <{\rho }^{(0)},\\ c_0+(c_1-c_0)·\frac{\rho -{\rho }^{(0)}}{{\rho }^{(1)}-{\rho }^{(0)}},& {\rho }^{(0)}\le \rho \le {\rho }^{(1)},\\ c_1,& \rho >{\rho }^{(1)}\end{array}& (88)\end{array}$

with parameters ${\rho }^{(0)},{\rho }^{(1)}\in {ℝ}_{+}$ and c₀, c₁ ∈ ℝ₊. In the LETKF method, the analysis ensemble is inflated around the analysis ensemble mean. In the LAPF and LMCPF method, particles are resampled from the background ensemble, shifted (in case of the LMCPF) and then randomly perturbed to increase the ensemble variability. Due to these differences in the multiplicative inflation approach, the application of a scaled version of ρ is necessary and yielded better results in experiments. The boundaries c₀ and c₁ are tuning parameters. Due to the random drawing around each resampled particle, the parameters c₀ and c₁ should be chosen smaller than the parameters ρ⁽⁰⁾, ρ⁽¹⁾ in the LETKF method. These parameters describe the upper and lower bound of ρ.

All in all, the steps of selecting, moving and drawing can be combined in the matrix W_LMCPF, i.e.,

$\begin{array}{ll}{W}_{\text{LMCPF}}:=\stackrel{⌣}{W}+W^{(\text{shift})}\stackrel{⌣}{W}+\sigma (\rho )·{\left[B_{\text{ens}}^{(a)}\right]}^{1/2}·Z.& (89)\end{array}$

with $\stackrel{⌣}{W}$ defined in Equation (68), W^(shift) following Equation (83) and a random matrix Z ∈ ℝ^L×L with standard normally distributed random numbers as entries. Then, the full analysis ensemble is obtained by

$\begin{array}{ll}{(x^{(a,l)})}_{l=1,\dots ,L}={\stackrel{-}{x}}^{(b)}·𝟙+X·W_{\text{LMCPF}}& (90)\end{array}$

where 𝟙 ∈ ℝ^1×L describes a row vector with ones as entries and X the ensemble pertubation matrix defined in Equation (11).

In Feng et al. [56], two nonlinear filters are compared which can preserve the first and second moments of the classical particle filter. First, the local particle filter in its version introduced in Poterjoy et al. [57] represent a localized adaption of the classical particle filter. Second, the local nonlinear ensemble transform filter (LNETF; [16]) is an approximation to the classical particle filter as well but instead of a classical resampling step a deterministic square root approach is followed. This is based on ideas of LETKF. Compared to the local particle filter and LNETF, the LMCPF uses a Gaussian mixture probability density function to approximate the background. With the stratified resampling step the particles are resampled following the posterior distribution, which is exact for Gaussian mixtures and Gaussian observation error. Due to the assumption of Gaussian mixture densities, the resampled particles are shifted which results in the exact mean vectors of the Gaussians of the posterior pdf, and also, temporarily, the exact covariances. To increase the variability of the ensemble, new particles are drawn from the posterior distribution as follows. Around each particle, new particles are randomly drawn from a Gaussian distribution with the exact mean vector and the exact covariance multiplied with an inflation factor. In contrast to the local particle filter, there is no rescaling of the ensemble applied in the LMCPF method. That means, the LMCPF will preserve the moments of a Gaussian mixture filter approximately up to sampling errors and inflation.

3.3. Localized Ensemble Transform Kalman Filter

The Localized Ensemble Transform Kalman Filter (LETKF) is first introduced in Hunt et al. [4] and is widely used in numerical weather prediction (e.g., [58]). The LETKF is based on equations of the Ensemble Kalman Filter (EnKF; [1, 3, 59]) transformed and performed in ensemble space. As the LAPF and LMCPF the observation error is chosen to be Gaussian distributed with the pdf described in Equation (10). In contrast to the methods described previously, this method assumes the background ensemble to represent a Gaussian distribution as well, i.e.,

$\begin{array}{ll}{p}^{(b)}(x):=c^{(b)}·e^{-\frac{1}{2}{(x-{\stackrel{-}{x}}^{(b)})}^T{G}^{-1}(x-{\stackrel{-}{x}}^{(b)})},x\in {ℝ}^n.& (91)\end{array}$

G denotes the estimated background covariance matrix following Equation (33) with γ = 1/(L − 1), i.e.,

$\begin{array}{ll}G:=\frac{1}{L-1}X{X}^T\in {ℝ}^{n\times n}.& (92)\end{array}$

To distinguish from the more general version of the covariance matrix introduced in Section 3.2 about the LMCPF method, the standard covariance estimator is named G. The transformed version in ensemble space—which is spanned by the columns of X in Equation (11)—is then given by

$\begin{array}{ll}{G}_{\text{ens}}:=\frac{1}{L-1}{I}_L\in {ℝ}^{L\times L}& (93)\end{array}$

with the L × L - identity matrix I_L. The application of Bayes' formula (9) to the background distribution p^(b) and the observation error pdf Equation (10) leads to the Gaussian analysis pdf

$\begin{array}{ll}{p}^{(a)}(x)=c^{(a)}{e}^{\left(-\frac{1}{2}{(x-{\stackrel{-}{x}}^{(a)})}^T{(G^{(a)})}^{-1}(x-{\stackrel{-}{x}}^{(a)})\right)}& (94)\end{array}$

with the covariance matrix

$\begin{array}{ll}{G}^{(a)}={(G^{-1}+H^T{R}^{-1}H)}^{-1}& (95)\end{array}$

and the expectation vector

$\begin{array}{ll}{\stackrel{-}{x}}^{(a)}={\stackrel{-}{x}}^{(b)}+G^{(a)}{H}^T{R}^{-1}(y-H{\stackrel{-}{x}}^{(b)}).& (96)\end{array}$

The derivation can be found for example in Nakamura and Potthast [52] or in Evensen et al. [3]. A more common formulation of the update equations can be derived by rearrangement of Equations (95) and (96). Following Lemma 5.4.2 in Nakamura and Potthast [52], an equivalent form of the covariance matrix is given by

$\begin{array}{ll}{G}^{(a)}={(I_n-G{H}^T(R+HG{H}^T))}^{-1}G={(I_n-K)}^{-1}G& (97)\end{array}$

with the Kalman gain matrix K ∈ ℝ^n×n and identity matrix $I_n\in {ℝ}^{n\times n}$. The covariance matrix in ensemble space is derived in Equations (70)–(98), i.e.,

$\begin{array}{ll}{G}_{\text{ens}}^{(a)}:={((L-1)·I_L+A)}^{-1}& (98)\end{array}$

with identity matrix $I_L\in {ℝ}^{L\times L}$ and A defined in Equation (18). The insertion of Equation (75) applied to $G_{\text{ens}}^{(a)}$ in the definition of ${\stackrel{-}{x}}^{(a)}$ in Equation (96) leads to

$\begin{array}{ll}{\stackrel{-}{x}}^{(a)}={\stackrel{-}{x}}^{(b)}+X{((L-1)·I+A)}^{-1}{X}^T{H}^T{R}^{-1}(y-H{\stackrel{-}{x}}^{(b)})& (99)\end{array}$

$\begin{array}{ll}={\stackrel{-}{x}}^{(b)}+X·G_{\text{ens}}^{(a)}{Y}^T{R}^{-1}(y-{ȳ}^{(b)}).& (100)\end{array}$

That means, the analysis mean in ensemble space is given by

$\begin{array}{ll}{\stackrel{-}{\beta }}^{(a)}:=G_{\text{ens}}^{(a)}{Y}^T{R}^{-1}(y-{ȳ}^{(b)})\in {ℝ}^L.& (101)\end{array}$

There are multiple approaches to obtain the full analysis ensemble in dependence on the analysis covariance matrix. The LETKF is based on the square root method. The weighting matrix W_LETKF is defined by the square root

$\begin{array}{ll}{W}_{\text{LETKF}}={\left[(L-1)G_{\text{ens}}^{(a)}\right]}^{\frac{1}{2}}& (102)\end{array}$

which is related to the covariance matrix by

$\begin{array}{ll}{G}_{\text{ens}}^{(a)}=(L-1)W_{\text{LETKF}}{(W_{\text{LETKF}})}^T.& (103)\end{array}$

Additionally, the posterior covariance is inflated. To this end, an adaptive inflation factor ρ based on observation minus background statistics is derived by Equations (86) and (87). Then, the full analysis ensemble is calculated by

$\begin{array}{ll}{(x^{(a,l)})}_{l=1,\dots ,L}={\stackrel{-}{x}}^{(a)}·𝟙+X·\sqrt{\rho }·W_{\text{LETKF}}& (104)\end{array}$

where 𝟙 ∈ ℝ^1×L describes a row vector with ones as entries and X the ensemble pertubation matrix defined in Equation (11).

4. Study of Individual Steps of LMCPF

The LMCPF method can be divided in three parts: stratified resampling (Section 3.2.1), shift of particles (Section 3.2.2) and drawing new particles from a Gaussian mixture distribution (Section 3.2.3). In this section, we discuss the behavior of the ensemble during the different parts of a single data assimilation step performed by the LMCPF method.

4.1. Stratified Resampling

The stratified resampling step represents the main idea of the particle filter method. Only the particles with sufficient weight are chosen. In the LAPF and LMCPF methods, the resampling step is carried out in the ensemble space in order to reduce the dimension and prevent filter collapse. This step occurs in both methods but different particle weights are used. The relative weights of the LAPF Equation (26) depend on the distance of the particles to the observation and the observation error covariance. In case of the LMCPF, the exact weights Equation (66) additionally depend on the particle uncertainty parameter κ.

Figure 2 illustrates the relation between these two weights. If κ tends to zero, the normalized Gaussian mixture weights tend to the classical particle filter weights, which are used in the LAPF and were previously used in the LMCPF method. The particle weights are derived from the case illustrated in Figure 3. The approximate weights in Figure 2 suggest that in the LAPF method only one particle would have been chosen as one particle gets all the weight. Furthermore, the exact weights approach each other for larger κ. That means, more particles would be chosen in the stratified resampling step for larger κ. If κ tends to infinity, the exact weights tend to one so that the probability to sample a particle is the same for each particle.

FIGURE 2

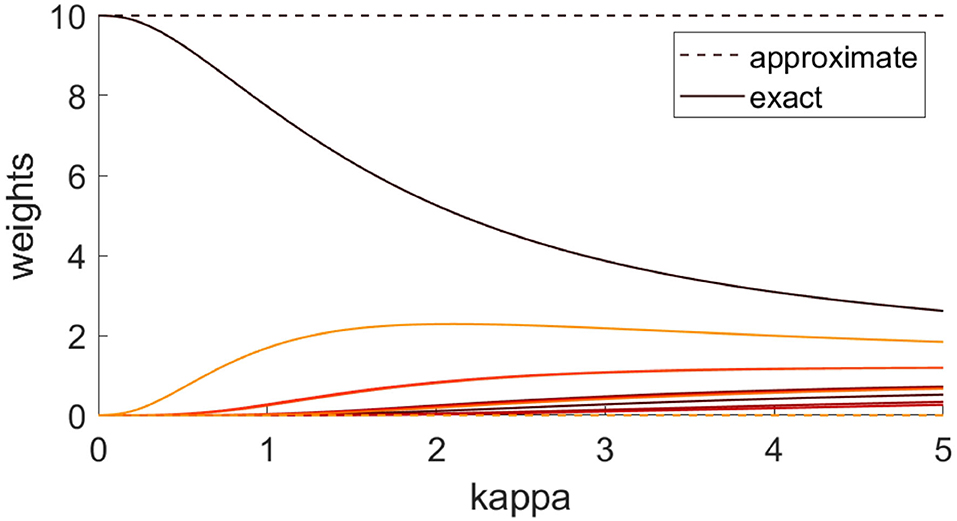
Figure 2. The exact Gaussian mixture weights w^(a,l) Equation (66) are compared against the approximate weights ${\tilde{w}}^{(a,l)}$ Equation (26), which are used in the LAPF method. Each color denotes the pair of weights (approximate and exact) for one of the 10 particles. The particle weights come from the scenario illustrated in Figure 3. For the exact weights, the particle uncertainty parameter κ is varied.

FIGURE 3

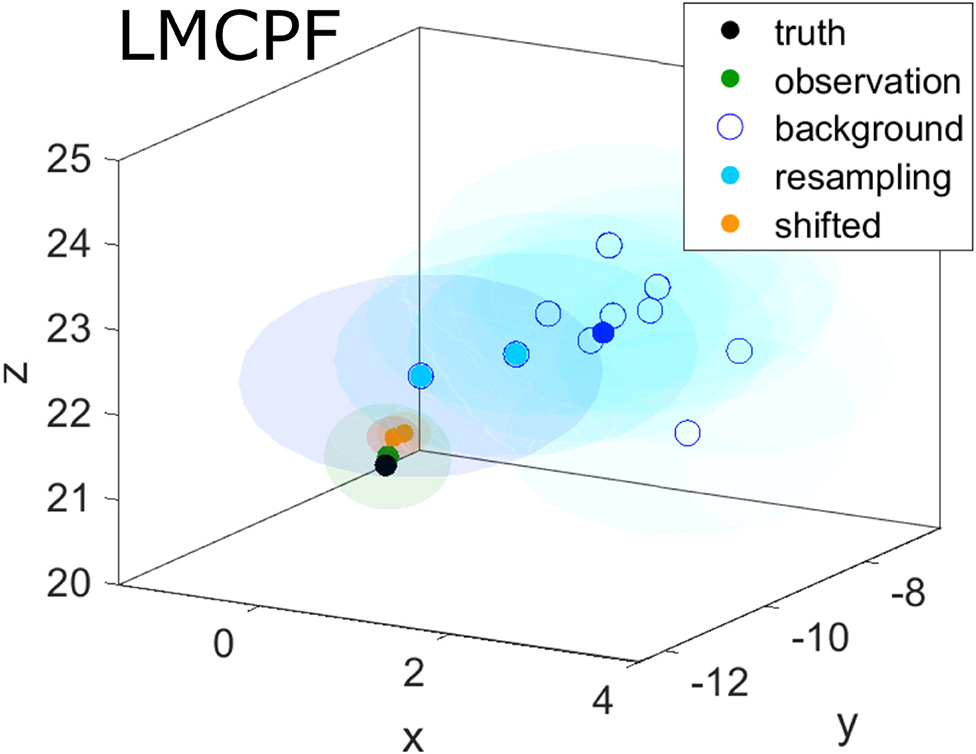
Figure 3. A single assimilation step is carried out with the LMCPF method. The observation (green point) is located outside of the background ensemble of size L = 10 with the ensemble mean represented by the dark blue point. The particles chosen in the stratified resampling step (light blue points) are shifted toward the observation (orange points). The particle uncertainty parameter κ is set to one. The shaded areas denote Gaussian ellipsoids with respect to the corresponding covariance matrices. Darker colored ellipsoids around the background particles denote larger weights w^(a,l) defined in Equation (66).

Since the relative weights depend on the distance of the particles to the observation, these background particles, which are close to the observation, are chosen. This is illustrated in Figure 3 as well as in the example with a bimodal background distribution in Figure 4. In the bimodal case, all the particles of the mode close to the observation are resampled. In both examples, the observation is located outside of the background ensemble. After the stratified resampling step, the particles are still far from the observation. In Figure 4B, the shifted ensemble mean of the LETKF method is even closer to the observation than the nearest background particles. That leads to the idea, to use a Gaussian mixture representation in the LMCPF, to include the shifting step of the LETKF, which is discussed in the next part.

FIGURE 4

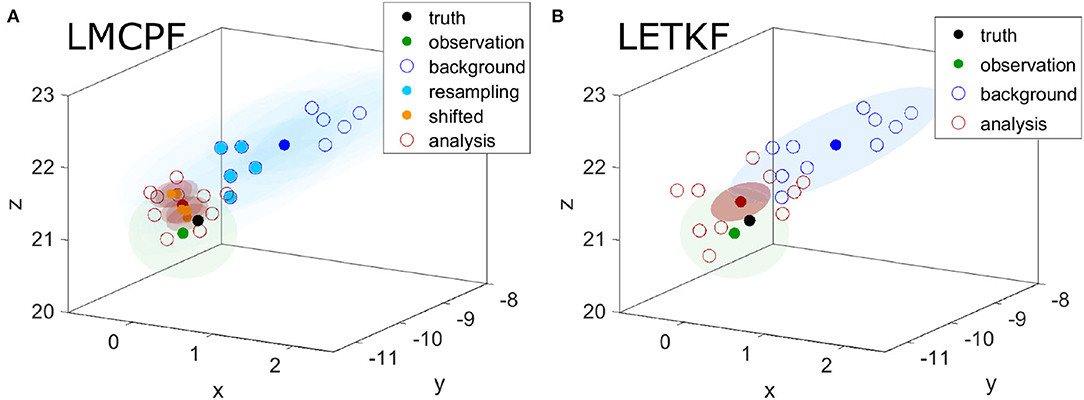
Figure 4. The background ensemble (blue circles) is generated from a bimodal distribution and the observation (green point) is located near one of the modes. The dark blue point illustrates the background ensemble mean. In (A), the assimilation step is performed with the LMCPF method and in (B) with the LETKF method. The light blue points in (A) illustrate the resampled particles and the orange points describe the shifted particles for κ = 1. The analysis particles resulting from LMCPF and LETKF are represented by the red circles and the red point illustrates the analysis ensemble mean. In the LMCPF method, these particles are randomly generated from Gaussian distributions with the shifted particles as expectation vectors. The shaded areas denote Gaussian ellipsoids with respect to the corresponding covariance matrices.

4.2. Shift of Particles

In contrast to the ensemble Kalman filter method, particle filters do not shift particles toward the observation but only choose the nearest ones, so that the ensemble mean is pulled toward the observation. In the LMCPF, each remaining particle is shifted as the ensemble mean in the ensemble Kalman filter method. Furthermore, the shift is affected by the particle uncertainty described by the background covariance matrix. Modification of the parameter κ in Equation (34) yields changes in the valuation of the particle uncertainty. If κ is set to a larger value, there is less confidence in the background ensemble. Hence, the confidence in the observation ascends, relatively seen. Finally, this results in a stronger shift of the remaining particles toward the observation. To validate this intuition mathematically, the spectral norm of the posterior covariance matrix

$\begin{array}{ll}{B}_{\text{ens}}^{(a)}={\left(\frac{L-1}{\kappa }{I}_L+A\right)}^{-1}& (105)\end{array}$

with κ > 0, the identity matrix $I_L\in {ℝ}^{L\times L}$ and projected observation error covariance matrix

$\begin{array}{ll}A=Y^T{R}^{-1}Y\in {ℝ}^{L\times L}& (106)\end{array}$

is observed. The spectral norm is induced from the euclidean vector norm and is defined by the square root of the maximal eigenvalue of A^TA. In the case of complex matrices, the transpose matrix is replaced by the adjoint matrix. Matrix A is symmetric as the observation error covariance matrix R is a symmetric matrix by definition. Furthermore, every symmetric matrix is normal. Let be U ∈ ℝ^L×L the matrix with eigenvectors of the normal matrix A as columns and D ∈ ℝ^L×L the diagonal matrix with the respective eigenvalues as diagonal entries ordered from maximal to minimal eigenvalue such that

$\begin{array}{ll}A=UD{U}^T& (107)\end{array}$

holds. Since U is a unitary matrix, i.e., $U{U}^T=I_L$, the inverse term of $B_{\text{ens}}^{(a)}$ can be reshaped to

$\begin{array}{ll}\frac{L-1}{\kappa }{I}_L+UD{U}^T=U\left(\frac{L-1}{\kappa }{I}_L+D\right)U^T.& (108)\end{array}$

That means, U also describes the unitary matrix of the eigenvalue decomposition of the inverse of $B_{\text{ens}}^{(a)}$ and the eigenvalues are given by

$\begin{array}{ll}{\lambda }_i=\frac{L-1}{\kappa }+{\mu }_i,i=1,\dots ,L& (109)\end{array}$

with eigenvalues (μ_i)_i of A. We remark that μ_i > 0 holds for all i = 1, …, L as A is positive definite. The spectral norm of the inverse matrix equals the inverse of the smallest eigenvalue min{λ_i|i = 1, …, L}, i.e.,

$\begin{array}{ll}{\Vert B_{\text{ens}}^{(a)}\Vert }_2={\left(\frac{L-1}{\kappa }+{\displaystyle \underset{i=1,\dots ,L}{min}}({\mu }_i)\right)}^{-1}.& (110)\end{array}$

On the basis of this term, we can easily see that larger values for κ leads to a larger spectral norm of B^(a).

Furthermore, the shift vectors are defined by

$\begin{array}{ll}{\beta }^{(\text{shift},l)}={\left(\frac{L-1}{\kappa }{I}_L+A\right)}^{-1}A(C-e_l),l=1,\dots ,L.& (111)\end{array}$

To discover the shifting strength for different κ, the spectral norm of $B_{\text{ens}}^{(a)}$ multiplied with A is examined. With the eigenvalue decomposition of A, we obtain

$\begin{array}{l}{\left(\frac{L-1}{\kappa }{I}_L+UD{U}^T\right)}^{-1}UD{U}^T\\ ={(U^T)}^{-1}{\left(\frac{L-1}{\kappa }{I}_L+D\right)}^{-1}{U}^{-1}UD{U}^T& (112)\end{array}$

$\begin{array}{ll}=U{\left(\frac{L-1}{\kappa }{I}_L+D\right)}^{-1}D{U}^T& (113)\end{array}$

which follows from the property U⁻¹ = U^T of a unitary matrix U. This results in the spectral norm

$\begin{array}{ll}{\Vert B_{\text{ens}}^{(a)}A\Vert }_2={\displaystyle \underset{i=1,\dots ,L}{max}}\left\{{\left(\frac{L-1}{\kappa }+{\mu }_i\right)}^{-1}{\mu }_i\right\}& (114)\end{array}$

which gets larger for greater κ.

In Figure 3, the shift of the two particles, which are chosen in the stratified resampling step results in particles close to the observation even for κ = 1. For this parameter choice, the background error covariance matrix B equals the standard covariance estimator. The shaded areas around the dots describe the uncertainty. Compared to the background uncertainty, the observation error covariance matrix R = 0.3²·I is smaller, which explains the strong shift toward the observation. In comparison, the difference between background and observation uncertainty is smaller in the bimodal case in Figure 4. This results in shifted particles, which are not as close to the observation as in Figure 3.

4.3. Draw Particles From Gaussian Mixture Distribution

In the LMCPF as well as in the LAPF method, new particles are drawn from a Gaussian mixture distribution but different covariance matrices are applied. In the LAPF, an inflated version of the background error covariance matrix in ensemble space 1/(L − 1) · I is used. The covariance matrix is adapted by the spread control factor σ(ρ)², which is derived in Equation (88). In contrast, the newly derived covariance matrix $B_{\text{ens}}^{(a)}$ Equation (98) in ensemble space is applied in an inflated version in the LMCPF.

The draw from a Gaussian mixture distribution is carried out by drawing new particles from Gaussian distributions around each chosen particle. For all Gaussian distributions, the same covariance matrix is applied. In case of the LMCPF, the spectral norm of the covariance matrix $B_{\text{ens}}^{(a)}$ results in a larger value if the particle uncertainty parameter κ is set to a greater value. This counteracts the effect that a stronger shift toward the observation vector leads to smaller distances among the particles.

Figure 4 shows the results of one LMCPF and LETKF step for a bimodal background distribution. The Gaussian ellipsoids cover random draws from the same three dimensional distribution with a high probability. Nevertheless, the analysis particles of LMCPF and LETKF are located outside of the ellipsoids. The particles are resampled in the L − 1-dimensional ensemble space and not in the three-dimensional model space. This leads to a wider analysis ensemble for L > n than we would obtain by drawing in the n-dimensional model space. In practice, the dimension of the model space is much larger than the dimension of the ensemble space so that this case does not occur.

In comparison to the particle filter method, the analysis ensemble derived by the LETKF method maintains the structure of the background ensemble and is only shifted and contracted. In that case, the ensemble mean, which represents the state estimate, is not located in an area with high probability density but in between the two modes (see Figure 4B). The analysis ensemble aims to approximate the uncertainty distribution of the state estimate. This more realistic uncertainty estimation is one of the advantages of the particle filter methods over the ensemble Kalman filter.

5. Results for Longer Assimilation Periods

In the following, the results of longer data assimilation experiments for the Lorenz 1963 model as well as the 40-dimensional Lorenz 1996 model are discussed. Beside the comparison of root-mean-square errors following Equations (115) and (116) for different methods, the development of the effective ensemble size [see Equations (119) and (120)] in the particle filter methods are observed. For both models, the initial ensemble size is set to L = 20 in the following experiments. Further parameters of the model configuration and experimental setup, which are used in this section, are summarized in Table 1.

TABLE 1

Table 1. Parameters of the model configuration and experimental setup for the Lorenz 1963 (L63) and 1996 (L96) models.

For the 40-dimensional Lorenz 1996 model, the methods are used in a localized form, as described at the beginning of Section 3. The localization depends on the localization radius r_loc, which affects the number of observations used in the analysis step. Moreover, the optimal localization radius depends on the method as well as the model parameters. For the LETKF method, we choose r_loc in between 4 and 7 in depending on the model error, the integration time Δ_t and the observation noise after the investigation of different localization radii. With respect to the LMCPF with exact weights, the localization radius r_loc is set to a value between 4 and 6 in the experiments of this section. In addition, experiments revealed larger effective ensemble sizes for smaller localization radii. Moreover, an automatic restart was introduced for all methods to catch extreme cases.

5.1. Definition of RMSE and Effective Ensemble Size

To compare different data assimilation methods, a measure is needed. In general, the goodness of a DA method is associated with the distance between the background or analysis state estimate and the truth, or alternatively the observation if the truth is not available. For that purpose, the normalized euclidean norm or root-mean-square-error (RMSE) is used to calculate the distance of background or analysis state estimate and the truth at time t_k, i.e.,

$\begin{array}{ll}{e}_k^{(b)}:=e^{(b)}(t_k)=\frac{1}{\sqrt{n}}{\Vert {\stackrel{-}{x}}_k^{(b)}-x_k^{true}\Vert }_2,& (115)\end{array}$

$\begin{array}{ll}{e}_k^{(a)}:=e^{(a)}(t_k)=\frac{1}{\sqrt{n}}{\Vert {\stackrel{-}{x}}_k^{(a)}-x_k^{true}\Vert }_2,& (116)\end{array}$

where n ∈ ℕ denotes the number of variables of the underlying model and ${\stackrel{-}{x}}_k^{(b)},{\stackrel{-}{x}}_k^{(a)}$ describe the background or analysis ensemble means. For a time period given, where data assimilation is carried out at the measurement points t₁, …, t_K, the averaged errors are denoted by

$\begin{array}{ll}{e}^{(b)}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{e}_k^{(b)},& (117)\end{array}$

$\begin{array}{ll}{e}^{(a)}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{e}_k^{(a)}.& (118)\end{array}$

In terms of particle filter methods, the development of the effective ensemble size is an important quantity to examine the stability of the filter. The effective ensemble size is defined by

$\begin{array}{ll}{L}_{\text{eff}}=\frac{1}{{\displaystyle {\sum }_{l=1}^L}{(w^{(a,l)}/L)}^2}& (119)\end{array}$

with the relative particle weights in ensemble space w^(a,l) of the LMCPF described in Equation (66) or with the classical particle filter weights ${\tilde{w}}^{(a,l)}$ of the LAPF defined in Equation (26). In general, particle filter methods suffer in high-dimensional spaces from filter degeneracy due to the finite ensemble size (see [6]). In that case, the effective ensemble size tends to one, which means that the weights become strongly non-uniform. With respect to the 40-dimensional Lorenz 1996 model, the effective ensemble size is computed at each localization point and the average at each data assimilation cycle is derived. The mean effective ensemble size over all localization points is denoted by

$\begin{array}{ll}{\stackrel{-}{L}}_{\text{eff}}=\frac{1}{P}{\displaystyle \sum _p}{L}_{\text{eff}}(p)& (120)\end{array}$

where P describes the number of localization points (P = n for Lorenz 1996) and L_eff is calculated at each localization point using the respective weights.

5.2. LMCPF Results in Dependence of the Particle Uncertainty Parameter κ

The results of data assimilation methods vary in dependence of the model parameters integration time Δ_t of the dynamical model, the model error between true and model run and observation noise σ_obs. The chaotic behavior of the Lorenz systems means that small differences in the initial conditions can lead to significantly different future trajectories. In average, greater propagation or forecast time intervals result in greater perturbations of the model run. The nonlinearity of the Lorenz models causes the propagation of some Gaussian distributed ensemble to result in non-Gaussian structures even at shorter lead times.

Figure 5 shows the integration of a Gaussian distributed ensemble over time with Lorenz 1963 model dynamics. For Δ_t = 0.3 and Δ_t = 0.5, the resulting ensemble is clearly non-Gaussian so that the main assumption of the Kalman filter to the background distribution does not hold. As a consequence, we expect improvements of LMCPF over LETKF especially for longer forecast times.

FIGURE 5

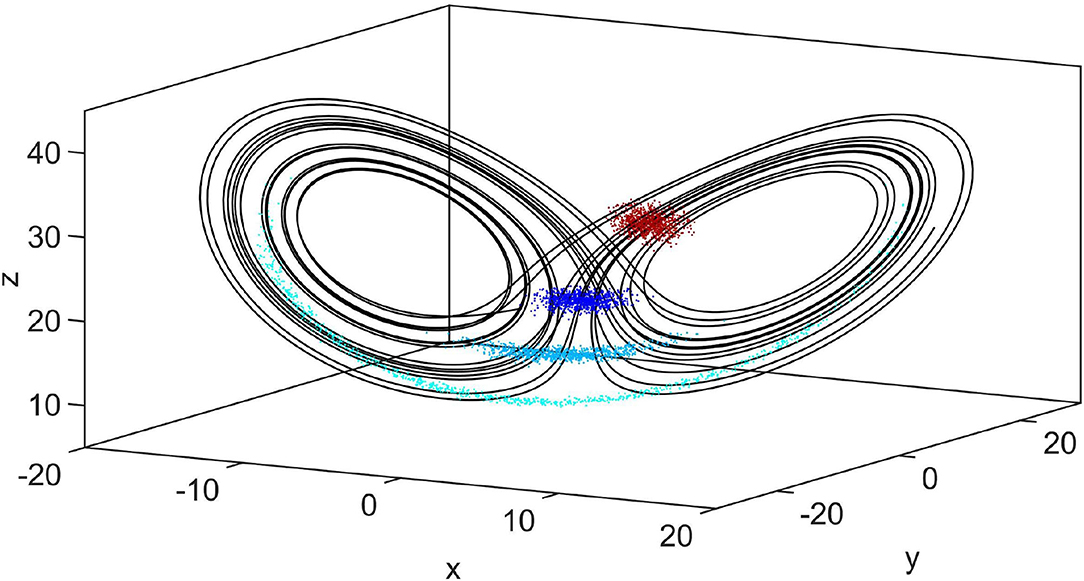
Figure 5. A thousand particles drawn from a Gaussian distribution (red points) are integrated in time with respect to the Lorenz 1963 model dynamics for Δ_t = 0.15 (blue), Δ_t = 0.3 (lightblue) and Δ_t = 0.5 (cyan) time units.

Moreover, model error means that true states, respectively, observations are generated by a slightly different dynamical model than the first guess from the previous analysis ensemble. For the Lorenz systems, the model error is produced by the application of different values for the Prandtl number σ (Lorenz 1963) and for the forcing term F (Lorenz 1996). In NWP systems, the atmospheric model is known to have errors. Hence, it is important to investigate the application of data assimilation methods in case of model error. Naturally, we expect the model run to differ stronger from the true run for greater differences in the model parameters.

In addition, the observation noise σ_obs strongly affects the data assimilation results. As in the case of the model error, this is no surprise, since the observation is used in data assimilation to obtain an analysis state. The LMCPF is quite sensitive to the observation noise because the resampling as well as the shift moves the ensemble toward the observation. To generate the observations for experiments with the Lorenz models, the true trajectory is randomly perturbed at time points, where data assimilation is performed. If some observation is far from the truth by chance, an overestimation of the importance of this observation might lead to worse results of the LMCPF compared to LETKF or LAPF.

There are six parameters in the LMCPF method to adapt the method to model and observation error as well as the integration time. The five parameters ρ₀, ρ₁, c₀, c₁ and α are used to control the spread of the analysis ensemble in the last step, where new particles are drawn from a Gaussian mixture distribution (see Section 3.2.3). But the sixth, the particle uncertainty parameter κ, respectively, γ defined in Equation (34), is the most important parameter since the variable affects the spread of the analysis ensemble as well as the movement of the particles toward the observation.

In the following, the results for LMCPF compared to LETKF are shown for different settings of Lorenz 1963 and 1996. To identify a reasonable particle uncertainty parameter κ, the parameter is varied. In Figure 6, experiments for different forecast lengths Δ_t are performed with respect to the Lorenz 1963 model. The observation error standard deviation is chosen as σ_obs = 0.5 and only the first variable is observed. The true trajectory is generated with the Prandtl number σ^true = 10, while the forecast ensemble is integrated with σ = 12 to introduce model error. For each parameter setting, 1, 000 data assimilation cycles are carried out with both methods, whereas the average errors over the last 900 cycles are computed. That means the first 100 steps are not used. Furthermore, each experiment is repeated ten times with different seeds to generate different random numbers and the average error is reported. The mean background errors [see Equations (117) and (118)] of both methods are compared by

$\begin{array}{ll}\delta =\frac{e_{\text{LETKF}}^{(b)}-e_{\text{LMCPF}}^{(b)}}{e_{\text{LETKF}}^{(b)}}·100.& (121)\end{array}$

Positive values (blue arrays) for δ denote better results for LMCPF than LETKF. Following Figure 5, the background ensemble is less Gaussian distributed for longer forecast lengths. Figure 6 illustrates the improvement of LMCPF over LETKF in particular for Δ_t = 0.5. In case of Δ_t = 0.15, the results for LMCPF are worse than for LETKF. For a longer forecast length, the RMSE of background minus truth is lower than the RMSE of LETKF for a wider range of values for κ.

FIGURE 6

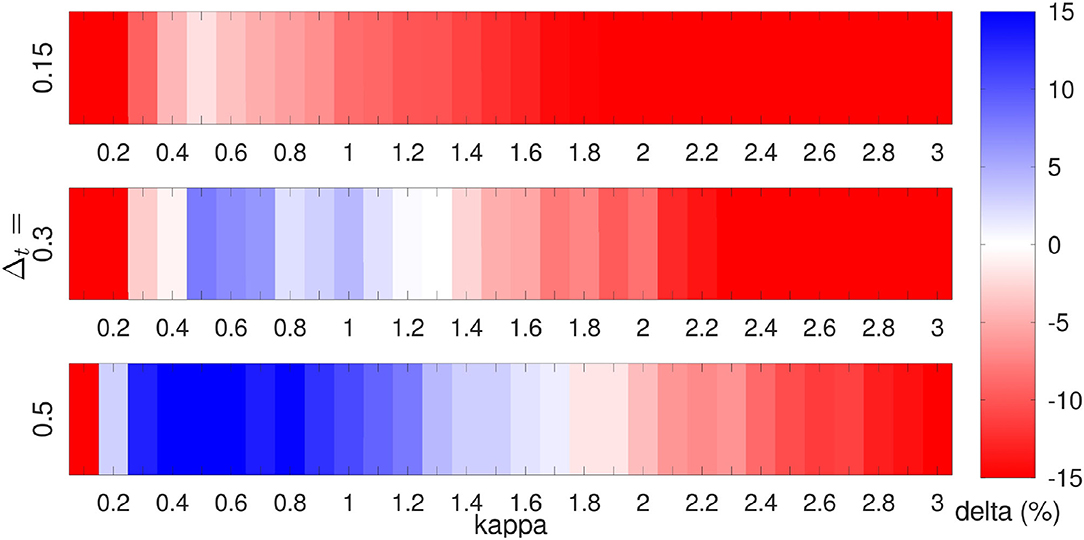
Figure 6. Comparison of background errors of LMCPF and LETKF following Equation (121) for different forecast lengths Δ_t = 0.15, Δ_t = 0.3 and Δ_t = 0.5. Positive values denote a smaller RMSE of truth minus background for the LMCPF method than the LETKF. For each parameter combination, 1, 000 data assimilation steps are carried out for the Lorenz 1963 model whereas the last 900 steps are used to compute the statistics. The experiments are repeated 10 times with different seeds and the average error is reported. The true trajectory is generated with σ^true = 10, the integration of the ensemble of states is performed with σ = 12 and the observation noise equals σ_obs = 0.5. Only the first variable is observed. The ensemble size is set to L = 20 for both methods.

In Figure 7, the results for a range of values of κ are shown for the 40-dimensional Lorenz 1996 model with respect to different model errors. Similar to Figure 6, the background errors of LMCPF and LETKF are compared by Equation (121). One thousand data assimilation cycles are carried out, whereas the first 100 steps are considered as spin-up time and are not used in the computation of the mean errors. Moreover, the experiments are repeated ten times with different random seeds. To receive the results displayed in Figure 7, the truth is generated with the forcing term F^true = 8, while the forecast ensemble is derived with different forcing terms between F = 8 and F = 9.5. In addition, the observation error standard deviation is set to σ_obs = 0.5 and a longer forecast length Δ_t = 0.5 is applied. The results indicate, that in most cases there is some particle uncertainty parameter κ, so that the LMCPF outperforms the LETKF.

FIGURE 7

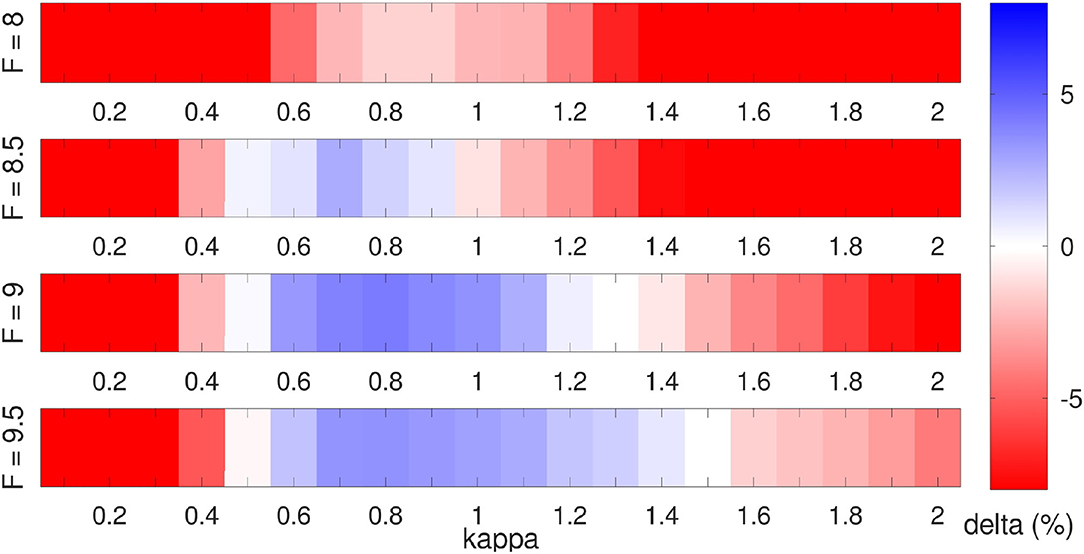
Figure 7. Comparison of background errors of LMCPF and LETKF following Equation (121). Positive values denote a smaller RMSE of truth minus background for the LMCPF method than the LETKF. For each parameter combination, 1, 000 data assimilation steps for the Lorenz 1996 model are carried out whereas the last 900 steps are used to compute the statistics. The experiments are repeated ten times with different seeds and the average error is reported. The true trajectory is generated with F^true = 8, the forecast length is set to Δ_t = 0.5 and the observation noise equals σ_obs = 0.5. Every second variable is observed. The ensemble size is set to L = 20 for both methods.

Following Lei and Bickel [60], longer forecast lengths (Δ_t > 0.4) lead to highly non-Gaussian ensembles for the 40-dimensional Lorenz 1996 model with forcing term F = 8. To verify this, we integrated a standard Gaussian distributed ensemble (L = 10, 000) in time for Δ_t = 0.5 and with forcing term F = 8. The distance of the resulting distribution to a Gaussian distribution with the same mean and variance can be measured by the distance of the skewness and kurtosis to the characteristic values 0 and 3 for skewness and kurtosis of a Gaussian distribution. For the integrated ensemble, we obtain 0.56 as absolute skewness averaged over all N = 40 model variables. The averaged absolute distance of the empirical kurtosis of the integrated ensemble to the characteristic value 3 of a Gaussian distribution is 0.99. This indicates a non-Gaussian ensemble.

An increasing value of F up to 9.5 leads to a larger distance of the background to the true state or the observations which denotes a larger systematic model bias. Figure 7 illustrates that for larger model error, the RMSE of LMCPF is lower than for LETKF for a wider range of values for κ. That means, the parameter adjustment of the LMCPF is easier for larger model error. In case of no model error for the forcing term F = 8, the distance between observations and background is smaller than in cases with model error. In theory, we suggest that smaller values for the particle uncertainty parameter κ yield better results in that case since this leads to less uncertainty in the background. If κ tends to zero, the LMCPF gets more similar to LAPF. For the LAPF, we have observed a greater sensitivity to sampling errors. To this end, experiments for increased ensemble size (L = 100) were performed which showed better scores of LMCPF than LETKF in case of no model error and for smaller values of κ. Finally, the perfect model scenario with small distances between background and observation is a difficult case for the LMCPF with small ensemble sizes while this case is less relevant for the application in real NWP systems. In realistic applications, model errors occur and the applicable ensemble size is relatively small compared to the model dimension.

Furthermore, the effective ensemble size depends on the parameter κ. If κ tends to infinity, the effective ensemble size tends to the upper boundary L. This can be explained by Figure 2, which illustrates that the particle weights approach each other if κ tends to infinity. This means, that all the particles get the same weight, which results in the effective ensemble size L_eff = L. With respect to the experiments in Figure 7, the mean effective ensemble size varies for κ > 0.5 between L_eff = 8 and L_eff = 15. The variabilty of the effective ensemble size for different model errors is negligible. As remark, further experiments with different localization schemes and localization radii have shown that smaller localization radii lead to larger effective ensemble sizes up to a certain point. To ensure that the ability of the LMCPF to outperform the LETKF (see Figure 7) do not depend solely on the special selection on forcing terms F^true and F, additional combinations between 6.5 and 9.5 were tested.

In Figures 6, 7, the results for different integration times and model errors are shown. Figure 8 illustrates the changes for different observation standard deviations σ_obs. On the one hand, the LMCPF is able to outperform the LETKF for a wider range of values for κ. On the other hand, there is the tendency that for larger observation standard deviation smaller values for κ lead to good results. As the parameter κ adapts the particle uncertainty, smaller values decrease the uncertainty of the background ensemble and relatively increase the uncertainty of the observation. That means the particles are pulled less strongly in the direction of the observation.

FIGURE 8

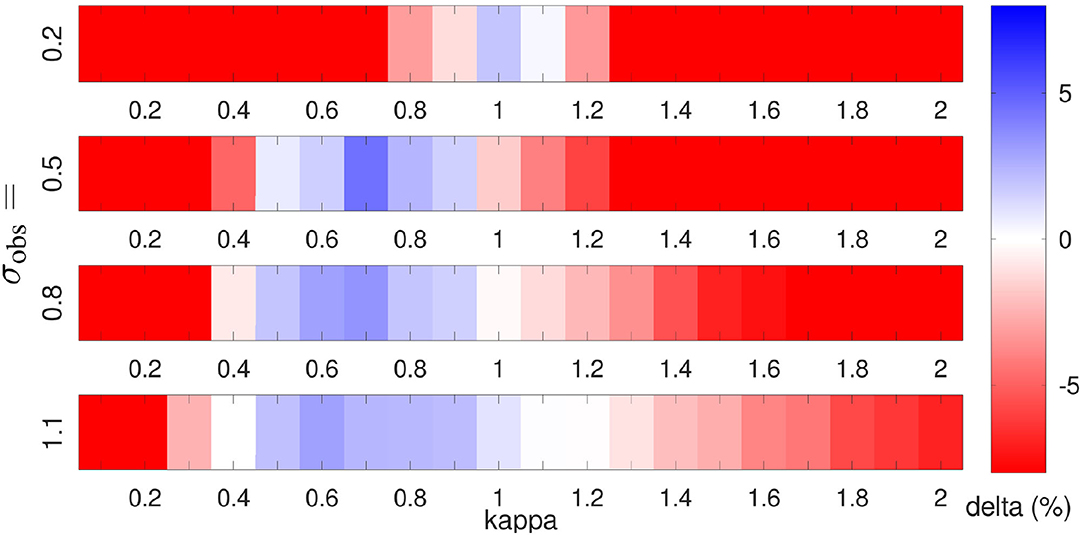
Figure 8. The background errors of LMCPF and LETKF following Equation (121) are compared for different observation error standard deviations σ_obs. Positive values denote a smaller RMSE of truth minus background for the LMCPF method than the LETKF. For each parameter combination, 1, 000 data assimilation steps for the Lorenz 1996 model are carried out whereas the last 900 steps are used to compute the statistics. The experiments are repeated ten times with different seeds and the average error is reported. The true trajectory is generated with F^true = 8 and the integration of the ensemble of states is performed with F = 8.5. The forecast length is set to Δ_t = 0.5. Every second variable is observed. The ensemble size is set to L = 20 for both methods.

In addition, we compared LMCPF and LETKF in case of non-Gaussian distributed observations. To this end, observations are generated with errors following a univariate non-Gaussian double exponential Laplace distribution [16], which are also applied in [56], and an equivalent experiment to Figure 7 was performed. The observation error standard deviation is chosen as σ_obs = 0.5 again. There is no significant improvement of LMCPF compared to LETKF in case of non-Gaussian observations. Since both methods assume Gaussian distributed observation errors by definition, the results confirmed the expectation, that LMCPF does not have an advantage over LETKF in case of non-Gaussian observations. But there is the possibility to adapt the LMCPF in future to account for non-Gaussian observation error. Similar to the idea of a Gaussian mixture filter, the observation error distribution may be approximated by a sum of Gaussians. This would lead to new particle weights and shift vectors.

5.3. LMCPF With Gaussian Mixture and Approximate Weights

In the first version of the LMCPF method presented in Walter et al. [32], the particle weights are approximated by the classical particle filter weights in ensemble space, which are used in the LAPF method. This is reasonable if the covariance B of the Gaussians kernels is small compared to the distance of observation minus background particles. But this assumption may not be justified in practice. If the uncertainty parameter κ tend to zero the assumption is fulfilled and the exact Gaussian mixture weights tend to the approximate weights (see Figure 2).

In Figure 9, the LMCPF method with exact Gaussian mixture weights [see Equation (66)] is compared to the LMCPF method with approximate weights [see Equation (26)] in the case that every second variable is observed. To compare the methods for a variety of model parameters, the forecast length is set to Δ_t = 0.3 for the experiments in the following sections. The results of LMCPF with exact and approximate weights are comparable but the overall background and analysis errors are higher for the version with approximate weights. Moreover, the adaptive inflation parameters ρ₀, ρ₁, c₀, c₁ and α are set to the same values for both methods and both methods have a similar ensemble spread averaged over the whole experiment. Furthermore, the ensemble spread is overestimated for both methods compared to the background, respectively, analysis error.

FIGURE 9

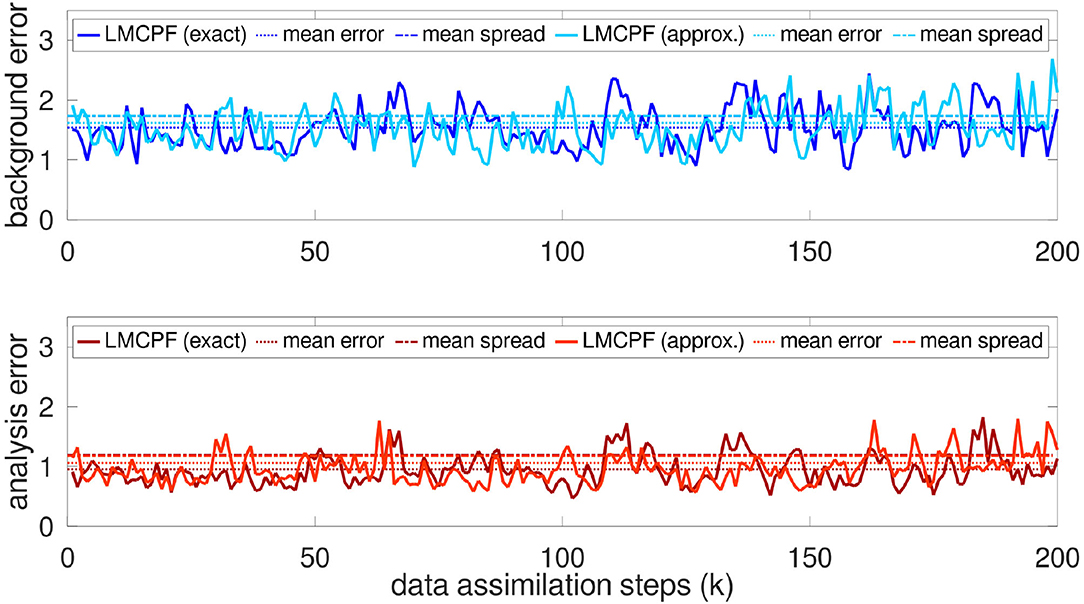
Figure 9. The evolution of the background and analysis errors [see Equations (115) and (116)] for LMCPF with exact and approximate weights is illustrated for the last 200 data assimilation steps of an experiment over 1, 000 steps. For both methods, the ensemble size is set to L = 20. Every second variable of the 40-dimensional Lorenz 1996 model is observed. The forcing terms are set to F^true = 8 and F = 9.5 and the forecast length is set to Δ_t = 0.3. The observation standard deviation is chosen as σ_obs = 0.5 and the observation error covariance matrix as diagonal matrix $R={\sigma }_{\text{obs}}^2·I_m$. The particle uncertainty parameter is set to κ = 1.1 for the LMCPF with exact weights and to κ = 1.0 for the LMCPF with approximate weights. The background error mean of the last 900 data assimilation steps of the LMCPF with exact weights equals e^(b) ≈ 1.54 and the analysis error mean is approximately e^(a) ≈ 0.95. The respective error means for the LMCPF with approximate weights are given by e^(b) ≈ 1.62 and e^(a) ≈ 1.06.

In Figure 10, the development of the effective ensemble size L_eff over the last 200 assimilation steps of this experiment is plotted for the LMCPF with exact and approximate weights as well as the LAPF method. The effective ensemble size of the LMCPF with approximate weights is only slightly higher than for the LAPF method, while the line of LMCPF with exact weights is significantly higher. Also, the localization radius has a large effect on the effective ensemble size. Smaller localization radii r_loc lead to larger effective ensemble sizes. Regarding the results in Figure 10, for the LMCPF method with exact weights, the localization radius is set to r_loc = 4, while for the other two methods, the radius is chosen as r_loc = 2. That means, for the same localization radius the effective ensemble size of LMPCF with exact weights would be even larger. Moreover, the localization radius is an important parameter to achieve stable results in case of the LAPF method. For the LMCPF method, the application of the exact Gaussian mixture weights lead to higher effective ensemble sizes so that the filter performance does not depend so heavily on the localization radius and optimal results are obtained for higher localization radii than for the version with approximate weights. Further experiments for longer forecast lengths (Δ_t = 0.5 and Δ_t = 0.8) have also shown that the effective ensemble size decreases for increasing integration time for all three particle filter versions. While the effective ensemble size of the LMCPF with exact weights still take values around L_eff = 10 for an initial ensemble size of L = 20, the variable decreases to values around L_eff = 3 for LAPF and LMCPF with approximate weights. The increase of the effective ensemble size shows the improvement of the stability of the LMCPF method with exact particle weights. In case of a larger effective ensemble size, more information of the background ensemble is used. If only few particles are chosen in the stratified resampling step, the ensemble spread depends more on the adaptive spread control parameters ρ₀, ρ₁, c₀, c₁ and α. In a worst case scenario where only one particle is chosen, all analysis particles are drawn from the same Gaussian distribution with inflated covariance matrix. Small changes in the covariance matrix of the Gaussian distribution effect the ensemble spread stronger compared to drawing the analysis particles from Gaussians with different expectation vectors. Using the exact Gaussian mixture weights, Kotsuki et al. [39] also detected an improvement of the stability of the LMCPF method with respect to the inflation parameters within an intermediate AGCM. Nevertheless, the application of the analysis covariance matrix $B_{\text{ens}}^{(a)}$ [see Equation (98)] in the Gaussian mixture distribution, from which new particles are drawn in the last step, leads for both LMCPF versions to more stable results with respect to the spread control parameters compared to the LAPF method.

FIGURE 10

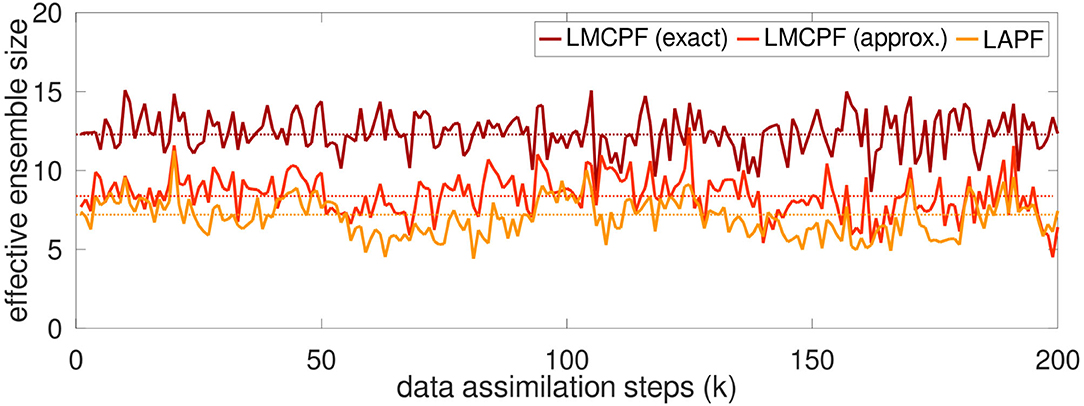
Figure 10. The effective ensemble size ${\stackrel{-}{L}}_{\text{eff}}$ defined in Equation (120) of the LMCPF method with exact and approximate weights as well as the LAPF method is shown for the last 200 steps of the data assimilation experiment described in Figure 9. The ensemble size is set to L = 20 which is the highest value ${\stackrel{-}{L}}_{\text{eff}}$ can take on. The dotted lines denote the mean effective ensemble size over the whole experiment except a spin-up phase (last 900 data assimilation steps).

5.4. Comparison of LMCPF, LAPF, and LETKF

In this section, the three localized methods LMCPF, LAPF and LETKF are compared with respect to the 40-dimensional Lorenz 1996 model.

Figures 11, 12 describe the results for the true forcing term F^true = 8 and F = 9 for the model integration with integration time Δ_t = 0.3. Compared to the overall results in Figure 9 for an experiment with larger model error F = 9.5, the RMSE of background or analysis mean minus truth for the LMCPF method takes lower values. Furthermore, the results for the last 200 data assimilation steps of the experiment in Figure 11 illustrate that the higher errors for the LAPF method mostly come from high peaks at some points, while the errors are comparable for most regions. The tuning of the spread control parameters is essential to obtain good results for the LAPF. Compared to the LMCPF, the filter is more sensitive to these parameters. Additionally, background and analysis errors of the LMCPF method are lower than the errors of the LETKF and the LAPF methods for the majority of the shown time steps. The mean errors over the whole period except a spin-up phase, take lower values even if there are high peaks at some steps. Some outliers occur for each of the three methods.

FIGURE 11

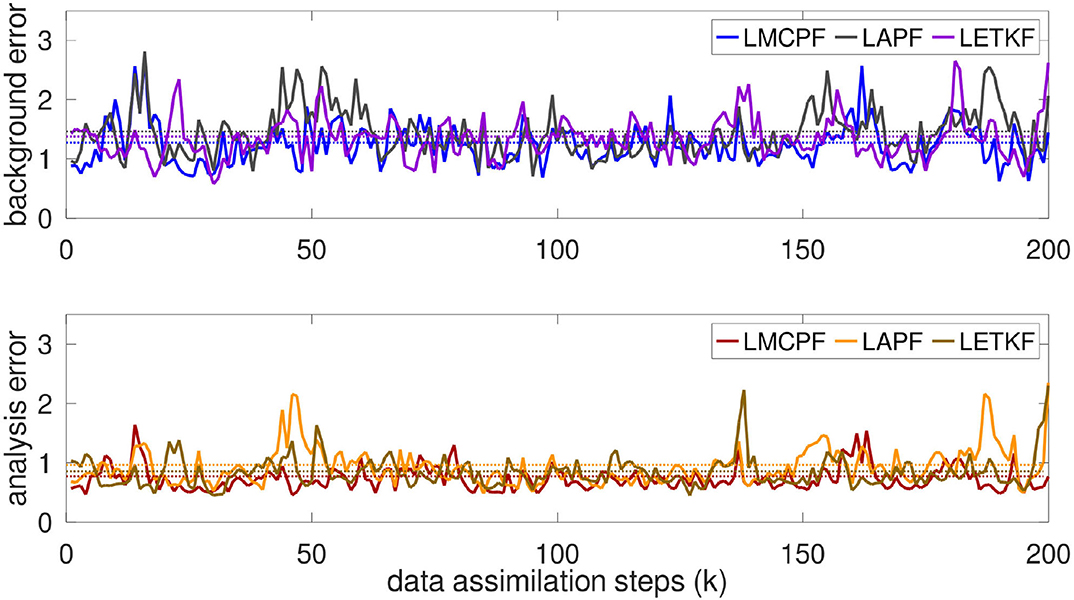
Figure 11. The evolution of the background errors and analysis errors [see Equations (115) and (116)] for LMCPF (κ = 1.1), LETKF and LAPF is illustrated for the last 200 steps of an experiment over 1, 000 steps. The dotted lines denote the mean errors over the whole experiment except a spin-up phase (last 900 data assimilation steps). For all methods, the ensemble size is set to L = 20. Every second variable of the 40-dimensional Lorenz 1996 model is observed. The forcing terms are set to F^true = 8 and F = 9. The forecast length is set to Δ_t = 0.3. The observation standard deviation is chosen as σ_obs = 0.5 and the observation error covariance matrix as diagonal matrix $R={\sigma }_{\text{obs}}^2·I_m$. The background error mean of the last 900 data assimilation steps of the LMCPF equals e^(b) ≈ 1.28 and the analysis error mean is approximately e^(a) ≈ 0.77. The respective error means for the LETKF are given by e^(b) ≈ 1.38 and e^(a) ≈ 0.86, respectively by e^(b) ≈ 1.46 and e^(a) ≈ 0.97 for the LAPF.

FIGURE 12

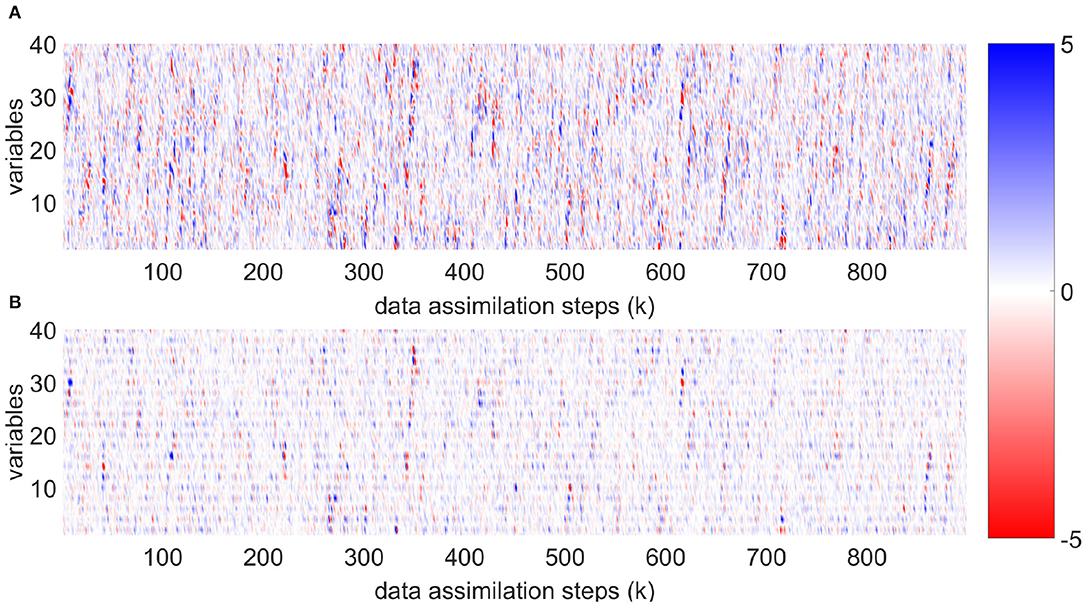
Figure 12. (A) shows the difference of background mean and truth for the LMCPF method for all 40 variables for the experiment described in Figure 11. In (B), the analysis mean minus truth is illustrated for the LMCPF method.

The RMSE development gives an impression for the overall performance of the filters. In contrast, Figure 12 illustrates the behavior for individual variables over the full period except a spin-up phase of 100 data assimilation steps. The difference between the background (Figure 12A) and analysis (Figure 12B) mean and the true trajectory is shown for the LMCPF method. For the experiment, every second variable of the 40 nodes of the Lorenz 1996 model is observed. The vertical structure in Figure 12B indicates a lower distance of analysis mean and truth for observed variables. Figure 12A shows that the background errors for observed and unobserved variables are largely mixed and the vertical structure can only be guessed at some points. This results from the relatively long integration time and the large model error induced by the different model parameter F = 9 in the time integration of the ensemble.

In this study, we focused on the Lorenz 1996 model with 40 variables. This setting is widely used for tests of data assimilation methods and tuning of filter parameters is possible in a reasonable amount of time. Nevertheless, it is important to investigate if the particle filter methods still work for much higher dimensions. To this end, we made first experiments with respect to the Lorenz 1996 model with 1, 000 variables. LAPF and LMCPF (as well as LETKF) run stably with initial ensemble size L = 40 and no filter divergence occured. Moreover, LAPF and LMCPF with approximate weights were already tested with respect to the global ICON model in the data assimilation framework at DWD.

6. Conclusion

Standard algorithms for data assimilation in the application of NWP in high-dimensional spaces are in general ensemble methods, where the ensemble describes the sample of an underlying distribution. The ensemble Kalman filter is an example for a standard algorithm, which is based on normality assumptions. However, the application of nonlinear models to a Gaussian distribution leads to a loss of the normality property in general. In future, the dynamical models used in NWP will get even more nonlinear due to higher resolution and more complex physical schemes, so that this approach might be not optimal in highly nonlinear situations. Hence, there is a need for fully nonlinear data assimilation methods, which are applicable in high dimensional spaces.

This work covers two nonlinear particle filter methods, which are already implemented and tested in the operational data assimilation system of the German Weather Service (DWD). Previous studies of the localized adaptive particle filter (LAPF; [31]) and the localized mixture coefficients particle filter (LMCPF; [32]) showed mixed results for the global NWP system at DWD. The particle filter methods were compared to the local ensemble transform Kalman filter (LETKF). With this manuscript, we examine the question if the LMCPF is able to outperform the LETKF, with respect to a standard NWP setup and standard NWP scores for the dynamical models Lorenz 1963 and Lorenz 1996. The experiments are performed with a revised version of the LMCPF method. The exact particle weights are derived in this work. Previously, the weights were approximated by those of the LAPF. Recently, the revised method is also presented in Kotsuki et al. [39] and tested for an intermediate AGCM. The effective ensemble size is increased for the exact weights, which results in a more stable filter with respect to the parameters of the LMCPF. In case of higher effective ensemble sizes, more background information is contained, while the filter degenerates if the effective ensemble size tends to one. In this study, we demonstrated that the LMCPF is able to outperform the LETKF method with respect to the root-mean-square-error (RMSE) of background/analysis ensemble mean minus truth in case of model error for both systems. That means, the inital question, if the LMCPF is capable to outperform the LETKF within an experimental design reflecting a standard NWP setup and standard NWP scores, can be answered with yes. The experiments with Lorenz 1963 show that the longer the forecast length is chosen, which results in a higher nonlinearity, the better are the scores of LMCPF compared to LETKF. In that case, the LMCPF outperforms the LETKF for a wide range of parameter settings of the LMCPF. Even if the particle uncertainty parameter κ, which affects the ensemble spread as well as the shift toward the observation, is not perfectly adjusted, the RMSE of background ensemble mean minus truth is lower than the error of LETKF. A similar effect is visible for larger systematic model error, which is exemplarily shown with respect to the dynamical system Lorenz 1996. Moreover, further experiments for all of these localized methods, LMCPF (with exact and approximate particle weights), LAPF and LETKF, suggest, that the revised LMCPF is an improvement compared to the previous version of the LMCPF as well as the LAPF and is able to outperform the LETKF.

In the application of data assimilation methods in complex NWP systems, the behavior of the methods is overlaid by a multitude of other processes. In this work, we present the individual ingredients of the LMCPF method in one assimilation step with respect to the Lorenz 1963 model. In case of a bimodal background distribution, the analysis ensemble of the LMCPF method builds a more realistic uncertainty estimation than for the LETKF. Furthermore, the improvement of LMCPF over LAPF is demonstrated in the case of a large distance between the particles and the observation, respectively, true state. In contrast to the LAPF, the analysis ensemble, generated by the LMCPF method, is pulled stronger toward the observation due to the additional shift.

All in all, the results suggest that particle filter methods and the LMCPF in particular represent a serious alternative to the LETKF in nonlinear environments in the future. As next steps, we want to test the improved LMCPF method with respect to the global ICON model as well as the convective-scale ICON-LAM. Additionally, the application within a higher dimensional Lorenz 1996 model (starting from 1, 000 variables) is interesting to investigate further. Moreover, we plan to focus on further scores to compare LMCPF to LETKF.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

NS, RP, and AR conceived the study. Execution of the numerical calculations were performed by NS. Writing the publication was done by NS. Revising the manuscript was done by RP and NS. All authors contributed to the article and approved the submitted version.

Funding

Funding is provided by Deutscher Wetterdienst (German Meteorological Service).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Bastian von Harrach from Goethe-University for scientific support.

References

1. Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J Geophys Res Oceans. (1994) 99:10143–62. doi: 10.1029/94JC00572

CrossRef Full Text | Google Scholar

2. Evensen G, van Leeuwen PJ. An ensemble kalman smoother for nonlinear dynamics. Mon Weather Rev. (2000) 128:1852–67. doi: 10.1175/1520-0493(2000)128<1852:AEKSFN>2.0.CO;2

CrossRef Full Text | Google Scholar

3. Evensen G. Data Assimilation: The Ensemble Kalman Filter. Earth and Environmental Science. 2nd ed. Dordrecht: Springer (2009). Available online at: http://books.google.de/books?id=2_zaTb_O1AkC

Google Scholar

4. Hunt BR, Kostelich EJ, Szunyogh I. Efficient data assimilation for spatiotemporal chaos: a local ensemble transform Kalman filter. Physica D. (2007) 230:112–26. doi: 10.1016/j.physd.2006.11.008

CrossRef Full Text | Google Scholar

5. van Leeuwen PJ. Particle filtering in geophysical systems. Mon Weather Rev. (2009) 137:4089–114. doi: 10.1175/2009MWR2835.1

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Snyder C, Bengtsson T, Bickel P, Anderson J. Obstacles to high-dimensional particle filtering. Mon Weather Rev. (2008) 136:4629–40. doi: 10.1175/2008MWR2529.1

CrossRef Full Text | Google Scholar

7. Bickel P, Li B, Bengtsson T. Sharp failure rates for the bootstrap particle filter in high dimensions. In: Pushing the Limits of Contemporary Statistics: Contributions in Honor of Jayanta K Ghosh. Beachwood, OH (2008). p. 318–29.

Google Scholar

8. Gordon NJ, Salmond DJ, Smith AFM. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc F Radar Signal Process. (1993) 140:107–13. doi: 10.1049/ip-f-2.1993.0015

CrossRef Full Text | Google Scholar

9. van Leeuwen PJ, Künsch HR, Nerger L, Potthast R, Reich S. Particle filters for high-dimensional geoscience applications: a review. Q J R Meteorol Soc. (2019) 145:2335–65. doi: 10.1002/qj.3551

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Stordal A, Karlsen H, Nævdal G, Skaug H, Vallès B. Bridging the ensemble Kalman filter and particle filters: the adaptive Gaussian mixture filter. Comput Geosci. (2011) 15:293–305. doi: 10.1007/s10596-010-9207-1

CrossRef Full Text | Google Scholar

11. Frei M, Künsch HR. Bridging the ensemble Kalman and particle filters. Biometrika. (2013) 100:781–800. doi: 10.1093/biomet/ast020

CrossRef Full Text | Google Scholar

12. Robert S, Künsch H. Localizing the Ensemble Kalman particle filter. Tellus A. (2017) 69:1–14. doi: 10.1080/16000870.2017.1282016

CrossRef Full Text | Google Scholar

13. Robert S, Leuenberger D, Künsch HR. A local ensemble transform Kalman particle filter for convective-scale data assimilation. Q J R Meteorol Soc. (2018) 144:1279–96. doi: 10.1002/qj.3116

CrossRef Full Text | Google Scholar

14. Nakano S, Ueno G, Higuchi T. Merging particle filter for sequential data assimilation. Nonlinear Process Geophys. (2007) 14:395–408. doi: 10.5194/npg-14-395-2007

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xiong X, Navon IM, Uzunoglu B. A note on the particle filter with posterior gaussian resampling. Tellus A. (2006) 58:456–60. doi: 10.1111/j.1600-0870.2006.00185.x

CrossRef Full Text | Google Scholar

16. Tödter J, Ahrens B. A second-order exact ensemble square root filter for nonlinear data assimilation. Mon Weather Rev. (2015) 143:1347–67. doi: 10.1175/MWR-D-14-00108.1

CrossRef Full Text | Google Scholar

17. Bishop CH, Etherton BJ, Majumdar SJ. Adaptive sampling with the ensemble transform Kalman filter. Part I: theoretical aspects. Mon Weather Rev. (2001) 129:420–36. doi: 10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2

CrossRef Full Text | Google Scholar

18. Reich S. A nonparametric ensemble transform method for bayesian inference. SIAM J Scientific Comput. (2013) 35:A2013–24. doi: 10.1137/130907367

CrossRef Full Text | Google Scholar

19. Neal RM. Sampling from multimodal distributions using tempered transitions. Stat Comput. (1996) 6:353–66. doi: 10.1007/BF00143556

CrossRef Full Text | Google Scholar

20. Del Moral P, Doucet A, Jasra A. Sequential monte carlo samplers. J R Stat Soc B. (2006) 68:411–36. doi: 10.1111/j.1467-9868.2006.00553.x

CrossRef Full Text | Google Scholar

21. Emerick AA, Reynolds AC. Ensemble smoother with multiple data assimilation. Comput Geosci. (2013) 55:3–15. doi: 10.1016/j.cageo.2012.03.011

CrossRef Full Text | Google Scholar

22. Beskos A, Crisan D, Jasra A. On the stability of sequential Monte Carlo methods in high dimensions. Ann Appl Probab. (2014) 24:1396–445. doi: 10.1214/13-AAP951

CrossRef Full Text | Google Scholar

23. van Leeuwen PJ. Nonlinear ensemble data assimilation for the ocean. In: Seminar on Recent Developments in Data Assimilation for Atmosphere Ocean, 8–12 September 2003 ECMWF. Shinfield Park; Reading: ECMWF (2003). p. 265–86.

Google Scholar

24. Reich S. A Gaussian-mixture ensemble transform filter. Q J R Meteorol Soc. (2012) 138:222–33. doi: 10.1002/qj.898

CrossRef Full Text | Google Scholar

25. Reich S, Cotter C. Probabilistic Forecasting and Bayesian Data Assimilation. Cambridge: Cambridge University Press (2015).

Google Scholar

26. Liu Q, Wang D. Stein variational gradient descent: a general purpose Bayesian inference algorithm. In: Lee DD, Sugiyama M, Luxburg UV, Guyon I, Garnett R, editors. Advances in Neural Information Processing Systems, Vol. 29. Curran Associates, Inc. (2016). p. 2378–86. Available online at: https://proceedings.neurips.cc/paper/2016/file/b3ba8f1bee1238a2f37603d90b58898d-Paper.pdf (accessed June 10, 2022).

Google Scholar

27. Lu J, Lu Y, Nolen J. Scaling limit of the stein variational gradient descent: the mean field regime. SIAM J Math Anal. (2019) 51:648–71. doi: 10.1137/18M1187611

CrossRef Full Text | Google Scholar

28. Poterjoy J. A localized particle filter for high-dimensional nonlinear systems. Mon Weather Rev. (2016) 144:59–76. doi: 10.1175/MWR-D-15-0163.1

CrossRef Full Text | Google Scholar

29. Poterjoy J, Sobash RA, Anderson JL. Convective-Scale data assimilation for the weather research and forecasting model using the local particle filter. Mon Weather Rev. (2017) 145:1897–918. doi: 10.1175/MWR-D-16-0298.1

CrossRef Full Text | Google Scholar

30. Penny SG, Miyoshi T. A local particle filter for high-dimensional geophysical systems. Nonlinear Process Geophys. (2016) 23:391–405. doi: 10.5194/npg-23-391-2016

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Potthast R, Walter A, Rhodin A. A localized adaptive particle filter within an operational nwp framework. Mon Weather Rev. (2019) 147:345–62. doi: 10.1175/MWR-D-18-0028.1

CrossRef Full Text | Google Scholar

32. Rojahn, A., Schenk, N., van Leeuwen, P. J., and Potthast, R. (2022). Particle filtering and Gaussian mixtures – On a localized mixture coefficients particle filter (LMCPF) for global NWP. Preprint. doi: 10.48550/arXiv.2206.07433

CrossRef Full Text | Google Scholar

33. Alspach D, Sorenson H. Nonlinear Bayesian estimation using Gaussian sum approximations. IEEE Trans Automat Contr. (1972) 17:439–48. doi: 10.1109/TAC.1972.1100034

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Anderson JL, Anderson SL. A monte carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon Weather Rev. (1999) 127:2741–58. doi: 10.1175/1520-0493(1999)127<2741:AMCIOT>2.0.CO;2

CrossRef Full Text | Google Scholar

35. Chen R, Liu J. Mixture Kalman Filter. J Roy Statist Soc Ser B. (2000) 62:493–508. doi: 10.1111/1467-9868.00246

CrossRef Full Text | Google Scholar

36. Bengtsson T, Snyder C, Nychka D. Toward a nonlinear ensemble filter for high-dimensional systems. J Geophys Res Atmospheres. (2003) 108:8775. doi: 10.1029/2002JD002900

CrossRef Full Text | Google Scholar

37. Kotecha JH, Djuric PM. Gaussian particle filtering. IEEE Trans Signal Process. (2003) 51:2592–601. doi: 10.1109/TSP.2003.816758

CrossRef Full Text

38. Hoteit I, Pham DT, Triantafyllou G, Korres G. A new approximate solution of the optimal nonlinear filter for data assimilation in meteorology and oceanography. Mon Weather Rev. (2008) 136:317–34. doi: 10.1175/2007MWR1927.1

CrossRef Full Text | Google Scholar

39. Kotsuki S, Miyoshi T, Kondo K, Potthast R. A Local Particle Filter and Its Gaussian Mixture Extension: Comparison With the LETKF Using an Intermediate AGCM. (2022). doi: 10.5194/gmd-2022-69

CrossRef Full Text

40. Zängl G, Reinert D, Rípodas P, Baldauf M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: description of the non-hydrostatic dynamical core. Q J R Meteorol Soc. (2015) 141:563–79. doi: 10.1002/qj.2378

CrossRef Full Text | Google Scholar

41. Lorenz EN. Deterministic nonperiodic flow. J Atmosphere Sci. (1963) 20:130–41. doi: 10.1175/1520-04691963020<0130:DNF>gt;2.0.CO;2

CrossRef Full Text | Google Scholar

42. Goodliff M, Amezcua J, Leeuwen PJV. Comparing hybrid data assimilation methods on the Lorenz 1963 model with increasing non-linearity. Tellus A. (2015) 67:26928. doi: 10.3402/tellusa.v67.26928

CrossRef Full Text | Google Scholar

43. Miller RN, Ghil M, Gauthiez F. Advanced data assimilation in strongly nonlinear dynamical systems. J Atmospher Sci. (1994) 51:1037–56. doi: 10.1175/1520-0469(1994)051<1037:ADAISN>2.0.CO;2

CrossRef Full Text | Google Scholar

44. Lorenz EN. Predictability: a problem partly solved. In: Seminar on Predictability, 4-8 September 1995, vol. 1. ECMWF. Shinfield Park, Reading: ECMWF (1995). p. 1–18.

PubMed Abstract

45. Li H, Kalnay E, Miyoshi T. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter. Q J R Meteorol Soc. (2009) 135:523–33. doi: 10.1002/qj.371

CrossRef Full Text | Google Scholar

46. van Leeuwen PJ. Nonlinear data assimilation in geosciences: an extremely efficient particle filter. Q J R Meteorol Soc. (2010) 136:1991–9. doi: 10.1002/qj.699

CrossRef Full Text | Google Scholar

47. Frei M, Künsch HR. Sequential state and observation noise covariance estimation using combined ensemble Kalman and particle filters. Mon Weather Rev. (2012) 140:1476–95. doi: 10.1175/MWR-D-10-05088.1

CrossRef Full Text | Google Scholar

48. Nerger L, Janjić T, Schröter J, Hiller W. A regulated localization scheme for ensemble-based Kalman filters. Q J R Meteorol Soc. (2012) 138:802–12. doi: 10.1002/qj.945

CrossRef Full Text | Google Scholar

49. Papoulis A, Pillai SU. Probability, Random Variables, and Stochastic Processes. 3rd Edn. Boston, MA: McGraw-Hill (1991).

Google Scholar

50. Kirchgessner P, Nerger L, Bunse-Gerstner A. On the choice of an optimal localization radius in ensemble Kalman filter methods. Mon Weather Rev. (2014) 142:2165–75. doi: 10.1175/MWR-D-13-00246.1

CrossRef Full Text | Google Scholar

51. Gaspari G, Cohn SE. Construction of correlation functions in two and three dimensions. Q J R Meteorol Soc. (1999) 125:723–57. doi: 10.1002/qj.49712555417

CrossRef Full Text | Google Scholar

52. Nakamura G, Potthast R. Inverse Modeling: An Introduction to the Theory and Methods of Inverse Problems and Data Assimilation. Bristol: IOP Publishing (2015).

Google Scholar

53. Carpenter J, Cliffordy P, Fearnhead P. An improved particle filter for non-linear problems. IEE Proc Radar Sonar Navig. (2000) 146:2–7. doi: 10.1049/ip-rsn:19990255

CrossRef Full Text | Google Scholar

54. Anderson BDO, Moore JB. Optimal Filtering. Hoboken, NJ: Prentice-Hall (1979).

Google Scholar

55. Desroziers G, Berre L, Chapnik B, Poli P. Diagnosis of observation, background and analysis-error statistics in observation space. Q J R Meteorol Soc. (2005) 131:3385–96. doi: 10.1256/qj.05.108

CrossRef Full Text | Google Scholar

56. Feng J, Wang X, Poterjoy J. A comparison of two local moment-matching nonlinear filters: local particle filter (LPF) and local nonlinear ensemble transform filter (LNETF). Mon Weather Rev. (2020) 148:4377–95. doi: 10.1175/MWR-D-19-0368.1

CrossRef Full Text | Google Scholar

57. Poterjoy J, Wicker L, Buehner M. Progress toward the application of a localized particle filter for numerical weather prediction. Mon Weather Rev. (2019) 147:1107–26. doi: 10.1175/MWR-D-17-0344.1

CrossRef Full Text | Google Scholar

58. Schraff C, Reich H, Rhodin A, Schomburg A, Stephan K, Periáñez A, et al. Kilometre-scale ensemble data assimilation for the COSMO model (KENDA). Q J R Meteorol Soc. (2016) 142:1453–472. doi: 10.1002/qj.2748

CrossRef Full Text | Google Scholar

59. Evensen G. The ensemble kalman filter: theoretical formulation and practical implementation. Ocean Dynamics. (2003) 53:343–67. doi: 10.1007/s10236-003-0036-9

CrossRef Full Text | Google Scholar

60. Lei J, Bickel P. A moment matching ensemble filter for nonlinear non-gaussian data assimilation. Mon Weather Rev. (2011) 139:3964–73. doi: 10.1175/2011MWR3553.1

CrossRef Full Text | Google Scholar