
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat., 29 April 2022
Sec. Statistical and Computational Physics
Volume 8 - 2022 | https://doi.org/10.3389/fams.2022.879140
This article is part of the Research TopicData-Driven Modeling and Optimization in Fluid Dynamics: From Physics-Based to Machine Learning ApproachesView all 11 articles
The control of general nonlinear systems is a challenging task in particular for large-scale models as they occur in the semi-discretization of partial differential equations (PDEs) of, say, fluid flow. In order to employ powerful methods from linear numerical algebra and linear control theory, one may embed the nonlinear system in the class of linear parameter varying (LPV) systems. In this work, we show how convolutional neural networks can be used to design LPV approximations of incompressible Navier-Stokes equations. In view of a possibly low-dimensional approximation of the parametrization, we discuss the use of deep neural networks (DNNs) in a semi-discrete PDE context and compare their performance to an approach based on proper orthogonal decomposition (POD). For a streamlined training of DNNs directed to the PDEs in a Finite Element (FEM) framework, we also discuss algorithmical details of implementing the proper norms in general loss functions.
- Conceptual: Due to the quadratic nature of the Navier-Stokes equations, any encoder-decoder with a linear decoding part provides an affine LPV approximation of the state-space equations. We propose the use of convolutional neural networks (CNNs).
- Algorithmical: An efficient realization of the correct FEM norms within the training of a neural network. As a result, we provide basic routines that combine the Finite Element package FEniCS and the Machine Learning toolbox PyTorch.
- Numerically: A very low-dimensional, that is 3-dimensional, performant LPV approximation of a flow around a cylinder in the vortex shedding regime.
The computer-aided controller design for a nonlinear control system
with an input u and an input operator B typically resorts to system insights (like in backstepping [1], feedback linearization [2, Ch. 5.3], or sliding mode control [3]), or the repeated computation for subobtimal control laws like in model predictive control (MPC) [4]. The holistic but general approach via the Hamilton-Jacobi-Bellmann (HJB) equations is only feasible for very moderate system sizes or calls for model order reduction; see e.g., Breiten et al. [5] for a relevant discussion and an application in fluid flow control.
For general large-scale systems, MPC schemes seem to be a good choice since modern hardware and optimization algorithms can well mitigate the computational complexity while the continuous update of the prediction realizes a feedback loop as it is needed to react on inevitable perturbations in simulations and measurements. Nonetheless, stability guarantees for MPC schemes are difficult to establish a priori and the solving of nonlinear optimization problems at runtime limits their performance in particular for large-scale systems.
In view of these two limiting factors, alternatives are presented by methods that base on extended linearizations or state-dependent coefficients (SDC) (see e.g., Banks et al. [6]) schemes that are particular realizations of the representation of a nonlinear model as a linear parameter varying (LPV) system.
In an exact SDC representation, the flow f of the model is factorized as
with a suitable A : ℝn → ℝn,n which exists under mild conditions. The SDC is a special case of an LPV representation
with ρ : ℝn → ℝr and N : ℝr → ℝn,n suitably chosen and, possibly, r < n.
While these representations are exact reformulations of the model, a low-dimensional (r ≪ n) and affine-linear parameter dependency might only exist as an approximation
If an approximation can be afforded, many numerical approaches for the derivation of low-dimensional LPV representations apply. In fact, any model order reduction scheme that encodes the state in a reduced coordinate ρ = μ(υ) ∈ ℝk and lifts it back to can turn an SDC representation into a low-dimensional LPV approximation via
Even more, if the state-dependent coefficient matrix N is affine-linear in its argument and if the lifting λ is affine-linear, then the resulting LPV approximation is affine-linear. We will make use of this observation when discussing the Navier-Stokes equations and when designing the low-dimensional encodings.
An immediate advantage in view of large-scale systems is that for these pointwise linear problems, linear methods for controller design apply. Generally, an a-priori proof that a controller will stabilize the system is by no means easier in an LPV context. Nonetheless, conditions that can be checked or monitored numerically have been developed; see e.g., Benner and Heiland [7] for a result on SDC systems or [8] for a result for (affine) LPV systems.
This paper investigates the use of convolutional neural networks in combination with bases obtained from a POD to design such approximative LPV systems with affine parameter dependency:
We focus on Navier-Stokes equations but the methodology applies to any system with states that are distributed in a spatial domain like spatially discretized approximations to PDE models.
The motivation for this study is the potential use of low-dimensional LPV representations in controller design. For example, for affine-linearly parametrizable coefficients as in Equation (1), one can derive series expansions (see e.g., Beeler et al. [9]) of the solution to the associated parameter-dependent Riccati equations and exploit them for efficient controller design; cp. [10]. Furthermore, if the image of ρ for the given system can be confined to a polygon, then one can provide a globally stabilizing controller (see e.g., Apkarian et al. [11]) through the scheduling of a set of linear controllers. Both approaches, however, hinge on a small dimension of ρ(υ) since the series expansion has to be considered in all parameter directions and since the scheduling requires the solution of a coupled system of r linear matrix inequalities of the size of the system dimension.
In view of these considerations, this work provides a particular solution to the following general problem:
Problem 1. Given a nonlinear system ,
(a) how to encode a current state υ(t) ∈ ℝn in a low dimensional parameter ρ(t) ∈ ℝr and
(b) how to provide embeddings so that
Existing general solutions for this task are known to result in larger dimensions of the parametrization ρ; see Koelewijn and Tóth [12] for relevant references and a neural network based approach toward a reduced order of ρ.
In any case, the existing strategies were designed for ODE models of moderate size rather than the treatment of high-dimensional nonlinear models that are associated with PDEs.
Therefore, we propose the use of model reduction techniques to derive LPV approximations with low parameter dimensions independently of the system size. Similar efforts can be spotted in earlier works (see e.g., Hashemi and Werner [13] where the Burgers' equation was considered) though with a different strategy: the model reduction techniques were used for reducing the overall system so that the natural SDC representation could be interpreted as a low-dimensional LPV approximation.
In what we propose, however, the system dimensions are not touched in order to ensure accuracy and feature-completeness, but only parts of the nonlinear functions are replaced by de– and encoded variables to provide the low-dimensional LPV representation. Certainly, if controllers are to be designed, a state-space reduction might be necessary but can then be directed to the purpose of the controller model rather than the actual state equations.
In a regime that is dominated by convection, the encoding of a state of a Navier-Stokes equation in a very-low dimensional coordinate system cannot be simply done by a linear projection. This has been observed in numerical studies of flow problems and specifically analyzed for equations with wave like patterns [14, 15].
Successful low-dimensional parametrizations for convective phenomena have been established using a nonlinear preprocessing like the detection and explicit treatment of wave patterns; see e.g., Reiss et al. [16] for a method of adaptive shifting of POD modes along with wave fronts and [17] for a recent update that resorts to neural networks. A more generic approach was used in Sarna and Benner [18], where a superposition of the phase space of hyperbolic and parabolic parts was introduced and successfully exploited for efficient reduction of parabolic parts. A purely neural network based appraoch that explicitly addresses wave patterns has been discussed in Deo and Jaiman [19].
Recently, the use of neural networks for finding low-dimensional coordinates has been proposed, e.g., as an alternative to established POD techniques [20–23] or as an enhancement to them [24].
Considering fluid flow or Burgers' equations, it has been observed that neural networks can significantly outperform POD approaches at very-low dimensions in terms of approximation quality; see e.g., Lee and Carlberg [20, Figure 3] or Kim et al. [21, Figure 2]. However, the effort for setting up the surrogate model (cp. [24, Table 3] or [20, Section 8]) as well as the evaluation at runtime can be inferior to a plain POD approach; compare, e.g., the reported speed-ups in Kim et al. [21, Table 1].
We note that we can easily tolerate these performance limitations, as the major motivation of our work is to establish a model approximation of a particular structure.
In summary of the preceding considerations, we state that the presented investigations are motivated by and directed to support the following working hypotheses:
Working Hypothesis 1.
1. Neural networks can efficiently encode the state of a PDE and thus provide very low dimensional parametrizations.
2. For the synthesis of a controller model for a nonlinear PDE, the use of high-dimensional data and demanding computations is appropriate.
We briefly introduce the PDE model of interest, the concept of convolutional neural networks, and state relevant observations.
The incompressible Navier-Stokes equations
is a set of partial differential equations that is widely used to model incompressible fluid flows in a domain Ω ⊂ ℝd, d = 2, 3, on a time interval [0, T] ⊂ ℝ in terms of the evolution of the velocity field v: [0, T] × Ω → ℝd and the pressure field p: [0, T] × Ω → ℝ. Here, Re is the so-called Reynolds number that parametrizes the flow setup and f contains forces that act on the flow like gravity or, in a flow control setup, external inputs.
As we will detail below (in Section 4.1) after a spatial discretization and by means of divergence-free coordinates, the flow model reads
and is readily expressed as a so-called state-dependent coefficient system
with
Remark 1. The decomposition is by no means unique. In particular, a similarly natural factorization exists and any combination
for a scalar s can be considered, too. Such a blending of the coefficients can be used to improve the model performance as we did in our numerical examples; cp. Remark 5.
In what follows, we will consider LPV systems that generalize state-dependent coefficient (SDC) systems by encoding the state in a parameter variable ρ. We will refer to ρ(υ) as the code of v and also distinguish an associated encoder
It will be convenient to refer to a decoder as
by the vague requirement that for all v of interest although an inverse to μ may not exist and although the inference of μ and μ−1 may be unrelated in practice.
Given an encoder μ and a decoder μ−1, an LPV approximation to the state-dependent coefficient (Equation 5) is readily given as
Remark 2. A particular property of quadratic systems and, thus, of the Navier-Stokes equations is that the natural choices of the state-dependent coefficient N(υ) are linear, i.e., N(λ1υ1 + λ2υ2) = λ1N(υ1) + λ2N(υ2). Accordingly, if the decoder μ−1 is affine-linear, i.e.,
for a shift ṽ0 and a some vectors , then the induced LPV representation is affine-linear as
Remark 3. If the decoder μ−1 or the SDC relation v → A(υ) is nonlinear, then an additional approximation step is needed for an affine-linear LPV representation; see Koelewijn and Tóth [12].
Generally, a neural network of NL layers can be expressed as a recursively defined map
that maps the input variable x(0) onto the output variable . It is defined in terms of the layer widths nℓ, the weights meaning the coefficients of the matrix and the bias term , and the activation function σ : ℝ → ℝ that is applied componentwise to the vectors .
The term of training a neural network refers to determining the weights by an optimization toward an optimality criterion (the loss function) evaluated at given sample points.
In convolutional neural networks, the linear map W(ℓ) in each a layer is defined by a number of convolution kernels that convolve the current state. Typically, a linear contraction follows that merges neighboring states. The advantages of convolutional layers for PDE data is manifold.
• In each layer, the learnable parameters are given by the parameters of the convolution kernels so that the amount of parameters is independent of the possibly large state dimensions
• The convolution acts upon neighboring states which can respect and, notably, detect coherent spatial structures as they may be inherent in states of PDEs.
• The contraction operation reduces the number of variables in each channel in every layer so that a CNN can be designed to provide low-dimensional encodings.
An immediate obstacle that stands against the use of CNNs for PDEs is the need of tensorized grids, whereas a simulation of complex phenomena typically requires a locally refined and unstructured grid. We overcome this issue by simply interpolating the state values from the FEM grid to a tensorized grid.
For an introduction to the techniques of CNNs, we refer to O'Shea and Nash [25]. An application for spatially distributed data as in our case is well explained in Lee and Carlberg [20].
The provision of a low-dimensional affine-linear LPV approximation
for the Navier-Stokes equations amounts to learning or computing
• an encoder μ: υ ↦ ρ and
• an embedding or lifting .
Note that λ can be defined without a decoder μ−1. On the other hand, for the Navier-Stokes case, if an affine-linear decoder is given, then λ: ρ ↦ N(μ−1(ρ)) readily provides an affine-linear parametrization; cp. Remark 2.
As a benchmark and for later use as a basis for the decoding, we consider the LPV representation that is induced by a POD reduction. Here, one uses a projection basis
that consists of the r leading singular vectors of a matrix of snapshots like
The POD reduction itself bases on the property that the projection minimizes the average projection error over the given data set (Equation 7), meaning that
is minimal over all r-dimensional linear projections of the data set, where the subscript M stands for a weight in the norm induced, e.g., by the symmetric positive (mass) matrix of an underlying an FEM scheme; cp. [26].
Accordingly, with
the POD basis Vr defines a r-dimensional encoding via , a decoding via , and an embedding λ for the LPV approximation via
Remark 4. As it is common practice, for a better approximation quality and for consistency reasons, the data for the POD and, thus, also the POD bases, are shifted by a vector vs. which will be chosen to be the initial value in the simulations. Accordingly, the correct reconstruction reads , which simply adds a constant and a few linear terms to the approximation or the corresponding loss functions.
In this setup, we investigate whether a CNN can replace the POD encoding of the state
and also provide an enhanced decoding to POD coordinates via a full linear map W
and the embedding via the p-dimensional POD basis .
In this approach, the CNN and the matrix is learned as neural network
with the loss function
If , and the resulting embedding outperforms the standard -dimensional POD reduction, then this approach provides a countable improvement in terms of dimensionality.
Moreover, the loss functions can be changed in order to direct the learning to best approximate the resulting convective behavior as described in the following subsection.
With the same approach but with
as the loss function, the training of the decoder can be directed toward the actual goal—the low-dimensional parametrization of the convection part. Note the M−1 norm, that is the discrete version of the norm of N(υ) as a functional on the state space L2(Ω).
In this section, we discuss implementation issues as the arise in the numerical treatment of incompressible Navier-Stokes equations by finite elements and the inclusion of FEM-norms in learning algorithms.
A spatial discretization (see e.g., Behr et al. [27]) of the incompressible Navier-Stokes equations (2) leads to a system of type
where M is a positive definite (mass) matrix, where N(υ) is the matrix that realizes the convection for a state υ(t), where A0 encodes the diffusion part, where JT and J stand for the discrete gradient and divergence operator, and where the vectors f and g accommodate possible inhomogenities and boundary conditions.
In order to eliminate the inhomogeneity and possibly nonzero boundary conditions, one may shift the state by some vector vs. that fulfills the boundary conditions and the algebraic constraint, i.e., Jυs = g, so that the shifted system for υd(t) = υ(t) − υs reads
where
Finally, with the reasonable assumption that JTM−1J is invertible, we find that with the projector Π = I − M−1JT(JM−1JT)J it holds that υd = Πυd and that the solution υd is completely defined through the projected system (see e.g., Heiland [28, Thm. 8.6])
The practical implications are as follows: in a simulation, one needs to consider all data shifted by a constant vector vs. that fulfills the boundary conditions so that the snapshots υi can be assumed to comply with zero Dirichlet conditions. Then a reduced parametrization will target the shifted space with zero boundary conditions and can be lifted to the physical space by adding vs. again.
Generally, the projection Π needs not be computed explicitly as it will be implicitly realized during the time integration; [29]. However, if only the velocity is of interest, the model could be trained to best approximate ΠTN(υ)υ which resides on a submanifold of dimension (nv−rank Π). If however, the pressure is of interest too, the LPV approximation should be trained toward a good representation of
as the part (I − ΠT) defines how the convection enters the pressure approximation.
As mentioned above, in order to employ standard CNNs, the data on an FEM mesh has to be interpolated to a tensorized mesh. For that and for a generic 2D flow setup we proceed as follows.
Let Ω ⊂ ℝ2 be the computational domain and let (ξ1, ξ2) ∈ Ω denote the spatial coordinates. Let
be the ansatz space of the finite element discretization. Then every solution snapshot υi has the function representation via
where [υi]j is the j-th component of the vector of coefficients υi. Accordingly, it can be interpolated onto a tensorization
of two 1D grids
into a 2 × nx × ny tensor vi as
We denote this interpolation operator with the operator . The application of P to the data points υi is the first operation in the processing of the υi's in a CNN.
For the implementation of the learning based on FEM data, we need to include M or M−1 in the loss functions without breaking the automated computation of sensitivities1. For the realization of the M norm, we can resort to sparse factorizations M = FFT and use the equivalence of . In this way, the M-norm can realized in standard ML packages that have the 2-norm implemented as the mean square error loss function and that also support sparse matrix multiplication.
For the realization of M−1, where no sparse factorization can be provided, we compute a M−1 optimal (cp. [26, Lem. 2.5]) snapshot basis for N(υi)υi, i = 1, …, k of dimension kc. With that we can best approximate
where F is a factor of M = FFT and where we have used that L is orthogonal so that it does not affect the 2-norm. In this way, the M−1 norm of N(υi)υi can be well approximated with the standard mean-squared error and a premultiplication by the dense matrix .
We consider the well-known benchmark example of a 2D flow around a cylinder in a channel. In nondimensionalized coordinates the channel covers the rectangle [0, 5] × [0, 1] with the cylinder of radius R = 0.05 centered at . The regime is parametrized by the Reynolds number Re that is computed using the velocity of the inflow parabola averaged over the inflow boundary and the radius and set to Re = 40 in the presented simulations. As the starting value for t = 0, we impose the associated steady-state Stokes solution. With this initialization the flow immediately starts the transition into the characteristic periodic vertex-shedding regime which seems to be well developed at around t = 8. A snapshot of the domain and the developed flow at t = 8 is presented in Figure 1.
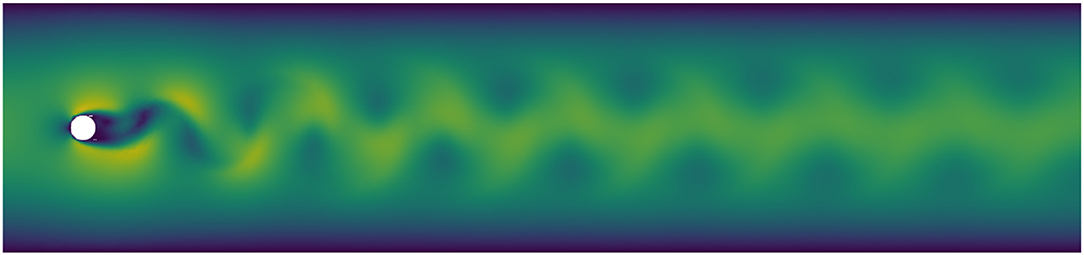
Figure 1. Snapshot of the domain and the magnitude of the fully developed velocity field at Re = 40.
We will use data from the initial phase from t = 0 till t = 8 to generate low-dimensional LPV models. The performance of the reduced-order models will be directed toward how well the periodic regime is captured on a time frame till t = 50.
For the spatial discretization, we use P2 − P1 Taylor-Hood finite elements on a nonuniform grid that results in 42764 degrees of freedom in the velocity approximation. For the time integration we use the implicit one-step Crank-Nicolson scheme for the linear part and the explicit 2-step Adams-Bashforth scheme for the nonlinear part which combines into a 2nd order approximation. The finite element discretization was realized in the FEM toolbox FEniCS [30], the time integration and the connection to PyTorch (which was used for the setup, training and evalution of the (C)NNs) was handled via the SciPy interface dolfin-navier-scipy [31].
The solution is monitored via the induced forces onto the cylinder periphery that we compute by testing the (numerically computed) residual of the FEM solution (υ(t), p(t)) against (a numerical realization of) the function ϕ that takes on the value (1, 1) at the cylinder boundary and (0, 0) elsewhere:
where Ω is the computational domain; see Babuǎka and Miller [32]. Since the flow passes the channel in ξ1 direction, the first component of represents the current drag and the second component represents the lift force.
Once the semi-discrete model is defined, the overall procedure of setting up and evaluating a low-dimensional LPV surrogate model can be summarized in four major steps:
1. Data Aquisition and Preparation. This step generates the data used for computing the POD basis and for the CAE model training. For that, a simulation on the base of the original model is performed and solution snapshots at dedicated time instances are stored. In view of being used for the training of the CAE model, among others, the data is interpolated to a tensor grid.
2. Training of the Encoder and Decoder. By means of the snapshot data, a POD basis is computed. Also, the interpolated data are used to optimize the parameters of the CAE encoder and decoder.
3. Setup of the LPV Approximation. The CAE and the POD encoder and decoders that approximate a current velocity υ(t) by for some basis and the code ρ(t) is used to approximate the actual nonlinear N(υ(t))υ(t) term in the model by a low-dimensional LPV approximation Ñ(ρ(t))υ(t).
4. Simulation with the LPV Model. Finally, simulations of the original model with the nonlinearity replaced by the LPV approximation are performed and evaluated.
All these steps are explained in detail in the following subchapters.
The data [V] for the training of the CNN and the computation of POD bases Ṽ and of the states υi and of the convection field N(υi)υi is collected from the simulation on the time interval [0, te] at ndp equally spaced data points.
For the use for training of the CNN, the states data υi is interpolated to the tensor grid by means of the interpolation operator to give the data set
Additionally, we recorded the maximal and minimal values of the data in [V] and linearly scaled all interpolations to the range of [−1, 1]. The scaled and partially doubled data, we will denote by [V+].
Note that the interpolation to the tensor grid is not lossless in particular in the considered case where the dimension of the tensorized data is 2 x 63 x 127 = 16,002 is much smaller than the data on the full FEM grid, where the tensor grid is not adapted to the problem whatsoever, and where geometrical features of the domain are not represented in the tensorized data; cp. Figure 2.
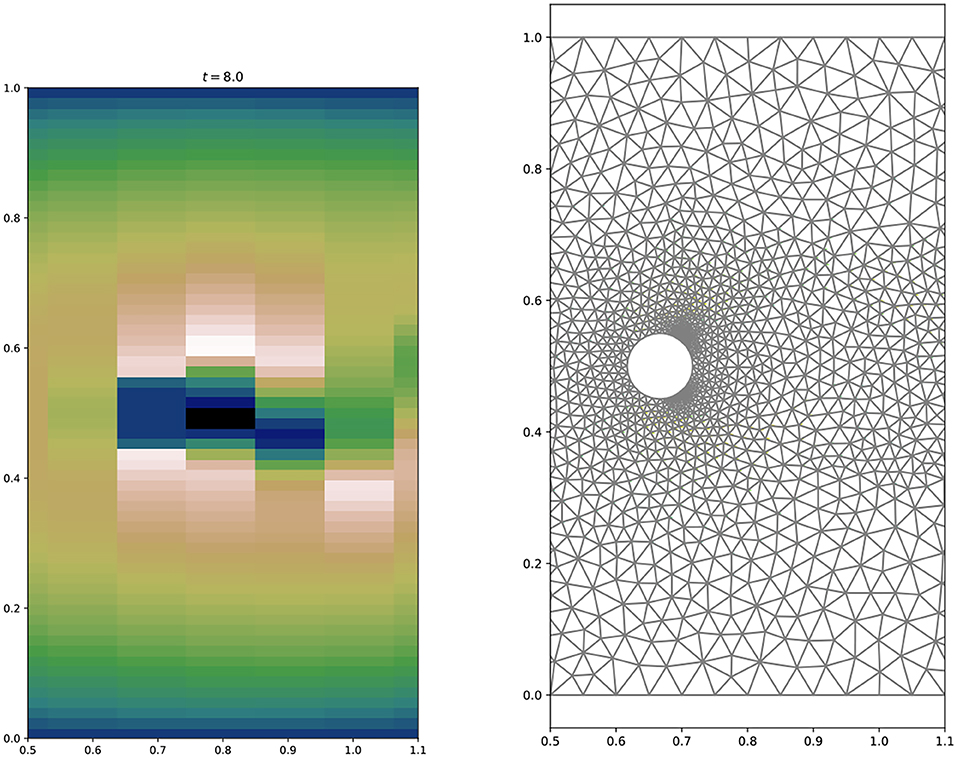
Figure 2. Close up view of the computational domain with the FEM mesh (right) and the data representation on the tensorized mesh (left).
At first, as preliminary tests showed, the trained neural network performed poorly on the first data points, e.g., the initial phase of the simulation. To shift the focus of the training toward the initial phase, we doubled a defined amount of the data points as follows: for a given percentage p, a subgrid of the snapshot time instances was computed that contained p percent of the data points exponentially distributed of the time range of the data. Hereby, the time differences between the data points were smallest at the beginning and grew exponentially toward the end of the time range. The selected data was appended to the data set. In this way, no additional information was added but due to the unequal distribution of the doubled data points, the iterative training of the CNN will focus more on the initial phase. As done in the presented numerical study, this doubling of data can be repeated with varying percentages.
We define the CNN for the encoding via a number Ncl of convolutional layers followed by a fully connected linear layer with activation that maps the output of the repeated convolutions onto a vector of size cs—the code size. This encoding part will be denoted by CAE and we will write
to express that a velocity state υ(t) has been encoded to ρ(t) of dimension cs via the neural network. Note the inclusion of the interpolation P to the tensor grid.
For the decoding, we use a truly linear layer of input dimension cs and output dimension k, so that with a POD basis Ṽ of dimension k the reconstruction reads
where W is the k × cs-matrix that realizes the linear layer that maps and where vs. is the shift vector that was used to center the POD data; cp. Remark 4.
The parameters of the architecture of the CAE-model used in the presented numerical results are given in Table 1. See also Figure 3 for an illustration.
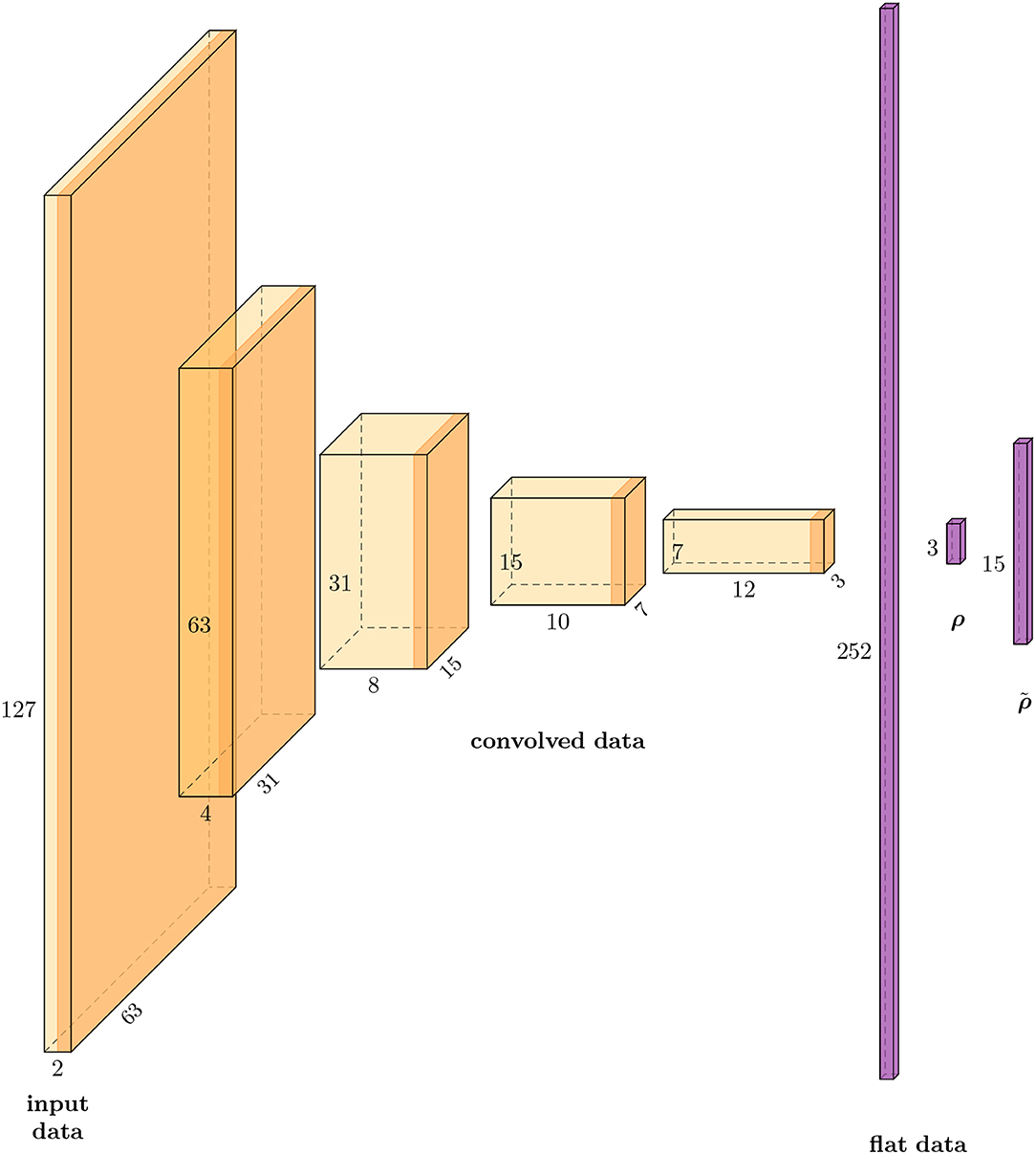
Figure 3. Schematic illustration of the data sizes in each layer of the CAE-3 network that was used in the numerical example: Four convolutional layers, one reshape of the data to the vector (flat data), a full linear layer that reduces the data to ρ and a linear layer without activation for the decoding to .
The parameters of CAE as well as the coefficients of W are then trained to fit the data of [V+] with respect to the loss function
For that, the data [V+] is randomly split into batches of size Bs, the mean value of Equation (11) over a batch is computed, and the parameters of CAE and W updated according to a stochastic gradient method. This procedure is repeated over the same data in a number of epochs.
With the decoder matrix W, the POD basis Ṽ, and the CAE model for variable code sizes cs at hand, we approximate the actual nonlinearity N(υ)υ by the linear-affine LPV approximation
of dimension cs where ρ =CAE(υ).
For comparison, we considered the plain POD LPV approximation
with the POD basis Ṽcs of dimension cs and the POD coordinates .
Remark 5. The blending
of the two natural LPV representations was found to be beneficial since N(·)ρ tended to damp out the fluctuations whereas N(ρ)(·) triggered the unsteady behavior very well but led to blowups regardless whether the CAE or the POD approximation was considered. This observation can be explained by known stabilizing effect of linearizations of the first type (cp., e.g., the convergence analysis of iterative linearization schemes in Karakashian [33]) whereas in a linearization like N(·)ρ the ρ undergoes a differentiation which can explain the tendency for a blow-up.
Certainly, the value of s can be another parameter in the optimization of the approximation. For simplicity, we simply fixed it to .
For a variable code size cs that eventually defines the dimension of the affine-linear LPV approximation, we checked the performance of the CAE-cs-model and compared it to a POD approximation of the same dimension.
Since the cylinder wake is a chaotic system, in the sense that, e.g., the transition to the periodic regime is severely influenced by perturbations, a direct comparison of trajectories is uninformative. Therefore, we plotted the resulting curves of drag and lift for the full order simulation FOM and the approximations on top of each other to get a qualitative expression of the approximation. An informative comparison, however, can be derived from the analysis how well the approximations capture the limit cycle of the periodic regime. For that, we plot the phase portrait of drag vs. lift.
For the smallest investigated code size cs=3 (cp. Figure 4) we found that the CAE-3 approximation departed from the FOM-simulation in the initial phase but captured the limit cycle well with but a small distortion of the symmetry and an overestimation of the drag by about 2%. The POD-3-simulation, i.e., the LPV approximation by a POD basis of dimension 3, did not reach a clear limit cycle within the comparatively long time horizon and did not well reproduce the nominal values of drag and lift either.
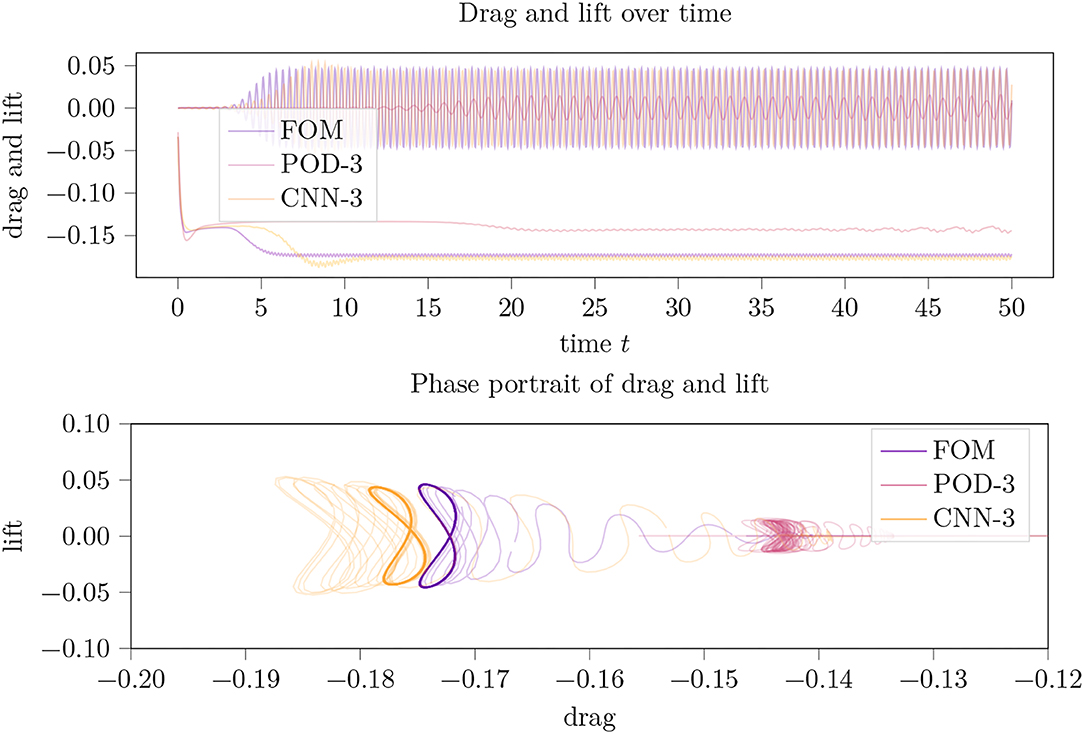
Figure 4. Drag and lift trajectories (top) over time and their phase portrait (bottom picture) for an LPV approximation of the incompressible flow around a 2D cylinder using a parameter dimension of cs = 3.
For an increased code size cs=5, the POD approximation qualitatively and quantitatively (cp. Figure 5) improved to approximately the same level as CAE-3. The CAE approximation for this code size did not perform well at all.
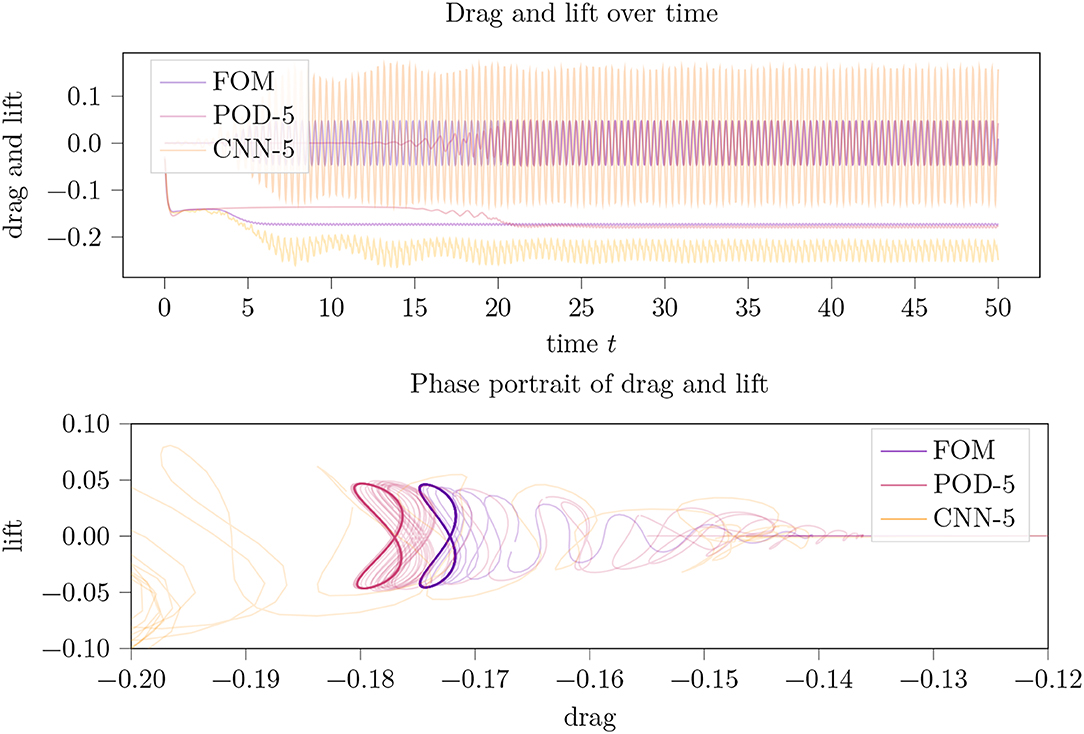
Figure 5. Drag and lift trajectories (top) over time and their phase portrait (bottom picture) for an LPV approximation of the incompressible flow around a 2D cylinder using a parameter dimension of cs = 5. In the phase portrait plot, parts of CAE-5 were truncated.
For cs=8, the POD approximation improved only marginally whereas the CAE-model approximation reached a limit cycle again though with a huge distortion of the symmetry and a significant overestimation of drag and lift (cp. Figure 6).
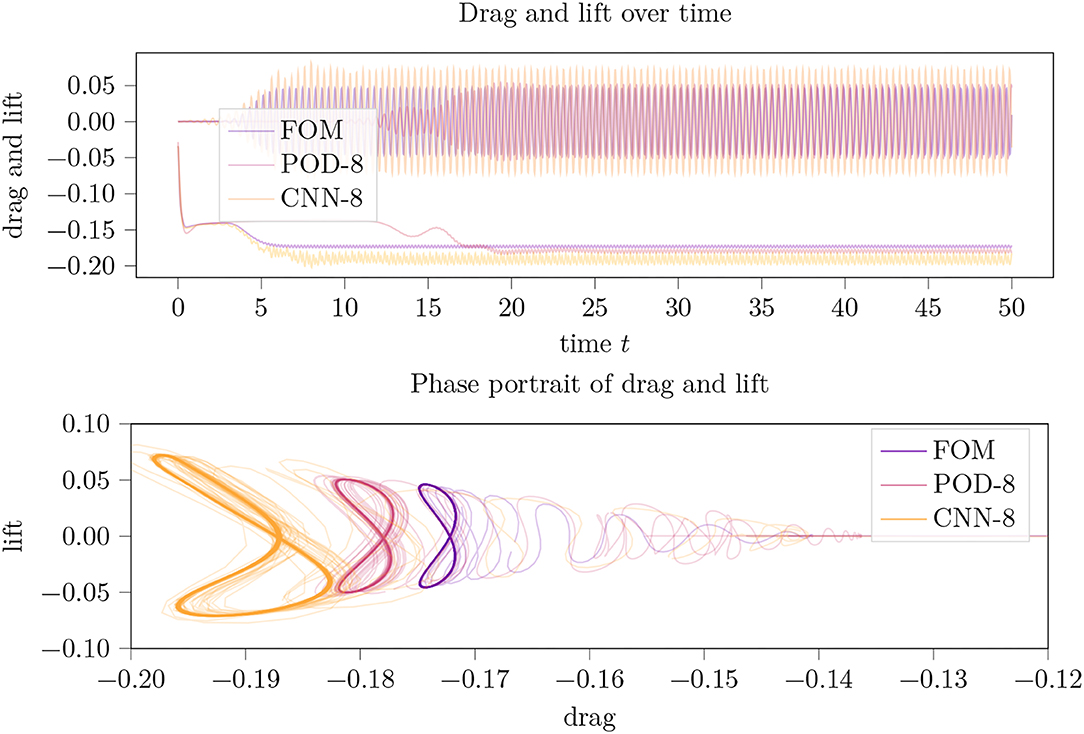
Figure 6. Drag and lift trajectories (top) over time and their phase portrait (bottom picture) for an LPV approximation of the incompressible flow around a 2D cylinder using a parameter dimension of cs = 8.
Since, theoretically, the CAE-8 and CAE-5 model contain the CAE-3 model, their failure in the approximation basically means a failure of the optimization of the model parameters during the training. The manifold ways of adapting the parameters of the network architecture as well as those of the optimization procedure offers many ways of improving.
Even more, the interpolation to the uniform tensor grid (cp. Figure 2) means a significant loss of information so that slight improvements here, e.g., through a local refinement that preserves the tensor structure, will likely improve the approach.
Nonetheless, the good performance of CAE-3 fully supports our initial working hypotheses that a convolutional neural network can provide a very low-dimensional encoding targeted to an efficient affine LPV approximation of the incompressible Navier-Stokes equations. In this case, it took a parameter space of dimension cs=3 to well approximate the nonlinear incompressible Navier-Stokes equations of dimension 42764 just in the velocity part.
Finally, for a rough orientation about the computational costs, we provide the computational times as they can be read off the log files (i.e., only a single wall clock measurement). All experiments have been conducted on a computing cluster but without GPU support and restricted to two computing kernels. The training of the individual CAE models took about 30 min, the simulation of the full order model over the full time frame from t = 0 to t = 50 took about 80 min. The same simulation but with the POD reduced LPV model took about 130 min, whereas the CAE model took 420 min. The computational overhead of the POD model is mainly due to the blending that requires the evalution of the nonlinearity twice as often. This also holds true for the CAE model but accounts only for a part of the overtime.
Certainly, these timings can be improved significantly. However, the focus of the presented work was on reducing the model in terms of its structure by replacing the nonlinear term by a low-dimensional LPV formulation.
To evaluate the robustness of the presented method, we conduct the same experiments at Re = 60, i.e., in a regime that is even more convection-dominated and that is expected to be more difficult to approximat by a linear projection method. The results are displayed in Figure 7 and are well inline with those reported for Re = 40 before. The CAE-3-model outperformed all POD-configurations, once a satisfactory setup of hyperparameters was found. In fact, for the training of the CAE-model for Re = 60 we added another batch p=20 percent of data focussed on the initial phase (cp. Table 2) while for the simulation we set (cp. Remark 5). Both updates to the Re = 40 case are natural as in this regime, the initial phase is shorter and the simulation is less stable. Interestingly, the POD-models gave a solid performance at small cs, but deteriorated for larger sizes of the POD basis. An explanation for this behavior might lie in the sensitivity of the problem and in numerical errors in the POD vector computation. We also note that adding stability to the system by an even smaller s was of no help as it damped the periodic behavior (with a result similar to the POD-3 approximation in Figure 7).
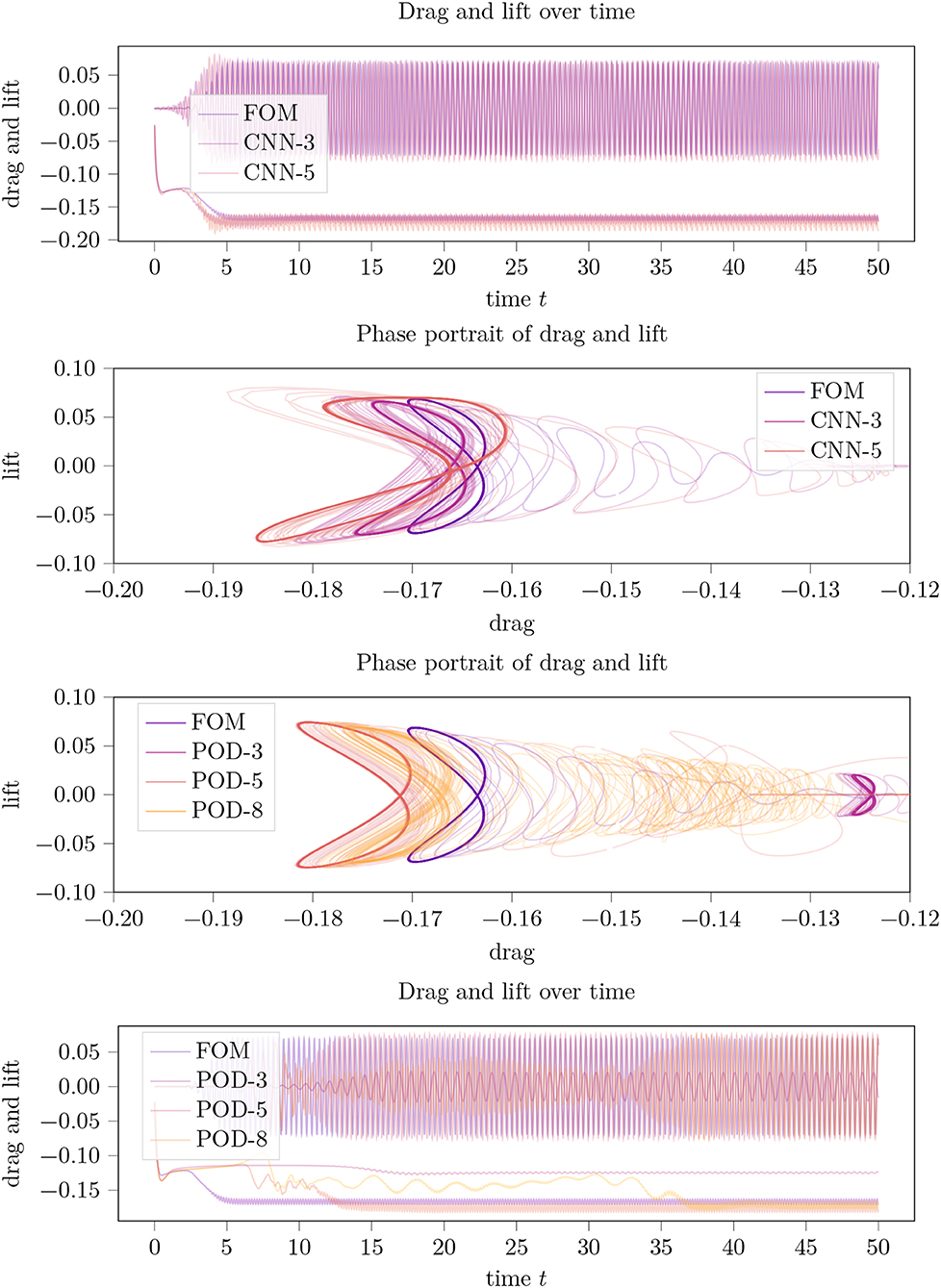
Figure 7. Summarized results for the case of Re = 60. Drag and lift trajectories over time and their phase portraits for an LPV approximation of the incompressible flow around a 2D cylinder using a variable parameter dimension cs in the POD and CAE approximation and in comparison to the full order model (FOM).
In the presented work, we have provided a proof of concept on how CNNs in combination with POD can be used to generate very low-dimensional LPV approximations to nonlinear systems. For the considered Navier-Stokes equations and, generally, for any quadratic system, the LPV approximation is affine-linear if only the decoding from the coded variable ρ to the state reconstruction ṽ is a linear map.
The myriad of parameters that can be tuned in the design of DNNs and their training have not been investigated in depth (once a satisfying working setup has been found). Accordingly, there is a huge potential for improvements since the well working CAE-3 example is certainly no global optimum and the larger code sizes could, theoretically, be tuned for better approximations. A systematic investigation of the parameters is left to future research efforts.
Another future research direction is the direct identification of the parametrization matrices Ni, i = 0, …, r, for an affine-linear LPV-representation
without resorting to POD coordinates. It was mentioned in Koelewijn and Tóth [12], that a neural network without the nonlinear activation that approximates ρ(υ) → N(ρ(υ)) is such an affine-linear map with coefficients Ñi defined through the weighting matrices of the neural net. Accordingly, the same architectures and optimization algorithms can be used to design the parametrization from scratch. However, in the large-scale setting, it is not feasible to learn (and even just to store) these coefficients. A general approach to that would be sparsity enforcing methods in the learning of the weights. A more specific approach could consider transposed convolutional layers that reverses the convolutions and contractions but without the nonlinear activations. Certainly, the concatenated operations of the transposed convolutions and the reversal of the interpolation from the FEM to the tensor grid can be represented as one sparse operator. This is subject to further investigations.
The code used to compute the numerical results is available from https://doi.org/10.5281/zenodo.6401953.
JH conducted the basic research and the numerical experiments and wrote the manuscript. PB contributed relevant references and proofread and enhanced the manuscript. RB contributed to the numerical experiments and generated plots. All authors contributed to the article and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. ^A particularly powerful feature of DNN architectures that comes with the explicit formulation of DNNs in terms of fundamental functions is that the gradients of the current realization with respect to the parameters can be computed by algorithmic differentiations in a straight-forward way. All packages for neural networks make use of this functionality during the training of the network. Once, new functional dependencies are introduced, e.g., in the loss function, one has to take care that this so called back propagation of gradients is maintained.
1. Kokotovic PV. The joy of feedback: nonlinear and adaptive. IEEE Control Syst Mag. (1992) 12:7–17. doi: 10.1109/37.165507
2. Sontag ED. Mathematical Control Theory. 2nd Edn. Texts in Applied Mathematics. New York, NY: Springer-Verlag (1998).
3. Dodds SJ. Sliding mode control and its relatives. In: Feedback Control. Linear, Nonlinear and Robust Techniques and Design with Industrial Applications. London: Springer London (2015). p. 705–92.
4. Grüne L, Pannek J. Nonlinear model predictive control. Theory and algorithms. Cham: Springer (2017).
5. Breiten T, Kunisch K, Pfeiffer L. Feedback stabilization of the two-dimensional Navier-Stokes equations by value function approximation. Appl Math Optim. (2019) 80:599–641. doi: 10.1007/s00245-019-09586-x
6. Banks HT, Lewis BM, Tran HT. Nonlinear feedback controllers and compensators: a state-dependent Riccati equation approach. Comput Optim Appl. (2007) 37:177–218. doi: 10.1007/s10589-007-9015-2
7. Benner P, Heiland J. Exponential stability and stabilization of extended linearizations via continuous updates of riccati-based feedback. Internat J Robust Nonlinear Control. (2018) 28:1218–32. doi: 10.1002/rnc.3949
8. Apkarian P, Noll D. Controller design via nonsmooth multidirectional search. SIAM J Control Optim. (2006) 44:1923–49. doi: 10.1137/S0363012904441684
9. Beeler SC, Tran HT, Banks HT. Feedback control methodologies for nonlinear systems. J Optim Theory Appl. (2000) 107:1–33. doi: 10.1023/A:1004607114958
10. Alla A, Kalise D, Simoncini V. State-dependent Riccati equation feedback stabilization for nonlinear PDEs. arXiv 2106. 07163. (2021) doi: 10.48550/arXiv.2106.07163
11. Apkarian P, Gahinet P, Becker G. Self-scheduled H∞ control of linear parameter-varying systems: a design example. Autom. (1995) 31:1251–61. doi: 10.1016/0005-1098(95)00038-X
12. Koelewijn PJW, Tóth R. Scheduling dimension reduction of LPV models-a deep neural network approach. In: 2020 American Control Conference, ACC 2020. Denver, CO, USA, July 1-3, 2020. Denver, CO: IEEE (2020). p. 1111–7.
13. Hashemi SM, Werner H. LPV modelling and control of burgers' equation. IFAC Proc Volumes. (2011) 44:5430–5. doi: 10.3182/20110828-6-IT-1002.03318
14. Dahmen W, Plesken C, Welper G. Double greedy algorithms: reduced basis methods for transport dominated problems. ESAIM Math Model Numer Anal. (2014) 48:623–63. doi: 10.1051/m2an/2013103
15. Ohlberger M, Rave S. Reduced basis methods: success, limitations and future challenges. In: Proceedings of the Conference Algoritmy. Vysoké Tatry, Slovakia (2016). p. 1–12.
16. Reiss J, Schulze P, Sesterhenn J, Mehrmann V. The shifted proper orthogonal decomposition: a mode decomposition for multiple transport phenomena. SIAM J Sci Comput. (2018) 40:A1322–44. doi: 10.1137/17M1140571
17. Papapicco D, Demo N, Girfoglio M, Stabile G, Rozza G. The neural network shifted-proper orthogonal decomposition: a machine learning approach for non-linear reduction of hyperbolic equations. arXiv[Preprint].arXiv:2108.06558. (2021). doi: 10.1016/j.cma.2022.114687
18. Sarna N, Benner P. Data-Driven model order reduction for problems with parameter-dependent jump-discontinuities. arXiv[Preprint].arXiv:2105.00547. (2021). doi: 10.1016/j.cma.2021.114168
19. Deo IK, Jaiman R. Learning wave propagation with attention-based convolutional recurrent autoencoder net. arXiv[Preprint].arXiv:2201.06628. (2022). doi: 10.48550/arXiv.2201.06628
20. Lee K, Carlberg KT. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J Comput Phys. (2020) 404:108973. doi: 10.1016/j.jcp.2019.108973
21. Kim Y, Choi Y, Widemann D, Zohdi T. Efficient nonlinear manifold reduced order model. arXiv[Preprint].arXiv:2011.07727. (2020). doi: 10.48550/arXiv.2011.07727
22. Mojgani R, Balajewicz M. Physics-aware registration based auto-encoder for convection dominated PDEs. arXiv[Preprint].arXiv.2006.15655. (2020). doi: 10.48550/arXiv.2006.15655
23. Nikolopoulos S, Kalogeris I, Papadopoulos V. Non-intrusive surrogate modeling for parametrized time-dependent PDEs using convolutional autoencoders. arXiv[Preprint].arXiv.2101.05555. (2021). doi: 10.1016/j.engappai.2021.104652
24. Fresca S, Manzoni A. POD-DL-ROM: enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. arXiv[Preprint].arXiv:2103.0160. (2021). 2103. 0160. doi: 10.1016/j.cma.2021.114181
25. O'Shea K, Nash R. An introduction to convolutional neural networks. arXiv[Preprint].arXiv.1511.08458. (2015). doi: 10.48550/arXiv.1511.08458
26. Baumann M, Benner P, Heiland J. Space-Time Galerkin POD with application in optimal control of semi-linear parabolic partial differential equations. SIAM J Sci Comput. (2018) 40:A1611–41. doi: 10.1137/17M1135281
27. Behr M, Benner P, Heiland J. Example setups of navier-stokes equations with control and observation: spatial discretization and representation via linear-quadratic matrix coefficients. arXiv[Preprint].arXiv:1707.08711. (2017). doi: 10.48550/arXiv.1707.08711
28. Heiland J. Decoupling and Optimization of Differential-Algebraic Equations with Application in Flow Control (Dissertation). TU Berlin (2014).
29. Altmann R, Heiland J. Continuous, semi-discrete, and fully discretized navier-stokes equations. In: Campbell S. Ilchmann A, Mehrmann V, Reis T, editors. Applications of Differential-Algebraic Equations: Examples and Benchmarks. Differential-Algebraic Equations Forum. Springer (2019). p. 277–312.
30. Logg A, Mardal KA, Wells G editors. Automated Solution of Differential Equations by the Finite Element Method. The Fenics Book. Vol. 84. Berlin: Springer (2012).
31. Heiland J. dolfin_navier_scipy: a python Scipy FEniCS interface. Zenodo. (2019). Available online at: https://github.com/highlando/dolphin_navier_scipy. Github/Zenodo.
32. Babuǎka I, Miller A. The post-processing approach in the finite element method-part 1: calculation of displacements, stresses and other higher derivatives of the displacements. Int J Numer Meth Eng. (1984) 20:1085–109. doi: 10.1002/nme.1620200610
Keywords: model reduction and model simplification, Navier-Stokes equation, data driven learning, linear parameter varying (LPV), convolutional neural network
AMS subject classifications: 65M22, 76D05.
Citation: Heiland J, Benner P and Bahmani R (2022) Convolutional Neural Networks for Very Low-Dimensional LPV Approximations of Incompressible Navier-Stokes Equations. Front. Appl. Math. Stat. 8:879140. doi: 10.3389/fams.2022.879140
Received: 18 February 2022; Accepted: 22 March 2022;
Published: 29 April 2022.
Edited by:
Traian Iliescu, Virginia Tech, United StatesReviewed by:
Omar Abu Arqub, Al-Balqa Applied University, JordanCopyright © 2022 Heiland, Benner and Bahmani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jan Heiland, aGVpbGFuZEBtcGktbWFnZGVidXJnLm1wZy5kZQ==
†ORCID: Jan Heiland orcid.org/0000-0003-0228-8522
Peter Benner orcid.org/0000-0003-3362-4103
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.