- 1Advanced Research Computing, Virginia Tech, Blacksburg, VA, United States
- 2Department of Mathematics, Virginia Tech, Blacksburg, VA, United States
In this work, we explore how the emergence of collective motion in a system of particles is influenced by the structure of their domain. Using the Vicsek model to generate flocking, we simulate two-dimensional systems that are confined based on varying obstacle arrangements. The presence of obstacles alters the topological structure of the domain where collective motion occurs, which, in turn, alters the scaling behavior. We evaluate these trends by considering the scaling exponent and critical noise threshold for the Vicsek model, as well as the associated diffusion properties of the system. We show that obstacles tend to inhibit collective motion by forcing particles to traverse the system based on curved trajectories that reflect the domain topology. Our results highlight key challenges related to the development of a more comprehensive understanding of geometric structure's influence on collective behavior.
1. Introduction
Collective behavior associated with living in groups is documented across the animal kingdom [1]. Although they are simpler organisms than animals, bacteria also demonstrate the ability to generate complex collective motion when they occur in sufficiently dense swarms [2]. Similarly to the recognizable aligned motion in fish schools and bird flocks, bacteria in swarms can align their motion locally to achieve organized spatio-temporal patterns [3, 4]. However, in natural environments, bacterial swarms may exist on structures with complex geometries [5] and the relationship between these geometries and the resulting collection motion is as yet unstudied. Experiments show evidence of individual bacteria colliding with obstacles and reversing their direction of motion [6], but no experiments exist showing how these reversals necessarily influence the motion of a group of bacteria. In this article, we seek to understand how complex domain geometries impact collective motion through the model system of a particle swarm obeying a flocking model which is well-studied in the physics literature.
The Vicsek model is widely used to study phase transitions in active matter [7–10]. The modeling framework is particularly useful to advance understanding for biological systems, since biological agents frequently align their motion with each other, leading to a variety of interesting emergent phenomena. Collective motion can be considered as a super-diffusive phenomenon, due to the fact that particles that align their trajectories tend to move a greater distance compared to particles that collide and interfere with each other [11]. Whereas basic diffusion can be modeled with a random walk, the Vicsek model enables spontaneous alignment of particles, which results in symmetry-breaking due to the non-conservative nature of the alignment process. Particles move at constant speed, with their trajectories determined by interactions with other particles and random noise η. Inter-particle interactions and noise are competing effects that determine the strength of collective behavior generated by the model.
The dynamics of collective motion depend in part upon the structure of the space where the motion occurs. Collective motion on two-dimensional surfaces is important to a wide range of applications including the movement of crowds [12, 13], herd animals [14], and microbial activity such as biofilm growth on surfaces [15]. Since the interactions between particles are local, information exchange within such systems is constrained by the structure of the space where the particle interactions occur. In particular, the presence of obstacles alters the topology of the domain where motion occurs, which exerts independent influence over the aggregate behavior in the system. The structure of the domain can be characterized based upon invariant properties, which are integral measures that provide an averaged measure of the geometry [16, 17]. The theoretical basis for geometric characterization has been established in several seminal works from the previous century. Weyl's tube formula establishes that the volume within a small distance of any closed surface in ℝ3 is predicted from the surface area and Euler characteristic [18]. Hadwiger's characterization theorem asserts that the geometry for an object in ℝn is characterized by n + 1 scalar measures [19, 20]. The Lesbesgue measure for the object and its boundary are the first two invariants. The remaining quantities can be identified as integrals of the boundary curvature invariants, with the Euler characteristic being among these measures [21]. Euler characteristic has a well-established link to percolation, with χ = 0 defining the boundary between percolating and non-percolating structures [22, 23]. A two-dimensional surface is associated with three isotropic measures, which are the surface area A, perimeter length L, and total curvature K. The total curvature K relates to the topology of the structure (equivalently captured based on the Euler characteristic), which represents a discrete contribution to the system dynamics. The capacity for geometric invariants to characterize complex structures has been explored in detail for three-dimensional systems [24]. In this work, we consider how these inherently geometric effects influence the scaling behavior for the Vicsek model.
Confined diffusion provides a natural analog for these studies [25]. Persistent random walk models are routinely used to develop mechanistic understanding into anomalous diffusion phenomena [26]. Geometric effects often play an important role in anomalous diffusion, most notably in systems that involve confinement, e.g., due to the presence of a complex microstructure [27, 28]. Because the presence of obstacles inhibits diffusion, confinement is widely associated with sub-diffusive scaling. Crowding has been identified as an important source of sub-diffusion in cellular systems [29]. The mechanism itself may be self-reinforcing, and anomalous diffusion can be considered as a driving mechanism for spatial heterogeneity [30]. Geometric barriers have a natural tendency to inhibit information exchange within a system. Since these effects are antagonistic in comparison to the super-diffusive tendencies associated with collective motion, it is interesting to consider their interaction. Within this context, the influence of geometry is of interest due to the possibility that confinement may frustrate a superdiffusive process. Viswanathan et al. [31] established a criterion to characterize super-diffusive phenomena based on the correlation timescale for orientation persistence in random walks. Due to particle alignment the Vicsek model leads to superdiffusive behavior when the contribution of random noise is sufficiently small. The introduction of obstacles, in the form of disk-like versus particle-like agents, has been shown to alter the emergence of order in the Vicsek model depending on the characteristics of collision which are defined [32].
In this article, we explore how geometric constraints, imposed by static obstacles in the domain, alter the scaling behavior recovered from the Vicsek model. We demonstrate that the diffusion coefficient, critical noise threshold, and scaling exponents are each sensitive to the topology of the space where motion occurs. Introducing obstacles changes the domain topology and forces particles to travel along curved trajectories; based on the fact that geodesic curves cannot intersect with the obstacles, particles cannot travel long distances along straight-line trajectories when obstacles are present. This geometric effect leads to fundamental changes to the scaling behavior. Since geometry is an inherent component in many physical problems, we suggest that structural effects may inhibit universality for other systems. In the sections that follow, we provide a straightforward demonstration of these effects and consider their consequences for collective motion.
2. Modeling
2.1. Flocking Model
Vicsek et al. [7] presented an elegant model of flocking for groups of self-propelled particles which has garnered interest across science and engineering particularly for the phase transitions it shows between ordered and disordered group behavior. The model considers particles moving at a constant speed in a two-dimensional, periodic domain and which perform an averaging protocol with the heading directions of their nearby neighbors corrupted by additive noise. In this work, we introduce obstacles into the domain and study their effect on group alignment using the order parameter from Vicsek et al. [7] and a measure of the particles' diffusion.
Consider a two-dimensional periodic domain with side length L containing N particles. Particle j, for j = 1, …, N, has position and velocity at time step t ∈ ℕ∪{0}. We define particle j's heading direction as
which updates at successive time steps according to
where k denotes the index for all neighbors k≠j such that the distance between particle j and k is less than R. The random noise source term ξj is uniformly distributed, independent, random variables with −π ≤ ξj(t) ≤ π. The amplitude for the noise is scaled by η ∈ [0, 1]. Particle j's velocity and position are then updated as
where c > 0 is the constant particle speed (see Table 1) and . Note that vj has unit length. In this work, we consider the presence of obstacles in the particles' domain. When the updated position xj(t + 1) is inside the boundary of an obstacle, we take xj(t + 1) = xj(t) and set vj(t + 1) = − vj(t) to model elastic collisions with the obstacles.
Critical behavior in the Vicsek model is assessed by an order parameter based on the mean particle velocity. The so-called polarization φ is defined at time step t as
When particles are not aligned, φ is close to zero. When the system is more ordered, φ is close to 1. It is the transition from the disordered phase to the ordered phase in steady state, driven by the magnitude of the noise η, that the Vicsek model is generally constructed to consider. Stationary conditions are determined such that the statistics of the particles' polarization do not change based on translations of the time window along the time axis. In the standard Vicsek model, the critical transition is well-described by
where |τ| is the distance of η to some critical noise ηc (i.e., τ = η − ηc) and β is the associated critical exponent.
It is well-known that finite size effects alter the scaling behavior. As particles in the system align their motion, a correlation structure develops such that the motion of adjacent particles are strongly correlated. In an infinite system, the length scale for spatial correlations can be arbitrarily large. In a finite-size system with length scale L, the correlation length cannot exceed L. In such systems the stationary scaling behavior should obey the relation [33].
where is a suitable scaling function and ν determines the scaling behavior for finite size systems. In this work, we further consider the role of the domain structure on the scaling behavior for the Vicsek model. We will demonstrate that, as the topology for the domain is altered, critical phase transitions will necessarily change as well.
2.2. Diffusion
Diffusion provides a conceptual framework to measure how particles pervade in the domain as a function of the obstacle geometry and the collective behavior resulting from the Vicsek model. For this work, we use a definition of the diffusion coefficient based on the mean square displacement M covered by the particles over time, which is defined as
where t0 is selected as a time step when the system exhibits steady-state behavior and ||·|| is the Euclidean norm. In standard diffusion, M(t) grows linearly with time based on the diffusion coefficient D such that
Due to the collective behavior generated by interactions in systems using low noise, particles may behave super-diffusively or sub-diffusively based on the power law
When P = 1, the particles move according to standard diffusion; the sub-diffusive regime is associated with P < 1 and the super-diffusive regime with P > 1. For the Vicsek model, super-diffusive effects are driven by the tendency for particles to align their motion with nearby particles [31]. A competing effect is due to the influence of obstacles, which prevent particles from moving long distances along a straight-line path. When obstacles are present, particles must follow a curved trajectory to traverse the system, and thus the mean-squared displacement will be smaller per unit time on average. All possible paths must necessarily conform to the topology of the domain structure, and the shortest distance paths will be geodesic curves that inherit their curvature from the space where movement can occur. This leads to sub-diffusive behavior in confined systems. We will consider the diffusion coefficient as a measure of these effects in the case where these two basic forces compete due to the obstacle arrangement and noise.
2.3. Geometric Measure Theory for Anisotropic Systems
The tendency for the Vicsek model to produce polarization presents intriguing possibilities with respect to geometric interactions. Structural effects can also produce anisotropic tendencies, which have potentially interesting interactions with emergent collective motion. Measure theory provides a formal mathematical basis for the characterization of complex geometric structures. The Minkowski tensors derived by Schröder-Turk et al. [34] provided a quantitative basis to assess the role of geometry in such contexts. Here, we consider this approach applied in the context of two-dimensional systems.
Consider the set Ω ∈ ℝ2 with boundary ∂Ω, which represents the domain where motion can occur, meaning that the particle trajectories xj(t) ∈ Ω for all j. The scalar invariants are well-known in the context of the Minkowski-Steiner formula, which has provided the basis for influential theoretical works [18, 19, 21]. These invariants are the quermassintegrals,
where k is the boundary curvature. The quermassintegrals define a complete set of measures to account for the rotation-invariant properties of a structure. For two-dimensional sets, the relevant invariants relate to the surface area, perimeter length and total curvature, the latter being directly proportional to the Euler characteristic, χ = W2/π. Note that for a 2D structure there is only a single curvature invariant, whereas higher dimensional structures will be associated with additional invariants (e.g., due to both mean and Gaussian curvature for the case of a three-dimensional surface). Therefore, as the dimension of the space increases, so too does the set of invariants. The scalar invariants have proven to be a powerful tool to characterize the properties and behavior of complex materials [16, 24, 35–38].
Scalar measures are limited in the sense that they can only describe the isotropic properties of a material. Generalized tensor-valued measures are able to characterize the anisotropic structure of sets. Following the convention used by Schröder-Turk et al., this leads to the following definition for the Minkowski tensors, which extend the set of measures considered in Equation (9) to include vector and tensor-valued quantities. Below we summarize the original approach, restricting the result to two-dimensional systems in the interest of clarity. The first of the vector-valued quantities is defined as
where x is the position vector. The measure is a geometric analog for the center of mass. The normalized value will exactly coincide with the center of mass of a structure if the material is homogeneous (uniform mass density). It is noted that, while the definitions given by Schröder-Turk et al. do not satisfy translation invariance; this can be achieved by determining all other measures relative to the geometric center. The vector-valued boundary invariants are, therefore,
where and n is the unit vector normal to the structure boundary. For the cases relevant to this work, ∂M is a closed curve and .
Second order tensors are also be defined using this approach, which is of particular significance due to the application of Alesker's theorem [39]. Any additive, continuous functional F depending on the structure can be represented as a sum that involves a limited set of shape contributions
where the coefficients do not depend on Ω and the unit tensor Q≡e1e1 + e2e2, where e1 and e2 are unit vectors that constitute an orthonormal basis for ℝ2. Independent shape information is thereby contained in the basis constructed from the scalar invariants based on QW0, QW1, and QW2, and the tensors , , , , and , which are defined as given below. A geometric analog of the inertia tensor is obtained in the form
The tensor-valued boundary invariants are
These boundary invariants characterize structural asymmetries based on the location of boundary and its curvature. For two-dimensional systems, Equations (14)–(16) define a set of seven geometric tensors that account for the anisotropic properties of a structure. The measures are geometric in that the expressions involve only units of length. Each of the tensors listed in Equation (16) satisfy both the homogeneity condition as well as the translation invariance condition. In the present context, we will consider the role of the topology in particular, which is embedded in the tensor invariant . Using the fact that n is a unit normal vector,
where Tr is the trace of a matrix. The eigenvalues of thereby relate to the directional contribution of the total curvature. Since the total curvature is proportional to the Euler characteristic, a topological invariant, the connectivity can be considered in an anisotropic context based on . In this work, we focus our attention on how topology influences the scaling behavior in the Vicsek model. We show that these effects are of considerable consequence, noting that a comprehensive geometric treatment should also consider the full set of tensor invariants given in Equations (14)–(16). For sufficiently isotropic structures, the scalar measures should provide an adequate characterization of geometric contribution to the scaling behavior.
3. Simulations
We consider simulations of the 2D Vicsek model subject to fifteen different geometric constraints as depicted in Figure 1, where the white area indicates where particles may move and the black areas are obstacles. Periodic boundary conditions are applied in all cases with the understanding that a periodic rectangular 2D domain is homeomorphic to a torus. The geometries shown in Figure 1 thereby correspond to surfaces of a torus with holes punched in it. The cases have one (A), two (B), or six (C) disjoint circular obstacles and, for each of these, the obstacles increase in size as the case number increases. Noting that χ = 0 for a torus, the Euler characteristic for each structure is determined from the number of obstacles; as long as no two obstacles contact each other, each obstacle is associated with a single geodesic loop in the domain with a corresponding unit decrease to the Euler characteristic. Structures on the top row therefore have χ = −1, the second row χ = −2, and the third row χ = −6. Moving from left to right in each row, the structures have fixed topology but an increasing ratio of obstacle perimeter to area.
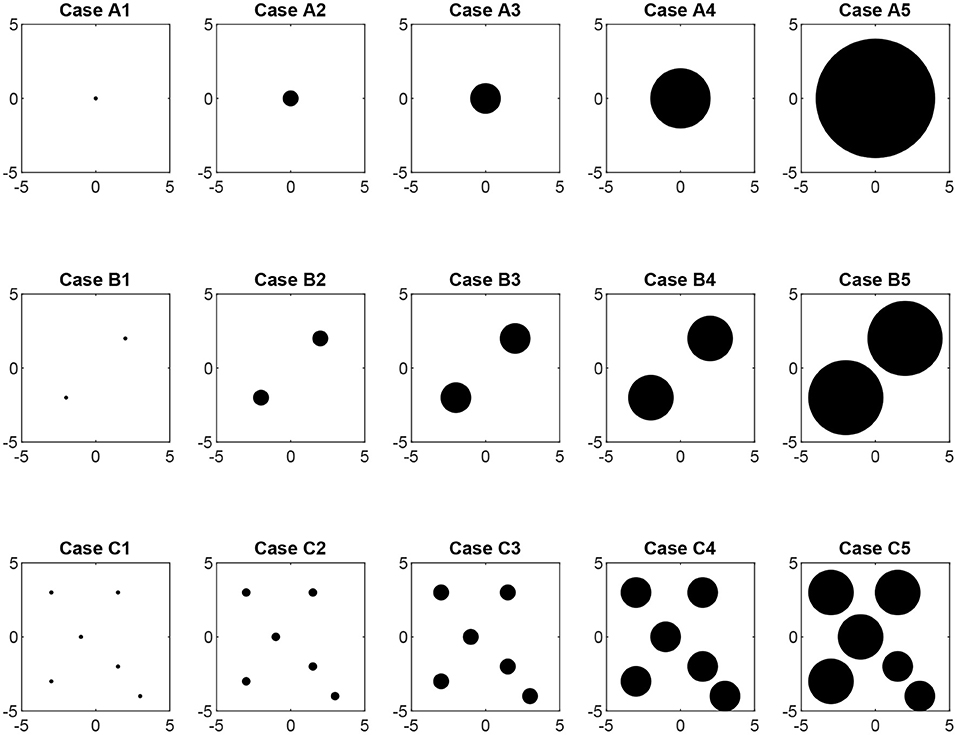
Figure 1. Fifteen cases of obstacle topologies. Particle motion occurs within the white region. Each row corresponds to a different topology, with one obstacle on the first row, two disjoint obstacles on the second row and six disjoint obstacles on the third row. Each column has comparable surface area where particles are allowed to move.
The number of particles is chosen so that the particle density is constant for all simulations. This choice was made to exclude the possibility for critical transitions based on the particle density. The number of particles, therefore, decreases as the total obstacle area is increased. For example, in case A5, the effective domain area is A = L2 − (obstacle area) = (10)2 − π(42) ≈ 100 − 50.3 = 49.7 and so the number of particles required to maintain a constant density between cases is N = ρ × A = ⌈(2)(49.7)⌉ = 100, i.e., half the number as in a case with no obstacles.
In addition to the fifteen domains with obstacles, two control cases are considered to better understand the results of this study. The first (“control 1”) is the native Vicsek model in a 2D domain with no obstacles. This condition allows for assessing the role of the obstacles in the emergence of group order. The second (“control 2”) defines the particles as performing random walks independent of each other, thus, neglecting any interaction defined by the averaging rule in Equation (2). This condition allows for extracting the role of group alignment on the diffusion metrics.
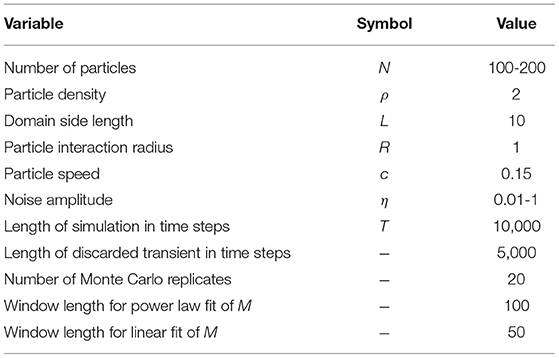
Simulations of the model were performed with Matlab (version 2019a, Mathworks, Natick, MA, USA). A 5,000-time-step transient was eliminated to allow for computing polarization, mean square distance, and corresponding diffusion metrics in the steady-state regime. For each value of the selected parameters and domain cases, we performed 20 Monte Carlo replicates with random initial conditions for particle positions and velocities. This, and the elimination of the transient in each simulation, serves to remove the effect of initial conditions. In the following figures of the results, error bars indicate mean values ± one standard deviation with statistics taken over the 20 replicate simulations. A summary of the simulation parameters is given in Table 1.
4. Results
Simulation results, presented in Figure 2, show a phase transition between ordered and disordered states analogous to the native Vicsek model. When the obstacles are very small (cases A1, B1, and C1), the system behaves almost identically to the Vicsek model without obstacles (control 1). This is expected in situations where the length scale for the obstacles is smaller than the length-scale for particle interactions. The system shows lower polarization as the number and size of obstacles increase for the cases with low noise. This is because particle collisions with obstacles frustrate the persistent alignment of particles, making it less probable for flocks of particles to travel together for long distances. This decrease in polarization is most profound when more obstacles are present, e.g., comparing cases A5, B5, and C5. This effect persists as η approaches the transition from the ordered to the disordered phase.
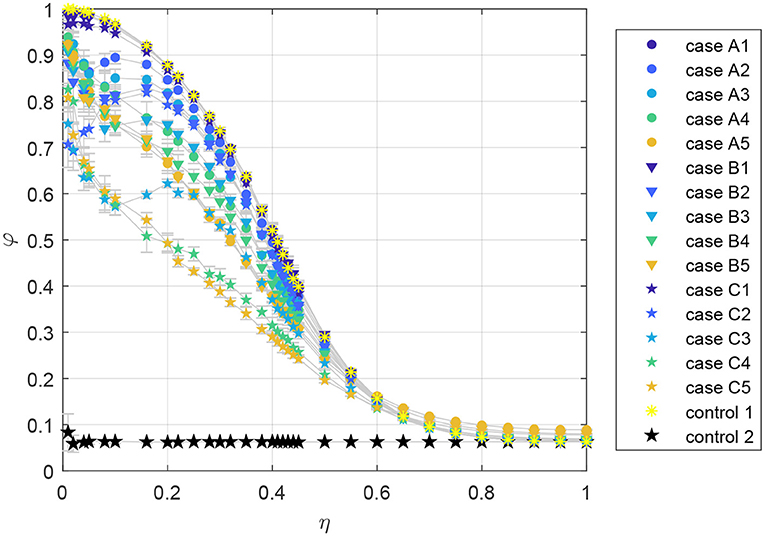
Figure 2. Steady-state polarization φ as a function of the noise amplitude η for fifteen obstacle cases, control 1 (interaction but no obstacles), and control 2 (no interaction, no obstacles). Plots show mean values over 20 Monte Carlo replicates and the error bars in gray indicate ± one standard deviation.
Since the polarization curves show shallower decay as the obstacle area is increased, it is natural to ask what is the critical value of η which evidences the disordered state, denoted ηc as in Vicsek et al. [7]. For each case, values of ηc are determined by performing a non-linear least-squares regression based on the form
where the parameters a, b, and ηc are computed independently per case. Best-fit values for ηc and b are provided along with the geometric descriptors of the cases in Table 2. For cases with one or two obstacles (A1–A5, B1–B5), the value of ηc increases as the area of the obstacles increases, and the values of cases with different number of obstacles but similar areas have comparable values. However, the relationship between obstacle area and critical noise is more complex for cases with six obstacles (C1–C5), suggested by the non-monotonic trend in ηc with changing geometry. Since the contribution due to topology is inherently discrete, non-monotonic and even discontinuous transitions should not be considered surprising.

Table 2. Geometric measures of the domain structure with fitted critical noise amplitude ηc and scaling exponent b.
With the horizontal axis shifted by ηc and set on logarithmic scale, the polarization curves are shown in Figure 3. For all cases, the function Equation (18) adequately represents the scaling behavior as η → ηc, indicating that this is an appropriate functional form. For a single obstacle, the exponent b shows a clear increasing trend with increasing obstacle size. The trend observed for a single obstacle is no longer evident with more obstacles (see Table 2). It is clear from cases A5, B5, and C5 in Figure 1 that arrangements with more obstacles correspond to obstacles with a smaller radius of curvature. Since the average particle trajectories must curve to avoid the obstacles, this length scale will necessarily alter the scaling behavior. There is a clear shift for the critical noise ηc.
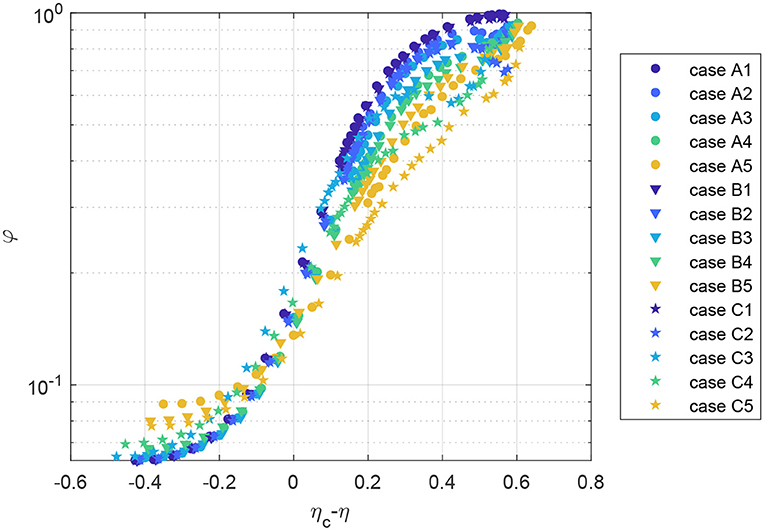
Figure 3. Mean steady-state polarization φ as a function of the distance from the critical noise ηc for fifteen obstacle cases.
As we consider values of η further from ηc, we see that the presence of obstacles suppresses the effect of polarization due in the collective motion regime (ηc − η > 0). However, we also note that the obstacles lead to small amounts of polarization even in noise-dominated regimes (ηc − η < 0). This is because the obstacle arrangement is not perfectly isotropic, so the particle motion will tend to have a preferred orientation.
The effect of the obstacles on group order can be interpreted by considering the motion of the particles as a process of mass diffusion in the domain. Figure 4 gives the diffusion coefficient for all cases and noise values in the left column of plots. From a first viewing of the plots, we can see that increasing the noise parameter decreases the diffusion in the system, which can be explained by noticing that higher noise induces more convoluted paths for each particle. Similarly to the polarization plots, the cases with small obstacles (A1, B1, and C1) are virtually indistinguishable. As a note, the plots for D with noise equal to 1 go to a value of ≈ 0.02.
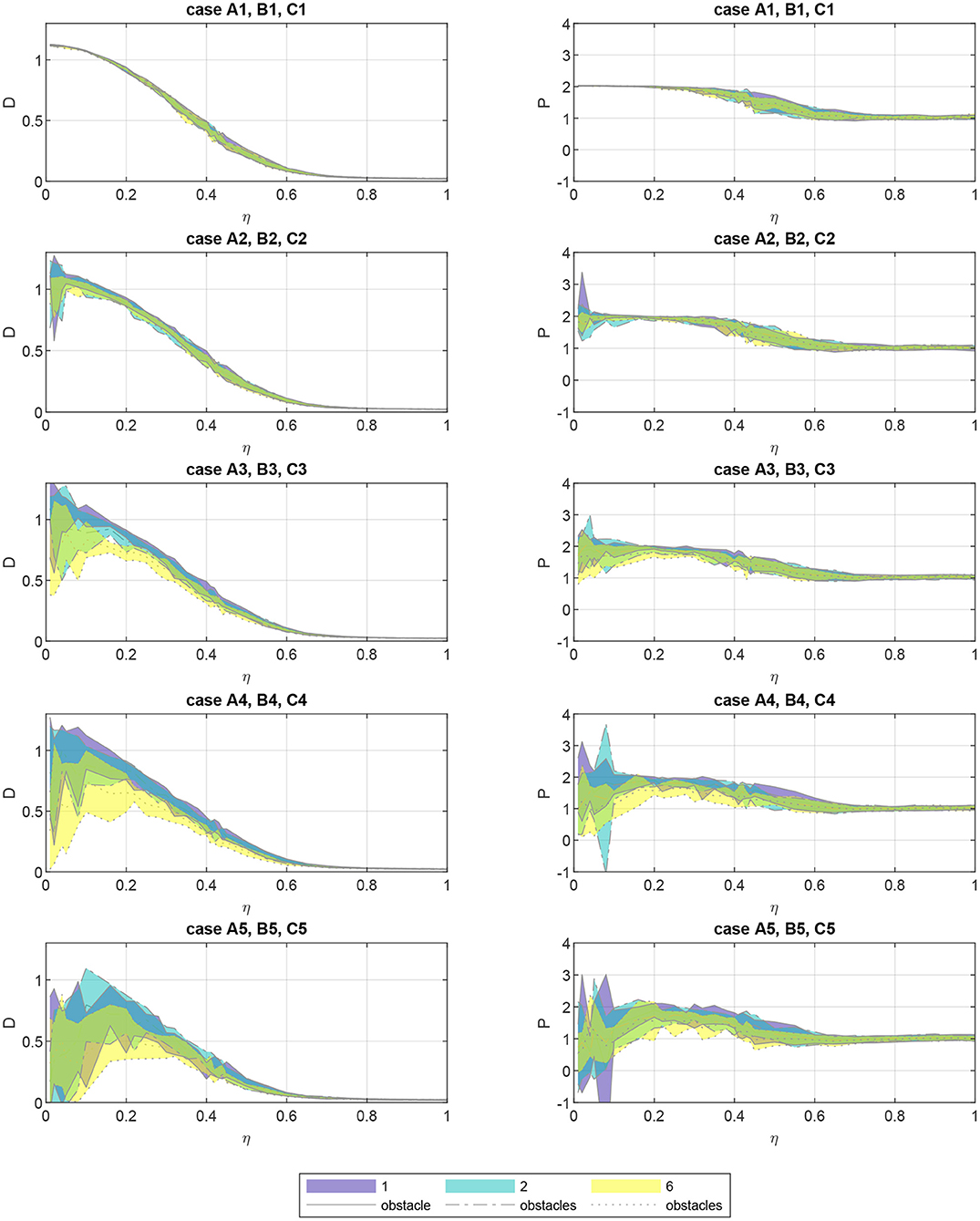
Figure 4. Diffusion coefficient D (left plots) and the diffusion exponent P (right plots) as a function of the noise amplitude η for the fifteen obstacle cases. Cases are indicated in figure titles. Cases are grouped by the number of obstacles by color (see legend), and are placed on the same subplot when obstacles (whether 1, 2, or 6) are approximately the same size. The individual obstacle size increases for lower subplots. Shaded regions indicate mean ± one standard deviation over the 20 Monte Carlo replicates.
We see the effect of increasing obstacle area in the low noise conditions, since particle paths are less likely to traverse long distances and intersect obstacles when noise is high. For the low noise conditions, the mean diffusion coefficient decreases and the variation among replicates (shown as ± one standard deviation in the shaded area) increases as obstacle area rises. This effect is more noticeable for larger numbers of obstacles, as shown by the lower values for the yellow shaded areas with six obstacles (C1–C5) in comparison to the purple and blue areas for one (A1–A5) and two (B1–B5) obstacles, respectively.
These trends are echoed by the diffusion exponent P, shown in the right column of plots in Figure 4. When the obstacles are small, all cases show super-diffusion, although the exponent decreases with increasing noise. As the obstacle area is increased, the variation between replicates grows, shown again by the shaded areas, particularly for the low noise conditions. The effect of the obstacles is so strong that it qualitatively changes the nature of mass diffusion in the system, pushing the mean diffusion exponent less than one and into a sub-diffusive regime in many cases. It should be noted that, although the plots seem to show values for P < 0, this is not the case. The shaded region indicates the mean P± one standard deviation over the 20 replicates, and the lower bound for this area may be negative when the mean and standard deviation, both positive, are low and high, respectively.
The control cases shed light on the possible sources for these trends. Figure 5 shows the diffusion coefficient and exponent for the two control cases. In the left plot, we see that the diffusion coefficient is significantly larger for the Vicsek model (control 1) than for a system of independent particles (control 2) when noise is low, and that increasing noise decreases diffusion in either case. Furthermore, both cases can be classified as super-diffusive when noise is near zero, but this effect is quickly replaced by standard diffusion with increasing noise when particles are independent (control 2). For interacting particles (control 1), the super-diffusivity is more robust to noise, but is replaced by standard diffusion in high noise conditions. This can be explained if the super-diffusivity results from the coordination between the particles, which is lost as noise dominates the collective behavior.
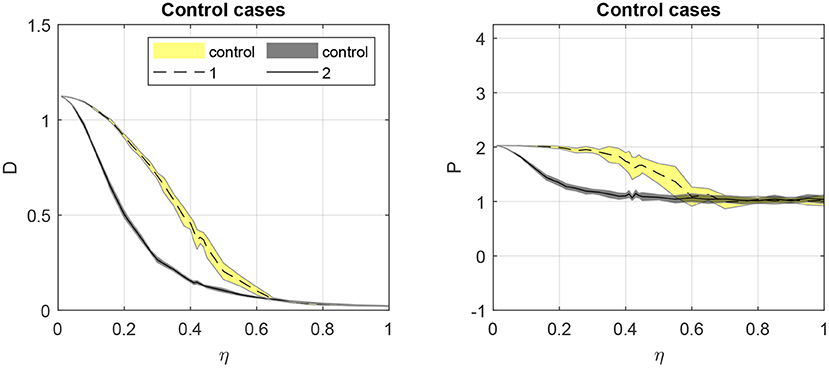
Figure 5. Diffusion coefficient D (left) and the diffusion exponent P (right) as a function of the noise amplitude η for the two control cases. Control 1 is the native Vicsek model with no obstacles in the domain; control 2 is random walker dynamics with no interactions between the particles. Shaded regions indicate mean ± one standard deviation over the 20 Monte Carlo replicates.
5. Discussion
In this work, we consider the extent to which critical phenomena are influenced by geometric structure in the context of the Vicsek model. We simulate dynamics of the Vicsek model on 2D surfaces with varying topology, and we study the ramifications for scaling behavior and the critical phase transition. The effects of geometric structure can be considered within the broader context of length scale effects within the system. Length scale effects can be understood based on three scales. In the native Vicsek model, length scale effects in the system are controlled by the particle interaction radius R and system size L control, which determine scaling effects with respect to density and finite size. The third length scale associated with our model with obstacles is the size of obstacles based on their radius of curvature. The operative length scales in the system are non-dimensionalized based on the radius for particle interactions; direct particle-particle interactions occur within radius R = 1. The physical size of the system and the length scale for geometric structure are normalized accordingly. Since the topology can be directly related to the total curvature, structures with a larger magnitude Euler characteristic will have a smaller average radius of curvature at fixed area. This is visually apparent from Figure 1. The domain topology is measured based on the Euler characteristic, already a non-dimensional measure. The Euler characteristic is a natural link to incorporate scaling studies associated with percolation, which can be considered alongside other finite-size scaling effects in the system [9, 33].
While the limitations of finite-size are well-established for the Vicsek model, finite size systems are in many cases better suited to represent the inherent inhomogeneities in many actual natural and biological systems. Geometric invariants provide a quantitative basis to assess these effects in a practical setting. Noting that the polarization in the system introduces anisotropic effects, scalar geometric invariants cannot be expected to completely parameterize the problem. A more complete description for the aniostropic effects can be formulated in terms of the Minkowski tensors [34]. The relevant tensor-valued measures are presented in this work for two-dimensional systems. In a system that is isotropic, scalar geometric effects will be sufficient to characterize leading order effects with respect to the polarization strength.
The effects of domain structure are directly evident from the diffusion coefficient, which is evaluated using the mean-square displacement. Competing effects are observed based on the super-diffusive tendency for particles to align their movement and the sub-diffusive tendency associated with confined systems. As the domain becomes more topologically complex, this influences the diffusive scaling behavior by forcing particles to follow more curved trajectories that avoid the obstacles. For a fixed timescale, the mean-squared distance for the particle trajectories will be smaller due to the fact that they must traverse a greater distance along the curved trajectory, since the most efficient pathways will follow geodesic curves. This is a basic reason why confinement leads to sub-diffusion. In the Vicsek model, confinement frustrates the typically super-diffusive tendencies of collective motion. Since particle-particle alignment is favored for ηc − η > 0, the scaling exponents indicate that the Vicsek model is super-diffusive. However, the effect is suppressed when the number of obstacles is increased, as shown in Figure 4. We also note that the obstacles have a significant impact on low noise cases, when particle polarization tends to be the most significant. Particle collisions with obstacles tend to break up groups of particles so that the collective motion is less persistent at large length and time scales. In some situations, noise may even enhance alignment when obstacles are present. The crossover between these two regimes is also clearly evident from Figure 3 based on cases B2, C2 and C3.
When we consider this work in the context of the phenomenon of bacterial swarming, we see that the Vicsek model echoes phase transitions between disordered to ordered behavior from experimental studies on bacterial swarms. For instance, swarms of Bacillus subtilis show phase transitions with varying particle density or mean speed [3]. Based on our results, we would expect that bacterial collective motion would be impacted by obstacles similarly to the particles in our model; that is, the introduction of obstacles into the domain would promote more disorder in the system, with the effect enhanced by more and smaller obstacles. Such an expectation is supported by noting that microscopy shows Bacillus subtilis reversing its heading direction when it collides with obstacles, which would create a negative effect of the reversed particle in the polarization and reduce the order in the system as a whole [6]. Experimental work considering these collisions with respect to the group behavior would be a next step to trace the role of geometry in these transitions.
In summary, geometric structure and domain topology in particular have important consequences for collective motion. While structural effects are an essential component for a very wide range of natural and engineered systems, the scaling behavior for collective motion will be altered by even a basic level of structural complexity. Results from geometric measure theory provide a basis to quantitatively assess the associated effects, an approach that can be extended to consider arbitrarily complex structures. Problems of practical interest can be easily identified that involve arbitrary two-dimensional surfaces as well as three-dimensional systems. The study of complex structures necessarily collides with the study of finite-size effects, since geometric structure introduces additional length scales into the system. This work focuses on the scaling behavior associated with the critical noise, with the particle density held constant. Based on the literature on the Vicsek model, the system's behavior is expected to be sensitive to particle density as well. Further characterization of these effects is an important component to understanding collective motion in a practical setting.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The repository can be found at: https://github.com/JamesEMcClure/ObstacleVicsek.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
NA was supported by the National Science Foundation under grant 1751498.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Wu Y. Collective motion of bacteria in two dimensions. Quant Biol. (2015) 3:199–205. doi: 10.1007/s40484-015-0057-7
3. Cisneros LH, Kessler JO, Ganguly S, Goldstein RE. Dynamics of swimming bacteria: Transition to directional order at high concentration. Phys Rev E. (2011) 83:061907. doi: 10.1103/PhysRevE.83.061907
4. Gachelin J, Rousselet A, Lindner A, Clement E. Collective motion in an active suspension of Escherichia coli bacteria. New J Phys. (2014) 16:025003. doi: 10.1088/1367-2630/16/2/025003
5. Al-Amshawee S, Yunus MYBM. Geometry of biofilm carriers: a systematic review deciding the best shape and pore size. Groundwater Sustain Develop. (2021) 12:100520. doi: 10.1016/j.gsd.2020.100520
6. Cisneros L, Dombrowski C, Goldstein RE, Kessler JO. Reversal of bacterial locomotion at an obstacle. Phys Rev E. (2006) 73:030901. doi: 10.1103/PhysRevE.73.030901
7. Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys Rev Lett. (1995) 75: 1226–9. doi: 10.1103/PhysRevLett.75.1226
8. Vicsek T, Zafeiris A. Collective motion. Phys Rep. (2012) 517:71–140. doi: 10.1016/j.physrep.2012.03.004
9. Baglietto G, Albano EV, Candia J. Criticality and the onset of ordering in the standard Vicsek model. Interface Focus. (2012) 2:708–14. doi: 10.1098/rsfs.2012.0021
10. Ginelli F. The physics of the Vicsek model. Eur Phys J Special Top. (2016) 225:2099–117. doi: 10.1140/epjst/e2016-60066-8
11. Nagy M, Daruka I, Vicsek T. New aspects of the continuous phase transition in the scalar noise model (SNM) of collective motion. Phys A Stat Mech Appl. (2007) 373:445–54. doi: 10.1016/j.physa.2006.05.035
12. Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature. (2000) 407:487–90. doi: 10.1038/35035023
13. Warren WH. Collective motion in human crowds. Curr Direct Psychol Sci. (2018) 27:232–40. doi: 10.1177/0963721417746743
14. Giardina I. Collective behavior in animal groups: theoretical models and empirical studies. HFSP J. (2008) 2:205–19. doi: 10.2976/1.2961038
15. Stewart PS. Diffusion in biofilms. J Bacteriol. (2003) 185, 1485–1491. doi: 10.1128/JB.185.5.1485-1491.2003
16. Mecke KR. Integral geometry in statistical physics. International Journal of Modern Physics B. 1998;12(09):861–899.
17. Mecke KR. “Additivity, convexity, and beyond: applications of Minkowski Functionals in statistical physics,” In: Statistical Physics and Spatial Statistics. Berlin: Springer (2000). p. 111–84.
20. Klain DA. A short proof of Hadwiger's characterization theorem. Mathematika. (1995) 42, 329–339.
22. Mecke K, Wagner H. Euler characteristic and related measures for random geometric sets. J Stat Phys. (1991) 64:843–50.
23. Bobrowski O, Skraba P. Homological percolation and the Euler characteristic. Phys Rev E. (2020) 101:032304. doi: 10.1103/PhysRevE.101.032304
24. McClure JE, Ramstad T, Z Li Z, Armstrong RT, Berg S. Modeling geometric state for fluids in porous media: evolution of the euler characteristic. Transp Porous Media. (2020) 133:229–50. doi: 10.1007/s11242-020-01420-1
25. van Drongelen R, Pal A, Goodrich CP, Idema T. Collective dynamics of soft active particles. Phys Rev E. (2015) 91:032706. doi: 10.1103/PhysRevE.91.032706
26. Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1–77. doi: 10.1016/S0370-1573(00)00070-3
27. Condamin S, Tejedor V, Voituriez R, Bénichou O, Klafter J. Probing microscopic origins of confined subdiffusion by first-passage observables. Proc Natl Acad Sci USA. (2008) 105:5675–80. doi: 10.1073/pnas.0712158105
28. Massignan P, Manzo C, Torreno-Pina JA, García-Parajo MF, Lewenstein M, Lapeyre GJ. Nonergodic Subdiffusion from Brownian Motion in an Inhomogeneous Medium. Phys Rev Lett. (2014) 112:150603. doi: 10.1103/PhysRevLett.112.150603
29. Weiss M, Elsner M, Kartberg F, Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys J. (2004) 87:3518–24. doi: 10.1529/biophysj.104.044263
30. Oliveira FA, Ferreira RMS, Lapas LC, Vainstein MH. Anomalous diffusion: a basic mechanism for the evolution of inhomogeneous systems. Front Phys. (2019) 7:18. doi: 10.3389/fphy.2019.00018
31. Viswanathan GM, Raposo EP, Bartumeus F, Catalan J, da Luz MGE. Necessary criterion for distinguishing true superdiffusion from correlated random walk processes. Phys Rev E. (2005) 72:011111. doi: 10.1103/PhysRevE.72.011111
32. Martinez R, Alarcon F, Rodriguez DR, Aragones JL, Valeriani C. Collective behavior of Vicsek particles without and with obstacles. Eur Phys J E. (2018) 41:91. doi: 10.1140/epje/i2018-11706-8
33. Baglietto G, Albano EV. Finite-size scaling analysis and dynamic study of the critical behavior of a model for the collective displacement of self-driven individuals. Phys Rev E. (2008) 78:021125. doi: 10.1103/PhysRevE.78.021125
34. Schröder-Turk GE, Mickel W, Kapfer SC, Klatt MA, Schaller FM, Hoffmann MJF, et al. Minkowski Tensor Shape Analysis of Cellular, Granular and Porous Structures. Adv Mater. (2011) 23:2535–53. doi: 10.1002/adma.201100562
35. Mecke KR, Stoyan D. Statistical Physics and Spatial Statistics: The Art of Analyzing and Modeling Spatial Structures and Pattern Formation. vol. 554. Springer Science & Business Media (2000).
36. Arns CH, Knackstedt MA, Pinczewski WV, Mecke KR. Euler-Poincaré characteristics of classes of disordered media. Phys Rev E. (2001) 63:031112. doi: 10.1103/PhysRevE.63.031112
37. Armstrong RT, McClure JE, Robins V, Liu Z, Arns CH, Schlüter S, et al. Porous media characterization using minkowski functionals: theories, applications and future directions. Transp Porous Media. (2019) 130:305–35. doi: 10.1007/s11242-018-1201-4
38. Rabot E, Wiesmeier M, Schlüter S, Vogel HJ. Soil structure as an indicator of soil functions: a review. Geoderma. (2018) 314:122–37. doi: 10.1016/j.geoderma.2017.11.009
Keywords: anomalous diffusion, collective behavior, Euler characteristic, integral geometry, Vicsek model
Citation: McClure JE and Abaid N (2022) Effect of Topology and Geometric Structure on Collective Motion in the Vicsek Model. Front. Appl. Math. Stat. 8:829005. doi: 10.3389/fams.2022.829005
Received: 04 December 2021; Accepted: 11 February 2022;
Published: 08 March 2022.
Edited by:
Jean Clairambault, Institut National de Recherche en Informatique et en Automatique (INRIA), FranceReviewed by:
M. N. Kuperman, Bariloche Atomic Centre (CNEA), ArgentinaShahin Rouhani, Sharif University of Technology, Iran
Copyright © 2022 McClure and Abaid. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James E. McClure, bWNjbHVyZWpAdnQuZWR1
 James E. McClure
James E. McClure Nicole Abaid
Nicole Abaid