Iterator-Based Design of Generic C++ Algorithms for Basic Tensor Operations

Numerical tensor calculus has recently gained increasing attention in many scientific fields including quantum computing and machine learning which contain basic tensor operations such as the pointwise tensor addition and multiplication of tensors. We present a C++ design of multi-dimensional iterators and iterator-based C++ functions for basic tensor operations using mode-specific iterators only, simplifying the implementation of algorithms with recursion and multiple loops. The proposed C++ functions are designed for dense tensor and subtensor types with any linear storage format, mode and dimensions. We demonstrate our findings with Boost's latest uBlas tensor extension and discuss how other C++ frameworks can utilize our proposal without modifying their code base. Our runtime measurements show that C++ functions with iterators can compute tensor operations at least as fast as their pointer-based counterpart.

1. Introduction

Numerical tensor calculus can be found in many application fields, such as signal processing [1], computer graphics [2, 3], and data mining [4, 5] in which tensors are attained by, e.g., discretizing multi-variate functions [6] or by sampling multi-modal data [7]. Tensors are interpreted as generalized matrices with more than two dimensions and are, therefore, also referred to as hypermatrices [8]. Similar to matrix computations, most numerical tensor methods are composed of basic tensor operations such as the tensor-tensor, tensor-matrix, tensor-vector multiplication, the inner and outer product of two tensors, the Kronecker, Hadamard and Khatri-Rao product [9–11]. Examples of such methods containing basic tensor operations are the higher-order orthogonal iteration, the higher-order singular value decomposition [12], the higher-order power method and variations thereof.

High-level libraries in Python or Matlab, such as NumPy, TensorLy, or TensorLab¹ offer a variety of tensor types and corresponding operations for numerical tensor computations. However, in case of tensor multiplication operations tensors are dynamically unfolded in order to make use of optimized matrix operations, consuming at least twice the memory than their in-place alternatives [13]. Depending on the program, Python or Matlab can also introduce runtime overhead due to just-in-time compilation or interpretation and automatic resource management.

To offer fast execution times with minimal memory consumption, many tensor libraries are implemented in C++ which provides a simple, direct mapping to hardware and zero-overhead abstraction mechanism [14, 15]. Their programming interface is close to the mathematical notation supporting elementwise and complex multiplication tensor operations [16–21]. All libraries offer a family of tensor classes that are parameterized by at least the element type. The library presented in [21] also parameterize the tensor template by the tensor order and dimensions. Tensor elements are linearly arranged in memory either according to the first-order or the last-order storage format. Most libraries use expression templates to aggregate and delay the execution of mathematical expressions for a data-parallel and even out-of-order execution [17, 19]. Some libraries can express the general form of the tensor-tensor multiplication with Einstein's summation convention using strings or user-defined objects. For instance, expressions like C["ijk"]=A["ilj"]∗B["kl"] or C(i,j,k)=A(i,l,k)∗B(k,l) specify a 2-mode multiplication of a 3-dimensional with a matrix. The interface can be very convenient utilized if the application or numerical method uses a fixed tensor order or contraction mode. However, many numerical methods such as the higher-order orthogonal iteration consist of variable tensor multiplications preventing the use of aforementioned expressions. In such cases, flexible interfaces and functions similar to the one presented in [22] are required allowing, e.g., the contraction mode to depend on other variables. A comprehensive and recent overview of the tensor software landscape is provided in [23] including all of the previously mentioned C++ libraries.

Most of the above mentioned libraries implement tensor operations using pointers, single and multi-indices. Accessing tensor elements with multi-indices, however, can slow down the execution of a recursively defined tensor function by a factor that is equal to the recursion depth and tensor order [24]. Using single indices or raw pointers on the other hand requires a combination of induction variables with mode-specific strides. This can be inconvenient and error-prone, especially when library users want to modify or extend C++ functions. The authors in [25] suggest to parameterize C++ functions in terms of tensor types and their proxies with which mode-specific iterators can be generated using the member functions begin and end. Index operations are hidden from the user by offering a simple iterator increment operation that is able to adjust its internal data pointer according to a predefined stride. However, their begin and end functions do not allow to specify a mode. The authors in [26] propose to use member functions begin and end of a tensor type that can generate mode-specific iterators. The mode is a non-type template parameter of the iterator requiring the recursion index and the contraction modes to be compile-time parameters. Similar to the aforementioned approaches, tensor functions are defined in terms of tensor types which makes the specification of iterator requirements difficult.

In this article, we present iterator-based C++ algorithms for basic tensor operations that have been discussed in [22] as part of a Matlab toolbox. Our software implementation follows the design pattern that has been used in the Standard Template Library (STL) and separates tensor functions from tensor types with the help of iterators only [27]. The separation helps to define iterator and function templates that are not bound to particular tensor and iterator types, respectively. We present C++ functions such as for_each and transform that perform unary and binary operations on tensor and subtensor elements. Our discussion also includes more complex multiplication operations such as tensor-vector (ttv), tensor-matrix (ttm), and the tensor-tensor multiplication (ttt). While we demonstrate their usability with Boost's uBlas tensor extension, the proposed C++ templates can be instantiated by tensor types that provide pointers to a contiguous memory region.

To our best knowledge, we are the first to propose a set of basic tensor functions that can process tensor types without relying on a specific linear data layout, eliminating the need to provide multiple algorithms for similar types. While a discussion of optimization techniques for data locality or parallel execution of tensor operations are beyond the scope of this article, we provide algorithmic changes to all proposed tensor functions to increase spatial locality. Moreover, we demonstrate that the introduced iterator abstraction does not penalize the performance of iterator-based C++ functions. On the contrary, our performance measurements with approximately 1,800 differently shaped tensors show that iterator- based functions compute elementwise tensor operations and the tensor-vector product at least as fast as pointer-based functions.

The remainder of the paper is organized as follows: Section 2 introduces mathematical notations used in this work and provides an overview of data organization for dense tensor and subtensor types. Section 3 describes Boost's uBlas tensor extension and class templates for tensors and subtensors. Section 4 introduces multi-dimensional iterators for a family of tensor types supporting any linear storage format. Section 5 discusses the design and implementation of tensor operations using multi-dimensional iterators. Section 6 presents runtime measurements of iterator- and pointer-based implementations of two elementwise tensor operations. Lastly, section 7 presents some conclusions of our work.

2. Preliminaries

2.1. Mathematical Notation

A tensor is defined as an element of the tensor space that is given by the tensor product of vector spaces typically over the real or complex numbers [28]. For given finite basis of the vector spaces, tensors can be represented by multi-dimensional arrays [8]. We do not distinguish between tensors and multi-dimensional arrays and allow their elements to be bool or integer types. The number of dimensions is called the tensor order and is denoted by the letter p. Tensors are denoted by bold capital letters with an underscore, e.g., A with A = (a_i)_i∈I where i is a multi-index i = (i₁, i₂, …, i_p) with i_r ∈ I_r for all 1 ≤ r ≤ p. The r-th index set I_r is defined as I_r: = {1, 2, …, n_r} for all 1 ≤ r ≤ p with n_r ∈ ℕ. n = (n₁, …, n_p) is called a dimension tuple of a p-dimensional tensor. The Cartesian product of all index sets of a p-order tensor A is called the multi-index set I with I = I₁ × I₂ × ⋯ × I_p. Elements of a p-dimensional tensor A are given by A(i₁, i₂, …, i_p) = a_i1i2…ip or A(i) = a_i with i ∈ I. Matrices have two dimensions and will be represented without an underscore B. Vectors are given by small bold letters such as b where one of the first two dimensions are equal to or greater than one. A tensor is a scalar if all dimensions are equal to one and denoted by small, non-bold letters.

A subtensor A′ of a tensor A is a reference to a specified region or domain of A and has the same order p and data layout π as the referenced tensor. It can be regarded as a lightweight handle with a dimension tuple n′ where the subtensor dimensions satisfy $n_r^{\prime }\le n_r$ for 1 ≤ r ≤ p. The r-th index set $I_r^{\prime }$ of a subtensor and its multi-index set I′ are analogously defined to I_r with $I_r^{\prime }\subseteq I_r$ and I, respectively. Each dimension $n_r^{\prime }$ and the corresponding index subset $I_r^{\prime }$ are determined by f_r, t_r, and l_r where f_r ∈ I_r and l_r ∈ I_r are the lower and upper bound of the index range with 1 ≤ f_r ≤ l_r ≤ n_r. The integer t_r defines the step size for the r-th dimension satisfying t_r ∈ ℕ for 1 ≤ r ≤ p. The shape tuple ${\mathbf{\text{n}}}^{\prime }=(n_1^{\prime },\dots ,n_p^{\prime })$ of a subtensor is given by $\lfloor n_r^{\prime }=(l_r-f_r)/t_r+1\rfloor$. Elements of a p-dimensional subtensor A′ are given by A′(i′) = a_i′′ with i′ ∈ I′.

Assuming a simple linear (flat) memory model, dense tensors shall be stored contiguously in memory. The (absolute) memory locations of tensor elements are given by k = k₀ + j · δ with k₀ ∈ ℕ₀ being the memory location of the first tensor element and δ being the number of bytes required to store tensor elements. We call $J:=\left\{0,1,\dots ,{\prod }_{r=1}^p{n}_r-1\right\}$ the single index set of A where each j ∈ J is the relative position of the j-th tensor element denoted by A[j]. A subtensor A′ of a tensor A has its own single index set J′ with ${\prod }_{r=1}^p{n}_r^{\prime }$ elements. We write A′[j′] to denote the j′-th subtensor element.

2.2. Data Organization and Layout

The tensor layout or storage format of a dense tensor defines the ordering of its elements within a linearly addressable memory and, therefore, the transformation between multi-indices and single indices. A p-order tensor A with a dimension tuple n, has (∏_rn_r)! possible orderings where only a subset of those are considered in practice. In case of two dimensions, most programming languages arrange matrix elements either according to the row- or column-major storage format. More sophisticated non-linear layout or indexing functions have been investigated for instance in [29, 30] with the purpose to increase the data locality of dense matrix operations.

The most prominent element layouts are first- and last-order storage formats. The former format is defined in the Fortran, the latter in the C and C++ language specification, respectively. Any linear layout can be expressed in terms of a permutation tuple π. The q-th element π_q corresponds to an index subscript r of a multi-index i_r with the precedence q where i_r ∈ I_r and 1 ≤ q, r ≤ p. In case of the first-order format, the layout tuple is defined as π_F: = (1, 2, …, p) where the precedence of the dimension ascends with increasing index subscript. The layout tuple of the last-order storage format is given by π_L: = (p, p − 1, …, 1).

Given a layout tuple π and the shape tuple n, elements of a stride tuple w are given by w_πr = 1 for r = 1 and $w_{{\pi }_r}={\prod }_{q=1}^{r-1}{n}_{{\pi }_q}$ otherwise, with 1 ≤ w_πq ≤ w_πr for 1 ≤ q < r ≤ p, see also Equation (2) in [24]. The q-th stride w_q is a positive integer and defines the number of elements between two elements with an identical multi-index except that their q-th index differs by one. Fortran stores tensor elements according to the first-order storage format with ${\mathbf{\text{w}}}_F=(1,n_1,n_1·n_2,\dots ,{\prod }_{r=1}^{p-1}{n}_r)$. In case of the last-order storage format π_L = (p, p − 1, …, 1), the stride tuple is given by ${\mathbf{\text{w}}}_L=({\prod }_{r=2}^p{n}_r,{\prod }_{r=3}^p{n}_r,\dots ,n_p,1)$ which is used by the C and C++ language for the data layout of the built-in multi-dimensional arrays.

3. Boost.uBlas Tensor Extension

Initially equipped with basic matrix and vector operations, Boost's uBlas has been recently extended with tensor templates and corresponding tensor operations to support multi-linear algebra applications². Tensor order, dimensions and contraction modes (if applicable) of the tensor and subtensor types are runtime variable. Common arithmetic operators are overloaded and evaluated using expression templates. In the following, we will only use the namespace std to denote the standard library namespace and skip boost::numeric::ublas. Boost's uBlas tensor extension offers a variety of basic dense tensor operations offering at least four important tensor functionality categories that have been discussed in [23].

3.1. Tensor and Subtensor Templates

The tensor template class represents a family of tensor types and adapts a contiguous container such as std::vector. It is designed to organize multi-dimensional data and to provide access with multi-indices and single indices.

template  <class T,

           class F = first_order,

           class C = std::vector<value_type>>

class tensor;

The element type T of tensor needs to fullfill the requirements specified by the container type C and needs to support all basic arithmetic scalar operations such as addition, subtraction, multiplication, and division. The container C type must satisfy the requirements of a contiguous container. By default, if no container class is specified, std::vector is used. Public member types such as value_type, size_type, difference_type, pointer, reference, and iterator are derived from the container type which stores elements of type value_type and takes care of the memory management. The memory space for tensor is dynamically allocated by std::vector::allocator_type. Public member functions are provided in order to construct, copy and move tensors. Data elements can be assigned to the tensor using the assignment operator =. Elements can be accessed with a single index using the access operator [] and multi-indices with the function call operator (). The user can conveniently create subtensors with the function call operator (). Size and capacity member functions such as size(), empty(), clear(), and data() are provided as well. The user has multiple options to instantiate tensor types. The default constructor creates an empty tensor of order zero with an empty shape tuple. The following expression instantiats a three-dimensional tensor A with the extents 4, 2, and 3 with elements of type double.

auto A = tensor<float>{4,2,3};

The user can also specify dimensions for each mode using the extents class from which the tensor order and size of the data vector is derived. The layout tuple is initialized according to the first-order storage format if not specified otherwise. Once the layout and dimensions are initialized, the constructor computes strides according to the computation in subsection 2.2 and Equation (2) in [24]. The following code snippet shows a possible instantiation of a three-dimensional tensor with a last-order storage format.

auto A = tensor<double,last_order>(extents{4,2,3});

The copy assignment operators () of the tensor class template are responsible for copy data and protecting against self-assignment. The user can expect the source and destination tensor class instances to be equal and independent after the copy operation. Two tensors are equal if they have the same shape tuple, tensor order and elements with the same multi-index independent of their layout tuple. Besides the type of the data elements, the user can change the content and the size of all member variables at runtime. The subtensor template class is a proxy of tensor for conveniently reference a subset of tensor elements.

template  <class T>

class subtensor;

The tensor template specializes subtensor with tensor<value_type,container> such that tensor::subtensor_t equals subtensor<tensor<value_type,container». In general, T needs to provide an overloaded access operator and function call operator for accessing contiguously stored tensor elements. The subtensor template contains a reference of the viewed tensor instance, i.e., subtensor::tensor_t, a pointer to the first element of type value_type*, extent ranges of a single dimension using the class span, extents of type size_type, strides of type size_type and also provides the same public member types and methods as tensor allowing both types to be used in free functions interchangeably. A subtensor instance neither owns nor tracks the referenced tensor object. It might become invalid whenever the corresponding tensor instance does not exist any more.

The constructor of subtensor takes a reference of subtensor::tensor_t and might take range types such as span and std::integral types as additional arguments that specify the multi-index space of a subtensor instance. The r-th span instance defines an index set $I_r^{\prime }$ that is a subset of the index set I_r of a selected tensor instance. A subtensor instance without any span objects references all elements of a subtensor::tensor_t object. The tensor template provides an overloaded function call operator with a template parameter pack which simplifies the construction of a subtensor subject. For instance, if A is of type tensor<float> with a dimension tuple (3, 4, 2), then S of the following expression is of type subtensor<tensor<float>> and has the dimensions 2, 2, 1.

auto S = A ( span(1,2), span(2,3), 1 );

The pointer to the first subtensor element is computed by adding an offset j^* to the pointer of the first tensor element. The offset j^* is computed by combining p lower bounds f of the span instances using the index function λ in Equation (1) in [24] such that $j^{*}={\lambda }_{\mathbf{\text{w}}}(\mathbf{\text{f}})$ with f = (f₁, …, f_p) where w is the stride tuple of a tensor and f_r is the lower bound of the r-th span instance.

3.2. Multi-Index Access

The tensor template provides multiple overloaded function call operators for conveniently accessing elements with multi-indices and scalar memory indices. The function call operator is a variadic template that computes the inner product of the stride and multi-index tuple in order to transform multi-indices onto single indices. Hence, the user can define the following statement which converts a three-dimensional tensor A into an identity tensor with ones in the superdiagonals.

for(auto i = 1u; i <= n; ++i)

  A(i,i,i) = 1.0;

Note that the statement is valid independent of A's layout tuple. The template tensor additionally allows to dynamically specify multi-indices using std::vector. In that case the argument of the function call is given by std::vector<std::size_t>(p,i) where p is the tensor order. Using multi-indices abstracts from the underlying data layout and enables the user to write layout invariant programs as all elements have a unique multi-index independent of the data layout. Note that accessing elements of a p-dimensional tensor A with multi-indices involves a multi-index to memory index transformation that is given by ${\lambda }_{\mathbf{\text{w}}}(\mathbf{\text{i}})=\sum _{r=1}^p{w}_r(i_r-1)$ where p is the tensor order with p > 1 and w is the stride tuple of A, see also Equation (1) in [24]. For fixed stride tuples w_F and w_L, the index functions λ_wF and λ_wL coincide with definitions provided in [25, 29]. Tensor elements can also be accessed with a single index using the overloaded access operator of tensor. This is convenient whenever the complete memory index set needs to be accessed independent of the tensor layout or order of data access is not relevant for the implementation of the tensor operation. For instance, A with any dimensions and storage format can be initialized by the following statement.

for(auto j = 0u; j  <  A.size(); ++j)

  A[j] = 0;

In contrast to an access with multi-indices, accessing tensor elements with single indices does not involve index transformations. However, most of the more complex tensor operations such as the tensor transposition require some type of multi-index access.

Subtensor elements can be similarly accessed using multi-indices with the subtensor's overloaded function call operator. Given the previously defined subtensor instance S with the dimensions (2,2,1), all diagonal elements can be set to 1 using a single for-loop where m is equal to 2.

for(auto i = 1; i  <= m; ++i)

  S(i,i,1) = 1;

Similar to the tensor case, the relative memory location needs to be computed as well, using index function λ transforming every index ${\mathbf{\text{i}}}^{\prime }\in I_r^{\prime }$ into an index of the set I_r with $j=j^{*}+{\lambda }_{\mathbf{\text{w}}\prime \prime }({\mathbf{\text{i}}}^{\prime })$ where j^* is the relative memory location of the first subtensor element. Elements of the stride tuple w′′ is given by $w_r^{″}=w_r^{\prime }{t}_r$ for 1 ≤ r ≤ p in which w′ is computed with n′. The subtensor template also provides an overloaded access operator with a single index. The following statement sets all subtensor elements to zero.

for(auto j = 0u; j  <  S.size(); ++j)

  S[j] = 0;

In contrast to the tensor case, accessing a relative memory location of subtensor's element with a single index involves its transformation using the index function λ and its inverse λ⁻¹. Given a valid single index j′ ∈ J′ and the relative memory location of the first subtensor element j^*, the relative memory location j ∈ J of a subtensor element at index j′ is given by $j=j^{*}+{\lambda }_{\mathbf{\text{w}}\prime \prime ,\mathbf{\text{w}}\prime }(j\prime )$ with λ_{w′′, w′} being a composition of the index functions λ_w′′ and ${\lambda }_{\mathbf{\text{w}}\prime }^{-1}$. The latter is the inverse index function is given by ${\lambda }_{\mathbf{\text{w}}}^{-1}(j)=\mathbf{\text{i}}$ where i_r = x_r/w_r + 1 with x_πr = x_πr+1−w_πr+1·(i_πr+1 − 1) for r < p and i_πp = ⌊j/w_πp⌋ + 1, see also [24].

4. Multi-Dimensional Iterator

C++ iterators are class templates that can traverse and access C++ container elements. They help to decouple the dependency between C++ container and C++ algorithms by parameterizing the latter in terms of iterators only. The following class template multi_iterator simplifies the iteration over a multi-index set of a tensor or subtensor independent of their storage formats and helps to decouple tensor types from tensor functions.

template<class iterator>

class multi_iterator;

The template parameter iterator should be a valid template parameter for std::iterator_traits with which iterator attributes can be queried. The tensor and subtensor templates can specialize multi_iterator with their corresponding pointer or iterator type. The constructor of multi_iterator initializes three private member variables, the current pointer of type std::iterator_traits<iterator>::pointer, a pointer to the strides of type const std::size_t* and a stride of type std::size_t. The following statement specializes the multi-dimensional iterator template and instantiates it.

auto it = multi_iterator<pointer>(k,w,1);

The argument k is a pointer to the first tensor element and w a pointer to the first stride tuple element. The last argument 1 selects the second stride from w. The copy-assignment operator of iterator copies the current position k, the pointer to the stride tuple w, and the stride wc. We consider two dimension-based iterators i1 and i2 equal if the current positions i1.k, i2.k and the strides i1.wc, i2.wc of the iterators are equal. Therefore, the statement (i1=i2) == i2 is considered true as both iterators have equal position and stride after the assignment (i1=i2).

The following example illustrates the difference of two ranges that are created by the random access iterator type iterator of std::vector and the multi_iterator<pointer> type. Let A be a three-dimensional dense tensor with elements of type float contiguously stored according to the first-order storage format. Let also k be a pointer to the first element of A initialized with A.data(). Given 4, 3, 2 be A's extents and w the stride tuple with (1,4,12), respectively, the two statements instantiate iterator pairs.

iterator                 first(k    ),  last(k+w[2]    );

multi_iterator<pointer> mfirst(k,w,1), mlast(k+w[2],w,1);

The first half-open range [first,last) covers all tensor elements with memory indices from 0 and to 12. The second range only covers elements with the multi-indices (1, i, 1) for 1 ≤ i ≤ 2 which corresponds to a mode-2 tensor fiber, i.e., the first row of the frontal tensor slice. Applying the index function λ, the relative memory positions of A's elements are at position 0, 4 and 8. The iteration over the second mode of A can be performed with both iterator pairs.

for(;  first !=  last;  first+=w[1]) {  *first = 5.0; }

for(; mfirst != mlast; mfirst+=1   ) { *mfirst = 5.0; }

The statements initialize the first row of A. The first statement uses the C++ standard random-access iterator first which is explicitly incremented with the second stride w[1]. The same operation can be accomplished with the multi-dimensional iterator mfirst which is initialized and internally incremented with the second stride w[1]. Our implementation of multi-dimensional iterators can also be used with C++ algorithms of the standard library. For instance, std::fill can be used together with mfirst and mlast to initialize the first row of A.

std::fill(mfirst, mlast, 5.0);

The user can introduce member functions begin and end of tensor and subtensor or implement free functions, both simplifying the instantiation of multi-dimensional iterators. The user needs to specify a one-based mode that is greater than zero and equal to or smaller than the tensor order. Both functions could also allow to specify a multi-index with std::vector<std::size_t> and define the displacement within the multi-index space except for the dimension dim. In the following, begin and end shall be member functions of the tensor and subtensor types. The aforementioned initialization of A's first row can be performed in one line which first generates mode-specific iterates using begin and end for the first mode.

std::fill(A.begin(1),A.end(1),5.0);

Note that the user can perform the initialization independent of A's storage format. Moreover, fibers with different modes using C++ algorithms of the standard library can be combined. The following statement for instance computes the inner product of a mode-3 and mode-2 fiber.

std::inner_product(A.begin(3),A.end(3),

                   B.begin(2),0.0);

LISTING 1

Listing 1. Nested-loop with multi-dimensional iterators for tensor types of order 3 with any linear storage format.

Again, A and B can be of different types (such as tensor or subtensor) with different storage formats. The user can invoke begin and end function with no mode or mode 0 with which the single-index space of a tensor or subtensor can be iterated through.

  std::fill(A.begin(),A.end(), 0.0);

Note that range-based for-loops can also be used instead of std::fill. Similar to the tensor type, the multi_iterator template provides two methods begin and end with which multi-dimensional iterators can be instantiated. The new instantiated iterators have the same pointer position and stride tuple reference but a new stride depending on the argument which specifies the mode. For instance, a multi-dimensional iterator it can be used to define a multi-dimensional iterator pair that is able to iterate along the third mode.

auto first = it.begin(3),  auto last = it.end(3);

Listing 1 illustrates the initialization of a three-dimensional tensor or subtensor A with multi-dimensional iterators. The code example consists of three nested for-loops. Within each loop a multi-dimensional iterator it{r} is initialized using the begin and end member function of either the tensor A or a multi-dimensional iterator of the previous loop. The iterator number corresponds with the position within the stride tuple so that it{r} will be internally incremented with the w[r-1] stride in case of tensors and with w[r-1]*s[r-1] in case of subtensors where s[r-1] is the step size. The inner loop assigns value v to the column elements of the (it3,it2)-th frontal slice. The innermost loop can be replaced with the following statement.

std::fill(it1.begin(1), it1.end(1), v);

In contrast to the iterator design in [25, 26], our iterator instances are able to clone themselves for different modes. Tensor A in the outer-most loop is replaceable by a multi-dimensional iterator it3 that is generated in a previous statement with the expression A.begin(3). In the next section we present tensor functions that iterate over the multi-index space of multi-dimensional tensors and subtensors with arbitrary storage format using multi-dimensional iterators only.

5. Tensor Functions

The following tensor functions implement basic tensor operations and iterate over the multi-index space of tensor types using multi-dimensional iterators combining multiple tensor elements. The user is not forced to use the aforementioned multi-dimensional iterator class templates. Yet the multi-dimensional iterator should be able to iterate over a specific mode and must provide begin and end member functions that can generate multi-dimensional iterators with the same capabilities. Most of the following tensor functions require input iterator attributes of the standard library.

Similar to the basic linear algebra subroutines (BLAS), we distinguish between first-level and higher-level tensor algorithms. The former generalize function templates of the C++ standard library for tensor types and have identical function names with almost the same function signature. They combine elements of one or more tensor or subtensor instances with the same multi-index and are often referred to as pointwise or elementwise tensor operations. Higher-level tensor operations have a more complex control-flow and tensor elements with different multi-indices such as the tensor-tensor multiplication.

All of the following C++ tensor functions implement tensor operations with multiple loops and contain two optimizations that have been suggested in [24] optimizing index computation (minimum-index) and inlining recursive function by compile-time optimization (inline). Comparing the tree-recursive and equivalent iteration-based implementations that have presented in [24], we favor the tree-recursion which has fewer lines of C++ code, is easier to understand and is only about 8% slower if the leading dimension of the tensors or subtensors is greater than or equal to 256.

5.1. First-Level Tensor Operations

The following proposed first-level tensor C++ function templates are akin to the ones provided by the algorithms library of the C++ standard library and combine elements with the same multi-index. With similar functions signatures, tensor functions pose different iterator requirements and has in most cases tensor order as an additional parameter. Almost all C++ tensor functions contain a function object (predicate) that is applied to every input element. The user can utilize existing function objects of the C++ standard library, define its own class or use lambda-expressions which is why first-level C++ tensor functions can be regarded as higher-order functions for tensors.

It should be noted that dense and contiguously stored tensors, C++ functions from the standard library such std::transform or std::inner_product can be used. However, the usage of loops utilizing a single-index or alike in case of subtensors slows down the performance by a factor which is proportional to the subtensor order [24]. If the leading dimension n_π1 of a tensor is large enough and greater than 512, the experiments in [24] show that the control- and data-flow overhead of a multi-loop approach only slows down the computation by at most 12%. In extreme cases where the leading dimension is smaller than 64, we observed a slow down of about 50%. This observation favors the usage of one implementation with nested recursion and multiple loops for dense tensors and their subtensors if the leading dimensions are in most cases greater than 256.

The implementation of basic tensor functions can be derived from the previous example in listing 1. In contrast to the C++ algorithms, first-level tensor function templates iterate over multiple ranges using multi-dimensional iterators. The function for_each in listing 2 applies the function object fn of type UnaryFn to every tensor element that is accessed by multi-dimensional iterator pairs first and last. Given a tensor or subtensor A of order p with p>0, for_each in listing 2 needs to be performed with an iterator pair A.begin(p) and A.end(p). The parameter r corresponds to the inverse recursion depth which is initialized with the tensor order p and decremented until the base case of the recursion is reached where r is equal to 1. for_each calls itself std::distance(first,last) times in line 6 with a new range defined by first.begin(r-1) and first.end(r-1) where first is an iterator instance of the previous function call. When the base case with r=1 is reached, std::for_each is called in line 7 with the range specified by first.begin(1), first.end(1). If for_each is called with an r smaller than p, for_each skips p-r modes and only applies fn on the first r modes. If r is greater than p, any memory access is likely to cause a segmentation fault. If the user calls for_each with r=0, std::for_each is directly called and iterated along the single index space of the tensor or subtensor.

LISTING 2

Listing 2. Implementation of for_each with multi-dimensional iterators.

Note that for_each calls itself n₂⋯n_p times if the tensor or subtensor is of order p > 1 and has the dimensions n₁, n₂, …, n_p. Given a tensor or subtensor A of order p with any linear storage format and a unary function object fn, the arguments of for_each should be p, A.begin(p), A.end(p), and fn. For instance, adding a scalar v to all elements of A can be performed if fn is defined as std::bind(std::plus <>{},_1,v) or using a lambda function with the same computation.

//A:=A+v;

for_each(p, A.begin(p), A.end(p), [v](auto &a){a+=v;});

The user can implement elementwise subtraction, multiplication, division operations by defining a binary function object from the standard library such as std::bind(std::multiplies< >{},_1,v). It is also possible to define bitwise tensor operations, e.g., std::bind(std::bit_or< >{},_1,v) if v satisfies the template parameter requirements of the binary operation. The user can conveniently create complex elementwise tensor operations that contain a sequence of scalar operations for each element. For instance, raising all tensor or subtensor elements to the power of 2, dividing the result by v and adding the value w is given by the following expression.

//A:=A.^2/v+w;

for_each(p, A.begin(p), A.end(p),

                          [v,w](auto &a){a*=a/v+w;});

In contrast to calling simple overloaded operators of tensor or subtensor types, this statement does not create temporary tensor objects and is as efficient as expression templates.

Function transform, presented in listing 3, has a signature which is similar to the one of std::transform. It operates on two multi-dimensional ranges which are defined by the iterators fin, lin of type InputIt and fout of type OuputIt defining the input and output ranges, respectively. Akin to the for_each implementation, the one-dimensional ranges are given by iterators that are instantiated either by the previous recursive call or when transform is initially called. For demonstration purposes, the inverse recursion depth and its initial value is specified using a non-type template parameter r. The if condition is modified with the constexpr specifier so that r>1 is evaluated at compile time. A C++ compiler can decide to inline the recursive calls which leads faster runtimes in case of small dimensions [24]. Once the base case with r=1 is reached std::transform performs the unary operation op on elements of tensor fibers that are given by the ranges [fin,lin) and [fout, fout+std::distance(fin,lin)).

LISTING 3

Listing 3. Implementation of transform with multi-dimensional iterators.

Given p+1-dimensional tensors or subtensors A and C with the shape tuple n and any linear storage format. Let also op be a unary operation of type UnaryOp. The multiplication of a scalar v with the elements of A is accomplished by calling transform as follows.

// C:= A+v;

transform<p>(A.begin(p), A.end(p), C.begin(p),

                           [v](auto a){  return a*v;});

Given p+1-dimensional tensors or subtensors A, B, and C with the shape tuple n and any linear storage format. Let also op be a binary operation of type BinaryOp that can process elements of A and B. Elementwise addition of A and B can be performed by calling transform as follows.

// C:= A+B;

transform<p>(A.begin(p), A.end(p),

             B.begin(p), C.begin(p), std::plus < >{});

Users can implement their own multi-dimensional iterators supporting the input iterator type traits with the begin and end method for initializing iterators. The copy and transform functions have the same signature except the unary operator which can be left out in case of copy. Moreover, copy can be regarded as a specialization of transform where the unary function op returns a single element that is provided by the input iterator. With r specifying the inverse recursion depth, our implementation of copy is given by the following function call.

transform<r>(fin, lin, fout, [](auto a){return a;}));

Transposing a tensor can be accomplished using the copy function with minor modifications. Let tau of type, e.g., std::array<unsigned,p> be an additional standard container for the index permutation as a function parameter and let the function name copy be changed to transpose. An out-of-place tensor-transposition is performed with

// C := A^{tau};

transpose <p>(A.begin(tau[p-1]), A.end(tau[p-1]),

              C.begin(p), tau);

The recursive function call in transpose needs to be changed accordingly, replacing the argument p with r-1. Note this simple implementation of the tensor transposition does not conserve data locality only for both tensors unless the permutation tuple is trivial. A high-performance version of the transposition operation is given in [31].

An implementation of the inner product of two tensors or subtensors with any linear storage format is given in listing 4. The function signature and body corresponds to a modified transform function. The std::inner_product computes the inner product of tensor or subtensor fibers multiple times using results init of previous function calls. Computing the inner product of two tensors or subtensors A and B is given by the following function call.

// c :=  <A,B>;

auto inner = inner_product<p>(A.begin(p), A.end(p),

                              B.begin(p), Value{});

The initial value is given by the default constructor of Value which should be implicitly convertible to the elements type of A and B. The frobenius norm of a tensor A can be implemented using the inner_product as follows.

// c: = fnorm(A) = sqrt(inner(A,A));

auto c = std::sqrt(inner_product<p>(A.begin(p),A.end(p),

                                    A.begin(p),Value{}));

The computation of the frobenius norm is given by first executing the unary operation [](auto const& a){return a*a;} with transform and accumulate all elements of the output tensor C using the accumulate function.

LISTING 4

Listing 4. Implementation of inner_product with multi-dimensional iterators.

5.2. Higher-Level Tensor Operations

Higher-level tensor operations perform one or more inner products over specified dimensions and, therefore, exhibit a higher arithmetic intensity ratio compared to first-level tensor operations. Prominent examples are the general tensor-times-tensor multiplication with variations.

5.2.1. Tensor-Vector Multiplication

One such variation is the q-mode tensor-vector multiplication where q equals the contraction dimension. Let A be a tensor or subtensor of order p > 1 with dimensions n and any linear storage format. Let b be a vector with dimension n_q with 1 ≤ q ≤ p. Let C be a tensor or subtensor of order p − 1 with dimensions n′ = (n₁, …, n_q−1, n_q+1, …, n_p). The q-mode tensor-vector multiplication computes $1/n_q{\prod }_{r=1}^p{n}_r$ inner products, i.e., fiber-vector multiplications, according to

$\begin{array}{ll}\underset{\_}{\text{C}}(i_1,\dots ,i_{q-1},i_{q+1},\dots ,i_p)={\displaystyle \sum _{i_q=1}^{n_q}}\underset{\_}{\text{A}}(i_1,\dots ,i_q,\dots ,i_p)·\text{b}(i_q)& (1)\end{array}$

with 1 ≤ i_r ≤ n_r. If p = 2, the tensor-vector multiplication computes a vector-matrix product of the form c = b^T · A for q = 1 and a matrix-vector product of the form c = A · b for q = 2. Vector b is multiplied with the frontal slices of A if p is greater than 2 and q = 1 or q = 2.

Function ttv in listing 5 implements the general tensor-times-vector multiplication where the contracting dimension q is a one-based compile time parameter computing all contractions for 1 < q ≤ p. The second template parameter ra corresponds to the inverse recursion depth and ranges from 1 ≤ r ≤ p. The third template parameter rc depends on q so that r_c = r_a − 1 for q < r_a ≤ p and r_c = r_a for 1 ≤ r_a ≤ q. The algorithm used in ttv is based on the algorithm 1 that has been proposed in [32]. The implementation can be regarded as an extension of the previously discussed functions with similar signature and body. The first if-statement is introduced to skip and place the iteration along the q-th dimension inside the base case. Therefore, iterators for the next recursion are generated for A based on the current position of fa. The second if-statement contains the recursive call that can be found in all previous listings. The else-statement contains the base case of the recursion which is executed if ra=1. The base case multiplies vector b with a selected slice of A and stores the results in the corresponding fiber of C. Given a tensor A of order p, a vector b and a tensor C of order p-1, all with the same element type and storage format, then

// C = A *q b

ttv<q,p,p-1>(A.begin(p), b.begin(),C.begin(p-1));

computes the q-mode tensor-times-vector product for 1 < q ≤ p. Note that spatial data locality for A is maximized when stride $w_q^a$ satisfies $w_q^a\le w_{r_a}^a$ for all r_a ≠ q which is the case for a storage format with a layout tuple (q, π₂, …, π_p). For that purpose, C stride $w_1^c$ needs to satisfy $w_1^c\le w_{r_c}^c$ for all r_c ≠ q. Assuming that only one storage format, the spatial data locality can be increased for any linear storage format by modifying the recursion order according to the storage format and reordering the loops in the base case as suggested in [32]. This is accomplished by using the layout vectors π of A and C that contain indices with w_πr ≤ w_πr+1 for all 1 ≤ r < p. Replacing indices ra and rc with pia[ra-2] and pic[rc-2] allows to generate iterators with strides that are decreasing with the recursion depth. The base case needs to be changed as well with the following code snippet that computes a slice-vector product accessing A and C for any linear storage format.

auto ta = pia[0];

auto tc = pic[0];

  

for(auto faq=fa.begin(q); faq!=fa.end(q); ++faq,++fb){

     auto op = [b=*fb](auto const& a,  auto const& c)

                                       {return c+a*b;});

  

    std::transform(faq.begin(ta), faq.end(ta),

                   fc. begin(tc), fc. begin(tc), op);

}

Instead using std::inner_product, the base case scales A's fibers with b and writes the result in C's corresponding fibers. If A and B are contiguously stored, memory access can be performed in a coalesced manner. The algorithm can be further optimized for temporal data locality and parallel execution. Interested readers are referred to [32].

LISTING 5

Listing 5. Implementation of the q-mode tensor-vector product with iterators for q<1.

5.2.2. Tensor-Matrix Multiplication

A generalization of the q-mode tensor-vector multiplication and a specialization of the tensor-tensor multiplication is the q-mode tensor-matrix multiplication. Let A be a tensor or subtensor of order p > 1 with dimensions n and any linear storage format. Let B be a matrix with dimensions (n_q, $n_q^{\prime }$) with 1 ≤ q ≤ p. Let C be a tensor or subtensor of order p with dimensions n′ = (n₁, …, m, …, n_p). The q-mode tensor-matrix multiplication computes $(m/n_q){\prod }_{r=1}^p{n}_r$ inner products, i.e., fiber-vector multiplications, according to

$\begin{array}{ll}\underset{\_}{\text{C}}(i_1,\dots ,j,\dots ,i_p)={\displaystyle \sum _{i_q=1}^{n_q}}\underset{\_}{\text{A}}(i_1,\dots ,i_q,\dots ,i_p)·\text{B}(j,i_q)& (2)\end{array}$

with 1 ≤ i_r ≤ n_r and 1 ≤ j ≤ m. If p = 2, a matrix-matrix product C = B · A for q = 1 and C = A·B^T for q = 2, respectively. Matrix B is multiplied with the frontal slices of A accordingly if p greater than 2 and q = 1 or q = 2.

The implementation of the q-mode tensor-matrix multiplication is almost identical to ttv except for the base case, minor modifications for the recursion cases and the function signature.

template<unsigned q,  unsigned r,

         class InputIt1, class InputIt2, class OutputIt>

void ttm(InputIt1 fa, InputIt1 la, InputIt2 fb,

           OutputIt fc)

The contracting dimension q is a one-based compile time parameter of ttm which performs a valid computation for 1 < q ≤ p. As both tensors or subtensors have the same order, ttm requires only one template parameter r which equates to ra in ttv. The implementation of ttm's base-case computes a matrix-slice product of the form C = A · B^T by multiplying a two-dimensional slice of A with a transposed B and storing the results in corresponding fibers of C. The base case is presented in the following code section and executed when r=1.

for(auto fb1=fb; fa!=la; ++fa, ++fc,fb0 = fb)

     for(auto fcq=fc.begin(q);fcq!=fc.end(q);++fcq,++fb1)

      *fcq = std::inner_product(fa.begin(q),fa.end(q),

                                fb1.begin(2),*fcq);

When r=1, iterators fa, la, and fc have been instantiated by previously generated iterators with their begin and end methods for r=1. We postulate that fb is initialized with begin for the first dimension with r=1. The first for-loop iterates over the first mode of A and C using fa and fc. The second for-loop iterates over mode q of C with the starting address of the previous iterator and first mode of B and calling std::inner_product with A's fiber and one column of B. Given a tensor or subtensor A of order p, a matrix B and a tensor or subtensor C of order p, with similar element types and any linear data layout, then

// C = A *q B;

ttm<q,p> (A.begin(p), B.begin(1), C.begin(p));

computes the q-mode tensor-times-matrix product. Note that spatial data locality for A and C is high when their strides w_q satisfy w_q ≤ w_r for all r ≠ q. Assuming that only one storage format, the spatial data locality can be increased for any linear storage format similar to ttv. This is done by utilizing the layout vectors π of both tensors and by replacing the index r with pi[r-2] that allows to generate iterators with decreasing strides and recursion depth. The loop ordering inside the base case of ttm is changed from (n₁,n_q,m) to (m,n_q,n_π1). In that case A and C are accessed in a coalesced manner for any linear storage format if the tensors are contiguously stored in memory where one fiber of C is accessed n_q times. The algorithm can be further optimized for temporal data locality and parallel execution.

5.2.3. Tensor-Tensor Multiplication

The tensor-tensor product is the general form of the tensor-matrix and tensor-vector multiplication. Let A and B be tensors or subtensors of order p_a and p_b with dimensions n_a and n_b, respectively. Given two permutation tuples φ and ψ of length p_a and p_b and the number of contractions q with q_a = p_a − q and q_b = p_b − q, the q-fold tensor-tensor multiplication computes elements of tensor or subtensor C of order p_c = q_a + q_b with dimensions n_c and using permutation tuples φ and ψ according to

$\begin{array}{ll}\underset{\_}{\text{C}}({\text{i}}_c)={\displaystyle \sum _{j_1=1}^{m_1}}\cdots {\displaystyle \sum _{j_q=1}^{m_q}}\underset{\_}{\text{A}}({\text{i}}_a)·\underset{\_}{\text{B}}({\text{i}}_b),& (3)\end{array}$

where the shape tuples satisfy $n_{r_c}^c=n_{r_a}^a$ for 1 ≤ r_c ≤ q_a with r_a = φ_r, $n_{r_c}^c=n_{r_b}^b$ for 1 ≤ r ≤ q_b with r_c = q_b + r and r_b = ψ_r, $m_r=n_{r_a}^a=n_{r_b}^b$ for 1 ≤ r ≤ q with r_a = φ_r+qa and r_b = ψ_r+qb. The first q elements of φ and ψ specify the contraction modes, while the remaining q_a and q_b elements specify the free (non-contraction) modes. The k-mode tensor-matrix and k-mode tensor-vector multiplication are specializations of the q-fold tensor-tensor multiplication which corresponds to the k-mode tensor-vector multiplication, if q = 1, p_a > 1, p_b = 1 and φ = (1, …, k − 1, k + 1, …, p_a, k), ψ = (1). The k-mode tensor-matrix multiplication is given if q = 1, p_a > 1, p_b = 2 and φ = (1, …, k − 1, k + 1, …, p_a, k), ψ = (1, 2).

Function ttt in listing 6 implements the tensor-times-tensor multiplication as defined in Equation (3) for any number of contractions q>1. The contraction is performed with tensors or subtensors A and B of order pa and pb with any linear storage format and without unfolding A or B. The free and contraction modes reside within the permutation tuple phi and psi that must be a container with random access capabilities. Function ttt is defined with four non-type template parameter. The first three ra, rb, and rc are the current modes of each corresponding tensor or subtensor and should be initially instantiated with pa and pb and pc, respectively. The last non-type parameter q of ttt and equals to the number of contraction modes.

LISTING 6

Listing 6. Template Function ttt using multi-dimensional iterators implementing Equation (3).

The control flow of ttt contains four main branches of which three contain a for-loop with a recursive function call. The first for-loop is exectued q_b times and iterates over free index spaces of B and C with s = ψ_rb for q < r_b ≤ p_b and q_a < r_c ≤ p_c without adjusting iterators of A. The second for-loop is executed q_a times and iterates over free index spaces of A and C where s = φ_ra for q < r_a ≤ p_a and 1 ≤ r_c ≤ q_a without adjusting iterators of B. The third for-loop is executed q times and iterates over the contraction index spaces of A and B where s = φ_ra and r = ψ_rb for 1 < r_{a, b} ≤ q without adjusting iterators of C. If r_a = 1 and r_b = 1 the base case is reached and ttt performs an inner product with iterators that have been previously instantiated.

The q-mode tensor-tensor multiplication can be interpreted as a mix of the inner and outer tensor product with permutation tuples. The latter is partly accomplished by the q_a + q_b-fold execution with the first and second for-loop. However, input tensor elements of A and B are not multiplied to complete the outer product operation. Instead an inner product over q modes is computed for the recursion levels r > q_a + q_b. The last two branches could be replaced by the inner_product in listing 4 using the permutation tuples phi and psi. The minimum recursion depth is 1 when q = 1 and q_{a, b} = 0, while the maximum recursion depth equals q + q_a + q_b with q > 0 and q_a,b > 0.

Given tensors or subtensors A of order 3, B of order 4 and C of order 3 with similar element types, any linear data layout. Let the dimension tuples of A and B be n_a = (4, 3, 2) and n_b = (5, 4, 6, 3), respectively. Let also q = 2 be the number of contractions and φ = (1, 2, 3) and ψ = (2, 4, 1, 2) be the elements of the permutation tuples phi and psi, respectively. Given the dimensions $(n_3^a,n_1^b,n_2^b)$, i.e., (2,5,6), then

// C = A(_i,_j,_)*B(_,_i,_,_j)

ttt < pa,pb,pc,q>(phi,psi,

                  A.begin(pa),B.begin(pb),C.begin(pc));

performs a 2-mode tensor-tensor multiplication of A and B according to phi, psi, and q. Spatial data locality for A and B is high when for q > 0 their strides $w_{{\phi }_1}^a$ and $w_{{\psi }_1}^b$ satisfy $w_{{\phi }_1}^a\le w_r^a$ for all r ≠ φ₁ and $w_{{\psi }_1}^b\le w_r^b$ for all r ≠ ψ₁, respectively. Performance analysis and optimization techniques for the general tensor-tensor multiplication are discussed in [33, 34].

6. Runtime Analysis

This section presents runtime results of the transform function (listing 3) and the function inner_product (listing 4). The runtime measurements also include pointer-based implementations that have been presented in [24]. We have also included runtime results of the ttv function (listing 5) that has been discussed in [32] as a sequential implementation for the tensor-times-vector multiplication. All pointer and iterator-based functions have identical with respect to their control-flow in which the recursion index is a template parameter.

6.1. Setup

The following runtime measurements have been performed with 1792 differently shaped tensors ranging from 32 to 1024 MiB for single- and 64 to 2048 MiB for double-precision floating-point numbers. The order of the tensors ranges from 2 to 14 while dimensions range from 256 to 32768. Dimension tuples are arranged within multiple two-dimensional arrays so that runtime data could be visualized as three-dimensional surfaces or contour plots in terms of the tensor order and tensor size. The contour plots consist of 100 height levels that correspond to averaged throughputs. We will refer to the contour plots as throughput maps. Spatial data locality is always preserved meaning that relative memory indices are generated according to storage format. Tensor elements are stored according to the first-order storage format. This setup is identical to the tensor test set that has been presented in [24]. For the tensor-times-vector multiplication, we have used a setup that is akin to the one described in [32]. All tensors are asymmetrically shaped ranging from 64 to 2048 MiB for single- and 128 to 4096 MiB for double-precision floating-point numbers. The tensor order ranges from 2 to 10 and the contraction mode has been set to 1 in order to preserve spatial data locality for all tensor objects.

The experiments have been carried out on a Core i9-7900X Intel Xeon processor with 10 cores and 20 hardware threads running at 3.3 GHz. It has a theoretical peak memory bandwidth of 85.312 GB/s resulting from four 64-bit wide channels with a data rate of 2666MT/s with a peak memory bandwidth of 21.328 GB/s. The sizes of the L3 cache and each L2 cache are 14MB and 1024KB. The source code has been compiled with GCC v9.3 using the highest optimization level -Ofast and -march=native. The benchmark results of each function are the average of 10 runs on a single core.

6.2. Results

Figure 1 contains two throughput maps of a pointer- and iterator-based transform function. Both implement an elementwise tensor addition of the form C:=A+v; using unary function object [v](auto a){return a+v;}. The throughput of transform with pointers and iterators are most effected when the tensor size smaller than 128. We assume that this is caused by the caching mechanism which is still able to hold some data inside the last level cache and to speed up the computation. This effect diminishes when the tensor size is greater than 256 MiB. The throughput also contains a slight variation for different tensor order. For tensor sizes greater than 256 MiB, pointer-based implementation of transform computes the tensor addition with approximately 12.2 GB/s varying with at most 10% from the mean value. The iterator-based implementation is more consistent and only slows down to approximately 12.2 GB/s if the tensor order is 4 and 5. The std::transform function of the C++ standard library, the pointer-based and iterator-based transform function reach a median throughput of 13.71, 12.01, and 12.60 GB/s for 95% of test cases and a maximum throughput of 15.57, 13.50, and 13.71 GB/s.

FIGURE 1

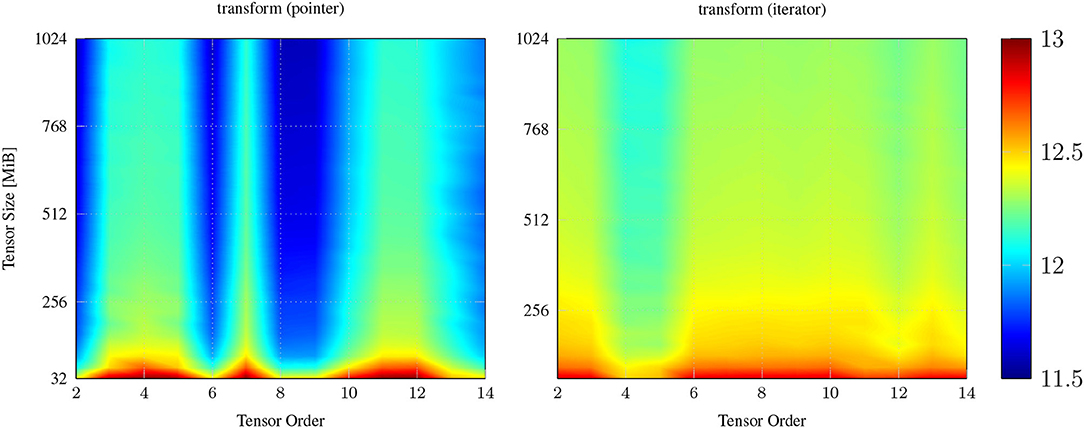
Figure 1. Single core throughput in GB/s of the transform function with pointers (left) that has been discussed in [24] and iterators (right) that is presented in listing 3. Iterator-based transform function reaches a median throughput of 12.60 GB/s and is about 2% to 5% faster than its pointer-based counterpart.

The runtime behavior of the inner_product implementations is similar, see Figure 2. The std::inner_product function of the C++ standard library, the pointer-based and iterator-based inner_product function reach a median throughput of 14.8, 12.03, and 12.47 GB/s for 95% of test cases. They exhibit maximum throughput of 15.36, 12.59, and 12.82 GB/s mostly when the tensor size is equal to 32 MiB. We have made similar runtime observations for other elementwise tensor operations such as for_each where the iterator-based implementation is in many cases 1 to 5% faster than their corresponding pointer-based counterparts.

FIGURE 2

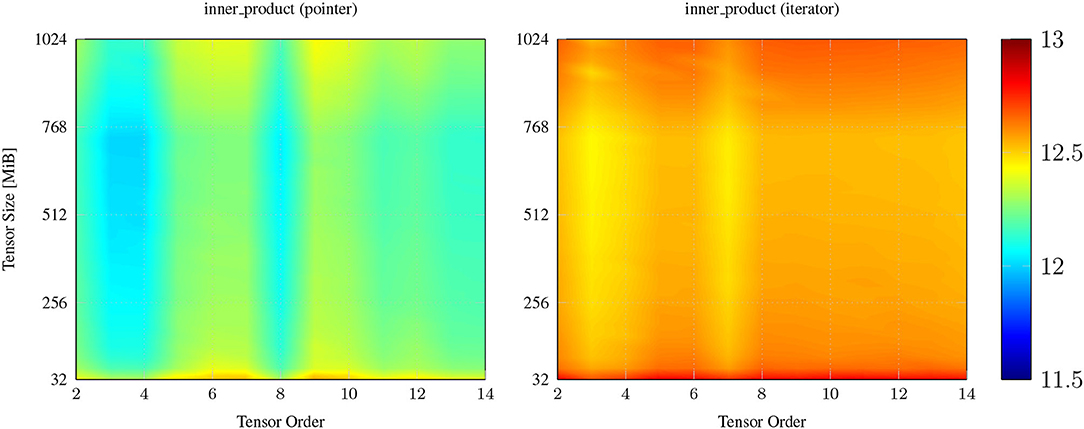
Figure 2. Single core throughput in GB/s of the inner_product function with pointers (left) that has been discussed in [24] and with iterators (right) that is presented in listing 4. Iterator-based inner_product function reaches a median throughput of 12.47 GB/s and is about 2 to 5% faster than its pointer-based counterpart.

Similar results are obtained for iterator-based and pointer-based implementations of the tensor-times-vector operations where both C++ functions compute the tensor-vector-product with 2.09 (single-precision) GFLOPS for about 95% test-cases. This can be observed in Figure 3 which contains throughput maps for the iterator-based and pointer-based implementation of the tensor-times-vector operation. The iterator-based function ttv in listing 5 reaches a peak throughput of 2.92 GFLOPS when tensor size and order are around 64 MiB and 10, respectively. The pointer-based counterpart exhibits a maximum throughput of 2.74 GFLOPS with the same tensor dimensions and is about 6.5% slower than the iterator-based function. Those performance peaks happen for larger tensor order when the first (contraction) dimension of the input tensor is relatively small. This results in a higher reuse of cache lines that belong to the input vector and output tensor fiber.

FIGURE 3

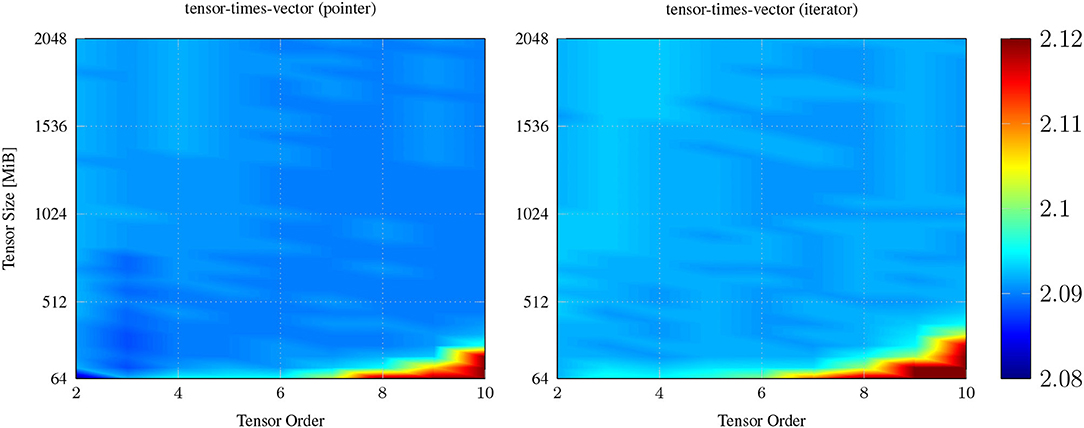
Figure 3. Single core throughput in GFLOPS of the ttv function with pointers (left) and with iterators (right) that is presented in listing 3. Iterator-based ttv function computes the tensor-vector product with median throughput of 2.09 GFLOPS and performs as fast as the pointer-based implementation.

7. Conclusions

We have presented generic C++ functions for basic tensor operations that have been discussed in [22] as part of a Matlab toolbox for numeric tensor computations. Following design pattern of the Standard Template Library, all proposed C++ functions are defined in terms of only multi-dimensional iterators and avoid complex pointer arithmetic. The set of the C++ functions includes elementwise tensor operations and more complex tensor operations such as tensor-tensor multiplication. All C++ functions perform the corresponding computation in-place and in a recursive fashion using two optimizations that have been discussed in [24]. We have introduced a multi-dimensional iterator that can be instantiated by Boost's uBlas tensor and subtensor types. Other C++ frameworks can utilize the proposed C++ functions for any linear storage format by implementing the proposed or their own multi-dimensional iterator fulfilling a minimal set of iterator requirements. Our performance measurements show that the iterator-based functions compute elementwise tensor operations and the tensor-times-vector product at least as fast as their corresponding pointer-based counterparts. Our iterator-based design method is applicable to other tensor operations such as the metricized-tensor times Khatri-Rao product (MTTKRP) which is used to decompose tensors according to the PARAFAC model [35, 36]. This implies that multi-dimensional iterators can be used for efficiently implementing tensor operations. In future, we intend to design C++ concepts for multi-dimensional iterator or ranges. We also would like to integrate optimization techniques that have been discussed in [32, 33] and to enable parallel execution of different type of tensor operations.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://numpy.org, http://tensorly.org, https://www.tensorlab.net.

2. ^See GSoC18 link for the project description, Github link for the initial implementation and Github link for the most current development.

References

1. Savas B, Eldén L. Handwritten digit classification using higher order singular value decomposition. Pattern Recognit. (2007) 40:993–1003. doi: 10.1016/j.patcog.2006.08.004

CrossRef Full Text | Google Scholar

2. Vasilescu MAO, Terzopoulos D. Multilinear image analysis for facial recognition. In: Proceedings of the 16th International Conference on Pattern Recognition. Vol. 2 Quebec City, QC (2002). p. 511–514.

Google Scholar

3. Suter SK, Makhynia M, Pajarola R. TAMRESH - tensor approximation multiresolution hierarchy for interactive volume visualization. In: Proceedings of the 15th Eurographics Conference on Visualization. EuroVis '13. Chichester (2013). p. 151–60.

Google Scholar

4. Kolda TG, Sun J. Scalable tensor decompositions for multi-aspect data mining. In: Proceedings of the 8th IEEE International Conference on Data Mining. (Pisa) 2008. p. 363–72.

Google Scholar

5. Rendle S, Balby Marinho L, Nanopoulos A, Schmidt-Thieme L. Learning optimal ranking with tensor factorization for tag recommendation. In: Proceedings of the International Conference on Knowledge Discovery and Data Mining. Paris (2009). p. 727–36.

Google Scholar

6. Khoromskij B. Tensors-structured numerical methods in scientific computing: survey on recent advances. Chemometr. Intell. Lab. Syst. (2012) 110:1–19. doi: 10.1016/J.CHEMOLAB.2011.09.001

CrossRef Full Text | Google Scholar

7. Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Rev. (2009) 51, 455–500. doi: 10.1137/07070111X

CrossRef Full Text | Google Scholar

8. Lim LH. Tensors and hypermatrices. In: Hogben L, editor. Handbook of Linear Algebra, 2nd Edn. Chapman and Hall (2017).

Google Scholar

9. Cichocki A, Zdunek R, H PA, Amari S. Nonnegative Matrix and Tensor Factorizations, 1st Edn. John Wiley & Sons, (2009).

Google Scholar

10. da Silva JD, Machado A. Multilinear algebra. In: L. Hogben, editor. Handbook of Linear Algebra, 2nd Edn. Chapman and Hall, (2017).

Google Scholar

11. Lee N, Cichocki A. Fundamental tensor operations for large-scale data analysis using tensor network formats. Multidimensional Syst Signal Process. (2018) 29:921–60. doi: 10.1007/s11045-017-0481-0

CrossRef Full Text | Google Scholar

12. Lathauwer LD, Moor BD, Vandewalle J. A multilinear singular value decomposition. SIAM J Matrix Anal Appl. (2000) 21:1253–78. doi: 10.1137/S0895479896305696

CrossRef Full Text | Google Scholar

13. Li J, Battaglino C, Perros I, Sun J, Vuduc R. An input-adaptive and in-place approach to dense tensor-times-matrix multiply. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. SC '15. Austin, TX (2015). p. 1–12.

Google Scholar

14. Stroustrup B. Foundations of C++. In: Programming Languages and Systems - 21st European Symposium on Programming. Vol. 7211 of Lecture Notes in Computer Science. Tallinn (2012). p. 1–25.

Google Scholar

15. Stroustrup B. Software development for infrastructure. Computer. (2012) 45:47–58.

Google Scholar

16. Veldhuizen TL. Arrays in Blitz++. In: Caromel D, Oldehoeft RR, Tholburn M, editors. Lecture Notes in Computer Science. ISCOPE. Vol. 1505. Berlin: Springer (1998). p. 223–30.

Google Scholar

17. Reynders III, JV, Cummings JC. The POOMA framework. Comput Phys. (1998) 12:453–59.

18. Landry W. Implementing a high performance tensor library. Sci Program. (2003) 11:273–90.

PubMed Abstract | Google Scholar

19. Solomonik E, Matthews D, Hammond J, Demmel J. Cyclops tensor framework: Reducing communication and eliminating load imbalance in massively parallel contractions. In: Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing. IPDPS '13. Cambridge, MA (2013). p. 813–24.

Google Scholar

20. Harrison AP, Joseph D. Numeric tensor framework: exploiting and extending Einstein notation. J Comput Sci. (2016) 16:128–39. doi: 10.1016/j.jocs.2016.05.004

CrossRef Full Text | Google Scholar

21. Poya R, Gil AJ, Ortigosa R. A high performance data parallel tensor contraction framework: Application to coupled electro-mechanics. Comput Phys Commun. (2017) 216:35–52. doi: 10.1016/j.cpc.2017.02.016

CrossRef Full Text | Google Scholar

22. Bader BW, Kolda TG. Algorithm 862: MATLAB tensor classes for fast algorithm prototyping. ACM Trans Math Softw. (2006) 32:635–53. doi: 10.1145/1186785.1186794

CrossRef Full Text | Google Scholar

23. Psarras C, Karlsson L, Bientinesi P. The landscape of software for tensor computations. CoRR. 2021;abs/2103.13756.

Google Scholar

24. Bassoy C, Schatz V. Fast higher-order functions for tensor calculus with tensors and subtensors. In: Shi Y, Fu H, Tian Y, Krzhizhanovskaya VV, Lees MH, Dongarra J, et al., editors. Computational Science—ICCS 2018. Springer International Publishing (2018). p. 639–52.

Google Scholar

25. Garcia R, Lumsdaine A. MultiArray: a C++ library for generic programming with arrays. Softw Pract Exp. (2005) 35:159–88. doi: 10.1002/spe.630

CrossRef Full Text | Google Scholar

26. Aragón AM. A C++ 11 implementation of arbitrary-rank tensors for high-performance computing. Comput Phys Commun. (2014) 185:1681–96. doi: 10.1016/j.cpc.2014.01.005

CrossRef Full Text | Google Scholar

27. Stepanov A. The standard template library. Byte. (1995) 20:177–8.

28. Hackbusch W. Numerical tensor calculus. Acta Numerica. (2014) 23:651–742. doi: 10.1017/S0962492914000087

CrossRef Full Text | Google Scholar

29. Chatterjee S, Lebeck AR, Patnala PK, Thottethodi M. Recursive array layouts and fast parallel matrix multiplication. In: Proceedings of the Eleventh Annual ACM symposium on Parallel algorithms and architectures. SPAA '99. New York, NY (1999). p. 222–31.

Google Scholar

30. Elmroth E, Gustavson F, Jonsson I, Kågström B. Recursive blocked algorithms and hybrid data structures for dense matrix library software. SIAM Rev. (2004) 46:3–45. doi: 10.1137/S0036144503428693

CrossRef Full Text | Google Scholar

31. Springer P, Su T, Bientinesi P. HPTT: a high-performance tensor transposition C++ library. In: Proceedings of the 4th ACM SIGPLAN International Workshop on Libraries, Languages, and Compilers for Array Programming. Barcelona (2017). p. 56–62.

Google Scholar

32. Bassoy C. Design of a high-performance tensor-vector multiplication with BLAS. In: Rodrigues JMF, Cardoso PJS, Monteiro JM, Lam R, Krzhizhanovskaya VV, Lees MH, et al., editors. Computational Science – ICCS 2019 Lecture Notes in Computer Science. Vol. 11536. Cham: Springer. (2019). p. 32–45.

Google Scholar

33. Springer P, Bientinesi P. Design of a high-performance GEMM-like tensor-tensor multiplication. ACM Trans Math Softw. (2018) 44:1–29. doi: 10.1145/3157733

CrossRef Full Text | Google Scholar

34. Matthews DA. High-performance tensor contraction without transposition. SIAM J Sci Comput. (2018) 40:C1–C24. doi: 10.1137/16M108968X

CrossRef Full Text | Google Scholar

35. Ballard G, Knight N, Rouse K. Communication lower bounds for matricized tensor times Khatri-Rao product. In: 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS). Vancouver, BC: IEEE (2018). p. 557–67.

Google Scholar

36. Bader BW, Kolda TG. Efficient MATLAB computations with sparse and factored tensors. SIAM J Sci Comput. (2008) 30:205–31. doi: 10.1137/060676489

CrossRef Full Text | Google Scholar