- 1Fondazione the Microsoft Research-University of Trento Centre for Computational and Systems Biology (COSBI), Rovereto, Italy
- 2Department of Cellular, Computational and Integrative Biology (CIBIO), University of Trento, Trento, Italy
- 3Department of Mathematics and Geosciences, University of Trieste, Trieste, Italy
Parkinson's disease (PD) is the second most common neurodegenerative disorder worldwide, yet there is no disease-modifying therapy up to this date. The biological complexity underlying PD hampers the investigation of the principal contributors to its pathogenesis. In this context, mechanistic models grounded in molecular-level knowledge provide virtual labs to uncover the primary events triggering PD onset and progression and suggest promising therapeutic targets. Multiple modeling efforts in PD research have focused on the pathological role of α-synuclein (αsyn), a presynaptic protein that emerges from the intricate molecular network as a crucial driver of neurodegeneration. Here, we collect the advances in mathematical modeling of αsyn homeostasis, focusing on aggregation and degradation pathways, and discussing potential modeling improvements and possible implications in PD therapeutic strategy design.
1. Introduction
Parkinson's disease (PD) is a debilitating neurodegenerative disorder with currently no disease-modifying therapy or cure [1]. The high prevalence of PD on the global scale and its exponential growth over the last few decades suggest the imminent outbreak of a non-infectious pandemic propelled by aging and industrialization as unconventional vectors of this rapidly growing neurological disorder [2]. Given the enormous strain that a pandemic would put on the healthcare system and the resulting human and economic toll, it is no surprise that investigating PD pathogenesis has rapidly become a serious public health concern. Since 1817, when the “shaking palsy” was first described [3], considerable progress has been made in understanding PD, from the clinical symptoms to the molecular mechanisms. Such progress has yet to translate into effective treatments that can hamper or even reverse PD progression. The current gold-standard therapy (Levodopa or L-Dopa treatment) manages motor symptoms but cannot stop neurodegeneration [4]. It counterbalances dopamine (DA) deficiency in the basal ganglia by relying on the pharmacological input of the DA precursor L-Dopa. Indeed, impairments in the dopaminergic pathway and the subsequent neuronal death in the substantia nigra pars compacta stand out as a primary hallmark of the disease [1].
Human and molecular genetic research has soon uncovered PD's multifactorial nature, thus unveiling a complex molecular network [1, 5]. In addition to impairments in DA metabolism, numerous processes such as protein aggregation, defective degradation, neuroinflammation, and oxidative stress contribute to disease onset and progression through various feedback mechanisms (see Fujita et al. [6] for a comprehensive disease map). The presynaptic amyloidogenic protein α-synuclein (αsyn) emerges from the intricate molecular landscape as a key driver of PD pathogenesis [1]. Here, we focus on two mechanisms governing its homeostasis, i.e., the aggregation and degradation pathways. Figures 1A, 2A display the biological mechanisms involved in these pathways. Their link to PD neurodegeneration is supported by multiple experimental and genome-wide association studies [5, 7, 8]. Even though multiple studies have highlighted the significant contribution of these processes to PD neurodegeneration [9–11], the interplay between the uncontrolled accumulation of αsyn aggregates and impairments in the degradation mechanisms is still unclear [12].
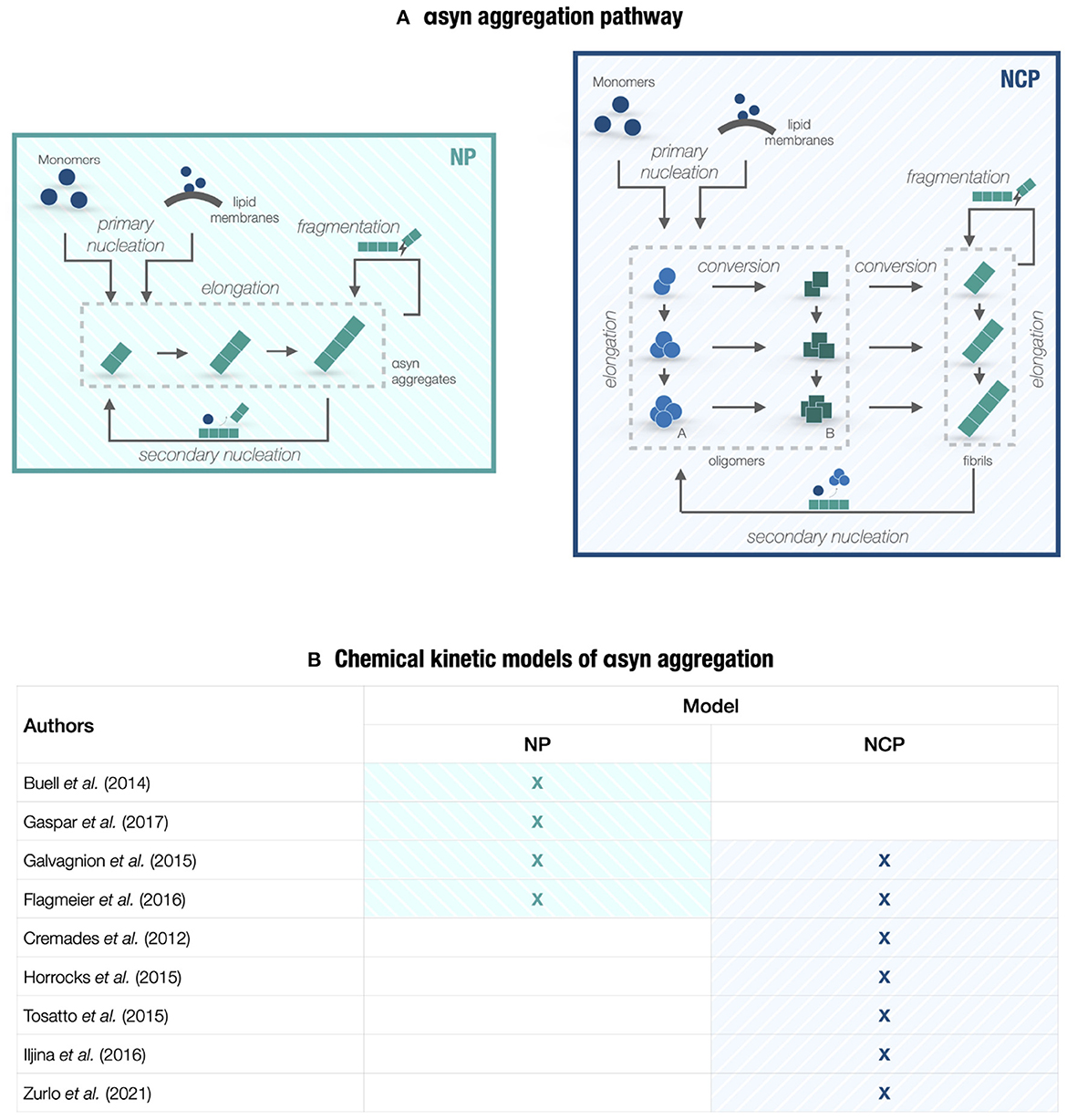
Figure 1. Chemical kinetic models of αsyn aggregation. (A) A conceptual scheme of the PD molecular landscape underlying models in Section 2. The kinetic of αsyn aggregation can be represented by either a nucleation-polymerization (NP) process or a nucleation-conversion-polymerization (NCP) process. The pathway includes homogeneous primary nucleation from monomers, heterogeneous primary nucleation catalyzed by lipid membranes, aggregate elongation by monomer addition, structural conversion between oligomeric species (type-A and type-B oligomers) and fibrillar species (if we consider NCP models), fibril fragmentation, and heterogeneous secondary nucleation on fibril surfaces. Reverse processes, such as monomer dissociation and reverse conversion, are not shown since they are negligible at the early aggregation steps. (B) Table collecting the chemical kinetic models of αsyn aggregation considered in Section 2 that provide mechanistic insights into PD neurodegeneration. The studies are based on the master equation approach and focus either on NP or NCP models.
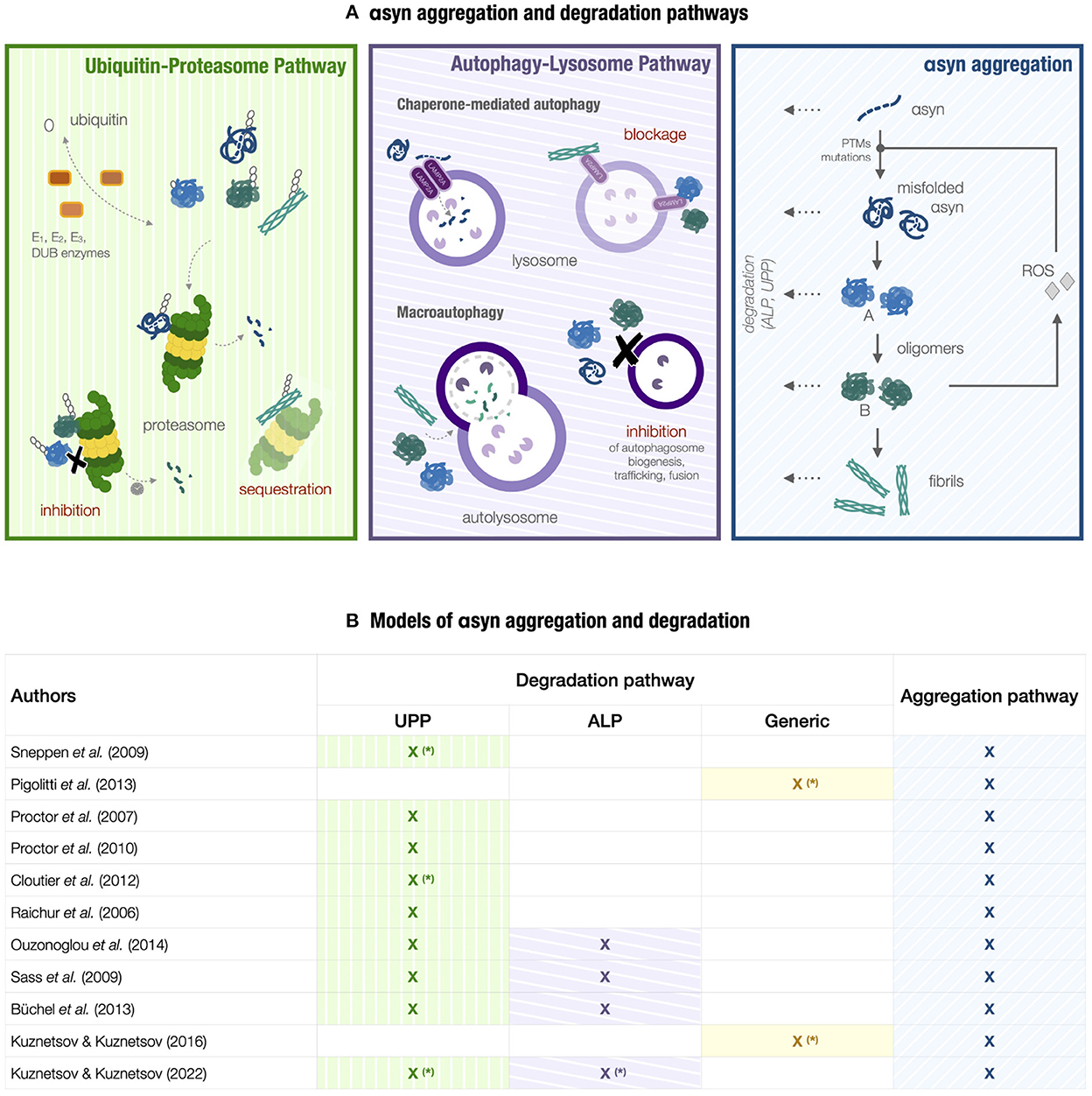
Figure 2. Models of αsyn aggregation and degradation. (A) A conceptual scheme of the PD molecular landscape underlying models in Section 3. A high-level representation of αsyn aggregation (light-blue box) is integrated into a more complex network involving the ubiquitin-proteasome pathway (UPP) and the autophagy-lysosome pathway (ALP) (green and purple boxes, respectively), reactive oxygen species (ROS) production, and the corresponding feedback loops. The aggregation process involves αsyn misfolding, the conformational change between type-A and type-B oligomers, the conversion from oligomers to fibrils, and degradation of αsyn species. Factors triggering αsyn misfolding can be post-translational modifications (PTMs), αsyn mutations, and high ROS levels. UPP degradation, including ubiquitination and proteasome-mediated degradation, is impaired by fibrils sequestering the proteasome and oligomers inhibiting proteasomal activity either by proteasome overload or directly due to their inherent toxicity. Pathogenic αsyn also interferes with ALP components [69]. Fibrils and oligomers can block CMA degradation by obstructing LAMP2A receptors and inhibiting their assembly [67, 85, 125]. Macroautophagy is the main degradation route for αsyn aggregates. In return, misfolded αsyn and its aggregates can exert an overall inhibitory effect on macroautophagy and hamper its activity by interfering with autophagosome formation, maturation, and trafficking, in addition to lysosomal fusion and transport [126, 127]. (B) Table collecting the models considered in Section 3. The term Generic indicates a generic degradation mechanism, either proteasome or lysosome-mediated. The models denoted by the symbol (*) incorporate degradation mechanisms either as pseudo-first-order reactions or enzymatic reactions; the remaining models are characterized by a more detailed representation of the degradation pathways.
Given the intricate biological picture outlined so far, identifying the specific role of αsyn aggregation and degradation pathways would support therapeutic strategies currently under investigation [13], e.g., small molecule inhibition, αsyn antibodies, and autophagy stimulation, or even pave the way for new pharmacological approaches. To this end, the experimental analysis calls for a quantitative systems pharmacology (QSP) approach at the interface between pharmacological research and systems biology [14]. As recently highlighted in Geerts et al. [15], Abrams et al. [16], Bloomingdale et al. [17], and Bloomingdale et al. [18], QSP models indeed hold great potential in neuroscience as they provide a systems-level understanding of complex biological processes and insights into their response to drugs. Specifically, modeling efforts in PD research are moving toward multiscale QSP models that describe molecular, cellular, whole-brain, and organism levels to assess how the effects of a molecular perturbation can scale up to influence the clinical outcome [19].
Starting from the molecular level, various mechanistic models falling within the systems biology framework have tackled PD complexity. As highlighted by previous studies on systems biology models for neurodegenerative disorders [20, 21], they have mainly focused on protein aggregation, synaptic transmission, apoptosis, oxidative stress, and genetic components rather than protein degradation. The relatively small number of models that include degradation processes is likely to rise along with increasing evidence that supports the critical role of the protein clearance machinery in PD [10, 22]. With this in mind, we collect the advances in mathematical modeling of αsyn aggregation and degradation by the ubiquitin-proteasome pathway, macroautophagy, and chaperone-mediated autophagy. As shown in Figures 1, 2, we divide the mechanistic models into two groups: (i) Single-pathway models of αsyn aggregation representing the chemical kinetics of the process (i.e., chemical kinetic models); (ii) Multiple-pathway models of αsyn homeostasis focusing on the interplay between αsyn aggregation and degradation mechanisms (i.e., degradation models). We discuss their potential improvements and possible implications in PD therapy development.
2. Mechanistic models of αsyn aggregation kinetics
Protein aggregation and misfolding are central features in the molecular network of neurodegeneration [23]. It is therefore no surprise that a large part of the modeling effort targeting PD investigates the chain of microscopic events in αsyn aggregation. These studies fall into a broader line of research devoted to uncovering the generality of amyloid formation by focusing on the chemical and physical aspects of this phenomenon [24, 25]. Here, we analyze mechanistic models that extend the formalism of chemical kinetics to the aggregation process; we thus refer to them as chemical kinetic models (see Figure 1B). These models adopt a master equation approach building on the pioneering work by Oosawa and Kasai [26] to provide a mathematical formulation of each molecular step in the process and derive the corresponding rate constants. To gain novel biological insights and formulate new scientific queries, in silico models evolve along with increasingly advanced experimental procedures in a virtuous cycle of model calibration and validation against in vitro quantitative measurements [23].
2.1. αsyn misfolding and aggregation and PD neurodegeneration
Soluble αsyn is an aggregation-prone protein with an intrinsically disordered conformation that prevents its spontaneous self-assembly [27]. Many factors can trigger αsyn misfolding and accumulation, such as high αsyn concentrations, genetic mutations, increased reactive oxygen species (ROS) levels, and interaction with lipid membranes [28]. The process initiates upon structural changes that expose the highly amyloidogenic region of the protein to the cytosol. Misfolded monomers slowly aggregate into oligomeric species, thus creating nucleation seeds. In return, seeding-competent oligomers can rapidly accumulate and elongate by monomer addition forming protofibrils and insoluble fibrils (Figure 1A). Multiple αsyn species eventually gather into amyloid inclusions known as Lewy bodies (LBs) and Lewy neurites (LNs), which represent one of PD's main molecular hallmarks [29].
A considerable body of research points to the harmful effect of αsyn aggregation and its crucial contribution to PD neurodegeneration. For instance, the SNCA gene, encoding for αsyn, was the first gene associated with PD [30]. Still, there is no agreement on the specific mechanisms of toxicity. Seeding and spreading ability and inherent toxicity are the functional and structural factors that determine the overall toxicity of aggregates [27, 31]. According to in vitro and in vivo experimental evidence, the most cytotoxic species are oligomers with a partially folded structure similar to mature fibrils [28, 31, 32]. Due to their conformation, some oligomeric species can create pores within the cell membrane, thus enhancing its permeability and dysregulating calcium homeostasis [33]. They can also impair mitochondrial function and proteolytic machinery. On the other hand, small fibril fragments have been identified as major-spreading agents in PD because of their high seeding efficiency and internalization ability [28]. According to one of the leading hypotheses for αsyn propagation, pathogenic species are assumed to spread in a prion-like manner [34]; they are released in the extracellular space and then endocytosed by neighboring neurons, where they recruit non-native monomers acting as seeds for further aggregation. As a result, protein aggregates propagate across interconnected brain areas over decades, eventually resulting in PD neurodegeneration [1].
Considerable progress has been made in understanding the kinetic of αsyn misfolding and aggregation, however, there is no agreement on many aspects of this mechanism. Chemical kinetic models can provide valuable insights into understanding, for example, the relative contribution of different microscopic events to the process, the structural and functional features of αsyn aggregate species [32], and the relationship between αsyn aggregation and LB formation and maturation [35, 36].
2.2. The master equation approach
The aggregation pathway of a generic amyloidogenic protein can be represented by a minimal set of fundamental reactions, regulating the transition from soluble monomers to fibrils through various intermediate states. As shown in Figure 1A, we can differentiate between primary reactions, i.e., homogeneous primary nucleation and elongation, and secondary reactions, i.e., heterogeneous secondary nucleation and fibril fragmentation [37, 38]. Homogeneous nucleation initiates the aggregation process by combining monomers into newly formed aggregates that, in turn, elongate by monomer addition. By integrating these reactions, fibril fragmentation and heterogeneous nucleation on aggregate surfaces multiply the aggregate number in a positive feedback loop with elongation, thus ensuring self-replication. Their relative contribution to the aggregation process depends on the specific protein considered [25]. Primary and secondary reactions can incorporate more complex events, such as interaction with lipid membranes and multistep nucleation. The master equation approach [26, 39] translates the reaction network into an infinite system of coupled non-linear differential equations describing, in probabilistic terms, the time course of the species involved, from monomers to filaments identified by their monomer count.
The main goal of this approach is to find an analytical solution for the system to describe its reaction time course. As a result, the analytical solution can be fitted to experimental data to identify kinetic rate constants and provide mechanistic insights into the aggregation process. Since the master equation formulation is often analytically and numerically intractable, specific approximation methods can be employed to reduce the system to two differential equations describing the time evolution of aggregate number and mass concentrations, i.e., readily available observables. Multiple efforts have channeled into a formal analysis of this minimal closed system. Knowles and colleagues [25, 37, 40] proposed fixed-point approaches to derive explicit solutions for the entire time course of aggregates. All the identified parameters had a clear physical meaning related to the underlying molecular events. Furthermore, analytical solutions exhibited scaling laws used in model fitting to determine the importance of primary and secondary reactions [41]. For instance, in the case of breakable fibrils [25], the authors found that the reaction time course mainly depended on a parameter combining elongation and fragmentation rate constants. By analyzing the relationship between this parameter and the observables, such as half-time and maximal growth rate, the authors showed that even small perturbations in the fragmentation reaction significantly affected the aggregation process. This procedure was implemented in a global fitting tool for chemical kinetic models of in vitro protein aggregation (AmyloFit) [38].
Model parsimony and data accuracy are essential requirements for the fitting protocol. A parsimonious model can be fitted to a wide range of experimental data acquired for different initial monomer concentrations and in the presence and absence of preformed aggregate seeds. Techniques for measuring aggregate species vary from fluorescent dyes (e.g., thioflavin T) to mass spectrometry for aggregate mass concentration and single-molecule fluorescence for oligomer concentrations [38, 42, 43]. With improvements in experimental approaches come recent advances in the mathematical framework, including the investigation of stochastic aggregation kinetics [44], the spatial dependence of protein aggregation [45], and the nature of oligomeric species [32, 46].
2.3. Chemical kinetic models of αsyn aggregation
A significant number of chemical kinetic models address αsyn aggregation and its implications in PD.
2.3.1. Nucleation-polymerization models
NP models describe aggregation as fibril formation by monomer addition, which follows a nucleation event and escalates by secondary reactions. This process is represented by a characteristic sigmoidal growth curve, identified by a lag phase, a growth phase, and a plateau [25]. By relying on the kinetic theory of aggregation that revolves around the master equation approach, multiple studies have combined experimental analysis with these mechanistic models to investigate underlying microscopic events and the effect of varying experimental conditions.
Buell et al. [47] focused on the effect of pH on αsyn aggregation in the presence and absence of preformed fibril seeds. Homogeneous and heterogeneous nucleations and fragmentation were negligible in purely monomeric solutions at neutral pH. Adding preexisting aggregates to the solution enhanced the aggregation rate and shortened the lag phase of the sigmoidal growth curve. To obtain the elongation rate constant, the authors used a minimal model involving only an elongation reaction saturating at high monomer concentrations (i.e., two-step elongation). On the other hand, a mildly acidic pH uncovered a much faster aggregation, that is, a longer lag phase and a more rapid growth phase, due to either surface-catalyzed nucleation or fibril fragmentation. Building on Buell et al. [47] and Gaspar et al. [48] determined the pH-dependent role of these two events by relying on the theoretical analysis of a model that includes primary and secondary reactions. According to an experimental analysis supported by a global fitting procedure [38], the autocatalytic nature of aggregation was mainly determined by secondary nucleations of monomers on fibril surfaces. These studies provided insightful information on physiological mechanisms; for example, they showed that even a slight pH change associated with different intracellular environments might enhance the production of toxic aggregates.
Small lipid vesicles can alter αsyn aggregation as much as pH levels [49]. Upon interaction with lipid membranes, the protein adopts a stable α-helical conformation [50]. Galvagnion et al. [49] showed that an imbalance between free and membrane-bound αsyn states can trigger amyloid formation by enhancing heterogeneous primary nucleation on lipid surfaces. To confirm and quantify these results, the authors employed an NP model including this nucleation reaction, two-step elongation, and the conversion between intermediate species [42]. Relying on Buell et al. [47] and Galvagnion et al. [49], Flagmeier et al. [51] investigated how mutations in αsyn influence the fate of amyloid fibrillation. The authors performed three experiments to separately analyze initiation, elongation, and multiplication steps for all αsyn variants. Each experiment was associated with a mechanistic model: the NP model from Galvagnion et al. [49] for lipid-induced aggregation; and linear polymerization models for strongly and weakly seeded aggregation processes at neutral and mildly acidic pH. Experimental and theoretical results agreed that the rate of surface-catalyzed nucleation on lipid membranes and fibril surfaces could vary by several orders of magnitude across different mutations.
2.3.2. Nucleation-conversion-polymerization models
The NP models are coarse-grained to the extent that they do not explicitly account for αsyn intermediate species. The modeling choice mainly relates to the absence of accurate measurements of oligomer concentrations in the aggregation process. Oligomers are indeed transient and highly heterogeneous species. The development of new methods to report their levels has motivated the transition to NCP models [46, 52]. These models include the structural interconversion from disordered clusters to oligomers with a partially formed fibrillar structure, eventually growing into fibrils.
Multiple studies on αsyn aggregation have provided experimental and theoretical support to this updated kinetic theory [53–56]. Single-molecule Förster Resonance Energy Transfer (FRET) experiments can distinguish two oligomeric populations associated with low and high FRET levels. Type-A oligomers are early-formed, disordered, highly degradable, and mildly toxic species, whereas type-B oligomers are later-forming, more compact, degradation-resistant, and ROS-promoting species [42, 55]. Both oligomeric species appear as required subsequent steps in the aggregation process [57]. As displayed in Figure 1A, NCP models tailored for αsyn aggregation include primary nucleation, which generates type-A oligomers from monomers, and the structural conversion from type-A to type-B oligomers and then fibrils [42, 55]. Both fibrillar and oligomeric species increase in size by monomer-dependent elongation. In this reaction network, the conformational change between oligomeric species emerges as a crucial step for initiating αsyn aggregation. Upon fitting the model to experimental data, Cremades et al. [42] showed that the corresponding kinetic rate is slow, thus providing a sufficient lag time for the protein quality control machinery to hamper the pathological process. A potential therapeutic strategy may employ molecular chaperones or small molecules to regulate this reaction. A follow-up study [55] used the NCP model to quantify seeding ability and conditions for type-B oligomers and fibrils, with implications on prion-like spreading. Model predictions showed that fibrils were more prone to seed aggregation, whereas oligomers mainly contributed to the increase of oxidative stress.
The studies reported above focused on the early stages of αsyn aggregation; thus, they did not require full-time analytical solutions. To extend the analysis to the entire time course, Dear et al. [46] provided a general mathematical framework for NCP models. The authors proposed a reaction network with a single oligomeric state. Such a coarse-grained model is suitable to avoid overfitting in the analysis of experimental data on total oligomer concentration that, as such, does not account for differences between oligomeric populations, e.g., see Zurlo et al. [56]. Moreover, the model is instrumental in classifying oligomers according to theoretically defined metrics: persistence or half-life, abundance, and productivity, i.e., the propensity to form fibrils rather than dissociate. The authors proved that oligomers were more prone to dissociation than fibrillation as a universal feature. Results focusing on αsyn oligomers showed that they were very kinetically stable, more persistent than monomers, relatively abundant, and highly productive compared to other proteins.
Overall, chemical kinetic models contribute to a detailed mechanistic understanding of αsyn aggregation by combining theoretical results and in vitro data acquired through advanced techniques. By exploring a wide range of in silico experimental conditions, these models return coherent predictions that can be useful for studying PD. Further investigation in this direction should focus on whether and how these results apply to in vivo settings to provide insights into the mechanisms of neurodegeneration and, possibly, inform therapeutic strategy design [58].
3. Mechanistic models of αsyn aggregation and degradation pathways
Given the central role of degradation in regulating αsyn homeostasis, multiple models have investigated this process in relation to PD neurodegeneration, including models solely focused on αsyn aggregation and degradation or miscellaneous models that include additional pathogenic processes (e.g., ROS production and defective dopamine metabolism). These degradation models offer a heterogeneous picture in terms of specific mechanisms they consider, granularity, and modeling approaches [21] (see Figure 2B). The biological processes can be represented by varying degrees of detail, and the modeling formalism can range from ordinary differential equations (ODEs) and algebraic equations to stochastic simulations, partial differential equations, or flux balance analysis [20, 21].
3.1. Defective protein degradation machinery and PD neurodegeneration
The proteolytic machinery combined with the molecular chaperone system ensures the renewal of functional components and regulates the fate of altered proteins to avoid the build-up of intracellular damage. In PD and other neurodegenerative diseases, degradation efficiency declines with age and oxidative stress [59], thus increasing misfolded αsyn and aggregate levels. On the other hand, αsyn aggregation can hamper the proteolytic machinery causing the accumulation of other cellular components [60]. The interplay of αsyn aggregation and impairment of degradation in multiple negative feedbacks poses a causality dilemma [61]: which pathological process comes first? There is still no clear answer. Degradation defects and αsyn aggregation can be either primary or secondary events of neurodegeneration [12, 62]. The investigation of their role in PD is even more challenging due to interfering factors such as increased oxidative stress and mitochondrial dysfunctions [1, 59]. Systems biology models can help elucidate these contributions by providing in silico benchmarks to assess these hypotheses.
3.1.1. The ubiquitin-proteasome pathway
UPP is the dominant clearance route for mislocated, misfolded, damaged, and short-lived proteins. Target substrates are selectively tagged by polyubiquitin chains through multiple enzymatic reactions and then transferred to the proteasome. Ubiquitinating and deubiquitinating enzymes such as PARKIN and UCH-L1 play a central role in modulating protein degradation in PD, as indicated by UPP-related familial cases [8, 60]. For instance, UCH-L1 maintains a stable pool of monomeric ubiquitin; an imbalance of this pool can lead to poor substrate labeling with consequent impaired proteasomal degradation. Furthermore, the presence of LBs as a PD molecular hallmark corroborates the correlation between proteasomal dysfunctions and PD pathogenesis. Indeed, LBs mainly consist of ubiquitin-tagged αsyn aggregate, ubiquitinated proteins, and UPP components [60, 63, 64]. According to multiple studies [11, 65], their composition suggests a potential cytoprotective role for LBs, which may act as sinks for poorly degraded proteins to reduce the toxic effect of protein accumulation and slow down neurodegeneration. Still, it is unclear whether these cytoplasmic inclusions represent a harmful or defense molecular mechanism for the neuron. UPP dysfunctions and αsyn aggregation create a negative feedback loop. Genetic and age-related impairments in UPP may hamper the proper degradation of misfolded aggregate-prone αsyn. On the other hand, αsyn species refractory to proteasomal degradation, such as mutant αsyn forms, oligomers, and fibrils, can inhibit proteasomal activity by sequestering the proteasome. In addition, the interaction with oligomers and oxidatively damaged αsyn may directly alter proteasome subunits, as shown in the green box in Figure 2A.
3.1.2. The autophagy-lysosome pathway
ALP removes long-lived proteins, lipids, and dysfunctional organelles, such as aging mitochondria (i.e., mitophagy), thus maintaining neuronal homeostasis. It includes three degradation mechanisms: macroautophagy, chaperone-mediated autophagy (CMA), and microautophagy. Experimental findings indicate that both UPP and ALP degradation of αsyn can occur [66]. The autophagic mechanisms are involved in physiological αsyn turnover and αsyn aggregates degradation (see the purple box in Figure 2A). Specifically, wild-type αsyn monomers are degraded mainly by CMA [67], which relies on molecular chaperones to recognize a specific motif on the target substrate. Upon chaperone binding, the cargo interacts with the membrane receptor LAMP2A, which assembles into multimeric translocation complexes. The substrate then enters the lysosome lumen, where it is rapidly degraded. CMA also clears ALP and UPP-related proteins, such as LRRK2, UCH-L1, DJ-1, and GCase [68]. Furthermore, macroautophagy represents the main clearance route for αsyn aggregates due to the inaccessibility of the CMA degradation motif [62]. This degradation mechanism consists in the formation of autophagosomes, i.e., double-membrane vesicles surrounding the cargo and fusing with lysosomes to allow hydrolase-mediated degradation in the lysosomal lumen. In selective macroautophagy, specific autophagosome membrane receptors target protein aggregates. The link between impaired autophagy and PD neurodegeneration conceals a complex interaction network between αsyn aggregates and the lysosomal proteolytic machinery. Growing evidence supports the negative effect of αsyn aggregation on autophagy acting on multiple levels [62, 69], as displayed in Figure 2A. At the same time, defective ALP cannot handle harmful αsyn species, thus leading to their accumulation. Such defects can originate from various sources, such as increased oxidative stress, aging, and dysfunctional proteins related to genetic PD forms, namely, LRRK2, DJ-1, and GBA [5], and with a physiological role in ALP.
3.2. Degradation models
3.2.1. UPP models
Relying on experimental evidence pointing to the essential contribution of UPP to neurodegeneration [70, 71], Sneppen et al. [72] provided a minimal theoretical model of the interplay between impairments in proteasomal degradation and αsyn fibrillation. The proteasome ensured protein homeostasis by keeping the amount of αsyn aggregates low. On the other hand, insoluble αsyn fibrils sequestered this proteolytic machinery and formed a slowly-degraded complex, thus reducing proteasome function. Computational simulations of this ODE system supported by stability analysis showed a bifurcation behavior. When the fibril level exceeded a particular threshold related to proteasome production capacity, the double-negative feedback broke αsyn homeostasis in favor of a pulsatile oscillatory regime characterized by spikes and long periods of low proteasome concentrations. As a result, the system alternated between the hypothetical recovery of proteolytic activity and the uncontrolled accumulation of harmful aggregates and fibrils. Several oscillations eventually built up toxicity over decades, thus explaining the slow progression of PD neurodegeneration. The authors therefore associated proteasome overload and the subsequent oscillatory regime with the onset of sporadic PD phenotype. In a follow-up study [73], the stochastic analysis of the core negative feedback confirmed and generalized the above phenomenon for the whole protein clearance machinery. The bifurcation behavior characterized by a healthy homeostatic state and an oscillatory disease state indeed emerged for both UPP and ALP degradation. In addition, stochastic simulations captured dynamical differences between the two degradation systems, modeled as enzymatic reactions slowly reducing aggregate concentrations. Lysosomes were assumed to be more efficient but less abundant than proteasomes. Fibril-mediated sequestration of the proteasome therefore led to regular and almost deterministic oscillations, whereas lysosome overload resulted in irregular fluctuations.
In contrast to the high-level representation of the UPP in Sneppen et al. [72], Pigolotti et al. [73], and Proctor et al. [74, 75] proposed a detailed description of this pathway by including mono- and polyubiquitination, proteasome binding, ATP-dependent degradation, and proteasome inhibition by protein aggregates. These studies were devoted to the mathematical modeling of the aging process, which contributes to the decline of proteolytic activity and the build-up of oxidative stress due to flawed mitochondria [76, 77]. Both models indeed investigated the role of the proteasomal degradation pathway in age-related neurodegeneration. In Proctor et al. [74], Proctor and colleagues first presented a stochastic model for aggregation and proteasomal degradation of a generic protein under normal homeostasis and aging. The authors then tailored the system to assess the UPP role in αsyn aggregation during PD neurodegeneration [75]. The final model included additional modules representing αsyn metabolism and UCH-L1 deubiquitination activity in proteasomal degradation. This stepwise approach relied on the idea that the molecular landscape of neurodegeneration can be arranged in building blocks, as most biological processes are assumed to be modular [20, 78]. Both general and specific models proved to be functional for investigating the negative feedback of protein aggregate formation and UPP impairment. Employing the more general model [74], the authors explored the impact of various experimental procedures, e.g., shutting down a ubiquitin-protein ligase or the proteasome activity. The results suggested that depleted ubiquitin pools might contribute to proteostasis impairment. In addition, relying on the model tailored for PD [75], the authors analyzed the effects of both mutated and oxidatively damaged UCH-L1. Stochastic simulations indicated that proteasome inhibition might not be the triggering event for neurodegeneration but rather an exacerbating factor accelerating αsyn aggregation and inclusion formation. Both models were validated against data gathered in ad-hoc designed experiments, in a virtuous cycle of model refinement and in vitro experiments.
3.2.2. UPP and ROS models
Since oxidative stress and impairments in UPP degradation are interconnected, multiple studies have analyzed their synergistic effect on αsyn homeostasis. Cloutier et al. [79] provided a mathematical model accounting for the interplay between αsyn aggregation, ROS production, and proteasome-mediated degradation. Given the variety of molecular processes involved, the authors were able to evaluate the impact of multiple risk factors on αsyn metabolism. For instance, perturbations of system parameters related to oxidative stress and protein clearance capacity reproduced the high variability of LB concentration in PD forms [79, 80]. Moreover, supported by experimental verification [81], deterministic simulations of the model uncovered a bistable process whereby the system irreversibly switched from a healthy to a disease state, identified by high misfolded αsyn and ROS levels, in response to toxin exposure, genetic mutations, and aging. On the other hand, the model could not recapitulate the oscillatory regime due to decreased levels of available clearance machinery obtained in Sneppen et al. [72] and Pigolotti et al. [73]. To identify the primary mechanisms determining the bifurcation behavior, the authors reduced the system to focus only on the double-positive feedback between αsyn misfolding and ROS production [82]. This minimal version retained the bistable behavior, thus associating PD onset with a switch-like transition in response to enhanced ROS concentrations. In line with [72, 73], the central idea remained that neurodegeneration results from the transition between two dynamical behaviors.
Raichur et al. [83] also presented a model targeting the interplay between oxidative stress, αsyn aggregation, and UPP dysfunctions. Compared to Cloutier et al. [79], this system displayed a more granular description of the UPP pathway, from ubiquitination and proteasome recognition to degradation. The close molecular detail of ROS production and UPP degradation provided in the model inevitably hampered the theoretical analysis. On the other hand, the explicit representation of proteasome-mediated degradation enabled the authors to explore different scenarios of UPP-related genetic predisposition: mutations in UCH-L1, PARKIN, and DJ-1 genes, combined with age-related oxidative stress. These familial PD forms determined the accumulation of ubiquitinated proteins, leading to a more rapid αsyn aggregation than sporadic forms. Furthermore, the synergistic combination of ROS production and UPP-related genetic mutations fueled αsyn aggregation. These results pointed to therapeutic strategies involving restored UPP functionality or enhanced ALP activity in combination with antioxidant treatments.
3.2.3. UPP and ALP models
The modeling picture outlined so far focuses on the ubiquitin-proteasome pathway, while the autophagy-lysosome pathway is under-represented despite its critical role in αsyn turnover; when considered, autophagic clearance has often been incorporated as a pseudo-first-order reaction. This is not the case of Ouzounoglou et al. [84], who provided a detailed representation of selective macroautophagy, CMA, and proteasome-mediated degradation, focusing on the inhibitory feedback between αsyn oligomers and the CMA receptor LAMP2A. Upon model calibration and validation against αsyn overexpression data from human neuroblastoma cells, the authors performed stochastic simulations to explore different interventions with neuroprotective potentials, such as shutting off DA production, increasing LAMP2A levels, and reducing αsyn synthesis. The resulting predictions of increased cell viability were in agreement with experimental evidence and literature [85, 86].
To provide valuable insights into the role of αsyn degradation in neurodegeneration, a mechanistic model should integrate ALP and UPP degradation mechanisms, ideally accounting for the crosstalk between these pathways. In this direction, Sass et al. [87] proposed a model targeting asyn aggregation, UPP and ALP degradation, and DA metabolism and based on the biochemical system theory. A granular representation of these mechanisms and their interactions facilitated the analysis of specific system perturbations in both disease and treated states (e.g., enhanced αsyn fibrillation and aggregation rate). Including DA metabolism in the model also enabled the authors to simulate the impairment of DA vesicle packaging and available treatments related to its shortage, such as L-Dopa therapy combined with monoamine oxidase inhibitors. Increasing model complexity even further, Büchel et al. [88] presented an extended model of a dopaminergic neuron that includes the highest number of molecular components among the available PD models of αsyn homeostasis [20]. The model described 11 biological processes, including DA metabolism and transport, αsyn aggregation, oxidative stress, UPP and ALP clearance mechanisms, and specific details on PARKIN and DJ-1 proteins. Here, the modeling approach adopted was crucial to tackle model complexity. The authors employed flux balance analysis to investigate the steady-state behavior of the model rather than deterministic or stochastic analysis based on mass action kinetics. The qualitative prediction of multiple in silico experiments pointed to increased ROS, neurotoxin MPTP, and αsyn levels as crucial factors in PD neurodegeneration.
3.2.4. αsyn degradation and axonal transport models
The degradation models analyzed so far do not account for the spatial dependence of αsyn aggregation and degradation mechanisms. However, αsyn homeostasis and disease progression may strongly depend on intraneuronal protein propagation. Along this line, Kuznetsov and Kuznetsov [89, 90] investigated αsyn axonal transport and how its perturbation between the somatic and synaptic compartments affected the aggregation and degradation processes. By relying on a two-compartment ODE model [90], the authors predicted axonal death due to αsyn accumulation at the synaptic terminal, pointing to defective protein clearance machinery as the primary cause for αsyn aggregation onset compared to reduced αsyn production and transport [90]. Differences in the degradation of αsyn monomers and aggregates were determined by assuming distinct half-lives. Furthermore, building on recent findings on the absence of αsyn fibrils in LB inclusions [36], the authors proposed a mathematical model of αsyn aggregation, degradation, and transport to test the hypothetical autocatalytic nature of LB formation and its impact on protein accumulation [91]. Here, the authors assumed spatial-dependent proteasomal and autophagic degradation mechanisms. The study pointed to the central role of the autophagic clearance pathway in LB formation and PD progression; defective autophagy may favor the aggregation of membrane-bound organelles catalyzed by αsyn aggregates and, thus, LB formation. Most degradation models do not differentiate between αsyn fibrillation and LB formation, whereas chemical kinetic models do not even include these cytoplasmic inclusions. The detailed implementation of LB formation and maturation would allow for the investigation of LB neuroprotective role [65, 91].
The wide variety of degradation models reflects the multifactorial nature of PD. Such a modeling effort has provided multiple insights into the interplay between αsyn aggregation and protein degradation by spanning various levels of molecular detail, from coarse-grained to highly granular representations (see Figure 2B). Minimal models have been used to uncover dynamical features of disease progression (e.g., Sneppen et al. [72], Pigolotti et al. [73], and Cloutier et al. [82]). More detailed models (e.g., Proctor et al. [75] and Ouzounoglou et al. [84]) have proven to be suitable for testing the effects of potential treatments. Overall, degradation models move toward an integrative representation of PD pathogenesis. Future work may focus on the crosstalk between UPP and ALP pathways, the interplay between autophagy and apoptosis in PD neurodegeneration [92], and the integration of other control systems for protein homeostasis such as the molecular chaperone system [93].
4. Discussion
Mechanistic modeling grounded in molecular-level knowledge is a powerful tool for tackling PD biological complexity. By exploring the intricate interaction network of neurodegeneration through in silico experiments, mathematical models can investigate the key drivers of PD pathogenesis, discover promising targets, and even simulate the effect of potential single or combination therapies. Given the pivotal role of αsyn homeostasis in PD, this review has provided a collection of available mathematical models of αsyn aggregation and degradation pathways.
Chemical kinetic models focus on a single molecular pathway and rely on a unifying kinetic theory that translates into the consistency of modeling formalism (i.e., master equations approximated to ODE systems). In contrast, degradation models describe multiple biological processes and adopt a wide range of approaches to analyze the dynamical features of the system. The latter are modeled as deterministic and stochastic simulations based on mass action kinetics; yet, there are some exceptions, such as flux balance analysis, mainly related to the complexity of the reaction network considered. Stochastic approaches [94, 95] have been employed to analyze biological processes with low molecular counts and capture their inherent fluctuations. Future investigation may explore the role of intrinsic noise in PD onset and progression since it can unpredictably affect the system behavior, for example, by triggering the transition from a healthy to a disease state leading to PD onset [21, 79].
4.1. Integrating chemical kinetic and degradation models
Both chemical kinetic and degradation models include a representation of αsyn aggregation. As shown in Figures 1A, 2A (light-blue box), chemical kinetic models account for each molecular step separately, whereas degradation models employ macro-variables for different αsyn aggregate species according to their size and functional features. The master equation approach returns parameters that physically relate microscopic events to macroscopic observables. On the other hand, a higher-level representation of the process enables the targeting of additional pathways and the investigation of their interplay in the molecular network. A modeling opportunity lies at the intersection of the two groups: degradation models can be integrated with a chemical kinetic representation of the aggregation process. In this way, they can benefit from the kinetic rate constants derived from fitting to the wide variety of in vitro data available. At the same time, chemical kinetic models can be extended to include UPP and ALP pathways, converging toward an in vivo representation. These integrated models can be employed to determine the relative importance of each microscopic event in relation to degradation mechanisms (e.g., the structural interconversion between type-A and type-B oligomers), thus suggesting specific target species and reactions. Recent studies have moved a few steps toward model integration [73, 96]. Here, clearance mechanisms are approximated by pseudo-first-order reactions to facilitate theoretical analysis. Further investigation should focus on an explicit representation of the degradation processes, especially the ALP pathway, considering the growing interest in the role of autophagy in neurodegeneration [7, 22, 97]. However, this choice translates into an increased complexity of the system itself. Future work should favor an integrative representation of pathological mechanisms that balances high granularity and analytical or computational tractability [98].
4.2. In vitro/in vivo translation
Integrating chemical kinetic and degradation models is part of the modeling efforts currently chasing the mechanistic representation of αsyn aggregation in vivo. To this end, both groups of models would benefit from calibration and validation against measurements of aggregate levels in living systems. However, the availability of this quantitative information is limited by technical difficulties in monitoring the time evolution of aggregates and addressing the heterogeneous and elusive nature of oligomers [58]. As a result, chemical kinetic models have been trained mainly on in vitro data. Among the limitations of using this type of data is the unclear relevance of the results on a disease time scale, moving from the few hours or days of test-tube experiments to the decades of PD progression [21]. In addition, in vitro aggregation assays typically rely on initial protein concentrations that far exceed αsyn levels detected intracellularly and in post-mortem brain extracts from PD patients and controls [99–101]. On the other hand, concentrations used in vitro are comparable to those estimated in vivo at presynaptic terminals [102–105]. Such a potential discrepancy in αsyn concentrations may hamper translatability due to the strong dependence of aggregation rates on initial protein levels [58, 106]. Nevertheless, studying aggregation mechanisms in silico can bridge in vitro and in vivo settings. For example, in vitro studies paired with chemical kinetic models showed that adding lipid vesicles to the solution accelerates in vitro aggregation, which occurs at lower bulk concentrations [47, 48]. This result may suggest a similar mechanism in living systems, given αsyn intracellular localization at presynaptic terminals and its physiological role in vesicular trafficking. Moreover, according to a recent perspective paper [58], the late onset of amyloid formation in sporadic PD may emerge from the intrinsic properties of aggregation kinetics, specifically from a combination of dominant secondary processes and prion-like spreading. Age-related defects in protein degradation may also work in concert with secondary events in the aggregation process to drive amyloid formation. Qualitative similarities between in vitro and in vivo aggregation mechanisms support this scenario. Indeed, biophysical features of amyloid formation detected in test-tube experiments seem to be preserved in living systems [58, 107]. On the other hand, a quantitative analysis of the aggregation kinetics in vivo is lacking. Current studies focus on the applicability of in vitro molecular-level mechanistic studies to living systems and the related modeling limitations and opportunities, as extensively discussed in Meisl et al. [108]. Molecular models combining the kinetic of αsyn aggregation and multiple biological pathways underlying PD neurodegeneration can assist in vitro to in vivo translation [109].
4.3. Modulating the protein aggregation pathway
PD research efforts seek to provide a solid foundation for therapeutic strategy design in PD. Not only can mechanistic models of αsyn homeostasis identify candidate target mechanisms, but they can also support the development of various anti-aggregation treatments currently under study. In this context, chemical kinetic models provide a theoretical framework for analyzing the inhibitory effect of multiple compounds on the aggregation process. Employing a nucleation-polymerization model that accounts for interactions with a new general component, Michaels et al. [110] identified different regimes of inhibition related to specific combinations of kinetic rate constants and binding affinities, thus optimizing the inhibitor efficacy of the compound. Furthermore, a follow-up study simulated the impact of therapeutic interventions on key oligomeric features by tuning specific rate constants [111]. This analysis suggested that inhibiting the primary nucleation event that dominates lipid-induced αsyn aggregation strongly reduces the peak and overall concentration of the oligomeric population. As shown in [112], this mechanism of action characterizes the natural aminosterol compound known as trodusquemine, which interferes with αsyn aggregation by blocking its interaction with lipid membranes and thus inhibits lipid-induced primary nucleation and fibril-mediated secondary nucleation. Also, it can suppress aggregation-related cytotoxicity by hampering oligomer interaction with cell membranes [113]. In addition to small molecules, potential therapeutic strategies targeting different αsyn species and reactions include peptides and peptidomimetics, antibodies, and molecular chaperones [13]. In this respect, chemical kinetic studies have recently investigated the mechanism of action of specific molecular chaperones [114, 115] and antibodies [116] on amyloid beta aggregation in Alzheimer's disease (e.g., Brichos and Aducanumab, respectively); the results were in good agreement with clinical outcomes. These studies should be extended to Parkinson's disease, e.g., supporting clinical trials that involve anti-αsyn antibodies such as prasinezumab and cinpanemab.
4.4. Targeting protein degradation pathways
Inhibiting specific molecular steps of the aggregation pathway is not the only possible intervention targeting impaired αsyn homeostasis. Genetic-based strategies reducing protein synthesis have been proposed to avoid aggregation in the first place, such as employing antisense oligonucleotides, RNA interference, and β2-adrenoreceptor agonists [13]. However, side effects may arise from protein downregulation due to αsyn physiological role in presynaptic vesicle trafficking. Mechanistic models should be employed to determine a critical range for αsyn expression levels, facilitating the transition from preclinical to clinical trials. However, currently available models do not include a genetic level representation; thus, transcription and translation inhibitions can be simulated only by varying the rate constant associated with αsyn production. Another strategy consists in modulating UPP and ALP degradation mechanisms to hamper αsyn aggregation and PD neurodegeneration. Autophagy can be enhanced selectively or as a whole. An overall ALP enhancement driven by chemical compounds such as rapamycin and trehalose has limited applicability in PD since it may interfere with essential physiological processes and the homeostasis of proteins other than αsyn [62]. The same limitations hold for therapeutic strategies focusing on overall UPP degradation [117]. In contrast, selective targeting of specific molecular steps in proteasomal degradation, CMA, and macroautophagy may be a promising strategy [62]. UPP-related candidate treatments include stimulating ubiquitination and regulating the activity of chaperone systems. In addition, selective ALP activators may act by modulating LAMP2A assembly and translocation, enhancing autolysosome fusion, and targeting lysosomal function. Ideally, mechanistic models can support the development of current and future interventions of this type. However, further research is needed to reach this goal. Most degradation models analyzed here lack a granular representation of autophagic pathways that would allow the simulation of these selective strategies. Still, they can provide insightful information on the role of UPP and ALP degradation pathways in neurodegeneration as the first step toward in silico-aided therapeutic strategies against PD.
4.5. Toward multiscale QSP models for PD
The points discussed above highlight the need for multiscale QSP models that can link molecular mechanisms to cellular and tissue-level events and, finally, clinical manifestations. These models would leverage the large amount of available data associated with neuroimaging techniques and disease-rating scales for motor symptoms (MDS-UPDRS) and cognitive impairment (MoCa and MMSE) [1, 118]. This type of data has already been employed by quantitative models that address the heterogeneity of the PD clinical picture by accounting only for physical symptoms [119]. In addition to quantitative tools supporting PD diagnosis, a mechanistic understanding of the molecular processes underlying PD pathogenesis and how they connect to the clinical endpoints is essential to inform drug discovery and development. The models in this review represent a starting point in this sense. Being confined at the molecular level, they have to settle for surrogate endpoints such as ROS, αsyn aggregate, and LB levels to identify disease phenotypes. Moving to the cellular, tissue, and organ levels through network-based, epidemiological, and compartmental PK/PD approaches [120–123], these models can account for αsyn prion-like propagation between neurons and across multiple brain areas, using potential PD biomarkers such as αsyn concentrations in plasma and CSF [124] and magnetic resonance imagining measurements.
Overall, this review makes a case for using mechanistic models of αsyn homeostasis as valuable tools to uncover PD pathogenesis, suggesting their integration into a QSP framework to provide blueprints for therapeutic interventions.
Author contributions
ER and FR designed, wrote, and edited the manuscript. AA provided a preliminary version of some sections. LM and ED discussed the results and edited the manuscript. All the authors reviewed the manuscript.
Acknowledgments
The authors would like to thank Dr. Gianluca Selvaggio for his helpful suggestions, comments, and support in preparing this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Poewe W, Seppi K, Tanner CM, Halliday GM, Brundin P, Volkmann J, et al. Parkinson disease. Nat Rev Dis Primers. (2017) 3:17013. doi: 10.1038/nrdp.2017.13
2. Dorsey ER, Sherer T, Okun MS, Bloem BR. The emerging evidence of the Parkinson pandemic. J Parkinsons Dis. (2018) 8:S3-S8. doi: 10.3233/JPD-181474
3. Parkinson J. An essay on the shaking palsy. J Neuropsychiatry Clin Neurosci. (2002) 14:223–36. doi: 10.1176/jnp.14.2.223
4. LeWitt PA, Fahn S. Levodopa therapy for Parkinson disease: a look backward and forward. Neurology. (2016) 86(14 Supplement 1):S3-S12. doi: 10.1212/WNL.0000000000002509
5. Blauwendraat C, Nalls MA, Singleton AB. The genetic architecture of Parkinson's disease. Lancet Neurol. (2020) 19:170–8. doi: 10.1016/S1474-4422(19)30287-X
6. Fujita KA, Ostaszewski M, Matsuoka Y, Ghosh S, Glaab E, Trefois C, et al. Integrating pathways of Parkinson's disease in a molecular interaction map. Mol Neurobiol. (2014) 49:88–102. doi: 10.1007/s12035-013-8489-4
7. Gan-Or Z, Dion PA, Rouleau GA. Genetic perspective on the role of the autophagy-lysosome pathway in Parkinson disease. Autophagy. (2015) 11:1443–57. doi: 10.1080/15548627.2015.1067364
8. Walden H, Muqit MM. Ubiquitin and Parkinson's disease through the looking glass of genetics. Biochemical Journal. (2017) 474:1439–51. doi: 10.1042/BCJ20160498
9. Vekrellis K, Xilouri M, Emmanouilidou E, Rideout HJ, Stefanis L. Pathological roles of α-synuclein in neurological disorders. Lancet Neurol. (2011) 10:1015–25. doi: 10.1016/S1474-4422(11)70213-7
10. Navarro-Romero A, Montpeyó M, Martinez-Vicente M. The emerging role of the lysosome in Parkinson's disease. Cells. (2020) 9:2399. doi: 10.3390/cells9112399
11. Olanow CW, McNaught KSP. Ubiquitin-proteasome system and Parkinson's disease. Mov Disord. (2006) 21:1806–23. doi: 10.1002/mds.21013
12. Xilouri M, Brekk OR, Stefanis L. Alpha-synuclein and protein degradation systems: a reciprocal relationship. Mol Neurobiol. (2013) 47:537–51. doi: 10.1007/s12035-012-8341-2
13. Fields CR, Bengoa-Vergniory N, Wade-Martins R. Targeting alpha-synuclein as a therapy for Parkinson's disease. Front Mol Neurosci. (2019) 12:299. doi: 10.3389/fnmol.2019.00299
14. Azer K, Kaddi CD, Barrett JS, Bai JP, McQuade ST, Merrill NJ, et al. History and future perspectives on the discipline of quantitative systems pharmacology modeling and its applications. Front Physiol. (2021) 12:637999. doi: 10.3389/fphys.2021.637999
15. Geerts H, Wikswo J, Graaf PH, Bai JPF, Gaiteri C, Bennett D, et al. Quantitative systems pharmacology for neuroscience drug discovery and development: current status, opportunities, and challenges. CPT Pharmacometr Syst Pharmacol. (2020) 9:5–20. doi: 10.1002/psp4.12478
16. Abrams R, Kaddi CD, Tao M, Leiser RJ, Simoni G, Reali F, et al. A quantitative systems pharmacology model of Gaucher disease type 1 provides mechanistic insight into the response to substrate reduction therapy with eliglustat. CPT Pharmacometr Syst Pharmacol. (2020) 9:374–83. doi: 10.1002/psp4.12506
17. Bloomingdale P, Karelina T, Cirit M, Muldoon SF, Baker J, McCarty WJ, et al. Quantitative systems pharmacology in neuroscience: novel methodologies and technologies. CPT Pharmacometr Syst Pharmacol. (2021) 10:412–9. doi: 10.1002/psp4.12607
18. Bloomingdale P, Karelina T, Ramakrishnan V, Bakshi S, Véronneau-Veilleux F, Moye M, et al. Hallmarks of neurodegenerative disease: a systems pharmacology perspective. CPT Pharmacometr Syst Pharmacol. (2022) 11: 1399–429. doi: 10.1002/psp4.12852
19. Stephenson D, Ollivier C, Brinton R, Barrett J. Can innovative trial designs in orphan diseases drive advancement of treatments for common neurological diseases? Clin Pharmacol Therapeut. (2022) 111:799–806. doi: 10.1002/cpt.2528
20. Lloret-Villas A, Varusai T, Juty N, Laibe C, NovÈre NL, Hermjakob H, et al. The impact of mathematical modeling in understanding the mechanisms underlying neurodegeneration: evolving dimensions and future directions. CPT Pharmacometr Syst Pharmacol. (2017) 6:73–86. doi: 10.1002/psp4.12155
21. Bakshi S, Chelliah V, Chen C, van der Graaf PH. Mathematical biology models of Parkinson's disease. CPT Pharmacometr Syst Pharmacol. (2019) 8:77–86. doi: 10.1002/psp4.12362
22. Klein AD, Mazzulli JR. Is Parkinson's disease a lysosomal disorder? Brain. (2018) 141:2255–62. doi: 10.1093/brain/awy147
23. Chiti F, Dobson CM. Protein misfolding, amyloid formation, and human disease: a summary of progress over the last decade. Annu Rev Biochem. (2017) 86:27–68. doi: 10.1146/annurev-biochem-061516-045115
25. Knowles TP, Waudby CA, Devlin GL, Cohen SI, Aguzzi A, Vendruscolo M, et al. An analytical solution to the kinetics of breakable filament assembly. Science. (2009) 326:1533–7. doi: 10.1126/science.1178250
26. Oosawa F, Kasai M. A theory of linear and helical aggregations of macromolecules. J Mol Biol. (1962) 4:10–21. doi: 10.1016/S0022-2836(62)80112-0
27. Gracia P, Camino JD, Volpicelli-Daley L, Cremades N. Multiplicity of α-synuclein aggregated species and their possible roles in disease. Int J Mol Sci. (2020) 21:8043. doi: 10.3390/ijms21218043
28. Hijaz BA, Volpicelli-Daley LA. Initiation and propagation of α-synuclein aggregation in the nervous system. Mol Neurodegener. (2020) 15:1–12. doi: 10.1186/s13024-020-00368-6
29. Spillantini MG, Schmidt ML, Lee VMY, Trojanowski JQ, Jakes R, Goedert M. Alpha-Synuclein in Lewy bodies. Nature. (1997) 388:839–40. doi: 10.1038/42166
30. Polymeropoulos MH, Lavedan C, Leroy E, Ide SE, Dehejia A, Dutra A, et al. Mutation in the α-synuclein gene identified in families with Parkinson's disease. Science. (1997) 276:2045–7. doi: 10.1126/science.276.5321.2045
31. Froula JM, Castellana-Cruz M, Anabtawi NM, Camino JD, Chen SW, Thrasher DR, et al. Defining α-synuclein species responsible for Parkinson's disease phenotypes in mice. J Biol Chem. (2019) 7294:10392–406. doi: 10.1074/jbc.RA119.007743
32. Cremades N, Chen SW, Dobson CM. Structural characteristics of α-synuclein oligomers. Int. Rev. Cell Mol. Biol. (2017) 329:79–143. doi: 10.1016/bs.ircmb.2016.08.010
33. Alam P, Bousset L, Melki R, Otzen DE. α-synuclein oligomers and fibrils: a spectrum of species, a spectrum of toxicities. J Neurochem. (2019) 9150:522–34. doi: 10.1111/jnc.14808
34. Brundin P, Melki R, Kopito R. Prion-like transmission of protein aggregates in neurodegenerative diseases. Nat Rev Mol Cell Biol. (2010) 11:301–7. doi: 10.1038/nrm2873
35. Hardenberg MC, Sinnige T, Casford S, Dada ST, Poudel C, Robinson EA, et al. Observation of an α-synuclein liquid droplet state and its maturation into Lewy body-like assemblies. J Mol Cell Biol. (2021) 13:282–94. doi: 10.1093/jmcb/mjaa075
36. Shahmoradian SH, Lewis AJ, Genoud C, Hench J, Moors TE, Navarro PP, et al. Lewy pathology in Parkinson's disease consists of crowded organelles and lipid membranes. Nat Neurosci. (2019) 22:1099–109. doi: 10.1038/s41593-019-0423-2
37. Cohen SI, Vendruscolo M, Welland ME, Dobson CM, Terentjev EM, Knowles TP. Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J Chem Phys. (2011) 135:08B615. doi: 10.1063/1.3608916
38. Meisl G, Kirkegaard JB, Arosio P, Michaels TCT, Vendruscolo M, Dobson CM, et al. Molecular mechanisms of protein aggregation from global fitting of kinetic models. Nat Protoc. (2016) 11:252–72. doi: 10.1038/nprot.2016.010
39. Michaels TC, Knowles TP. Mean-field master equation formalism for biofilament growth. Am J Phys. (2014) 82:476–83. doi: 10.1119/1.4870004
40. Cohen SI, Vendruscolo M, Dobson CM, Knowles TP. Nucleated polymerization with secondary pathways. II. Determination of self-consistent solutions to growth processes described by non-linear master equations. J Chem Phys. (2011) 135:08B611. doi: 10.1063/1.3608917
41. Michaels TC, Dear AJ, Knowles TP. Scaling and dimensionality in the chemical kinetics of protein filament formation. Int Rev Phys Chem. (2016) 35:679–703. doi: 10.1080/0144235X.2016.1239335
42. Cremades N, Cohen SIA, Deas E, Abramov AY, Chen AY, Orte A, et al. Direct observation of the interconversion of normal and toxic forms of α-synuclein. Cell. (2012) 149:1048–59. doi: 10.1016/j.cell.2012.03.037
43. Perrett S, Buell AK, Dobson CM, Knowles TP. The physical chemistry of the amyloid phenomenon: thermodynamics and kinetics of filamentous protein aggregation. Essays Biochem. (2014) 56:11–39. doi: 10.1042/bse0560011
44. Michaels TC, Dear AJ, Knowles TP. Stochastic calculus of protein filament formation under spatial confinement. New J Phys. (2018) 20:055007. doi: 10.1088/1367-2630/aac0bc
45. Cohen S, Rajah L, Yoon C, Buell A, White D, Sperling R, et al. Spatial propagation of protein polymerization. Phys Rev Lett. (2014) 112:098101. doi: 10.1103/PhysRevLett.112.098101
46. Dear AJ, Michaels TCT, Meisl G, Klenerman D, Wu S, Perrett S, et al. Kinetic diversity of amyloid oligomers. Proc Natl Acad Sci USA. (2020) 117:12087–94. doi: 10.1073/pnas.1922267117
47. Buell AK, Galvagnion C, Gaspar R, Sparr E, Vendruscolo M, Knowles TP, et al. Solution conditions determine the relative importance of nucleation and growth processes in α-synuclein aggregation. Proc Nat Acad Sci USA. (2014) 111:7671–6. doi: 10.1073/pnas.1315346111
48. Gaspar R, Meisl G, Buell AK, Young L, Kaminski CF, Knowles TP, et al. Secondary nucleation of monomers on fibril surface dominates α-synuclein aggregation and provides autocatalytic amyloid amplification. Q Rev Biophys. (2017) 50:172. doi: 10.1017/S0033583516000172
49. Galvagnion C, Buell AK, Meisl G, Michaels TC, Vendruscolo M, Knowles TP, et al. Lipid vesicles trigger α-synuclein aggregation by stimulating primary nucleation. Nat Chem Biol. (2015) 11:229–34. doi: 10.1038/nchembio.1750
50. Fusco G, De Simone A, Gopinath T, Vostrikov V, Vendruscolo M, Dobson CM, et al. Direct observation of the three regions in α-synuclein that determine its membrane-bound behaviour. Nat Commun. (2014) 5:1–8. doi: 10.1038/ncomms4827
51. Flagmeier P, Meisl G, Vendruscolo M, Knowles TP, Dobson CM, Buell AK, et al. Mutations associated with familial Parkinson's disease alter the initiation and amplification steps of α-synuclein aggregation. Proc Nat Acad Sci USA. (2016) 113:10328–33. doi: 10.1073/pnas.1604645113
52. Garcia GA, Cohen SI, Dobson CM, Knowles TP. Nucleation-conversion-polymerization reactions of biological macromolecules with prenucleation clusters. Physical Review E. (2014) 89:032712. doi: 10.1103/PhysRevE.89.032712
53. Horrocks MH, Tosatto L, Dear AJ, Garcia GA, Iljina M, Cremades N, et al. Fast flow microfluidics and single-molecule fluorescence for the rapid characterization of α-synuclein oligomers. Anal Chem. (2015) 87:8818–26. doi: 10.1021/acs.analchem.5b01811
54. Tosatto L, Horrocks MH, Dear AJ, Knowles TPJ, Serra MD, Cremades N, et al. Single-molecule FRET studies on alpha-synuclein oligomerization of Parkinson's disease genetically related mutants. Sci Rep. (2015) 5:16696. doi: 10.1038/srep16696
55. Iljina M, Garcia GA, Horrocks MH, Tosatto L, Choi ML, Ganzinger KA, et al. Kinetic model of the aggregation of α-synuclein provides insights into prion-like spreading. Proc Natl Acad Sci USA. (2016) 113:E1206–215. doi: 10.1073/pnas.1524128113
56. Zurlo E, Kumar P, Meisl G, Dear AJ, Mondal D, Claessens MMAE, et al. In situ kinetic measurements of α-synuclein aggregation reveal large population of short-lived oligomers. PLoS ONE. (2021) 16:e0245548. doi: 10.1371/journal.pone.0245548
57. Dear AJ, Meisl G, Šarić A, Michaels TCT, Kjaergaard M, Linse S, et al. Identification of on- and off-pathway oligomers in amyloid fibril formation. Chem Sci. (2020) 11:6236–47. doi: 10.1039/C9SC06501F
58. Sinnige T. Molecular mechanisms of amyloid formation in living systems. Chem Sci. (2022) 13:7080–97. doi: 10.1039/D2SC01278B
59. Szweda PA, Friguet B, Szweda LI. Proteolysis, free radicals, and aging. Free Radical Biol Med. (2002) 33:29–36. doi: 10.1016/S0891-5849(02)00837-7
60. Tai HC, Schuman EM. Ubiquitin, the proteasome and protein degradation in neuronal function and dysfunction. Nat Rev Neurosci. (2008) 19:826–38. doi: 10.1038/nrn2499
61. Ciechanover A, Brundin P. The ubiquitin proteasome system in neurodegenerative diseases: sometimes the chicken, sometimes the egg. Neuron. (2003) 40:427–46. doi: 10.1016/S0896-6273(03)00606-8
62. Scrivo A, Bourdenx M, Pampliega O, Cuervo AM. Selective autophagy as a potential therapeutic target for neurodegenerative disorders. Lancet Neurol. (2018) 17:802–15. doi: 10.1016/S1474-4422(18)30238-2
63. Kuzuhara S, Mori H, Izumiyama N, Yoshimura M, Ihara Y. Lewy bodies are ubiquitinated. Acta Neuropathol. (1988) 75:345–53. doi: 10.1007/BF00687787
65. McNaught KSP, Olanow CW, Halliwell B, Isacson O, Jenner P. Failure of the ubiquitin-proteasome system in Parkinson's disease. Nat Rev Neurosci. (2001) 2:589–94. doi: 10.1038/35086067
66. Webb JL, Ravikumar B, Atkins J, Skepper JN, Rubinsztein DC. α-Synuclein is degraded by both autophagy and the proteasome. J Biol Chem. (2003) 278:25009–13. doi: 10.1074/jbc.M300227200
67. Cuervo AM, Stefanis L, Fredenburg R, Lansbury PT, Sulzer D. Impaired degradation of mutant α-synuclein by chaperone-mediated autophagy. Science. (2004) 305:1292–5. doi: 10.1126/science.1101738
68. Hou X, Watzlawik JO, Fiesel FC, Springer W. Autophagy in Parkinson's disease. J Mol Biol. (2020) 432:2651–72. doi: 10.1016/j.jmb.2020.01.037
69. Xilouri M, Brekk OR, Stefanis L. Autophagy and Alpha-Synuclein: relevance to Parkinson's disease and related synucleopathies. Mov Disord. (2016) 31:178–92. doi: 10.1002/mds.26477
70. McNaught KSP, Perl DP, Brownell AL, Olanow CW. Systemic exposure to proteasome inhibitors causes a progressive model of Parkinson's disease. Ann Neurol. (2004) 56:149–62. doi: 10.1002/ana.20186
71. Cuervo AM, Wong ESP, Martinez-Vicente M. Protein degradation, aggregation, and misfolding. Mov Disord. (2010) 25:S49-S54. doi: 10.1002/mds.22718
72. Sneppen K, Lizana L, Jensen MH, Pigolotti S, Otzen D. Modeling proteasome dynamics in Parkinson's disease. Phys Biol. (2009) 6:036005. doi: 10.1088/1478-3975/6/3/036005
73. Pigolotti S, Lizana L, Otzen D, Sneppen K. Quality control system response to stochastic growth of amyloid fibrils. FEBS Lett. (2013) 587:1405–10. doi: 10.1016/j.febslet.2013.03.018
74. Proctor CJ, Tsirigotis M, Gray DA. An in silico model of the ubiquitin-proteasome system that incorporates normal homeostasis and age-related decline. BMC Syst Biol. (2007) 1:1–18. doi: 10.1186/1752-0509-1-17
75. Proctor CJ, Tangeman PJ, Ardley HC. Modelling the role of UCH-L1 on protein aggregation in age-related neurodegeneration. PLoS ONE. (2010) 5:e13175. doi: 10.1371/journal.pone.0013175
76. Kirkwood TB, Boys RJ, Gillespie CS, Proctor CJ, Shanley DP, Wilkinson DJ. Towards an e-biology of ageing: integrating theory and data. Nat Rev Mol Cell Biol. (2003) 4:243–49. doi: 10.1038/nrm1051
77. Mc Auley MT, Guimera AM, Hodgson D, Mcdonald N, Mooney KM, Morgan AE, et al. Modelling the molecular mechanisms of aging. Biosci Rep. (2017) 37:177. doi: 10.1042/BSR20160177
78. Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. (1999) 402:C47-C52. doi: 10.1038/35011540
79. Cloutier M, Wellstead P. Dynamic modelling of protein and oxidative metabolisms simulates the pathogenesis of Parkinson's disease. IET Syst Biol. (2012) 6:65. doi: 10.1049/iet-syb.2011.0075
80. Foltynie T, Brayne C, Barker RA. The heterogeneity of idiopathic Parkinson's disease. J Neurol. (2002) 249:138–145. doi: 10.1007/PL00007856
81. Finnerty NJ, O'Riordan SL, Lowry JP, Cloutier M, Wellstead P. Continuous real-time in vivo measurement of cerebral nitric oxide supports theoretical predictions of an irreversible switching in cerebral ROS after sufficient exposure to external toxins. J Parkinsons Dis. (2013) 3:351–62. doi: 10.3233/JPD-130198
82. Cloutier M, Middleton R, Wellstead P. Feedback motif for the pathogenesis of Parkinson's disease. IET Syst Biol. (2012) 6:86. doi: 10.1049/iet-syb.2011.0076
83. Raichur A, Vali S, Gorin F. Dynamic modeling of alpha-synuclein aggregation for the sporadic and genetic forms of Parkinson's disease. Neuroscience. (2006) 142:859–70. doi: 10.1016/j.neuroscience.2006.06.052
84. Ouzounoglou E, Kalamatianos D, Emmanouilidou E, Xilouri M, Stefanis L, Vekrellis K, et al. In silico modeling of the effects of α-synuclein oligomerization on dopaminergic neuronal homeostasis. BMC Syst Biol. (2014) 8:1–18. doi: 10.1186/1752-0509-8-54
85. Xilouri M, Vogiatzi T, Vekrellis K, Park D, Stefanis L. Aberrant α-synuclein confers toxicity to neurons in part through inhibition of chaperone-mediated autophagy. PLoS ONE. (2009) 4:e5515. doi: 10.1371/journal.pone.0005515
86. Vekrellis K, Xilouri M, Emmanouilidou E, Stefanis L. Inducible over-expression of wild type α-synuclein in human neuronal cells leads to caspase-dependent non-apoptotic death. J Neurochem. (2009) 109:1348–62. doi: 10.1111/j.1471-4159.2009.06054.x
87. Sass MB, Lorenz AN, Green RL, Coleman RA. A pragmatic approach to biochemical systems theory applied to an α-synuclein-based model of Parkinson's disease. J Neurosci Methods. (2009) 178:366–77. doi: 10.1016/j.jneumeth.2008.12.014
88. Büchel F, Saliger S, Dräger A, Hoffmann S, Wrzodek C, Zell A, et al. Parkinson's disease: dopaminergic nerve cell model is consistent with experimental finding of increased extracellular transport of α-synuclein. BMC Neurosci. (2013) 14:136. doi: 10.1186/1471-2202-14-136
89. Kuznetsov IA, Kuznetsov AV. Mathematical models of α-synuclein transport in axons. Comput Methods Biomech Biomed Engin. (2016) 19:515–26. doi: 10.1080/10255842.2015.1043628
90. Kuznetsov IA, Kuznetsov AV. What can trigger the onset of Parkinson's disease - A modeling study based on a compartmental model of α-synuclein transport and aggregation in neurons. Math Biosci. (2016) 278:22–9. doi: 10.1016/j.mbs.2016.05.002
91. Kuznetsov IA, Kuznetsov AV. Can the lack of fibrillar form of alpha-synuclein in Lewy bodies be explained by its catalytic activity? Math Biosci. (2022) 344:108754. doi: 10.1016/j.mbs.2021.108754
92. Tavassoly I, Parmar J, Shajahan-Haq A, Clarke R, Baumann WT, Tyson JJ. Dynamic modeling of the interaction between autophagy and apoptosis in mammalian cells. CPT Pharmacometr Syst Pharmacol. (2015) 4:263–272. doi: 10.1002/psp4.29
93. Proctor CJ, Soti C, Boys RJ, Gillespie CS, Shanley DP, Wilkinson DJ, et al. Modelling the actions of chaperones and their role in ageing. Mech Ageing Dev. (2005) 126:119–31. doi: 10.1016/j.mad.2004.09.031
94. Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. (1977) 81:2340–61. doi: 10.1021/j100540a008
95. Wilkinson DJ. Stochastic Modelling for Systems Biology. Chapman and Hall/CRC (2018). doi: 10.1201/9781420010664
96. Thompson TB, Meisl G, Knowles TPJ, Goriely A. The role of clearance mechanisms in the kinetics of pathological protein aggregation involved in neurodegenerative diseases. J Chem Phys. (2021) 154:1650. doi: 10.1063/5.0031650
97. Senkevich K, Gan-Or Z. Autophagy lysosomal pathway dysfunction in Parkinson's disease; evidence from human genetics. Parkinsonism Related Disord. (2020) 73:60–71. doi: 10.1016/j.parkreldis.2019.11.015
98. Ribba B, Grimm H, Agoram B, Davies M, Gadkar K, Niederer S, et al. Methodologies for quantitative systems pharmacology (QSP) models: design and estimation. CPT Pharmacometr Syst Pharmacol. (2017) 6:496–8. doi: 10.1002/psp4.12206
99. Banks SM, Medeiros AT, McQuillan M, Busch DJ, Ibarraran-Viniegra AS, Sousa R, et al. Hsc70 ameliorates the vesicle recycling defects caused by excess α-synuclein at synapses. eNeuro. (2020) 7:ENEURO.0448-19.2020. doi: 10.1523/ENEURO.0448-19.2020
100. Hannestad JK, Rocha S, Agnarsson B, Zhdanov VP, Wittung-Stafshede P, Höök F. Single-vesicle imaging reveals lipid-selective and stepwise membrane disruption by monomeric α-synuclein. Proc Natl Acad Sci USA. (2020) 117:14178–86. doi: 10.1073/pnas.1914670117
101. Paleologou KE, Kragh CL, Mann DM, Salem SA, Al-Shami R, Allsop D, et al. Detection of elevated levels of soluble α-synuclein oligomers in post-mortem brain extracts from patients with dementia with Lewy bodies. Brain. (2009) 132:1093–101. doi: 10.1093/brain/awn349
102. Bodner CR, Dobson CM, Bax A. Multiple tight phospholipid-binding modes of α-synuclein revealed by solution NMR spectroscopy. J Mol Biol. (2009) 390:775–90. doi: 10.1016/j.jmb.2009.05.066
103. Westphal CH, Chandra SS. Monomeric synucleins generate membrane curvature. J Biol Chem. (2013) 288:1829–40. doi: 10.1074/jbc.M112.418871
104. Wilhelm BG, Mandad S, Truckenbrodt S, Kröhnert K, Schäfer C, Rammner B, et al. Composition of isolated synaptic boutons reveals the amounts of vesicle trafficking proteins. Science. (2014) 344:1023–8. doi: 10.1126/science.1252884
105. Perni M, Galvagnion C, Maltsev A, Meisl G, Müller MB, Challa PK, et al. A natural product inhibits the initiation of α-synuclein aggregation and suppresses its toxicity. Proc Nat Acad Sci USA. (2017) 114:E1009–17. doi: 10.1073/pnas.1701964114
106. Meisl G, Knowles TP, Klenerman D. The molecular processes underpinning prion-like spreading and seed amplification in protein aggregation. Curr Opin Neurobiol. (2020) 61:58–64. doi: 10.1016/j.conb.2020.01.010
107. Sinnige T, Stroobants K, Dobson CM, Vendruscolo M. Biophysical studies of protein misfolding and aggregation in in vivo models of Alzheimer's and Parkinson's diseases. Q Rev Biophys. (2020) 53:25. doi: 10.1017/S0033583520000025
108. Meisl G, Knowles TP, Klenerman D. Mechanistic models of protein aggregation across length-scales and time-scales: from the test tube to neurodegenerative disease. Front Neurosci. (2022) 16:909861. doi: 10.3389/fnins.2022.909861
109. Cassotta M, Geerts H, Harbom L, Outeiro TF, Pediaditakis I, Reiner O, et al. The future of Parkinson's disease research: a new paradigm of human-specific investigation is necessary… and possible. ALTEX. (2022) 39:694–709. doi: 10.14573/altex.2203161
110. Michaels TC, Šarić A, Meisl G, Heller GT, Curk S, Arosio P, et al. Thermodynamic and kinetic design principles for amyloid-aggregation inhibitors. Proc Natl Acad Sci USA. (2020) 117:24251–7. doi: 10.1073/pnas.2006684117
111. Michaels TC, Dear AJ, Cohen SI, Vendruscolo M, Knowles TP. Kinetic profiling of therapeutic strategies for inhibiting the formation of amyloid oligomers. J Chem Phys. (2022) 156:164904. doi: 10.1063/5.0077609
112. Perni M, Flagmeier P, Limbocker R, Cascella R, Aprile FA, Galvagnion C, et al. Multistep inhibition of α-synuclein aggregation and toxicity in vitro and in vivo by trodusquemine. ACS Chem Biol. (2018) 13:2308–19. doi: 10.1021/acschembio.8b00466
113. Limbocker R, Mannini B, Ruggeri FS, Cascella R, Xu CK, Perni M, et al. Trodusquemine displaces protein misfolded oligomers from cell membranes and abrogates their cytotoxicity through a generic mechanism. Commun Biol. (2020) 3:435. doi: 10.1038/s42003-020-01140-8
114. Arosio P, Michaels TCT, Linse S, Månsson C, Emanuelsson C, Presto J, et al. Kinetic analysis reveals the diversity of microscopic mechanisms through which molecular chaperones suppress amyloid formation. Nat Commun. (2016) 7:10948. doi: 10.1038/ncomms10948
115. Cohen SIA, Arosio P, Presto J, Kurudenkandy FR, Biverstal H, Dolfe L, et al. A molecular chaperone breaks the catalytic cycle that generates toxic Aβ oligomers. Nat Struct Mol Biol. (2015) 22:207–13. doi: 10.1038/nsmb.2971
116. Linse S, Scheidt T, Bernfur K, Vendruscolo M, Dobson CM, Cohen SIA, et al. Kinetic fingerprints differentiate the mechanisms of action of anti-Aβ antibodies. Nat Struct Mol Biol. (2020) 27:1125–33. doi: 10.1038/s41594-020-0505-6
117. Dantuma NP, Bott LC. The ubiquitin-proteasome system in neurodegenerative diseases: precipitating factor, yet part of the solution. Front Mol Neurosci. (2014) 7:70. doi: 10.3389/fnmol.2014.00070
118. Roberts P, Spiros A, Geerts H. A humanized clinically calibrated quantitative systems pharmacology model for hypokinetic motor symptoms in Parkinson's disease. Front Pharmacol. (2016) 7:6. doi: 10.3389/fphar.2016.00006
119. Sarbaz Y, Pourakbari H. A review of presented mathematical models in Parkinson's disease: black-and gray-box models. Med Biol Eng Comput. (2016) 54:855–68. doi: 10.1007/s11517-015-1401-9
120. Carbonell F, Iturria-Medina Y, Evans AC. Mathematical modeling of protein misfolding mechanisms in neurological diseases: a historical overview. Front Neurol. (2018) 9:37. doi: 10.3389/fneur.2018.00037
121. Bloomingdale P, Bakshi S, Maass C, van Maanen E, Pichardo-Almarza C, Yadav DB, et al. Minimal brain PBPK model to support the preclinical and clinical development of antibody therapeutics for CNS diseases. J Pharmacokinet Pharmacodyn. (2021) 48:861–71. doi: 10.1007/s10928-021-09776-7
122. Bloomingdale P, Bumbaca-Yadav D, Sugam J, Grauer S, Smith B, Antonenko S, et al. PBPK-PD modeling for the preclinical development and clinical translation of tau antibodies for Alzheimer's disease. Front Pharmacol. (2022) 13:867457. doi: 10.3389/fphar.2022.867457
123. Lin L, Hua F, Salinas C, Young C, Bussiere T, Apgar JF, et al. Quantitative systems pharmacology model for Alzheimer's disease to predict the effect of aducanumab on brain amyloid. CPT Pharmacometr Syst Pharmacol. (2022) 11:362–372. doi: 10.1002/psp4.12759
124. Parnetti L, Gaetani L, Eusebi P, Paciotti S, Hansson O, El-Agnaf O, et al. CSF and blood biomarkers for Parkinson's disease. Lancet Neurol. (2019) 18:573–86. doi: 10.1016/S1474-4422(19)30024-9
125. Martinez-Vicente M, Talloczy Z, Kaushik S, Massey AC, Mazzulli J, Mosharov EV, et al. Dopamine-modified α-synuclein blocks chaperone-mediated autophagy. J Clin Invest. (2008) 118:777–88. doi: 10.1172/JCI32806
126. Wong YC, Holzbaur EL. Autophagosome dynamics in neurodegeneration at a glance. J Cell Sci. (2015) 128:1259–67. doi: 10.1242/jcs.161216
Keywords: Parkinson's disease, neurodegeneration, alpha-synuclein aggregation, protein degradation mechanisms, mathematical modeling, systems biology, mechanistic models
Citation: Righetti E, Antonello A, Marchetti L, Domenici E and Reali F (2022) Mechanistic models of α-synuclein homeostasis for Parkinson's disease: A blueprint for therapeutic intervention. Front. Appl. Math. Stat. 8:1060489. doi: 10.3389/fams.2022.1060489
Received: 03 October 2022; Accepted: 30 November 2022;
Published: 16 December 2022.
Edited by:
Narayan P. Subramaniyam, Tampere University, FinlandReviewed by:
Riccardo Capelli, University of Milan, ItalyVaibhav Maheshwari, Takeda Oncology, United States
Copyright © 2022 Righetti, Antonello, Marchetti, Domenici and Reali. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Federico Reali, cmVhbGlAY29zYmkuZXU=
 Elena Righetti
Elena Righetti Alice Antonello3
Alice Antonello3 Luca Marchetti
Luca Marchetti Enrico Domenici
Enrico Domenici Federico Reali
Federico Reali