- School of Mathematics and Statistics, Xiamen University of Technology, Xiamen, China
This paper aims to address the tracking problem of uncertain fractional-order permanent magnet synchronous motors with parametric uncertainties. To guarantee the system stability and offset the effect of parametric uncertainties, an adaptive backstepping composite learning neural control scheme based on interval excitation is presented. Moreover, dynamic surface technique is exploited to overcome the technical limitation of “explosion of complexity” caused by standard backstepping framework. In virtue of stability analysis and illustrative simulation, it is confirmed that the proposed control scheme not only attenuates the tracking error as small as possible, but also achieves satisfactory parametric convergence with high estimation precision.
1. Introduction
Fractional calculus is an important mathematical discipline with a history of several centuries. In recent decades, fractional differential equations have made great progress in engineering, mechanics, physics, chemistry, and many other fields. Compared with classical mathematical models governed by integer-order differential equations, most fractional-order models have abundant advantages in describing the memory and genetic characteristics of the process [1, 2]. In addition, owing to the particularity of fractional calculus, fractional-order systems always exhibit rich dynamic behaviors [3–8].
Permanent magnet synchronous motor (PMSM) [9] has a great deal of advantages such as low production cost, high energy consumption, strong robustness, compact structure, superior performance, high inertia torque ratio, large power capacity. The existing results show that integer-order PMSM has chaotic characteristics under some certain operating conditions. So far, several chaos control methods [10–14] have been put forward to attenuate the effect of chaotic oscillation and maintain the stable operation of integer-order PMSM. Fractional order PMSM [15–18] reflects the same complex chaotic dynamics, because fractional calculus provides a powerful tool for describing the genetic and infinite memory properties of different substances more accurately and essentially. Thus, the establishment of a chaos control scheme for fractional-order PMSM instead of the traditional one is of vast significance.
Radial basis function network (RBFNN) [19] has been widely concerned and applied due to its valuable characteristics of approximation for coping with functional uncertainty in controlled systems. The approximation ability of RBFNNs can greatly reduce the difficulty of modeling procedure in practical control problems and hence facilitates to simplify the controller design. Although a majority of the existing neural control approaches facilitates to realize error convergence, the approximation abilities of RBFNNs are generally restricted for the reason that the persistent excitation (PE) condition [20] must be met during the overal adaptation process. Actually, the PE condition for the implementation of traditional adaptive neural control is very strict and sometimes even infeasible in practical applications. In Wang and Hill [21], a neural control method based on a practical PE condition was proposed to guarantee the exponential stability of the closed-loop system as well as the exact approximation of RBFNNs. However, the parametric convergence rate via such a learning-based neural control method or its outgrowths (e.g., [22–24]) is highly dependent on the strength of PE, which may lead to very slow learning speed in general. Aiming to overcome this limitation, several scholars put forward useful composite learning control strategies [25–30]. Composite learning significantly relaxes the PE condition into the interval excitation (IE) condition. The essential idea of this method is to synthesize the online data and the historical data for the generation of a so-called prediction error and then to configure a composite adaptive law integrated with the tracking error and the prediction error for the better update of adaptive parameters.
Based on the above theoretical background, this paper studies the tracking issue of fractional-order PMSM. A neural network-based adaptive composite learning control approach is proposed, which can accurately estimate unknown functions under certain parameter design conditions. It will be proven that expected tracking performance and fast parametric convergence are realized once the proposed method is applied.
The main innovations of this work are worthy of emphasis as 2-fold: (1) Relying on fractional-order Lyapunov stability criterion, a novel fractional-order adaptive nerual-network chaos controller is constructed to achieve robust tracking performance. Compared with the existing researches [10–14] on integer-order PMSM, the tracking control problem of fractional-order PMSM dynamic model studied in the article is more challenging and significant due to the memory and genetic characteristics of fractional calculus. (2) A composite learning algorithm is proposed. Different from the conventional adaptive control methods [15–18] under the PE condition for fractional-order PMSM, the proposed composite learning adaptive control method relaxes the stringer PE condition into the IE condition which is relatively easy to be implemented. It will be proven that the designed composite learning algorithm not only updates the adaptive parameters of RBFNNs via taking advantage of the online data, but also effectively promote the estimation accuracy of all unknown functions.
The architecture of this article is organized as below. In Section 2, the fundamental background of fractional calculus, radial basis function network, persistent excitation, and interval excitation are recalled. Section 3 describes the considered problem formulation, and then, an adaptive neural-network controller based on composite learning scheme is systematically elaborated. It is verified that the proposed method facilitates to achieve satisfactory tracking performance and highly accurate parametric estimation under interval excitation condition. In Section 4, a numerical simulation is carried out to evaluate the feasibility of the proposed approach. In Section 5, the whole conclusion of the paper and the prospect of future research are summarized.
2. Preliminaries
2.1. Fractional calculus
In this overall article, ℕ (resp. ℝ, ℝn, ℝ+, ℂ) means the family of all non-zero natural numbers (resp. real numbers, n dimensional real vectors, positive numbers, complex numbers). Given a k ∈ ℕ, Ck is the family of all differentiable functions with continuous i-order derivatives for all i = 1, 2, ⋯ , k. L∞ denotes the space of all bounded signals. sign(·) expresses the signum function. The transpose of an x ∈ ℝn is denoted by xT. .
Definition 1. Podlubny [2] The β-order Caputo fractional derivative for a given differentiable function φ(t) is formulated by
with k − 1 ≤ β < k in which k ∈ ℕ. When t0 = 0, we write simply instead of .
Definition 2. Podlubny [2] A mapping Eβ,γ :ℂ → ℂ with double parameters β, γ ∈ ℝ+ is called the Mittag-Leffler function, defined as
Particularly, . Let Eβ(z) ≜ Eβ,1(z) whenever γ = 1.
Lemma 1. Podlubny [2] Given β ∈ (0, 2), γ ∈ ℝ. For an arbitrary z ∈ ℂ, if the argument arg(z) satisfies
with βπ/2 < θ ≤ min{π, βπ}, then the value of Eβ,γ(z) is limited within the estimation range:
where C ∈ ℝ+ is a constant.
Lemma 2. Gong [4] Let V(t) be a continuous nonnegative function. Suppose that
where λ > 0, ρ ≥ 0. Then
where M = max{1, C}, C ∈ ℝ+ is defined as in Lemma 1.
Lemma 3. Podlubny [2] Let x(t) and y(t) be differentiable functions, C ∈ ℝ, β ∈ (0, 1). Then (1) (2) , where m, n ∈ ℝ are constants.
Lemma 4. Aguila-Camacho et al. [3] Let x(t) be a differentiable function, β ∈ (0, 1). Then
2.2. Radial basis function network
Recall the notion of radial basis function network (RBFNN) [19]. An RBFNN is represented by
where is referred to as the output of RBFNN, x(t) ∈ ℝn is referred to as the input of RBFNN, is a weight vector with m being the number of neural nodes, and Ψ(x(t)) ∈ ℝm is a vector of radial basis functions, the jth coordinate ψj(x(t)) of Ψ(x(t)) is usually defined to be the Gaussian function, that is
where describes the center of the receptive field, means the width of ψj(x(t)).
Lemma 5. Sanner and Slotine [19] For any continuous function f(x(t)) defined over a compact set Ωr and any small positive scalar , one can find an RBFNN, denoted by Θ*TΨ(x(t)), such that
in which Θ* is the optimal RBFNN parameter, described by
Lemma 6. Kurdila et al. [20] Given an x(t) ∈ ℝn. Then, there exists a positive scalar ψ irrelevant with x(t) such that the regressor Ψ(x(t)) defined in Equation (1) satisfies max{||Ψ(x(t))||, ||Ψ(ẋ(t))||} ≤ ψ.
Definition 3. Pan et al. [25] Let μ > 0 be an excitation strength and τ0 > 0 be a time duration. A time-varying vector Ψ(t) is said to be of persistent excitation (PE), provided that for all t > τ0, where Im×m is an m × m unit matrix.
Definition 4. Pan et al. [25] Let μ > 0 be an excitation strength and τ0 > 0 be a time duration. A time-varying vector Ψ(t) is said to be of interval excitation (IE) over the interval [Te − τ0, Te] with Te > τ0, if .
3. Main results
3.1. Problem formulation
Permanent magnet synchronous motor (PMSM) is a sort of special mechanical device whose dynamic behaviors manifest exclusive chaotic attractor. An integer-order PMSM dynamic system [10] can be modeled by
where ω, id, and iq symbolize the angular velocity, the d-axis current, and the q-axis current, respectively. σ and γ are two positive coefficients.
Put ω = x1, iq = x2 and id = x3 in Equation (2), respectively. By substituting the β-order derivative operator with 0 < β < 1 for , we generalize the aforesaid formulation into an uncertain fractional-order PMSM dynamic system in the state-space form as follows:
where (i = 1, 2, 3) is a measurable state vector, (i = 1, 2, 3) is an unknown bounded continuous nonlinear function, y(t) ∈ ℝ is the system output, and ud(t) ∈ ℝ is the control input.
Let the initial values be x1(0) = x2(0) = x3(0) = 0.8. When β = 0.98, σ = 3, and γ = 30, the chaotic attractor appears in the dynamic behaviors of fractional-order PMSM, see Figure 1.
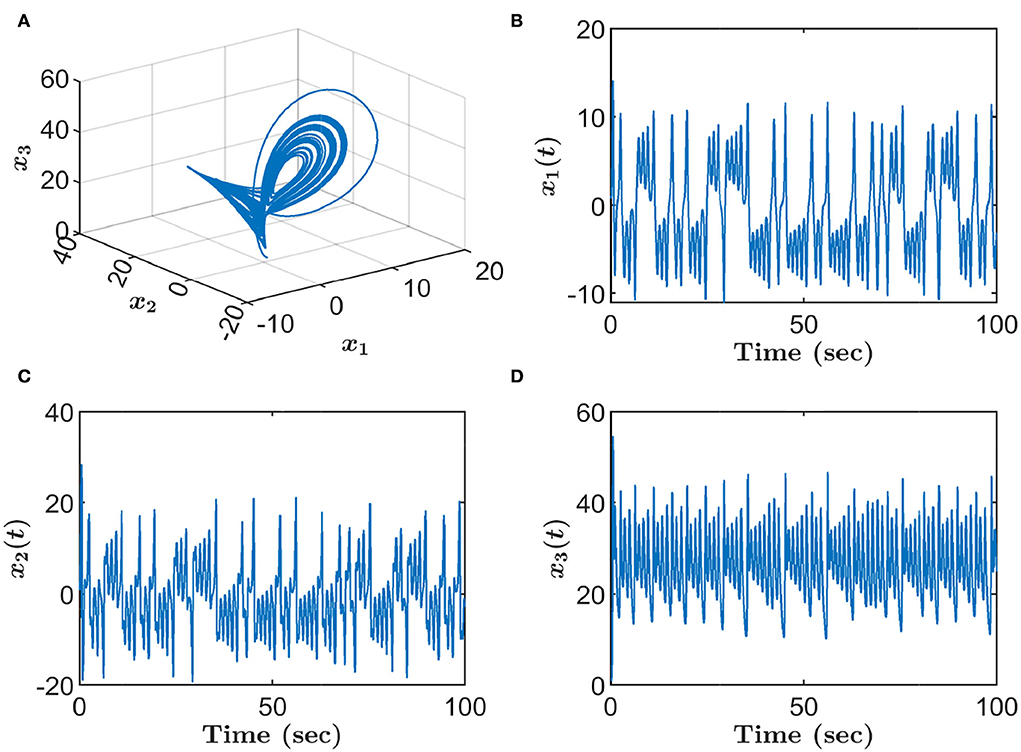
Figure 1. Chaotic attractor of fractional-order PMSM with β = 0.98, σ = 3, and γ = 30. (A) 3D phase portrait. (B) Time evolution of x1. (C) Time evolution of x2. (D) Time evolution of x3.
The system controller will be designed in the next subsection such that the output signal y(t) is driven to track the desired signal yd(t). To accomplish this tracking task, one needs to invoke the following assumption.
Assumption 1. Both of the signals yd(t) and are known, bounded and smooth.
3.2. Control design
Next, let us expound the backstepping control design process for fractional-order PMSM.
Denote the virtual inputs by α1(t) and α2(t) for the first subsystem and the second subsystem, respectively. Let α1(t) and α2(t) pass the following fractional-order dynamic surfaces
respectively, where are given constants, and the filter outputs αi,c(t) satisfy the initial conditions αi,c(0) = αi(0). Suppose that the parameters φi are selected suitably large. According to Liu et al. [27, Lemma 3], there are constants such that |αi,c(t) − αi(t)| ≤ ζi for all t ≥ 0.
Consider the following coordinate translation:
In light of Lemma 5, the existence of optimal RBFNN parameters for i = 1, 2, 3 is guaranteed so that
respectively, in which εfi(t) represents the approximation error variable, which satisfies for some given scalar . The parametric estimation error is taken as .
Step 1. From Equations (3) and (7), it holds
Hence, owing to Equations (5), (6), and (8), computing the fractional time derivative of e1(t) yields
where z1(t) = α1,c(t) − α1(t) is the filter error.
The virtual control function for the first subsystem is defined by
where k1 is a positive known constant.
Incorporating Equation (10) into Equation (9) infers
It is worth noting that |z1(t)| ≤ ζ1. By Young inequality, multiplying both sides of Equation (11) by e1(t) induces
In general, the traditional adaptation law can only make sure that the parametric estimation error is bounded under the PE condition. However, the PE condition is sometimes too stringent to be fulfilled, and thus, satisfactory parametric convergence cannot be ensured. Motivated by this reason, a composite learning approach will be studied in the sequel to achieve higher precision of with the removal of the rigorous PE condition.
Define a mapping by
where τ1 > 0 is a certain integration duration.
Suppose that m1(t) ≥ μ1I with μ1 > 0 standing for the exciting strength, whenever is of IE on t ∈ [Te1 − τ1, Te1] for a time instant Te1 > τ1. Take into account the next prediction error defined by
where is expressed as
The fractional-order composite learning adaptation law is designed as
where ϱ1, η1, and are known constants.
Construct an auxiliary variable H1(t) by
Apparently, it is observed from Equation (8) that
Multiply both sides of Equation (16) by . Then, it is inferred that
Invoking Equations (15) and (17), we can gain access to the precise value of H1(t) as
Consequently, the value of can be acquired precisely as
Substituting Equation (18) into Equation (14), one arrives at
Consider the next quadratic Lyapunov function:
Invoking Lemmas 3 and 4, simple manipulation on the fractional differentiation of Equation (20) renders
Application of Young's inequality gives
Moreover, by using Young's inequality and Lemma 6, it is shown that
with ψ1 > 0 being a constant which is independent of and the number of neural nodes.
Considering Equations (12)–(14) and Equation (19)–(23), we conclude
where a1 = min{2k1, η1 + ϱ1(2ϖ1μ1 − 1)}, .
Step 2. According to Equations (3) and (7), we have
With the aid of Equations (6) and (25), we can derive
where z2(t) = α2,c(t) − α2(t) is the filter error.
The virtual controller is provided as
with k2 > 0 being a design parameter.
Substituting Equation (27) into Equation (26) induces
Multiply both sides of Equation (28) by e2(t). Employing Lemma 4 and Young inequality, we argue
Let be of IE over the interval [Te2 − τ2, Te2] for some τ2 > 0 and Te2 > τ2.
Define the following prediction error
where and are formulated by
and
respectively. Presume that m2(t) ≥ μ2I, where μ2 is the exciting strength.
Choose the composite learning-based adaptation law as below:
where ϱ2, η2, and ϖ2 are given positive scalars.
Define the following auxiliary term:
On account of Equation (25), it is trivially seen that
Multiply both sides of Equation (33) by . Then, it is inferred that
Due to Equations (32) and (34), the computational result of H2(t) is attainable, that is
Accordingly, the precise value of is determined by
Define the Lyapunov function by
By Lemmas 3 and 4, taking the fractional derivative of Equation (35) leads to
Analogs to Equations (22) and (23), it is easily verified that
in which is a positive constant irrelevant with and the number of neural nodes.
By means of Equations (29), (31), and (36)–(38), we get
where a2 = min{a1, 2k2, η2 + ϱ2(2ϖ2μ2 − 1)}, .
Step 3. In virtue of Equations (3) and (7), we know
On the basis of Equations (3) and (6), it is not difficult to check
Configure the actual control law as
where k3 is a given positive scalar.
By substituting Equation (42) into Equation (41), it is directly implied that
Multiply both sides of Equation (43) by e3(t). Then according to Lemma 4, it follows that
Define a mapping by
with τ3 > 0 being the length of an integral interval.
Inspired by the similar argument in Step 2, we construct the prediction error by
where is described as
respectively. Let the IE condition be fulfilled, that is, m3(t) ≥ μ3I with a positive scalar μ3 being the exciting strength, which implies is of IE on t ∈ [Te3 − τ3, Te3] for some Te3 > τ3.
Introduce the adaptation law from composite learning as follows:
with ϱ3, η3, and ϖ3 being positive design parameters.
To figure out the value of , let us define an auxiliary variable H3(t) by
Equivalently, Equation (40) can be rewritten as
Multiplying both sides of Equation (47) by , we can see
From Equations (46) and (48), it is deduced that
Thereby, calculating the accurate value of leads to
Select the candidate of Lyapunov function V3 as the following formula:
In virtue of Lemma 4, taking the fractional derivative of Equation (50) implies
Analogs to Equations (37) and (38), it is easily verified that
in which is a positive constant irrelevant with and the number of neural nodes.
Synthesizing Equations (39), (44), (45), and (51)–(53) with Lemma 6, we arrive at
where a3 = min{a2, 2k3, η3 + ϱ3(2ϖ3μ3 − 1)}, .
By virtue of Equation (54) and Lemma 2, it is straightly examined that
for all t ≥ 0, where C ∈ ℝ+ is a certain constant, M = max{1, C}. Therefore, and for i = 1, 2, 3, which indicates . This demonstrates the boundedness of the whole signals in the closed-loop system.
Given a sufficient small positive scalar ϵ = ϵ1 + ϵ2 where and ϵ2 > 0. By Equation (55), as t → ∞, we have
Based on Equations (55) and (56), if all design parameters are selected adequately, then there exists a certain T > 0 such that whenever t ≥ T and hence V3(t) ≤ ϵ. Consequently, the dynamic errors ei and converge toward a compact region of the origin, and the radius of the bounded region can be adjusted as small as possible.
Summarizing the above arguments, we obtain the following main result with respect to the system stability.
Theorem 1. Take into account the system Equation (3) with Assumption 1. Suppose that the control scheme comprises the virtual control functions Equations (10) and (27), the actual control law Equation (42), together with the composite learning laws (Equations 14, 45). Then, all the closed-loop signals are bounded, and the error variables ei, (i = 1, 2, 3) converge toward a small enough compact region of the origin.
Remark 1. In Xue et al. [8], a class of second-order command filter was extended into fractional form:
where α(t) is the filter input, φ ∈ ℝ+, λ ∈ [0, 1]. The main advantage of Equation (57) is that its approximation accuracy for the input α(t) is much better than that of fractional-order dynamic surface (Equation 4) used in this paper. However, in contrast with Equation (57 which needs to satisfy that both and are bounded, Equation (4) only requires the boundedness of and shows less conservation.
4. Simulation research
In this part, let us validate the efficiency of the proposed control scheme.
Pay attention to the practical model of fractional-order PMSM as follows:
where β = 0.98, σ = 3, γ = 30, , and are unknown functions. The initial value of the full-state vector is considered as . Let the target signal be yd(t) = 2 + 0.5sin(0.5t) + 0.5sin(t).
Due to the uncertainty of f1 and f2, we take advantage of three RBFNNs and in the simulation to approximate f1 and f2, respectively. The single input of the first RBFNN is x1, and the radial basis function is composed of twenty-one Gaussian functions which are uniformly distributed over the interval [−2, 2]. With respect to the second RBFNN , we regard its input variables as x1 and x2, and eight Gaussian functions evenly distributed on the interval [−2, 2] are given for each input to induce the corresponding radial basis function. Thus, the number of all neural-network nodes related to is selected as 8 × 8 = 64.
The design parameters are now selected as follows. First, let the input gain parameters are k1 = k2 = k3 = 15. Second, the gain parameters of the dynamic surfaces are considered as φ1 = φ2 = 80. Third, set the integration duration to be τd = 15 and the finalization time instants for IE to be Te1 = Te2 = Te3 = 20. At last, choose ϱi = 30 and ηi = ϖi = 0.001 with i = 1, 2, 3 for the composite learning adaptive control.
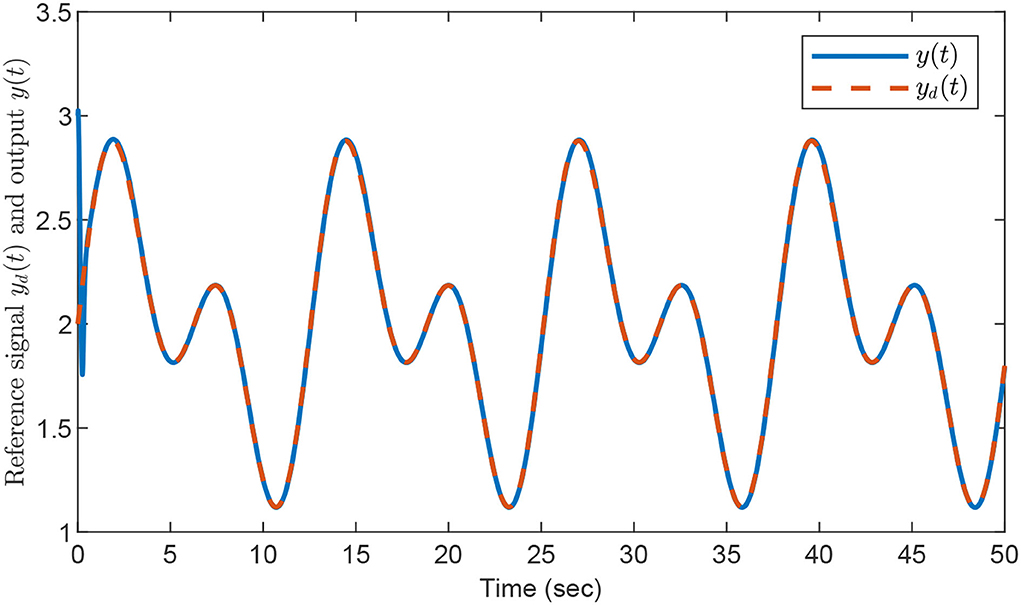
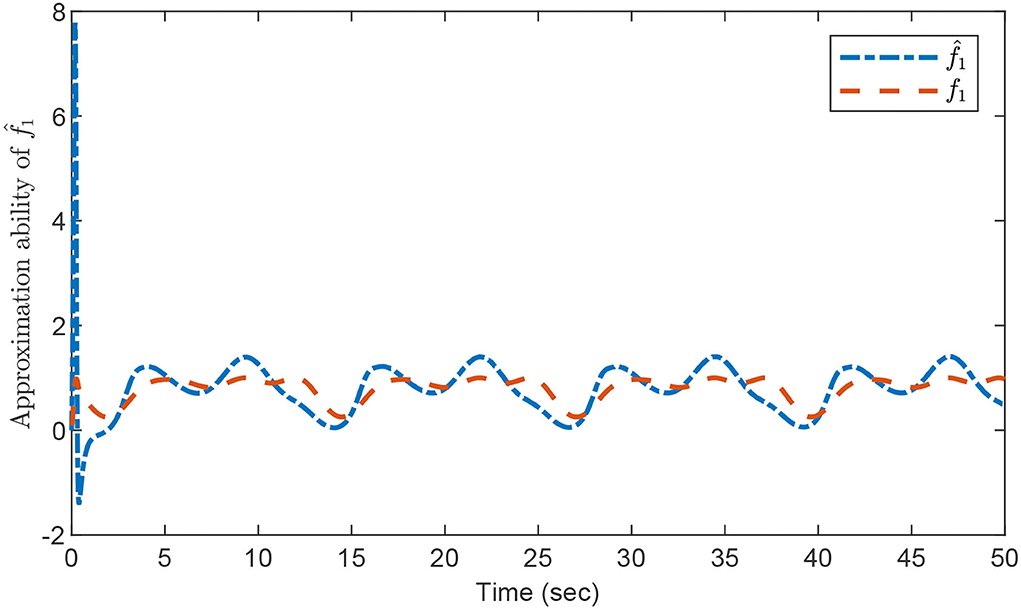
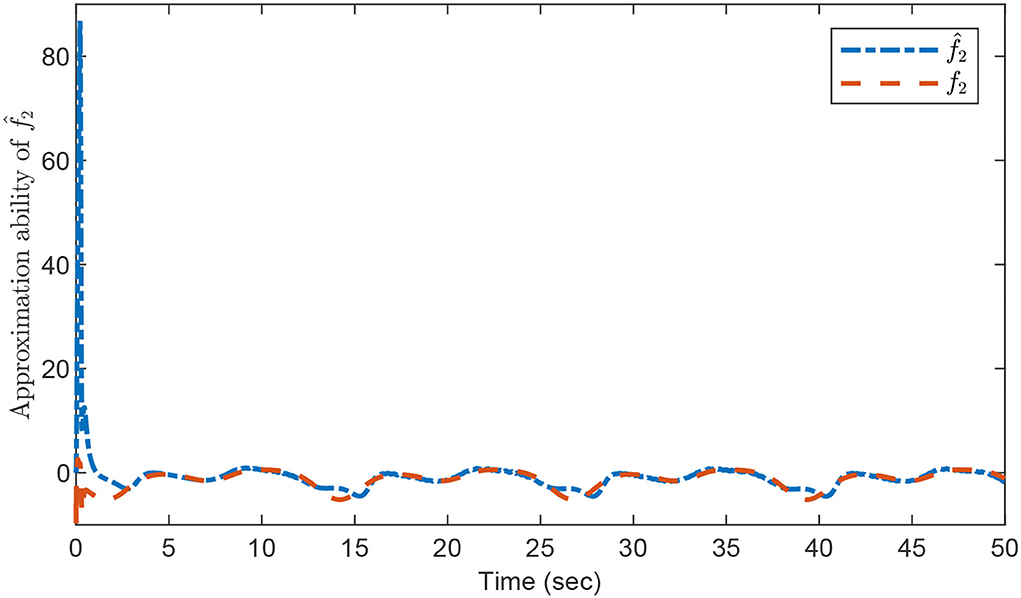
The relevant performance results are illustrated in Figures 2–4. Figure 2 shows that fast system response is achieved and the output signal y(t) can track the target trajectory yd(t) closely as desired. The approximation abilities of the estimations for fi with i = 1, 2 via the designed composite learning algorithm are displayed in Figures 3, 4, respectively. By using the introduced composite learning adaptive control method under the IE condition, one can observe that excellent estimation preciseness is obtained, which confirms the robustness of the introduced composite learning neural control approach as well as its powerful capability of chaos suppression.
5. Conclusion
In the article, the tracking control of fractional-order PMSMs is studied by establishing an adaptive backstepping composite learning neural control scheme. Neural networks are applied to serve as functional approximations, and a composite learning adaptive control algorithm is constructed to guarantee the high estimation accuracy of adaptation parameters. Employing the extended Lyapunov stability criterion, it is proven that the proposed control method achieves robust control performance and plays a vital role in tackling the tracking control problem of uncertainty fractional-order PMSMs. The simulation example reveals that the provided control method can improve the tracking efficiency. In future, we will focus on the study of fractional permanent magnet motor system with complicated characteristics of control input, such as input saturation, input dead-zone, and input delay.
Author contributions
CW: conceptualization, methodology, formal analysis, investigation, validation, software, data curation, and writing.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 11302184), the Fujian Provincial Natural Science Foundation (Grant No. 2021J011194), and Research Climbing Program of Xiamen University of Technology (Grant No. XPDKQ20020).
Acknowledgments
The author would like to convey his acknowledgments to the editors and the reviewers for their helpful comments and recommendations.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley-Interscience Publication (1993).
3. Aguila-Camacho N, Duarte-Mermoud MA, Gallegos JA. Lyapunov functions for fractional order systems. Commun Nonlinear Sci Num Simulat. (2014) 19:2951–7. doi: 10.1016/j.cnsns.2014.01.022
4. Gong P. Distributed tracking of heterogeneous nonlinear fractional-order multi-agent systems with an unknown leader. J Franklin Inst. (2017) 354:2226–44. doi: 10.1016/j.jfranklin.2017.01.001
5. Han SI. Fractional-Order command filtered backstepping sliding mode control with fractional-order nonlinear disturbance observer for nonlinear systems. J Franklin Inst. (2020) 357:6760–76. doi: 10.1016/j.jfranklin.2020.04.055
6. Liu H, Pan Y, Cao J, Zhou Y, Wang H. Positivity and stability analysis for fractional-order delayed systems: a T-S fuzzy model approach. IEEE Trans Fuzzy Syst. (2021) 29:927–39. doi: 10.1109/TFUZZ.2020.2966420
7. Song S, Park JH, Zhang B, Song X. Observer-based adaptive hybrid fuzzy resilient control for fractional-order nonlinear systems with time-varying delays and actuator failures. IEEE Trans Fuzzy Syst. (2021) 29:471–85. doi: 10.1109/TFUZZ.2019.2955051
8. Xue G, Lin F, Li S, Liu H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf Sci. (2022) 600:189–208. doi: 10.1016/j.ins.2022.03.084
9. Li Z, Park JB, Joo YH, Zhang B, Chen G. Bifurcations and chaos in a permanent-magnet synchronous motor. IEEE Trans Circ Syst I Fundament Theory Appl. (2002) 49:383–7. doi: 10.1109/81.989176
10. Yu J, Chen B, Yu H, Gao J. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping. Nonlinear Anal. (2011) 12:671–81. doi: 10.1016/j.nonrwa.2010.07.009
11. Yang X, Yu J, Wang QG, Zhao L, Yu H, Lin C. Adaptive fuzzy finite-time command filtered tracking control for permanent magnet synchronous motors. Neurocomputing. (2019) 337:110–9. doi: 10.1016/j.neucom.2019.01.057
12. Zhou S, Sui S, Tong S. Adaptive neural networks optimal control of permanent magnet synchronous motor system with state constraints. Neurocomputing. (2022) 504:132–40. doi: 10.1016/j.neucom.2022.06.114
13. Basin M, Rodriguez-Ramirez P, Ramos-Lopez V. Continuous fixed-time convergent controller for permanent-magnet synchronous motor with unbounded perturbations. J Franklin Inst. (2020) 357:11900–13. doi: 10.1016/j.jfranklin.2019.11.059
14. Gil J, You S, Lee Y, Kim W. Nonlinear sliding mode controller using disturbance observer for permanent magnet synchronous motors under disturbance. Expert Syst Appl. (2023) 214:119085. doi: 10.1016/j.eswa.2022.119085
15. Li C, Yu S, Luo X. Fractional-order permanent magnet synchronous motor and its adaptive chaotic control. Chin Phys B. (2012) 21:168–73. doi: 10.1088/1674-1056/21/10/100506
16. Xue W, Li Y, Cang S, Jia H, Wang Z. Chaotic behavior and circuit implementation of a fractional-order permanent magnet synchronous motor model. J Franklin Inst. (2015) 352:2887–98. doi: 10.1016/j.jfranklin.2015.05.025
17. Lu S, Wang X, Li Y. Adaptive neural network finite-time command filtered tracking control of fractional-order permanent magnet synchronous motor with input saturation. J Franklin Inst. (2020) 357:13707–33. doi: 10.1016/j.jfranklin.2020.10.021
18. Zhang S, Wang C, Zhang H, Ma P, Li X. Dynamic analysis and bursting oscillation control of fractional-order permanent magnet synchronous motor system. Chaos Solit Fractals. (2022) 156:111809. doi: 10.1016/j.chaos.2022.111809
19. Sanner RM, Slotine JJE. Gaussian networks for direct adaptive control. IEEE Trans Neural Netw. (1992) 3:837–63. doi: 10.1109/72.165588
20. Kurdila AJ, Narcowich FJ, Ward JD. Persistency of excitation in identification using radial basis function approximants. SIAM J Control Optim. (2006) 33:625–42. doi: 10.1137/S0363012992232555
21. Wang C, Hill DJ. Learning from neural control. IEEE Trans Neural Netw. (2006) 17:130–46. doi: 10.1109/TNN.2005.860843
22. Wang C, Wang M, Liu T, Hill DJ. Learning from ISS-modular adaptive NN control of nonlinear strict-feedback systems. IEEE Trans Neural Netw Learn Syst. (2012) 23:1539–50. doi: 10.1109/TNNLS.2012.2205702
23. Wang M, Wang C, Liu X. Dynamic learning from adaptive neural control with predefined performance for a class of nonlinear systems. Inf Sci. (2014) 279:874–88. doi: 10.1016/j.ins.2014.04.038
24. Pan Y, Yu H. Biomimetic hybrid feedback feedforward neural-network learning control. IEEE Trans Neural Netw Learn Syst. (2017) 28:1481–7. doi: 10.1109/TNNLS.2016.2527501
25. Pan Y, Sun T, Liu Y, Yu H. Composite learning from adaptive backstepping neural network control. Neural Network. (2017) 95:134–42. doi: 10.1016/j.neunet.2017.08.005
26. Xu B, Sun F, Pan Y, Chen B. Disturbance observer based composite learning fuzzy control of nonlinear systems with unknown dead zone. IEEE Trans Syst Man Cybern Syst. (2017) 47:1854–62. doi: 10.1109/TSMC.2016.2562502
27. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybern. (2020) 50:2557–67. doi: 10.1109/TCYB.2019.2938754
28. Guo Y, Qin H, Xu B, Han Y, Fan QY, Zhang P. Composite learning adaptive sliding mode control for AUV target tracking. Neurocomputing. (2019) 351:180–6. doi: 10.1016/j.neucom.2019.03.033
29. Guo K, Pan Y, Zheng D, Yu H. Composite learning control of robotic systems: a least squares modulated approach. Automatica. (2020) 111:108612. doi: 10.1016/j.automatica.2019.108612
Keywords: fractional-order permanent magnet synchronous motors, composite learning, dynamic surface control, backstepping control, radial-basis-function neural networks
Citation: Wang C (2022) Adaptive composite learning dynamic surface control for chaotic fractional-order permanent magnet synchronous motors. Front. Appl. Math. Stat. 8:1059756. doi: 10.3389/fams.2022.1059756
Received: 10 February 2022; Accepted: 26 October 2022;
Published: 22 November 2022.
Edited by:
Heng Liu, Guangxi University for Nationalities, ChinaReviewed by:
Guangming Xue, Guangxi University of Finance and Economics, ChinaShumin Ha, Shaanxi Normal University, China
Copyright © 2022 Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chenhui Wang, Y2h3YW5nQHhtdXQuZWR1LmNu; d2NoMDUxNkAxNjMuY29t
 Chenhui Wang
Chenhui Wang