- 1School of Applied Mathematics, Getulio Vargas Foundation, Rio de Janeiro, Brazil
- 2Department of Mathematical Sciences, College of Science, United Arab Emirates University, Al-Ain, United Arab Emirates
In this paper, we propose a fractional-order viral infection model, which includes latent infection, a Holling type II response function, and a time-delay representing viral production. Based on the characteristic equations for the model, certain sufficient conditions guarantee local asymptotic stability of infection-free and interior steady states. Whenever the time-delay crosses its critical value (threshold parameter), a Hopf bifurcation occurs. Furthermore, we use LaSalle’s invariance principle and Lyapunov functions to examine global stability for infection-free and interior steady states. Our results are illustrated by numerical simulations.
1 Introduction
Various mathematical models have been developed to describe, within-host, the dynamics of various viral infections, with a focus on virus-to-cell transmission, such as human immunodeficiency virus (HIV) [1], COVID-19 [2,3], hepatitis C virus (HCV) [4], hepatitis B virus (HBV) [5], and human T-cell lymphotropic virus 1 (HTLV-1) [6]. Classical viral infection models are composed of the interactions between susceptible cells, infected target cells, and free viruses. Furthermore, some authors studied latent infection to describe the mechanism of latency. Wang et al. [7] investigated the HIV model with latent infection incorporating both modes of time-delays and transmissions between viral entry and viral production or integration and also discussed the basic reproductive number, showing existence of asymptotic stability of endemic equilibrium points. Wen et al. [8] studied the virus-to-cell and cell-to-cell HIV virus transmission dynamics with latently infected cells. Pan et al. [9] discussed the HCV infection model, which includes the routes of infection and spread, such as virus-to-cell and cell-to-cell transmission dynamics, and explained numerically the four different HCV models.
The infection persists when the virus weakens and suppresses the immune response. Immune system response refers to the process that when the virus enters the human body, the immune system receives the signal of virus attack and spreads it to the immune organs, which secrete lymphocytes to purge the virus. Moreover, the adaptive immune response plays a crucial role in the control of infection process. When the virus spreads in the human body, the human body produces double modes of immune responses: one is the B cell that makes humoral immune response and the other is the cytotoxic T lymphocyte (CTL) that makes cellular immune response. Previous studies have shown that the humoral immune response is more active than the cellular immune responses. Elaiw et al. [10] discussed the dynamical behaviors of viral infection models with latently infected cells, humoral immune response, and general non-linear incidence rate function. The authors in [11] investigated the global asymptotic stability of reaction–diffusion viral infection model with homogeneous environments and non-linear incidence in heterogeneous and humoral immunity. Wang et al. [12] discussed the global stability results of HIV viral infection model with latently infected cells, B-cell immune response, Beddington–DeAngelis functional response, and various time-delays. The authors in [13] reported the stability and bifurcation results of generalized viral infection system with humoral immunity and distributed delays in virus production and cell infection, and time lags described the time needed to activate the immune response.
The fractional-order modeling provides more reliable, accurate, and precise information about the dynamics of biological models. Description of memory and hereditary properties make it superior to the classical-order model. Additionally, non-integer–order models can easily demonstrate and explore the dynamics between two non-local points and are more comprehensive to discuss real-world problems for the global dynamics. In recent years, various ideas and theories about the fractional-order derivatives have been developed and introduced (see [14–16]). Rakkiyappan et al. [17] discussed the fractional-order Zika viral infection model with different time-delays, such as the latency infection in the infected host and in a vector, and sufficient conditions for stability and bifurcation results with respect to time lags. The authors in [18] analyzed the local stability results of fractional-order Ebola viral infection model with time-delayed immune response (cytotoxic T-lymphocyte term) in heterogeneous complex networks. Rihan et al. [19] studied the fractional-order dynamics of hepatitis C virus (HCV) incorporating the intracellular delay between the initial infection of a cell by HCV and the release of new virions and the interferon-α (IFN-α) treatment. Tamilalagan et al. [20] reported the characteristic dynamics for the non-integer–order HIV infection model with CTL immune responses and antibody and also compared it with that of the integer-order model. The authors reported in [21] derived the sufficient conditions of stability and optimal control results for the fractional-order HIV model with transmission dynamics. Researchers investigated fractional-order viral infection models to understand how the immune system works and examined how immune cells eliminate virus [22,23].
With motivation of the above-mentioned studies, in this paper, we extend the integer-order differential model into the fractional-order model for the virus-immune system with latently infected cell compartments. We incorporate fractional order and time-delay to represent long-run and short-run memory. As part of the Holling type II functional response, viral pathogens spread from virus to cell and from cell to cell. To avoid dimensional mismatches in the fractional equations, a parameter modification is used. We derive the positivity and boundedness of the solution for the considered model. We examine the local stability of existing equilibrium points and the bifurcation results of the considered model. We also discuss some necessary conditions for global stability using a novel suitable Lyapunov function combined with LaSalle’s invariance principle. The rest of this paper is organized as follows: In Section 2, we formulate the viral infection model and also study the positivity and boundedness of the solution. Local and global stability results of such a model are derived in Section 3 and Section 4, respectively. The numerical simulations are provided in Section 5, to validate the obtained theoretical results. Section 6 contains conclusion.
2 Model Formulation
In the process of viral infection, the immune system plays a critical role. Viral dynamics can be modeled properly to provide insights into understanding the disease and the clinical treatments used to treat it. In adaptive immune responses, lymphocytes are responsible for specificity and memory. The two main types of lymphocytes are B cells and T cells. The function of T cells is to recognize and kill infected cells, while the function of B cells is to produce antibodies to neutralize the viruses. Researchers have studied the effects of immune responses such as CTL responses and antibody responses [24–27]. Some other researchers have also taken into account the effect of CTL responses and intracellular delays [16,19,28]. The mathematical model that describes the effect of humoral immune response on virus dynamics is presented as [29]
where x(t), y(t), v(t), and w(t) represent the concentration of uninfected target cells, actively infected cells, free viruses, and antibodies/B cells at time t, respectively. The uninfected cells x(t) are assumed to produce/grow at a constant rate
Herein, we upgrade the model (1) to include the latent infection component. We assume that the uninfected cell x(t) becomes infected by free virus or by direct contact with an infected cell at the rate
with initial values x(0) > 0, l(0) > 0, y(s) = χ(s) > 0, v(0) > 0, w(0) > 0, s ∈ [ − τ, 0] and χ(s) being the smooth function. Here, Dα is the Caputo fractional derivative of order α. l(t) denotes the concentrations of infected cells in the latent stage at t. We avoid dimensional mismatches for the fractional order model, define the parameter values
Definition 1 [15]. The Caputo derivative of fractional order α for a function f(t) is described as
where
The Laplace transform of Caputo derivative is described as
where
Remark 1. The fractional derivative α ∈ (0, 1) is defined by Caputo sense [15], so introducing a convolution integral with a power-law memory kernel is a good way to describe memory effects in dynamical systems. The decaying rate of the memory kernel is determined by α. A lower value of α corresponds to slower-decaying time-correlation functions which result in long-run memory.
Theorem 1. For any initial values x(0) > 0, l(0) > 0, y(s) = χ(s) > 0, v(0) > 0, w(0) > 0, s ∈ [ − τ, 0], the model (2) has a unique solution in [0, + ∞). Moreover, this solution remains positive and bounded.
Proof 1. Assume that
Here, Z(t) = (x(t),l(t),y(t),v(t),w(t))T, and
From [30,31] and Eq. 3, we found
Next, we prove the boundedness, adding the first three equations in Eq. 2:
Suppose that d ≤ min{m, a}, we get
If t → ∞, then we get
If t → ∞, then we get
The model (2) has the following equilibrium points:
• Infection-free equilibrium point
• Immune response–free equilibrium point
• Endemic equilibrium point
Here, we derive the threshold quantity
Based on the method of next-generation matrix [32–34], the threshold quantity
Therefore,
Note that
3 Local Stability
In this section, we discussed the local stability and bifurcation results of equilibrium point by using the linearization technique and Jacobian matrix. The linearized system of Eq. 2 at any equilibrium point
Apply the Laplace transform of Eq. 4, so that
where
and
The characteristic equation becomes
and
Theorem 2. If
Proof 2. The characteristic equation of Eq. 2 at
Since some coefficients of the above equations are delay-dependent, we utilize the geometric method, discussed in [35], to explore the possible stability switch in a general delay differential system with delay-dependent parameters. For the underlying model, we prove the stability of equilibrium points by direct comparison of the modulus of Eq. 6. When
Dividing by (sα + m + γ)(sα + μ)(sα + a) on both sides of Eq. 6, we get
This leads to contradiction because
where
Clearly,
Next, we derive the local stability at the endemic equilibrium state
Suppose the time-delay τ = 0, then the characteristic equation (5) is
where p1 = ρ1, p2 = ρ2 + ρ6, p3 = ρ3 + ρ7, p4 = ρ4 + ρ8, and p5 = ρ5 + ρ9. The endemic equilibrium point
Suppose τ > 0, then Eq. 5 becomes
We aim to prove that Eq. 7 has no pure imaginary roots for τ > 0. Let us assume that Eq. 7 has a pure imaginary and then substitute s = iν, ν > 0 in Eq. 7 to get
Separate the real and imaginary parts as
From Eq. 8,
Clearly,
Then,
The ν values get from U1, U2, V1, and V2.
This equation
Take the derivative of Eq. 7 with respect to τ for checking the transversality condition at τ = τ*, then
Then,
where
We arrive at the following result.
Theorem 3. For the model (2), the following results hold:
i) If τ = 0, then
ii) If τ > 0, then
The local asymptotic stability at the immune response–free equilibrium point
4 Global Stability
Lemma 1 [36]. Let
Theorem 4. If
Proof 3. We define the non-negative definite function at
Applying the fractional-order derivatives and using Lemma 1, we get
Based on the assumptions
Theorem 5. Assume that
Proof 4. We define the non-negative definite function at
Applying the fractional derivative on both sides, using Lemma 1, and assuming
Clearly, by using Lyapunov–LaSalle’s invariant principle and [37], DαV(t) < 0, the equilibrium point
5 Numerical Simulation
The numerical results of fractional-order delay differential system (2) are discussed, using implicit Euler’s scheme in [38]. The parameter values are as follows: λ = 8, d = 1, β1 = 5, β2 = 5, φ = 0.5, m = 2, γ = 100, a = 10, k = 10, μ = 10, ξ = 1, g = 1, and h = 1
Figure 1 shows the stable behaviors of the model (2) which converge to the infection-free steady state
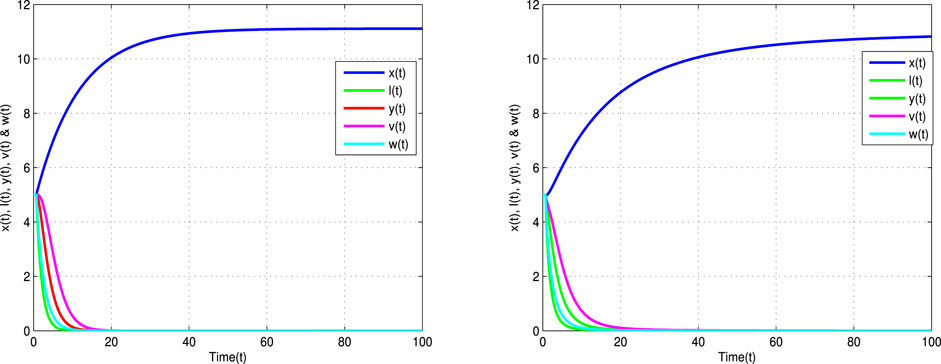
FIGURE 1. Time trajectories for uninfected cells x(t), latently infected cells l(t), infected cells y(t), viruses v(t), and antibodies w(t) of Eq. 2 with α = 1 (left banner) and α = 0.9 (right banner) and
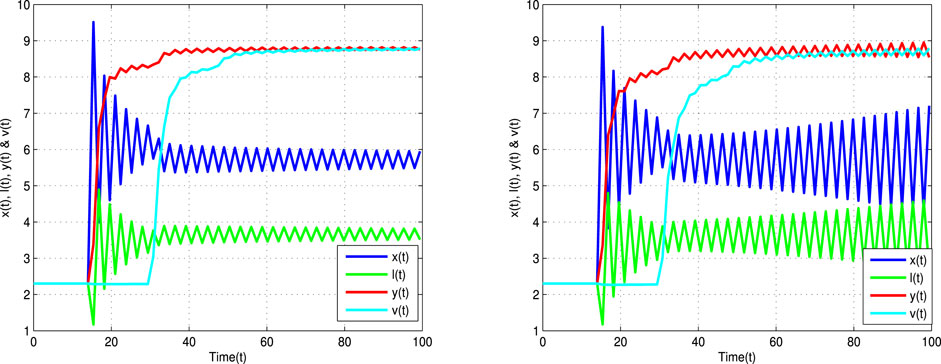
FIGURE 2. Time trajectories for uninfected cells x(t), latently infected cells l(t), infected cells y(t), and viruses v(t) of Eq. 2 with τ = 14 > τ* = 13.5, α = 0.9 (left banner) and α = 0.8 (right banner).
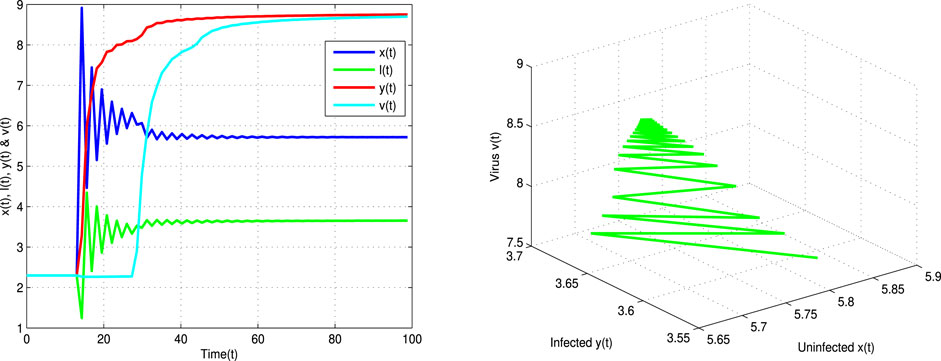
FIGURE 3. Time and space plane trajectories for uninfected cells x(t), latently infected cells l(t), infected cells y(t), and viruses v(t) of Eq. 2 with τ = 13 < τ* = 13.5 and α = 0.9.
Figure 4 displays the time trajectories of the considered model (2), which converge to the endemic equilibrium point
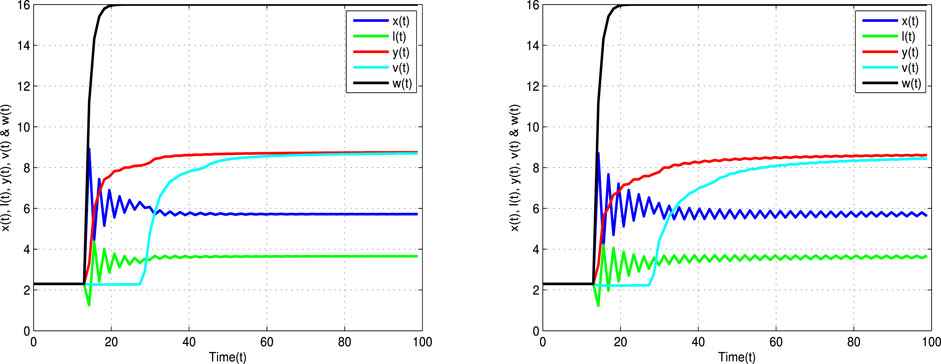
FIGURE 4. Time trajectories for uninfected cells x(t), latently infected cells l(t), infected cells y(t), viruses v(t), and antibodies w(t) of Eq. 2 with τ = 13 < τ* = 13.5, α = 0.9 (left banner) and α = 0.8 (right banner).
Remark 2. These are the results from the fractional-order viral infection model with latent infection and delay, which are different, complement, and expand upon those in [7,9,12]. The fractional-order stability regions in Figures 1–4 are larger than the corresponding integer-order stability regions in [7,12]. In a fractional-order model, the unstable equilibrium of an integer-order model may be a stable model. Furthermore, time-delays enhance the dynamics of the model and increase its complexity.
6 Concluding Remarks
Although the classical integer-order differential models can be useful for the study of disease dynamics, the fractional-order models are more useful for exploring disease dynamics. Several factors contribute to this, including data fitting, memory effects, and crossover effects. The fractional calculus is a powerful tool to describe physical and biological systems that have long-term memory and long-range spatial interactions. This paper examines the global dynamics of a fractional-order viral infection model with latent infection. We studied the positivity and boundedness of the solutions. Based on this formula, we derived the basic reproductive number
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, and further inquiries can be directed to the corresponding author.
Author Contributions
FR was involved in project conceptualization and supervision, writing the original draft, and reviewing and editing the paper. CR was responsible for data visualization and validation, running the software, and performing the methodology.
Funding
This research was funded by UAE University, fund # 12S005-UPAR 2020.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Kang, C, Miao, H, and Chen, X. Global Stability Analysis for a Delayed Hiv Infection Model with General Incidence Rate and Cell Immunity. Engin Lett (2016) 24:392–8.
2. Rihan, FA, and Velmurugan, G. Dynamics and Sensitivity of Fractional-Order Delay Differential Model for Coronavirus (Covid-19) Infection. Prog Fractional Differ Appl (2021) 7:43–61.
3. Rihan, FA, and Alsakaji, HJ. Dynamics of a Stochastic Delay Differential Model for COVID-19 Infection with Asymptomatic Infected and Interacting People: Case Study in the UAE. Results Phys (2021) 28:104658. doi:10.1016/j.rinp.2021.104658
4. Dahari, H, Lo, A, Ribeiro, RM, and Perelson, AS. Modeling Hepatitis C Virus Dynamics: Liver Regeneration and Critical Drug Efficacy. J Theor Biol (2007) 247:371–81. doi:10.1016/j.jtbi.2007.03.006
5. Yousfi, N, Hattaf, K, and Tridane, A. Modeling the Adaptive Immune Response in HBV Infection. J Math Biol (2011) 63:933–57. doi:10.1007/s00285-010-0397-x
6. Stilianakis, N, and Seydel, J. Modeling the T-Cell Dynamics and Pathogenesis of Htlv-I Infection. Bull Math Biol (1999) 61:935–47. doi:10.1006/bulm.1999.0117
7. Wang, X, Tang, S, Song, X, and Rong, L. Mathematical Analysis of an Hiv Latent Infection Model Including Both Virus-To-Cell Infection and Cell-To-Cell Transmission. J Biol Dyn (2017) 11:455–83. doi:10.1080/17513758.2016.1242784
8. Wen, Q, and Lou, J. The Global Dynamics of a Model about Hiv-1 Infection In Vivo. Ricerche mat. (2009) 58:77–90. doi:10.1007/s11587-009-0048-y
9. Pan, S, and Chakrabarty, SP. Threshold Dynamics of Hcv Model with Cell-To-Cell Transmission and a Non-cytolytic Cure in the Presence of Humoral Immunity. Commun Nonlinear Sci Numer Simulat (2018) 61:180–97. doi:10.1016/j.cnsns.2018.02.010
10. Elaiw, AM, and AlShamrani, NH. Global Properties of Nonlinear Humoral Immunity Viral Infection Models. Int J Biomath (2015) 08:1550058. doi:10.1142/s1793524515500588
11. Luo, Y, Zhang, L, Zheng, T, and Teng, Z. Analysis of a Diffusive Virus Infection Model with Humoral Immunity, Cell-To-Cell Transmission and Nonlinear Incidence. Physica A: Stat Mech its Appl (2019) 535:122415. doi:10.1016/j.physa.2019.122415
12. Wang, Y, Lu, M, Lu, M, and Jiang, D. Viral Dynamics of a Latent Hiv Infection Model with Beddington-Deangelis Incidence Function, B-Cell Immune Response and Multiple Delays. Mbe (2021) 18:274–99. doi:10.3934/mbe.2021014
13. Hattaf, K. Global Stability and Hopf Bifurcation of a Generalized Viral Infection Model with Multi-Delays and Humoral Immunity. Physica A: Stat Mech its Appl (2020) 545:123689. doi:10.1016/j.physa.2019.123689
14. Kilbas, AA, Srivastava, HM, and Trujillo, JJ. Theory and Applications of Fractional Differential Equations. North Holland Mathematics Studies, Vol. 204. Amsterdam: Elsevier Science (2006).
16. Rihan, FA. Delay Differential Equations and Applications to Biology. Singapore: Springer (2021).
17. Rakkiyappan, R, Preethi Latha, V, and Rihan, FA. A Fractional-Order Model for Zika Virus Infection with Multiple Delays. Complexity (2019) 4178073. doi:10.1155/2019/4178073
18. Latha, VP, Rihan, FA, Rakkiyappan, R, and Velmurugan, G. A Fractional-Order Model for Ebola Virus Infection with Delayed Immune Response on Heterogeneous Complex Networks. J Comput Appl Math (2018) 339:134–46. doi:10.1016/j.cam.2017.11.032
19. Rihan, FA, Arafa, AA, Rakkiyappan, R, Rajivganthi, C, and Xu, Y. Fractional-order Delay Differential Equations for the Dynamics of Hepatitis C Virus Infection with IFN-α Treatment. Alexandria Eng J (2021) 60:4761–74. doi:10.1016/j.aej.2021.03.057
20. Tamilalagan, P, Karthiga, S, and Manivannan, P. Dynamics of Fractional Order Hiv Infection Model with Antibody and Cytotoxic T-Lymphocyte Immune Responses. J Comput Appl Math (2021) 382:113064. doi:10.1016/j.cam.2020.113064
21. Naik, PA, Zu, J, and Owolabi, KM. Global Dynamics of a Fractional Order Model for the Transmission of Hiv Epidemic with Optimal Control. Chaos, Solitons & Fractals (2020) 138:109826. doi:10.1016/j.chaos.2020.109826
22. Danane, J, Allali, K, and Hammouch, Z. Mathematical Analysis of a Fractional Differential Model of Hbv Infection with Antibody Immune Response. Chaos Solitons Fractals (2020) 136:109787. doi:10.1016/j.chaos.2020.109787
23. Shi, R, Lu, T, and Wang, C. Dynamic Analysis of a Fractional-Order Delayed Model for Hepatitis B Virus with Ctl Immune Response. Virus Res (2020) 277:197841. doi:10.1016/j.virusres.2019.197841
24. Wang, K, Wang, W, and Liu, X. Global Stability in a Viral Infection Model with Lytic and Nonlytic Immune Responses. Comput Math Appl (2006) 51:1593–610. doi:10.1016/j.camwa.2005.07.020
25. Wang, K, Wang, W, and Liu, X. Viral Infection Model with Periodic Lytic Immune Response. Chaos, Solitons & Fractals (2006) 28:90–9. doi:10.1016/j.chaos.2005.05.003
26. Wang, X, and Wang, W. An Hiv Infection Model Based on a Vectored Immunoprophylaxis experiment. J Theor Biol (2012) 313:127–35. doi:10.1016/j.jtbi.2012.08.023
27. Wodarz, D. Hepatitis C Virus Dynamics and Pathology: The Role of Ctl and Antibody Responses. J Gen Virol (2003) 84:1743–50. doi:10.1099/vir.0.19118-0
28. Song, X, Wang, S, and Dong, J. Stability Properties and Hopf Bifurcation of a Delayed Viral Infection Model with Lytic Immune Response. J Math Anal Appl (2011) 373:345–55. doi:10.1016/j.jmaa.2010.04.010
29. Murase, A, Sasaki, T, and Kajiwara, T. Stability Analysis of Pathogen-Immune Interaction Dynamics. J Math Biol (2005) 51:247–67. doi:10.1007/s00285-005-0321-y
30. Atangana, A. Derivative with a New Parameter: Theory, Methods and Applications. Academic Press (2015).
32. Sardar, T, Rana, S, Bhattacharya, S, Al-Khaled, K, and Chattopadhyay, J. A Generic Model for a Single Strain Mosquito-Transmitted Disease with Memory on the Host and the Vector. Math Biosciences (2015) 263:18–36. doi:10.1016/j.mbs.2015.01.009
33. Sardar, T, Rana, S, and Chattopadhyay, J. A Mathematical Model of Dengue Transmission with Memory. Commun Nonlinear Sci Numer Simulation (2015) 22:511–25. doi:10.1016/j.cnsns.2014.08.009
34. van den Driessche, P, and Watmough, J. Reproduction Numbers and Sub-threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Math Biosci (1802) 180:29–48. doi:10.1016/s0025-5564(02)00108-6
35. Beretta, E, and Kuang, Y. Geometric Stability Switch Criteria in Delay Differential Systems with Delay Dependent Parameters. SIAM J Math Anal (2002) 33:1144–65. doi:10.1137/s0036141000376086
36. Li, H-L, Zhang, L, Hu, C, Jiang, Y-L, and Teng, Z. Dynamical Analysis of a Fractional-Order Predator-Prey Model Incorporating a Prey Refuge. J Appl Math Comput (2017) 54:435–49. doi:10.1007/s12190-016-1017-8
37. Sene, N. Stability Analysis of the Fractional Differential Equations with the Caputo-Fabrizio Fractional Derivative. J Fract Calculus Appl (2020) 1:160–72.
Keywords: bifurcation, fractional order, viral infection model, stability, time-delay
Citation: Rajivganthi C and Rihan FA (2021) Global Dynamics of a Delayed Fractional-Order Viral Infection Model With Latently Infected Cells. Front. Appl. Math. Stat. 7:771662. doi: 10.3389/fams.2021.771662
Received: 06 September 2021; Accepted: 10 November 2021;
Published: 08 December 2021.
Edited by:
Axel Hutt, Inria Nancy—Grand-Est Research Centre, FranceReviewed by:
Dibakar Ghosh, Indian Statistical Institute, IndiaTomás Lázaro, Universitat Politecnica de Catalunya, Spain
Copyright © 2021 Rajivganthi and Rihan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. A. Rihan, ZnJpaGFuQHVhZXUuYWMuYWU=
 C. Rajivganthi
C. Rajivganthi F. A. Rihan
F. A. Rihan