- Complex Multiscale Dynamics, Division of Games Technology and Mathematics, Abertay University, Dundee, United Kingdom
In recent years unmanned aerial vehicles (UAVs) have become smaller, cheaper, and more efficient, enabling the use of multiple autonomous drones where previously a single, human-operated drone would have been used. This likely includes crisis response and search and rescue missions. These systems will need a method of navigating unknown and dynamic environments. Typically, this would require an incremental heuristic search algorithm, however, these algorithms become increasingly computationally and memory intensive as the environment size increases. This paper used two different Swarm Intelligence (SI) algorithms: Particle Swarm Optimisation and Reynolds flocking to propose an overall system for controlling and navigating groups of autonomous drones through unknown and dynamic environments. This paper proposes Particle Swarm Optimisation Pathfinding (PSOP): a dynamic, cooperative algorithm; and, Drone Flock Control (DFC): a modular model for controlling systems of agents, in 3D environments, such that collisions are minimised. Using the Unity game engine, a real-time application, simulation environment, and data collection apparatus were developed and the performances of DFC-controlled drones—navigating with either the PSOP algorithm or a D* Lite implementation—were compared. The simulations do not consider UAV dynamics. The drones were tasked with navigating to a given target position in environments of varying size and quantitative data on pathfinding performance, computational and memory performance, and usability were collected. Using this data, the advantages of PSO-based pathfinding were demonstrated. PSOP was shown to be more memory efficient, more successful in the creation of high quality, accurate paths, more usable and as computationally efficient as a typical incremental heuristic search algorithm when used as part of a SI-based drone control model. This study demonstrated the capabilities of SI approaches as a means of controlling multi-agent UAV systems in a simple simulation environment. Future research may look to apply the DFC model, with the PSOP algorithm, to more advanced simulations which considered environment factors like atmospheric pressure and turbulence, or to real-world UAVs in a controlled environment.
1 Introduction
It is the role of crisis response teams to react to disaster situations such as out of control wildfires or major earthquakes. These teams often must work in dangerous, volatile environments with limited knowledge of the current situation. Such environments can pose a serious risk to the health of the responders. The ability for teams to deploy inexpensive, unmanned vehicles in place of human responders could limit the risk to human life and, thus, could be a valuable part of crisis response procedures [1].
Unmanned Aerial Vehicles (UAVs), commonly referred to as drones, are aircraft which operate without an onboard human pilot. Instead, these vehicles are either controlled remotely by a human pilot, remotely with an autonomous control system, or with an onboard, autonomous navigation system [2]. In recent years UAV technology has advanced rapidly with numerous different applications proposed and explored. Search and rescue operations have been identified as a key task where UAV technology could be of significant benefit [3].
This paper will explore the application of Swarm Intelligence (SI) concepts as a method of controlling and navigating systems of autonomous UAVs in unknown environments. Games technology will be used to provide a simulation environment in which the algorithm can be tested. Additionally, this paper will describe how the core concepts could be applied to games applications, combining concepts from both UAV dynamics and games technology with the aim of enhancing both fields.
A crisis response mission that utilises remotely operated UAVs requires constant real-time communication with each of the deployed drones. This communication link can be considered an operational vulnerability as a disruption, or failure, of this link would significantly limit the effectiveness of the drones consequently limiting the success of the overall mission. To address this vulnerability, research has begun to explore SI as a method of controlling a group of deployed drones [4]. SI explores the decentralised, self-organisation of multi-agent systems (MASs). SI can be considered a route to Artificial Intelligence where the application of SI techniques can lead to emergent, intelligent behaviour capable of solving a broad range of problems [5]. SI techniques often require little, or no, direct communication between agents, thus, a system using a SI approach to control drones engaged in a crisis response operation would be better able to handle communication disruption than a remote-control approach [4].
The flocking behavioural model is a well-documented SI concept that can produce collision-free collective motion within a MAS. Reynolds flocking [6] is a ruleset that can be used to produce flocking behaviour algorithmically and has been utilised in both simulation and real-world environments [7, 8]. The scope of Reynolds flocking is limited, the ruleset alone does not provide any obstacle avoidance (only avoiding collisions with other agents) nor can it provide any pathfinding capabilities. For a complete drone control model, both, obstacle avoidance and pathfinding would have to be handled using additional techniques.
Pathfinding, the calculation of an optimal path between two points, is a foundational problem in computer science. Typically, this problem has been approached from a graph-theory perspective where a graph representation of the environment is required. For use in dynamic environments, prominent graph-based algorithms, such as Lifelong Planning A* or D* often suffer bottlenecks and cycle repetition and, as the size of the graph grows, become increasingly computationally, and memory, expensive [9].
To address this limitation, this paper will propose the Particle Swarm Optimisation Pathfinding (PSOP) algorithm as a method of onboard, autonomous navigation in dynamic environments for groups of UAVs. The algorithm will use the SI metaheuristic, Particle Swarm Optimisation (PSO) [10] as the basis of an environment-size agnostic pathfinding algorithm to be used as part of an overall model for controlling flocks of UAVs. This model—the Drone Flock Control (DFC) model—also proposed by this paper, will combine the novel PSOP algorithm, with Reynolds flocking, and an obstacle avoidance AI implementation to create a performant solution for multi-agent, autonomous UAV control in unknown, dynamic environments.
In addition to its real-world applications, the DFC model could be used in game applications. Regularly, within games, there is a desire to have a group of non-playable characters (NPCs) navigate an environment. This could be a horde of enemies, gameplay mechanics like target-seeking abilities, or simply fauna to make an environment feel alive.
With the strict computational and memory resource restrictions of games applications, the available resources for NPC pathfinding is often very limited. As game environments grow increasingly large and more complex, using A* based pathfinding approaches can often become prohibitively expensive in these large environments [11]. One solution to this has been to reduce the granularity of the graph used by the search algorithm, where the same game environment is represented with a lower resolution graph. However, paths created with a very low granularity graph—whilst traversing the fewest number of nodes—may be far from optimal as far apart nodes are unable to detect fine details in the environment, such as small gaps that could be used as a shortcut.
The PSOP algorithm, proposed by this paper, may provide a better alternative for NPC pathfinding than A* based approaches for situations with multiple agents. It is hypothesised that the computational and memory requirements of the PSOP algorithm will be agnostic to the environment size and will have no limitations on search granularity. Additionally, the DFC model may be suitable as a method of controlling the complete motion of an NPC group—particularly in situations where flocking behaviour was desired, like for the control of a flock of birds.
The aim of this paper is to combine two different SI algorithms: PSO and Reynolds flocking, to propose a model for controlling a system of autonomous UAVs capable of navigating unknown and evolving environments. The project will design, implement, and test a PSO-based dynamic pathfinding algorithm and the computational and memory efficiency of this approach will be compared to that of a traditional graph-based pathfinding method. A real-time application will be created to provide a simulation environment in which test scenarios can be run. Quantitative data, describing the performances of both the SI-based and graph-based pathfinding algorithms, will be collected. This data will be analysed to assess the suitability of the proposed pathfinding algorithm for use with a multi-agent UAV system. Deterministic pathfinding algorithms, that guarantee an optimal path is found, grow rapidly in computational and memory expense as environment size grows. A SI metaheuristic-based pathfinding algorithm, whilst unable to guarantee an optimal path, will likely be far more scalable than graph-based algorithms. It is hypothesised that the computational and memory requirements of the proposed SI pathfinding algorithm (PSOP) will be unaffected by the environment size, and thus, as the environment size grows, the PSOP algorithm is expected to increasingly outperform a traditional graph-based algorithm for the navigation of a multi-agent system.
The paper is structured as follows: Section 2 describes the development and implementation of the DFC model and the PSOP algorithm including performance testing; Section 3 presents and discusses the results from the performance testing; and, Section 4 summarises the results, placing the results in the wider context and discusses further developments.
2 Methodology
To achieve the stated aims of the paper, both the DFC model and the PSOP algorithm were designed and implemented. Additionally, a real-time application was created to provide a test environment in which the proficiency of the PSOP algorithm could be compared to that of a contemporary pathfinding approach. The following section will deliver a comprehensive description of the development process and will discuss the reasoning behind key development decisions. Performance testing and data analysis processes will also be discussed.
2.1 Project Development
Unity [12] was chosen as the development environment as it is an industry standard game engine. Using Unity allowed access to a powerful physics subsystem and ensured that rendering would be performant—without the need for extensive setup. The proposed DFC model, PSOP algorithm, and D* Lite implementation were implemented in C# and a real-time application was created to facilitate testing and data collection. The application that was created is capable of instantiating and controlling a system of drones within a simulation environment. The application also defines an objective for the drones to complete and records data relating to the group’s performance in achieving that objective. A concise menu was created to allow users of the application to run multiple tests with various parameters without requiring changes to the code or the use of the engine.
2.2 Particle Swarm Optimisation Pathfinding (PSOP) Algorithm
The main focus of this project is the proposal, design, and implementation of an environment-size agnostic approach to cooperative pathfinding. The proposed algorithm, PSOP, utilises the PSO algorithm [10] to iteratively improve the quality of an agent’s position, where position quality is an estimate of how useful that position is as a point on a path from the start to the target. The PSO algorithm was identified as an effective method of iteratively improving a candidate solution in a search-space, using multiple agents—or particles—to improve search-time by sharing information about position quality between agents. This approach is highly applicable to multi-agent pathfinding, and thus, the proposed PSOP algorithm builds directly upon the structure of the PSO algorithm. A record is kept of the highest quality position found personally by each agent (pBest) and the highest quality position found by any agent (gBest). Each timestep, the quality of the current position is assessed using the PSOP heuristic (see Section 2.2.1) with pBest and gBest updated if required. The algorithm then updates the velocity of each agent using the formula:
where v(t) is the velocity at timstep t; w, c1, c2 are constants; r1, r2 ∈ [0, 1]; and, p, pbest, gbest are the current position, the position of pBest, and the position of gBest respectively. The values of the constants are shown (Table 1). The values for c1 and c2 were selected to match the canonical PSO algorithm [10]. Inertia was not described as part of the original PSO algorithm, however, an inertia (or w) value in the range [0.9, 1.2] was found to improve the performance of the algorithm [13] and thus was included in the PSOP algorithm. Internal development testing found improved performance when this value was lowered—likely caused by the DFC model already considering the drone’s inertia (see Section 2.3).
2.2.1 PSOP Heuristic
Borrowing from the heuristic used by the A* algorithm, the PSOP heuristic considers the Euclidean distance between the agent and the target—favouring positions that are closer to the target by taking the inverse of the distance. Additionally, the PSOP heuristic considers how obstructed the direct path from the current position to the target,
where
where θ is the angle between
2.2.2 pBest and gBest
When applied in dynamic environments, it is highly likely that positions that were once of high quality could lose quality, for example, if an obstacle moves between the position and the target—referred to as positions becoming stale. Stale positions could negatively impact on the algorithm’s ability to effectively find the target by causing the velocity of the agent to be calculated using incorrect information. One solution to the problem, would require drones to periodically recheck pBest and gBest positions. This approach is conceptually similar to the ‘finder and tracker’ adaptation that can be applied to the PSO algorithm to allow it to be applied to a dynamic search-space [14]. This adaptation assigns each particle to one of two roles: finder or tracker. When a candidate solution (position) of sufficient quality is discovered by a finder, tracker particles are assigned to the position and follow the peak as the environment evolves. The approach chosen by this paper, however, was to use a confidence system. The quality value of both pBest and gBest are decayed over time so that recently discovered positions of high quality are favoured over older positions—drones are less confident in the quality of older positions. This approach negates any need for positions to be actively rechecked. The implementation created by this project uses a linear decay controlled by the ‘quality decay factor’, however, any function of time t could be used.
2.3 Drone Flock Control Model
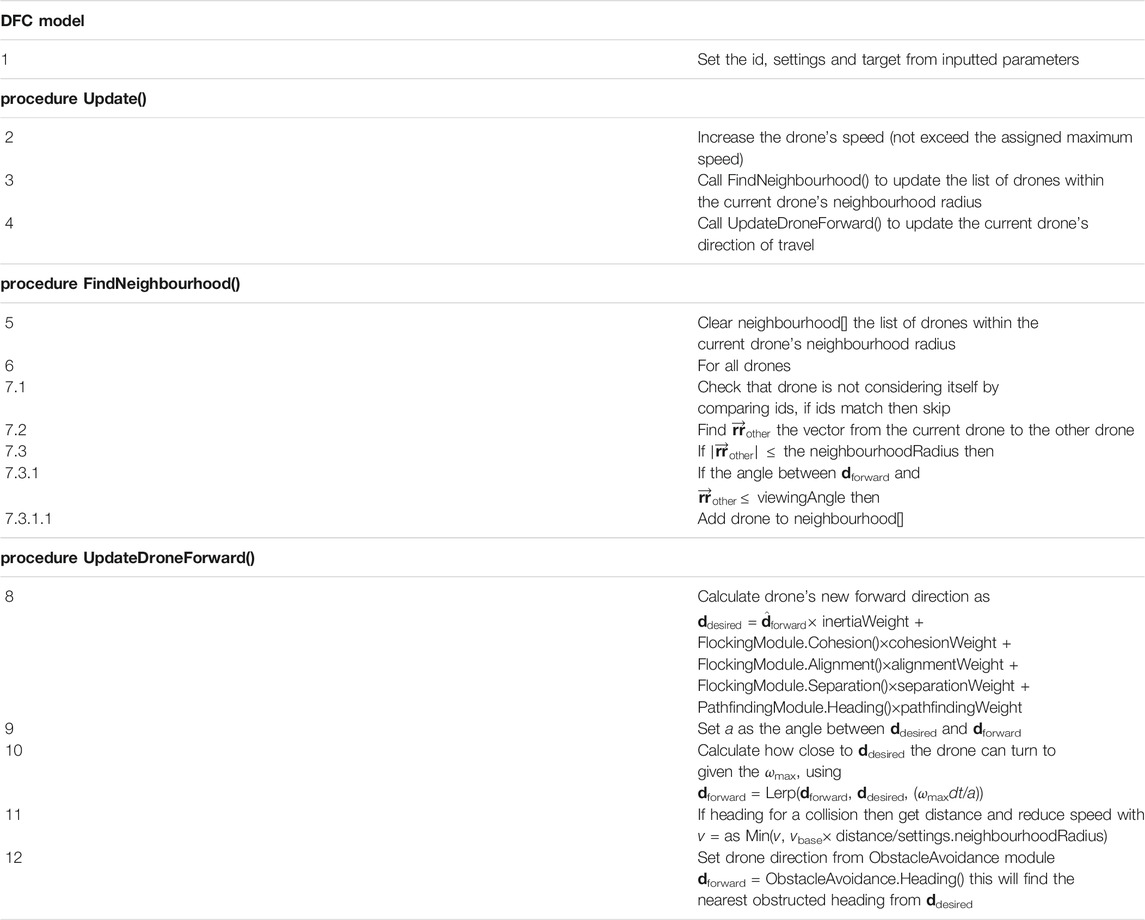
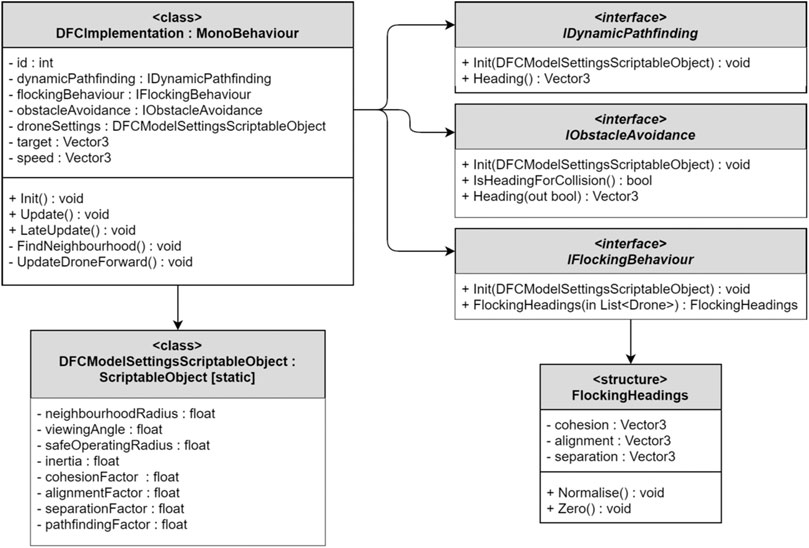
DFC is a model for facilitating the cooperative motion of a multi-agent system in a 3D environment. Designed to be run locally by each member of the flock, the DFC model determines a velocity vector at each timestep by assessing three factors: the flocking module, pathfinding module, and the obstacle avoidance module. Each module contributes between one and three vectors to the model and the velocity is calculated as the weighted sum of these vectors plus weighted inertia (the product of the velocity at the previous timestep and its weight) (Table 2). The model requires a neighbourhood radius, maximum viewing angle, and safe operating radius in order to determine which of the other drones and which obstacles should be considered by the different modules (see Figure 1). During development several issues were caused by conflicts between the obstacle avoidance module and the other two modules. Both drone-to-drone and drone-to-environment collisions were occurring because the flocking and pathfinding modules were contributing vectors that opposed the vector proposed by the obstacle avoidance module. To address this, the model was updated to first assess the velocity using inertia, flocking, and pathfinding, then updating the obstacle avoidance module. Only using the obstacle avoidance to update the velocity if the module has assessed that a collision would occur.
2.3.1 Drone Flock Control Implementation
The DFC model implementation inherits from MonoBehaviour—the base class from which Unity scripts must derive [15]. This allows the model’s implementation to be attached directly to a Unity GameObject. The functionality of each of the DFC modules (flocking, obstacle avoidance, and pathfinding) are defined with module-specific C# interfaces [16]. Each interface describes a contract in code for what behaviour a module must implement (Figure 1). This approach creates an abstract, general structure for how the DFC model should be implemented, separate from the specific implementation created for this project. This allows further work to easily use and extend the DFC model to meet domain specific challenges.
2.3.2 Drone Settings
In the engine, the weight values—used by the DFC model to calculate the weighted sum—are held in a ScriptableObject, this container also stores the neighbourhood, viewing angle, and safe-operating distance values—collectively this data is referred to as the drone settings. Using a ScriptableObject to store the drone settings requires just one copy of the data to be stored. This copy can be accessed by all drones in a simulation, thus, if a change to the drone settings is required then only the centrally stored data needs to be updated for the change to affect all drones. During the implementation of the project’s test plan, fixed values were used for the drone settings across all testing scenarios (Table 3). These values were selected following internal development testing.
2.4 Flocking Module
Reynolds flocking [6] had previously been identified as an effective approach to facilitating collision-free motion for multi-agent systems. Additionally, Reynolds flocking is an extremely well documented approach to autonomous UAV control, previously used by numerous research groups [7, 17]. Thus, Reynolds flocking was chosen to form the basis of the flocking component implementation used in this paper. There are numerous examples of Reynolds flocking implementations in both 2D and 3D environments (e.g. [7, 17]). Many of these implementations include adaptions to either improve the algorithm or to address a specific challenge. This paper, however, implements the standard algorithm described by Reynolds.
2.5 Obstacle Avoidance Module
As obstacle avoidance was not the focus of this paper, the implementation of the obstacle avoidance module utilises a simple but effective AI algorithm. The algorithm determines if the drone is currently heading for a collision. If so, then rays are cast in increasing distance from the current direction of travel, until an unobstructed direction is found. Provided that the explored directions are always evenly spaced and are of equal or increasing angle from the direction of travel, then this method will identify an unobstructed heading that requires a, close to, minimal alteration from the current heading. Whether a given heading is obstructed is determined using the raycast functionality included as part of Unity’s physics subsystem [15]. The directions of increasing angle from the direction of travel are calculated at startup-time using the “Fibonacci Spiral Sphere” to find evenly distributed points on a unit sphere. When required by a drone, the array of directions is transformed to start from the drone’s current direction of travel.
2.6 Pathfinding Module
The role of the pathfinding module is to direct the drone along a path that will lead to some target location. There is no requirement for the target to be at a fixed location, however, this paper will look specifically at pathfinding to a stationary target. The only requirement of the pathfinding module is to provide a single heading (a vector3 value) to represent the direction that the module is recommending as the direction of travel for the drone. The project will explore the use of two different styles of pathfinding implementations: graph-based, single-agent, deterministic pathfinding; and, a cooperative, non-deterministic pathfinding approach. Specifically, this paper will compare a DFC compatible implementation of the incremental heuristic search algorithm, D* Lite to an implementation of the PSOP algorithm.
2.6.1 PSOP Implementation
As it was designed for use in multi-agent systems, implementing the PSOP algorithm for use with the DFC model required no changes from the algorithm’s canonical form. The one notable technical hurdle is the shared awareness of gBest (see Section 2.2.2). This project’s implementation uses the singleton pattern to create a reference to which each drone’s PSOP implementation can refer. Real-world implementations, where each drone will have its own hardware, will, naturally, not be able to rely on globally accessible memory and thus a more involved solution would be required. For example, each flock member could store what they believe to be gBest and broadcast this to the other flock members periodically—updating their own whenever they receive a broadcast of a gBest that is better than the one they are currently aware of.
2.6.2 D* Lite Implementation
A C# implementation of the D* Lite algorithm [18] was adapted to integrate with the DFC model. Typically, the D* Lite algorithm requires the seeker to move to the next requested node for the algorithm to be updated. As the drones move with a fixed maximum speed and their velocity is not solely determined by the pathfinding module, there is no guarantee that, at the next timestep, the drone will be at the next position. The D* Lite implementation, thus, only searches for a new shortest path if either the seeker is at a different node from last time step or a new obstacle was found. The drones used a grid of nodes, one unit apart, as the graph representation of the environment. Obstacles were identified using the obstacle detection apparatus used by the obstacle avoidance module (see Section 2.5). During development it was found that in a small number of cases the algorithm was unable to update in the time required to be applied in real-time. To address this a 700-node expansion limit was applied to the algorithm when finding the shortest path. This did not appear to impact performance as, if the optimal path was not found after expanding 700 nodes, the correct general direction was usually determined and further calculation, if needed, could be completed as the drone moved closer to the target.
2.7 Testing
To assess the proficiency of the PSOP algorithm two types of drones were created, both controlled with the DFC model. One type of drone used PSOP as the pathfinding module (p-drones) and the other used a D* Lite implementation (d-drones). Flocks, comprised of either the p-drones or d-drones, were instantiated in the environment and tasked with achieving an objective.
2.7.1 The Environment
This project focused on the performance of the flock within an urban environment. The environment was created using user-positioned, cuboidal obstacles to represent buildings and other common urban structures such as signs and walls. These obstacles were implemented with Unity GameObjects and placed within a Unity scene (Figure 2). This approach was selected as it is in line with the methods used and described by similar research projects [19, 20]. A key requirement of the project was that the environment be dynamic, to facilitate this, moving spherical obstacles were added. These obstacles could move freely in three-dimensions. The obstacles did, however, avoid other obstacles using the same obstacle avoidance system as the drones (see Section 2.5). During pretesting it was noted that the dynamic obstacles—designed to move freely around the environment—were not encountering the drone flocks often enough to regularly disrupt the drones’ path planning. To address this a probabilistic targeting system was added where, each second, each dynamic obstacle would have a 4.17% chance of changing direction to move directly towards the centre of the flock. Additionally, obstacles would have a 12.5% chance, per second, of moving away from the flock, to prevent one area from becoming too crowded. The probabilities were set manually to produce a reasonable level of encounters between the drones and the dynamic obstacles. Please note that the simulations conducted do not use a simulator implementing UAV dynamics.
2.7.2 The Objective
The drones were required to find and follow a clear path from the starting location to a pseudorandom target point in the environment. The flock was said to have completed this objective when one of the flock members entered the region immediately surrounding the target—within a radius of four units. Please note that the environment size is measured in non-dimensional units. In this context, a radius of 4 units is deemed a reasonable threshold length scale for close proximity. This objective was selected to simulate a latent objective of a crisis response team in a disaster situation: making contact with a given location in an environment.
The start point and target point could not be chosen at random as some points would be unreachable—such as points that are inside obstacles. Thus, the environment defines multiple targetable regions that report every point within that region to the simulation manager. When a target was to be selected, the simulation manager selected a random point from the list of reported targetable points. The same system was used to select a starting position for the flock—using a “startable” region in place of the targetable regions. Additionally, the simulation manager only considered target points where the distance from the starting point to the target point was greater than a given minimum distance (defined as half the average edge length of the environment).
2.7.3 Testing Scenarios
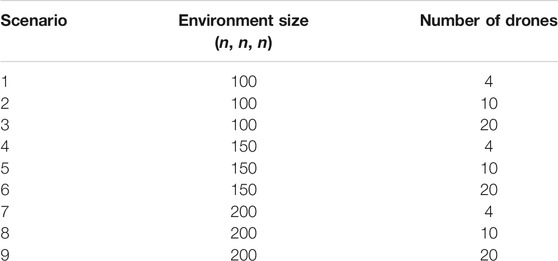
To obtain a robust understanding of the proficiency of the PSOP algorithm when compared to the D* Lite algorithm, a comprehensive test plan was proposed exploring the performance differences between p-drones and d-drones. The testing would specifically explore performance differences as the environment size increased and as the number of drones in the flock increased. The test plan comprised nine scenarios, each with a unique environment size and flock size combination. Each scenario would be simulated using first p-drones then d-drones (Table 4). To facilitate the presentation of strong claims about the proficiency of p-drones when compared to d-drones each scenario was repeated five times.
2.7.4 Data Gathering
Data was collected (Table 5) from the scenarios outlined in Table 4. Data was gathered per iteration of each scenario—with either one data point collected each frame (for Frametime and Memory Allocation) or one data point collected each iteration (for Initialisation Time, Search Time, and Collisions). The data for the Frametime and Memory Allocation was obtained by running the scenarios each five times. Within each iteration of the scenarios a large number of data was measured; for example, the number of frames recorded is of the order of 1,000 frames. This approach to data gathering allows the stochastic nature of the PSO algorithm to be taken into account and the calculated mean and median values of the Frametime and Memory Allocation to be statistically valuable. Statistics are presented as the average, and variance, of all iterations (n = 5) of a given scenario. Where a data point was collected each frame, statistics are presented as (weighted mean ± weighted SD) and as (mean ± SD) when only one data point was collected per iteration. All drones are controlled using the DFC model with p-drones using the PSOP pathfinding-module and d-drones using the D* Lite pathfinding-module. The testing was completed on a PC (see Table 6) running Windows 10 with minimal processes running in the background. The testing application was a Unity Standalone development build, with Windows as the target platform using 64-bit x86 architecture.
2.7.5 Data Analysis
Once the data has been gathered the mean frametime and memory allocation will be calculated for each iteration of each scenario. Using this intermediary data, the weighted mean for both the frametime and memory allocation of each scenario will be calculated using the formula:
where, for the i-th iteration of a given scenario, ni is the number of data points (frames) recorded that iteration and
3 Results and Discussion
In this paper we explore how the PSO algorithm could be used to facilitate dynamic pathfinding as part of a SI-based UAV control model. Results from our investigation are shown in Figures 3–9. It was hypothesised that the proposed PSO-based pathfinding algorithm would be agnostic to the environment size and would increasingly outperform a traditional graph-based algorithm as the environment size increased. The hypothesis was found to be partially correct as when compared to a contemporary graph-based pathfinding algorithm (D* Lite), the PSO-based pathfinding algorithm (PSOP) was more memory efficient and as computationally efficient as the D* Lite algorithm (Figures 3–5). This paper also found that the PSOP algorithm was more accurate and efficient for systems of 10 or 20 agents (Figures 6–8). Whilst the computational requirements of the PSOP algorithm were shown to be agnostic to the environment size, the algorithm’s memory requirements did increase as the environment size grew. This increase was, however, far lower than the observed increase in memory allocation required by the D* Lite algorithm. Overall, this paper finds that the PSOP algorithm is a far more suitable algorithm than D* Lite for use as part of a SI-based multi-agent UAV control model. This section will discuss, with reference to the data gathered during testing, how these conclusions were formulated and will analyse the effect of increasing the environment size on the performance of the algorithms.
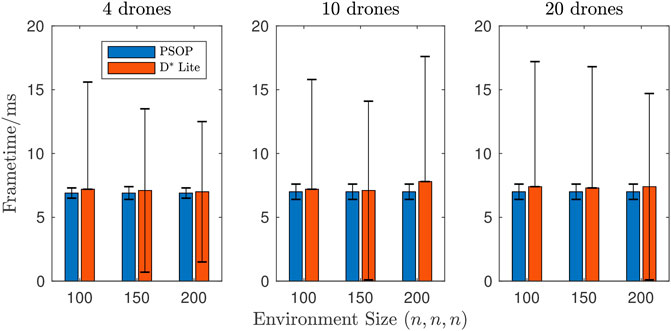
FIGURE 3. Weighted mean frametime by environment size. The 4 drones case shows similar performance between the two algorithms when using D* Lite; whereas, there is a slight performance benefit when using PSOP for the 10 and 20 drone cases.
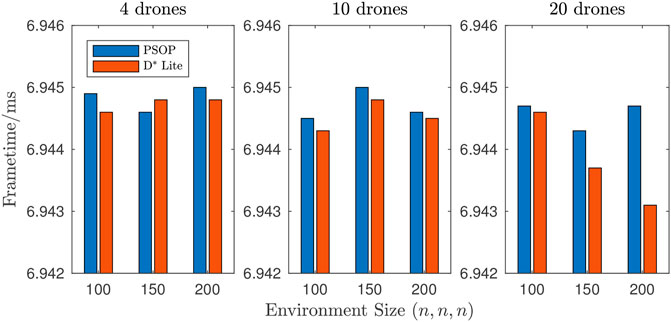
FIGURE 4. Weighted median frametime by environment size. Across all nine scenarios the weighted-median required frametimes were shown to be extremely similar with only a 0.027% variation between the highest and lowest weighted-median frametime.
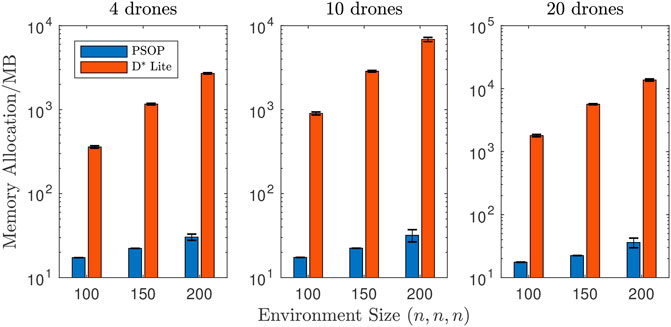
FIGURE 5. Weighted mean memory allocation by environment size. Across all nine scenarios, p-drones were shown to require far lower memory allocation than d-drones. For 4 drones the results show a far higher memory allocation, which increases more rapidly as the environment size increases, when using D* Lite. This trend is increasingly enhanced for 10 and 20 drones.
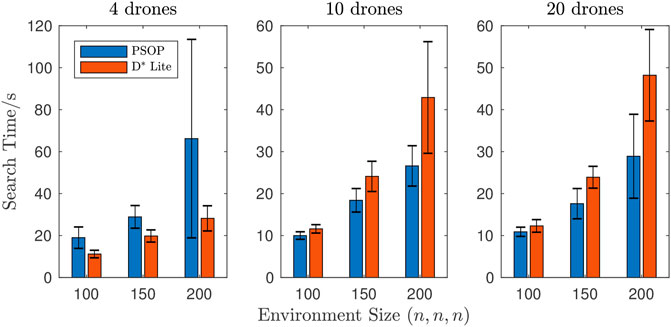
FIGURE 6. Mean time taken to complete objective by environment size. For a system of 4 drones, p-drones required longer to complete objectives than d-drones; whereas for systems of either 10 or 20 drones p-drones required less time to complete objectives when compared to d-drones. For 4 drones the PSOP method takes longer than D* Lite; however, this trend is reversed for 10 and 20 drones.
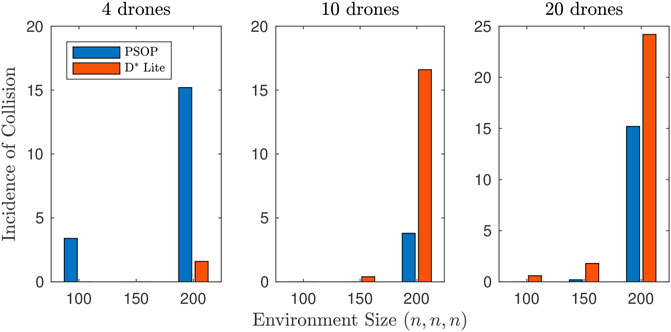
FIGURE 7. Mean incidence of collision by environment size (drone-to-environment). For a system of 4 drones, p-drones recorded a greater number of collisions between drones and the environment (6.2 collisions per scenario, average across all environment sizes) than d-drones (0.5 collisions per scenario, average across all environment sizes). Whereas for systems of either 10 or 20 drones p-drones recorded fewer collisions between drones and the environment (1.3 and 5.1 collisions per scenario respectively, average across all environment sizes) when compared to d-drones (5.7 and 8.9 collisions per scenario respectively, average across all environment sizes).
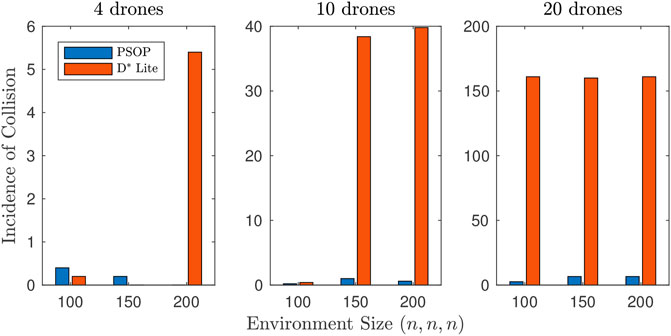
FIGURE 8. Mean incidence of collision by environment size (drone-to-drone). For collisions between two drones, p-drones recorded fewer incidences for systems of 4, 10, and 20 drones with 0.2, 0.6, and 5.3 collisions per scenario respectively for p-drones (average across all environment sizes) and 1.9, 26.2, and 160.7 collisions per scenario respectively for d-drones (average across all environment sizes).
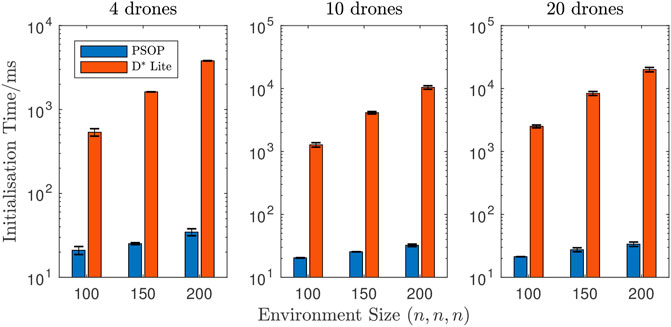
FIGURE 9. Mean time taken to initialise by environment size. Across all nine scenarios, p-drones were shown to require far less initialisation time than d-drones. Figure shows far higher initialisation time, which increases as function of environment size and number of drones, when using D* Lite. For p-drones, the initialisation time increased by 60.2% (on average across all drone system sizes) from environment size of (100 × 100 × 100) to environment size of (200 × 200 × 200) whereas d-drones saw an average increase of 693.0% for the same increase in environment size. Additionally, for p-drones the initialisation time increased by 2.0% (on average across all environment sizes) from a system of 4 drones to a system of 20 drones whereas d-drones saw an average increase of 417.8% for the same increase in number of drones.
3.1 Computational and Memory Performance
One aspect of pathfinding algorithm performance that is often discussed in the literature is computational performance. Typically, pathfinding algorithms are applied to graphs without any limitations to how data about the graphs can be collected; this is analogous to allowing the drones to move through the environment without any limitation on movement speed. This freedom allows the algorithms to run to completion without interruption—making it simple to record the total time taken to compute the path. Numerous studies have used this value as an indicator of an algorithm’s computational efficiency [21–23]. However, there are limitations to this approach, the value (typically in seconds) is specific to the graph and the hardware the algorithm was applied to. This makes it difficult to compare results between research groups as identical graphs (environments) and hardware are required for research groups to make meaningful comparisons with the work of other researchers. Another approach to determine computational efficiency is to assess the number of graph vertices that are accessed (also called expanded) [18, 22]. This metric does provide consistent results across different hardware but fails to consider how long it takes to select which vertex to next explore—this means that a lower number of accessed vertices does not guarantee that an algorithm will execute faster. Additionally, this metric only applies to graph-based pathfinding and, thus, cannot be used to assess the efficiency of the PSOP algorithm.
To assess the computational efficiency of the two algorithms, the total Frametime for each frame was recorded. Frametime is the interval between the previous frame and the current frame [15]. This is not an indicator of the time spent executing the pathfinding algorithm, but instead, the time spent for the whole application to update. As the same application was used for both algorithms the time required to update the application should be consistent, thus, this can be considered a systematic error. As the error is consistent and as a large volume of data was collected (one data point per frame) the data gathered is sufficient for meaningful conclusions to be made.
Across all nine scenarios, when the PSOP algorithm was used the frametime was marginally lower on average than when the D* Lite algorithm was used (Figure 3). This improvement is very small and infers that the PSOP and D* Lite algorithms computationally efficiency is comparable. However, across all nine scenarios, when the D* Lite algorithm was used there was significantly higher variance in the recorded frametime. This indicates that for most frames the D* Lite implementation was of similar computational expense to the PSOP implementation but there were some frames where the computational cost of D* Lite was far higher. This was likely caused by the need for the D* Lite implementation to update only when the drones entered a new grid cell, and thus, for most frames the update cost was minimal as the drones remained in the same cell as the previous timestep. A comparison of the median frametime adds credence to this interpretation as Figure 4 shows that, in most scenarios, median frametime was slightly lower (around 0.02%) when using D* Lite. To quantify this further, a Wilcoxon rank sum test [24] was performed, to do a left-tailed hypothesis test, where the alternative hypothesis states that the median of the PSOP data is less than the median of D* Lite, for each of the nine scenarios. The Wilcoxon test rejected the null hypothesis with p-values of
Another aspect of pathfinding algorithm performance that is often scrutinised is memory performance—the amount of memory that must be allocated for the algorithm to run (see Figure 5). As with the frametime, this value was recorded each frame and could be influenced by other factors and does not represent only the memory allocated for the pathfinding algorithm. This can again be considered a systematic error thus meaningful conclusions about memory allocation requirements can still be made.
The disparity in required memory allocation between when the PSOP algorithm was used and when D* Lite was used was far greater than the disparity in observed frametimes. The required allocation when using D* Lite was consistently two (or even three) orders of magnitude higher than PSOP with a similarly large disparity between the variance in memory allocation. Performing a Wilcoxon rank sum test, comparing the PSOP and D* Lite data for each of the scenarios, rejected the null hypothesis that the data samples are from continuous distributions with equal medians, with p-values of
This project hypothesised that the computational and memory performance of the PSOP algorithm would be unaffected by changes to the environment size and would thus increasingly outperform D* Lite as the environment size grew. This was partially correct as the PSOP algorithm did outperform D* Lite by increasing margins as the environment size increased and particularly in the amount of required memory allocation. This result was expected because as the environment size increases the number of nodes that the D* Lite implementation must represent increases as the cube of the length of the environment’s side whereas the PSOP is only ever required to store four individual values—regardless of the environment size. Further research is required to determine why the memory allocation when using PSOP increase as the environment size increased.
This paper’s findings are in line with the findings of other research groups using SI-based pathfinding algorithms. For example, Bee Algorithm pathfinding—a SI-based pathfinding algorithm—was found to be, both, more computationally and memory efficient then the A* algorithm and that the efficiency disparity grew larger as the environment size increased [25].
3.2 Pathfinding Performance
In the literature, there are inconsistencies in how the quality of pathfinding algorithms are evaluated. This makes the comparison of results between studies challenging. This paper uses three metrics to assess the performance of each algorithm: 1) the time taken to complete the objective (find the target); 2) the number of collisions between drones and obstacles; and, 3) the number of collisions between drones and other drones. The time taken 1) indicates the quality of the path created by an algorithm where a higher quality path enables the drones to find the target more rapidly. The drone-to-environment collision count 2) indicates how accurate the created path is where an accurate path efficiently evades obstacles. Finally, the drone-to-drone collision count 3) indicates how well each algorithm integrates with the DFC model’s other modules—as the objective of the other modules is to minimise collisions.
This approach is similar to the approach used by [26] who used algorithm run time and the number of conflicts (between the path and obstacles) as the metrics to assess algorithm quality. Other research teams have used the length of the path created by a given algorithm as the metric determining the quality [27]. This approach, however, was considered broadly unsuitable for this paper as the dynamic, non-deterministic nature of the test environment would mean variations in the length of the optimal path. This would make it challenging to determine whether a longer path was the result of a poorly performing algorithm or simply the optimal path through an environment with particularly challenging changes. Thus, a vast number of iterations would be required for consistent trends in path length to be identified.
For a system of only 4 drones, p-drones required significantly more time to find the target than d-drones (Figure 6) whilst causing a similar number of collisions with the environment (Figure 7). However, for systems of either 10 or 20 drones, in all cases, p-drones required less time to find the target (Figure 6). Due to the significant overlap of the error bars between PSOP and D* Lite, a Wilcoxon rank sum test was performed to assess the extent the performance of the two algorithms differs. Table 7 shows the p-values from the statistical test demonstrating that only scenarios 4, 6 and 9 have p < 0.05 and that the performance benefit of PSOP relative D* Lite is statistically significant; whereas, scenarios 5, 7 and 8 have p ≲ 0.1 and the performance benefits of PSOP are alluded to, but not statistically significant. This shows that the quality and accuracy of the PSOP algorithm’s paths improve as the algorithm accesses more information about candidate solutions. This is consistent with the findings of [28] who found that when using PSO-based pathfinding, in a game environment, an increase in the number of particles (agents) led to a decrease in the time taken to find a target.

TABLE 7. Table of p-values for Wilcoxon rank sum test results to compare the Search Time between the PSOP and D* Lite algorithms. The null hypothesis is that both data sets are samples from continuous distributions with equal medians.
For systems of either 10 or 20 drones, in all cases, p-drones recorded fewer collisions with the environment than drones using D* Lite (Figures 7 and 8). However, we can not say definitively that this trend is statistically significant since a Wilcoxon rank sum test only determined p < 0.05 for scenario 6, and so further experiments are required to investigate this further. Across almost all scenarios, p-drones recorded fewer drone-to-drone collisions than d-drones. This is confirmed by a Wilcoxon rank sum test, which shows that p < 0.008 for scenario 2 and 5–9. This is likely a result of PSOP providing more influence of the cognitive factor and the random weights, r1 and r2, decrease the chance that drones will have similar headings, whereas, the D* Lite algorithm often has nearby drones heading towards the same position, leading to a follow-the-leader style formation. This formation reduces the information available to the flocking module as only having fellow drones in front and behind reduces the number of drones within one’s neighbourhood. Thus, for systems of at least 10 drones, the PSOP algorithm can be considered a superior algorithm than D* Lite for use in a UAV control model that utilises Reynolds flocking.
For both pathfinding approaches, when the environment size increased the time taken to find the target also increased. Given that the maximum speed of the drones was constrained, it was expected that it would take longer for the drones to traverse a larger environment. Additionally, for both approaches, the number of collisions (both drone-to-environment and drone-to-drone) increased as the environment size increased. This is likely a result of objectives in larger environments taking longer to complete and requiring the circumvention of more obstacles—leading to increased opportunity for collisions to occur.
3.3 Ease of Implementation and Usability
An algorithm’s ease of implementation describes how simple an algorithm is to implement and maintain. Ease of implementation is a key factor, alongside efficiency, in determining an algorithm’s overall efficacy. Algorithms that are more straightforward to implement require less development time and are easier to modify, analyse, and debug. Whilst computational and memory efficiency are central considerations when selecting an algorithm to solve a given problem, algorithms with poor ease of implementation are difficult and time consuming to implement and, thus, may not be worth the performance benefits they bring. This is an especially important consideration in the field of games development as overall development time is typically a central economic consideration. The Maintainability Index (MI) [29] is a commonly used metric for describing the ease of implementation for a given section of code. This project used the MI variant that is available within Visual Studio 2019 [30] to assess the ease of implementation for the PSOP algorithm and for the D* Lite implementation. The MI variant used produces a value between 0 and 100 where a higher value indicates code that is easier to understand and maintain. The singular PSOP implementation class received a MI of 72 whereas the D* Lite class received only 66 in addition to the MI of 75 received by the second D* Lite implementation class that was required to communicate between the D* Lite class and the DFC model code. As higher MI values have been shown to indicate code with fewer defects [31] we can conclude that implementations of the PSOP algorithm are likely easier to understand, maintain, and contain fewer defects than D* implementations.
The final metric of algorithm performance that will be explored is initialisation time—the time required for the drones to setup ready to move. This is an important aspect of usability as initialisation time would likely be an important consideration for most uses of the DFC model. In real-world crisis response situations, time is often critical, therefore an algorithm that requires a long time to initialise may be considered unsuitable. Additionally, long load times can break a player’s emersion in a computer game as they can feel pulled out of the experience. Thus, game developers may avoid algorithms that would significantly increase the application load time.
This paper found that initialisation time when using D* Lite was consistently two or three orders of magnitude higher than when using PSOP (Figure 9). A Wilcoxon rank sum test shows that improvements in the initialisation time are statistically significant with p-values of
3.4 Limitations
There are two key limitations of this study. Firstly, this studies simulation fails to consider the effects of atmospheric pressure, wind, turbulence, gravity or UAV dynamics on the drones. Considering these factors has been viewed as an important part of the realism of UAV flight simulations [32] and therefore the findings of this project may be less applicable to real-world scenarios. Secondly, this study applied restrictions on the D* Lite implementation (see Section 2.6.2) for the algorithm to be applied to the real-time simulation. When finding the shortest path, the algorithm was restricted to searching only 700 nodes. This was necessitated by the available computing resources failing to facilitate a full search in the time required for the algorithm to be applied in real-time—especially in large environments for systems of many drones. During development, a restriction of around 700 appeared to maintain the algorithm’s performance whilst allowing this algorithm to be used in real-time. However, this means that the implementation is not the canonical D* Lite algorithm, and thus, some variations in performance may have occurred.
The collision avoidance algorithm used in this work is not optimal; however, the focus of the paper was not to characterise collision avoidance. As collision avoidance (between agents) is a key benefit of flocking behaviour this paper has demonstrated that some pathfinding approaches can synergise with this collision avoidance better than others. We have shown that PSOP naturally created flock formations that were better suited to flocking-based cooperative motion than the formation seen when using D*Lite. Having a high-powered collision avoidance system may have made it more challenging to draw conclusions about the suitability of the pathfinding algorithms for use with a flocking-based system. A well designed collision avoidance algorithm may have mitigated most (or all) collisions making it difficult to determine which pathfinding algorithm reduced the likelihood of collisions the most.
4 Conclusion
This paper has explored the use of SI techniques to facilitate intelligent, collective, and directed motion within flocks of UAVs and attempted to answer the question: How can the PSO algorithm be utilised to facilitate dynamic pathfinding as part of a Swarm Intelligence based UAV control model? Reynolds flocking was used with an obstacle avoidance AI implementation to create a modular model (DFC model) that enables collective motion where collisions are minimised. Additionally, a dynamic pathfinding algorithm, based upon the PSO algorithm, was proposed, implemented, and integrated into the DFC model to enable the model to facilitate pathfinding in a dynamic environment. Using the Unity game engine, a testing environment and data collection apparatus were developed. The DFC model using the PSOP algorithm was tested in this environment and compared to the performance of the DFC model when using a D* Lite implementation.
This study found that, using a heuristic that evaluates the quality of a position as a point along a path, the PSO algorithm could be successfully adapted to facilitate pathfinding in a dynamic environment for multi-agent systems. This study showed that, using this approach, the PSOP algorithm was able to produce higher quality and more accurate pathfinding than the D* Lite algorithm when applied to a SI-based multi-agent UAV control model operating in a dynamic environment. For example, in a large environment (200 × 200 × 200) with a system of 20 drones, when using PSOP an average of 26.6 s (with an average of 21.8 total collisions) was required to find the target, compared to 42.3 s (with an average of 185.2 total collisions) when using D* Lite. When using the PSOP algorithm a system of drones was shown to require similar computation time and far less allocated memory. For the same environment (200 × 200 × 200), 20 drones required on average 36 MB of allocated memory when using PSOP compared to 14,000 MB for D* Lite. Additionally, the PSOP algorithm was shown to require less time to initialise, and it was found that the PSOP algorithm was simpler to implement than D* Lite. This study concludes that using the PSO algorithm, as the basis of a pathfinding algorithm, is a viable approach to multi-agent navigation in dynamic environments. The PSOP algorithm shows great promise as a method of facilitating pathfinding for real-world UAVs and as a method of controlling NPCs within games applications.
The work presented here has implications both within the field of autonomous vehicle control and within the field of games technology. This study furthers the research into autonomous vehicle control presenting the application of SI algorithms to autonomous UAV control. This study has shown that PSO-based pathfinding can be a more effective approach than a typical graph-based algorithm for systems of multiple drones. As UAV technology continues to get cheaper, future crisis response teams may increasingly have access to multiple UAVs capable of autonomous navigation. As this study’s findings suggest, in this scenario cooperative pathfinding using a PSO-based algorithm may prove superior to traditional pathfinding algorithms—allowing the drones to navigate the environment faster and more efficiently, locating survivors faster, and ultimately saving lives.
Often in games applications there is a need for low-cost systems to control the movement and navigation of NPCs within game environments. This research describes a cooperative pathfinding approach free from the memory and scalability limitations of graph-based pathfinding and showed that this approach significantly outperformed D* Lite. This gives game developers a new approach to implementing intelligent group motion to their applications. The authors believe the DFC with the PSOP algorithm would be the ideal approach to controlling a group of nature-inspired NPCs in a three-dimensional environment, such as a group of flying enemies attacking the player or fireflies guiding the player through a complex area.
The research presented in this project may be expanded upon with future research focused on either SI-algorithms for real-world UAV control or for applications of SI-based pathfinding in games applications. The simulation used in this study does not consider environmental factors such as atmospheric pressure, wind, turbulence, and gravity. The simulation also does not consider UAV dynamics or hardware, thus, further research may look to apply the DFC model, with the PSOP algorithm, to a simulation that uses a modern environment model to consider these factors. The existing simulation could be improved through the application of AirSim [33]—a hi-fidelity physics simulation designed specifically for autonomous vehicle AI. Using the AirSim Unity package, the simulation could be extended to consider a range of environmental phenomena, real-world UAV dynamics, and technical engineering considerations, such as the different types of sensors available with real-world UAVs. Navigation systems that are proficient in AirSim simulations can be applied in the real-world without the need for adaptation [34]. Following further development to meet the challenges of an AirSim hi-fidelity simulation, the DFC model with the PSOP algorithm could be applied to real-world UAVs in a controlled environment.
In the domain of games development, algorithm performance is critical as games applications typically have strict framerate requirements. Further research into the PSOP algorithm in this domain may aim to optimise the performance of the algorithm. Parallelisation has been shown to improve the performance of the PSO algorithm [35], thus, further research may look to apply parallelisation techniques to the PSOP algorithm. The aim of this research would be to develop a highly performant pathfinding algorithm for use in games applications and may include adapting the work of [27]. Additionally, it has previously been noted that the movement of NPCs controlled using a PSO-based pathfinding algorithm navigate their environment with realistic motion that resembles intelligent behaviour [28]. Further research may wish to explore pathfinding with PSOP to find optimal parameter configurations and adaptions that facilitate environment navigation that appears highly lifelike and intelligent for a system of game NPCs.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.6084/m9.figshare.15015528.v1.
Author Contributions
CS and LP contributed to the project conceptualization, the development of the methodology, the visualization of the data and project administration. LP conducted the primary research and investigation process, the formal analysis of the data and wrote the first draft of the manuscript under the supervision of CS. Both authors contributed to manuscript revisions, read, and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to the referees for constructive comments and suggestions that have improved this paper. The authors are grateful for support from the Complex Multiscale Dynamics Research Group within the Division of Games Technology and Mathematics at Abertay University.
References
1. Scanlan, J, Flynn, D, Lane, D, Richardson, R, Richardson, T, and Sóbester, A. Extreme Environments Robotics: Robotics for Emergency Response, Disaster Relief and Resilience. UK-RAS White Papers. UK-RAS Network (2017).
2.ICAO. International Civil Aviation Organization Unmanned Aircraft Systems (UAS). [Dataset] (2011).
3. Hu, J, and Lanzon, A. An Innovative Tri-rotor Drone and Associated Distributed Aerial Drone Swarm Control. Robot Auton Syst (2018) 103:162–74. doi:10.1016/j.robot.2018.02.019
4. Innocente, M, and Grasso, P. Swarms of Autonomous Drones Self-Organised to Fight the Spread of Wildfires. In: Proceedings of the RSFF’18 Workshop; 2018 Jul 19–20; L’Aquila, Italy (2018).
5. Karaboga, D, and Akay, B. A Survey: Algorithms Simulating Bee Swarm Intelligence. Artif Intell Rev (2009) 31:61–85. doi:10.1007/s10462-009-9127-4
6. Reynolds, CW. Flocks, Herds and Schools: A Distributed Behavioral Model. SIGGRAPH Comput Graph (1987) 21:25–34. doi:10.1145/37402.37406
7. Hauert, S, Leven, S, Varga, M, Ruini, F, Cangelosi, A, Zufferey, J-C, and Floreano, D. Reynolds Flocking in Reality with Fixed-wing Robots: Communication Range vs. Maximum Turning Rate. In: 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems; 2011 Sept 25–30; San Francisco, CA (2011). p. 5015–20. doi:10.1109/IROS.2011.6095129
8. Watson, NR, John, NW, and Crowther, WJ. Simulation of Unmanned Air Vehicle Flocking. Proc Theor Pract Comput Graphics (2003) 2003:130–7. doi:10.1109/TPCG.2003.1206940
9. Silver, D. Cooperative Pathfinding. In: Proceedings of the First AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment-AIIDE’05; 2005 Jun 1–3; Marina del Rey, CA. AAAI Press (2005). p. 11722.
10. Kennedy, J, and Eberhart, R. Particle Swarm Optimization. In: Proceedings of ICNN’95 - International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, Australia, 4 (1995). p. 1942–8. doi:10.1109/ICNN.1995.488968
11. Cui, X, and Shi, H. A*-Based Pathfinding in Modern Computer Games. Int. J. Netw. Secur. (2011). 11(1):125–130.
13. Shi, Y, and Eberhart, R. A Modified Particle Swarm Optimizer. In: 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360); 1998 May 4–9; Anchorage, AK; (1998). p. 69–73. doi:10.1109/ICEC.1998.699146
14. Yazdani, D, Bb, A, Sepas-Moghaddam, A, and Meybodi, M. A Novel Multi-Swarm Algorithm for Optimization in Dynamic Environments Based on Particle Swarm Optimization. Appl Soft Comput (2013) 13:2144158. doi:10.1016/j.asoc.2012.12.020
15.Unity. Unity User Manual 2020.3. Unity Technologies (2020). Available at: http://docs.unity3d.com/Manual/index.thml
17. Basu, P, Redi, J, and Shurbanov, V. Coordinated Flocking of Uavs for Improved Connectivity of mobile Ground Nodes. In: IEEE MILCOM 2004 Military Communications Conference; 2004 Oct 31–Nov 3; Monterey, CA, 3 (2004). p. 1628–34. doi:10.1109/MILCOM.2004.1495182
18. Koenig, S, and Likhachev, M. Incremental a*. In: T Dietterich, S Becker, and Z Ghahramani, editors. Advances in Neural Information Processing Systems, Vol. 14. Cambridge, MA: MIT Press (2002).
19. De Filippis, L, Guglieri, G, and Quagliotti, F. Path Planning Strategies for Uavs in 3d Environments. J Intell Robot Syst (2012) 65:247–64. doi:10.1007/s10846-011-9568-2
20. Wu, J, Wang, H, Li, N, Yao, P, Huang, Y, and Yang, H. Path Planning for Solar-Powered Uav in Urban Environment. Neurocomputing (2018) 275:2055–65. doi:10.1016/j.neucom.2017.10.037
21. Sazaki, Y, Satria, H, and Syahroyni, M. Comparison of a* and Dynamic Pathfinding Algorithm with Dynamic Pathfinding Algorithm for Npc on Car Racing Game. In: 2017 11th International Conference on Telecommunication Systems Services and Applications (TSSA); 2017 Oct 26–27; Lombok, Indonesia (2017). p. 1–6.
22. Krishnaswamy, N. Comparison of Efficiency in Pathfinding Algorithms in Game Development. [Ph.D. Thesis] (2009).
23. Zarembo, I, and Kodors, S. Pathfinding Algorithm Efficiency Analysis in 2d Grid. Etr (2015) 2:46. doi:10.17770/etr2013vol2.868
24. Barlow, RJ. Statistics: A Guide to the Use of Statistical Methods in the Physical Sciences (Manchester Physics Series). reprint edn. Chichester, England: WileyBlackwell (1989).
25. Sabri, AN, Radzi, NHM, and Samah, AA. A Study on Bee Algorithm and a? Algorithm for Pathfinding in Games. In: 2018 IEEE Symposium on Computer Applications Industrial Electronics (ISCAIE); 2018 April 28–29; Penang Island, Malaysia (2018). p. 224–9. doi:10.1109/ISCAIE.2018.8405474
26. Burwell, K. Multi-agent Pathfinding for Unmanned Aerial Vehicles. Universitat Politècnica de Catalunya. Facultat d'Informàtica de Barcelona (2019).
27. Dang, W, Xu, K, Yin, Q, and Zhang, Q. A Path Planning Algorithm Based on Parallel Particle Swarm Optimization. In: D-S Huang, V Bevilacqua, and P Premaratne, editors. Intelligent Computing Theory. Cham: Springer International Publishing (2014). p. 82–90. doi:10.1007/978-3-319-09333-8_10
28. Díaz, G, and Iglesias, A. Swarm Intelligence Scheme for Pathfinding and Action Planning of Non-player Characters on a Last-Generation Video Game. Adv Intell Syst Comput (2017) 514:343–53. doi:10.1007/978-981-10-3728-3_34
29. Oman, P, and Hagemeister, J. Metrics for Assessing a Software System's Maintainability. In: Proceedings Conference on Software Maintenance 1992; 1992 Nov 9-12; Orlanda, FL (1992). p. 337–44. doi:10.1109/ICSM.1992.242525
31. Counsell, S, Liu, X, Eldh, S, Tonelli, R, Marchesi, M, Concas, G, and Murgia, A. Re-visiting the 'Maintainability Index' Metric from an Object-Oriented Perspective. In: 2015 41st Euromicro Conference on Software Engineering and Advanced Applications; 2015 Aug 26–28; Madeira, Portugal (2015). p. 84–7. doi:10.1109/SEAA.2015.41
32. Mancini, A, Cesetti, A, Iualè, A, Frontoni, E, Zingaretti, P, and Longhi, S. A Framework for Simulation and Testing of UAVs in Cooperative Scenarios. J Intell Robot Syst (2008) 54:307–29. doi:10.1007/s10846-008-9268-8
34. Shah, S, Dey, D, Lovett, C, and Kapoor, A. Airsim: High-Fidelity Visual and Physical Simulation for Autonomous Vehicles. In: FSR-2017; 2017 Sep 12–15; Zurich, Switzerland (2017). doi:10.1007/978-3-319-67361-5_40
Keywords: dynamic pathfinding, swarm intelligence, particle swarm optimisation, flocking, multi-agent systems and autonomous agents
Citation: Pyke LM and Stark CR (2021) Dynamic Pathfinding for a Swarm Intelligence Based UAV Control Model Using Particle Swarm Optimisation. Front. Appl. Math. Stat. 7:744955. doi: 10.3389/fams.2021.744955
Received: 29 July 2021; Accepted: 21 October 2021;
Published: 22 November 2021.
Edited by:
Lixin Shen, Syracuse University, United StatesReviewed by:
Si Li, Guangdong University of Technology, ChinaDaniel H. Stolfi, University of Luxembourg, Luxembourg
Copyright © 2021 Pyke and Stark. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Craig R. Stark, Yy5zdGFya0BhYmVydGF5LmFjLnVr
 Lewis M. Pyke
Lewis M. Pyke Craig R. Stark
Craig R. Stark