Longitudinal Modulation of Marangoni Wave Patterns in Thin Film Heated From Below: Instabilities and Control

Non-linear Marangoni waves, which are generated by the long-wave oscillatory instability of the conductive state in a thin liquid film heated from below in the case of a deformable free surface and a substrate of very low conductivity, are considered. Previously, the investigation of traveling Marangoni waves was restricted to the analysis of the bifurcation and stability with respect to disturbances with strongly different wave vectors. In the present article, for the first time, the modulational instability of traveling waves is investigated. We derive the amplitude equation for the modulated traveling wave, which describes non-linear interaction of the main convective pattern with the perturbations with slightly different wavenumbers. The amplitude equation differs from the conventional complex Ginzburg–Landau equation as it contains an additional term of the local liquid level rise. Linear stability analysis reveals two modulational instability modes: the amplitude modulational and the phase modulational (Benjamin–Feir) ones. It is shown that traveling rolls are stable against the longitudinal modulation for the uncontrolled convection. We also investigate the influence of the non-linear feedback control, which was applied previously to eliminate subcritical excitation of traveling rolls. Computations reveal both the modulational modes under the non-linear feedback control. The obtained results show that the modulational instabilities significantly influence the region of parameters where the non-linear feedback control is efficient for stabilization of waves.

Introduction

Marangoni instability arises at the interface due to the dependence of the surface tension on temperature (the Marangoni effect). This instability results in spatially periodic convective motion that can be either steady or oscillatory. In the latter case, the Marangoni wave patterns emerge, of which the most widespread kind is the traveling rolls.

The pattern selection analysis is based on the investigation of the non-linear interaction of perturbations with a specific wavelength (critical perturbations) that forms the stable spatially periodic patterns. However, above the instability threshold, there is a continuum of unstable perturbations with wavelengths slightly different from the critical one. Non-linear interaction with those perturbations can distort periodic patterns, whereas the modulated patterns may undergo the modulational (sideband) instabilities.

Modulational instabilities of convective patterns are crucial for the pattern selection and the development of the spatiotemporal chaos. The investigations of those instabilities are presented in many article (see [1]) as a review. However, only few of them are devoted to the modulations of non-stationary patterns (see [2–5] for review).

Here, we explore the modulational instability of traveling rolls that are formed due to the novel mode of the oscillatory Marangoni instability.⁶ This instability arises in a thin liquid film rested at the heated substrate of small heat conductivity in comparison with that of the liquid. Non-stationary patterns can be observed in this system, when the heat transfer from the interface is small and the surface tension of the liquid is large.

The article is organized as follows. In Thin Film Dynamics Under Feedback Control, the reader is introduced to the results of the previous research of the thin film dynamics under feedback control. The system of partial differential equations is presented that governs large-scale evolution of film thickness and the liquid temperature. The multiple scale expansion is applied to this system in Longitudinal Modulation. Here, the partial differential equation for the envelope function is derived. The stability analysis of traveling rolls is provided within the envelope equation. The results are summarized in Discussions.

Thin Film Dynamics Under Feedback Control

Long-wave Marangoni instability in a thin liquid film heated from below is governed by the following system of partial differential equations (see [6, 7], a derivation can be found in Supplementary Appendix SA):

$\frac{\partial h}{\partial t}=\nabla \cdot \left(\frac{h^3}{3}\nabla P+\mathrm{Ma}\frac{h^2}{2}\nabla f\right)\equiv \nabla \cdot \mathbf{j},(1)$

$h\frac{\partial \Theta }{\partial t}=\nabla \cdot h\nabla \Theta -\frac{1}{2}{(\nabla h)}^2-[\beta -\varkappa \left(f\right)]f+\mathbf{j}\cdot \nabla f+\nabla \cdot \left(\frac{h^4}{8}\nabla P+\mathrm{Ma}\frac{h^3}{6}\nabla f\right).(2)$

This system describes the joint large-scale evolution of the film thickness $h(x,y,t)$ and the liquid temperature $\Theta (x,y,t)$ (in fact, it is the temperature deviation from the conductive value $T=\Theta -z+{\mathrm{Bi}}^{-1}$).

The function $\varkappa \left(f\right)={\varkappa }_l+{\varkappa }_{q}f$ describes non-linear feedback control based on the measurement of the temperature perturbation on the free surface and imposing a corresponding local change of heat flux on the solid substrate [7, 8]. Applying a feedback control, one can govern the instabilities in this system. The linear control law affects the linear stability; thus, one can shift the instability threshold by varying ${\varkappa }_l$ [8]. The non-linear control term affects non-linear dynamics; therefore, we concentrate on the influence of ${\varkappa }_q$ in this study.

Here, $P=\mathrm{Ga}h-C{\nabla }^{2}h$, $\nabla =(\partial /\partial x,\partial /\partial y,0)$, $f=\Theta -h$.

Dimensionless parameters are as follows: $\mathrm{Ma}={\sigma }_{T}Q{H}^2\text{/}\rho \nu \chi$ is the Marangoni number, and $\mathrm{Ga}=g{H}^3\text{/}\nu \chi$ is the Galileo number. The capillary number С and the Biot number $\beta$ are rescaled as $\mathrm{Ca}={\epsilon }^{-2}C$ and $\mathrm{Bi}={\epsilon }^2\beta$, where $\mathrm{Ca}={\sigma }_{0}H\text{/}\rho \nu \chi$ and $\mathrm{Bi}=qH\text{/}m$. The small parameter $\epsilon$ is the ratio of film thickness to a typical horizontal length scale, or dimensionless wavenumber of perturbations. Here, $H$ is the mean liquid layer thickness, $Q$ is the temperature gradient across the layer, $g$ is the gravitational acceleration, and $q$ is the heat transfer coefficient; $\rho$, $m$, $\chi$, and $\nu$ are the density, thermal conductivity, thermal diffusivity, and kinematic viscosity of the liquid, respectively. ${\sigma }_0$ is the surface tension at the reference temperature, and ${\sigma }_T=d\sigma \text{/}dT$ is the temperature coefficient of surface tension. Let us recall the key assumptions that were used in the derivation of Eqs 1, 2. [6]. First, a thin film is assumed to be placed on the solid substrate of a very low thermal conductivity in comparison with the one of the liquids. In this case, a long-wave Marangoni instability emerges with a critical wavenumber determined by a small Biot number, that is, weak heat flux from the free surface. For a water layer, a Plexiglas wall is an appropriate “insulated for perturbations” substrate [9, 10]; meanwhile, the air above the water layer provides a weak heat transfer from the free surface.

Note that instability under consideration was previously studied in the full two-layer case. In the study in ref [11], the authors replaced the empirical law for the heat transfer from the free surface by the solution of adjoint problem in the ambient gas layer. In that case, the expression for the effective scaled Biot number is ${\mathrm{Bi}}_{eff}=\left(m_{gas}H\right)\text{/}\left(m{H}_{gas}\right)$, where $m_{gas}$ and $H_{gas}$ are thermal conductivity and thickness of a gas layer, respectively.

Another key assumption is that a moderately large capillary number Ca and a finite Galileo number Ga allow deformational Marangoni instability due to the free surface deflections. For a water layer, scalings $\mathrm{Ca}={\epsilon }^{-2}C$ and $\mathrm{Ga}=O\left(1\right)$ are valid for ultrathin films (thinner than 0.1 mm).

Linear Stability Analysis

Eqs 1, 2 have the base state solution $h_0={\Theta }_0=1$, which corresponds to the flat surface of motionless liquid with the linear temperature distribution across the layer. For uncontrolled convection, the stability analysis of small perturbations proportional to $\exp (i{k}_{x}x+i{k}_{y}y+\lambda t)$ provides the quadratic equation for the growth rate $\lambda$ [6].

${\lambda }^2+\lambda \left[\beta +k^2\left(1+\frac{G-\mathrm{Ma}}{3}\right)\right]+\frac{G{k}^2}{3}(\beta +k^2)-\frac{\mathrm{Ma}{k}^4(72+G)}{144}=0,(3)$

where $k^2=k_x^2+k_y^2$ is the wavenumber, $G\equiv \mathrm{Ga}+C{k}^2$. This equation has complex roots, which correspond to the oscillatory instability. At the stability border ($\mathrm{Re}\lambda =0$), the neutral curve, critical wavenumber, and the frequency of the neutral perturbations are as follows:

${\mathrm{Ma}}_0=3+3\frac{\beta }{k^2}+G,k_c^2=\sqrt{\frac{3\beta }{C}},(4)$

${\omega }_0\left(k\right)=\mathrm{Im}\lambda =\frac{k^2}{12}\sqrt{\left(72+G\right)\left({\mathrm{Ma}}^{\ast }-{\mathrm{Ma}}_0\right)},{\mathrm{Ma}}^{\ast }=\frac{48G(\beta +k^2)}{k^2(72+G)}.(5)$

The instability threshold can be changed by the linear feedback control [8] as it varies the heat transfer from the free surface, $\beta \to \beta -{\varkappa }_l$.

Pattern Selection

In the study mentioned in ref [6], stable oscillatory Marangoni patterns were revealed within systems (1)–(2). Depending on the values of parameters Ga, С, β, and ${\varkappa }_q$, either subcritical bifurcation or stable traveling rolls occur. Subcritical bifurcation means that the base state is unstable with respect to the growth of finite-amplitude disturbances, resulting in the film rupture even below the convection threshold. Such a behavior is beyond our scopes. Critical perturbations in the form of a single traveling wave near the instability threshold evolve according to the following differential equation (see Supplementary Appendix SB):

$\frac{\partial A}{\partial t_2}=\gamma A-K_0|A{|}^{2}A,(6)$

where coefficients $\gamma$ and $K_0$, which determine the stability of traveling rolls, depend on problem parameters Ga, С, β, and ${\varkappa }_q$. The linear instability takes place as ${\gamma }_r=\mathrm{Re}\gamma >0$, and stable traveling waves are developed as $K_{0r}=\mathrm{Re}{K}_0>0$.

Longitudinal Modulation

Amplitude Equation

Let us consider the oscillatory mode of instability near the convection threshold Ma_c with the wavenumber k_c and frequency ω_c = ω₀(k_c). The small parameter δ denotes the small deviation of actual Ma from its critical value:

$\mathrm{Ma}={\mathrm{Ma}}_c+{\delta }^2{\mathrm{Ma}}_2.(7)$

It is known that the periodic solution of (1)–(2) emerges due to the Hopf bifurcation. In this case, the solution amplitude is proportional to the square root of the bifurcation parameter in the vicinity of the bifurcation point. Besides, near the threshold, the solution evolves slowly in time compared to the period of oscillations $2\pi \text{/}{\omega }_0$. Consequently, the film thickness, the liquid temperature, and time derivative near the convection threshold can be presented as a series in powers of small δ [12].

$h=1+\delta h_1+{\delta }^2{h}_2+\mathrm{...},\Theta =1+\delta {\theta }_1+{\delta }^2{\theta }_2+\mathrm{...},\frac{\partial }{\partial t}=\frac{\partial }{\partial t_0}+\delta \frac{\partial }{\partial t_1}+{\delta }^2\frac{\partial }{\partial t_2}\mathrm{...}(8)$

As we aimed at investigating spatially periodic solution stability with respect to disturbances with slightly different wavenumbers, the spatial derivative should be expanded in a power series as well:

$\frac{\partial }{\partial x}=\frac{\partial }{\partial x_0}+\delta \frac{\partial }{\partial x_1}+\mathrm{...}(9)$

Next, we substitute expansions (7)–(9) into the non-linear system (1)–(2) and obtain the linear system in each order of a small parameter δ. At the first order, we arrive at the linear stability problem.

$\frac{\partial h_1}{\partial t_0}=\frac{\partial }{\partial x_0}\left(\frac{1}{3}\frac{\partial P_1}{\partial x_0}+\frac{{\mathrm{Ma}}_c}{2}\frac{\partial f_1}{\partial x_0}\right)\equiv \frac{\partial j_{x1}}{\partial x_0},(10)$

$\frac{\partial {\theta }_1}{\partial t_0}=\frac{{\partial }^2{\theta }_1}{\partial x_0^2}+\frac{1}{8}\frac{{\partial }^2{P}_1}{\partial x_0^2}+\frac{{\mathrm{Ma}}_c}{6}\frac{{\partial }^2{f}_1}{\partial x_0^2}-\beta f_1.(11)$

We consider the solution of this system in the form of the modulated traveling wave as follows:

$h_1=A(x_1,t_1,t_2)e^{i(k_c{x}_0+{\omega }_c{t}_0)}+c.c.,f_1=\alpha A(x_1,t_1,t_2)e^{i(k_c{x}_0+{\omega }_c{t}_0)}+c.c.(12)$

Here, $\alpha =-2(\mathrm{Ga}{k}^2+C{k}^4+3i{\omega }_0)\text{/}3{\mathrm{Ma}}_c{k}^2$, and “c.c.” denotes complex conjugate terms.

Dynamics of the envelope function $A(x_1,t_1,t_2)$ can be revealed from the solvability condition of the inhomogeneous system of equations at higher orders of δ.

$\left(i{\omega }_c+\frac{1}{6}\mathrm{M}{\mathrm{a}}_{\mathrm{c}}{k}_c^2+k_c^2+\beta \right)F_1^{\sec }=\frac{1}{2}\mathrm{M}{\mathrm{a}}_{\mathrm{c}}{k}_c^2{F}_2^{\sec },(13)$

where $F_1^{\sec }$ and $F_2^{\sec }$ are secular inhomogeneities in Eqs 1, 2, respectively.

At the second order in small δ, the solvability condition (13) results in a wave equation for the envelope function:

$\frac{\partial A}{\partial t_1}={\omega }_1\frac{\partial A}{\partial x_1},(14)$

${\omega }_1={\left(\frac{\partial {\omega }_0}{\partial k}\right)}_c=\frac{k_c^3}{144{\omega }_0}[C{k}_c^2(26C{k}_c^2+9\mathrm{Ga}-153)-2{\mathrm{Ga}}^2-54\mathrm{Ga}-432](15)$

where the subscript $c$ means $k=k_c$ and $\mathrm{Ma}={\mathrm{Ma}}_c$. Obviously, one can eliminate the first slow time $t_1$ by going over to the frame of reference $F^{\prime }$ that moves along $x_1$ with the group velocity ${\omega }_1$:

$A=A(X_1,t_2,\mathrm{...}),X_1=x_1+{\omega }_1{t}_1.(16)$

Within the moving frame of reference $F^{\prime }$, the solution at the second order of small δ can be presented as follows:

$h_2=a_{22}{A}^2{e}^{2i(k{x}_0+{\omega }_0{t}_0)}+h_{20}(X_1,t_2)+c.c.(17)$

$f_2=b_{21}\frac{\partial A}{\partial X_1}{e}^{i(k{x}_0+{\omega }_0{t}_0)}+b_{22}{A}^2{e}^{2i(k{x}_0+{\omega }_0{t}_0)}+b_{20}|A{|}^2+c.c.(18)$

The coefficients $a_{22}$, $b_{22}$, and $b_{20}$ are known from the bifurcation analysis for a single traveling wave [7]; they can be found in Supplementary Appendix SC. However, new terms with $b_{21}$ and $h_{20}$ appear in the case of a modulated wave. The coefficient $b_{21}$ comes from dependence $\alpha \left(k\right)$ in the first-order solution:

$b_{21}=-i{\left(\frac{\partial \alpha }{\partial k}\right)}_c=\frac{2(2iC{k}_c^4+6{\omega }_0-3{\omega }_1{k}_c)}{3M{a}_c{k}_c^3}$

The term $h_{20}$ emerges due to the interaction of the slowly growing oscillatory modes with wavenumbers $k_c$ with the slowly decaying modes with wavenumbers $k<<1$ corresponding to long-wave modulation of the layer thickness, which leads to a significant change of the expression for $h_2$ in the case where the envelope $A$ depends not only on $t_2$ but also on $X_1$.

The solvability condition of the equations at the third order in $\delta$ yields the one-dimensional amplitude equation, which governs a slow change in time and space of envelope function $A(X_1,t_2)$:

$\frac{\partial A}{\partial t_2}=\gamma A-K_0|A{|}^{2}A+{\lambda }_2\frac{{\partial }^{2}A}{\partial X_1^2}+\tilde{K}{h}_{20}A.(19)$

Here, $\gamma =(\partial \lambda \text{/}\partial \mathrm{Ma}){|}_c$, ${\lambda }_2=-1\text{/}2({\partial }^2\lambda \text{/}\partial k^2){|}_c$, $K_0$ is the Landau coefficient, and $\tilde{K}$ is defined below. For the sake of brevity, these coefficients are not given here; they can be found in the Supplementary Appendix SC.

The coefficient $\tilde{K}$ can be revealed from the investigation of dependence of $\lambda$ on $h_{20}$. Assume that the dimensional thickness of the film is changed, and it is equal to $H{h}_0$, instead of $H$. This leads to the change of non-dimensional parameters $\mathrm{Ga}\to \mathrm{Ga}{h}_0^3$ and $\mathrm{Ma}\to \mathrm{Ma}{h}_0^2$, according to their definitions. Note that the capillary number $C$ and the Biot number $\beta$ change as $C\to C{h}_0^3$ and $\beta \to \beta \text{/}{h}_0$ because of the rescaling of the wavenumber itself. Consequently, the growth rate changes as follows:

$\lambda (C,\beta ,\mathrm{Ga},\mathrm{Ma})\to \lambda (C{h}_0^3,\beta /h_0,\mathrm{Ga}{h}_0^3,\mathrm{Ma}{h}_0^2)$

Taking $h_0=1+{\delta }^2{h}_{20}$, we find

$\frac{d\lambda }{d{h}_{20}}={\delta }^2{\left(\frac{\partial \lambda }{\partial C}3C{h}_0^2-\frac{\partial \lambda }{\partial \beta }\frac{\beta }{h_0^2}+\frac{\partial \lambda }{\partial \mathrm{Ga}}3\mathrm{Ga}{h}_0^2+\frac{\partial \lambda }{\partial \mathrm{Ma}}2\mathrm{Ma}{h}_0\right)|}_c={\delta }^2\tilde{K}.(20)$

To determine $h_{20}(X_1,t_2)$, let us consider the parts of Eq. 1 at the third order in $\delta$ that do not depend on $x_0$, $t_0$ as follows:

$\frac{\partial h_{20}}{\partial t_1}=\frac{\partial }{\partial x_1}\left[ik{\mathrm{Ma}}_c(\alpha -{\alpha }^{\ast })\right|A{|}^2](21)$

For a traveling wave $A=A(X_1,t_1)=A(x_1+{\omega }_1{t}_1)$, Eq. 21 gives

$\frac{\partial h_{20}}{\partial X_1}=\frac{4{\omega }_0}{{\omega }_{1}k}\frac{\partial |A{|}^2}{\partial X_1}$

hence,

$h_{20}(X_1,t_2)=\frac{4{\omega }_0}{{\omega }_{1}k}|A{|}^2(X_1,t_2)+c\left(t_2\right).(22)$

Because of the conservation of the liquid’s volume, the value of $h_{20}$ averaged over a whole region of $X_1$ vanishes, ${\langle h_{20}(X_1,t_2)\rangle }_{X_1}=0$; therefore,

$c\left(t_2\right)=-\frac{4w_0}{{\omega }_{1}k}{\langle |A{|}^2(X_1,t_2)\rangle }_{X_1}$

and

$h_{20}(X_1,t_2)=\frac{4{\omega }_0}{{\omega }_{1}k}\left[\right|A{|}^2(X_1,t_2)-{\langle |A{|}^2(X_1,t_2)\rangle }_{X_1}](23)$

Thus, Eq. 19 reads as

$\frac{\partial A}{\partial t_2}=\gamma A-K_0|A{|}^{2}A+{\lambda }_2\frac{{\partial }^{2}A}{\partial X_1^2}+K_1[|A{|}^2(X_1,t_2)-\langle |A{|}^2(X_1,t_2){\rangle }_{X_1}]A(24)$

where $K_1=4{\omega }_0\tilde{K}\text{/}{\omega }_{1}k$.

As one can see, Eq. 24 is very much like the complex Ginzburg–Landau equation (CGLE), which usually describes modulational instabilities of patterns [13]. However, unlike numerous physical problems leading to the CGLE, the problem under consideration has an additional “soft” (stable but slowly evolving) mode corresponding to the large-scale modulation of the layer thickness. The existence of that mode is the consequence of the conservation of the liquid volume. The modulation of the wave amplitude $A$, according to (23), generates a corresponding modulation of the local layer thickness, which creates an additional term in the evolution equation. For a non-modulated wave, $\left|A\right|=const$; therefore, the additional term disappears.

By rescaling

$A=a\sqrt{\frac{{\gamma }_r}{K_{0r}}}{e}^{i{\gamma }_i{t}_2},\frac{\partial }{\partial t_2}={\gamma }_r\frac{\partial }{\partial t},\frac{\partial }{\partial X_1}=\sqrt{\frac{{\gamma }_r}{{\lambda }_{2r}}}\frac{\partial }{\partial x}(25)$

Eq. 24 is transformed to the standard form as follows:

$\frac{\partial a}{\partial t}=a-(1+iv)|a{|}^{2}a+(1+iu)\frac{{\partial }^{2}a}{\partial x^2}+(c_r+i{c}_i)[|a{|}^2-\langle |a{|}^2{\rangle }_x]a(26)$

Here,

$v=\frac{K_{0i}}{K_{0r}},u=\frac{{\lambda }_{2i}}{{\lambda }_{2r}},c_r=\frac{K_{1r}}{K_{0r}},c_i=\frac{K_{1i}}{K_{0r}}(27)$

The rescaling (25) is justified because ${\gamma }_r>0$ and ${\lambda }_{2r}>0$ (see Supplementary Appendix), and we consider only supercritical excitation of traveling rolls, that is, $K_{0r}>0$.

It can be convenient to present complex amplitude as $a=r\exp \left(i\varphi \right)$ and rewrite (26) as a system of two equations for real amplitude $r$ and phase $\varphi$ as follows:

$\frac{\partial r}{\partial t}=r-r^3+\frac{{\partial }^{2}r}{\partial x^2}-r{\left(\frac{\partial \varphi }{\partial x}\right)}^2-u\left(2\frac{\partial r}{\partial x}\frac{\partial \varphi }{\partial x}+r\frac{{\partial }^2\varphi }{\partial x^2}\right)+c_r(r^2-{\langle r^2\rangle }_x)r(28)$

$r\frac{\partial \varphi }{\partial t}=-v{r}^3+2\frac{\partial r}{\partial x}\frac{\partial \varphi }{\partial x}+r\frac{{\partial }^2\varphi }{\partial x^2}+u\left[\frac{{\partial }^{2}r}{\partial x^2}-r{\left(\frac{\partial \varphi }{\partial x}\right)}^2\right]+c_i(r^2-{\langle r^2\rangle }_x)r(29)$

Stability of Traveling Wave

Here, we investigate the stability of the particular solution of (26) that corresponds to the traveling wave with $k=k_c$:

$r_0=1,{\varphi }_0=-vt(30)$

Linearizing (28) and (29) around (30), we obtain the following eigenvalue problem for small disturbances $(\tilde{r},\tilde{\varphi })$:

$\tilde{\sigma }\tilde{r}=-2\tilde{r}+\frac{{\partial }^2\tilde{r}}{\partial x^2}-u\frac{{\partial }^2\tilde{\varphi }}{\partial x^2}+2c_r(\tilde{r}-{\langle \tilde{r}\rangle }_x)$

$\tilde{\sigma }\tilde{\varphi }=-2v\tilde{r}+u\frac{{\partial }^2\tilde{r}}{\partial x^2}+\frac{{\partial }^2\tilde{\varphi }}{\partial x^2}+2c_i(\tilde{r}-{\langle \tilde{r}\rangle }_x)$

where $\tilde{\sigma }$ is the growth rate.

For the solution in the form

$\tilde{r}=R{e}^{iqx},\tilde{\varphi }=\Phi e^{iqx},q\ne 0$

one obtains the dispersion relation as follows:

${\tilde{\sigma }}^2+2\tilde{\sigma }(1-c_r+q^2)+2q^2[1-c_r+u(v-c_i)]+(1+u^2)q^4=0(31)$

For small $q$, the dispersion relation has two roots, that is, two modes exist:

i) the amplitude mode with $\tilde{\sigma }=2(c_r-1)+O\left(q^2\right)$ and

ii) the phase mode with the asymptotic $\tilde{\sigma }\sim q^2\frac{c_r-1-u(v-c_i)}{c_r-1}$.

In Figure 1, the growth rate $\tilde{\sigma }\left(q\right)$ is presented for four different cases: $c_r-1>0$ and opposite, and $c_r-1-u(v-c_i)>0$ and opposite. As one can see, the traveling wave is unstable with respect to amplitude modulation, if $c_r>1$. If $c_r<1$, a phase modulation (Benjamin–Feir) instability is possible, if $c_r-1-u(v-c_i)>0$. Note that for a one-dimensional CGLE, only phase modulation instability occurs, if $1+uv<0$ [2, 3]. One can clearly see that we obtain this criterion if we drop additional terms in (26) that occurs due to the modulation of the local layer thickness.

FIGURE 1

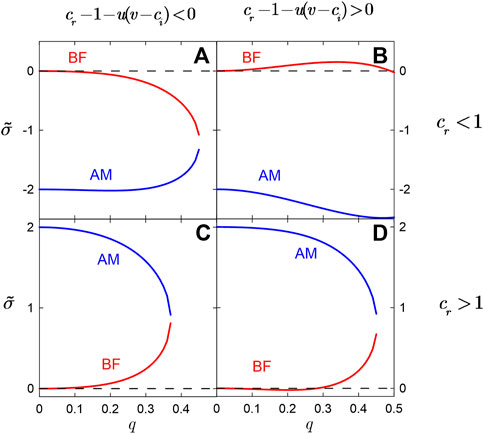
FIGURE 1. Growth rate of modulational instabilities as the function of wavenumber $q$ for different values of $c$ and $v$, $u=2$. (A) $c=iv$, (B) $c=i(v+2)$, (C) $c=2+i(v-1)$, (D) $c=2+iv$. Branches corresponding to the amplitude modulation instability and the phase modulation (Benjamin–Feir) instability are marked as “AM” and “BF,” respectively.

Here, we present the results of calculation of coefficient combinations that correspond to the modulational instabilities (i), (ii) depending on the problem parameters—Galileo number, Biot number, capillary number, and non-linear control gain. Recall that the oscillatory Marangoni instability is critical when ${\mathit{Ma}}^{\ast }>{\mathit{Ma}}_0$; otherwise, stationary instability occurs (see Eqs 4, 5). Therefore, traveling rolls can emerge only within a specific domain of parameters. For fixed $C=1000$, this domain is the closed area on the $\mathrm{Ga}-\beta$ plane bounded by the dashed line in Figure 2. Consequently, in our calculations, we are restricted by the values of the Galileo number Ga and rescaled Biot number $\beta$ lying within this area.

FIGURE 2

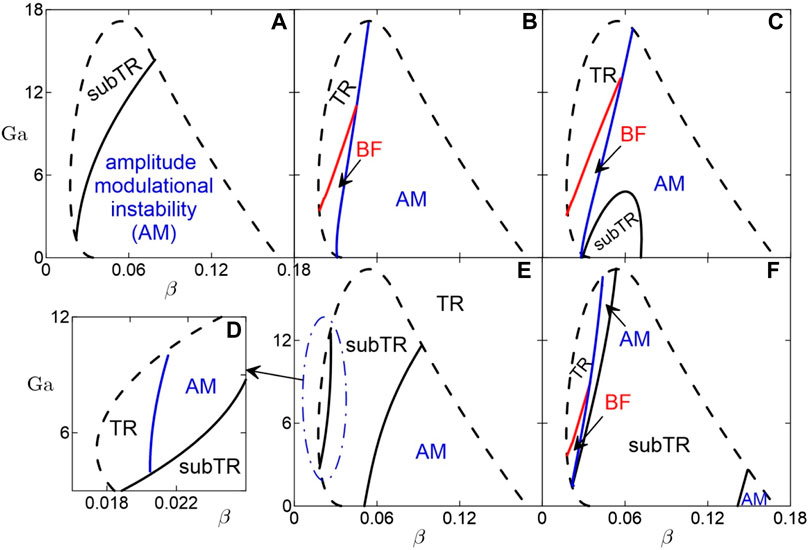
FIGURE 2. Domains of stability for traveling rolls against the longitudinal modulations for (A) uncontrolled convection; (B), (C) negative nonlinear feedback control gain ${\mathbf{\varkappa }}_q=-0.2,-0.3$, (E), (F) positive nonlinear feedback control gain ${\mathbf{\varkappa }}_q=0.1,0.3$. (D) Zoomed-in fragment of panel (E). Dashed lines indicate the area of the oscillatory convection. Within domains marked “subTR” traveling rolls bifurcate subcritically. “TR” marks domains of stability for traveling rolls. Benjamin-Feir instability and the amplitude modulational instability occurs within domains marked “BF” and “AM”, respectively.

It is known that traveling rolls can be unstable due to the subcritical excitation of instability, when disturbances grow without saturation. The boundary between domains of subcritical excitation and stability of traveling rolls is depicted in Figure 2 as a solid black line. Our analysis is valid only outside the domain of subcritical excitation that is marked “subTR” in Figure 2.

In view of these restrictions, we have calculated coefficients $uv,c_r$, and $c_i$ within the domain of stability of traveling rolls, that is, under the dashed line and the solid line in Figure 2A. We find that traveling rolls are unstable against both the amplitude modulation instability and the phase modulation instability.

Influence of the Feedback Control

It was mentioned earlier that the influence of the linear part of feedback control ${\varkappa }_l$ is trivial amplification/suppression of the heat transfer from the film surface as ${\beta }_{eff}=\beta -{\varkappa }_l$. Thus, the linear feedback control changes instability threshold ${\mathrm{Ma}}_0$ and shifts the whole plot in Figure 2A along the $\beta$-axis.

The non-linear part of feedback control ${\varkappa }_q$ changes non-linear dynamics by varying the Landau coefficient $K_0$ in the amplitude, Eq. 24 (see Supplementary Appendix SC). Thus, the non-linear feedback control influences the stability of traveling rolls against both the subcritical excitation and the longitudinal modulation.

Previously, it was shown that one can eliminate subcritical instability by applying non-linear feedback control with negative control gain [7]. For $-0.24<{\varkappa }_q<-0.07$, the domain of supercritical excitation of traveling rolls extends to the entire area, where the oscillatory mode is critical (within dashed lines in Figure 2). However, the non-linear control also affects dynamics of the modulated wave; thus, the stability of the traveling wave can be interrupted. Indeed, one can see from Figure 2B that for ${\varkappa }_q=-0.2$, the area of Benjamin–Feir instability occurs. With the increase in control gain, the domain of phase modulation instability expands; also, the domain of subcritical instability occurs (see Figure 2C).

If ${\varkappa }_q>0$, one cannot eliminate subcritical instability within the entire domain, where the oscillatory mode is critical [7]. It is seen from Figure 2D that for ${\varkappa }_q=0.1$, the subcritical instability on the left side of the plot is stabilized by the feedback control. However, a large domain of subcritical instability occurs at the bigger values of $\beta$. One can see from Figures 2D and E that a positive control gain suppresses the amplitude modulation instability within a small area of parameters. The growth of the positive control gain results in extension of the domain of subcritical instability (see Figure 2F). For ϰ_q = 0.3, the domain of stable traveling rolls extends and the area of the phase modulation instability occurs.

Discussions

We investigated the modulation instability of Marangoni wave patterns that emerge at the interface of a thin liquid film heated from below. Applying the multiple scale expansion to the system of PDEs for the film thickness and liquid temperature, we derive complex PDEs for the envelope function of the longitudinal modulated roll pattern. The equation for the envelope function is very much like the complex Ginzburg–Landau equation, except for the additional non-linear term proportional to the surface deformation. Previously, a similar additional term was obtained in the study given in ref [14], and it was connected to the interaction of two monotonic Marangoni instability modes: the short wave and the long wave. In our case, the additional term arises due to the non-linear interaction between the slowly growing mode with the critical wavelength and the slowly decaying large-scale mode. Note that the term with ${\langle A^2\rangle }_X$ in the amplitude equation for a monotonic instability was first obtained in the study mentioned in the ref [15].

The stability analysis of the traveling wave is provided within the CGLE-like equation for the envelope function. Two modes of instability were revealed: one caused by the amplitude modulation and the other caused by the phase modulation. The latter is similar to the Benjamin–Feir instability first discovered for the Stokes wave [16]. Note that the modulational instability was formerly studied in the framework of the CGLE, and only phase modulation instability was found. Thus, amplitude modulation instability is a completely new effect of the interaction with a stable soft mode. This interaction also modified the criterion for the phase modulation instability.

Calculations show that the uncontrolled roll patterns are unstable against the perturbations with slightly different wavelength. However, in the absence of the control, traveling rolls emerge through the subcritical bifurcation within certain parameter domains. Previously, it was demonstrated that one can eliminate subcritical bifurcation by applying the non-linear feedback control [7]. But besides that, non-linear feedback control affects pattern selection as well. In this article, we reveal that the non-linear feedback control can suppress an amplitude modulation instability or produce a phase modulation instability depending on the parameters. Thus, the non-linear feedback control can destabilize traveling rolls against the longitudinal modulation at the same time as it stabilizes traveling rolls against the subcritical excitation.

Here, we examined only longitudinal modulations of the traveling wave pattern. This is sufficient if the region has a shape of a rectangle, which is long only in one direction. If the thin film is infinite in the $x-y$ plane, a transverse modulation of the traveling wave is possible. Investigation of roll pattern stability against the transverse wave could be a good subject for the future studies.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

AS acknowledges financial support from the Russian Science Foundation (Grant No. 20-71-00070). A.N. acknowledges financial support from the Israel Science Foundation (Grant No. 843/18).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.697332/full#supplementary-material

References

1. Hoyle, R. Pattern Formation: An Introduction to Methods. Cambridge: Cambridge University Press (2006). p. 422. doi:10.1017/CBO9780511616051

CrossRef Full Text | Google Scholar

2. Nepomnyashchy, AA. Modulated Wave Motions Arising Due to the Instability of Spatially Periodic Secondary Motions. Proc Perm State Univ (1974) 316:105–113. In Russian.

Google Scholar

3. Yamada, T, and Kuramoto, Y. A Reduced Model Showing Chemical Turbulence. Prog Theor Phys (1976) 56:681–3. doi:10.1143/ptp.56.681

CrossRef Full Text | Google Scholar

4. Janiaud, B, Pumir, A, Bensimon, D, Croquette, V, Richter, H, and Kramer, L. The Eckhaus Instability for Traveling Waves. Physica D: Nonlinear Phenomena (1992) 55:269–86. doi:10.1016/0167-2789(92)90060-z

CrossRef Full Text | Google Scholar

5. Shklyaev, S, and Nepomnyashchy, A. Longwave Instabilities and Patterns in Fluids. New York: Birkhaeuser (2017). p. 456. doi:10.1007/978-1-4939-7590-7

CrossRef Full Text | Google Scholar

6. Shklyaev, S, Alabuzhev, AA, and Khenner, M. Long-wave Marangoni Convection in a Thin Film Heated from below. Phys Rev E (2012) 85:016328. doi:10.1103/PhysRevE.85.016328

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Samoilova, AE, and Nepomnyashchy, A. Nonlinear Feedback Control of Marangoni Wave Patterns in a Thin Film Heated from below. Physica D: Nonlinear Phenomena (2020) 412:132627. doi:10.1016/j.physd.2020.132627

CrossRef Full Text | Google Scholar

8. Samoilova, AE, and Nepomnyashchy, A. Feedback Control of Marangoni Convection in a Thin Film Heated from below. J Fluid Mech (2019) 876:573–90. doi:10.1017/jfm.2019.578

CrossRef Full Text | Google Scholar

9. Le Gal, P, and Croquette, V. Appearance of a Square Pattern in a Rayleigh-Bénard experiment. Phys Fluids (1988) 31:3440–2. doi:10.1063/1.866908

CrossRef Full Text | Google Scholar

10. Le Gal, P, Pocheau, A, and Croquette, V. Square versus Roll Pattern at Convective Threshold. Phys Rev Lett (1985) 54:2501–4. doi:10.1103/PhysRevLett.54.2501

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Samoilova, AE, and Shklyaev, S. Oscillatory Marangoni Convection in a Liquid-Gas System Heated from below. Eur Phys J Spec Top (2015) 224:241–8. doi:10.1140/epjst/e2015-02356-4

CrossRef Full Text | Google Scholar

12. Kevorkian, J, and Cole, JD. Multiplay Scale and Singular Perturbation Methods. New York: Springer (1996). p. 634. doi:10.1007/978-1-4612-3968-0

CrossRef Full Text | Google Scholar

13. Aranson, IS, and Kramer, L. The World of the Complex Ginzburg-Landau Equation. Rev Mod Phys (2002) 74:99–143. doi:10.1103/RevModPhys.74.99

CrossRef Full Text | Google Scholar

14. Golovin, AA, Nepomnyashchy, AA, and Pismen, LM. Interaction between Short-scale Marangoni Convection and Long-scale Deformational Instability. Phys Fluids (1994) 6:34–48. doi:10.1063/1.868090

CrossRef Full Text | Google Scholar

15. Garcia-Ybarra, PL, Castillo, JL, and Velarde, MG. Bénard-Marangoni Convection with a Deformable Interface and Poorly Conducting Boundaries. Phys Fluids (1987) 30:2655–61. doi:10.1063/1.866109

CrossRef Full Text | Google Scholar

16. Benjamin, TB, and Feir, JE. The Disintegration of Wave Trains on Deep Water Part 1. Theory. J Fluid Mech (1967) 27:417–30. doi:10.1017/S002211206700045X

CrossRef Full Text | Google Scholar

17. Tang, J, and Bau, HH. Stabilization of the No-Motion State in the Rayleigh–Bénard Problem. Proc R Soc A (1994) 447:58731. doi:10.1098/rspa.1994.0157

CrossRef Full Text | Google Scholar

18. Or, AC, Kelly, RE, Cortelezzi, L, and Speyer, JL. Control of Long-Wavelength Marangoni-Bénard Convection. J Fluid Mech (1999) 387:321–41. doi:10.1017/s0022112099004607

CrossRef Full Text | Google Scholar