Data Assimilation for Ionospheric Space-Weather Forecasting in the Presence of Model Bias

The dynamics of many models of physical systems depend on the choices of key parameters. This paper describes the results of some observing system simulation experiments using a first-principles model of the Earth’s ionosphere, the Thermosphere Ionosphere Electrodynamics Global Circulation Model (TIEGCM), which is driven by parameters that describe solar activity, geomagnetic conditions, and the state of the thermosphere. Of particular interest is the response of the ionosphere (and predictions of space weather generally) during geomagnetic storms. Errors in the overall specification of driving parameters for the TIEGCM (and similar dynamical models) may be especially large during geomagnetic storms, because they represent significant perturbations away from more typical interactions of the earth-sun system. Such errors can induce systematic biases in model predictions of the ionospheric state and pose difficulties for data assimilation methods, which attempt to infer the model state vector from a collection of sparse and/or noisy measurements. Typical data assimilation schemes assume that the model produces an unbiased estimate of the truth. This paper tests one potential approach to handle the case where there is some systematic bias in the model outputs. Our focus is on the TIEGCM when it is driven with solar and magnetospheric inputs that are systematically misspecified. We report results from observing system experiments in which synthetic electron density vertical profiles are generated at locations representative of the operational FormoSat-3/COSMIC satellite observing platforms during a moderate (G2, Kp = 6) geomagnetic storm event on September 26–27, 2011. The synthetic data are assimilated into the TIEGCM using the Local Ensemble Transform Kalman Filter with a state-augmentation approach to estimate a small set of bias-correction factors. Two representative processes for the time evolution of the bias in the TIEGCM are tested: one in which the bias is constant and another in which the bias has an exponential growth and decay phase in response to strong geomagnetic forcing. We show that even simple approximations of the TIEGCM bias can reduce root-mean-square errors in 1-h forecasts of total electron content (a key ionospheric variable) by 20–45%, compared to no bias correction. These results suggest that our approach is computationally efficient and can be further refined to improve short-term predictions (∼1-h) of ionospheric dynamics during geomagnetic storms.

1 Introduction

The ionosphere is a portion of the Earth’s mesosphere, thermosphere, and exosphere, corresponding to altitudes from approximately 60–1,000 km, in which interactions with solar radiation create a plasma consisting of neutral and ionized gases with free electrons. The plasma tends to be concentrated in layers whose composition and thickness vary diurnally. At night, the so-called E and F layers extend, respectively, from altitudes from about 90 to 150 km and from 150 to 500 km. During the daytime, the D layer appears (from about 60 to 90 km) and the F layer bifurcates into two thinner layers, ${\text{F}}_1$ and ${\text{F}}_2$. The various layers can reflect, refract, and absorb radio waves at particular frequencies, and for this reason, the ionosphere interferes with satellite communications. During solar storms, the Earth may be bombarded with streams of energetic particles that interact with the ionosphere and Earth’s magnetic field to induce electromotive forces that can extend all the way to the ground, disrupting high-voltage electric transmission grids [1]. The term “space weather” refers broadly to all of these dynamics. For a comprehensive overview of these issues, see the book by Kelley [2].

The development of a space-weather forecasting capability, comparable to that of operational tropospheric models, is a long-term research goal [1]. No systematic overview of ionospheric models or the associated open problems is attempted here; interested readers are referred to [3, 4] and references therein. Present-day models include both empirical descriptions (e.g., the International Reference Ionosphere, or IRI) and physics-based dynamical models (e.g., the Thermosphere Ionosphere Electrodynamics Global Circulation Model, or TIEGCM). The IRI has been under development since the late 1960’s to provide, among other things, monthly means of electron density profiles and plasma temperatures during quiet-time conditions [5], i.e., in the absence of geomagnetic storms that arise from shock waves in the solar wind and/or coronal mass ejections. The TIEGEM, developed by the High-Altitude Observatory at the National Center for Atmospheric Research [6], attempts to provide self-consistent solutions for the magnetohydrodynamics of the upper atmosphere. Dynamical models will be important for space-weather forecasting efforts during storm- as well as quiet-time conditions.

Our paper builds upon recent achievements in the understanding of transport and mixing using theoretical analysis, large-scale numerical simulations, and data analysis, and focuses on multi-scale ionospheric dynamics [1, 2, 7]. The ionosphere is a dynamic mixture of ions, electrons and neutral gases surrounding the earth. Understanding and modeling multi-scale ionospheric dynamics is a daunting but important challenge because of its critical role in space sciences and space weather. Significant progress has been made in developing computational models over the past several decades. However, current modeling capabilities need further development, especially with regard to neutral-plasma interactions driven by neutral fluid dynamics and electrodynamics physical processes over the large range of temporal and spatial scales that characterize the ionosphere. Advances are needed in physics-based predictive modeling and data assimilation to make accurate high-resolution forecasts. In particular, novel computational and data assimilation capabilities are required for operational communication, navigation, remote sensing, imaging and space weather applications.

Non-equilibrium processes, transport, and mixing are exceedingly challenging to study. Their dynamics often involve sharp changes of vector and scalar fields and may also include radiation transport and chemical reactions, and diffusion of species and electric charges, among other effects. Non-equilibrium dynamics of transport and mixing are inhomogeneous, anisotropic, non-local, and statistically unsteady. At macroscopic scales, non-equilibrium transport may lead to self-organization and order, thus offering new opportunities for diagnostics and control. Capturing properties of emerging coherent structures, interfaces and mixing, enabling their accurate description can aid better understanding of the Eulerian and Lagrangian dynamics, and developing new methods of control of non-equilibrium transport in nature and technology. Significant success was recently achieved in understanding of transport and mixing on the sides of theoretical analysis, large-scale numerical simulations, and data analysis. This success opens new opportunities for studies of fundamentals of non-equilibrium dynamics across the scales including Rayleigh-Taylor (RT) instabilities and turbulence [8–10], hydrodynamic RT turbulence mixing [11, 12], and plasma dynamics in the ionosphere [13–18].

Turbulent mixing induced by RT instabilities occurs in settings as varied as exploding stars (supernovae), inertial confinement fusion, and macroscopic flows in fluid dynamics such as ionospheric plasmas [19]. Since the discovery of the plasma instability phenomenon that occurs in the nighttime equatorial F-region ionosphere, and which is revealed by rising plumes identified as large-scale depletions or bubbles, considerable efforts have been made in the development of computer models that simulate the generation and evolution of the convective equatorial ionospheric storms or Equatorial Spread F (ESF) Dynamics [2, 3, 6, 11, 12, 14, 20–32]. Analyses and simulations of primary and secondary RT instabilities in the ESF triggered by the response of plasma density to neutral turbulent dynamics and wave breaking in the lower region of ionosphere were investigated for coupled systems (ions, electrons, neutral winds), thus enabling studies of mesoscale/microscale dynamics for a range of altitudes encompassing ionospheric D, E and F layers. At smaller scales, turbulent mixing induced by hydrodynamic instabilities plays an important role and considerable efforts has focused on discovering universal properties of turbulence in various settings. Neutral-plasma interactions and physical processes at ionospheric meso/microscales is currently a grand challenge for data-driven computational studies of ionospheric dynamics [2].

To provide useful forecasts, dynamical models require an accurate and computationally efficient data assimilation capability. Traditional approaches assume that the associated model produces unbiased forecasts. Several approaches have been suggested to handle model bias in data assimilation systems. Dee and da Silva [33, 34] suggested a two-stage approach that estimates separate gain matrices for the forecast state vector and for the bias correction. Biases in observations, such as satellite radiances, can be handled through Kalman filtering (e.g., [35]). Eyre [20] shows that forecast and analysis biases are functions of the relative weights given to bias-corrected and non-bias-corrected observations and the rate at which the forecast model relaxes to its climatology. Canter et al. [36] have explored the possibility of applying stochastic forcing to a forecast model, with an augmented state vector to estimate the model bias, with an application to a global ocean circulation model. Machine-learning approaches also have been tried to observation bias correction [26]. The approach applied in this paper is based on one suggested by Baek et al. [37], which attempts to compensate for the model bias in the handling of the observations, as described below.

Our principal focus is on the TIEGCM. We consider a period corresponding to a moderately strong (G2) geomagnetic storm, which can induce significant perturbations of the ionosphere from quiet-time conditions and affect the operation of satellite communication and power distribution networks. In particular, we are interested in the case where various model driving parameters are misspecified, as may occur during periods of particularly high solar activity [38], resulting in systematic errors in model predictions of electron density and related variables. Our approach extends prior work by Baek et al. [37], who described some approaches to handle model bias in a data assimilation system.

The Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC), and its successor, COSMIC-2 are designed, built, and operated by the United States. National Oceanographic and Atmospheric Administration and other agencies in collaboration with the Taiwan National Space Organization (to whom the satellite systems are known as FormoSat-3 and -7, respectively, and abbreviated as F3/C and F7/C2). The COSMIC networks measure total electron content in the ionosphere using a method called radio occultation [29].

Variations in solar activity determine the rates of ionization and heating within the ionosphere and thermosphere. In cases of high solar activity, the ionosphere and its drivers undergo significant changes: ionization and heating rates rise sharply, geomagnetic activity undergoes significant disturbances (geomagnetic storms), and the thermosphere expands, creating enhanced pressure fields and wind circulations that modify the composition of neutral and ionized gases. (See [39] for an overview of the effects of solar flares on the ionosphere and [40] for an overview of ionospheric storms.)

The modeling of extreme ionospheric events is of practical interest due to potential adverse effects associated with space weather disturbances, which range from satellite communication interruptions [41] and Earth imaging [21] to geomagnetically induced currents, which affect power transmission systems [42]. Although the benefits of modeling the ionosphere and thermosphere and their associated electrodynamical processes with a single general circulation model have been observed [31], other ionospheric drivers are specified with auxiliary empirical models.

The ionosphere is strongly coupled to the magnetosphere in high-latitude regions. The TIEGCM does not include a model for magnetospheric dynamics; the coupling is represented by empirical models [43]. At high altitudes, the TIEGCM uses ionospheric electric fields as provided by the Heelis [23] and Weimer [43] models. The parameterization of these latter models therefore has an important effect on TIEGCM outputs. Inputs to solar and geomagnetic parameterizations usually are measured directly and are physically meaningful, but nowcasting and short-term forecasting of parameters like the Kp remain a topic of continuing research [44, 45]. Challenges include limited station observability coverage and limited representation of associated physical mechanisms [46].

We describe two sets of observing system simulation experiments in which synthetic observations of electron density are assimilated into the TIEGCM using various choices of driving parameters (such as for the electric fields), to assess their effect on 1-h forecasts. The dynamics of the ionosphere respond rapidly to changes in solar activity. Even if the initial state vector of an ionospheric model is accurate, its predicted evolution may not be if external, time-evolving drivers of solar activity, geomagnetic conditions [47], and the state of the dynamically coupled thermosphere are incorrectly specified [48]. We find that simple models of the time evolution of the forecast bias can provide significant improvements to 1-h predictions of electron density and related quantities.

Ensemble Kalman Filter (EnKF) approaches have been shown to be effective in estimating the state of the coupled ionosphere-thermosphere system [24, 31] and ionospheric forcing parameters [32]. Improved estimates of electron density may also help improve estimation of other systems that are strongly coupled to the ionosphere, such as the magnetosphere [19]. An overview of parameter estimation strategies in data assimilation is presented in [49], and additional parameter estimation strategies with Ensemble Kalman filters for non-global parameters are discussed in [50]. Geomagnetic storms often have significant and persistent storm-time effects that modify the state of the ionosphere relative to quiet-time conditions [51], such as by changing electron densities in ways that are difficult to predict [52]. Such effects may be another source of systematic model biases that can be difficult to remedy by adjustments to input parameters alone.

In this paper, we propose a strategy to compute spatially varying corrections to compensate for model bias introduced from suboptimal parameterized inputs. Our approach is based on methodology originally proposed in [37]. We assume that a solar and magnetospheric parameter configuration, which is specified through some parameter estimation approach, is already in place. Our strategy treats the global distribution of model bias as a collection of bias correction parameters, which we estimate using an ensemble Kalman filter. The bias corrections are not used to adjust the model state vector directly. Instead, spatially varying bias corrections are applied in the evaluation of the observation operator, with the intent of reducing model bias in its electron density predictions prior to the assimilation of observations.

The application of spatially varying bias corrections extends the degrees of freedom in the predictions made with a given parameterized configuration and may be beneficial in capturing storm-time effects. The corrections are computed independently of parameterized inputs, so this strategy may be applied together with other direct parameter estimation approaches. Furthermore, this strategy helps provide a more gentle state estimation update due to the adjusted forecast predictions, which may help to avoid the introduction of spurious dynamical artifacts from drastic adjustments to the system state that may occur due to strong model bias presence during an extreme event. To our knowledge, this bias correction strategy has not been applied previously to an ionospheric model with operational capabilities.

The proposed bias estimation strategy, which is designed for high-dimensional ionospheric systems that are sparsely observed, is applied in observing system experiments focused on the September 2011 geomagnetic storm to compensate for model bias resulting from suboptimal parameterized solar and magnetospheric inputs. We use the Local Ensemble Transform Kalman Filter (LETKF) [25] to assimilate synthetic electron density vertical profiles into the Thermosphere Ionosphere Electrodynamics Global Circulation Model (TIEGCM). The synthetic observation profile locations are the representative of the COSMIC/FORMOSAT-3 satellite constellation [53] during September 26–27, 2011. The LETKF is a type of ensemble square-root filter that computes its analysis using a low-rank estimate of the forecast covariance matrix. The analysis is computed independently grid point by grid point, by assimilating nearby observations simultaneously. The LETKF has been applied in the ionosphere with an idealized regional model [54] and for space-weather specification during an extreme event with the TIEGCM by [7]. The LETKF has also been used with the Global Ionosphere-Thermosphere Model to estimate solar parameters during periods of low and high solar activity [22, 27].

2 Data Assimilation Scheme

The data assimilation algorithm used in this paper is the Local Ensemble Transform Kalman Filter (LETKF). We provide a brief overview of the algorithm below and refer to [25] for a full description. Its application to the TIEGCM is also presented in [7].

The LETKF begins with an ensemble of k global forecast (“background”) vectors at a particular model update (“analysis”) time $t_n$, which we denote by ${\left\{{\mathbf{u}}^{b\left(j\right)}\right\}}_{j=1}^k$. (Since all calculations here are performed at $t_n$, we omit the explicit dependence on time to simplify the notation.) The LETKF adjusts the ensemble of background state vectors, grid point by grid point, based on the available observations within a suitable neighborhood of each grid point (the radius of which is problem-, data-, and model specific). The individual analyses are aggregated to produce an ensemble of global analysis state vectors, which we denote as ${\left\{{\mathbf{u}}^{a\left(j\right)}\right\}}_{j=1}^k$. The analysis update is computed independently at each grid point as we now describe.

Consider a model grid point indexed, say, as L. We associate a “local window” to L, consisting of the space within a prescribed horizontal and vertical distance from L. The subscript L is used to emphasize that the following quantities are associated with a specific grid point and its associated local window. Let d denote the number of components of the model state vector to be analyzed (Often, atmospheric models include passive scalars as well as dynamical variables, so d may be less than the dimension of the actual state vector. In the case of the TIEGCM, the variables that are analyzed include electron and ion density and temperature.) Let L be a multi-index to identify each model grid point. We denote the background global model state vector for the jh ensemble as ${\mathbf{u}}^{b\left(j\right)}$ and let ${\mathbf{x}}_L^{b\left(j\right)}$ denote the components to be analyzed at grid point L. The local background ensemble mean is given by ${\overline{\mathbf{x}}}_L^b=k^{-1}{\displaystyle {\sum }_{j=1}^k{\mathbf{x}}_L^{b\left(j\right)}}.$ Let ${\mathbf{X}}_L^b$ be the $d\times k$ matrix of local background ensemble perturbations from the mean whose jth column is given by

${\mathbf{X}}_L^{b\left(j\right)}={\mathbf{x}}_L^{b\left(j\right)}-{\overline{\mathbf{x}}}_L^b.(1)$

The LETKF performs the Kalman filtering step in the column space S of ${\mathbf{X}}_L^b$ and finds a linear combination of the ensemble perturbations that minimizes the weighted least-squares sum given in Eq. 4.

Denote the $\ell$-vector of observations within the local window as ${\mathbf{y}}_L^o$ and its associated $\ell \times \ell$ covariance matrix as ${\mathbf{R}}_L$. The background observation predictions for the jth local forecast are denoted by the $\ell$-vector

${\mathbf{y}}_L^{b\left(j\right)}={\mathbf{H}}_{\mathbf{L}}\left[{\mathbf{u}}^{b\left(j\right)}\right],(2)$

where ${\mathbf{H}}_L$ is the local forward operator that relates model state quantities to the local observations. The operator defined by ${\mathbf{H}}_L$ may be a linear interpolation, or it may be a non-linear function whose linearization is assumed to provide a good approximation of ${\mathbf{H}}_L$ locally within the local window. The linearization is constructed by computing the $\ell \times 1$ ensemble mean of the predicted observations, ${\overline{\mathbf{y}}}_L^b=k^{-1}{\displaystyle {\sum }_{i=1}^k{\mathbf{y}}_L^{b\left(i\right)}}$, and the $\ell \times k$ observation perturbation matrix, ${\mathbf{Y}}_L^b$, whose jth column is given by ${\mathbf{Y}}_L^{b\left(j\right)}={\mathbf{y}}_L^{b\left(j\right)}-{\overline{\mathbf{y}}}_L^b$.

The ensemble mean of the analyzed local state at the grid point L is an adjustment of the background ensemble mean, consisting of a linear combination of local forecast perturbations given by

${\overline{\mathbf{x}}}_L^a={\overline{\mathbf{x}}}_L^b+{\mathbf{X}}_L^b{\overline{\mathbf{w}}}_L^a,(3)$

where ${\overline{\mathbf{w}}}_L^a$ minimizes the objective function

$J\left(\mathbf{w}\right)=\left(k-1\right){\mathbf{w}}^{\text{T}}\mathbf{w}+{\left[{\mathbf{y}}_L^o-{\overline{\mathbf{y}}}^b-{\mathbf{Y}}_L^b\mathbf{w}\right]}^{\text{T}}{\mathbf{R}}^{-1}\left[{\mathbf{y}}_L^o-{\overline{\mathbf{y}}}^b-{\mathbf{Y}}_L^b\mathbf{w}\right].(4)$

If $\mathbf{w}$ is a Gaussian random vector in S with mean and covariance ${\left(k-1\right)}^{-1}\mathbf{I}$, then the right-hand side of Eq. 3 has mean ${\overline{\mathbf{x}}}^b$ and the sample covariance ${\mathbf{P}}^b={\left(k-1\right)}^{-1}{\mathbf{X}}^b{\left({\mathbf{X}}^b\right)}^{\text{T}}$, which is just the ensemble estimate of the covariance matrix of the forecast model at L. The minimizer of J is given by ${\overline{\mathbf{w}}}_L^a={\tilde{\mathbf{P}}}_L^a{\left({\mathbf{Y}}_L^b\right)}^{\text{T}}{\mathbf{R}}_L^{-1}\left({\mathbf{y}}_L^o-{\overline{\mathbf{y}}}_L^b\right),$ where ${\tilde{\mathbf{P}}}_L^a$ is the analysis covariance matrix in S,

${\tilde{\mathbf{P}}}_L^a={\left[{\alpha }_L^{-1}\left(k-1\right)\mathbf{I}+{\left({\mathbf{Y}}_L^b\right)}^{\text{T}}{\mathbf{R}}_L^{-1}{\mathbf{Y}}_L^b\right]}^{-1}.$

To compensate for model nonlinearity, multiplicative covariance inflation is incorporated in the above formulation through the factor ${\alpha }_L$, calculated as described in [55]. The factor ${\alpha }_L$ varies by grid point and is applied to all components of each local state vector. The associated covariance matrix in model space is given by

${\mathbf{P}}_L^a={\mathbf{X}}_L^b{\tilde{\mathbf{P}}}_L^a{\left({\mathbf{X}}_L^b\right)}^{\text{T}}.(5)$

The ensemble of local analysis perturbations is constructed from the local background perturbations as

${\mathbf{X}}_L^a={\mathbf{X}}_L^b{\mathbf{W}}_L^a,(6)$

where ${\mathbf{W}}_L^a={\left[\left(k-1\right){\tilde{\mathbf{P}}}_L^a\right]}^{1/2}$ is the symmetric square root of ${\mathbf{P}}_L^a$. This choice of ${\mathbf{W}}_L^a$ yields an ensemble whose sample covariance, ${\left(k-1\right)}^{-1}{\mathbf{X}}_L^a{\left({\mathbf{X}}_L^a\right)}^{\text{T}}$, matches Eq. 5. The columns of ${\mathbf{X}}_L^a$ also sum to zero, so that the ensemble has the correct sample mean after ${\overline{\mathbf{x}}}_L^a$ is added to each of its columns to form each local analyzed state vector, ${\mathbf{x}}_L^{a\left(j\right)}$. The choice of symmetric square root for ${\mathbf{W}}_L^a$ ensures that the analysis perturbations sum to zero (for correct sample statistics) and that ${\mathbf{W}}_L^a$ depends continuously on ${\tilde{\mathbf{P}}}_L^a$, so that the analysis ensembles resulting from slightly different analysis covariances matrices do not differ significantly from one another (as could be the case with a Cholesky decomposition, for example) [25]. The analysis procedure described above is performed independently for each grid point. Collectively, the local analyses at each of the grid points, ${\mathbf{x}}_L^{a\left(j\right)}$, form the global analysis vector, ${\left\{{\mathbf{u}}^{a\left(j\right)}\right\}}_{j=1}^k$.

3 Bias Estimation Methodology

We consider the data assimilation problem in the context of a forecast model for which there is some systematic difference between its predicted state ${\mathbf{u}}_{n+1}^m$ of the ionosphere at time $t_{n+1}$ and the “true” state. More precisely, the vector ${\mathbf{u}}_{n+1}^m$ contains all the dynamical variables associated with the model’s depiction of ionospheric processes, such as electron density, thermospheric composition, etc., over the global model grid. We may regard the ionospheric model as a collection of maps ${\mathbf{M}}_n$, $n=\mathrm{1,2},\dots ,N$, that yield global model state vectors of the form

${\mathbf{u}}_{n+1}^m={\mathbf{M}}_n\left({\mathbf{u}}_n^m\right)(7)$

for discrete times $t_1,t_2,\dots ,t_N$ over some interval of interest. The ionospheric model approximates a corresponding “true” set of state vectors ${\mathbf{u}}_n^t$ at each time and grid point. That is, we may regard the sequence

${\mathbf{u}}_{n+1}^t={\mathbf{F}}_n\left({\mathbf{u}}_n^t\right)(8)$

as a finite-dimensional projection of the ionosphere’s evolution to the grid points of the ionospheric forecast model at each time $t_n$. A perfect model would produce a sequence ${\mathbf{u}}_n^m$ that is identical to ${\mathbf{u}}_n^t$ for each n, provided that the initial state of the ionosphere and its drivers is the same. In practice, however, the initial ionosphere-thermosphere state is not known precisely. Additionally, the specification of solar and magnetospheric drivers that produces each ${\mathbf{u}}_n^m$ differs from evolution operator that produces the “true” ionospheric state ${\mathbf{u}}_n^t$. Thus the vectors ${\mathbf{u}}_n^m$ and ${\mathbf{u}}_n^t$ differ.

Our approach is based on one suggested by Baek et al. [37], which they called “bias model II,” that assumes the dynamics of the ionospheric model evolve on a different attractor from the “true” dynamics of the ionosphere. In such a case, substituting ${\mathbf{u}}_n^t$ (or a vector close to it) into the model ${\mathbf{M}}_n$ may excite spurious dynamics because the dynamical drivers represented by the model differ from those of the truth. To avoid this situation, we regard the evolution of the state vector on the model attractor as a time-dependent translation of corresponding points on the true attractor. We compensate for the discrepancy between the truth and forecast state vectors within the data assimilation system, whose objective now is to find the model state vector that yields the best forecast. For this purpose, we define the model bias at each analysis time $t_n$ as

${\mathbf{c}}_{n+1}={\mathbf{F}}_n\left({\mathbf{u}}_n^t\right)-{\mathbf{M}}_n\left({\mathbf{u}}_n^m\right)(9)$

where

${\mathbf{u}}_n^m={\mathbf{u}}_n^t-{\mathbf{c}}_n.(10)$

Generally, the correction ${\mathbf{c}}_{n+1}$ depends on ${\mathbf{c}}_n$ as well as on ${\mathbf{F}}_n$ and ${\mathbf{M}}_n$. To make our scheme practicable within a data assimilation system, we adopt the approach of [37] and suppose that the corrections ${\mathbf{c}}_n$ evolve according to another dynamical system to produce the following augmented model:

${\mathbf{u}}_{n+1}^b={\mathbf{M}}_n\left({\mathbf{u}}_n^a\right)(11)$

${\mathbf{c}}_{n+1}^b={\mathbf{G}}_n\left({\mathbf{u}}_n^a,{\mathbf{c}}_n^a\right).(12)$

Here the subscript b refers to the “background” state vector (i.e., the forecast) and a to the “analyzed” state vector (i.e., the output of the data assimilation system).

The data assimilation procedure described in Section 2 proceeds as before, but it begins with an ensemble of augmented state vectors of the form ${\left[{\left({\mathbf{u}}_n^{b\left(j\right)}\right)}^{\text{T}}{\left({\mathbf{c}}_n^{b\left(j\right)}\right)}^{\text{T}}\right]}^{\text{T}},$ where j indexes each ensemble member. In lieu of Equation 2, the observation operator at time $t_n$ becomes

${\mathbf{y}}_L^{b\left(j\right)}={\mathbf{H}}_L\left({\mathbf{u}}_n^{b\left(j\right)}+{\mathbf{c}}_n^{b\left(j\right)}\right).(13)$

In other words, we compensate for the model error by adding a correction term to the model state vector whenever a comparison to observations is made. The data assimilation procedure produces an augmented analysis ensemble of the form ${\left[{\left({\mathbf{u}}_n^{a\left(j\right)}\right)}^{\text{T}}{\left({\mathbf{c}}_n^{a\left(j\right)}\right)}^{\text{T}}\right]}^{\text{T}},$ which is used as the initial condition in the subsequent forecasting step. We apply Eqs 11,12 to produce the augmented state vector ${\left[{\left({\mathbf{u}}_{n+1}^{b\left(j\right)}\right)}^{\text{T}}{\left({\mathbf{c}}_{n+1}^{b\left(j\right)}\right)}^{\text{T}}\right]}^{\text{T}}$ for the next analysis step.

The procedure described above yields a spatially varying state estimate of the model bias. The remaining component of our proposed algorithm is the propagation of the model bias estimates for which one needs a suitable model, ${\mathbf{G}}_n$, to describe their temporal evolution. The choice of ${\mathbf{G}}_n$ depends upon the problem, and a complete description of the time evolution of the model bias may not be available. Nevertheless, the main point of this paper is that even simple choices of ${\mathbf{G}}_n$ can yield a stable filter that significantly improves 1 h forecasts of electron density, compared to a non-bias-corrected LETKF scheme, despite systematic errors in the solar and magnetospheric parameterizations of the forecast model.

In principle, the bias correction procedure doubles the number of state variables that must be estimated from the same set of observations, which increases the variance in the analyzed fields. On the other hand, not all model biases contribute equally to the forecast error, and it may suffice to apply the bias correction procedure only to some of the components of the model state vector; that is, the components of ${\mathbf{c}}_n^b$ are taken to be zero except for those corresponding to fields of greatest forecast interest. In the numerical experiments described in this paper, we apply the bias estimation procedure only to the electron density component of the TIEGCM. Section 5 describes the results when the bias model ${\mathbf{G}}_n$ is persistence, i.e., ${\mathbf{c}}_{n+1}={\mathbf{c}}_n$. Section 6 describes the results when ${\mathbf{G}}_n$ implements an exponential growth and relaxation in the model bias.

4 Observing System Experiment Setup

This section describes the common aspects of the observing system experiments described in the next sections. Our setup is a “perfect model” experiment, in which the results of the data assimilation system are obtained with synthetic observations generated from the TIEGCM model with known driving parameters. In this way, the sources of model bias are controlled, the performance of the data assimilation system may be compared to a known truth, and improvements due to the proposed bias correction scheme may readily be quantified. The conclusion section suggests some issues that may be considered prior to any potential operational application.

The numerical experiments simulate a scenario in which an ionospheric forecast is driven with suboptimal specification of magnetospheric and solar inputs during a period of geomagnetic disturbance. Storm-time effects can be difficult to model and predict [44, 45]. For example, the study by [51] discusses the significant enhancement in F-layer electron density peak and altitude during the geomagnetic storm of December 15, 2006. The focus of the observing system experiments in this paper is on the September 26–27, 2011 geomagnetic storm event.

4.1 Ionosphere Model Description

The TIEGCM is a three-dimensional nonlinear model of the coupled ionosphere-thermosphere system. It solves the momentum and energy equations for neutral and plasma species and the electrodynamical coupling between the ionosphere and thermosphere. We use version 1.94 in this paper at a geographic resolution of $5^{\circ }\times 5^{\circ }$ in latitude and longitude. The vertical coordinate is on a log-pressure scale, with each pressure level defined as $\text{ln}\left(p_0/p\right)$, where p is pressure and $p_0=5\times {10}^{-7}\text{hPa}$ is a reference pressure that corresponds to about 200 km altitude, depending on solar conditions (One scale height corresponds to the change in altitude by which the pressure changes by a factor of e.) The pressure levels extend from −7 to 7 with half-scale height resolution and range from about 97 to 600 km, depending on solar conditions.

The main source of ionization in the ionosphere, and thus one of its primary dynamical drivers, is the absorption of solar radiation in the thermosphere, primarily by O₁ and neutral gases (O₂ and N₂). The TIEGCM represents effects of solar irradiance and its variability through auxiliary empirical models. The default solar input model, which we use in our TIEGCM configuration, is the EUVAC irradiance model [56]. The EUVAC model specifies important ionospheric processes related to solar activity, such as ionization and dissociation rates, and heating of neutral gases, ions, and electrons. The empirical representation of solar irradiance is parameterized with the $F_{10.7}$ index, which is a daily measurement radio flux at 10.7 cm wavelength, and its 81-day average. Solar proxy models parameterized with the $F_{10.7}$ index have been widely used in other recent ionospheric data assimilation studies, such as [28, 31].

Another key driver of ionospheric dynamics is geomagnetic activity. The ionosphere is strongly coupled to the magnetosphere in high-latitude regions and is typically approximated with auxiliary empirical models due its complexity. The magnetospheric input used in our simulations with the TIEGCM is the Heelis model [23], which specifies important high-latitude processes in the ionosphere, such as electric field patterns and auroral energy inputs, for different levels of geomagnetic disturbance.

The Kp index, a widely used index derived from the horizontal component of geomagnetic field disturbances, is an input to the Heelis model. It is to calculate Hp (Hemispheric Power), which is used in the parameterization of auroral precipitation, and the cross-tail potential (Cp), which specifies ion convection patterns in the polar regions. Kp indices are provided every 3 h and range in value from 0 to 9, to describe geomagnetic conditions ranging from quiet to extremely disturbed. Historical records of $F_{10.7}$ and Kp indices are provided by the National Oceanic and Atmospheric Administration (NOAA).

4.2 Ensemble Generation

We generate an ensemble of 40 forecasts with normally distributed values of $F_{10.7}$ and Kp, which in turn produce estimates of Hp and Cp. Each parameter is centered around the respective index values published for September 26–27, 2011. The standard deviation for the $F_{10.7}$ distribution is its 21-day standard deviation during the spin-up period, which we take to be from 5 to 25 September 2011, and the standard deviation for Kp is ±1.0. The respective standard deviations for $F_{10.7}$, Cp and Hp are $13\times {10}^{-22}\text{W}/{\text{m}}^2\text{Hz}$, $8.4\text{kV}$ and $7.2\text{GW}$, respectively. Figures 1A–C summarize the temporal evolution of the ensemble of forecast parameters (pink) and the ensemble mean (red) for each respective parameter. The horizontal axis for each figure is time in hours, starting from 00:30 UTC on September 26, 2011 to 23:30 UTC on September 27, 2011. The choice of 40 ensemble members represents a compromise between computational expense and accuracy of background forecast uncertainty. Forty ensemble members provided satisfactory results in observing system experiments with the Global Forecast System operational atmospheric model [57] and in the authors’ previous study using the TIEGCM [7]. We retain this ensemble size to facilitate comparisons with previous work.

FIGURE 1

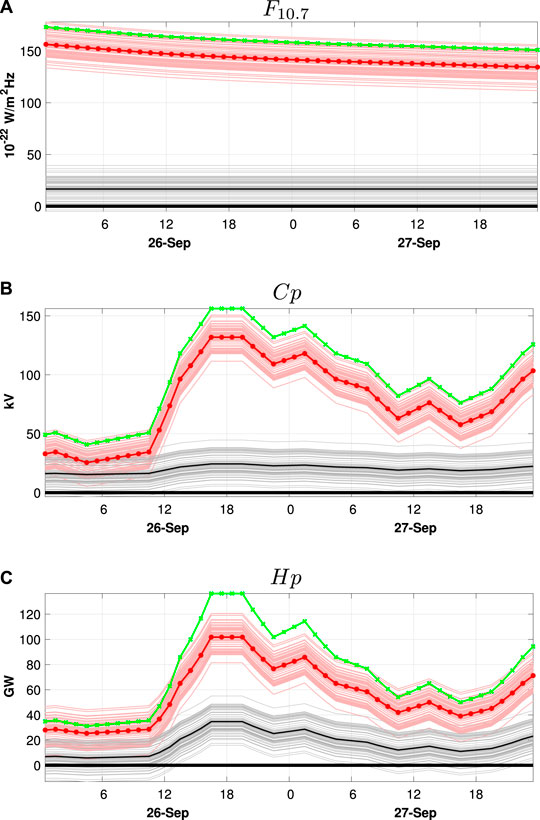
FIGURE 1. (A) Time series of $F_{10.7}$ indices in solar flux units $\left({10}^{-22}\text{W}/\left({\text{m}}^2\text{Hz}\right)\right)$, (B) cross-tail potential (Cp) in kV, and (C) hemispheric power (Hp) in GW. The horizontal axis is in hours, starting at 00:30 UTC on 26 September and ending at 23:30 UTC on September 27, 2011. The parameters used to drive the truth are shown in green, the parameters used to drive the ensemble of forecasts are shown in pink and their respective ensemble means are shown in red. The deviation of each parameter from those used in the control simulation is shown in gray, and the ensemble mean of the deviations is shown in black.

The control simulation is driven with forcing parameters that have the same temporal evolution as the published indices but are shifted as shown by the green curves in Figures 1A–C. This shift is introduced to simulate the scenario where the solar and magnetospheric inputs used to drive the forecast are a misspecification relative to the “true” state of the ionosphere-thermosphere system. The imposed bias on $F_{10.7}$, shown in Figure 1A for the ensemble (gray) and the ensemble mean (black), is $10\times {10}^{-22}\text{W}/{\text{m}}^2\text{Hz}$ and is kept constant throughout the simulation. The bias in the magnetospheric inputs is introduced by adding a shift of 1.0 units in the Kp index. The corresponding bias on Cp and Hp values is shown in Figures 1B,C. Although the bias in the Kp index is fixed, the resulting bias in the Cp and Hp indices varies temporally. Prior to the onset of the geomagnetic storm, which is about 12:30 UTC on 26 September, the bias in the magnetospheric inputs is relatively small and constant but increases considerably over the next 6 h. The strongest bias occurs during the main phase of the geomagnetic storm, which takes place at about 16:30–19:30 UTC on 26 September. As geomagnetic conditions relax over the next 12 h, the bias in the magnetospheric inputs also decreases accordingly.

In reality, of course, the errors between the published and “optimal” model forcing parameters are more complex, but, to our knowledge, have not been fully characterized. Insofar as the model’s response varies nonlinearly with the forcing parameters, and the magnitude of the bias in the magnetospheric inputs resembles the typical uncertainty during geomagnetically disturbed periods, we believe that our choice of ensemble of forcing parameters is as good as any for this illustration of bias correction. Nevertheless, future work should address this question in more detail.

4.3 The TIEGCM-LETKF Data Assimilation System

Our TIEGCM-LETKF data assimilation system runs as a discrete forecast/analysis sequence, in which the LETKF is used to assimilate observations available in the time interval $[t_n-0.5\text{h},t_n+0.5\text{h}]$ into the output of TIEGCM at the analysis time $t_n$. The assimilation of observations produces an analyzed state estimate at time $t_n$ that is used as the initial condition for the subsequent 1-h forecast to estimate the ionosphere-thermosphere system state at time $t_{n+1}=t_n+1\text{ h}$, where observations in the time interval $[t_{n+1}-0.5\text{ h},t_{n+1}+0.5\text{ h}]$ are assimilated. This forecast/analysis sequence is repeated throughout the duration of the simulation, starting at 00:30 UTC on September 26, 2011.

During each analysis calculation, only a subset of the TIEGCM state variables is included in the LETKF state vector and analyzed with the assimilated observations. State variables included in the LETKF state vector are electron density (Ne), neutral temperature (Tn), zonal (Un), and meridional (Vn) components of neutral winds, as well as atomic (O₁) and molecular (O₂) mass mixing ratios. The same forecast/analysis sequence and choice of analyzed state vector is used in [7]. Similar approaches are also used in other ionospheric data assimilation studies [28, 32].

The covariance inflation scheme used in this paper is the one proposed by [55], which also was used with the LETKF and TIEGCM in the observing system experiments presented in [7]. Other LETKF parameters, such as the ensemble size and localization radii, are also taken to be the same as in [7] to simplify comparisons with the results.

4.4 Observing Network

During each analysis step, observations are generated synthetically from the electron density component of the control simulation (“truth”), ${\mathbf{u}}^t$, with the observation locations and times given by the COSMIC network during September 26–27, 2011. Vertical profiles from the COSMIC network extend from about 80 to 800 km altitudes at a vertical resolution of about 10 km. There are about 85 globally distributed vertical profiles per 1-h interval. The COSMIC observation set is available at the COSMIC Data Analysis and Archive Center (CDAAC) at UCAR (http://cdaac-www.cosmic.ucar.edu). Synthetic observations are generated with additive Gaussian noise to represent observation processing noise: ${\mathbf{y}}^o=\mathbf{H}{\mathbf{u}}^t+\mathrm{ϵ}$, where $\mathbf{H}$ interpolates the electron density component of ${\mathbf{u}}^t$ to the respective observation locations and times during the given analysis step and $\mathrm{ϵ}$ is a Gaussian random vector with zero mean and covariance matrix $\mathbf{R}$. Observation errors are assumed to be independent, so $\mathbf{R}$ is diagonal.

Observations obtained through retrievals, such as COSMIC electron density profiles, have also been shown to have significant uncertainties associated with the inversion process, particularly at low altitudes [30, 58]. We include an approximation of the inversion error associated with these observations, as done in [7, 24]. In addition to standard observing errors, retrieval errors are correlated in possibly complicated ways, depending on the nature of the satellite observing platform, but here we treat them as independent. To compensate, the standard deviation of $\mathrm{ϵ}$ is assumed to scale as 10% of the of the electron density component of ${\mathbf{u}}^t$ at the observation locations. Although we have not studied the sensitivity of the forecast accuracy of the TIEGCM to the magnitude of observational errors, previous experiments [54] have demonstrated the stability and robustness of the LETKF to observation noise when using an idealized regional ionospheric model.

5 Numerical Experiment 1: Persistent Bias Evolution

In this section, we study how well the proposed bias estimation strategy can estimate the spatiotemporal evolution of model bias in the electron density field when the bias evolution operator is persistence, that is, ${\mathbf{G}}_n=\mathbf{I}$ and ${\mathbf{c}}_{n+1}={\mathbf{c}}_n$ for all analysis times $t_n$. The bias in the predicted electron density field is introduced with the misspecification of the solar and magnetospheric model inputs as shown in Figure 1. As noted in Section 3, we apply the bias correction methodology only to the electron density component of the TIEGCM model, as it is our primary interest in the simulations.

At the analysis time $t_n$, we denote the electron density component of the background state vectors, ${\left\{{\mathbf{u}}_n^{b\left(j\right)}\right\}}_{j=1}^k$, as ${\left\{{\mathbf{e}}_n^{b\left(j\right)}\right\}}_{j=1}^k$ and its ensemble mean as ${\overline{\mathbf{e}}}_n^{b\left(j\right)}$. Similarly, we denote the “true” electron density component from the control simulation as ${\mathbf{e}}_n^t$. We define the electron density bias to be given by the deviation of the forecast mean from the truth: ${\mathbf{b}}_n={\overline{\mathbf{e}}}_n^b-{\mathbf{e}}_n^t$.

Figure 2A shows the global distribution of electron density bias, in units of $\text{el}/{\text{cm}}^3$, at a fixed altitude of 375 km, which is about the altitude of the F-layer over the equatorial daytime ionosphere during this time period. The selected times show the distribution of electron density bias on September 26, 2011 before the major onset of geomagnetic disturbances (12:30 UTC), during the main phase of the geomagnetic storm (15:30 UTC, 18:30 UTC), and as geomagnetic disturbances begin to relax (21:30 UTC). The locations of the observed electron density profiles available for assimilation at each respective time are shown with the magenta markings.

FIGURE 2

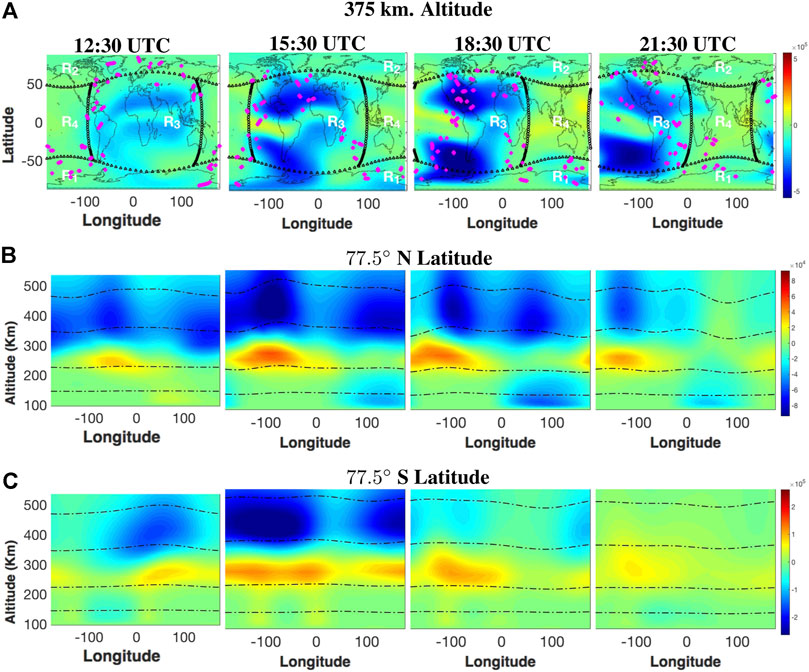
FIGURE 2. (A) Global maps of electron density bias in units of $\text{el}/{\text{m}}^3$, at a fixed 375 km altitude at the indicated times on September 26, 2011. The electron density bias is computed as deviation from the truth of the ensemble mean of the forecast $\left({\overline{e}}^b-e^t\right)$. The black curves denote the boundaries of the geographical regions, labeled in white, that partition the domain horizontally. The locations of the COSMIC vertical profiles at each time are shown with the magenta markings. (B) Vertical structure of electron density bias at a fixed 77.5° N latitude at 11:30, 15:30, 19:30 and 23:30 UTC on September 26, 2011. The vertical partitioning of the domain is denoted with the black curves, which correspond to pressure levels −2.5, 0, 2.5, and 5. (C) Analogous plots of the electron density bias vertical structure at a fixed 77.5° S latitude.

Also shown in Figure 2A are four geographical regions over which we examine the model bias. The boundaries for the Northern and Southern high-latitude regions (R₁ and R₂) are located at the ${30}^{\circ }$ magnetic co-latitudes. Processes associated with magnetospheric inputs are calculated explicitly by the TIEGCM below this co-latitude and imposed directly with the Heelis model above the ${20}^{\circ }$ magnetic co-latitudes. Between these co-latitude bands, a linear combination of the imposed parametric and model solutions is used. (The TIEGCM model description provides more information; see www.hao.ucar.edu/modeling/tgcm.) We also separate low-to-mid altitude regions in the daytime (R₃) from the nighttime (R₄).

A positive (negative) sign indicates that the background electron density overestimates (underestimates) the true electron density. Prior to the main phase of the geomagnetic storm, the most notable bias structure is in the daytime mid-latitude regions (R₃), where there is a negative bias. As geomagnetic conditions become increasingly disturbed, the misspecification in the magnetospheric input grows, resulting in the formation of a significant negative bias structure over the Southern Polar region (R₁). The negative bias structure continues to grow over regions R₁ and R₃ over the next few hours throughout the rest of the main storm phase. There is also a formation of negative bias in the Northern polar region (R₂) and a positive bias forming over the night-time low-to-mid latitude region (R₄). After the main phase (21:30 UTC), the negative bias in the polar regions is largely diminished but the bias over the daytime mid-latitudes remains relatively constant. This suggests that the misspecification of $F_{10.7}$, which is held constant throughout the simulation has its largest effect over the low-to-mid latitude regions. Over this time period, the temporal evolution of electron density bias has a pronounced westward drift of approximately ${15}^{\circ }/\text{h}$, so the persistent dynamics of the bias evolution operator, $\mathbf{G}$, provide a reasonable representation of the model error.

Figure 2B shows the vertical structure of the electron density bias at the ${77.5}^{\circ }$ N geographical latitude at the same times. The black horizontal curves denote model pressure levels −2.5, 0, 2.5, and 5, which correspond to altitudes of about 145, 215, 325, and 460 km, respectively. Throughout the main phase of the geomagnetic storm, the most notable bias is negative, occurring above 250 and 280 km altitudes in the day- and nighttime regions, respectively, which is about the altitude of the lower portion of the F-layer. Figure 2C shows the vertical structure of the electron density bias at the ${77.5}^{\circ }$S geographical latitude. Similarly, the most notable bias is observed above the 280 km altitude. However, there is pronounced positive bias at about a 250 km altitude, which is located slightly below the F-layer peak density.

5.1 Region-Averaged Bias Estimates

Following the procedure described in Section 3, the ensemble of global bias correction vectors at a given time $t_n$, ${\left\{{\mathbf{c}}_n^{b\left(j\right)}\right\}}_{j=1}^k$, is updated to form an ensemble of analyzed global bias correction vectors, ${\left\{{\mathbf{c}}_n^{a\left(j\right)}\right\}}_{j=1}^k$. Generally, each ${\mathbf{c}}_n^{b\left(j\right)}$ is an $md\times 1$ vector, where m is the number of grid points and d is the number of state variables being analyzed. As discussed at the end of Section 3, we consider bias corrections only for the electron density field. For simplicity in notation, we now regard each ${\mathbf{c}}_n^{b\left(j\right)}$ to be an $m\times 1$ vector corresponding to the electron density field corrections only.

The forecast/analysis cycle is initialized at time $t_0$ with electron density bias corrections at each grid point given by

${\mathbf{c}}_0^{b\left(j\right)}=\frac{1}{4}\left({\mathbf{e}}_0^{b\left(j\right)}-{\overline{\mathbf{e}}}_0^b\right),(14)$

which has ensemble mean and reflects the initial spatial correlations of the electron density field. The factor of 1/4 in Eq. 14 is incorporated to reduce the variance in the electron density bias estimate, which is generally expected to be smaller than that of the electron density field. The procedure described in Section 3 is then carried out for subsequent analysis steps to produce spatially and time varying bias estimates throughout the domain that are evolved according to ${\mathbf{G}}_n$, which in this section is taken to be the identity (persistence). For each grid point L, variance inflation is applied to the bias correction component so that its ensemble variance is at least 20% of the electron density component at L.

The model state vector is analyzed without the bias corrections for the first few analysis cycles after the forecast spinup so that errors associated with the unadjusted thermospheric state are reduced and the electron density bias is primarily dependent on the misspecification of the solar and magnetospheric inputs. We compute eight analysis cycles, from 16:30 to 23:30 UTC on September 25, 2011, before applying the bias correction strategy for the first time at 00:30 UTC on September 26, 2011.

To evaluate the skill of our bias estimation strategy, we examine the model bias estimates, averaged over the four geographical regions shown in Figure 2A. Consider one of the fixed bias regions $R=R_1,\dots ,R_4$ as defined above. Denote the electron density component of the jth forecast, ${\mathbf{e}}_L^{b\left(j\right)}$, averaged over all grid points $L\in R$, as $D_R^{b\left(j\right)}=N_R^{-1}{\displaystyle {\sum }_{L\in R}{\mathbf{e}}_L^{b\left(j\right)}},$ where $N_R$ is the number of grid points in R. Similarly, form the region-averaged electron density of the control simulation, $D_R^t=N_R^{-1}{\displaystyle {\sum }_{L\in R}{\mathbf{e}}_L^t}.$ The region-averaged deviation from the truth for the jth forecast is given by

$B_R^{b\left(j\right)}=D_R^{b\left(j\right)}-D_R^t,j=1,\dots ,k(15)$

which yields an ensemble of regionally averaged model bias estimates, whose ensemble mean, ${\overline{B}}_R^b=k^{-1}{\displaystyle {\sum }_{j=0}^k{B}_R^{b\left(j\right)}}$, is the most likely state of the regionally averaged model bias.

Figure 3A summarizes the temporal evolution of the region-averaged electron density bias in the Southern polar region (R₁) averaged between 1.0 and 5.5 pressure levels, which correspond to altitudes of about 260–485 km. The horizontal axis is time in hours, starting at 00:30 UTC on September 26 2011 and ending at 23:30 UTC on September 27, 2011, and the vertical axis is electron density in units of $\text{el}/{\text{cm}}^3$. The ensemble of spatially averaged background electron densities, ${\left\{D_R^{b\left(j\right)}\right\}}_{j=1}^k$ and their ensemble mean, ${\overline{D}}_R^b$, are denoted with the thin pink and thick curves, respectively. The analogous region-averaged electron density for the control simulation, $D_R^t$, is given by the green curve. The ensemble of bias correction parameters, ${\left\{C_R^{b\left(j\right)}\right\}}_{j=1}^k$ and their ensemble mean, ${\overline{C}}_R^b$, are shown with the cyan and thick blue curves, respectively. For direct comparison, the negative of the region-averaged forecast deviations, ${\left\{B_R^{b\left(j\right)}\right\}}_{j=1}^k$, is also shown with the thin gray curves and their respective ensemble mean, ${\overline{B}}_R^b$, is given by the thick black curve.

FIGURE 3

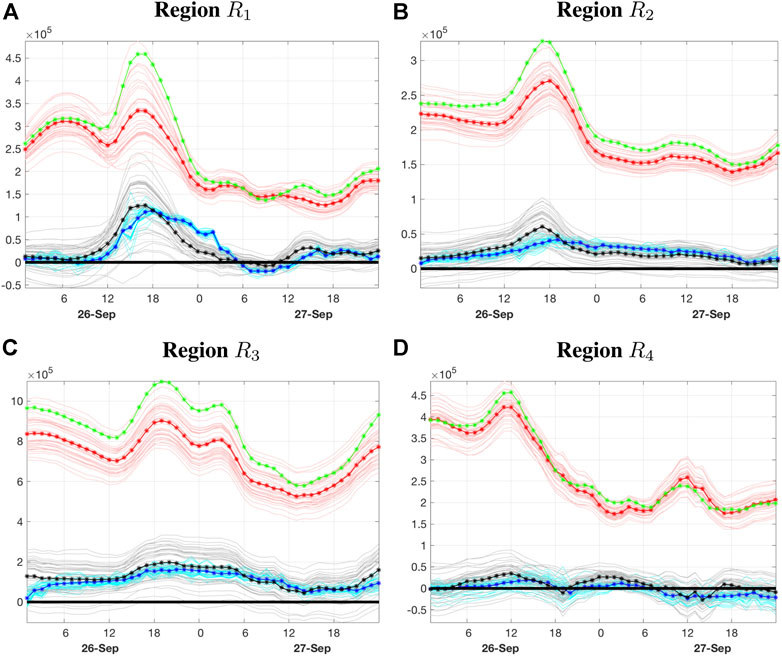
FIGURE 3. (A) Time series of the true electron density (green), in units of $\text{el}/{\text{cm}}^3$, averaged over region $R_1$ (as defined in Figure 2A), at the indicated altitudes. The electron density, averaged over the same region, for the background ensemble (pink) and its ensemble mean (red) are also shown. The deviation of the background ensemble and its ensemble mean from the truth are given by the thin gray and thick black curves, respectively. The time series of the ensemble of bias parameters and their ensemble mean are shown by the thin cyan and the thick blue curves, respectively. The horizontal axis is time in hours, starting at 00:30 UTC on September 26, 2011 and ending at 23:30 UTC on September 27, 2011. (B–D) Analogous time series of electron density, averaged over region $R_2$ (Northern polar region), region $R_3$ (daytime mid-latitudes), and region $R_4$ (night-time mid-latitudes), respectively.

The region-averaged electron density for the control simulation varies considerably within region R₁, particularly during the period of main geomagnetic disturbance, where the electron density increases sharply between 12:30 UTC and 16:30 UTC on 26 September. After the main storm phase, electron density content drops considerably and remains relatively constant throughout the rest of the simulation. The region-averaged electron density trajectories for the forecast evolve similarly. Prior to the onset of geomagnetic disturbances, the electron density bias is relatively small, but rises sharply during the main phase, peaking at around 16:30 UTC. The electron density bias is maintained until about 19:30 UTC, where it begins to drop considerably and remains relatively constant after 23:30 UTC on 26 September, until there is a small resurgence toward the end of the simulation.

Prior to the onset of geomagnetic disturbances (12:30 UTC), the bias strategy correctly detects the near-zero positive bias and continually adjusts its estimates as the model bias starts to increase during the transition into the main phase of the geomagnetic storm around 12:30 UTC. Although the temporal variations in the bias estimates evolve in a similar manner as the model bias, the temporal variations are not captured during this transitionary period in which the model bias increases and decreases sharply during the initial and relaxation phases, respectively. Most notably, the bias corrections adjust too slowly and underestimate the model bias peak during the initial storm phase. After the main phase, the model bias decreases sharply and although the bias corrections adjust, they do so too slowly and overestimate the model considerably after 20:30 UTC for the next 8 h.

The region-averaged bias over the daytime low-to-mid-latitude region (R₃), shown in Figure 3C, exhibits a relatively larger bias compared to the high-latitude regions but remains relatively constant throughout the simulation, since the misspecification of $F_{10.7}$, which is held constant throughout the simulation, is the primary driver of bias over this region. The bias correction parameters approach the model bias relatively quickly and follow its temporal variations well, particularly during the relaxation phase where the model bias decreases gradually. The bias in the night-time region (R₄), shown in Figure 3D, is considerably smaller than the bias in its surrounding regions. Its temporal evolution is relatively constant throughout the simulation and is well represented with the bias corrections.

5.2 Validation of Bias Correction

To validate the bias correction strategy, we compare 1-h predictions of electron density before and after the bias corrections are applied. Since the bias corrections are applied only during the evaluation of the forward operator, we evaluate the benefit of the bias corrections at the observed locations. In particular, we compare the prediction RMS error averaged over all vertical profiles within each of the geographical regions:

$\text{RMSE}={\left(\frac{{\displaystyle {\sum }_{i\in R}{\left({\overline{\mathbf{y}}}_i^b-{\mathbf{y}}_i^t\right)}^2}}{{\ell }_R}\right)}^{1/2},(16)$

where ${\mathbf{y}}_i^t$ and ${\overline{\mathbf{y}}}_i^b$ are the true and predicted electron densities at the ith observation location. The RMSE in Eq. 16 is averaged over the set of ${\ell }_R$ observations located in the given region R.

Figure 4A shows the RMSE time series of 1 h predictions over region $R_1$, where the blue and red curves are computed with Eq 16, by taking ${\overline{\mathbf{y}}}_i^b$ to be the forecast predictions before and after the bias corrections are applied, respectively. Prior to the main phase of the geomagnetic storm (12:30 UTC), there is little benefit in applying the bias corrections due to the relatively small bias present during this time period. Considerable benefits in using the bias correction are observed between 15:30 UTC and 19:30 UTC, where the RMSE of uncorrected predictions reaches its peak. Due to the misrepresentation of the model bias over region $R_1$ during the relaxation phase, as seen in Figure 3A, the bias corrections do not yield benefits in 1-h predictions and actually increase the forecast RMSE considerably throughout the relaxation storm phase. In Section 6, we show that using a growth-relaxation model for the bias evolution significantly improves the temporal variations of the model bias during this time period.

FIGURE 4

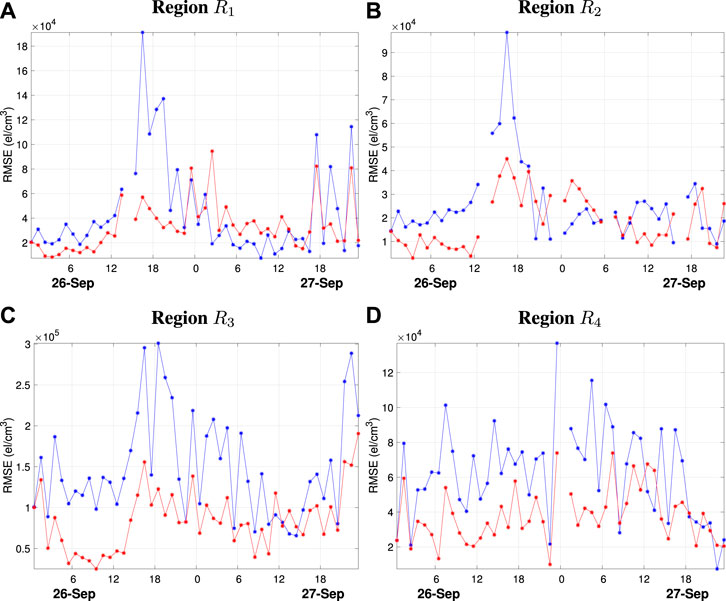
FIGURE 4. (A) Time series of the root mean squared error (RMSE) of 1 h forecasted electron density predictions, in $\text{el}/{\text{cm}}^3$, averaged over all the observed locations in region $R_1$ (as defined in Figure 2). The RMSE values are shown for predictions before (blue) and after (red) the bias correction is applied. (B–D) Analogous time series of region-averaged RMSE values and ratios for regions $R_2$, $R_3$ and $R_4$. In all figures, missing values indicate that there are no observations in that region during that time. All time series begin at 00:30 UTC on September 26, 2011 and end at 00:30 UTC on September 28, 2011, with 1 h intervals.

Figure 4B shows the analogous RMSE time series for region $R_2$, which is similar to that of region $R_1$ insofar as there is a peak in RMSE during the main phase of the geomagnetic storm, although it is smaller in magnitude. The improvements prior to the onset of geomagnetic disturbances are relatively small, but there is significant improvement of about 30% during the main phase. During the relaxation phase, the RMSE is about the same with and without the bias correction, so the bias corrections do not yield much benefit during this time period.

Figure 4C shows the analogous RMSE time series for the low-to-mid-latitude daytime region (R₃). The RMSE time series for this region has a less pronounced peak during the main phase and the improvement due to the applied bias corrections is consistent throughout the simulation, although there are a few time periods where the bias corrections offer little to no improvement near the end of the simulation. The RMSE time series for the night-time region (R₄) is shown in Figure 4D. In this region, the bias is also relatively constant and the benefits of applying the bias corrections are consistent.

The numerical experiments presented in this section show that the bias correction strategy usually improves 1-h forecasts throughout the domain, particularly during the main phase of the geomagnetic storm. However, some limitations of the strategy are observed during transitionary periods of the geomagnetic storm, where model bias undergoes relatively fast temporal variations. Most notably, the high-latitude bias corrections underestimate the sharp increase in model bias during the initial storm phase and overestimate the model bias as it sharply decreases during the relaxation storm phase. The misrepresentation of model bias during these time periods is primarily due to the choice of bias evolution operator, ${\mathbf{G}}_n$, which assumes the model bias remains constant during each forecasting step. Consequently, the predicted bias corrections partially diverge from the true state and yield inadequate background bias correction estimates over high-latitude regions. Due to the sparsity of observations, the bias estimates computed during each analysis step are not sufficiently adjusted to fully capture the temporal variations of the model bias.

6 Numerical Experiment 2: Bias Estimation With a Time-Varying Evolution Operator

Although a simple persistence model for the bias evolution provides some improvement in 1-h forecasts of electron density, the results show that there is considerable room for improvement. The question of how to optimize the bias evolution model is a topic for future investigation, but here we outline one potential approach to the problem.

Figure 5A shows a time series (blue dots) of the RMSE between the “true” values of the electron density and those of the ensemble mean, in units of $\text{el}/{\text{cm}}^3$, at pressure level 2.0 ($\sim 375\text{km}$ altitude). Given the systematic errors in the driving parameters (Figure 1) and the initial conditions, the chaotic dynamics of the model suggest that deviations from the truth should, on average, tend to grow exponentially, particularly during the intensification phase of the geomagnetic storm. After the storm passes, the dynamics relax back to a more typical state. From approximately 12 UTC to 15 UTC on 26 September, the RMSE of the electron density in the Southern polar region (R₁) grows exponentially, and from about 19 UTC to 23 UTC decays exponentially.

FIGURE 5

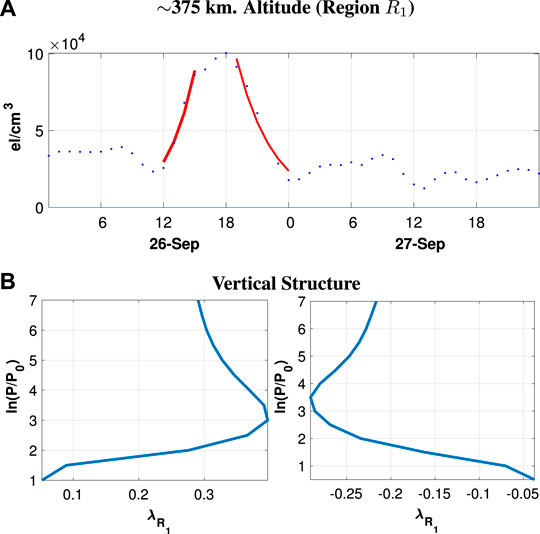
FIGURE 5. (A) RMSE time series of electron density bias in units of $\text{el}/{\text{cm}}^3$, at pressure level 3.5 (_∼375 km), averaged over all grid points in region $R_1$. The horizontal axis is time in hours. The growth and decay factors used in the bias evolution operator, ${\lambda }_{R_1}$, are shown by the red curves and are applied only during the times that these curves cover. (B) Vertical structure of each ${\lambda }_{R_1}$ during the initial (left) and relaxation (right) phases of the geomagnetic storm. The vertical axis is in pressure levels and the horizontal axis is the value of ${\lambda }_{R_1}$.

By their nature, model errors tend to be of a particular sign. For example, the representative bias results in Figure 2 show regions where the model consistently underestimates or overestimates the electron density. Consequently, we propose a growth-relaxation model for the bias evolution of the form

${\mathbf{G}}_n\left({\mathbf{c}}_n^a\right)=e^{{\lambda }_n}{\mathbf{c}}_n^a(17)$

to describe the temporal evolution of model bias estimates at each analysis time $t_n$, such that the bias estimate for the jth forecast is given by ${\mathbf{c}}_{n+1}^{b\left(j\right)}={\mathbf{G}}_n\left({\mathbf{c}}_n^{a\left(j\right)}\right).$ The parameter ${\lambda }_n$ may vary with time and location to describe an averaged rate of model bias growth or decay, depending on the storm phase. With this choice of ${\mathbf{G}}_n$, the model bias estimate depends only upon its current state, ${\mathbf{c}}_n^{a\left(j\right)}$.

6.1 Bias Propagation

Because the errors in the model driving parameters under geomagnetic storm conditions are not well characterized, suitable choices of the growth and decay rates for the evolution of the model bias must be determined empirically. The choices depend upon latitude, altitude, and time of year (i.e., Earth’s axial tilt). Detailed reanalyses of prior geomagnetic storms are needed, which we have not yet undertaken. For the sake of illustration, however, we consider an idealized procedure for finding time-dependent bias parameters and discuss the effect on the resulting forecast errors. Section 6.3 describes some potential future work on this topic.

We consider the RMSE of electron density, averaged over all grid points in the Southern polar region (R₁) at pressure level 2.0 as mentioned previously in Figure 5A (blue dots). Although the electron density bias a strong spatiotemporal variability (Figure 2), we perform a simple regression from 12 UTC to 15 UTC on 26 September of the RMSE (red curves in Figure 5) vs. time to determine the spatiotemporally averaged rate of bias increase, which we denote as ${\lambda }_n\left(R_1,2.0\right)$, where n indexes the analysis times from 12 UTC to 15 UTC. We proceed likewise to compute ${\lambda }_n\left(R_1,z\right)$ at each pressure level z above 0.5, which corresponds to the lower portion of the F-layer. Below this pressure level, we set ${\lambda }_n\left(R_1,z\right)=0$, because the model bias generally does not display a strong growth or decay at these pressure levels during transitionary periods of the storm, and it is also much weaker in magnitude relative to the topside ionosphere. We fit a corresponding exponential decay curve from 19:30 UTC to 23:30 UTC on 26 September at the same pressure levels.

Figure 5B shows the vertical structure of ${\lambda }_n\left(R_1,z\right)$ values used during the initial (left) and relaxation (right) storm periods for region $R_1$ above pressure levels 1.0 and 0.5, respectively. During the initial storm phase, the largest rate of growth is at about pressure level 3.0 (∼350 km altitude), which is about the top portion of the F-layer. Similarly, the greatest rates of decay are seen between pressure levels 3.0 and 4.0, which correspond to about 350 and 400 km altitudes. Growth-relaxation rates are computed similarly for regions R₂ and R₃ and are provided in Appendix. The growth-relaxation bias evolution model is not used in the night-time region (R₄), because the bias is not observed to have a pronounced growth or decay component like the other geographical regions.

The method just described is but one of many possible parameterizations of the bias evolution model. A more sophisticated approach might further localize the${\lambda }_n$’s in space and time, based on reanalyses of additional geomagnetic storm events. The next subsection discusses this issue in more detail.

6.2 Results

The time series of region-averaged bias estimates, in the case where the growth-relaxation model described in Section 6.1 is used for ${\mathbf{G}}_n$, are shown for regions R₁ and R₂ in Figures 6A,B. The quantities in these figures are computed as described in Section 5.1 and are analogous to Figures 3A,B. Regions R₁ and R₂ are the high-latitude regions over which rapid temporal variations occur during the transitionary periods of the geomagnetic storm. Comparison with Figures 3A,B reveals that the growth-relaxation model for ${\mathbf{G}}_n$ provides a considerably improved representation in the initial and relaxation phases of model bias throughout the main phase of the geomagnetic storm. The bias estimates still slightly underestimate the rapid growth of the model bias in region R₁ during the beginning of the initial phase between 11:30 and 13:30 UTC, but the application of ${\mathbf{G}}_n$ allows the bias estimates to quickly grow and adequately estimate the peak of the model bias at 16:30 UTC and also follow the sharp decrease in model bias following the main storm phase. The bias evolution in region R₂ is similarly well represented throughout the simulation with the growth-relaxation model for ${\mathbf{G}}_n$.

FIGURE 6

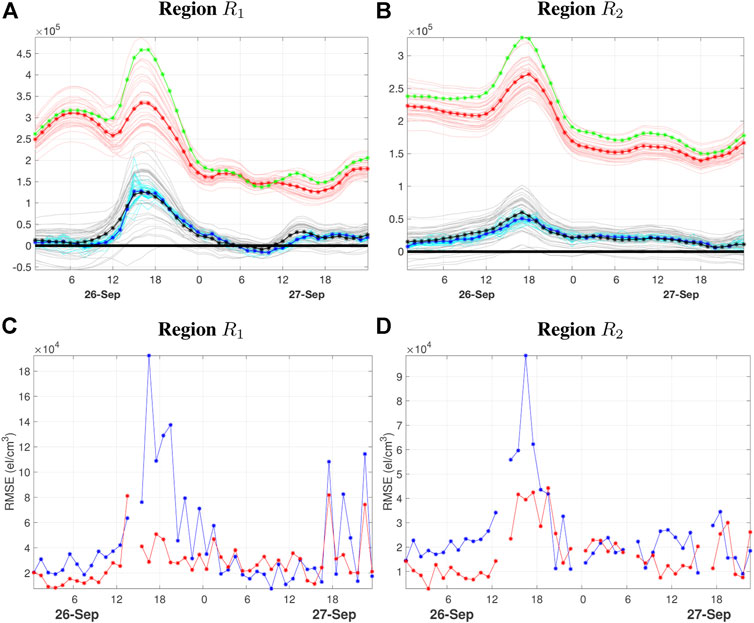
FIGURE 6. (A,B) Time series of bias correction parameters averaged over regions $R_1$ and $R_2$, respectively. The bias correction values in this figure are calculated in the same manner as Figures 3A,B, but in the case where the bias evolution operator described in Section 5 is used. (C,D) Time series of the root mean squared error (RMSE) of 1 h forecasted electron density predictions, in $\text{el}/{\text{cm}}^3$ in regions $R_1$ and $R_2$, respectively. The RMSE values in this figure are calculated in the same manner as Figures 4A,B, but in the case where the bias evolution operator described in Section 6 is used.

Figures 6C,D show the corresponding RMSE time series of 1-h electron density predictions over regions R₁ and R₂ in the case where the growth-relaxation model is used for $\mathbf{G}$. These RMSE time series are computed as described in Section 5.2 and are analogous to those shown in Figures 4A,B. An overall improvement is seen throughout the duration of the geomagnetic storm over regions R₁ and R₂. The most notable benefits of the bias corrections occur during the relaxation phase, where there is improvement of about 40 and 20% in regions R₁ and R₂, respectively, compared to the persistent bias evolution model.

Figure 7 summarizes the spatial distribution of the bias corrections at same representative times of the geomagnetic storm. For comparison, Figure 7A shows the same background electron density bias from Figure 2A, computed as ${\overline{\mathbf{e}}}^b-{\mathbf{e}}^t$. This quantity yields the model error in 1-h electron density predictions at each of the indicated altitudes and times. Figure 7B shows the global distribution of background bias corrections, ${\overline{\mathbf{c}}}^b$, at the same altitude and times as Figure 2A. Locations where the bias corrections are red (blue) correspond to regions where the bias corrections are positive (negative). Comparison with Figure 7A demonstrates that the spatial structure of bias corrections provides a reasonable estimate of the electron density bias, particularly over the daytime mid-latitude regions. Figure 7C shows the difference between Figure 7B and Figure 7A, which indicate what the remaining model error would be after the bias corrections are added at each grid point. Locations where the bias corrections overestimate (underestimate) the model bias are shown in red (blue).

FIGURE 7

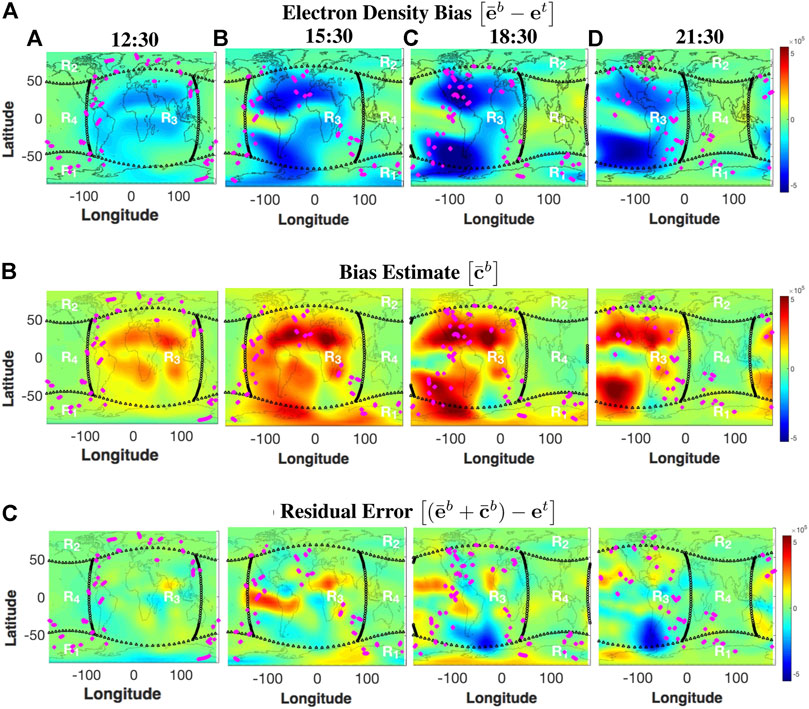
FIGURE 7. (A) Same global maps of electron density bias as shown in Figure 2A. (B) Spatial structure of the bias correction estimates, ${\overline{\mathbf{c}}}_L^b$, at the same times and altitudes. (C) Analogous global maps of electron density bias after the field of correction estimates is added.

Although there is considerable improvement in the overall bias distribution, there are a few locations where the bias correction scheme does not accurately represent the model bias, mainly in regions of sparse data coverage. Overall, the background prediction of electron density is improved at the observed locations, so that the data assimilation procedure may produce a more gentle update during the assimilation of the observations.

Figure 8A shows 1-h predictions of electron density averaged over all vertical profiles in region R₁ at 12:30, 15:30, 18:30 and 21:30 UTC on September 26, 2011. The horizontal axis is electron density in $\text{el}/{\text{cm}}^3$ and the vertical axis is altitude in km. The region-averaged observations are shown in green, and the analogously averaged electron density is shown for the background ensemble mean before (blue) and after (red) the bias corrections are applied. The vertical structure of the applied bias corrections is given by the black curves. The vertical structure of the bias corrections varies similarly to that of the electron density profiles, although the maximum corrections are applied above the F-layer and there are negative corrections applied at altitudes slightly below the F-layer at certain assimilation times. The applied bias corrections improve state estimates of the maximum electron density in the F2-layer (NmF2) and its altitude (hmF2) considerably, particularly during the main phase of the storm (15:30 UTC and 19:30 UTC). Analogous plots of bias corrections applied to regions R₂ and R₃ are shown in Figures 8B,C, respectively. Similar improvements in peak density and altitude are observed over these regions. The bias corrections for the most part correctly increase the electron density peak and its altitudes, but there are times where the electron density peak is correctly for improved agreement with the truth.

FIGURE 8

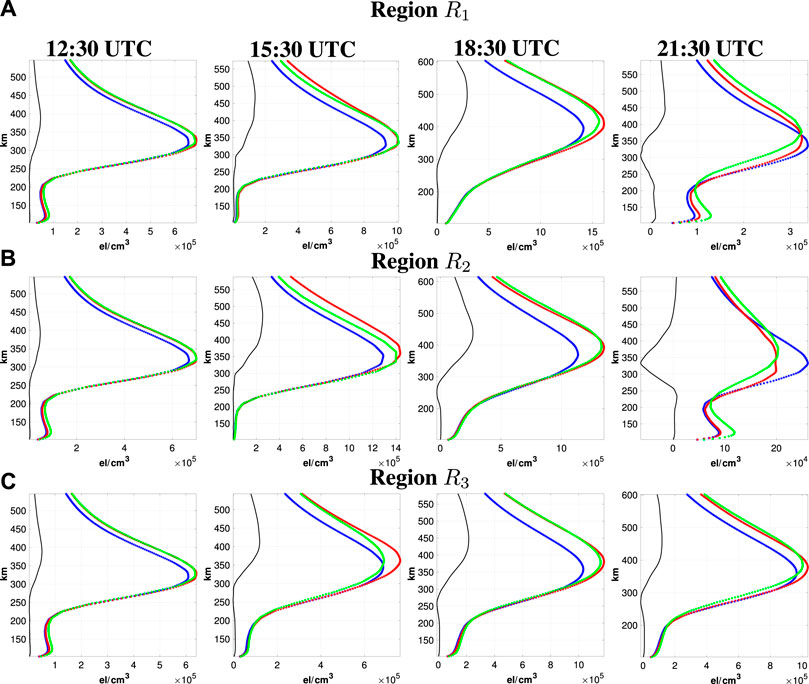
FIGURE 8. (A) Comparison of 1 h electron density vertical profile predictions at the indicated times on September 26, 2011. The green profile in each figure is the average of all COSMIC electron density vertical profiles located in region $R_1$ (as defined in Figure 2A). The forecasted electron density is also shown before (blue) and after (red) the bias correction, shown by the black curve, is applied. (B,C) Analogous comparison of electron density predictions over regions $R_2$ and $R_3$ at the same times. In all figures, the vertical axis is altitude in km and the horizontal axis is electron density in $\text{el}/{\text{cm}}^3$.

6.3 Discussion

The main point of this exercise is to show that it may be possible, using relatively few parameters, to devise a characterization of model error that can improve short-term forecasts. Further refinement of the bias estimation procedure, particularly in the time interval following the storm peak, should be possible.

The parameterization procedure described above uses the RMSE between the predicted and “true” values of the electron density (assuming a persistent-bias model) to determine the growth and decay factors ${\lambda }_n$ for the various polar regions and altitudes. The question of how to determine optimal values for the bias factors ${\lambda }_n$ beyond the data used for this particular geomagnetic storm is nontrivial and is deferred to a future study, but we outline some potential approaches here.

Various authors have sought to devise useful statistical characterizations of geomagnetic storms. No comprehensive review of these efforts is attempted here, but as an illustration, we mention the “epoch analysis” of [59], who analyzed disturbance time index (Dst) data from 305 geomagnetic storms. They define 1) the start time of each storm (i.e., the commencement of the main phase) as the time at which Dst first crosses zero; 2) the peak of the storm as the time at which Dst achieves a minimum value, $D_{\text{ min}}$; and 3) the ending time as when Dst recovers to values above $\frac{1}{10}{D}_{\text{ min}}$. (The Dst index is available from the WDC for Geomagnetism, Kyoto at http://wdc.kugi.kyoto-u.ac.jp/dstdir/.) They also define “intense” geomagnetic storms as those for which $D_{\text{ min}}<-100\text{ nT}$; “class 1” moderate storms, $-100\text{ nT}\le D_{\text{ min}}<-50\text{ nT}$; “class 2” moderate storms, $-50\text{ nT}\le D_{\text{ min}}<-30\text{ nT}$; and “weak” storms, $D_{\text{ min}}\ge -30\text{ nT}$.

The left half of the regression interval in Figure 5 corresponds approximately from the time when the Dst index first increases from its background value to when Dst first becomes negative (i.e., the start of the main storm phase). The right half corresponds approximately to the main phase of the storm, ending at the peak, when Dst reaches its relative minimum. One potential indicator of an impending geomagnetic storm is when the 1-h forecast errors begin to increase substantially; perhaps it will be possible to define a threshold value to initiate bias correction. Our initial numerical results suggest that once of the peak of the storm is reached, the forecast ensemble tracks the electron density reasonably well during the recovery phase without bias correction, although improvements may be possible.

By the criteria of [59], the September 26–27, 2011 storm would be classified as intense, because $D_{\text{ min}}=-118\text{ nT}$. Proceeding in a similar manner over prior geomagnetic storms, and using RMSE values between predicted and previously analyzed ionospheric quantities like total electron content (TEC), one might try to determine averaged values of the bias correction parameters as a function of storm intensity, latitude, altitude, season, etc., that are suitable for use with an operational data assimilation system.

The Dst is but one possible index to consider for this purpose. Other proposed ionospheric storm scales, such as one based on TEC and $f_0{F}_2$ statistics [60], might be better choices. Future work, using data from many prior geomagnetic storms, is needed to develop improved model bias parameterizations.

7 Conclusion

A general strategy for model bias correction is presented within a data assimilation system for complex and sparsely observed dynamical systems. The proposed strategy is applied in observing system experiments corresponding to extreme conditions, in which the geomagnetic storm of September 26–27, 2011 with a global ionospheric circulation model, the TIEGEM. Synthetic electron density vertical profiles, whose locations are given by the operational COSMIC satellite observing network during the time period of the storm, are assimilated using the LETKF. Systematic model bias in electron density predictions is simulated through the misspecification of parameterized solar and magnetospheric inputs to the TIEGCM, which specify key dynamics in the ionosphere. The spatial distribution of electron density bias is estimated through a state-augmentation approach. The bias estimates are applied in the evaluation of the forward operator, with the intent to reduce the effect of model errors in the predicted electron densities prior to the assimilation of observations. This methodology permits spatially varying estimation of model bias, which may be useful during extreme events, to account for storm-time effects that are not well represented with the parameterized representation of the solar and magnetospheric drivers alone.

The results of this study suggest that relatively simple models for bias correction can provide significant improvements in 1-h electron density forecasts when the model error arises from a systematic misspecification of the ionospheric driving parameters. Two such models are considered: one in which the bias is assumed constant, and another in which an exponential growth and relaxation process is assumed in the electron density.

The constant-bias assumption underestimates the growth in the model error during the initial storm phase and overestimates it during the relaxation storm phase, particularly for the electron density over high-latitude regions. This persistence model does not adjust the bias estimates quickly enough to capture their temporal variability. Additionally, the observing network is relatively sparse over high-latitude regions during the time period under study, which further slows the adjustment of the bias estimates. Nevertheless, the bias corrections yield considerable improvements in 1-h forecasts of electron density in certain regions prior to onset of the geomagnetic storm and during the initial and main phases; however, the 1-h forecasts are worse with the bias correction during the relaxation phase.

The benefits of the second bias-correction approach, which uses a growth-relaxation model for the electron density, are seen in 1-h electron density predictions over high-latitude regions during transitionary periods of the geomagnetic storm, when the temporal variations in model bias are most prominent. Model bias corrections over the Southern polar region (R₁) yield on average about 45 and 35% improvements in 1 h electron density predictions during the main and relaxation phases of the storm, respectively. The Northern polar region (R₂) displays a similar peak in model bias evolution, and bias corrections yield an improvement of about 45 and 20% during the main and relaxation phases, respectively. Over daytime low-latitude regions, a steady improvement of about 25% is observed throughout the simulation. One-hour predictions of the global distribution of model bias are approximated reasonably well with the bias correction strategy overall. The bias corrections also yield adequate estimates of the vertical structure of the model bias and considerably improves 1-h electron density predictions of the observed vertical profiles, including the adjustment of the F-layer peak and its altitude.

The experiments presented in this paper provide a proof of concept. The results are established with synthetically generated observations, which allows us to quantify specifically the effect of the bias correction on 1-h forecasts of electron density. The choice of bias evolution operator is important when there are significant temporal variations in the model’s dynamical variables and when the observing network is sparse. Extensions to real observations will be considered in future work.

The approach described in this paper may be an effective tool for model bias estimation during geomagnetic storms, provided that there are qualitative similarities in the temporal variations of model bias during these time periods. For example, the bias model employed in our numerical experiments may be applied during other geomagnetic storms in which positive and negative storm-time effects are expected during the initial and relaxation phases, respectively. Further studies of previous geomagnetic storms may help provide improved estimates of typical temporal variations in the electron bias evolution, which may depend on solar/geomagnetic activity, latitude, pressure level, and/or season.

The extension of this approach to real observations presents some open problems. One obvious question involves model errors arising from subgrid parameterizations and uncertainties in the solar and geomagnetic driving parameters. Representativeness error in the observations must also be considered. The results presented here suggest that relatively simple dynamical characterizations of the model bias can yield a stable filter and improve 1-h forecasts of electron density. Nevertheless, better choices of the bias evolution operator ${\mathbf{G}}_n$ surely can be found. Reanalyses of prior geomagnetic storm events and efforts to quantify the effect of different choices of solar and magnetospheric inputs may help to quantify the dynamical interaction between biases in multiple model variables. These questions will be the subject of future work.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JD, EK, and AM contributed to conception and design of the computational study. JD performed the data analysis. JD, EK, and AM wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The TIEGCM was obtained from the High Altitude Observatory, NCARData files containing solar and geomagnetic parameters used in this paper are published by NOAA and are packaged in the TIEGCM code. The COSMIC data information was obtained from the COSMIC Data Analysis and Archive Center (CDAAC) at UCAR (http://cdaac-www.cosmic.ucar.edu). This material is based upon work supported by the Air Force Office of Scientific Research under the award number FA9550-19-1–0064.

Appendix

Bias Estimation Algorithm Pseudocode

The following algorithm demonstrates the procedure used to compute the analysis at an arbitrary grid point L, and how the model bias corrections are applied and updated. We assume there are d components in the local state vector, ${\mathbf{x}}_L^b$, including the bias correction parameter, and that the ensemble is of size k. The quantities below are related to the grid point L and its associated local region, where we assume there are $\ell$ observations. The computations below may be performed independently (and in parallel) at each grid point L.

Analysis Computation

A detailed description of the analysis calculation and the associated computational complexity is provided in [25]. In the following suppose the forecast and bias estimates have been propagated to a time $t_n$, so that the global state vector is given by ${\mathbf{u}}_n^{b\left(j\right)}={\mathbf{M}}_n\left[{\mathbf{u}}_{n-1}^{a\left(j\right)}\right]$ and the global bias correction vector is given by ${\mathbf{c}}_n^b={\mathbf{G}}_{n-1}\left({\mathbf{c}}_{n-1}^a\right)$. Now consider the analysis update of a local state vector, ${\mathbf{x}}_L^{b\left(j\right)}$ at a fixed grid point L.

a. Construct the $d\times k$ matrix ${\mathbf{X}}_L^b$, corresponding to the augmented local state vector ${\left[{\left({\mathbf{x}}_L^{b\left(j\right)}\right)}^{\text{T}}{\left({\mathbf{c}}_L^{b\left(j\right)}\right)}^{\text{T}}\right]}^{\text{T}}.$

b. Construct the $\ell \times k$ matrix, ${\mathbf{Y}}_L^b={\mathbf{H}}_L\left({\mathbf{u}}^{b\left(j\right)}+{\mathbf{c}}^{b\left(j\right)}\right)$ as described in Section 3.

c. Form the $k\times \ell$ matrix ${\mathbf{G}}_L={\left({\mathbf{Y}}_L\right)}^{\text{T}}{\left({\mathbf{R}}_L\right)}^{-1}$

d. Compute the $k\times k$ analysis covariance matrix,

${\tilde{\mathbf{P}}}_L^a={\left[\left(k-1\right)\mathbf{I}/{\alpha }_L+{\mathbf{G}}_L{\mathbf{Y}}_L\right]}^{-1}.$

e. The analysis ensemble is constructed in terms of the “weight matrix”, ${\mathbf{W}}_L^a$, which is computed in two steps.

1) Compute the $k\times k$. symmetric square root of the analysis covariance matrix,

${\widehat{\mathbf{W}}}_L^a={\left[\left(k-1\right){\tilde{\mathbf{P}}}_L^a\right]}^{1/2}.$

2)Define the k-vector ${\overline{\mathbf{w}}}^a={\tilde{\mathbf{P}}}_L^a{\mathbf{G}}_L\left({\mathbf{y}}^o-{\overline{\mathbf{y}}}_L\right)$ and add it to each column ${\widehat{\mathbf{W}}}_L^a$ to form the $k\times k$ weight matrix ${\mathbf{W}}_L^a$.

f. Compute the analysis perturbation matrix ${\mathbf{X}}_L^a={\mathbf{X}}_L^b{\mathbf{W}}_L^a$.

g. The jth column of the analysis ensemble is formed by adding the background ensemble mean, ${\overline{\mathbf{x}}}_L^b$, to the jth column of ${\mathbf{X}}_L^a$, $j=\mathrm{1,2},\dots ,k$.

Propagate Ionospheric and Model Bias State Estimates

a. Apply forecast model ${\mathbf{M}}_n$ (given by the TIEGCM).

b. Compute ${\mathbf{u}}_{n+1}^{b\left(j\right)}={\mathbf{M}}_{n+1}\left({\mathbf{u}}_n^{a\left(j\right)}\right)$

c. Apply bias evolution operator $\mathbf{G}$ to compute ${\mathbf{c}}_{n+1}^b={\mathbf{G}}_{n+1}\left({\mathbf{c}}_n^a\right)$

References

1.N. R. C. S. S Board. Space Weather and Space Climatology: A Vision for Future Capabilities. In: Solar and Space Physics: A Science for a Technological Society. Washington, DC: National Academies Press, (2013). ch. 7, pp. 135–46.

Google Scholar

2. Kelley, MC. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, Vol. 96 of International Geophysics. 2nd ed. Cambridge, United States: Academic Press(2009).

3. Materassi, M, Forte, B, Coster, AJ, and Skone, S, eds. The Dynamical Ionosphere: A Systems Approach to Ionospheric Irregularity. Amsterdam, Netherlands: Elsevier (2020).

4. Schunk, R, and Nagy, A. Ionospheres: Physics, Plasma Physics, and Chemistry, Cambridge Atmospheric and Space Science Series. 2nd ed. Cambridge, UK: Cambridge University Press (2018).

5. Bilitza, D, and Reinisch, B. International Reference Ionosphere 2007: Improvements and New Parameters. Adv Space Res (2007). 42:599–609. doi:10.1016/j.asr.2007.07.048

CrossRef Full Text | Google Scholar

6.N. C. F. A. R. High-Altitude Observatory. Available at: https://www.hao.ucar.edu/modeling/tgcm/ (Accessed May 15, 2019).

Google Scholar

7. Durazo, JA, Kostelich, EJ, and Mahalov, A. Local Ensemble Transform Kalman Filter for Ionospheric Data Assimilation: Observation Influence Analysis during a Geomagnetic Storm Event. J Geophys Res Space Phys (2017). 122:9652–69. doi:10.1002/2017JA024274

CrossRef Full Text | Google Scholar

8. Abarzhi, S. Coherent Structures and Pattern Formation in Rayleigh-Taylor Turbulent Mixing. Phys Scr (2008). 78:015401. doi:10.1088/0031-8949/78/01/015401

CrossRef Full Text | Google Scholar

9. Abarzhi, SI. Review of Theoretical Modelling Approaches of Rayleigh-Taylor Instabilities and Turbulent Mixing. Philos Trans R Soc A (2010). 368:1809–28. doi:10.1098/rsta.2010.0020

CrossRef Full Text | Google Scholar

10. Abarzhi, S, and Rosner, R. A Comparative Study of Approaches for Modeling Rayleigh-Taylor Turbulent Mixing. Phys Scr (2010). T142:014012. doi:10.1088/0031-8949/2010/t142/014012

CrossRef Full Text | Google Scholar

11. Mahalov, A, and Moustaoui, M. Multiscale Nested Simulations of Rayleigh-Taylor Instabilities in Ionospheric Flows. J Fluid Eng (2013). 136:021202. doi:10.1115/1.4025657

CrossRef Full Text | Google Scholar

12. Mahalov, A. Multiscale Modeling and Nested Simulations of Three-Dimensional Ionospheric Plasmas: Rayleigh-Taylor Turbulence and Nonequilibrium Layer Dynamics at Fine Scales. Phys Scr (2014). 89:098001. doi:10.1088/0031-8949/89/9/098001

CrossRef Full Text | Google Scholar

13. Cheng, B, and Mahalov, A. General Results on Zonation in Rotating Systems with a β-Effect and the Electromagnetic Force. In: B Galperin, and P Read, editors. Zonal Jets: Phenomenology, Genesis, and Physics. Cambridge, UK: Cambridge University Press (2019). p. 209–19. doi:10.1017/9781107358225.012

CrossRef Full Text | Google Scholar

14. Galperin, B, and Read, P eds. Zonal Jets: Phenomenology, Genesis, and Physics. Cambridge, United Kingdom: Cambridge University Press (2019).

15. Tang, W, and Mahalov, A. Stochastic Lagrangian Dynamics for Charged Flows in the E-F Regions of Ionosphere. Phys Plasmas (2013). 20:032305. doi:10.1063/1.4794735

CrossRef Full Text | Google Scholar

16. Tang, W, and Mahalov, A. The Response of Plasma Density to Breaking Inertial Gravity Waves in the Lower Regions of Ionosphere. Phys Plasmas (2014). 21:042901. doi:10.1063/1.4870760

CrossRef Full Text | Google Scholar

17. Zhou, Y. Rayleigh-Taylor and Richtmyer-Meshkov Instability Induced Flow, Turbulence, and Mixing. I. Phys Rep (2017). 720–722:7201–136. doi:10.1016/j.physrep.2017.07.005 |

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhou, Y. Rayleigh-Taylor and Richtmyer-Meshkov Instability Induced Flow, Turbulence, and Mixing. II. Phys Rep (2017). 723–725:1–160. doi:10.1016/j.physrep.2017.07.008 |

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Merkin, VG, Kondrashov, D, Ghil, M, and Anderson, BJ. Data Assimilation of Low-Altitude Magnetic Perturbations into a Global Magnetosphere Model. Space Weather (2016). 14:165–84. doi:10.1002/2015SW001330

CrossRef Full Text | Google Scholar

20. Eyre, JR. Observation Bias Correction Schemes in Data Assimilation Systems: A Theoretical Study of Some of Their Properties. Q J R Meteorol Soc (2016). 142:2284–91. doi:10.1002/qj.2819

CrossRef Full Text | Google Scholar

21. Gilman, M, Smith, E, and Tsynkov, S. Transionospheric Synthetic Aperture Imaging. Cham: Birkäuser (2017). doi:10.1007/978-3-319-52127-5

CrossRef Full Text

22. Godinez, HC, Lawrence, E, Higdon, D, Ridley, A, Koller, J, and Klimenko, A. Specification of the Ionosphere-Thermosphere Using the Ensemble Kalman Filter. In: S Ravela, and A Sandu, editors. Dynamic Data-Driven Environmental Systems Science, DyDESS. Cham: Birkäuser (2014). p. 274–83.

Google Scholar

23. Heelis, RA, Lowell, JK, and Spiro, RW. A Model of the High-Latitude Ionospheric Convection Pattern. J Geophys Res (1982). 87:6339–45. doi:10.1029/JA087iA08p06339

CrossRef Full Text | Google Scholar

24. Hsu, CT, Matsuo, T, Wang, W, and Liu, JY. Effects of Inferring Unobserved Thermospheric and Ionospheric State Variables by Using an Ensemble Kalman Filter on Global Ionospheric Specification and Forecasting. J Geophys Res Space Phys (2014). 119:9256–67. doi:10.1002/2014ja020390

CrossRef Full Text | Google Scholar

25. Hunt, BR, Kostelich, EJ, and Szunyogh, I. Efficient Data Assimilation for Spatiotemporal Chaos: A Local Ensemble Transform Kalman Filter. Phys D Nonlinear Phenomena (2007). 230:112–26. doi:10.1016/j.physd.2006.11.008

CrossRef Full Text | Google Scholar

26. Jin, J, Lin, HX, Segers, A, Xie, Y, and Heemink, A. Machine Learning for Observation Bias Correction with Application to Dust Storm Data Assimilation. Atmos Chem Phys (2019). 19:10009–26. doi:10.5194/acp-2019-298

CrossRef Full Text | Google Scholar

27. Koller, J, Brennan, S, Godinez, H, Higdon, D, Koller, J, and Lawrence, E. Integrated Modeling of Perturbations in Atmospheres for Conjunction Tracking. In: AMOS Conference: LA-UR-13-26931 (2013).

Google Scholar

28. Lee, IT, Matsuo, T, Liu, JY, Wang, W, and Lin, CH. Assimilation of FORMOSAT-3/COSMIC Electron Density Profiles into a Coupled Thermosphere/ionosphere Model Using Ensemble Kalman Filtering, J Geophys Res (2012). 117:A10318. doi:10.1029/2012ja017700

CrossRef Full Text | Google Scholar

29. Li, W, Huang, L, Zhang, S, and Chai, Y. Assessing Global Ionosphere TEC Maps with Satellite Altimetry and Ionospheric Radio Occultation Observations. Sensors (2019). 19:5489. doi:10.3390/s19245489 |

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kuo, JY, Lin, CY, Lin, CH, Tsai, HF, Solomon, SC, Sun, YY, et al. Artificial Plasma Cave in the Low-Latitude Ionosphere Results from the Radio Occultation Inversion of the FORMOSAT-3/COSMIC. J Geophys Res (2010). 115. doi:10.1029/2009JA015079

CrossRef Full Text | Google Scholar

31. Matsuo, T, and Araujo-Pradere, EA. Role of Thermosphere-Ionosphere Coupling in a Global Ionospheric Specification. Radio Sci (2011). 46:RS0D23. doi:10.1029/2010rs004576

CrossRef Full Text | Google Scholar

32. Matsuo, T, Lee, IT, and Anderson, J. Upper Atmosphere Data Assimilation with an Ensemble Kalman Filter. Washington, DC: AGU (2013). p. RS0D23.

33. Dee, DP. Bias and Data Assimilation. Q J R Meteorol Soc (2005). 131:3323–43. doi:10.1256/qj.05.137

CrossRef Full Text | Google Scholar

34. Dee, DP, and da Silva, AM. Data Assimilation in the Presence of Forecast Bias. Q J R Meteorol Soc (1998). 124:269–95. doi:10.1002/qj.49712454512

CrossRef Full Text | Google Scholar

35. Aravéquia, JA, Szunyogh, I, Fertig, EJ, Kalnay, E, Kuhl, D, and Kostelich, EJ. Evaluation of a Strategy for the Assimilation of Satellite Radiance Observations with the Local Ensemble Transform Kalman Filter. Mon Weather Rev (2011). 139:1932–51. doi:10.1175/2010MWR3515.1

CrossRef Full Text | Google Scholar

36. Canter, M, Barth, A, and Beckers, J-M. Correcting Circulation Biases in a Lower-Resolution Global General Circulation Model with Data Assimilation. Ocean Dyn (2017). 67:281–98. doi:10.1007/s10236-016-1022-3

CrossRef Full Text | Google Scholar

37. Baek, SJ, Hunt, BR, Kalnay, E, Ott, E, and Szunyogh, I. Local Ensemble Kalman Filtering in the Presence of Model Bias. Tellus A Dyn Meteorol Oceanogr (2006). 58:293–306. doi:10.1111/j.1600-0870.2006.00178.x

CrossRef Full Text | Google Scholar

38. Codrescu, SM, Codrescu, MV, and Fedrizzi, M. An Ensemble Kalman Filter for the Thermosphere-Ionosphere. Space Weather (2018). 16:57–68. doi:10.1002/2017SW001752

CrossRef Full Text | Google Scholar

39. Tsurutani, BT, Verkhoglyadova, OP, Mannucci, AJ, Lakhina, GS, Li, G, and Zank, GP. A Brief Review of Solar Flare Effects on the Ionosphere. Radio Sci (2009). 44:RS0A17. doi:10.1029/2008rs004029

CrossRef Full Text | Google Scholar

40. Buensanto, M. Ionospheric Storms - A Review. Space Sci Rev (1999). 88:563–601. doi:10.1029/2010RG000340

CrossRef Full Text | Google Scholar

41. Dubey, S, Wahi, R, and Gwal, AK. Ionospheric Effects on Gps Positioning. Adv Space Res (2006). 38:2478–84. doi:10.1016/j.asr.2005.07.030

CrossRef Full Text | Google Scholar

42. Stauning, P. Power Grid Disturbances and Polar Cap Index during Geomagnetic Storms. J Space Weather Space Clim (2013). 3:A22. doi:10.1051/swsc/2013044

CrossRef Full Text | Google Scholar

43. Weimer, DR. Improved Ionospheric Electrodynamic Models and Application to Calculating Joule Heating Rates. J Geophys Res (2005). 110:A05306. doi:10.1029/2004JA010884

CrossRef Full Text | Google Scholar

44. Tan, Y, Hu, Q, Wang, Z, and Zhong, Q. Geomagnetic Index kp Forecasting with LSTM. Space Weather (2018). 16:406–16. doi:10.1002/2017SW001764

CrossRef Full Text | Google Scholar

45. Wing, S, Johnson, JR, Jen, J, Meng, C-I, Sibeck, DG, Bechtold, K, et al. Kp Forecast Models. J Geophys Res Space Phys (2005). 110:A04203. doi:10.1029/2004ja010500

CrossRef Full Text | Google Scholar

46. Xu, W. Uncertainty in Magnetic Activity Indices. Sci China Ser E Technol Sci (2008). 51:1659–64. doi:10.1007/s11431-008-0261-z

CrossRef Full Text | Google Scholar

47. Pi, X, Mannucci, AJ, Iijima, BA, Wilson, BD, Komjathy, A, Runge, TF, et al. Assimilative Modeling of Ionospheric Disturbances with FORMOSAT-3/COSMIC and Ground-Based GPS Measurements. Terr Atmos Ocean Sci (2009). 20:273–85. doi:10.3319/TAO.2008.01.04.01(F3C)

CrossRef Full Text | Google Scholar

48. Chartier, AT, Jackson, DR, and Mitchell, CN. A Comparison of the Effects of Initializing Different Thermosphere-Ionosphere Model Fields on Storm Time Plasma Density Forecasts. J Geophys Res Space Phys (2013). 118:7329–37. doi:10.1002/2013ja019034

CrossRef Full Text | Google Scholar

49. Ruiz, JJ, Pulido, M, and Miyoshi, T. Estimating Model Parameters with Ensemble-Based Data Assimilation: A Review. J Meteorol Soc Jpn (2013). 91:79–99. doi:10.2151/jmsj.2013-201

CrossRef Full Text | Google Scholar

50. Bellsky, T, Berwald, J, and Mitchell, L. Nonglobal Parameter Estimation Using Local Ensemble Kalman Filtering. Monthly weather Rev (2014). 142:2150–64. doi:10.1175/mwr-d-13-00200.1

CrossRef Full Text | Google Scholar

51. Pedatella, NM, Lei, J, Larson, KM, and Forbes, JM. Observations of the Ionospheric Response to the 15 December 2006 Geomagnetic Storm: Long-Duration Positive Storm Effect. J Geophys Res Space Phys (2009). 114. doi:10.1029/2009JA014568

CrossRef Full Text | Google Scholar

52 Chartier, AT, Matsuo, T, Anderson, JL, Collins, N, Hoar, TJ, Lu, G, et al. Ionospheric Data Assimilation and Forecasting during Storms. J Geophys Res Space Phys (2016). 121:764–78. doi:10.1002/2014JA020799

CrossRef Full Text | Google Scholar

53. Rocken, C, Kuo, YH, Schreiner, WS, Sokolovskiy, S, and McCormick, C. COSMIC System Description, Terr Atmos Ocean Sci (2000). 11:21–52.doi:10.3319/tao.2000.11.1.21(cosmic)

CrossRef Full Text | Google Scholar

54. Durazo, J, Kostelich, E, Mahalov, A, and Tang, W. Observing System Experiments with an Ionospheric Electrodynamics Model. Phys Scr (2016). 91:044001. doi:10.1088/0031-8949/91/4/044001

CrossRef Full Text | Google Scholar

55. Miyoshi, T. The Gaussian Approach to Adaptive Covariance Inflation and its Implementation with the Local Ensemble Transform Kalman Filter. Mon Weather Rev (2011). 139:1519–35. doi:10.1175/2010mwr3570.1

CrossRef Full Text | Google Scholar

56. Richards, PG, Fennelly, JA, and Torr, DG. EUVAC: A Solar EUV Flux Model for Aeronomic Calculations. J Geophys Res (1994). 99:8981–92. doi:10.1029/94JA00518

CrossRef Full Text | Google Scholar

57. Szunyogh, I, Kostelich, EJ, Gyarmati, G, Kalnay, E, Hunt, BR, Ott, E, et al. A Local Ensemble Transform Kalman Filter Data Assimilation System for the NCEP Global Model, Tellus A Dyn Meteorol Oceanogr (2008). 60:113–30. doi:10.1111/j.1600-0870.2007.00274.x

CrossRef Full Text | Google Scholar

58. Hunt, X, Schreiner, WS, Lei, J, Sokolovskiy, SV, Rocken, C, Hunt, DC, et al. Error Analysis of Abel Retrieved Electron Density Profiles from Radio Occultation Measurements. Ann Geophys (2010). 28:217–22. doi:10.5194/angeo-28-217-2010

CrossRef Full Text | Google Scholar

59. Yokoyama, N, and Kamide, Y. Statistical Nature of Geomagnetic Storms. J Geophys Res (1997). 102:14215–22. doi:10.1029/97ja00903

CrossRef Full Text | Google Scholar

60. Nishioka, M, Tsugawa, T, Jin, H, and Ishii, M. A New Ionospheric Storm Scale Based on TEC and f₀f₂ Statistics. Space Weather (2017). 15:228–39. doi:10.1002/2016sw001536

CrossRef Full Text | Google Scholar