- 1NORCE Norwegian Research Center, Bergen, Norway
- 2University of Bergen, Bergen, Norway
With large amounts of simultaneous data, like inverted seismic data in reservoir modeling, negative effects of Monte Carlo errors in straightforward ensemble-based data assimilation (DA) are enhanced, typically resulting in underestimation of parameter uncertainties. Utilization of lower fidelity reservoir simulations reduces the computational cost per ensemble member, thereby rendering the possibility of increasing the ensemble size without increasing the total computational cost. Increasing the ensemble size will reduce Monte Carlo errors and therefore benefit DA results. The use of lower fidelity reservoir models will however introduce modeling errors in addition to those already present in conventional fidelity simulation results. Multilevel simulations utilize a selection of models for the same entity that constitute hierarchies both in fidelities and computational costs. In this work, we estimate and approximately account for the multilevel modeling error (MLME), that is, the part of the total modeling error that is caused by using a multilevel model hierarchy, instead of a single conventional model to calculate model forecasts. To this end, four computationally inexpensive approximate MLME correction schemes are considered, and their abilities to correct the multilevel model forecasts for reservoir models with different types of MLME are assessed. The numerical results show a consistent ranking of the MLME correction schemes. Additionally, we assess the performances of the different MLME-corrected model forecasts in assimilation of inverted seismic data. The posterior parameter estimates from multilevel DA with and without MLME correction are compared to results obtained from conventional single-level DA with localization. It is found that multilevel DA (MLDA) with and without MLME correction outperforms conventional DA with localization. The use of all four MLME correction schemes results in posterior parameter estimates with similar quality. Results obtained with MLDA without any MLME correction were also of similar quality, indicating some robustness of MLDA toward MLME.
1 Introduction
Sound decision-making in petroleum reservoir management depends on provision of reliable production forecasts from petroleum reservoir models, including provision of the uncertainty in the forecasts. The reliability is increased by utilization of available data for calibration of the models. Ensemble-based data assimilation (DA) methods, using statistically correct formulations, have accordingly become popular for automated reservoir history matching [1–4].
Monte Carlo approximations play crucial roles in ensemble-based DA. Due to computational cost limitations, the ensemble size is limited to roughly one hundred. Using straightforward ensemble-based DA, the degrees of freedom of the problem would equal the ensemble size, and such an approach would result in significant Monte Carlo errors. The negative effects of Monte Carlo errors are enlarged in the presence of large amounts of data to be assimilated simultaneously, for example, inverted seismic data, resulting in underestimation of variance of the unknown parameters and, in more severe cases, even in ensemble collapse.
The most widely used treatment for Monte Carlo errors is distance-based localization. The basic assumption underlying this method is that true correlations between a parameter and a datum decrease when the distance between their respective locations increases, and disappear if the distance exceeds a critical distance. This assumption may not always hold for subsurface problems. Different correlation functions and their utilization in DA can be found in References [5–7]. A proper choice of correlation function, as well as the critical distance in particular, depends on parameter and data types as well as on other problem settings. This reduces the robustness of distance-based localization, also for problems where its basic assumption does hold.
Simply increasing the ensemble size will, of course, reduce Monte Carlo errors, but it will also increase computational cost. Utilization of a lower cost and lower fidelity model renders the possibility of increasing the ensemble size without increasing the total computational cost. The use of a lower fidelity reservoir model will however introduce modeling errors in addition to those already present in conventional fidelity simulation results. The underlying assumption when applying lower fidelity models in DA is therefore that the gain in reducing Monte Carlo errors is larger than the loss in numerical simulation accuracy. If the abovementioned additional modeling errors could be approximately accounted for, utilization of lower fidelity models would be even more attractive. DA using various types of lower fidelity models has been applied to several inverse problems, for example, within petroleum reservoir modeling [8–10] and atmospheric science [11]. Note that since lower fidelity simulations are applied to the forecast step and localization is applied to the analysis step, the two techniques can be combined, if desired.
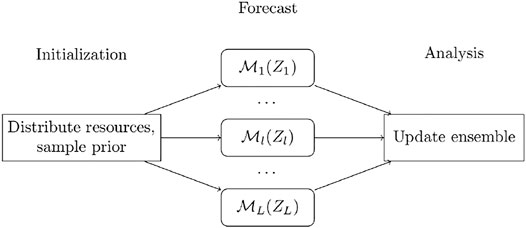
Multilevel simulations utilize a selection of models for the same entity that constitute hierarchies in both fidelities and computational costs (multilevel models). The idea is to decrease Monte Carlo errors without increasing numerical errors too much. There are a number of ways to realize multilevel models. We choose to construct them by spatial coarsening of the conventional simulation grid to several levels of coarseness and correspondingly upscale the associated grid-based parameter functions. Multilevel data assimilation (MLDA) [12–16] utilizes multilevel simulations in the forecast step. Since inverted seismic data are given on the conventional grid (denoted as the fine grid from now on), MLDA with such data must be able to handle differences in grid levels between data and model forecasts.
Modeling errors are ubiquitous in all numerical simulations in the geosciences. In the context of a coarse-grid numerical model, three types of modeling errors can be envisioned: Type 1: the discrepancy between the physical reality and the solution obtained with a mathematical model attempting to model the physical reality; Type 2: the discrepancy between the solution obtained with that mathematical model and the model forecast from a numerical model resulting from discretization of the mathematical model; and Type 3: the discrepancy between the model forecast from that numerical model and the model forecast from a numerical model with a coarser simulation grid.
Assuming a normal distribution for the errors, a Bayesian framework for jointly accounting for Type 1 and Type 2 modeling errors in DA was presented in Reference [17]. The effect of Type 2 modeling errors on the solution to linear Gaussian inverse problems was analyzed in Reference [18]. (Neither Ref. [17] nor Ref. [18] were concerned with Type 3 modeling errors.) In this study, we quantify and approximately account for Type 3 modeling errors for each level in multilevel assimilation of spatially distributed data, such as inverted seismic data. (We will use the term multilevel modeling error (MLME) to denote this error from now on.) To this end, three computationally inexpensive approximate MLME correction schemes are developed, and their abilities to correct multilevel model forecasts for reservoir models with different types of MLME are assessed and compared to a previously proposed (also computationally inexpensive) MLME correction scheme. Additionally, we assess the performances of the different MLME-corrected model forecasts in assimilation of bulk impedance data. The posterior parameter estimates from MLDA with and without MLME correction are compared to results obtained from conventional single-level DA with localization.
The rest of this article is framed as follows. Section 2 is devoted to explaining MLDA and introducing a recently devised algorithm for it. Section 3 introduces MLME and the four proposed schemes for addressing it. Section 4 explains the reservoir models used for assessment of the performance of MLME correction schemes in MLDA. In Section 5, we describe the numerical investigations, which are followed by their results in Section 6. Finally, in Section 7, we summarize and conclude the study.
2 Multilevel Data Assimilation
The forecast step in ensemble-based DA takes the initial states and parameters as input and generates the model forecasts. In this work, the forecast step of MLDA is performed using a hierarchy of nested forward models,
In order to give a description for a full cycle of MLDA of spatially distributed data, multilevel models should be discussed. Additionally, since the MLDA uses the ensemble approximations of the mean and covariance of the model forecasts, which are in different resolutions for different levels, a robust transformation scheme should be devised for converting the model forecasts from one resolution to another. These two topics will be discussed in Sections 2.1 and 2.2, respectively. They will be followed by sections on upscaling of the observation data (Section 2.3) and formulation of multilevel statistics for mean and covariance of the model forecasts (Section 2.4). Afterward, a description of a recently devised method for MLDA of spatially distributed data, which will be used in our numerical experiments, is given in Section 2.5.
2.1 Multilevel Models
Let
As for coarsening the grid of the forward models, the authors of Reference [15] proposed a robust technique, which was also used in Reference [16]. This technique occurs in a sequence of steps. In each step, neighboring cells of the grid at the previous step are merged into a coarser cell, unless they are to be kept fine deliberately. A representation of the grid coarsening process for an
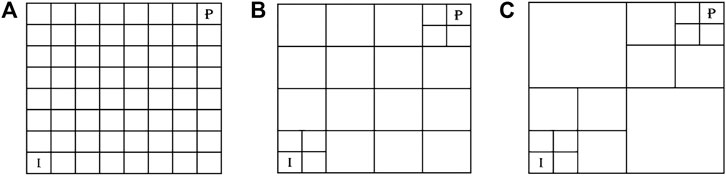
FIGURE 2. Grid coarsening proposed by [15] performed on an 8 × 8 grid (A) finest level and (B, C) coarser levels.
The parameters associated with the grid are upscaled in such a way that the physics of the problem do not change drastically. Upscaling of the parameters will be further discussed in Section 4.
2.2 Transformation of Model Forecasts
The discrepancy in coarseness of the multilevel grids results in the spatially distributed model forecasts to be in different resolutions for different levels. Therefore, in order to be able to compute the multilevel sample statistics of the model forecast, a robust transformation scheme should be devised for converting a model forecast from the resolution at one level to another.
In the problem at hand, transformation of the model forecast requires either upscaling or downscaling. To this end, a standard volume-weighted arithmetic averaging technique is used. Accordingly, we define a set of linear transformations,
Figure 3 gives two examples of transformation of a spatially distributed model forecast, one from a coarser grid to a finer grid and one vice versa. Each model forecast component is represented in its corresponding spatial grid cell.
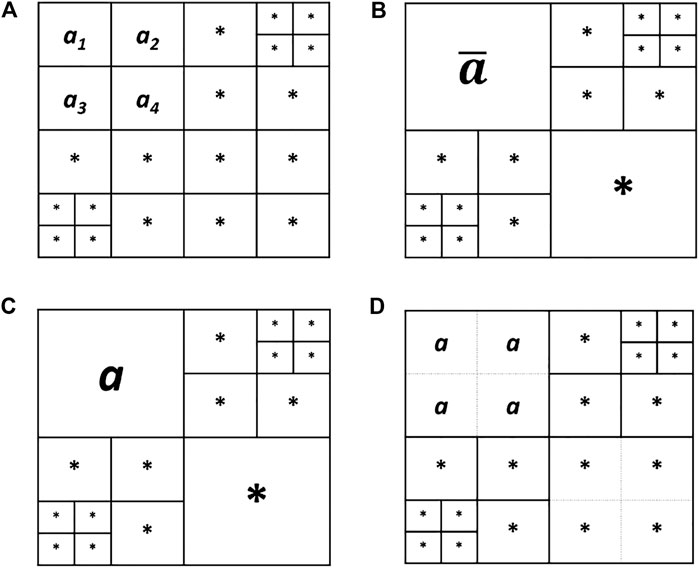
FIGURE 3. Transformation of model forecast between two levels p (finer) and q (coarser) (A) model forecast in resolution of level p, (B) transformation of model forecast from resolution of level p to the resolution of level q, (C) model forecast in resolution of level q, and (D) transformation of model forecast from resolution of level q to the resolution of level p.
As can be seen in Figure 3, in the upscaling procedure, the arbitrarily named model forecast components
2.3 Upscaling of Observation Data
As part of the DA process, the mismatch between the model forecasts and observation data is to be calculated. Here, it is assumed that inverted seismic data are given in the resolution of the finest simulation grid. Accordingly, for each of the levels, either the observation data should be upscaled to the resolution of model forecast or the model forecast should be downscaled to the resolution of the observation data. In this study, we take the former approach. Since the observation data are in the resolution of the finest model, using the same transformation functions as those designed for model forecasts on the fine observation data will result in upscaling of observation data into the preferred resolution.
2.4 Multilevel Statistics
Assuming we have approximations of the model forecasts, Y, being a function of the unknown parameter vector Z in several levels, a statistically correct scheme for approximation of multilevel statistics for Y is required. As for MLDA, the first two central moments of the model forecast are of foremost interest. Accordingly, formulations for these multilevel statistics are proposed.
Assuming the model with the highest fidelity,
where
In addition, the parameter forecast cross-covariance can be written as follows:
Using these ML moments enables us to utilize the classic DA formulations for updating the ensemble as will be presented in Section 2.5.
2.5 Multilevel Hybrid Ensemble Smoother
Utilizing statistics given by Eqs. 1–3, the authors of Reference [16] formulated an MLDA algorithm that rendered the possibility of assimilation of spatially distributed data, for example, inverted seismic data, in a multilevel manner. This DA algorithm was called multilevel hybrid ensemble smoother (MLHES). In this work, we briefly explain MLHES and utilize it in our numerical experiments. An iterative version of MLHES has also been developed1.
Initially, a total of
The correction for MLME then would be performed as
where
After MLME correction, there will be a separate analysis step for each of the levels. The updated parameter vector of an arbitrary ensemble member is given by
where the observation data realization,
where the multilevel statistics
After the analysis step, the estimates of mean and covariance of the posterior parameter field are computed based on a pool composed of all realizations
A pseudo-code of MLHES is presented in Appendix 1.
3 Multilevel Modeling Error
Let R denote some spatially varying physical property, and let W denote the forecast of a mathematical model attempting to model R. Furthermore, let
which can be rewritten as
The first term on the right-hand side of Eq. 11 represents the error in the mathematical model’s forecast of physical reality, and the second term represents the discretization error when simulating with a numerical model on the fine grid. We will consider the last term, which represents the error due to numerical simulation on the level-l grid, instead of on the fine grid.
The expression
and develop techniques for estimating
3.1 Multilevel Modeling Error Correction
Assuming fine model forecasts to be sufficiently accurate, ideally, the model forecasts at each level should be upscaled fine model forecasts to the resolution of that level, that is, the correction in Eq. 5 should be
The techniques developed here are therefore computationally cheap adjunctions which can be added to many MLDA algorithms with minor modifications. The four schemes formulated and investigated in this work are named as mean bias correction (MB), stochastic correction (ST), deterministic correction (DE), and telescopic correction (TE).
Figure 4A depicts general formation of the sub-ensembles from the prior ensemble for Z. The realizations in each sub-ensemble are put in the same line as the forward model that is used for their simulation; consider each of the unit cells in the rows as a realization of the prior and each row as a sub-ensemble. Figures 4B–D describe the requirements on prior realizations for different MLME correction schemes; if parts of two sub-ensembles are of the same color, those realizations are shared between those sub-ensembles and are to be simulated using both corresponding forward models.
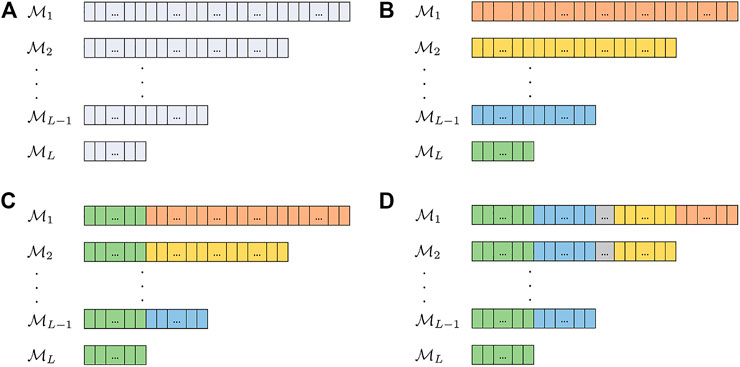
FIGURE 4. (A) Division of the prior ensemble for Z into L sub-ensembles, (B) mean bias Correction prior setting, (C) stochastic and deterministic corrections prior settings, and (D) telescopic correction prior setting.
3.1.1 Mean Bias Correction
This technique was used in Reference [12] for correction of the production data for their mean bias. There, the correction was formulated as
where
where E(YL) and E(Yl) are sample means of the model forecasts at levels L and l, respectively. Using this correction, the mean of the corrected forecast at every level would be equal to the upscaled mean of the forecast given by the most accurate (finest) model.
As can be seen in Figure 4B, in mean bias correction, as opposed to the rest of MLME correction schemes, the prior realizations are run on each of the forward models without any requirement to be run by other forward models.
3.1.2 Stochastic Correction
Simulating the sub-ensemble
In the stochastic formulation, assuming a normal distribution for
where
As seen in Figure 4C and Eq. 15, this correction scheme requires the realizations at sub-ensemble L to be simulated using all the forward models.
3.1.3 Deterministic Correction
Assume that
Under linearity assumption, we would have
To calculate the Jacobian of
where
and the local linearity assumption gives the approximation
We would then use the ensemble for approximation of both mean and Jacobian of
where the superscript
3.1.4 Telescopic Correction
This scheme utilizes the idea in deterministic correction in a telescopic manner so that it can benefit from the multilevel structure of the problem. The MLME can be written as
and Eq. 25 holds because all the transformations are linear and from a finer level to a coarser level. Accordingly, we can write
where
This reformulation of the error term renders the possibility to approximate
where
The idea here is that even though the errors in approximation aggregate in the summation in Eq. 26, the increase in the ensemble size would reduce Monte Carlo errors and the approximation of
In order to be able to perform this correction, a nested structure in the prior realizations is necessary. In other words, as seen in Figure 4D, all the realizations simulated by a forward model should also be computed using all the less accurate forward models than that model.
4 Test Models
We are interested in assessing the quality of MLME correction schemes in reservoir history matching of inverted seismic data using MLHES. In accordance with it, three different reservoir models are considered. These reservoir models have some shared properties. They are two-dimensional, with
In each of the reservoir models used in this work, the general structure is modified with the aim of increasing the MLME. These reservoir models are explained separately in Sections 4.1–4.3, and samples from the prior distribution of Z for each of the reservoir models can be found in Figure 5.
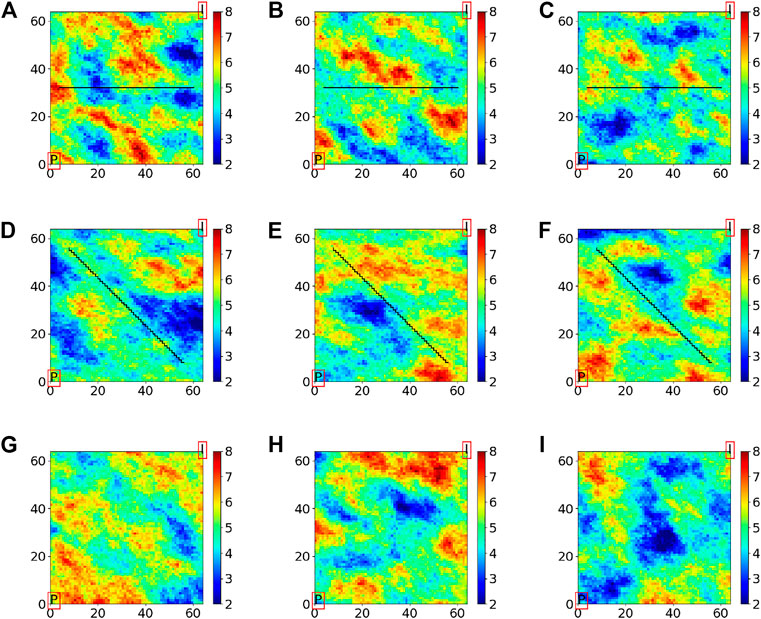
FIGURE 5. Samples from the prior distributions for log permeability for the three experiments, (A)–(C) Experiment I, (D)–(F) Experiment II, and (G)–(I) Experiment III.
The forward models used for forecast
The flow segment of the forward models is performed using Eclipse 100 [19]. Coarsening the grid is done by using the Eclipse keyword COARSEN, which merges groups of predefined neighboring cells to form a coarser grid. The upscaling of permeabilities is performed using pore-volume–weighted arithmetic averaging, and transmissibilities between two neighboring coarse cells in each direction are calculated based on harmonic averaging in that direction and summing it in other directions [19]. As for the petro-elastic segment of the forward model, an in-house model based on standard rock physics [20], [21, Report 1] was used.
4.1 Reservoir Model I
A nonpermeable fault has been added to the field with its normal vector pointing north, its eastern most point 4 grid cells away from the east side of the field, and its western most point 4 grid cells away from the west side of the field. From Figures 5A–C, it is clear that flow from the injector to the producer has to pass through one of the narrow openings at the ends of the fault. Hence, there will be strong variations in the solution variables in these regions. Grid coarsening is therefore expected to produce stronger MLME for this example than for a similar example, but where no fault was present.
4.2 Reservoir Model II
An oblique fault stretching from 8 grid cells away from the northwest corner to 8 grid cells away from the southeast corner is added to the general reservoir model structure. In addition to the complexities similar to those associated with Reservoir Model I, as can be seen in Figure 6, the coarsening scheme in the presence of such a fault, which will be discussed in Section 5.2, results in some permeability values that are located on one side of the fault in the fine grid to contribute to an upscaled permeability value located on the other side of the fault in the coarsened grid. This introduces another type of MLME to the model.
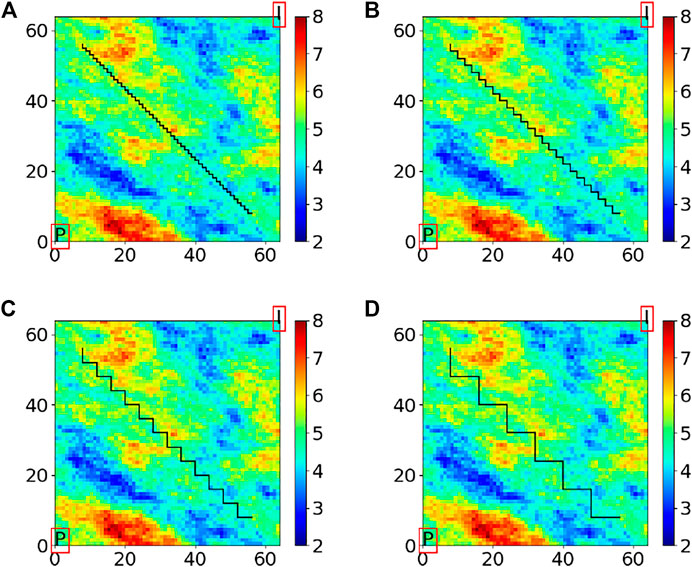
FIGURE 6. Approximation of the fault for simulations, (A) original fault and (B–D) approximations at coarser levels.
4.3 Reservoir Model III
This reservoir model uses the general structure of the models without addition of faults and is used for investigation of a different type of MLME, which is formed by simplifying the grid coarsening scheme.
5 Numerical Investigation
In order to assess the quality of the MLME correction schemes presented in this work, three experiments are conducted. The experiments are performed on the reservoir models discussed in Section 4.
The observation data are two sets of time-lapse bulk impedance data taken based on a baseline (day zero of production) and two vintages, which are different for each experiment and will be mentioned separately. These observation data are generated using the results of simulation from a random draw of the prior distribution. As the inverted seismic data are spatially correlated, we use a correlated covariance matrix for the data error. In doing so, a variogram with the specifications given in Table 2 is considered. The marginal standard deviation of each observation value is given as
where
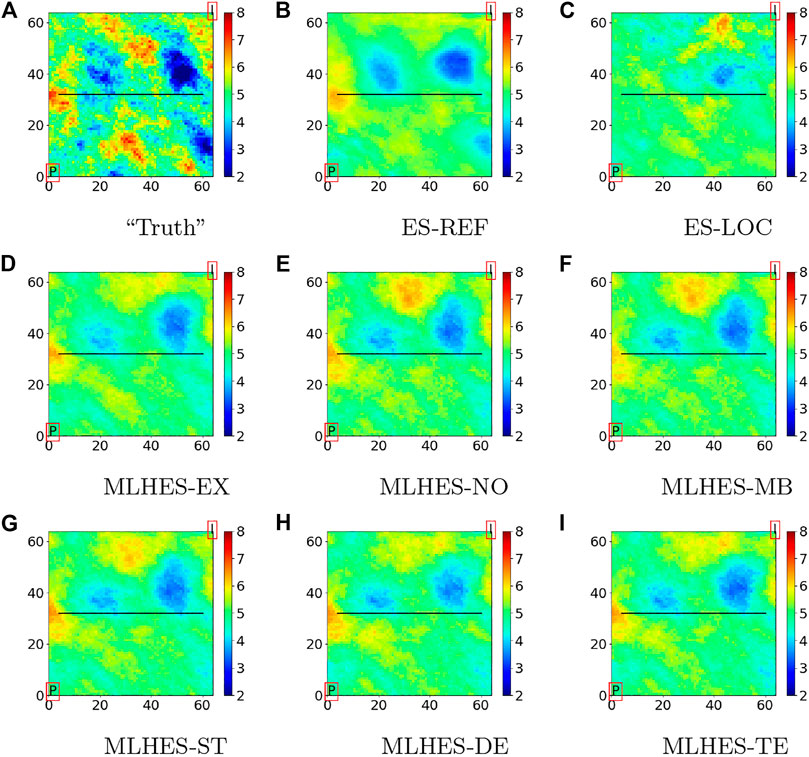
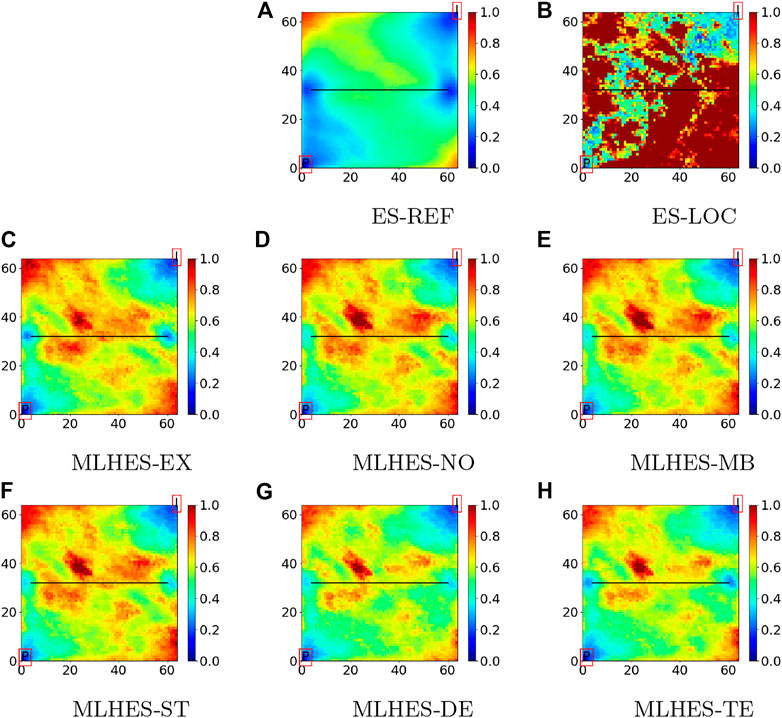
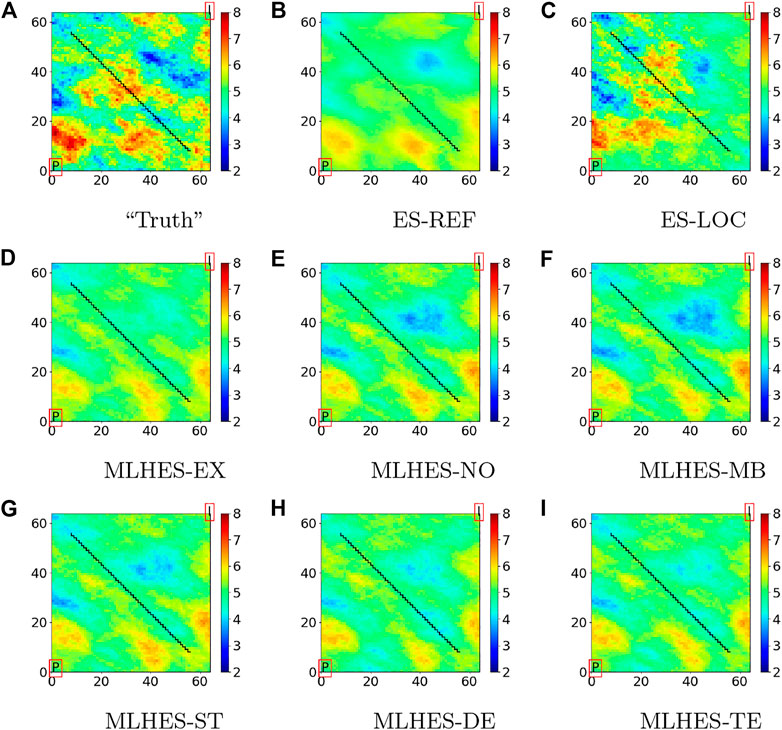
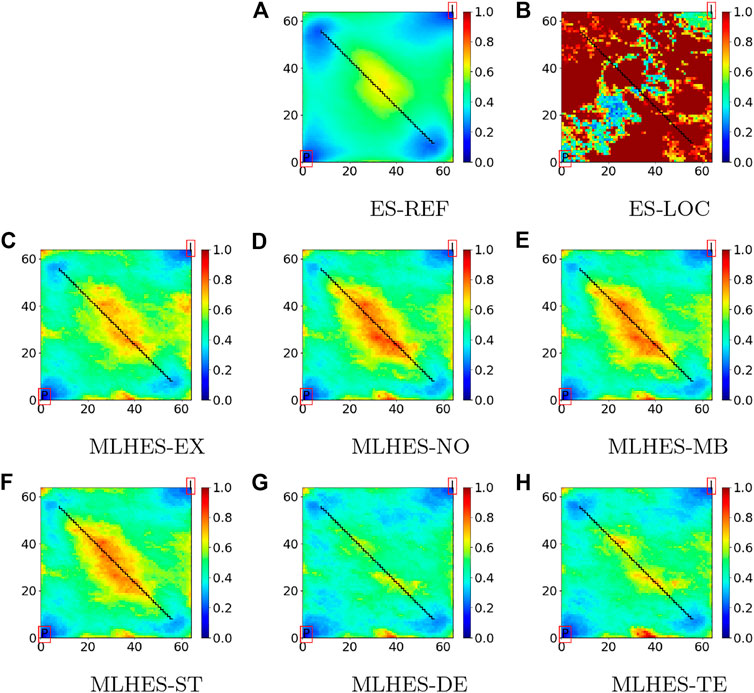
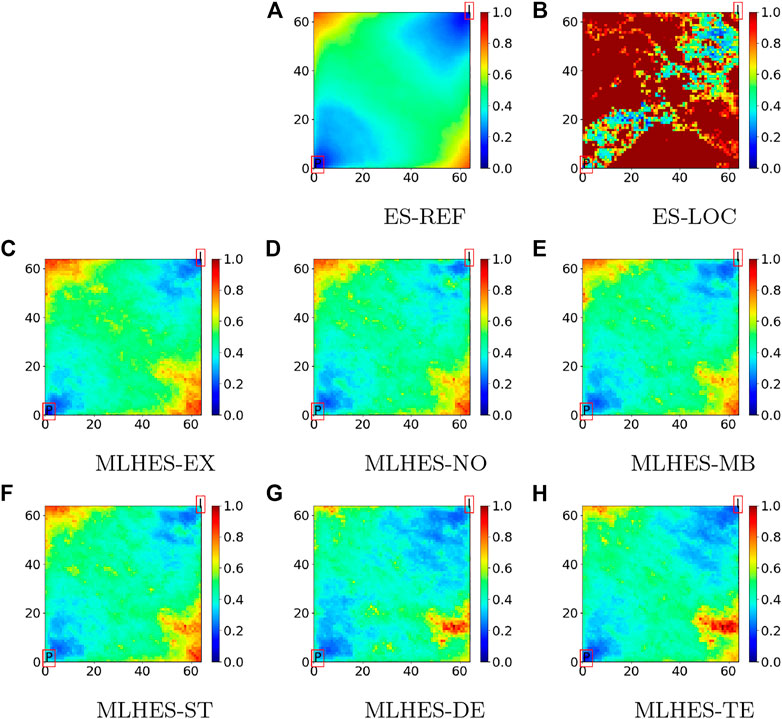
For each numerical experiment, we will compare plots of results (mean and variance fields) obtained with five versions of the MLHES to those obtained with ES with distance-based localization (ES-LOC). The five versions are MLHES with mean bias correction (MLHES-MB), MLHES with stochastic correction (MLHES-ST), MLHES with deterministic correction (MLHES-DE), MLHES with telescopic correction (MLHES-TE), and MLHES with no correction (MLHES-NO).
The gold standard (reference solution) for the comparison will be results obtained using ES with 10,000 ensemble members (ES-REF). By utilizing such an unrealistically large ensemble, we obtain results that are visually indistinguishable from the best results that can be achieved using ES.
Furthermore, we will show plots of results obtained with a scheme with exact correction for the MLME (MLHES-EX). These results are obtained by running fine-scale simulations with the same total ensemble size as for the multilevel simulations and thereafter upscaling model forecasts (with the appropriate sub-ensemble sizes) to the respective levels. Obviously, MLHES-EX is computationally much costlier than the rest of the MLHES variants, and it is included only to assess the effect of completely removing the MLME on posterior results. Finally, we will show plots of the log permeability realization used when generating the synthetic data (“truth”).
A fixed computational power is considered for all runs (except for ES-REF and MLHES-EX). As the dominant cost of the DA process is pertaining to simulations of forward models, where iterative linear solvers dominate the computational costs for large problems, the computational cost pertaining to each ensemble member to be simulated using the forward model
Considering this equation, we set
For ES with distance-based localization, the tapering function for localization is based on Reference [23]. As for the MLHES, regarding weights of the hybrid mean and covariance matrices,
The unknown parameter vector in all the experiments is the logarithmic permeability field. The prior fields are based on three spherical variograms, all having mean 5 and variance 1, and specific characterizations given in Table 3. Samples from the prior distributions are given in Figure 5.
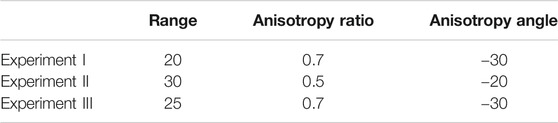
TABLE 3. Specific characterizations of variograms of the prior distribution, the unit for range is grid cells.
5.1 Experiment I
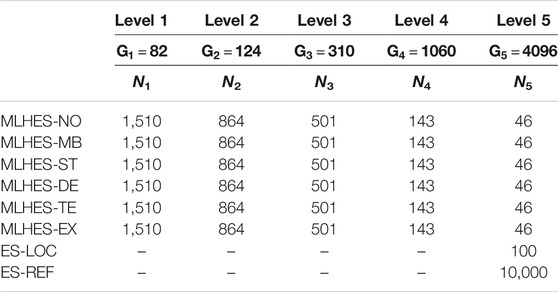
This experiment is conducted on Reservoir Model I with five levels corresponding to 82, 124, 310, 1,060, and 4,096 grid cells, respectively. A summary of the resource allocation for the different runs carried out in this experiment can be found in Table 4. The observation data for this experiment are generated based on seismic vintages at 4,000 and 8,000 days after production starts.
5.2 Experiment II
This experiment is conducted on Reservoir Model II. In this experiment, the presence of the oblique fault in the field interferes with coarsening the model. One way to handle this issue would be to avoid coarsening the grid around the fault area; however, this would reduce the computational advantage of the multilevel scheme. In order to keep the grid coarsening as it is, the fault is approximated with bigger “zigzags,” as depicted in Figure 6, for one realization of the logarithmic permeability field at different levels of coarseness. This makes the experiment to be more challenging than Experiment I, since in addition to coarsening the grid and upscaling the parameters, a structural characterization of the field (the fault) is also approximated.
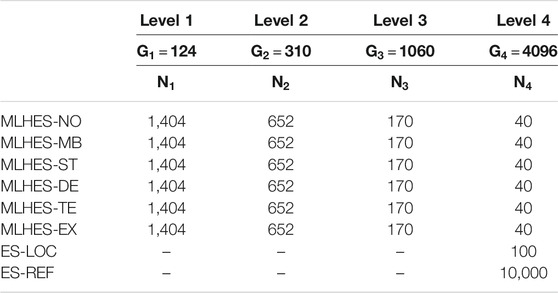
MLHES is run with four levels corresponding to 124, 310, 1,060 and 4,096 grid cells, respectively. A summary of the resource allocation for the different algorithms carried out in this experiment can be found in Table 5. The observation data are generated based on seismic vintages at 5,000 and 10,000 days after beginning of production.
5.3 Experiment III
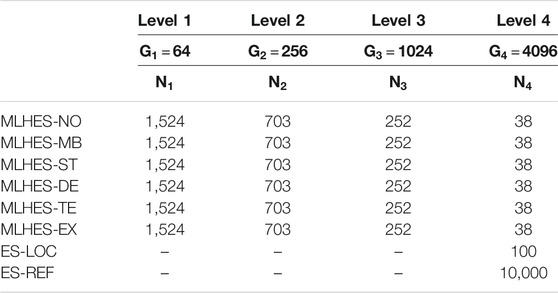
This experiment is conducted on Reservoir Model III. The coarsening of the grid is performed uniformly, so that also the regions near the wells are coarsened. Hence, a different type of MLME is generated. The number of grid cells is now complete powers of 2. Forming four levels of coarseness, the number of grid cells are 64, 256, 1,024, and 4,096. A summary of the resource allocation for the different algorithms carried out in this experiment can be found in Table 6. The observation data are generated based on seismic vintages at 4,000 and 8,000 days after production starts.
6 Numerical Results
The numerical results are assessed in two ways. First, we perform a quantitative analysis of the MLME-corrected model forecasts. Second, we perform a qualitative analysis of the results obtained when using the MLME-corrected forecasts in MLDA.
As for a quantitative analysis of success of MLME correction schemes, the normalized correction ratio for model forecasts at level l,
is considered. Here,
NCRl is different for different realizations. In order to assess the success of each of the correction schemes jointly for all realizations, the sample median of each of the elements of NCRl is computed. The median is chosen since the mean of NCRl is not a good indicator of success (NCRl has a lower bound at zero but has no upper bound, and outliers would affect it disproportionately). Then, the mean of the elements of the sample median of NCRl are reported for different levels in all MLME correction schemes for the three experiments.
As for the qualitative assessment of the DA results, the mean and the variance of the posterior unknown parameters are compared between different algorithms. We have not considered any specific formulation for computation of the final multilevel statistics. Accordingly, the simplest formulation is chosen, that is, reuniting all the sub-ensembles and treating them as one ensemble for computation of a posteriori mean and variance fields. ES-LOC was tested with several ranges for localization (critical distances), and the best results are presented for each of the experiments.
6.1 Results of Experiment I
As can be seen in Table 7,
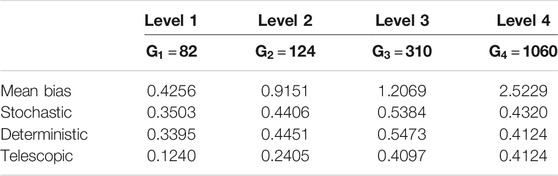
TABLE 7. Experiment I: Mean of the elements of the median vector of
Visual analysis of the mean permeability fields, given in Figure 7, shows that all MLHES variants are reasonably similar and more similar to ES-REF than ES-LOC is. This can be further confirmed by comparison of the variance fields given in Figure 8. The ES-LOC results presented here are based on the localization range of 40 grid cells. Additionally, no superiority of some MLME correction schemes over others is evident in visual assessment of the posterior mean and variance fields. The results from all MLHES variants are reasonably similar to the MLHES-EX results.
6.2 Results of Experiment II
Based on the trends in
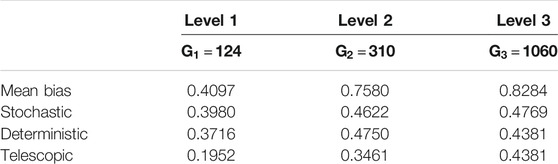
TABLE 8. Experiment II: Mean of the elements of the median vector of
6.3 Results of Experiment III
From Table 9, it is seen that
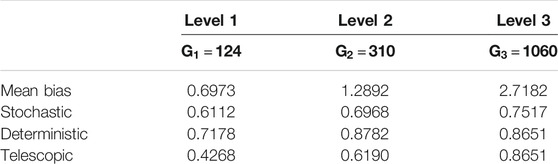
TABLE 9. Experiment III: Mean of the elements of the median vector of
Visual analysis of the mean permeability fields, given in Figure 11, shows that all MLHES variants are reasonably similar and more similar to ES-REF than ES-LOC. This can be further confirmed by comparison of the variance fields given in Figure 12. The ES-LOC results presented here are based on the localization range of 40 grid cells. Additionally, no superiority of some MLME correction schemes over others is evident in visual assessment of the posterior mean and variance fields. The results from all MLHES variants are reasonably similar to the MLHES-EX results.
7 Summary and Conclusion
With large amounts of simultaneous data, like inverted seismic data in reservoir modeling, negative effects of Monte Carlo errors in straightforward ensemble-based data assimilation (DA) are enhanced, typically resulting in underestimation of parameter uncertainties. Multilevel simulations utilize a selection of models for the same entity that constitute hierarchies both in fidelities and computational costs. Multilevel data assimilation (MLDA) utilizes multilevel simulations in the forecast step. MLDA therefore renders the possibility of decreasing Monte Carlo errors without increasing the total computational cost, but MLDA will also introduce multilevel modeling errors (MLME) that are not present in conventional simulation results. The underlying assumption is therefore that the gain in reducing the Monte Carlo error is larger than the loss in introducing the MLME. If the MLME could be approximately accounted for, however MLDA performance could be further improved.
We have estimated and approximately accounted for the MLME. Four computationally inexpensive approximate MLME correction schemes have been considered. We have denoted these schemes mean bias correction, stochastic correction, deterministic correction, and telescopic correction. The three latter schemes have been developed in this work. The abilities of the four schemes to correct for the MLME have been assessed in two ways, utilizing numerical experiments with three selected reservoir models.
First, statistics for the normalized correction ratios for model forecasts at each level were compared. The results showed that the correction schemes were capable of reducing the MLME, but the amount of reduction depended on the case and on the level. In general, the MLME correction schemes were more successful in correcting the MLME in the coarser levels than the finer ones, with telescopic correction showing the best performance followed by deterministic correction, stochastic correction, and mean bias correction.
Second, we assessed the performances of the different MLME-corrected model forecasts in assimilation of inverted seismic data, using the multilevel hybrid ensemble smoother (MLHES). The resulting posterior mean and variance fields with and without MLME correction were visually compared to results obtained from conventional ensemble smoother (ES) with localization, utilizing results obtained with conventional ES with an unrealistically large ensemble size as the gold standard. It was found that MLHES with and without MLME correction outperformed conventional ES with localization.
The use of all four MLME correction schemes, and in fact also MLDA without MLME correction, mostly resulted in posterior parameter estimates with similar quality. For each example, we also ran a computationally much more costly MLDA variant where the MLME had been exactly accounted for in the model forecasts (termed MLHES-EX in Sections 5–6). No differences in quality between results obtained with MLHES-EX and results obtained with several of the computationally inexpensive MLDA variants were found in all three examples. We have run several examples in addition to those presented in the article. In none of these examples did the computationally inexpensive MLDA variants produce poor results, and straightforward MLHES (i.e., without any MLME correction) produced results of similar quality. Altogether, these results indicate that the MLHES is reasonably robust toward MLMEs.
Further investigation concerning the robustness of MLHES with and without MLME correction can be conducted for additional reservoir models with different types of MLMEs than those considered here. On the other hand, the MLME correction techniques can be further developed. Their current versions address the MLME of spatially distributed data on their associated grid cells independently, that is, spatial correlations of the MLME are not considered. It would be interesting to consider spatial correlation of the MLME in future work.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MN is a Ph.D. student, and TB, KF, and TM are supervising him in his research. Accordingly, MN did the details of the research and most of writing with the help of his supervisors.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge financial support from the NORCE research project “Assimilating 4D Seismic Data: Big Data Into Big Models” which is funded by industry partners, Aker BP ASA, Equinor Energy AS, Lundin Energy Norway AS, Repsol Norge AS, Shell Global Solutions International B.V., Total E&P Norge AS, and Wintershall Dea Norge AS, as well as the Research Council of Norway (PETROMAKS2). We also thank Schlumberger for providing academic software licenses to ECLIPSE.
Footnotes
1Nezhadali, M., Bhakta, T., Fossum, K., and Mannseth, T. Iterative multilevel assimilation of inverted seismic data. Submitted
References
1. Chen, Y, and Oliver, DS. Ensemble Randomized Maximum Likelihood Method as an Iterative Ensemble Smoother. Math Geosci (2012). 44(1):1–26. doi:10.1007/s11004-011-9376-z
2. Emerick, AA, and Reynolds, AC. Ensemble Smoother with Multiple Data Assimilation. Comput Geosci (2013). 55:3–15. doi:10.1016/j.cageo.2012.03.011
3. Luo, X, Bhakta, T, and Nævdal, G. Correlation-based Adaptive Localization with Applications to Ensemble-Based 4d-Seismic History Matching. SPE J (2018). 23(02):396–427. doi:10.2118/185936-pa
4. Lorentzen, RJ, Bhakta, T, Grana, D, Luo, X, Valestrand, R, and Nævdal, G. Simultaneous Assimilation of Production and Seismic Data: Application to the Norne Field. Comput Geosci (2019). 12:1–14. doi:10.1007/s10596-019-09900-0
5. Gaspari, G, and Cohn, SE. Construction of Correlation Functions in Two and Three Dimensions. Q.J R Met. Soc. (1999). 125(554):723–57. doi:10.1002/qj.49712555417
6. Chen, Y, and Oliver, DS. Cross-covariances and Localization for Enkf in Multiphase Flow Data Assimilation. Comput Geosci (2010). 14(4):579–601. doi:10.1007/s10596-009-9174-6
7. Emerick, A, and Reynolds, A. Combining Sensitivities and Prior Information for Covariance Localization in the Ensemble Kalman Filter for Petroleum Reservoir Applications. Comput Geosci (2011). 15(2):251–69. doi:10.1007/s10596-010-9198-y
8. He, J, Sarma, P, and Durlofsky, LJ. Reduced-order Flow Modeling and Geological Parameterization for Ensemble-Based Data Assimilation. Comput Geosciences (2013). 55:54–69. doi:10.1016/j.cageo.2012.03.027
9. Tarrahi, M, Elahi, SH, and Jafarpour, B. Fast Linearized Forecasts for Subsurface Flow Data Assimilation with Ensemble Kalman Filter. Comput Geosci (2016). 20(5):929–52. doi:10.1007/s10596-016-9570-7
10. Fossum, K, and Mannseth, T. Coarse-scale Data Assimilation as a Generic Alternative to Localization. Comput Geosci (2017). 21(1):167–86. doi:10.1007/s10596-016-9602-3
11. Hatfield, S, Subramanian, A, Palmer, T, and Düben, P. Improving Weather Forecast Skill through Reduced-Precision Data Assimilation. Monthly Weather Rev (2018). 146(1):49–62. doi:10.1175/mwr-d-17-0132.1
12. Fossum, K, Mannseth, T, and Stordal, AS. Assessment of Multilevel Ensemble-Based Data Assimilation for Reservoir History Matching. Comput Geosci (2020). 24(1):217–39. doi:10.1007/s10596-019-09911-x
13. Hoel, H, Law, KJH, and Tempone, R. Multilevel Ensemble Kalman Filtering. SIAM J Numer Anal (2016). 54(3):1813–39. doi:10.1137/15m100955x
14. de Moraes, RJ, Hajibeygi, H, and Jansen, JD. A Multiscale Method for Data Assimilation. Comput Geosciences (2019). 12:1–18. doi:10.5194/egusphere-egu21-3880
15. Fossum, K, and Mannseth, T. “A Novel Multilevel Method for Assimilating Spatially Dense Data,” in ECMOR XVI-16th European Conference on the Mathematics of Oil Recovery, Vol. 2018. London: European Association of Geoscientists & Engineers (2018). 1–12.
16. Nezhadali, M, Bhakta, T, Fossum, K, and Mannseth, T. “A Novel Approach to Multilevel Data Assimilation,” in ECMOR XVII, Vol. 2020. London: European Association of Geoscientists & Engineers (2020). 1–13.
17. Evensen, G. Accounting for Model Errors in Iterative Ensemble Smoothers. Comput Geosci (2019). 23(4):761–75. doi:10.1007/s10596-019-9819-z
18. Kaipio, J, and Somersalo, E. Statistical Inverse Problems: Discretization, Model Reduction and Inverse Crimes. J Comput Appl Math (2007). 198(2):493–504. doi:10.1016/j.cam.2005.09.027
19. Schlumberger, L. Eclipse Reservoir Simulation Software V2016 (2016). Technical Description Manual.
20. Batzle, M, and Wang, Z. Seismic Properties of Pore Fluids. Geophys. (1992). 57(11):1396–408. doi:10.1190/1.1443207
21. Fahimuddin, A. 4D Seismic History Matching Using the Ensemble Kalman Filter (EnKF): Possibilities and challenges. Ph.D. Thesis. The University of Bergen (2010). doi:10.2118/131453-ms
23. Furrer, R, and Bengtsson, T. Estimation of High-Dimensional Prior and Posterior Covariance Matrices in Kalman Filter Variants. J Multivar. Anal (2007). 98(2):227–55. doi:10.1016/j.jmva.2006.08.003
24. Chavent, C, and Liu, J. Multiscale Parametrization for the Estimation of a Diffusion Coefficient in Elliptic and Parabolic Problems. IFAC Proc Vol. (1989). 22(4):193–202. doi:10.1016/s1474-6670(17)53542-9
25. Grimstad, A-A, and Mannseth, T. Nonlinearity, Scale, and Sensitivity for Parameter Estimation Problems. SIAM J Sci Comput (2000). 21(6):2096–113. doi:10.1137/s1064827598339104
Appendix A: MLHES pseudo-code

Keywords: data assimilation, multilevel, modeling error, seismic data, reservoir model
Citation: Nezhadali M, Bhakta T, Fossum K and Mannseth T (2021) Multilevel Assimilation of Inverted Seismic Data With Correction for Multilevel Modeling Error. Front. Appl. Math. Stat. 7:673077. doi: 10.3389/fams.2021.673077
Received: 26 February 2021; Accepted: 10 May 2021;
Published: 01 June 2021.
Edited by:
Behnam Jafarpour, University of Southern California, Los Angeles, United StatesReviewed by:
Sanjay Srinivasan, Pennsylvania State University (PSU), United StatesLu Xiong, Middle Tennessee State University, United States
Copyright © 2021 Nezhadali, Bhakta, Fossum and Mannseth. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammad Nezhadali, bW9uZUBub3JjZXJlc2VhcmNoLm5v
 Mohammad Nezhadali
Mohammad Nezhadali Tuhin Bhakta
Tuhin Bhakta Kristian Fossum
Kristian Fossum Trond Mannseth
Trond Mannseth