- 1Mathematical Sciences Institute, Australian National University, Canberra, ACT, Australia
- 2Research School of Physics, Australian National University, Canberra, ACT, Australia
Fuzzing is a systematic large-scale search for software vulnerabilities achieved by feeding a sequence of randomly mutated input files to the program of interest with the goal being to induce a crash. The information about inputs, software execution traces, and induced call stacks (crashes) can be used to pinpoint and fix errors in the code or exploited as a means to damage an adversary’s computer software. In black box fuzzing, the primary unit of information is the call stack: a list of nested function calls and line numbers that report what the code was executing at the time it crashed. The source code is not always available in practice, and in some situations even the function names are deliberately obfuscated (i.e., removed or given generic names). We define a topological object called the call-stack topology to capture the relationships between module names, function names and line numbers in a set of call stacks obtained via black-box fuzzing. In a proof-of-concept study, we show that structural properties of this object in combination with two elementary heuristics allow us to build a logistic regression model to predict the locations of distinct function names over a set of call stacks. We show that this model can extract function name locations with around 80% precision in data obtained from fuzzing studies of various linux programs. This has the potential to benefit software vulnerability experts by increasing their ability to read and compare call stacks more efficiently.
1 Introduction
A black-box fuzzing campaign is one conducted without explicit knowledge of the source code or its intermediate representations. Generally, methods in this area require a brute-force generation of inputs. This can lead to masses of crashes where many are duplicates of one another. For practitioners, untangling the output of a black-box fuzzing campaign is a time-consuming task. The goal of this article is to investigate methods that alleviate the difficulty of comprehending such results.
1.1 Call Stacks
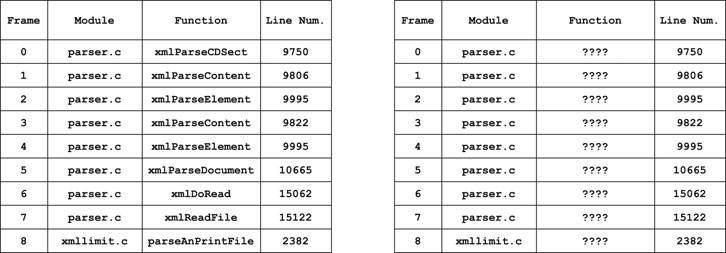
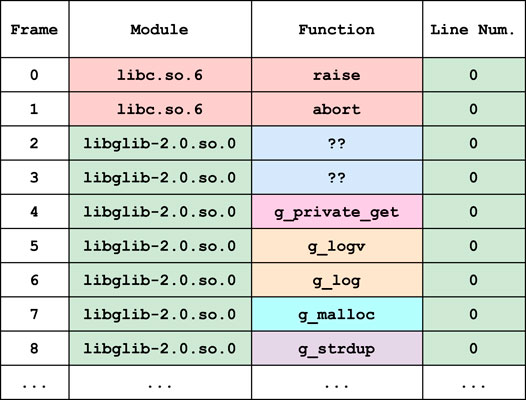
When a program crashes, the slew of error text it returns to the user is referred to as the call-stack (Example in Figure 1). The call-stack is a record of the nested functions traced out by the program in its final moments and is one of the few pieces of information available to us when analyzing black-box fuzzing. The lines in the call-stack are called frames, and while contingent on the operating system’s debugging syntax, decompose roughly into three columns: 1) the module (or filename), 2) the function and 3) the line number. We will refer to the set of all constituent modules, functions and line numbers in a set of call-stacks
Further complicating matters is that—depending on whether the source code is available—call-stacks may have partial information excluded. In particular, when fuzzing programs without possession of source code or full knowledge of terms, the partially obscured call-stack may be the only source of information available.
1.2 Goals
The ANU researchers [1] provided to us a data set of call stacks generated by fuzzing several Linux programs with the afl fuzzing algorithm (See [2]). They were interested in answering two key research questions:
1. Clustering and Deduplication: determining the extent to which there are discernible clusters in the set of call-stacks.
2. Term Removal: quantifying how much information about function terms can be recovered given they are obscured (for example, as in Figure 1).
While the first question has been studied in a number of contexts [3, 4], to the best of our knowledge no attempt has been made at the second. In this paper, we show that once the data has been suitably whitelisted, the set of crashes contain a high number of exact duplicate call-stacks. This observation highlights a fundamental lack of diversity in the data generated by fuzzing, and alone is enough to answer the first question to a large extent.
To address the question of function term removal, we introduce a model of call-stack information using finite topological spaces, posets and the theory of [5]. This not only helps to quantify the significance of removing function terms, but is a useful object to capture the dependencies between terms in the set of call-stacks.
2 Data-Set Overview
Six common Linux programs were fuzzed using the program afl. Key aspects of the program: the binary name, file extension, and version are presented in Table 1. Call-stacks were generated within the framework of the GDB debugger using the AddressSanitizer (ASAN) [6] tool.

TABLE 1. The number of crashes generated by fuzzing each program, and the number of unique crashes after whitelisting and removed exact duplicates. Within the set of call-stacks, some files were either blank or unable to be opened. We discarded such files, as appears in the second column from the right.
Upon recommendation by the ANU cyber-security researchers, we performed several pre-processing whitelisting steps to each call-stack text file. Firstly, frames appearing up to and including the ASAN error frame were considered superfluous and hence deleted. In crashes that did not call the ASAN module, frames up to assert_fail were deleted. For every file, the two final generic end-of-file frames were deleted. Finally, we extracted three salient features from each frame: the module, the function and intra-module line number, and discarded the other information in the call-stack file.
Unlike the afl protocol–where crashes are de-duplicated based on a hashing scheme–we labeled two call-stacks to be deplicates whenever their text files were identical after the pre-processing described above. A striking result of frequency analysis is that there are dramatically fewer distinct crashes relative to total crashes (see Figure 1). Further, the frequency of distinct crashes is unevenly distributed. Across programs, the call-stack data displayed largely the same pattern: most of the weight was distributed among a few crashes, with the rest rarely occurring (See Figure 2).
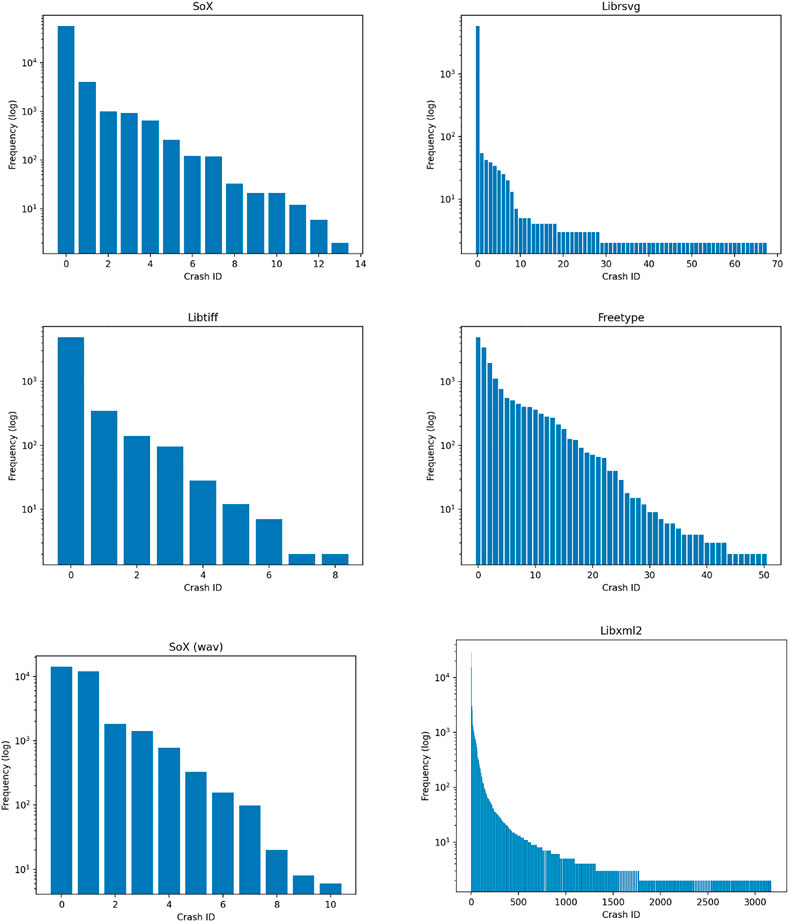
FIGURE 2. Frequency (logarithmic scale) distribution of crashes in each binary, where the crash ID is with respect to distinct call-stacks.
3 Topological Model
In this section, we propose a model to frame the complex dependency relationships between the terms
Recall that in any topological space X, the open neighborhood
3.1 Call-Stack Topology
Given a set of call-stacks
Unlike many topologies we are familiar with, e.g., topologies generated by open balls in a metric space, the call-stack topology is seldom Hausdorff. In our context, the looser criterion of a
Since distinct terms can appear in the same subset of call-stacks,
The following simple lemma shows that one may characterize equivalence classes in the Kolmogorov quotient of the call-stack topology by examining the set of call-stacks directly rather than the topology. For
Lemma 1. For a set of call-stacks
PROOF. The definition of the equivalence relation is
Suppose that
Conversely, suppose that
where each
According to the above lemma, equivalence classes in the Kolmogorov quotient of the call-stack topology consist of terms that occur in the same set of call-stacks. The intuition is that by taking the Kolmogorov quotient, we only consider terms up to the information of which call-stacks they appear in. The composition of equivalence classes in such a quotient will be a key feature for analysis in our application.
In theory, calculating such equivalence classes requires knowledge of open neighbourhoods and, ergo, the entire gamut of open sets in the call-stack topology. Aside from providing useful intuition, the above lemma also ensures that we can avoid this computationally expensive task, attaining equivalence classes indirectly by comparing the call-stack neighbourhoods of pairs of terms.
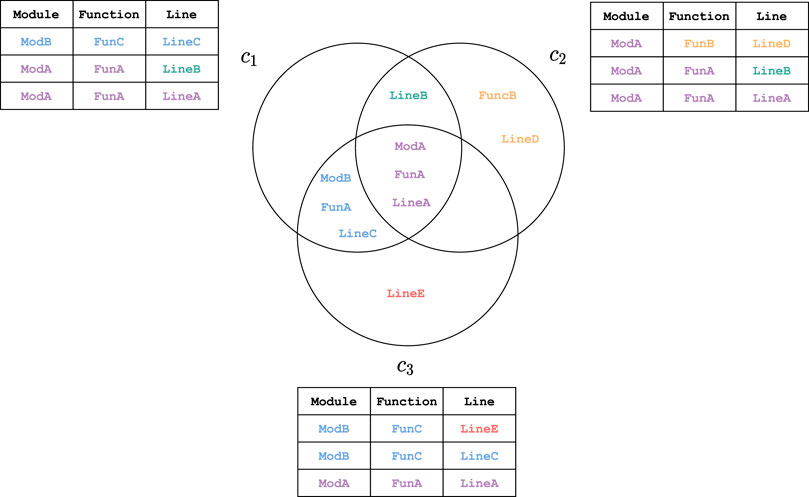
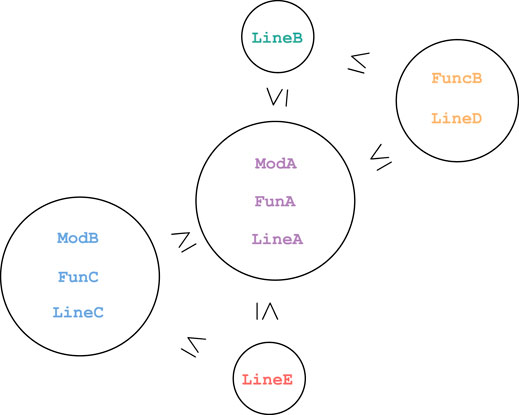
Example 1. In Figure 3, we depict a set of three call-stacks. In the center of the Figure, the three circles each represent a generating set for the call-stack topology
3.2 Call-Stack Partial Order
In this section we equip the set of call-stack terms with the additional structures of a pre-order and partial order. Our approach in later sections is to use this structure to examine relations between terms in different equivalence classes. For any topological space, one may use the structure of the open sets to define a pre-order over its points called the specialization pre-order. This may be defined in the following equivalent statements.
Definition 1. For a topological space X, the specialization pre-order
or equivalently
The specialization pre-order forms a partial order over X precisely when X is a
Definition 2. The call-stack pre-order on a set of call-stacks
Definition 3. The call-stack poset on a set of call-stacks
Unlike the call-stack topology
As is the case for equivalence classes, the call-stack partial order can be computed without explicitly calculating the open sets in the call-stack topology.
Lemma 2. Two classes of terms
Proof. Suppose first that
where there exists j such that
In the other direction, suppose that
The above lemma suggests how one should interpret the call-stack partial order: two sets of terms
Example 2. In Figure 4, we depict the call-stack poset corresponding to the example call-stack topology provided in Example 1. Each circle contains an equivalence class of terms that have identical call-stack neighbourhoods. Lemma 2 tells us that an order relation
3.3 Function Term Obfuscation
One of the key research questions is how much information can be extracted from the call-stack when terms are removed. Let
be the set of call stacks with the term t removed. Note here that each
Lemma 3. Suppose
1.
2.
Proof. For
One can summarize the above result as the fact that
Corollary 1. Let
Then
In other words, whenever we remove function terms from the model, the structure of the call-stack poset is unchanged away from classes comprised solely of function terms. When a function term t shares an equivalence class with non-function terms, these may be used to recover its structural dependency information even when t is removed. The point of the above theorems is to motivate the idea that many attributes of the call-stack poset are retained in the case where some terms are missing.
4 Function Term Reconstruction
The goal of this paper is to reconstruct information about function terms from call-stacks in which they are obscured. In this section, we present a small-scale experiment on our linux data set using features extracted from the call-stack topology model.
Accordingly, we must first define what we mean by ‘function information.’ When the function names are missing, it is not possible to recover them explicitly from the call-stack data. The next best data, and what we choose to focus on in this paper, is to recover the set of positions within the call-stacks that share a common function name. This notion is captured in the following definition.
Definition 4. For a term
where
If t appears in multiple frames
By performing logistic regression over features extracted from the call-stack model, we will show that a surprising number of function frame traces can be recovered without any explicit knowledge of function names. This is particularly striking given that the user also knows nothing about the internal structure of the program. Additionally, we provide an algorithm for generating fake function names based on the guessed frame traces, making sets of call stacks more human-readable in the setting where function names are missing.
4.1 Preliminary Analysis of Call-Stack Equivalence Classes and Poset Structure
To motivate the use of our novel tools in the task of recovering function frame traces, we first present a basic analysis of the data through the lens of the call-stack topology and poset. In particular, we study the characteristics of equivalence classes—their size and the types of terms of which they comprise—as well as the order relations and dependencies they exhibit on one another.
4.1.1 Basic Statistics
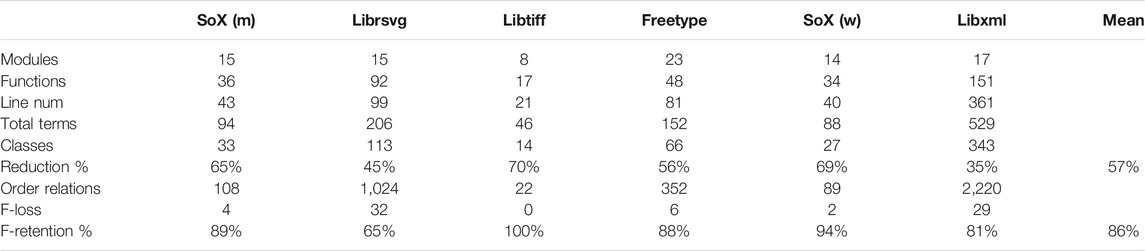
Recall that the equivalence classes in the call-stack topology consist of terms that occur in the same set of call stacks. Table 2 shows the extent of reduction from the number of terms to their equivalence classes under the quotient operation.
Our primary interest is to understand the effect of obscuring function terms. Corollary 1 states that removing the function terms only alters the model’s structure at equivalence classes consisting of function terms alone. Accordingly, we say a function term f is retained under the quotient operation when it is equivalent to a non-function term t. Notably, in the case
Table 2 shows that, on average,
4.1.2 Patterns Relating Line Numbers and Function Terms
When two terms are in the same equivalence class, they occur in the same set of call-stacks. However, our topological model encodes none of the information about which frame they occur in. Our toy example (Example 1) suggested that line numbers and functions in the same equivalence class tend to occupy similar frames in the call-stack. In a thorough examination of the data, we observed two patterns, demonstrating each with the example call stacks in Figure 5.
• Pattern 1: When multiple line numbers belong to an equivalence class, they are usually paired with functions in the same frame except for the line number in the bottom frame. The lowest line number appears to act as a switch point between blocks of terms, instigating a run of function calls that are either seen in only one call-stack or always together. In Figure 5, this occurs in the brown and green equivalence classes of the example on the left.
• Pattern 2: When a single line number is in an equivalence class with a function, it is likely paired with a function one frame above. In Figure 5, this occurs in the purple and orange boxes of the left call-stack, and the purple, orange and green boxes of the right.
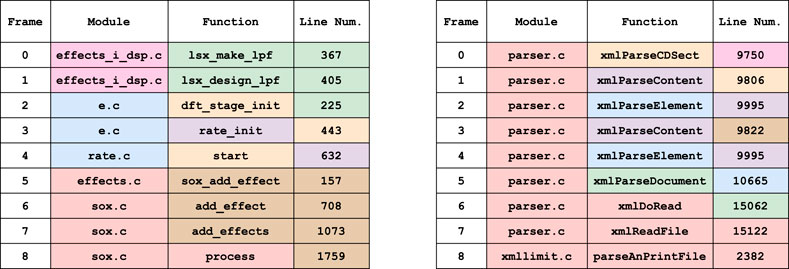
FIGURE 5. Example call stacks from the Linux data exhibiting the behavior described by the two patterns. The left and right examples are taken from two separate libraries, where each of the seven colors represents an equivalence class in the call-stack topology; that is, a set of terms which have identical call-stack neighbourhoods.
It is important to state that neither pattern reflects an underlying mathematical truth. Rather, they seem to be a symptom of programming convention. Namely, as source code tends to decompose into many different simple functions nested within one another, runs of frames in the call-stack tend to cycle through distinct function names. Further, these patterns only apply in the case that a line number occurs in the same set of crashes as a function, in which case we assume that they describe how the frames of a function and line number are related.
4.2 Method
Our method for frame trace recovery is centered around leveraging structure of the call-stack topology and poset. To do so, we generate the call-stack equivalence classes
Once such objects are constructed, our approach consists of the following two steps.
1. Classifying Equivalence Classes: Within the incomplete data model, the terms of an equivalence class
2. Pairing Frame Traces: The second step of our method is to apply our two observations above to obtain a heuristic for predicting frame trace locations of function terms. This is done by selecting line numbers within a given equivalence class whose frame traces are likely to be paired with a function term frame trace in the complete data. The frame traces of these line numbers serve as our set of predictions for function frame traces and enable us to partially reconstruct the data set.
4.2.1 Classifying Equivalence Classes Within Libxml
The first step in our method of frame trace recovery is learning to detect when an equivalence class contains a function term. Before tackling the task of classifying equivalence classes in the incomplete data, we restrict our focus to a small study of libxml, which offers the largest base of terms and equivalence classes from which to garner information. We outline our method here to examine the relationship between the structure of an equivalence class within the libxml call-stack poset and the types of terms that it contains.
Consider the following three binary classification problems over the equivalence classes
1. Modules: each equivalence class
2. Functions: each equivalence class
3. Line Numbers: each equivalence class
We address each of the above by performing a simple logistic regression based on four features in the call-stack model. For an equivalence class
1. The size
2. The frequency (number of call-stacks) of the class
3. The weighted in-degree
of the class within the order graph of the call-graph poset
4. The weighted out-degree
of the class within the order graph of the call-graph poset
The names given to features 3 and 4 reference the fact that a poset p can be represented as a graph whose nodes are elements of p and edges are order relations
Lastly, for normalization each of the four variables is scaled by minimum and maximum to lie within
Since the classification labels are unbalanced, the classes were re-weighted according to the to sci-kit learn class re-weighting scheme. To prevent over-fitting, the data was randomly split into an
As a baseline to compare the statistical significance of our method, we propose the following binary classification null-model. Firstly, we empirically derive three probabilities from the ratio of the number of equivalence classes containing each term over the total number of equivalence classes. For each type of term, the null-model randomly guesses whether each class contains that particular term type with the empirically derived probability
4.2.2 Classifying Incomplete-Data Equivalence Classes
Once we have attained logistic regression weights for the libxml data, we then apply them to other programs. An important point of this stage is that, unlike the libxml program experiment, we withhold the full-data with function names as a validation set. This means that the call-stack topology and poset are generated for each program from the call-stacks
From each of these objects, we extract the same four features as above, normalizing in the same way to ensure that the learned libxml weights scale appropriately. The goal of this stage is to predict whether an equivalence class in the incomplete data is likely to contain a function in the full-data, thus predicting a set of call-stacks which share a common missing function term.
4.2.3 Pairing Line Numbers With Function Frame Traces
The outline of our approach to predicting function frame traces is to 1) guess when a line number in the incomplete-data model was likely to have been in an equivalence class with a function name and 2) generating predicted frame traces for functions from line number frame traces using our two heuristics. Algorithm LABEL:predict_FTs ties these two steps together, taking in the set of obscured call-stacks
Algorithm 1PredictFTs
In our algorithm, the logistic regression weights in Line 3 learned over libxml serve as the basis for detecting whether there exists a function in each line number’s equivalence class. Using only the libxml weights ensures that when we predict function frame traces, we require no information about function names in other programs beforehand.
The logistic regression is learned over the full-term model of libxml then performed over the call-stack topology models generated without terms in other programs. There are two significant obstacles that the model must overcome to be successful. Firstly, the model must exhibit transference if the regression weights from libxml are to work for other programs. Secondly, the model must be robust to term removal given that it classifies over a model without function terms. On the second point, Corollary 1 states that the call-stack model retains much of its structure when function terms are removed, which suggests that the logistic regression weights have a chance of still being applicable.
The role of the logistic regression model is primarily to act as a gate-keeper, probabilistically determining when a given line number is not in the same class as any function. This prevents the model from over-predicting instances where a function’s frame trace should be paired to that of a line number. The method drop bottom lineum in Line 5 removes the line number with the lowest average frame trace from the set, which is necessary to apply pattern 1.
4.3 Results
4.3.1 Learning Libxml Logistic Regression Weights
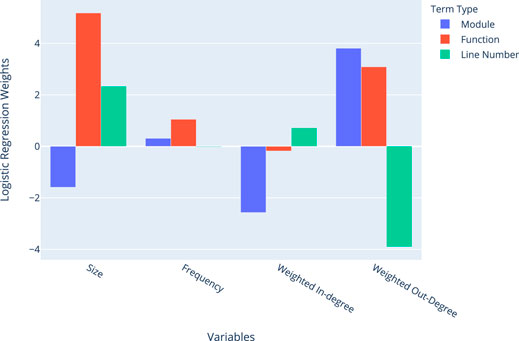
In Table 3 we present the results of our binary classification experiment within the libxml data described in Subsection 4.2.1. The results show that the inclusion of call-stack topology features significantly improves the quality of prediction across terms when compared with the null model. To quantify the effect of each feature in classification, we plot the logistic regression weights in Figure 6. In all cases, the frequency of a term has little effect on classification. For individual term types, there are several observations about the model variables that detect its presence in an equivalence class.
• Modules are likely to be in smaller equivalence classes with lower weighted in-degree and higher weighted out-degree. This means more terms depend on them than they depend on.
• Functions are likely to be in large equivalence classes, with high out-degree. This means many terms are likely to depend on them.
• Line Numbers are likely to be in larger equivalence classes, with a low weighted out-degree. This means terms are unlikely to depend on line numbers.

TABLE 3. Proportion of equivalence classes containing each term type, and logistic regression F1 score and AUC improvements on the null-model for the libxml call-stacks.
Each observation agrees with the structure of library dependencies, where line numbers depend on functions, and functions depend on modules. The logistic regression model is notably adept at detecting the presence of function terms within a given equivalence class.
4.3.2 Frame Trace Recovery
The PredictFts algorithm is run over each Linux program. Since the function term information in libxml was used to generate the logistic regression weights, we exclude it from the analysis. To measure the results, we compare the set of predicted function frame traces generated by the algorithm against the set of actual function frame traces in each set of call stacks.
Table 4 contains the results of each experiment with three different cut-off probabilities 0.4, 0.5 and 0.6. Despite the heavy reliance on fairly naïve heuristics, our model has a reasonable mean precision of above 0.75 is each case. Notably, both precision and recall of frame traces are relatively stable across each program. This suggests that the libxml logistic regression weights and the heuristics both exhibit some degree of transference across programs.
In Figure 7, we analyze the effect of the cut-off probability parameter in detail. When this parameter is high, the algorithm requires a large degree of confidence that an equivalence class contains a function term before predicting a frame trace. This is reflected in an increasing precision and decreasing recall as the cut-off probability increases.
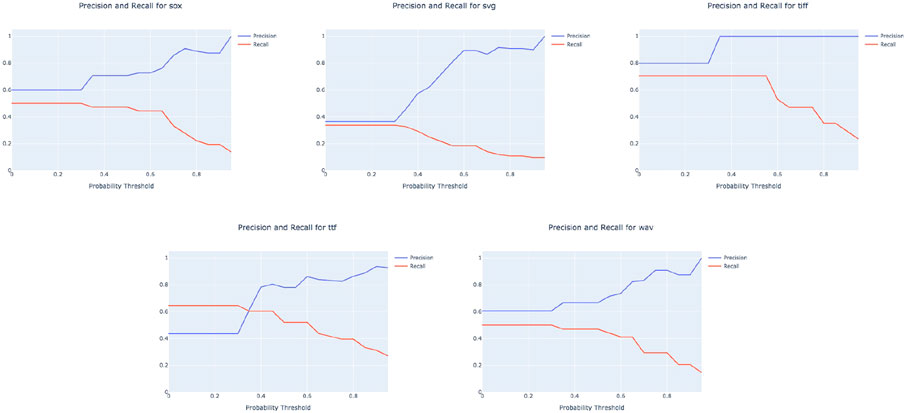
FIGURE 7. Precision and recall for the PredictFTs algorithm on each program indexed by the cut-off probability parameter.
The cut-off probability parameter indirectly allows the user to dictate the importance of precision at the expense of recall. Given that the purpose of our experiment is to reliably reconstruct what function names we can, the importance of precision outweighs that of recall. Indeed, there exist function names in the data that could not possibly be recalled from the module and line number information alone. For example, large swathes of function names are hidden behind the repeated line number 0 in the librsvg data (Figure 8), rendering their recall impossible by our method.
Example 3. To make call stacks without function terms more readable we insert random words into each predicted frame trace. Keeping with the afl theme, we sample random words from the surnames of champion players from the Richmond Tigers Australian Football League (AFL) team. These words are consistent across the set of call stacks, making it easier for the user to visually compare different call stacks.
Figure 9 demonstrates two reconstructed call stacks from the SoX program. In the original call-stacks, the coloring represents equivalence classes in the model. We color the reconstructed call-stacks the same, noting that when we attempt to reconstruct we do not know what equivalence classes will contain functions a priori.
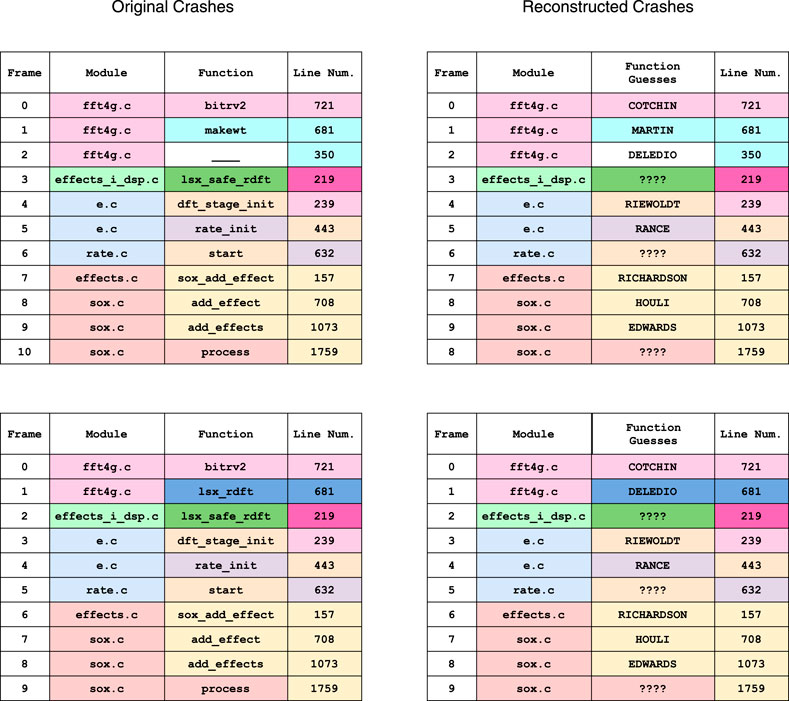
FIGURE 9. Two call stacks from the SoX data set, along with their reconstructions using the PredictFTs algorithm.
As is evident, words representing functions are consistent across the set of call-stacks when frame traces are correctly predicted. The ???? terms in the reconstructed call-stacks represent function frame traces that the algorithm did not attempt to predict.
In Figure 10, we explain which fake function names were paired with which line numbers. We describe how each fake function name pairs with an original in the case that it was a correct prediction, as well as which of the two heuristics were used to pair it with the frame trace of a given line number. The only incorrect prediction was the fake function name DELEDIO, which erroneously predicted that the line number 219 was paired with a function in the original call-stack set via heuristic 2.
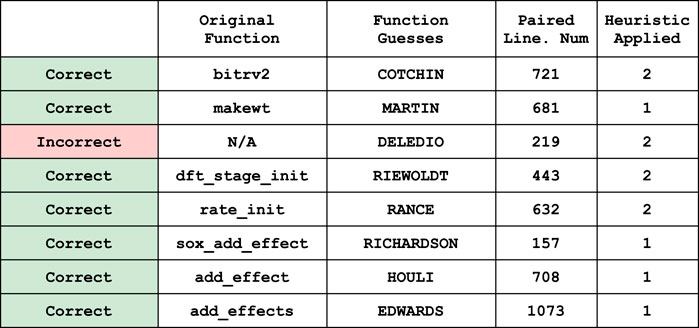
FIGURE 10. The list of functions whose frame trace was recovered, and the fake function names and line numbers that were paired.
5 Related Work
There is a large collection of research centered on crash triage, in particular in crash de-duplication. The most common tasks are either 1) to automatically de-duplicate full bug-reports submitted to open-source software or 2) to bucket crashes by dissimilarity. In contrast to the setting considered in this paper, most research concerns full bug reports where call-stacks are only a subset of the entire information. In particular, the language in user-reported comments is incorporated, and in some cases the central object [9].
Some of the highest rates of an expert-validated crash duplicate recall are attributed when program execution traces are also recorded [10]. Including call stacks in bug report data has been shown to increase de-duplication recall of full bug reports significantly [11] validating that they are an important object of study in crash triage. We refrained from using the common methods outlined in the above research, showing that a reasonable whitelisting and de-duplication was enough to significantly reduce the number of call-stacks.
Other models of call-stacks exist, albeit with slightly different machinery. For example, the crash-graph defined in [12] serves as a way to graphically compare the similarity between call-stacks. The use of such a model for function frame trace recovery could be an avenue for future research.
6 Limitations
One of the main limitations of our work is that it is performed on a relatively small data-set. Indeed there are less than 100 distinct call-stacks in each Linux program we have tested, barring the libxml data used to generate the logisitic regression weights. When the set of call-stacks is not very diverse, there may be a tendency to only see function terms with a single line number, making them easier to recover using our method.
A second limitation of our model is that it relies on two fairly naïve patterns. It is not clear if 1) such patterns yield similar results on larger data-sets or 2) whether such patterns could be improved upon or replaced with a more scientific approach. At present, the heuristic method means that our model can only predict function terms that are consistently associated with a single line number across the call-stack set. Our hope is that more sophisticated pattern recognition techniques applied to our topological model could accommodate cases such as frames that pair a particular function with various line numbers. In particular, since the call-stack poset can be thought of as a graph, we expect that more sophisticated techniques from the graph-learning literature could be leveraged 1) in lieu of our logistic regression model and 2) to derive better heuristics and push recall beyond
7 Conclusion
In summary, our main contribution has been to present a novel topological model to address the problem of function term reconstruction in call-stack data. We performed a small-scale experiment, providing an algorithm to predict the frame-traces of function terms which have been obscured in the call-stack data. Despite the limitations, the performance of the model is relatively encouraging, showing that more information about obscured function terms can be recovered than one may initially suspect. In the future, we envision further research could be done within this framework to improve the recall of the PredictFTs algorithm.
We also showed that there is a fundamental lack of diversity in our call-stack data, and we hypothesize that the brute-force nature of fuzzing means that this will probably occur in most data-sets generated by a fuzzer. It is an open question whether our method will work on larger, more diverse call-stack data-sets. Given that some level of dependence between terms is required to form equivalence classes, there is no guarantee that similar results will be achieved.
Lastly, the topological model used here is an example of a larger framework defined in [13]. The extended model is used to tackle applications in gray-box fuzzing, with the goal being to help guide fuzzing campaigns to generate more diverse call-stack data. The use of these models of dependency relations may be applicable in broader contexts outside of fuzzing, such as analyzing dependencies between genes in medical data.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
VR conceived the project and helped source the data. KM conducted the research and wrote the manuscript with assistance and guidance from VR. Both authors discussed the results and analysis at length.
Funding
KM received funding from the Australian Commonwealth Department of Defense under the project title “Mathematical methods for analysis and classification of call-stack data sets”. VR was supported by ARC Future Fellowship FT140100604 in the early stages of the project.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are indebted to W.P. Malcolm for suggesting that topological data analysis might be usefully applied to study call-stacks, for assistance in sourcing the data, and many fascinating conversations about probability theory. The paper would not exist without the data provided by Adrian Herrera. The authors gratefully acknowledge many helpful discussions with AH about the art of fuzzing, software compilers, and call-stack jargon.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.668082/full#supplementary-material
References
1. Gunadi, H, and Herrera, A. Experiment Data for MoonLight: Effective Fuzzing with Near-Optimal Corpus Distillation (2019). doi:10.1109/icicos48119.2019.8982513
2. Zalewski, M. Technical Whitepaper for AFL-Fuzz (2014). doi:10.3726/978-3-653-03549-0 https://lcamtuf.coredump.cx/afl/technical_details.txt.
3. Bartz, K, Stokes, J, and Platt, J. Finding Similar Failures Using Callstack Similarity. Redmond WA: Microsoft Corporation (2009).
4. Modani, N, Gupta, R, Lohman, G, Syeda-Mahmood, T, and Mignet, L. Automatically Identifying Known Software Problems. In: Proceedings - International Conference on Data Engineering (2007). Istanbul, Turkey. doi:10.1109/ICDEW.2007.4401026
5. McCord, MC. Singular Homology Groups and Homotopy Groups of Finite Topological Spaces. Duke Math J (1966). 33:465–74. doi:10.1215/S0012-7094-66-03352-7
6. Serebryany, K, Bruening, D, Potapenko, A, and Vyukov, D. AddressSanitizer: A Fast Address Sanity Checker. In: Proceedings of the 2012 USENIX Conference on Annual Technical Conference. Boston, MA: USENIX Association, USENIX ATC’12 (2012). p. 28.
7. Pirttimäki, T. A Survey of Kolmogorov Quotients (2019). https://arxiv.org/abs/1905.01157.
9. Runeson, P, Alexandersson, M, and Nyholm, O. Detection of Duplicate Defect Reports Using Natural Language Processing. In: Proceedings - International Conference on Software Engineering (2007). Barcelona, Spain. doi:10.1109/ICSE.2007.32
10. Xiaoyin, W, Lu, Z, Tao, X, Anvik, J, and Sun, J. An Approach to Detecting Duplicate Bug Reports Using Natural Language and Execution Information. In: Proceedings - International Conference on Software Engineering (2008). Germany. doi:10.1145/1368088.1368151
11. Lerch, J, and Mezini, M. Finding Duplicates of Your yet Unwritten Bug Report. In: Proceedings of the European Conference on Software Maintenance and Reengineering. Geneva, Italy: CSMR (2013). doi:10.1109/CSMR.2013.17
Keywords: fuzzing, crash-triage, software vulnerability research, call-stack analysis, topology, TDA, specialization pre-order
Citation: Maggs K and Robins V (2021) Topology-Inspired Method Recovers Obfuscated Term Information From Induced Software Call-Stacks. Front. Appl. Math. Stat. 7:668082. doi: 10.3389/fams.2021.668082
Received: 15 February 2021; Accepted: 03 May 2021;
Published: 28 May 2021.
Edited by:
Frédéric Chazal, Inria Saclay-Île-de-France Research Center, FranceReviewed by:
André Lieutier, Dassault Systèmes, FranceVincent Rouvreau, Inria Saclay-Île-de-France Research Center, France
Copyright © 2021 Maggs and Robins. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vanessa Robins, dmFuZXNzYS5yb2JpbnNAYW51LmVkdS5hdQ==
 Kelly Maggs
Kelly Maggs Vanessa Robins
Vanessa Robins