Spatio-Temporal Inversion Using the Selection Kalman Model

Data assimilation in models representing spatio-temporal phenomena poses a challenge, particularly if the spatial histogram of the variable appears with multiple modes. The traditional Kalman model is based on a Gaussian initial distribution and Gauss-linear forward and observation models. This model is contained in the class of Gaussian distribution and is therefore analytically tractable. It is however unsuitable for representing multimodality. We define the selection Kalman model that is based on a selection-Gaussian initial distribution and Gauss-linear forward and observation models. The selection-Gaussian distribution can be seen as a generalization of the Gaussian distribution and may represent multimodality, skewness and peakedness. This selection Kalman model is contained in the class of selection-Gaussian distributions and therefore it is analytically tractable. An efficient recursive algorithm for assessing the selection Kalman model is specified. The synthetic case study of spatio-temporal inversion of an initial state, inspired by pollution monitoring, suggests that the use of the selection Kalman model offers significant improvements compared to the traditional Kalman model when reconstructing discontinuous initial states.

1 Introduction

Data assimilation in models representing spatio-temporal phenomena is challenging. Most statistical spatio-temporal models are based on assumptions of temporal stationarity, possibly with a parametric, seasonal trend model [1]. We consider spatio-temporal phenomena where the dynamic spatial variables evolve according to a set of differential equations. Such phenomena will, in statistics, normally be modeled as hidden Markov models [2]. The celebrated Kalman model [3] is one of the most frequently used hidden Markov models.

In studies of hidden Markov models, it is natural to distinguish between filtering and smoothing [2]. Filtering entails predicting the spatial variable at a given time with observations up to that point in time. Smoothing entails predicting the spatial variable given observations both at previous and later times. Filtering is naturally based on recursive temporal updating while smoothing appears as more complicated since updating must also be made backwards in time. We focus on a particular smoothing challenge, namely to assess the initial state given observations at later times and we denote the task spatio-temporal inversion.

Spatio-temporal inversion is of interest in many applications. In petroleum engineering, initial water saturation is often unknown. Ensemble smoothing techniques [4–6] are commonly used to evaluate this parameter and improve fluid flow prediction. In air pollution monitoring [7], inverse trajectory methods are used to identify potential source contribution. Source mapping of wildfire origin from airborne smoke observations is a spectacular example [8]. Evaluation of groundwater pollution mostly focuses on the future pollution of the pollutant, but as emphasized in [9], the identification of the heterogeneous source may be complicated.

We study a continuous spatial variable, a random field (RF), with temporal behavior governed by a set of differential equations. The spatio-temporal variable is discretized in space and time, and the hidden Markov model is cast in a Bayesian framework. The prior model consists of an initial spatial model and a forward spatio-temporal model, representing the evolution of the spatio-temporal phenomenon. The likelihood model represents the observation acquisition procedure. The corresponding posterior model, fully defined by the prior and likelihood models, represents the spatio-temporal phenomenon given the available observations. The traditional Kalman model constitutes a very particular hidden Markov model [3] with a Gaussian initial model and a linear forward function with Gaussian error term (Gauss-linear) forward model, and a Gauss-linear likelihood model. Since the class of Gaussian models is closed under linear operations, the posterior distribution is also Gaussian in the Kalman model, and the posterior model parameters are analytically tractable. Based on this posterior Gaussian model, both filtering and smoothing can easily be performed. In particular, the spatio-temporal inversion can be obtained by integrating out the spatial variables at all time points except the initial one, which is a simple task in Gaussian models. Most spatio-temporal models used in statistical studies are defined in the traditional Kalman model framework [10, 11]. Moreover, most of these models are based on spatial stationarity and consider filtering. Their focus is primarily on computational efficiency, not on model flexibility.

The fundamental Gauss-linear assumptions of the traditional Kalman model are often not suitable in real studies. The initial spatial variable may appear as non-Gaussian and/or the forward and/or the likelihood functions are non-linear. In the control theory community, linearizations such as the extended Kalman filter [12] or quantile-based representation such as the unscented Kalman filter [13] are recommended in these cases. These approaches are suitable for models with mild deviations from Gauss-linearity. Statisticians will more naturally use various Monte-Carlo based approaches such as the particle filter [2] or the ensemble Kalman Filter (EnKF) [14]. The particle filter is a sequential Monte Carlo algorithm with data assimilation made by reweighting the particles. To avoid singular solutions, resampling is usually required during the assimilation. The need for resampling makes the definition of an efficient corresponding particle smoother difficult. The EnKF is also a sequential Monte Carlo algorithm with data assimilation based on linear updates of each ensemble member. The sequential linear updates cause the ensemble distribution to drift toward Gaussianity. A corresponding ensemble smoother [15] is available but the ensemble drift toward Gaussianity makes it difficult to preserve non-Gaussianity in the posterior distribution. The discrete representation of the spatial variable makes the spatio-temporal model high-dimensional, and according to [16, 17], the EnKF is preferable to the particle filter in high dimensional models. Lastly, brute force Markov chain Monte Carlo (McMC) [18] algorithms may be used for spatio-temporal inversion, but the increasing coupling of the temporal observations makes these algorithms inefficient. Focus in our study is on the spatial initial state of the spatio-temporal phenomenon, and we aim at reproducing clearly non-Gaussian marginal features, such as multi-modality, skewness and peakedness. Several models with such features are presented in the literature.

In [19], a hidden Markov model with a skew-Gaussian initial model is defined, and for Gauss-linear forward and likelihood models, it is demonstrated that the filtering is analytically tractable. The skew-Gaussian model is based on a selection concept, and the current spatio-temporal model will later be defined along these lines.

In [16, 20–24], the initial model in the hidden Markov model is defined to be a Gaussian mixture model representing multimodality. These studies all consider filtering problems and the filter algorithms are based on a combination of clustering/particle filter and Kalman filter/EnKF. The Gaussian mixture model contains a latent categorical mode indicator, which in a spatial setting must have spatial coupling, for example in the form of a Markov RF [25]. Data assimilation in such categorical Markov RFs, either by particle filter or EnKF, appears as very complicated [23, 24], particularly in a smoothing setting.

The spatio-temporal case we consider in the current study has a non-Gaussian spatial initial model, while both the forward and likelihood models are Gauss-linear. We study this special case since it has a particularly elegant analytical solution. Further, we study spatio-temporal inversion, which entails smoothing to assess the initial spatial variable given observations up to current time, as it constitutes a particularly challenging problem. To our knowledge, no reliable methodology exists for solving such a spatio-temporal inverse problem.

In the hidden Markov model considered in this study, the initial spatial model is assigned a selection-Gaussian RF [26], which may capture multi-modality, skewness and/or peakedness in the spatial histogram of the initial spatial variable. Recall that the forward and likelihood models are assumed to be Gauss-linear. Since the class of selection-Gaussian models is closed under linear operations [26] the posterior model will also be selection-Gaussian. The posterior model parameters are then analytically tractable. A general algorithm for assessing this posterior selection-Gaussian model is defined. Based on this posterior model, both smoothing and filtering can be performed. We denote this special hidden Markov model the selection Kalman model. The class of Gaussian models is a central member in the class of selection-Gaussian models [26], hence one may consider the selection Kalman model to be a generalization of the Kalman model. We develop the results presented above and demonstrate the use of the selection Kalman model on a synthetic case study of spatio-temporal inversion. This entails assessing the initial spatial variable in a dynamic model based on a limited set of observations.

The characteristics of the class of selection-Gaussian models are central in the development of the selection Kalman model properties. These characteristics are thoroughly discussed in [26], which is inspired by the results presented in [27, 28]. In these papers, the general concept of the selection-Gaussian pdf is defined in a probabilistic setting. In [19], the one-sided selection concept is used to define a skew Kalman filter in a non-spatial setting.

In this paper $y\sim f\left(y\right)$ denotes a random variable $y$ distributed according to the probability density function (pdf) $f\left(y\right)$, or alternatively according to the corresponding cumulative distribution function (cdf) $F\left(y\right)$. Moreover, ${\phi }_n\left(y;\mu ,\Sigma \right)$ denotes the pdf of the Gaussian n-vector $y$ with expectation n-vector $\mu$ and covariance $\left(n\times n\right)$-matrix $\Sigma$. Further ${\Phi }_n\left(A;\mu ,\Sigma \right)$ denotes the probability of the aforementioned Gaussian n-vector $y$ to be in $A\subset {\mathrm{ℝ}}^n$. We also use $i_n$ to denote the all-ones n-vector and $I_n$ to denote the identity $\left(n\times n\right)$-matrix.

In Section 2, the problem is set. In Section 3, the traditional Kalman model is cast in a Bayesian hidden Markov model framework. The generalization to the selection Kalman model is then defined, and the analytical tractability is investigated. Further a general recursive algorithm for assessing the posterior distribution is specified. In Section 3, a synthetic case study of the advection-diffusion equation is discussed to showcase the ability of the selection Kalman model to solve the spatio-temporal inversion problem. The goal is to reconstruct the initial state. Results from the selection Kalman model and the traditional Kalman model are compared. In section 4, conclusions are presented.

2 Problem Setting

The case is defined in a spatio-temporal setting. Consider the variable $\left\{r_t\left(x\right);x\in {\mathrm{ℒ}}_r,t\in \mathrm{}\right\};r_{\cdot }(\cdot )\in ℝ$, with ${\mathrm{ℒ}}_r$ a grid of size n over a two-dimensional spatial area of interest while $\mathrm{}:\left\{\mathrm{0,1},\dots ,T\right\}$ is a regular discretization in time. Let $t=T$ represent current time while $t=0$ represents the initial time. The spatial variable $\left\{r_0\left(x\right);x\in {\mathrm{ℒ}}_r\right\}$ is a discretized representation of the initial state which later will be assumed to be unknown. Figure 1 displays the initial state that we evaluate in the case study. It is a spatial field with two areas: the blue area is at low value and the yellow area is at much higher value. One may consider the yellow area as the release of a pollutant at time $t=0$.

FIGURE 1

FIGURE 1. Initial state with observation locations $(\cdot )$ and monitoring locations $(\times )$.

The spatio-temporal variable evolves in time, $\left\{r_{t+1}\left(x\right);x\in {\mathrm{ℒ}}_r\right\}={\omega }_t\left[\left\{r_t\left(x\right);x\in {\mathrm{ℒ}}_r\right\}\right]$ where ${\omega }_t(\cdot )$ is a dynamic function usually represented by a set of discretized differential equations. Figure 2 shows the temporal evolution of the field presented in Figure 1 according to a set of differential equations. The spatio-temporal variable is not fully observable, it can only be measured at a number of observation sites. The observations at the observation sites are collected with some measurement error, they appear as time series denoted $\left\{d_t=\left(d_t^1,\dots ,d_t^m\right),t\in \mathrm{}\right\}$ where m is the number of observation sites. The five observation locations in the case study are represented by dots in Figure 1. Figure 3 displays the observations collected at these observation locations. The typical challenge is to infer the spatio-temporal variable $\left\{r_t\left(x\right);x\in {\mathrm{ℒ}}_r,t\in \mathrm{}\right\}$ based on the observed time series $\left\{d_t;t\in \mathrm{}\right\}$. It constitutes a complex spatio-temporal inverse problem. In the current study we focus on assessing the initial spatial variable $\left\{r_0\left(x\right);x\in {\mathrm{ℒ}}_r\right\}$ from the observed time series $\left\{d_t;t\in \mathrm{}\right\}$.

FIGURE 2

FIGURE 2. Spatio-temporal diffusion.

FIGURE 3

FIGURE 3. Observations at the observation locations and true curve.

3 Model Definition

Consider the unknown temporal n-vector $r_t$, representing the discretized spatial variable $\left\{r_t\left(x\right);x\in {\mathrm{ℒ}}_r\right\}$, for $t\in {\mathrm{}}_r:\left\{\mathrm{0,1},\dots ,T,T+1\right\}$. Define the variable $r=\left\{r_0,r_1,\dots ,r_T,r_{T+1}\right\}$ and let $r_{i:j}$ denote $\left\{r_i,r_{i+1},\dots ,r_j\right\},\forall \left(i,j\right)\in {\mathrm{}}_r^2,i\le j$. Moreover assume that the temporal m-vectors of observations $d_t$ for $t\in {\mathrm{}}_d:\left\{\mathrm{0,1},\dots ,T\right\}$ are available, and define $d=\left\{d_0,d_1,\dots ,d_T\right\}$ and $d_{i:j}=\left\{d_i,\dots ,d_j\right\}$ accordingly. The objective of this study is to assess $\left[r_0|d\right]$. To that end, we define a Kalman type model, represented as a hidden Markov model in a Bayesian inversion framework.

3.1 Bayesian Inversion

The Kalman type model, phrased as Bayesian inversion, requires the specification of a prior model for $r$ and a likelihood model for $\left[d|r\right]$. The model specified below defines a hidden Markov model as displayed in Figure 4.

FIGURE 4

FIGURE 4. Graph of the hidden Markov model.

3.1.1 Prior Model

The prior model on $r$ synthesizes the knowledge and experience with the spatial variable of interest, and it consists of an initial distribution and a forward model:

Initial Distribution

The prior distribution for the initial state $r_0$ is denoted $f\left(r_0\right)$.

Forward Model

The forward model given the initial state $\left[r_{1:T+1}|r_0\right]$ is defined as,

$f\left(r_{1:T+1}|r_0\right)={\displaystyle \prod }_{t=0}^{T}f\left(r_{t+1}|r_t\right)(1)$

with,

$\left[r_{t+1}|r_t\right]={\omega }_t\left(r_t,{\epsilon }_t^r\right)\sim f\left(r_{t+1}|r_t\right)(2)$

where ${\omega }_t\left(\cdot ,\cdot \right)\in {ℝ}^n$ is the function that propagates $r_t$ forward in time, with ${\epsilon }_t^r$ a random component. Since ${\omega }_t\left(\cdot ,\cdot \right)$ only involves the variable at the previous time step, $r_t$, the forward model is a Markov chain.

3.1.2 Likelihood Model

The likelihood model on $\left[d|r\right]$ provides a link between the variable of interest $r$ and the observations $d$ and is defined as,

$f\left(d|r\right)={\displaystyle \prod }_{t=0}^{T}f\left(d_t|r_t\right)(3)$

with,

$\left[d_t|r_t\right]={\psi }_t\left(r_t,{\epsilon }_t^d\right)\sim f\left(d_t|r_t\right)(4)$

where ${\psi }_t\left(\cdot ,\cdot \right)\in {ℝ}^m$ is the likelihood function with ${\epsilon }_t^d$ a random component. The likelihood model is defined assuming conditional independence and single state response and is thus in factored form.

3.1.3 Posterior Model

Bayesian inversion endeavors to assess the posterior distribution of $\left[r|d\right]$,

$\begin{array}{l}f\left(r|d\right)={\left[{\displaystyle \int f\left(d|r\right)f\left(r\right)dr}\right]}^{-1}\times f\left(d|r\right)f\left(r\right)\\ =const\times f\left(d_0|r_0\right)f\left(r_0\right)\\ \times {\displaystyle \prod _{t=1}^{T}f\left(d_t|r_t\right)f\left(r_t|r_{t-1}\right)f\left(r_{T+1}|r_T\right)}\\ =f\left(r_0|d\right){\displaystyle \prod _{t=1}^{T}f\left(r_t|r_{t-1},d_{t:T}\right)f\left(r_{T+1}|r_T\right)}\end{array}(5)$

which is a non-stationary Markov chain for the hidden Markov model with a likelihood model in factored form as defined above [29]. Assessing such a posterior distribution is usually difficult as both the normalizing constant and the conditional transition matrices are challenging to calculate.

3.2 Kalman Type Models

The current study is limited to Kalman type models. They comprise an initial and a process part.

Initial Distribution

The initial distribution is identical to the initial distribution of the prior model $f\left(r_0\right)$, and as such captures the characteristics of the initial state of the process. Two model classes are later discussed: the Gaussian and the selection-Gaussian classes.

Process Model

The process model includes the forward model and likelihood models defined in Section 3.1. It thus characterizes the process dynamics and the observation acquisition procedure. The forward model is defined by,

$\left[r_{t+1}|r_t\right]=A_t{r}_t+{\epsilon }_t^r$

$f\left(r_{t+1}|r_t\right)={\phi }_n\left(r_{t+1};A_t{r}_t,{\Sigma }_t^{r|r}\right)(6)$

with forward $\left(n\times n\right)$-matrix $A_t$ and n-vector error term ${\epsilon }_t^r$ defined as centered Gaussian with covariance $\left(n\times n\right)$-matrix ${\Sigma }_t^{r|r}$. The forward model is therefore Gauss-linear. The likelihood component is defined by,

$\left[d_t|r_t\right]=H{r}_t+{\epsilon }_t^d$

$f\left(d_t|r_t\right)={\phi }_p\left(d_t;H{r}_t,{\Sigma }_t^{d|r}\right)(7)$

with the observation $\left(m\times n\right)$-matrix $H$ and the m-vector error term ${\epsilon }_t^d$ defined as centered Gaussian with covariance $\left(m\times m\right)$-matrix ${\Sigma }_t^{d|r}$. The likelihood model is also Gauss-linear. This process model coincides with the frequently used traditional Kalman model [3].

3.3 Traditional Kalman Model

The traditional Kalman model is defined by letting the initial distribution be in the class of Gaussian pdfs,

$r_0\sim f\left(r_0\right)={\phi }_n\left(r_0;{\mu }_0^r,{\Sigma }_0^r\right)(8)$

with initial expectation n-vector ${\mu }_0^r$ and positive definite covariance $\left(n\times n\right)$-matrix ${\Sigma }_0^r$. The Gaussian initial distribution is parametrized by ${\Theta }^G=\left({\mu }_0^r,{\Sigma }_0^r\right)$. In our spatial study, this initial distribution will be a discretized stationary Gaussian RF. The process model is Gauss-linear and identical to the traditional Kalman type.

This traditional Kalman model is analytically tractable. The posterior distribution $f\left(r|d\right)$ is Gaussian and the posterior distribution parameters can be calculated by algebraic operations on the parameters of the initial distribution, process model and the observed data. Therefore the assessment of the posterior distribution does not require computationally demanding integrals. The analytical tractability follows from the recursive reproduction of Gaussian pdfs:

• The initial model $f\left(r_0\right)$ is Gaussian and the likelihood model $f\left(d_0|r_0\right)$ is Gauss-linear, hence the joint model $f\left(r_0,d_0\right)$ is Gaussian. Consequently, the conditional model $f\left(r_0|d_0\right)$ is Gaussian.

• The conditional model $f\left(r_0|d_0\right)$ is Gaussian and the dynamic model $f\left(r_1|r_0\right)$ is Gauss-linear, hence the joint conditional model $f\left(r_1,r_0|d_0\right)$ is Gaussian.

By recursion, we obtain that $f\left(r|d\right)=f\left(r_0,\dots ,r_{T+1}|d_0,\dots ,d_T\right)$ is Gaussian. Note in particular that since $f\left(r|d\right)$ is Gaussian, so is $f\left(r_0|d\right)$. This pdf is obtained by marginalization of $f\left(r|d\right)$ which, for the Gaussian case, amounts to removing rows from the expectation vector and rows and columns from the covariance matrix. Additionally, the joint pdf $f\left(r,d\right)$ can be assessed using a simple recursive algorithm, see Supplementary Appendix Algorithm A1 in Supplementary Appendix A.

From the joint Gaussian pdf $f\left(r,d\right)$, the posterior distribution $f\left(r|d\right)$ can be analytically assessed. In spatial models, the grid dimension n may be large while the number of data collection sites m usually is small. Supplementary Appendix Algorithm A1 requires storing the covariance $\left[n\left(T+2\right)+m\left(T+1\right)]\times [n\left(T+2\right)+m\left(T+1\right)\right]$-matrix of the Gaussian vector $\left[r,d\right]$ which is hardly ever necessary in practice where the target distribution is clearly identified. Only the spatial variables of interest need to be stored, which entails that only the covariance $\left[n+m\left(T+1\right)]\times [n+m\left(T+1\right)\right]$-matrix of $\left[r_0,d\right]$ need to be stored in our spatio-temporal inversion study.

3.4 Selection Kalman Model

The selection Kalman model is defined by letting the initial distribution be in the class of selection-Gaussian pdfs [27, 28]. This class is defined by considering an auxilary n-vector $\tilde{r}$ with pdf from the Gaussian class,

$f\left(\tilde{r}\right)={\phi }_n\left(\tilde{r};{\mu }_{\tilde{r}},{\Sigma }_{\tilde{r}}\right)(9)$

with expectation n-vector ${\mu }_{\tilde{r}}$ and covariance $\left(n\times n\right)$-matrix ${\Sigma }_{\tilde{r}}$. In our spatial study this pdf will represent a discretized stationary Gaussian RF. Define further an auxiliary q-vector $\nu$ by a Gauss-linear extension,

$\left[\nu |\tilde{r}\right]={\mu }_{\nu }+{\Gamma }_{\nu |\tilde{r}}\left(\tilde{r}-{\mu }_{\tilde{r}}\right)+{\epsilon }_{\nu |\tilde{r}}(10)$

with the expectation q-vector ${\mu }_{\nu }$, and the regression $\left(q\times n\right)$-matrix ${\Gamma }_{\nu |\tilde{r}}$ and the centered Gaussian q-vector ${\epsilon }_{\nu |\tilde{r}}$, independent of $\tilde{r}$, with covariance $\left(q\times q\right)$-matrix ${\Sigma }_{\nu |\tilde{r}}$. In the current spatial study the dimension of $\tilde{r}$ and $\nu$ will be identical. Generally, we have,

$f\left(\nu |\tilde{r}\right)={\phi }_q\left(\nu ;{\mu }_{\nu |\tilde{r}},{\Sigma }_{\nu |\tilde{r}}\right)(11)$

with ${\mu }_{\nu |\tilde{r}}={\mu }_{\nu }+{\Gamma }_{\nu |\tilde{r}}\left(\tilde{r}-{\mu }_{\tilde{r}}\right)$. As a consequence, $\left[\tilde{r},\nu \right]$ is jointly Gaussian,

$\left[\begin{array}{c}\tilde{r}\\ \nu \end{array}\right]\sim f\left(\tilde{r},\nu \right)={\phi }_{n+q}\left(\left[\begin{array}{c}\tilde{r}\\ \nu \end{array}\right];\left[\begin{array}{c}{\mu }_{\tilde{r}}\\ {\mu }_{\nu }\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{\tilde{r}}& {\Sigma }_{\tilde{r}}{\Gamma }_{\nu |\tilde{r}}^T\\ {\Gamma }_{\nu |\tilde{r}}{\Sigma }_{\tilde{r}}& {\Sigma }_{\nu }\end{array}\right]\right)(12)$

with the covariance $\left(q\times q\right)$-matrix ${\Sigma }_{\nu }={\Gamma }_{\nu |\tilde{r}}{\Sigma }_{\tilde{r}}{\Gamma }_{\nu |\tilde{r}}^T+{\Sigma }_{\nu |\tilde{r}}$. Define a selection subset $A\subset {ℝ}^q$, and define the class of selection-Gaussian pdfs by $r_A=\left[\tilde{r}|\nu \in A\right]$. In the current spatial study the set A will be separable in ${\mathrm{ℝ}}^q$. Generally, it follows that,

$\begin{array}{l}f\left(r_A\right)=f\left(\tilde{r}|\nu \in A\right)\\ ={\left[{\Phi }_q\left(A;{\mu }_{\nu },{\Sigma }_{\nu }\right)\right]}^{-1}\\ \times {\Phi }_q\left(A;{\mu }_{\nu |\tilde{r}},{\Sigma }_{\nu |\tilde{r}}\right)\times {\phi }_n\left(\tilde{r};{\mu }_{\tilde{r}},{\Sigma }_{\tilde{r}}\right)\end{array}(13)$

This class of pdfs is parametrized by ${\Theta }^{SG}=\left({\mu }_{\tilde{r}},{\Sigma }_{\tilde{r}},{\mu }_{\nu },{\Gamma }_{\nu |\tilde{r}},{\Sigma }_{\nu |\tilde{r}},A\right)$ for all valid parameter sets. The class of selection-Gaussian pdfs is very flexible and may represent multi-modality, skewness and peakedness [26].

Four one-dimensional selection-Gaussian pdfs are displayed in Figure 5 in order to demonstrate the influence of the selection set $A\subset ℝ$. The bivariate variable $\left[\tilde{r},\nu \right]$ is bi-Gaussian and identical in all displays, while the selection sets are marked as solid gray bars along the vertical ν-axis. Figure 5A contains a selection set comprised of two segments symmetric about the expectation of ν, making the selection-Gaussian pdf along the horizontal axis bimodal and symmetric. Figure 5B contains a selection set of two asymmetric segments, making the selection-Gaussian pdf bimodal and asymmetric. Figure 5C contains a selection set of three segments symmetric about the expectation of ν, making the selection-Gaussian pdf trimodal and symmetric. Lastly, Figure 5D contains a selection set comprised of only one segment, making the selection-Gaussian pdf skewed. This selection concept can be extended to higher dimensions and even to discretized spatial models.

FIGURE 5

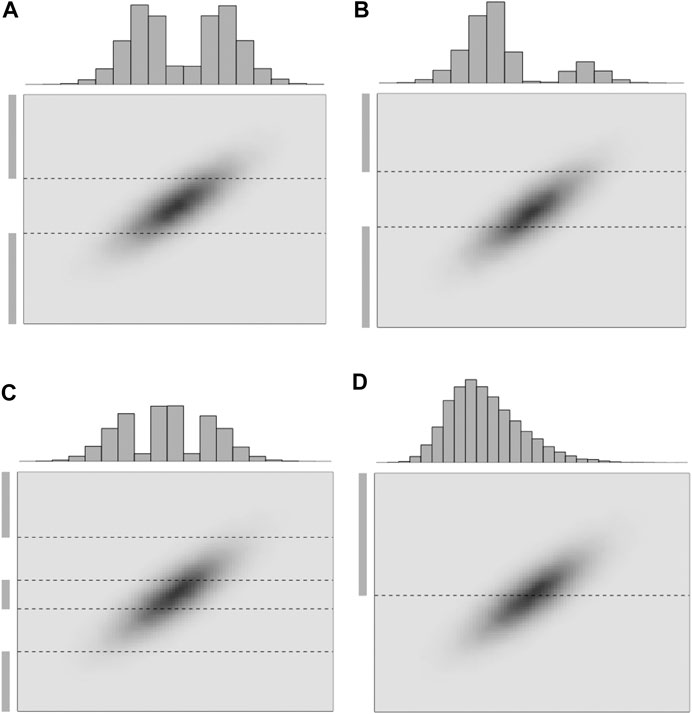
FIGURE 5. Realizations of 1D selection-Gaussian pdfs (histogram) with varying selection sets $A\subset {ℝ}^n$ (solid gray bars) for a bi-Gaussian pdf $\left[\tilde{r},\nu \right]$ (dark gray).

Note that assigning a null-matrix to ${\Gamma }_{\nu |\tilde{r}}$ entails that $f\left(\tilde{r},\nu \right)=f\left(\tilde{r}\right)f\left(\nu \right)$ and selection on $\nu$ does not influence $\tilde{r}$. It follows that $f\left(r_A\right)=f\left(\tilde{r}\right)$ is Gaussian. The selection-Gaussian model can therefore be seen as a generalization of the Gaussian one. Assume that the conditional independence, $f\left(d_t,\nu |{\tilde{r}}_t\right)=f\left(d_t|{\tilde{r}}_t\right)f\left(\nu |{\tilde{r}}_t\right)$, holds for all t, it can then be demonstrated [26] that the following recursive reproduction of selection-Gaussian pdfs holds:

• The initial model $f\left(r_{A,0}\right)$ is selection-Gaussian and the likelihood model $f\left(d_0|r_{A,0}\right)$ is Gauss-linear, hence the joint model $f\left(r_{A,0},d_0\right)$ is selection-Gaussian. Moreover, the conditional model $f\left(r_{A,0}|d_0\right)$ is selection-Gaussian.

• The conditional model $f\left(r_{A,0}|d_0\right)$ is selection-Gaussian and the dynamic model $f\left(r_{A,1}|r_{A,0}\right)$ is Gauss-linear, the joint conditional model $f\left(r_{A,1},r_{0,A}|d_0\right)$ is therefore selection-Gaussian.

By recursion, we obtain that $f\left(r_A|d\right)=f\left(r_{A,0},\dots ,r_{A,T+1}|d_0,\dots ,d_T\right)$ is selection-Gaussian. Recall that these characteristics are similar to those of the class of Gaussian pdfs that make the traditional Kalman model analytically tractable. The selection Kalman model is defined with an initial distribution from the class of selection-Gaussian pdfs and a process model which is Gauss-linear and identical to the traditional Kalman type. From the characteristics of the class of selection-Gaussian distributions, it follows that the posterior distribution $f\left(r_A|d\right)$ is in the class of selection-Gaussian distributions and so is $f\left(r_{A,0}|d\right)$.

Consider the augmented $\left(n+q\right)$-vector $\left[{\tilde{r}}_0,\nu \right]$ which together with the selection set $A\in {ℝ}^q$ defines the initial state $r_{A,0}=\left[{\tilde{r}}_0||\nu \in A\right]$. The recursive algorithm, see Algorithm 1, is initiated with this augmented vector which is Gaussian. The conditional independence $f\left(d_t,\nu |{\tilde{r}}_t\right)=f\left(d_t|{\tilde{r}}_t\right)f\left(\nu |{\tilde{r}}_t\right)$ entails that $f\left(d_t|r_{A,t}\right)=f\left(d_t|r_t\right)$, which is Gauss-linear for all t.

Algorithm 1 provides the Gaussian pdf of the $\left[n\left(T+2\right)+q+m\left(T+1\right)\right]$-vector $\left[\tilde{r},\nu ,d\right]$. From the joint Gaussian pdf $f\left(\tilde{r},\nu ,d\right)$, the pdf $f\left(r_{A,0}|d\right)=f\left({\tilde{r}}_0|\nu \in A,d\right)$ can be assessed by first marginalizing $\tilde{r}$ and thereafter sequentially conditioning on $d$ and then on $\nu$. The final step, conditioning on $\nu \in A$, is computer demanding even though $\nu$ has only dimension q. Rejection sampling is only possible for very low values of q. We therefore use the Metropolis-Hastings algorithm, a McMC method, detailed in [26] and extended from [30]. Algorithm 1 requires storing the covariance $\left[n\left(T+2\right)+q+m\left(T+1\right)]\times [n\left(T+2\right)+q+m\left(T+1\right)\right]$ -matrix of the augmented Gaussian vector $\left[\tilde{r},\nu ,d\right]$ which can usually be avoided in practice. Only the spatial variables of interest need to be stored, which entails that only the covariance $\left[n+q+m\left(T+1\right)]\times [n+q+m\left(T+1\right)\right]$-matrix of $\left[{\tilde{r}}_0,\nu ,d\right]$ need to be stored in our spatio-temporal inversion study.

ALGORITHM 1

Algorithm 1. Joint Selection Kalman Model

4 Synthetic Study

The synthetic study is introduced in Section 2, and we discuss it in larger detail in this section.

4.1 Model

Consider a discretized spatio-temporal continuous RF representing the evolution of a temperature field $\left\{r_t\left(x\right),x\in {\mathrm{ℒ}}_r\right\}$, $t\in {\mathrm{}}_r:\left\{\mathrm{0,1},.\dots ,T,T+1\right\}$; $r_t\left(x\right)\in ℝ$, as defined in Section 2. The number of spatial grid nodes is $n=21\times 21$, while temporal reference T is the current time up to $T=50$. The discretized spatial field at time t is represented by the n-vector $r_t$.

The initial temperature field $r_0$, given in Figure 1, is assumed to be unknown. It is divided into two distinct areas: the blue area where the temperature is set at 20°C and the yellow area where the temperature is set at 45°C. Assume that, given the initial temperature field, the field evolves according to the advection-diffusion equation, a linear partial differential equation,

$\frac{\partial r_t\left(x\right)}{\partial t}-\lambda {\nabla }^2{r}_t\left(x\right)+c\cdot \nabla r_t\left(x\right)=0(14)$

$\nabla r_t\left(x\right)\cdot n=0(15)$

with $\lambda \in {ℝ}_{+}$ the known diffusivity coefficient, $n$ the outer normal to the domain and $c=\left[c_1,c_2\right]$ the known velocity field. The forward model is defined as,

$\left[r_{t+1}|r_t\right]=A{r}_t+{\epsilon }_t^r(16)$

$f\left(r_{t+1}|r_t\right)={\phi }_n\left(r_{t+1};A{r}_t,{\Sigma }_t^{r|r}\right)(17)$

where the $\left(n\times n\right)$-matrix $A$ is obtained by discretizing the advection-diffusion equation using finite differences, see Supplementary Appendix B for finite differences scheme and parameter values, while the centered Gaussian n-vector ${\epsilon }_t^r$, with covariance $\left(n\times n\right)$-matrix ${\Sigma }_t^{r|r}=0\times I_n$ represents model error. Under these assumptions, the forward model is exact which constitutes a limiting case to Gauss-linear models. The evolution of the temperature field is described in Figure 2.

The observations are acquired at $m=5$ different locations on the spatial grid ${\mathrm{ℒ}}_r$ at each temporal node in ${\mathrm{}}_d$ providing the set of m-vectors $\{d_t,t\in {\mathrm{}}_d\}$. The observation locations are represented with dots in Figure 1. The corresponding likelihood model is defined as,

$\left[d_t|r_t\right]=H{r}_t+{\epsilon }_t^d(18)$

$f\left(d_t|r_t\right)={\phi }_m\left(d_t;H{r}_t,{\Sigma }_t^{d|r}\right)(19)$

where the observation $\left(m\times n\right)$-matrix $H$ is a binary selection matrix, see Supplementary Appendix B, while the centered Gaussian m-vector ${\epsilon }_t^d$ with covariance $\left(m\times m\right)$-matrix ${\Sigma }_t^{d|r}={\sigma }_{d|r}^2\times I_m$ with ${\sigma }_{d|r}=0.1$, represents independent observation errors. Under these assumptions, the likelihood model is Gauss-linear. The observations are displayed as time series in Figure 3. Note that ${\Sigma }_t^{r|r}$ and ${\Sigma }_t^{d|r}$ are in this example constant through time.

The forward and likelihood models are Gauss-linear. In order to fully defined the selection Kalman model and traditional Kalman model, we must specify the prior distribution for the initial temperature field for both approaches.

We assume we know the initial temperature field has large areas with low temperatures in the range $\left[5°C,25°C\right]$ and possibly, smaller areas with high temperatures in the range $\left[40°C,55°C\right]$. The exact location, extent and temperature of these smaller areas are unknown. The prior is therefore spatially stationary in both models.

The prior distribution is set to be selection-Gaussian for the selection Kalman model. Such a prior model can represent multimodality. The model is constructed according to [26] and is defined considering an auxiliary discretized stationary Gaussian RF,

$f\left(\widetilde{r_0}\right)={\phi }_n\left({\tilde{r}}_0;{\mu }_{\tilde{r}}{i}_n,{\sigma }_{\tilde{r}}^2{\Sigma }_{\tilde{r}}^{\rho }\right)(20)$

with expectation and variance levels, ${\mu }_{\tilde{r}}$ and ${\sigma }_{\tilde{r}}^2$ respectively. The spatial correlation $\left(n\times n\right)$-matrix ${\Sigma }_{\tilde{r}}^{\rho }$ is defined by an isotropic second order exponential spatial correlation function ${\rho }_{\tilde{r}}\left(\tau \right)=\exp \left(-{\tau }^2/{\delta }^2\right);\tau \in {ℝ}_{+}$. Define the auxiliary n-vector $\nu$ given ${\tilde{r}}_0$,

$\left[\nu |{\tilde{r}}_0\right]=\gamma \left({\tilde{r}}_0-{\mu }_{\tilde{r}}{i}_n\right)+{\epsilon }^{\nu }(21)$

$f\left(\nu |{\tilde{r}}_0\right)={\phi }_n\left[\nu ;\gamma \left({\tilde{r}}_0-{\mu }_{\tilde{r}}{i}_n\right),\left(1-{\gamma }^2\right)I_n\right](22)$

$=\stackrel{n}{{\displaystyle \prod }_{i=1}}{\phi }_1\left[{\nu }_i;\gamma \left({\tilde{r}}_{0,i}-{\mu }_{\tilde{r}}\right),\left(1-{\gamma }^2\right)\right](23)$

with coupling parameter $\gamma \in {ℝ}_{\left[-\mathrm{1,1}\right]}$ and centered Gaussian independent n-vector ${\epsilon }^{\nu }$ with variance $\left(1-{\gamma }^2\right)$. Note that this pdf is in factored form. Consequently the joint pdf of $\left[{\tilde{r}}_0,\nu \right]$ is,

$\left[\begin{array}{c}{\tilde{r}}_0\\ \nu \end{array}\right]\sim {\phi }_{2n}\left(\left[\begin{array}{c}{\tilde{r}}_0\\ \nu \end{array}\right];\left[\begin{array}{c}{\mu }_{\tilde{r}}{i}_n\\ 0i_n\end{array}\right],\left[\begin{array}{cc}{\sigma }_{\tilde{r}}^2{\Sigma }_{\tilde{r}}^{\rho }& {\sigma }_{\tilde{r}}^2\gamma {\Sigma }_{\tilde{r}}^{\rho }\\ {\sigma }_{\tilde{r}}^2\gamma {\Sigma }_{\tilde{r}}^{\rho }& {\sigma }_{\tilde{r}}^2{\gamma }^2{\Sigma }_{\tilde{r}}^{\rho }+\left(1-{\gamma }^2\right)I_n\end{array}\right]\right)(24)$

Define a separable selection set $A\subset {ℝ}^n$ such that $A=B^n,B\subset ℝ$. Therefore, the prior distribution is represented by the discretized selection-Gaussian RF $r_{A,0}$ defined as,

$r_{A,0}=\left[{\tilde{r}}_0|\nu \in A\right](25)$

$\begin{array}{l}f\left(r_{A,0}\right)={\left[{\Phi }_n\left(A;0i_n,{\sigma }_{\tilde{r}}^2{\gamma }^2{\Sigma }_{\tilde{r}}^{\rho }+\left(1-{\gamma }^2\right)I_n\right)\right]}^{-1}\\ \times \stackrel{n}{{\displaystyle \prod }_{i=1}}{\Phi }_1\left[A_i;\gamma \left({\tilde{r}}_i-{\mu }_{\tilde{r}}\right),\left(1-{\gamma }^2\right)\right]\\ \times {\phi }_n\left(r_{A,0};{\mu }_r{i}_n,{\sigma }_{\tilde{r}}^2{\Sigma }_{\tilde{r}}^{\rho }\right)\end{array}(26)$

Note that after selection on the auxiliary variable $\nu$ is made, the expectation and variance of the resulting $r_{A,0}$ will no longer be ${\mu }_{\tilde{r}}{i}_n$ and ${\sigma }_{\tilde{r}}^2{\Sigma }_{\tilde{r}}^{\rho }$.

The parameters values are listed in Table 1 and they are chosen to reflect what is assumed about the initial temperature field. The prior marginal distribution is bimodal, the dominant mode is centered about $18°C$ while the smaller mode is centered about $40°C$ as shown in Figure 6. The spread of the dominant mode covers the assumed temperature range for the low temperature areas while the spread of the smaller mode covers the assumed range for the high temperature areas. Realizations from the prior distribution and associated spatial histograms are shown in Figure 7A. They exhibit large areas at low temperatures and smaller areas at higher temperatures. Similarly to the marginal distribution, the spatial histograms cover the assumed range for high and low temperature areas.

TABLE 1

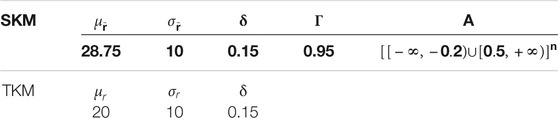
TABLE 1. Parameter values for the selection Gaussian initial model (SKM) and the Gaussian initial model (TKM).

FIGURE 6

FIGURE 6. Prior marginal distribution of the initial temperature field for the selection Kalman model.

FIGURE 7

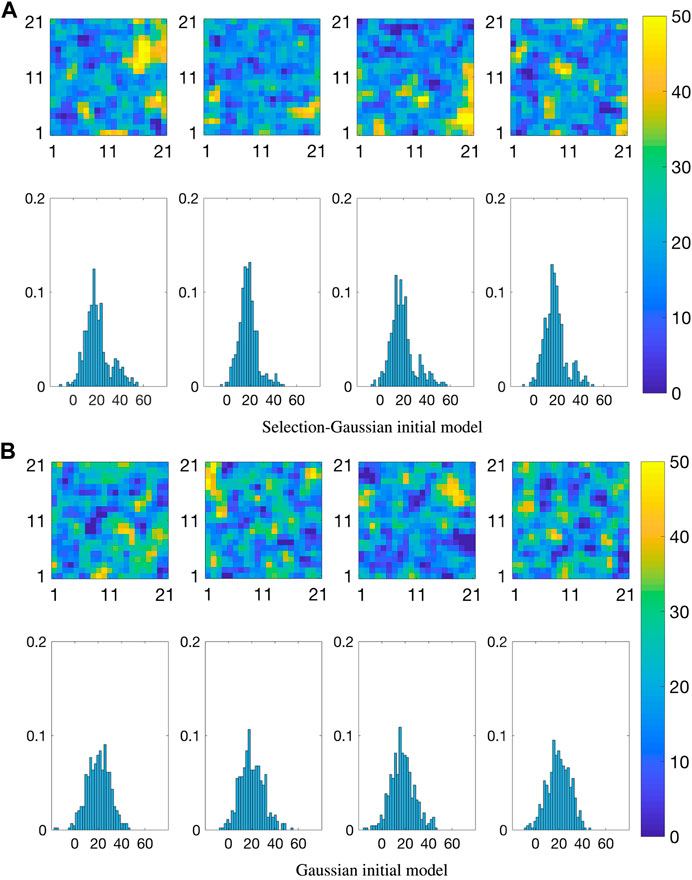
FIGURE 7. Realizations from the prior distribution of the initial state; maps (upper), spatial histograms (lower).

The prior distribution for the traditional Kalman model is Gaussian and is defined as,

$f\left(r_0\right)={\phi }_n\left(r_0;{\mu }_r{i}_n,{\sigma }_r^2{\Sigma }_r^{\rho }\right)(27)$

with expectation and variance levels, ${\mu }_r$ and ${\sigma }_r^2$, respectively and spatial correlation $\left(n\times n\right)$-matrix ${\Sigma }_r^{\rho }$ defined by a second order spatial correlation function ${\rho }_r\left(\tau \right)=\exp \left(-{\tau }^2/{\delta }^2\right);\tau \in {ℝ}_{+}$. The parameter values are listed in Table 1.

Figure 7B displays four realizations with associated spatial histograms from the prior distribution for the traditional Kalman model. The mean and variance levels are chosen so that the prior covers the assumed range for the high and low temperature areas as can be seen in the spatial histograms.

Figure 7B can be compared to Figure 7A, and one observes that only the selection-Gaussian distribution can capture bi-modality in the spatial histograms. In studies with real data, the prior model specification must of course be based on experience with the phenomenon under study.

In the next section, we demonstrate the effect of specifying different initial models in the spatio-temporal inversion model.

4.2 Results

The challenge is to restore $r_0$ based on the observations $d=\left\{d_0,\dots ,d_T\right\}$ by evaluating the posterior distribution in the selection Kalman model $f\left(r_{A,0}|d_0,\dots ,d_T\right)$ and in the traditional Kalman filter $f\left(r_0|d_0,\dots ,d_T\right)$. We compare the results from these two models that have been specified in the previous section. The posterior distributions are analytically tractable for both the selection Kalman model and the traditional Kalman model. They are calculated using Algorithm 1 and Supplementary Appendix Algorithm A1 respectively. In order to evaluate the results, we present various characteristics of the posterior distributions for increasing values of current time T:

1. Marginal pdfs at four monitoring locations represented by crosses and numbered $\mathrm{1,2,3,4}$ in Figure 1,

$f\left(r_{A,0,i}|d_{0:T}\right)={\displaystyle \int f\left(r_{A,0}|d_{0:T}\right)d{r}_{A,0,-i}}i=1,\dots ,4(28)$

and similarly for $f\left(r_{0,i}|d_{0:T}\right)$ based on $f\left(r_0|d_{0:T}\right)$. The index $-i$ stands for all the indices in $1,\dots ,n$ but the ith index.

2. Spatial prediction based on a marginal maximum a posteriori (MMAP) criterion,

$\begin{array}{l}{\widehat{r}}_{A,0}=MMAP\left\{r_{A,0}|d_{0:T}\right\}\\ =\left\{MAP\left\{r_{A,0,j}|d_{0:T}\right\};j=\mathrm{1,2},\dots ,n\right\}\\ =\left\{\arg \max \left\{f\left(r_{A,0,j}|d_{0:T}\right)\right\},j=\mathrm{1,2},\dots ,n\right\}\end{array}(29)$

and similarly for ${\widehat{r}}_0$ based on $f\left(r_0|d_{0:T}\right)$. This MMAP criterion is used as the marginal posterior model may be multi-modal. For uni-modal symmetric posterior distributions such as the Gaussian one, the MMAP predictor coincides with the expectation predictor.

3. The MMAP prediction and the associated 0.80 prediction interval along a horizontal profile A-A’, see Figure 1. The prediction interval is computed as the highest density interval (HDI) [31], which entails that the prediction intervals may consist of several intervals for multimodal posterior pdfs.

4. Realizations From the Posterior Pdfs $f\left(r_{A,0}|d_{0:T}\right)$ and $f\left(r_0|d_{0:T}\right)$.

Figure 8 displays the marginal posterior pdfs based on the selection Kalman model at the four monitoring locations, vertically, for increasing current time T, horizontally. At current time $T=0$, all pdfs are virtually identical to the marginal pdf of the stationary initial model. As current time T increases, and the observations are assimilated, one observes substantial differences between the marginal pdfs at the monitoring locations. The height of the high-value mode increases depending on the proximity of monitoring location to the yellow area, as expected. The posterior marginal pdf at observation location one clearly indicates that it lies in the yellow area already at current time $T=20$ as the high-value mode is increasing. At location two the high-value mode also increases somewhat at $T=20$, but does not increase more thereafter. This monitoring location is outside the yellow area, although fairly close to it. Location three is far from both the yellow area and observation locations and the posterior marginal pdf remains almost identical to the prior model. Lastly, location four is far from the yellow area but close to an observation location at which the observations remain stationary, hence the low-value mode grows to be completely dominant.

FIGURE 8

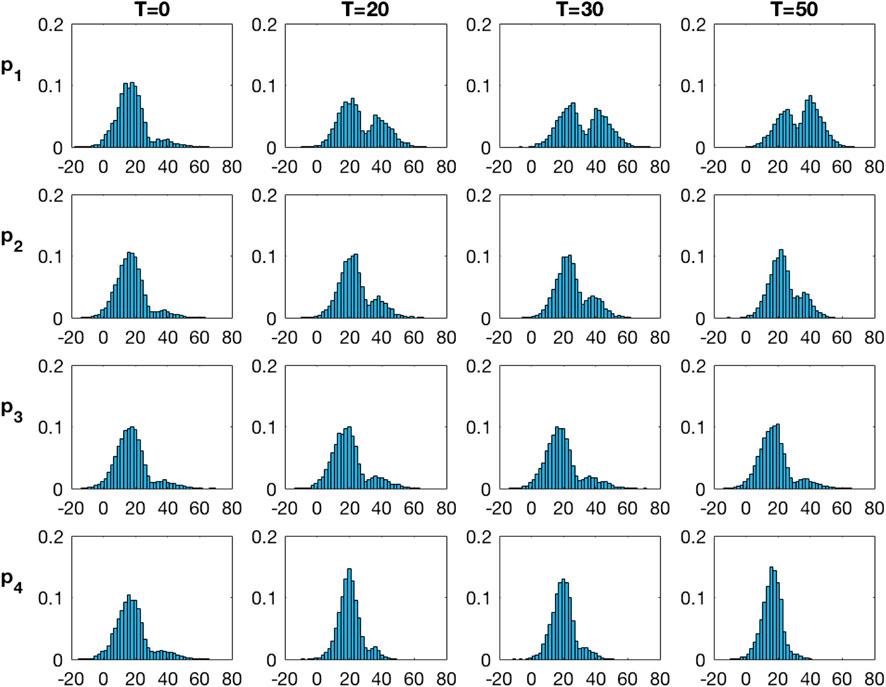
FIGURE 8. Marginal pdfs at monitoring locations for increasing current time T from the inversion with the selection Kalman model.

Figure 9 displays the marginal pdfs from the traditional Kalman model. These marginal posterior pdfs are also virtually identical at current time $T=0$. As current time T increases the marginal pdfs at the monitoring locations are indeed different as they are shifting. However, this shift is difficult to observe. By using the selection Kalman model, the indications of a yellow area at the correct location can be observed from current time $T=20$, while one can hardly observe any indications of it if the traditional Kalman model is used.

FIGURE 9

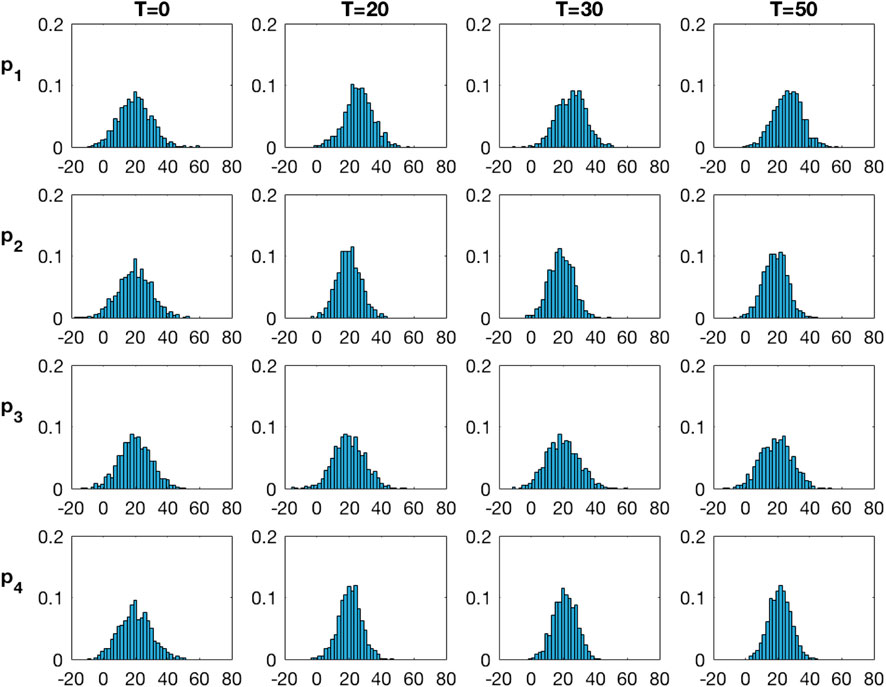
FIGURE 9. Marginal pdfs at monitoring locations for increasing current time T from the inversion with the traditional Kalman model.

The upper panels of Figure 10 display the MMAP spatial prediction based on the selection Kalman model for increasing current time T. At current time $T=0$, the predictions are virtually constant bar some boundary effect as the initial prior model is stationary. As current time T increases, indications of the yellow appear at $T=30$, it is however at $T=50$ that correct location and spatial extent are identified. The prediction value of the yellow area is very close to the correct value of 45. The blue area value is predicted with some variability around the expected 20. The lower panels of Figure 10 present the corresponding spatial predictions based for the traditional Kalman model. As current time T increases, indications of something occurring in the yellow area appears, but the location is uncertain and the spatial extent only vaguely outlined. Moreover the predicted value in the yellow area is much lower than the correct value 45. The background value is however fairly precisely predicted around the expected 20. The circular features centered about the observation locations that appear on the predictions based on the selection Kalman model in Figure 10 are not artifacts. These features are also present on the predictions based on the traditional Kalman model, although less prominent.

FIGURE 10

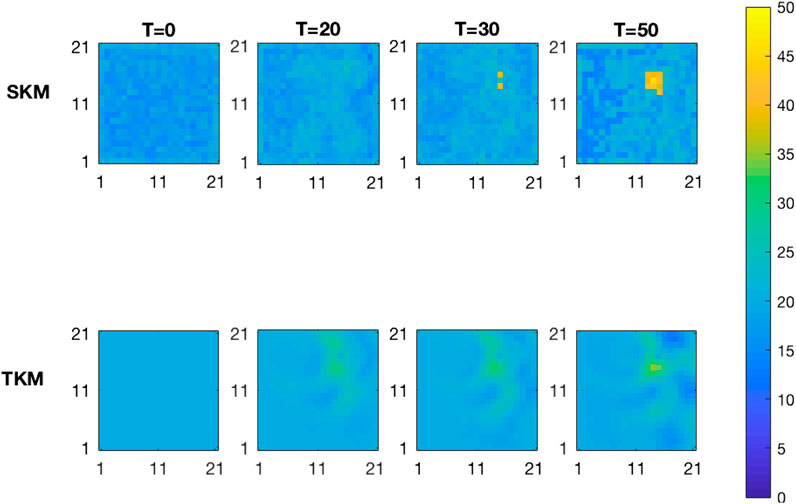
FIGURE 10. MMAP predictions of the initial state for increasing current time T from the inversion with the selection Kalman model (SKM-upper) and with the traditional Kalman model (TKM-lower).

We evaluate the root mean square error (RMSE) values of the two models at time $T=50$. The RMSE criterion is used to quantify the difference between the MMAP predictions in Figure 10 and the truth in Figure 1. The RMSE for the selection Kalman model is 2.76 while the RMSE of the traditional Kalman model is 3.33 The selection Kalman model therefore offers a $18\%$ reduction in RMSE compared to the RMSE of the traditional Kalman model.

Figure 11 displays the MMAP predictions with associated 0.80 prediction intervals along the horizontal profile A-A’. The prediction from the selection Kalman model captures the yellow area while the prediction from the traditional Kalman model barely indicates the yellow area. The prediction intervals follow the same pattern. Note, however, that the prediction intervals of the selection Kalman model may appear as two intervals close to the yellow area since the marginal posterior models are bimodal. By using the selection Kalman model, the location, spatial extent and value of the yellow area is very precisely predicted at current time $T=50$. Predictions based on the traditional Kalman model are less precise and rather blurred.

FIGURE 11

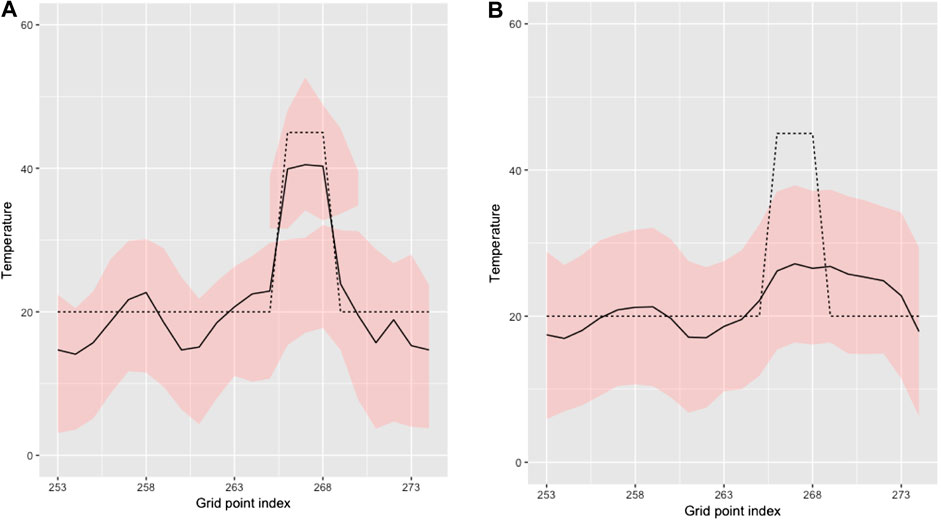
FIGURE 11. MMAP predictions (solid black line) with HDI 0.8 (red) intervals in cross section A-A′ of initial state at current time $T=50$ with selection Kalman model (left) and with traditional Kalman model (right). True cross section (dotted line).

Figure 12 displays realizations from the posterior pdfs at $T=50$. For the selection Kalman model, see Figure 12A, the yellow area is precisely reproduced in the majority of realizations while for traditional Kalman model, see Figure 12B, the yellow area is only vaguely indicated. Note however that the realizations from the selection Kalman model reflect the bimodality of the prior model outside the central area where the five spot observation design provides the most information. These observations are consistent with the results observed in Figures 8, 9.

FIGURE 12

FIGURE 12. Realizations from the posterior distribution of the initial state at current time $T=50$.

Conditioning on the observed data takes the same time for both methods but the selection Kalman model requires sampling from a high dimensional truncated Gaussian pdf in order to evaluate the posterior distribution which means that the computational demand for the selection Kalman model is higher than that of the traditional Kalman model. For $n=441$, as in our study, it takes an average of $7.4s$ to generate 100 realizations from a selection-Gaussian on our laptop computer, so a little over 12 min to generate the 10,000 realizations used to estimate the MMAP for the selection Kalman model. Note that the sampling becomes increasingly more resource consuming as the grid dimension increases and the computational time can be reduced by introducing parallelization in the algorithm.

To demonstrate the generality of the selection Kalman model, we define an alternative true initial state with two yellow areas, see Figure 13A. We used the same model parameters as in the primary case. The prior distribution for both the selection Kalman model and the traditional Kalman model are identical to the first case. Note in particular that the number of yellow areas is not specified. The observed time series will of course be different, see Figure 13B. These time series have many similarities with the ones from the primary case. We inspect the marginal pdfs at two monitoring locations, one inside each yellow area, as they evolve with current time T, see Figure 14A. Both marginal pdfs are identical at current time T = 0, and as current time T increases the height of the high-value mode increases, indicating that both monitoring locations are within the yellow areas. In Figure 14B the corresponding MMAP predictions are displayed for increasing current time T. We observe that location, areal extent and value of both yellow areas are well reproduced, but not as well as for the first case since identifying two sources is more complicated. The identification challenge is of course increasing with an increasing number of yellow areas. Figure 14B also displays the MMAP prediction for the traditional Kalman model for the two-yellow-area case, where location, areal extent and value are hard to evaluate, similarly to the first test case.

FIGURE 13

FIGURE 13. Set up from the two yellow area test case.

FIGURE 14

FIGURE 14. Results from the two-yellow-area test case.

5 Conclusion

We define a selection Kalman model based on a selection-Gaussian initial distribution and Gauss-linear dynamic and observation models. This model may represent spatial phenomena with initial states with spatial histograms that are multimodal, skewed and/or peaked. The selection Kalman model is demonstrated to be contained in the class of selection-Gaussian distributions and hence analytically tractable. The analytical tractability makes the assessment of the selection-Gaussian posterior model fast and reliable. Moreover, an efficient recursive algorithm for assessing the selection Kalman model is specified. Note that the traditional Kalman model is a special case of the selection Kalman model, hence the latter can be seen as a generalization of the former.

A synthetic spatio-temporal inversion case study with Gauss-linear forward and observation models is used to demonstrate the characteristics of the methodology. We specify both a selection Kalman model and a traditional Kalman model and evaluate their ability to restore the initial state based on the observed time series. The time series are noisy observations of the variable of interest collected at a set of sites. The selection Kalman model outperforms the traditional Kalman model. The former model identifies location, areal extent and value of the yellow area very reliably. The traditional Kalman model only provides blurry indications with severe under-prediction of the yellow area. We conclude that for spatio-temporal inversion where the initial spatial state has bimodal or multimodal spatial histograms, the selection Kalman model is far more suitable than the traditional Kalman model.

The selection Kalman model has potential applications far beyond the simple case evaluated in this case study. For all spatio-temporal problems where multimodal spatial histograms appear, the selection Kalman model should be considered. The model can easily be extended to a selection extended Kalman model, along the lines of the extended Kalman model. A more challenging and interesting extension is the definition of a selection ensemble Kalman model including non-linear dynamic and observation models. Research along these lines is currently taking place.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MC and HO contributed equally to this manuscript in every matter except implementation for which was carried out exclusively by MC.

Funding

The research is a part of the Uncertainty in Reservoir Evaluation (URE) activity at the Norwegian University of Science and Technology (NTNU).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This manuscript is a rewrite of a preprint which can be found at https://arxiv.org/abs/2006.14343.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.636524/full#supplementary-material.

References

1. Handcock, MS, and Wallis, JR. An approach to statistical spatial-temporal modeling of meteorological fields. J Am Stat Assoc (1994). 89:368–78. doi:10.1080/01621459.1994.10476754

CrossRef Full Text | Google Scholar

2. Cappé, O, Moulines, E, and Ryden, T. Inference in hidden Markov models (Springer series in statistics). Berlin, Heidelberg: Springer-Verlag (2005).

3. Kalman, RE. A new approach to linear filtering and prediction problems. J Basic Eng (1960). 82:35–45. doi:10.1115/1.3662552

CrossRef Full Text | Google Scholar

4. Emerick, AA, and Reynolds, AC. Ensemble smoother with multiple data assimilation. Comput Geosci (2013). 55:3–15. doi:10.1016/j.cageo.2012.03.011

CrossRef Full Text | Google Scholar

5. Evensen, G, Raanes, PN, Stordal, AS, and Hove, J. Efficient implementation of an iterative ensemble smoother for data assimilation and reservoir history matching. Front Appl Math Stat (2019). 5:47. doi:10.3389/fams.2019.00047

CrossRef Full Text | Google Scholar

6. Liu, M, and Grana, D. Time-lapse seismic history matching with iterative ensemble smoother and deep convolutional autoencoder. Geophysics (2019). 85:1–63. doi:10.1190/geo2019-0019.1

CrossRef Full Text | Google Scholar

7. Hopke, PK. Review of receptor modeling methods for source apportionment. J Air Waste Manag Assoc (2016). 66:237–59. doi:10.1080/10962247.2016.1140693

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cheng, MD, and Lin, CJ. Receptor modeling for smoke of 1998 biomass burning in Central America. J Geophys Res Atmos (2001). 106:22871–86. doi:10.1029/2001JD900024

CrossRef Full Text | Google Scholar

9. Kjeldsen, P, Bjerg, PL, Rügge, K, Christensen, TH, and Pedersen, JK. Characterization of an old municipal landfill (Grindsted, Denmark) as a groundwater pollution source: landfill hydrology and leachate migration. Waste Manage Res (1998). 16:14–22. doi:10.1177/0734242X9801600103

CrossRef Full Text | Google Scholar

10. Wikle, CK, and Cressie, N. A dimension-reduced approach to space-time Kalman filtering. Biometrika (1999). 86:815–29. doi:10.1093/biomet/86.4.815

CrossRef Full Text | Google Scholar

11. Todescato, M, Carron, A, Carli, R, Pillonetto, G, and Schenato, L. Efficient spatio-temporal Gaussian regression via Kalman filtering. Automatica (2020). 118:109032. doi:10.1016/j.automatica.2020.109032

CrossRef Full Text | Google Scholar

12. Jazwinski, AH. Stochastic processes and filtering theory. New York, NY: Academic Press (1970).

13. Julier, SJ, and Uhlmann, JK. New extension of the Kalman filter to nonlinear systems. In: I Kadar, editor. Signal processing, sensor fusion, and target recognition VI (SPIE), 3068 (1997). p. 182–93. doi:10.1117/12.280797

CrossRef Full Text | Google Scholar

14. Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J Geophys Res (1994). 99:101–43. doi:10.1029/94JC00572

CrossRef Full Text | Google Scholar

15. Evensen, G, and van Leeuwen, PJ. An ensemble Kalman smoother for nonlinear dynamics. Monthly Weather Rev (2000). 128:1852–67. doi:10.1175/1520-0493(2000)128<1852:AEKSFN>2.0.CO;2

CrossRef Full Text | Google Scholar

16. Li, R, Prasad, V, and Huang, B. Gaussian mixture model-based ensemble Kalman filtering for state and parameter estimation for a PMMA process. Processes (2016). 4:9. doi:10.3390/pr4020009

CrossRef Full Text | Google Scholar

17. Katzfuss, M, Stroud, JR, and Wikle, CK. Ensemble Kalman methods for high-dimensional hierarchical dynamic space-time models. J Am Stat Assoc (2020). 115:866–85. doi:10.1080/01621459.2019.1592753

CrossRef Full Text | Google Scholar

18. Robert, C, and Casella, G. Monte Carlo statistical methods. Springer Texts in Statistics. New York, NY: Springer (2005).

19. Naveau, P, Genton, MG, and Shen, X. A skewed Kalman filter. J Multivariate Anal (2005). 94:382–400. doi:10.1016/j.jmva.2004.06.002

CrossRef Full Text | Google Scholar

20. Ackerson, G, and Fu, K. On state estimation in switching environments. IEEE Trans Automatic Control (1970). 15:10–7. doi:10.1109/TAC.1970.1099359

CrossRef Full Text | Google Scholar

21. Chen, R, and Liu, JS. Mixture Kalman filters. J R Stat Soc Ser B (Statistical Methodology) (2000). 62:493–508. doi:10.1111/1467-9868.00246

CrossRef Full Text | Google Scholar

22. Smith, KW. Cluster ensemble kalman filter. Tellus A (2007). 59:749–57. doi:10.1111/j.1600-0870.2007.00246.x

CrossRef Full Text | Google Scholar

23. Dovera, L, and Della Rossa, E. Multimodal ensemble Kalman filtering using Gaussian mixture models. Comput Geosciences (2011). 15:307–23. doi:10.1007/s10596-010-9205-3

CrossRef Full Text | Google Scholar

24. Bengtsson, T, Snyder, C, and Nychka, D. Toward a nonlinear ensemble filter for high-dimensional systems. J Geophys Res Atmos (2003). 108. doi:10.1029/2002JD002900

CrossRef Full Text | Google Scholar

25. Ulvmoen, M, and Omre, H. Improved resolution in Bayesian lithology/fluid inversion from prestack seismic data and well observations: Part 1—methodology. Geophysics (2010). 75(2):R21–R35. doi:10.1190/1.3294570

CrossRef Full Text | Google Scholar

26. Omre, H, and Rimstad, K. Bayesian spatial inversion and conjugate selection Gaussian prior models. Methodology. Preprint: arXiv:1812.01882 (2018).

Google Scholar

27. Arellano-Valle, RB, Branco, MD, and Genton, MG. A unified view on skewed distributions arising from selections. Can J Stat (2006). 34:581–601. doi:10.1002/cjs.5550340403

CrossRef Full Text | Google Scholar

28. Arellano-Valle, R, and del Pino, G. From symmetric to asymmetric distributions: a unified approach. In: M Genton, editor. Skew-elliptical distributions and their applications: a journey beyond normality. New York, NY: Chapman and Hall/CRC) (2004). p. 113–33.

Google Scholar

29. Moja, S, Asfaw, Z, and Omre, H. Bayesian inversion in hidden Markov models with varying marginal proportions. Math Geosci (2018). 51:463–84. doi:10.1007/s11004-018-9752-z

CrossRef Full Text | Google Scholar

30. Robert, CP. Simulation of truncated normal variables. Stat Comput (1995). 121–5. doi:10.1007/BF00143942

CrossRef Full Text | Google Scholar

31. Hyndman, RJ. Computing and graphing highest density regions. The Am Statistician (1996). 50:120–6. doi:10.2307/2684423

CrossRef Full Text | Google Scholar