Continuous-Time Portfolio Selection: A Cursory Survey

In this article we provide a short survey on continuous-time portfolio selection. We explain the pioneering contribution of Merton and the use of dynamic programming. Then, we discuss Bismut's application of the Pontryagin maximum principle to portfolio selection and the dual martingale approach. We also explain two models with potential applicability to practice: life-cycle models with explicit consideration of retirement and models with protection against decline in spending power.

JEL Classification Codes: E21, G11

1. Introduction

In this article we provide a short survey on continuous-time portfolio selection. Continuous-time portfolio selection has played a pivotal role in modern theory of asset pricing by developing the intertemporal capital asset pricing model [1]. It is now a central theme of research in quantitative finance.

Continuous-time portfolio selection was born and grown, when there was a need to develop a multi-period model of asset management. The models of Markowitz [2] and Roy [3] provided a foundation of modern portfolio analysis, establishing risk-return trade-off as a central concept in the analysis. The models, however, were static and did not accommodate changes in economic environment. Merton [4, 5] made a pioneering contribution by casting portfolio selection in a multi-period continuous-time framework.

Optimal control theory and continuous-time stochastic analysis were main tools for Merton's pioneering research. He used Bellman's dynamic programming to solve the portfolio selection problem. Pontryagin's maximum principle was another achievement in optimal control theory. Bismut [6] extended the maximum principle to stochastic processes and applied it to the continuous-time portfolio selection problem. He showed that the problem could be solved more easily by the maximum principle. The dual martingale approach was developed based on Bismut's contribution and has provided an efficient approach to solve the problem in a complete financial market; the dual value function satisfies a linear partial differential equation, whereas the value function of the primal problem satisfies a highly non-linear Hamilton-Jacobi-Bellman equation.

We explain two classes of models which have potential to be applied to practice, life-cycle models with retirement and models protecting against decline in consumption. Models of the first class can be used as a tool for lifetime planning, including saving and investment for retirement. Models of the second class can be used when it is necessary for individuals or institutions to protect against decline in spending power.

The rest of the article proceeds as follows. Sections 2 and 3 provide basic framework for continuous-time portfolio selection: section 2 explains the static model of investment and section 3 explains development of dynamic models and Merton's contribution. Sections 4, 5, and 6 explain methodological development: section 4 explains the maximum principle and Bismut's approach, section 5 discusses the dual martingale approach, and section 6 provides a brief survey on attempts to provide concrete solutions to the portfolio selection problem. Sections 7 and 8 explain two applications: section 7 explains life-cycle models including choice of optimal retirement time and section 8 discusses models protecting against decline in spending power. Section 9 concludes.

2. Portfolio Selection: Risk-Return Tradeoff

Traditionally people chose investment portfolios based on two methods, fundamental analysis and technical analysis. Fundamental analysis refers to discovering the fundamental value (or intrinsic value) of an asset by using publicly available information, e.g., news about companies, markets, and economy. Fundamental analysts forecast future cash flows from an asset based on the information and discount them by an appropriate discount rate and calculate the fundamental value (see e.g., [7]). Technical analysis focuses on analyzing price charts and forecasts future price trend based on the information in the charts.

The idea of risk was always there, as the famous maxim “do not put all your eggs in one basket.” Fundamental analysts used discount rates higher than the risk-free rate for risky cash flows. Risk was, however, at the background of investors' thoughts, never coming in front.

Academic research changed the practice. Two academic papers, one by Markowitz [2] and another by Roy [3], brought the idea of risk to the foreground and provided a technically feasible framework to construct an investment portfolio based on the trade-off between risk and return.

Markowitz proposes to construct a portfolio by using a solution to the following problem:

Problem 1.

${\displaystyle \underset{\theta }{max}}{\theta }^{\prime }\mu$

subject to

$\begin{array}{l}{\theta }^{\prime }\Sigma \theta \le {\sigma }_M,\end{array}$

where θ is the vector of dollar amounts (or alternatively, weights) invested in assets, μ is the vector of mean returns on assets and Σ is their covariance matrix.

Problem 1 asks to find a portfolio which maximizes the mean return given maximum possible variance. Both Markowitz and Roy use variance as a measure of risk and seek to find a portfolio with restriction on its variance. The analysis to construct an investment portfolio based on answers to Problem 1 is called the mean variance analysis, and has been the major tool for investment analysis.

3. Dynamic Models of Portfolio Selection: Samuelson and Merton

The mean variance approach has been a main paradigm for practical investment analysis. The main reason for its success is its simplicity; one needs only to estimate the means, covariances of asset returns. Of course, there exist problems such as solving an optimization problem and estimating the large covariance matrix when the number of assets is large. The problems, however, have provided a continuous impetus for research and the practical implementation of the approach has been one of the most active research areas. A more serious economic issue about the mean variance approach is its static nature; it is based on one-period models and does not consider changes which occur in the economic environment over a time span longer than the one period model can accommodate. The problem is not just technical and asks to develop a dynamic framework for investment, which takes the changing economic environment explicitly into consideration.

Samuelson [8] studies a multi-period model of investment in discrete time and provides a solution using the dynamic programming developed by Bellman [9, 10]. Merton [1, 4, 5] extends Samuelson's analysis by formulating the problem in continuous time. We provide an explanation of Merton's model.

The economy is described by a vector $X_t={(X_{1,t},\dots X_{M,t})}^{\prime }$ of state variables, which satisfies the dynamics

$\begin{array}{ll}d{X}_t=\nu (t,X_t)dt+\Sigma (t,X(t))d{B}_t,& (1)\end{array}$

where $B_t=(B_{1,t},\dots ,B_{K,t}^{\prime })$ is an K-dimensional standard Brownian motion and ′ denotes the transpose of a matrix¹.

There exist one risk-free asset and N risky assets. The price of the riskless asset P_0,t evolves according to

$\begin{array}{ll}\frac{d{P}_{0,t}}{P_{0,t}}=r(t,X_t)dt.& (2)\end{array}$

The (cum-dividend) price $P_t={(P_{1,t},\dots ,P_{N,t})}^{\prime }$ evolves following the dynamics

$\begin{array}{ll}\frac{d{P}_t}{P_t}=\mu (t,X_t)dt+\sigma (t,X_t)d{B}_t.& (3)\end{array}$

We normalize P_0,0 = 1, P₀ = 1, where 1 is the N − vector of 1's.

An investor's objective is to maximize the utility function

$\begin{array}{ll}U=𝔼\left[{\displaystyle {\int }_0^T}{e}^{-\delta t}u(c_t)dt+e^{-\delta T}V(W_T)\right],& (4)\end{array}$

where 𝔼 denotes expectation, δ is the subjective discount rate, u is a concave strictly increasing function, called felicity function, c_t is the rate of consumption at t and W_T is the investor's wealth at T. We will use simpler notation r_t, μ_t, ν_t, Σ_t, σ_t for r(t, X_t), μ(t, X_t), ν(t, X_t), Σ(t, X_t), σ(t, X_t), respectively.

Samuelson and Merton's framework of maximizing the utility function has been a standard framework for studying portfolio selection. We will utilize the same framework in this survey [see explanations following (33), (34), (43)].

Let ${\pi }_t={({\pi }_{1,t},\dots ,{\pi }_{N,t})}^{\prime }$, where π_i,t denotes the dollar amount invested in the i-th asset at time t. We assume self-financing of the agent's wealth, i.e., there exists no inflow into the agent's wealth nor outflow of from it. Under the self-financing assumption, the investor's wealth at time t, W_t, satisfies the dynamics: given initial wealth W₀ = W [see pages 1560–1561 of Karatzas et al. [11] for more details],

$\begin{array}{l}d{W}_t=\left[r_t(W_t-c_t-{\displaystyle \sum _{i=1}^N{\pi }_{i,t}})+{\mu }_t^{\prime }{\pi }_t\right]dt+{\pi }_t^{\prime }{\sigma }_{t}d{B}_t\\ =\left[r_t{W}_t-c_t+({\mu }_t-r_{t}1{)}^{\prime }{\pi }_t)\right]dt+{\pi }_t^{\prime }{\sigma }_{t}d{B}_t.& (5)\end{array}$

We require that

$\begin{array}{ll}{W}_t\ge 0\text{\hspace{1em} for every }t\in \left[0,T\right].& (6)\end{array}$

The condition precludes an arbitrage opportunity [12].

State variable X_t, wealth W_t, and time t provide sufficient information to answer the investor's optimization problem, and consequently, the maximized value of the investor's utility can thus be expressed as a function of (t, W_t, X_t), which we will call the value function and denote by V(t, W_t, X_t), or simply by V if there is no possibility of confusion.

The investor's optimization problem is time consistent and satisfies Bellman's principle of optimality. The principle implies the Hamilton-Jacobi-Bellman (HJB) equation

$\begin{array}{ll}{\displaystyle \underset{c_t,{\pi }_t}{max}}\frac{𝔼\left[dV\right]}{dt}-\delta V=0.& (7)\end{array}$

By Itô's lemma we have

$\begin{array}{l}d{V}_t=[V_t+V_W(r{W}_t-c_t+({\mu }_t-r_{t}1{)}^{\prime }{\pi }_t)+V_X^{\prime }{\nu }_t\\ +\frac{1}{2}{V}_{WW}{\pi }_t^{\prime }{\sigma }_t^{\prime }{\sigma }_t{\pi }_t\\ +\frac{1}{2}{\Sigma }_t^{\prime }{V}_{XX}{\Sigma }_t+V_{WX}^{\prime }{\Sigma }_t{\sigma }_t^{\prime }{\pi }_t]dt\\ +(V_W^{\prime }{\sigma }_t+V_X^{\prime }{\Sigma }_t)d{B}_t,& (8)\end{array}$

where we use the subscript notation for partial derivatives². Accordingly, Equation (7) implies

$\begin{array}{l}\underset{c_t,{\pi }_t}{\max }[V_t+V_W(r{W}_t-c_t+{({\mu }_t-r_{t}1)}^{\prime }{\pi }_t)\\ +V_X^{\prime }{\nu }_t+\frac{1}{2}{V}_{WW}{\pi }_t^{\prime }{\sigma }_t^{\prime }{\sigma }_t{\pi }_t\\ +\frac{1}{2}{\Sigma }_t^{\prime }{V}_{XX}{\Sigma }_t+V_{WX}^{\prime }{\Sigma }_t{\sigma }_t^{\prime }{\pi }_t]\\ -\delta V=0.& (9)\end{array}$

The first-order conditions are given by the following

$\begin{array}{ll}{c}_t={(u^{\prime })}^{-1}(V_W),& (10)\end{array}$

$\begin{array}{ll}{\pi }_t=-\frac{V_W}{V_{WW}}{({\sigma }_t{\sigma }_t^{\prime })}^{-1}({\mu }_t-r_{t}1)+\frac{V_{WX}^{\prime }}{V_{WW}}{\Sigma }_t{\sigma }_t^{\prime }{({\sigma }_t{\sigma }_t^{\prime })}^{-1}.& (11)\end{array}$

Merton [1] derives the HJB equation and the expression for optimal consumption and portfolio in the first-order conditions. According to Equation (11) the investor's optimal portfolio of risky assets has two components: the first component is an investment in the mean-variance efficient portfolio and the second component is an investment to cope with changes in the economic environment. The first is the investment in the efficient portfolio in the static mean variance analysis, and is called the myopic component. The second component exists due to changes in the investment opportunity. Merton's framework extends the mean variance analysis to a dynamic setting in which the economy changes over the course of time.

The HJB equation is highly non-linear when the optimal consumption and portfolio in the first-order-conditions are substituted for c_t and π_t. Merton [4, 5] provide a concrete solution to the HJB equation for the case the investment opportunity is constant, i.e., r(t, X_t), μ(t, X_t), σ(t, X_t) do not depend on X_t and are constant. He discovers the solution by guessing-and-verifying, i.e., he conjectures a specific form for the solution and verifies it to be a solution by plugging it into the equation.

4. Maximum Principle

The investor's optimization problem in Merton's continuous time model is a stochastic optimal control problem. Merton employs Bellman's approach to optimal control problems to solve the consumption/portfolio selection problem. Pontryagin et al. [13] propose another approach to optimal control problems and derive the maximum principle. Dorfman [14] applies the principle to the theory of economic growth. Bismut [6] extends it to a stochastic environment and applies it to Merton's problem [15]. Here we explain Bismut's approach. Bismut considers the case with a deterministic investment opportunity. We assume N = 1 for simplicity of exposition. We consider the following equation for the adjoint variable p_t³:

$\begin{array}{ll}d{p}_t={\mu }_{p,t}dt+{\theta }_{p,t}d{B}_t,p_0=\lambda .& (12)\end{array}$

Then, we can define the Hamiltonian ${H}$_t of the system as follows

$\begin{array}{ll}{{H}}_t\equiv e^{-\delta t}u(c_t)+p_t(r_t{W}_t-c_t+({\mu }_t-r_t){\pi }_t)+{\theta }_{p,t}{\sigma }_t{\pi }_t.& (13)\end{array}$

The maximum principle can now be stated as follows:

$\begin{array}{ll}\frac{\partial {{H}}_t}{\partial c_t}=e^{-\delta t}{u}^{\prime }(c_t)-p_t=0,& (14)\end{array}$

$\begin{array}{ll}\frac{\partial {{H}}_t}{\partial {\pi }_t}=({\mu }_t-r_t)p_t+{\theta }_{p,t}{\sigma }_t=0,& (15)\end{array}$

$\begin{array}{ll}{e}^{-\delta T}{V}^{\prime }(W_T)=p_T,& (16)\end{array}$

and the expected change in p_t is given by

$\begin{array}{ll}{\mu }_{p,t}=-\frac{\partial {{H}}_t}{\partial W_t}=-r_t{p}_t,& (17)\end{array}$

Equation (15) implies

$\begin{array}{ll}{\theta }_{p,t}=-{\theta }_t{p}_t,\text{\hspace{1em}where\hspace{1em}}{\theta }_t\equiv \frac{{\mu }_t-r_t}{{\sigma }_t}.& (18)\end{array}$

The quantity θ_t is commonly called the market price of risk or the Sharpe ratio of the risky asset. Now Equations (17) and (18) imply the following dynamics for p_t:

$\begin{array}{ll}\frac{d{p}_t}{p_t}=-r_{t}dt-{\theta }_{t}d{B}_t,p_0=\lambda & (19)\end{array}$

Hence, p_t is given by

$\begin{array}{ll}{p}_t=\lambda e^{-{\displaystyle {\int }_0^t}(r_s+\frac{1}{2}{\theta }_s^2)ds-{\displaystyle {\int }_0^t}{\theta }_s{B}_s}.& (20)\end{array}$

and optimal consumption $c_t^{*}$ is determined by

$\begin{array}{ll}{c}_t^{*}={\left(u^{\prime }\right)}^{-1}(y_t),& (21)\end{array}$

where y_t is the marginal utility of consumption at optimum defined by

$\begin{array}{ll}{y}_t\equiv e^{\delta t}{p}_t.& (22)\end{array}$

Thus, the optimal consumption policy ${(c_t)}_{t=0}^T$ is determined once the initial value λ of the marginal value of capital is known.

We will now proceed to determine the initial value λ of p_t.

By the martingale property, we have

$\begin{array}{l}{W}_0=H_0{W}_0=𝔼\left[{\displaystyle {\int }_0^t}{H}_s{c}_{s}ds+H_t{W}_t\right]\text{for }t\in \left[0,T\right].\end{array}$

where

$\begin{array}{ll}{H}_t\equiv e^{-{\displaystyle {\int }_0^t}(r_s+\frac{1}{2}{\theta }_s^2)ds-{\displaystyle {\int }_0^t}{\theta }_s{B}_s},& (23)\end{array}$

In particular,

$\begin{array}{ll}{W}_0=𝔼\left[{\displaystyle {\int }_0^T}{H}_t{c}_{t}dt+H_T{W}_T\right].& (24)\end{array}$

We have shown that the dynamic wealth evolution equation implies the budget constraint (24), which we will call the static budget constraint. Conversely, suppose that a consumption policy ${(c_t)}_{t=0}^T$ satisfying (24) is given. Then, by the martingale representation theorem (Theorem 4.2, Ch. 3, [16]), there exists an admissible ${({\pi }_t)}_{t=0}^T$ such that capital evolves according to the wealth evolution equation. This shows that the dynamic capital evolution equation and the budget constraint are equivalent.

We would like to find λ which makes the resource constraint hold as equality. For this purpose we plug the optimal consumption in (21) into the left-hand side of (24) and derive the following:

$\begin{array}{l}{W}_0=𝔼\left[{\displaystyle {\int }_0^T}{H}_t{c}_t^{*}dt+H_T{W}_T^{*}\right]\\ =𝔼\left[{\displaystyle {\int }_0^T}{H}_t{(u^{\prime })}^{-1}(\lambda H_t)dt+H_T{(V^{\prime })}^{-1}(\lambda H_T)\right],& (25)\end{array}$

where $W_T^{*}$ is the wealth at T when the agent follows the optimal consumption and portfolio strategies. We can find λ from the above equation.

5. The Dual Martingale Approach

Bismut's stochastic maximum principle and its application to consumption/portfolio selection allows one to transform the dynamic wealth evolution equation into a static budget constraint. Bismut rederives Merton's solution for the case where the investment opportunity set is deterministic. Pliska [17], Duffle and Huang [18], Karatzas et al. [19], and Cox and Huang [20] extend the idea to a general case.

Let

$\begin{array}{ll}{\theta }_t\equiv {({\sigma }_t)}^{-1}({\mu }_t-r_{t}1)& (26)\end{array}$

and define

$\begin{array}{ll}{H}_t\equiv e^{-{\displaystyle {\int }_0^t}{r}_{s}ds}{Z}_t\text{ where }{Z}_t\equiv e^{-\frac{1}{2}{\displaystyle {\int }_0^t}|{\theta }_s{|}^{2}ds-{\displaystyle {\int }_0^t}{\theta }_s^{\prime }d{B}_s}.& (27)\end{array}$

H_t in Equation (27) is called the stochastic discount factor and is equal to that in Equation (23) if the θ_t and r_t are deterministic.

If θ_t satisfies a regularity condition, then Z_t is a martingale and in this case we can show that the wealth evolution equation and the following static budget constraint is equivalent:

$\begin{array}{ll}𝔼\left[{\displaystyle {\int }_0^T}{H}_t{c}_{t}dt+H_T{W}_T\right]\le W_0.& (28)\end{array}$

Then, one can obtain a solution to the consumption/portfolio selection problem by using the Lagrangian:

$\begin{array}{l}\text{L}=𝔼\left[{\displaystyle {\int }_0^T}{e}^{-\delta t}u\left(c_t\right)dt+e^{-\delta T}V\left(W_T\right)\right]\\ +\lambda \left(W-𝔼\left[{\displaystyle {\int }_0^T}{H}_t{c}_{t}dt+H_T{W}_T\right]\right).& (29)\end{array}$

The Lagrangian based on the static budget constraint provides a fundamental tool to solve a portfolio selection problem in continuous time [see explanations following (39) and (44)].

The first-order conditions are

$\begin{array}{ll}{c}_t^{*}={(u^{\prime })}^{-1}(y_t),,W_T^{*}={(V^{\prime })}^{-1}(y_T).& (30)\end{array}$

where $y_t\equiv \lambda e^{\delta t}{H}_t$.

We can determine λ by plugging the optimal consumption and bequest into the budget constraint which holds as equality at the optimum.

Defining the dual value function J at t by

$\begin{array}{l}J(t,y_t)\equiv {𝔼}_t[{\displaystyle {\int }_t^T{e}^{-\delta (s-t)}}(u(c_s)-c_s{y}_s)ds\\ +e^{-\delta (T-t)}(V(W_T)-y_T{W}_T)],& (31)\end{array}$

where $y_s=e^{\delta s}{H}_s$ and ${𝔼}_t\left[·\right]=𝔼\left[·\mid {{F}}_t\right]$. Notice that J can be expressed as a function of (t, y_t) and the Feynman-Kac theorem implies J satisfies a linear PDE. Under suitable regularity conditions the following duality relationship is valid:

$\begin{array}{ll}V={\displaystyle \underset{\lambda >0}{inf}}\left[J+\lambda W_0\right].& (32)\end{array}$

6. Concrete Solutions

Merton proposed the continuous-time consumption/portfolio selection problem in a stochastic economic environment. Concrete solutions, however, were not obtained for the stochastically changing economic environment until 1990s. Brennan et al. [21] obtain a concrete solution by solving the non-linear HJB equation numerically. Kim and Omberg [22] obtain a closed-form solution to the HJB equation for the case where the dynamics of asset prices follow affine processes. In this case one can transform the partial differential equation into an ordinary differential equation of the Riccati type and obtain a closed-form solution in special cases. Liu [23] extends Kim and Omberg's approach to a general stochastic market environment and proposes an approach to obtain a concrete solution by solving the Riccati equations numerically.

7. Retirement and Life-Cycle Portfolio Selection

So far we have treated the optimal consumption/investment problem without consideration of lifetime planning or retirement. Lifetime planning, including labor supply decisions, is a crucial feature for practical application of the theory. Retirement is a major concern of an individual; it represents enjoying more leisure but a once-and-for-all cessation of wage income for the individual. In this section we provide a survey on recent research which studies lifetime planning and the effects of a retirement decision on optimal portfolio and consumption.

Bodie et al. [24] study a model of flexible labor supply before retirement, introducing a trade-off between labor and leisure. They consider an agent with the following utility function:

$\begin{array}{ll}U=𝔼\left[{\displaystyle {\int }_0^T}{e}^{-\delta t}u(c_t,L_t)dt+e^{-\delta T}V(W_T)\right],& (33)\end{array}$

where T is the time of retirement, L_t is the rate of leisure the agent enjoys at time t, u(c, L) is increasing and concave in c and L, and V(W_T) is the continuation utility function of wealth at retirement. The maximum possible leisure rate is 1, and 1 − L_t is the labor supply of the agent. The agent receives wage income at a rate equal to w_t(1 − L_t) where w_t is the wage rate at t; the lower the leisure, the higher the labor supply, and the higher the income. Bodie et al. [25] extend the model by considering stochastic investment opportunity and wage rate.

These studies, however, assume the retirement time as fixed and exogenously given. Including choice of retirement time in the life-cycle consumption and portfolio selection model raises a technical challenge, since it involves optimal choice of retirement time, an optimal stopping problem, as well as choice of consumption and portfolio at each instant. Karatzas and Wang [26] make a contribution in this regard by characterizing a condition for the existence of a solution to the mixture problem of optimal stopping and optimal choice of consumption. Choi and Shim [27] study the open problem proposed by Karatzas and Wang [26] in which the agent continues to consume and invest after the retirement. An infinitely-lived live agent chooses optimal retirement time as well as consumption and portfolio. The agent's period utility function has two components before retirement, utility of consumption and disutility of labor; disutility of labor is subtracted from utility of consumption. Thus, retirement is a choice to avoid disutility of labor foregoing labor income.

Fahri and Panageas [28] study the choice of retirement time, optimal consumption and investment. They assume the agent has a Cobb-Douglas utility of labor and leisure and the choice of leisure is binomial, i.e., a constant level before retirement which jumps to a higher level after retirement. They also consider a finite horizon problem to understand the effect of aging on the choices. Choi et al. [29] study a similar problem with a flexibility in leisure choice. They introduce the choice of retirement time in a model similar to that of Bodie et al. [24], namely, the period utility function is a constant elasticity of substitution (CES) function and the labor/leisure choice is flexible up to a certain limit. After retirement the agent enjoys a full level of leisure, which is higher than the maximum leisure before retirement. Dybvig and Liu [30] study a model similar to that of Fahri and Panageas [28] and investigate implications for portfolio selection and asset pricing, considering liquidity constraints and uninsurable income risk.

Yang and Koo [31] investigate the model of Choi and Shim [27] in a finite horizon with a general period utility function and provide conditions for the existence of a solution and establish properties of optimal policies. Their analysis depends on the theory of partial differential equations (PDEs). In particular, they use the comparison theorem for the PDEs to characterize the optimal retirement boundary and to establish comparative static results.

Bae et al. [32] investigate the optimal consumption, investment, and retirement time problem of infinitely lived agent who receives a constant stream of social insurance payment after retirement. They adopt the approach of Yang and Koo [31] and analyze the properties of optimal consumption, investment, and retirement time analytically.

To understand the portfolio selection problem with retirement option in detail, we explain the problem studied by Choi and Shim [27]. They use dynamic programming. We use, however, the dual martingale approach explained in section 5, following Yang and Koo [31].

The objective of the agent is to maximize the following utility function

$\begin{array}{ll}U=𝔼\left[{\displaystyle {\int }_0^{\infty }}{e}^{-\delta t}(u(c_t)-l{𝟙}_{t<\tau })dt\right]& (34)\end{array}$

where l is a constant describing disutility of labor and τ is the retirement time of the agent. The agent receives a stream of labor income at a constant rate ϵ before retirement.

For simplicity of exposition, we assume that the financial market is composed of one risky asset and one riskless asset and the expectation μ and volatility σ of the rate of return on the risk asset are constant and the risk-free rate r is also constant. The agent's wealth satisfies the following dynamics at time t.

$\begin{array}{lll}\hfill d{W}_t=\left[r{W}_t-c_t+ϵ{𝟙}_{t<\tau }+(\mu -r){\pi }_t\right]dt+{\pi }_t\sigma d{B}_t.& & (35)\end{array}$

The agent's wealth satisfies following conditions

$\begin{array}{lll}\hfill W_t\ge -\frac{ϵ}{r},t\in [0,\tau ),W_t\ge 0,t\in [\tau ,\infty ).& & (36)\end{array}$

Let θ ≡ (μ − r)/σ and $H_t\equiv e^{-rt}{Z}_t$ where $Z_t\equiv e^{-\frac{1}{2}{\theta }^{2}t-\theta B_t}$ as in section 5. Then, by applying the dual martingale approach in 5, we have the following static budget constraint, adopted to the existence of a stopping time:

$\begin{array}{lll}\hfill 𝔼\left[{\displaystyle {\int }_0^{\tau }}{H}_t{c}_{t}dt+H_{\tau }\left(W_{\tau }+\frac{ϵ}{r}\right)\right]\le W+\frac{ϵ}{r},\forall \tau \in {S},& & (37)\end{array}$

where ${S}$ is the set of ${F}$ stopping times taking values in [0, ∞].

The objective function of the agent can be rewritten as

$\begin{array}{ll}\hfill U=𝔼\left[{\displaystyle {\int }_0^{\tau }}{e}^{-\delta t}(u(c_t)-l)dt+e^{-\delta \tau }\underset{\_}{U}(W_{\tau })\right],& (38)\end{array}$

where U denotes the value function of the investor after retirement, i.e., it is the investor's maximized utility of after retirement.

For a fixed stopping time τ, we consider the following Lagrangian:

$\begin{array}{ll}\begin{array}{l}\text{L}=𝔼\left[{\displaystyle {\int }_0^{\tau }}{e}^{-\delta t}\left(u\left(c_t\right)-l\right)dt+e^{-\delta \tau }\underset{\_}{U}\left(W_{\tau }\right)\right]\\ +\lambda \left[W+\frac{ϵ}{r}-𝔼\left[{\displaystyle {\int }_0^{\tau }}{H}_t{c}_{t}dt+H_{\tau }\left(W_{\tau }+\frac{ϵ}{r}\right)\right]\right].\end{array}& (39)\end{array}$

The first-order conditions yield

$\begin{array}{ll}{c}_t^{*}={(u^{\prime })}^{-1}(y_t)\text{for }t\ge 0,\text{and }{W}_{\tau }^{*}={({\underset{\_}{U}}^{\prime })}^{-1}(y_{\tau }),& (40)\end{array}$

where $y_t\equiv \lambda e^{\delta t}{H}_t$.

The dual value function $\widehat{V}$ is defined by

$\begin{array}{lll}\hfill \widehat{V}\equiv {\displaystyle \underset{\tau \in {S}}{sup}}𝔼\left[{\displaystyle {\int }_0^{\tau }}{e}^{-\delta t}(ũ(y_t)-l)dt+e^{-\delta \tau }\underset{\_}{\widehat{V}}(y_{\tau })\right],& & (41)\end{array}$

where ũ(y) is the convex conjugate of u, i.e., $ũ(y)\equiv \underset{c\ge 0}{max}(u(c)-yc),$⁴ $\underset{\_}{\widehat{V}}(y)\equiv \underset{\_}{\widehat{V}}(y)-y\frac{ϵ}{r}$ and Ṽ(y) is the dual value function of the post-retirement problem.

One can show that the dual value function satisfies a variational inequality and obtain the optimal stopping time τ^* as the first hitting time of a boundary characterizing a unique solution to the variational inequality. The following duality relationship is valid [31].

$\begin{array}{ll}V(W)={\displaystyle \underset{y>0}{inf}}\left[\widehat{V}(y)+y\left(W+\frac{ϵ}{r}\right)\right].& (42)\end{array}$

8. Protection of Spending Power

In this section we discuss models which explicitly consider protection of spending power. In the 1980s portfolio insurance strategies, designed to provide a floor value for a portfolio, were popular. The strategies bought put options or used synthetic replication of put options. Brennan and Schwartz [34], Basak [35, 36], and Grossman and Zhou [37] investigate effects of portfolio insurance on equilibrium asset prices and returns. There may exist adverse equilibrium effects of portfolio insurance, as some of the literature has shown. Moreover, the strategies impose terminal dates for protection of wealth arbitrarily, without having a rationale for the choice. People usually roll the strategies over when the target dates come. Dybvig [38] shows that rollover of portfolio insurance is inefficient.

In order to avoid the arbitrariness of the target dates, people consider putting restrictions continuously on flow of consumption, not on wealth on an arbitrary future date. A typical restriction is the monotonicity constraint, which stipulates that consumption can never decline over time. An investor's consumption strategy subject to the constraint is called consumption ratcheting. Based on the original idea of Duesenberry [39] and Dybvig [40] formulates an economic model for consumption ratcheting and provides optimal consumption and portfolio strategies in closed form. Riedel [41] extends the results of Dybvig [40] to a general utility function with a pricing kernel generated by a Lévy process, and Watson and Scott [42] consider a finite horizon model. Riedel [41] and Watson and Scott [42], however, do not consider investment strategies in their models. In a recent work Jeon et al. [43] analyze optimal portfolio strategies in consumption ratcheting models both with a finite horizon and with an infinite horizon.

We will now provide an explanation of the infinite-horizon consumption ratcheting model, following the approach by Jeon et al. [43]. For an exogenously given consumption level c₀₋, an investor's objective is to maximize the following utility function by choosing a non-decreasing consumption process c and portfolio π of assets:

$\begin{array}{ll}U\equiv 𝔼\left[{\displaystyle {\int }_0^{\infty }}{e}^{-\delta t}u(c_t)dt\right],& (43)\end{array}$

where the utility function u(c) is a twice continuously differentiable, strictly concave, strictly increasing function with a suitable regularity condition. Since the consumption process is non-decreasing, we need

$\begin{array}{l}{W}_0>\frac{c_{0-}}{r},\end{array}$

i.e., wealth is greater than the level which is necessary to sustain the previously given level of consumption. By using the static budget constraint developed in section 5, we can write down the Lagrangian as follows:

$\begin{array}{ll}\begin{array}{l}\text{L}\equiv 𝔼\left[{\displaystyle {\int }_0^{\infty }}{e}^{-\delta t}u\left(c_t\right)dt\right]+\lambda \left(W_0-𝔼\left[{\displaystyle {\int }_0^{\infty }}{H}_t{c}_{t}dt\right]\right)\\ =𝔼\left[{\displaystyle {\int }_0^{\infty }}{e}^{-\delta t}\left(u\left(c_t\right)-\lambda e^{\delta t}{H}_t{c}_t\right)dt\right]+\lambda W_0,\end{array}& (44)\end{array}$

where $y_t=\lambda e^{\delta t}{H}_t$.

From the Lagrangian (44), we choose the non-decreasing consumption process ${(c_t)}_{t=0}^{\infty }$ to maximize L and thus introduce the dual problem⁵.

$\begin{array}{ll}J(y,c)={\displaystyle \underset{(c_t)\in {ND}(c)}{sup}}𝔼\left[{\displaystyle {\int }_0^{\infty }}{e}^{-\delta t}(u(c_t)-y_t{c}_t)dt\right],& (45)\end{array}$

where ${ND}(c)$ denotes the set of all non-decreasing, right continuous with left limits processes ${(e_t)}_{t=0}^{\infty }$ starting at c.

According to Jeon et al. [43], we can show that the following duality relationship holds:

$\begin{array}{ll}V(W_0,c_{0-})={\displaystyle \underset{y>0}{inf}}(J(y,c_{0-})+y{W}_0).& (46)\end{array}$

The dual problem in (45) involves the choice of a non-decreasing process ${(c_t)}_{t=0}^{\infty }$ which is called a singular control problem. By a standard approach to the singular control problem (see [44], [45]), the dual value function J(y, c) satisfies the following HJB equation:

$\begin{array}{ll}\begin{array}{l}max\left\{{L}J(y,c)+u(c)-yc,J_c(y,c)\right\}=0,\\ \text{ for }(y,c)\in (0,\infty )\times (0,\infty ),\end{array}& (47)\end{array}$

where the differential operator ${L}$ is given by

$\begin{array}{l}{L}=\frac{{\theta }^2}{2}{y}^2\frac{{\partial }^2}{\partial y^2}+(\delta -r)y\frac{\partial }{\partial y}-\delta .\end{array}$

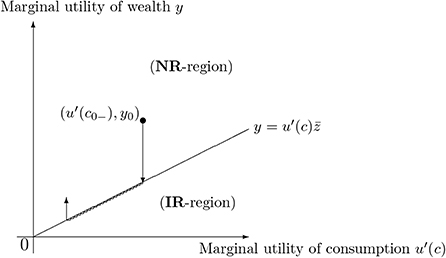
From the HJB Equation (47), the agent's optimal consumption strategy can be characterized by two regions in the state space, the inaction region NR and the increasing region IR. There exists a free boundary $\bar{z}$ such that the two regions NR and IR can be represented by

$\begin{array}{ll}\begin{array}{l}\text{N}\text{R}=\left\{(y,c)\mid J_c(y,c)<0\right\}=\left\{(y,c)\mid y>\bar{z}{u}^{\prime }(c)\right\},\\ \text{ I}\text{R}=\left\{(y,c)\mid J_c(y,c)=0\right\}=\left\{(y,c)\mid y\le \bar{z}{u}^{\prime }(c)\right\}.\end{array}& (48)\end{array}$

If the initial consumption level c₀₋ is such that (y₀, c₀₋) lies in the increasing region IR, it jumps immediately to the inaction region NR. Suppose the level of consumption is such that (y₀, c₀₋) lies in side the NR region. The level of consumption stays constant while the marginal utility of wealth process y_t is inside the NR-region. The consumption is adjusted upward if and only if the process y_t goes below $u^{\prime }(c_{t-})\bar{z},$ so that the pair (y₀, c₀₋) is restored to the inaction region. Figure 1 illustrates the regions and adjustment of consumption.

FIGURE 1

Figure 1. NR and IR regions and consumption adjustment.

If we define the discretionary wealth as wealth in excess of the perpetuity value of current consumption (the level of wealth required to maintain the current rate of consumption) we can show that the optimal portfolio π is proportional to the discretionary wealth, i.e.,

$\begin{array}{ll}{\pi }_t=\frac{\theta \left(1-m_2\right)}{\sigma }\left(x_t-\frac{c_t}{r}\right),\text{for all }t\ge 0.& (49)\end{array}$

This relationship is independent of the agent's felicity function and depends only on the subjective discount rate and the market parameters as shown by Dybvig [40] and Koo et al. [46]. Dybvig [47] discusses potential application of the consumption ratcheting model to practical asset management.

Choi et al. [48, 49] study an extension of the model in which the agent can adjust consumption downward with mental adjustment costs and explore its application to practical asset management.

9. Conclusion

We have provided a survey on continuous-time portfolio selection. We have explained technological development such as the dynamic programming method, application of the maximum principle, and the dual martingale approach. We have also explained models of practical importance.

Of course, we cannot discuss all the important contributions in this short survey. For example, we have not explained models with frictions such as transaction costs, uninsurable income risk, and taxes. We leave them as topics for a separate survey.

Author Contributions

HK has initiated the survey and done major part of writing. SB has contributed mainly to Retirement and Life Cycle Portfolio Selection. JJ has contributed mainly to Protection of Spending Power.

Funding

This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2019S1A5A2A03054249). JJ gratefully acknowledges the support of the National Research Foundation of Korea (NRF) grant funded by the Korea government (Grant No. NRF-2017R1C1B1001811).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^The Brownian motion is defined on a filtered probability space $(\Omega ,{F},{({{F}}_t)}_{t\ge 0},P)$, where the filtration ${({{F}}_t)}_{t\ge 0}$ is generated by the Brownian motion (B_t)_t≥0 and augmented by null sets.

2. ^That is, $V_t=\frac{\partial V}{\partial t},V_W=\frac{\partial V}{\partial W_t},V_X=\frac{\partial V}{\partial X_t},V_{WW}=\frac{{\partial }^{2}V}{\partial W^2},V_{XX}=\frac{{\partial }^{2}V}{\partial X^2}.$

3. ^p_t is different from the asset price P_t in (3) and is the adjoint variable.

4. ^See Rockafellar [33] for definition and use of the convex conjugate of a concave function in convex analysis.

5. ^Usually, the dual problem of a maximization problem involves minimization. Here the problem still involves a maximization. We, however, call it the dual problem, since the important variable is the marginal utility of wealth y_t, the dual variable to wealth, in the problem.

References

1. Merton R. An intertemporal capital asset pricing model. Econometrica. (1973) 4:867–87. doi: 10.2307/1913811

CrossRef Full Text | Google Scholar

2. Markowitz H. Portfolio selection. J Finan. (1952) 7:77–91. doi: 10.1111/j.1540-6261.1952.tb01525.x

CrossRef Full Text | Google Scholar

3. Roy A. Safety first and the holding of assets. Econometrica. (1952) 20:431–49. doi: 10.2307/1907413

CrossRef Full Text | Google Scholar

4. Merton R. Lifetime portfolio selection under uncertainty: the continuous-time case. Rev Econ Stat. (1969) 51:247–57. doi: 10.2307/1926560

CrossRef Full Text | Google Scholar

5. Merton R. Optimum consumption and portfolio rules in a continuous-time model. J Econ Theor. (1971) 3:373–413. doi: 10.1016/0022-0531(71)90038-X

CrossRef Full Text | Google Scholar

6. Bismut JM. Conjugate convex functions in optimal stochastic control. J Math Anal Appl. (1973) 44:384–404. doi: 10.1016/0022-247X(73)90066-8

CrossRef Full Text | Google Scholar

7. Graham B, Dodd D. Security Analysis. New York, NY: McGraw-Hill (2008).

Google Scholar

8. Samuelson P. Lifetime portfolio selection by dynamic stochastic programming. Rev Econ Stat. (1969) 51:239–46. doi: 10.2307/1926559

CrossRef Full Text | Google Scholar

9. Bellman R. Dynamic programming and stochastic control processes. Inform Control. (1958) 1:228–39. doi: 10.1016/S0019-9958(58)80003-0

CrossRef Full Text | Google Scholar

10. Bellman R. Dynamic Programming. New Jersey, NJ: Princeton University Press (2009).

Google Scholar

11. Karatzas I, Lehoczky J, Shreve SE. Optimal portfolio and consumption decisions for a “Small Investor” on a finite horizon. SIAM J Control Optim. (1987) 25:1557–86. doi: 10.1137/0325086

CrossRef Full Text | Google Scholar

12. Dybvig P, Huang C. Nonnegative wealth, absence of arbitrage, and feasible consumption streams. Rev Finan Stud. (1988) 62:675–68.

Google Scholar

13. Pontryagin L, Boltyanskii V, Gamkrelidze R, Mishchenko E. The Mathematical Theory of Optimal Processes Translated by K. Trirogoff. Cambridge: Cambridge University Press (1962).

Google Scholar

14. Dorfman R. An economic interpretation of optimal control theory. Am Econ Rev. (1969) 59:817–31.

Google Scholar

15. Bismut JM. Growth and optimal intertemporal allocation of risks. J Econ Theor. (1975) 10:239–57. doi: 10.1016/0022-0531(75)90053-8

CrossRef Full Text | Google Scholar

16. Karatzas I, Shreve SE. Methods of Mathematical Finance. New York, NY: Springer-Verlag (1998).

Google Scholar

17. Pliska SR. A stochastic calculus model of continuous trading: optimal portfolios. Math Oper Res. (1986) 11:371–82. doi: 10.1287/moor.11.2.371

CrossRef Full Text | Google Scholar

18. Duffie D, Huang CF. Implementing arrow-debreu equilibria by continuous trading of few long-lived securities. Econometrica. (1985) 53:1337–56. doi: 10.2307/1913211

CrossRef Full Text | Google Scholar

19. Karatzas I, Lehoczky JP, Sethi S, Shreve SE. Explicit solution of a general consumption/investment problem. Math Oper Res. (1986) 11:261–94. doi: 10.1287/moor.11.2.261

CrossRef Full Text | Google Scholar

20. Cox J, Huang C. Optimal consumption and portfolio polices when asset prices follow a diffusion process. J Econ Theor. (1989) 49:33–83. doi: 10.1016/0022-0531(89)90067-7

CrossRef Full Text | Google Scholar

21. Brennan MJ, Schwartz ES, Lagnado R. Strategic asset allocation. J Econ Dyn Control. (1997) 21:1377–403. doi: 10.1016/S0165-1889(97)00031-6

CrossRef Full Text | Google Scholar

22. Kim T, Omberg E. Dynamic nonmyopic portfolio behavior. Rev Finan Stud. (1996) 9:141–61. doi: 10.1093/rfs/9.1.141

CrossRef Full Text | Google Scholar

23. Liu J. Portfolio selection in stochastic environments. Rev Finan Stud. (2007) 20:1–39. doi: 10.1093/rfs/hhl001

CrossRef Full Text | Google Scholar

24. Bodie Z, Merton R, Samuelson W. Labor supply flexibility and portfolio choice in a life cycle model. J Econ Dyn Control. (1992) 16:427–49. doi: 10.1016/0165-1889(92)90044-F

CrossRef Full Text | Google Scholar

25. Bodie Z, Detemple J, Otruba S, Walter S. Optimal consumption portfolio choices and retirement planning. J Econ Dyn Control. (2004) 28:1115–48. doi: 10.1016/S0165-1889(03)00068-X

CrossRef Full Text | Google Scholar

26. Karatzas I, Wang H. Utility maximization with discretionary stopping. SIAM J Control Optim. (2000) 39:306–29. doi: 10.1137/S0363012998346323

CrossRef Full Text | Google Scholar

27. Choi KJ, Shim G. Disutility, optimal retirement, and portfolio selection. Math Finan. (2006) 16:443–67. doi: 10.1111/j.1467-9965.2006.00278.x

CrossRef Full Text | Google Scholar

28. Fahri E, Panageas S. Saving and investing for early retirement: a theoretical analysis. J Finan Econ. (2007) 83:87–121. doi: 10.1016/j.jfineco.2005.10.004

CrossRef Full Text | Google Scholar

29. Choi KJ, Shim G, Shin Y. Optimal portfolio, consumption-leisure and retirement choice problem with CES utility. Math Finan. (2008) 18:445–72. doi: 10.1111/j.1467-9965.2008.00341.x

CrossRef Full Text | Google Scholar

30. Dybvig PH, Liu H. Lifetime consumption and investment: retirement and constrained borrowing. J Econ Theor. (2010) 145:885907. doi: 10.1016/j.jet.2009.08.003

CrossRef Full Text | Google Scholar

31. Yang Z, Koo H. Optimal consumption and portfolio selection with early retirement option. Math Oper Res. (2018) 43:1378–404. doi: 10.1287/moor.2017.0909

CrossRef Full Text | Google Scholar

32. Bae SY, Jeon J, Koo HK, Park K. Economic effects of social insurance for the elderly. In: Working Paper. (2019).

Google Scholar

33. Rockafellar R. Convex Analysis. New Jersey, NJ: Princeton University Press (1996).

Google Scholar

34. Brennan M, Schwartz E. Portfolio insurance and financial market equilibrium. J Bus. (1996) 62:455–72. doi: 10.1086/296472

CrossRef Full Text | Google Scholar

35. Basak S. A general equilibrium model of portfolio insurance. Rev Finan Stud. (1995) 8:1059–90. doi: 10.1093/rfs/8.4.1059

CrossRef Full Text | Google Scholar

36. Basak S. A comparative study of portfolio insurance. J Econ Dyn Control. (2002) 26:1217–41. doi: 10.1016/S0165-1889(01)00043-4

CrossRef Full Text | Google Scholar

37. Grossman S, Zhou Z. Equilibrium analysis of portfolio insurance. J Finan. (1996) 51:1379–403. doi: 10.1111/j.1540-6261.1996.tb04073.x

CrossRef Full Text | Google Scholar

38. Dybvig P. A comparative study of portfolio insurance. Rev Finan Stud. (1988) 1:67–88. doi: 10.1093/rfs/1.1.67

CrossRef Full Text | Google Scholar

39. Duesenberry JS. Income, Saving, and the Theory of Consumer Behaviory. Cambridge, MA: Harvard University Press (1949).

Google Scholar

40. Dybvig PH. Dusenberry's racheting of consumption: optimal dynamic consumption and investment given intolerance for any decline in standard of living. Rev Econ Stud. (1995) 62:287–31. doi: 10.2307/2297806

CrossRef Full Text | Google Scholar

41. Riedel F. Optimal consumption choice with intolerance for declining standard of living. J Math Econ. (2009) 45:449–64. doi: 10.1016/j.jmateco.2009.03.010

CrossRef Full Text | Google Scholar

42. Watson J, Scott J. Ratchet consumption over finite and infinite planning horizons. J Math Econ. (2014) 54:84–96. doi: 10.1016/j.jmateco.2014.09.001

CrossRef Full Text | Google Scholar

43. Jeon JK, Koo HK, Shin YH. Portfolio selection with consumption ratcheting. J Econ Dyn Control. (2018) 92:153–82. doi: 10.1016/j.jedc.2018.05.003

CrossRef Full Text | Google Scholar

44. Davis MHA, Norman AR. Portfolio selection with transaction costs. Math Oper Res. (1990) 15:676–713. doi: 10.1287/moor.15.4.676

CrossRef Full Text | Google Scholar

45. Fleming WH, Soner HM. Controlled Markov Processes and Viscosity Solutions. New York, NY: Springer-Verlag (2006).

Google Scholar

46. Koo B, Koo H, Koo J, Hyun J. A generalization of dybvig's result on portfolio selection with intolerance for decline in consumption. Econ Lett. (2012) 117:646–9. doi: 10.1016/j.econlet.2012.08.027

CrossRef Full Text | Google Scholar

47. Dybvig PH. Using asset allocation to protect spending. Finan Anal J. (1999) 55:49–62. doi: 10.2469/faj.v55.n1.2241

CrossRef Full Text | Google Scholar

48. Choi KJ, Jeon JK, Koo HK. An Intertemporal Preference with Risk and Loss Aversion. In: Working Paper. (2019).

Google Scholar

49. Choi KJ, Jeon JK, Koo HK. An Intertemporal Preference with Risk and Loss Aversion: Implications for Portfolio Selection and Aggregate Consumption. In: Working Paper. (2019).

Google Scholar