
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat., 25 March 2020
Sec. Dynamical Systems
Volume 6 - 2020 | https://doi.org/10.3389/fams.2020.00003
This article is part of the Research TopicRecurrence Analysis of Complex Systems DynamicsView all 9 articles
We use Recurrence Quantification Analysis (RQA) to study features of Generalized Synchronization (GS) between El Niño-Southern Oscillation (ENSO) and monthly hydrological anomalies (HyAns) of rainfall and streamflows in Colombia. To that end, we check the sensitivity of the RQA concerning diverse HyAns estimation methods, which constitutes a fundamental procedure for any climatological analysis at inter-annual timescales. In general, the GS and its sensitivity to HyAns methods are quantified by means of time-lagged joint recurrence analysis. Then, we link the GS results with the dynamics of major physical mechanisms that modulate Colombia's hydroclimatology, including the Caribbean, the CHOCO and the Orinoco Low-Level Jets (LLJs), and the Cross-Equatorial Flow (CEF) over northwestern Amazonia (southern Colombia). Our findings show that RQA exhibits significant differences depending on the HyAns methods. GS results are similar for the HyAns methods with variable annual cycle but the time-lags seem to be sensitive. On the other hand, our results make evident that HyAns in the Pacific, Caribbean, and Andean regions of Colombia exhibit strong (weak) GS with the ENSO signal during La Niña (El Niño), when hydrological anomalies are positive (negative). Results from the GS analysis allow us to identify spatial patterns of non-linear dependence between ENSO and the Colombian's climatology. The mentioned moisture transport sources constitute the interdependence mechanism and contribute to explain hydrological anomalies in Colombia during the phases of ENSO. During La Niña (El Niño), GS is strong (weak) for the Caribbean and the CHOCO LLJs whereas GS is moderate (strong) for the Orinoco LLJ. Moreover, moisture advection by the Caribbean and CHOCO LLJs exhibit synchrony with HyAns at 0–2 (2–4) months-lags over north-western Colombia and the Orinoco LLJ moisture advection synchronizes with HyAns at similar month-lags over the Amazon region of Colombia. Furthermore, our results suggest a strong (weak) GS between negative (positive) Sea Surface Temperatures (SST) anomalies in the Eastern Pacific and rainfall anomalies in Colombia. In contrast, GS is strong (weak) for positive (negative) SST anomalies in the Central Pacific. Our GS results contribute to advance our understanding on the regional effects of both phases of ENSO in Colombia, whose socio-economical, environmental and ecological impacts cannot be overstated. This work provides a novel approach that reveals new insights into the impact of ENSO on northern South America.
Synchronization is a well-known phenomenon that occurs when different oscillatory systems adjust the time scales of their oscillations due to mutual interaction [1, 2]. Diverse types of synchronization can be determined, such as frequency synchronization (FS), phase synchronization (PS), identical synchronization (IS), generalized synchronization (GS), and lag synchronization (LS) [3]. Particularly, GS emerges when the state of the driven system is completely determined by the state of the driving system [4]. Hence, for two signals x and y that have a functional link y ≃ f(x), GS techniques help to identify their synchronization or interrelationships even when their amplitudes behave differently. Diverse methods have been proposed to study synchronization, such as those based on recurrences [5–10], phase differences [1, 11–13], and quasi-simultaneous appearance of events [14–17]. In particular, the method based on recurrences (recurrence plots and RQA) is based on properties from the non-linear dynamical systems, such as the Poincaré Recurrence Theorem [18] and the Takens' theorem regarding the artificial reconstruction of strange attractors [19, 20].
In the last two decades, methods based on recurrences have proven to be very useful in different areas, such as earth sciences, engineering, and applied physics, among others [10, 21, 22]. Specifically, join recurrence plots (JRPs) have been used to study simultaneous recurrences and the detection of generalized synchronization in different systems [23]. Recently, RQA has proved to be useful in diverse areas, such as economy, physiology, earth sciences, astrophysics, and engineering [10, 22]. In particular, RQA has been used to investigate complex synchronization scenarios between coupled chaotic oscillators [24], emergence of GS in networks of structurally different time-delay systems [25, 26], and precursors and synchronization of components of the tectonic system [27], among others. The oscillatory nature of diverse hydroclimate phenomena is well-known, such as those associated with the annual cycle of insolation (12 months), and the quasi-periodic El Niño-Southern Oscillation (3–4 years), which constitutes the most important modulator of interannual climate variability worldwide [28]. In turn, ENSO itself exhibits phase-locking with the annual cycle [29], and affects the annual cycle of hydroclimatic variability in tropical South America and elsewhere [28]. Thus, GS and RQA provide powerful theoretical and quantitative frameworks to understand the non-linear interaction between ENSO and hydroclimatic processes in the region.
As far as we know, RQA has not been used to test the sensitivity of different methods to estimate hydro-climatic anomalies at interannual timescales (hereafter HyAns). The recent work by Salas et al. [30] demonstrated that HyAns exhibit significant differences in terms of magnitude, timing, and sign, depending on the estimation method. Furthermore, they also demonstrated that linear and non-linear quantifiers of dependence can be significantly affected by how HyAns are defined [30, 31]. Then, in this work, we test the sensitivity of the GS metrics using the four HyAns methods assessed by Salas et al. [30, 31], namely: (i) the Traditional Annual Cycle or constant climatology (HyAns–TAC), (ii) F-filtering of the Annual Cycle by moving averages (HyAns–FAC), (iii) Annual cycle extracted by Singular Spectrum Analysis or Singular-Spectrum Annual Cycle (HyAns–SSAC) and, (iv) the Modulated Annual Cycle or variable climatology (HyAns–MAC). We also aim to provide advances regarding the robustness of the GS quantifiers based on recurrences for climate analysis at inter-annual timescales.
Colombia experiences positive (negative) anomalies in rainfall and streamflows, during the cold (warm) phase of ENSO, whose magnitude and timing vary across the main geographic regions of the country (Caribbean, Andes, Pacific, Orinoco, and Amazon) [30–38]. Associated with those anomalies, there are extreme hydro-meteorological events of important socio-economical, environmental and ecological impacts. As such, the GS provides a new framework to further understand the impacts on ENSO on the hydroclimatology of Colombia, and the physical mechanisms responsible for such anomalies using a non-linear dynamical systems approach based on recurrences [10]. In general, we investigate GS between hydrological records of monthly series of rainfall and streamflows in Colombia and diverse variables related to moisture transport mechanisms influencing the Colombian hydrology during the extreme phases of ENSO. In particular, our GS-analysis is carried out at inter-annual timescales considering the extreme phases of ENSO (La Niña and El Niño) separately. Three main moisture-ladden Low-Level Jets are considered as major mechanisms associated with hydroclimatic anomalies in Colombia, namely: (i) the Caribbean LLJ [39], (ii) the Chorro del Occidente Colombiano (hereafter CHOCO LLJ) [40, 41], and (iii) the Orinoco LLJ [42] also known as the Eastern Andean LLJ or Corriente de los Andes Orientales (CAO) [43, 44] (hereafter Orinoco LLJ). Furthermore, we also consider (iv) the Cross-Equatorial Flow (CEF) [45] as a possible mechanism of meridional moisture transport from the Amazon River basin to the Colombian territory. Additionally, in order to contrast our analysis with the available literature, we consider the SST gradient between the Pacific Ocean off the Colombian coast and the El Niño 1+2 zone, which makes part of the physical mechanism behind the CHOCO LLJ dynamics [40].
Also, we study the emergence of GS between two different types of ENSO and the Colombian hydrology, given that several recent works have shown that major SST warming has occurred frequently in the central Pacific (hereinafter CP El Niño), notably different from the eastern Pacific warming pattern during canonical El Niño events [46–49] (hereinafter EP El Niño). Moreover, the CP El Niño exerts distinct socio-economical, environmental and ecological impacts around the globe [46–49]. Andreoli et al. [47] stated that the different SST anomaly patterns in the tropical Pacific affect the large-scale (Walker circulation and troposferic Rossby waves) and local atmospheric circulation patterns over northern South America producing different anomaly precipitation patterns. In particular, few works have studied the influence of the different types of El Niño events on Colombian's hydroclimatology [50–53]. Those works indicate that SST anomalies on the Eastern Pacific (EP) and the Central Pacific (CP) ocean are related with positive or negative hydrologic anomalies in the country depending on the location. At this point, there is not a clear consensus on the relationship between the different SST anomalies in the tropical Pacific and its influence on the hydrologic response in Colombia. Recently, Sullivan et al. [46] proposed robusts indices for the EP El Niño, CP El Niño, and the Mixed-type El Niño, which are based on the normalized SST anomalies in the Niño3, Niño4, and Niño3.4 areas of the tropical Pacific Ocean, respectively. Therefore, we aim to quantify GS using those indices to infer clues on the influence of the different types of ENSO on Colombia hydrology.
The objectives of this work are manifold: (i) To quantify non-linear inter-dependencies between the ENSO signal and the anomalies of hydrological variables in Colombia using the GS approach based on RQA; (ii) To assess the sensitivity of the GS-metrics based on RQA using diverse methods used to define hydro-climatic anomalies; (iii) To evaluate the impact of ENSO on the Colombian hydrology through its effect on the sources of moisture that feed the water cycle dynamics over Colombia; (iv) To calculate GS between different types of El Niño indices (Central Pacific, Eastern Pacific, and Mixed) and the Colombian hydrology; and (v) To examine by means of GS metrics the propagation of the ENSO signals over Colombia.
To achieve the mentioned objectives we revise and characterize hydrological anomalies over Colombia during the phases of ENSO. Besides, a quantification of the linear and non-linear associations among the different variables seems necessary to elucidate new insights and explanations. In particular, we look for evidences about the influence of the aforementioned moisture sources on Colombian hydrology during ENSO. To that end, we consider the behavior of the moisture advection through the Caribbean, CHOCO, and Orinoco LLJs as well as the CEF during the phases of ENSO. Furthermore, our physical interpretation of GS results are based on Gill's theory [54] that states that weakening (strengthening) of the low-level winds is related to the increase (decrease) of the SSTs, which subsequently increase (decrease) of evaporation, increase (decrease) of moisture convergence, and increase (decrease) of rainfall in some regions [32, 39, 55].
This work is outlined as follows: section 2 describes the datasets and the region of study. Section 3 presents the RQA, the GS-index, the statistical tests for RQA. Results are discussed in section 4 and the final remarks are drawn in section 5.
We use monthly rainfall and streamflows series from the five major regions of Colombia: Caribbean, Andes, Pacific, Orinoco and Amazon. Figure 1 shows six macro-climatic zones, namely: Nino3.4 and Nino1+2 in the tropical Pacific Ocean, as well as the zones related to the Caribbean, CHOCO, and Orinoco LLJs, and the Cross Equatorial Flow (CEF). Details are provided in sections 2.1, 2.3, and 2.4.
To classify the ENSO events, we use the monthly Multivariate ENSO Index (MEI) [56], which is based on six variables over the tropical Pacific: sea-level pressure, zonal and meridional surface wind components, sea and air surface temperatures, and total cloud fraction. It is considered to be a more reliable estimator of the ENSO state compared to other indexes, such as Nino3.4 (based solely on sea surface temperatures) or the Southern Oscillation Index (SOI), which is based on sea-level pressures [57, 58]. Values of the MEI index greater (lesser) than +0.5 (−0.5) define the occurrence of El Niño (La Niña) events, whereas the remaining periods will be referred to as neutral. The information of precipitation and streamflows was classified according to El Niño and La Niña months, following the classification previously described.
We use the monthly Extended Reconstructed Sea Surface Temperatures (ERSSTv5) in the El Niño 3.4 region (hereafter SST3.4), in the area 5° N–5° S and 170–120° W. Details in https://www.cpc.ncep.noaa.gov. The mentioned SST3.4 time series was filtered using a 12-months moving average filter to extract the inter-annual variability. Then, we calculate the GS index between SST3.4 and rainfall and streamflows series in Colombia.
A recent study proposed three simple indices to represent the EP El Niño, CP El Niño, and the mixed type of El Niño (Mixed-type), which can be used for understanding, prediction, and impact assessment [46]. In general, those indices are based on the SST in the Niño3 and Niño 4 regions, which coincide with the areas that exhibit maximum SST warm anomalies of the EP and CP El Niño, respectively [46]. Indices for EP type, CP type, and Mixed-type El Niño are calculated as [46]:
• EP = Niño3normalized – 0.5 * Niño4normalized,
• CP = Niño4normalized – 0.5 * Niño3normalized,
• Mixed-type = EP + CP ≃ Niño3.4normalized,
where Niño3normalized, Niño4normalized, and Niño3.4normalized denote the normalized SSTs anomalies in the Niño3 (5°S–5°N, 150–90°W), Niño4 (5°S–5°N, 160–150°W), and Niño3.4 (5°S–5°N, 170–120°W) regions, respectively [46].
Figure 2 shows the MEI index and its classification in La Niña, El Niño, and Neutral as explained in section 2.1.1. Furthermore, Figure 2A shows the EP El Niño index, Figure 2B shows the CP El Niño index and, Figure 2C shows the Mixed-type El Niño as defined in Ref. [46].
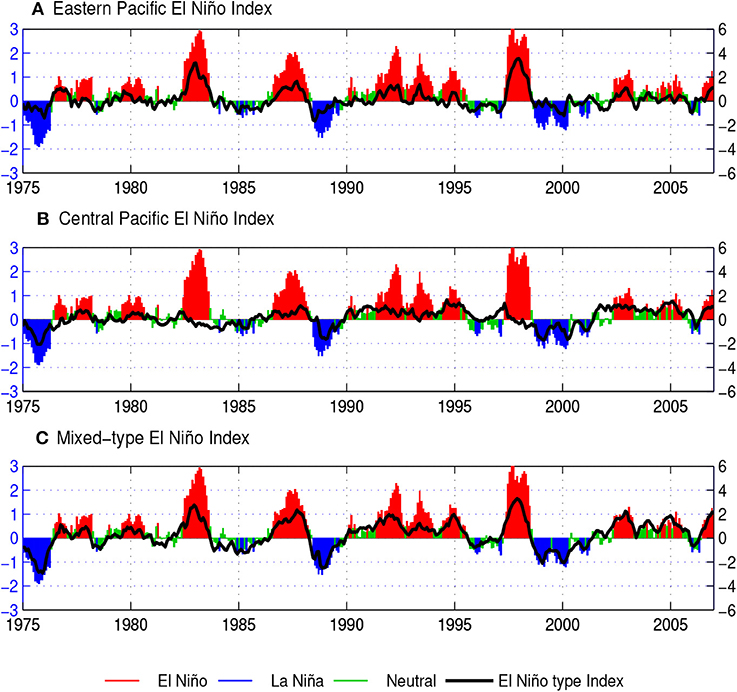
Figure 2. Indices for different types of El Niño in the period 1975-2006: (Left axis) MEI index denoting La Niña (blue), El Niño (red), and Neutral (green) phases of ENSO. (Right axis-black line) Eastern Pacific (EP) type (A), Central Pacific (CP) type (B), and Mixed-type (C).
• Dataset 1: We use data from a reanalysis of Colombian rainfall performed by Hurtado-Montoya and Mesa [59], which produced monthly precipitation fields, spanning the period from 1975 to 2006, at a spatial resolution of 5 min of arc, in the region 5°S–15°N and 80–65°W. Those authors used a set of 2,270 rain gauges from diverse institutions including Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia (IDEAM), Empresas Públicas de Medellín (EPM), Centro Nacional de Investigaciones del Café (CENICAFE), and The Global Historical Climatology Network (GHCN). In addition, they also used satellite information from the Global Precipitation Climatology Project(GPCP)-V2, National Centers for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR), Tropical Rainfall Measuring Mission (TRMM), and the Geostationary Satellite System (GOES). Finally, the monthly precipitation fields resulted from a combination of the available data and the implementation of the PRISM model over the Colombian territory. The resulting data set is freely available upon request to one the authors (O. J. M) [59].
• Dataset 2: We also use data from a set of 937 rain gauges from IDEAM, at monthly resolution, having record lengths of 40 years, for the period 1976–2015, with less than 10% missing records. The geographical distribution of this data set is as follows: 38 time series in the Pacific region, 631 in the Andes, 228 in the Caribbean, 30 in the Orinoco, and 10 in the Amazon region (see Figure 3B).
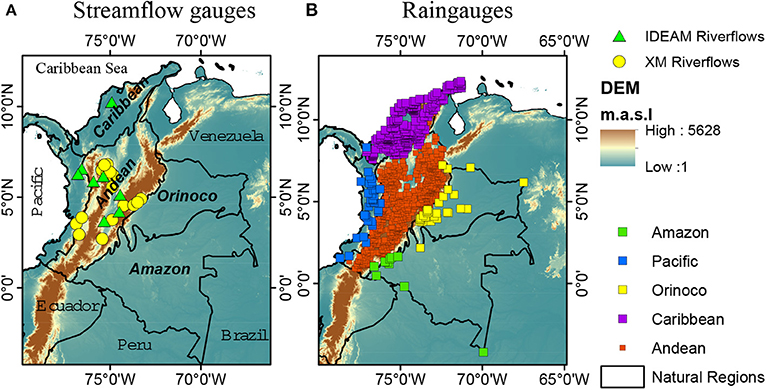
Figure 3. National context including the Colombian Natural Regions as well as the streamflows and rainfall gauges. (A) Streamflow gauges. (B) Raingauges.
We use monthly average streamflows data from seven IDEAM's river gauging stations having common record lengths of 38 years, from 1976 to 2013 (see Table S1). Furthermore, we use a set of 18 time series from XM (url: www.xm.com.co), at monthly time-scale, with record lengths 40 years from 1976 to 2015 (see Table S2). Most river gauging stations are located in the Andean region, whereas long-term data in the Orinoco and Amazon regions are not available (see Figure 3A).
Table 1 details the sample size used to quantify dependency among diverse variables for each dataset. The samples were defined once each month is classified as El Niño, La Niña, and Neutral according to the MEI index (details in section 2.1).
In order to investigate the influence of the Low Levels Jets (LLJs) as rainfall-generating moisture transport mechanisms and therefore as physical mechanisms behind the emergence of GS, we use data from the NCEP/NCAR Reanalysis Project [60]. Moisture advection is calculated as the product between the monthly mean zonal winds and the monthly mean specific humidity at 925 hPa. In particular, moisture advection is calculated over the following geographic zones, which are associated with the three LLJs surrounding Colombia, namely: (i) The Caribbean LLJ moisture advection is calculated over the region 12.5–17.5°N, 80–70°W. This region is selected based on the work by Wang [39], who studied the variability of the Caribbean LLJ; (ii) The CHOCO LLJ moisture advection is quantified over the region 2–8°N, 82–77.5°W. This region was used in study [40], which deals with the characterization and influence of the CHOCO LLJ on ocean-land-atmosphere interactions over the far eastern Pacific; and (iii) The Orinoco LLJ moisture advection is calculated over the region 6–10°N, 70–65°W. This region is located over the vast Llanos (plains) region over the Colombia-Venezuela border and, selected according to previous works [42–44].
In particular, the CHOCO LLJ dynamics is related to the SST gradient in the far eastern tropical Pacific. That is, the surface air temperature gradient between the Pacific Ocean off the Colombian coast (2–8°N, 77.5–82°W) and the El Niño 1+2 region (10–0°, 90–80°W) from the sea level to 925 hPa [40]. Hence, we calculate the SST gradient between both zones and its association with rainfall and streamflows in Colombia using the GS metrics. We will contrast the GS results obtained between ENSO and the Colombian hydrology (rainfall and streamflows) with those obtained between LLJs and the Colombian hydrology to infer similarities and differences.
The Cross-Equatorial Flow can be related to the hydrological dynamics over eastern and southeastern Colombia (Orinoco and Amazon regions) and the northern-most Amazon basin [45]. Hence, as in the previous section, we estimate the moisture advection as the product between the mean meridional winds and the mean specific humidity at 925 hPa, using data from the NCEP/NCAR Reanalysis Project [60], over the region 5°S–5°N, 65–75°W [45].
Recurrence in phase space is a fundamental property of diverse types of dynamical systems [10]. This recurrence behavior can be characterized and quantified by means of the so-called Recurrence Plots (RP), which is a modern tool of non-linear data analysis that allows to visualize and quantify properties of higher-dimensional phase space trajectories [61]. The construction of the RP from a time series, xi, requires the representation of the m-dimensional phase space of the system X. For single time series, xi, it is necessary to reconstruct the dynamics using the time delay embedding technique as [19, 62],
where m is the embedding dimension and ω is the time delay. The false nearest neighbors (FNN) is the most used method to quantify m, whereas the Auto-Information Function (AIF) is commonly used to quantify the time-delay [10, 63–65]. Once m and ω have been estimated, the RP is calculated using the pair-wise proximity test to obtain the recurrence of x for the times i and j as,
where N is the number of data points, N′ = N − (m − 1)ω is the dimension of phase space vectors, ϵ is the threshold to the proximity between the phase space vectors. According to the literature, ϵ must be selected as a few percent (not larger than 10%) of the maximum phase space diameter [22, 66, 67]. is the spatial distance between vectors in phase space. ‖ · ‖ denotes any norm in phase space (e.g., Manhattan, Euclidean, or maximum norm) [22], and Θ(·) is the Heaviside function, such as Θ(x) = {1 ∣ x > 0;0 ∣ x ≤ 0} [10]. The plot of the recurrence binary matrix RX provides the RP. Then, the probability that one system recurs to a certain state is equal to the column-average of the recurrence matrix [10].
On the other hand, the Joint Recurrence Plot (JRP) is used to study the possible influence between two different physical systems, constituting a measure of their simultaneous recurrence. The joint recurrence matrix is defined as the Hadamard product of the RPs of the single RPs of systems X and Y [10, 68, 69],
Hence, the probability of finding a simultaneous recurrence at time i in both systems X and Y is equal to the column-average of the JRXY matrix [69],
The same procedure can be carried out considering the relationship between the system X and the time lagged system Y(τ). Then, if both systems X and the time lagged Y(τ) are independent, . In contrast, if both systems are in GS, we expect approximately the same recurrences, .
The computation of the recurrence matrices is most appropriate using a fixed amount of nearest neighbors, Nn, for each column in the matrix than a fixed threshold [6, 10]. This corresponds to the original definition of RP [61]. Therefore, according to [10], and are equal and fixed by Nn, i.e., . Taking the recurrence rate (RR) as RR = Nn/N,
where S(τ) is a time series with values ranging between 0.0 and 1.0, and τ is a time-lag between time series xi and yi+τ [10]. Consequently, it is possible to define a global index for GS based on the average joint probability of recurrence (hereafter GS-index) by choosing the maximum value of S(τ) and normalizing it [10],
where GS ranges from 0 (independent) to 1 (correlated). In order to avoid potential pitfalls in RQA, our procedures are based on pivotal literature on recurrences [10, 22, 65].
The existence of GS between the systems X(t) and Y(t + τ) requires a statistical test to verify the significance of the GS-index at time-lag τ. Consequently, it is possible to test the significance of the GS-index based on the joint recurrence matrix between the trajectory in phase space of the original system X (ENSO in our case) and a representative number of phase space trajectories of the system Y (precipitation and streamflows in our case), which are independent copies of the underlying system Y [also called twin surrogates (TS)] [70, 71]. This ensures surrogates that are uncorrelated or not synchronized with each other. Then, TS are phase space trajectories sharing the same neighborhood up to the threshold ϵ such that , k = 1, …, N′. In this work, TS are constructed using the algorithm by Thiel et al. [70, 71], which is included in the CRP Toolbox for MATLAB provided by TOCSY, available at http://tocsy.agnld.uni-potsdam.de [10].
The null hypothesis is that each TS is an independent trajectory of the system, corresponding to different initial conditions. In this work, we test the significance of the GS-index between X and Y(τ) using 100 TS of the Y system (hydrological variables), i.e., to calculate the GS-index for each pair of X and the TS and obtain their distribution. Finally, we compare the GS-index for the original time series x(t) and y(t) with the 95th percentile (95% confidence boundary) of the test distribution. The time-lags τ where the GS-index, GS(τ), takes values out the confidence band imply values for which the null hypothesis is rejected, i.e., the systems X and Y are significantly dependent. In order to test for the null hypothesis, we carry out a multiple testing procedure following the Šidák-Bonferonni Equations [72, 73], and perform five independent tests limiting the risk of making at least one Type I error to an overall value of α[PF] = 0.05 (PF means alpha per family of tests) and then we use α[PT] ≈ 0.01 (PT means alpha per test).
Taking into account that precipitation and streamflows exhibit different kind of anomalies depending on the ENSO phase (warm or cold), we quantify the probability of joint recurrence, , at time i (Equation 5) for the cold (La Niña) and warm (El Niño) phases of ENSO separately. After that, we calculate the joint recurrence matrix (Equation 4) and then , where τ is the time-lag. Then, we look for the columns in the JRP that correspond to the classification of ENSO phases as per the MEI index (section 2.1). Finally, we calculate during La Niña and El Niño conditions.
For the different types of El Niño indices (EP, CP, and Mixed-type), we carry out a similar procedure. We quantify the probability of joint recurrence, , for each index using all data and also periods as per the MEI classification, separately.
Diverse methods commonly used to estimate hydro-climatic anomalies (HyAns) exhibit differences that may induce strong biases and error sources toward the interdependence analysis and modeling of climate time series [30]. Such differences may generate ambiguities for the physical interpretation of results [30], and thus the need to consider the uncertainty in HyAns estimation and its consequences for quantification of interdependence using linear and non-linear techniques. In this sense, Salas et al. [31] showed that phase synchronization metrics based on Generalized Phase Differences [13] are sensitive to seasonal-residual frequencies in time series of anomalies.
Hence, we verify the sensitivity of GS metrics based on RQA using the four HyAns methods assessed by [30, 31], namely: (i) the Traditional Annual Cycle or constant climatology (HyAns–TAC), (ii) F-filtering of the Annual Cycle by moving average (HyAns–FAC), (iii) Annual cycle extracted by Singular Spectrum Analysis or Singular-Spectrum Annual Cycle (HyAns–SSAC) and, (iv) the Modulated Annual Cycle or variable climatology. In this way, we evaluate the robustness of our GS approach in relation to the diverse HyAns estimation methods.
According to Salas et al. [30], the HyAns–FAC method is appropriate for climatological purposes owing to the following properties: (i) a firm mathematical foundation, (ii) a varying climatology (annual cycle), (iii) an adequate separation of noise, intra-annual, seasonal and inter-annual components, since (iv) it does not leave significant residual seasonal frequencies in HyAns, (v) its extreme values are in a middle range in comparison with the HyAns-SSAC and HyAns-MAC methods, (vi) its autocorrelation function is comparable with HyAns-SSAC and HyAns-MAC, and (vii) its computational cost is one-tenth of HyAns-SSAC and hundredths times less than HyAns-MAC.
First, we quantify rainfall anomalies over Colombia considering both phases of ENSO (El Niño and La Niña), as explained in section 2.1. Rainfall anomalies were calculated using a F-Filtering of the annual cycle by moving averages, which filters out adequately the seasonal signal [74, 75]. Figure 4 shows that during La Niña, Colombia experiences wetter (drier) than normal periods in the Pacific, Andean, and Caribbean (Orinoco and Amazon) regions. In contrast, during El Niño, Colombia evidences drier (wetter) than normal periods in the Pacific, Andean and Caribbean (Orinoco and Amazon) regions. On the other hand, Figure 4 shows that, during La Niña (El Niño), the Orinoco and Amazon regions exhibit negative (positive) rainfall anomalies throughout the year. It is worth noting that the influence of both phases of ENSO on streamflows in the Amazon region of Colombia does not show a clear-cut pattern of positive or negative anomalies [76]. Hence, ENSO's influence on rainfall anomalies in Colombia depends on the phase of ENSO (La Niña or El Niño) and the region of the country (see Figure S11).
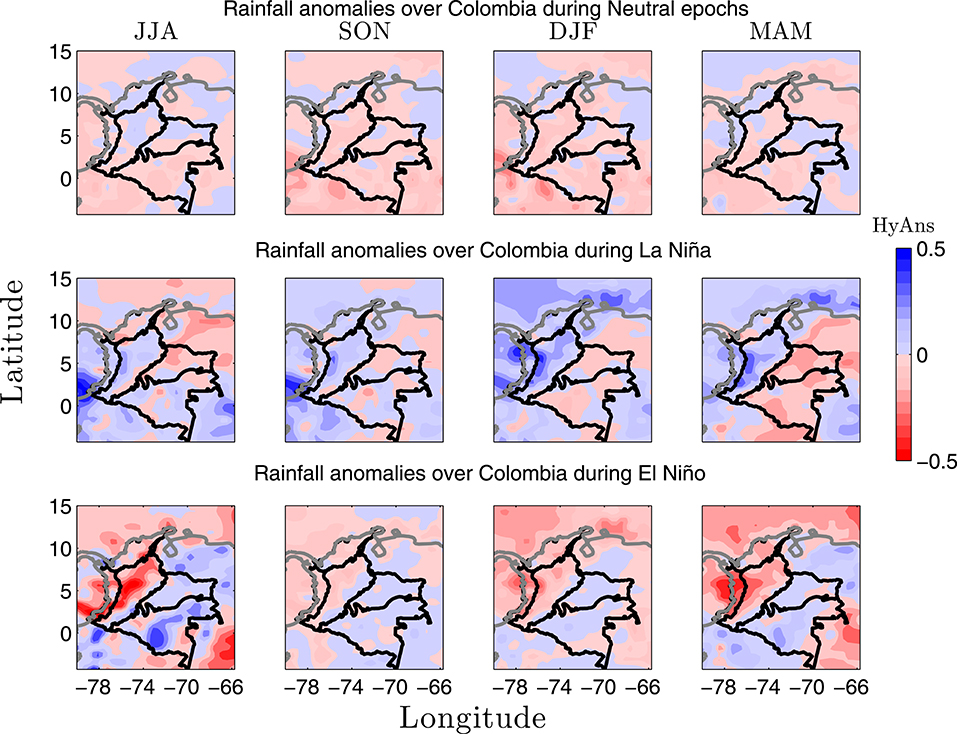
Figure 4. Seasonal average rainfall anomalies (HyAns) in Colombia during ENSO. Data set No. 1. Rainfall anomalies were calculated using F-Filtering of the annual cycle by moving averages, which is previously mentioned as the HyAns–FAC method. (Gray line) Northern South American coast line. (Black line) Borders of the Colombia's natural regions.
Second, we quantify the linear association between SST anomalies in the tropical Pacific and rainfall anomalies over Colombia during ENSO using Pearson correlations, r. We calculate r using the complete monthly time series to capture the big picture. Figure 5 suggests that positive (negative) rainfall anomalies over the Pacific, the Andean and the Caribbean regions are significantly correlated with negative (positive) SST anomalies in the tropical Pacific Ocean. Furthermore, the spatial patterns of statistical significance of r are in agreement with the spatial patterns of positive (negative) rainfall anomalies in Colombia during ENSO (see Figure 4). However, it is worth noting that correlation patterns between SST3.4 anomalies and rainfall anomalies could differ during the phases of ENSO, and that Pearson correlations only quantify the linear association. This points out the need to explore non-linear techniques to quantify the dependence between hydrological anomalies in Colombia and the ENSO signal considering La Niña and El Niño phases.
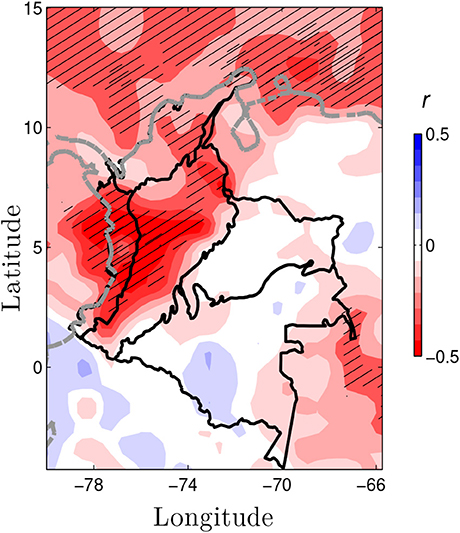
Figure 5. Pearson correlation, r, between rainfall anomalies in Colombia and SST3.4 anomalies. (Dashed gray line) Northern South American coast line. (Black line) Borders denote Colombia's natural regions. The hatched areas indicate that r is significant at 5%. The significance levels are calculated considering the Effective Degrees of Freedom due to autocorrelation in timeseries [77].
Low-Level Jets (LLJs) are important rainfall-formation mechanisms and their non-linear interdependence with the regional hydroclimatology requires an adequate characterization of moisture advection anomalies [78–81]. To that end, we characterize the annual cycle of moisture advection anomalies by the Caribbean LLJ, the CHOCO LLJ, and the Orinoco LLJ as well as by the Cross-Equatorial Flow (CEF) during the phases of ENSO. To this end, we use data from the NCEP/NCAR Reanalysis Project [60] and calculate moisture advection as the product between the mean zonal or meridional winds and the mean specific humidity at 925 hPa averaged over the geographic areas described in section 2.3. We estimate moisture advection anomalies in such a way that positive or negative anomalies represent increase or decrease of moisture advection, respectively. Furthermore, after an exhaustive verification of NCEP/NCAR 925 hPa data in the period 1970–2015, the moisture advection by the Caribbean and the Orinoco LLJs have a predominant easterly direction whereas the moisture advection by the CHOCO LLJ exhibits a clear-cut westerly direction during 80% of time. Likewise, the CEF exhibits dominant northerly (southerly) moisture advection from October to March (April to September).
Figure 6A shows that the Caribbean LLJ exhibits positive (negative) zonal moisture advection anomalies during El Niño (La Niña) for the period from May to November, with a peak in July for both positive and negative cases, which coincides with the variation of Caribbean LLJ winds during June–July–August (JJA) and December–January–February (DJF) [39, 55]. In particular, this result coincides with the observation that during La Niña, the easterly Caribbean LLJ winds are weak (strong) in JJA (DJF), whereas during El Niño, the easterly Caribbean LLJ winds are strong (weak) in JJA (DJF) [39]. Furthermore, Figure 6B shows that zonal moisture advection anomalies by the CHOCO LLJ are positive (negative) during La Niña (El Niño) from July to December. These results are consistent with those reported by Poveda and Mesa [40]. Moreover, Figure 6C shows that moisture advection anomalies by the Orinoco LLJ are positive (negative) during El Niño (La Niña) in JJA. Finally, Figure 6D shows that the CEF exhibits positive (negative) moisture advection anomalies during La Niña (El Niño) from April to October for the southerly winds, whereas the CEF exhibits negative (positive) during La Niña (El Niño) from November to March for the northerly winds.
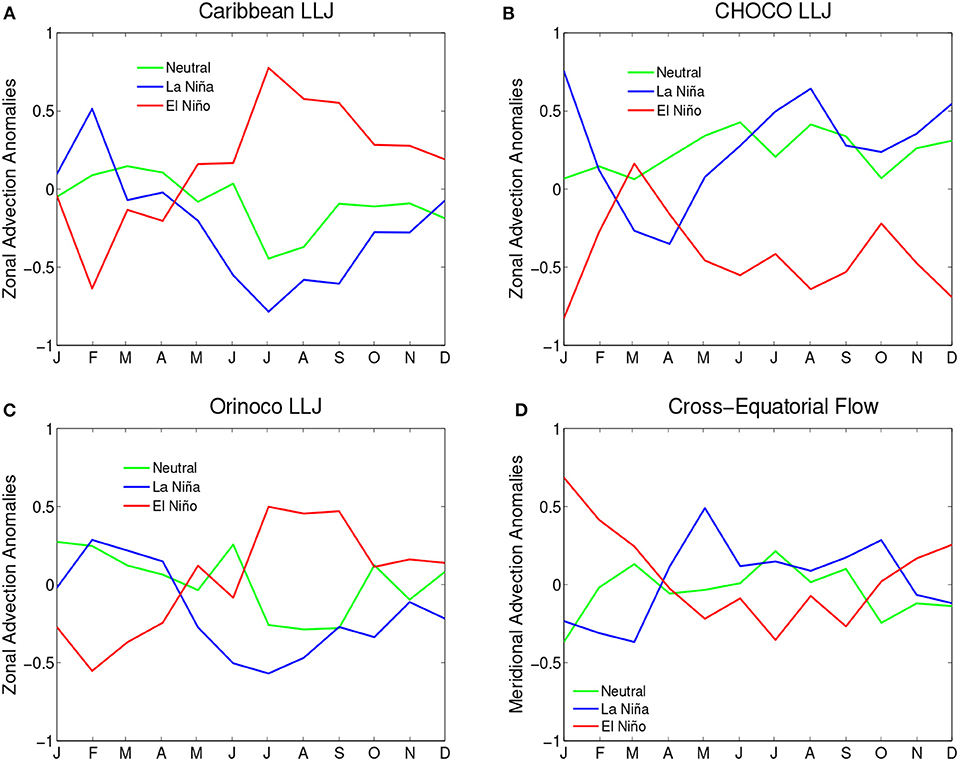
Figure 6. Annual cycle of standardized moisture advection anomalies during ENSO using data from the NCEP/NCAR Reanalysis Project for the period 1970–2015. (A) Zonal moisture advection by the Caribbean LLJ. (B) Zonal moisture advection anomalies by the CHOCO LLJ. (C) Zonal moisture advection anomalies by the Orinoco LLJ. (D) Meridional moisture advection by the Cross-Equatorial Flow.
The annual cycles of moisture advection anomalies, as well as the annual cycle of hydrological anomalies during ENSO, are important information sources for the interpretation of results of non-linear metrics, such as GS. In the following sections, we will revisit these findings in order to interpret the GS results from a physical point of view.
Detection of GS using the recurrence quantification analysis (RQA) requires to adequately select the time delay, ω, and the embedding dimension, m. The time delay, ω, for each time series is calculated as the time that the auto information function (AIF) takes to decay to 1/e of its value at zero lag (see section 3.1). Figure 7A shows that all the time series exhibit an exponential decay until a time delay ω ≈ 8 months. The embedding dimension, m, is calculated using the false nearest neighbors (FNN). Figure 7B shows that according to FNN an appropriate embedding dimension for all time series is m = 2.
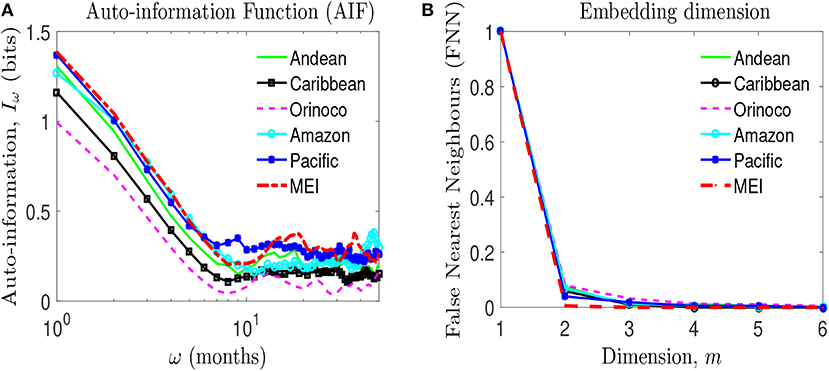
Figure 7. Estimation of the time delay and the embedding dimension for monthly precipitation averaged over the natural regions of Colombia (from data set No. 1) and MEI index. (A) Time delay, ω, using the auto-information function (AIF). (B) Embedding dimension, m, using false nearest neighbors (FNN).
Hereafter, all analyses are carried out using the fixed amount of nearest neighbors (FAN) whereas the significance tests are based on 100 twin surrogates. On the other hand, in this work, the threshold of proximity between the phase space vectors was selected as ϵ = 10% according to Refs. [22, 66, 67].
We use a time series of rainfall anomalies for the Andean region (monthly precipitation spatially averaged over the Andean region) and quantify the GS-index using the four HyAns methods: HyAns–TAC, HyAns–FAC, HyAns–SSAC, and HyAns–MAC [30] (see section 3.4). To that end, we select sample data classified according to El Niño and La Niña months, as per the MEI definition (see section 2.1). Figure 8 shows the GS-index for the mentioned HyAns methods. In general, our findings reveal that the HyAns–TAC method exhibits the lowest GS values in relation to the other methods, during both La Niña and El Niño. This behavior can be explained by the presence of noise, intra-annual, and significant-residual seasonal frequencies in anomalies, when those are estimated using HyAns–TAC [30]. Hence, we consider that the HyAns–TAC method is not reliable for the RQA and purposes of this study.
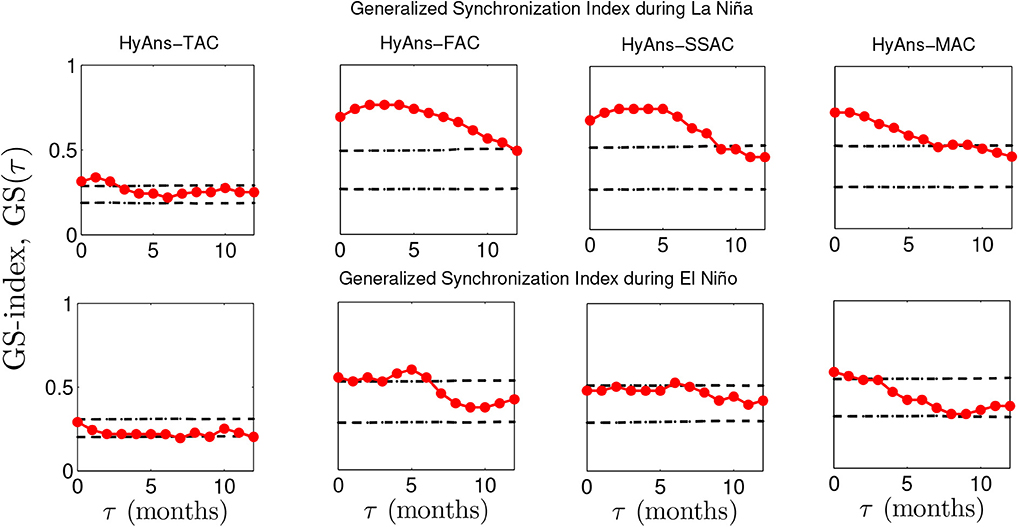
Figure 8. Generalized synchronization index (GS-index) between the ENSO signal (MEI index) and monthly rainfall anomalies in the Andean region estimated using the four HyAns methods: HyAns–TAC, HyAns–FAC, HyAns–SSAC, HyAns–MAC. (Top row) La Niña and (bottom row) El Niño. Period 1976–2015. τ denotes the time lag. (Dashed black lines) 95% confidence boundaries.
In addition, Figure 8 shows the GS-index between the ENSO signal and rainfall anomalies using diverse HyAns methods. In general, the GS-index exhibits higher values during La Niña than during El Niño, for the HyAns–FAC, HyAns–SSAC, and HyAns–MAC methods. In this sense, Poveda and Mesa [33, 82] showed that the ratio between hydrological anomalies and the long-term mean is higher during La Niña than during El Niño. In agreement with this finding, Salas et al. [31] showed that the strength of phase synchronization index between rainfall anomalies and the ENSO signal also is stronger during La Niña than during El Niño.
In terms of the time-lag between the ENSO signal and rainfall anomalies over the Andean region of Colombia, Figure 8 shows that during La Niña, the HyAns–FAC, HyAns–SSAC, and HyAns–MAC methods suggest a 2–4 months-lag whereas, during El Niño, the HyAns–FAC, and HyAns–SSAC methods show a 4–6 months-lag. Furthermore, the HyAns–FAC and HyAns–MAC methods show time-lag differences during El Niño. As a conclusion, the magnitude of the GS-index is not highly sensitive to the diverse HyAns methods whereas the time-lag between time series could be affected by the HyAns methods.
Hereafter, time series are filtered using the F-filtering of the annual cycle by a moving average procedure (HyAns–FAC) in order to remove the intra-annual, semi-annual and annual frequency bands. Furthermore, we verify that the time series only contain information at inter-annual timescales using the test by Ahdesmäki et al. [83].
As a first step, we quantify GS between SST3.4 anomalies and rainfall and streamflows anomalies over Colombia. In general, Figure 9 evidences that rainfall anomalies are in GS with SST anomalies in the central tropical Pacific. In particular, the GS calculation using all data points, regardless of ENSO phases, leads to lower GS-values but whose significant values are consistent with the results considering the Neutral, La Niña, and El Niño. Furthermore, our findings show that the GS is strong (weak) during La Niña where rainfall exhibits positive (negative) anomalies. The lowest GS values are shown in the Neutral condition. During La Niña, the GS occurs mainly over western Colombia, that is the northern and western Andean region as well as the Pacific and the Caribbean regions. In turn, mentioned regions exhibit positive rainfall anomalies. Note that the Amazon region also exhibits significant GS but, during this cold phase of ENSO, rainfall anomalies are negative. During El Niño, the GS is significant mainly over the Pacific and the Andean regions where rainfall exhibits negative anomalies. At this point, our results confirm the influence of both ENSO phases over Colombia [33, 36]. Moreover, our findings confirm that those regions exhibiting strong (weak) phase synchronization during La Niña (El Niño) [31] also exhibit GS. Hence, the systems (ENSO and rainfall in some regions of Colombia) exhibit a functional relationship.
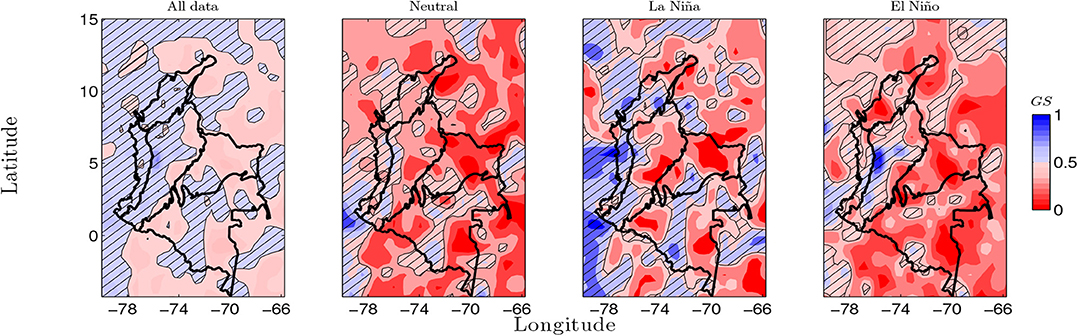
Figure 9. Generalized synchronization index between SST3.4 anomalies and rainfall anomalies in Colombia, Data set No. 1, period 1975–2006. The hatched contours indicates zones where the GS is significant at 5%.
On the other hand, streamflows are the hydrological response to interactions, at catchment scale, between landscape characteristics (soils, vegetation, geology, the topology of drainage networks, hydraulic properties, etc.) and climate and weather events [84]. In addition, the catchment plays a filtering role to the high frequency nature of precipitation in association with evapotranspiration and soil moisture dynamics [85]. In this sense, it is to be expected that marked long-term patterns of precipitation appear also in long-term characteristics of streamflows. Figure 10 shows the GS index between SST3.4 anomalies and streamflow anomalies. Our results are consistent with those found for rainfall anomalies. First, our findings demonstrate that using all data points, regardless of ENSO phases, leads to lower GS-values. Furthermore, the GS index is higher during La Niña than during El Niño. In particular, streamflow anomalies exhibiting strong GS are located in the Caribbean region and the north-western Andean region. These results could be associated with the GS-patterns between rainfall anomalies and moisture advection from the Caribbean and CHOCO LLJs discussed next (see Figure S3).
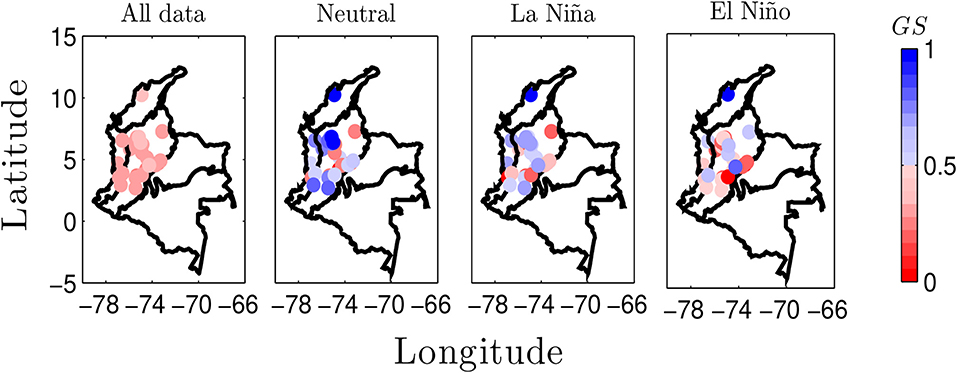
Figure 10. Generalized synchronization index between SST3.4 anomalies and river flow anomalies from the IDEAM and XM datasets, period 1976–2013.
Figure 11 shows the GS-index between the moisture advection of the aforementioned low-level jets (LLJ) and rainfall anomalies throughout Colombia, the columns denote the GS-results considering all data and the different samples for the phases of ENSO (Neutral, La Niña, and El Niño). Figure 11 (top row) shows the GS-index between the moisture advection by the Caribbean LLJ and rainfall anomalies in Colombia. Our results reveal that rainfall anomalies over the Caribbean, the northern-Pacific, and the northern-Andean regions are related to moisture advection by the Caribbean LLJ. In particular, during La Niña, the GS-index exhibits the strongest values and the largest area, whereas during El Niño the GS-values and area of influence are smaller. These findings are in support of the Caribbean LLJ influence on the hypothesis that the Caribbean LLJ influence the hydro-climatic response over northern South America and, particularly, over northern Colombia [32, 39, 55]. Furthermore, these results confirm the influence of the Caribbean LLJ anomalies during ENSO on the positive (negative) rainfall anomalies over northern Colombia. References [39] and [55] showed that during JJA, rainfall in the Caribbean (including the Caribbean region of Colombia) exhibits significant correlations with the Caribbean LLJ index. Moreover, it is postulated that the Caribbean LLJ induces changes in moisture flux divergence in the Caribbean, which enhance convection and increase rainfall [55]. In this sense, weakening (strengthening) of the Caribbean LLJ winds is associated with increasing (decreasing) rainfall anomalies over northern Colombia [32]. Coherently, our findings reveal that positive rainfall anomalies during La Niña coincide with negative moisture advection by the Caribbean LLJ from May to November, which is evidenced as moderate GS. In contrast, our results show that negative rainfall anomalies during El Niño exhibit weak GS (see Figures 4, 6A). These results can be explained because the Caribbean LLJ has an opposite relationship with ENSO in the boreal winter and summer. During the winter a weak (strong) easterly Caribbean LLJ corresponds to warm (cold) SST anomalies in the tropical Pacific, whereas during the summer a strong (weak) easterly Caribbean LLJ is associated with warm (cold) SST anomalies in the tropical Pacific [39]. Furthermore, during El Niño, the Caribbean and Central America region experiences less precipitation in July-August, suggesting that Caribbean LLJ may modulate precipitation anomalies [86].
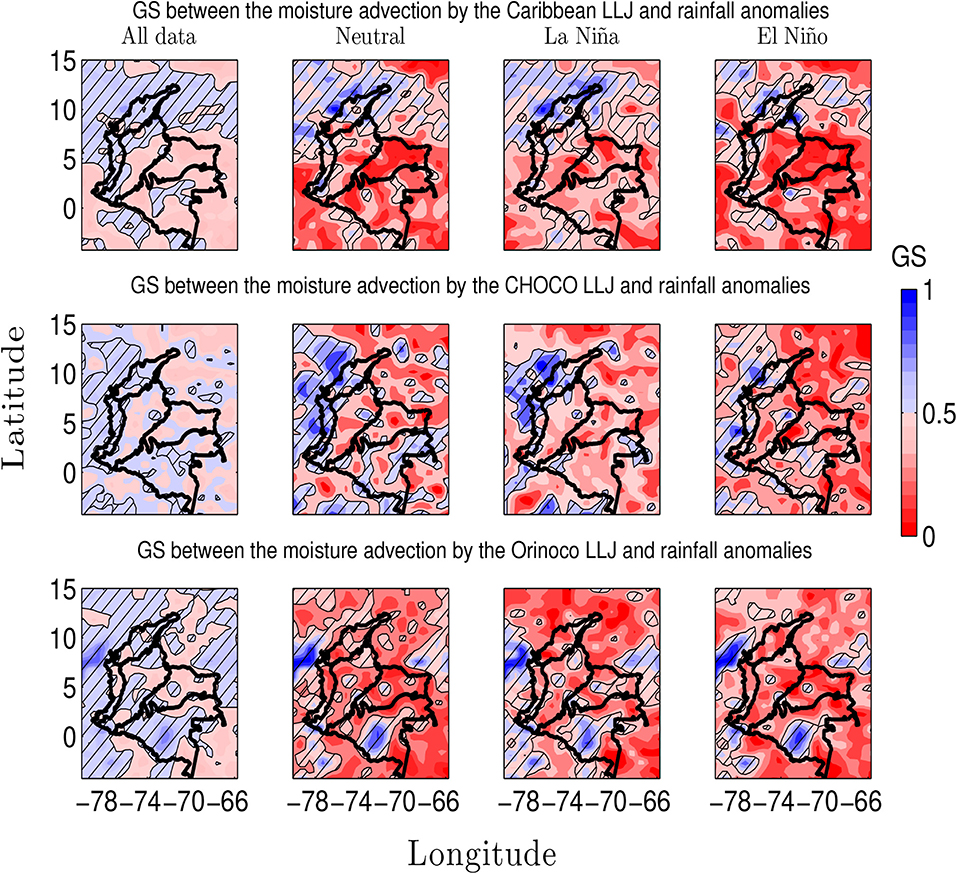
Figure 11. Generalized synchronization index between the moisture advection of the low level jets and rainfall anomalies throughout Colombia. (Top row) Caribbean LLJ. (Middle row) CHOCO LLJ. (Bottom row) Orinoco LLJ. Dataset No. 1, period 1975–2006. The hatched contours indicates zones where the GS is significant at 5%.
On the other hand, Figure 12 (top row) shows the maximum time-lags in areas of significant GS between moisture advection anomalies by the Caribbean LLJ and rainfall anomalies during the ENSO phases. During La Niña and Neutral phases, synchrony between the Caribbean LLJ moisture anomalies and rainfall anomalies in northern Colombia corresponds to time-lags between 0 and 2 months. During El Niño, such synchrony over northern Colombia occurs at time-lags between 0 and 4 months, suggesting that during El Niño, the time-lag between the Caribbean LLJ moisture anomalies and rainfall anomalies could be longer than during La Niña.
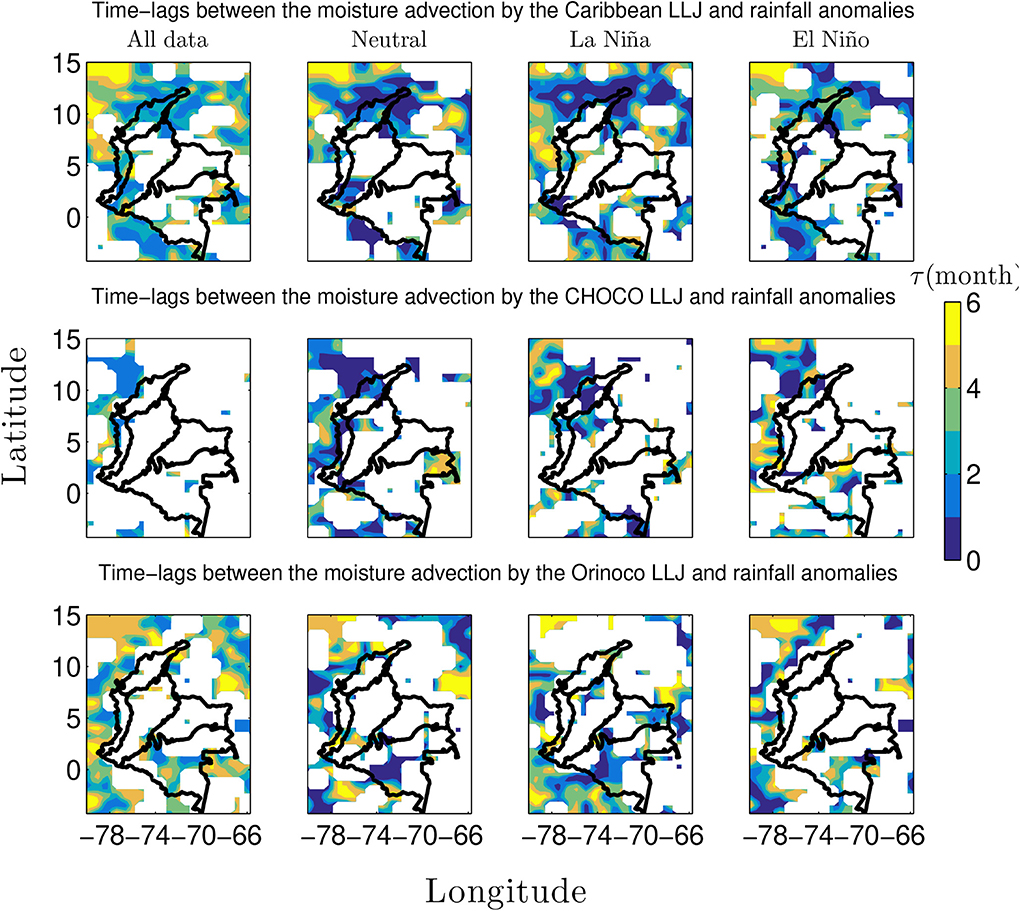
Figure 12. Time-lags between the moisture advection by the low level jets and rainfall anomalies throughout Colombia. (Top row) Caribbean LLJ. (Middle row) CHOCO LLJ. (Bottom row) Orinoco LLJ. Dataset No. 1, period 1975–2006. White indicates zones where GS is not significant at 5%.
Figure 11 (middle row) shows the GS-index between moisture advection by the CHOCO LLJ and rainfall anomalies in Colombia. Results evidence that rainfall anomalies over the entire tropical Pacific, the southern Caribbean, and the western Andean regions can be associated with moisture advection by the CHOCO LLJ. During La Niña and Neutral phases, the GS values are higher than during El Niño epochs (in most places). Furthermore, the GS-significant-areas are larger during the Neutral and El Niño than during La Niña epochs. References [36, 40, 87] argue that positive (negative) rainfall anomalies in western Colombia during La Niña (El Niño) can be explained in terms of the increasing (decreasing) moisture advection of the CHOCO LLJ as a result of the increase (decrease) in the temperature gradient between surface air temperatures over the Pacific coast off Colombia and El Niño 1+2 zone during June–July–August and September–October–November. During La Niña, positive rainfall anomalies coincide with positive moisture advection anomalies by the CHOCO LLJ, both signals exhibiting prominent peaks in the same period, which is reflected as strong GS over northwestern Colombia (see Figure 6B; Figure S12; Figure 11, middle row, third column, La Niña). In contrast, during El Niño, GS between negative rainfall anomalies and negative moisture advection by the CHOCO LLJ is weak, although GS is also significant (see Figure 11, middle row, last column, El Niño). Additionally, we also calculate GS between the sea surface temperature gradient in the previously mentioned regions and rainfall anomalies in Colombia. Our findings confirm the influence of the far-eastern Pacific SST gradient on rainfall anomalies on western Colombia and are consistent with those shown for GS between the CHOCO LLJ and SST3.4 (see Figure S1).
On the other hand, Figure 12 (middle row) shows the maximum time-lags in areas of significant GS between moisture advection anomalies by the CHOCO LLJ and rainfall anomalies during the ENSO phases. During La Niña and Neutral phases, synchrony between rainfall anomalies and the CHOCO LLJ moisture anomalies in north-western Colombia corresponds to time-lags between 0 and 2 months. During El Niño, such synchrony over north-western Colombia occurs at time-lags between 2 and 6 months, suggesting that during El Niño, the time-lag between the CHOCO LLJ moisture anomalies and rainfall anomalies could be longer than during La Niña.
Figure 11 (bottom row) shows the GS-index between moisture advection anomalies by the Orinoco LLJ and rainfall anomalies in Colombia. Our GS-analysis suggests that such positive (negative) moisture advection influences the positive (negative) hydro-climatic anomalies in the Colombian Amazon region during El Niño (La Niña), GS is moderate (strong) and the areas are larger (smaller). In contrast, these GS results can not be easily associated with rainfall anomalies in the Orinoco region (see Figures 4, 6C). Hence, these findings point out the need of further research regarding the response of the Orinoco LLJ to ENSO's phases in order to advance the understanding of hydro-climatic anomalies of these regions. Note that the Pacific coast exhibits significant GS, which need to be further investigated. Figure 12 (bottom row) shows the maximum time-lags in areas of significant GS between moisture advection anomalies by the Orinoco LLJ and rainfall anomalies during the ENSO phases. Results suggest a simultaneous relation between moisture by the Orinoco LLJ and rainfall anomalies over the Amazon region. During La Niña and Neutral phases, synchrony between rainfall anomalies and the Orinoco LLJ moisture anomalies in southern Colombia (Amazon region) corresponds to time-lags between 0 and 2 months. During El Niño, such synchrony occurs at time-lags between 2 and 4 months, suggesting that during El Niño, the time-lag between the Orinoco moisture anomalies and rainfall anomalies could be longer than during La Niña.
Figure 13 (top row) shows the GS-index between moisture advection by the Cross-Equatorial Flow (CEF) and rainfall anomalies in Colombia. Our results evidence that rainfall anomalies in the Amazon region are related to the meridional moisture advection by the CEF. Hence, our results support those presented by Wang and Fu [45] regarding the influence of the CEF over hydro-climatology of the northern Amazon River basin (southern Colombia).
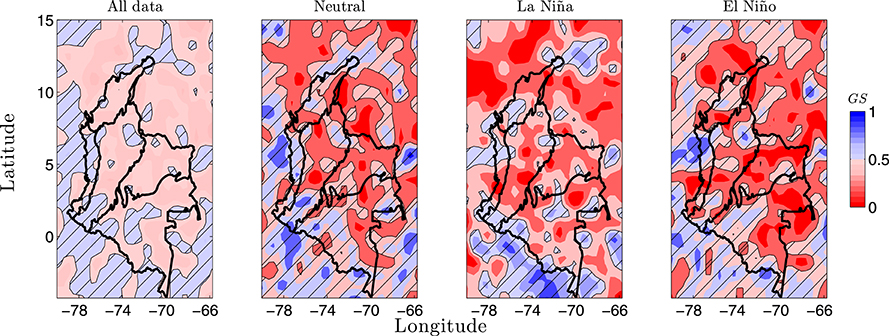
Figure 13. Generalized synchronization index between the moisture advection by the cross-equatorial flow and rainfall anomalies. Dataset No. 1, period 1975–2006. The hatched contours indicate zones where the GS is significant at 5%.
In addition, our findings show that the GS-significant-areas are larger (smaller) during El Niño (La Niña) as well as the GS is strong (weak) during La Niña (El Niño). In particular, the GS results reveal a connection between the Amazon region of Colombia (north-western most Amazon River basin) and the western Colombia Pacific coast. This result supports the recent works on aerial rivers connecting Amazonia and the Colombian Pacific [88], as well as the existence of an Atmosphere-Land Bridge between the Pacific and the tropical North Atlantic through the Amazon River basin [89, 90]. In this sense, Figure 4 does not show a clear annual cycle of rainfall anomalies in these regions (see also Figure S12). Nonetheless, Figure 6D evidences positive (negative) southerly moisture advection anomalies by the CEF during La Niña (El Niño) in the austral winter as well as negative (positive) northerly moisture advection anomalies by the CEF during La Niña (El Niño) in the austral summer. This results provide new insights on the influence of the Orinoco LLJ and the CEF winds over the Amazon region as modulators of rainfall anomalies during ENSO. The influence of the Orinoco LLJ seems to be stronger than the influence of the CEF over the Amazon region of Colombia (see Figure 11 bottom row). Moreover, our results suggest that the influence of the CEF is stronger in the Pacific region (western Colombia) than in the Amazon region of Colombia. However, further research is needed regarding the CEF dynamics during ENSO and its influence on the Orinoco and Amazon regions of Colombia. At this point, there is not clear evidence on the influence of the CEF over the Orinoco region. Additionally, the analysis of time-lags do not show clear patterns (see Figure S2, top row).
Figure 14 (left column) shows GS between the different types of El Niño indices and rainfall anomalies in Colombia using all data. These results suggest that the three indices exhibit GS with rainfall anomalies over the Caribbean, the Pacific, and the Andean regions whereas the Orinoco and the Amazon regions do not exhibit such interdependence. Furthermore, these results agree with the work by Salas et al. [31], which stated that rainfall anomalies are phase-locked with SST anomalies in the Caribbean, the Pacific, and Andean regions, whereas the Orinoco and the Amazon regions do not exhibit such phase-locking. Hence, our GS results suggest that rainfall anomalies in some regions of Colombia (the driven system) are mainly determined by ENSO (the driving system).
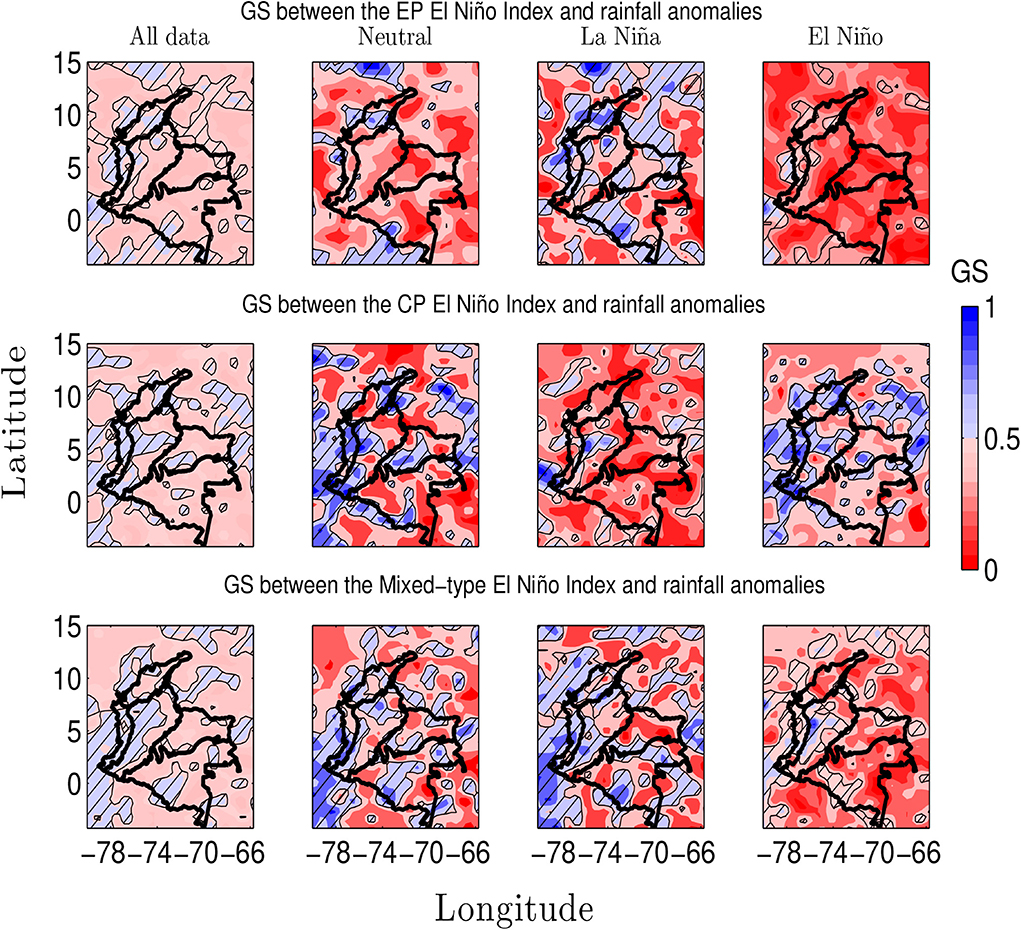
Figure 14. Generalized synchronization between indices for different types of ENSO and rainfall anomalies throughout Colombia. (Top row) Eastern Pacific (EP) El Niño type. (Middle row) Central Pacific (CP) El Niño type. (Bottom row) Mixed-type El Niño. Dataset No. 1, period 1975–2006. The hatched contours indicates zones where the GS is significant at 5%.
Additionally, we quantify GS between each index-type of ENSO and rainfall anomalies in Colombia considering the ENSO phases. We aim to characterize the GS-patterns during El Niño, La Niña and Neutral phases using the same reference periods than in previous analysis as per MEI classification (see Figure 2). Figure 14 (top row) evidences that the EP index exhibits a strong (weak) GS with rainfall anomalies in Colombia during La Niña (El Niño) over vast (small) areas of the continental Colombian territory. Figure 2A shows that during La Niña (El Niño) phase the EP index shows negative (positive) SST anomalies. This GS-result can be explained because cold (warm) SST anomalies over the Eastern Pacific produces a higher (smaller) temperature gradient between the Pacific Ocean off the Colombian coast and the El Niño 1+2 region that increase (decrease) of the moisture advection by the CHOCO LLJ [36, 40].
In contrast, Figure 14 (middle row) evidences that the CP index exhibits a strong (weak) GS with rainfall anomalies during El Niño (La Niña) phase over vast areas of the continental Colombian territory. Figure 2A evidences that during El Niño (La Niña) the EP index shows positive (negative) SST anomalies that are higher (smaller) than those experienced in the Central Pacific (Figure 2A). Hence, we hypothesize that cooling (warming) of SSTs in the far eastern tropical Pacific are more associated with higher positive (negative) rainfall anomalies in Colombia than the cooling (warming) of SSTs in the central Pacific. The cooling (warming) of SSTs in the Central Pacific seems to modulate rainfall anomalies in Colombia in different ways given that the increase (decrease) of SSTs in the central tropical Pacific are sandwiched by anomalous cooling (warming) over the eastern and western tropical Pacific, which influences the far-eastern tropical Pacific (the Pacific Ocean off the Colombian coast) and the Caribbean sea [48, 49, 91]. Hence, the characteristics of such anomalous cooling (warming) over the eastern and western portions of the Central Pacific affect the SST gradients between the Pacific Ocean off the Colombian coast and the El Niño 1+2 as well as the response in the Caribbean sea, which affects the hydro-climatic response over Colombia. This result is in agreement with the study of Navarro-Monterroza et al. [52] regarding different effects of CP and EP El Niños on rainfall anomalies in Colombia.
A similar procedure was carried out to quantify GS between the Mixed-type El Niño indices and rainfall anomalies in Colombia. Figure 14 (bottom row) evidences that the Mixed-type El Niño index exhibits strong (weak) GS with rainfall anomalies during La Niña (El Niño) in the Caribbean, the Andean and Pacific regions. These results are comparable with the GS-patterns between the SST3.4 anomalies and rainfall anomalies (see Figure 9) as expected because both, the Mixed-type El Niño Index and SST3.4 anomalies, are calculated over the same tropical Pacific zone (Niño3.4).
We analyzed time-lags between the different types of El Niño indices and hydrological (rainfall and streamflows) anomalies in Colombia but our results do not show clear evidence of synchrony or temporal propagation of spatial patterns (see Figures S5–S10).
We use Recurrence Quantification Analysis (RQA) with the aim to study features of Generalized Synchronization (GS) between ENSO and the hydrological anomalies (rainfall and streamflows) over Colombia, taking into account the uncertainty in the non-linear recurrence metrics induced by the different methods to estimate hydro-climatic anomalies (HyAns). Our results suggest that the GS quantifier based on RQA can be significantly affected when anomalies are defined on a constant climatology (HyAns–TAC method). On the other hand, the GS-metric exhibits similar magnitude for the HyAns methods that consider a non-constant annual cycle (HyAns–FAC, HyAns–SSAC, and HyAns–MAC), whereas the time-lags between signals could be sensitive to the HyAns method used.
Our findings allow us to conclude that the hydrology of Colombia exhibits GS with ENSO. Moreover, the physical mechanisms associated with such GS could be different for each region of Colombia. Our results reveal that advection of moisture by the studied Low-Level Jets (LLJs) and the Cross-Equatorial Flow are part of the physical mechanisms influencing the hydrological anomalies in Colombia during ENSO.
We identified that GS-patterns between advection of moisture by each of the three LLJs and hydrology change, in terms of magnitude and spatial distribution, depending on the phase of ENSO (La Niña and El Niño). In this sense, there are three main results, which advance our understanding about the hydrological anomalies in Colombia at interannual timescales: (i) rainfall anomalies in the Caribbean, northern-Pacific, and northern-Andean regions are mostly related with moisture advection by the Caribbean LLJ. During La Niña (El Niño), rainfall and streamflows in these regions exhibit positive (negative) anomalies, and GS is strong (weak) with the largest (smallest) areas of significant correlation; (ii) rainfall anomalies in the entire Pacific region, the southern Caribbean region, and the western Andean region can be associated with the advection of moisture by the CHOCO LLJ. During La Niña (El Niño), hydrological variables experiment positive (negative) anomalies and, GS is strong (weak) whereas the significant spatial GS-areas are small (large); (iii) rainfall anomalies in the Colombian Amazon region are correlated with the advection of moisture by the Orinoco LLJ. During La Niña (El Niño), the Amazon and Orinoco regions experience negative (positive) hydrological anomalies but only the Amazon region shows weak (strong) GS.
We provide evidence of propagation patterns over Colombia regarding the influence of the LLJs and CEF over the studied hydrological anomalies: (i) During La Niña, the Caribbean LLJ moisture anomalies exhibit synchrony with rainfall anomalies in northern Colombia at 0–2 months lags. During El Niño, the Caribbean LLJ moisture advection leads rainfall anomalies at 2–4 months lags. During Neutral and La Niña conditions, time-lags are similar. (ii) During La Niña, the CHOCO LLJ moisture anomalies exhibit synchrony with rainfall anomalies over north-western Colombia at 0–2 months lags. During El Niño, CHOCO LLJ moisture anomalies lead rainfall anomalies at 2–4 months lags. During Neutral and La Niña, time-lags are similar; (iii) the Orinoco LLJ exhibits synchrony with rainfall anomalies over the Amazon region (not so over the Orinoco region); (iv) north-western Colombia (the Caribbean region and the northern Pacific region) experiences a conjoint influence of the Caribbean LLJ and the CHOCO LLJ.
We also study the GS between the moisture advection by the Cross-Equatorial Flow (CEF) and rainfall anomalies in Colombia. Our results indicate that rainfall anomalies in the Colombian Amazon region are correlated to the CEF. During La Niña (El Niño), GS is strong (weak) whereas the GS spatial patterns are small (large). It is remarkable that our GS results reveal a connection between the Amazon region of Colombia (west-northernmost Amazon River basin) and the western Colombian Pacific coast. This result can be associated with aerial rivers connecting the Pacific and the Amazon River basin, which had been stated in several previous works [88, 90, 92]. In particular, the Orinoco LLJ exhibits stronger GS in the Amazon region of Colombia than the CEF and the analysis of time-lags do not show clear synchronous evolution of signals, which requires more research.
We quantify GS between three indices for the different types of El Niño (EP and CP) and hydrological variables in Colombia. Our results suggest a strong (weak) GS between negative (positive) SST anomalies in the Eastern Pacific and rainfall anomalies in Colombia. In contrast, our results exhibit a strong (weak) GS between positive (negative) SST anomalies in the Central Pacific and rainfall anomalies. These findings evidence a different influence of the types of ENSO on hydrologic anomalies in Colombia. Further research is needed regarding the effects of the different types of El Niño on physical mechanisms influencing Colombian hydro-climatology.
This work uses a novel approach that reveals new insights regarding the impacts of ENSO given the non-linear nature of the GS method. First-order approximation of the relation between ENSO and Colombian rainfall anomalies seems to be linear, but it is hardly the whole picture. From our analysis, we can conclude that non-linearity is also important although probably there are other ways to go deeper into this relation but this first step is an important contribution. In particular, our findings contribute to explain the hydrological anomalies over Colombia in terms of diverse physical mechanisms of moisture transport during ENSO. Furthermore, we take into account the uncertainty in the analysis with respect to different ways to define anomalies, which is a fundamental procedure to avoid biases in the interpretation of results for climatological purposes at inter-annual timescales. Notwithstanding, further research is needed regarding the seasonal spatio-temporal patterns of GS at inter-annual timescales, the differences in results considering the different flavors of ENSO, and the differences in the estimation of time-lags in relation to the HyAns methods.
Further research is needed regarding the effects of the different types of El Niño on physical mechanisms influencing Colombian hydro-climatology, e.g., How do the different types of ENSO affect the dynamics of low-levels jets surrounding Colombia? How do the different types of ENSO affect the dynamics of the Cross-Equatorial Flow from the Amazon River Basin? How do the different types of ENSO affect diverse land surface-atmosphere interactions at continental, regional, and local scales? How do synchronization patterns change with seasons? These topics are outside the scope of this investigation and need to be further investigated.
The datasets generated for this study are available on request to the corresponding author.
HS prepared the data and performed the computations. All authors designed, proposed, discussed, and analyzed the data and results. All authors wrote and reviewed the manuscript.
The work of HS was supported by COLCIENCIAS—Grant for National Doctorates 617-2 and partially funded by the Humboldt University of Berlin IRTG 1740 and Institución Universitaria Colegio Mayor de Antioquia, Project El Chorro de los Andes Orientales—CHAO—y su relación con la hidro-climatología de Colombia. The work of GP and ÓM was supported by Universidad Nacional de Colombia at Medellin. The work by NM was supported by Deutsche Forschungsgemeinschaft (DFG) GRK 2043/1 Natural risk in a changing world (NatRiskChange).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We are grateful to NOAA for NCEP/NCAR data, U.S. Geological Survey (USGS HydroSHEDS) for the Digital Elevation Models, A. F. Hurtado for the reanalysis data of Colombian precipitation, IDEAM for rainfall and streamflow data, XM for streamflow data. Recurrence analysis was carried out with the CRP Toolbox for MATLAB developed by NM and available at http://tocsy.pik-potsdam.de/CRPtoolbox.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2020.00003/full#supplementary-material
1. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge: Cambridge University Press (2001).
2. Balanov A, Janson N, Postnov D, Sosnovtseva O. Synchronization: From Simple to Complex. Heidelberg: Springer-Verlag Berlin (2009).
3. Brown R, Kocarev L. A unifying definition of synchronization for dynamical systems. Chaos. (2000) 10:344–9. doi: 10.1063/1.166500
4. Rulkov NF, Sushchik MM, Tsimring LS, Abarbanel HDI. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys Rev E. (1995) 51:980–94. doi: 10.1103/PhysRevE.51.980
5. Schiff SJ, So P, Chang T, Burke RE, Sauer T. Detecting dynamical interdependence and generalized synchrony through mutual prediction in a neural ensemble. Phys Rev E. (1996) 54:6708–24. doi: 10.1103/PhysRevE.54.6708
6. Arnhold J, Grassberger P, Lehnertz K, Elger CE. A robust method for detecting interdependences: application to intracranially recorded EEG. Phys D. (1999) 134:419–30. doi: 10.1016/S0167-2789(99)00140-2
7. Le Van Quyen M, Martinerie J, Adam C, Varela FJ. Non-linear analyses of interictal EEG map the brain interdependences in human focal epilepsy. Phys D. (1999) 127:250–66. doi: 10.1016/S0167-2789(98)00258-9
8. Quiroga RQ, Kraskov A, Kreuz T, Grassberger P. Performance of different synchronization measures in real data: a case study on electroencephalographic signals. Phys Rev E. (2002) 65:041903. doi: 10.1103/PhysRevE.65.041903
9. Zbilut J, Webber Jr C. Recurrence Quantification Analysis. New York, NY: Wiley Online Library. (2006).
10. Marwan N, Romano MC, Thiel M, Kurths J. Recurrence plots for the analysis of complex systems. Phys Rep. (2007) 438:237–329. doi: 10.1016/j.physrep.2006.11.001
11. Rosenblum MG, Pikovsky AS, Kurths J. From phase to lag synchronization in coupled chaotic oscillators. Phys Rev Lett. (1997) 78:4193–96. doi: 10.1103/PhysRevLett.78.4193
12. Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al. Detection of n: m phase locking from noisy data: application to magnetoencephalography. Phys Rev Lett. (1998) 81:3291–4. doi: 10.1103/PhysRevLett.81.329
13. Rosenblum M, Pikovsky A, Kurths J, Schäfer C, Tass PA. Phase synchronization: from theory to data analysis. Handb Biol Phys. (2001) 4:279–321. doi: 10.1016/S1383-8121(01)80012-9
14. Stolbova V, Martin P, Bookhagen B, Marwan N, Kurths J. Topology and seasonal evolution of the network of extreme precipitation over the Indian subcontinent and Sri Lanka. Nonlin Process Geophys. (2014) 21:901–17. doi: 10.5194/npg-21-901-2014
15. Malik N, Bookhagen B, Marwan N, Kurths J. Analysis of spatial and temporal extreme monsoonal rainfall over South Asia using complex networks. Clim Dyn. (2012) 39:971–87. doi: 10.1007/s00382-011-1156-4
16. Rheinwalt A, Boers N, Marwan N, Kurths J, Hoffmann P, Gerstengarbe F.-W., et al. Non-linear time series analysis of precipitation events using regional climate networks for Germany. Clim Dyn. (2016) 46:1065–74. doi: 10.1007/s00382-015-2632-z
17. Agarwal A, Marwan N, Rathinasamy M, Merz B, Kurths J. Multi-scale event synchronization analysis for unravelling climate processes: a wavelet-based approach. Nonlin Process Geophys. (2017) 24:599–611. doi: 10.5194/npg-2017-19
18. Poincaré H. Sur la probleme des trois corps et les q́quations de la dynamique. Acta Math. (1890) 13:1–271.
19. Takens F. Detecting strange attractors in turbulence. In: Rand D, Young LS, , editors. Dynamical Systems and Turbulence, Lecture Notes in Mathematics, Vol. 898. Berlin: Springer (1981). p. 366–81.
20. Sauer T, Yorke J, Casdagli AM. Embedology. J Stat Phys. (1991) 65:579–616. doi: 10.1007/BF01053745
21. Marwan N. A historical review of recurrence plots. Eur Phys J Spec Top. (2008) 164:3. doi: 10.1140/epjst/e2008-00829-1
22. Webber CL, Marwan N. Recurrence Quantification Analysis: Theory and Best Practices. Cham; Heidelberg; New York, NY; Dordrecht; London: Springer (2014).
23. Romano MC, Thiel M, Kurths J. Generalized synchronization indices based on recurrence in phase space. AIP Conf Proc. (2004) 742:330–6. doi: 10.1063/1.1846494
24. Feldhoff JH, Donner RV, Donges JF, Marwan N, Kurths J. Geometric signature of complex synchronisation scenarios. Europhys Lett. (2013) 102:3. doi: 10.1209/0295-5075/102/30007
25. Senthilkumar DV, Suresh R, Lakshmanan N, Kurths J. Global generalized synchronization in networks of different time-delay systems. Europhys Lett. (2013) 103:5. doi: 10.1209/0295-5075/103/50010
26. Suresh R, Senthilkumar DV, Lakshmanan M, Kurths J. Emergence of a common generalized synchronization manifold in network motifs of structurally different time-delay systems. Chaos Solit Fract. (2016) 93:235–45. doi: 10.1016/j.chaos.2016.10.016
27. Hobbs B, Ord A. Nonlinear dynamical analysis of GNSS data: quantification, precursors and synchronisation. Prog Earth Planet Sci. (2018) 5:36. doi: 10.1186/s40645-018-0193-6
28. Sarachik ES, Cane MA. The El Niño—Sourthern Oscillation Phenomenon. Cambridge: Cambridge University Press (2010).
29. Stein K, Timmermann A, Schneider N. Phase synchronization of the El Niño-sourthern oscillation with the annual cycle. Phys Rev Lett. (2011) 107:128501. doi: 10.1103/PhysRevLett.107.128501
30. Salas HD, Poveda G, Mesa OJ, Boers N, Kurths J. Uncertain estimation of anomalies and its importance for analysis and modeling of climate time series. Sci Rep. (Submitted).
31. Salas HD, Poveda G, Mesa OJ, Kurths J. Regional hydro-climatic anomalies in Colombia and their association with ENSO: a phase synchronization approach. J Geophys Res. (Submitted).
32. Arias PA, Martínez, Vieira SC. Moisture sources to the 2010–2012 anomalous wet season in northern South America. Clim Dyn. (2015) 45:2861–84. doi: 10.1007/s00382-014-2437-5
33. Poveda G, Mesa OJ. Feedbacks between hydrological processes in tropical South America and large-scale ocean–atmospheric phenomena. J Clim. (1997) 10:2690–702. doi: 10.1175/1520-0442(1997)010<2690:FBHPIT>2.0.CO;2
34. Poveda G, Jaramillo A, Gíl MM, Quiceno N, Mantilla RI. Seasonally in ENSO related precipitation, river discharges, soil moisture, and vegetation index in Colombia. Water Resour Res. (2001) 37:2169–78. doi: 10.1029/2000WR900395
35. Waylen P, Poveda G. El Niño-southern oscillation and aspects of western South American hydro-climatology. Hydrol Process. (2002) 16:1247–60. doi: 10.1002/hyp.1060
36. Poveda G, Álvarez DM, Rueda OA. Hydro-climatic variability over the Andes of Colombia associated with ENSO: a review of climatic processes and their impact on one of the Earth's most important biodiversity hotspots. Clim Dyn. (2010) 36:2233. doi: 10.1007/s00382-010-0931-y
37. Bedoya-Soto JM, Poveda G, Sauchyn D. New insights on land surface-atmosphere feedbacks over tropical South America at interannual timescales. Water. (2018). 10:1095. doi: 10.3390/w10081095
38. Bedoya-Soto JM, Poveda G, Trenberth KE, Vélez-Upegui JJ. Interannual hydroclimatic variability and the 2009–2011 extreme ENSO phases in Colombia: from Andean glaciers to Caribbean lowlands. Theor Appl Climatol. (2018) 135:1531–44. doi: 10.1007/s00704-018-2452-2
39. Wang C. Variability of the Caribbean Low-Level Jet and its relations to climate. Clim Dyn. (2007) 29:411–22. doi: 10.1007/s00382-007-0243-z
40. Poveda G, Mesa OJ. On the existence of Lloró (the rainiest locality on earth): enhanced ocean-land-atmosphere interaction by a low-level jet. Geophys Res Lett. (2000) 27:1675–8. doi: 10.1029/1999GL006091
41. Yepes J, Poveda G, Mejíac JF, Moreno L, Rueda C. CHOCO-JEX: a research experiment focused on the Chocó low-level jet over the far eastern Pacific and western Colombia. Bull Am Meteorol Soc. (2019) 100:779–96. doi: 10.1175/BAMS-D-18-0045.1
42. Jiménez-Sánchez G, Markowski PM, Jewtoukoff V, Young GS, Stensrud DJ. The Orinoco low-level jet: an investigation of its characteristics and evolution using the WRF model. J Geophys Res Atmos. (2019) 124:10696–711. doi: 10.1029/2019JD030934
43. Montoya G, Pelkowski J, Eslava JA. Sobre los alisios del nordeste y la existencia de una corriente en el Piedemonte Oriental Andino. Rev Acad Colomb Cienc. (2001) 25:363–70. Available online at: http://www.accefyn.com/revista/vol_25.htm
44. Torrealba E, Amador J. La corriente en chorro de bajo nivel de los Llanos Venezolanos de Sur América. Rev Climatol. (2010) 10:1–20. Available online at: http://hdl.handle.net/10669/76170
45. Wang H, Fu R. Cross-equatorial flow and seasonal cycle of precipitation over South America. J Clim. (2002) 15:1591–608. doi: 10.1175/1520-0442(2002)015<1591:CEFASC>2.0.CO;2
46. Sullivan A, Luo JJ, Hirst AC, Bi D, Cai W, He J. Robust contribution of decadal anomalies to the frequency of central-Pacific El Niño. Sci Rep. (2016) 6:38540. doi: 10.1038/srep38540
47. Andreoli RV, de Oliveira SS, Kayano MT, Viegas J, de Souza RAF, Candido LA. The influence of different El Niño types on the South American rainfall. Int J Climatol. (2017) 37:1374–90. doi: 10.1002/joc.4783
48. Ashok K, Behera SK, Rao SA, Weng H, Yamagata T. El Niño Modoki and its possible teleconnection. J Geophys Res. (2007) 112:1–27. doi: 10.1029/2006JC003798
49. Ashok K, Yamagata T. The El Niño with a difference. Nature. (2009) 461:481–4. doi: 10.1038/461481a
50. Córdoba-Machado S, Palomino-Lemus R, Gámiz-Fortis SR, Castro-Díez Y, Esteban-Parra MJ. Assessing the impact of El Niño Modoki on seasonal precipitation in Colombia. Glob Planet Change. (2015) 124:41–61. doi: 10.1016/j.gloplacha.2014.11.003
51. Córdoba-Machado S, Palomino-Lemus R, Gámiz-Fortis SR, Castro-Díez Y, Esteban-Parra MJ. Influence of tropical Pacific SST on seasonal precipitation in Colombia: prediction using El Niño and El Niño Modoki. Clim Dyn. (2015) 44:1293–310. doi: 10.1007/s00382-014-2232-3
52. Navarro-Monterroza E, Arias PA, Vieira SC. El Niño-southern oscillation Modoki and its effects on the spatiotemporal variability of precipitation in Colombia. Rev Acad Colomb Cienc Ex Fis Nat. (2019) 43:120–32. doi: 10.18257/raccefyn.704
53. Serna LM, Arias PA, Vieira SC. The Choco and Caribbean low-level jets during El Niño and El Niño Modoki events. Rev Acad Colomb Cienc Ex Fis Nat. (2018) 42:410–21. doi: 10.18257/raccefyn.705
54. Gill AE. Some simple solutions for heat-induced tropical circulation. Quart J R Met Soc. (1980) 106:447–62. doi: 10.1002/qj.49710644905
55. Martin ER, Schumacher C. The caribbean low-level jet and its relationship with precipitation in IPCC AR4 models. J Clim. (2011) 24:5935–50. doi: 10.1175/JCLI-D-11-00134.1
56. Wolter K, Timlin MS. Measuring the strength of ENSO events—how does 1997/1998 rank? Weather. (1998) 53:315–24. doi: 10.1002/j.1477-8696.1998.tb06408.x
57. Rasmusson E, Carpenter T. Variations in tropical sea surface temperature and surface winds fields associated with the Southern Oscillation/El Niño, Mon Weather Rev. (1982) 110:354–84. doi: 10.1175/1520-0493(1982)110<0354:VITSST>2.0.CO;2
58. Trenberth K, Stepaniak D. Indices of El Niño evolution. J Clim. (2001) 14:1697–701. doi: 10.1175/1520-0442(2001)014<1697:LIOENO>2.0.CO;2
59. Hurtado-Montoya A, Mesa OJ. Reanalysis of monthly precipitation fields in Colombian territory. Dyna. (2014) 81:251–8. doi: 10.15446/dyna.v81n186.40419
60. Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, et al. The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc. (1996) 77:437–71. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2
61. Eckmann JP, Kamphorst SO, Ruelle D. Recurrence plots of dynamical systems. Europhys Lett. (1987) 4:973–7. doi: 10.1209/0295-5075/4/9/004
62. Packard NH, Crutchfield JP, Farmer JD, Shaw RS. Geometry from a time series. Phys Rev Lett. (1980) 45:712–6. doi: 10.1103/PhysRevLett.45.712
63. Fraser AM, Swinney HL. Independent coordinates for strange attractors from mutual information. Phys Rev A. (1986) 33:1134–40. doi: 10.1103/PhysRevA.33.1134
65. Marwan N. How to avoid potential pitfalls in recurrence plot based data analysis. Int J Bifurc Chaos. (2011) 21:1003–17. doi: 10.1142/S0218127411029008
66. Mindlin GM, Gilmore R. Topological analysis and synthesis of chaotic time series. Phys D. (1992) 58:229–42. doi: 10.1016/0167-2789(92)90111-Y
67. Zbilut JP, Webber CL Jr. Embeddings and delays as derived from quantication of recurrence plots. Phys Lett A. (1992) 171:199–203. doi: 10.1016/0375-9601(92)90426-M
68. Romano MC, Thiel M, Kurths J, Von Bloh W. Multivariate recurrence plots. Phys Lett. (2004) 330:214–23. doi: 10.1016/j.physleta.2004.07.066
69. Marwan N, Zou Y, Wessel N, Riedl M, Kurths J. Estimating coupling directions in the cardiorespiratory system using recurrence properties. Philos Trans R Soc A. (2013) 371:20110624. doi: 10.1098/rsta.2011.0624
70. Thiel M, Romano MC, Kurths J, Rolfs M, Kliegl R. Twin surrogates to test for complex synchronisation. Europhys Lett. (2006) 75:535–41. doi: 10.1209/epl/i2006-10147-0
71. Thiel M, Romano MC, Kurths J, Rolfs M, Kliegl R. Generating surrogates from recurrences. Philos Trans R Soc A Math Phys Eng Sci. (2008) 366:545–57. doi: 10.1098/rsta.2007.2109
73. Abdi H. Bonferroni and Šidák corrections for multiple comparisons. In: Salkind NJ, , editor. Encyclopedia of Measurement and Statistics. Thousand Oaks, CA: Sage. (2007).
74. Douglass DH. The Pacific sea surface temperature. Phys Lett. (2011) 376:128–35. doi: 10.1016/j.physleta.2011.10.042
75. Douglass DH, Knox RS. The sun is the climate pacemaker I. Equatorial Pacific Ocean temperatures. Phys Lett. (2015) 379:823–9. doi: 10.1016/j.physleta.2014.10.057
76. Arango-Ruda E, Poveda G. Efectos de El Niño y La Niña sobre la hidrología de la Amazonia colombiana. Colomb Amazón. (2018) 11:33–58. doi: 10.17533/udea.boan.v33n55a01
77. Afyouni S, Smith SM, Nichols TE. Effective degrees of freedom of the Pearson's correlation coefficient under autocorrelation. Neuroimage. (2019) 199:609–25. doi: 10.1016/j.neuroimage.2019.05.011
78. Bonner WD. Climatology of the low level jet. Mon Weather Rev. (1968) 96:833–50. doi: 10.1175/1520-0493(1968)096<0833:COTLLJ>2.0.CO;2
79. Stensrud DJ. Importance of low-level jets to climate: a review. J Clim. (1996) 9:1698–711. doi: 10.1175/1520-0442(1996)009<1698:IOLLJT>2.0.CO;2
80. Gimeno L, Dominguez F, Nieto R, Trigo R, Drumond A, Reason CJC, et al. Major mechanisms of atmospheric moisture transport and their role in extreme precipitation events. Annu Rev Environ Resour. (2016) 41:117–41. doi: 10.1146/annurev-environ-110615-085558
81. Hoyos I, Dominguez F, Cañón-Barriga J, Martínez JA, Nieto R, Gimeno L, et al. Moisture origin and transport processes in Colombia, northern South America. Clim Dyn. (2017) 50:971–90. doi: 10.1007/s00382-017-3653-6
82. Poveda G, Mesa OJ. The extreme phases of ENSO (El Niño and La Niña) y its influence on the Colombian hydrology. Ingen Hidrául Méx. (1996) XI:21–37.
83. Ahdesmäki M, Lähdesmäki H, Pearson R, Huttunen H, Yli-Harja O. Robust detection of periodic time series measured from biological systems. BMC Bioinformatics. (2005) 6:117. doi: 10.1186/1471-2105-6-117
84. Troch PA, Carrillo G, Sivapalan M, Wagener T, Sawicz K.Climate-vegetation-soil interactions and long-term hydrologic partitioning: signatures of catchment co-evolution. Hydrol Earth Syst Sci. (2013) 17:2209–17. doi: 10.5194/hess-17-2209-2013
85. Andrés-Doménech I, García-Bartual R, Montanari A, Marco JB. Climate and hydrological variability: the catchment filtering role. Hydrol Earth Syst Sci. (2015) 19:379–87. doi: 10.5194/hess-19-379-2015
86. Muñoz E, Bussalacchi AJ, Nigam S, Ruiz-Barradas A. Winter and summer structure of the Caribbean low-level jet. J Clim. (2007) 21:1260–76. doi: 10.1175/2007JCLI1855.1
87. Rueda OA, Poveda G. Space-time variability of the CHOCO jet and its effect on the Colombian Pacific coast hydroclimatology. Meteorol Colomb. (2006) 10:132–45.
88. Sakamoto MS, Ambrizzi T, Poveda G. Moisture sources and life cycle of convective systems over western Colombia. Adv Meteorol. (2012) 2011:1–11. doi: 10.1155/2011/890759
89. García-Serrano J, Cassou C, Douville H, Giannini A, Doblas-Reyes FJ. Revisiting the ENSO teleconnection to the tropical North Atlantic. J Clim. (2017) 30:6945–57. doi: 10.1175/JCLI-D-16-0641.1
90. Builes-Jaramillo A, Ramos AMT, Poveda G. Atmosphere-land bridge between the Pacific and tropical North Atlantic SST's through the Amazon river basin during the 2005 and 2010 droughts. Chaos. (2018) 28:085705. doi: 10.1063/1.5020502
91. Weng H, Behera SK, Yamagata T. Anomalous winter climate conditions in the Pacific rim during recent El Niño Modoki and El Niño events. Clim Dyn. (2009) 32:663–74. doi: 10.1007/s00382-008-0394-6
Keywords: recurrence quantification analysis, ENSO, tropical rainfall, streamflows, interdependence, hydro-climatic anomalies
Citation: Salas HD, Poveda G, Mesa ÓJ and Marwan N (2020) Generalized Synchronization Between ENSO and Hydrological Variables in Colombia: A Recurrence Quantification Approach. Front. Appl. Math. Stat. 6:3. doi: 10.3389/fams.2020.00003
Received: 30 May 2019; Accepted: 12 February 2020;
Published: 25 March 2020.
Edited by:
Peter Ashwin, University of Exeter, United KingdomReviewed by:
Xinsong Yang, Chongqing Normal University, ChinaCopyright © 2020 Salas, Poveda, Mesa and Marwan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hernán D. Salas, aGRzYWxhc0B1bmFsLmVkdS5jbw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.