
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat. , 14 January 2020
Sec. Mathematics of Computation and Data Science
Volume 5 - 2019 | https://doi.org/10.3389/fams.2019.00067
This article is part of the Research Topic Artificial Intelligence in Insurance and Finance View all 12 articles
Word embeddings have introduced a compact and efficient way of representing text for further downstream natural language processing (NLP) tasks. Most word embedding algorithms are optimized at the word level. However, many NLP applications require text representations of groups of words, like sentences or paragraphs. In this paper, we propose a supervised algorithm that produces a task-optimized weighted average of word embeddings for a given task. Our proposed text embedding algorithm combines the compactness and expressiveness of the word-embedding representations with the word-level insights of a BoW-type model, where weights correspond to actual words. Numerical experiments across different domains show the competence of our algorithm.
Word embeddings, or a learned mapping from a vocabulary to a vector space, are essential tools for state-of-the-art Natural Language Processing (NLP) techniques. Dense word vectors, like Word2Vec [1] and GLoVE [2], are compact representations of a word's semantic meaning, as demonstrated in analogy tasks [3] and part-of-speech tagging [4].
Most downstream tasks, like sentiment analysis and information retrieval (IR), are used to analyze groups of words, like sentences or paragraphs. For this paper, we refer to this more general embedding as a “text embedding.”
In this paper we propose a supervised algorithm that produces embeddings at the sentence-level that consist on an weighted average of an available pre-trained word-level embedding. The resulting sentence-level embedding is optimized for the corresponding supervised learning task. The weights that the proposed algorithm produces can be use to estimate the importance of the words with respect to the supervised task. For example, when classifying movie reviews into one of two classes: action movies or romantic movies, words like “action,” “romance,” “love,” and “blood,” will get precedence over words, like “movie,” “i,” and “theater.” This leads to the shifting of the text-level vector toward words with larger weights, as can be seen in Figure 1.
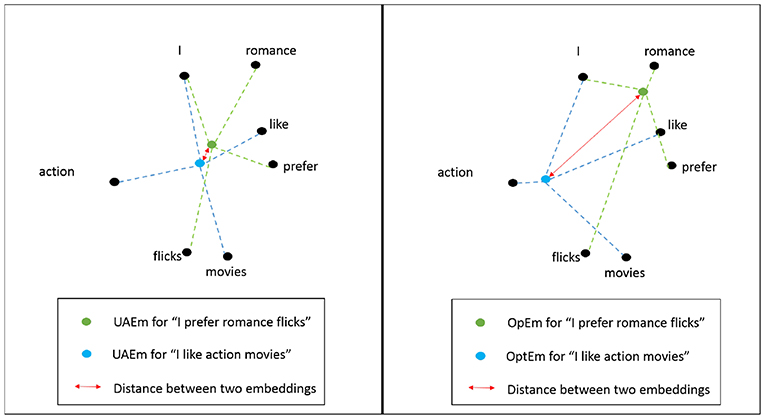
Figure 1. Unweighted (UAEm) (left) and Optimal embeddings (OptEm) (right) of two movie reviews in feature space. Distance between the two reviews increases for OptEm representation of the text.
When we use an unweighted averaged word embedding (UAEm) [5] for representing the two reviews, we see that all the words get the same importance, due to which the reviews—“I like action movies” and “I prefer romance flicks”—end up close to each other in the vector space. Our algorithm, on the other hand, identifies “romance” and “action” as two important words in the vocabulary for the supervised task, and assigns weights with high absolute value to these words. This leads to shifting of the representation of the two reviews toward their respective important words in the vector space, increasing the distance between them. This indicates that, for the task of differentiating an action movie review from a romantic movie review, our algorithm produces a representation at the review level more adequate for discriminating between the two kinds of reviews.
Our algorithm has many advantages over simpler text embedding approaches, like bag-of-words (BoW) and the averaged word-embedding schemes discussed in section 2. In section 4, we show results from experiments on different datasets. In general, we observed that our algorithm is competitive with other methods. Unlike the simpler algorithms, our approach finds a task-specific representation. While BoW and some weighting schemes, like tf-idf, rely only on word frequencies to determine word importance, our algorithm computes how important the word is to a specific task. We believe that for some applications, this task-specific representation is important for performance; one would expect the importance of words to be very different whether you are trying to do topic modeling or sentiment analysis.
It is important to note that other deep-learning-based approaches for text classification also implicitly optimize the text-level representation from word-level embedding in the top layers of the neural network. However, in order to train such models large datasets are needed. Our empirical results show that our proposed representation is in general competitive with traditional deep learning based text classification approaches and outperforms them when the training data is relatively small.
Additionally, by generating importance weights to each one of the words in the vocabulary, our algorithm yields a more interpretable result than looking at the weights corresponding to the word-embedding dimensions that have no human-interpretable meaning. Effectively, our text embedding algorithm combines the compactness and expressiveness of the word-embedding representations with the human-interpretability of a BoW-type model.
Furthermore, in contrast with some deep-learning-based approaches, our approach does not impose constraints or require special processing (trimming, padding) with respect to the length of the sentence or text to be classified. In summary, we can summarize the contributions of the paper as follows:
• Our algorithm provides a task optimized text embedding from word level embeddings.
• Our algorithm outperforms other more complex algorithms when training data is relatively small in size.
• Our algorithm can be implemented by leveraging existing libraries in a trivial way as it only requires access to a SVM implementation.
• Our resulting task specific text embedding are as compact as the original word level embedding while providing word level insights similar to a BOW type model.
The rest of the paper is organized as follows: in section 2, we discuss related work. Later, in section 3, we present a detailed explanation and mathematical justification to support our proposed algorithm. In section 4, we present and described our proposed algorithm.
Various representation techniques for text have been introduced over the course of time. In the recent years, none of these representations have been as popular as the word embeddings, such as Word2Vec [1] and GLoVE [2], that took contextual usage of words into consideration. This has led to very robust word and text representations.
Text embedding has been a more challenging problem over word embeddings due to the variance of phrases, sentences, and text. Le and Mikolov [6] developed a method to generate the embeddings that outperforms the traditional bag-of-words approach [7]. More recently, deeper neural architectures have been developed to generate these embeddings and to perform text classification tasks [8] and some of these architectures involve sequential information of text, such as LSTMs [9], BERT [10], and XLNET [11]. Furthermore, recently developed attention models can also provide insights about word importance, however they require large amounts of training data.
Methods have been developed that use word embeddings to generate text embeddings without having to train on whole texts. These methods are less costly than the ones that train directly on whole text, and can be implemented faster.
Unweighted average word embedding [5] generated text embeddings by computing average of the embeddings of all the words occurring in the text. This is one of the most popular methods of computing text embeddings from trained word embeddings, and, though simple, has been known to outperform the more complex text embedding models especially in out-of-domain scenarios. Arora et al. [12] provided a simpler method to enhance the performance of text embedding generated from simple averaged embedding by the application of PCA.
The unsupervised text embedding methods face the problem of importance-allocation of words while computing the embedding. This is important, as word importance determines how biased the text embedding needs to be toward the more informative words. DeBoom et al. [13] introduced a method that would assign importance to the words based on their tf-idf scores in the text.
Our method generates weights based on the importance of the words perceived through a supervised approach. We use classifiers to determine the weights of the words based on their importance captured through the procedure. The advantage of this method over other methods is that we keep the simplicity of Wieting's algorithm [5], while incorporating the semantically agreeable weights for the words.
A sentence, paragraph, or document can be represented using a given word-level embedding (wle) as follows:
where,
• is a vectorial representation or embedding at the sentence, text or document level (we will refer it as tle in rest of the paper) of ith sample;
• we will assume that Ai is the ith row of a matrix A ∈ Rm×n containing a collection of m documents, k is the number of words in the wle corpus V;
• λj ∈ R is a weighting factor associated with the jth word vj ∈ V. Note that for the widely used averaged tle (text2vec) representation [5], λj = 1, ∀j;
• δij is a normalized occurrence count. It is the number of times jth word appears in the document i divided by the total number of words in the document i.
Our proposed algorithm assumes that we have a supervised classification problem for which we want to find an optimal representation at the document (text) level from the word embeddings.
More concretely, we consider the problem of classifying m points in the n-dimensional real space Rn, represented by the m × n matrix A, according to membership of each point Ai in the classes +1 or −1 as specified by a given m × m diagonal matrix D with ones or minus ones along its diagonal.
In general, this linear classification problem can formulated as follows:
where,
• e ∈ ℝm×1 is a column of ones;
• y ∈ ℝm×1 is a slack vector;
• (w, γ) ∈ ℝ(n+1) ×1 represents the separating hyperplane.
• L is a loss function that is used to minimize the misclassification error.
• R is a regularization function used to improve generalization.
• c is a constant that controls the trade-off between error and generalization.
Note that, if L(.)= and R(.)=, then Equation (2) corresponds to an SVM formulation [14]. The corresponding unconstrained convex optimization problem is given as:
which we will denote by
From (1), we can rewrite A as:
That is,
where Δ ∈ ℝm×k; is a matrix of occurrences count with δij in the (i, j) position. , and V ∈ ℝk×n is the matrix whose rows are all the word2vec vectors considered in the word2vec corpus or dictionary.
From (3) and (6),
where λ = (λ1, …, λk).
Formulation (7) is a biconvex optimization problem, which can be solved using alternate optimization [15]. By solving this problem, not only do we obtain an SVM-type classifier, but also learn the optimal importance weights for each word in our corpus (λ1, …, λk) which can be used to interpret classification results for the specific tasks at hand. Though we could have restricted the λi to be positive, we choose to leave them unconstrained in order to make our algorithm more scalable and computationally efficient. Another interesting consideration would be to add a relative importance constrained on addition to the non-negativity bounds of the form:
but again, we choose not to for computationally efficiency. We will explore this option in the future.
In (7), if we fix Λ to a constant , we have:
We can obtain the corresponding optimal solution for (w, γ) by solving (w∗, γ∗) = SVM(Ã, D, c).
On the other hand, if we fix , we get
where .
Similarly, from (7) and (10) and making , we have
since is a constant.
We can obtain an approximate optimal (λ, γ) by solving . Note that this solution will consider a regularization term for λ.
We are ready now to describe our proposed alternate optimization (AO) algorithm to solve formulation (7).
One of the advantages of the algorithm is that it can be easily implemented by using existing open-source SVM libraries, like the ones included in scikit-learn [16] or a more recent GPU-based fast SVM implementation like ThunderSVM [17].
The optimal text embedding algorithm, then, inherits the convergence properties and characteristics of the AO problems [15]. It is important to note that the set of possible solutions to which Algorithm 1 can converge can include certain type of saddle points (i.e., a point that behaves like a local minimizer only when projected along a subset of the variables). However, it is stated in the paper [15] that it is extremely difficult to find examples where converge occurs to a saddle point rather than to a local minimizer.
In order to further reduce the computational complexity of the proposed algorithm, we can consider a simplified loss function L(.)= and R(.)=. Then formulation (7) becomes the corresponding unconstrained convex optimization problem:
Fixing , from (9) and (12), we have
This formulation corresponds to a least-squares or Proximal SVM formulation [18, 19], and its solution can be obtained by solving a simple system of linear equations. We will denote formulation (13) by
If then the solution to (13) is given by
On the other hand, fixing , we have
since is a constant. Hence,
Furthermore,
From (17) and (18),
For some problems, ΔTΔ can be ill-conditioned, which may lead to incorrect values for λ. In order to improve conditioning we add a Tikhonov regularization perturbation [20]. (19) becomes
where ϵ is a very small value.
Note that (ΔTΔ + ϵI)−1 involves calculating the inverse of a k × k matrix, where k is the number of words in the word2vec dictionary. In some cases, k can be much larger than m, the number of training set examples. If this is the case, we can use the Sherman-Morrison-Woodbury formula [21]:
with Z = ϵI, u = v = ΔT. Then (ΔTΔ + ϵI)−1 becomes
which involves inverting an m × m matrix with m << k.
The λ we obtained is a vector of weights of the words that would be used in (1) to calculate text2vec of a given sample.
Algorithm 1 can be modified to consider formulation (3) instead of (13) by making two simple changes:
1. Substitute line 6 of Algorithm 1 by: Solve Equation (15) to obtain (wi, γ);
2. Substitute line 8 of Algorithm 1 by: Solve Equation (19) to obtain λi;
We used binary classification as the task for evaluating our algorithm performance by comparing it to the following methods:
1. UAEm: Unweighted average of the word vectors that comprise the sentence or document [5].
2. WAEm: Weighted averaged text representations. We computed WAEm using tf-idf coefficients as the weights as described in De Boom et al. [13].
3. FastText [22], an open-source, free, library that allows users to learn text representations and text classifiers. The classifiers are based in a simple shallow model instead of deep one which allows the framework to train models in a fast manner.
4. AdvCNN [8] is a CNN based deep network which comprises of parallel convolutional layers with varying filter widths and it achieves state-of-the-art performance on sentiment analysis and question classification.
5. VanillaCNN is a custom CNN architecture we designed and is similar to Kim [8] except that in this case there is only one convolutional layer instead of parallel layers.
Note that in both the CNN experiments we have initialized the embedding layer with pre-trained word2vec models and these vectors are kept static.
We implemented two versions of our Algorithm 1: SVM-based (SVM-OptEm) (Formulation 3) and least square SVM-based (LSSVM-OptEm) (Formulation 12).
In SVM-OptEm, we used a support vector machine (SVM) [23] as the classifier. We used a scikit-learn [24] implementation of SVM for the experiments.
In LSSVM-OptEm, we used a least square support vector machine (LS-SVM) [23] as the classifier.
To showcase the performance of our model, we chose fifteen different binary classification tasks over the subsets of different datasets. Twelve public datasets are briefly described in Table 1.
We also performed experiments on three datasets belonging to the insurance domain.
• BI-1 and BI-2: These datasets consist of the claim notes with binary classes based on topic of phone conversation. These notes were taken by call representative of the company after the phone call was completed. For BI-1, we classified the call notes into two categories based on claim complexity: simple and complex. For BI-2, we wanted to identify notes that documented a failed attempt made by the call representative to get in touch with the customer. It is important to note that the corpus is same for these two datasets but the classification task is different.
• TRANSCRIPTS: These datasets consist of the phone transcripts with two classes: pay-by-phone calls and others. These transcripts were generated inside the company for the calls received at the call center. Each call would be assigned a class based on the purpose of the call.
We chose to work on different word2vec-based word embeddings. These word embeddings have either been pre-trained models or in-house trained models. These embeddings were used on the datasets based on their contextual relevance.
• wikipedia [38]: The skip-gram model was trained on English articles in Wikipedia by FastText [39].
• google-news [40]: The model was trained on Google News Data, and is available on the Google Code website [41].
• amzn: The skip-gram model was trained in-house on amazon reviews [27, 28]. Gensim [42] was used to train the model.
• yelp: The skip-gram model was trained in-house on yelp reviews [37]. Gensim was used to train the model.
• transcript: The continuous bag-of-words model was trained in-house on the transcripts generated in the of the calls from call centers. Gensim was used to train the model over approximately 3 million transcripts.
• claim-notes: The continuous bag-of-words model was trained in-house on the notes taken by call representatives after the call was completed. C-based code from Google Word2vec website [41] was used to train the model over approximately 100 million notes.
We used different word2vec models to verify that our models works well independently of the underlying embedding representation. Moreover, it also gives better contextual representation of words for these datasets.
The method of processing employed on text was similar to the one done for training the word2vec models. This ensured the consistency of word-occurrence in the dataset in lieu to the model that would be used for mapping the words.
Different word2vec models had different processing procedures, such as substitutions based on regular expressions, removal of non-alphabetical words, and lowercasing the text. Accordingly, text-processing was done for the training data.
To compare performance of the algorithms tested, we decided to use area under curve (AUC) for evaluation. This metric was chosen in order to remove the possibility of unbalanced datasets affecting the efficacy of the accuracy of the models.
The performance of our models for the experiments can be seen in Table 2.
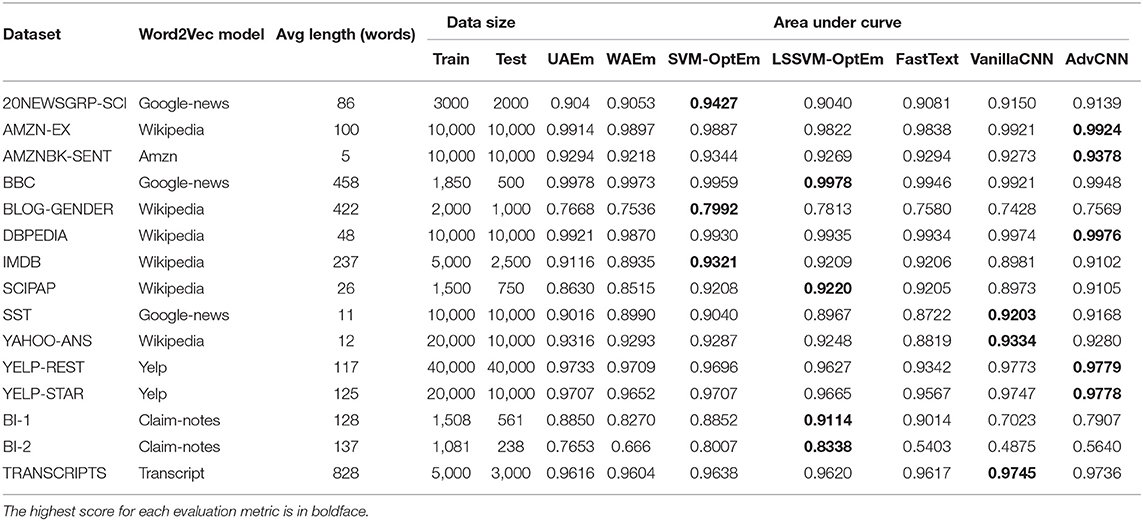
Table 2. Binary text classification AUC and accuracy results for test data for: UAEm, WAEm, VanillaCNN, AdvCNN, the SVM-based implementation (SVM-OptEm) and the least square SVM-based implementation (LSSVM-OptEm).
Our algorithm provides better or comparable performance against UAEm and WAEm. This performance is achieved over multiple iterations, as seen in Figure 2. The number of iterations required to reach the best performance for our model varies with the dataset and training size.
It is important to note that our proposed algorithm tends to achieve better AUC performance when the training data is small which it is the case for many scenarios in the insurance domain where labels are difficult and expensive to obtain. This fact make the algorithm a good choice for active learning frameworks where labels are scarce specially at early iterations of such approaches.
In general, our algorithm approached an “equilibrium” stage for the vector λ, as seen in Figure 3. In other words, as the algorithm iterate, the norm of the difference between the current weights and the weights from the previous iteration of the words approaches zero. This behavior is seen consistently for all the experimental cases. This shows that our algorithm exhibits good convergence behavior as expected.
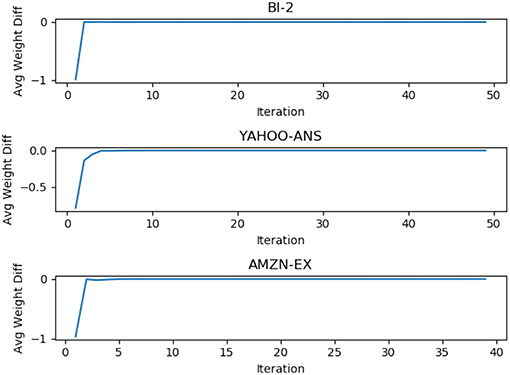
Figure 3. Average of weight difference over iteration for three datasets. This difference approaches zero over iterations.
One of the advantages our model holds over UAEm and WAEm is that our model can be used to extract the most important words in the training set. As our model reconfigures the weights of the words at each iteration, it also indirectly reassigns the degree of importance to these words. We can obtain these words by taking the absolute values of the weights assigned to these words at the end of the iteration. This information can be used for improving different algorithms, such as visual representation of text and topic-discovery, and as features for other models.
Figure 4 shows weights of top 15 words for three of our datasets. Weights assigned to the words are based on the role they play in helping the classifier determine the class of any given sample.
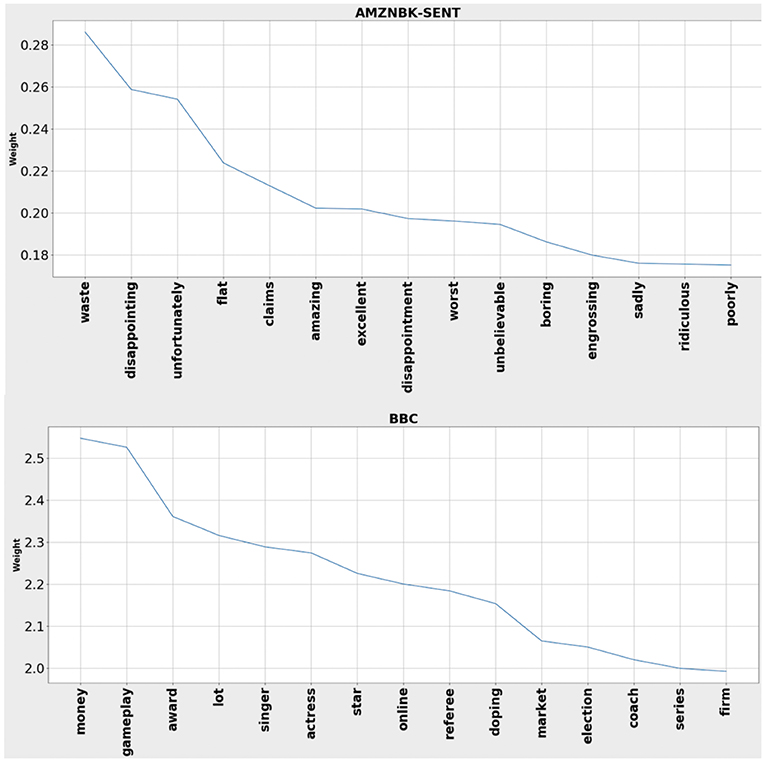
Figure 4. Weights of top 15 words identified by OptEm for two of the datasets used in our experiments. The words appear to be very informative; some can be easily associated to corresponding class.
Table 3 shows the top 10 words for three of our datasets. The words are determined by taking the absolute value of the weights i.e., λ* learned from the algorithm and rank them in descending order. For a human eye, these words clearly makes sense with respect to the given classification task. For example,
1. AMZN-EX classification task is to predict items belonging to eletronics category based on reviews.
2. YAHOO-ANS classification task is to predict health related questions.
3. DBPEDIA classification task is to predict artistic articles.
We also found that words that are least informative about the given task have weights(λ*) close to zero.
Following our results presented in Table 2, we want to highlight the following observations:
• Our method is competitive with more sophisticated models. As a matter of fact, we are winning on 7 out of 15 text classification tasks from various domains.
• Our method seems to significantly outperform other approaches when the dataset size is relatively small in size. This might be very relevant in situations where labeling data is expensive to obtain which is often the case in many industrial applications.
Our paper provides an alternative way of sentence/document-level representation for supervised text classification, based on optimization of the weights of words in the corresponding text to be classified. This approach takes labels into consideration when generating optimal word's weights for these words. Numerical experiments show that our proposed algorithm is competitive with respect with other state-of-the-art techniques and outperformed CNNs when the training data was small and we even show that this approach is not sensitive to document lengths.
Our model also brings additional benefits to the table. It provides a ranking of the relevance of the words with respect to the text classification problem at hand. This ranking of words by importance can be used for different NLP applications related to the same task, such as extraction-based summarization, context-matching, and text cleaning. By learning the optimal weights of the words, our model also tends to remove or ignore less informative words, thus performing its own version of feature selection. Our text embedding algorithm combines the compactness and expressiveness of the word-embedding representations with the human-interpretability of a BoW-type model.
We intend to extend this work to make the proposed algorithm more scalable in order to incorporate larger, more complex classification models and tasks, such as multi-label, multi-class classification and summarization.
We want to explore using other normalizations and constraints to the weight vector. One possibility is to explore 1-norm regulation for the weight vector to make it more sparse and have a more aggressive feature (word) selection. Another interesting direction is to consider group regularization similar [43], where the groups of words are suggested by a graph naturally defined by the distances between the words provided by the word embedding. In this way, semantically similar words would be weighted similarly and the result of the algorithm would be a clustering of terms by semantic meaning or topics that are relevant to the classification problem at hand.
The datasets generated for this study are available on request to the corresponding author.
GF was the technical advisor and the central figure for driving this project to completion. SG was responsible for running all the initial set of experiments and dataset preparation. TK was responsible for finishing all of the remaining experiments and manuscript writing. DC was part of research discussions and brainstorming.
Authors were employed by the company American Family Insurance. The authors declare that this study received funding from American Family Insurance. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
1. Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space. In: Proceedings of ICLR Workshop. Scottsdale, AZ (2013).
2. Pennington J, Socher R, Manning CD. GloVe: global vectors for word representation. In: Empirical Methods in Natural Language Processing (EMNLP) (2014). p. 1532–43. Available online at: http://www.aclweb.org/anthology/D14-1162
3. Levy O, Goldberg Y. Linguistic regularities in sparse and explicit word representations. In: CoNLL. Ann Arbor, MI (2014).
4. Lin C, Ammar W, Dyer C, Levin LS. Unsupervised POS induction with word embeddings. CoRR. (2015) abs/1503.06760. Available online at: http://arxiv.org/abs/1503.06760.
5. Wieting J, Bansal M, Gimpel K, Livescu K. Towards universal paraphrastic sentence embeddings. CoRR. abs/1511.08198 (2015).
6. Le Q, Mikolov T. Distributed representations of sentences and documents. In: Proceedings of the 31st International Conference on International Conference on Machine Learning - Volume 32. ICML'14. (2014). p.II–1188–II–1196. Available online at: http://dl.acm.org/citation.cfm?id=3044805.3045025
8. Kim Y. Convolutional neural networks for sentence classification. arXiv preprint arXiv:14085882. (2014). doi: 10.3115/v1/D14-1181
9. Palangi H, Deng L, Shen Y, Gao J, He X, Chen J, et al. Deep sentence embedding using long short-term memory networks: analysis and application to information retrieval. IEEE/ACM Trans Audio Speech Lang Proc. (2016) 24:694–707. doi: 10.1109/TASLP.2016.2520371
10. Devlin J, Chang MW, Lee K, Toutanova K. Bert: pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:181004805 (2018). doi: 10.18653/v1/N19-1423
11. Yang Z, Dai Z, Yang Y, Carbonell J, Salakhutdinov RR, Le QV. Xlnet: generalized autoregressive pretraining for language understanding. In: Wallach H, Larochelle H, Beygelzimer A, d'Alch é-Buc F, Fox E, Garnett R, editors. Advances in Neural Information Processing Systems 32. Curran Associates, Inc. (2019). p. 5754–64. Available online at: http://papers.nips.cc/paper/8812-xlnet-generalized-autoregressive-pretraining-for-language-understanding.pdf
12. Arora S, Liang Y, Ma T. A simple but tough-to-beat baseline for sentence embeddings. In: 5th International Conference on Learning Representations, ICLR 2017 (Toulon). Available online at: https://openreview.net/forum?id=SyK00v5xx
13. De Boom C, Van Canneyt S, Demeester T, Dhoedt B. Representation learning for very short texts using weighted word embedding aggregation. Pattern Recogn Lett. (2016) 80:150–6. doi: 10.1016/j.patrec.2016.06.012
14. Lee YJ, Mangasarian OL. SSVM: a smooth support vector machine for classification. Comput Optim Appl. (2001) 20:5–22. doi: 10.1023/A:1011215321374
15. Bezdek JC, Hathaway RJ. Convergence of alternating optimization. Neural Parallel Sci Comput. (2003) 11:351–68.
16. scikit-learn. Support Vector Machines (2017). Available online at: http://scikit-learn.org/stable/modules/svm.html
17. Wen Z, Shi J, Li Q, He B, Chen J. ThunderSVM: a fast SVMlibrary on GPUs and CPUs. J Mach Learn Res. (2018) 19:797–801.
18. Fung G, Mangasarian OL. Proximal support vector machine classifiers. In: Provost F, Srikant R, editors. Proceedings KDD-2001: Knowledge Discovery and Data Mining. San Francisco, CA; New York, NY: Asscociation for Computing Machinery (2001). p. 77–86. Available online at: Ftp://ftp.cs.wisc.edu/pub/dmi/tech-reports/01-02.ps
19. Suykens JAK, Vandewalle J. Least squares support vector machine classifiers. Neural Process Lett. (1999) 9:293–300. doi: 10.1023/A:1018628609742
20. Neumaier A. Solving ill-conditioned and singular linear systems: a tutorial on regularization. SIAM Rev. (1998) 40:636–66. doi: 10.1137/S0036144597321909
21. Golub GH, Van Loan CF. Matrix Computations, 3rd Edn. Baltimore, MD: Johns Hopkins University Press (1996).
22. Joulin A, Grave E, Bojanowski P, Mikolov T. Bag of tricks for efficient text classification. In: Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 2, Short Papers. Valencia: Association for Computational Linguistics (2017). p. 427–31.
23. Cortes C, Vapnik V. Support-vector networks. Mach Learn. (1995) 20:273–97. doi: 10.1023/A:1022627411411
24. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in Python. J Mach Learn Res. (2011) 12:2825–30.
25. Lang K. NewsWeeder: learning to filter netnews. In: Proceedings of the 12th International Machine Learning Conference. Tahoe City, CA (1995). p. 331–9.
26. Blitzer J, Dredze M, Pereira F. Biographies, bollywood, boom-boxes and blenders: domain adaptation for sentiment classification. In: Proceedings of the Association for Computational Linguistics (ACL) (2007).
27. McAuley J, Targett C, Shi Q, van den Hengel A. Image-based recommendations on styles and substitutes. In: Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR '15. New York, NY: ACM (2015). p. 43–52. Available online at: http://doi.acm.org/10.1145/2766462.2767755
28. He R, McAuley J. Ups and downs: modeling the visual evolution of fashion trends with one-class collaborative filtering. In: Proceedings of the 25th International Conference on World Wide Web. WWW '16. Republic and Canton of Geneva: International World Wide Web Conferences Steering Committee (2016). p. 507–17. Available online at: https://doi.org/10.1145/2872427.2883037
29. Greene D, Cunningham P. Practical solutions to the problem of diagonal dominance in kernel document clustering. In: Proc. 23rd International Conference on Machine learning (ICML'06). Pittsburgh, PA: ACM Press (2006). p. 377–84.
30. Mukherjee A, Liu B. Improving gender classification of blog authors. In: Proceedings of the 2010 Conference on Empirical Methods in Natural Language Processing, EMNLP '10. Stroudsburg, PA: Association for Computational Linguistics (2010). p. 207–17. Available online at: http://dl.acm.org/citation.cfm?id=1870658.1870679
31. DBPedia. DBPedia (2018). Available online at: http://wiki.dbpedia.org/
32. Lehmann J, Isele R, Jakob M, Jentzsch A, Kontokostas D, Mendes PN, et al. DBpedia - A large-scale, multilingual knowledge base extracted from wikipedia. Semant Web J. (2015) 6:167–95. doi: 10.3233/SW-140134
33. Zhang X, Zhao J, LeCun Y. Character-level convolutional networks for text classification. In: Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 1, NIPS'15. Cambridge, MA: MIT Press (2015). p. 649–57. Available online at: http://dl.acm.org/citation.cfm?id=2969239.2969312
34. Maas AL, Daly RE, Pham PT, Huang D, Ng AY, Potts C. Learning word vectors for sentiment analysis. In: Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies. Portland, OR: Association for Computational Linguistics (2011). p. 142–50. Available online at: http://www.aclweb.org/anthology/P11-1015
35. Lichman M. UCI Machine Learning Repository. Irvine, CA (2013). Available online at: http://archive.ics.uci.edu/ml
36. Socher R, Perelygin A, Wu J, Chuang J, Manning CD, Ng AY, et al. Parsing With compositional vector grammars. In: EMNLP (2013).
37. Yelp. Yelp Dataset Challenge (2018). Available online at: https://www.yelp.com/dataset/challenge
38. Bojanowski P, Grave E, Joulin A, Mikolov T. Enriching word vectors with subword information. arXiv preprint arXiv:160704606. (2016). doi: 10.1162/tacl_a_00051
39. Facebook. FastText (2018). Available online at: https://fasttext.cc/
40. Mikolov T, Sutskever I, Chen K, Corrado G, Dean J. Distributed representations of words and phrases and their compositionality. In: Proceedings of the 26th International Conference on Neural Information Processing Systems - Volume 2. NIPS'13. Curran Associates Inc. (2013). p. 3111–9. Available online at: http://dl.acm.org/citation.cfm?id=2999792.2999959
41. Google. Word2Vec (2018). Available online at: https://code.google.com/archive/p/word2vec/
42. Řehůřek R, Sojka P. Software framework for topic modelling with large corpora. In: Proceedings of the LREC 2010 Workshop on New Challenges for NLP Frameworks. Valletta : ELRA (2010). p. 45–50. Available online at: http://is.muni.cz/publication/884893/en
Keywords: NLP (national language processing), word embedding, text classification, SVM—support vector machine, text representation models
Citation: Gupta S, Kanchinadam T, Conathan D and Fung G (2020) Task-Optimized Word Embeddings for Text Classification Representations. Front. Appl. Math. Stat. 5:67. doi: 10.3389/fams.2019.00067
Received: 09 August 2019; Accepted: 16 December 2019;
Published: 14 January 2020.
Edited by:
Yiming Ying, University at Albany, United StatesReviewed by:
Shao-Bo Lin, Xi'an Jiaotong University (XJTU), ChinaCopyright © 2020 Gupta, Kanchinadam, Conathan and Fung. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Teja Kanchinadam, dGthbmNoaW5AYW1mYW0uY29t
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.