Weak Chimeras in Modular Electrochemical Oscillator Networks

We investigate the formation of weak chimera states in modular networks of electrochemical oscillations during the electrodissulution of nickel in sulfuric acid. In experiment and simulation, we consider two globally coupled populations of highly non-linear oscillators which are weakly coupled through a collective resistance. Without cross coupling, the system exhibits bistability between a one- and a two-cluster state, whose frequencies are distinct. For weak cross coupling and initial conditions for the one- and two-cluster states for populations 1 and 2, respectively, weak chimera dynamics are generated. The weak chimera state exhibits localized frequency synchrony: The oscillators in each population are frequency-synchronized while the two populations are not. The chimera state is very robust: The behavior is maintained for hundreds of cycles for the rather heterogeneous natural frequencies of the oscillators. The experimental results are confirmed with numerical simulations of a kinetic model for the chemical process. The features of the chimera states are compared to other previously observed chimeras with oscillators close to Hopf bifurcation, coupled with parallel resistances and capacitances or with a non-linear delayed feedback. The experimentally observed synchronization patterns could provide a mechanism for generation of chimeras in biological systems, where robust response is essential.

Introduction

Synchronization of oscillatory chemical reactions is an important dynamical phenomenon with relevance to many physical and biological processes [1]. Early studies focused on the dynamics of continuous, stirred tank reactors (CSTRs) where coupling is through active or passive mass transfer, or by electrical means [2–6]. Different types of interactions were able to induce different synchronization patterns, e.g., in-phase, anti-phase, and out-of-phase entrainment. The CSTR technology however is difficult to scale up to a large population of reactors [7, 8]. Belousov-Zhabotinsky (BZ) microdroplets [9, 10], beads [11, 12], microwell arrays [13], and nanodroplets [14] provide ways to study synchronization of populations. In oscillatory electrochemical systems, electrode arrays can be applied to investigate coupled systems, up to about 100 oscillators [15]. Globally coupled electrochemical oscillators indeed showed a variety of synchrony patterns with various levels of coherence, including full synchrony [16] and other stable [17] and intermittent [18] cluster states.

Understanding what coupling properties—topology, delay, symmetry, and non-linearity —influence synchronization in dynamical models [1, 19] provides guidelines for the design of experiments. In particular, phase-model-based predictions turned out to be useful for identification of synchronization patterns in experiments [17, 18]. While the importance of phase models in interpreting synchronization structures was emphasized in early studies [5], some reluctance remained among chemists to adopt phase models in the theoretical description of chemical reactions due to their simplified nature [20]. Only one angular variable, the phase, is used to uniquely identify the state of the chemical reactions. However, oscillatory chemical reactions typically require at least two chemical species [20]. While phase descriptions can be rigorously justified for weak interaction [21], the full range of interactions in chemical systems include strong and highly non-linear coupling. Hence, pure phase model description should be used with care. Nonetheless, many dynamical phenomena, e.g., clustering [17], desynchronization [22, 23], and slow switching [18] were interpreted and designed using phase model approaches.

Chimeras, synchrony patterns with coexisting domains of coherence and incoherence in networks of identical oscillators, have attracted a tremendous amount of attention in the last decades [24, 25]. They were originally reported by Kuramoto and Battogtokh in rings of non-locally coupled oscillators where the coupling strength depends on the distance between oscillators [26]. These traditional chimeras have been studied theoretically in the continuum limit of infinitely many oscillators [26, 27]. By contrast, the concept of a “weak chimera” [28, 29] provides a rigorous characterization of chimeras in networks of finitely many oscillators and capture features of the chimeras originally described by Kuramoto and Battogtokh: Weak chimeras in networks of identical oscillators are characterized by localized frequency synchrony, i.e., there are oscillators that are synchronized in frequency and others which have distinct frequencies.

The theoretically predicted chimera states challenged the fundamental understanding of the non-linear dynamics of chemical reactions and the experimental techniques that enabled the construction of networks of coupled chemical reactions. Can we design networks and choose experimental conditions favorable for the chimera state?

As the theory of chimera states is quickly growing [24, 25], developments of experimental and data analysis techniques were also needed to identify and classify partially synchronized states as chimera states [30]. The BZ bead system with optical feedback technique is a promising approach that can generate various types of chimera patterns in different configurations [31–34]. In electrochemistry, non-linear electrical coupling during silicon dissolution generates localized patterns that possess many features similar to chimeras [35–40]. The beating mercury drop system also showed that while homogeneous coupling generates rather synchronized states, inhomogeneous coupling results in partial synchronization similar to a chimera [41]. Current oscillations of nickel electrodissolution, in the transpassive dissolution region, on electrode arrays exhibit a wide range synchronization patterns [15]. Oscillation occurs due to the hidden negative differential resistance of the electrodissolution process [42]. Two different types of chimeras were identified [43–45]. On a ring with long-range interaction, a short-lived synchrony pattern, similar to the traditional chimera was found [44, 45]. When non-linear coupling was generated with a computer feedback, weak chimeras [28, 29, 46] were obtained with a four-oscillator network, where two pairs of elements were locked in-phase and anti-phase configurations with distinct frequencies [43].

In this paper, we report the occurrence of weak chimera states in a modular network of electrochemical oscillators with the electrodissolution of nickel in sulfuric acid. First, for comparison with previous results, an overview is given on the characteristics of chimera states in the nickel electrodissolution system [43–45]. In these previous experiments, the chimera state was observed either in a device [44, 45] with relatively short life-time, or in a computer feedback system [43] with long life-time. Here we seek long life-time chimeras in a device. Numerical simulations are performed to explore parameter space and identify experimental conditions for which weak chimera states can be observed with strongly non-linear oscillators in the presence of linear (or difference) coupling through the electrode potential. Finally, experiments are performed to show the existence of the weak chimeras in the electrochemical system.

Materials and Methods

Figure 1 shows the experimental setup and the three different network topologies. Each approach uses different techniques to generate favorable experimental conditions for the chimera state.

FIGURE 1

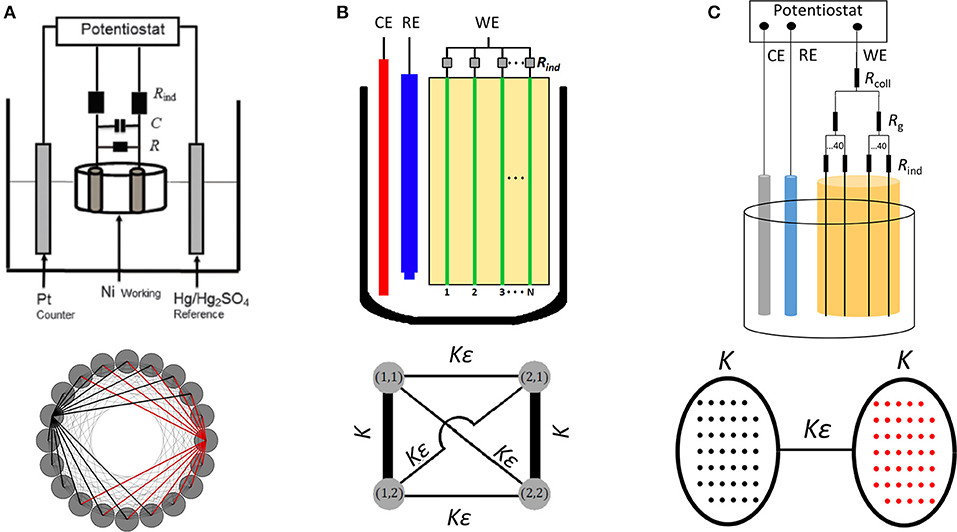
Figure 1. Schematics of the experimental setups (top) for the different types of network topologies (bottom). (A) Non-local ring network with 20 nodes and 140 links. R_ind: individual resistance. C: capacitance. R: cross resistance. (B) Weakly non-linear oscillator and highly non-linear delayed feedback in two pairs of oscillators with weak cross-coupling. CE: Counter electrode. RE: Reference electrode. WE: Working electrode. K: coupling strength. ε: cross coupling factor. N: number of oscillators in a general configuration. (C) Highly non-linear oscillators and linear interactions in two populations of electrodes with weak, global cross coupling. R_coll: collective resistance. R_g: group resistance.

Ring Network With Non-local Coupling

A standard three-electrode electrochemical cell for the ring network with non-local coupling [44] is shown in Figure 1A. This approach used an electrode array, in which the electrode pairs are coupled by parallel resistance/capacitance circuit elements. An array of nickel wires (only two are shown in the figure) were used as the working electrode. A Hg/Hg₂SO₄ saturated K₂SO₄ is the reference, and a platinum rod is the counter electrode. The electrodes were immersed in a 3 M H₂SO₄ solution. The cell temperature was maintained at 10°C by a circulating bath. The working electrode array has 1 mm diameter wires, embedded in epoxy, with a spacing of 2 mm. With this large spacing the potential drop in the electrolyte is sufficiently small (about 0.1 mV), so that without the presence of additional coupling, the oscillations do not show synchronization [16]. The working electrodes were connected to a potentiostat through an external resistance (R_ind) for each wire. The potentiostat sets the constant circuit potential, and the currents, measured from the potential drops across the individual resistances, were digitized using a National Instrument PCI 6255 data acquisition board at a rate of 200 Hz (Note that each wire has the same circuit potential in this configuration).

The properties of individual oscillations for a wire of a given diameter can be changed by the circuit potential (V), the attached total external resistance, the concentration of the sulfuric acid, and the temperature. Once the properties of the individual oscillators are set, the wires in the electrode arrays can be coupled externally for a given topology. As shown in the bottom panel of Figure 1A, the network topology consists of 20 nodes with 140 links. Each node is an oscillatory nickel electrodissolution reaction, which takes place on the surface of the electrode. The links of the network are established through a coupling resistance R [45] and capacitance C. To induce some delay in the coupling current a capacitor in parallel was added to each coupling resistor [47]. In the network, each node is coupled to seven of its nearest neighbors of the ring network in both directions.

Network With Spatially Distributed Non-linear Delayed Feedback

The experimental setup with non-linear feedback shown in Figure 1B [43]. The system consisted of four oscillators divided into two populations with stronger coupling in the populations and a weaker coupling between them (Figure 1B bottom). The oscillators are coupled through linear and quadratic delayed feedback. The same electrode array can be used as with the non-local ring network. (To further eliminate coupling through the electrolyte, the electrodes had 3 mm spacing.) A multichannel potentiostat (ACM Instruments Gill IK64) was used. The potential V_σ,k(t) of the wire k in population σ ∈ {1, 2} with respect Hg/Hg₂SO₄ sat K₂SO₄ reference electrode, was set with a multichannel potentiostat interfaced with a real-time Labview controller. The electrode potentials E_σ,k(t) of the four wires were converted using the currents (I_σ,k(t)): E_σ,k(t) = V_σ,k(t) − I_σ,k(t)R_ind, with R_ind = 1 kOhm. The electrode potentials were adjusted for offset with, $E_{\sigma ,k}=E_{\sigma ,k}-o$, where o is the time averaged electrode potential (The quantity o was measured before the experiments, for a timeframe of about 100 oscillations). The circuit potential of each wire is adjusted by the feedback using the equation:

$\begin{array}{ll}{V}_{\sigma ,k}(t)=V_0+K{\displaystyle \sum _{\kappa ,j\in \left\{1,2\right\}}}{K}_{\kappa \sigma }h({\overline{E}}_{\kappa ,j}(t-\tau ))& (1)\end{array}$

where K_κσ determines the network topology, K is the total feedback gain, τ is the global delay, and

$\begin{array}{l}h({\overline{E}}_{\kappa ,j}(t))=k_1\left[{\overline{E}}_{\kappa ,j}(t)-{\overline{E}}_{\kappa ,j}(t-{\tau }_{Ex})\right]\\ +k_2\left[{\overline{E}}_{\kappa ,j}{(t)}^2+{\overline{E}}_{\kappa ,j}{(t-{\tau }_{Ex})}^2\right]& (2)\end{array}$

is the feedback. For each population, K₁₁ = K₂₂ = 1. Coupling between the population is set to K₁₂ = K₂₁ = ε, where ε is the cross-coupling factor. The linear and quadratic feedback gains, k₁ and k₂, respectively, are applied to induce the required dynamics. The delay τ_Ex was set to be equal to half of the period of the uncoupled oscillators. See [43] for more details on the choice of the parameters k₁, k₂, and τ_Ex. V₀ = 1, 160 mV and the natural frequency (i.e., the frequency of the oscillation without coupling) was about 0.45 Hz. In a typical experiment of about 500 oscillations, the natural frequency change is about 2–3 mHz.

Modular Network

Figure 1C shows the experimental setup for a modular network consisting of coupled oscillator populations. In the bottom of Figure 1C a schematic of the network topology is shown: A total of 80 oscillators are divided into two populations of 40. The same working electrode array, reference and counter electrodes, and electrolyte was used as with the feedback experiment above. The cell was connected to a single channel potentiostat (ACM Instruments, Gill AC), and an individual resistance (R_ind) was added to each electrode. Additionally, two group resistances (R_g) and a collective resistance (R_coll) were used to generate the intra- and inter-population coupling, respectively.

Results and Discussions

To put our results in context, we start out with reviewing the chimera states observed earlier with non-local ring network (section Chimera State with Non-local Ring Network Close to Hopf Bifurcation) and weak chimeras with non-linear feedback (section Weak Chimera with Non-linear Feedback). In section Weak Chimera in Modular Networks with Strongly Non-linear Oscillators, new results are presented in a modular network of highly non-linear oscillators coupled through differences in the electrode potentials.

Chimera State With Non-local Ring Network Close to Hopf Bifurcation

Here we considered oscillations in the experimental system that occur close to Hopf bifurcation [48]. Normally, the natural frequency of the oscillations has a range of about 16 mHz and frequency of 0.4 Hz [45]. To ensure nearly identical oscillators, the range of the natural frequencies was carefully tuned to fall below 0.5 mHz by small changes of the individual resistances, as shown in Figure 2A. Coupling through resistors corresponds to a Kuramoto-model-like behavior (i.e., with nearly sinusoidal phase interaction function) [47]. When coupling is through capacitance, the coupling signal is delayed with a phase of about π/2 [47]. A combination of resistive and capacitive coupling was applied such that the coupling parallel RC circuit had a time constant 2.35 s, which approximately matches the oscillation period of 2.5 s [45]. Such coupling, in our experiments, ensured that the oscillations synchronized at relatively weak strengths, with a delay sufficient for the chimera states to arise. As the coupling was turned on, the population split into a domain of synchronized (electrodes 1–4, 17–20) and desynchronized (electrodes 5–16) elements, as shown in Figure 2B. The frequency of the synchronized elements is 0.389 Hz and the desynchronized elements have lower frequencies (Figure 2A). Additionally, these frequencies form a semi-circle as a function of the position of the elements. This distribution was predicted theoretically for the chimera state [26]. Note that for this chimera state some oscillators are synchronized in frequency, while others are not. Figure 2C shows a snapshot of the currents. The elements 1–4 and 17–20 have very similar values and the desynchronized elements have a broader distribution. This chimera state has a limited lifetime of about 80–100 oscillations. This lifetime is in accordance with theoretical predictions [49] and numerical simulations with experiment-based phase models [45] describing the chemical process. The observations thus show that the experimentally observed dynamical state is similar to the traditional Kuramoto chimera state, induced by non-local interactions in a ring topology [49]. Later efforts were focused on characterizing the impact of oscillator heterogeneity (i.e., “remnant” chimeras obtained without adjustments of natural frequencies) [45], and increasing the lifetime of the chimera states with a more non-linear system [43].

FIGURE 2

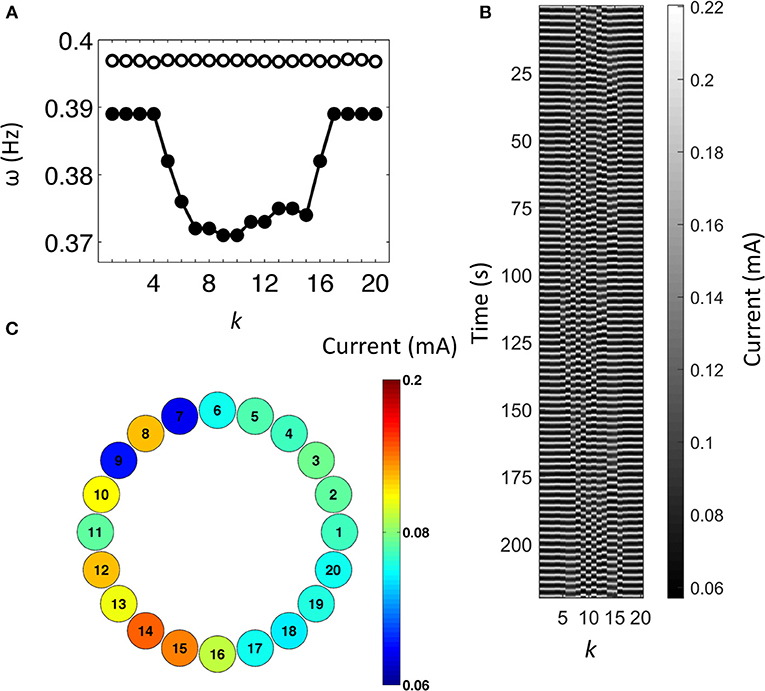
Figure 2. Experimental traditional chimera state in a non-locally coupled regular network. (A) Frequency of the oscillators. Open circles: natural frequency. Solid circles: frequency with coupling. (B) Space-time plot of the current in gray scale. (C) Snapshot of the current of the electrodes. V = 1,094 mV, R_ind = 1 kOhm, R = 499 kOhm, C = 4.7 μF.

Weak Chimera With Non-linear Feedback

Weak chimeras can arise in modular oscillator networks consisting of multiple populations with stronger coupling within populations and weaker coupling between different populations [28]. In a phase model, with a pair of oscillators, bistability between an in-phase, and an anti-phase solution with distinct frequencies can be observed. Under such conditions, a chimera state forms in a network of two pairs of two oscillators, where one of the two strongly coupled oscillator pairs exhibit in-phase, the other anti-phase state. The two synchronized pairs of oscillators have different frequencies, resulting in a weak chimera [29].

We used a synchronization engineering [18] technique to design a combination of first and second order feedbacks to induce a dynamics that represents the desired phase model. When this feedback is applied to two oscillators [43], there is region global delay τ with bistability between in-phase and anti-phase synchronization (see Figure 3A). For τ = 0 s, the electrodes are in-phase synchronized; increasing the value until τ ≈ 0.8 s the dynamics shift to anti-phase synchronization. Now, when we started from anti-phase synchronization and the global delay was decreased, there was a critical point where the dynamics shifted back into in-phase synchronization at about 0.2 s. Consequently, there is a region from τ ≈ 0.2 s to τ ≈ 0.8 s in which both states can exist and are stable. A delay of τ ≈ 0.51 s was chose for investigation of the chimera state.

FIGURE 3

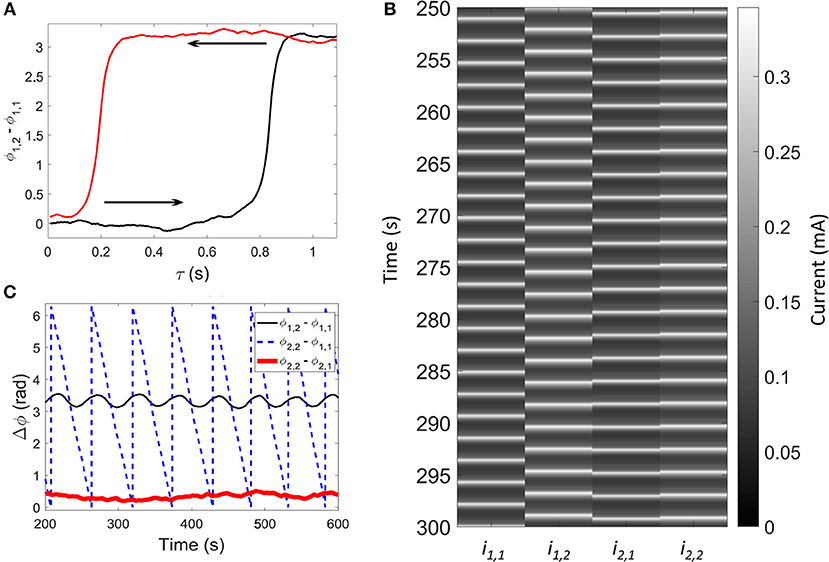
Figure 3. Experimental weak chimera state with non-linear feedback. (A) Hysteresis between the in-phase and anti-phase synchronization, as a function of the global coupling delay, τ; black line: forward sweep; red line: backward sweep. (B,C) Weak chimera state with τ = 0.51 s and ε = 0.1. (B) Space time plot of the current of the four oscillators. (C) Time series of the phase difference within population 1 (black thin line φ_{1, 2} − φ_{1, 1}), population 2 (red thick line, φ_{2, 2} − φ_{2, 1}), and for two elements between the populations (blue dashed line, φ_{2, 2} − φ_{1, 1}). Feedback parameters: K = 0.52, k₁ = 0.22, k₂ = 2.0 1/V.

As shown in Figure 3B, in the four-oscillator network with weak cross coupling (ε = 0.1), population 1 is in anti-phase while population 2 is in-phase synchronized [43]. The phase difference between elements are shown in Figure 3C. For elements in the same population, the phase difference remains nearly the same (in- or anti-phase), but the phase difference between one element in population 1 and population 2 is growing. This state thus represents a weak chimera. With the weak chimera, the in- and anti-phase populations can remain desynchronized even in the presence of the cross coupling. Note that the oscillations of the phase difference for the anti-phase pair arise due to the presence of coupling from the two nearly in phase oscillators in the other populations. These oscillators speed up and slow down the anti-phase pair (due to their weak cross coupling) as their phase difference drifts apart [43].

Weak Chimera in Modular Networks With Strongly Non-linear Oscillators

We now consider networks of two coupled populations with a larger number of oscillators per population and inherent non-linearities through the phase response curve and the oscillators' waveforms. For a phase description, these properties lead to non-sinusoidal phase interaction, which can give multistability between in-phase synchrony and other cluster states with global coupling [17, 50, 51]. This suggests that weak chimeras can occur for coupled populations. In contrast to the setup in the previous section, the coupling is not mediated by a computer but through a resistance, i.e., the electrode potential difference between the electrodes results in a coupling current that can induce chemical changes [47]. First, we demonstrate the approach with model simulations, and then confirm the findings in experiments.

Numerical Simulations

We used the kinetic scheme proposed by Haim et al. [52] of nickel electrodissolution to model the behavior of a single electrode. The model was written for two variables, the dimensionless electrode potential e and the total surface coverage of the nickel oxide and hydroxide θ. For 40 electrodes coupled through a combination of individual (R_ind) and global (collective) (R_coll) resistance, the charge and mass balance equations are the following [53]:

$\begin{array}{llll}\frac{d{e}_i}{dt}& =& \frac{V-e_i}{R}-J_F(e_i,{\theta }_i)+K{\displaystyle \sum _{j=1}^{40}}(e_j-e_i)& (3)\end{array}$

$\begin{array}{llll}{\Gamma }_i\frac{d{\theta }_i}{dt}& =& \frac{exp(0.5e_i)}{1+C_{h}exp(e_i)}(1-{\theta }_i)-\frac{b{C}_{h}exp(2e_i){\theta }_i}{c{C}_h+exp(e_i)}& (4)\end{array}$

where i = 1, …, 40, V is the dimensionless circuit potential, R = 20 is the dimensionless individual total resistance, J_F(e, θ) is the Faraday current density calculated by the equation

$\begin{array}{ll}{J}_F(e,\theta )=\left[\frac{C_{h}exp(0.5e)}{1+C_{h}exp(e)}+aexp(e)\right](1-\theta ),& (5)\end{array}$

and Γ_i is the surface capacity. Γ_i were randomly chosen between 9.999 ×10⁻³ and 10.001 ×10⁻³ for simulating the heterogeneities of the different natural frequencies of the oscillators [54]. Moreover, C_h = 1600, a = 0.3, b = 6 × 10⁻⁵ and c = 0.001 are kinetic parameters. The global coupling occurs through the electrode potential equation (last term in Equation 3). K is the global coupling strength, K = R_c/(R_indR) and R = R_ind + 40R_c [53]. Equation 3 is the charge balance: Current can be generated by charging the electrical double layer, the charge transfer electrochemical reactions (Faradayic current), and through coupling to the electrode potentials of the other wires. Nickel electrodissolution and water electrolysis are the two major chemical steps that contribute to the Faradayic current density in Equation 5 [52]. The oxide layer, whose coverage is given by Equation 4, blocks parts of the electrode from dissolution and water electrolysis. Without coupling (K = 0), Equations (3–5) exhibit a supercritical Hopf bifurcation at V = 10.2. The numerical simulations are performed at somewhat elevated circuit potentials (V > 24), where the oscillations exhibit non-linear waveforms.

Figure 4A shows the frequency of the synchronized oscillations as a function of the circuit potential (V) with K = 2 × 10⁻⁴ for the one- and two-cluster states for 24.3 ≤ V ≤ 25.3. At low V, only the one-cluster state exists. For 24.9 ≤ V ≤ 25.3 there is bistability between the one- and two-cluster states. Note the frequencies of both the one- and the two-cluster states decrease with increasing the potential and that the two-cluster states have slightly larger frequencies. In previous study [17], a phase model analysis was performed, which showed that very close to a Hopf bifurcation the phase coupling function exhibits only first harmonic components, and thus only one-cluster state is possible with positive coupling. The two-cluster state arises because of the presence of higher harmonics in the phase coupling function, which are induced by higher harmonics in both the infinitesimal phase response function and the oscillation waveform [17]. These non-linearities have been interpreted with higher-order correction terms of the amplitude equations close to a Hopf bifurcation [55], or with integrate-and-fire type models with a refractory period [56].

FIGURE 4

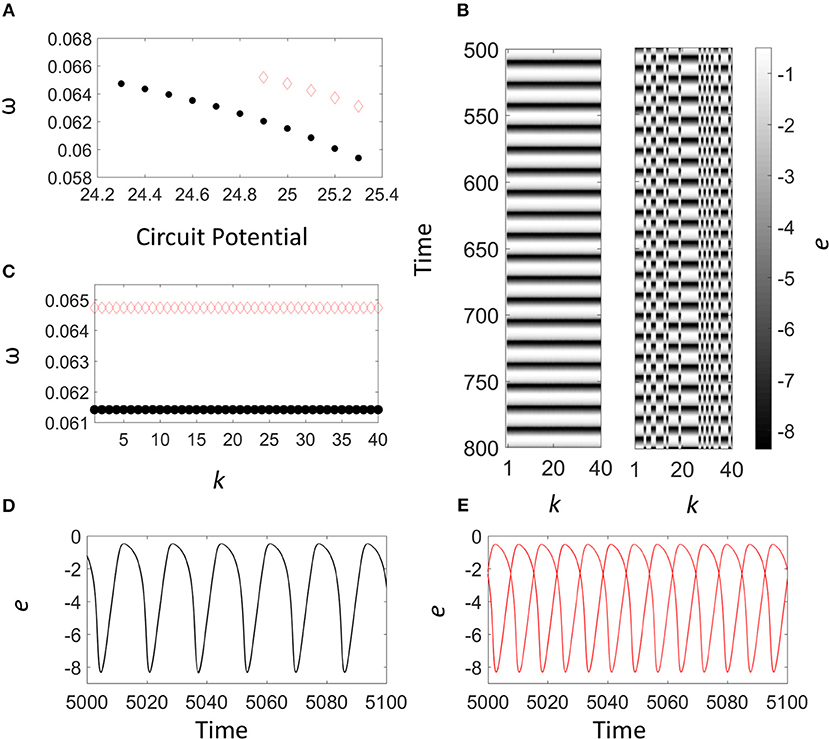
Figure 4. Numerical simulation: Cluster formation with global coupling (K = 2×10⁻⁴). (A) Frequency of the one- (black solid circles) and the two-cluster states (red empty diamonds) as a function of the circuit potential, V. (B) Space time plot of the electrode potential for the one- and the two-cluster states. (C) Frequency of the elements in the one- (black solid circles) and two-cluster (red empty diamonds) states. (D,E) Time series of the electrode potentials for the elements in the one- (black line) and two-cluster (red line) states. In panels (B–D), V = 25.0.

The behavior at V = 25.0 of the one- and the two-cluster states are shown in Figures 4B–E. In the one-cluster state, the electrode potentials (Figure 4D) follow the same variations. In the two-cluster state (Figure 4E), there are two groups of 20 elements that are in nearly anti-phase configuration. Note that in contrast to previous studies [43–45], the waveforms are not very harmonic and exhibit a moderate relaxation character.

The space time plot for the one- and two-cluster state (the left and right panel, respectively) are shown in Figure 4B. The one cluster exhibits uniform oscillations, while in the two-cluster state there are two groups in an approximate anti-phase configuration (Note that in the two clusters the configurations depend on initial conditions. Here we consider initial conditions opposite of the limit cycle, randomized in space). The frequencies of the elements are shown in Figure 4C. The two-cluster state has about 5% higher frequency (ω = 0.06474) than the one cluster (ω = 0.06142) state, with frequency difference Δω = 3.32 ×10⁻³. Because there is bistability between the one-cluster and the two-cluster states with differing frequency, the conditions may favor the formation of weak chimera states in networks. We note that oscillator heterogeneity was added to the model to better represent the experimental scenario. The same bistability also occurs for uniform populations (i.e., with Γ_i = 0.01 for all oscillators).

As a simple modular network obtained from the globally coupled oscillator populations, we introduce some cross coupling between two populations. For the electrode potential, the equations are:

$\begin{array}{l}\frac{d{e}_l}{dt}=\frac{V-e_l}{R}-J_F(e_l,{\theta }_l)+K{\displaystyle \sum _{j=1}^{40}}(e_j-e_l)+\epsilon K{\displaystyle \sum _{k=41}^{80}}(e_k-e_l)\\ l=1,2,...,40& (6)\end{array}$

$\begin{array}{l}\frac{d{e}_i}{dt}=\frac{V-e_i}{R}-J_F(e_i,{\theta }_i)+\epsilon K{\displaystyle \sum _{j=1}^{40}}(e_j-e_i)+K{\displaystyle \sum _{k=41}^{80}}(e_k-e_i)\\ i=41,42,...,80& (7)\end{array}$

(The equations for surface coverages are the same, i.e., Equation 4). There is a strong global coupling within the populations, K, and weak global cross coupling between the populations εK, where ε is the cross-coupling factor (0 ≤ ε ≤ 1).

With ε = 0.05 with initial conditions corresponding to the one (or two)-cluster states for all the oscillators, the expected one (or two) cluster state was obtained. Figure 5 shows the behavior with ε = 0.05 from initial conditions for population 1 (elements 1–40) with in-phase, and population 2 (elements 41–80) with conditions opposite of the limit-cycle randomized in space (Other parameters are the same as in Figure 4). Figure 5A shows the frequency of the elements. The two-cluster still has about 5% higher frequency (ω = 0.06485) than the one-cluster (ω = 0.06157) but the frequency difference is slightly lower than that without coupling, Δω = 3.28 × 10⁻³. The grayscale plot (Figure 5B) shows that the first forty elements (population 1) exhibit uniform oscillations while the elements 41–80 (population 2) form two clusters in anti-phase configurations. As shown in Figure 5C, the phase difference of the elements in the one-cluster state remains constant, approximately 2π (or zero), while in the two-cluster the phase difference between two elements in different clusters has small amplitude oscillations around π. For a pair of elements in different populations, we observed a phase drifting behavior, further confirming the chimera state. The presence of the desynchronized behavior between the populations could also be seen in the times series data of the electrode potentials (Figure 5D). Under these conditions, the presence of the chimera state is a unique behavior of the network interactions. With global coupling (ε = 1.0), the chimera state disappears: With initial conditions similar to the chimera state in Figure 5 we obtained a one-cluster, in-phase synchronized state.

FIGURE 5

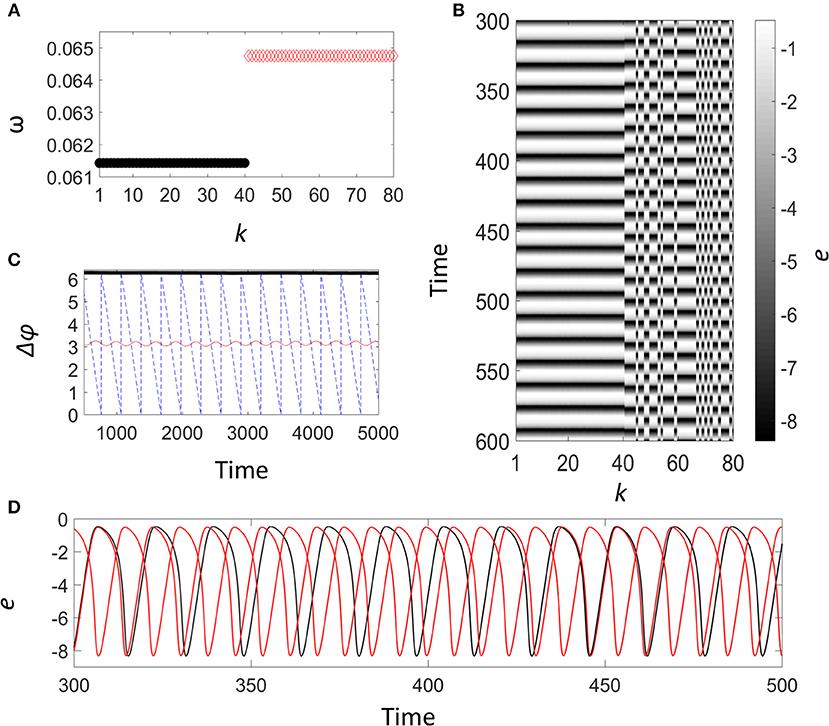
Figure 5. Numerical simulation: Weak chimera state in the modular network with weak cross coupling. V = 25, K = 2 × 10⁻⁴ and ε = 0.05. (A) Frequency of elements (population 1: black solid circles; population 2: red open diamonds). (B) Space time plot of the electrode potential. Population 1: k = 1,…,40. Population 2: k = 41,…,80. (C) Phase difference between two elements in population one, (black thick line φ₁ − φ₂), populations 2 red thin line, (φ₄₁ − φ₄₅), and between populations (blue dashed, φ₁ − φ₄₁). (D) Time series of the electrode potential for the chimera state; population 1: black line, populations 2: red line.

Experiments

Without coupling, the oscillators exhibit slight heterogeneity, and the natural frequencies have a standard deviation of about 14 mHz. To confirm the weak chimera state, we performed a set of experiments following the guidelines developed in the simulations. First, we used only population 1 (40 electrodes), and coupled them globally (i.e., R_coll = 0 Ohm, R_g = 10 Ohm in Figure 1C). With K = 16.7 μS, the frequencies of the elements in the one- and two-cluster states are shown in Figure 6. For V ≤ 1, 220 mV, only the one-cluster state is stable. The frequencies decrease with increasing circuit potential. For 1, 230 mV ≤ V ≤ 1, 270 mV a two-cluster state was also found (This two-cluster state can be obtained by increasing the circuit potential past V = 1, 270 mV, where the one-cluster state breaks up, and decreasing the potential). Thus, in this region, there is bistability between the one- and two-cluster states and, similar to the simulations, the two-cluster state has slightly larger frequency than the one-cluster state. Note that the occurrence of such bistability between one- and two-cluster states was predicted by experiment-based phase models [17].

FIGURE 6

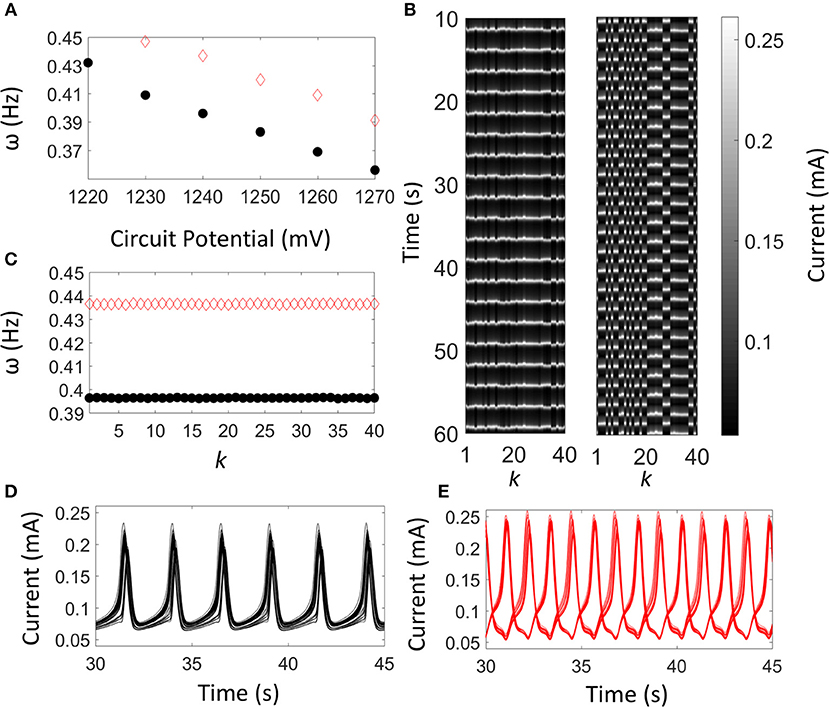
Figure 6. Experiments: Cluster formation with global coupling. (A) Frequency of the one- (black solid circles) and the two-cluster state (red empty diamonds) as a function of the circuit potential, V. The one cluster state was obtained by increasing the circuit potential from V = 1.100 V. The two-cluster state can be obtained by increasing the circuit potential past V = 1, 270 mV, where the one-cluster state breaks up, and decreasing V. (B) Space time plot of the current for the one- and two-cluster states. (C) Frequency of the elements in the one- (black solid circles) and two-cluster (red empty diamonds) states. (D,E) Time series of the current of the elements in the one- (black line) and two-cluster (red line) states. R_ind = 600 Ohm, R_g = 10 Ohm, R_coll = 0 Ohm, K = 16.7 μS. In panels (B–E), V = 1,240 mV.

As an example of the behavior observed in this region, the dynamics is shown at V = 1, 240 mV. The time series data for the one- and two-cluster states also confirm that this state was found with oscillation waveform of relaxation character (see Figures 6D,E). The grayscale plots (Figure 6B) show the one- (left) and two-cluster states (right). The elements in the one-cluster state oscillate nearly uniformly, while those in the two-cluster states form two groups, oscillating in anti-phase. The two-cluster state forms an almost balanced configuration with 18 and 22 elements in each cluster. As in the simulation, the two-cluster state has a higher frequency (ω = 0.437 Hz) than the one-cluster (ω = 0.396 Hz); the frequency increase is about 10% with a frequency difference of 41 mHz (see Figure 6C).

Now we consider the modular network with two populations of 40 electrodes. The oscillators in each population are coupled with R_g. As shown in Figure 1C, the two populations are coupled through a collective resistance R_coll. The resistance R_coll induces global coupling between every electrode pair, with coupling strength K_coll = R_coll/[(R_ind + 40R_g)R_eq], where R_eq = R_ind + 40R_g + 80R_coll. The group resistance induces coupling only within a population, i.e., K_g = R_g/[R_ind(R_ind + 40R_g)]. The total coupling thus K = K_g + K_coll, and ε = K_g/K.

Figure 7A shows the frequency of the one- and two-cluster states in the network configuration with K = 17μS and ε = 0.03. In this set of experiments, the frequency of the one- and the two-cluster states with ε = 0 was 0.384 Hz and 0.413 Hz, respectively; the frequency difference was 29 mHz with the two-cluster state having about 8% higher frequency than the one-cluster state. With ε = 0.03, the frequency difference between the populations decreased to 27 mHz; the frequency of the two-cluster state (0.418 Hz) was about 7% higher than that of the one-cluster state (0.391 Hz). The grayscale plot (Figure 7B) of the chimera state shows that the first forty elements (population 1) are in-phase synchronized and elements 41–80 (population 2) form two clusters, in anti-phase configuration, with 17 and 23 elements in each cluster. The phase differences are shown in Figure 7C. The elements in population 1 are nearly in-phase with a phase difference close to 2π (or zero). The clusters in the two-cluster population are approximately in anti-phase; the phase difference shows the characteristics small amplitude oscillations around π (The high frequency modulation on top of the slow oscillation is due to in-cycle fluctuation of the phase; averaged phase models cannot explain such fluctuations). Finally, elements in between population 1 and 2 exhibit phase drifting. The lack of frequency synchrony can also be seen in the current time series in Figure 7D.

FIGURE 7

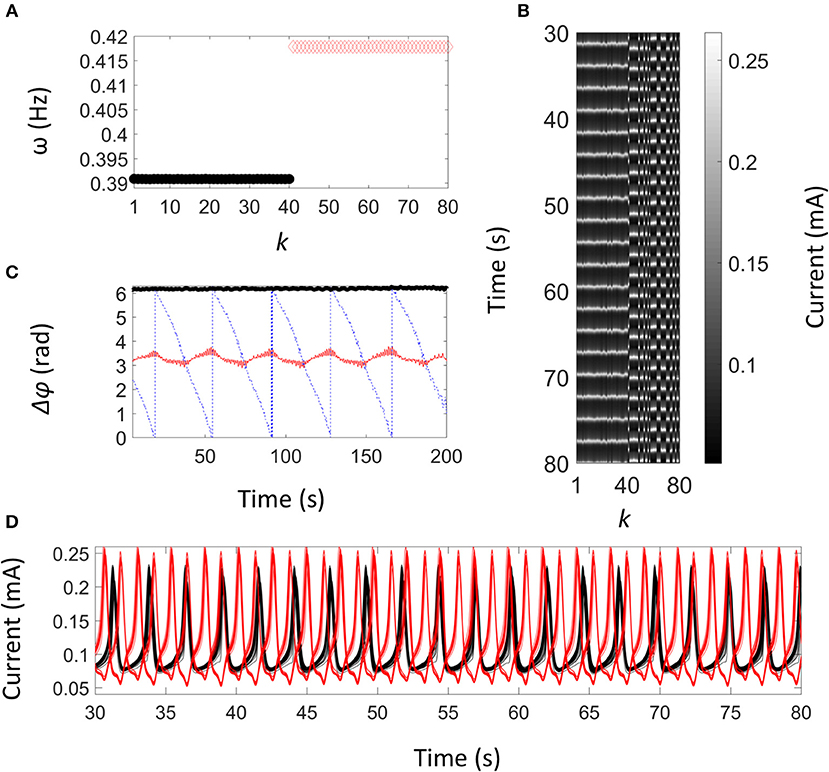
Figure 7. Experiments: Weak chimera state in modular network with weak cross coupling. (A) Frequency of elements (population 1: black solid circles; population 2: red open diamonds). (B) Space time plot of the current oscillations. Population 1: k = 1,…,40. Population 2: k = 41,…,80. (C) Phase difference between two elements in population one (black thick line φ₁ − φ₂), populations 2 red thin line (φ₄₁− φ₄₅), and between populations (blue dashed, φ₁ − φ₄₁). (D) Time series of the currents of the elements in the chimera state; population 1: black line, population 2: red line. V = 1,250 mV, R_ind = 580 Ohm, R_g = 9 Ohm, R_coll = 0.5 Ohm, K = 17.0 μS, ε = 0.03.

We also performed a long-term experiment to check for the robustness of the chimera state. The chimera state was stable for about 1,000 cycles, after which a one-cluster state was observed. In this parameter region, the system parameters exhibit a slow drift toward the Hopf bifurcation point. One explanation for the loss of the chimera state is that during this slow drift the oscillations become less non-linear for the chimera state to occur as the parameters leave the region where bistability is present.

We also confirmed that by increasing the coupling strength, the chimera state breaks down. While for ε = 0.1 stable chimera state occurs, with ε = 0.2 (with similar coupling strengths and initial conditions) only in-phase behavior can be observed in the experiments.

Conclusions

Robust weak chimera states were observed in a modular network of two populations of globally coupled electrochemical oscillators with simple resistive cross coupling between populations that is sufficiently weak (ε < 0.2). There are important differences in the observed chimera states compared to those in our previous studies [43–45]. A ring network of electrochemical oscillators, close to Hopf bifurcation, showed chimera state with long-range interactions [44, 45]. This chimera state was not very robust in the sense that even small heterogeneities destroyed the behavior, and only chimera “remnants” occurred. From an engineering perspective, even the relatively small system size (20 electrodes) required large number (140) of coupling resistors and capacitances. In addition, the chimera state only occurred as a transient behavior, for about 80–100 cycles. In the weak chimera state reported here, global coupling within and between the modules can be induced with one resistance each; this design greatly simplifies the experimental setup. Because the chimera state is very robust it does not require adjustment of natural frequencies, and the chimera state is sustained for many hundreds of cycles.

In identifying the experimental conditions for the chimera state, we relied on our previous study [43], where two populations of weakly non-linear oscillators were coupled with a strongly non-linear feedback mechanism. However, here we assumed that the same type of non-linearities can be obtained with linear (difference) coupling of highly non-linear oscillators. Such conditions (1, 230 mV ≤ V ≤ 1, 270 mV) were found far from the Hopf bifurcation (V ≈ 1.10 V) in the electrochemical system. While the parameter region favorable for the chimera state is relatively small (40 mV) compared to the region of oscillations (~200 mV), we note that we focused here on weak chimeras of a particular type with one- and two-cluster states with distinct frequencies. Weak chimeras could also occur with other initial conditions (e.g., with balanced and unbalanced two-cluster states) and parameter regions with other types of desynchronized clusters, e.g., two- and three-cluster states; see also Bick et al. [29].

Similar weak chimera states could be observed in many other chemical systems. For example, other electrochemical systems and the BZ reaction can generate rich variety of clusters, in particular, when the sign of the coupling strength can also be varied (e.g., excitatory and inhibitory coupling) [31, 39]. The weak chimera state could contribute to exploring chimeras in robust biological systems, e.g., circadian clocks [57], and dynamical diseases [58]; see also [59] for a recent review. Along these lines, we showed that an integrate-and-fire neuron model, with refractory period can generate bistability between cluster states in globally coupled populations [56]. Other possible biological system could include the oscillatory glycolysis, where highly non-linear feedback mechanisms are common [60].

Author Contributions

IK and CB conceived the presented idea. CB encouraged IK and JO-E to investigate the weak chimeras in modular networks. IK and JO-E planned the experiments and the numerical simulations. JO-E performed the experiments and numerical simulations, and processed the data. JO-E took the lead in writing the manuscript. IK and CB revised the manuscript. IK supervised the project. All authors provided critical feedback and helped shape the research, analysis, and manuscript.

Funding

IK acknowledges support from National Science Foundation CHE-1465013 grant.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Pikovsky AS, Rosenblum MG, Kurths J. Synchronization: A Universal Concept in Non-Linear Sciences. Cambridge: Cambridge University Press (2001). doi: 10.1017/CBO9780511755743

CrossRef Full Text | Google Scholar

2. Marek M, Stuchl I. Synchronization in two interacting oscillatory systems. Biophys Chem. (1975) 3:241–8. doi: 10.1016/0301-4622(75)80016-0

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Crowley MF, Field RJ. Electrically coupled Belousov-Zhabotinskii oscillators. 1. Experiments and simulations. J Phys Chem. (1986) 90:1907–15. doi: 10.1021/j100400a033

CrossRef Full Text | Google Scholar

4. Crowley MF, Epstein IR. Experimental and theoretical studies of a coupled chemical oscillator: phase death, multistability and in-phase and out-of-phase entrainment. J Phys Chem. (1989) 93:2496–502. doi: 10.1021/j100343a052

CrossRef Full Text | Google Scholar

5. Fujii H, Sawada Y. Phase-difference locking of coupled oscillating chemical systems. J Chem Phys. (1978) 69:3830–2. doi: 10.1063/1.437048

CrossRef Full Text | Google Scholar

6. Nakajima K, Sawada Y. Experimental studies on the weak coupling of oscillatory chemical reaction systems. J Chem Phys. (1980) 72:2231–4. doi: 10.1063/1.439466

CrossRef Full Text | Google Scholar

7. Booth V, Erneux T, Laplante J-P. Experimental and numerical study of weakly coupled bistable chemical reactors. J Phys Chem. (1994) 98:6537–40. doi: 10.1021/j100077a019

CrossRef Full Text | Google Scholar

8. Dechert G, Zeyer K, Lebender D, Schneider F. Recognition of phase patterns in a chemical reactor network. J Phys Chem. (1996) 100:19043–8. doi: 10.1021/jp9616066

CrossRef Full Text | Google Scholar

9. Toiya M, Vanag VK, Epstein IR. Diffusively coupled chemical oscillators in a microfluidic assembly. Angew Chem Int Ed. (2008) 47:7753–5. doi: 10.1002/anie.200802339

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Toiya M, Gonzalez-Ochoa HO, Vanag VK, Fraden S, Epstein IR. Synchronization of chemical micro-oscillators. J Phys Chem Lett. (2010) 1:1241–6. doi: 10.1021/jz100238u

CrossRef Full Text | Google Scholar

11. Taylor AF, Tinsley MR, Wang F, Huang ZY, Showalter K. Dynamical quorum sensing and synchronization in large populations of chemical oscillators. Science. (2009) 323:614–7. doi: 10.1126/science.1166253

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Taylor AF, Tinsley MR, Wang F, Showalter K. Phase clusters in large populations of chemical oscillators. Angew Chem Int Edit. (2011) 50:10161–4. doi: 10.1002/anie.201008248

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Okano T, Miyakawa K. Feedback-controlled dynamics in a two-dimensional array of active elements. Phys Rev E. (2009) 80:026215. doi: 10.1103/PhysRevE.80.026215

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Vanag VK, Epstein IR. Pattern formation in a tunable medium: the Belousov-Zhabotinskii reaction in an aerosol OT microemulsion. Phys Rev Lett. (2001) 87:228301. doi: 10.1103/PhysRevLett.87.228301

CrossRef Full Text | Google Scholar

15. Wickramasinghe M, Kiss IZ. Synchronization of Electrochemical Oscillators. Engineering of Chemical Complexity. New Jersey: Wolrd Scientific (2013). p. 215–36. doi: 10.1142/9789814390460_0011

CrossRef Full Text | Google Scholar

16. Kiss IZ, Zhai Y, Hudson JL. Emerging coherence in a population of chemical oscillators. Science. (2002) 296:1676–8. doi: 10.1126/science.1070757

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kiss IZ, Zhai YM, Hudson JL. Predicting mutual entrainment of oscillators with experiment-based phase models. Phys Rev Lett. (2005) 94:248301. doi: 10.1103/PhysRevLett.94.248301

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kiss IZ, Rusin CG, Kori H, Hudson JL. Engineering complex dynamical structures: sequential patterns and desynchronization. Science. (2007) 316:1886–9. doi: 10.1126/science.1140858

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Manrubia SC, Mikhailov AS, Zanette DH. Emergence of Dynamical Order: Synchronization Phenomena in Complex Systems. Singapore: World Scientific. (2004). doi: 10.1142/9789812562463

CrossRef Full Text | Google Scholar

20. Epstein IR, Pojman JA. An Introduction to Non-Linear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos. Oxford: Oxford University Press (1998).

Google Scholar

21. Nakao H. Phase reduction approach to synchronisation of non-linear oscillators. Contemp Phys. (2016) 57:188–214. doi: 10.1080/00107514.2015.1094987

CrossRef Full Text | Google Scholar

22. Zhai YM, Kiss IZ, Kori H, Hudson JL. Desynchronization and clustering with pulse stimulations of coupled electrochemical relaxation oscillators. Physica D. (2010) 239:848–56. doi: 10.1016/j.physd.2009.06.004

CrossRef Full Text | Google Scholar

23. Zhai Y, Kiss IZ, Hudson JL. Control of complex dynamics with time-delayed feedback in populations of chemical oscillators: desynchronization and clustering. Ind Eng Chem Res. (2008) 47:3502–14. doi: 10.1021/ie0708632

CrossRef Full Text | Google Scholar

24. Panaggio MJ, Abrams DM. Chimera states: co-existence of coherence and incoherence in networks of coupled oscillators. Nonlinearity. (2015) 28:R67–87. doi: 10.1088/0951-7715/28/3/R67

CrossRef Full Text | Google Scholar

25. Omel'Chenko OE. The mathematics behind chimera states. Nonlinearity. (2018) 31:R121–64. doi: 10.1088/1361-6544/aaaa07

CrossRef Full Text | Google Scholar

26. Battogtokh D, Kuramoto Y. Coexistence of coherence and incoherence. Non-lin Phenom Complex Syst. (2002) 5:380–5.

Google Scholar

27. Abrams DM, Strogatz SH. Chimera states for coupled oscillators. Phys Rev Lett. (2004) 93:174102. doi: 10.1103/PhysRevLett.93.174102

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ashwin P, Burylko O. Weak chimeras in minimal networks of coupled phase oscillators. Chaos. (2015) 25:013106. doi: 10.1063/1.4905197

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Bick C, Ashwin P. Chaotic weak chimeras and their persistence in coupled populations of phase oscillators. Nonlinearity. (2016) 29:1468–86. doi: 10.1088/0951-7715/29/5/1468

CrossRef Full Text | Google Scholar

30. Kemeth FP, Haugland SW, Schmidt L, Kevrekidis IG, Krischer K. A classification scheme for chimera states. Chaos. (2016) 26:094815. doi: 10.1063/1.4959804

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tinsley MR, Nkomo S, Showalter K. Chimera and phase-cluster states in populations of coupled chemical oscillators. Nat Phys. (2012) 8:662–5. doi: 10.1038/nphys2371

CrossRef Full Text | Google Scholar

32. Nkomo S, Tinsley MR, Showalter K. Chimera states in populations of non-locally coupled chemical oscillators. Phys Rev Lett. (2013) 110:244102. doi: 10.1103/PhysRevLett.110.244102

CrossRef Full Text | Google Scholar

33. Nkomo S, Tinsley MR, Showalter K. Chimera and chimera-like states in populations of non-locally coupled homogeneous and heterogeneous chemical oscillators. Chaos. (2016) 26:094826. doi: 10.1063/1.4962631

CrossRef Full Text | Google Scholar

34. Totz JF, Rode J, Tinsley MR, Showalter K, Engel H. Spiral wave chimera states in large populations of coupled chemical oscillators. Nat Phys. (2018) 14:282–5. doi: 10.1038/s41567-017-0005-8

CrossRef Full Text | Google Scholar

35. Haugland SW, Schmidt L, Krischer K. Self-organized alternating chimera states in oscillatory media. Sci Rep. (2015) 5:9883. doi: 10.1038/srep09883

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kemeth FP, Haugland SW, Krischer K. Symmetries of chimera states. Phys Rev Lett. (2018) 120:214101. doi: 10.1103/PhysRevLett.120.214101

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Schmidt L, Krischer K. Clustering as a prerequisite for chimera states in globally coupled systems. Phys Rev Lett. (2015) 114:034101. doi: 10.1103/PhysRevLett.114.034101

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Schmidt L, Krischer K. Chimeras in globally coupled oscillatory systems: from ensembles of oscillators to spatially continuous media. Chaos. (2015) 25:064401. doi: 10.1063/1.4921727

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Schmidt L, Schönleber K, Krischer K, García-Morales V. Coexistence of synchrony and incoherence in oscillatory media under non-linear global coupling. Chaos. (2014) 24:013102. doi: 10.1063/1.4858996

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Schönleber K, Zensen C, Heinrich A, Krischer K. Pattern formation during the oscillatory photoelectrodissolution of n-type silicon: turbulence, clusters and chimeras. New J Phys. (2014) 16:063024. doi: 10.1088/1367-2630/16/6/063024

CrossRef Full Text | Google Scholar

41. Kumar P, Verma DK, Parmananda P. Partially synchronized states in an ensemble of chemo-mechanical oscillators. Phys Lett A. (2017) 381:2337–43. doi: 10.1016/j.physleta.2017.05.032

CrossRef Full Text | Google Scholar

42. Koper MTM. Oscillations and complex dynamical bifurcations in electrochemical systems Adv Chem Phys. (1996) 92:161–298. doi: 10.1002/9780470141519.ch2

CrossRef Full Text | Google Scholar

43. Bick C, Sebek M, Kiss IZ. Robust weak chimeras in oscillator networks with delayed linear and quadratic interactions. Phys Rev Lett. (2017) 119:168301. doi: 10.1103/PhysRevLett.119.168301

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wickramasinghe M, Kiss IZ. Spatially organized dynamical states in chemical oscillator networks: synchronization, dynamical differentiation, and chimera patterns. PLoS ONE. (2013) 8:e80586. doi: 10.1371/journal.pone.0080586

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Wickramasinghe M, Kiss IZ. Spatially organized partial synchronization through the chimera mechanism in a network of electrochemical reactions. Phys Chem Chem Phys. (2014) 16:18360–9. doi: 10.1039/C4CP02249A

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Thoubaan M, Ashwin P. Existence and stability of chimera states in a minimal system of phase oscillators. Chaos. (2018) 28:103121. doi: 10.1063/1.5044750

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wickramasinghe M, Kiss IZ. Synchronization of electrochemical oscillators with differential coupling. Phys Rev E. (2013) 88:062911. doi: 10.1103/PhysRevE.88.062911

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kiss IZ, Kazsu Z, Gáspár V. Tracking unstable steady states and periodic orbits of oscillatory and chaotic electrochemical systems using delayed feedback control. Chaos. (2006) 16:033109. doi: 10.1063/1.2219702

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Wolfrum M, Omel'chenko OE. Chimera states are chaotic transients. Phys Rev E. (2011) 84:015201. doi: 10.1103/PhysRevE.84.015201

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Ashwin P, Swift JW. The dynamics of n weakly coupled identical oscillators. J Non-lin Sci. (1992) 2:69–108. doi: 10.1007/BF02429852

CrossRef Full Text | Google Scholar

51. Okuda K. Variety and generality of clustering in globally coupled oscillators. Physica D. (1993) 63:424–36. doi: 10.1016/0167-2789(93)90121-G

CrossRef Full Text | Google Scholar

52. Haim D, Lev O, Pismen LM, Sheintuch M. Modeling periodic and chaotic dynamics in anodic nickel dissolution. J Phys Chem. (1992) 96:2676–81. doi: 10.1021/j100185a051

CrossRef Full Text | Google Scholar

53. Zhai Y, Kiss IZ, Hudson J. Emerging coherence of oscillating chemical reactions on arrays: experiments and simulations. Ind Eng Chem Res. (2004) 43:315–26. doi: 10.1021/ie030164z

CrossRef Full Text | Google Scholar

54. Kiss IZ, Wang W, Hudson JL. Experiments on arrays of globally coupled periodic electrochemical oscillators. J Phys Chem B. (1999) 103:11433–44. doi: 10.1021/jp992471h

CrossRef Full Text | Google Scholar

55. Kori H, Kuramoto Y, Jain S, Kiss IZ, Hudson JL. Clustering in globally coupled oscillators near a Hopf bifurcation: theory and experiments. Phys Rev E. (2014) 89:062906. doi: 10.1103/PhysRevE.89.062906

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Kori H, Kiss IZ, Jain S, Hudson JL. Partial synchronization of relaxation oscillators with repulsive coupling in autocatalytic integrate-and-fire model and electrochemical experiments. Chaos. (2018) 28:045111. doi: 10.1063/1.5022497

CrossRef Full Text | Google Scholar

57. Rattenborg NC, Amlaner CJ, Lima SL. Behavioral, neurophysiological and evolutionary perspectives on unihemispheric sleep. Neurosci Biobehav Rev. (2000) 24:817–42. doi: 10.1016/S0149-7634(00)00039-7

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Andrzejak RG, Rummel C, Mormann F, Schindler K. All together now: analogies between chimera state collapses and epileptic seizures. Sci Rep. (2016) 6:23000. doi: 10.1038/srep23000

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bick C, Goodfellow M, Laing CR, Martens EA. Understanding the dynamics of biological and neural oscillator networks through mean-field reductions: a review. eprint arXiv:190205307. (2019).

Google Scholar

60. Dhumpa R, Truong TM, Wang X, Bertram R, Roper MG. Negative feedback synchronizes islets of langerhans. Biophys J. (2014) 106:2275–82. doi: 10.1016/j.bpj.2014.04.015

PubMed Abstract | CrossRef Full Text | Google Scholar