Joan-Pau Sánchez
Rita Neves
Hodei Urrutxua- 1Centre of Autonomous and Cyber-Physical Systems, School of Aerospace, Cranfield University, Bedfordhire, United Kingdom
- 2European Institute for Aviation Training and Accreditation, Universidad Rey Juan Carlos, Madrid, Spain
In simple terms, an asteroid retrieval mission envisages a spacecraft that rendezvous with an asteroid, lassos it and hauls it back to the Earth's neighborhood. Speculative engineering studies for such an ambitious mission concept appeared in scientific literature at the beginning of the space age. This early work employed a two-body dynamical framework to estimate the Δv costs entailed with hauling an entire asteroid back to Earth. The concept however has experienced a revival in recent years, stimulated by the inclusion of a plan to retrieve a small asteroid in NASA's 2014 budget. This later batch of work is well aware of technological limitations, and thus envisages a much more level-headed space system, capable of delivering only the most minimal change of linear momentum to the asteroid. As a consequence, the design of retrieval trajectories has evolved into strategies to take full advantage of low energy transfer opportunities, which must carefully account for the simultaneous gravitational interactions of the Sun, Earth, and Moon. The paper reviews the published literature up to date, and provides a short literature survey on the historical evolution of the concept. This literature survey is particularly focused on the design of asteroid retrieval trajectories, and thus the paper provides a comprehensive account of: the endgame strategies considered so far, the different dynamical models and the trajectory design methodologies.
Introduction
Our Solar System is crisscrossed by millions of minor bodies, including asteroids and comets. Significant attention is devoted to these small and irregular objects, since they ultimately hold the key to understand the formation and evolution of our Solar System. NASA, ESA, JAXA, and recently the China National Space Administration (CNSA) have conceived and launched a series of missions to obtain data from such bodies; particularly, from near Earth asteroids (NEAs). Among all asteroids, NEAs have stepped into prominence because they are the easiest celestial bodies to reach from the Earth, while also representing a potential impact threat to our planet [1].
Furthermore, in recent years, the concept of utilization of in-space resources has also been receiving a renewed and notable support. In-space resources would clearly benefit science and exploration, since their utilization in space would enable otherwise unaffordable mission scenarios. An increasing number of scientists and engineers are now advocating for the necessary technologies to prospect, mine and utilize materials in space [2]. Asteroids present particularly appealing concentrations of potentially valuable resources, as well as a plethora of useful materials [3]; e.g., volatiles, such as water, may be found in carbonaceous chondrite asteroids, while metals, semi-conductors and rare Earth elements are present in metal-rich asteroids or ordinary chondrites.
Amid these trends, asteroid retrieval or capture missions were proposed. This mission concept envisages a spacecraft that rendezvous with an asteroid, lassos it and hauls it back to the Earth's neighborhood, so that it can be more easily accessed. The mission has clear synergies with all three of the above aspects of asteroid missions: science, planetary defense and resource utilization.
The paradigm of in-space utilization of asteroid resources was conceived together with the pioneering of rocketry at the start of twentieth century [4]. Thus, with the beginning of the space race, rocketry futurists, such as Cole and Cox [5], began to envisage ambitious mission scenarios where asteroids would be moved from their original orbits by means of large nuclear propulsion systems, for subsequent extraction of their resources. However, a much more level-headed mission concept, and serious effort to develop it, was pursued more recently; within NASA's Asteroid Initiative. Announced in 2013, the Asteroid Initiative included, among other activities, the Asteroid Redirect Robotic Mission (ARRM), which initially1 aimed at hauling an asteroid to a distant retrograde lunar orbit [6].
It is immediately clear that capturing an asteroid, whose mass may be several orders of magnitude larger than that of a typical interplanetary spacecraft (~103 kg), will require an extremely powerful propulsion system and/or an extremely low-energy transfer. This short paper concerns with the latter topic: the body of literature studying trajectory opportunities to retrieve asteroids has seen a many-fold increase in the last few years. Hence, the objective of this paper is to compile a short literature review and state-of-the-art of the trajectory design methodologies for the retrieval of asteroids.
The paper is structured as follows: section Introduction provides a general background introduction and a statement of the aim of the paper. Section Trajectories to Move an Asteroid contains the main literature survey, which follows a rough chronological order, where exceptions to the strict chronology are allowed for the sake of clarity. Section Trajectories to Move an Asteroid's literature survey focuses only on published work that has tackled the problem of designing trajectories to retrieve asteroids. Section Concluding Remarks instead provides a non-comprehensive literature review of a limited number of issues that relate to the trajectory design for asteroid retrieval.
Trajectories to Move an Asteroid
Conceptually, the trajectory design for asteroid retrieval missions can be sketched into two distinctive elements: the Earth delivery trajectory and the endgame orbit. The former accounts for the transfer and rendezvous trajectory with the target asteroid (outbound leg) and the Earth delivery trajectory to bring the asteroid into the planet's neighborhood (inbound leg). On the other hand, the endgame2 orbit refers to the selection of the particular destination orbit where the captured asteroid is to be placed. The dynamical richness of the Earth-Moon system offers a variety of appealing endgame options; Figure 1 shows a schematic view of the endgame options that have been considered so far in the literature. Table 1 summarizes inbound leg delivery trajectories and endgame strategies as published by some of the literature reviewed in the following paragraphs.
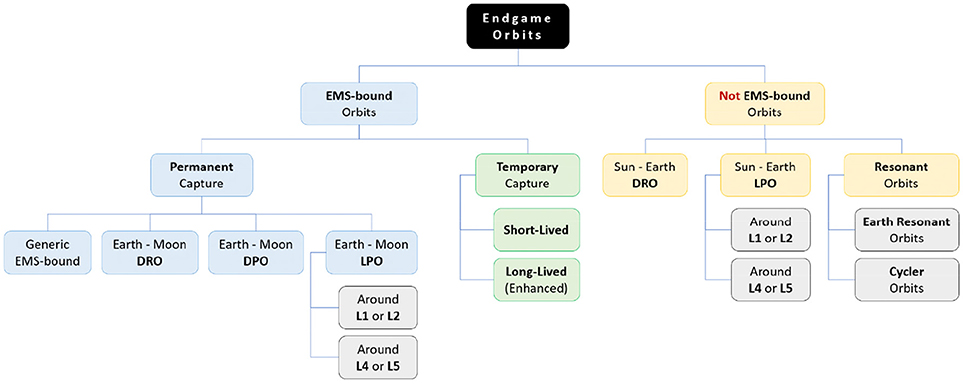
Figure 1. Endgame options tree for asteroid retrieval missions. EMS, Earth-Moon System; DRO, Distant Retrograde Orbit; DPO, Distant Prograde Orbit; LPO, Libration Point Orbit.
Table 1. Summary of asteroid retrieval missions found in the literature.
The nineteenth century began with the discovery of asteroids, namely main belt objects, while it was not until the beginning of the twentieth century that NEAs were discovered. With only 50 known NEA by the late 70's [16], asteroids were already recognized as potential interplanetary stepping stones, prior to an eventual human mission to Mars [17], as well as potential targets for space resources [18].
Bender et al. [16] conducted the first comprehensive trajectory analysis for the retrieval of asteroids into Earth-bound orbits, i.e., with a characteristic energy (C3) smaller than 0 km2/s2. In their work, round-trip trajectories are shown to be possible with Δv from 6 km/s, as computed in a patched conics approximation and including Earth, Moon, and Venus gravity assists. O'Leary et al. [19] argued that minimizing the Δv of the out-bound leg reduces the total wet mass of the retrieval spacecraft, since the in-bound Δv was assumed to be achieved with a mass driver system and considering asteroidal reaction mass (i.e., the propellant for the return trip was expected to be obtained from in-situ resources). Nevertheless, the conceived retrieval spacecraft was still a colossal space endeavor, requiring on-orbit assembly and a total of 50 Space Shuttle launches [19]. This was due to the fact that the early population of NEAs was entirely made up with very large objects, since these are much brighter and easier to detect.
By early 2000, the population of known asteroids had already increased sufficiently to allow a sensible statistical analysis [20, 21]. Thus, instead of focusing on known objects, Sanchez and McInnes [22] analyze the orbital region that is accessible given a limiting Δv threshold, and study the statistical number of asteroids that should be found considering a state-of-the-art asteroid probability density function [21]. Using a free-phase patched conics approximation, Sanchez and McInnes [22] hypothesize that there should be a 10-m diameter asteroid that could be retrieved with only 30 m/s Δv.
Even a 10-m diameter boulder, whose density may range anywhere from 1.3 to 5.3 g/cm3 depending on composition and structure [23], is likely to be from 100s to 1000s of times heavier than the standard interplanetary spacecraft. Hence, propulsion systems with high exhaust velocity would appear to be the most suitable systems to haul large inert masses. This is identified in Brophy et al. [24], where a high-power solar electric propulsion mission is conceived to haul a 2-m notional boulder to rendezvous with the ISS. Similarly, Hasnain et al. [25] investigate the necessary thrust to haul a series of known low inclination asteroids into Earth-bound orbits, by means of implementing a sub-optimal control law and a constant thrust assumption in a patched conics dynamical framework.
Earlier, Massonnet and Mayssignac [26] argue that asteroids that could be easily maneuvered, as of with a small Δv, must be energetically close to the Earth. Following a similar framework, Baoyin et al. [7] search for asteroids with an Earth close approach well within the sphere of influence of the Earth. The work then implements an impulsive Δv maneuver such that the zero velocity curves (ZVC) in the elliptical restricted three-body problem (ER3BP) close at both Sun-Earth L1 and L2 points. Such an approach would effectively capture an asteroid, and Baoyin et al. [7] identify one object, 2009 BD, which could have been captured with a Δv of 410 m/s during its close encounter in 2009.
Asteroids energetically close to the Earth are also nearly co-orbital, thus Bombardelli et al. [27] implement a sub-optimal low-thrust control law to modify the asteroid period in order to insert the body into a Quasi-Satellite Orbit (QSO) around the Earth (also known as Sun-Earth Distant Retrograde Orbits). On the other hand, both Massonnet and Mayssignac [26] and García Yárnoz et al. [9] focus instead on the endgame of capturing asteroids into Sun-Earth libration point orbits (LPOs).
García Yárnoz et al. [9] present a systematic approach to design impulsive retrieval transfers into the stable hyperbolic manifold of Sun-Earth LPOs in the Circular Restricted Three-Body Problem (CR3BP). Easily Retrievable Objects (EROs) are then identified as all those asteroids that can be captured with a total Δv maneuver of <500 m/s, and an initial list of 12 such objects is provided.
The original ARRM concept was proposed in 2011 after a feasibility study workshop at the Keck Institute of Space Studies [8]. In Landau et al. [28] a round-trip retrieval trajectory to asteroid 2008 HU4 is shown to be able to retrieve up to 1,300 tons of material (i.e., ~7-m object). The retrieval spacecraft uses a high-power (~40 kW) solar electric propulsion, has a wet mass of 18 tons, of which 5.5 tons are dry mass. The retrieval trajectories benefit from out-bound and in-bound lunar gravity assists to increase or decrease the Earth-relative orbital energy (i.e., C3), as well as Earth-Earth leveraging transfers [29]. The endgame option is a lunar Distant Retrograde Orbit (LDRO), although options that are not Earth-bound are also discussed in Strange et al. [10].
It is thus widely agreed that a level-headed asteroid retrieval mission must use high-power electric propulsion and should target asteroids that are energetically close to the Earth. This implies that the design of low-thrust, low-energy trajectories must both: (1) solve the optimal control problem defined by a low-thrust trajectory; and (2) take into account dynamical models that carefully consider the simultaneous gravitational interaction of multiple bodies (i.e., Sun, Earth, and Moon). Lladó et al. [30] solve the optimal control problem for the low-thrust retrieval of 39 small asteroids. The transfer is computed in a two-body dynamical framework, however the targeted final state is that of the Sun-Earth L2 point as computed using JPL ephemeris model. Mingotti et al. [31] employ instead a CR3BP framework to solve the optimal control for the retrieval of the 12 EROs identified by García Yárnoz et al. [9]. Sánchez and García Yárnoz [32] present similar optimal control low-thrust solutions for 17 EROs. All [30–32] solve the optimal control problem using direct transcription methods, although their generation of necessary first guess solutions present a diverse range of techniques. He et al. [33] tackled the same optimal control problem in the restricted four-body dynamical framework (i.e., Sun, Earth, and Moon) within the context of a trajectory design competition, which proposed an asteroid retrieval mission as optimization challenge.
Granvik et al. [34] predict that one 3-m diameter asteroid should be on a temporarily captured orbit around the Earth every 10 years, due to a natural capture phenomenon that occurs in the dynamics of a multi-body system. Urrutxua et al. [11] studied how these temporary captures could be extended. In the specific case of 2006 RH120 (~3-m diameter object), an asteroid which temporarily orbited the Earth for about 1 year in 2007, Urrutxua et al. [11] show how its stay could have been lengthened to 5 years with a Δv of only 32 m/s. Extending the temporary capture to a more permanent one is considered by Verrier and Mcinnes [35], who discuss a chaos-assisted capture mechanism associated with Kolmogorov–Arnold–Moser (KAM) orbits. Verrier and McInnes [35] demonstrate the process within the dynamical framework of the planar Hill problem. De Sousa-Silva and Terra [36] discuss a similar long-term capture within regions of effective stability near the triangular points L4 and L5 of the Earth-Moon system CR3BP.
Both Verrier and McInnes [35] and De Sousa-Silva and Terra [36] agree with Urrutxua et al. [11] on the fact that, in order for these highly sensitive capture trajectories to be applicable to real test cases, high-precision numerical ephemerides are indispensable. In particular, as discussed by both Granvik et al. [34] and Urrutxua et al. [11], the Moon plays a paramount role in the temporary capture of asteroids. This is also investigated by Gong and Li [13] who, in a planar restricted three-body framework, characterize the heliocentric orbit conditions that lead to a capture after a Moon fly-by. The process is also demonstrated in an ephemeris model (DE405) for a few test cases.
The active role of the Moon in the process of capturing an asteroid is also investigated by Mingotti et al. [31] and Tan et al. [14]. In these cases, however, the design strategy focuses on exploiting the stable hyperbolic manifold structures associated with periodic orbits in the Earth-Moon CR3BP. Tan et al. [14] target Earth-Moon LPOs, while Mingotti et al. [37] also consider LDRO and Lunar Distant Prograde Orbits (LDPO). In both cases, the intrinsic instability of these orbits is exploited by back-propagating a set of stable hyperbolic manifolds, which can be targeted by the asteroid-spacecraft system. While the generation of the stable hyperbolic manifold structures is performed in the CR3BP, the back-propagation and/or targeting are carried out in a restricted four-body problem considering Sun, Earth, and Moon.
Finally, the role of the Earth, not only as destination of retrieval trajectories, but also as leverage to reduce the final retrieval Δv is explored by Bao et al. [12] and Neves and Sánchez [15]. Bao et al. [12] explore the use of Earth-Earth leveraging transfers, as well as Moon fly-bys, to facilitate the capture of asteroids. The approach however is a relatively high-energy, in the sense that Lambert arcs and patched conic approximation are considered. Instead, Neves and Sánchez [15] present a methodology to benefit from Earth encounters that occur well outside the classic sphere of influence. The methodology allows exploiting the chaotic sensitivity of the multi-body problem, albeit at the cost of extremely long transfers.
One more exotic capture mechanism was recently described in Tan et al. [38]. As in previous scenarios, Tan et al. [38] also target stable hyperbolic invariant manifolds associated with Sun-Earth LPOs; however, in this case, the change of velocity needed to carry out the capture is produced by a linear momentum exchange. This is achieved by modifying the trajectory of a smaller asteroid so that this either impacts the targeted capture asteroid or performs a tethered fly-by.
In summary, it is noteworthy to highlight the diverse set of endgame orbits that have been considered in the literature (see Figure 1). Each endgame strategy implies a different set of methodologies to approach the design of the retrieval transfer. A substantial amount of work has not targeted a specific final capture orbit, but instead considered the energy conditions to enable permanent (or long-term stable) capture within the Earth's sphere of influence [7, 11–13, 25]. The other common approach has been to target a specific final orbit for the captured object; such as, Lunar Distant Retrograde Orbits (LDROs), as for NASA's ARRM concept [28, 31, 39], Sun-Earth LPOs [9, 26, 32, 40], or Earth-Moon LPOs [14, 31]. Additionally, Near Rectilinear Lunar Halo Orbits (NRHO) have recently been considered, as these have attracted attention as possible locations for a potential cis-lunar space station [41]. Note that the trajectory design techniques used to target many of the above final capture orbits benefit from their intrinsic instability; in the sense that one can construct the so-called stable hyperbolic invariant manifold structures associated to these orbits, which can be used for efficient targeting of the retrieval transfer. However, some of the proposed final orbits are instead linearly stable [35, 36], and do not have such a mathematical construct associated with them.
Concluding Remarks
The intrinsic stability or instability of the final capture orbit has been often quoted as a critical issue for the choice of an appropriate location for the retrieved asteroid [8, 42]. Ideally, one would choose a stable orbit if this implies a well-behaved long term evolution of the uncontrolled trajectory. However, as shown by Roa and Handmer [43]3, a small deviation from a nominally stable LDRO may still trigger the escape from the Moon neighborhood. In contrast, station-keeping requirements for unstable orbits may be smaller than the standard station-keeping Δv budget for a geostationary satellite [44], as in the case of JWST [45]. Another important aspect which has not been yet fully explored is that of the navigability and controllability of the retrieval trajectory. Ceriotti and Sanchez [46] consider the impact of uncertainties in the insertion into the stable invariant manifolds associated with Sun-Earth LPOs. However, a full analysis considering navigation errors, uncertainties and maneuverability is still lacking.
The majority of the work has focused on the design of the in-bound retrieval trajectories. This should perhaps be expected, since the in-bound retrieval legs are key to the feasibility of the mission, especially regarding propulsion performance and propellant consumption. This is a clear consequence of the much larger mass that needs to be hauled on the way back, unless, of course, asteroidal reaction mass is considered [19, 47]. However, due to the long synodic period of easily retrievable objects, the out-bound trajectories need to be considered carefully indeed, to avoid a significant impact on the propulsion system and propellant consumption [48].
Note that the reviewed literature has only discussed the design of trajectories under the framework of gravitational forces. To the knowledge of the authors, no paper on trajectory design for asteroid retrieval missions has yet considered a non-gravitational acceleration, such as that caused by solar radiation pressure impinging on a solar sail [49]. Nevertheless, the benefit of a propulsion system requiring no reaction mass was identified early on within the wider literature on in-space resource utilization, (e.g., [50]). It must be noted however that the directionality of the thrust vector is heavily constrained for a solar sail [51], while the low thrust transfers discussed here assume a thrust vector that can be freely oriented.
Finally, from the discussion in section Trajectories to Move an Asteroid, the targeted population for low energy retrieval trajectories can be clearly identified as that of small asteroids in Earth-like orbits [9, 34]. As of July 2018, more than 18,000 NEAs have been discovered4, from which about 3,500 are boulder-sized (<30 m diameter) and may potentially be candidates to be moved with near- to mid-term propulsion technology, akin to the ones reported in Table 1. While important uncertainties on the amount of boulder-size near-Earth asteroids yet exist [52, 53], this number is likely to be in the order of thousands of millions. Hence, the completeness level of the easily retrievable asteroid population is extremely low. New wide-field ground-based surveys, such as the Large Synoptic Survey Telescope, are likely to increase these levels by several orders of magnitude [54, 55].
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
RN would like to acknowledge the support of the Amelia Earhart Fellowship grant and the Coachmakers' Eric Beverley Bursary. HU wishes to acknowledge funding from grant ESP2017-87271-P (MINECO/AEI/FEDER, UE).
Footnotes
1. ^The concept later evolved into a plan to haul a multi-ton boulder from the surface of a larger NEA, and was finally cancelled in 2017.
2. ^Term borrowed from chess, meaning the closing stage of a game, in which only a few pieces are left on the board; it is also used figuratively to refer to the final stage of some action or process (e.g., negotiation, dispute, contest, war, …).
3. ^Roa and Handmer [43] perturb a LDRO by adding a small Δv within the CR3BP framework.
References
1. Alvarez LW, Alvarez W, Asaro F, Michel HV. Extraterrestrial cause for the cretaceous-tertiary extinction. Science (1980) 208:1095–108. doi: 10.1126/science.208.4448.1095
2. Elvis M. Let's mine asteroids — for science and profit. Nature (2012) 485:549. doi: 10.1038/485549a
3. Lewis JS, Hutson ML. Asteroidal resource opportunities suggested by meteorite data. In Lewis JS, Matthews MS, Guerrieri ML, editors. Resources of Near-Earth Space. Tucson, AZ: University of Arizona Press (1993). p. 523–42.
4. Tsiolkovsky KE. The Exploration of Cosmic Space by Means of Reaction Devices. Scientific Review (1903).
5. Cole DM, Cox DW. Islands in Space: The Challenge of Planetoids Philadelphia, PA: Chilton Books (1964).
6. Gates M, Muirhead B, Naasz B, Mcdonald M, Mazanek D, Stich S, et al. NASA's Asteroid Redirect Mission concept development summary. In: 2015 IEEE Aerospace Conference. Big Sky, MT (2015). p. 1–13.
7. Baoyin H-X, Chen Y, Li J-F. Capturing near earth objects. Res Astron Astrophys. (2010) 10:587–98. doi: 10.1088/1674-4527/10/6/008
8. Brophy J, Culick F, Friedman L, Allen C, Baughman D, Bellerose J, et al. Asteroid Retrieval Feasibility Study. Pasadena, CA: Keck Institute for Space Studies, Califonia Institute of Technology, Jet Propulsion Laboratory (2012).
9. García Yárnoz D, Sanchez JP, Mcinnes CR. Easily retrievable objects among the NEO population. Celest Mech Dynam Astron. (2013) 116: 367–88. doi: 10.1007/s10569-013-9495-6
10. Strange NJ, Landau D, Longuski J, Chodas P. Identification of retrievable asteroids with the tisserand criterion. In: AIAA/AAS Astrodynamics Specialist Conference. San Diego, CA: American Institute of Aeronautics and Astronautics (2014).
11. Urrutxua H, Scheeres DJ, Bombardelli C, Gonzalo JL, Peláez J. Temporarily captured asteroids as a pathway to affordable asteroid retrieval missions. J Guid Control Dyn. (2015) 38:2132–45. doi: 10.2514/1.G000885
12. Bao C, Yang H, Barsbold B, Baoyin H. Capturing near-Earth asteroids into bounded Earth orbits using gravity assist. Astrophys Space Sci. (2015) 360:61. doi: 10.1007/s10509-015-2581-3
13. Gong S, Li J. Asteroid capture using lunar flyby. Adv Space Res. (2015) 56:848–58. doi: 10.1016/j.asr.2015.05.020
14. Tan M, Mcinnes C, Ceriotti M. Direct and indirect capture of near-Earth asteroids in the Earth–Moon system. Celest Mech Dynam Astron. (2017) 129:57–88. doi: 10.1007/s10569-017-9764-x
15. Neves R, Sánchez JP. Multi-fidelity design of low-thrust resonant captures for near-earth asteroids. J Guid Control Dyn. (2018). [Epub ahead of print].
16. Bender DF, Dunbar SR, Ross DJ. Round-trip missions to low-delta-V asteroids and implications for material retrieval. NASA Special Publ. (1979) 161–72.
17. Niehoff JC. Round-trip mission requirements for asteroids 1976 AA and 1973 EC. Icarus (1977) 31:430–8. doi: 10.1016/0019-1035(77)90146-4
18. O'neill GK. Space resources and settlements. In: Billingham J, Gilbreath W, O'leary B, editors. 1977 Summer Study. Washington, DC: NASA (1979).
19. O'leary B, Gaffey MJ, Ross DJ, Salkeld R. Retrieval of asteroidal materials. In: Billingham J, Gilbreath W, O'Leary B, editors. Space Resources and Settlements. Washington, DC: NASA (1979).
20. D'abramo G, Harris AW, Boattini A, Werner SC, Harris AW, Valsecchi GB. A simple probabilistic model to estimate the population of near-earth asteroids. Icarus (2001). 153:214–7. doi: 10.1006/icar.2001.6650
21. Bottke WF, Morbidelli A, Jedicke R, Petit J-M, Levison HF, Michel P, et al. Debiased orbital and absolute magnitude distribution of the near-earth objects. Icarus (2002) 156:399–433. doi: 10.1006/icar.2001.6788
22. Sanchez JP, Mcinnes CR. Asteroid resource map for near-earth space. J Spacec Rockets (2011) 48:153–65. doi: 10.2514/1.49851
23. Chesley SR, Chodas PW, Milani A, Yeomans DK. Quantifying the risk posed by potential earth impacts. Icarus (2002) 159:423–32. doi: 10.1006/icar.2002.6910
24. Brophy JR, Gershman R, Landau D, Polk J, Porter C, Yeomans D, et al. Asteroid return mission feasibility study. In: 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit 2011 (2011).
25. Hasnain Z, Lamb C, Ross SD. Capturing near-earth asteroids around earth. Acta Astron. (2012) 81:523–31. doi: 10.1016/j.actaastro.2012.07.029
26. Massonnet D, Mayssignac B. A captured asteroid: our david's stone for shielding earth and providing the cheapest extraterrestrial material. Acta Astron. (2006) 59:77–83. doi: 10.1016/j.actaastro.2006.02.030
27. Bombardelli C, Urrutxua H, Peláez J. Earth delivery of a small NEO with an ion beam shepherd. In: McAdams JV, McKinley DP, Berry MM, Jenkins KL, editors. Advances in the Astronautical Sciences. Vol. 143. Charleston, SC: Univelt, Inc. (2012). p. 371–8.
28. Landau D, Dankanich J, Strange N, Bellerose J, Llanos P, Tantardini M. Trajectories to Nab a NEA (Near-Earth Asteroid). In: AAS/AIAA 23rd Space Flight Mechanics Meeting. Kauai: American Astronautical Society (2013).
29. Sims JA, Longuski JM, Staugler AJ. Vinf leveraging for interplanetary missions: multiple-revolution orbit techniques. J Guid Control Dyn. (1997) 20:409–15. doi: 10.2514/2.4064
30. Lladó N, Ren Y, Masdemont JJ, Gómez G. Capturing small asteroids into a Sun–Earth Lagrangian point. Acta Astron. (2014) 95:176–88. doi: 10.1016/j.actaastro.2013.11.007
31. Mingotti G, Sánchez JP, Mcinnes CR. Combined low-thrust propulsion and invariant manifold trajectories to capture NEOs in the Sun–Earth circular restricted three-body problem. Celest Mech Dyn Astron. (2014) 120:309–36. doi: 10.1007/s10569-014-9589-9
32. Sánchez JP, García Yárnoz D. Asteroid retrieval missions enabled by invariant manifold dynamics. Acta Astron. (2016) 127:667–77. doi: 10.1016/j.actaastro.2016.05.034
33. He S, Zhu Z, Peng C, Ma J, Zhu X, Gao Y. Optimal design of near-Earth asteroid sample-return trajectories in the Sun–Earth–Moon system. Acta Mech Sin. (2016) 32:753–70. doi: 10.1007/s10409-015-0527-1
34. Granvik M, Vaubaillon J, Jedicke R. The population of natural Earth satellites. Icarus (2012) 218:262–77. doi: 10.1016/j.icarus.2011.12.003
35. Verrier PE, Mcinnes CR. Low-energy capture of asteroids onto kolmogorov–arnold–moser tori. J Guid Control Dyn. (2014) 38:330–5. doi: 10.2514/1.G000797
36. De Sousa-Silva PA, Terra MO. Long term capture of asteroids for resources and scientific exploitation using hyperbolic objects in the solar system. In: Proceedings of the International Astronautical Congress, IAC. Jerusalem (2015). p. 5410–9.
37. Mingotti G, Sánchez JP, Mcinnes C. Low energy, low-thrust capture of near earth objects in the Sun-Earth and Earth-Moon restricted three-body systems. In: AIAA/AAS Astrodynamics Specialist Conference. San Diego, CA: American Institute of Aeronautics and Astronautics (2014).
38. Tan M, Mcinnes CR, Ceriotti M. Low-energy near-earth asteroid capture using momentum exchange strategies. J Guid Control Dyn. (2018) 41:632–43. doi: 10.2514/1.G002957
39. Strange N, Landau D, Mcelrath T, Lantoine G, Lam T. Overview of mission design for NASA Asteroid Redirect Robotic Mission concept. In: 33rd International Electric Propulsion Conference (IEPC2013). Washington, DC: NASA. Jet Propulsion Laboratory (2013).
40. Sanchez JP, García Yárnoz D, Alessi EM, Mcinnes CR. Gravitational capture opportunities for asteroid retrieval missions. In: 63nd International Astronautical Congress. Naples: International Astronautical Federation (2012).
41. Strange N, Brophy J, Alibay F, Mcguire M.L, Muirhead B, Hack K.J. High power solar electric propulsion and the Asteroid Redirect Robotic Mission (ARRM). In: 2017 IEEE Aerospace Conference (2017). p. 1–10.
42. Muirhead BK, Brophy JR. Asteroid redirect robotic mission feasibility study. In: Aerospace Conference, 2014 IEEE. Big Sky, MT (2014). p. 1–14.
43. Roa J, Handmer CJ. Quantifying hazards: asteroid disruption in lunar distant retrograde orbits. arXiv preprint arXiv:1505.03800 (2015).
44. Simó C, Gómez G, Llibre J, Martínez R, Rodríguez J. On the optimal station keeping control of halo orbits. Acta Astronautica (1987) 15:391–7. doi: 10.1016/0094-5765(87)90175-5
45. Dichmann DJ, Alberding CM, Yu WH. Stationkeeping Monte Carlo simulation for the James Webb space telescope. In: International Symposium on Space Flight Dynamics 2014. Laurel, MD (2014).
46. Ceriotti M, Sanchez JP. Control of asteroid retrieval trajectories to libration point orbits. Acta Astron. (2016) 126:342–53. doi: 10.1016/j.actaastro.2016.03.037
48. Englander JA, Cardiff EH. Asteroid retrieval via direct launch and solar electric propulsion. In: Wilson RS, Zanetti R, Mackison DL, Abdelkhalik O, editors. Advances in the Astronautical Sciences. Vol. 152. Santa Fe, NM: Univelt, Inc. (2014). p. 1137–1153.
49. Mcinnes C. Solar Sailing: Technology, Dynamics and Mission Applications. London: Springer (2004).
50. Drexler KE. High performance solar sails and related reflecting devices. In: 4th Conference on Space Manufacturing Facilities Princeton University. Princeton, NJ: American Institute of Aeronautics and Astronautics (1979).
51. Dachwald B, Seboldt W. Multiple near-Earth asteroid rendezvous and sample return using first generation solar sailcraft. Acta Astron. (2005) 57:864–75. doi: 10.1016/j.actaastro.2005.04.012
52. Fedorets G, Granvik M, Jedicke R. Orbit and size distributions for asteroids temporarily captured by the Earth-Moon system. Icarus (2017) 285:83–94. doi: 10.1016/j.icarus.2016.12.022
53. Granvik M, Morbidelli A, Jedicke R, Bolin B, Bottke WF, Beshore E, et al. Debiased orbit and absolute-magnitude distributions for near-Earth objects. Icarus (2018) 312:181–207. doi: 10.1016/j.icarus.2018.04.018
54. Fedorets G, Granvik M, Jones L, Jedicke R. Discovering asteroids temporarily captured by the Earth with LSST. Honolulu, HI: IAU General Assembly (2015).
Keywords: near-earth asteroids, asteroid capture, low-energy trajectories, low-thrust trajectories, ballistic capture
Citation: Sánchez J-P, Neves R and Urrutxua H (2018) Trajectory Design for Asteroid Retrieval Missions: A Short Review. Front. Appl. Math. Stat. 4:44. doi: 10.3389/fams.2018.00044
Received: 28 February 2018; Accepted: 11 September 2018;
Published: 02 October 2018.
Edited by:
Elisa Maria Alessi, Consiglio Nazionale Delle Ricerche (CNR), ItalyReviewed by:
John R. Brophy, Jet Propulsion Laboratory, United StatesEnrico Stoll, Technische Universitat Braunschweig, Germany
Copyright © 2018 Sánchez, Neves and Urrutxua. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joan-Pau Sánchez, anAuc2FuY2hlekBjcmFuZmllbGQuYWMudWs=