Generic convergence of infinite products of nonexpansive mappings with unbounded domains

We study the generic convergence of infinite products of nonexpansive mappings with unbounded domains in hyperbolic metric spaces.

1. Introduction and the Main Result

Let (X, ρ) be a metric space and let R¹ denote the real line. We say that a mapping c : R¹ → X is a metric embedding of R¹ into X if ρ(c(s), c(t)) = |s − t| for all real s and t. The image of R¹ under a metric embedding will be called a metric line. The image of a real interval [a, b] = {t ∈ R¹: a ≤ t ≤ b} under such a mapping will be called a metric segment.

Assume that (X, ρ) contains a family M of metric lines such that for each pair of distinct points x and y in X, there is a unique metric line in M which passes through x and y. This metric line determines a unique metric segment joining x and y. We denote this segment by [x, y]. For each 0 ≤ t ≤ 1, there is a unique point z in [x, y] such that

$\rho (x,z)=t\rho (x,y)\text{and}\rho (z,y)=(1-t)\rho (x,y).$

This point is denoted by (1 − t)x ⊕ ty. We say that X, or more precisely, (X, ρ, M), is a hyperbolic metric space if

$\rho (\frac{1}{2}x\oplus \frac{1}{2}y,\frac{1}{2}x\oplus \frac{1}{2}z)\le \frac{1}{2}\rho (y,z)$

for all x, y, and z in X. An equivalent requirement is that

$\rho (\frac{1}{2}x\oplus \frac{1}{2}y,\frac{1}{2}w\oplus \frac{1}{2}z)\le \frac{1}{2}(\rho (x,w)+\rho (y,z))$

for all x, y, z, and w in X. A set K ⊂ X is called ρ-convex if [x, y] ⊂ K for all x and y in K.

It is clear that all normed linear spaces are hyperbolic in this sense. A discussion of more examples of hyperbolic spaces and, in particular, of the Hilbert ball can be found, for example, in Goebel and Reich [1] and Reich and Shafrir [2].

Let (X, ρ, M) be a complete hyperbolic metric space, and let K ⊂ X be a nonempty, closed and ρ-convex subset of (X, ρ). For each C: K → K, set C⁰(x) = x for all x ∈ K. Denote by 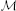the set of all sequences {A_t}^∞_{t = 1} of mappings A_t : K → K, t = 1, 2, …, such that for all integers t ≥ 1,

$\begin{array}{cc}\rho (A_t(x),A_t(y))\le \rho (x,y)\text{ for all}x,y\in K.& \left(1.1\right)\end{array}$

For each x ∈ X and each r > 0, set

B(x, r) = {y ∈ X: ρ(x, y) ≤ r} and B_K(x, r) = B(x, r) ∩ K.

Fix θ ∈ K. For each M, ϵ > 0, set

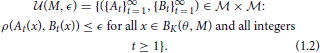
We equip the set 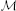with the uniformity which has the base

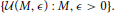
It is not difficult to see that the uniform space 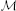is metrizable (by a metric d) and complete.

Denote by 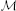_* the set of all {A_t}^∞_{t = 1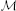} ∈ for which there exists a point $\tilde{x}$ ∈ K satisfying

$\begin{array}{cc}{A}_t(\tilde{x})=\tilde{x}\text{ for all integers}t\ge 1.& \left(1.3\right)\end{array}$

Denote by 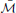_* the closure of the set 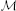_* in the uniform space 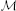. We consider the topological subspace 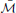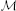_* ⊂ equipped with the relative topology and the metric d.

In this paper we study the asymptotic behavior of (unrestricted) infinite products of generic sequences of mappings belonging to the space 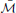_* and obtain convergence to a unique common fixed point. More precisely, we establish the following result, which generalizes the corresponding result in Reich and Zaslavski [3] (see also [4] and [5]). That result was obtained in the case where the set K was bounded.

Theorem 1.1. There exists a set 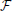⊂ 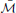_* which is a countable intersection of open and everywhere dense subsets of the complete metric space (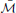_*, d) such that for each {B_t}^∞_{t = 1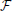} ∈ , the following properties hold:

(a) there exists a unique point x ∈ K such that B_t(x) = x for all integers t ≥ 1;

(b) if t ≥ 1 is an integer and y ∈ K satisfies B_t(y) = y, then y = x;

(c) for each ϵ > 0 and each M > 0, there exist a number δ > 0 and a neighborhood 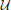of {B_t}^∞_{t = 1} in the metric space 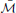_* such that if {C_t}^∞_{t = 1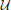} ∈ , t ∈ {1, 2, …}, and if y ∈ B_K(θ, M) satisfies ρ(y, C_t(y)) ≤ δ, then ρ(y, x) ≤ ϵ;

(d) for each ϵ > 0 and each M > 0, there exist a neighborhood 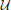of {B_t}^∞_{t = 1} in the metric space 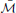_*, a number δ > 0 and a natural number q such that if {C_t}^∞_{t = 1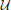} ∈ , m ≥ q is an integer, r: {1, …, m} → {1, 2, …}, and if {x_i}^m_{i = 0} ⊂ K satisfies

$\rho (x_0,\theta )\le M$

and

$\rho (C_{r(i)}(x_{i-1}),x_i)\le \delta ,i=1,\dots ,m,$

then

$\rho (x_i,\overline{x})\le ϵ,i=q,\dots ,m.$

2. Proof of Theorem 1.1

Elements of the space 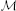will occasionally be denoted by a boldface letters: A = {A_t}^∞_{t = 1}, B = {B_t}^∞_{t = 1}, C = {C_t}^∞_{t = 1}, respectively.

Let A = {A_t}^∞_{t = 1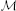} ∈ _* and γ ∈ (0, 1). There exists a point x_A ∈ K such that

$\begin{array}{cc}{A}_t(x_A)=x_A\text{ for all integers}t\ge 1.& \left(2.1\right)\end{array}$

For each integer t ≥ 1 and each x ∈ K, set

$\begin{array}{cc}{A}_{\gamma ,t}(x)=(1-\gamma )A_t(x)\oplus \gamma x_A.& \left(2.2\right)\end{array}$

By (1.1), (2.1), and (2.2), for all integers t ≥ 1 and all points x, y ∈ K,

$\begin{array}{cc}\begin{array}{l}\rho (A_{\gamma ,t}(x),A_{\gamma ,t}(y))\\ =\rho ((1-\gamma )A_t(x)\oplus \gamma x_A,(1-\gamma )A_t(y)\oplus \gamma x_A)\\ \le (1-\gamma )\rho (A_t(x),A_t(y))\le (1-\gamma )\rho (x,y)\end{array}& \left(2.3\right)\end{array}$

and

$\begin{array}{cc}{A}_{\gamma ,t}(x_A)=x_A.& \left(2.4\right)\end{array}$

In view of (2.2–2.4),

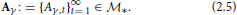
Let n be a natural number. Fix a number

$\begin{array}{cc}r(A,n)>n+2+\rho (\theta ,x_A),& \left(2.6\right)\end{array}$

a number

$\begin{array}{cc}M(A,n)>r(A,n)+\rho (\theta ,x_A)+2,& \left(2.7\right)\end{array}$

a positive number

$\begin{array}{cc}\delta (A,\gamma ,n)<{(8n)}^{-1}\gamma & \left(2.8\right)\end{array}$

and an integer

$\begin{array}{cc}q(A,\gamma ,n)>4+4nr(A,n){\gamma }^{-1}.& \left(2.9\right)\end{array}$

There exists an open neighborhood V(A, γ, n) of {A_{γ, t}}^∞_{t = 1} in 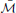_* such that

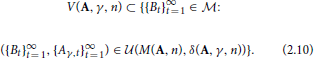
Assume that

$\begin{array}{cc}{\left\{C_t\right\}}_{t=1}^{\infty }\in V(A,\gamma ,n),& \left(2.11\right)\end{array}$

$\begin{array}{cc}m\ge q(A,\gamma ,n)& \left(2.12\right)\end{array}$

is an integer,

$\begin{array}{cc}r:\{1,\dots ,m\}\to \{1,2,\dots \},& \left(2.13\right)\end{array}$

and that a sequence {x_i}^m_{i = 0} ⊂ K satisfies

$\begin{array}{cc}\rho (x_0,\theta )\le n& \left(2.14\right)\end{array}$

and

$\begin{array}{cc}\rho (C_{r(i)}(x_{i-1}),x_i)\le \delta (A,\gamma ,n),i=1,\dots ,m.& \left(2.15\right)\end{array}$

We now show by induction that for all integers i = 0, …, m,

$\begin{array}{cc}\rho (x_i,x_A)\le r(A,n),& \left(2.16\right)\end{array}$

$\begin{array}{cc}\rho (x_i,\theta )\le M(A,n)& \left(2.17\right)\end{array}$

and if i < m, then

$\begin{array}{cc}\rho (x_{i+1},x_A)\le (1-\gamma )\rho (x_i,x_A)+2\delta (A,\gamma ,n).& \left(2.18\right)\end{array}$

Assume that p ∈ {0, …, m − 1}, (2.16) and (2.17) hold for all i = 0, …, p and that (2.18) holds for all nonnegative integers i < p. [Note that in view of (2.6), (2.7), and (2.14), our assumption holds for p = 0]. It follows from (2.3), (2.4), and (2.15) that

$\begin{array}{cc}\begin{array}{l}\rho (x_{p+1},x_A)\le \rho (x_{p+1},C_{r(p+1)}(x_p))+\rho (C_{r(p+1)}(x_p),x_A)\\ \le \delta (A,\gamma ,n)+\rho (C_{r(p+1)}(x_p),x_A)\\ \le \delta (A,\gamma ,n)+\rho (C_{r(p+1)}(x_p),\\ A_{\gamma ,r(p+1)}(x_p))+\rho (A_{\gamma ,r(p+1)}(x_p),x_A)\\ \le \delta (A,\gamma ,n)+\rho (C_{r(p+1)}(x_p),A_{\gamma ,r(p+1)}(x_p))\\ +(1-\gamma )\rho (x_p,x_A).\end{array}& \left(2.19\right)\end{array}$

By (2.17), which holds for i = p, (1.2), (2.10), and (2.11),

$\begin{array}{cc}\rho (C_{r(p+1)}(x_p),A_{\gamma ,r(p+1)}(x_p))\le \delta (A,\gamma ,n).& \left(2.20\right)\end{array}$

Relations (2.19) and (2.20) imply that

$\begin{array}{cc}\rho (x_{p+1},x_A)\le (1-\gamma )\rho (x_p,x_A)+2\delta (A,\gamma ,n).& \left(2.21\right)\end{array}$

Thus, (2.18) holds for i = p. It follows from (2.16), which holds for i = p, (2.6), (2.8), and (2.21) that

$\begin{array}{l}\rho (x_{p+1},x_A)\le (1-\gamma )r(A,n)+2\delta (A,\gamma ,n)\\ \le (1-\gamma )r(A,n)+2^{-1}\gamma \le r(A,n).\end{array}$

By the above relation and (2.7),

$\begin{array}{l}\rho (x_{p+1},\theta )\le \rho (x_{p+1},x_A)+\rho (x_A,\theta )\\ \le r(A,n)+\rho (x_A,\theta )\le M(A,n).\end{array}$

Hence (2.16) and (2.17) hold for i = p + 1 and the assumption made for p also holds for p + 1. Therefore, our assumptions hold for p = m, (2.16) and (2.17) hold for all i = 0, …, m, and (2.18) holds for all i = 0, …, m − 1.

We claim that for all i = q(A, γ, n), …, m,

$\begin{array}{cc}\rho (x_i,x_A)\le n^{-1}.& \left(2.22\right)\end{array}$

First we show that there exists i ∈ {0, …, q(A, γ, n)} such that (2.22) holds.

Assume the contrary. Then

$\begin{array}{cc}\rho (x_i,x_A)>n^{-1},i=0,\dots ,q(A,\gamma ,n).& \left(2.23\right)\end{array}$

By (2.8), (2.18), and (2.23), for all integers i = 0, …, q(A, γ, n) − 1,

$\begin{array}{l}\rho (x_i,x_A)-\rho (x_{i+1},x_A)\\ \ge \gamma \rho (x_i,x_A)-2\delta (A,\gamma ,n)\\ \ge \gamma n^{-1}-2\delta (A,\gamma ,n)\ge \gamma {(2n)}^{-1}.\end{array}$

In view of the above inequality and (2.16),

$\begin{array}{l}r(A,n)\ge \rho (x_0,x_A)\ge \rho (x_0,x_A)-\rho (x_{q(A,\gamma ,n)},x_A)\\ ={\displaystyle \sum _{i=0}^{q(A,\gamma ,n)-1}(\rho (}{x}_i,x_A)-\rho (x_{i+1},x_A))\ge q(A,\gamma ,n)\gamma {(2n)}^{-1}\end{array}$

and so,

$q(A,\gamma ,n)\le 2nr(A,n){\gamma }^{-1}.$

This contradicts (2.9). The contradiction we have reached proves that there indeed exists an integer j ∈ {0, …, q(A, γ, n)} such that

$\begin{array}{cc}\rho (x_j,x_A)\le n^{-1}.& \left(2.24\right)\end{array}$

Next we claim that (2.2) holds for all integers i ∈ {j, …, m}.

Indeed, by (2.24), inequality (2.22) is true for i = j. Now assume that i ∈ {j, …, m}, i < m and (2.22) holds. There are two cases:

$\begin{array}{cc}\rho (x_i,x_A)\le {(2n)}^{-1};& \left(2.25\right)\end{array}$

$\begin{array}{cc}\rho (x_i,x_A)>{(2n)}^{-1}.& \left(2.26\right)\end{array}$

Assume now that (2.25) holds. In view of (2.8), (2.18), and (2.25),

$\begin{array}{l}\rho (x_{i+1},x_A)\le (1-\gamma )\rho (x_i,x_A)+2\delta (A,\gamma ,n)\\ \le {(2n)}^{-1}+2\delta (A,\gamma ,n)\le n^{-1}.\end{array}$

Assume that (2.26) holds. Then it follows from (2.8), (2.18), (2.22), and (2.26) that

$\begin{array}{l}\rho (x_{i+1},x_A)\le (1-\gamma )\rho (x_i,x_A)+2\delta (A,\gamma ,n)\\ =\rho (x_i,x_A)-\gamma \rho (x_i,x_A)\\ +2\delta (A,\gamma ,n)\\ \le n^{-1}-\gamma {(2n)}^{-1}+2\delta (A,\gamma ,n)\le n^{-1}.\end{array}$

Thus, in both cases,

$\rho (x_{i+1},x_A)\le n^{-1}.$

This means that we have shown by induction that (2.22) is indeed valid for all i = q(A, γ, n), …, m. Clearly, we have proved that the following property holds:

(P) For each

${\left\{C_t\right\}}_{t=1}^{\infty }\in V(A,\gamma ,n),$

each integer m ≥ q(A, γ, n), each

$r:\{1,\dots ,m\}\to \{1,2,\dots \}$

and each sequence {x_i}^m_{i = 0} ⊂ K which satisfies

$\rho (x_0,\theta )\le n$

and

$\rho (C_{r(i)}(x_{i-1}),x_i)\le \delta (A,\gamma ,n),i=1,\dots ,m,$

we have

$\rho (x_i,x_A)\le n^{-1},i=q(A,\gamma ,n),\dots ,m.$

Set

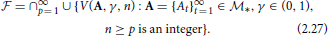
By (1.1), (2.1), and (2.2), for each A = {A_t}^∞_{t = 1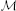} ∈ _*, each γ ∈ (0, 1), each integer t ≥ 1 and each x ∈ K, we have

$\begin{array}{cc}\begin{array}{l}\rho (A_{\gamma ,t}(x),A_t(x))=\rho ((1-\gamma )A_t(x)\oplus \gamma x_A,A_t(x))\\ \le \gamma \rho (A_t(x),x_A)\le \gamma \rho (x,x_A)\\ \le \gamma (\rho (x,\theta )+\rho (\theta ,x_A)).\end{array}& \left(2.28\right)\end{array}$

In view of (1.2) and (2.28),

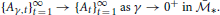
When combined with (2.27), this implies that 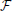is a countable intersection of open and everywhere dense subsets of _*.

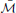Assume that

and M, ϵ > 0. Choose a natural number p such that

$\begin{array}{cc}p>8M+8\text{ and}{(8p)}^{-1}<ϵ.& \left(2.30\right)\end{array}$

By (2.27) and (2.29), there exist

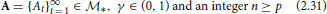
such that

$\begin{array}{cc}{\left\{B_t\right\}}_{t=1}^{\infty }\in V(A,\gamma ,n).& \left(2.32\right)\end{array}$

Let

$\begin{array}{cc}x\in B_K(\theta ,M),& \left(2.33\right)\end{array}$

let t ≥ 1 be an integer and consider the sequence {Bⁱ_t(x)}^∞_{i = 0}. By (2.30)–(2.33) and property (P) (applied to {C_s}^∞_{s = 1} = {B_s}^∞_{s = 1} and r(j) = t, j = 1, 2, …), for all integers i ≥ q(A, γ, n), we have

$\begin{array}{cc}\rho (B_t^i(x),x_A)\le n^{-1}<ϵ.& \left(2.34\right)\end{array}$

Since ϵ is an arbitrary positive number, we conclude that for each point z ∈ B_K(θ, M) and each integer t ≥ 1, {Bⁱ_t(z)}^∞_{i = 0} is a Cauchy sequence. Since M is any positive number, we see that for each integer t ≥ 1 and each z ∈ K, there exists

$\underset{i\to \infty }{\lim }{B}_t^i(z)$

in (X, ρ). In view of (3.34), for every integer t ≥ 1 and every z ∈ B_K(θ, M),

$\rho (\underset{i\to \infty }{\lim }{B}_t^i(z),x_A)\le ϵ.$

This implies that for each pair of points z₁, z₂ ∈ B_K(θ, M) and for each pair of natural numbers t₁, t₂,

$\rho (\underset{i\to \infty }{\lim }{B}_{t_1}^i(z_1),\underset{i\to \infty }{\lim }{B}_{t_2}^i(z_2))\le 2ϵ.$

Since ϵ, M are arbitrary positive numbers, we may conclude that for each pair of integers t₁, t₂ ≥ 1 and each pair of points z₁, z₂ ∈ K,

$\underset{i\to \infty }{\lim }{B}_{t_1}^i(z_1)=\underset{i\to \infty }{\lim }{B}_{t_2}^i(z_2).$

Let x ∈ K be such that

$\begin{array}{cc}\overline{x}=\underset{i\to \infty }{\lim }{B}_t^i(z)\text{ for all}z\in K\text{ and all integers}t\ge 1.& \left(2.35\right)\end{array}$

In view of (2.35),

$\begin{array}{cc}{B}_t(\overline{x})=\overline{x}\text{ for all integers}t\ge 1.& \left(2.36\right)\end{array}$

It immediately follows from (2.35) and (2.36) that properties (a) and (b) hold. We claim that property (c) also holds.

Let

${\left\{C_t\right\}}_{t=1}^{\infty }\in V(A,\gamma ,n),t\in \{1,2,\dots ,\},y\in B_K(\theta ,M)$

and assume that

$\begin{array}{cc}\rho (y,C_t(y))\le \delta (A,\gamma ,n).& \left(2.37\right)\end{array}$

Set

$\begin{array}{cc}\begin{array}{l}{y}_t=y,t=0,1,\dots ,\\ r(i)=t,i=1,2,\dots .\end{array}& \left(2.38\right)\end{array}$

It follows from (2.37) and (2.38) that for all integers t ≥ 1,

$\begin{array}{cc}\rho (y_i,C_{r(i)}(y_{i-1}))=\rho (y,C_t(y))\le \delta (A,\gamma ,n).& \left(2.39\right)\end{array}$

By (2.30), (2.31), (2.37–2.39) and property (P) applied to any integer m ≥ q(A, γ, n) and x_i = y_i, i = 0, …, m,

$\rho (y_i,x_A)\le n^{-1},i=q(A,\gamma ,n),\dots ,m,$

and

$\begin{array}{cc}\rho (y,x_A)\le n^{-1}.& \left(2.40\right)\end{array}$

In view of (2.30), (2.31), (2.34), (2.35), and (2.40),

$\begin{array}{cc}\rho (y,\overline{x})\le \rho (y,x_A)+\rho (x_A,\overline{x})\le 2n^{-1}<ϵ.& \left(2.41\right)\end{array}$

Thus, property (c) does hold, as claimed.

Finally, we show that property (d) holds too. It follows from (2.34) and (2.35) that

$\rho (x_A,\overline{x})\le n^{-1}.$

Assume that

${\left\{C_t\right\}}_{t=1}^{\infty }\in V(A,\gamma ,n),$

let m ≥ q(A, γ, n) be an integer, r: {1, …, m} → {1, 2, …}, and let {x_i}^m_{i = 0} ⊂ K satisfy

$\rho (x_0,\theta )\le M$

and

$\rho (C_{r(i)}(x_{i-1}),x_i)\le \delta (A,\gamma ,n),i=1,\dots ,m.$

By the relations above and property (P),

$\begin{array}{cc}\rho (x_i,x_A)\le n^{-1},i=q(A,\gamma ,n),\dots ,m.& \left(2.42\right)\end{array}$

It now follows from (2.30), (2.31), (2.41), and (2.42) that for all integers i = q(A, γ, n), …, m,

$\rho (x_i,\overline{x})\le \rho (x_i,x_A)+\rho (x_A,\overline{x})\le 2n^{-1}<ϵ.$

Thus, property (d) indeed holds. This completes the proof of Theorem 1.1.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

SR was partially supported by the Israel Science Foundation (Grant No. 389/12), by the Fund for the Promotion of Research at the Technion and by the Technion General Research Fund.

References

1. Goebel K, Reich S. Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. New York, NY; Basel: Marcel Dekker (1984).

2. Reich S, Shafrir I. Nonexpansive iterations in hyperbolic spaces. Nonlin Anal. (1990) 15:537–58.

Google Scholar

3. Reich S, Zaslavski AJ. Convergence of generic infinite products of nonexpansive and uniformly continuous operators. Nonlin Anal. (1999) 36:1049–65.

Google Scholar

4. Reich S, Zaslavski AJ. Inexact powers and infinite products of nonlinear operators. Int J Math Stat. (2010) 6:89–109.

Google Scholar

5. Reich S, Zaslavski AJ. Genericity in Nonlinear Analysis, Developments in Mathematics, Vol. 34. New York, NY: Springer (2014).