Dynamic RIS partitioning in NOMA systems using deep reinforcement learning

The rapid evolution of wireless communication technologies necessitates innovative solutions to meet the increasing performance requirements of future networks, particularly in terms of spectral efficiency, energy efficiency, and computational efficiency. Reconfigurable Intelligent Surfaces (RIS) and Non-Orthogonal Multiple Access (NOMA) are emerging as promising technologies to enhance wireless communication systems. This paper explores the dynamic partitioning of RIS elements in NOMA systems using Deep Reinforcement Learning (DRL) to optimize resource allocation and overall system performance. We propose a novel DRL-based framework that dynamically adjusts the partitioning of RIS elements to maximize the achievable sum rate and ensure fair resource distribution among users. Our architecture leverages the flexibility of RIS to create an intelligent radio environment, while NOMA enhances spectral efficiency. The DRL model is trained online, adapting to real-time changes in the communication environment. Empirical results demonstrate that our approach closely approximates the performance of the optimal iterative algorithm (exhaustive search) while reducing computational time by up to 90 percent. Furthermore, our method eliminates the need for an offline training phase, providing a significant advantage in dynamic environments by removing the requirement for retraining with every environmental change. These findings highlight the potential of DRL-based dynamic partitioning as a viable solution for optimizing RIS-aided NOMA systems in future wireless networks.

1 Introduction

Wireless communication has witnessed a significant transformation, from its origins with radio waves to the upcoming era of 6G technology. This progression began with basic radio communications and advanced through successive generations, each marking a leap in enhancing global connectivity. The introduction of 4G was a major advancement, delivering high-speed data transmission and setting the stage for the widespread adoption of mobile broadband. The current generation, 5G, is revolutionizing the field with its promise of very high speeds and minimal delay, enabling advancements like the Internet of Things (IoT) and the development of smart urban environments. Looking ahead, 6G is expected to further expand the horizons of connectivity and foster innovations on a large scale Giordani et al. (2020).

The constant quest for improved communication services, combined with the rapid evolution of wireless technologies, has propelled the continuous exploration and development of advanced wireless communication strategies. In this context, non-orthogonal multiple access (NOMA) has been identified as a key technology poised to enhance the efficiency of future wireless systems, thanks to its capacity to cater to distinct operational needs Makki et al. (2020). As we witness an exponential increase in global communication demands, the adoption of advanced multiple-access technologies like NOMA becomes essential.

Recently, reconfigurable intelligent surfaces (RISs) have emerged as an innovative technology in the field of advanced communication systems, offering notable advantages such as cost efficiency and the ability to create intelligent radio environments Basar et al. (2019); Liu et al. (2021). Their ability to modify the communication channel and environment in an eco-friendly and cost-effective manner has garnered significant attention, establishing RISs as a strong alternative to extensive multiple-input multiple-output (MIMO) systems and a key component in the next-generation of communication systems Khaleel and Basar (2021). RISs facilitate the modulation of signals in an energy-efficient way at a reduced cost, thereby playing a crucial role in securing and optimizing multi-user communication Huang et al. (2019).

However, the dynamic nature of wireless networks necessitates advanced strategies for the efficient allocation and partitioning of RIS elements, especially in multi-user environments. Addressing this need, Deep Reinforcement Learning (DRL) offers a promising approach by enabling systems to learn optimal partitioning strategies through interaction with the environment, without relying on predefined models or extensive offline training phases. This research builds upon our previous work Gevez et al. (2024), extending the exploration of RIS-aided NOMA systems through the application of DRL to optimize RIS partitioning for two users.

1.1 Literature review

To provide a comprehensive understanding of the significant advancements and persistent challenges in Reconfigurable Intelligent Surface (RIS)-aided NOMA systems, we review the existing literature. This review highlights key developments, innovative solutions, and areas requiring further exploration within the domain. By examining the current state of the art, we aim to identify the gaps that our research seeks to address, thereby contributing to the ongoing discourse and advancement of RIS-aided NOMA technologies.

Non-Orthogonal Multiple Access (NOMA): NOMA is primarily categorized into code-domain NOMA (CD-NOMA) and power-domain NOMA (PD-NOMA). CD-NOMA uses unique sparse spreading sequences for signal multiplexing across non-orthogonal frequency bands, effectively reducing user interference Liu and Yang (2021). Recent studies have explored new approaches in CD-NOMA to further improve spectral efficiency and reduce interference. For instance, Zhang X. et al. (2021) introduced an advanced sparse code design that significantly enhances the performance of CD-NOMA systems in dense user environments. Similarly, Kim et al. (2022) proposed a new coding scheme that improves the decoding accuracy in high-interference scenarios, making CD-NOMA more robust for practical applications.

Conversely, PD-NOMA, which enjoys more widespread application, allows the simultaneous sharing of time and frequency resources among users by differentiating signals based on their power levels Islam et al. (2017). Using successive interference cancellation (SIC), this method enables the differentiation of signals by their power intensity, allowing the coexistence of multiple users within the same non-orthogonal radio frequencies. Recent advancements in PD-NOMA have focused on optimizing power allocation strategies to enhance security and efficiency. For example, Liu J. et al. (2022) proposed a new power allocation scheme that improves the security of PD-NOMA systems against eavesdropping attacks while maintaining high spectral efficiency. Additionally, Wang T. et al. (2023) developed an adaptive power control algorithm that dynamically adjusts power levels based on real-time channel conditions, significantly improving overall system performance.

However, the traditional application of SIC in PD-NOMA requires a shared power strategy, which could inadvertently expose signals to potential security breaches. To address this, Chen Q. et al. (2023) developed an enhanced SIC mechanism that incorporates dynamic power adjustment to mitigate security risks without compromising system performance. Furthermore, Huang Y. et al. (2023) introduced a hybrid SIC approach that combines machine learning techniques with traditional SIC to predict and mitigate interference more effectively. These recent contributions highlight the continuous evolution of NOMA technologies in enhancing the efficiency, security, and robustness of wireless communication systems.

1.1.1 Reconfigurable Intelligent Surfaces (RISs)

Reconfigurable Intelligent Surfaces (RISs) have gained prominence as a cost-effective and energy-efficient solution to enhance wireless environments. Recent surveys, particularly those by Basar et al. (2023), clearly outline the development of RISs within 6G wireless communication technologies. These comprehensive reviews highlight RISs’ key advancements, showing their potential to overcome current challenges in signal efficiency, connectivity, and system performance.

Building on these insights, Wu et al. (2023) explore the integration of RIS with machine learning algorithms, showing how intelligent surfaces can adapt dynamically to changing wireless environments to optimize performance. Furthermore, Tang et al. (2022) provide an in-depth analysis of the potential of RIS to significantly enhance the capacity and reliability of wireless networks, especially in dense urban settings.

Recent studies also explore the application of RIS in millimeter-wave (mmWave) and terahertz communication systems. For example, Li et al. (2022) discuss the use of RIS to overcome the high path loss and signal blockage issues inherent in mmWave and terahertz bands, showcasing substantial improvements in signal strength and coverage. Additionally, Yang et al. (2023) investigate the deployment strategies of RIS in heterogeneous networks, highlighting their ability to facilitate seamless connectivity and robust performance in multi-tier network architectures.

Such scholarly efforts highlight RIS technology as a key development in the evolution of future wireless networks, setting a new standard for research and application in the field Basar et al. (2023); Wu et al. (2023); Tang et al. (2022); Li et al. (2022); Yang et al. (2023).

1.1.2 Machine learning (ml) in wireless communications

Machine learning (ML), particularly deep learning (DL) and DRL, has shown great potential in optimizing wireless communication systems. These approaches enable systems to learn and adapt to changing environments, enhancing performance without the need for manual configuration. For example, DL has been utilized for tasks such as user clustering, which significantly reduces computational demand and enables optimal power distribution through sequential decoding (Cui et al., 2018).

Recent advancements have further explored the integration of traditional ML models with DL techniques. Gao et al. (Mar. 2021) combined Gaussian mixture models with K-means clustering to effectively align interference and manage increasing network traffic. This hybrid approach has proven beneficial in dynamically adapting to fluctuating network conditions.

DRL has emerged as a particularly powerful tool in this domain, offering advanced methods for optimizing complex wireless communication tasks. For instance, Yang et al. (2021) applied DRL to optimize phase configurations in a NOMA framework supported by RIS, significantly enhancing spectral efficiency.

Recent studies have delved deeper into DRL’s applications in wireless communications. Wang et al. (2022) explored the use of DRL for resource allocation in heterogeneous networks, demonstrating its ability to achieve near-optimal performance with reduced computational overhead. Furthermore, Zhang et al. (2023b) investigated DRL-based dynamic spectrum access, showing substantial improvements in spectrum utilization and interference management.

Moreover, Li et al. (2023) developed a robust DRL framework to manage the inherent uncertainties in wireless environments, enhancing the reliability and efficiency of communication systems. Additionally, Sun et al. (2023) proposed a multi-agent DRL approach for cooperative spectrum sharing, which significantly improves network throughput and reduces latency.

Recent research by Chen R. et al. (2023) focused on DRL for real-time beamforming in massive multiple-input multiple-output (MIMO) systems, achieving notable gains in energy efficiency and signal quality. Another study by Huang L. et al. (2023) introduced a joint DRL framework for simultaneous optimization of power allocation and interference management in ultra-dense networks.

These advancements highlight the important role of ML, particularly DRL, in evolving next-generation wireless communication systems, driving significant improvements in efficiency, adaptability, and overall performance.

1.1.3 RIS-NOMA Integration

The study of different phase adjustment strategies in RIS-aided NOMA systems reveals a balance among reliability and system complexity, proposing a simplified phase selection method for random phase shifting to improve signal reception Ding et al. (2020). Recent research by Chen et al. (2021) further explores optimized phase adjustment algorithms, demonstrating substantial improvements in signal reception and overall system performance.

Furthermore, a partitioning algorithm designed to boost spectrum efficiency by improving the ergodic rate for all users, while ensuring fairness, has been put forward Khaleel and Basar (2022). Recent advancements by Zhao et al. (2022) have refined this algorithm, enhancing spectrum efficiency and user fairness in more dynamic network environments.

Additionally, a new simultaneously transmitting and reflecting (STAR)-RIS-aided NOMA scheme has been introduced. This scheme utilizes the unique capabilities of STAR-RIS to manage incident signals by either transmitting or reflecting them, thus integrating a NOMA framework to cater to diverse user needs through innovative signal management Zuo et al. (2021). Building on this, Zhang et al. (2023a) presented an advanced STAR-RIS design that further optimizes the balance between transmission and reflection, achieving higher spectral efficiency and better user experience.

Recent studies have also focused on integrating ML techniques with RIS-NOMA systems. Wang X. et al. (2023) proposed a ML-based optimization framework for RIS-NOMA, which dynamically adjusts system parameters to maximize performance. Another significant contribution is from Xu et al. (2023b), who introduced an adaptive ML-based framework for optimizing the placement and configuration of RIS in NOMA systems, achieving improved performance metrics in terms of both throughput and latency. This approach has shown significant potential in enhancing system adaptability and efficiency.

In conclusion, the integration of ML techniques with RIS-NOMA systems represents a significant advancement in the field of wireless communications. By leveraging the adaptability and efficiency of ML algorithms, these systems can dynamically optimize parameters to improve performance, spectral efficiency, and energy consumption. The continuous evolution of RIS-NOMA integration, driven by innovative ML-aided approaches, promises to significantly enhance the capabilities and robustness of future wireless communication networks.

1.2 Motivation

Integrating NOMA with RIS presents a promising solution to address the limitations of traditional communication systems, such as increased processing times. Despite these efforts, traditional allocation approaches face challenges, especially in large-scale systems, where they can lead to increased processing times. Our preceding research Gevez et al. (2024) ventured into a novel technique for distributing RIS elements, harnessing supervised learning to refine the partitioning of RIS and mitigate interference among users in non-line-of-sight (NLOS) scenarios. This initiative represents a significant step towards optimizing communication systems for the future, ensuring more efficient and effective utilization of RIS in enhancing wireless connectivity.

Building on our previous work, which utilized supervised learning for RIS partitioning, this study introduces a novel DRL-based framework. Our approach dynamically adjusts RIS partitioning to optimize resource allocation and enhance system performance. The proposed framework significantly improves upon previous methodologies by eliminating the offline training phase, thus enhancing adaptability to real-time network changes.

The enhancements detailed in this work are rooted in a deep understanding of the dynamic nature of wireless networks and the critical role of RIS in maximizing NOMA system performance. The contributions of our current study are characterized by several key advancements:

$•$ Introduction of a DRL-based framework for the dynamic optimization of RIS partitioning between two users, marking a significant evolution from the static and semi-static allocation strategies prevalent in our earlier work.

$•$ Removal of the offline training phase, a critical improvement that addresses one of the major limitations identified in earlier literature. This modification not only simplifies the deployment process but also enhances the model’s ability to adapt to real-time changes in network conditions.

$•$ Demonstration of the model’s ability to achieve near-optimal partitioning of RIS elements, thereby significantly enhancing both the sum achievable rate and fairness of the system. The real-time adaptability of our approach ensures near-optimal system performance even under rapidly changing conditions.

$•$ Provision of a detailed analysis that underscores the practical implications of employing DRL for the dynamic partitioning of RIS in NOMA systems. The findings from this study contribute to the broader discourse on the deployment of intelligent technologies in future wireless networks, paving the way for further innovation.

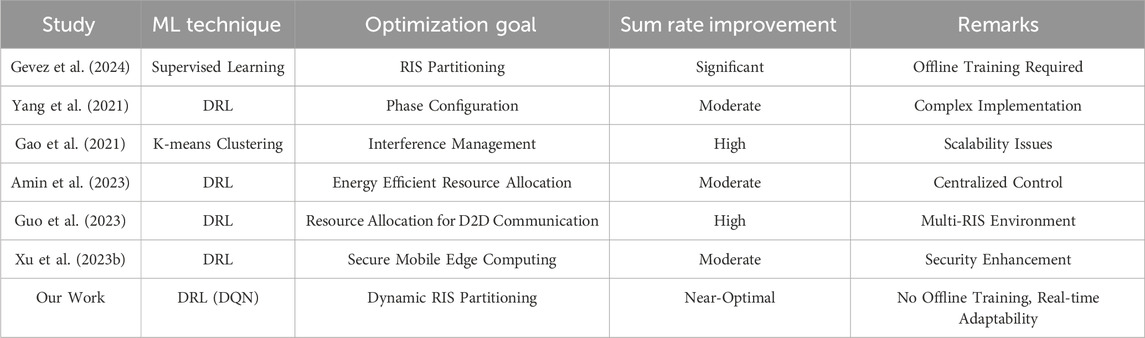
Table 1 contextualizes our work within the landscape of machine-learning-assisted RIS-aided NOMA literature focusing on sum rate optimization. Gevez et al (2024) used supervised learning for RIS partitioning, achieving significant improvements but requiring extensive offline training. Yang et al (2021) applied deep reinforcement learning (DRL) for phase configuration, yielding moderate gains with complex implementation. Gao et al (Mar. 2021) used K-means clustering for interference management, resulting in high sum rate gains but facing scalability issues. Recent works such as Amin et al (2023) employed DRL for energy-efficient resource allocation, achieving moderate improvements but with centralized control limitations. Additionally, Guo et al (2023) investigated DRL for resource allocation in device-to-device (D2D) communication, showing high sum rate improvements in a multi-RIS environment. Xu et al (2024) explored DRL for secure mobile edge computing, achieving moderate improvements with a focus on security enhancement. Our work, using the DRL-based dynamic RIS partitioning, achieves near-optimal sum rate improvements without the need for offline training, providing significant real-time adaptability advantages over traditional methods.

Table 1

Table 1. Comparison of machine-learning-assisted RIS NOMA studies focusing on sum rate.

The results indicate that our DRL-based approach achieves near-optimal sum rate improvements without the need for offline training, providing significant real-time adaptability advantages over traditional methods. This study enhances the understanding of the applicability and effectiveness of DRL in optimizing RIS-aided NOMA systems, setting a new benchmark for future research and practical implementations.

Our work employs a Deep Q-Network (DQN) for dynamic RIS partitioning, achieving near-optimal sum rate improvements without the need for offline training. This real-time adaptability is crucial for dynamic environments. Unlike other studies, our approach eliminates the offline training phase, enhancing practical deployment.

In summary, this paper addresses a crucial aspect of enhancing RIS-aided NOMA systems and represents an improvement over our previous contributions. By focusing on the dynamic and efficient partitioning of RIS elements through DRL, we present a model that combines theoretical innovation with practical applicability, setting a new standard for the deployment and operation of advanced wireless communication systems.

By addressing the limitations of previous methods and providing a scalable, efficient solution, our research significantly advances the field of RIS-aided NOMA systems. This study enhances sum rate and fairness and ensures adaptability to changing network conditions, positioning our work as a substantial contribution to the literature.

This paper is organized as follows: Section 1 delves into the system model, detailing the architecture and key components of our uplink-NOMA communication setup. Section 2 provides an analytical analysis of outage probability, establishing a theoretical framework for assessing system reliability. In Section 3, we introduce our novel DRL scheme, discussing its methodology, strategy, and the unique benefits it offers for dynamic RIS partitioning. Section 4 presents numerical results derived from comprehensive simulations, showcasing the effectiveness of our DRL-based approach in comparison to traditional methods. We conclude in Section 5 with a discussion on the implications of our findings for the future of wireless communication systems, emphasizing the advancements made through the application of DRL in optimizing RIS-aided NOMA systems. Throughout, we highlight our contributions to the field and suggest directions for future research.

2 System model

In this part of our study, we introduce the architecture of our uplink-NOMA communication setup, which includes transmissions from two single-antenna users to a single-antenna Base Station (BS). This model operates within a quasi-static, frequency-flat Rayleigh fading channel environment. Rayleigh fading is chosen in this work because it effectively models the multipath propagation effects encountered in Non-Line-of-Sight (NLOS) outdoor environments, such as those found in sporting events. This makes it particularly suitable for evaluating the performance of wireless communication systems in realistic, dynamic environments like outdoor sports venues Goldsmith (2005).

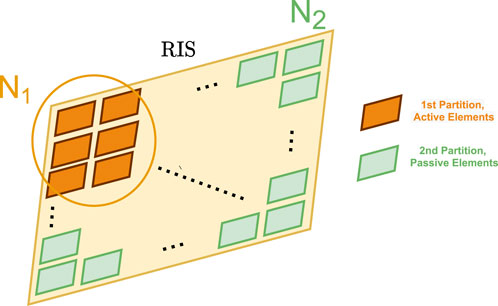
The scenario is set within a two-dimensional, 20 m by 20 m outdoor area, with both users located at ground level, as illustrated in Figure 1. While the RIS and the first user (U-1) are fixed in position, the second user (U-2) has the liberty to move around a predefined zone. Information about deployment positions and their corresponding RIS partitioning schemes are stored in a dedicated database.

Figure 1

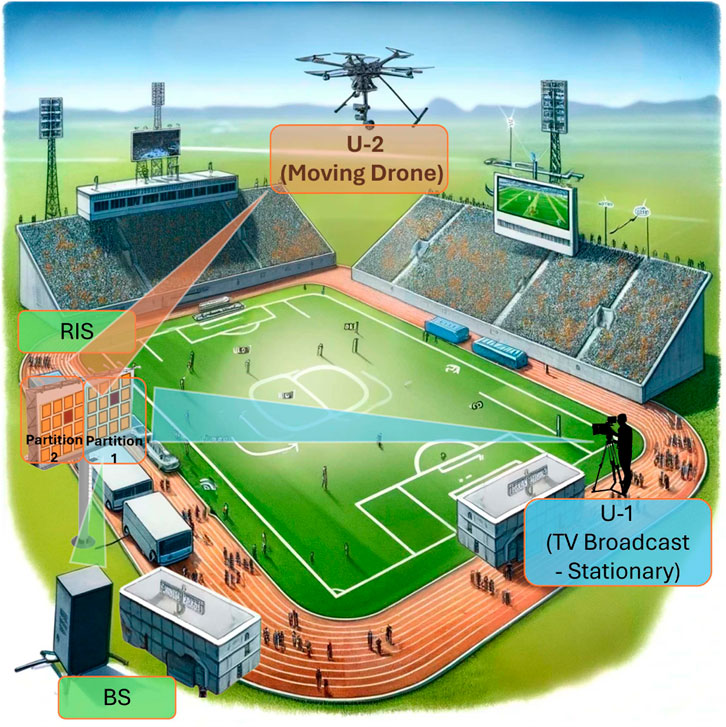
Figure 1. System scheme for a two-user uplink scenario in an outdoor environment. (This figure is generated using AI.)

To illustrate a practical example of an outdoor scenario involving one static and one mobile user with a partitioned RIS, consider an outdoor sporting event. In this scenario, a static broadcasting unit (U-1) is stationed at a fixed location to manage real-time event coverage and communication with the central BS. Simultaneously, a mobile user (U-2), such as a camera drone, navigates the event area to capture and stream live footage. The RIS is strategically partitioned into two sections to dynamically optimize the signal reflection towards both the static and mobile users. This setup demonstrates the applicability of our model in real-world dynamic environments, where the RIS can adaptively enhance communication performance for both fixed and moving entities, ensuring robust and efficient data transmission. To determine the precise locations for U-2’s various points, sophisticated positioning techniques are employed, following the guidance of references such as Witrisal et al. (2016).

Despite the practical challenges in obtaining perfect Channel State Information (CSI), it remains a common assumption in studies concerning RIS-aided NOMA, including notable references like Zhang et al. (2022); Liu Y. et al. (2022); Zhang Z. et al. (2021). The acquisition of CSI is assumed to be feasible through methodologies proposed in literature, notably Wei et al. (2021) and Noh et al. (2022). Our communication process transmits single-carrier signals from users to the BS via a single hybrid-RIS. The RIS comprises $N=N_1+N_2$ reflective elements, where $N_1$ and $N_2$ represent the number of elements allocated for U-1 and U-2, respectively. To address the power variance between users necessary for NOMA, our system utilizes an innovative RIS partitioning approach, ensuring both users transmit at the same power level. This partitioning strategy is illustrated in Figure 2.

Figure 2

Figure 2. Illustration of RIS partitioning with active and passive elements.

A DRL model is harnessed to find the best partitioning strategy that optimizes both the network throughput and fairness among users. For baseline comparison, the optimal iterative algorithm for dynamic RIS partitioning, as detailed in Khaleel and Basar (2022), employs an exhaustive search method to find the best allocation of RIS elements. This method systematically evaluates all possible partitioning configurations to maximize the sum rate and ensure fairness among users. While this approach guarantees finding the optimal solution, it is computationally intensive and time-consuming, especially as the number of RIS elements increases. With precise CSI, the RIS is adeptly configured, aligning $N_1$ active reflectors towards U-1 and $N_2$ passive elements towards U-2, which forms the basis for the BS’s received signal formula.

In consideration of these factors, the signal that is received at the BS can be described in Eq. 1 as follows:

$\begin{array}{ll}\hfill y& =\sqrt{P_t}{\displaystyle \sum _{i=1}^2}\left(\sqrt{\alpha }{\mathbf{h}}_i^{\text{T}}{\mathbf{\theta }}_{\text{act}}{\mathbf{h}}_{BS}+{\mathbf{g}}_i^{\text{T}}{\mathbf{\theta }}_{\text{pas}}{\mathbf{g}}_{BS}\right)x_i\hfill \\ \hfill & +\sqrt{\alpha }\mathbf{z}{\mathbf{\theta }}_{\text{act}}{\mathbf{h}}_{BS}+n_0,\hfill \end{array}(1)$

Here, ${\mathbf{h}}_i={[h_i^1,\dots ,h_i^{N_1}]}^{\text{T}}$ and ${\mathbf{g}}_i={[g_i^1,\dots ,g_i^{N_2}]}^{\text{T}}$, along with ${\mathbf{h}}_{BS}={[h_{BS}^1,\dots ,h_{BS}^{N_1}]}^{\text{T}}$ and ${\mathbf{g}}_{BS}={[g_{BS}^1,\dots ,g_{BS}^{N_2}]}^{\text{T}}$, denote the Rayleigh fading channel coefficients connecting the $i_{th}$ user with the $n_1^{th}$ and $n_2^{th}$ elements of the RIS’s active and passive segments, and the links to the BS, correspondingly. Furthermore, $x_i$ signifies the modulated signal transmitted by the $i_{th}$ user, possessing a unit power $(\mathbb{E}[|x{|}^2]=1)$, $P_t$ refers to the transmission power of the users, and $\alpha$ indicates the gain factor for the RIS’s actively reflecting elements. Additionally, $\mathbf{z}={[z^1,\dots ,z^{N_1}]}^{\text{T}}$ represents the noise vector from the active component’s amplification of the RIS, where $z^{n_1}$ is the noise contribution from the amplifier at the $n_1^{th}$ element of the RIS, obeying a $\mathcal{C}\mathcal{N}(0,{\sigma }_z^2)$ distribution. Moreover, $n_0$ is the additive white Gaussian noise sample (AWGN) at the BS, with a distribution of $\mathcal{C}\mathcal{N}(0,N_0)$, ${\mathbf{\theta }}_{\text{act}}=\text{diag}(e^{j{\varphi }^1},\dots ,e^{j{\varphi }^{N_1}})\in {\mathbb{C}}^{N_1\times N_1}$ and ${\mathbf{\theta }}_{\text{pas}}=\text{diag}(e^{j{\xi }^1},\dots ,e^{j{\xi }^{N_2}})\in {\mathbb{C}}^{N_2\times N_2}$ are phase adjustment matrices for the RIS, where $e^{j{\varphi }^{n_1}}=e^{-j\angle (h_1^{n_1}{h}_{BS}^{n_1})}$ and $e^{j{\xi }^{n_2}}=e^{-j\angle (g_2^{n_2}{g}_{BS}^{n_2})}$ introduce phase shifts by the RIS’s $n_1^{th}$ and $n_2^{th}$ elements, respectively.

A user benefiting from both coherent alignment and amplification exhibits significantly greater strength compared to another user coherently aligned without amplification, as seen in the scenario where the passive side supports the user. Thus, the SINR for the first and the second user is given in Eq. 2, which is at the top of this page.

$\begin{array}{cc}\hfill & {\gamma }_1=\frac{P_t\left(|\sqrt{\alpha }{\sum }_{n_1=1}^{N_1}|h_1^{n_1}\Vert h_{BS}^{n_1}|+{\sum }_{n_2=1}^{N_2}{g}_1^{n_2}{\mathrm{\theta }}_{\text{pas}}^{n_2}{g}_{BS}^{n_2}{|}^2\right)}{P_t\left(|\sqrt{\alpha }{\sum }_{n=1}^{N_1}{h}_2^{n_1}{\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}+{\sum }_{n_2=1}^{N_2}|g_2^{n_2}||g_{BS}^{n_2}{\Vert }^2\right)+{\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|{\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}{|}^2+N_0},\hfill \\ \hfill & {\gamma }_2=\frac{P_t\left(|\sqrt{\alpha }{\sum }_{n_1=1}^{N_1}{h}_2^{n_1}{\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}+{\sum }_{n_2=1}^{N_2}|g_2^{n_2}||g_{BS}^{n_2}{\Vert }^2\right)}{{\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|{\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}{|}^2+N_0}.\hfill \end{array}(2)$

In light of the SINR calculations obtained, the data transmission rate for the $i_{th}$ user can be determined by $R_i={\log }_2(1+{\text{SINR}}_i)$, and the overall achievable sum rate is expressed in Eq. 3 as follow

$R_{\mathit{sum}}={\displaystyle \sum _{i=1}^2}{R}_i={\displaystyle \sum _{i=1}^2}{\log }_2\left(1+{\mathrm{S}\mathrm{I}\mathrm{N}\mathrm{R}}_i\right).(3)$

3 Analytical analysis of outage probability

This section presents an analytical exploration of the outage probability to validate the reliability of outcomes obtained from parametric simulations. Leveraging the central limit theorem—which posits that the average of a large number of samples approximates a normal distribution—it can be deduced that with a substantial number of reflective elements, the cumulative channel effects tend towards a Gaussian distribution. For notational ease, we transform parts of the SINR formula by introducing auxiliary variables such as $K=\sqrt{\alpha }{\sum }_{n_1=1}^{N_1}|h_1^{n_1}||h_{BS}^{n_1}|$, $L={\sum }_{n_2=1}^{N_2}{g}_1^{n_2}{\mathrm{\theta }}_{\text{pas}}^{n_2}{g}_{BS}^{n_2}$, $M=\sqrt{\alpha }{\sum }_{n_1=1}^{N_1}{h}_2^{n_1}{\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}$, $O={\sum }_{n_2=1}^{N_2}|g_2^{n_2}||g_{BS}^{n_2}|$, $P={\mathrm{\theta }}_{\text{act}}^{n_1}{h}_{BS}^{n_1}$, and $Q=N_0$. This leads to the updated SINR expressions as in Eqs 4 and 5 for both users as follows:

${\gamma }_1=\frac{P_t|K+L{|}^2}{P_t|M+O{|}^2+{\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|Q{|}^2+P},(4)$

${\gamma }_2=\frac{P_t|M+O{|}^2}{{\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|Q{|}^2+P}.(5)$

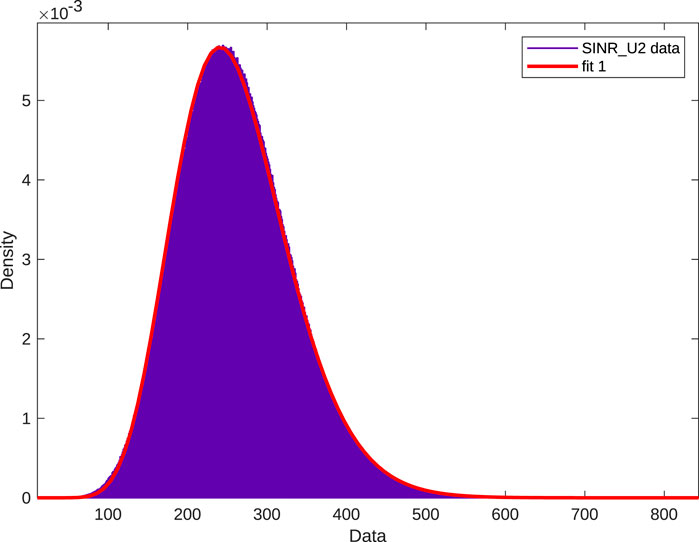
The adaptation of SINRs for user U-2 to a Gamma distribution, as depicted in Figure 3 with the reflective element count at 128 and the transmission power $P_t$ at eight dBm, results from the squared sum of channel products $|K+L{|}^2$ and $|M+O{|}^2$, adhering to a chi-squared distribution with two degrees of freedom. Figure 3, generated using the MATLAB fitting tool, provided the parameters necessary for subsequent analysis, thereby ensuring the accuracy and reliability of our methodology.

Figure 3

Figure 3. Fitting the SINR distribution for the secondary user with a probability distribution.

The Gamma distribution’s parameters, namely, the shape $(a)$ and scale $(b)$, with estimated values for $a=12.871$ and $b=20.275$, and their respective standard errors 0.005682 and 0.009129, facilitate the simulation of data or statistical inferences about the population’s parameters. Notably, the Gamma distribution is constrained to positive values, as indicated by $0<y<\infty$, with the estimated mean and variance being 260.959 and 5,291.19, respectively.

We particularly examine U-2, which is serviced by the passive component of the RIS. The outage probability $(P_{\text{out},2})$ is determined using $P_{\text{out},2}=P({\text{SINR}}_2<2^{R_{\text{th}}/BW}-1)$, where the SINR is below the threshold $R_{\text{th}}$ (bits per second), ensuring U-2’s quality of service (QoS) across a bandwidth $(BW)$. The formula for the cumulative distribution function (CDF) is described in Eq. 6:

$P_{\text{out},2}=P\left(\frac{P_t|M+O{|}^2}{{\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|Q{|}^2+P}<v\right),(6)$

where $v=2^{R_{\text{th}}/BW}-1$. This equation is effectively represented as the CDF of a random variable $G$, hence $P(G<g)=F_G(g)$, where $F_G(g)$ symbolizes the CDF of $G$. The variable $G$ signifies the difference between $P_t|M+O{|}^2$ and ${\sigma }_z^2\alpha {\sum }_{n_1=1}^{N_1}|Q{|}^{2}v$, which introduces complexity due to its representation as a difference of chi-squared distributions. However, through the application of characteristic functions (CFs), evaluating such distributions is made possible. The main challenge lies in calculating the probability density function (PDF) of the difference between non-central and central chi-squared distributions, as this PDF involves an infinite series incorporating Whittaker functions, related to the confluent hypergeometric function. The CF of $G$ is derived on Eq. 7 as:

${\mathrm{\Psi }}_G\left(\omega \right)=\frac{1}{{\left(1-2j\omega {\sigma }^2\right)}^{n/2}}\exp \left(\frac{j\omega {\mu }^2}{1-2j\omega {\sigma }^2}\right),(7)$

where $G$ sums squares of $n$ independent Gaussian variables $A_i$, each with mean ${\mu }_i$ and variance ${\sigma }^2$. By adjusting $\mu$ and $\sigma$ to the mean and variance of the summation terms, we obtain the CF of $G$. Considering the uncorrelated nature of the Gaussian variables, we express $|M+O{|}^2$ in terms of their real and imaginary parts, as ${[\mathfrak{R}(M)+\mathfrak{R}(O)]}^2+{[\mathfrak{I}(M)]}^2$, where $\mathfrak{R}(\cdot )$ and $\mathfrak{I}(\cdot )$ extract the real and imaginary components, respectively. With the sum of independent variables, the characteristic functions of these components are multiplied, leading to Eq. 8 as:

${\mathrm{\Psi }}_G\left(w\right)={\mathrm{\Psi }}_{P_t|M+O{|}^2}\left(w\right){\mathrm{\Psi }}_{\left(-{\sigma }_z^2\alpha {\displaystyle {\sum }_{s=1}^S}|Q{|}^{2}v\right)}\left(w\right),(8)$

substituting ${\mu }_i$ and ${\sigma }_i$ for the mean and variance of their respective terms. The Gil-Pelaez inversion theorem then allows for calculating the CDF of the differential chi-squared variables in Eq. 9 as:

$F_G\left(g\right)=\frac{1}{2}-{\int }_0^{\infty }\frac{\mathfrak{I}\left\{e^{-jwg}{\mathrm{\Psi }}_G\left(w\right)\right\}}{w\pi }dw,(9)$

where $F_G(g)$ denotes the CDF of $G$ and ${\mathrm{\Psi }}_G(w)$ its CF. Utilizing the CDF for the difference between chi-squared variables enables the computation of the outage probability for the communication system.

4 Deep reinforcement learning scheme

In our system model, we incorporate a dynamic DRL approach tailored for real-time application. This DRL model is specifically designed to conduct online partitioning of the RIS, enabling the system to adapt instantaneously to variations in the communication environment. Unlike traditional methods that rely on offline training and static partitioning strategies, our model leverages the inherent adaptability of DRL to assess and modify the RIS configuration on the fly. This online partitioning is crucial for operational efficiency, particularly in scenarios where user positions and channel conditions are subject to frequent changes. By employing online partitioning, our DRL model ensures that the RIS can dynamically adjust the allocation of its reflecting elements to users, thereby optimizing the signal reflection properties in real time and maintaining the robustness of the NOMA communication system.

This model’s online partitioning capability is essential for maintaining operational efficiency in scenarios marked by continuous changes in user positions and channel conditions. It ensures that the RIS can dynamically adjust its reflecting elements across users, optimizing signal reflection properties in real time and upholding the integrity of the NOMA system’s functionality.

A key aspect of our DRL model is its ability to match the performance of iterative algorithms and supervised learning schemes in configuring RIS partitioning while reducing computational complexity and operational time. This efficiency does not come at the expense of significantly outperforming these conventional methods in metrics such as fairness or total sum rate; rather, the DRL framework achieves a performance level on par with these methodologies, supplemented by the critical advantages of enhanced real-time adaptability. This efficiency and adaptability represent an important advancement in operational efficiency and computational economy.

The model makes achieving optimal partitioning strategies not just a theoretical possibility but a practical reality, streamlined and viable within the stringent demands of dynamic system environments. By reducing computational demands with the capacity for real-time system adaptation, our DRL approach manages the trade-offs between performance, efficiency, and complexity.

4.1 DRL strategy

DRL is an advanced machine learning approach that combines artificial neural networks with a reinforcement learning architecture. This enables autonomous agents to learn optimal behaviors within complex environments by interacting with the environment, observing the outcomes of their actions, and adapting their strategies to maximize a numerical reward signal. At the core of DRL is the agent-environment interaction, where the agent performs actions, and the environment responds with new states and rewards as depicted in Figure 4. These components are mathematically formulated as the state space, action space, and reward function.

Figure 4

Figure 4. DRL Agent-Environment interaction.

Implemented within the MATLAB Deep Learning Toolbox The MathWorks, Inc (2023), DRL utilizes MATLAB’s computational tools to streamline the development and training of neural networks that approximate the policy and value functions—the central mechanisms by which the agent assesses its current policy and estimates the expected outcomes of its actions. The toolbox provides a framework for defining the problem’s specific DRL components, such as custom observation and action spaces, and for integrating them with neural network layers and training algorithms. By using these tools, it is possible to efficiently construct and train DRL agents for a wide array of applications, leveraging MATLAB’s optimization routines and GPU-accelerated computing capabilities to handle the extensive computations involved in the training process.

The environment in DRL is modeled as a Markov Decision Process (MDP), where the transition between states is determined by the actions of the agent. The state is represented as a multi-dimensional array or a custom data structure that reflects the agent’s perception of the environment. A well-designed state representation is crucial for the agent’s ability to learn the optimal policy. When the agent selects an action based on its policy, the environment reacts by transitioning to a new state and returning a reward. This reward is a scalar value that signals the agent about the effectiveness of the action. MATLAB’s toolbox facilitates the definition of this action-reaction mechanism, allowing the simulation of the environment’s dynamics through the step function in our environment. The step function contains all wireless communication configurations of our scenario defined in Section 2.

In this study, we selected the DQN algorithm with two hidden layers each with 256 hidden units to address the dynamic partitioning of RIS elements in NOMA systems. The DQN algorithm is well-suited for environments with discrete action spaces, which align with the nature of RIS element partitioning tasks. Unlike algorithms such as Deep Deterministic Policy Gradient (DDPG), which are designed for continuous action spaces, DQN efficiently handles the discrete decision-making required in our context Lillicrap et al. (2015). DQN is known for its high sample efficiency, meaning it can learn effective policies with fewer interactions with the environment.

This efficiency is crucial for our application, where the cost of environment interactions can be high in terms of time and computational resources. The DQN algorithm has demonstrated stability and reliable convergence properties in various applications Mnih et al. (2015). This stability is essential for ensuring that the DRL model can consistently find near-optimal solutions for RIS partitioning without significant fluctuations or instability during training. Preliminary experiments and literature review indicated that DQN performs well in scenarios similar to ours Hessel et al. (2018). The empirical evidence supports its ability to achieve high performance in terms of maximizing the sum rate and ensuring fair resource allocation among users.

4.1.1 State Space

The state space $\mathcal{S}$ is a reflection of the system’s multi-dimensional nature, comprising the current and past transmit power levels, the proximities between U-2 and the RIS, and the allocation of RIS elements. Formally, the state at any time step $t$ is represented in Eq. 10 as:

$s_t=\left[P_t,P_{t-1},d_t^{U2,RIS},d_{t-1}^{U2,RIS},N_t\right],(10)$

where $P_t$ indicates the transmit power at time $t$, and $N_t$ signifies the number of RIS elements focused towards U-1. The inclusion of both current and historical data ensures that the agent has the contextual awareness needed to make informed decisions. The terms $d_t^{U2,RIS}$ and $d_{t-1}^{U2,RIS}$ represent the current and past distances between U-2 and the RIS, respectively. The inclusion of these distances is important; $d_t^{U2,RIS}$ affects the real-time signal reflection properties, whereas $d_{t-1}^{U2,RIS}$ provides historical context that helps the DRL agent infer the mobility pattern of U-2. Together, they enable the agent to make more informed decisions regarding the RIS element allocation, ensuring that the dynamic adjustments are both responsive to current conditions and anticipatory of future system state transitions.

4.1.2 Action Space

To navigate through $\mathcal{S}$, we delineate an action space $\mathcal{A}$, crucial for the system’s dynamic response. The action $a_t$ at time $t$ determines the forthcoming partitioning of the RIS:

$a_t=\left[N_{t+1}\right],(11)$

where $N_{t+1}$ is the count of RIS elements allotted to U-1 for the next time step. This approach ensures the RIS’s continuous evolution in alignment with the users’ needs.

4.1.3 Reward Function

The reward function $\mathcal{R}$ guides the DRL agent towards a balanced policy, emphasizing the importance of fairness. Ensuring equitable treatment of all users necessitates the strategic allocation of reflecting elements ($N_1$ and $N_2$) to each, considering the interference caused by the sub-surfaces allocated to others. Consequently, the objective function in our proposed method leverages Jain’s Fairness Index (JFI) presents in Eq. 12, aligning with our DRL strategy’s reward mechanism as detailed in Khaleel and Basar (2021):

$\begin{array}{cc}\hfill JFI& =\underset{N_1,N_2}{\max }\frac{{\left(\frac{1}{2}{\sum }_{i=1}^2{\bar{R}}_i\right)}^2}{\frac{1}{2}{\sum }_{i=1}^2{\bar{R}}_i^2},\hfill \\ \hfill & \text{s.t.}{\displaystyle \sum _{i=1}^2}{N}_i=N,N_i\in \left\{1,\dots ,\left(N-1\right)\right\}\hfill \end{array}(12)$

where ${\bar{R}}_i$ signifies the average ergodic rate obtained from numerous random channel realizations, and $N_i$ represents the number of reflecting elements dedicated to the $i_{th}$ user. This approach underlines the core principle of our DRL strategy: optimizing system fairness and efficiency by dynamically adjusting the RIS element allocation in response to the real-time communication environment. The immediate reward $r_t$ which is presented in Eq. 13, is based on JFI, promoting an equitable allocation of resources:

$r_t=f\left(JFI\right),(13)$

where the index is a calculated metric of fairness based on the users’ data rates. This incentivizes not only throughput maximization but also the sustenance of fairness across the NOMA landscape.

The DRL agent employs a policy network parameterized by weights $\theta$, which is iteratively refined through interactions with the environment. The network is tasked with deducing a mapping from observed states to actions that can potentially amplify the cumulative reward.

4.1.4 Policy Optimization

The learning process aims to find the optimal policy, mathematically modeled as a gradient ascent on expected rewards which is presented in Eq. 14 as follows:

${\theta }^{*}=\underset{\theta }{\text{argmax}}\mathbb{E}\left[{\displaystyle \sum _{t=0}^T}{\gamma }^t{r}_t\right],(14)$

where $\gamma$ stands as the discount factor, adding a foresight dimension by quantifying the importance of future rewards, and $T$ denotes the temporal span of the decision-making horizon.

Empirical simulations corroborate the DRL scheme’s effectiveness, showcasing its capability to swiftly adapt to environmental changes while fostering fairness among the users. Through this adaptive mechanism, we achieve a balance between system responsiveness and operational integrity, demonstrating the viability of DRL in managing the demands of RIS-aided NOMA systems.

5 Simulation results

In this section, we present the results of our computer simulations aimed at evaluating the effectiveness of DRL-based partitioning within the established uplink NOMA communication system framework. This study extends our communication model to incorporate DRL as the principal mechanism for partitioning RIS, diverging from traditional approaches. Our analysis compares the DRL-based partitioning strategy against an iterative algorithm and the supervised learning-based method detailed in the literature.

The simulations are conducted at an operational frequency of 1.8 GHz, representative of sub-6 GHz frequencies commonly used in current wireless communication systems. The choice of reflective elements for the RIS ($N_{\text{RIS}}$ = 128, 256, and 512) aligns with these operational frequencies, providing a practical context for evaluation. Channel parameters include quasi-static frequency-flat Rayleigh fading channels with a path loss model based on free-space propagation. The channel gains follow a Rayleigh distribution, and the path loss is calculated using the Friis transmission equation. Specifically, the path loss exponent is set to 2, reflecting typical urban outdoor environments. The small-scale fading is modeled as a zero-mean complex Gaussian random variable with unit variance, simulating the multipath effect commonly encountered in urban scenarios. Additionally, the system assumes a constant noise power setting of −90 dBm, derived from a bandwidth of 20 MHz and a noise figure of 10 dB. For a comprehensive overview of the system setup, the reader is referred to Section 2.

Our simulation methodology employs $10^4$ random channel realizations to ensure robustness and reliability in the comparative analysis. This approach enables a comprehensive assessment of the partitioning strategies, focusing on the advancements and performance improvements introduced by the application of DRL over the iterative algorithm and the previously employed supervised learning technique. The comparative analysis is critical for elucidating the relative strengths and potential limitations of each partitioning method, contributing valuable insights into the ongoing advancement of RIS-NOMA communication systems.

Our neural network within the DRL model employs a multi-layered neural network characterized by fully connected layers designed to process an input with five distinct features. The network architecture is composed of two hidden layers, each consisting of 256 neurons, with rectified linear unit (ReLU) activation functions facilitating the introduction of non-linearity, enabling the model to capture complex relationships within the data. In our neural network design, the input layer comprises three neurons, each representing the transmit power, the number of reflecting elements, and the distance in meters. The output layer consists of a single neuron, corresponding to the one-dimensional action space in our reinforcement learning framework. This output neuron determines the number of reflecting elements required for a single user. Consequently, the number of elements allocated to the other user is simply the total number of reflecting elements minus the number allocated to the first user. This framework is versatile and can be applied to any RIS design with varying numbers of reflecting elements and transmit power levels. This configuration results in a total of approximately 100.2K learnable parameters, encompassing the weights and biases across all layers, which are iteratively adjusted during the training process. The sequential composition of these layers forms a robust framework for the DRL algorithm to dynamically optimize the partitioning of RIS elements between two users in a NOMA system, with the network’s depth and breadth calibrated to capture the intricacies of the wireless environment and user interactions.

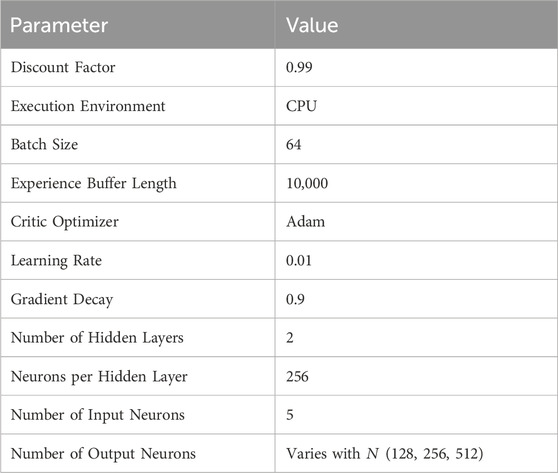
Table 2 presents the parameters and hyperparameters used for the DRL simulation employing the DQN algorithm. The agent options include a discount factor of 0.99, which ensures future rewards are appropriately weighted, aiding in the long-term optimization of the system. The execution environment is set to CPU, providing a balance between computational efficiency and resource availability. A batch size of 64 is chosen to stabilize the learning process, while an experience buffer length of 10,000 allows the agent to learn from a diverse set of past experiences, enhancing the robustness of the policy.

Table 2

Table 2. Simulation parameters and hyperparameters for DRL-based partitioning.

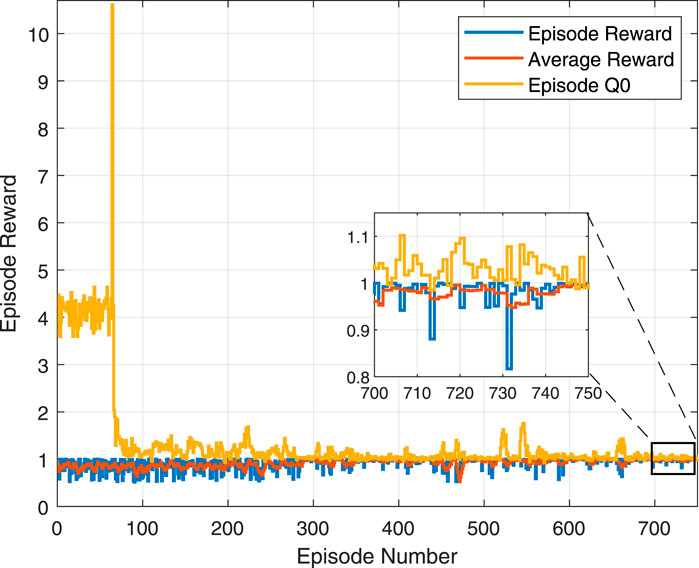
The critic optimizer utilizes the Adam optimizer with a learning rate of 0.01, which facilitates efficient and adaptive learning rates during training. The gradient decay of 0.9 helps in maintaining the momentum of gradients, preventing oscillations and aiding in faster convergence. The neural network consists of 256 hidden neurons per layer, providing sufficient capacity to model complex relationships in the data, which is crucial for accurately approximating the Q-values in the DQN algorithm. These carefully chosen parameters collectively ensure that the DRL model is both efficient and effective, optimizing the RIS partitioning strategy to improve system performance.Figure 5 illustrates the progression of the episodic reward over time through 750 episodes of partitioning training using the DRL framework for the RIS with 128 reflecting elements. Notably, there is significant variance in the early episodes, where a peak is observed, indicating a possible exploration of the action space or initial adjustments of the model’s parameters. As training progresses, the reward stabilizes, demonstrating the model’s convergence towards an optimal policy. The trend shows a clear decrease in variability and an increase in the consistency of the episodic reward, suggesting that the DRL model is learning effectively over time.

Figure 5

Figure 5. Convergence of the DRL algorithm over training episodes.

JFI, which ranges from 0 to 1, is a key component of the reward function to ensure fair resource allocation among users. During the initial exploration phase of the DRL algorithm (episode Q0), the agent explores various actions to learn the environment and understand the impact of different RIS partitioning strategies. The high reward values observed in this phase, though seemingly exceeding 1, result from an additional scaling factor applied to the JFI or from cumulative rewards over multiple steps, not from JFI alone. This exploration can sometimes yield high cumulative rewards, indicating that the agent has identified potentially optimal actions early in the training process.

Higher reward values are better as they signify better system performance in terms of sum rate and fairness. As training progresses, the agent shifts from exploration to exploitation, focusing on actions that consistently yield higher rewards, ensuring the agent converges towards an optimal strategy that maximizes the system’s performance. In summary, the episode reward values for episode Q0 indicate the potential of the agent to find effective actions early on, possibly due to cumulative rewards or scaling factors. As training progresses, the reward values stabilize, guiding the agent towards an optimal solution, aligning with the objectives of our DRL framework.

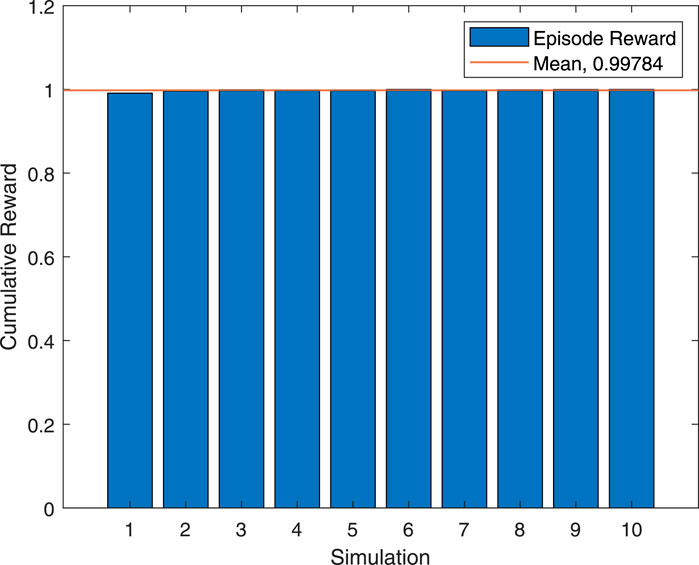
In Figure 6, the cumulative rewards over ten separate simulations for the same RIS configuration are depicted as uniform bars with a dashed line indicating the mean of the episodic rewards. The small error bars suggest low variance, which is indicative of consistent performance across these simulations. The consistency here confirms the reliability of the DRL approach under various initial conditions, showing the model’s robustness.

Figure 6

Figure 6. Cumulative rewards over separated simulations.

The training performance metrics from the MATLAB Deep Learning Toolbox provide further insight into the effectiveness of the learning session. An episodic reward of 0.9887, very close to the average reward of 0.98842, indicates that the agent is performing at a stable level by the end of the training session. The Episode Q0 value, standing at 1.013, is particularly noteworthy. The “Episode Q0 value” refers to the initial Q-value at the start of an episode in reinforcement learning, which quantifies the expected returns (rewards) from taking the best possible action in the initial state of the episode. It is a reflection of the quality of the state-action values being learned, suggesting that the agent has developed a strong prediction capability for expected returns. This means that right from the beginning of an episode, the agent is well-informed about the potential rewards of its actions, demonstrating an effective learning and decision-making process.

Collectively, these results and training metrics underscore a successful training session, where the DRL model demonstrates both convergence to an effective policy and stability across multiple simulations, with performance metrics confirming the agent’s capacity to learn and predict the optimal actions within the defined environment.

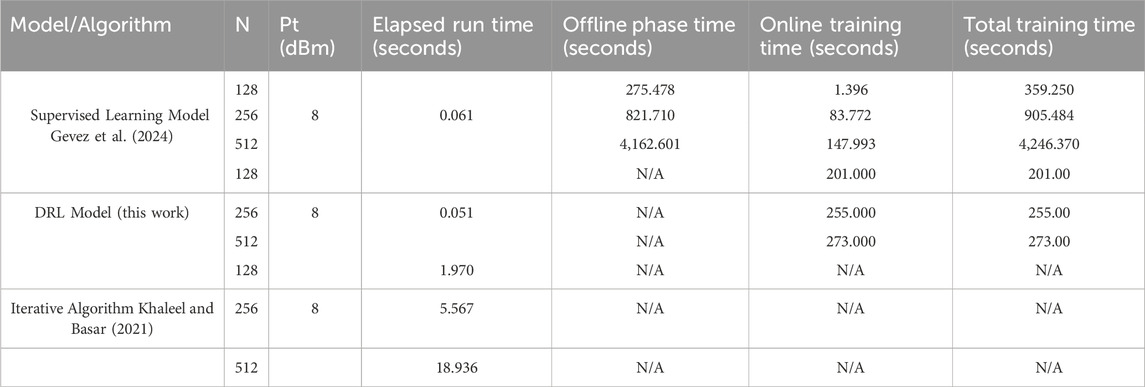
Table 3 provides a detailed comparison of the time efficiency associated with different partitioning strategies for a RIS-NOMA communication system, specifically comparing a supervised learning model, a DRL Model, and an Iterative Algorithm across three scenarios characterized by varying numbers of RIS elements ($N$ = 128, 256, 512). A significant highlight from this comparison is the substantial reduction in the offline phase time observed in the DRL Model, which does not report an offline phase time, suggesting a significant efficiency improvement in the model’s training and deployment process.

Table 3

Table 3. Performance comparison.

For the supervised learning model, the offline phase time increases with the number of RIS elements: 275.478 s for $N$ = 128, escalating to 821.709 s for $N$ = 256, and reaching 4,162.601 s for $N$ = 512. This exponential increase underscores the scalability challenge inherent in the supervised learning approach as the complexity of the system grows.

In contrast, the DRL Model bypasses the traditional offline phase entirely, indicating an inherent efficiency in adapting to system changes dynamically. This model exhibits online training times of 201 s for $N$ = 128, increasing modestly to 255 s for $N$ = 256, and 273 s for $N$ = 512. These figures translate into total training times of 3.35, 4.25, and 4.55 min, respectively, showcasing a significantly streamlined process compared to the supervised learning model.

The Iterative Algorithm, while not directly comparable due to its different operational paradigm (lacking a distinct offline training phase and online training time), shows elapsed run times that increase with the number of RIS elements, from 1.969,608 s for $N$ = 128 to 18.936,179 s for $N$ = 512. However, this approach’s lack of an offline phase or delineated training times presents a different set of operational efficiencies and constraints.

This comparison elucidates the substantial time efficiency advantages offered by the DRL Model, particularly in the context of offline phase reduction. Such efficiency not only enhances the model’s practical applicability but also positions DRL as a superior method for managing the complexities associated with optimizing RIS partitioning in high-dimensional communication systems. The DRL Model’s ability to operate without the need for an extensive offline phase underscores its potential for real-time adaptive system optimization, setting a new benchmark for performance and efficiency in RIS-NOMA system management.

The analysis begins with an evaluation of the ergodic sum rate across various transmit power levels $(P_t)$. Specifically, Figure 7A compares the DRL model’s performance with the sum algorithm, revealing its capability to closely emulate the optimal ergodic sum rate trajectories produced by our baseline. This comparison highlights the effectiveness of the DRL in optimizing RIS partitioning in real-time scenarios and delves into user fairness in power allocation. Building upon this, Figure 7B incorporates the supervised learning scheme into the comparative landscape, showing a parallel in performance scalability with increasing $P_t$ across all methods.

Figure 7

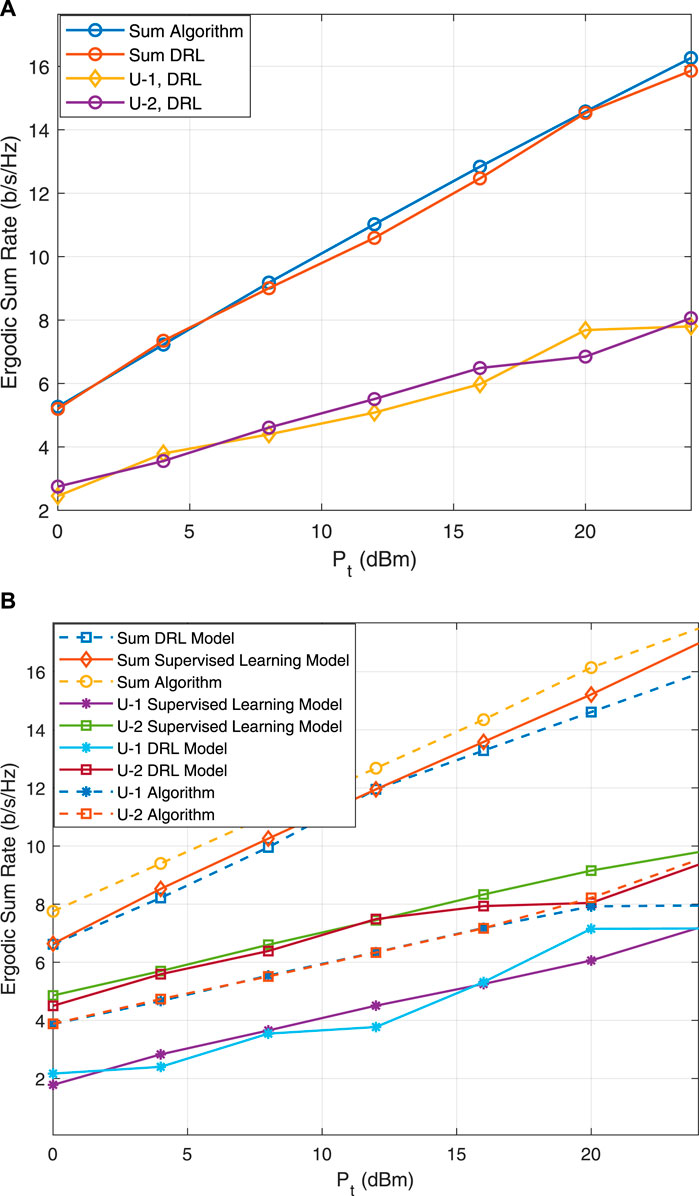
Figure 7. Comparison of achievable user rates and overall ergodic sum rates using the trained DRL model versus an iterative algorithm. Analysis includes U-2 (A) within the training area (U-2 at $x=13,y=13$), and (B) beyond the training area (U-2 at $x=8,y=8$).

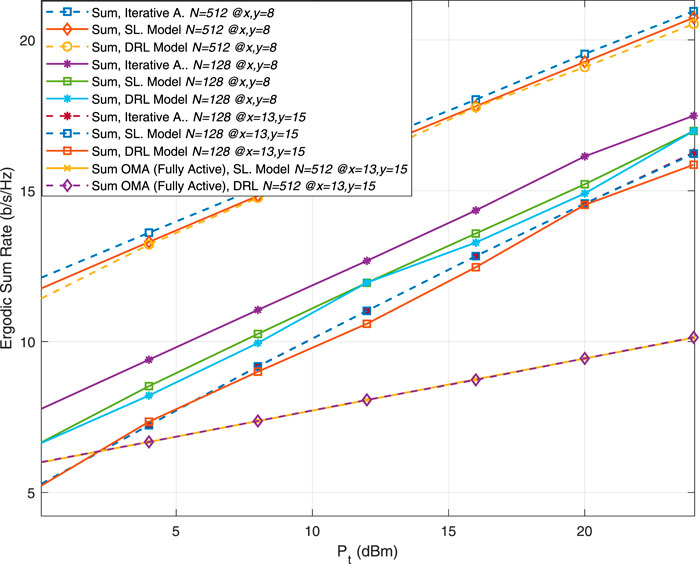
Progressing to Figure 8, the DRL model’s robustness and scalability are demonstrated through its performance across diverse system configurations. An enhancement in sum rate performance is observed with an increase in training point coordinates—from the initial position at $x=8,y=8$, 2 m away from the nearest training area, to the final position at $x=13,y=15$, directly within the training area—and an increase in the number of reflecting elements. This spatial progression in the training points underscores the significance of location in the context of training efficacy.

Figure 8

Figure 8. Comparison of total rates for varying numbers of reflective elements and training points.

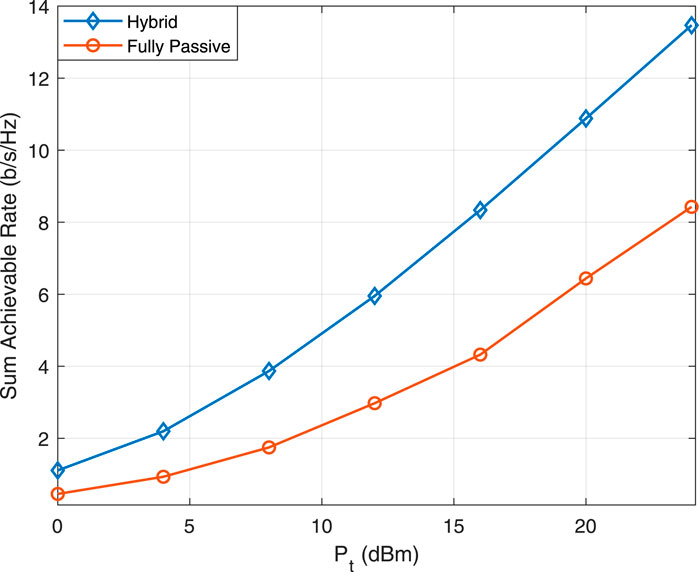
In the environment of Orthogonal Multiple Access (OMA) systems, the findings suggest that DRL models can match with Supervised Model especially as the number of reflecting elements is increased, which is of particular relevance in scenarios where OMA is employed and labeled data may not be readily available. The consistently upward trend in sum rate with increasing transmission power $P_t$ across all models and configurations reaffirms the expected positive correlation between transmission power and improved signal quality, aligning with established principles in the field of wireless communications Ding et al. (2022).

In Figure 9, the discourse transitions to an examination of the sum achievable rate for varying $P_t$ levels, contrasting hybrid approaches with fully passive strategies. Figure 10 elucidates the outage probability under various conditions for both the DRL and supervised learning models, with part (a) considering the ideal case of perfect SIC $(Ep=0)$ and Figure 10B accounting for SIC errors $(Ep\ne 0)$. Achievable rate thresholds in the calculation of outage probability are set to 6.5, 7.5, and 8.5 Mbps/Hz for 128, 256, and 512 reflecting elements, respectively. In Figure 10A, the DRL model exhibits commendable alignment with the supervised learning model, showcasing its capability to emulate the performance of the latter. This outcome is further underscored by the proximity of both models to the theoretical outage probability curve, which is expounded upon in Section 3. Such closeness indicates that the DRL model not only learns optimally in a perfect SIC scenario but also confirms the theoretical underpinnings that govern system behavior.

Figure 9

Figure 9. Comparison of achievable total rates for hybrid versus entirely passive NOMA systems.

Figure 10

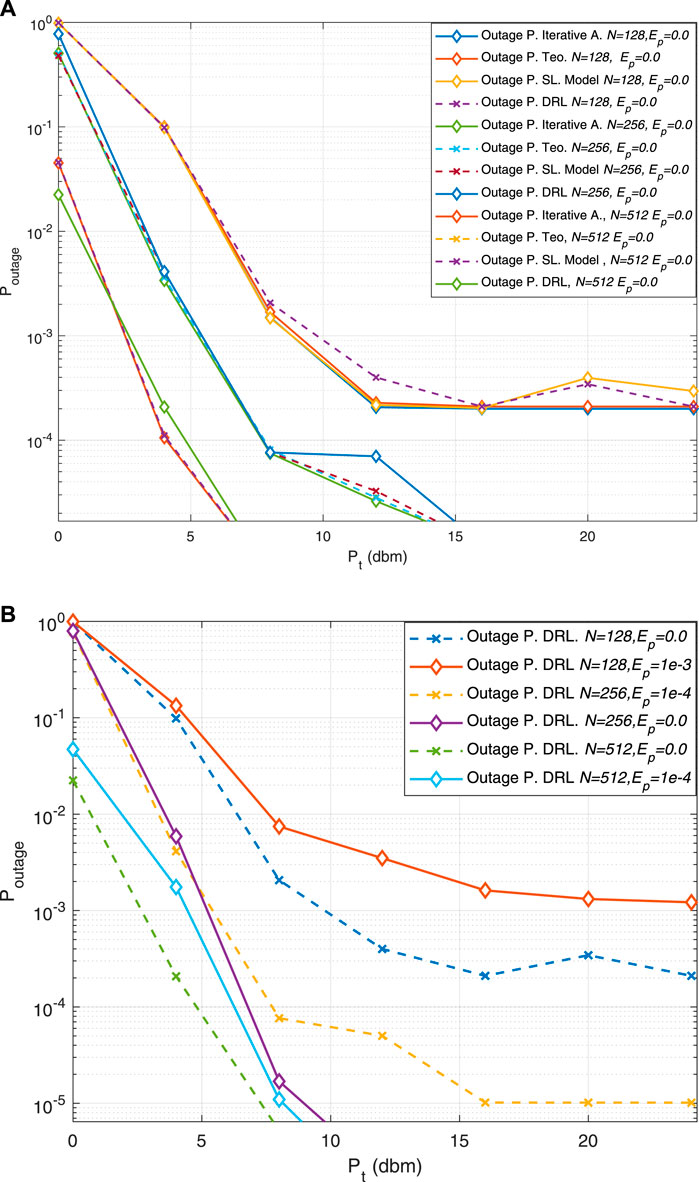
Figure 10. Comparative analysis of outage probability for U-2 utilizing the trained model versus an iterative algorithm, under diverse Quality of Service (QoS) requirements and sizes of RIS. The comparison contemplates: (A) scenarios with perfect SIC, and (B) scenarios accounting for errors in SIC $(Ep)$.

Figure 10B extends the analysis into a realistic domain where SIC is imperfect, manifesting a slight divergence from the theoretical ideal. Despite this, the DRL model demonstrates resilience by approximating the performance of the supervised learning model, signifying its robustness and adaptability in complex environments.

Moreover, Figure 10 illustrates the comparison between the theoretical outage probability, derived from our mathematical analysis in Section 3, and the empirical results obtained from the DRL-based and iterative algorithms. The relevance of the mathematical analysis of the outage probability in Section 3 is paramount as it provides a foundational framework that validates our empirical findings. By leveraging the central limit theorem to approximate the cumulative channel effects towards a Gaussian distribution, we establish a robust theoretical basis for assessing SINR under various conditions.

The theoretical curves shown in Figure 10 align closely with the empirical data, particularly under ideal conditions (perfect SIC). This close alignment demonstrates the robustness of our theoretical framework and its ability to predict system performance accurately. The DRL model’s performance, which closely matches the theoretical predictions, underscores its efficacy in achieving near-optimal outage probabilities even in practical scenarios.

Overall, the comparative analysis between the theoretical expectations and the empirical results obtained from the DRL and supervised learning models, as depicted in Figure 10, provides compelling evidence of the DRL model’s potential to revolutionize future communication systems. The DRL model’s ability to approach the supervised learning model under both perfect and imperfect SIC conditions establishes it as a promising paradigm for ensuring communication reliability in the face of operational challenges.

Our results indicate that while DRL significantly reduces overall computational and time complexities, its online training time is substantially higher than that of supervised learning approaches, presenting a trade-off between real-time adaptability and training duration. For instance, the online training time for DRL is 201 s for $N=128$ RIS elements, compared to 1.3962 s for the supervised learning model. In highly dynamic environments, where user positions and channel conditions frequently change, DRL’s real-time adaptability is advantageous despite the longer online training phase, allowing the system to start responding early and continuously improve performance. Conversely, in low-dynamic environments, the extended online training time may not be justifiable, making a long offline training phase of supervised learning more efficient. These models can respond almost instantaneously within the trained scenarios but may require re-training for significant changes. Dynamic changes necessitating DRL adaptation include user movement, varying user demands, and environmental changes, with DRL optimizing resource allocation in real-time. The continuous learning of DRL ensures the system provides adaptability and service improvement even before reaching optimal performance. Thus, DRL is more suitable for dynamic environments requiring real-time adaptability, while supervised learning is efficient in static environments with infrequent changes, guiding the development of robust RIS-aided NOMA systems.

While our proposed DRL-based dynamic RIS partitioning framework shows significant promise, several limitations should be acknowledged. The assumption of perfect CSI is common but challenging to achieve in practice, and any imperfections can affect performance. Additionally, the scalability of our model to larger systems with multiple users and RIS elements remains an area for further investigation, as increased complexity could impact efficiency. Furthermore, although the framework eliminates the offline training phase, the online training time required, particularly in dynamic environments, may pose constraints on real-time applicability. Addressing these limitations through advanced DRL algorithms, robust methods for handling imperfect CSI, and real-world implementations will be essential for the practical deployment and success of DRL-based dynamic RIS partitioning in future wireless communication networks.

6 Conclusion

In this paper, we have presented a novel DRL scheme to optimize the performance of RIS-aided NOMA systems. This scheme not only offers a dynamic and efficient approach to closely approximate the performance of optimal iterative algorithms but also significantly reduces computational and time complexities. By eliminating the offline training phase—a major limitation identified in our previous work on supervised learning—we have successfully demonstrated the potential of DRL in enhancing the real-time adaptability of RIS configurations to changing environments and user demands. The proposed DRL framework marks a significant step forward in the practical application and deployment of RIS-aided communication systems, potentially transforming future wireless networks with its robustness and responsiveness to the evolving communication landscape.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YG: Writing–original draft, Writing–review and editing. YT: Writing–original draft, Writing–review and editing. EB: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study is supported by The Scientific and Technological Research Council of Turkey (TUBITAK) through the 2247-A National Leader Researchers Program (Project Number: 121C254), Project Titled: “Deep Learning Based Novel Next Generation Communication Systems.”

Acknowledgments

The authors acknowledge the use of OpenAI’s generative AI technologies, ChatGPT (version GPT-4o) and DALL-E (version DALL-E 2), in Figure 1.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amin, S., Sheikh, J., and Malik, B. (2023). A deep reinforcement learning for energy efficient resource allocation intelligent reflecting surface (irs) driven non-orthogonal multiple access (noma). Phys. Commun. 56, 101151. doi:10.1016/j.phycom.2023.102148

CrossRef Full Text | Google Scholar

Basar, E., Alexandropoulos, G. C., Liu, Y., Wu, Q., Jin, S., Yuen, C., et al. (2023). Reconfigurable intelligent surfaces for 6g:Guo emerging hardware architectures, applications, and open challenges. arXiv Prepr. arXiv:2312.16874. doi:10.48550/arXiv.2312.16874

CrossRef Full Text | Google Scholar

Basar, E., Di Renzo, M., De Rosny, J., Debbah, M., Alouini, M.-S., and Zhang, R. (2019). Wireless communications through reconfigurable intelligent surfaces. IEEE Access 7, 116753–116773. doi:10.1109/access.2019.2935192

CrossRef Full Text | Google Scholar

Chen, J., Ma, X., and Zhang, L. (2021). Optimized phase adjustment for enhanced performance in ris-noma systems. IEEE Trans. Wirel. Commun. 20, 5205–5218. doi:10.1109/TWC.2021.3076231

CrossRef Full Text | Google Scholar

Chen, Q., Zhang, L., and Sun, S. (2023a). Enhanced successive interference cancellation for secure pd-noma. IEEE Commun. Lett. 27, 89–93. doi:10.1109/LCOMM.2023.3234567

CrossRef Full Text | Google Scholar

Chen, R., Zhang, X., and Li, Y. (2023b). Deep reinforcement learning for real-time beamforming in massive mimo systems. IEEE Trans. Wirel. Commun. 22, 3456–3469. doi:10.1109/TWC.2023.3187621

CrossRef Full Text | Google Scholar

Cui, J., Ding, Z., Fan, P., and Al-Dhahir, N. (2018). Unsupervised machine learning-based user clustering in millimeter-wave-NOMA systems. IEEE Trans. Wirel. Commun. 17, 7425–7440. doi:10.1109/twc.2018.2867180

CrossRef Full Text | Google Scholar

Ding, Z., Lv, L., Fang, F., Dobre, O. A., Karagiannidis, G. K., Al-Dhahir, N., et al. (2022). A state-of-the-art survey on reconfigurable intelligent surface-assisted non-orthogonal multiple access networks. Proc. IEEE 110, 1358–1379. doi:10.1109/jproc.2022.3174140

CrossRef Full Text | Google Scholar

Ding, Z., Schober, R., and Poor, H. V. (2020). On the impact of phase shifting designs on IRS-NOMA. IEEE Wirel. Commun. Lett. 9, 1596–1600. doi:10.1109/lwc.2020.2991116

CrossRef Full Text | Google Scholar

Gao, X., Liu, Y., Liu, X., and Song, L. (2021). Machine learning empowered resource allocation in IRS aided MISO-NOMA networks. ArXiv. doi:10.1109/TWC.2021.3122409

CrossRef Full Text | Google Scholar

Gevez, Y., Arslan, E., and Basar, E. (2024). A supervised learning-assisted partitioning solution for ris-aided noma systems. IEEE Trans. Cognitive Commun. Netw., 1. doi:10.1109/tccn.2024.3373637

CrossRef Full Text | Google Scholar

Giordani, M., Polese, M., Mezzavilla, M., Rangan, S., and Zorzi, M. (2020). Toward 6G networks: use cases and technologies. IEEE Commun. Mag. 58, 55–61. doi:10.1109/mcom.001.1900411

CrossRef Full Text | Google Scholar

Goldsmith, A. (2005). Wireless communications. Cambridge: Cambridge University Press.

Google Scholar

Guo, L., Jia, J., Zou, Y., Chen, J., Yang, L., and Wang, X. (2023). Resource allocation for multiple riss assisted noma empowered d2d communication: a mamp-dqn approach. Ad Hoc Netw. 138, 103083. doi:10.1016/j.adhoc.2023.103163

CrossRef Full Text | Google Scholar

Hessel, M., Modayil, J., Van Hasselt, H., Schaul, T., Ostrovski, G., Dabney, W., et al. (2018). “Rainbow: combining improvements in deep reinforcement learning,” in Proceedings of the AAAI conference on artificial intelligence, USA, February 20–27, 2024. doi:10.1609/aaai.v32i1.11796

CrossRef Full Text | Google Scholar

Huang, C., Zappone, A., Alexandropoulos, G. C., Debbah, M., and Yuen, C. (2019). Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 18, 4157–4170. doi:10.1109/twc.2019.2922609

CrossRef Full Text | Google Scholar

Huang, L., Zhang, H., and Wang, X. (2023a). Joint drl for power allocation and interference management in ultra-dense networks. IEEE Trans. Wirel. Commun. 22, 4820–4833. doi:10.1109/TWC.2023.3190456

CrossRef Full Text | Google Scholar

Huang, Y., Wu, Q., and Zhang, R. (2023b). Hybrid sic with machine learning for improved interference mitigation in pd-noma. IEEE Trans. Wirel. Commun. 72, 354–365. doi:10.1109/TWC.2022.3247865

CrossRef Full Text | Google Scholar

Islam, S. M. R., Avazov, N., Dobre, O. A., and Kwak, K.-s. (2017). Power-domain non-orthogonal multiple access (NOMA) in 5G systems: potentials and challenges. IEEE Commun. Surv. Tutorials 19, 721–742. doi:10.1109/comst.2016.2621116

CrossRef Full Text | Google Scholar

Khaleel, A., and Basar, E. (2021). Reconfigurable intelligent surface-empowered MIMO systems. IEEE Syst. J. 15, 4358–4366. doi:10.1109/jsyst.2020.3011987

CrossRef Full Text | Google Scholar

Khaleel, A., and Basar, E. (2022). A novel noma solution with ris partitioning. IEEE J. Sel. Top. Signal Process. 16, 70–81. doi:10.1109/jstsp.2021.3127725

CrossRef Full Text | Google Scholar

Kim, D., Park, J., and Lee, S. (2022). Enhanced coding scheme for cd-noma in high-interference scenarios. IEEE Commun. Lett. 26, 789–793. doi:10.1109/LCOMM.2022.3141258

CrossRef Full Text | Google Scholar

Li, S., Tang, J., and Han, Z. (2023). Robust drl for wireless communication systems: challenges and solutions. IEEE Trans. Wirel. Commun. 22, 1014–1027. doi:10.1109/TWC.2023.3154234

CrossRef Full Text | Google Scholar

Li, X., Chen, W., Zhang, H., Zhang, S., and Yang, L. (2022). Advanced signal processing for reconfigurable intelligent surface aided mmwave and terahertz communication. IEEE J. Sel. Areas Commun. 40, 1768–1782. doi:10.1109/JSAC.2022.3157843

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971.

Google Scholar

Liu, J., Zhao, W., and Li, Y. (2022a). Secure power allocation for pd-noma systems against eavesdropping. IEEE Trans. Wirel. Commun. 21, 1657–1668. doi:10.1109/TWC.2022.3154629

CrossRef Full Text | Google Scholar

Liu, Y., Liu, X., Mu, X., Hou, T., Xu, J., Di Renzo, M., et al. (2021). Reconfigurable intelligent surfaces: principles and opportunities. IEEE Commun. Surv. Tutorials 23, 1546–1577. doi:10.1109/comst.2021.3077737

CrossRef Full Text | Google Scholar

Liu, Y., Mu, X., Liu, X., Di Renzo, M., Ding, Z., and Schober, R. (2022b). Reconfigurable intelligent surface-aided multi-user networks: interplay between NOMA and RIS. IEEE Wirel. Commun. 29, 169–176. doi:10.1109/mwc.102.2100363

CrossRef Full Text | Google Scholar

Liu, Z., and Yang, L.-L. (2021). Sparse or dense: a comparative study of code-domain NOMA systems. IEEE Trans. Wirel. Commun. 20, 4768–4780. doi:10.1109/twc.2021.3062235

CrossRef Full Text | Google Scholar

Makki, B., Chitti, K., Behravan, A., and Alouini, M.-S. (2020). A survey of NOMA: current status and open research challenges. IEEE Open J. Commun. Soc. 1, 179–189. doi:10.1109/ojcoms.2020.2969899

CrossRef Full Text | Google Scholar

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. nature 518, 529–533. doi:10.1038/nature14236

PubMed Abstract | CrossRef Full Text | Google Scholar

Noh, S., Lee, J., Lee, G., Seo, K., Sung, Y., and Yu, H. (2022). Channel estimation techniques for RIS-assisted communication: millimeter-wave and sub-thz systems. IEEE Veh. Technol. Mag. 17, 64–73. doi:10.1109/mvt.2022.3158765

CrossRef Full Text | Google Scholar

Sun, X., Liu, J., and Popovski, P. (2023). Multi-agent drl for cooperative spectrum sharing in wireless networks. IEEE Trans. Commun. 71, 1890–1902. doi:10.1109/TCOMM.2023.3176541

CrossRef Full Text | Google Scholar

Tang, W., Chen, M. Z., Chen, X., Dai, J. Y., Han, Y., and Renzo, M. D. (2022). Wireless communications with reconfigurable intelligent surfaces: path loss modeling and experimental measurement. IEEE Trans. Wirel. Commun. 21, 1295–1310. doi:10.1109/TWC.2022.3180987

CrossRef Full Text | Google Scholar

The MathWorks, Inc (2023). MATLAB deep reinforcement learning toolbox user’s guide. Natick, Mass.

Google Scholar

Wang, T., Yang, X., and Chen, Z. (2023a). Adaptive power control for pd-noma based on real-time channel conditions. IEEE Trans. Commun. 71, 101–110. doi:10.1109/TCOMM.2022.3218954

CrossRef Full Text | Google Scholar

Wang, X., Wang, L., and Zhang, J. (2023b). Machine learning-based optimization framework for ris-noma systems. IEEE Trans. Commun. 71, 1890–1902. doi:10.1109/TCOMM.2023.3176541

CrossRef Full Text | Google Scholar

Wang, X., Wang, L., Zhang, J., and Chen, Y. (2022). Deep reinforcement learning for resource allocation in heterogeneous networks. IEEE Trans. Wirel. Commun. 21, 3503–3516. doi:10.1109/TWC.2022.3146228

CrossRef Full Text | Google Scholar

Wei, L., Huang, C., Alexandropoulos, G. C., Yuen, C., Zhang, Z., and Debbah, M. (2021). Channel estimation for RIS-empowered multi-user MISO wireless communications. IEEE Trans. Commun. 69, 4144–4157. doi:10.1109/tcomm.2021.3063236

CrossRef Full Text | Google Scholar

Witrisal, K., Hinteregger, S., Kulmer, J., Leitinger, E., and Meissner, P. (2016). “High-accuracy positioning for indoor applications: RFID, UWB, 5G, and beyond,” in IEEE Int. Conf. on RFID (RFID), China, 12-14 September 2022 (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Wu, Q., Zheng, B., You, C., Zhu, L., Shen, K., Shao, X., et al. (2023). Intelligent surfaces empowered wireless network: recent advances and the road to 6g. arXiv preprint arXiv:2312.16918.

Google Scholar

Xu, J., Xu, A., Chen, L., Chen, Y., Liang, X., and Ai, B. (2024). Deep reinforcement learning for ris-aided secure mobile edge computing in industrial internet of things. IEEE Trans. Industrial Inf. 20, 2455–2464. doi:10.1109/tii.2023.3292968

CrossRef Full Text | Google Scholar

Xu, R., Zhang, Y., and Liu, L. (2023b). Adaptive ml-based framework for optimizing ris placement and configuration in noma systems. IEEE Trans. Commun. 71, 2150–2163. doi:10.1109/TCOMM.2023.3198765

CrossRef Full Text | Google Scholar

Yang, F., Hasna, M. O., and Alouini, M. (2023). Deployment strategies of reconfigurable intelligent surfaces in heterogeneous networks. IEEE Trans. Wirel. Commun. 72, 854–867. doi:10.1109/TWC.2023.3227890

CrossRef Full Text | Google Scholar

Yang, Z., Liu, Y., Chen, Y., and Al-Dhahir, N. (2021). Machine learning for user partitioning and phase shifters design in ris-aided noma networks. IEEE Trans. Commun. 69, 7414–7428. doi:10.1109/tcomm.2021.3100866

CrossRef Full Text | Google Scholar

Zhang, X., Li, H., and Wang, Y. (2021a). Advanced sparse code design for cd-noma in dense user environments. IEEE Trans. Commun. 69, 1234–1246. doi:10.1109/TCOMM.2021.3049276

CrossRef Full Text | Google Scholar

Zhang, Y., Wu, Q., and Renzo, M. D. (2023a). Advanced star-ris design for optimized transmission and reflection in noma frameworks. IEEE Trans. Commun. 71, 1046–1074. doi:10.1109/TCOMM.2023.3168975

CrossRef Full Text | Google Scholar

Zhang, Y., Wu, Q., and Renzo, M. D. (2023b). Dynamic spectrum access in cognitive radio networks: a drl-based approach. IEEE Trans. Cognitive Commun. Netw. 9, 15–28. doi:10.1109/TCCN.2023.3217845

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, J., Liu, Y., Wu, Q., He, B., and Yang, L. (2022). On the secrecy design of STAR-RIS assisted uplink NOMA networks. IEEE Trans. Wirel. Commun. 21, 11207–11221. doi:10.1109/twc.2022.3190563

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, C., Jiang, C., Jia, F., Ge, J., and Gong, F. (2021b). Improving physical layer security for reconfigurable intelligent surface aided NOMA 6G networks. IEEE Trans. Veh. Technol. 70, 4451–4463. doi:10.1109/tvt.2021.3068774

CrossRef Full Text | Google Scholar

Zhao, H., Li, X., and Wang, Y. (2022). Enhanced partitioning algorithm for spectrum efficiency and fairness in ris-noma systems. IEEE Trans. Wirel. Commun. 21, 2543–2557. doi:10.1109/TWC.2022.3146228

CrossRef Full Text | Google Scholar

Zuo, J., Liu, Y., Ding, Z., and Song, L. (2021). “Simultaneously transmitting and reflecting (star) ris assisted noma systems,” in IEEE Global Communications Conference (GLOBECOM), China, 8–12 December 2024, 1–6.

CrossRef Full Text | Google Scholar