- 1Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany
- 2Max-Planck-Zentrum für Physik und Medizin, Erlangen, Germany
- 3Center of Membrane Biochemistry and Lipid Research, University Clinic and Faculty of Medicine, Dresden, Germany
- 4Institute for Clinical Chemistry and Laboratory Medicine, University Clinic and Faculty of Medicine, Dresden, Germany
- 5Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
The dauer larva is a specialized stage of worm development optimized for survival under harsh conditions that have been used as a model for stress resistance, metabolic adaptations, and longevity. Recent findings suggest that the dauer larva of Caenorhabditis elegans may utilize external ethanol as an energy source to extend their lifespan. It was shown that while ethanol may serve as an effectively infinite source of energy, some toxic compounds accumulating as byproducts of its metabolism may lead to the damage of mitochondria and thus limit the lifespan of larvae. A minimal mathematical model was proposed to explain the connection between the lifespan of a dauer larva and its ethanol metabolism. To explore theoretically if it is possible to extend even further the lifespan of dauer larvae, we incorporated two natural mechanisms describing the recovery of damaged mitochondria and elimination of toxic compounds, which were previously omitted in the model. Numerical simulations of the revised model suggested that while the ethanol concentration is constant, the lifespan still stays limited. However, if ethanol is supplied periodically, with a suitable frequency and amplitude, the dauer could survive as long as we observe the system. Analytical methods further help to explain how feeding frequency and amplitude affect lifespan extension. Based on the comparison of the model with experimental data for fixed ethanol concentration, we proposed the range of feeding protocols that could lead to even longer dauer survival and it can be tested experimentally.
1 Introduction
Caenorhabditis elegans is a well-known free-living nematode studied as a model organism to address a broad range of biomedical questions from genetics, cell biology, and human disease conditions to nematode control Sydney (1974); Corsi et al. (2015). In the context of how organisms may adapt to stressful environmental conditions, C. elegans larval stage called “dauer” is of particular interest Riddle (1988); Hu (2007); Erkut and Kurzchalia (2015). A developing C. elegans larva at the L1 stage can turn into an alternative dauer larva developmental stage under harsh environments such as lack of food or high population density Riddle (1988); Hu (2007); Erkut and Kurzchalia (2015). To be able to survive these conditions, C. elegans dauer develop a strong cuticle that covers its whole body, such that most of the matter exchange across its body boundary shuts down. As a result, it was long believed that C. elegans dauer survive solely on stored lipids and are not able to uptake any carbon source from their environment Riddle (1988); Hu (2007); Erkut and Kurzchalia (2015). However, our recent findings Kaptan et al. (2020) showed that C. elegans dauer can utilize ethanol as an external carbon source, see Figure 1. Remarkably, at optimal concentrations, ethanol could expand the lifespan of dauer larvae twofold for a wild type and up to fourfold for some mutants. Ethanol can penetrate across the cuticle and thus gets channeled in the metabolic pathways of C. elegans dauer larvae. The enzymes responsible for the first metabolic steps are SODH-1 and ALH-1 which transform ethanol to acetate which can be activated into acetyl-COA and enters the major metabolic pathways of the TCA cycle, glyoxylate shunt, gluconeogenesis, and lipid metabolism, thus augmenting the metabolic pathways that dauers use for energy production Kaptan et al. (2020); Erkut and Kurzchalia (2015); Penkov et al. (2020); Burnell et al. (2005); Wadsworth and Riddle (1989). SODH-1 and ALH-1 are found to be upregulated in the presence of ethanol, whereas in sodh-1 mutant, the ethanol is no longer incorporated and does not affect the lifespan of dauer. Experiments with radioactively-labeled ethanol have shown that it can be utilized for the production and accumulation of stored lipids, thus providing an effectively unlimited source of energy to dauer larvae in case of permanent ethanol supply Kaptan et al. (2020).
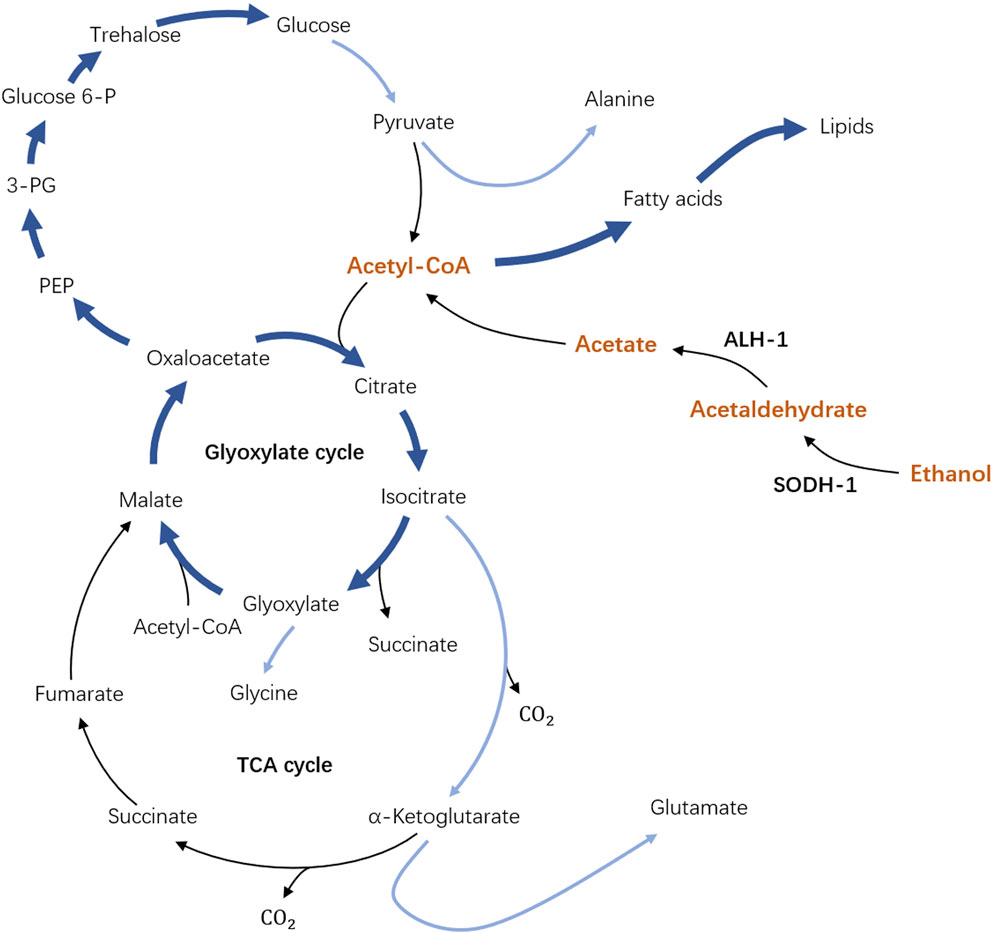
FIGURE 1. Schematics of the metabolic pathway of dauer larvae in the presence of external ethanol. In dependence on SODH-1 and ALH-1 enzymes, external ethanol is broken up and activated to Acetyl-COA (part of the pathway shown in orange) which is the key element of the original unperturbed metabolic pathway. Importantly, the arrows now pointing from Acetyl-CoA to fatty acids show the possibility of lipid storage accumulation in the presence of ethanol.
This led us to the question of why even in the presence of this energy source dauers do exhibit a longer lifespan but then eventually die. To help to answer this question, we proposed a mathematical model describing the relation between the lifespan of Caenorhabditis elegans dauer and the supplied ethanol based on the known metabolic pathway of dauer larvae. We assumed that the dauer dies either due to the lack of energy or due to the accumulation of some not yet identified toxic compound(s) Kaptan et al. (2020) that could resemble the so-called “lipotoxicity” factors in mammalian systems Burnell et al. (2005); Schooneman et al. (2013); DeFronzo (2010). As experimentally observed, the death of worms was preceded by the deterioration of mitochondria. We also assumed that these two mechanisms led to mitochondria damage and then to death. This model was very successful in explaining experimental data on the lifespans of dauer and various mutants in the presence of and without ethanol.
While identifying the exact toxic component that limits the lifespan of dauer is still an ongoing research project, we were interested in exploring whether or not the lifespan could be extended even further. To this end, we assume there are two self-recovery mechanisms, namely, regeneration of mitochondria and detoxification, and we test what they lead to. These two mechanisms alone still result in dauer’s death if the feeding protocol is constant. However, when we use a periodic supply of ethanol in the model, an unlimited lifespan can emerge according to the numerical simulation. By comparing model predictions with existing data on constant feeding, we also suggest feeding protocols that can be directly tested in future experiments on dauer.
Certainly, the unlimited lifespan for the wild-type C. elegans dauer larvae even under the proposed feeding protocol sounds unfeasible and is a regime predicted by an idealized theoretical model that proposes two recovery mechanisms. However, testing this model prediction in experiments will provide crucial insights into the metabolism of dauers if there is any significant extension of the lifespan for periodic feeding that would support the hypothesis of the existence of recovery mechanisms that could be further explored.
2 Methods
2.1 Mathematical model
A minimal model of the metabolic network of C. elegans dauer larvae was introduced in Kaptan et al. (2020) and accurately reproduced the lifespans of dauer with and without ethanol for wild-type worms and various mutations. The framework of the model follows the largely coarse-grained metabolic pathway of dauer. All the chemical components falling into the category of “available energy” are combined and called “acetate”, which is the central representative component of this category. Similarly, the components corresponding to “stored energy” and “consumed energy” are denoted as lipids and carbohydrates, respectively. Acetate and lipids could transform into each other as the balance between free and stored energy. At the same time, acetate continuously transforms into carbohydrates unidirectionally to support the main functions of an organism including mitochondria. If the production of carbohydrates drops below a certain minimal threshold, mitochondria start to get damaged and the dauer dies. In the presence of ethanol, acetate gains an influx proportional to its concentration. During the process of releasing stored lipids, toxic compounds are produced as a side product and as the second major reason that causes damage to the mitochondria alongside the lack of carbohydrate production.
Our model also included the effect of genes that were identified as regulatory factors through genetic experiments with loss-of- or reduction-of-function mutations Kaptan et al. (2020). We use daf-2(e1370) strain as a proxy for the control strain in our current study. The differences between wild-type dauers and daf-2 mutants were previously discussed in Kaptan et al. (2020). Specifically, this strain has a Daf-c (dauer constitutive) phenotype due to a conditional, temperature-activated mutation that induces dauer formation even on ample food and at a low population density. It undergoes controlled dauer formation upon temperature switch and provides two advantages compared to the wild-type: i) daf-2 animals enter dauer state more synchronously and, thus, the age variations are minor; ii) as they enter dauer state under unrestricted food supply, they might be able to store more lipids prior to entering dauer arrest. Otherwise, there is a well-documented agreement in the field that daf-2 dauer larvae recapitulate to a high degree the signaling and metabolic processes in wild-type worms undergoing dauer formation Hu (2007). Loss-of-function mutation in the aak-2/AMPKα in daf-2(e1370);aak-2(gt33) double mutants causes an enhanced lipolysis rate, which leads to a reduced lifespan compared to the control strain under both feeding conditions with and without ethanol Penkov et al. (2020); Narbonne and Roy (2009). A reduction-of-function allele in the class I PI3-kinase age-1(hx546) (single mutant), on the other hand, is supposed to have a reduced lipid synthesis rate. This assumption is based on experimental results with the mutant age-1 in dauer state Kaptan et al. (2020). Its lifespan is similar to control dauer when there is no ethanol supply but has a large increase when the ethanol is supplied Kaptan et al. (2020).
The goal of this work is to identify potential ways of how the dauer could survive even for a longer time. Thus, here, we consider mechanisms by which the model will be able to produce an unlimited lifespan while still remaining consistent with the results of the previous experiments. There are two essential and rather natural mechanisms that have been omitted in the original model Kaptan et al. (2020) while having potential for lifespan extension: detoxification Xu et al. (2005); Chen (2011) and a possibility for mitochondria to regenerate Palikaras and Tavernarakis (2014); Ni et al. (2015); Chan (2012) (see green arrows in Figure 2). We will show in the following that the model containing these two mechanisms predicts the possibility for lifespan extension under periodic supply protocol of ethanol.
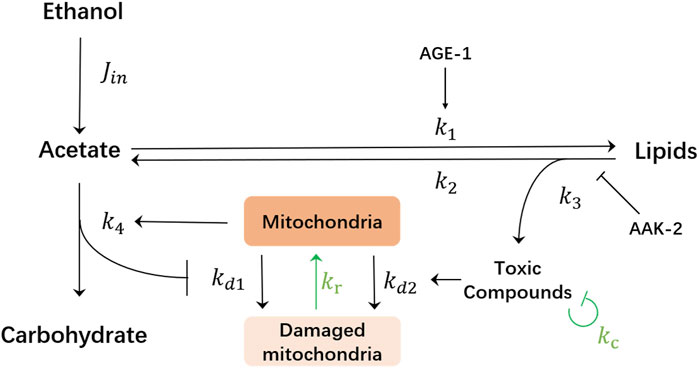
FIGURE 2. Schematics of the mathematical model of the metabolic network of C. elegans dauer larvae. Externally supplied ethanol is transformed into the acetate creating its influx jin, which can be either constant or varies in time depending on the respective supplied ethanol concentration. Acetate (ch. acetyl-CoA in Figure 1) is then used either for energy production and carbohydrate synthesis or can be stored in lipids. Mitochondria undergo damage from lack of carbohydrate production or accumulation of toxic compounds as the product of lipolysis. Aak-2 kinase exerts the inhibitory effect on the lipolysis, thus the aak-2 mutation leads to an enhanced lipolysis rate. Age-1 kinase stimulates lipid synthesis and thus age-1 mutation would lead to the reduction of lipid synthesis. Green arrows indicate two hypothesized mechanisms of recovery by degradation of toxic compounds with the rate kc and mitochondria regeneration with the rate kr.
To demonstrate this, we first formalize the schematics in Figure 2 into the system of ordinary differential equations that describe the chemical reaction network of ethanol metabolism Fromm and Hargrove (2011):
Here “a” and “l” denote the concentrations of the acetate and lipids, respectively, while “c” represents the concentration of toxic compound(s), and m designates the wellbeing of mitochondria. The consumption of acetate for simplicity is assumed to be unidirectional (not explicitly modeled in the system) with the rate k4, but acetate can also be stored in lipids, see Eq. 1. In the presence of external ethanol, an influx jin of acetate is included as the source. This influx jin is assumed to be proportional to the external ethanol concentration. Lipids get created from acetate with rate k1 while they are released through the lipolysis process with rate k2, Eq. 2. The toxic compound(s) c is produced as the side product of lipolysis with proportionality factor k3 and spontaneous degradation rate kc, Eq. 3. The variable m ranges from 1 to 0 and denotes the wellbeing of mitochondria, where m = 1 means a fully functional mitochondria and m = 0 means a fully damaged one. Mitochondria can be damaged with a rate kd1 if the carbohydrate production k4a falls below the minimal required “energy” flux jm, or with a rate kd2 when the toxic compound c accumulates above a certain threshold concentration ch (Θ in the equation is the Heaviside step function). There are many known mechanisms of mitochondria surveillance and maintenance Palikaras and Tavernarakis (2014); Ni et al. (2015); Chan (2012). Here, for simplicity, we suggest a phenomenological law of mitochondria recovery. When mitochondria do not suffer any damage (i.e., there is enough ethanol and the toxic compound is below the critical threshold) they can regenerate. The regeneration rate is proportional to the current damage level of mitochondria (1 − m) with a rate constant kr. This term ensures that the value of m recovers toward one from any state of 0 < m < 1.
While most of the reaction rates in the above equations are considered constant for simplicity, some rates do depend on variables. The first example is the linear dependence of k4 on m, which assumes that the energy production requires functional mitochondria:
where
Here, l1 is a characteristic lipid concentration at which the conversion starts to saturate and
where
The model including the self-recovery mechanism, however, should also reproduce the lifespan of dauers with and without ethanol, as well as different mutants as was observed experimentally Kaptan et al. (2020). This also means that this model should result in a finite lifespan under a constant ethanol supply. However, the novel possibility for lifespan extension may now emerge for non-constant feeding, where the supplied ethanol concentration varies in time, for instance, according to a periodic sinusoidal protocol. We next show by using numerical simulations that the model reproduces experimental observations under constant feeding and predicts the lifespan extension under periodic feeding protocol.
3 Results
3.1 Constant ethanol supply
We first check if the model with the self-recovery can recapitulate experimental observations with a constant ethanol supply. Parameters used in the simulations were chosen by checking whether the lifespan ratios between mutants (daf-2, daf-2;aak-2, and age-1) with and without ethanol generated by simulations fit the previous experimental results Kaptan et al. (2020). When one set of parameters is considered the control strain without ethanol feeding, the corresponding parameter set of daf-2;aak-2 mutant is defined by increasing the value of
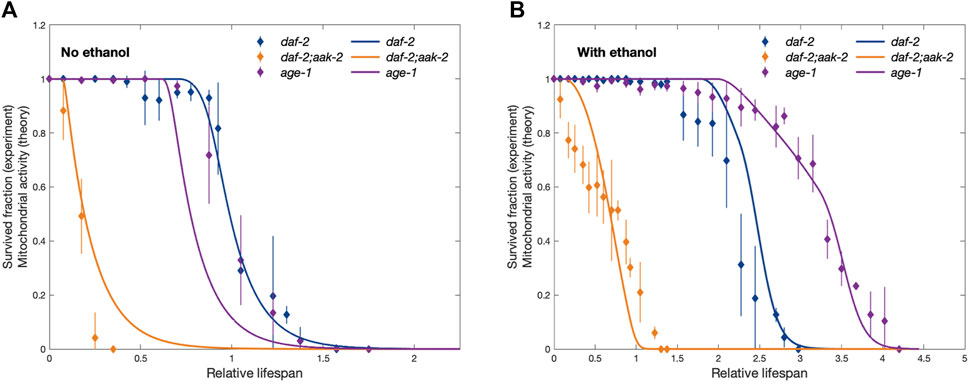
FIGURE 3. Comparison between experimentally observed lifespan of dauers of different strains (dashed lines) showing the fraction of survived dauers as a function of time and the corresponding simulation results (solid lines) showing the activity of mitochondria. Panels (A) and (B) correspond to no ethanol and provided ethanol conditions, respectively. The time axis is rescaled for the experimental curves by the time at which the fraction of survived daf-2 strain dauers used as a control drops to 0.5 (50%) in no ethanol condition (t =40 days). Similarly, for the simulation results, the time axis is rescaled by the time at which the activity of mitochondria in control conditions with no ethanol drops to 50%. This rescaling allows for direct theory-experiment comparison even if we do not link simulation time to real-time units. Experimental data is taken from Kaptan et al. (2020), and error bars show standard deviation.
The detailed dynamics of one of the parameter sets for control strain with and without feeding is shown as an example in Figure 4. When there is no feeding, dauer breaks down storage lipids to keep its acetate level and thus the carbohydrate production rate. As the lipids run out, the mitochondria are damaged for lack of carbohydrate production which results in the death of dauer. When ethanol is supplied at a sufficient level, starvation no longer becomes a concern. However, the toxic compound continuously accumulates and as it goes beyond the threshold at some point, the mitochondria start to take damage and finally the larvae die. The details of the simulation including the numerical methods Fromm and Hargrove (2011); Murray (1989); Strogatz (2000) and parameters are provided in Supplementary Appendix S1.
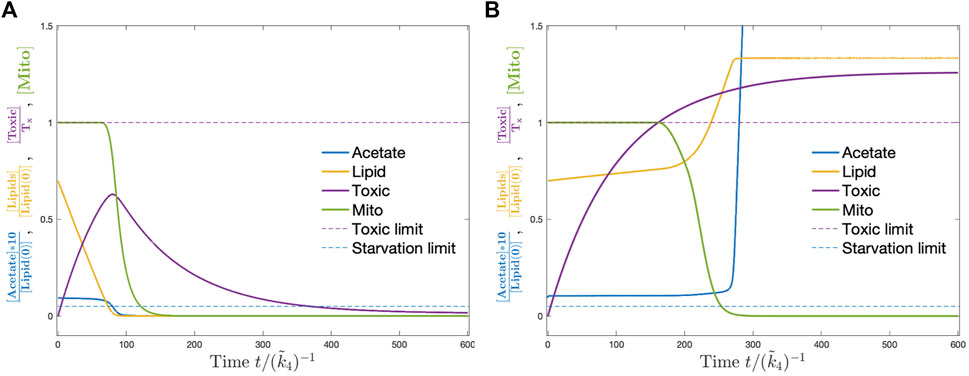
FIGURE 4. Dynamics of the model corresponding to control strain without (A) and with ethanol (B). Without ethanol supply, the dauer consumes the stored lipids (yellow) which keep acetate levels (blue) and mitochondria (green) at constant levels. Toxic compounds accumulate (magenta). When lipids are used up, the acetate level drops below the critical threshold (dashed blue line) and mitochondria start to get damaged till the larvae die due to starvation. With ethanol supply, acetate never ends and mitochondria start to damage after the toxic compounds go above a critical threshold (dashed magenta line). Then, dauer dies due to the accumulation of toxic compounds.
As the above two examples show, starvation or accumulation of toxic compounds is the reason for mitochondria damage and the resulting death of larvae. We can demonstrate more generally the condition for the finite lifespan of dauers for a constant ethanol concentration.
Figure 5 shows the lifespan of dauer as a function of the external ethanol influx. If either starvation damage kd1 or toxic damage kd2 is removed, the dauer may have an infinite lifespan when the ethanol concentration is sufficiently high or low, respectively. If, however, these two lifespans vs. influx curves intersect at some value of jin, lifespan will always remain finite, and as for any given ethanol concentration and the corresponding influx, there will be at least one reason that the dauer dies within the limited time determined by kd1 or kd2.
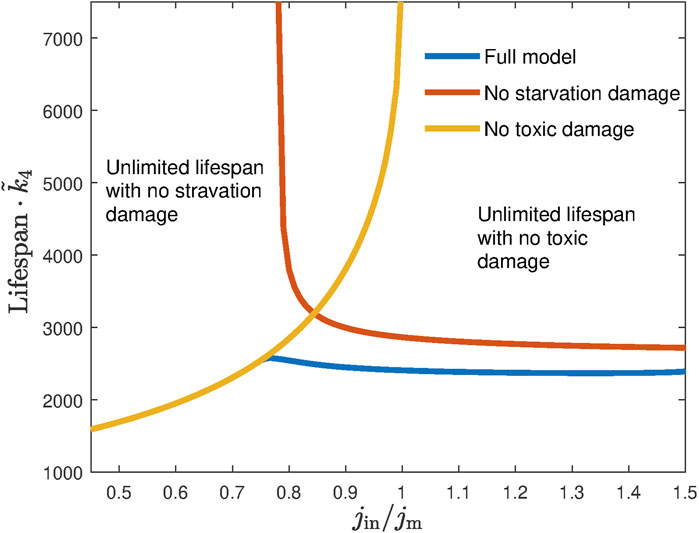
FIGURE 5. No lifespan extension is possible when larvae are fed with constant ethanol influx. The red and yellow lines show the lifespan as a function of the ethanol influx (normalized by minimal energy flux jm required for mitochondria wellbeing) in the absence of toxic damage and no starvation damage, respectively. While both cases have regions of influx supporting infinite lifespan, they do not overlap, leading to the overall final lifespan when both damages are present (blue line).
If the two curves (with each of the damage removed) do not intersect, they would form boundaries of a domain in between where the value of jin would support an infinite lifespan. As we mentioned above, in experiments, the dauer always survives the finite time in the presence of ethanol, thus defining for us the parameter range that has to be chosen in simulations.
3.2 Periodic ethanol supply
The above results show that ethanol supply keeps mitochondria operational, but the accumulating toxic compounds damage the mitochondria. Here, we hypothesize that periodic ethanol supply might be the key to an unlimited lifespan of dauer. While periods of supply might be used to replenish lipid storage and repair mitochondria, periods of no feeding can be used to degrade the accumulated toxic compounds. We now test this hypothesis numerically. For simplicity, we use a sinusoidal feeding protocol with a feeding amplitude A, feeding frequency ωE, and a positive baseline value j0:
With a proper parameter choice, the numerical simulations of the model show that the mitochondria damage and regenerate periodically until the end of simulations no matter how long these last.
Indeed, this situation becomes possible when parameters are tuned such that the periodic feeding permits the worm to accumulate toxic compounds while intaking ethanol and fuelling mitochondria but then remove them with a diet at the cost of some mitochondria damage, which can, however, be regenerated during the next intake cycle. These simulations suggest that the periodic feeding protocol does provide a theoretical possibility of an unlimited lifespan extension (Figure 6). We next investigate in more detail how this effect depends on model parameters.
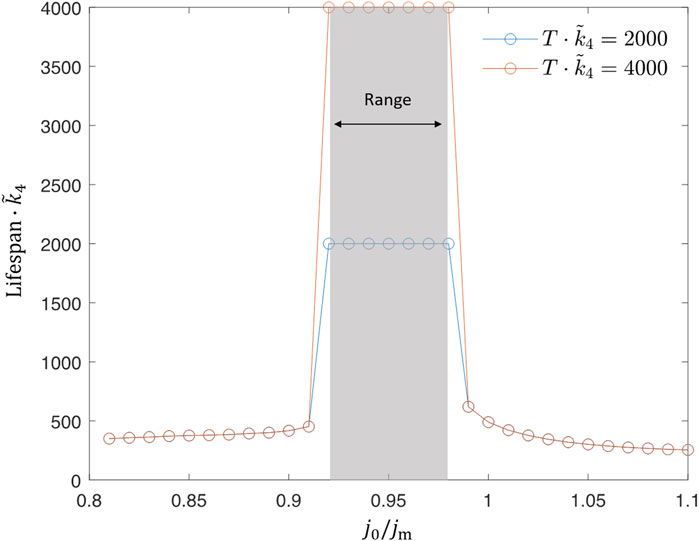
FIGURE 6. Example of a lifespan extension as a result of periodic feeding. The baseline value j0/jm =0.8 while A = j0. The feeding frequency ωE is the same as the oscillatory frequency of acetate level a shown in blue. The inset shows oscillations of toxicity near but below the toxic limit, while mitochondria are almost fully active.
Numerically, an unlimited lifespan can be defined as survival until the end of the simulation regardless of the simulation time. However, in practice, the time for which we can observe the system is always limited. Thus, we set a certain threshold value Tmax for the survival time. If a dauer survives until Tmax in simulation, we say the lifespan of the dauer is unlimited under this set of parameters. Our analytical considerations also suggest that there may exist a true infinite lifespan given a certain set of parameters in the model.
3.3 Effect of feeding parameters
A single simulation does not reflect the whole picture but only indicates a possibility. To quantify the robustness of lifespan extension, we defined a new value “range” w as the size of the interval within which the baseline influx j0 may vary so that the dauer exhibits an unlimited lifespan, see Figure 7. The range w of this baseline interval thus quantifies the ability of a certain set of parameters (ωE, A) to support the extension of lifespan. We note that the lifespan seems to go through a sharp transition from a finite to an infinite value, first when approaching from the side of low baseline value and second when approaching from the side of large baseline levels. The transition at low influx seems to be a jump-like switch (as we could only test numerically). The high influx condition is amenable to analytical analysis and we could show that it has a shape of a logarithmic divergence (see Supplementary Appendix S3). By quantifying the survival ability with the value of w and studying its dependence on feeding parameters, ωE and A would eventually help us to identify the optimal experimental conditions where the lifespan extension of dauer could be tested.
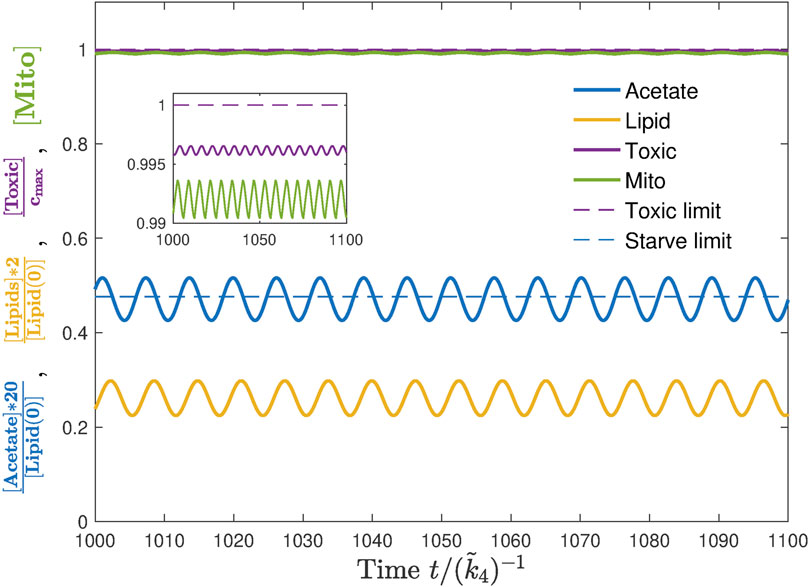
FIGURE 7. Range w is the size of an interval of j0 where the dauer experiences lifespan extension. Its value is obtained numerically by scanning over the baseline value j0 while keeping ωE and A fixed. For each j0, we run multiple simulations corresponding to various initial lipid storage l(0) and take the largest w from those simulations as the range w corresponding to this j0. The baseline value j0 can be smaller than the minimal energy flux jm as the oscillations with large enough amplitude A make jin larger than jm for a certain fraction of the feeding period. Here, we also show that the range does not strongly depend on the chosen threshold,
We next plot the range w as a function of feeding amplitude A and frequency ωE, see Figure 8.
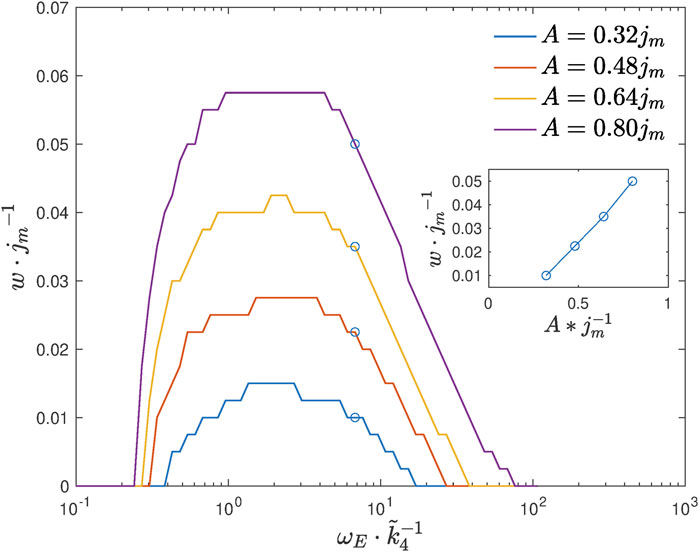
FIGURE 8. Range w as a function of the feeding frequency ωE for different values of amplitude A. The inset shows a linear-like dependence of the range on amplitude in the region of high-feeding frequencies.
According to the simulation results, we see that lifespan extension is possible when the feeding frequency is within a certain interval. The experiment with the feeding frequency ωE corresponding to the maximal range w is expected to give the highest chance to observe the effect. The simulations also suggest that the range w grows with feeding amplitude A in an almost linear way if the feeding frequency is high enough. This is because, at a high-frequency region, the range w is proportional to the oscillation amplitude of acetate, which can be explained by an approximate analytical solution. (For details of the analysis, see Supplementary Appendix S2).
The range-frequency curves can potentially help us to identify suitable feeding frequencies and amplitudes for which it is most likely to observe lifespan extension in experiments. To do so, we still need to connect our mostly dimensionless equations to realistic parameters. This is not too straightforward since not all parameters of the enzymatic kinetics as well as chemical concentrations in the dauer were measured yet. However, for the case of the feeding frequency, we may take a short-cut where we can determine the timescale by equalling the control lifespan without ethanol in the model defined as the time where m falls to, for example, 0.5, compared to that in experiment defined as respective 50% survival and restore all reaction rates in real-time units. Also, the feeding amplitude is simply set as large as possible (see below) so there is no more information needed. Figure 9 shows the range vs. period (given in hours) relation for control strain and daf-2;aak-2 mutants under maximal feeding amplitude. The maximal feeding amplitude is defined as A = min[j0] (i.e., the smallest j0 among all j0 used in scanning, such that the influx jin is always positive). Another definition A = j0 for all j0 is also possible and leads to similar results.
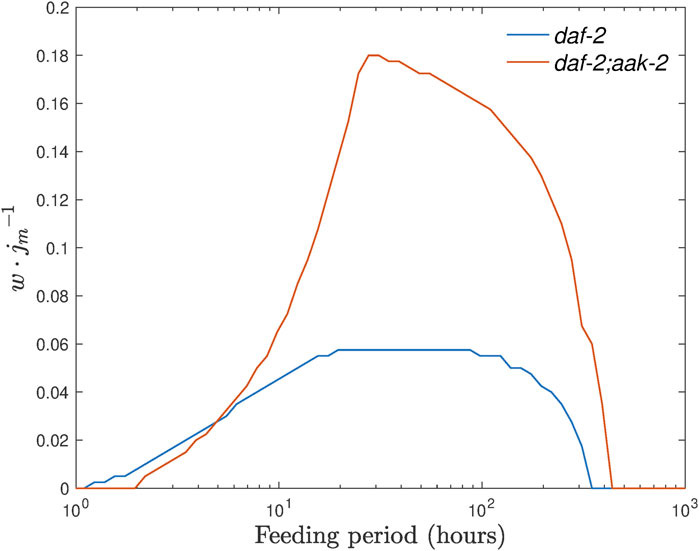
FIGURE 9. Range of the baseline ethanol supply levels where we expect to see unlimited survival of dauer larvae shown for control and daf-2;aak-2 strains as a function of the feeding period T =2π/ωE. Here, it is assumed that the amplitude A takes the value of min[j0].
These simulations not only suggest an optimal feeding period for both strains but also indicate that daf-2;aak-2 mutant is a better option for the experiment, not only for the larger range value but also for the smaller optimal feeding period. It requires a feeding period of the order of 10 h (so the media for larvae can be changed once a day) and the effect should be seen much earlier, as the original lifespan of daf-2;aak-2 is much shorter, and thus overall a shorter experiment could be carried out.
4 Discussion and conclusion
Previously, we have shown that the lifespan of Caenorhabditis elegans dauer larvae can be greatly extended due to the metabolism of externally provided ethanol. With the help of the mathematical model of this metabolic pathway, we proposed that the lifespan remains limited due to the accumulation of toxic compounds resulting from the process of lipolysis. So far, however, we have neglected the possibility of mechanisms that help dauer to recover from this damage. Therefore, two biological self-recovery mechanisms, namely, detoxification and mitochondria regeneration, were introduced into the model. Importantly, despite self-recovery mechanisms for constant ethanol supply, the model reproduces the experimental observations of extended but limited lifespan.
However, when the feeding protocol is periodic, an unlimited lifespan can emerge. The possibility of an unlimited lifespan can be explained by the switch between two feeding phases, where the first one at high ethanol concentration repairs the mitochondria at the cost of toxic compounds’ accumulation, while the second one, at low ethanol concentration, has the toxic compounds degraded but also damages the mitochondria slightly. For this process to keep the dauer surviving, both mitochondria regeneration and toxic compounds detoxification mechanisms are required to function.
Specifically in the context of dauer larvae survival in the wild Schulenburg and Félix (2017); Frézal and Félix (2015); Félix and Duveau (2012), our results might indicate that the time-varying availability of ethanol supply (when feeding phases are interspersed with starvation and toxic compound degradation) might be more beneficial for lifetime extension. One could speculate that fluctuating environmental conditions might be more common than a steady and abundant ethanol supply.
To characterize the unlimited lifespan predicted by the model systematically, we defined a range of baseline feeding fluxes, which quantifies the ability of a certain set of feeding parameters to support the unlimited lifespan. The dependence of this range on feeding frequency and amplitude was studied numerically with some supporting analytical arguments. This dependence combined with previous data helped us to suggest a suitable feeding period and amplitude that can now be tested experimentally.
While an unlimited lifespan is not uncommon in nature and is exemplified in worms by some planarian flatworm species Tan et al. (2012), observing this for the short-lived wild-type C. elegans dauer larvae is not likely. Our model, proposed and experimentally tested for constant ethanol supply, suggests that under the assumption of the existence of two recovery mechanisms (mitochondria repair and degradation of toxins) in a rather broad range of parameters, an unlimited lifespan is theoretically possible. Any significant extension of the lifespan for periodic feeding in the experiment would support the hypothesis of the existence of recovery mechanisms. Furthermore, an extended but limited lifespan would trigger the search for other yet unknown mechanisms that serve as limiting factors. Importantly, it also highlights the importance of ultimately identifying candidates of toxic compounds which, in the model, are the main cause of death when starvation is overcome by ethanol. This study treats the identity of toxic compounds openly and does not specify the concrete mechanisms of mitochondria recovery and detoxification. Ultimately, for our comprehensive understanding of dauer larvae lifespan extension mechanisms and the generalization of those to other organisms, we need to push toward identifying the exact biological players of toxicity and recovery competition.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
XZ investigation, methodology, writing–original draft preparation. SP methodology, writing—review and editing. TK conceptualization, writing–review and editing. VZ conceptualization, writing—review and editing, supervision. All authors contributed to the article and approved the submitted version.
Funding
SP was supported by funds from TU Dresden’s Institutional Strategy, financed by the Excellence Initiative of the Federal (Saxony) and State (Germany) Governments. TK acknowledges financial support from the Max Planck Society. XZ, VZ, and TK acknoledges financial support from Volkswagen Foundation “Life?” initiative. Grant number: 96527 The full name of funder: Volkswagen Stiftung URL of funder: https://www.volkswagenstiftung.de/en. We acknowledge financial support by Deutsche Forschungsgemeinschaft and Friedrich-Alexander-Universität Erlangen-Nürnberg within the funding programme “Open Access Publication Funding”.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fragi.2023.1031161/full#supplementary-material
References
Burnell, A. M., Houthoofd, K., O’Hanlon, K., and Vanfleteren, J. R. (2005). Alternate metabolism during the dauer stage of the nematode caenorhabditis elegans. Exp. Gerontol. 40, 850–856. doi:10.1016/j.exger.2005.09.006
Chan, D. C. (2012). Fusion and fission: interlinked processes critical for mitochondrial health. Annu. Rev. Genet. 46, 265–287. doi:10.1146/annurev-genet-110410-132529
Chen, C.-H. (2011). Activation and detoxification enzymes: Functions and implications. Berlin, Heidelberg: Springer.
Corsi, A. K., Wightman, B., and Chalfie, M. (2015). A transparent window into biology: A primer on caenorhabditis elegans. Genetics 200, 387–407. doi:10.1534/genetics.115.176099
DeFronzo, R. A. (2010). Insulin resistance, lipotoxicity, type 2 diabetes and atherosclerosis: the missing links. The claude bernard lecture 2009. Diabetologia 53, 1270–1287. doi:10.1007/s00125-010-1684-1
Erkut, C., and Kurzchalia, T. V. (2015). The c. elegans dauer larva as a paradigm to study metabolic suppression and desiccation tolerance. Planta 242, 389–396. doi:10.1007/s00425-015-2300-x
Félix, M.-A., and Duveau, F. (2012). Population dynamics and habitat sharing of natural populations of caenorhabditis elegans and c. briggsae. BMC Biol. 10, 59–19. doi:10.1186/1741-7007-10-59
Frézal, L., and Félix, M.-A. (2015). C. elegans outside the petri dish. elife 4, e05849. doi:10.7554/eLife.05849
Fromm, H. J., and Hargrove, M. S. (2011). “Enzyme kinetics,” in Essentials of biochemistry (Berlin, Heidelberg: Springer), 201–213.
Kaptan, D., Penkov, S., Zhang, X., Gade, V. R., Raghuraman, B. K., Galli, R., et al. (2020). Exogenous ethanol induces a metabolic switch that prolongs the survival of caenorhabditis elegans dauer larva and enhances its resistance to desiccation. Aging Cell 19, e13214. doi:10.1111/acel.13214
Narbonne, P., and Roy, R. (2009). Caenorhabditis elegans dauers need lkb1/ampk to ration lipid reserves and ensure long-term survival. Nature 457, 210–214. doi:10.1038/nature07536
Ni, H.-M., Williams, J. A., and Ding, W.-X. (2015). Mitochondrial homeostasis: the interplay between mitophagy and mitochondrial biogenesis. Redox Biol. 4, 6–13. doi:10.1016/j.redox.2014.11.006
Palikaras, K., and Tavernarakis, N. (2014). Mitochondrial homeostasis: the interplay between mitophagy and mitochondrial biogenesis. Exp. Gerontol. 56, 182–188. doi:10.1016/j.exger.2014.01.021
Penkov, S., Raghuraman, B. K., Erkut, C., Oertel, J., Galli, R., Ackerman, E. J. M., et al. (2020). A metabolic switch regulates the transition between growth and diapause in C. elegans. BMC Biol. 18, 31. doi:10.1186/s12915-020-0760-3
Schooneman, M. G., Vaz, F. M., Houten, S. M., and Soeters, M. R. (2013). Acylcarnitines: reflecting or inflicting insulin resistance? Diabetes 62, 1–8. doi:10.2337/db12-0466
Schulenburg, H., and Félix, M.-A. (2017). The natural biotic environment of caenorhabditis elegans. Genetics 206, 55–86. doi:10.1534/genetics.116.195511
Sydney, B. (1974). The genetics of caenorhabditis elegans. Genetics 77, 71–94. doi:10.1093/genetics/77.1.71
Tan, T. C., Rahman, R., Jaber-Hijazi, F., Felix, D. A., Chen, C., Louis, E. J., et al. (2012). Telomere maintenance and telomerase activity are differentially regulated in asexual and sexual worms. Proc. Natl. Acad. Sci. 109, 4209–4214. doi:10.1073/pnas.1118885109
Wadsworth, W. G., and Riddle, D. L. (1989). Developmental regulation of energy metabolism in caenorhabditis elegans. Dev. Biol. 132, 167–173. doi:10.1016/0012-1606(89)90214-5
Keywords: dauer larvae, lifespan extension, metabolic network, mathematical model, ethanol, periodic feeding
Citation: Zhang X, Penkov S, Kurzchalia TV and Zaburdaev V (2023) Periodic ethanol supply as a path toward unlimited lifespan of Caenorhabditis elegans dauer larvae. Front. Aging 4:1031161. doi: 10.3389/fragi.2023.1031161
Received: 18 November 2022; Accepted: 14 August 2023;
Published: 05 September 2023.
Edited by:
Terytty Yang Li, Fudan University, ChinaReviewed by:
Andrea Scharf, Missouri University of Science and Technology, United StatesStefan Klumpp, University of Göttingen, Germany
Copyright © 2023 Zhang, Penkov, Kurzchalia and Zaburdaev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vasily Zaburdaev, dmFzaWx5LnphYnVyZGFldkBmYXUuZGU=
 Xingyu Zhang
Xingyu Zhang Sider Penkov3,4
Sider Penkov3,4 Vasily Zaburdaev
Vasily Zaburdaev