Graph Theory Analysis Reveals Resting-State Compensatory Mechanisms in Healthy Aging and Prodromal Alzheimer’s Disease

Several theories of cognitive compensation have been suggested to explain sustained cognitive abilities in healthy brain aging and early neurodegenerative processes. The growing number of studies investigating various aspects of task-based compensation in these conditions is contrasted by the shortage of data about resting-state compensatory mechanisms. Using our proposed criterion-based framework for compensation, we investigated 45 participants in three groups: (i) patients with mild cognitive impairment (MCI) and positive biomarkers indicative of Alzheimer’s disease (AD); (ii) cognitively normal young adults; (iii) cognitively normal older adults. To increase reliability, three sessions of resting-state functional magnetic resonance imaging for each participant were performed on different days (135 scans in total). To elucidate the dimensions and dynamics of resting-state compensatory mechanisms, we used graph theory analysis along with volumetric analysis. Graph theory analysis was applied based on the Brainnetome atlas, which provides a connectivity-based parcellation framework. Comprehensive neuropsychological examinations including the Rey Auditory Verbal Learning Test (RAVLT) and the Trail Making Test (TMT) were performed, to relate graph measures of compensatory nodes to cognition. To avoid false-positive findings, results were corrected for multiple comparisons. First, we observed an increase of degree centrality in cognition related brain regions of the middle frontal gyrus, precentral gyrus and superior parietal lobe despite local atrophy in MCI and healthy aging, indicating a resting-state connectivity increase with positive biomarkers. When relating the degree centrality measures to cognitive performance, we observed that greater connectivity led to better RAVLT and TMT scores in MCI and, hence, might constitute a compensatory mechanism. The detection and improved understanding of the compensatory dynamics in healthy aging and prodromal AD is mandatory for implementing and tailoring preventive interventions aiming at preserved overall cognitive functioning and delayed clinical onset of dementia.

Introduction

Opposing effects of aging on brain functions have been reported: elderly individuals show decreased activity in some brain regions but increased activity in others (Cabeza and Dennis, 2012). These findings were challenging to the traditional assumption that aging is only linked with a simple pattern of cognitive and neural decline, supported by a body of research demonstrating an overall reduction of structural and functional brain integrity in Alzheimer’s Disease (AD).

A few studies investigated how the brain of AD patients reorganizes itself, which was interpreted as effects of brain plasticity (delEtoile and Adeli, 2017). Contrary to the initial belief, these and other studies have shown that “neuroplasticity” is not solely confined to children (Dennis et al., 2013) but is also observable in the healthy aging brain (Fuchs and Flügge, 2014) and even under the circumstances of neurodegeneration (Enciu et al., 2011), including Alzheimer’s Disease (delEtoile and Adeli, 2017). The latter findings gave rise to the concept of “neuronal compensation.”

Despite its popularity, the concept of compensation remains somewhat ambiguous, as the underlying neural mechanisms to date are still poorly understood. At least in part, this elusiveness is due to the complexity of defining the characteristics of compensation and the challenge to assess these characteristics in vivo (Gregory et al., 2017). To this end, various theoretical models of compensation in healthy aging and in the presence of neurodegeneration (Gregory et al., 2017) have been suggested. Most current theories of compensation were developed in task-based contexts, while compensatory processes in resting-state networks in healthy brain aging and early neurodegeneration have only rarely been addressed. However, resting-state studies offer several advantages over task-based ones, as they place low demands on the experimental design, compliance, instructions to be followed by participants, and training demands.

Cabeza et al. suggested that some essential criteria ought to be fulfilled for an observed increase in connectivity to reflect compensation (Cabeza et al., 2018). For example, increased connectivity should directly or indirectly be related to a neural resource deficiency or the supply demand gap (Lövdén et al., 2010; Cabeza and Dennis, 2012). The latter could be due to brain atrophy, reduced cerebral perfusion, or neurotransmitter deficiency (Cabeza et al., 2018). In the context of resting-state network connectivity, we propose four criteria to indicate compensatory mechanisms. First, the brain region must show a significant increase in functional connectivity. Second, the increase in functional connectivity must be accompanied by a decline of brain integrity in that region, e.g., volume reduction (Cabeza and Dennis, 2012). Third, the region must be specifically related to cognitive processing, to rule out non-selective neural recruitment (Cabeza, 2002; Logan et al., 2002). Finally, the connectivity increase of that region must be positively correlated with cognitive performance, thereby differentiating compensation from unspecific and maladaptive recruitment, in which greater connectivity is not associated with better cognitive performance (Cabeza and Dennis, 2012) or even with worse performance (Bakker et al., 2012).

We incorporated graph theory analysis in our novel criterion-oriented framework to investigate the resting-state compensation in healthy brain aging and prodromal AD. We hypothesized that during both healthy aging and MCI with biomarkers indicative of Alzheimer’s disease, brain regions show compensatory mechanisms, characterized by a significant increase of degree centrality, despite atrophy. Moreover, we assumed that degree centrality increases in these regions would be positively correlated with cognitive performance, indicating effective compensation.

Materials and Methods

Participants

The current study was part of the RIMCAD-study (Retroactive Interference during Memory Consolidation in Aging and Dementia) conducted by the Memory Clinic Köln Jülich. The Ethics Committee of the Faculty of Medicine of Cologne University had approved the RIMCAD-study. Out of the RIMCAD study’s larger pool of participants, three experimental groups were defined for the present study: (i) Fifteen young healthy controls (young HC), (ii) fifteen senior healthy controls (senior HC), and fifteen MCI patients (see Table 1). As MCI encompasses a heterogeneous population (Petersen et al., 2001), we solely recruited prodromal AD participants per the IWG-2 criteria and Dubois et al. (2014, 2016), with at least one positive AD biomarker. Biomarkers suggestive of AD included an abnormal amyloid deposition (either assessed by positron-emission-tomography or by an abnormal concentration of cerebrospinal fluid (CSF) β-amyloid 42), or an abnormal concentration of phospho-tau or a total tau/β-amyloid 42 ratio greater than 0.52 in CSF samples (Duits et al., 2015). All of the MCI patients were amnestic and 40% of them showed additional deficits in executive functions. Informed written consent had been obtained by all participants and upon completion of the study, they received financial compensation. All participants were right-handed, which was assessed using the Edinburgh Handedness Inventory (Oldfield, 1971) and had a normal or corrected-to-normal vision. As for the exclusion criteria, the participants were screened for neurological and psychiatric disorders, including a history of traumatic brain injury, epilepsy, Parkinson’s Disease, Multiple Sclerosis, depression, mania, or schizophrenia. Besides, past and present drug or alcohol abuse, as well as respiratory, cardiovascular, and gastro-intestinal, or kidney-related diseases were exclusion criteria. Moreover, contraindications to undergoing MRI, such as claustrophobia, non-removable piercings, a pacemaker, or magnetic implants, were checked beforehand. Notably, we ascertained our sample size by performing a post-hoc analysis using G^∗Power 3.1 (Faul et al., 2007) and IBM SPSS, version 23.0.

TABLE 1

Table 1. Demographic data of MCI, senior HC, and young groups.

MRI Data Acquisition and Preprocessing

All participants in the study underwent MRI imaging at the Research Centre Jülich. Structural MRI and resting-state functional MRI were collected at a 3T MAGNETOM Trio scanner (Siemens, Erlangen, Germany). T1-weighted structural images were obtained using a rapid gradient echo sequence with the following parameters: repetition time (TR) = 2250 ms, echo time (TE) = 3.03 ms, flip angle (FA) = 9°, field of view (FOV) = 256 × 256 mm ², voxel size = 1 mm isotropic, 176 gapless interleaved sagittal slices. During the resting-stage image acquisition, which took 7 min, patients were instructed to stay awake with open eyes and not to think of anything particular. For the functional images echo planar imaging (EPI) with the following parameters was used: TR = 3000 ms, TE = 30 ms, FA = 90°, FOV = 200 × 200, voxel size = 2.5 × 2.5 × 2.8, interleaved oblique slices parallel to the infra-supratentorial line with a gap of 0.28 mm.

Data were preprocessed using the default preprocessing pipeline of the CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012). The first four images of 155 volumes were removed to allow the signal to reach equilibrium. Functional images were realigned to the first acquired volume in the session. Subsequently, echo planar images (EPIs) were co-registered to the high-resolution T1 structural image, and normalized to the Montreal Neurological Institute (MNI) stereotactic space and resampled at 2 × 2 × 2 mm³ voxel size. The normalized images were spatially smoothed with an 8-mm full-width at half maximum (FWHM) isotropic Gaussian kernel. Head movement parameters were checked individually and excluded at a relative displacement criterion of ± 3 mm. After preprocessing the MRI data, 246 ROI were extracted using the Brainnetome Atlas (Fan et al., 2016) and imported into the CONN toolbox.

To address motion-related artifacts (Conwell et al., 2018), we incorporated frame-wise displacement (FD) calculated proposed by Jenkinson et al. (2002) as a covariate of no interest in our models. The method by Jenkinson et al. is preferable over other methods of FD calculation due to its consideration of voxel-wise differences in its derivation (Yan et al., 2013).

Graph Theory Analysis

Graph theory is a standard framework for the mathematical representation of networks. A network can be represented as a graph by G (N, K), with N, indicating the number of nodes and K as the number of edges in the graph G. The degree centrality (DC) is a simple measurement of connectivity between a single node and all other nodes in a network, representing the importance of a node in a network. The degree of node i is the number of edges connected to it and is calculated as k_i = ΣjεGa_ij (a_ij is the ith row and jth column element of adjacency matrix A) (Wang, 2010). In graph theory and network analysis, indicators of centrality identify the major nodes within a graph and a hub is a node with a number of edges that exceeds the average (see Figure 1).

FIGURE 1

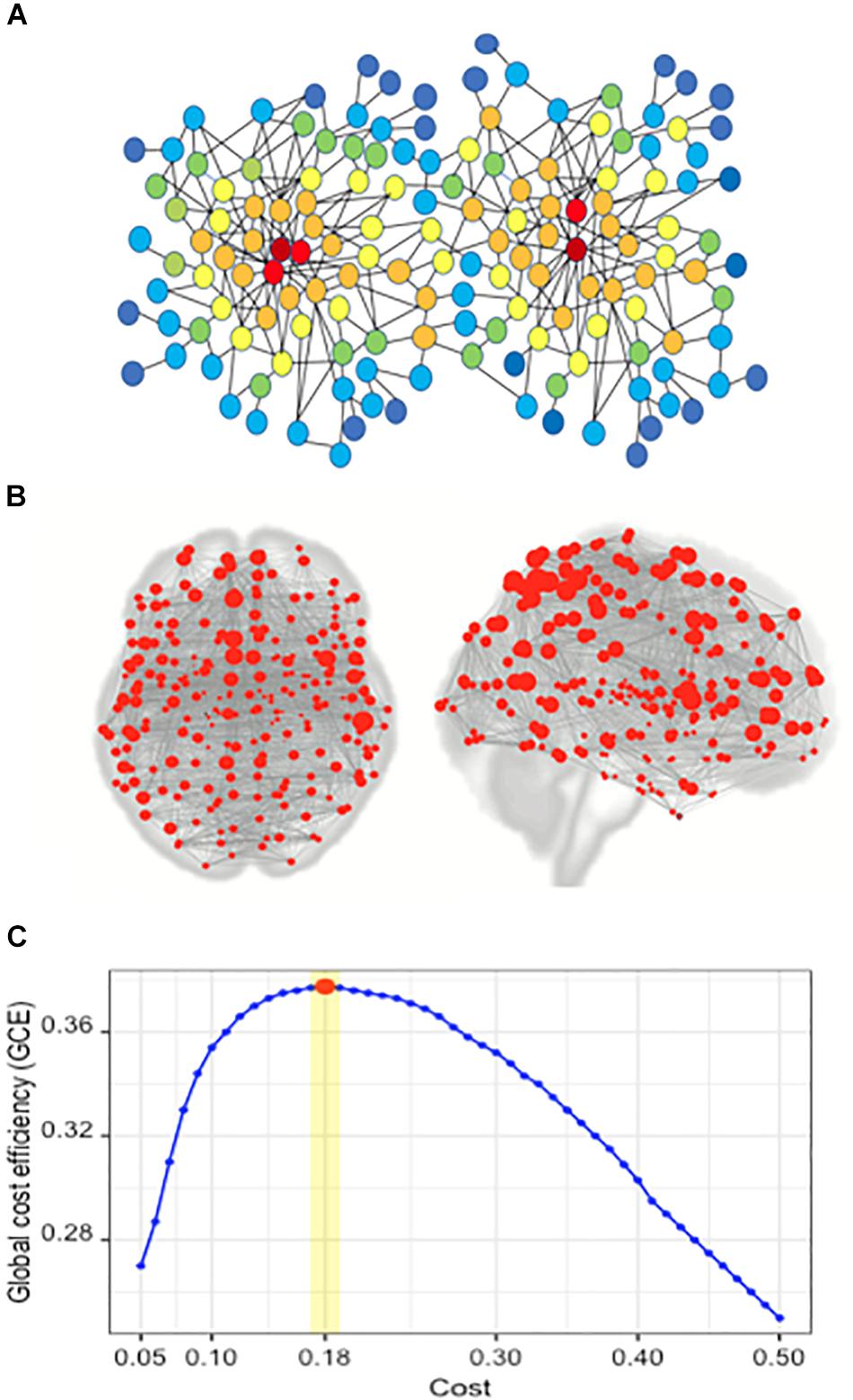
Figure 1. Network and the concept of degree centrality; the brain network of the Brainnetome atlas’ ROIs; finding the optimal cost. (A) In the illustrated network, the red nodes have the highest degree centrality, and the color spectrum from red to blue represents the gradual reduction of degree centrality. (B) Red circles represent the nodes in a brain network, composed of 246 nodes. In this network, each node is one of the 246 ROIs of the Brainnetome Atlas. (C) Plot of global cost efficiency vs. Cost averaged across all subjects in young HC, senior and MCI groups.

In order to apply graph theory analysis to fMRI scans, BOLD (blood oxygen level dependent) time series of brain activity were used, and the 246 imported Brainnetome Atlas ROIs served as the nodes of the network.

We incorporated Brainnetome Atlas (Fan et al., 2016) on CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012) to generate connectivity matrices, by averaging the time series of the BOLD (blood oxygenation level dependent) signals of all voxels in each ROI and calculating the Pearson’s correlation of these average signals between ROIs.

The proportion of the remained robust connections to the total number of connections is defined as Cost, ranging from 0 to 1. On one hand, setting very large values to Cost results in keeping weaker edges and noisy connections and on the other hand, assigning very small values to Cost removes too many edges, which consequently generates a disconnected graph. By adjusting the Cost as a threshold in a network of n nodes (N), one can optimize the global cost efficiency (GCE) of the network (Bassett et al., 2009; Bullmore and Sporns, 2009; Khazaee et al., 2016), which is calculated as:

$$GCE=GE-Cost(1)$$

$$GE=\frac{1}{n}\sum _{i\in N}{E}_i=\frac{1}{n}\sum _{i\in N}\frac{{\sum }_{j\in N,j\ne i}{d}_{ij}^{-1}}{n-1}(2)$$

Where GE and E_i are, respectively, the global efficiency and the efficiency of node i. And, d_ij is the shortest path length between nodes i and j.

Furthermore, the weighted connectivity matrices can be transformed into binary ones by applying an optimal threshold on connectivity matrices (Bassett et al., 2009; Dimitriadis et al., 2010).

The CONN toolbox allows the computation of both global and nodal graph measures on binary and weighted networks. At the single-subject level, we performed a ROI-to-ROI analysis incorporating all ROIs of the Brainnetome Atlas (Fan et al., 2016). We explored the optimal Cost value which maximizes the GCE. Different Cost values ranging from 0.05 to 0.5 by a step of 0.01 were examined. The optimal values of Cost were 0.18 ± 0.01 across all subjects; a maximum GCE of 0.37 was achieved (Figure 1). Then, the generated weighted connectivity matrices were transformed into binary matrices using a Cost of 0.18, as the mean of the optimal range on positive correlations.

Following ROI-to-ROI analyses at the subject level, we conducted analyses at the group level. Graph theory analyses on the three groups of young HC, senior HC, and MCI subjects were performed, and the adjacency matrices and network measures of each ROI were exported. Between-group differences on degree centrality were determined using two-tailed t-tests with a p < 0.05 (FDR-corrected) in two separate contrasts including (1) young HC vs. senior HC and MCI, (2) senior HC vs. MCI. For the first contrast, sex and education were applied as covariates of no interest, for the second contrast age was included in addition to sex and education. After group level comparisons, the DC measure of the ROIs with significantly higher DC was extracted for further correlation analysis with neuropsychological tests.

Brainnetome Atlas

The Brainnetome Atlas (Fan et al., 2016) includes 246 ROIs (210 cortical and 36 subcortical subregions) (see Figure 1), which are assigned to brain functions based on meta-analyses of tasked-based functional imaging techniques (Fan et al., 2016). Most human brain atlases lack fine-grained parcellations and fail to provide all aspects of functional connectivity. Using non-invasive multimodal imaging techniques, the Brainnetome Atlas was designed to provide a connectivity-based parcellation framework, which identifies the subdivisions of the human brain, revealing new dimensions of connectivity architecture. In particular, the atlas combines brain connectivity with cytoarchitecture and other microscale information. The delineated structures in the Brainnetome Atlas are mapped to mental processes by referring to the BrainMap database (Laird et al., 2009; Balsters et al., 2014; Fox et al., 2014), to provide an initial estimate of the mental processes sustained by each cortical and subcortical region of the Brainnetome Atlas (Fan et al., 2016). The functional characteristics of each subarea in the Brainnetome Atlas are based on the behavioral domains and paradigm class meta data labels of the BrainMap database¹, employing forward and reverse inferences (Eickhoff et al., 2011; Cieslik et al., 2013; Clos et al., 2013; Fox et al., 2014; Fan et al., 2016).

Volumetric Analysis

To locate the regions fulfilling criteria for compensation, as defined in the introduction, and to distinguish ROIs with significant atrophy, a volumetric analysis was performed using the computational anatomy toolbox (CAT12, Version 12.1)², an extension of statistical parametric mapping (SPM12; Wellcome Centre for Human Neuroimaging)³ implemented in MATLAB R2015b (The MathWorks, Natick, United States). After segmentation of all T1 images into gray matter (GM), white matter (WM), and cerebrospinal fluid, all images were normalized to the MNI space using DARTEL with six iterations and the integrated DARTEL template in MNI space (Mechelli et al., 2005; Ashburner, 2009) using the registration step, local GM and WM volumes were preserved by modulating their Jacobian determinants. Subsequently, the normalized GM were smoothed by Gaussian filter (FWHM = 8 × 8 × 8 mm), from which the GM volumes of the ROIs with a significant increase of DC as generated in the group contrast were extracted for the statistical analysis.

Neuropsychological Tests

Out of a larger pool of neuropsychological tests within the RIMCAD-study (for a comprehensive description see Conwell et al., 2018), we selected the Verbal Learning and Memory Test (VLMT), a German version of the Rey Auditory Verbal Learning Test (RAVLT) (Lux et al., 1999) as a test of memory performance (Zhao et al., 2015), and The Trail Making Test (TMT) (Rodewald et al., 2012) as an indicator of cognitive flexibility (Kinsella et al., 2007).

We aimed to refine and uniform the test results by generating a total VLMT value by averaging the standardized z-scores of the VLMT trials I–V (total learning), VI (recall after interference), and VII (delayed recall), and a delta TMT value by subtracting the TMT-B from the TMT-A values.

Correlation Analysis Between Compensatory ROIs and Neuropsychological Tests

Per correlation analysis, we examined if a higher connectivity was correlated with a better performance, as postulated in the fourth criterion in the introduction. To assess the correlation, we first exported all the graph measures following the graph theory analysis embedded in the group level result section of the CONN toolbox. After that, we specifically extracted the DC measures of all the significant ROIs in the senior HC and MCI subjects. Next, we tested the correlation between DC of compensatory ROIs and the neuropsychological test results in senior HC and MCI subjects using a linear regression function with least square fit, implemented in MATLAB R2015b (The MathWorks, Natick, United States), and corrected for multiple comparisons. For visualization purposes, R (R Core Team, 2013) along with ggplot2 package (Wickham, 2016) has been used.

Seed-to-ROI Analysis

We also performed Seed-to-ROI analyses using the compensatory ROIs as seeds and all 246 ROIs in the Brainnetome Atlas as target ROIs. Seed-to-ROI correlation matrices were defined as the Fisher-transformed bivariate correlation coefficients between two ROIs BOLD signals⁴.

$$r(i,j)=\frac{{\sum }_t{R}_i(t)R_j(t)}{\sqrt{{\sum }_t{R}_i{(t)}^2{\sum }_t{R}_j{(t)}^2}}$$

$$Z(i,j)=tan{h}^{-1}r(i,j)$$

Ri(t) = BOLD signals within i^th ROI, centered to zero mean.r(i,j) = correlation coefficients between i^th and j^th ROIs.Z(i,j) = Fisher-transformed correlation coefficient.

Seed-to-ROI correlation analyses were conducted at the single-subject level of the CONN toolbox as bivariate correlations without weighting.

Results

We assessed the imaging and neuropsychological data of all participants (N = 45) in three groups of young HC, senior HC and MCI. All three groups did not differ significantly in education level and sex. There was no significant difference in age among the senior HC and MCI groups (p > 0.05). In each step of the following analyses the normal distribution of the data was approved by the Shapiro-Wilk test in R.

Graph Theory Analysis and the ROIs With a Significant Increase of DC

We observed an increase of DC in the senior HC and MCI group vs. young HC in three ROIs: the right superior parietal lobule, rostral area 7 (Brainnetome label: SPL_R_5_1), the right and left precentral gyri caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2 and PrG_L_6_2) (Figures 2A,C, 3A, increases of DC depicted in circles of blue shades, decreases in red shades; see also Table 2). Furthermore, the comparison between the senior HC and the MCI group revealed an increase of DC in the right middle frontal gyrus, lateral areal 10 (Brainnetome label: MFG_R_7_7) (Figures 2B,C, 3A and Table 2).

FIGURE 2

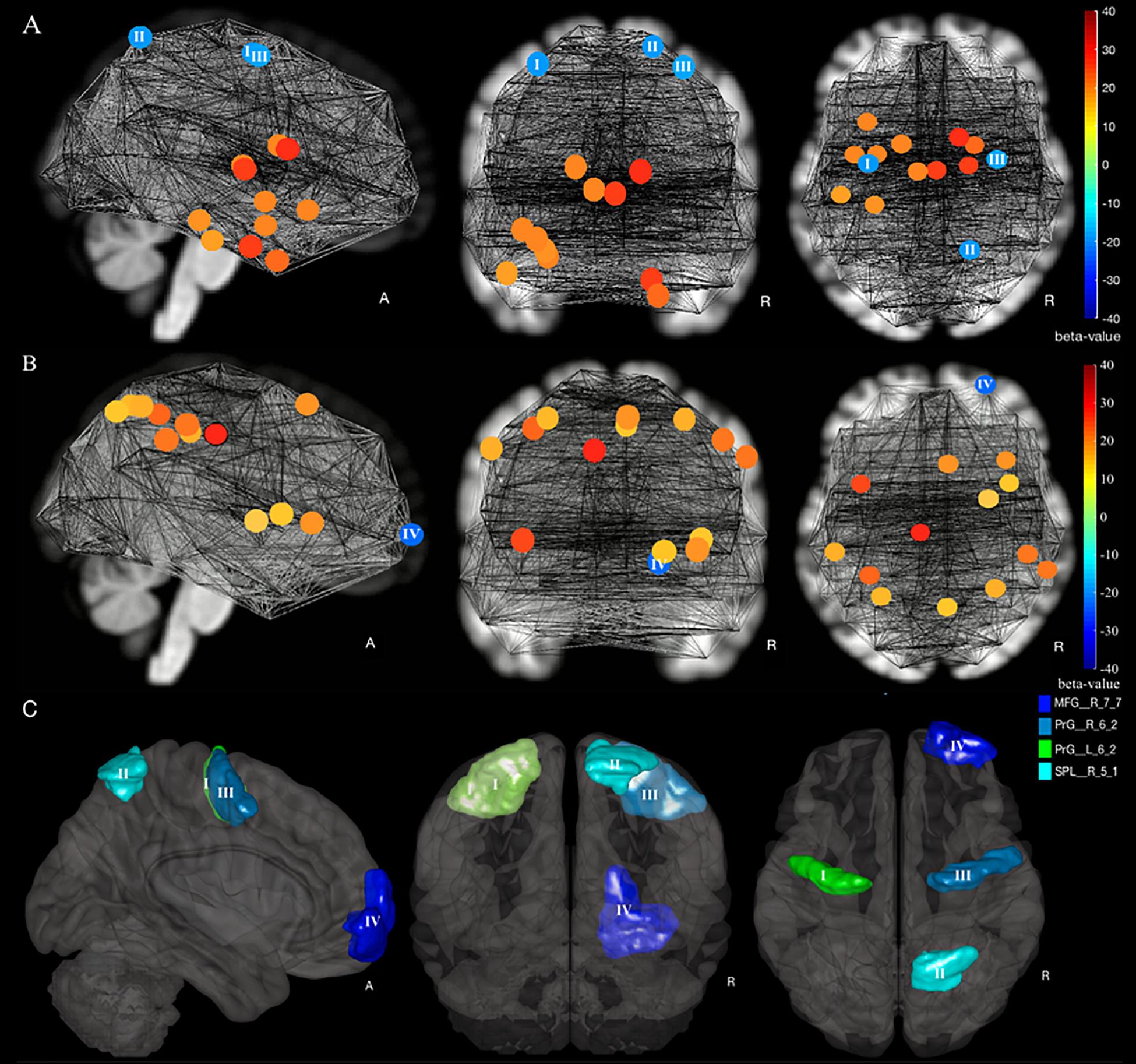
Figure 2. Increase and decrease of degree centrality in a comparison of young HC, senior HC, and MCI. (A) Young HC vs. senior HC and MCI contrast, in which blue shade circles represent a significant increase, and red shade circles represent a significant decrease of DC in Senior HC and MCI subjects compared to young HC (p < 0.05, FDR-corrected). (B) Senior HC vs. MCI contrast, in which blue shade circles represent a significant increase, and red shade circles represent a significant decrease of DC in MCI subjects compared to senior HC (p < 0.05, FDR-corrected). The significant ROIs are according to labeling by the Brainnetome atlas (I) PrG_L_6_2, (II) SPL_R_5_1, (III) PrG_R_6_2, and (IV) MFG_R_7_7. (C) All four compensatory ROIs stem from the two intergroup contrasts.

FIGURE 3

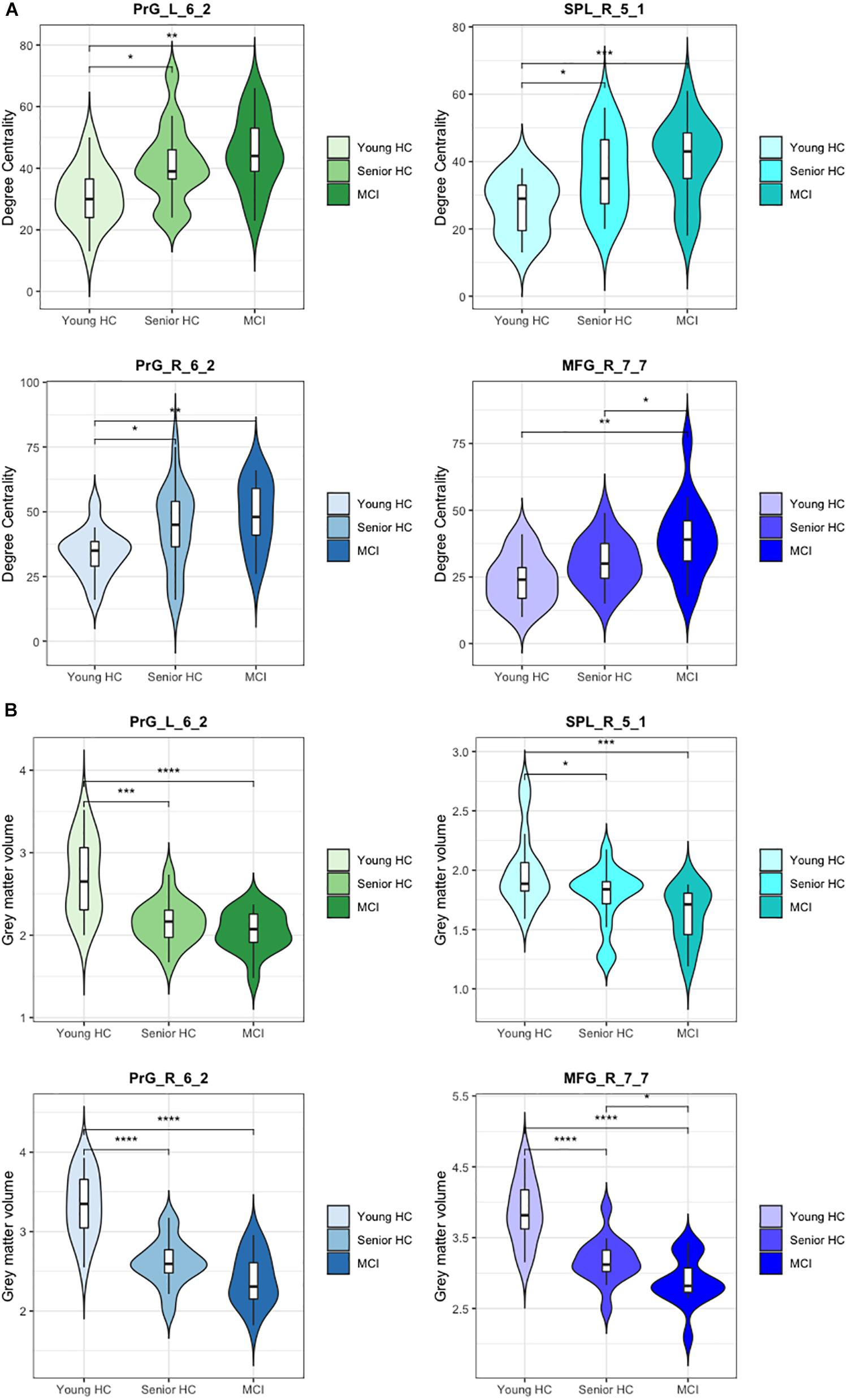
Figure 3. Degree centrality and gray matter volume of compensatory ROIs. Illustration of (A) the degree centrality and (B) the gray matter volume of the right and the left precentral gyri caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2 and PrG_L_6_2), the superior parietal lobe, rostral area 7 (Brainnetome label: SPL_R_5_1), and the right middle frontal gyrus, lateral area 10 (Brainnetome label: MFG_R_7_7). (*) indicates statistical significance (p < 0.05, FDR-Corrected), (**) indicates statistical significance (p < 0.01, FDR-Corrected), (***) indicates statistical significance (p < 0.005, FDR-Corrected), (****) indicates statistical significance (p < 0.001, FDR-Corrected).

TABLE 2

Table 2. The coordinates of the ROIs with a significant increase of DC in the intergroup contrasts.

Importantly, the post-hoc estimation of our sample size using G^∗Power 3.1 and IBM SPSS for α = 0.05 and the effect size = 0.39, which was calculated by MANOVA [F(4,40) = 6.5, p = 0.0001, partial η² = 0.39] from the results of the graph theory analysis, showed a power (1-ß) of 0.80.

Volumetric Analysis of the Compensatory ROIs

As defined in our criteria of compensatory mechanisms, the respective ROIs must show a concurrent increase of DC with a decrease of gray matter volume. Having corrected for the total intracranial volume, volumetric analysis revealed a significant decrease in gray matter volume of the compensatory ROIs. As presented in Figure 3, all four compensatory ROIs (Table 2) exhibited significant volume reduction in the senior HC and MCI group in comparison to the young HC (p < 0.05, FDR-corrected). Although further gradual volume reductions were detected in the MCI group compared to the senior HC in all four compensatory ROIs, this was only significant in the right middle frontal gyrus (p < 0.05, FDR-corrected).

Correlation Analysis Between DC, Total VLMT, and Delta TMT Values

As shown in Table 3 and Figure 4, the DC of the right precentral gyrus, caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2), the right superior parietal lobe, rostral area 7 (Brainnetome label: SPL_R_5_1), and the right middle frontal gyrus, lateral area 10 (Brainnetome label: MFG_R_7_7) was significantly correlated with the total VLMT values in MCI group (p < 0.05, corrected for multiple comparisons). Likewise, the DC of the right and the left precentral gyri, caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2, PrG_L_6_2), and the right superior parietal lobe, rostral area 7 (Brainnetome label: SPL_R_5_1) was significantly correlated with the delta TMT values in MCI group (p < 0.05, corrected for multiple comparisons). As two participants in the MCI group failed to complete TMT assessment, two data points are missing. After correcting for multiple comparisons, the correlation between the DC measures of the compensatory ROIs, total VLMT, and delta TMT values revealed no significant association in senior HC (see Table 4).

TABLE 3

Table 3. Correlation between DC of cognition-related compensatory ROIs, total VLMT, and delta TMT scores in MCI.

FIGURE 4

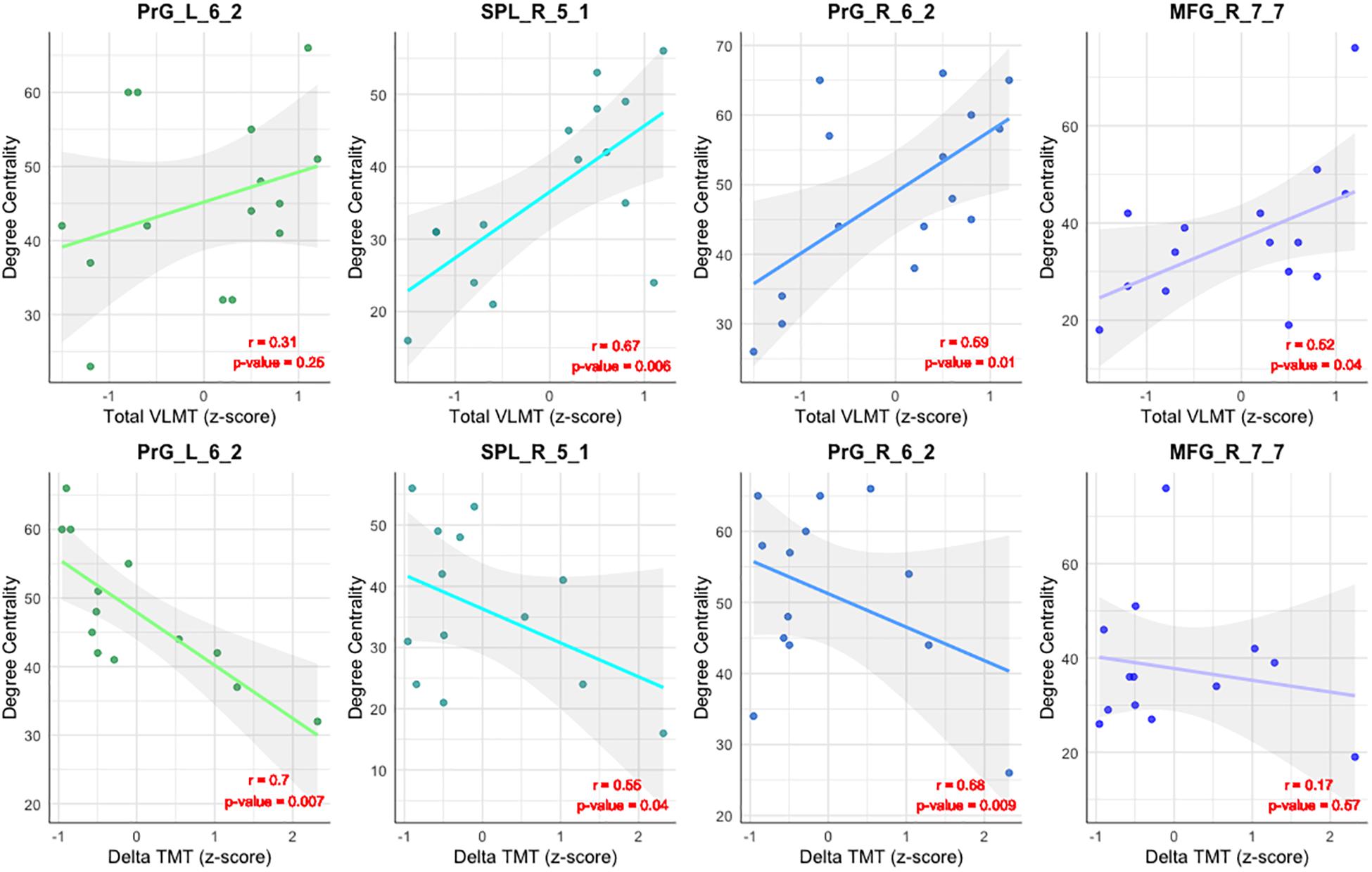
Figure 4. Correlation between DC and neuropsychological tests. Illustration of the correlation between the DC of the compensatory ROIs [the right and the left precentral gyri, caudal dorsolateral area 6 (Brainnetome label: PrG_R_6_2 and PrG_L_6_2), the superior parietal lobe, rostral area 7 (SPL_R_5_1), and the right middle frontal gyrus, lateral area 10 (Brainnetome label: MFG_R_7_7)], and the total VLMT score (upper row) and Delta TMT in MCI (lower row).

TABLE 4

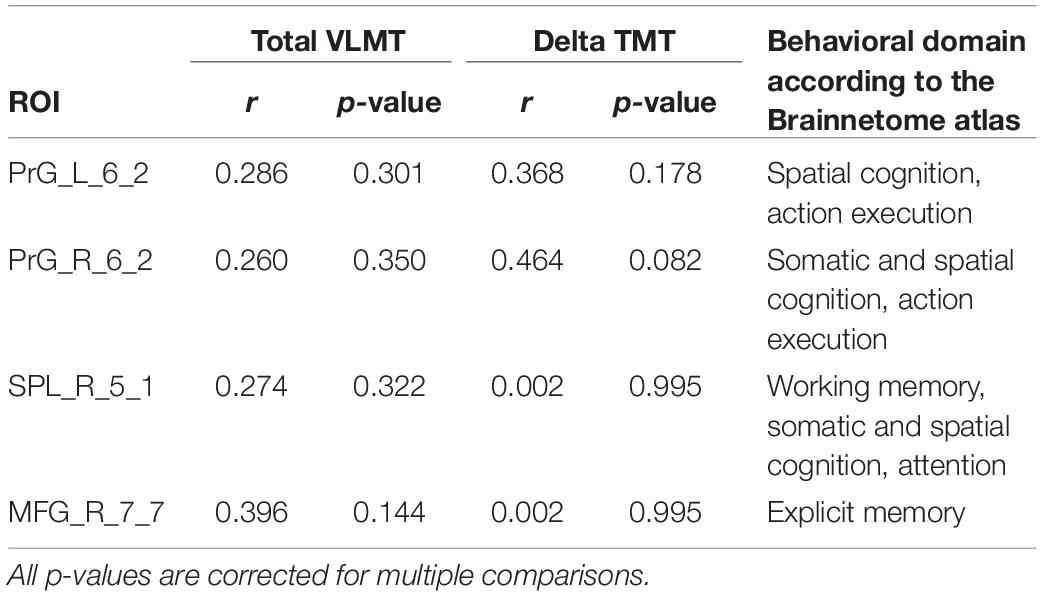
Table 4. Correlation between DC of cognition-related compensatory ROIs, total VLMT, and delta TMT scores in senior HC.

Seed-to-ROI Analysis

As shown in Figure 5, the compensatory ROIs in the right and the left precentral gyri (Brainnetome label: PrG_R_6_2 and PrG_L_6_2) and the right superior parietal lobe (Brainnetome label: SPL_R_5_1) demonstrated a significant increase of connectivity with cognition-associated regions, including multiple ROIs in the occipital lobes, the cuneus, fusiform gyri, and pre- and postcentral gyri. The compensatory ROI in the right middle frontal gyrus (Brainnetome label: MFG_R_7_7) also showed a significant increase in connectivity with cognition-associated ROIs in the left superior frontal gyrus and the left orbital gyrus.

FIGURE 5

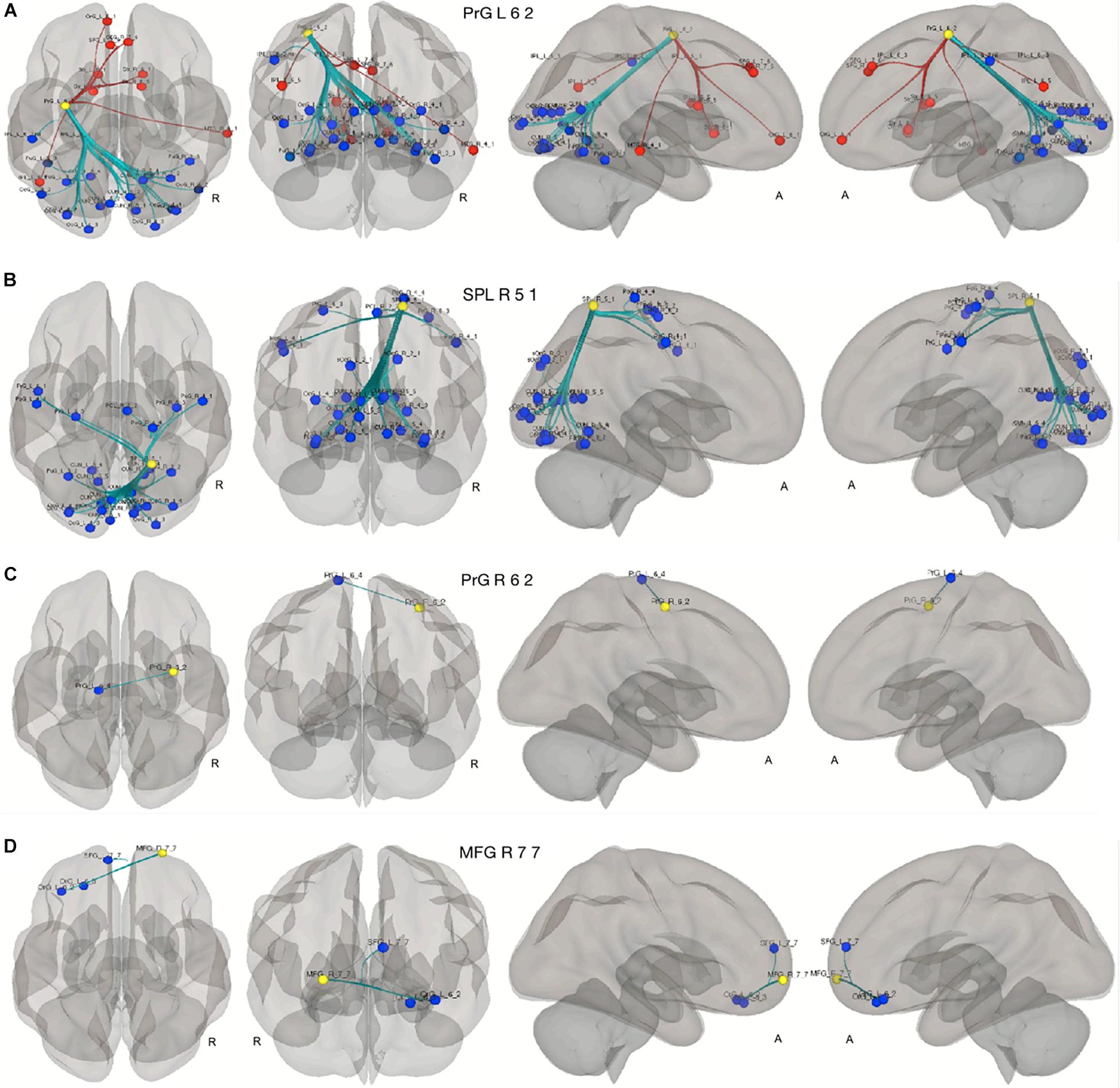
Figure 5. Seed to ROI analysis of the compensatory ROIs. The yellow circles represent the compensatory ROIs. The colored circles depict the ROIs with a significant increase (blue) or decrease (red) of connectivity with the corresponding compensatory ROIs in our two contrasts. (A–C) young HC > senior HC and MCI (p < 0.05, FDR-corrected). (D) Senior HC > MCI (p < 0.05, FDR-corrected).

Discussion

This study contributes to the ongoing discussion on compensatory mechanisms in neurodegenerative diseases. The primary purpose of this work was to draw attention to the dynamics and dimensions of compensation in healthy brain aging and MCI with AD biomarkers from a new perspective, namely the contribution of resting-state connectivity derived by graph theory. To the best of our knowledge, graph theory analysis has sparsely been used for the detection of compensatory effects in the AD continuum. We identified four cognition-related ROIs with characteristics of compensation in a resting-state-fMRI design, applying connectivity measures. The compensatory ROIs were the right superior parietal gyrus (rostral area 7), the right- and the left precentral gyri (caudal dorsolateral area 6), and the right middle frontal gyrus (lateral area 10). In these ROIs, we observed an increase of DC, indicating more robust connectivity, despite regional atrophy. This finding indicates that regional structural deterioration of the brain does not necessarily reflect regional brain function. Although the DC of the compensatory ROIs was well correlated with the cognitive performance in MCI patients, this correlation could not be observed in senior healthy controls. And, this finding is in good accordance with the concept of compensation, which is considered to reflect the brain’s attempt to compensate for the cognitive decline by increasing neural activity or connectivity. In the additional seed-to-ROI analyses using the aforementioned compensatory ROIs as seeds or hubs, we observed a significant increase of connectivity between these ROIs and cognition- and memory-associated ROIs in the caudal cuneus, the fusiform gyrus, the occipital polar cortex, the middle occipital gyrus, and the pre- and the postcentral gyri. The cognitive domains covered by these ROIs include language, semantic, and spatial cognition (Fan et al., 2016). Besides, and of particular relevance in the context of dementia, some of these ROIs were associated with learning and sequence recall (Fan et al., 2016), which is in line with our observation that the DC of the compensatory ROIs showed a significant correlation with memory, cognitive flexibility, and executive functioning, as derived by VLMT and TMT values.

In the context of task-based fMRI-experiments, various compensatory patterns of activity increases associated with brain aging have been proposed. According to one account, the hemispheric asymmetry of the prefrontal lobes observed in younger subjects is reduced in older adults. This pattern is called “Hemispheric Asymmetry Reduction in Older Adults” or HAROLD (Cabeza, 2002). Subsequent work suggested that such a mechanism may also be observed in the parietal lobe (Piefke et al., 2012). Another account suggested an increase of activity in prefrontal cortex in elderly individuals together with a. reduction of occipital lobe activity. This pattern was termed “Posterior-Anterior Shift with Aging” or PASA (Davis et al., 2008). Furthermore, a compensatory mechanism in healthy brain aging and AD was suggested by an increase in functional connectivity in the prefrontal cortex (Gregory et al., 2017) even though postmortem, in vivo, and brain imaging studies provided evidence for atrophy in the prefrontal cortex. This led to the frontal lobe hypothesis, which posits that cognitive inefficiencies in aging are predominantly due to the structural and functional deterioration of the frontal lobes (Cabeza and Dennis, 2012). The CRUNCH model (compensatory-related utilization of neural circuits) extends the models mentioned above and explains in general terms aging-related changes in activity related to compensation without restricting it to cerebral areas (Reuter-Lorenz and Cappell, 2008).

While the models mentioned above were revealed by task-based-fMRI designs and analyses focusing on regional activation rather than connectivity, our results based on connectivity showed comparable patterns. First of all, we were able to demonstrate successful compensation in the right middle frontal gyrus (lateral area 10) in MCI patients. Besides, we observed that in the transition from healthy aging to MCI, among all of the compensatory ROIs, volume reduction is only significantly pronounced in this prefrontal ROI, which vicariously addresses the frontal lobe hypothesis. We also demonstrated successful compensation in the right- and the left precentral gyri (caudal dorsolateral area 6), which have been consistently indicated in numerous studies as a key structure utilizing working memory tasks (Howard et al., 2003; Narayanan et al., 2005; Meltzer et al., 2008; Kirschen et al., 2010; Huang et al., 2013; Noy et al., 2015; Kambara et al., 2017). In line with these findings, there is some evidence, that an increase of resting-state nodal centrality in the right middle frontal gyrus and the right precentral gyrus in MCI might effectively serve as a compensatory mechanism, playing an essential role in MCI patients to recruit additional cognitive resources to achieve a normal level of cognition (Yao et al., 2010). Also, previous studies have provided evidence for task-specific compensatory recruitment of parietal lobe in brain aging (Huang et al., 2012; Piefke et al., 2012), and in this study, we could detect a resting-state compensatory recruitment of the right superior parietal gyrus (rostral area 7) in MCI patients. As an extension of the above-noted links between our results and previous studies, it is worth noting that our findings regarding compensatory connectivity change in the frontal and the parietal lobes could be considered as the resting-state counterparts of the HAROLD (Cabeza, 2002; Piefke et al., 2012) and/or CRUNCH (Reuter-Lorenz and Cappell, 2008)model of task-based compensation. By investigating the PASA phenomenon in the task-based and resting-state networks using graph measures, McCarthy et al. reported a bilateral increase of DC in the pre- and post-central gyri, and the superior parietal gyrus in the healthy aging and early AD (McCarthy et al., 2014). These findings are in line with our observations in the right- and the left precentral gyri (caudal dorsolateral area) and the right superior parietal gyrus (rostral area 7). McCarthy et al. (2014) have also observed a clear pattern of declining DC in posterior regions in the aged group, when compared to the young group. The latter lends support to our findings in the seed-to-ROI analysis, in which we observed an anterior-to-posterior tendency in the left precentral gyrus (caudal dorsolateral area 6) and the right superior parietal gyrus (rostral area 7).

Despite the converging evidence of our results and previous studies, it is worth noting that our findings regarding compensatory connectivity change in the frontal and parietal lobes could be considered as the resting-state counterparts of the HAROLD (Cabeza, 2002; Piefke et al., 2012) and/or CRUNCH (Reuter-Lorenz and Cappell, 2008) model of task-based compensation. Investigating the PASA phenomenon in task-based and resting-state networks using graph measures, McCarthy et al. reported a bilateral increase of DC in the pre- and post-central gyri, and the superior parietal gyrus in healthy aging and early AD (McCarthy et al., 2014). This is in line with our findings in the right- and the left precentral gyri (caudal dorsolateral area 6) and the right superior parietal gyrus (rostral area 7). McCathy et al. also reported a declining DC in posterior regions in the aged group when compared to a group of young subjects (McCarthy et al., 2014). These findings support our graph theory-based method, which reveals resting-state compensatory mechanisms in healthy aging and prodromal Alzheimer’s disease.

Finally, a critical issue for the relevance of these findings is their applicability and translation to the clinical and interventional settings. In general terms, non-invasive stimulation methods such as transcranial magnetic stimulation (TMS) may improve the neural performance of various brain regions (Solé-Padullés et al., 2006; Cotelli et al., 2008) and the compensatory ROIs might be used as targets of non-invasive stimulations.

There are several limitations to consider in our current study: First, our dataset is composed of only a small number of MCI patients characterized by beta-amyloid (Ab) and tau biomarkers. Thus, a study with a larger patient cohort is warranted to confirm these results. Second, we referred to the previous version of the A/T/N classification framework (Jack et al., 2016) as the diagnostic criteria for our participants. Whereas in the previous version of the framework (Jack et al., 2016), an isolated positive beta-Amyloid (A+) biomarker status was sufficient for AD classification, in the latest version (Jack et al., 2018), having both a beta-Amyloid (A+) and phospho-Tau (T+) biomarker status is required for an AD classification. Third, the CSF biomarkers were not available for the participants in the senior HC group. As some of the healthy elderly individuals might already have AD pathologies, including their biomarkers status would have been advantageous in interpreting the results. Fourth, in this study we only focused on group level comparisons. However, testing these criterions in an individual level have concrete preferences in terms of personalized medicine for the application in clinical practice, and it is an issue which merits further discussion. Group comparison fMRI studies have been extensively used to realize the generic aspect of brain function, usually by averaging across individuals to optimize the signal-to-noise ratio (SNR). Averaging the data has also a statistical advantage which is leveraged in group comparisons. However, the group comparison studies have fallen short of an appropriate characterization of brain function in the individual level. By far, the most frequently used approach to interpret the fMRI-derived results in an individual level is to relate them to other individual measures in the same subjects such as test scores or behavioral measures (Dubois and Adolphs, 2016; Dubois et al., 2016), which has also been the method of choice in our study. Nevertheless, another proposed approach is to shift from correlation analysis to a predictive (machine-learning inspired) framework to improve generalizability and interpretability of fMRI-derived results at the individual level (Linden, 2012; Gabrieli et al., 2015; Yarkoni and Westfall, 2017). Fifth, in this paper we exclusively investigated the applicability of our proposed framework of compensation using Brainnetome atlas in cerebral regions. However, the role of cerebellum in cognition, memory and learning (Schmahmann, 2010) could potentially expand the scope of cognitive compensation beyond the purview of cerebrum. Therefore, it will be essential to explore compensatory mechanism in cerebellum using other functional brain atlases with cerebellum coverage.

In conclusion, using combined graph theory analysis of resting-state fMRI data and volumetric analyses of structural MRI, we here show new characteristics of compensation in healthy brain aging and early neurodegeneration. Moreover, using an ROI-based atlas with fine parcellation, a more precise map of compensatory regions could be identified. The identified compensatory regions were well associated with the cognitive performance scores in MCI subjects, which offers new insights into the compensatory mechanism of memory and executive functions. Based on these findings, preferably more longitudinal studies with a broader spectrum of various categories and stages of cognitive impairment such as subjective memory impairment, early MCI, late MCI, amnestic vs. non-amnestic type of MCI, mild to moderate and severe AD are warranted to elucidate further the dynamics and dimensions of resting-state compensatory mechanism in neurodegenerative processes with cognitive decline. For future studies, analyses on individual level using a predictive machine-learning based framework seem to be a promising approach to further our understanding of the compensatory mechanisms.

Data Availability Statement

The datasets for this article are not publicly available because public access to the dataset has not been yet approved. Requests to access the datasets should be directed to QB, qumars.YmVoZmFyQHVrLWtvZWxuLmRl.

Ethics Statement

The studies involving human participants were reviewed and approved by the Ethics Committee of the Faculty of Medicine of Cologne University, Cologne, Germany. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

QB, OO, GF, and BR designed the experiment. OO and BR collected the data. QB, SB, OO, NR, JD, and RF analyzed the data. QB, SB, OO, NR, JD, RF, BR, and GF wrote, revised, and approved the manuscript. All authors listed in the author list fully qualify for authorship and contributed significantly to the work.

Funding

This work was supported by a grant from the Marga and Walter Boll Foundation, Kerpen, Germany, to GF. OO was supported by the Köln Fortune Program, Faculty of Medicine, University of Cologne.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^ www.brainmap.org/taxonomy
2. ^ http://dbm.neuro.uni-jena.de/cat/
3. ^ http://www.fil.ion.ucl.ac.uk/spm/software/spm12
4. ^ https://web.conn-toolbox.org/measures/roi-to-roi

References

Ashburner, J. (2009). Computational anatomy with the SPM software. Magn. Reson. Imaging 27, 1163–1174. doi: 10.1016/j.mri.2009.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Balsters, J. H., Laird, A. R., Fox, P. T., and Eickhoff, S. B. (2014). Bridging the gap between functional and anatomical features of cortico-cerebellar circuits using meta-analytic connectivity modeling. Hum. Brain Mapp. 35, 3152–3169. doi: 10.1002/hbm.22392

PubMed Abstract | CrossRef Full Text | Google Scholar

Bakker, A., Krauss, G. L., Albert, M. S., Speck, C. L., Jones, L. R., Stark, C. E., et al. (2012). reduction of hippocampal hyperactivity improves cognition in amnestic mild cognitive impairment. Neuron 74, 467–474. doi: 10.1016/j.neuron.2012.03.023

CrossRef Full Text | Google Scholar

Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A., Weinberger, D. R., and Coppola, R. (2009). Cognitive fitness of cost-efficient brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 106, 11747–11752. doi: 10.1073/pnas.0903641106

PubMed Abstract | CrossRef Full Text | Google Scholar

Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198. doi: 10.1038/nrn2575

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabeza, R. (2002). Hemispheric asymmetry reduction in older adults: the HAROLD model. Psychol. Aging 17, 85–100. doi: 10.1037/0882-7974.17.1.85

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabeza, R., Albert, M., Belleville, S., Craik, F. I. M., Duarte, A., Grady, C. L., et al. (2018). Maintenance, reserve and compensation: the cognitive neuroscience of healthy ageing. Nat. Rev. Neurosci. 19, 701–710. doi: 10.1038/s41583-018-0068-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabeza, R., and Dennis, N. A. (2012). Frontal lobes and aging. Princ. Front. Lobe Funct. 37, 628–652. doi: 10.1093/acprof:oso/9780195134971.001.0001

CrossRef Full Text | Google Scholar

Cieslik, E. C., Zilles, K., Caspers, S., Roski, C., Kellermann, T. S., Jakobs, O., et al. (2013). Is There “One” DLPFC in cognitive action control? evidence for heterogeneity from co-activation-based Parcellation. Cereb. Cortex 23, 2677–2689. doi: 10.1093/cercor/bhs256

PubMed Abstract | CrossRef Full Text | Google Scholar

Clos, M., Amunts, K., Laird, A. R., Fox, P. T., Eickhoff, S. B., and Vogt, O. (2013). Tackling the multifunctional nature of Broca’s region meta-analytically: co-activation-based parcellation of area 44 HHS Public access. Neuroimage 83, 174–188. doi: 10.1016/j.neuroimage.2013.06.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Conwell, K., von Reutern, B., Richter, N., Kukolja, J., Fink, G. R., and Onur, O. A. (2018). Test-retest variability of resting-state networks in healthy aging and prodromal Alzheimer’s disease. Neuroimage Clin. 19, 948–962. doi: 10.1016/J.NICL.2018.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotelli, M., Manenti, R., Cappa, S. F., Zanetti, O., and Miniussi, C. (2008). Transcranial magnetic stimulation improves naming in Alzheimer disease patients at different stages of cognitive decline. Eur. J. Neurol. 15, 1286–1292. doi: 10.1111/j.1468-1331.2008.02202.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis, S. W., Dennis, N. A., Daselaar, S. M., Fleck, M. S., and Cabeza, R. (2008). Qué PASA? the posterior-anterior shift in aging. Cereb. Cortex 18, 1201–1209. doi: 10.1093/cercor/bhm155

PubMed Abstract | CrossRef Full Text | Google Scholar

delEtoile, J., and Adeli, H. (2017). Graph theory and brain connectivity in Alzheimer’s disease. Neuroscientist 23, 616–626. doi: 10.1177/1073858417702621

PubMed Abstract | CrossRef Full Text | Google Scholar

Dennis, M., Spiegler, B. J., Juranek, J. J., Bigler, E. D., Snead, O. C., and Fletcher, J. M. (2013). Age, plasticity, and homeostasis in childhood brain disorders. Neurosci. Biobehav. Rev. 37, 2760–2773. doi: 10.1016/j.neubiorev.2013.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Dimitriadis, S. I., Laskaris, N. A., Tsirka, V., Vourkas, M., Micheloyannis, S., and Fotopoulos, S. (2010). Tracking brain dynamics via time-dependent network analysis. J. Neurosci. Methods 193, 145–155. doi: 10.1016/J.JNEUMETH.2010.08.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubois, B., Feldman, H. H., Jacova, C., Hampel, H., Molinuevo, J. L., Blennow, K., et al. (2014). Advancing research diagnostic criteria for Alzheimer’s disease: the IWG-2 criteria. Lancet Neurol. 13, 614–629. doi: 10.1016/S1474-4422(14)70090-0

CrossRef Full Text | Google Scholar

Dubois, B., Hampel, H., Feldman, H. H., Scheltens, P., Aisen, P., Andrieu, S., et al. (2016). Preclinical Alzheimer’s disease: definition, natural history, and diagnostic criteria. Alzheimer Dement. 12, 292–323. doi: 10.1016/j.jalz.2016.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubois, J., and Adolphs, R. (2016). Building a science of individual differences from fMRI. Trends Cogn. Sci. 20, 425–443. doi: 10.1016/j.tics.2016.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Duits, F. H., Prins, N. D., Lemstra, A. W., Pijnenburg, Y. A. L., Bouwman, F. H., Teunissen, C. E., et al. (2015). Diagnostic impact of CSF biomarkers for Alzheimer’s disease in a tertiary memory clinic. Alzheimers Dement. 11, 523–532. doi: 10.1016/j.jalz.2014.05.1753

PubMed Abstract | CrossRef Full Text | Google Scholar

Eickhoff, S. B., Bzdok, D., Laird, A. R., Roski, C., Caspers, S., Zilles, K., et al. (2011). Co-activation patterns distinguish cortical modules, their connectivity and functional differentiation. Neuroimage 57, 938–949. doi: 10.1016/j.neuroimage.2011.05.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Enciu, A. M., Nicolescu, M. I., Manole, C. G., Mureşanu, D. F., Popescu, L. M., and Popescu, B. O. (2011). Neuroregeneration in neurodegenerative disorders. BMC Neurol. 11:75. doi: 10.1186/1471-2377-11-75

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., et al. (2016). The human brainnetome atlas: a new brain atlas based on connectional architecture. Cereb. Cortex 26, 3508–3526. doi: 10.1093/cercor/bhw157

PubMed Abstract | CrossRef Full Text | Google Scholar

Faul, F., Erdfelder, E., Lang, A. G., and Buchner, A. (2007). G^∗Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 39, 175–191. doi: 10.3758/bf03193146

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, P. T., Lancaster, J. L., Laird, A. R., and Eickhoff, S. B. (2014). Meta-analysis in human neuroimaging: computational modeling of large-scale databases. Annu. Rev. Neurosci. 37, 409–434. doi: 10.1146/annurev-neuro-062012-170320

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuchs, E., and Flügge, G. (2014). Adult neuroplasticity: more than 40 years of research. Neural Plast. 2014:541870. doi: 10.1155/2014/541870

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabrieli, J. D. E., Ghosh, S. S., and Whitfield-Gabrieli, S. (2015). Prediction as a humanitarian and pragmatic contribution from human cognitive neuroscience. Neuron 85, 11–26. doi: 10.1016/j.neuron.2014.10.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Gregory, S., Long, J. D., Klöppel, S., Razi, A., Scheller, E., Minkova, L., et al. (2017). Operationalizing compensation over time in neurodegenerative disease. Brain 140, 1158–1165. doi: 10.1093/brain/awx022

PubMed Abstract | CrossRef Full Text | Google Scholar

Howard, M. W., Rizzuto, D. S., Caplan, J. B., Madsen, J. R., Lisman, J., Aschenbrenner-Scheibe, R., et al. (2003). Gamma oscillations correlate with working memory load in humans. Cereb. Cortex 13, 1369–1374. doi: 10.1093/cercor/bhg084

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, C.-M., Polk, T. A., Goh, J. O., and Park, D. C. (2012). Both left and right posterior parietal activations contribute to compensatory processes in normal aging. Neuropsychologia 50, 55–66. doi: 10.1016/j.neuropsychologia.2011.10.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, S., Seidman, L. J., Rossi, S., and Ahveninen, J. (2013). Distinct cortical networks activated by auditory attention and working memory load. Neuroimage 83, 1098–1108. doi: 10.1016/j.neuroimage.2013.07.074

PubMed Abstract | CrossRef Full Text | Google Scholar

Jack, C. R., Bennett, D. A., Blennow, K., Carrillo, M. C., Dunn, B., Haeberlein, S. B., et al. (2018). NIA-AA research framework: toward a biological definition of Alzheimer’s disease. Alzheimers Dement. 14, 535–562. doi: 10.1016/j.jalz.2018.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Jack, C. R., Bennett, D. A., Blennow, K., Carrillo, M. C., Feldman, H. H., Frisoni, G. B., et al. (2016). A/T/N: an unbiased descriptive classification scheme for Alzheimer disease biomarkers. Neurology 87, 539–547. doi: 10.1212/WNL.0000000000002923

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenkinson, M., Bannister, P., Brady, M., and Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17, 825–841. doi: 10.1006/nimg.2002.1132

CrossRef Full Text | Google Scholar

Kambara, T., Brown, E. C., Jeong, J. W., Ofen, N., Nakai, Y., and Asano, E. (2017). Spatio-temporal dynamics of working memory maintenance and scanning of verbal information. Clin. Neurophysiol. 128, 882–891. doi: 10.1016/j.clinph.2017.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Khazaee, A., Ebrahimzadeh, A., and Babajani-Feremi, A. (2016). Application of advanced machine learning methods on resting-state fMRI network for identification of mild cognitive impairment and Alzheimer’s disease. Brain Imaging Behav. 10, 799–817. doi: 10.1007/s11682-015-9448-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Kinsella, G., Storey, E., and Crawford, J. R. (2007). “Executive function and its assessment,” in Neurology and Clinical Neuroscience, ed. A. H. V. Schapira (Amsterdam: Elsevier Inc.), 83–95. doi: 10.1016/B978-0-323-03354-1.50011-0

CrossRef Full Text | Google Scholar

Kirschen, M. P., Chen, S. H. A., and Desmond, J. E. (2010). Modality specific cerebro-cerebellar activations in verbal working memory: an fMRI study. Behav. Neurol. 23, 51–63. doi: 10.3233/BEN-2010-0266

PubMed Abstract | CrossRef Full Text | Google Scholar

Laird, A. R., Eickhoff, S. B., Kurth, F., Fox, P. M., Uecker, A. M., Turner, J. A., et al. (2009). ALE meta-analysis workflows via the brainmap database: progress towards a probabilistic functional brain atlas. Front. Neuroinform. 3:23. doi: 10.3389/neuro.11.023.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Linden, D. E. J. (2012). The challenges and promise of neuroimaging in psychiatry. Neuron 73, 8–22. doi: 10.1016/j.neuron.2011.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Logan, J. M., Sanders, A. L., Snyder, A. Z., Morris, J. C., and Buckner, R. L. (2002). Under-recruitment and nonselective recruitment: dissociable neural mechanisms associated with aging. Neuron 33, 827–840. doi: 10.1016/S0896-6273(02)00612-8

CrossRef Full Text | Google Scholar

Lövdén, M., Bäckman, L., Lindenberger, U., Schaefer, S., and Schmiedek, F. (2010). A theoretical framework for the study of adult cognitive plasticity. Psychol. Bull. 136, 659–676. doi: 10.1037/a0020080

PubMed Abstract | CrossRef Full Text | Google Scholar

Lux, S., Helmstaedter, C., and Elger, C. E. (1999). Normierungsstudie zum Verbalen Lern- und Merkfähigkeitstest (VLMT). Diagnostica 45, 205–211. doi: 10.1026//0012-1924.45.4.205

CrossRef Full Text | Google Scholar

McCarthy, P., Benuskova, L., and Franz, E. A. (2014). The age-related posterior-anterior shift as revealed by voxelwise analysis of functional brain networks. Front. Aging Neurosci. 6:301. doi: 10.3389/fnagi.2014.00301

PubMed Abstract | CrossRef Full Text | Google Scholar

Mechelli, A., Price, C. J., Friston, K. J., and Ashburner, J. (2005). Voxel-based morphometry of the human brain: methods and applications. Curr. Med. Imag. 1:726.

Google Scholar

Meltzer, J. A., Zaveri, H. P., Goncharova, I. I., Distasio, M. M., Papademetris, X., Spencer, S. S., et al. (2008). Effects of working memory load on oscillatory power in human intracranial EEG. Cereb. Cortex 18, 1843–1855. doi: 10.1093/cercor/bhm213

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayanan, N. S., Prabhakaran, V., Bunge, S. A., Christoff, K., Fine, E. M., and Gabrieli, J. D. E. (2005). The role of the prefrontal cortex in the maintenance of verbal working memory: an event-related fMRI analysis. Neuropsychology 19, 223–232. doi: 10.1037/0894-4105.19.2.223

PubMed Abstract | CrossRef Full Text | Google Scholar

Noy, N., Bickel, S., Zion-Golumbic, E., Harel, M., Golan, T., Davidesco, I., et al. (2015). Intracranial recordings reveal transient response dynamics during information maintenance in human cerebral cortex. Hum. Brain Mapp. 36, 3988–4003. doi: 10.1002/hbm.22892

CrossRef Full Text | Google Scholar

Oldfield, R. C. (1971). The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9, 97–113. doi: 10.1016/0028-3932(71)90067-4

CrossRef Full Text | Google Scholar

Petersen, R. C., Doody, R., Kurz, A., Mohs, R. C., Morris, J. C., Rabins, P. V., et al. (2001). Current concepts in mild cognitive impairment. Arch. Neurol. 58, 1985–1992. doi: 10.1001/archneur.58.12.1985

PubMed Abstract | CrossRef Full Text | Google Scholar

Piefke, M., Onur, ÖA., and Fink, G. R. (2012). Aging-related changes of neural mechanisms underlying visual-spatial working memory. Neurobiol. Aging 33, 1284–1297. doi: 10.1016/j.neurobiolaging.2010.10.014

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2013). A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Reuter-Lorenz, P. A., and Cappell, K. A. (2008). Neurocognitive aging and the compensation hypothesis. Curr. Direc. Phychol. Sci. 17, 177–182. doi: 10.1111/j.1467-8721.2008.00570.x

CrossRef Full Text | Google Scholar

Rodewald, K., Bartolovic, M., Debelak, R., Aschenbrenner, S., Weisbrod, M., and Roesch-Ely, D. (2012). Eine normierungsstudie eines modifizierten trail making tests im deutschsprachigen raum. Zeitschrift Neuropsychol. 23, 37–48. doi: 10.1024/1016-264X/a000060

CrossRef Full Text | Google Scholar

Schmahmann, J. D. (2010). The role of the cerebellum in cognition and emotion: personal reflections since 1982 on the dysmetria of thought hypothesis, and its historical evolution from theory to therapy. Neuropsychol. Rev. 20, 236–260. doi: 10.1007/s11065-010-9142-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Solé-Padullés, C., Bartrés-Faz, D., Junqué, C., Clemente, I. C., Molinuevo, J. L., Bargalló, N., et al. (2006). Repetitive transcranial magnetic stimulation effects on brain function and cognition among elders with memory dysfunction. a randomized sham-controlled study. Cereb. Cortex 16, 1487–1493. doi: 10.1093/cercor/bhj083

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J. (2010). Graph-based network analysis of resting-state functional MRI. Front. Syst. Neurosci. 4:16. doi: 10.3389/fnsys.2010.00016

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitfield-Gabrieli, S., and Nieto-Castanon, A. (2012). Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2, 125–141. doi: 10.1089/brain.2012.0073

PubMed Abstract | CrossRef Full Text | Google Scholar

Wickham, H. (2016). ggplot2, 2nd Edn. New York City, NY: Springer International Publishing. doi: 10.1007/978-3-319-24277-4

CrossRef Full Text | Google Scholar

Yan, C.-G., Cheung, B., Kelly, C., Colcombe, S., Craddock, R. C., Di Martino, A., et al. (2013). A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. Neuroimage 76, 183–201. doi: 10.1016/j.neuroimage.2013.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, Z., Zhang, Y., Lin, L., Zhou, Y., Xu, C., Jiang, T., et al. (2010). Abnormal cortical networks in mild cognitive impairment and Alzheimer’s disease. PLoS Comput. Biol. 6:e1001006. doi: 10.1371/journal.pcbi.1001006

PubMed Abstract | CrossRef Full Text | Google Scholar

Yarkoni, T., and Westfall, J. (2017). Choosing prediction over explanation in psychology: lessons from machine learning. Perspect. Psychol. Sci. 12, 1100–1122. doi: 10.1177/1745691617693393

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Q., Guo, Q., Liang, X., Chen, M., Zhou, Y., Ding, D., et al. (2015). Auditory verbal learning test is superior to rey-osterrieth complex figure memory for predicting mild cognitive impairment to Alzheimer’s disease. Curr. Alzheimer Res. 12, 520–526. doi: 10.2174/1567205012666150530202729

PubMed Abstract | CrossRef Full Text | Google Scholar