Numerical and boundary condition effects on the prediction of detonation engine behavior using detailed numerical simulations

High-fidelity numerical simulations of an experimental rotating detonation engine with discrete fuel/air injection were conducted. A series of configurations with different feed-plenum pressures but with constant equivalence ratio were studied. Detailed chemical kinetics for the hydrogen/air system is used. A resolution study for the full rotating detonation engine (RDE) system simulation is also conducted. Two kinds of boundary conditions, a total pressure boundary and a constant mass flow rate boundary, are used to assess the effects of the inlet boundary. As mass flow rate is increased, the total pressure boundary causes more error in the axial pressure distribution while the constant mass flow rate gives a better solution for all cases ran. The simulations confirm experimental findings, and reproduce qualitative as well as some of the quantitative trends. These results demonstrate that a) fuel-air mixing is highly non-uniform within the detonation chamber, leading to variations in local equivalence ratio, b) the fuel and oxidizer injectors experience significant backflow as the detonation wave passes over, but recover at different rates which further augments the inefficiencies in mixing, and c) parasitic combustion in the mixing region makes the detonation wave weak by extending the reaction zone across the wave.

1 Introduction

Pressure gain combustion is increasingly being seen as a viable pathway to increasing efficiency of gas turbine engines (Raman et al., 2023; Lu and Braun 2014; Zhou et al., 2016). Unlike constant pressure thermodynamic cycles used in the current generation of gas turbines, pressure gain combustors use a modified cycle where the heat release is accompanied by an increase in pressure. This pressure gain can then offset other losses and directly increase the useful work available from the hot fluid. Alternatively, this pressure gain could be used to reduce the number of compressor stages upstream, which in itself reduces the material and operational cost of the gas turbine. While different methods to realize pressure gain have been considered (Kailasanath 2003; Zhou et al., 2016; Lisanti and Roberts 2016; Kailasanath 2011), rotating detonation engines (RDEs) are emerging as a practical design (Zhou et al., 2016; Lu and Braun 2014). RDEs employ detonations to obtain compact heat release rather than deflagration-based processes in conventional gas turbine combustors. While RDEs have been studied for many decades, recent progress driven by improved designs and material characteristics has increased their practical viability (Rankin et al., 2017; Rankin et al., 2015b; Anand et al., 2016; Anand et al., 2017; Rhee et al., 2017; Kindracki et al., 2011; Lentsch et al., 2005; Wang et al., 2014; Shank et al., 2012). The presence of a propagating detonation wave, however, leads to a number of design challenges: a) large pressure and density gradients introduce thermal and mechanical loads on the combustor walls, b) the detonation front can propagate upstream into the fuel and air feed plenums which can endanger the safety and reliability of the device, and c) the combustor should be able to utilize the pressure gain effectively instead of dissipating the compression work achieved close to the front. In response to these issues, recent RDE designs have moved towards a non-premixed injection system. Here, the fuel and air streams enter the combustion chamber through separate injectors. The design augments turbulence-induced mixing in order to have a large region of near-homogeneous mixture that is processed by the azimuthal wave. However, as in other turbulence-driven combustion systems, there is invariably some level of inefficiency leading to losses (Raman et al., 2023). The focus of this work is in understanding the structure of the flow field and the detonation wave in such non-premixed combustors, with the goal of gaining insight into the mixing and reaction processes.

In a typical RDE configuration, the detonation waves (there could be more than one) move azimuthally through a thin annulus region, passing over fuel/air injectors that issue fluids axially into the chamber. While this is for a typical configuration, other variations where the entire cylindrical region is used (Yao et al., 2017) or the detonation passes radially (Huff et al., 2019; Sato et al., 2017) have also been studied (Zhou et al., 2016). The design of the injectors is a critical challenge in RDEs (Duvall et al., 2018; Rankin et al., 2017). If the pressure in the annulus is less than the critical pressure, the throat is choked, leading to constant mass flow rate. However, as the detonation wave passes over the injectors, it can temporally unchoke the combustor and can lead to flow stoppage (Sato et al., 2021a). Depending on the pressure upstream of the throat, the flow will recover over a finite time (Prakash et al., 2021). If the upstream pressure is higher, then the flow will recover faster. However, higher-pressure inflow will require additional compression upstream, which will reduce the overall efficiency of the combustion device. Hence, a major research objective is to develop practical injectors with lower feed pressures that can still ensure stable and efficient detonations.

When lower injection pressures are used, a main issue is the upstream propagation of burnt gases behind the detonation wave. This can lead to mixing with the feed streams leading to altered ignition and detonation properties. Detailed imaging of the injection plenum (Roy et al., 2017) shows that high-pressure waves from the detonation chamber travel upstream into the oxidizer plenum and disrupt the oncoming flow. Further, wave interactions inside the plenum can setup unwanted instabilities as well (Anand et al., 2017). Consequently, the unsteady recovery of the injectors is an important contributor to the stability of the detonation process. However, due to the extreme environment inside RDEs, it is difficult to experimentally probe such a system. Most experimental measurements are limited to pressure probes (Kindracki et al., 2011; Kindracki 2015; Fotia et al., 2016), while image-based diagnostics are only beginning to be used (Rankin et al., 2017; Chacon and Gamba 2018; Bohon et al., 2019).

In this context, numerical simulations provide a convenient approach to studying the flow structure inside injectors. While many RDE simulations have been carried out in the past (Schwer and Kailasanath 2013; Schwer and Kailasanath 2011; Cocks et al., 2016; Tsuboi et al., 2016; Uemura et al., 2013; Meng and Jian-Ping 2011; Sato et al., 2017; Paxson 2014; Wolański 2013), computations of full-scale RDE geometries are still sparse (Zhou et al., 2016; Wolański 2013; Sato et al., 2021b; Sato et al., 2021a; Sato and Raman 2020; Cocks et al., 2016). Wang and co-workers (Meng and Jian-Ping 2011; Zhou et al., 2016) have conducted detailed simulations of wave initiation and stabilization but using one-step chemical kinetics. Cocks et al. (2016) simulated the Air Force Research Laboratory (AFRL) 6-inch experimental configuration using detailed chemical kinetics and full resolution of the injector sections. This simulation showed that the injector response can affect the nature of the detonation process, but the level of interaction depends on injection and detonation pressures. Further, it was demonstrated that detonations sustain more in the richer mixtures found inside the chamber due to non-uniform mixing of fuel and air streams. Yellapantula et al. (2017) simulated the same configuration focusing on the detonation chamber, but used an unsteady RANS approach to find that the detonation structure matched experimental OH luminescence images. This study also showed that multiple waves can be observed in the combustor for certain flow conditions.

Another aspect of the numerical simulation of RDEs is the inlet boundary conditions. The choked relation is used to decide the inflow properties for the ideal two-dimensional unwrapped simulations (Schwer and Kailasanath 2010; Sato et al., 2018a). However, this boundary condition cannot be applied to the full RDE system due to flashback of the burnt gases. There are two possible choices for the inlet boundary conditions, the total pressure boundary (Sato et al., 2018b; Sato and Raman 2020) and the constant mass flow boundary (Cocks et al., 2016; Sato et al., 2021b; Sato et al., 2021a). It is known that both of the boundary conditions successfully sustain detonation waves in the chamber. Nevertheless, the effect of those boundary conditions on the dynamics in the detonation chamber is unknown. One of the goals of this study is to assess the effect of the inlet boundary on the detonation structure and the macroscopic system performance.

With this background, the main focus of the current study is to extend the analysis of the AFRL experiments using high-resolution simulation of the detonation chamber and the upstream fuel/air plenums for a series of operating conditions. Hydrogen/air detonation with multiple mass flow rates but a fixed stoichiometric equivalence ratio is considered. Moreover, detailed chemical kinetics is used to ensure that mixture inhomogeneity caused by non-uniform and unsteady fuel/air flow profiles is fully captured. The impact of grid resolution on the simulations is studied. Additionally, two kinds of inlet boundary conditions, the total pressure boundary and the constant mass flow rate boundary, are examined. The choice of a boundary condition is non-trivial due to the strong correlation between detonation behavior and inflow conditions. Analysis of instantaneous and cycle-averaged data is used to understand the detonation structure and injector dynamics.

2 Simulation configuration and numerical approach

The simulation configuration used here corresponds to the 6-inch diameter based RDE experiment conducted at AFRL (Rankin et al., 2017; Rankin et al., 2015b; Rankin et al., 2015a; Cocks et al., 2016; Cocks et al., 2015). A schematic of this configuration is provided in Figure 1. The detonation chamber has an inner diameter of 138.7 mm, and an outer diameter of 153.9 mm, with an annulus thickness of 7.6 mm. The height of the detonation chamber is 101.6 mm. The fuel and air streams are injected from separate plenums located upstream of the combustion chamber. Fuel enters the detonation chamber through 120 holes each with a diameter of 0.89 mm. Air enters circumferentially through a 123 mm diameter slot with a height of 1.78 mm. Further details of the experimental configuration and the measurement techniques can be found in Rankin et al. (2017) and Rankin et al. (2015b).

FIGURE 1

FIGURE 1. Simulated RDE configuration and computational mesh near a single injector region.

The experimental campaign contains a large set of individual studies (Rankin et al., 2017). Here, the focus is on understanding the effect of mass flow rate on detonation structure, which is obtained by varying the total pressure far upstream of the detonation chamber in both the oxidizer and fuel plenums. The pressure is varied such that the overall mass flow rates correspond to a globally stoichiometric mixture. Three cases are studied here, corresponding to cases 2.2.2.1, 3.2.2.1 and 4.2.2.1 in Rankin et al. (2017), which are denoted here as cases 1, 2 and 3, respectively.

The governing equations for fluid flow based on the Euler formulation can be written in concise form as

$\frac{\partial \rho }{\partial t}+\frac{\partial \rho u_i}{\partial x_i}=0,(1)$

$\frac{\partial \rho u_i}{\partial t}+\frac{\partial \rho u_i{u}_j}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial {\tau }_{ij}}{\partial x_j},(2)$

$\frac{\partial \rho E}{\partial t}+\frac{\partial \rho u_{j}H}{\partial x_j}=\frac{\partial }{\partial x_j}k\frac{\partial T}{\partial x_j}+\frac{\partial {\tau }_{ij}{u}_i}{\partial x_j},(3)$

and

$\frac{\partial \rho Y_i}{\partial t}+\frac{\partial \rho u_j{Y}_i}{\partial x_j}=\frac{\partial }{\partial x_j}\rho D\frac{\partial Y_i}{\partial x_j}+\dot{\omega }{M}_i,(4)$

where ρ is the mass density, u, v, w are x, y, and z velocity components, respectively, p is the pressure, E is the total energy, and H is the total enthalpy. The viscous stress τ is obtained as

${\tau }_{ij}=-2/3\mu \frac{\partial u_k}{\partial x_k}{\delta }_{ij}+\mu \left(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j}\right),(5)$

For a N-species chemical mechanism, Y_i is the mass fraction and ${\dot{\omega }}_i$ is the species production rate, with i = 1, …, N. The terms μ, k, and D are diffusion coefficients, where μ is dynamic viscosity, k is thermal conductivity, and ρD represents the total species diffusion coefficient defined as ρD = ρ∑_iY_iD_i.

The simulations are performed using an in-house solver developed at the University of Michigan (UM). This solver, termed UMdetFOAM, is based on the OpenFOAM framework (OpenFOAM 2016) and solves the governing equations listed above. In order to minimize numerical dissipation while ensuring stability, the flux terms are discretized using a Monotonic Upstream-centered Scheme for Conservation Laws (MUSCL)-based Harten-Lax-van Leer-Contact (HLLC) scheme (Toro et al., 1994). The chemical source terms are treated explicitly through a detailed multi-step mechanism for hydrogen/air with 9 species and 19 steps (Mueller et al., 1999). Other mechanisms tested using canonical one-dimensional detonation cases did not yield significant differences in both the species profiles and macroscopic parameters such as wave speed. In the solver, the chemical source terms are handled by integration with the CANTERA (Goodwin et al., 2012) open source package. The time-dependent equations are advanced using a second-order two-stage Runge-Kutta (RK) scheme. A fractional time-stepping method is used to integrate the chemical source terms, where the convection terms are advanced in two half-steps, with the chemical source term advanced in between these half-steps. The solver has been extensively tested for detonation-containing flows, and numerical convergence for a variety of flow configurations has been studied (Sato et al., 2018b; Sato and Raman 2020; Sato et al., 2021a; Sato et al., 2021b; Prakash et al., 2020). A brief examination of the effects of numerics and interpolation methods on the RDE simulation results shown in this study is provided in the Supplementary Material.

The computational grid used in this study is shown in Figure 1. The simulation domain has been extended from the original experimental geometry in order to provide sufficient distance for the pressure waves at the detonation chamber exit to dissipate without reflecting back into the chamber. The main focus here is on the inflow section, where turbulent mixing as well as the reverse flow affects the dynamics of the combustor. The mesh is predominantly hexahedral. The post-detonation plenum contains a very limited number of computational cells, designed specifically to numerically dissipate the waves. The minimum cell size in the detonation chamber is 2 × 10⁻⁴ m. Similar resolution has been used in other studies (Pal et al., 2021; Prakash and Raman 2021; Strakey et al., 2016), and this resolution is smaller than the induction length for a premixed hydrogen/air detonation at these conditions (Prakash and Raman 2019). Capturing induction length is important for detonation simulations, as failure to capture induction length properly has been shown to negatively affect the peak density and propagation of self-sustaining detonation waves (Hsu and Jemcov, 2000), which can ultimately impact macroscopic flow properties. Prior analysis indicates that the detonation structures are weaker in such discrete injector configurations, with a significant deflagration region behind the shock (Prakash et al., 2018; Burr and Yu 2017). As seen in the results section that follows, the detonation structures span several grid points in the calculations. Both the total pressure boundary condition and the constant mass flow rate boundary condition are used at the inflow planes for the oxidizer and fuel plenums, while zero gradient conditions are used at the exit plane in the post-detonation plenum. Non-slip and adiabatic walls are applied to all simulations in this paper.

Similar to other studies (Yao et al., 2015), it was observed that the time required to reach steady detonation operation is highly dependent on the simulation initiation approach. Here, the following procedure is used. First, the fuel and oxidizer streams are allowed to propagate through the plenum into the detonation chamber without any ignition. For this purpose, the fuel and oxidizer plenums are filled with their corresponding gases, with initial conditions of boundary total pressure and boundary total temperature. At the second step, chemical reactions are turned off and the jets are allowed to mix in the detonation chamber. Once choked flow is established in the injectors, and the mixing structure does not change appreciably, high pressure, temperature, and velocity conditions corresponding to one-dimensional post-detonation values are patched onto a small volumetric region inside the detonation chamber. The detonation wave establishes over some transient time, after which steady operation is observed. All discussions below are based on results over 10 cycles after the first 15 cycles to ensure that steady states are achieved.

3 Results

3.1 Grid convergence

To author’s knowledge, the refinement study for the full RDE system simulation has not been studied in the community while it is well-studied for the 1D and unfolded 2D RDE simulation (Sato et al., 2018b; Sato and Raman 2020; Schwer and Kailasanath 2011). Unlike those simplified configurations, the resolution in the full system simulation would affect 1) incomplete detonation process due to the non-premixed injector, 2) the downstream flow field due to numerical dissipation, and 3) the macroscopic performance parameters of the system such as wave speed, thrust, and specific impulse. With this in mind, before discussing the detailed physics of the full RDE system simulation, the grid convergence study is discussed in this section.

For the refinement study, three different grids are used. The base mesh has 2 × 10⁻⁴ m resolution (40 million control volumes) in the detonation chamber. Previous computational studies of RDEs using intentionally coarse grids (Paxson 2014; Paxson et al., 2015) show that even at moderately coarser resolutions than this one, macroscopic properties such as specific impulse and axial pressure distribution still provide reasonable agreement with experiments. Nevertheless, this base resolution is decided based on the convergence study for a 1D detonation tube problem (Sato et al., 2018b), analytical induction length calculations for stoichiometric hydrogen/air detonation at similar conditions (Prakash and Raman, 2019), and prior full RDE system simulations (Sato et al., 2021b; Sato et al., 2021a; Cocks et al., 2016). Additionally, a coarse mesh and fine mesh are simulated to conduct a basic investigation of the resolution effect on the RDE simulations based on the chosen base resolution. As such, no formal grid convergence index is used, but rather a direct comparison of macroscopic flow properties is made between the base, coarse, and fine mesh to experimental data. The resolutions of the coarse mesh and fine mesh are 4 × 10⁻⁴ m (10 million control volumes) and 1 × 10⁻⁴ m (76 million control volumes), respectively. For the fine mesh, 1 × 10⁻⁴ m resolution is given up to a height of 3 cm from the chamber bottom to resolve detonation waves and the other region of the chamber is set to 2 × 10⁻⁴ m resolution. The simulation is conducted with NS equations with non-slip and adiabatic walls. Since the flow in the chamber is dominantly supersonic due to the detonation waves and the choked injectors, additional refinement is not given near the wall in this grid convergence test while it is taken into account for the main simulation with the total pressure boundary condition (Section 3.2). For the fuel and oxidizer inlet boundary, total pressure boundary values of 239 kPa and 276 kPa are used as shown in Table 1.

TABLE 1

TABLE 1. Details of the test cases of the resolution study as well as summary of macroscopic results from the simulations compared against experimental data.

3.1.1 General flow-field comparison

Figure 2 shows the pressure field on the outer wall, mid-channel, and top view at 1 cm above the chamber bottom for each grid. A self-sustained detonation wave is observed with all tested grids in this study. The wave vertically stands followed by an oblique shock wave. The detonation front is almost flat in the radial direction with more compression near the outer wall. In terms of the detonation height, the angle of the oblique shock wave, the vertical detonation front, the pressure propagating back to the plenum system, and the number of waves, no particular differences are observed although there are minor grid effects on the flow field. For example, the high-pressure region in the post-detonation region broadens as the grid is refined. This is because the sharp pressure gradients caused by detonation waves dissipate out as the grid becomes coarse. Dissipation in the axial direction within the chamber will be compared in the next subsection.

FIGURE 2

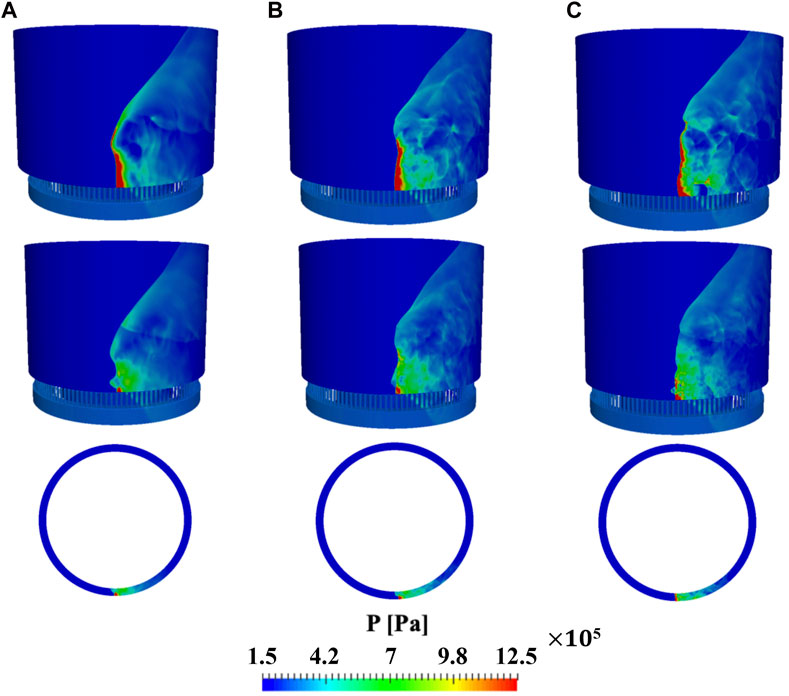
FIGURE 2. Instantaneous pressure field of RDE with different resolution mesh for (A) coarse mesh case, (B) base mesh case, and (C) fine mesh case. Outer wall (top row), mid-channel (middle row), and top view at 1 cm above the chamber bottom (bottom row).

3.1.2 Axial pressure distribution

As for quantitative performance, the axial averaged pressures obtained in the simulations and CTAP data from the corresponding experiment are compared in this section. For the simulation data, the numerical probes are put at the same locations as in the experiment. The axial averaged pressures for the coarse mesh, base mesh, fine mesh, and experiment are shown in Figure 3. Zero (cm) corresponds to the bottom of the detonation chamber. Overall, all grid cases are in good agreement with the experiment. Near the chamber bottom, the simulations exhibit relatively higher pressure due to the detonation wave. This pressure rise gradually decreases by the 3 cm mark which is indicative of the detonation height. The higher pressure near the chamber bottom suggests that the mixing process is active in this region which will be discussed in Section 3.2.4. The first point above the chamber bottom is under-predicted from the experiment because of the under-predicted mass flow rate at the injection exit, which will be discussed in Section 3.2.6 and Section 3.2.10. Downstream of the detonation wave, the product gases expand towards the exit which gradually decreases the pressure. Overall, the axial averaged pressures for all grid cases are almost indistinguishable. This result concludes that the coarse mesh (4 × 10⁻⁴ m) does not deteriorate the averaged profile of the detonation wave and the downstream flow field due to numerical dissipation.

FIGURE 3

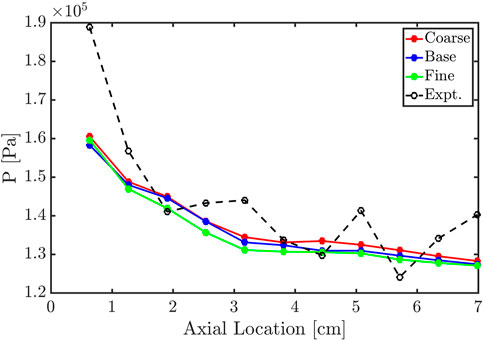
FIGURE 3. Comparison of temporally-averaged pressure measurement on the chamber wall between simulation and experiment for the resolution study.

Finally, the macroscopic performance of the system is compared for all grid cases. First, the averaged pressure at 2.54 cm above the chamber bottom is extracted. It is found that the values are in very good agreement with the experiment for all tested grids. Regarding the wave speed, all grid cases show a similar wave speed to the experiment within 5% error. The wave speed is converged even with the coarse mesh which is a similar observation to the 1D detonation tube problem (Sato et al., 2018b). For the upstream and downstream comparison, the air mass flow rate, thrust, and specific impulse are extracted. For both the air mass flow rate and the thrust, errors are within 4% for each case which suggests that increasing or decreasing mesh resolution by a factor of 2 (to the finer or coarser mesh respectively) does not affect the pressure propagation into the plenum system and the dissipation process in the downstream. With this resolution study in mind, the base grid size (2 × 10⁻⁴ m) is used for the main simulation.

3.2 Main simulation

3.2.1 Simulation with the total pressure boundary

With the results from the resolution study, the grid size for the main simulation is set to 2 × 10⁻⁴ m. The geometry is the same as the resolution study as shown in Figure 1. For the main simulation, two kinds of boundary conditions, total pressure boundary and constant mass flow rate boundary, are imposed on the fuel and oxidizer inlet for each case. To assess the boundary effect, layers are added near the wall to resolve the boundary layer for the total pressure boundary cases although the diffusion effects are limited in the system due to the predominantly supersonic flow (Sato and Raman, 2019). A grid is used with a near-wall resolution of 2 × 10⁻⁵ m, stretching with a ratio of 1.15 to the base resolution, which results in 58 million control volumes. The resolution in the layer is less than y+ = 50 in most of the domains. Non-slip and adiabatic conditions are employed (Cocks et al., 2016). The complete mesh contains roughly 60 million grid cells. The simulations are run on the Pleiades NASA supercomputer cluster with 6,000 cores. The computational time to complete each case is 3.6 million core hours on average.

For RDE operation, it is critical to investigate how the pressure in the plenum (the mass flow rate) would affect the flow field and performance of the system. The prior experiment reveals that increasing mass flow rate impacts the detonation height, detonation strength, and the number of waves in the chamber (Rankin et al., 2017). Although this macroscopic data is available experimentally, it is hard to capture the flow field due to its extremely harsh environment in the facility. With this in mind, three different cases are simulated in this study based on the experiment (Rankin et al., 2017). The simulations are initiated in the same manner as described in the previous section. For the total pressure boundary simulations, the total pressure is set to the values tabulated in Table 2, and the total temperature on the inlet is set to 300 K. The data is extracted after the flow fields reach the steady state (at least after 15 cycles).

TABLE 2

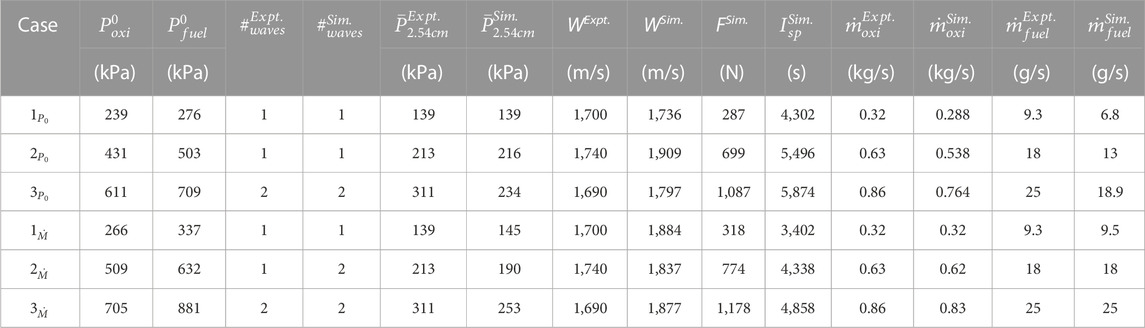
TABLE 2. Details of the test cases with the total pressure boundary and the constant mass flow rate boundary as well as summary of macroscopic results from the simulations compared against experimental data.

3.2.2 General behavior (total pressure boundary)

Figure 4 shows the characteristic features of the RDE flow field at a given time instant. The most notable feature is the detonation front, which shows a relatively non-smooth surface unlike a typical premixed detonation wave (Schwer and Kailasanath, 2010). It is also seen that the unreacted gases in front of the wave have a profile of fill heights, with the highest axial penetration observed close to the detonation front. This is due to the fact that as the detonation wave passes over the injectors, it blocks these feed streams. The expansion behind the detonation wave decreases the pressure after a finite distance, which allows the feed streams to resume the injection of fuel and oxidizer. This delayed response causes the characteristic slope of the fill heights. The product gases expand towards the outflow, which produces a change in the flow direction. Moreover, the interaction of the detonation wave with the product gases creates an oblique shock wave. Note that the effect of the detonation wave will be observed within the injection plenum as well, depending on the particular design. These features and the injector response will be discussed in more detail in Section 3.2.4. Since the exit to the combustion chamber is open to the atmosphere, the detonated products will be expanded out through the exit plane.

FIGURE 4

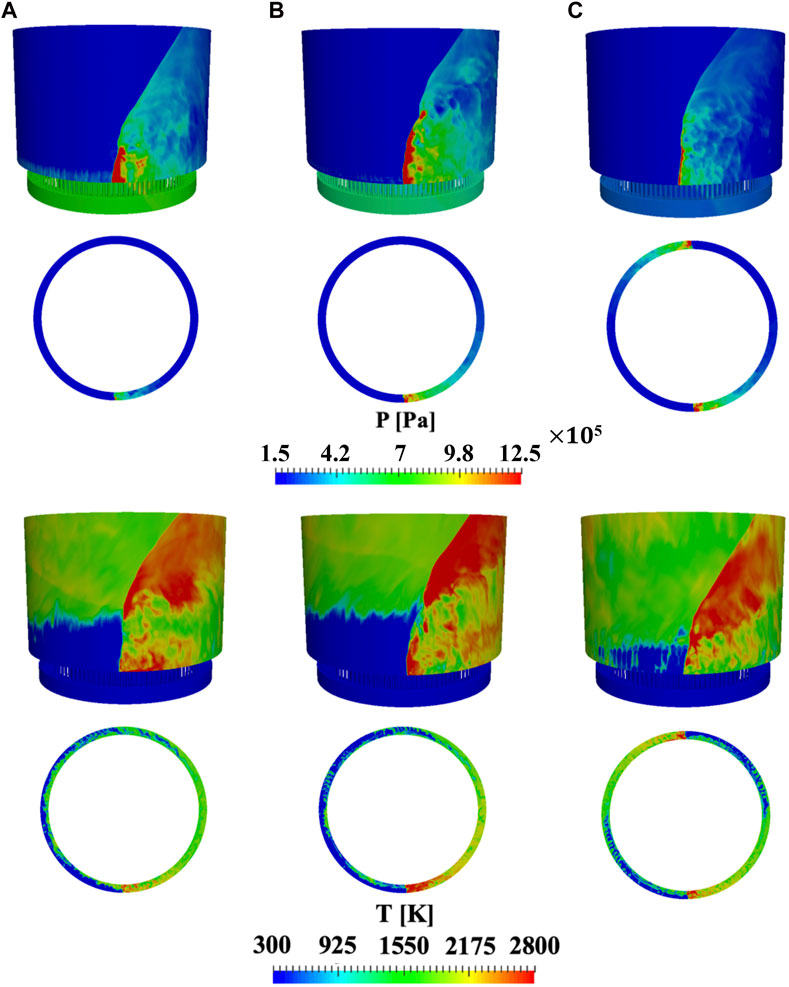
FIGURE 4. Instantaneous pressure field (top) and temperature field (bottom) of RDE with different injection conditions with the total pressure boundary condition. (A) case 1, (B) case 2, (C) case 3.

The instantaneous pressure field on the outer wall and from the top view at 1 cm above the chamber bottom displaying the detonation wave is shown in Figure 4 for the three cases. It is seen that cases 1 and 2 show a single wave while case 3 shows a two-wave system, which matches the corresponding experiments. Prior studies have postulated that the number of waves is based on the cell size and the fill height (Bykovskii et al., 2006). Consistent with the presence of multiple waves, the height of individual detonation waves decreases as plenum pressure (mass flow rate) increases. Figure 4 also shows that the detonation wave is stronger near the outer wall than near the inner wall. Further, the front appears curved normal to the wall, with a trailing weaker detonation or deflagration front near the inner wall. As plenum pressure increases, case 2 and case 3 are able to form the detonation waves in the mid-channel region. It is also seen that the pressure in the post-detonation region decreases for case 3 which is most likely due to the presence of multiple waves.

Figure 4 also shows the temperature field on the outer wall for each case. For all cases, the temperature field captures a similar detonation structure to that of the unfolded 2D RDE simulations (Schwer and Kailasanath 2010; Sato et al., 2018a). The detonation waves convert re-filled unreacted gases (the blue region near the chamber bottom) into product gases. An oblique shock wave is formed from the top of the detonation front which propagates towards the outlet. While the unfolded 2D RDE simulation reveals the vortex structure caused by the contact surface below the oblique shock wave, this structure is not clear in the full system simulations. For case 3 (two-wave mode), it is seen that the re-filling height is almost half of the other cases (one-wave mode). This height is almost the same as the detonation height, indicating that the detonation height is controlled by the re-filling height. Finally, the axial cutting planes at 1 cm above the chamber bottom are compared. Case 2 reveals higher temperature in a broader post-detonation region than that of case 1, indicating that more heat is released across the wave front as plenum pressure (mass flow rate) increases. However, this region becomes shorter for case 3 as the single wave is split into two waves. When the number of waves increases, the mixing timescale is affected and limited re-filling occurs, causing detonation waves to consume smaller amounts of mixture and become weaker as a result. An interesting point here is that the product gases for case 3 are replaced with the freshly re-filled gases at nearly a quarter cycle while it takes at least a half cycle for case 1 and case 2. This indicates that the re-filling time scales adjust to the number of waves to keep the waves self-sustained, which will be discussed in Section 3.2.4.

3.2.3 Detonation structure with a radial air inlet

To assess the more detailed dynamics in the chamber and compare to the idealized 2D calculation (Schwer and Kailasanath, 2010; Sato et al., 2018a), it is useful to look at the unwrapped flow field extracted from the full system simulation. Figure 5 shows the unwrapped flow field of pressure, temperature, equivalence ratio, and Mach number at the mid-diameter of the chamber. The flow field is extracted at the mid-channel of the detonation chamber. Compared to the flow field on the outer wall, the unreacted region at the mid-channel shows a more stratified structure. Several reasons account for this stratified structure. First, the product gases are not completely pushed away due to the freshly re-filled gases. This incomplete re-filling structure induces weaker detonations than that of CJ values, which will be discussed in Section 3.2.5. The second reason is that the mixture is not completely mixed due to the non-premixed injector scheme. The mixing process likely depends on the mass flow rate as well as the injector types employed for the system (Sato et al., 2021b).

FIGURE 5

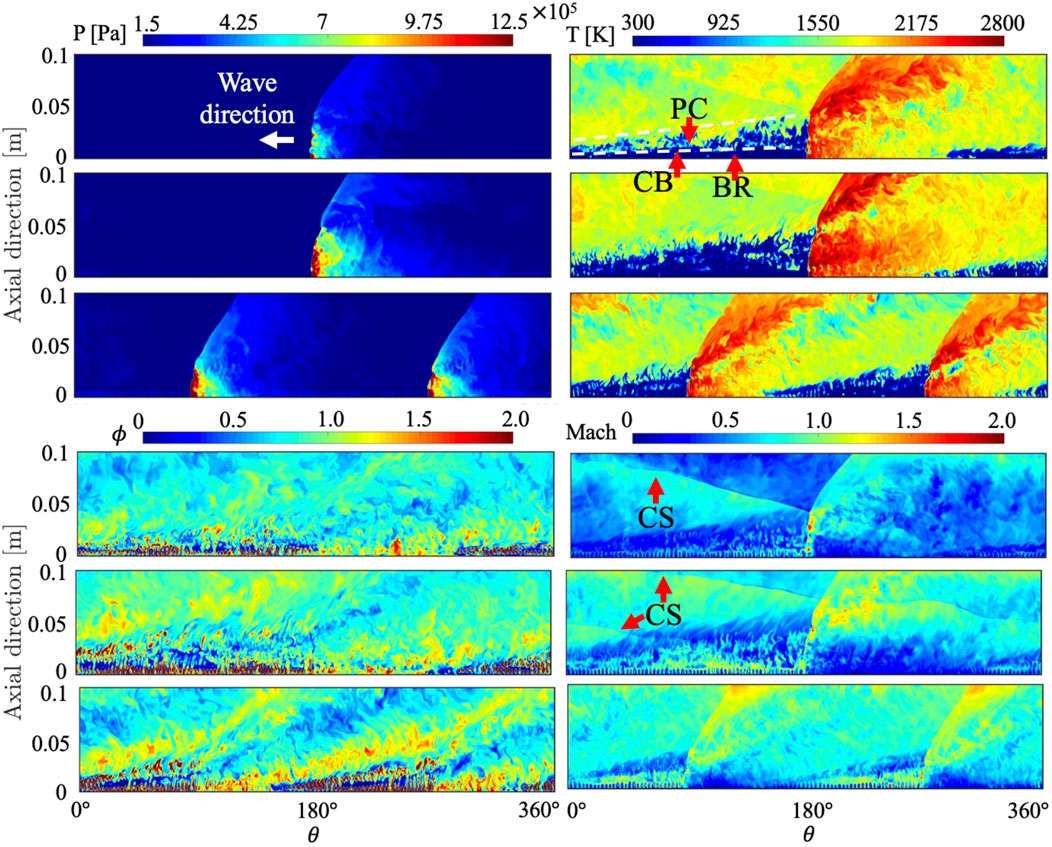
FIGURE 5. Instantaneous pressure, temperature, equivalence ratio, and Mach number on the unwrapped plane at the mid-channel with the total pressure boundary condition. Top: case 1, middle: case 2, bottom: case 3.

Figure 5 also reveals that the mixture is pre-burnt at various locations before the wave, which is consistent with observations using a different injector scheme in both the experiment and simulation (Chacon and Gamba 2019a; Sato et al., 2021b): a contact burning region (CB) divides the parasitic combustion (PC), where the mixture begins burning in the pre-detonation region, and the buffer region (BR), where the re-filling process is dominant over parasitic combustion. With the radial air injector scheme in this study, the BR appears near the chamber bottom while the axial air injector scheme reveals that PC appears near the chamber bottom (Chacon and Gamba 2019a; Sato et al., 2021b). It is reported that parasitic combustion makes a detonation wave weaker, which reduces wave speed and peak pressure at the wave (Chacon and Gamba 2019a; Sato et al., 2021b; Sato et al., 2021a; Sato and Raman 2020). This structure is seen for all cases regardless of the number of waves (mass flow rates). It is suggested that such a structure depends on the mixing process in the chamber that is created by a certain injector scheme.

The equivalence ratio profile in Figure 5 gives more insight into the parasitic combustion region. Near the chamber bottom, poorly mixed fuel and air are present which corresponds to the BR. At a certain distance from the chamber, ϕ = 1 begins appearing which can be consumed through parasitic combustion. Generally, parasitic combustion can be induced by residual products from the previous cycle and secondary waves (Chacon and Gamba 2019a; Sato et al., 2021b; Sato et al., 2021a; Chacon and Gamba 2019b). Finally, the Mach contour also reveals an interesting structure. For cases 1 and 2, a contact surface (CS) can be found across which the Mach number decreases. Due to the CS, both subsonic and supersonic flow comes out from the chamber depending on the location. A similar CS structure is also found in the idealized 2D calculation (Schwer and Kailasanath 2010; Sato et al., 2018a). For case 3, however, the CS disappears and only supersonic flow comes out at the exit. In other words, increasing the mass flow rate eliminates the CS that decelerates the expanding flow in the post-detonation region. For a real system, supersonic exit flow does not allow any feedback from the exhaust system that is attached to the exit of the chamber.

3.2.4 Averaged flow profiles and injection dynamics

The previous section discussed the detailed detonation structure on an unwrapped flow field in the circumferential direction. It will be useful to look at the flow field from a different angle because of the highly three-dimensional structure. Figure 6 shows azimuthally averaged temperature and mixture fraction on an injection cutting plane. The color bar for the mixture fraction is limited between 0 and 0.1 because the stoichiometric mixture fraction is Z_st = 0.0284. The temperature profile reveals a similar structure for case 1 and 2 regardless of the difference in the mass flow rate. Low temperature appears near the chamber bottom due to re-filling mixture, followed by gradually increasing temperature towards the exit. This temperature distribution matches the observation on an unwrapped field where mixture is burned near the bottom and product gases expand in the post-detonation region. Interestingly, case 3 reveals that high temperature appears near the outer wall at the bottom of the chamber. This is likely because of the presence of multiple waves in the system which act to impose high temperature product gases on the outer wall more frequently.

FIGURE 6

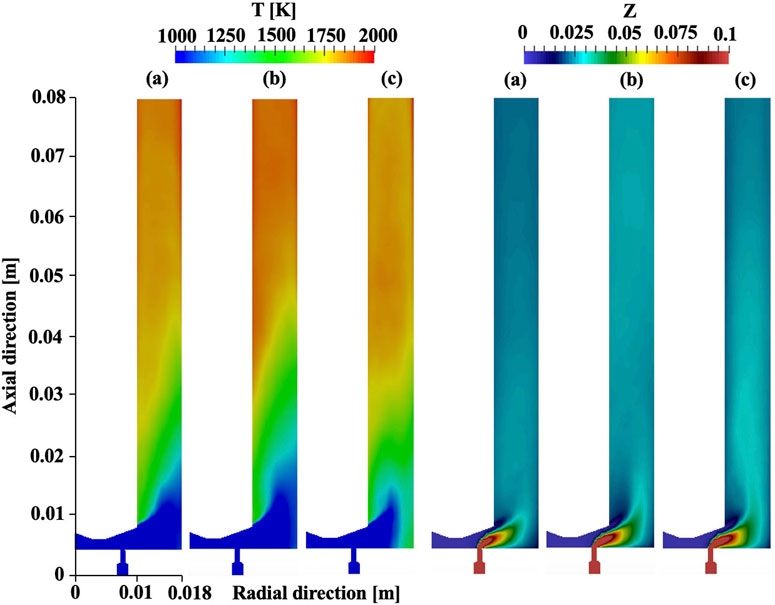
FIGURE 6. Azimuthal averaged temperature and mixture fraction for (A) case 1, (B) case 2, and (C) case 3 with the total pressure boundary condition.

For the mixture fraction, it is seen that the fuel stream is pushed into the chamber due to the axially flowing air stream for all cases. After flowing into the chamber, those streams start to actively get mixed. The stoichiometric region appears 1) at the intersection between the fuel and air streams and 2) at some distance from the chamber bottom and outer wall most likely due to recirculation in the area. It is also seen that the air stream hits the outer wall and creates a lean layer near the outer wall (note that the air inlet is continuous over 360° while the fuel injectors are discrete). As mass flow rate increases, the stoichiometric region extends further into the downstream region as well.

The mixing process is highly chaotic for RDE systems due to the non-premixed injection scheme. It is not just because the fuel and air are separately injected, but also because the injector experiences blocking/flashback due to the detonation wave in the chamber. After the injector is initially blocked, it takes some recovery time to restart the re-filling process into the chamber. These dynamics add complexity to the mixing process of RDE systems. With this in mind, it is critical to assess the injection dynamics over a cycle for both the fuel and air injectors.

Figure 7 shows the averaged injection velocity for the fuel and air inlets as a function of cycle-normalized time. The sudden drop in velocity shows that both injectors are blocked as the detonation wave passes. Only case 3 reveals two flashbacks over a cycle due to the two-wave mode operation. For cases 1 and 2 (one-wave mode), the velocity quickly recovers after a sudden suppression. For the air inlet, the recovery process takes on a curved shape in time which takes about a half cycle to recover to the original value. Interestingly, case 3 finds that the recovery timescale adjusts to the number of waves in the chamber, and the recovery process is complete such that the system can sustain the multiple waves. This observation matches the temperature field in Figures 4, 5 where the re-filling is completed sufficiently enough to sustain the multiple waves. For the fuel injection, flashback can also be observed although the dynamics of it slightly differ from that of the air inlet. The dropped velocity stalls at a minimum point for a certain duration. This is computed as such because the velocity of the fuel injector shows large fluctuations near the minimum point before starting the recovery process. After the stalled point, the velocity sharply recovers to the original value without drawing a curve. These stiff dynamics of the fuel injector are also seen for case 3 which shows the multiple wave mode. This recovery process and difference in the recovery process form a complex mixing in the chamber that leads to a highly chaotic detonation structure.

FIGURE 7

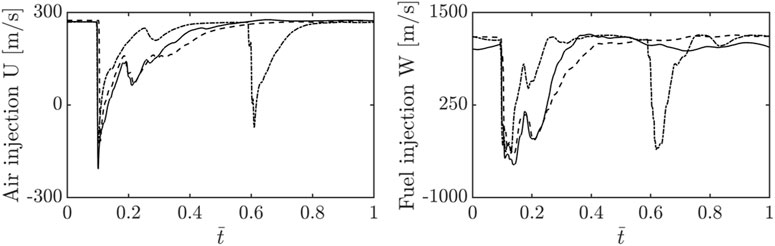
FIGURE 7. Variation in injection velocity with cycle-averaged time for oxidizer and fuel inlets with the total pressure boundary condition. The solid line, dashed line, and dotted line show cases 1, 2, and 3 respectively.

3.2.5 Averaged shock-normal profile

The last section reveals that the detonation structure is highly chaotic due to the non-premixed injection causing a different recovery timescale. While ZND theory suggests that the sharp pressure rise at the wave front induces the high rate of chemical reaction in the post-region which makes the wave self-sustained, the structure could be different in RDE systems due to the complex dynamics mentioned above. As such, it will be useful to look at the profiles across the wave in RDE systems to understand the detailed flame structure.

To determine the structure of the detonation wave itself, a time-averaged profile in the wave reference frame is obtained. The flow properties are extracted across the wave front at the mid-channel at 1 cm above the lower wall of the detonation chamber. Figure 8 shows the profiles in terms of the distance from the shock front. The product gases from the previous cycle can be seen in the post-detonation region as mentioned in Section 3.2.3. The oxidization process can be seen for every case where the fuel and oxidizer are consumed to produce fresh products causing a sharp increase in the pressure. Nevertheless, the oxidization process is significantly weaker compared to the ideal case (Sato et al., 2018b). Comparing case 1 and case 2, the peak of the heat release is closer to the wave front for case 2. This is indicative of the stronger detonation wave as mass flow rate is increased. For case 3, the heat release reaches its peak with a sharper gradient although the peak heat release appears at a similar location to case 2. The heat released in the narrower region supplies more energy to the wave front, resulting in a peak pressure up to nearly 15 atm for case 3.

FIGURE 8

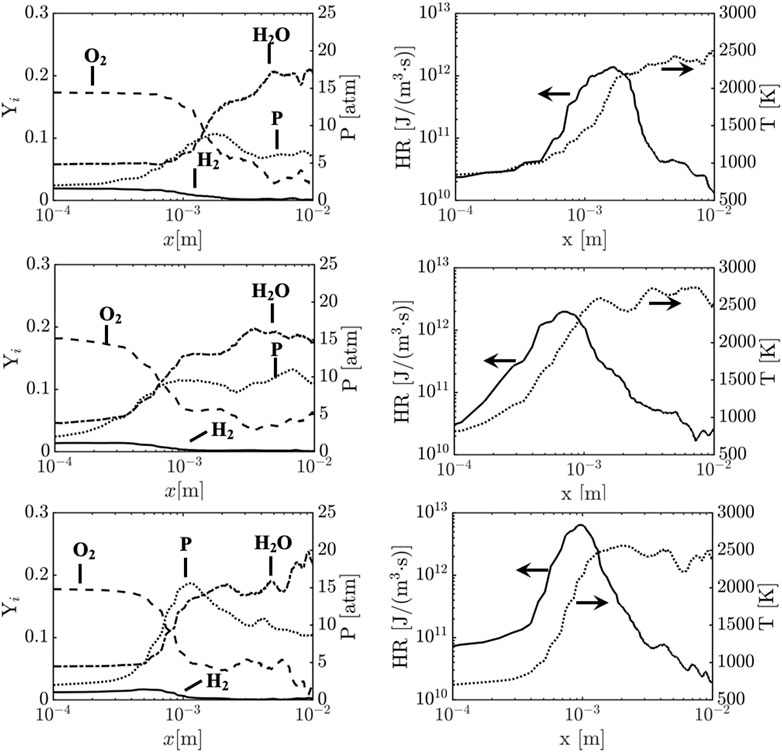
FIGURE 8. One-dimensional shock-normal averaged species and pressure profile (left), and temperature (......) and heat release(---) (right). x = 0 indicates shock location. The data is obtained at the mid-channel 1 cm from the center of the air inlet throat. Top: case 1, middle: case 2, bottom: case 3.

The relation between the compression and chemical reaction can be seen when plotting heat release and temperature on top of each other as shown in Figure 8. For all cases, the heat release sharply increases before that of the temperature. Furthermore, the temperature is nearly at 1,000 K before the wave front where the finite value of heat release also can be seen. This structure suggests that the reaction region extends across the wave due to parasitic combustion which causes the longer induction length and lower peak pressure value (P_CJ = 27 atm) at the wave front. This extension of the reaction zone becomes shorter as mass flow rate is increased (note that the x-axis is in log-scale.). It should also be noted though that peak pressure values are generally lower than CJ pressures due to limited spatial resolution of the Von-Neumann peak, in addition to the averaged 1D profiles coming from multi-dimensional detonation simulations that cannot fully match the 1D assumptions made in CJ calculations.

3.2.6 Axial pressure and macroscopic performance of the system

Finally, the axial variation in average pressure is considered. Table 2 shows the average pressure measured on the outer wall at 2.54 cm above the detonation chamber bottom wall for both experiments and simulations. For case 1 and case 2, the simulation is in good agreement with the experiment within 1.5% errors. A more detailed comparison of wall pressure profiles is provided in Figure 9. Overall, the chamber pressures decrease with increasing axial distance due to expansion effects. Although the simulations capture the experimental trend for case 1 and case 2, case 3 (two-wave mode) underestimates the axial averaged pressure. In other words, as waves split into multiples, the pressure rise due to the detonation is under-predicted in the simulation. Despite the difference for case 3 in the axial averaged pressure, the wave speed is within 10% error between the experiment and the simulation as shown in Table 2. Compared to the result of the base mesh in the resolution study, the main simulation that has boundary layer resolution for case 1 does not show particular differences. This result indicates that the diffusion effects are negligible in the system due to the predominantly supersonic flow, as the reaction timescales through the detonation waves are much shorter than the timescales of boundary layer growth radially in the chamber (Radulescu and Hanson, 2005). Finally, the fuel and air mass flow rate is compared between the experiment and the simulation. Overall, the simulation is in good agreement with the experiment, with a nearly 10% error for the air mass flow rate and a fuel mass flow rate that is under-predicted by 25%. Note that the mass flow rate is calculated at the injector exit for the simulation data while it is measured at the upstream part of the plenum system in the experiment. The total pressure boundary condition does not ensure the target mass flow rate into the chamber. To feed the target mass flow rate, the constant mass flow rate boundary is necessary, which will be discussed in the next section.

FIGURE 9

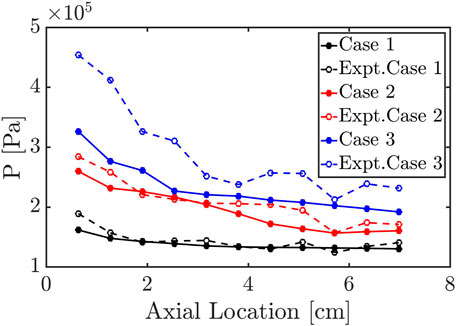
FIGURE 9. Comparison of temporally-averaged pressure measurement on the chamber wall between simulation and experiment with the total pressure boundary condition.

3.2.7 Simulation with the constant mass flow rate boundary condition

As Table 2 reveals for the total pressure boundary condition, the total pressure boundary can match the plenum pressure to the experimental values at cost of the error in the mass flow rate into the chamber. The error is caused by the following: 1) the numerical error, 2) the mass flow rate is regulated far upstream of the plenum system in the experiments while the mass flow rate is calculated at the injector exit in the simulations, 3) the experimental plenum system has more complex geometry in the upstream region. Of these, the second issue needs further elaboration. It should be noted that in experimental setups, the mass flow into a feed plenum is fixed by a choked inflow, with the pressures upstream at much higher values to ensure that this flow rate does not change with time. Typically, this feed plenum then distributes air and fuel to the discrete injectors. As the RDE operates, some of the injectors are blocked, and the mass flow needs to be redirected to other open injectors. In order to compensate for this reduced flow area, the pressure in the plenum will increase until the system reaches a steady state (Chacon et al., 2019). The time taken to reach this steady state will depend, among other factors, on the size of the feed plenum and the strength of the detonation waves. Since RDE calculations are typically quite expensive (computationally), boundary conditions need to be specified to partially capture the effect of this plenum pressurization. The total pressure condition uses the steady-state pressure conditions as a way of mimicking this behavior, but cannot preserve the mass flow rate. Another option is to directly impose the constant mass flow rate boundary condition. In this case, there is no guarantee that the measured pressure in the plenum can be recovered, especially when the entire feed plenum is not simulated. The constant mass flow rate boundary condition ensures that the targeted mass flow rate is supplied into the chamber while the plenum pressure is obtained from the simulation. The overall differences caused by these two types of boundary conditions will be discussed in Section 3.2.10.

The simulations with the constant mass flow rate boundary condition are conducted for the same experimental runs as the total pressure boundary condition. The simulated cases are tabulated in Table 2. The simulations are initiated in the same manner as discussed in Section 2. For the mesh with the constant mass flow rate boundary condition, the base cell size is 2 × 10⁻⁴ m which is the same size as the total pressure boundary condition. The boundary layer resolution is not added as the previous section suggests that the diffusion effect at the wall is negligible. The extended plenum region in Figure 1 is restricted up to 2 cm from the detonation chamber for the constant mass flow rate boundary condition. This is done so that the plenum is easily pressurized due to pressure waves propagating back from the chamber to ensure the target mass flow at the injection exit. The total number of control volumes is 40 million. Each simulation takes approximately 1.008 million core hours to complete using 3000 CPU cores on the NASA Pleiades supercomputer. The main goal of this simulation is to understand the effect on the simulated results by the different boundary conditions and to give more insight to the community for the choice of the inlet boundary condition.

3.2.8 Detonation structure with the constant mass flow rate boundary condition

The unwrapped flow-field is shown in Figure 10 in the same manner as in Figure 5. The constant mass flow rate boundary reveals a similar structure as the total pressure boundary in terms of PC, CB, and BR. For case 2, the constant mass flow rate boundary splits the wave into two waves while the experimental observation suggests a one-wave mode. It should be noted that the mass flow rate into the chamber is under-predicted with the total pressure boundary while the constant mass flow rate boundary captures the target mass flow rate very well. This difference can be explained by the higher plenum pressure with the constant mass flow rate as shown in Table 2. The constant mass flow rate boundary allows the plenum system to be pressurized due to pressure waves from the chamber. The higher plenum pressure locally increases the pressure of the injected gases which affects the reactivity of the mixture. Because of the higher mass flow rate with the constant mass flow rate boundary, case 1 reveals a higher detonation height with a single-wave mode. Interestingly, the height of the BR does not differ from that of the total pressure boundary while the PC region becomes taller. This suggests that the recirculation region becomes taller for the same number of waves as mass flow rate increases.

FIGURE 10

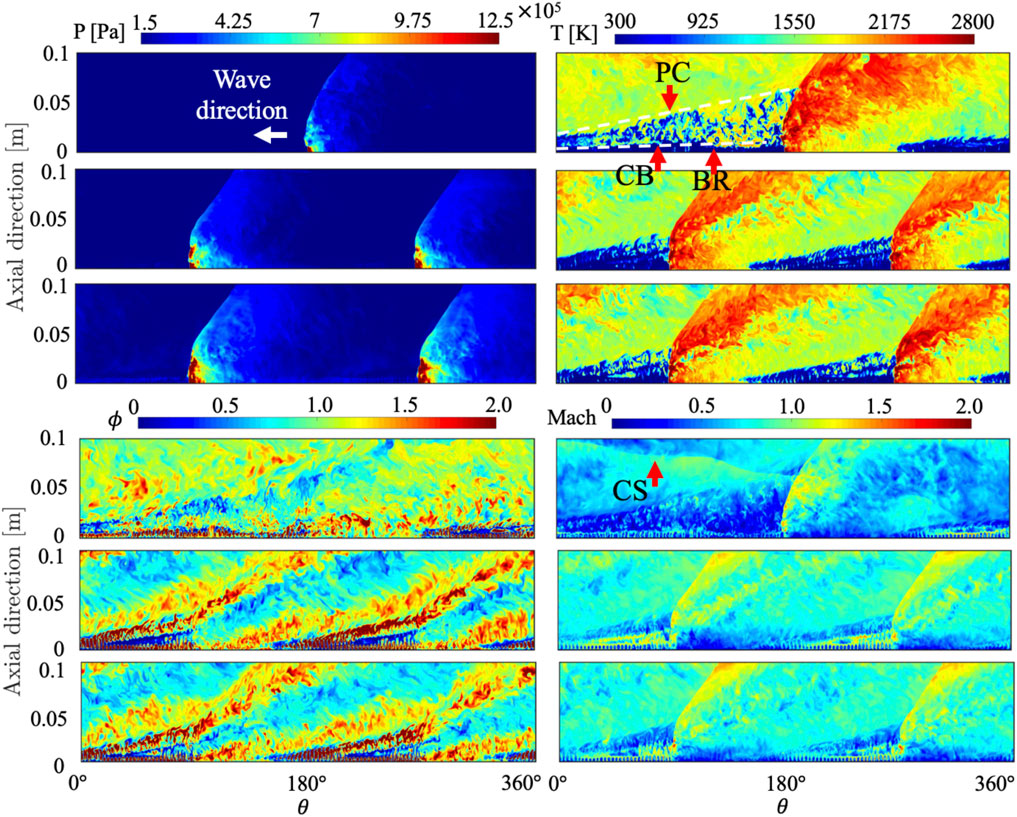
FIGURE 10. Instantaneous pressure, temperature, equivalence ratio, and Mach number on the unwrapped plane at the mid-channel with the constant mass flow rate boundary condition. Top: case 1, middle: case 2, bottom: case 3.

The extended mixing region is also confirmed in Figure 10. The equivalence ratio flow field finds that the broad region of ϕ = 1 appears in the same region of the PC. It should be noted that overall the equivalence ratio flow fields get richer than those of the total pressure boundary cases because the fuel mass flow rate is under-predicted and the system experiences lean operation with the total pressure boundary. The Mach contour also shows a similar trend to Figure 5 although case 2 for the constant mass flow rate boundary does not reveal a CS. This observation suggests that the number of waves has control over the existence of a CS which affects the Mach number (subsonic or supersonic) at the exit.

Nevertheless, despite the minor difference in the flow field, the constant mass flow rate boundary generally reveals the same structure in terms of PC, BR, and CS on an unwrapped field as in the total pressure boundary. It is critical that the general structure remains regardless of the inlet boundary conditions.

3.2.9 Averaged flow profiles and injection dynamics with the constant mass flow rate boundary condition

This section will discuss the averaged profile on an injection cutting plane and the injection dynamics with the constant mass flow rate boundary. Figure 11 shows azimuthally averaged temperature and heat release on an injection cutting plane. The mixture fraction profiles are not shown here because they are very similar to ones for the total pressure boundary cases shown in Figure 6. For cases 2 and 3, the relatively high temperature (nearly 1,500 K) appears near the edge of the chamber bottom and the outer wall. This observation is seen only for case 3 with the total pressure boundary condition which is the two-wave mode. This indicates that this region experiences more heating due to the higher frequency of the flame. Interestingly, it is seen that the temperature downstream in the chamber is higher for case 1 (single wave) than the other cases. This suggests that the longer timescale of exhausting product gases averagely creates hotter gases in the downstream region.

FIGURE 11

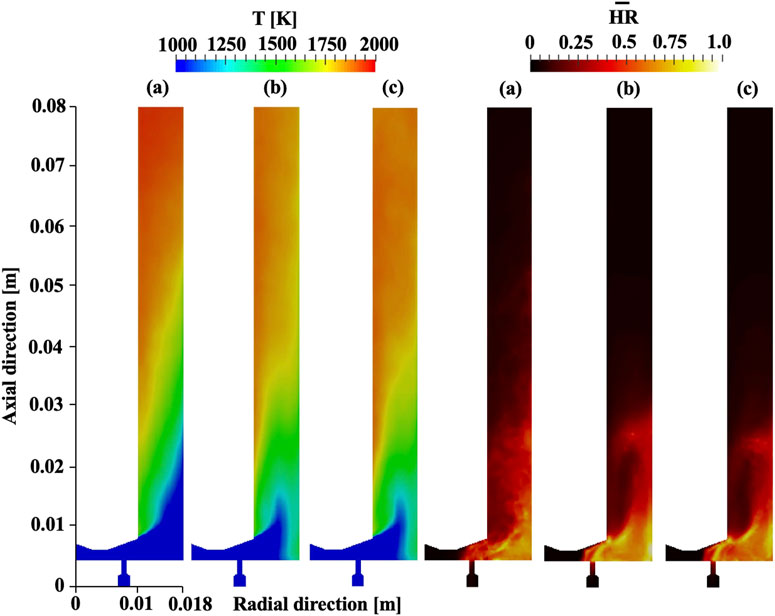
FIGURE 11. Azimuthal averaged temperature and heat release for (A) case 1, (B) case 2, and (C) case 3 with the constant mass flow rate boundary condition.

The right figure in Figure 11 shows the averaged heat release on an injection cutting plane. The value is normalized by the maximum heat release on the plane. For all cases, heat is released near the chamber bottom where the mixed mixture also appears as shown in Figure 6. The heat release appears not only in the detonation chamber but also in the injector region. Nevertheless, the injector prevents the heat release from coming into the plenum system due to the choked condition. Furthermore, there is less heat release near the inner wall for all cases, which is indicative of poor mixing in those regions. In fact, heat release can be seen at the intersection between the fuel and air streams and the recirculation region in Figure 6. Cases 1 and 2 reveal a relatively higher heat release fraction in the broad region near the chamber bottom while case 3 shows a local peak value at the intersection of the two streams. It is also seen for the other injection geometry (axial air injection) that the high heat release fraction is restricted to this local stream intersection region as mass flow rate increases (Sato et al., 2021a; Prakash et al., 2020).

Figure 12 shows the averaged injection velocity history over one cycle with the constant mass flow rate boundary which is plotted in the same manner as in Figure 7. The velocity goes to negative values due to the pressure wave from the chamber for all cases with the constant mass flow rate boundary as well. For the air injection, the recovery timescale becomes shorter than that of the total pressure boundary. This is because the higher plenum pressure induces a quicker response of the injectors as discussed in Section 3.2.8. For case 2, the two-wave mode with the total pressure boundary reduces the recovery timescale for each wave so that the re-filling process can sustain multiple waves. For the fuel injector, the same trend can be seen as with the air injector. For a single-wave mode (case 1), the velocity recovers to the original value within nearly $\bar{t}$ = 0.15.

FIGURE 12

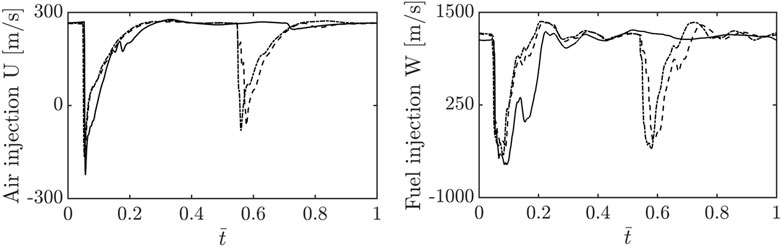
FIGURE 12. Variation in injection velocity with cycle-averaged time for oxidizer and fuel inlets with the constant mass flow rate boundary condition. The solid line, dashed line, and dotted line show case 1, 2, and 3 respectively.

3.2.10 Comparison between the total pressure boundary condition and the constant mass flow rate boundary condition

The comparison between the total pressure boundary and the constant mass flow rate boundary is discussed in this section. First, the axial pressure with the constant mass flow rate boundary is plotted in Figure 13 in the same manner as in Figure 9. Overall, the simulations are in good agreement with the experimental CTAP data. The simulation results capture the general trend that the gases are compressed near the chamber bottom and expand towards the exit. Especially for case 3, the constant mass flow rate boundary reveals better agreement with the experiment than the total pressure case. This result indicates that the under-predicted mass flow rate with the total pressure boundary makes the detonation wave weak. This is because lower mass flow rates (and correspondingly lower feed pressures) lengthen the recovery time of injectors, leading to the formation of a less uniform fuel-air mixture before detonation wave arrival (Sato et al., 2021a). As such, the unsteady behavior of injector flow, which increases with decreasing mass flow rate, causes large variations in local equivalence ratio, which have been found to directly contribute to variable detonation speeds and strengths (Prakash and Raman 2021; Sato et al., 2021a), thus affecting the entire detonation structure and flow within the chamber (Prakash et al., 2020).

FIGURE 13

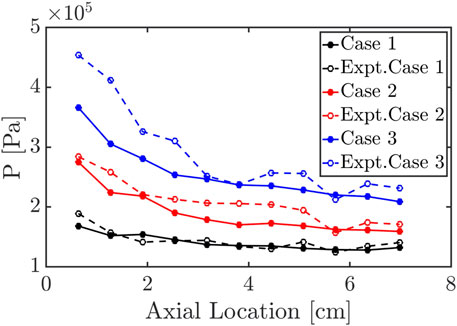
FIGURE 13. Comparison of temporally-averaged pressure measurement on the chamber wall between simulation and experiment with the constant mass flow rate boundary condition.

For the macroscopic performance in the system, the plenum pressures for the constant mass flow rate boundary cases are over-computed against the experimental values (which are also the total pressure boundary values) as shown in Table 2. This is likely because the experimental plenum system has longer and more complex geometry in the upstream region as discussed in Section 3.2.8. For the mass flow rate at the injector exit, the total pressure boundary under-predicts the value nearly 20% for both injectors which causes the differences in the detonation structure and the injection dynamics as discussed in Section 3.2.9. For the wave speed, both boundary conditions over-predict the experimental values. As a general trend for both boundary conditions, the wave speed becomes faster for the same number of waves as mass flow rate increases. The error in the wave speed is within 15% against the experimental values, which is on the same order as other prior studies (Sato et al., 2021a; Sato et al., 2021b; Prakash et al., 2021; Prakash et al., 2020).

Overall, the total pressure boundary and the constant mass flow rate boundary ensure agreement with the experiment in terms of different properties. The total pressure boundary can capture plenum pressure and wave speed better compared to the constant mass flow rate boundary. However, it under-predicts the axial pressure distribution likely due to the erroneous mass flow rate. On the other hand, the mass flow rate boundary ensures the right amount of mass flow rate into the chamber. The downside of this boundary condition though is that the plenum pressure is higher than the experiment. This also indicates, however, that the longer plenum system in the experiment is causing some loss between the pressure probe in the plenum and the location of measurement of the mass flow rate. In terms of the axial pressure distribution, the constant mass flow rate reveals better agreement with the experimental CTAP data.

4 Conclusion

A series of high-resolution simulations using detailed chemical kinetics and a discrete injection process including plenum flow is conducted. The use of detailed chemical kinetics provides a full view of the detonation structure. The simulation configuration is based on the AFRL 6-inch RDE experiment using hydrogen/air at stoichiometric conditions. Three cases, corresponding to three different plenum pressures and resulting mass flow rates, are studied with the total pressure and the constant mass flow rate boundary conditions. The simulations indicate that multiple waves can be sustained as higher mass flow rates are considered. Similar to the experiments, the waves become weaker, moving with lower velocities at higher mass flow rates for the same number of waves.

Spatially, the detonation waves are stronger near the outer wall but devolve into strong deflagrations near the inner wall. The reason for the radial difference in detonation structure comes from the fuel/air stratification due to incomplete mixing. Simulations show that the different stiffness associated with the injectors lead to non-uniform fueling of the detonation chamber, even when the global flow rates are steady in long-time averages. Most importantly, the injector recovery timescale adjusts to the number of waves in the chamber.

Regarding the detonation front structure, it is found that the residual product gases from the previous cycles remain, which could cause the incomplete combustion process. Parasitic combustion appears above the buffer region near the chamber bottom which is bounded by the contact burning region. For the lower mass flow rate, a contact surface decelerates the Mach number which made the outflow subsonic. As the wave splits into multiples, the contact surface disappears which results in supersonic outflow. The averaged profiles on an injection cutting plane find that the averaged temperature structure varies depending on the number of waves in the chamber. For the multiple wave mode, the temperature near the outer wall at the chamber bottom increases because flames pass more frequently. The mixture fraction suggests that the mixing happens at some distance from the chamber. It is also found that the air stream hits and flows along the outer wall where the mixing is not created. As mass flow rate increases, the mixing region broadened towards the downstream as well. The averaged heat release suggests that the reaction actively happens at the intersection of the fuel and air streams and in the recirculation region.

The cycle-averaged injection velocity reveals that the fuel injector generally shows stiffer dynamics than that of the oxidizer. As mass flow rate increases, the recovery process becomes stiffer due to higher plenum pressure. The recovery timescale adjusts to the number of waves in the chamber so that re-filling is completed before the next wave comes in. The different timescales of the recovery process lead to complex mixing behavior which results in an incomplete and highly three-dimensional detonation structure.

The shock-normal profile shows that the structure across the wave is very different from the ideal detonation tube case. For case 1, the averaged peak pressure drops by more than 60% compared to the CJ value. Product gases appear in the pre-detonation region due to parasitic combustion and residual gases from the previous cycle, which makes the wave weaker than the ideal detonation wave. The heat release profiles suggest that the reaction region is extended across the wave as well. It is also observed that the induction length becomes shorter as mass flow rate increases.

The resolution study reveals that macroscopic properties such as wave speed, oxidizer mass flow rate, axial averaged pressure, and thrust converge even with the grid size of 4 × 10⁻⁴ m. This study employed 2 × 10⁻⁴ m to capture the detailed profile across the wave although the resolution study indicates that one can use 4 × 10⁻⁴ m only to assess the macroscopic properties of the RDE system.

A comparison between the total pressure boundary and the constant mass flow rate boundary conditions is also conducted. Overall, the detonation structures and the injection dynamics reveal a similar structure with minor differences that are caused by the different mass flow rates (the higher pressure in the plenum system). The constant mass flow rate boundary allows the pressurizing process in the chamber to adjust the mass flow at the injector exit. Due to this, case 2 operates in a two-wave mode for the constant mass flow rate boundary. The constant mass flow rate boundary ensures the target mass flow rate at the injector exit plane (nearly within 2% error) while the total pressure boundary reveals much larger error (nearly 20%). Due to the higher pressure in the plenum for the constant mass flow rate boundary, the injection dynamics get stiffer than those of the total pressure boundary. Overall, the axial pressures, wave speeds, and oxidizer mass flow rates are in good agreement with the experiments. As a conclusion, both boundary conditions capture the general trends of the detonation structure and the injection dynamics. However, depending on the quantity of interest such as plenum pressure or axial pressure distribution within the detonation chamber, one must choose the appropriate boundary condition for the inlet.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

TS, CVB, and VR contributed to the conception and design of the study. TS and CVB performed analysis. TS wrote the first draft of the manuscript. TS and CVB wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

DOE-NETL Grant DE-FE0025315 with Dr. Mark Freeman as program monitor. Allocation of Computational Resources: NCSA Blue Waters System, NASA Pleiades Supercomputer. Support from an NDSEG Fellowship through AFRL.

Acknowledgments

The authors gratefully acknowledge financial support from DOE-NETL through grant DE-FE0025315 with Dr. Mark Freeman as program monitor. The authors are grateful for the generous allocation of computational resources on the NCSA Blue Waters System as well as the NASA Pleiades Supercomputer. The authors thank Dr. Brent Rankin (AFRL) for sharing the RDE experimental data. The authors also acknowledge support from an NDSEG Fellowship through AFRL.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpace.2023.1123249/full#supplementary-material

References

Anand, V., George, A. S., Driscoll, R., and Gutmark, E. (2016). Analysis of air inlet and fuel plenum behavior in a rotating detonation combustor. Exp. Therm. Fluid Sci. 70, 408–416. doi:10.1016/j.expthermflusci.2015.10.007

CrossRef Full Text | Google Scholar

Anand, V., George, A. S., and Gutmark, E. (2017). Amplitude modulated instability in reactants plenum of a rotating detonation combustor. Int. J. Hydrogen Energy 42, 12629–12644. doi:10.1016/j.ijhydene.2017.03.218

CrossRef Full Text | Google Scholar

Bohon, M., Bluemner, R., Paschereit, C., and Gutmark, E. (2019). High-speed imaging of wave modes in an RDC. Exp. Therm. Fluid Sci. 102, 28–37. doi:10.1016/j.expthermflusci.2018.10.031

CrossRef Full Text | Google Scholar

Burr, J., and Yu, K. (2017). “Detonation wave propagation in an open channel with transverse jets,” in 53rd AIAA/SAE/ASEE joint propulsion conference, 4908.

Google Scholar

Bykovskii, F. A., Zhdan, S. A., and Vedernikov, E. F. (2006). Continuous spin detonations. J. Propuls. Power 22, 1204–1216. doi:10.2514/1.17656

CrossRef Full Text | Google Scholar

Chacon, F., Feleo, A., and Gamba, M. (2019). “Impact of inlet area ratio on the operation of an axial air inlet configuration rotating detonation combustor,” in AIAA propulsion and energy 2019 forum, 4450.

CrossRef Full Text | Google Scholar

Chacon, F., and Gamba, M. (2019a). Detonation wave dynamics in a rotating detonation engine. In AIAA scitech 2019 forum. 0198.

CrossRef Full Text | Google Scholar

Chacon, F., and Gamba, M. (2018). Development of an optically accessible continuous wave rotating detonation engine. In 2018 joint propulsion conference. 4779.

CrossRef Full Text | Google Scholar

Chacon, F., and Gamba, M. (2019b). Study of parasitic combustion in an optically accessible continuous wave rotating detonation engine. In AIAA scitech 2019 forum. 0473.

CrossRef Full Text | Google Scholar

Cocks, P. A., Holley, A. T., Greene, C. B., and Haas, M. (2015). “Development of a high fidelity RDE simulation capability,” in 53rd AIAA Aerospace sciences meeting, 1823.

CrossRef Full Text | Google Scholar

Cocks, P. A., Holley, A. T., and Rankin, B. A. (2016). “High fidelity simulations of a non-premixed rotating detonation engine,” in 54th AIAA Aerospace sciences meeting, 2016–0125.

CrossRef Full Text | Google Scholar

Duvall, J., Chacon, F., Harvey, C., and Gamba, M. (2018). Study of the effects of various injection geometries on the operation of a rotating detonation engine. In 2018 AIAA Aerospace sciences meeting. 0631.

CrossRef Full Text | Google Scholar

Fotia, M. L., Schauer, F., Kaemming, T., and Hoke, J. (2016). Experimental study of the performance of a rotating detonation engine with nozzle. J. Propuls. Power 32, 674–681. doi:10.2514/1.b35913

CrossRef Full Text | Google Scholar

Goodwin, D., Malaya, N., Moffat, H., and Speth, R. (2012). Cantera: An object oriented software toolkit for chemical kinetics, themodynamics, and transport processes.Version 2.1.1

Google Scholar

Hsu, K., and Jemcov, A. (2000). “Numerical investigations of detonation in premixed hydrogen-air mixture-assessment of simplified chemical mechanisms,” in Fluids 2000 conference and exhibit, 2478.

CrossRef Full Text | Google Scholar

Huff, R., Polanka, M. D., McClearn, M. J., Schauer, F. R., Fotia, M. L., and Hoke, J. L. (2019). Design and operation of a radial rotating detonation engine. J. Propuls. Power 35, 1143–1150. doi:10.2514/1.b37578

CrossRef Full Text | Google Scholar

Kailasanath, K. (2003). Recent developments in the research on pulse detonation engines. AIAA J. 41, 145–159. doi:10.2514/2.1933

CrossRef Full Text | Google Scholar

Kailasanath, K. (2011). “The rotating-detonation-wave engine concept: A brief status report,” in 49th AIAA Aerospace sciences meeting, 2011–0580.

CrossRef Full Text | Google Scholar

Kindracki, J. (2015). Experimental research on rotating detonation in liquid fuel–gaseous air mixtures. Aerosp. Sci. Technol. 43, 445–453. doi:10.1016/j.ast.2015.04.006

CrossRef Full Text | Google Scholar

Kindracki, J., Wolański, P., and Gut, Z. (2011). Experimental research on the rotating detonation in gaseous fuels–oxygen mixtures. Shock Waves 21, 75–84. doi:10.1007/s00193-011-0298-y

CrossRef Full Text | Google Scholar

Lentsch, A., Bec, R., Serre, L., Falempin, F., Daniau, E., Piton, D., et al. (2005). Overview of current French activities on PDRE and continuous detonation wave rocket engines. AIAA 3232, 2005.

CrossRef Full Text | Google Scholar

Lisanti, J. C., and Roberts, W. L. (2016). Design of an actively valved and acoustically resonant pulse combustor for pressure-gain combustion applications. In 54th AIAA Aerospace sciences meeting. San Diego; California. 0899.

CrossRef Full Text | Google Scholar

Lu, F., and Braun, E. M. (2014). Rotating detonation wave propulsion: Experimental challenges, modeling, and engine concepts. J. Propuls. Power 30, 1125–1142. doi:10.2514/1.b34802

CrossRef Full Text | Google Scholar

Meng, L., and Jian-Ping, W. (2011). Three dimensional simulation for the effects of fuel injection patterns in rotating detonation engine. Irvine, CA: 23rd ICDERS.

Google Scholar

Mueller, M., Kim, T., Yetter, R., and Dryer, F. (1999). Flow reactor studies and kinetic modeling of the H₂/O₂ reaction. Int. J. Chem. Kinet. 31, 113–125. doi:10.1002/(sici)1097-4601(1999)31:2<113:aid-kin5>3.0.co;2-0

CrossRef Full Text | Google Scholar

OpenFOAM (2016). The open source CFD toolbox. http://openfoam.org.

Google Scholar

Pal, P., Kumar, G., Drennan, S. A., Rankin, B. A., and Som, S. (2021). Multidimensional numerical modeling of combustion dynamics in a non-premixed rotating detonation engine with adaptive mesh refinement. J. Energy Resour. Technol. 143. doi:10.1115/1.4050590

CrossRef Full Text | Google Scholar

Paxson, D. E., Fotia, M., Hoke, J., and Schauer, F. (2015). “Comparison of numerically simulated and experimentally measured performance of a rotating detonation engine,” in 53rd AIAA Aerospace sciences meeting, 1101.

Google Scholar

Paxson, D. E. (2014). Numerical analysis of a rotating detonation engine in the relative reference frame. National Harbor, MD: National Aeronautics and Space Administration, Glenn Research Center.

Google Scholar

Prakash, S., Fiévet, R., Raman, V., Burr, J. R., and Yu, K. H. (2018). “Numerical study of the detonation wave structure in a linear model detonation engine,” in 2018 joint propulsion conference, 4966.

CrossRef Full Text | Google Scholar

Prakash, S., Fiévet, R., Raman, V., Burr, J., and Yu, K. H. (2020). Analysis of the detonation wave structure in a linearized rotating detonation engine. AIAA J. 58, 5063–5077. doi:10.2514/1.j058156

CrossRef Full Text | Google Scholar

Prakash, S., and Raman, V. (2019). Detonation propagation through inhomogeneous fuel-air mixtures. China: 27th ICDERS Beijing.

Google Scholar

Prakash, S., Raman, V., Lietz, C. F., Hargus, W. A., and Schumaker, S. A. (2021). Numerical simulation of a methane-oxygen rotating detonation rocket engine. Proc. Combust. Inst. 38, 3777–3786. doi:10.1016/j.proci.2020.06.288

CrossRef Full Text | Google Scholar

Prakash, S., and Raman, V. (2021). The effects of mixture preburning on detonation wave propagation. In Proceedings of the combustion Institute 38, 3749–3758. doi:10.1016/j.proci.2020.06.005

CrossRef Full Text | Google Scholar

Radulescu, M., and Hanson, R. (2005). Effect of heat loss on pulse-detonation-engine flow fields and performance. J. Propuls. Power 21, 274–285. doi:10.2514/1.10286

CrossRef Full Text | Google Scholar

Raman, V., Prakash, S., and Gamba, M. (2023). Non-idealities in rotating detonation engines. Annu. Rev. Fluid Mech. 55, 639–674. doi:10.1146/annurev-fluid-120720-032612

CrossRef Full Text | Google Scholar

Rankin, B. A., Fotia, M. L., Paxson, D. E., Hoke, J. L., and Schauer, F. R. (2015a). Experimental and numerical evaluation of pressure gain combustion in a rotating detonation engine. In 53rd AIAA Aerospace sciences meeting. 0877.

CrossRef Full Text | Google Scholar

Rankin, B. A., Richardson, D. R., Caswell, A. W., Naples, A. G., Hoke, J. L., and Schauer, F. R. (2017). Chemiluminescence imaging of an optically accessible non-premixed rotating detonation engine. Combust. Flame 176, 12–22. doi:10.1016/j.combustflame.2016.09.020

CrossRef Full Text | Google Scholar

Rankin, B. A., Richardson, D. R., Caswell, A. W., Naples, A., Hoke, J. L., and Schauer, F. R. (2015b). “Imaging of OH* chemiluminescence in an optically accessible nonpremixed rotating detonation engine,” in 53rd AIAA Aerospace sciences meeting, 2015–1604.

CrossRef Full Text | Google Scholar

Rhee, H., Ishiyama, C., Higashi, J., Kawasaki, A., Matsuoka, K., Kasahara, J., et al. (2017). “Experimental study on a rotating detonation turbine engine with an axial turbine,” in 26th international colloquium on the dynamics of explosions and reactive systems, 1–6.

Google Scholar

Roy, A., Ferguson, D. H., Sidwell, T., O’Meara, B., Strakey, P., Bedick, C., et al. (2017). 55th AIAA Aerospace Sciences Meeting, 1–16.Experimental study of rotating detonation combustor performance under preheat and back pressure operation

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, T., Chacon, F., Gamba, M., and Raman, V. (2021a). Mass flow rate effect on a rotating detonation combustor with an axial air injection. Shock Waves 31, 741–751. doi:10.1007/s00193-020-00984-7

CrossRef Full Text | Google Scholar

Sato, T., Chacon, F., White, L., Raman, V., and Gamba, M. (2021b). Mixing and detonation structure in a rotating detonation engine with an axial air inlet. Proc. Combust. Inst. 38, 3769–3776. doi:10.1016/j.proci.2020.06.283

CrossRef Full Text | Google Scholar

Sato, T., and Raman, V. (2020). Detonation structure in ethylene/air-based non-premixed rotating detonation engine. J. Propuls. Power 36, 752–762. doi:10.2514/1.b37664

CrossRef Full Text | Google Scholar

Sato, T., and Raman, V. (2019). “Dynamics of rotating detonation engines with a pintle-type injector,” in 24th ISABE conference, 1909–1920.

Google Scholar

Sato, T., Voelkel, S., and Raman, V. (2018a). “Analysis of detonation structures with hydrocarbon fuels for application towards rotating detonation engines,” in 2018 joint propulsion conference, 4965.

CrossRef Full Text | Google Scholar

Sato, T., Voelkel, S., and Raman, V. (2018b). “Detailed chemical kinetics based simulation of detonation-containing flows,” in Turbo expo: Power for land, sea, and air (American Society of Mechanical Engineers), 4A. Combustion, Fuels, and Emissions.

CrossRef Full Text | Google Scholar

Sato, Y., Matsuo, A., Higashi, J., Ishiyama, C., Matsuoka, K., and Kasahara, J. (2017). Numerical investigation on the behavior of detonation waves in a disk-shaped rotating combustor. MA: 26th ICDERS Boston.

Google Scholar

Schwer, D., and Kailasanath, K. (2013). Fluid dynamics of rotating detonation engines with hydrogen and hydrocarbon fuels. Proc. Combust. Inst. 34, 1991–1998. doi:10.1016/j.proci.2012.05.046

CrossRef Full Text | Google Scholar

Schwer, D., and Kailasanath, K. (2010). “Numerical investigation of rotating detonation engines,” in 46th AIAA/ASME/SAE/ASEE joint propulsion conference & exhibit, 6880.

CrossRef Full Text | Google Scholar

Schwer, D., and Kailasanath, K. (2011). Numerical investigation of the physics of rotating-detonation-engines. Proc. Combust. Inst. 33, 2195–2202. doi:10.1016/j.proci.2010.07.050

CrossRef Full Text | Google Scholar

Shank, J. C., King, P. I., Karnesky, J., Schauer, F., and Hoke, J. L. (2012). “Development and testing of a modular rotating detonation engine,” in 50th AIAA Aerospace sciences meeting, 2012–0120.

CrossRef Full Text | Google Scholar

Strakey, P., Ferguson, D., Sisler, A., and Nix, A. (2016). “Computationally quantifying loss mechanisms in a rotating detonation engine,” in 54th AIAA Aerospace sciences meeting, 0900.

CrossRef Full Text | Google Scholar

Toro, E. F., Spruce, M., and Speares, W. (1994). Restoration of the contact surface in the HLL-riemann solver. Shock Waves 4, 25–34. doi:10.1007/bf01414629

CrossRef Full Text | Google Scholar

Tsuboi, N., Eto, S., Hayashi, A. K., and Kojima, T. (2016). Front cellular structure and thrust performance on hydrogen–oxygen rotating detonation engine. J. Propuls. Power 33, 100–111. doi:10.2514/1.b36095

CrossRef Full Text | Google Scholar

Uemura, Y., Hayashi, A. K., Asahara, M., Tsuboi, N., and Yamada, E. (2013). Transverse wave generation mechanism in rotating detonation. Proc. Combust. Inst. 34, 1981–1989. doi:10.1016/j.proci.2012.06.184

CrossRef Full Text | Google Scholar

Wang, Y., Wang, J., Li, Y., and Li, Y. (2014). Induction for multiple rotating detonation waves in the hydrogen–oxygen mixture with tangential flow. Int. J. Hydrogen Energy 39, 11792–11797. doi:10.1016/j.ijhydene.2014.05.162

CrossRef Full Text | Google Scholar

Wolański, P. (2013). Detonative propulsion. Proc. Combust. Inst. 34, 125–158. doi:10.1016/j.proci.2012.10.005

CrossRef Full Text | Google Scholar

Yao, S., Liu, M., and Wang, J. (2015). Numerical investigation of spontaneous formation of multiple detonation wave fronts in rotating detonation engine. Combust. Sci. Technol. 187, 1867–1878. doi:10.1080/00102202.2015.1067202

CrossRef Full Text | Google Scholar

Yao, S., Tang, X., Luan, M., and Wang, J. (2017). Numerical study of hollow rotating detonation engine with different fuel injection area ratios. Proc. Combust. Inst. 36, 2649–2655. doi:10.1016/j.proci.2016.07.126

CrossRef Full Text | Google Scholar

Yellapantula, S., Tangirala, V., Singh, K., and Haynes, J. (2017). 26th International Colloquium on the Dynamics of Explosions and Reactive Systems, 1–7.A numerical study of H₂-air rotating detonation combustor

PubMed Abstract | Google Scholar

Zhou, R., Wu, D., and Wang, J. (2016). Progress of continuously rotating detonation engines. Chin. J. Aeronautics 29, 15–29. doi:10.1016/j.cja.2015.12.006

CrossRef Full Text | Google Scholar