Minimal length multi-segment clothoid return paths for vehicles with turn rate constraints

Continuous curvature recovery paths are needed to accurately return a fixed wing autonomous vehicle with turn rate constraints back to a missions path in the correct direction after collision avoidance. Clothoid paths where curvature is linearly dependent to arc length can be used to make multi-segment splines with continuous curvature, but require optimization to ensure that the path is of minimal length while meeting curvature and sharpness limits. The present work considers the problem of returning a fixed wing aircraft back to its original path facing the correct direction after a leaving it during collision avoidance by presenting a method of optimizing a three segment clothoid spline to be of minimal length while meeting fixed wing turn rate constraints and targeting a path function. The impact of this work is enabling accurate path recovery after collision avoidance with minimal length paths that minimize the time spent off a missions planned route, giving better control over time of arrival for the planned route and more time to complete mission objectives.

1 Introduction

Uncrewed Aerial Vehicles (UAV) are used for a variety of applications ranging from high altitude military surveillance to small hobbyist vehicles (Stacy et al., 2002; Ariyur and Fregene, 2008; Giernacki et al., 2017; Moon et al., 2019). UAVs under autonomous operations require a path to complete their objectives, but they may occasionally depart their planned trajectory due to obstacle avoidance. Collision avoidance methods can be utilized to route around conflict areas that were not previously considered (Harman, 1989; Albaker and Rahim, 2009; Erzberger et al., 2012; Kochenderfer et al., 2012; Jeannin et al., 2015; Deaton and Owen, 2020; English and Wilhelm, 2020; Browne et al., 2022). Returning to the planned route requires an updated plan to efficiently intercept the previous path and keep tracking the mission. Direct return to the original path utilizing trajectory tracking controllers (Coulter, 1992; Park et al., 2004) may result in excess deviation from original path for fixed wing turn rate restricted vehicles. Instead, a return route targeting a position optimized to the UAVs flight characteristics will bring the UAV back to the planned trajectory minimizing deviation (Browne et al., 2022). Recovery paths that return a UAV to a mission route must target both a position and heading that intercept the mission’s trajectory, as the vehicle is required to be both on target and facing the desired direction. Three segment clothoids can join any set of positions, tangents, and curvatures with a continuous curvature spline (Bertolazzi and Frego, 2018a), but do not have any considerations for fixed wing maneuverability constraints. Optimization of the clothoid mission interception routes would be required to meet turn rate constraints and minimize the path length to provide more time to complete mission objectives.

The present work details a method of optimizing a three segment clothoid spline to meet turn rate limits and minimize total path length. The method for generating three segment clothoid splines utilizes a heuristic to set the arc lengths for the first and third segments (Bertolazzi and Frego, 2018a). External optimization of the clothoid arc lengths was needed to satisfy fixed wing turning limits, but moving the rejoin position along the target path was required to ensure a solution would exist. Optimization of the rejoin position on a target trajectory and the initial/final arc lengths were explored externally to meet curvature and curvature rate requirements. The optimization process was first evaluated through varied configurations with different departure angles, initial positions, and maximum bank angles to ensure convergence throughout expected conditions. Simulated path following was investigated to ensure the aircraft is capable of accurately following the clothoid routes and intercept the target trajectory. Comparison to direct return interception methods were made to evaluate the effectiveness of clothoid path recovery. Utilization of optimized clothoid curves will improve path following performance when a UAV intercepts a trajectory, leading to increased accuracy in estimating travel times and more time on a mission’s path to complete objectives. The contribution of this work was a method of optimizing a three segment clothoid curve that represents a path interception and balances finding a minimal length path with meeting curvature/sharpness limits determined from fixed wing vehicle turning limitations.

2 Literature review

Fixed wing UAVs provide a platform for a variety of tasks including aerial reconnaissance (Stacy et al., 2002; Ariyur and Fregene, 2008). However, due to the requirement of continuous forward velocity to remain airborne, they have turn rate limits that must be accounted for when planning missions. Restrictions on typical non-fighter fixed wing maneuvering include a maximum bank angle, where the United States federal aviation administration advises a maximum of 25 degrees of bank angle (United States Department of Transportation Federal Aviation Administration) for most cases to prevent unsafe operation during flight. High altitude reconnaissance UAVs can not safely sustain bank angles over 25° (Pastor et al., 2018) and mission routes made for these vehicles must accommodate their limits. Minimum turn radius for a fixed wing vehicle can be modeled as a function of airspeed and the bank angle (Owen et al., 2015) where bounds on the maximum bank angle and bank angle rate can be used to determine a minimum turn radius and rate, these constraints are then used to ensure mission paths are flyable.

Deviation from the mission occurs when an obstacle that would cause a collision is detected on the planned route. Avoidance paths are then utilized to prevent a collision with detected obstacles. Methods include temporarily changing altitude, turning away from the obstacle until a safe distance is met, or search algorithms to compute avoidance paths (Harman, 1989; Albaker and Rahim, 2009; Erzberger et al., 2012; Kochenderfer et al., 2012; Jeannin et al., 2015; Deaton and Owen, 2020; English and Wilhelm, 2020; Browne et al., 2022). After a safe distance is met when avoiding an obstacle, the UAV must intercept its original route to continue its mission. Methods of accomplishing path interception include targeting a waypoint further along the route (McNally et al., 2001; Erzberger et al., 2012) or allowing a trajectory tracking controller to return the UAV to the route by providing heading commands that guide the UAV either towards or along the route (Coulter, 1992; Park et al., 2004). Approaching a path with trajectory tracking guidance often causes the to UAV overshoot the path before recovering (Coulter, 1992) as the vehicle heading request does not meet turning capabilities of the aircraft. Overshooting causes excess path deviation, increases the length of time to reach steady state path following, and results in greater controller effort. Potential field methods have been utilized to guide a vehicle towards a target goal and around obstacles (Khatib, 1985; Liu and Zhao, 2016; Choi et al., 2020), however they may not return to a planned route after avoidance. Path planning methods exist that are capable of planning a route around known obstacles then updating when conflicts are detected (Zhuang et al., 2016; Blasi, D’Amato, Mattei, Notaro), however these methods typically plan a new shortest path instead of returning to the original planned trajectory. Receding horizon control which continuously optimizes and plans new routes (Kuwata and How, 2004; Schouwenaars et al., 2004; Keviczky and Balas, 2005; Andersson et al., 2018; Hoang-Dinh et al., 2022), and path replanning which plans a new route around detected obstacles then returning to planned route have been investigated (Mehdi et al., 2015; Bertolazzi et al., 2018a; Chai and Hassani, 2019), but both need of continuous computation and sensor limitations may reduce their desirability for certain applications. Recovery routes that bring the UAV back to a position and direction on the planned path can be utilized to achieve smooth path interception (Browne et al., 2022). However, optimization is required to meet the turn rate limits of the airframe to ensure that the aircraft returns to its mission without further deviation and in minimal time.

Fixed wing UAVs require continuous curvature paths with bounds on the maximum curvature and sharpness if they are to be capable of accurately following them (Al Nuaimi, 2014). Generation of a path with a continuous curvature requires a function with a controllable curvature. Clothoids are functions where curvature is linearly dependent on its arc length and can be used to meet both a targeted position and direction while maintaining a continuous curvature. The equations for the spatial positions x and y as a function of the arc length s is presented (Bertolazzi and Frego, 2018a),

$x\left(s\right)=x_0+{\int }_0^s\cos \left(\frac{1}{2}{\kappa }^{\prime }{\tau }^2+{\kappa }_0\tau +{\theta }_0\right)d\tau (1)$

$y\left(s\right)=y_0+{\int }_0^s\sin \left(\frac{1}{2}{\kappa }^{\prime }{\tau }^2+{\kappa }_0\tau +{\theta }_0\right)d\tau (2)$

where κ is the curvature, θ is the tangent angle, θ₀ is the initial angle, and τ is the integration variable. Combination of multiple clothoids into a spline can be utilized to generate continuous curvature paths (Meek and Walton, 1992; Fraichard and Scheuer, 2004; Wilde, 2009; Gim et al., 2017; Bertolazzi and Frego, 2018a; Bertolazzi and Frego, 2018b) by matching the curvature where the clothoid segments meet. Three clothoid segments can be used to generate a continuous curvature spline that meets initial/final positions and headings in any configuration (Bertolazzi and Frego, 2018a; Bertolazzi and Frego, 2018b). The system of equations for the three segment clothoid has eight equations and 10 unknowns, requiring two more known variables to solve the system. Solving the clothoid spline requires a heuristic function to set the initial/final segment lengths to reduce the unknowns (Bertolazzi and Frego, 2018a). The remaining clothoid properties for the three segment spline are then found by utilizing a newtons method solver (Bertolazzi and Frego, 2018a). The three segment clothoid spline with its initial and final arc lengths set by a heuristic is not guaranteed to meet any curvature or sharpness constraints for the path, however optimization of the initial/final clothoid lengths could be used to meet curvature and sharpness constraints while minimizing total path length.

Non-Linear Programming (NLP) approaches can be utilized for optimization of the three segment clothoid. NLP methods can account for both minimization of an objective function and obeying applied constraints (Bracken and McCormick, 1968). NLP optimization methods include Sequential quadratic programming (SQP) (Boggs and Tolle, 2000) which finds a minimal point for a problem by iterating through the gradient created by the objective function and its constraints using finite difference methods to update each iteration (Boggs and Tolle, 2000). Minimization of the path length of a three segment clothoid while meeting curvature and sharpness limits can be accomplished with SQP however a defined cost function and constraints are needed for successful optimization.

Different approaches have been taken for finding an optimal path that joins two positions and trajectories required for recovery paths, geometric approaches for generation of minimal length paths have been investigated (Scheuer and Laugier, 1998; Scheuer and Fraichard, 2000a; Scheuer and Fraichard, 2000b; Fraichard and Scheuer, 2004), however they provide different configurations in which a path could be made and not a general solution. Generalized solution for multi-segment clothoid curves that join two points and headings was proposed in (Gim et al., 2017) but minimizes the total path sharpness, reducing its usefulness in the case after collision avoidance where rejoining the original path as quickly as possible is desired. Optimization of a sequence of clothoids with considerations for automotive vehicle constraints was accomplished (Frego et al., 2016a; Frego et al., 2016b; Frego et al., 2017; Bertolazzi et al., 2018a), however the solution requires a separate search algorithm to compute a sequence of points for the clothoid segments to meet at. Clothoid recovery paths with considerations for minimal turn radius were utilized in (Browne et al., 2022), however the paths are generated using a three segment clothoid spline (Bertolazzi and Frego, 2018a) that utilizes a heuristic function to set initial/final arc lengths, potentially creating a longer than necessary path without considerations for max sharpness. Bezier curves have been utilized for path generation (Hassani and Lande, 2018; Weintraub et al., 2020) however they have a nonlinear curvature and require complex models for computation of control points. Minimal length continuous curvature paths that target a mission’s route are needed for timely and accurate path rejoin after leaving the mission route due to presence of obstacles.

3 Methods

Optimization of interception paths that balance minimal length with satisfaction of curvature and sharpness limits was investigated. Three segment clothoid splines were utilized to create continuous curvature paths that target a position and heading on a missions route, but required optimization to meet curvature and sharpness constraints. Determination of an optimal rejoin position on a target path that ensures the return route would meet aircraft turning limits while keeping the total length as short as possible was investigated, however three segment clothoid splines were further optimized by changing the initial and final arc segment lengths. The present work detailed a process to minimize the length of a three segment clothoid spline with set initial position, heading and curvature, a target path function, and a max curvature and sharpness for path recovery after collision avoidance.

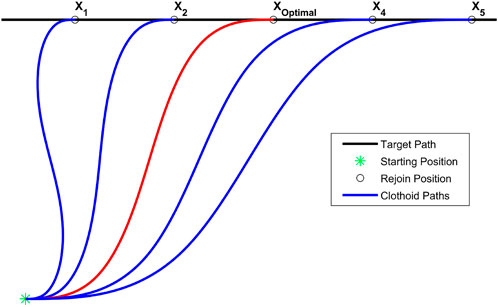
Curvature and sharpness constraints may not always be capable of being met for a three segment clothoid in cases where the ending position is near the starting point, however by utilizing a target path the optimizer may move the final position and heading along the path to find a point that minimizes the total path length while satisfying the constraints. Rejoin position on a target path too close to the starting point may not meet curvature or sharpness bounds while a point too far away would have excess length. Clothoid routes targeting different points on a path is presented in Figure 1, where the points X_1,2 on the target trajectory do not meet curvature/sharpness limits and X_4,5 meet the constraints but are of excess length.

FIGURE 1

FIGURE 1. Example of clothoid return paths with multiple possible rejoin positions.

Curvature and sharpness limits were determined from the maximum bank angle ϕ_max and bank angle rate ${\dot{\varphi }}_{\max }$. Maximum path curvature was found as a function of the vehicles velocity V, gravity g, and the maximum bank angle ϕ_max (Owen et al., 2015), max sharpness was then determined through differentiating the curvature function with respect to time.

${\kappa }_{\mathit{max}}=\frac{g}{V^2}\tan \left({\varphi }_{\mathit{max}}\right)(3)$

${\kappa }_{\mathit{max}}^{\prime }=\frac{g}{V^3}{\dot{\varphi }}_{\mathit{max}}{\sec }^2\left({\mathit{\varphi }}_{\max }\right)(4)$

Changing the rejoin point along a target trajectory as a design variable can be utilized to meet curvature and sharpness constraints, however the final heading ψ₁ and curvature κ₁ must be updated for each rejoin position (x₁, y₁) to generate an interception path that can smoothly transition to the target route. Determination of ending conditions require a target route capable of being represented by a continuous path function,

$y_1=f_{\mathit{path}}\left(x_1\right)(5)$

where (x₁, y₁) represent the rejoin position of the clothoid spline. Tangent angle and curvature were then determined using the path function to match the ending conditions of the return path with the target trajectory. The final heading of the return path was determined by finding the angle of the target trajectory at the rejoin position x₁,

${\psi }_1={\tan }^{-1}\left(f_{\mathit{path}}^{\prime }\left(x_1\right)\right)(6)$

where ψ₁ is the heading angle that matches the return path to the target. The ending curvature for the return path targeting a mission path function was found by determining the curvature of the target trajectory at the rejoin position x₁,

${\kappa }_1=\frac{f_{\mathit{path}}^{″}\left(x_1\right)}{{\left(1+{\left(f_{\mathit{path}}^{\prime }\left(x_1\right)\right)}^2\right)}^{\frac{3}{2}}}(7)$

where κ₁ is the curvature that matches the final curvature on the return route with the target trajectory. Moving the target rejoin point along a path function and updating the ending conditions of the return route to match the mission path allows for an optimizer to minimize the total clothoid path length while ensuring that curvature and sharpness constraints are satisfied.

Intial/final arc lengths of a three segment clothoid are changed as design variables to further optimize the length and curvature/sharpness alongside the rejoin position on a target route. The arc lengths of the three segment clothoid must be kept long enough that the sharpness limit is met, while kept short enough that the curvature constraint is satisfied. Chosen arc lengths must fall in a region that satisfies both the curvature and sharpness bounds while reducing the overall path length, Figure 2 presents a contour plot of the total path length with a static rejoin position vs. the arc lengths (s₀, s₁). The curvature and sharpness constraints shown in Figure 2 create an acceptable region for the arc lengths within the constraints where the path length can be minimized by utilizing a cost function and non-linear constraints. Optimization of the initial/final arc lengths alongside a rejoin position on a target route was utilized to further optimize total path length and meet curvature/sharpness constraints.

FIGURE 2

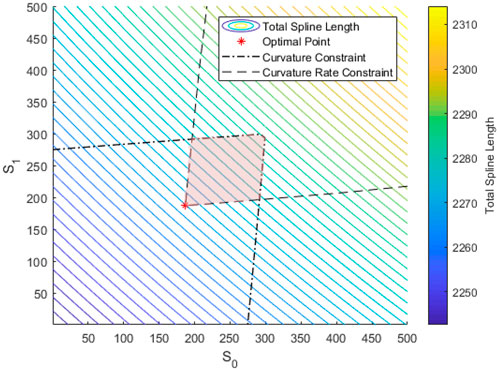
FIGURE 2. Contour plot of three segment clothoid spline length vs. initial/final arc lengths with curvature and sharpness constraints where the red shaded region represents the area where constraints can be satisfied.

Optimization of the clothoid return path was accomplished by utilizing a non-linear program where a cost function evaluated from the clothoid spline was minimized to find the minimum value while obeying set constraints. The cost function used to optimize the three segment clothoid to be of minimal length was the summed lengths of the clothoid segments,

$f_{\mathit{cost}}=s_0+s_m+s_1(8)$

where s₀ is the initial segment length, s_m is the middle segment length, and s₁ is the final segment length. The design variables for the cost function were the initial/final clothoid arc lengths s₀ and s₁, and the rejoin position x₁. The middle segment length s_m was found through solving the system of equations for the three segment clothoid where the solution is defined by the design variables. The cost function in Eq. 8 provides a method for reducing the length of the clothoid but more was required to prevent curvature and sharpness limits from being violated. Application of nonlinear constraints in the form of inequalities was utilized to ensure curvature and sharpness constraints are met. Clothoid curvature increases and decreases linearly, implying that the maximum curvature is found at the ends of a clothoid segment, and since the start and end of the spline are set by the initial conditions, the maximum curvature would occur at the start and end of the middle clothoid segment,

$|\kappa \left(s_0\right)|\le {\kappa }_{\mathit{max}}\mathrm{a}\mathrm{n}\mathrm{d}|\kappa \left(s_0+s_m\right)|\le {\kappa }_{\mathit{max}}(9)$

where κ(s₀) is the curvature at the end of the first segment, and κ(s₀ + s_m) is the curvature at the end of the second segment. Clothoid sharpness is constant throughout each segment as the curvature changes linearly and in a three segment clothoid spline there are three different curvature rates,

$|{\kappa }_0^{\prime }|\le {\kappa }_{\mathit{max}}^{\prime }\mathrm{a}\mathrm{n}\mathrm{d}|{\kappa }_m^{\prime }|\le {\kappa }_{\mathit{max}}^{\prime }\mathrm{a}\mathrm{n}\mathrm{d}|{\kappa }_1^{\prime }|\le {\kappa }_{\mathit{max}}^{\prime }(10)$

where ${\kappa }_x^{\prime }$ is the sharpness for the corresponding clothoid segment. Location of the curvature and sharpness constraints on the clothoid spline is presented in Figure 3, where curvature constraints are evaluated at the ends of the middle segment and sharpness constraints exist for each segment.

FIGURE 3

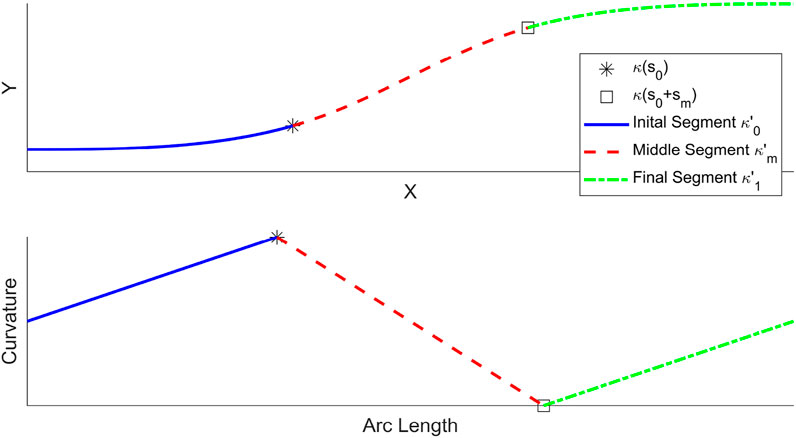
FIGURE 3. Example of three segment clothoid spline showing locations where curvature and sharpness limits are evaluated.

The initial guess for the optimization algorithm used to minimize the length of the three segment clothoid spline was required to provide a starting position on the gradient created by the initial/final arc lengths and the target rejoin position vs. the total return path length. Determining a reasonable initial guess for the optimizer would ensure that the system converges to the correct position and help prevent the optimizer from converging to a potential local minima by starting near the minimum point. The guess for the initial and final clothoid length can be found with the curvature and sharpness constraints to find the distance it would take for the path to reach the maximum curvature at the max curvature rate,

$s_{\mathit{guess}}=\frac{{\kappa }_{\mathit{max}}-{\kappa }_0}{{\kappa }_{\mathit{max}}^{\prime }}(11)$

where κ_max is the maximum allowable curvature, κ₀ is the initial curvature, and ${\kappa }_{\max }^{\prime }$ is the max allowable curvature rate. The initial guess for the target rejoin position will differ based on the target path function and the fixed wing vehicle turning limitations requiring the guess function to be determined for each mission.

Sequential quadratic programming implementation (Han, 1977; Powell, 1978; Powell and Watson, 1978) was utilized to minimize the NLP formed by the cost function from Eq. 8 and subjected to the constraints presented in Eqs 9–10. Initial position, heading and velocity of the aircraft must be provided, however since a fixed wing aircraft will move during the computation of the route, initial position for the return path should be a point along the current trajectory that will be passed through. Limits to the curvature and sharpness are first determined from the vehicle’s maneuverability constraints, then an initial guess for the optimizer is determined. Rejoin position, final vehicle heading, and curvature are then determined each iteration to provide starting and ending conditions to smoothly intercept the trajectory. Three segment clothoid splines were computed every iteration with the assistance of a library (Bertolazzi et al., 2018b) to solve the system of equations for the three segment clothoid where the return path could then be evaluated against the constraints and cost function. When the optimizer converges to a minimal cost route it returns a rejoin position and initial/final arc lengths that produce a minimal length clothoid interception route that meets the curvature and sharpness constraints. The method utilized to generate minimal length clothoid splines that satisfy curvature and sharpness constraints is shown in Algorithm 1.

Algorithm 1. Three Segment Clothoid Spline Optimization.

Validation of the optimization process was accomplished through evaluations over a range of potential initial headings, positions and maximum bank angles while intercepting a straight line target trajectory to ensure the process converges to a minimal length path meeting fixed wing turn rate limits. Straight line targets routes were utilized as they are often used to connect distant waypoints and present a consistent target for optimization, allowing distance from the path to be investigated by moving along one axis. Investigation of path following and interception performance required simulating a fixed wing aircraft and measuring how accurately it followed the route. Dynamics of a fixed wing UAV were modeled with a system that assumes a constant altitude and velocity, V, a maximum bank angle, ϕ_max, and rate, ${\dot{\varphi }}_{\max }$ (Techy et al., 2010). A bound on the maximum allowed UAV bank angle ϕ_max and bank angle rate ${\dot{\varphi }}_{\max }$ is placed on the vehicles heading to account for fixed wing vehicle maneuverability limits. The model is presented,

$\vec{X}\left(t\right)=\vec{X}\left(t-dt\right)+V\left[\begin{array}{c}\hfill \cos \left(\psi \left(t\right)\right)\hfill \\ \hfill \sin \left(\psi \left(t\right)\right)\hfill \end{array}\right]dt(12)$

$\psi \left(t\right)=\psi \left(t-dt\right)+\left(\frac{g}{V}\tan \left(\varphi \left(t\right)\right)\right)dt(13)$

$\varphi \left(t\right)=\varphi \left(t-dt\right)+\dot{\varphi }\left(t\right)dt(14)$

where ψ is the vehicle’s heading, ϕ is the airframe’s bank angle, and g is gravity. PD control is used to convert heading commands determined from guidance to bounded bank angle rates, leading the vehicle along the clothoid towards its target trajectory. Deviation from the path is measured by Cross Track Error (XTE),

$XTE=\sqrt{{\left(\begin{array}{c}\hfill X-X_C\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill Y-Y_C\hfill \end{array}\right)}^2}(15)$

where (X, Y) is the position of the aircraft and (X_C, Y_C) is the closest point on the path to the aircraft. Flyable routes would have low total XTE during path interception as the trajectory would account for the turning limits of the vehicle enabling accurate path recovery.

Three segment clothoid optimization provides a general solution for generating a route from a starting position and heading and returning to a path function. Curvature and sharpness limits were placed on the clothoid return route to prevent fixed wing turning limits from being violated. Target rejoin position for the clothoid was adjusted to minimize the total path length and ensure constraints can be met, initial/final arc length of the three segment clothoid curve are adjusted to further optimize the spline. Minimal length return paths meeting UAV turning limits enable timely and accurate path recovery to allow the aircraft to complete mission objectives.

4 Results

Clothoid return routes targeting a path function were optimized to be of minimal length with limits placed on curvature and sharpness to ensure that the paths met fixed wing turning rate limits. The heuristic approach for clothoid spline generation (Bertolazzi and Frego, 2018a) was compared to optimizing the initial/final arc lengths of the three segment spline to investigate how much was gained through optimizing the arc lengths. The optimization process was tested at varied heading angles, positions, and maximum bank angles while targeting a straight line path to verify that it would admit a minimal length flyable return route throughout the tested cases. Straight line targets were utilized as they are commonly used to connect distant waypoints and require a flyable return path to bring a UAV back to the route after collision avoidance to ensure that it does not stay off course. Verification that the optimized clothoid return routes were flyable was accomplished through simulation of a fixed wing UAV with bank angle and bank angle rate constraints and a constant velocity. Comparison to direct return to the target trajectory was then made using both nonlinear guidance and pure pursuit methods to investigate the performance of clothoid recovery routes intercepting a path.

4.1 Clothoid recovery path generation

Optimized clothoid return routes provide a method of returning to a target trajectory with minimal deviation by optimizing the rejoin position and clothoid arc length that minimize the length of the path while meeting fixed wing turning limits. Example of an optimized clothoid return route with position starting at the origin pointing away from the target path at y = 750 with a 30° difference in angle from the target trajectory is presented in Figure 4A. The gradient of initial/final arc length and rejoin position vs. the total cost as determined by the cost function from Eq. 8 and nonlinear constraints from Eqs 9–10 is presented in Figure 4B, where the optimal point is the point that provides the smallest possible cost while satisfying the curvature and sharpness constraints. The optimizer finds the point of minimum cost by iterating through the gradient created by the arc lengths and rejoin position until the cost decreasing within the regions accepted by the constraints is less than the optimizer’s tolerance. The optimization process finds acceptable routes by moving the interception point along the target path and should converge to a flyable route in all cases where the curvature required to intercept the path is lessened as the interception point is moved further along the path, such as the straight line scenario. The nonlinear constraints and cost function provided a method of balancing total path length and max curvature and sharpness throughout a clothoid spline enabling accurate path interception after collision avoidance.

FIGURE 4

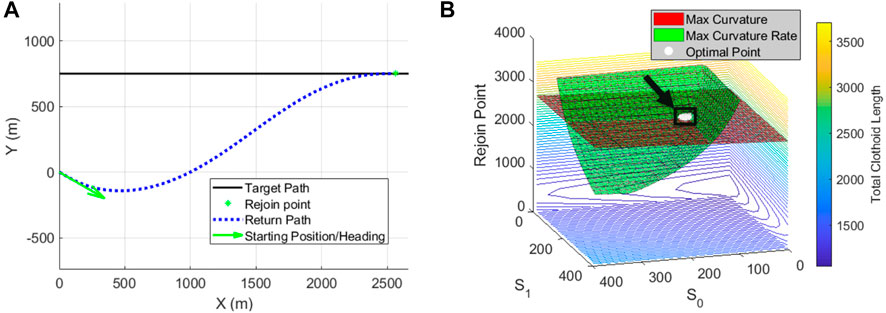
FIGURE 4. Example of an optimized 3-segment clothoid intercept path (A) and the gradient of total path length vs. final/initial arc length and rejoin position on target path (B).

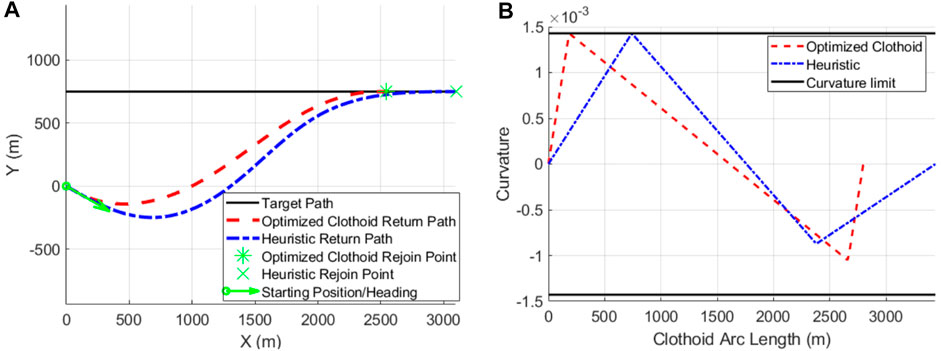
Optimized clothoid recovery routes change the initial and final arc lengths of the three segment clothoid spline alongside moving the rejoin position to balance meeting curvature and sharpness limits with minimizing the length of the route. The clothoid with optimized arc lengths was compared to using the heuristic method from (Bertolazzi and Frego, 2018a) for determining the arc lengths, rejoin position was optimized for both clothoids using the same cost function and nonlinear constraints. Clothoid recovery routes with the arc lengths set by a heuristic were previously utilized for clothoid path recovery after collision avoidance (Browne et al., 2022), where potential rejoin positions were sampled and the shortest clothoid route that met a curvature constraint was chosen, however optimization of the arc lengths could lead to a path length. The clothoid path with optimized arc lengths was found to be 18.6% shorter compared to the heuristic configuration for the case shown in Figure 5A. The initial and final segment lengths for the heuristic clothoid were found to be longer than the optimized clothoid and have a shallower curvature rate, as shown in Figure 5B, the smaller sharpness means that the aircraft would not turn as quickly leading to a longer path length. Optimization of the initial/final clothoid arc lengths allows for the clothoid spline to better utilize vehicle capabilities, leading to a shorter path length and less time spent away from the planned mission route.

FIGURE 5

FIGURE 5. Clothoid intercept path and heuristic clothoid (A) and curvature diagram (B).

Validation that the optimized clothoid return routes would converge to a minimal length path that met fixed wing turning limits throughout expected conditions was carried out by testing the optimization process with varied departure angle, initial position, and maximum bank angle. The optimization processes was first tested with varied initial heading angles with a static starting position, Figure 6A shows the generated paths with the varied initial headings. Initial position closer to the target trajectory could cause the return routes to cross over the target path before interception for heading angles pointing at the path while initial positions further away from the target trajectory would have a closer rejoin position. Total clothoid length vs. initial heading is presented in Figure 6B, showing the total path length decreasing when the UAV is facing the target path, and increasing when the UAV is pointing away from the target path. Tests of different starting positions and an initial heading angle parallel with the path for a three segment clothoid return path is shown in Figure 6C. The initial position first starts on the target trajectory and moves away from the path where it will converge to a S configuration where the shortest path will have the UAV turning straight toward the target instead of slowly converging alongside. The total clothoid length vs. the initial starting position of the three segment clothoid return paths is presented in Figure 6D where the path length increased with the total distance from the path. Maximum bank angle was varied from 5 to 89° to investigate the effect of curvature limits have on the optimization process and ensure that it admits a flyable return path. Clothoid return paths with varied maximum bank angle are shown in Figure 6E where the clothoid recovery routes target closer positions at higher bank angles, as shown in Figure 6F, and again form an S configuration where the UAV is able to fly towards the target route instead of transitioning alongside it. Optimized clothoid return paths were found to meet curvature and sharpness paths throughout the tested configurations, verifying that the method works under the evaluated conditions. The set of evaluations present all expected configurations and demonstrate that the optimization method will work as designed to provide a method of smooth path interception after collision avoidance enabling fast and accurate path recovery required to continue a mission and complete objectives without significant delay.

FIGURE 6

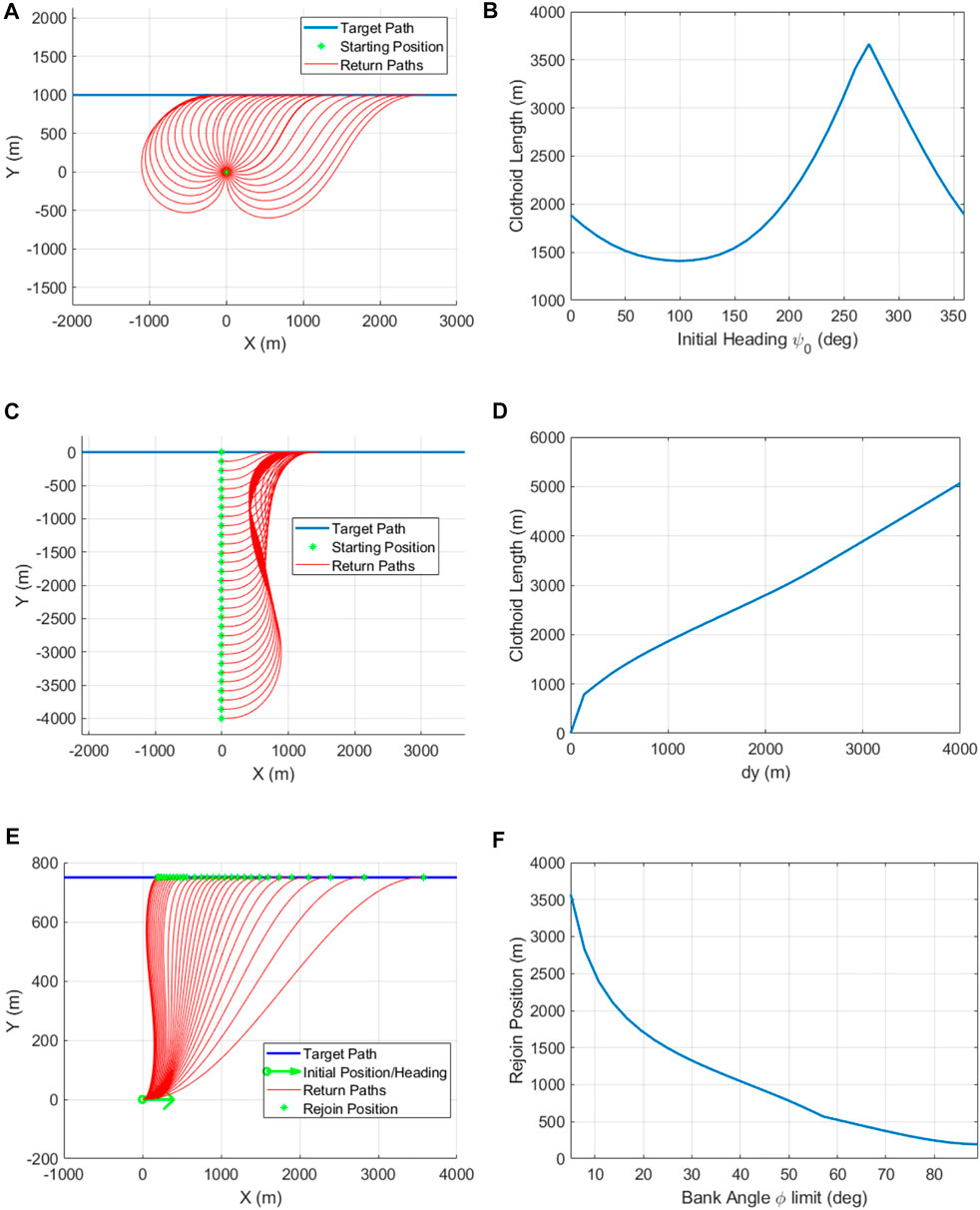
FIGURE 6. Clothoid intercept paths at varied departure angles (A) and total path length vs. heading (B), varied initial position (C) and total path length vs. position (D), and varied maximum bank angle (E) and rejoin position vs. max bank angle (F).

The clothoid interception path was optimized utilizing a Matlab implementation of SQP to find a minimal length return route meeting fixed wing turn rate limits. Computational time of the optimization function fmincon within Matlab averaged 0.054 s for the previously shown cases when utilizing a PC with a 6 core AMD Ryzen 5 3600 processor. Reduction of total execution time could be accomplished by approximating the clothoid computation with methods such as look up tables (Brezak and Petrovic, 2014). Online use of the optimization process would require the process to meet specific timing requirements on embedded machinery and has not yet been exhaustively tested.

4.2 Simulated clothoid path interception

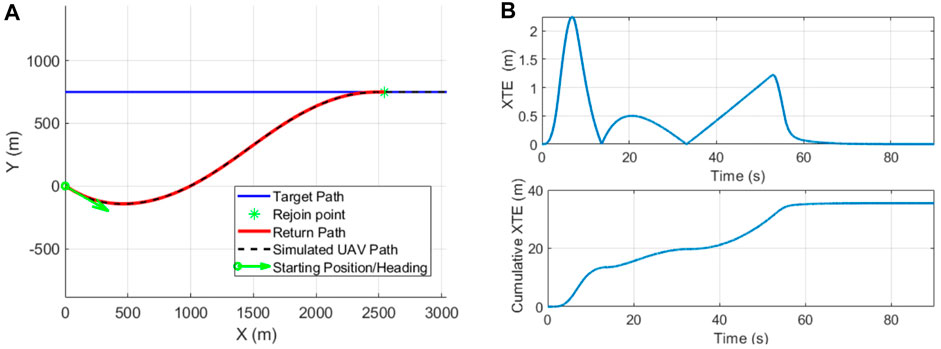
Simulation of UAV path following was carried out to compare and verify that optimized clothoid paths were flyable and capable of smooth and accurate path interception. UAV flight was modeled as described in Eqs 12–14 with bounded bank angle and bank angle rate constraints. Measurement of total deviation from the clothoid path through cross track error (XTE) was utilized to verify that the clothoid paths were flyable by showing small XTE and smooth convergence to the target trajectory. The UAV was tested in a common scenario pointing away from a straight line mission path at an angle of 30° with zero bank angle, then a clothoid path was computed accounting for the UAVs turning constraints to return it to the target trajectory. Path following results are presented in Figure 7A showing the UAVs path as it tracked the return path utilizing pure pursuit guidance then transitioned to the target path. Cross track error representing the total deviation from the clothoid recovery route is presented in Figure 7B, showing the total cross track error to be 35.4 m over the total length of the path and no deviation larger than 2.5 m at any given point. Low XTE from the clothoid recovery route and fast convergence to zero deviation once the straight line target was intercepted verifies that the return routes can be accurately flown by a fixed wing UAV enabling smooth and accurate path interception after collision avoidance.

FIGURE 7

FIGURE 7. Simulated clothoid path interception (A) and cross track error vs. travel time (B).

Investigation of commonly used path interception methods was carried out to evaluate the effectiveness of clothoid recovery routes compared to direct return methods. Pure pursuit (Coulter, 1992) and nonlinear guidance (Park et al., 2004) were utilized for direct return to a target trajectory by providing guidance commands given vehicle position, heading, and the target path to intercept and then track the mission path. Pure pursuit targeted a moving point at a look ahead distance along the target trajectory to provide guidance (Coulter, 1992). The look ahead distance for pure pursuit was tuned to follow the clothoid recovery route to ensure the guidance would provide accurate path following on both curved and straight trajectories and was used for both direct return and following the clothoid recovery route. Nonlinear guidance projected a fixed length L1 distance that intersected the target trajectory and the difference in angle between the L1 distance and the current heading was used to provide a guidance command (Park et al., 2004). The L1 distance for nonlinear guidance was tuned so that it would intersect the trajectory throughout the simulation to provide guidance for path interception and subsequent path following. Path interception was simulated where the UAV started at 750 m away and a 30° difference in heading pointing away from the target, Figure 8A presents the starting position, target path, and simulated path interception. Deviation from the target trajectory is presented in Figure 8B where pure pursuit crossed the target path first however then oscillated before settling along the path. Nonlinear guidance overshot the path but then smoothly recovered without excess oscillation however path interception following the clothoid return route showed no visible overshoot as the UAV approaches the target trajectory following the clothoid due to being capable of accurately tracking the clothoid recovery route. Bank angle throughout the simulated path interceptions is shown in Figure 8C, where the vehicles bank angle controls the change in heading angle required to follow a trajectory. Nonlinear guidance and pure pursuit both reached the maximum bank angle and remained banking for multiple seconds but pure pursuit then proceeded to oscillate between max positive and negative bank angle while it converged to the trajectory. Clothoid return bank angle was nearly identical to the curvature profile of a clothoid, reaching maximum bank angle, linearly approaching the negative max bank angle, and then returning to zero as it met the target, allowing smooth and accurate path interception after collision avoidance.

FIGURE 8

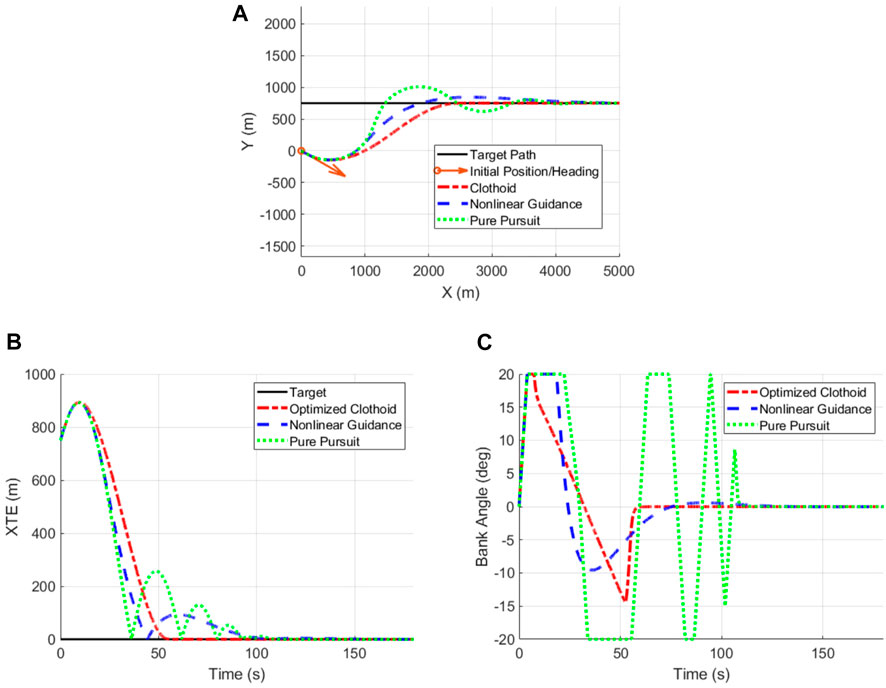
FIGURE 8. Simulated clothoid and direct return path recovery to a straight line target trajectory (A), cross track error vs. travel time (B) and bank angle vs. time (C).

Target routes consisting of circular arcs were explored for evaluation of path interception of a trajectory with a curvature to investigate a more difficult scenario then straight line targets. Path interception and following is presented in Figure 9A where visible overshoot can be seen for both the pure pursuit and nonlinear guidance methods, however all methods did converge to the path. XTE from the target trajectory is presented in Figure 9B where the oscillation of the pure pursuit method can be contrasted to the smooth convergence resulting from the clothoid return routes, nonlinear guidance converged slowly but avoided oscillation about the path. Clothoid intercept paths are capable of smooth and accurate convergence to their target trajectory because they meet a final position, heading and curvature along their target and are optimized to ensure that the route is flyable by meeting fixed wing dynamic limits. Flyable recovery routes enable smooth and accurate path interception for fixed wing aircraft after collision avoidance limiting time spent off mission.

FIGURE 9

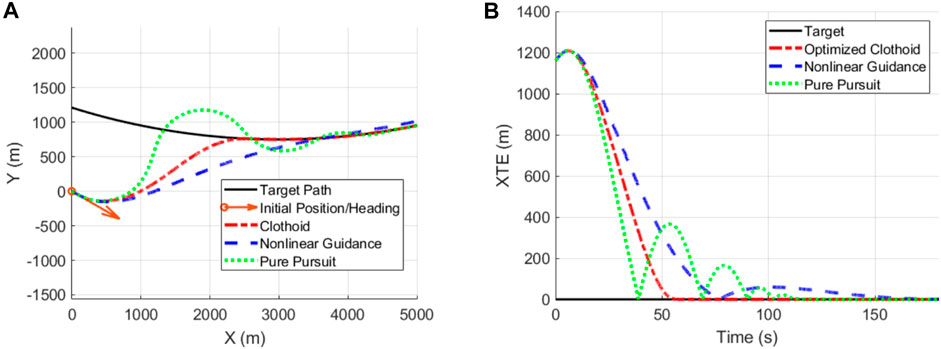
FIGURE 9. Simulated clothoid and direct return path interception to circular target trajectory (A) and cross track error vs. travel time (B).

5 Conclusion

Minimal time path interception was explored with optimization of a three segment clothoid targeting a path function representing a mission’s planned route to minimize the total spline length while satisfying fixed wing turn rate restrictions. The presented work proposed a method of optimizing three segment clothoid curves targeting a path function to be of minimal length while meeting the curvature and sharpness constraints of a vehicle. Optimization of a clothoid spline for minimal length and satisfaction of curvature/sharpness limits was accomplished by changing the rejoin position on a target path. Further reduction of overall path length was accomplished by optimizing the initial/final arc lengths in the three segment spline to meet fixed wing turning constraints and enable smooth path interception. Minimal length clothoid paths through optimization of the target rejoin position and initial/final arc lengths enable smooth and accurate path interception to a planned route.

The optimization method for balancing minimal length clothoid paths with satisfaction of fixed wing turn rate constraints was tested at varied initial headings, positions and maximum bank angles to verify that the method would admit minimal length solution meeting turning rate limits throughout the range of tested conditions representing typical scenarios for a fixed wing UAV. Simulated path following of the clothoid recovery route was carried out, verifying that fixed wing aircraft can accurately track the optimized paths and smoothly transition to a target trajectory. However both the dynamics model and clothoid return route only considered two dimensions, if desired for the interception route to include altitude changes another path primitive added to the three segment clothoid would be required to account for the third dimension. Clothoid path interception was compared to direct return to the target trajectory utilizing pure pursuit and nonlinear guidance techniques where simulated fixed wing aircraft showed the vehicle accurately tracking clothoid return routes and smoothly intercepting the target path while both pure pursuit and nonlinear guidance overshot the path before converging. Minimal length paths reduce the time it takes to intercept a path after collision avoidance allowing for more time to meet mission objectives. Flyable paths that can be accurately followed by considering fixed wing turning rate limits were desired as inaccurate path following could lead to unpredictable behavior off course, potentially preventing a UAV from accomplishing mission tasks. The impact of this work is a method of generating continuous curvature clothoid paths that balance curvature and sharpness constraints with minimizing overall path length to enable timely and accurate path interception.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/OUIDEAS/Optimized-Clothoid-Interception.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Ohio Federal Research Network through the project “Resilient and enhanced security UAS flight control.”

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al Nuaimi, M. (2014). Analysis and comparison of clothoid and dubins algorithms for UAV trajectory generation. Morgantown, WV, United States: MS, West Virginia University Libraries.

Google Scholar

Albaker, B. M., and Rahim, N. A. (2009). “A survey of collision avoidance approaches for unmanned aerial vehicles,” in 2009 international conference for technical postgraduates (TECHPOS) (Kuala Lumpur, Malaysia: IEEE), 1–7.

CrossRef Full Text | Google Scholar

Andersson, O., Ljungqvist, O., Tiger, M., Axehill, D., and Heintz, F. (2018). “Receding-horizon lattice-based motion planning with dynamic obstacle avoidance,” in 2018 IEEE conference on decision and control (CDC) (Miami Beach, FL: IEEE), 4467–4474.

CrossRef Full Text | Google Scholar

Ariyur, K. B., and Fregene, K. O. (2008). “Autonomous tracking of a ground vehicle by a UAV,” in 2008 American control conference (Seattle, WA: IEEE), 669–671.

CrossRef Full Text | Google Scholar

Bertolazzi, E., Bevilacqua, P., Biral, F., Fontanelli, D., Frego, M., and Palopoli, L. (2018). “Efficient Re-planning for robotic cars,” in 2018 European control conference (ECC) (Limassol: IEEE), 1068–1073.

CrossRef Full Text | Google Scholar

Bertolazzi, E., Bevilacqua, P., and Frego, M. (2018). Clothoids: A C++ library with Matlab interface for the handling of clothoid curves, 10.

Google Scholar

Bertolazzi, E., and Frego, M. (2018). Interpolating clothoid splines with curvature continuity. Math. Methods Appl. Sci. 41, 1723–1737, Mar. doi:10.1002/mma.4700

CrossRef Full Text | Google Scholar

Bertolazzi, E., and Frego, M. (2018). On the G2 hermite interpolation problem with clothoids. J. Comput. Appl. Math. 341, 99–116. doi:10.1016/j.cam.2018.03.029

CrossRef Full Text | Google Scholar

Blasi, L., D’Amato, E., Mattei, M., and Notaro, I. (5613). Path planning and real-time collision avoidance based on the essential visibility graph. Appl. Sci. 10, 5613. doi:10.3390/app10165613

CrossRef Full Text | Google Scholar

Boggs, P. T., and Tolle, J. W. (2000). “Sequential quadratic programming for large-scale nonlinear optimization,” in Numerical analysis 2000. Vol. IV: Optimization and nonlinear equations, 124, 123–137.

CrossRef Full Text | Google Scholar

Bracken, J., and McCormick, G. P. (1968). Selected applications of nonlinear programming. John Wiley & Sons.

Google Scholar

Brezak, M., and Petrovic, I. (2014). Real-time approximation of clothoids with bounded error for path planning applications. IEEE Trans. Robot. 30, 507–515. doi:10.1109/tro.2013.2283928

CrossRef Full Text | Google Scholar

Browne, J. P., Moleski, T. W., and Wilhelm, J. (2022). Minimal deviation from mission path after automated collision avoidance for small fixed wing uavs. AIAA SCITECH 2022 Forum 18. doi:10.2514/6.2022-0275

CrossRef Full Text | Google Scholar

Chai, Y., and Hassani, V. (2019). Hybrid collision avoidance with moving obstacles. IFAC-PapersOnLine 52 (21), 302–307. doi:10.1016/j.ifacol.2019.12.324

CrossRef Full Text | Google Scholar

Choi, D., Lee, K., and Kim, D. (2020). “Enhanced potential field-based collision avoidance for unmanned aerial vehicles in a dynamic environment,” in AIAA scitech 2020 forum (Orlando, FL: American Institute of Aeronautics and Astronautics).

CrossRef Full Text | Google Scholar

Coulter, R. C. (1992). Implementation of the pure pursuit path tracking algorithm. Carnegie-Mellon UNIV Pittsburgh PA Robotics INST. tech. rep.

Google Scholar

Deaton, J., and Owen, M. P. (2020). “Evaluating collision avoidance for small UAS using ACAS X,” in AIAA scitech 2020 forum (Orlando, FL: American Institute of Aeronautics and Astronautics).

CrossRef Full Text | Google Scholar

English, J., and Wilhelm, J. (2020). “Collision avoidance in OpenUxAS,” in AIAA scitech 2020 forum (Orlando, FL: American Institute of Aeronautics and Astronautics).

CrossRef Full Text | Google Scholar

Erzberger, H., Lauderdale, T. A., and Chu, Y.-C. (2012). Automated conflict resolution, arrival management, and weather avoidance for air traffic management. Proc. Institution Mech. Eng. Part G J. Aerosp. Eng. 226 (8), 930–949. doi:10.1177/0954410011417347

CrossRef Full Text | Google Scholar

Fraichard, T., and Scheuer, A. (2004). From reeds and shepp’s to continuous-curvature paths. IEEE Trans. Robot. 20, 1025–1035, Dec. doi:10.1109/tro.2004.833789

CrossRef Full Text | Google Scholar

Frego, M., Bertolazzi, E., Biral, F., Fontanelli, D., and Palopoli, L. (2016). “Semi-analytical minimum time solutions for a vehicle following clothoid-based trajectory subject to velocity constraints,” in 2016 European control conference (ECC) (Aalborg, Denmark: IEEE), 2221–2227.

CrossRef Full Text | Google Scholar

Frego, M., Bertolazzi, E., Biral, F., Fontanelli, D., and Palopoli, L. (2017). Semi-analytical minimum time solutions with velocity constraints for trajectory following of vehicles. Automatica 86, 18–28. doi:10.1016/j.automatica.2017.08.020

CrossRef Full Text | Google Scholar

Frego, M., Bevilacqua, P., Bertolazzi, E., Biral, F., Fontanelli, D., and Palopoli, L. (2016). “Trajectory planning for car-like vehicles: A modular approach,” in 2016 IEEE 55th conference on decision and control (CDC) (Las Vegas, NV, USA: IEEE), 203–209.

CrossRef Full Text | Google Scholar

Giernacki, W., Skwierczynski, M., Witwicki, W., Wronski, P., and Kozierski, P. (2017). “Crazyflie 2.0 quadrotor as a platform for research and education in robotics and control engineering,” in 2017 22nd international conference on methods and models in automation and robotics (MMAR) (Miedzyzdroje, Poland: IEEE), 37–42.

CrossRef Full Text | Google Scholar

Gim, S., Adouane, L., Lee, S., and Dérutin, J.-P. (2017). Clothoids composition method for smooth path generation of car-like vehicle navigation. J. Intell. Robot. Syst. 88, 129–146. doi:10.1007/s10846-017-0531-8

CrossRef Full Text | Google Scholar

Han, S. P. (1977). A globally convergent method for nonlinear programming. J. Optim. Theory Appl. 22 (3), 297–309. doi:10.1007/bf00932858

CrossRef Full Text | Google Scholar

Harman, W. H. (1989). Tcas: A system for preventing midair collisions, 437–458.

Google Scholar

Hassani, V., and Lande, S. V. (2018). Path planning for marine vehicles using bézier curves. IFAC-PapersOnLine 51 (29), 305–310. doi:10.1016/j.ifacol.2018.09.520

CrossRef Full Text | Google Scholar

Hoang-Dinh, K., Leibold, M., and Wollherr, D. (2022). A fast and close-to-optimal receding horizon control for trajectory generation in dynamic environments. Robotics 11, 72. doi:10.3390/robotics11040072

CrossRef Full Text | Google Scholar

Jeannin, J.-B., Ghorbal, K., Kouskoulas, Y., Gardner, R., Schmidt, A., Zawadzki, E., et al. (2015). “Formal verification of ACAS X, an industrial airborne collision avoidance system,” in 2015 international conference on embedded software (EMSOFT) (Amsterdam, Netherlands: IEEE), 127–136.

CrossRef Full Text | Google Scholar

Keviczky, T., and Balas, G. (2005). “Flight test of a receding horizon controller for autonomous UAV guidance,” in Proceedings of the 2005, American control conference (Portland, OR, USA: IEEE), 3518–3523.

Google Scholar

Khatib, O. (1985). “Real-time obstacle avoidance for manipulators and mobile robots,” in Proceedings. 1985 IEEE international conference on robotics and automation (St. Louis, MO, United States: Journal Abbreviation: Proceedings.), 2, 500–505.

Google Scholar

Kochenderfer, M. J., Holland, J. E., and Chryssanthacopoulos, J. P. (2012). Next-generation airborne collision avoidance system. Linc. LABORATORY J. 17-33, 17.

Google Scholar

Kuwata, Y., and How, J. (2004). “Three dimensional receding horizon control for UAVs,” in AIAA guidance, navigation, and control conference and exhibit (American Institute of Aeronautics and Astronautics). Providence, Rhode Island.

CrossRef Full Text | Google Scholar

Liu, Y., and Zhao, Y. (2016). “A virtual-waypoint based artificial potential field method for UAV path planning,” in 2016 IEEE Chinese guidance, navigation and control conference (CGNCC) (Nanjing, China: Journal Abbreviation), 949–953.

CrossRef Full Text | Google Scholar

McNally, D., Engelland, S., Bach, R., Chan, W., Brasil, C., Gong, C., et al. (2001). “Operational evaluation of the direct-to controller tool,” in USA FAA air traffic management R&D seminar (Santa Fe, NM, Unites States: FAA/EUROCONTROL), 14.

Google Scholar

Meek, D., and Walton, D. (1992). Clothoid spline transition spirals. Math. Comput. 59 (199), 117–133. doi:10.1090/s0025-5718-1992-1134736-8

CrossRef Full Text | Google Scholar

Mehdi, S. B., Choe, R., Cichella, V., Hovakimyan, N., and Kissimmee, Florida (2015). “Collision avoidance through path replanning using bézier curves,” in AIAA guidance, navigation, and control conference (American Institute of Aeronautics and Astronautics).

CrossRef Full Text | Google Scholar

Moon, H., Martinez-Carranza, J., Cieslewski, T., Faessler, M., Falanga, D., Simovic, A., et al. (2019). Challenges and implemented technologies used in autonomous drone racing. Intell. Serv. Robot. 12, 137–148. doi:10.1007/s11370-018-00271-6

CrossRef Full Text | Google Scholar

Owen, M., Beard, R. W., and McLain, T. W. (2015). Implementing dubins airplane paths on fixed-wing UAVs,” In Handbook of unmanned aerial vehicles. K. P. Valavanis, and G. J. Vachtsevanos, (Dordrecht: Springer Netherlands), 1677–1701.

CrossRef Full Text | Google Scholar

Park, S., Deyst, J., and How, J. (2004). “A new nonlinear guidance logic for trajectory tracking,” in AIAA guidance, navigation, and control conference and exhibit (Providence, Rhode Island: American Institute of Aeronautics and Astronautics).

CrossRef Full Text | Google Scholar

Pastor, E., Pérez-Batlle, M., Barrado, C., Royo, P., and Cuadrado, R. (2018). A macroscopic performance analysis of NASA’s northrop grumman RQ-4A. Aerospace 5 (6). doi:10.3390/aerospace5010006

CrossRef Full Text | Google Scholar

Powell, M. J. D. (1978). A fast algorithm for nonlinearly constrained optimization calculations. in Numerical analysis. G. A. Watson, (Berlin, Heidelberg: Springer Berlin Heidelberg). Series Title: Lecture Notes in Mathematics, 144–157.

CrossRef Full Text | Google Scholar

Powell, M. (1978). The convergence of variable metric methods for nonlinearly constrained optimization calculations. Nonlinear Program. 3, 27–63.

CrossRef Full Text | Google Scholar

Scheuer, A., and Fraichard, T. (2000). Continuous-curvature path planning for car-like vehicles,” in Proceedings of the 1997 IEEE/RSJ international conference on intelligent robot and systems. Innovative robotics for real-world applications (Grenoble, France: IROS ’97), 2, 997–1003.

Google Scholar

Scheuer, A., and Fraichard, T. (2000). Planning continuous-curvature paths for car-like robots. In Proceedings of IEEE/RSJ international conference on intelligent robots and systems. 33. Osaka, Japan: IROS ’96, 1304–1311.

Google Scholar

Scheuer, A., and Laugier, C. (1998). “Planning sub-optimal and continuous-curvature paths for car-like robots,” in Proceedings. 1998 IEEE/RSJ international conference on intelligent robots and systems. Innovations in theory, practice and applications (cat. No.98CH36190) (Victoria, BC, Canada: IEEE), 1, 25–31.)

Google Scholar

Schouwenaars, T., How, J., and Feron, E. (2004). “Receding horizon path planning with implicit safety guarantees,” in Proceedings of the 2004 American control conference (Boston, MA, USA: IEEE), 6, 5576–5581.

CrossRef Full Text | Google Scholar

Stacy, N., Craig, D., Staromlynska, J., Smith, R., and Ont, (2002).The Global Hawk UAV Australian deployment: Imaging radar sensor modifications and employment for maritime surveillance. In IEEE international geoscience and remote sensing symposium, (Toronto, Canada; IEEE), 699–701.

Google Scholar

Techy, L., Woolsey, C. A., Morgansen, K. A., and Anchorage, A. K. (2010). “Planar path planning for flight vehicles in wind with turn rate and acceleration bounds,” in 2010 IEEE international conference on robotics and automation (IEEE), 3240–3245.

CrossRef Full Text | Google Scholar

U.S. Department of Transportation Federal Aviation Administration (). Advisory circular, 120-91A. Tech. Rep.

Weintraub, I. E., Demers, Z. J. L., Shroyer, J., Ritsema, N. P., and Sluss, D. P. (2020). “Circular rejoin in 3D using bézier paths,” in 2020 IEEE conference on control technology and applications (CCTA) (Montreal, QC, Canada: IEEE), 600–605.

CrossRef Full Text | Google Scholar

Wilde, D. K. (2009). “Computing clothoid segments for trajectory generation,” in 2009 IEEE/RSJ international conference on intelligent robots and systems (St. Louis, MO, USA: IEEE), 2440–2445.

CrossRef Full Text | Google Scholar

Zhuang, Y., Sharma, S., Subudhi, B., Huang, H., and Wan, J. (2016). Efficient collision-free path planning for autonomous underwater vehicles in dynamic environments with a hybrid optimization algorithm. Ocean. Eng. 127, 190–199. doi:10.1016/j.oceaneng.2016.09.040

CrossRef Full Text | Google Scholar