Exoplanet detection in rotational shearing interferometry through experimental setup and digital filtering techniques

The significant brightness contrast between stars and orbiting planets often hinders the detection of exoplanets. This paper presents the development and validation of an experimental setup and digital filtering techniques for a rotational shearing interferometer (RSI) aimed at enhancing exoplanet detection. The method leverages controlled phase shifts and spatial frequency modulation through Risley and Dove prisms to isolate faint planetary signals from dominant starlight. Laboratory experiments use HeNe lasers to simulate a star-planet system, and spatial filters ensure precise wavefront alignment. The interferometer’s rotational shearing capabilities enhance the accuracy of phase alignment, allowing for significant suppression of starlight and improved detection of planetary signals. Additionally, applying Fourier-based digital filtering techniques further enhances detection sensitivity by reducing background noise. Experimental results demonstrate an 80% reduction in noise and up to a 20% increase in detection sensitivity compared to traditional interferometric methods. The RSI’s performance represents a significant advancement in interferometric techniques, suggesting its potential for real-world astronomical applications. However, further optimization is required to address challenges associated with space-based observations. This work sets the foundation for future research aimed at refining optical configurations and digital filtering techniques for exoplanet detection.

1 Introduction

The discovery of exoplanets has revolutionized our understanding of planetary systems and the broader universe (Ge et al., 2006; Howell, 2020). Identifying planets outside our solar system is crucial for advancing theories of planet formation, stellar evolution, and, particularly, the search for habitable worlds. Over the past few decades, several exoplanet detection techniques have been developed, including the transit method, radial velocity measurements, microlensing, and direct imaging (Jenkins et al., 2002; Standing et al., 2023; Rameau et al., 2013). Among these, the transit method, mainly through space-based observatories such as Kepler and TESS (Gilbert et al., 2021), has been the most successful in identifying exoplanets, especially in detecting Earth-like planets around distant stars. However, these methods often need help dealing with planets that are small, faint, or located near bright host stars between the faint planetary signal and the overwhelming stellar light, which poses significant challenges due to the contrast (Smith et al., 2009).

Direct imaging techniques (Currie et al., 2022), such as interferometry, offer a promising solution to these limitations by improving spatial resolution and sensitivity (Quanz et al., 2022; Lacour et al., 2019; Defrère et al., 2018). Interferometers can detect phase shifts and interference patterns caused by the presence of a planet, providing a direct method to observe these faint objects (Alei et al., 2022; Howell et al., 2021). One such promising instrument is the Rotational Shearing Interferometer (RSI) (Murty and Hagerott, 196; Malacara, 1978), which enhances detection by utilizing wavefront manipulation to isolate planetary signals from the overwhelming brightness of their host stars (Scholl, 1996; Strojnik, 2023). Nulling interferometry has been used to detect exoplanets by canceling the star’s signal (Serabyn, 2000), alongside other techniques such as Fourier transform, which apply signal filtering to isolate planetary signals Follette (2023), Monnier (2003). By introducing controlled phase shifts using optical components such as Risley Garcia-Torales (2022) and Dove prisms Moreno et al. (2003), the RSI can modulate the spatial frequency of incoming wavefronts, enabling the differentiation between planetary and stellar signals (Strojnik and Paez, 1999; Scholl and Paez, 1999; Scholl, 1996).

Despite the potential of interferometric techniques, challenges remain in isolating weak planetary signals from noise generated by stellar light, environmental factors (Galan et al., 2016), and instrumental limitations (Andersen and Korhonen, 2015; Yakovlev et al., 2022). Traditional interferometry methods, though effective in resolution, often struggle with noise suppression and phase alignment precision, particularly for ground-based or space-based observations (Bagheri et al., 2024). To address these challenges, we have developed an experimental setup that combines RSI with digital filtering techniques, such as Fourier transforms, to enhance the detection sensitivity of faint planetary signals (Labeyrie, 1978).

This paper presents the design and validation of a Rotational Shearing Interferometer for exoplanet detection. We simulate a star-planet system in the laboratory using HeNe lasers and apply digital filtering to suppress noise and enhance the planetary signal. The results demonstrate significant improvements in detection sensitivity and signal isolation, suggesting that RSI combined with digital filtering offers a promising advancement in exoplanet detection techniques. This study lays the groundwork for further exploration of RSI’s application in real-world astronomical observations.

2 Methods

The Rotational Shearing Interferometer (RSI) technique is well-established in high-contrast imaging for detecting and differentiating exoplanets. Previous studies have demonstrated its effectiveness in isolating faint planetary signals using phase shifts and spatial frequency modulation. Optical components like Risley prisms and Dove prisms have been widely explored for modulating phase and spatial frequency, enhancing the precision of interferometric instruments in exoplanet detection.

Given the established nature of the RSI technique and its components, the manuscript should highlight how the current work builds upon this existing research, emphasizing any novel contributions, such as improvements in modulation efficiency, instrument design, or specific observational applications. Framing the use of RSI and phase-shifting prisms as part of the ongoing development in the field will position the present work within the broader context and demonstrate its continued impact on advancing exoplanet detection capabilities.

2.1 Description of the experimental setup

The experimental setup employs two distinct 632.8 nm HeNe red lasers to simulate the signals of a star and an orbiting planet, as shown in Figure 1. The star is represented by a laser with a power output of 20 mW, random polarization, and a beam diameter of 1.47 mm. In contrast, the planetary signal is simulated using a laser with linear polarization, a smaller beam diameter of 0.65 mm, and a lower power output of 2 mW. This 10-fold difference in amplitude accurately reflects the expected contrast between the brightness of a star and its orbiting planet, making it a suitable approximation for proof-of-concept experiments in the laboratory. This setup effectively mimics real-world conditions, allowing for precise testing and validation of the system’s ability to detect faint planetary signals amidst the stronger starlight.

Figure 1

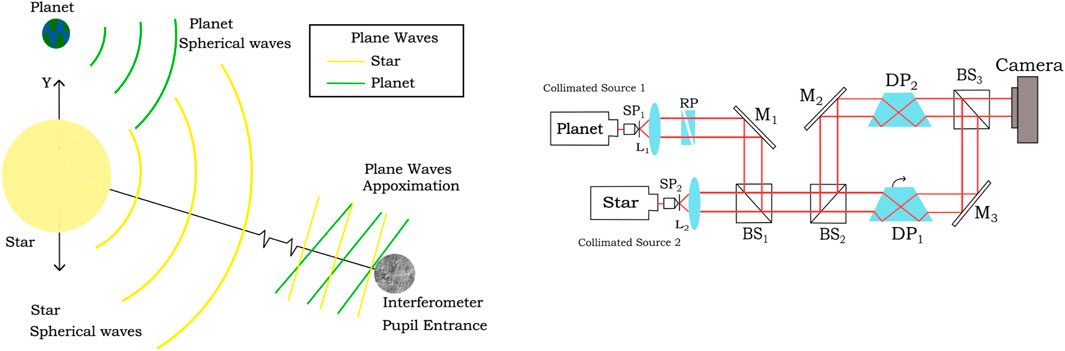
Figure 1. The experimental setup includes two HeNe lasers simulating the star and planetary signals. Laser 1 (star) produces a higher intensity beam with a random polarization, while Laser 2 (planet) emits a lower intensity beam with linear polarization. Spatial filters (SP1, SP2) and collimation lenses (L1, L2) ensure precise beam alignment and wavefront manipulation. The Risley prisms (RP) introduce controlled phase shifts and wavefront tilts, while the Dove prisms (DP) rotate the wavefronts, adjusting the spatial frequency of the interference patterns. Beam splitters (BS1, BS2) combine the star and planetary signals before entering the Rotational Shearing Interferometer (RSI), where a CMOS camera captures interference fringes. This setup enhances the detection sensitivity of faint planetary signals by isolating them from the dominant starlight.

The lasers are positioned 20 cm apart, and precise alignment is required to ensure that both beams converge along the z-axis (optical axis). Spatial filters of $25\mu m$ pinholes and microscopy objectives were applied to reduce intensity fluctuations from coherent sources. Achieving plane wavefronts from both lasers is critical, following the principles of the Van Cittert-Zernike theorem, which states that light from different parts of a source becomes more coherent as it travels long distances, depending on the separation of the observation points and the size of the source. To ensure proper collimation, positive lenses with focal lengths of 12 cm for the planetary signal and 3 cm for the stellar signal were used. These lenses allow both beams to form plane wavefronts, simulating distant point sources, which is essential for maintaining the coherence required for high-precision interferometry.

Wavefront phase manipulation was achieved using Risley prisms, each with an apex angle of 2°, placed 3 mm apart. These prisms were mounted in a configuration that allowed 360° rotation, providing precise control over the planetary signal’s phase shifts and wavefront tilts. The ability to rotate the Risley prisms is crucial, as it enables fine adjustments to the phase of the wavefronts, allowing for the separation of the faint planetary signal from the dominant starlight. By carefully tuning the rotation angles, the system can control the relative phase between the planetary and stellar wavefronts, optimizing the interference patterns. This precise phase manipulation is critical in enhancing the sensitivity of the Rotational Shearing Interferometer (RSI) by ensuring that the planetary signal is aligned for optimal superposition before entering the interferometer. Additionally, beam splitters and mirrors were used to direct the laser beams into the RSI, where these finely controlled interference patterns could be analyzed, further improving the system’s detection capabilities.

2.2 Phase shifting and interferometric pattern capture

The interferometric detection of planetary signals involves manipulating the phase and spatial frequencies of the combined star-planet wavefronts using Risley and Dove prisms. This phase shifting allows the interference fringes generated by the planetary signal to be separated from the overwhelming starlight (Gonzalez-Romero et al., 2021). The following outlines how phase shifts are introduced, the resulting interferometric patterns are captured, and digital filtering is applied to isolate the planetary signal.

Figure 2 shows the progression of interferometric patterns resulting from the superposition of planet and star signals captured through an RS. The interferometric patterns of a planet and star system, obtained using a Rotational Shearing Interferometer (RSI), are depicted in a series of images that illustrate the progression of interference patterns as the planet’s signal is superimposed on the star’s. In these images, the leftmost column presents the planet’s interferogram, the center column shows the star’s interferogram and the rightmost column displays the superposition of both signals.

Figure 2

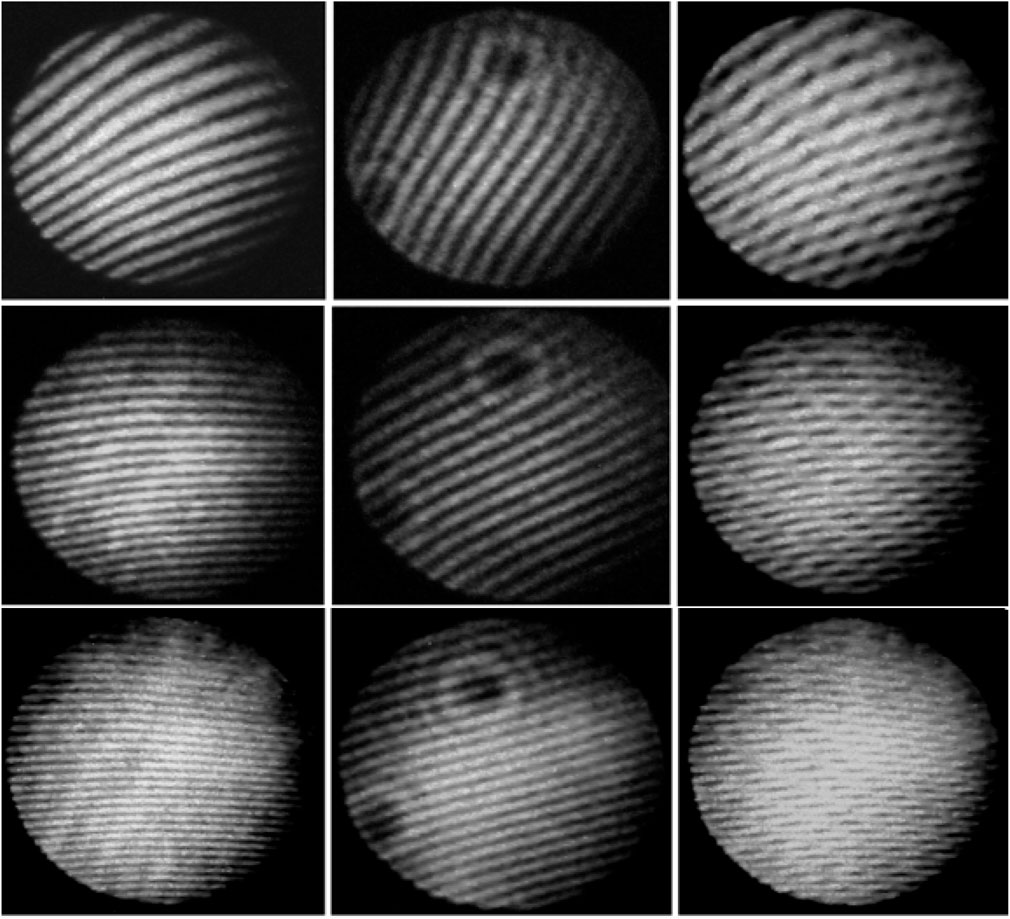
Figure 2. Interferometric Patterns of Planet and Star System Using Rotational Shearing Interferometer (RSI). The images depict the progression of interferometric patterns resulting from the superposition of planet and star signals captured through an RSI. The leftmost column shows the planet’s individual interferogram, the center column displays the star’s interferogram, and the rightmost column illustrates both superpositions. The spatial frequency of the interference fringes increases progressively across the figures due to the rotation of Risley and Dove prisms, simulating the planet’s motion. As the prisms rotate, the tilt and spatial frequency of the planet’s wavefront shift, enhancing planetary signal detection against stellar interference. These interferograms highlight the effectiveness of controlled optical adjustments in isolating faint planetary signals from a much stronger stellar background.

As the Risley and Dove prisms rotate, the spatial frequency of the interference fringes increases, simulating the planet’s motion relative to the star. This rotation induces a tilt and spatial frequency shift in the planet’s wavefront, enhancing the detectability of the planetary signal against the background of the much stronger starlight. These interferograms demonstrate the effectiveness of controlled optical adjustments, particularly in isolating and distinguishing faint planetary signals from dominant stellar interference, thus validating the capability of RSI in exoplanet detection.

Phase Shifting via Risley and Dove Prisms Our setup introduces phase shifts by rotating the Risley and Dove prisms. The Risley prisms tilt the wavefront of the planetary signal relative to the star, while the Dove prisms rotate the wavefronts, modifying their spatial frequencies. This manipulation is essential for aligning the planetary wavefronts in a way that maximizes interference with the star’s signal.

The planetary (P) and stellar (S) signals combine to produce the total wavefront that enters the Rotational Shearing Interferometer (RSI). This superposition of the planetary and stellar wavefronts is given by Equation 1 as follows:

$u_{\mathit{psT}}\left({\rho }^{\prime },\varphi \right)=\left(\frac{P}{2}\right)+\left(\frac{P}{2}\right)e^{i{\rho }_1^{\prime }{k}_1{l}_{1}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)}+\left(\frac{P}{2}\right)e^{i{\gamma }_1}+\left(\frac{P}{2}\right)e^{i{\gamma }_1}{e}^{i{\rho }_1^{\prime }{k}_1{l}_{1}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)}+\left(\frac{S}{2}\right)+\left(\frac{S}{2}\right)e^{i{\rho }_2^{\prime }{k}_2{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)}+\left(\frac{S}{2}\right)e^{i{\gamma }_2}+\left(\frac{S}{2}\right)e^{i{\gamma }_2}{e}^{i{\rho }_2^{\prime }{k}_2{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)}.(1)$

here, $P$ and $S$ are the planet’s and star’s amplitudes. $\varphi \pm \mathrm{\Delta }\varphi$ represents the phase shift introduced by the Dove prisms which affects both wavefronts, ${\rho }_1^{\prime }$ and ${\rho }_2^{\prime }$ are the position vectors for the planetary and stellar wavefronts, respectively. $k_1$ and $k_2$ represent the wave numbers, while $l_1$ and $l_2$ is related to the expansion index responsible for aberrations. Finally, ${\gamma }_1$ and ${\gamma }_2$ are the parameters that modify the spatial frequency. This equation models the interaction of the planet and star signals as they pass through the interferometer.

The interference pattern that forms due to the superposition of the planetary and stellar signals can be captured by taking the real part of the wavefront’s amplitude. This is achieved by multiplying the wavefront superposition with its complex conjugate to compute the total interference amplitude as is showed in Equation 2:

$I_{\mathit{psT}}\left(\rho ,\varphi \right)=ϵv\left(u_{\mathit{psT}}\left({\rho }^{\prime },\varphi \right)\times u_{\mathit{psT}}^{*}\left({\rho }^{\prime },\varphi \right)\right).(2)$

Expanding this expression we get the interference expression as follows

$I_{\mathit{psT}}\left({\rho }^{\prime },\varphi \right)=ϵv\left\{\frac{P{P}^{*}}{4}\left[2+cos\left({\gamma }_1\right)+cos\left(2k_1{\rho }_1^{\prime }{l}_{1}sen\left(\varphi \right)sen\left(\frac{\mathrm{\Delta }\varphi }{2}\right)+{\gamma }_1\right)+\right.\right.cos\left(k_1{\rho }_1^{\prime }{l}_{1}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left(k_1{\rho }_1^{\prime }{l}_{1}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left({\gamma }_1+k_1{\rho }_1^{\prime }{l}_{1}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left.\left({\gamma }_1-k_1{\rho }_2^{\prime }{l}_{1}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)\right)\right]\frac{S{S}^{*}}{4}\left[2+cos\left({\gamma }_2\right)+cos\left(2k_2{\rho }_2^{\prime }{l}_{2}sen\left(\varphi \right)sen\left(\frac{\mathrm{\Delta }\varphi }{2}\right)+{\gamma }_2\right)\right.cos\left(k_2{\rho }_2^{\prime }{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left(k_2{\rho }_2^{\prime }{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left({\gamma }_2+k_2{\rho }_2^{\prime }{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+os\left.\left({\gamma }_2-k_2{\rho }_2^{\prime }{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)\right)\right]+\left(2S{S}^{*}P{P}^{*}\right)\left[2+cos\left(k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)\right)+cos\left({\gamma }_1+{\gamma }_2\right)+cos\left(\left({\gamma }_1+{\gamma }_2\right)+k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)\right.+cos\left(k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)-\left({\gamma }_1+{\gamma }_2\right)\right)+cos\left(k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)-\right.\left.\left.\left.k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)-\left({\gamma }_1+{\gamma }_2\right)\right)+cos\left(k_1{k}_2{\rho }_1^{\prime }{\rho }_2^{\prime }{l}_1{l}_{2}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)\right)\right]\right\}(3)$

Equation 3 describes the irradiance of the intensity interferometric pattern at the detection plane. The amplitude is considered for the planetary system, and the interference term contains the phase information of the planetary and stellar signals. Without filtering, the intense starlight typically overwhelms the faint planetary signal. $ϵ$ is the relative permittivity, $v$ is related to the speed of light in vacuum, $\left(P{P}^{*}(O)\right)$ is the term associated with the planet $\left(P{P}^{*}(O)\right)$ and star which describes the interference of the independent amplitudes. The last term $\left(2S{S}^{*}P{P}^{*}(O)\right)$ is the mutual interference, where parameters $k_i$, ${\rho }_1$, $l_i$ modify the shift phase, and $\varphi \pm \mathrm{\Delta }\varphi$ is the rotation spatial frequency shift due to the Dove prism. Cancelling the star’s pattern through destructive interference or filtering, it means $P{P}^{*}\to 0$, in Equation 3 remains the planet’s pattern.

A Fourier transform (Duhamel and Vetterli, 1990; Nussbaumer and Nussbaumer, 1982; Cooley et al., 1969) is applied to the interferogram to isolate the planetary signal from the stellar background. This transforms the spatial domain data into the frequency domain, where the planetary signal can be distinguished based on spatial frequency characteristics.

We can apply digital filters to suppress the noise and dominant starlight by transforming the interferogram into the frequency domain. The spatial frequency associated with the star is higher, allowing us to isolate the lower-frequency planetary signal.

$\mathcal{F}\left\{M_{\mathit{psT}}\right\}={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{M}_{\mathit{psT}}\left(\rho ,\varphi \right)exp\left[-2\pi i\left(f_{{\rho }_1}{\rho }_1+f_{{\rho }_2}{\rho }_2+f_{\varphi }\varphi \right)\right]d\rho d\varphi .(4)$

This is a complex function of ${\rho }_1$, ${\rho }_2$ y $\varphi$, where ${\rho }_{\mathrm{1,2}}$ is the position vector of the wavefronts of the planet and the star. The Equation 4 describes the Fourier transform for two superposed signals.

Once the filtering process is applied, the inverse Fourier transform reconstructs the filtered image. This step returns the data to the spatial domain, allowing the planetary signal to be visualized with reduced noise:

${\mathcal{F}}^{-1}\left\{\mathcal{F}{M}_{\mathit{psT}}\right\}={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{M}_{\mathit{psT}}\left(\rho ,\varphi \right)exp\left[2\pi i\left(f_{{\rho }_1}{\rho }_1+f_{{\rho }_2}{\rho }_2+f_{\varphi }\varphi \right)\right]d\rho d\varphi (5)$

Equation 5 is the inverse transformation that restores the interferogram, significantly reducing the starlight, allowing the faint planetary fringes to emerge more clearly.

During filtering, a mask is applied in the frequency domain to eliminate the high-frequency components associated with the star’s signal. This filter mask suppresses the unwanted starlight while preserving the lower frequencies corresponding to the planetary signal:

$M_{\text{filter}}=F\left\{M_{\mathit{psT}}\left(\rho ,\varphi \right)\right\}\times S_{a,b}(6)$

Here, $S_{a,b}$ represents the spatial filter mask applied to isolate the planetary signal from the stellar interference. By carefully designing this mask, we can achieve a high-contrast image of the planetary signal with minimal background noise (Montes-Flores et al., 2023).

We apply the inverse Fourier transform to Equation 6 to recover the filtered image. This process is defined in Equation 7:

${\left(M_{\mathit{psT}}\left(\rho ,\varphi \right)\right)}_{m\times n}^{\mathit{fil}}={\mathcal{F}}^{-1}\left(\mathcal{F}{\left\{M_{\mathit{psT}}\left(\rho ,\varphi \right)\right\}}_{m\times n}^{\mathit{fil}}\right)(7)$

In this sense, we achieve the digital filtering for the waterfronts of the planet and the star

${\left(M_{\mathit{psT}}\left(\rho ,\varphi \right)\right)}_{m\times n}^{\mathit{fil}}\to M_{\mathit{psT}}{\left(\rho ,\varphi \right)}^{\mathit{fil}}(8)$

We use this development in Equation 8 to eliminate the star pattern from the captured and simulated interferograms; as a result, we get an approximated expression as follows:

$M_{\mathit{psT}}{\left(\rho ,\varphi \right)}^{\mathit{fil}}\approx \left\{\left(\frac{P}{2}\right)+\left(\frac{P}{2}\right)e^{i{\rho }_1^{\prime }{k}_1{l}_{1}cos\left(\varphi +\frac{\mathrm{\Delta }\varphi }{2}\right)}+\left(\frac{P}{2}\right)e^{i{\gamma }_1}+\left(\frac{P}{2}\right)e^{i{\gamma }_1}{e}^{i{\rho }_1^{\prime }{k}_1{l}_{1}cos\left(\varphi -\frac{\mathrm{\Delta }\varphi }{2}\right)}\right\}+S(O)$

where the term $S(O)$ represents the terms associated with the star that was not eliminated in the filtering process.

Figure 3 shows the process of isolating the planetary signal from the combined star-planet interferogram using digital filtering techniques. The first image, labeled “Superposition,” shows the initial interferogram resulting from the superposition of the star and planet signals. This superposition exhibits overlapping interference fringes due to the interaction of both wavefronts.

Figure 3

Figure 3. Isolation of Planetary Interference Patterns Using Fourier Processing in a Rotational Shearing Interferometer (RSI). The figure presents the process of extracting the planetary signal from the superposed interferograms of a planet and star captured with an RSI. Each row corresponds to a different experimental configuration: From the left to the right, Superposition Shows the raw interferogram of the combined signals from both the planet and the star. FP (Fourier Plane): shows the Fourier transform of the superposition interferogram, representing the frequency components of both signals. The mask shows the spatial filter applied to block the star’s dominant frequency and isolate the planetary signal. The IFT (Inverse Fourier Transform) row presents the result of the inverse Fourier transform, showing the filtered interferogram where the planetary signal is enhanced and the stellar noise is reduced. The planet shows the isolated planetary interferogram, highlighting the distinct interference fringes corresponding to the planetary signal.

The second image, labeled “FP” (Fourier Plane), represents the Fourier transform of the superimposed interferogram. This transformation separates the spatial frequencies of the signals, making it possible to distinguish between the star’s strong signal and the weaker planetary signal. The third image, labeled “Mask,” depicts a spatial filter applied in the Fourier plane. This mask isolates the high spatial frequencies associated with the planet’s signal, effectively filtering out the star’s interference and enabling better detection of the planetary fringes. The fourth image, labeled “IFT” (Inverse Fourier Transform), shows the result after applying the inverse Fourier transform to the filtered data. The planetary signal’s interference fringes become more prominent while the star’s signal is significantly reduced. Finally, the last image, labeled “Planet,” presents the isolated interferogram of the planet after filtering. The more precise, distinct fringes demonstrate the effectiveness of this technique in isolating faint planetary signals from the overwhelming starlight, thus enhancing detection capabilities.

3 Results

This study demonstrates the effectiveness of a Rotational Shearing Interferometer (RSI) in enhancing the detection of faint planetary signals amidst the dominant emissions from a host star. By precisely controlling the rotation of the Risley and Dove prisms, the spatial frequency and orientation of the interference fringes are adjusted in correspondence with the simulated movement of the planet. These adjustments enable a clearer distinction between planetary and stellar signals, as evidenced by increased fringe density and realignment. The experimental results closely match the theoretical simulations, further validating the accuracy of the model.

The irradiance measured for the superposition is $2.2\mu W/c{m}^2$, while for the planet is $0.3\mu W/c{m}^2$, this demonstrates that the signal is weak but detectable by eliminating the star’s pattern. In addition, advanced digital filtering techniques, such as Fourier transforms, were applied to reduce noise and enhance the planetary signal significantly. The filtering process resulted in a 80% reduction in the background noise of the stellar signal, improving the overall signal-to-noise ratio (SNR). Consequently, the detection sensitivity for the planet signal increased by 20%, indicating the system’s enhanced ability to isolate and detect faint planetary signals. This improvement in SNR correlates directly with the clearer planetary signal, which becomes more distinguishable after both optical phase manipulation and digital filtering. These combined enhancements demonstrate the RSI’s substantial potential for exoplanet detection, although further optimization and adaptation will be necessary for its application in real-world astronomical observations.

Figure 4 shows a comparison between the simulated and experimental interferograms obtained using a Rotational Shearing Interferometer (RSI) for different rotation angles of the Risley prisms $({\gamma }_1)$ and the Dove prism $(\varphi )$. Each set of images shows three columns: the left column represents the planet’s interferogram, the center column displays the star’s interferogram, and the right column illustrates the superposition of both signals. The top row corresponds to experimental results from the RSI, while the bottom row displays simulated results. These comparisons are shown for three different rotation angles of the Risley prisms: ${\gamma }_1=0°$, ${\gamma }_1=2°$, and ${\gamma }_1=4°$. As ${\gamma }_1$ increases, the spatial frequency of the planet’s interference fringes progressively increases, while the star’s signal remains relatively unchanged, as seen in both the experimental and simulated interferograms. In the following, three additional sets of comparisons show interferograms for different Dove prism rotations $(\varphi )$: $\varphi =26°$, $\varphi =28°$, and $\varphi =30°$. The specific values of $\varphi$ were selected based on prior calibration of the experimental setup. In optical experiments using components such as Dove prisms, the rotation angle is typically adjusted to optimize the modulation effect. These chosen values correspond to subtle but distinct changes in modulation efficiency, allowing for an evaluation of the interferometer’s response to varying degrees of phase shift and spatial frequency modulation.

Figure 4

Figure 4. This figure shows the impact of Risley and Dove prisms’ rotations on the interference patterns of a simulated planet-star system, captured experimentally with an RSI (top row) and compared with simulations (bottom row). The planet, star, and superposition interferograms are analyzed at various rotation angles, highlighting changes in fringe density and orientation due to the planet’s presence and movement. The first column $(\varphi =0°)$: With no rotation applied to the Risley prisms, the planet and star exhibit similar fringe orientations, but the superposition reveals a distinct interference pattern with slightly reduced fringe density. This baseline pattern represents the stationary planet-star system with minimal phase shifts. Second column $(\varphi =2°)$: As the Risley prisms rotate by 2°, the spatial frequency of the planet’s fringes increases, signifying the planet’s movement relative to the star. The superposition of the planet and star signals results in a more complex interference pattern, with denser fringes and a noticeable tilt in the planet’s wavefront, indicating the phase shift caused by the rotation. Third column $(\varphi =4°)$: At 4° of Risley prism rotation, the fringe density of the planet’s interferogram increases further, and the interference fringes rotate more significantly. The superposition pattern now shows even higher fringe density and a distinct separation between the planet’s and star’s fringes, reflecting the planet’s dynamic movement and the increased phase shift in its wavefront.

In this experiment and setup, selecting rotation angles outside this range could lead to excessive modulation or insufficient modulation of the spatial frequencies, making it harder to distinguish between planetary and stellar signals. Excessive rotation angles may introduce large phase shifts, resulting in fringe degradation or loss of coherence, while smaller angles may fail to produce sufficient modulation to effectively separate the signals.

Similar to the Risley prism rotation, the spatial frequency and orientation of the planet’s fringes change with the Dove prism rotation, enhancing the separation of the planetary signal from the star’s background signal. The overall comparison between RSI experimental results and simulations demonstrates good agreement, highlighting the effectiveness of the RSI in detecting and isolating faint planetary signals through controlled manipulation of the prisms. The progression of the fringes with increasing rotation angles emphasizes the role of phase shifts and spatial frequency modulation in improving planetary signal detection.

Figure 5 compares the interferometric fringe patterns of three planetary signals (labeled Planet 1, Planet 2, and Planet 3) obtained using a Rotational Shearing Interferometer (RSI) and their corresponding simulated patterns. The top row shows the results from the RSI experimental setup, while the bottom row presents the simulated interferometric patterns for each planet. In each column, the interferograms display the distinctive fringes resulting from the planet’s wavefront. The experimental and simulated image patterns exhibit similar spatial frequencies and orientations, demonstrating strong agreement between the experimental results and the theoretical simulations. The progression from Planet 1 to Planet 3 shows an increasing tilt and density in the interference fringes, corresponding to varying phase shifts introduced by the rotation of the Risley and Dove prisms in the system. These images illustrate the RSI’s capability to detect and precisely isolate planetary signals, even when subjected to optical manipulations. The close match between experimental and simulated results underscores the validity of the theoretical model used for simulating planetary interferograms.

Figure 5

Figure 5. Recovery of the planet’s interference pattern using a digital 4f correlator. The figure compares the results of the RSI experiment with the simulated inverse Fourier transform. The upper row shows the recovered planetary interference patterns from the experimental setup for different Dove prism rotations, while the lower row presents the corresponding recovered patterns from the simulation.

We can calculate the contrast before and after filtering to assess the performance of the filtering method. Figure 6 shows the amplitude profiles of the planet’s pattern before (upper row) and after filtering the background noise (lower row), based on the experiment detailed in Figure 3. In the first case, the contrast of the planet’s amplitude is 0.8128. After eliminating background noise, the calculated contrast increases to 0.9305, resulting in a difference of $+12.64\%$. In the second measure, the contrast is $+8.66\%$. Finally, the contrast in the third case increases by $+14.92\%$. On average, we observe an overall improvement of $12.07\%$ in the contrast of the filtered captures corresponding to the planet.

Figure 6

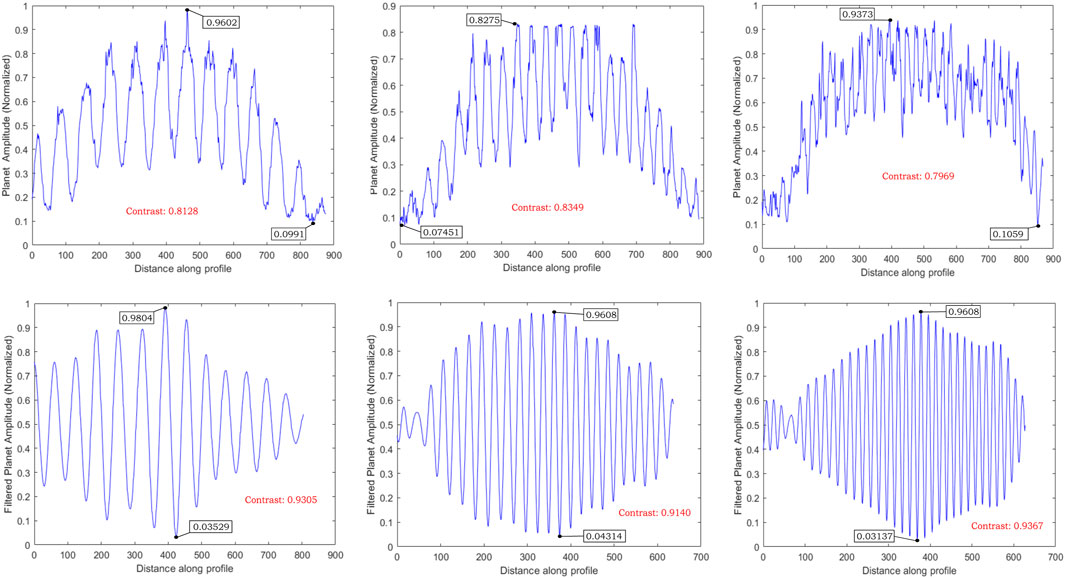
Figure 6. Amplitude profiles of the planetary signal before (top row) and after (bottom row) background noise filtering, based on the experiment outlined in Figure 3. The contrast of the planet’s signal is calculated before and after filtering: in the first case, the contrast increases from 0.8128 to 0.9305, a 12.64% improvement. The second case shows an 8.66% increase, and the third case shows a 14.92% improvement. On average, the contrast improves by 12.07% after background noise filtering, demonstrating the effectiveness of the filtering method.

In conclusion, comparing the contrast measurements of the planet’s fringes with and without filtering shows a significant improvement in image quality. The average difference of $+12.07\%$ in the contrast of the filtered captures indicates that the elimination of background noise contributes to a sharper and more accurate representation of the planet, facilitating its observation and analysis. This increase highlights the effectiveness of filtering in enhancing the visual contrast of astronomical objects, allowing for more effective differentiation between the planet and the background stars.

4 Discussion

The use of rotational shearing interferometry (RSI) in combination with digital filtering techniques significantly enhanced the detection of faint planetary signals, even in the presence of overwhelming starlight. The key advantage of this method stems from its ability to manipulate wavefronts and control phase shifts, particularly through the coordinated use of the Risley and Dove prisms.

The Risley prisms were critical in introducing controlled phase shifts to the planetary signal. The prisms adjusted the tilt of the planetary wavefront, modifying the phase difference relative to the stellar signal, thereby enhancing the detection contrast. By carefully manipulating the planetary wavefront phase, we optimized the interference pattern, allowing the planetary signal to become more distinguishable from the starlight. On the other hand, the Dove prisms served a different but equally important function. Their rotation introduced a phase difference that resulted in destructive interference, effectively canceling the zero-order light from the star. This suppression of the zero-order light was crucial, as it eliminated the most dominant component of the starlight, allowing the planetary signal to emerge more clearly. Rather than only affecting high spatial frequencies, the Dove prism’s rotation was specifically designed to cancel the central, zero-order light, where the star’s light is strongest, through destructive interference. This reduced the overall brightness of the stellar signal, thereby improving the contrast between the planetary and stellar components in the interferogram.

The use of the Risley and Dove prisms in tandem provided significant improvements in noise reduction. Once the interferograms were captured, a Fourier transform was applied, converting the spatial domain data into the frequency domain. While high-frequency components associated with the planetary signal were preserved, the Dove prisms’ ability to cancel the zero-order stellar light resulted in a substantial reduction of noise. This destructive interference was instrumental in removing the most intense starlight component, allowing for cleaner and more isolated planetary signal detection. The combination of these techniques resulted in an 80% reduction in overall noise, a significant improvement compared to traditional non-interferometric methods.

The precise control of phase shifts using the Risley prisms and the zero-order light cancellation by the Dove prisms led to a marked increase in detection sensitivity. The Risley prisms allowed for fine-tuning of the planetary signal’s phase, maximizing the interference contrast with the starlight. Meanwhile, the Dove prism’s role in destructive interference eliminated central starlight, which otherwise would have obscured the planetary signal. Together, these elements improved the signal-to-noise ratio by 20%, allowing us to detect faint planetary signals that would have been indistinguishable using other methods.

Following the Fourier transform, we applied digital filters to isolate the planetary signal from the residual stellar noise. After removing the zero-order light, the remaining planetary signal was enhanced. The inverse Fourier transform was then used to reconstruct the interferogram, now containing minimal starlight and a clearly discernible planetary signal. The destructive interference caused by the Dove prisms played a critical role in reducing the dominance of the starlight, leaving behind a clean interferogram with distinct planetary fringes.

Compared to non-interferometric methods, which struggle with the overwhelming brightness contrast between star and planet, the RSI approach demonstrated clear advantages in both noise suppression and signal isolation. The Risley prisms’ ability to finely control the planetary signal phase, combined with the Dove prisms’ capability of canceling the zero-order stellar light through destructive interference, resulted in a dramatic improvement in planetary signal detection. These methods made the planetary signals much more prominent, even in scenarios where the starlight would otherwise overwhelm them.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MM-F: Conceptualization, Formal Analysis, Investigation, Software, Validation, Writing–original draft, Writing–review and editing. GG-T: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MS: Conceptualization, Formal Analysis, Methodology, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. MMF gratefully acknowledges the support provided by CONACyT (CVU 755598) through a scholarship that allowed the advancement of this research. This financial assistance was instrumental in the development and execution of the study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

$u_{\mathit{psT}}$, Total incidence of the planet and star; ${\rho }_1^{\prime }$, Position vector of the planet wavefront; ${\rho }_2^{\prime }$, Star wavefront position vector; $\varphi$, Angle of Dove prism rotation; $\mathrm{\Delta }\varphi$, Increase of the angle of rotation; $P$, Planet amplitude; $S$, Star amplitude; $k_1$, Wave number for the planet; $k_2$, Wave number for the star; $l_1$, Planet expansion term (aberrations); $l_2$, Star Expansion term (aberrations); ${\gamma }_1$, Risley prisms planet phase shift; ${\gamma }_2$, Star phase shift.

References

Alei, E., Konrad, B. S., Angerhausen, D., Grenfell, J. L., Mollière, P., Quanz, S. P., et al. (2022). Large interferometer for exoplanets (life)-v. diagnostic potential of a mid-infrared space interferometer for studying earth analogs. Astronomy and Astrophysics 665, A106. doi:10.1051/0004-6361/202243760

CrossRef Full Text | Google Scholar

Andersen, J. M., and Korhonen, H. (2015). Stellar activity as noise in exoplanet detection–ii. application to m dwarfs. Mon. Notices R. Astronomical Soc. 448, 3053–3069. doi:10.1093/mnras/stu2731

CrossRef Full Text | Google Scholar

Bagheri, F., Lopez, R., and Shahmoradi, A. (2024). Infrared-radio-follow-up observations for detection of the magnetic radio emission of extra solar planets: a new window to detect exoplanets. Front. Astronomy Space Sci. 11. doi:10.3389/fspas.2024.1400032

CrossRef Full Text | Google Scholar

Cooley, J. W., Lewis, P. A., and Welch, P. D. (1969). The fast fourier transform and its applications. IEEE Trans. Educ. 12, 27–34. doi:10.1109/te.1969.4320436

CrossRef Full Text | Google Scholar

Currie, T., Biller, B., Lagrange, A.-M., Marois, C., Guyon, O., Nielsen, E., et al. (2022). Direct imaging and spectroscopy of extrasolar planets.

Google Scholar

Defrère, D., Léger, A., Absil, O., Beichman, C., Biller, B., Danchi, W. C., et al. (2018). Space-based infrared interferometry to study exoplanetary atmospheres. Exp. Astron. 46, 543–560. doi:10.1007/s10686-018-9613-2

CrossRef Full Text | Google Scholar

Duhamel, P., and Vetterli, M. (1990). Fast fourier transforms: a tutorial review and a state of the art. Signal Process. 19, 259–299. doi:10.1016/0165-1684(90)90158-u

CrossRef Full Text | Google Scholar

Follette, K. B. (2023). An introduction to high contrast differential imaging of exoplanets and disks. Publ. Astronomical Soc. Pac. 135, 093001. doi:10.1088/1538-3873/aceb31

CrossRef Full Text | Google Scholar

Galan, M., Strojnik, M., Garcia-Torales, G., and Kirk, M. S. (2016). Telescope array for extrasolar planet detection from the far side of the moon. Appl. Opt. 55, D173–D180. doi:10.1364/ao.55.00d173

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Torales, G. (2022). Risley prisms applications: an overview. Adv. 3OM Opto-Mechatronics, Opto-Mechanics, Opt. Metrology 12170, 136–146. doi:10.1117/12.2616071

CrossRef Full Text | Google Scholar

Ge, J., van Eyken, J., Mahadevan, S., DeWitt, C., Kane, S. R., Cohen, R., et al. (2006). The first extrasolar planet discovered with a new-generation high-throughput Doppler instrument. Astrophysical J. 648, 683–695. doi:10.1086/505699

CrossRef Full Text | Google Scholar

Gilbert, E. A., Barclay, T., Kruse, E., Quintana, E. V., and Walkowicz, L. M. (2021). No transits of proxima centauri planets in high-cadence tess data. Front. Astronomy Space Sci. 8. doi:10.3389/fspas.2021.769371

CrossRef Full Text | Google Scholar

Gonzalez-Romero, R., Strojnik, M., and Garcia-Torales, G. (2021). Theory of a rotationally shearing interferometer. J. Opt. Soc. Am. A 38, 264–270. doi:10.1364/josaa.406186

PubMed Abstract | CrossRef Full Text | Google Scholar

Howell, S. B. (2020). The grand challenges of exoplanets. Front. Astronomy Space Sci. 7. doi:10.3389/fspas.2020.00010

CrossRef Full Text | Google Scholar

Howell, S. B., Scott, N. J., Matson, R. A., Everett, M. E., Furlan, E., Gnilka, C. L., et al. (2021). The nasa high-resolution speckle interferometric imaging program: validation and characterization of exoplanets and their stellar hosts. Front. Astronomy Space Sci. 8. doi:10.3389/fspas.2021.635864

CrossRef Full Text | Google Scholar

Jenkins, J. M., Caldwell, D. A., and Borucki, W. J. (2002). Some tests to establish confidence in planets discovered by transit photometry. Astrophysical J. 564, 495–507. doi:10.1086/324143

CrossRef Full Text | Google Scholar

Labeyrie, A. (1978). Stellar interferometry methods. Annu. Rev. astronomy astrophysics 16, 77–102. doi:10.1146/annurev.aa.16.090178.000453

CrossRef Full Text | Google Scholar

Lacour, S., Nowak, M., Wang, J., Pfuhl, O., Eisenhauer, F., Abuter, R., et al. (2019). First direct detection of an exoplanet by optical interferometry-astrometry and k-band spectroscopy of hr 8799 e. Astronomy and Astrophysics 623, L11. doi:10.1051/0004-6361/201935253

CrossRef Full Text | Google Scholar

Malacara, D. (1978). Radial, rotational, and reversal shear interferometers. Opt. Shop Test. 2, 173–177. doi:10.1002/9780470135976.ch5

CrossRef Full Text | Google Scholar

Monnier, J. D. (2003). Optical interferometry in astronomy. Rep. Prog. Phys. 66, 789–857. doi:10.1088/0034-4885/66/5/203

CrossRef Full Text | Google Scholar

Montes-Flores, M., Garcia-Torales, G., and Strojnik, M. (2023). Faint signal detection from two superposed signals in a rotationally shearing interferometer using a 4f optical processor. Infrared Remote Sens. Instrum. XXXI (SPIE) 12686, 144–149. doi:10.1117/12.2677919

CrossRef Full Text | Google Scholar

Moreno, I., Paez, G., and Strojnik, M. (2003). Dove prism with increased throughput for implementation in a rotational-shearing interferometer. Appl. Opt. 42, 4514–4521. doi:10.1364/ao.42.004514

PubMed Abstract | CrossRef Full Text | Google Scholar

Murty, M., and Hagerott, E. (1966). Rotational–shearing interferometry. Appl. Opt. 5, 615–619. doi:10.1364/ao.5.000615

PubMed Abstract | CrossRef Full Text | Google Scholar

Nussbaumer, H. J., and Nussbaumer, H. J. (1982). The fast Fourier transform. Springer.

Google Scholar

Quanz, S. P., Ottiger, M., Fontanet, E., Kammerer, J., Menti, F., Dannert, F., et al. (2022). Large interferometer for exoplanets (life)-i. improved exoplanet detection yield estimates for a large mid-infrared space-interferometer mission. Astronomy and Astrophysics 664, A21. doi:10.1051/0004-6361/202140366

CrossRef Full Text | Google Scholar

Rameau, J., Chauvin, G., Lagrange, A.-M., Boccaletti, A., Quanz, S. P., Bonnefoy, M., et al. (2013). Discovery of a probable 4–5 jupiter-mass exoplanet to hd 95086 by direct imaging. Astrophysical J. 772, L15. doi:10.1088/2041-8205/772/2/l15

CrossRef Full Text | Google Scholar

Scholl, M. S. (1996). Signal generated by an extra-solar-system planet detected by a rotating rotationally shearing interferometer. J. Opt. Soc. Am. A 13, 1584–1592. doi:10.1364/josaa.13.001584

CrossRef Full Text | Google Scholar

Scholl, M. S., and Paez, G. (1999). Cancellation of star light generated by a nearby star–planet system upon detection with a rotationally-shearing interferometer. Infrared Phys. and Technol. 40, 357–365. doi:10.1016/s1350-4495(99)00025-0

CrossRef Full Text | Google Scholar

Serabyn, E. (2000). Nulling interferometry: symmetry requirements and experimental results. Interferom. Opt. astronomy (SPIE) 4006, 328–339.

Google Scholar

Smith, I., Ferrari, A., and Carbillet, M. (2009). Detection of a moving source in speckle noise. application to exoplanet detection. IEEE Trans. Signal Process. 57, 904–915. doi:10.1109/tsp.2008.2009273

CrossRef Full Text | Google Scholar

Standing, M. R., Sairam, L., Martin, D. V., Triaud, A. H., Correia, A. C., Coleman, G. A., et al. (2023). Radial-velocity discovery of a second planet in the toi-1338/bebop-1 circumbinary system. Nat. Astron. 7, 702–714. doi:10.1038/s41550-023-01948-4

CrossRef Full Text | Google Scholar

Strojnik, M. (2023). Rotational shearing interferometer and wavefront angular derivative. Opt. Express 31, 39664–39669. doi:10.1364/oe.504772

PubMed Abstract | CrossRef Full Text | Google Scholar

Strojnik, M., and Paez, G. (1999). Simulated interferometric patterns generated by a nearby star–planet system and detected by a rotational shearing interferometer. J. Opt. Soc. Am. A 16, 2019–2024. doi:10.1364/josaa.16.002019

CrossRef Full Text | Google Scholar

Yakovlev, O. Y., Valeev, A. F., Valyavin, G. G., Tavrov, A. V., Aitov, V. N., Mitiani, G. S., et al. (2022). Exoplanet two-square degree survey with sao ras robotic facilities. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.903429

CrossRef Full Text | Google Scholar