Sorting droplets beyond the Rayleigh limit under acoustic-gravity forces: a theoretical approach

The physics of droplets beyond the Rayleigh limit offers a novel acoustic sorting method that is fundamentally different from the techniques applied to sort droplets within the Rayleigh limit. Using this “acoustic sorting beyond Rayleigh limit” method, we theoretically demonstrate that by controlling the frequency $(f)$ and acoustic energy density $(E_{ac})$, smaller droplets can be suspended while larger ones settle against gravity, or larger droplets can be suspended while smaller ones settle. Intriguingly, this method also enables the suspension of intermediate-sized droplets, allowing both smaller and larger droplets to settle simultaneously. Furthermore, acoustic sorting is demonstrated for droplets of identical size but with varying interfacial tensions.

1 Introduction

Acoustophoresis, the manipulation of matter using acoustic fields, has its foundations since the late 18th century (Chladni, 1787; Faraday, 1831; Kundt and Lehmann, 1874). Significant advancements in the theoretical understanding of the acoustic radiation force $({\mathit{F}}_{ac})$ on particles within the Rayleigh limit ($d\ll \lambda$, where $d$ is the droplet diameter and $\lambda$ is the wavelength of the wave) were made by King (1934), Yosioka and Kawasima (1955), and Gor’kov (1962), with Gor’kov providing a simplified framework for calculating this force from the potential function. The acoustic radiation force acting on a particle $(d\ll \lambda )$ subjected to a standing wave along the $y$ direction (pressure $p=p_a\sin (ky)$ is given by,

${\mathit{F}}_{\mathit{a}\mathit{c}}=4\pi r^3{E}_{ac}\phi k\mathrm{s}\mathrm{i}\mathrm{n}\left(2ky\right){\mathit{e}}_{\mathit{y}},(1)$

where $E_{ac}=p_a^2/(4{\rho }_{\mathit{avg}}{c}_{\mathit{avg}}^2)$ is acoustic energy density, $r$ is the droplet radius, $E_{ac}$ is the acoustic energy density, $k=2\pi /\lambda$ is the wavenumber, $e_y$ is the unit vector along the wave direction, and $\phi$ is the contrast factor, which is a function of the density ratio and the compressibility ratio of particle and fluid. The acoustic radiation force (Equation 1) described above has been used to explain the levitation/suspension of particles (Gould and Coakley, 1974; Weiser and Apfel, 1982), droplets (Crum, 1971; Foresti et al., 2013), bubbles (Eller, 1968), and red blood cells (Baker, 1972; Dyson et al., 1971; Coakley et al., 1989) against gravity. In microfluidic systems, this force has enabled the development of two extensively utilized particle (such as beads, biological cells and droplets) sorting methods using acoustic fields (Lenshof et al., 2012; Wu et al., 2019), namely, size-based sorting and contrast factor-based sorting. Contrast factor $(\phi )$ based sorting is achieved when the physical properties of the particles differ, allowing the contrast factor of one particle to be made positive and that of another negative by adjusting the properties of the suspending liquid medium. This results in the particles experiencing opposing forces, with the former being directed toward the pressure node and the latter toward the pressure antinode, enabling their separation. This technique has been employed for separating polyethene particles of different densities (Gupta et al., 1995), isolating lipids from blood (Petersson et al., 2004), sorting encapsulated cells (Nam et al., 2012), separated bacteria from blood cell (Ohlsson et al., 2018), separated cancer cells from WBC (Karthick et al., 2018; Cushing et al., 2018). Size-based sorting, on the other hand, involves exposing two particles of different sizes (but with contrast factors of the same sign) to acoustic fields. The larger particle experiences a stronger acoustic force than the smaller one while moving against the drag force, allowing it to reach the pressure node or antinode more quickly due to its acoustic mobility $(\sim \phi r^2)$. This difference in movement, combined with the timely bifurcation or trifurcation of the outlet fluid streams, allows for effective size-based sorting. This size-based approach has been utilized for separating polystyrene particle mixtures of different sizes (Petersson et al., 2007), isolating blood components such as erythrocytes, leukocytes, and platelets (Shi et al., 2009), and separating cancer cells from blood (Thévoz et al., 2010; Augustsson et al., 2012; Li et al., 2015).

The acoustic radiation force $({\mathit{F}}_{ac})$ has been extended further to account for particles beyond the Rayleigh limit ($d>\sim \lambda$, droplet size greater than or approaching the order of the wavelength) in subsequent studies (Hasegawa, 1979a; Hasegawa, 1979b; Marston, 2017; Baasch and Dual, 2018; Pazos Ospina et al., 2022; Rueckner et al., 2023). These studies demonstrated that the behavior of particles beyond the Rayleigh limit differs significantly from that of particles within the Rayleigh limit. In a recent experimental study, it was shown that the acoustic power or acoustic energy density needed to suspend droplets beyond the Rayleigh limit varies significantly with their size, in contrast to smaller particles, where it remains independent of size (Thirisangu et al., 2023). They have also demonstrated a droplet sorting technique by suspending smaller droplets while allowing larger ones to settle. Following this, Thirisangu et al. (2024b) developed a unified theoretical framework in Eulerian form to examine the behaviour of droplets of arbitrary size subjected to acoustic fields, predicting their experimental observations of droplet migration, deformation, and splitting within microchannels. Extending the theoretical framework above by incorporating gravity, Thirisangu et al. (2024a), theoretically demonstrated that the suspension dynamics of droplets beyond the Rayleigh limit become highly size-dependent and non-monotonous, and could predict the experimental outcomes of droplet suspension observed in Thirisangu et al. (2023).

Building on the theoretical understanding gained from our previous work (Thirisangu et al., 2024a), we present a novel acoustic sorting method for droplets beyond the Rayleigh limit, specifically focusing on selective sorting of droplets across a wide range of sizes, including intermediate sizes. By controlling the wavelength and acoustic energy density, we demonstrate the ability to suspend larger droplets while smaller ones settle, or vice versa. Additionally, we present the methodology for sorting intermediate-sized droplets from a broad size range. Using this method, we further show the ability to sort droplets of the same size but with differing interfacial tensions through droplet splitting. Unlike size-based sorting methods, our approach enables droplets of the selected size to remain suspended, while droplets of other sizes settle indefinitely until the critical acoustic force is applied.

2 Physics of the problem

When immiscible inhomogeneous fluid (water droplet in the mineral oil) is subjected to gravity and acoustic fields as shown in Figure 1, the dynamics is governed by the incompressible mass continuity, momentum conservation, and advection-diffusion equations (Landau and Lifshitz, 1987; Thirisangu et al., 2024a), which are given below,

$\mathbf{\nabla }\cdot \mathit{v}=0,(\mathrm{2a})$

$\begin{array}{c}\hfill \rho \left[{\partial }_t\mathit{v}+\left(\mathit{v}\cdot \mathbf{\nabla }\right)\mathit{v}\right]=-\mathbf{\nabla }p+\eta {\mathbf{\nabla }}^2\mathit{v}+{\mathit{f}}_g+{\mathit{f}}_{\sigma }+{\mathit{f}}_{ac},\end{array}(\mathrm{2b})$

${\partial }_t\varphi +\mathit{v}\cdot \mathbf{\nabla }\varphi =\gamma \mathbf{\nabla }\cdot \left(ϵ\mathbf{\nabla }\varphi -\varphi \left(1-\varphi \right)\frac{\mathbf{\nabla }\mathit{\varphi }}{\left|\mathbf{\nabla }\mathit{\varphi }\right|}\right),(\mathrm{2c})$

where $\rho$ is the density, $\mathit{v}$ is the velocity, $\eta$ is the dynamic viscosity, $p$ is the pressure, $\varphi$ is the phase fraction ($\varphi =0$ for fluid 1 and $\varphi =1$ for fluid 2), and ${\mathit{f}}_g=-\rho g{\mathit{e}}_{\mathit{y}}$ is the gravitational force. ${\mathit{f}}_{\sigma }$ is the interfacial force which is expressed as $\sigma \kappa {\delta }_s\mathbf{n}$, where $\sigma$ is the surface tension, $\kappa$ is the curvature, ${\delta }_s$ is a surface Dirac delta function that becomes non-zero only at the interface between the fluids, and $\mathbf{n}$ is the unit normal. The parameter $ϵ$ defines the width of the transition region where $\varphi$ varies gradually from 0 to 1. To avoid singularities and enhance numerical stability, the droplet interface is modeled as diffusive in the simulations. To improve numerical stability, the parameter $\gamma$ regulates degree of reinitialization or stabilization of the level set function. For the standing acoustic wave applied along the y-direction (fast time scale pressure $p_f=p_a\sin (ky)$ and fast time scale velocity ${\mathit{v}}_f=\frac{p_a}{i{\rho }_0{c}_0}\cos (ky){\mathit{e}}_y$), the acoustic force $({\mathit{f}}_{ac})$ responsible for the movement of the droplets (inhomogeneous liquids) is expressed as follows (Thirisangu et al., 2024a; Thirisangu et al., 2024b),

${\mathit{f}}_{ac}=-2k{E}_{ac}\sin \left(2ky\right)\widehat{Z}{\mathit{e}}_{\mathit{y}}.(3)$

Figure 1

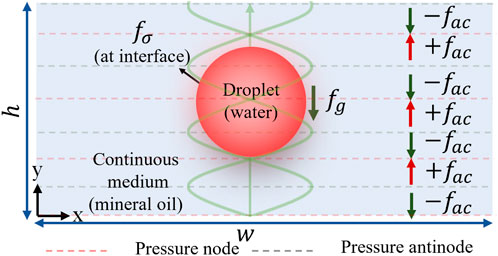
Figure 1. A schematic representation of a droplet with a size beyond the Rayleigh limit ($d>\sim \lambda$, droplet size greater than or approaching the order of wavelength), suspended in a continuous liquid medium under the influence of acoustic and gravity fields within a channel of width “w” and height “h.” A standing acoustic wave with a wavelength of $\lambda$ is established in the y-axis along the height of the channel.

Where $E_{ac}=p_a^2/(4{\rho }_{\mathit{avg}}{c}_{\mathit{avg}}^2)$ is the acoustic energy density, $k=2\pi /\lambda$ is the wavenumber, $p_a$ is the pressure amplitude, $\widehat{Z}=Z/Z_{\mathit{avg}}$ where $Z$ denotes impedance which is the product of density $(\rho )$ and speed of sound $(c)$, $Z_{\mathit{avg}}=(Z_1+Z_2)/2$, ${\rho }_{\mathit{avg}}$ is the average density of the fluids, $c_{\mathit{avg}}$ is the average speed of sound of the fluids and ${\mathit{e}}_y$ is the unit normal vector along the $y$ direction.

3 Numerical implementation

The numerical investigation of droplet behavior under acoustic fields is conducted by solving the governing equations simultaneously. These include the continuity equation (Equation 2a), the momentum equation (Equation 2b), and the advection-diffusion equation (Equation 2c), with the acoustic force equation (Equation 3) incorporated as a body force term. The simulations are performed using COMSOL Multiphysics 6.0, accounting for gravitational and interfacial forces within the computational framework. The interface of the droplet is modeled using phase field module, which are solved alongside the laminar flow equations. A time-dependent study is solved using the Implicit Backward Differentiation Formula. The flow field variables and the phase field variables are solved using the segregated Parallel Direct Solver. A two-dimensional channel with a width $(w)$ of 12 mm and a height $(h)$ of 6 mm is modeled, where a droplet is suspended in a continuous medium. An acoustic wave with wavelength $\lambda$ is applied along the height ($y$-direction) of the channel, while a no-slip boundary condition is imposed on all walls. Due to the closed nature of the domain, a pressure constraint is applied at a single point to stabilize the pressure field. The computational domain is discretized using a total of 804,596 grid elements, with a maximum grid size of 15 microns. Further refinement beyond this resolution does not significantly alter the flow field, as demonstrated in Figure 2. The material properties of the water droplet (${\rho }_{\text{water}}=1000kg/m^3$, $c_{\text{water}}=1480m/s$, and ${\eta }_{\text{water}}=0.8mPa.s$) and mineral oil (${\rho }_{\text{oil}}=857.5kg/m^3$, $c_{\text{oil}}=1440m/s$, and ${\eta }_{\text{oil}}=26.5mPa.s$) are taken from Hemachandran et al. (2019). In Sections 4.1, 4.2, selective sorting of the droplets beyond the Rayleigh limit is studied, when the interfacial force is strong enough to retain the droplet shape, where the following three cases are considered. Case I: Suspending the bigger droplet while settling the smaller droplet. Case II: Suspending the smaller droplet while settling the bigger droplet. Case III: Suspending the intermediate droplet while settling both the smaller and larger droplets. In Section 4.3, the sorting of the droplets, based on the interfacial tension is studied.

Figure 2

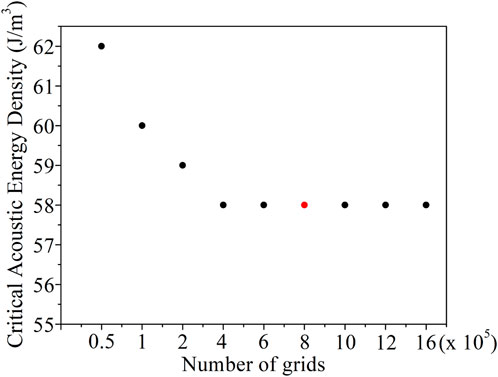
Figure 2. Grid independence analysis: The figure shows the critical acoustic energy density $(E_{cr})$ required to suspend a droplet with a diameter of 1.3 mm. A mesh with 804596 elements ensures grid convergence, as further refinement does not significantly influence the droplet dynamics, confirming grid independence.

4 Results and discussion

When an acoustic field is not present, a higher-density droplet (water) settles in a lower-density continuous medium (mineral oil) due to the balance between gravity and drag forces. In the presence of both gravity $({\mathit{f}}_g)$ and a plane standing acoustic wave field in $y$ direction $({\mathit{f}}_{ac})$, the droplet can either suspend $(f_{ac}\ge f_g)$ or settle $(f_{ac}<f_g)$. In this section, different sorting techniques for droplets beyond the Rayleigh limit $(d>\sim \lambda )$ are presented, using the interplay between acoustic $({\mathit{f}}_{ac})$ and gravitational $({\mathit{f}}_g)$ forces.

4.1 Acoustic sorting beyond the Rayleigh limit

As shown in Figure 3A, for the given two droplet sizes ($d_1=1.3$ mm and $d_2=1.8$ mm) beyond the Rayleigh limit $(d>\sim \lambda )$, at a frequency $f=720$ KHz ($\lambda =2$ mm) and $E_{ac}=12{\text{J/m}}^3$, the larger droplet $(d_2=1.8\text{mm})$ remains suspended as the net acoustic force acting on it dominates the gravitational force, whereas the smaller droplet $(d_1=1.3\text{mm})$ settles as gravitational force dominates over net acoustic force. By changing the frequency to $f=480$ KHz ($\lambda =3$ mm) and the acoustic energy density to $E_{ac}=20{\text{J/m}}^3$, the opposite of the above is observed where the bigger droplet ($d_2=1.8$ mm) settles, and the smaller droplet ($d_1=1.3$ mm) suspends as shown in Figure 3B. Remarkably, as illustrated in Figure 3C, droplets of intermediate size ($d_2=1.8$ mm) can be suspended while settling both the smaller ($d_1=1.3$ mm) and bigger ($d_1=2.6$ mm) droplets using an $E_{ac}=12{\text{J/m}}^3$ and $f=720$ KHz ($\lambda =2$ mm). This behavior is attributed to the dynamics of droplets beyond the Rayleigh limit, where the minimum acoustic energy density required to suspend the droplet (i.e., critical acoustic energy density, $E_{\text{cr}}$) is highly size-dependent and exhibits a non-monotonic pattern, as shown in Figure 3. In contrast, for droplets within the Rayleigh limit $(d\ll \lambda )$, such sorting is not feasible, as demonstrated by Crum (1971), that $E_{\text{cr}}$ is independent of droplet size, meaning that at a given $E_{\text{ac}}$, droplets of all sizes either suspend or settle. The $E_{cr}$ line separates the settling and suspending regime as shown in Figure 4A. If the applied $E_{ac}$ is less than the $E_{cr}$, the droplet settles, if $E_{ac}>E_{cr}$, the droplet suspends.

Figure 3

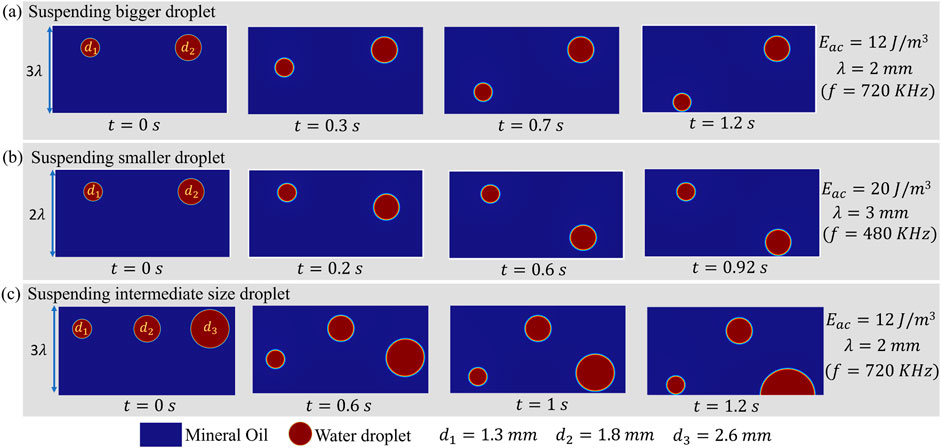
Figure 3. Sorting of droplets beyond the Rayleigh limit by controlling frequency (wavelength) and acoustic energy density: (a) Suspending a larger droplet $d_2=1.8$ mm while a smaller droplet $d_1=1.3$ mm settles at $E_{ac}=12{\text{J/m}}^3$ and $\lambda =2$ mm ($f=720$ KHz). (b) Suspending a smaller droplet $d_1=1.3$ mm while a larger droplet $d_2=1.8$ mm settles at $E_{ac}=20{\text{J/m}}^3$ and $\lambda =3$ mm ($f=480$ KHz). (c) Suspending an intermediate-sized droplet $d_2=1.8$ mm while both small droplet $d_1=1.3$ mm and large droplet $d_3=2.6$ mm settle at $E_{ac}=12{\text{J/m}}^3$ and $\lambda =2$ mm ($f=720$ KHz).

Figure 4

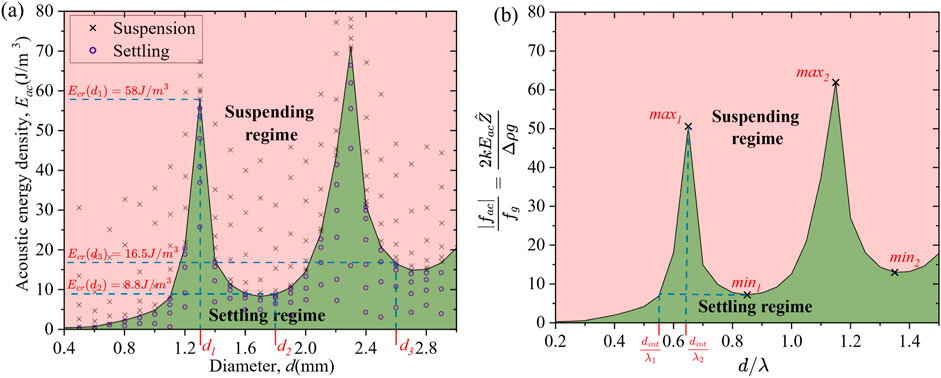
Figure 4. Suspending and Settling regimes of water droplets $(d>\sim \lambda )$ in the mineral oil due to interplay between acoustic $({\mathit{f}}_{ac})$ and gravity $({\mathit{f}}_g)$ forces: (a) The black solid line represents the minimum or critical acoustic energy density $(E_{\text{cr}})$ required to overcome gravity and suspend the droplets for the applied wavelength $\lambda =2$ mm. The $E_{\text{cr}}$ line separates the suspension and settling regimes. All data points are obtained from simulations. (b) A non-dimensionalized version of (a) involving the ratio $\left|f_{\text{ac}}\right|/f_{\text{g}}$ and $d/\lambda$.

To explain the results obtained in Figure 3, it is essential to understand the dependence of $E_{\text{cr}}$ on droplet size, shown in Figure 4. Although this has previously been explained in detail (Thirisangu et al., 2024a), we provide a summary nonetheless. When the droplets of size $d>\sim \lambda$ are subjected to acoustic fields, both positive and negative acoustic force regions exist within the droplet due to the presence of multiple nodes and antinodes (Figure 1). The portion of the droplet placed in the positive acoustic force region (quarter-wavelength below the pressure node) experiences an upward force (${\mathit{f}}_{ac}$ is positive), while the portion placed in the negative acoustic force region (quarter-wavelength above the pressure node) experiences a downward force (${\mathit{f}}_{ac}$ is negative). The partial cancellation of these opposing forces within the droplet reduces the net acoustic force acting against gravity, making the suspension of the droplet highly size-dependent. Additionally, as the droplet size increases, the net volume contributing to the positive acoustic force required to overcome gravity decreases significantly. This causes the critical acoustic energy $(E_{cr})$ needed for suspension to increase significantly, reaching a peak as shown in Figure 4A. The subsequent decrease in $E_{cr}$ after the peak is due to an increase in the available volume contributing to the positive net acoustic force acting on the droplet. Beyond this peak, $E_{cr}$ follows a pattern of alternating decreases and increases, with the magnitude of each successive peak or trough exceeding the previous one (Figure 4A). The above behavior of droplets reveals an intriguing phenomenon: larger droplets of some sizes require less $E_{cr}$ to suspend against gravity, whereas smaller droplets need higher $E_{cr}$ within the same wavefield $(f)$ as shown in the Figure 3.

With this understanding, the results of Figure 3 can be explained as follows. In Figure 3A, for the applied $E_{ac}=12$ ${\text{J/m}}^3$ $\&$ $\lambda =2$ mm, the bigger droplet ($d_2=1.8$ mm) suspends, as it is in the suspending regime (applied $E_{ac}=12{\text{J/m}}^3$ $>$ $E_{cr}(d_2)=8.8{\text{J/m}}^3$ as shown in Figure 4A), and the smaller droplet ($d_1=1.3$ mm) settles, as it is in the settling regime (applied $E_{ac}=12{\text{J/m}}^3$ $<$ $E_{cr}(d_1)=58{\text{J/m}}^3$ as shown in Figure 4A). For the same applied condition of $E_{ac}=12{\text{J/m}}^3$ $\&$ $\lambda =2$ mm as shown in Figure 3C, both the bigger droplet ($d_3=2.6$ mm), and smaller droplet ($d_1=1.3$ mm) settle, as both are in the settling regime (applied $E_{ac}=12{\text{J/m}}^3$ $<$ $E_{cr}(d_3)=16.5{\text{J/m}}^3$ $<$ $E_{cr}(d_1)=58{\text{J/m}}^3$ as shown in Figure 4A), but the intermediate sized droplet ($d_2=1.8$ mm) suspends, as it is in the suspending regime (applied $E_{ac}=12{\text{J/m}}^3$ $>$ $E_{cr}(d_2)=8.8{\text{J/m}}^3$ as shown in Figure 4A). It is to be noted that the plot given in Figure 4A cannot be used directly since the applied frequency (wavelength) has changed in Figure 3B. Instead, a similar plot to Figure 4A can be obtained for the required frequency (wavelength) from the non-dimensional plot in Figure 4B. For $E_{ac}=20{\text{J/m}}^3\&\lambda =3$ mm in Figure 3B, the bigger droplet ($d_2=1.8$ mm) settles, as it is in the settling regime (applied $E_{ac}=20{\text{J/m}}^3<E_{cr}(d_2)=87{\text{J/m}}^3$), and the smaller droplet ($d_1=1.3$ mm) suspends, as it is in the suspending regime (applied $E_{ac}=12{\text{J/m}}^3>E_{cr}(d_1)=13.2{\text{J/m}}^3$).

4.2 Sorting of arbitrary intermediate droplet sizes from a broad range

The following steps can be utilized to selectively sort intermediate-sized droplets $(d_{\text{int}})$ from a broad range $d_{\text{min}}$ to $d_{\text{max}}$.

Step 1. Determine ${\lambda }_1$ such that the $d_{\text{int}}/{\lambda }_1$ ratio falls before the first local maximum of $\left|f_{ac}\right|/f_g$ ($ma{x}_1$ as shown in the Figure 4B) and matches the value of the first local minimum of $\left|f_{ac}\right|/f_g$ ($mi{n}_1$ as shown in the Figure 4B). Set the frequency $f_1=c/{\lambda }_1$ to generate ${\lambda }_1$ and apply the corresponding $E_{cr}$ for $d_{\text{int}}$. As a result of this Step 1, droplets larger than $d_{\text{int}}$ will settle, while droplets of other sizes, including $d_{\text{int}}$, will remain suspended.

Step 2. Determine a ${\lambda }_2$ such that $d_{\text{int}}/{\lambda }_2$ corresponds to the first local maximum of $\left|f_{ac}\right|/f_g$ ($ma{x}_1$ as shown in the Figure 4B). Set the frequency $f_2$ accordingly. Apply the $E_{ac}$ slightly less than the $E_{cr}$ corresponding to $d_{\text{int}}$. As a result of this Step 2, smaller droplets remain suspended while the droplets of interest $(d_{\text{int}})$ begin to settle.

Step 3. While $d_{\text{int}}$ is settling, increase the $E_{ac}$ slightly more than the $E_{cr}$ corresponding to $d_{\text{int}}$. At the end of Step 3, $d_{\text{int}}$ is prevented from settling, allowing it to remain suspended within the fluid medium between the smaller droplets (stay at the top) and the larger droplets (settle at the bottom). This enables the sorting of arbitrary intermediate-sized droplets.

4.3 Sorting of the droplet based on the interfacial tension

Since the maximum Bond number $\left(Bo=\mathrm{\Delta }\rho g{r}^2/\sigma \right)$ is 0.063 (for a radius $r=1.5$ mm and $\sigma =50$ mN/m) for the results discussed until the previous sections, which is much less than 1, the interfacial force is strong enough to prevent the droplet from deforming or splitting. When interfacial effects weaken or the acoustic force becomes stronger, the opposing acoustic forces within the droplet compete, potentially leading to the droplet splitting into daughter droplets under suitable conditions (Thirisangu et al., 2024a). A combination of droplet splitting and the acoustic sorting method beyond the Rayleigh limit, as presented in Section 4.1, facilitates the sorting of droplets of the same size but with differing interfacial tensions, which will be discussed in this section.

Two droplets of the same size ($d_A=d_B=2$ mm), as shown in Figure 5, are subjected to an acoustic field with a wavelength of $\lambda =4$ mm. Droplet $A$ exhibits a strong interfacial force with an interfacial tension of ${\sigma }_A=50$ mN/m (Bond number $Bo=0.028$), and droplet $B$ exhibits a weak interfacial force with an interfacial tension of ${\sigma }_B=2\text{mN/m}$ $(Bo=0.699)$, are sorted in 2 steps (Note: The interfacial effects in practical fluids can be reduced by introducing surfactants). Step 1: Upon applying $E_{ac}$ $(200{\text{J/m}}^3)$ such that the droplet $B$ with the weak interfacial tension splits into two daughter droplets, while the droplet $A$ with the strong interfacial tension remains intact. Both droplet $A$ and the daughter droplets $(B^{\prime })$ remain suspended in the medium as long as $E_{ac}\gg E_{cr,A}>E_{cr,B^{\prime }}$ is applied, as shown in the Figure 5B. Step 2: Upon reducing the $E_{ac}$ to $10{\text{J/m}}^3$ $(E_{ac,A}>E_{ac}>E_{cr,B^{\prime }})$, the droplet $A$ settles, and the droplet $B$ suspends in the fluid medium, enabling the sorting of the droplets of same size with differing interfacial tension as shown in the Figure 5B. It is important to note that for the given wavelength ($\lambda =4$ mm), the $E_{cr}$ for the droplet $A$ ($d=2$ mm) is $14.5{\text{J/m}}^3$, and the $E_{cr}$ for the droplet $B^{\prime }$ ($d\approx 1$ mm) is $4.8{\text{J/m}}^3$.

Figure 5

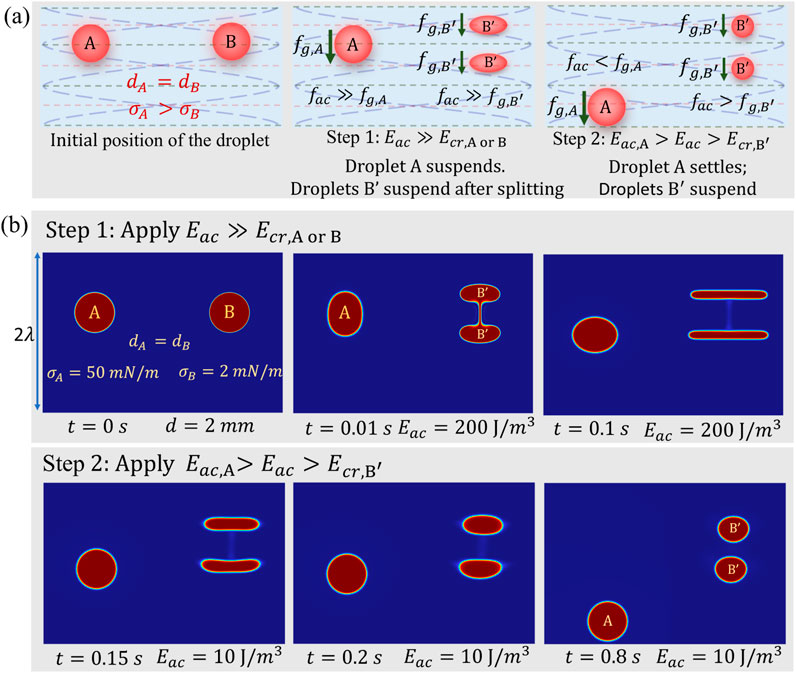
Figure 5. (a) A schematic representation of the sorting mechanism for two droplets of equal size $(d_A=d_B)$ with droplet A has a higher interfacial tension than droplet B $({\sigma }_A>{\sigma }_B)$. (b) Simulation results of the sorting process with the applied wavelength, $\lambda =4$ mm: Step 1: Apply $E_{ac}$ such that it suspends both the droplets and causes droplet B to split while ensuring droplet A remains intact. And Step 2: Reduce $E_{ac}$ $(E_{ac,A}>E_{ac}>E_{cr,B^{\prime }})$ such that droplet $A$ settles, and droplet $B$ suspends in the fluid medium.

5 Conclusion

The theoretical findings presented in this study on the acoustic sorting of droplets beyond the Rayleigh limit hold promise for enabling the development of advanced droplet-sorting devices. However, due to the high acoustic energy density $(E_{ac})$ or pressure amplitude $(p_a)$ involved, the experimental implementation of this technique requires pressurized systems to prevent cavitation. The study relies on a few assumptions: first, a predetermined $E_{ac}$ is employed without solving the first-order acoustic fields, and second, the acoustic body force $f_{ac}$ is derived using the Boussinesq approximation ($\mathrm{\Delta }\rho /{\rho }_{\mathit{avg}}\ll 1$ and $\mathrm{\Delta }c/c_{\mathit{avg}}\ll 1$) (Rajendran et al., 2022). In order to produce more accurate results on droplet dynamics, it is necessary to solve the bidirectionally coupled equations of fast-time acoustic fields and slow-time hydrodynamic motion, incorporating the divergence of the Reynolds stress tensor as the body force (Thirisangu et al., 2024b).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JT: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft. KS: Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Department of Science & Technology - Fund for Improvement of Science & Technology Infrastructure (DST-FIST) via Grant No: SR/FST/ET-I/2021/815.

Acknowledgments

The authors would like to express their sincere gratitude to Varun Kumar, Videsh, Anjan and Snekan for their valuable assistance in proofreading and providing insightful feedback during the preparation of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Augustsson, P., Magnusson, C., Nordin, M., Lilja, H., and Laurell, T. (2012). Microfluidic, label-free enrichment of prostate cancer cells in blood based on acoustophoresis. Anal. Chem. 84, 7954–7962. doi:10.1021/ac301723s

PubMed Abstract | CrossRef Full Text | Google Scholar

Baasch, T., and Dual, J. (2018). Acoustofluidic particle dynamics: beyond the Rayleigh limit. J. Acoust. Soc. Am. 143, 509–519. doi:10.1121/1.5021339

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, N. V. (1972). Segregation and sedimentation of red blood cells in ultrasonic standing waves. Nature 239, 398–399. doi:10.1038/239398a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Chladni, E. (1787). Entdeckungen uber die Theorie des Klanges. Leipzig, Germany: Weidmanns, Erben und Reich.

Google Scholar

Coakley, W. T., Bardsley, D. W., Grundy, M. A., Zamani, F., and Clarke, D. J. (1989). Cell manipulation in ultrasonic standing wave fields. J. Chem. Technol. Biotechnol. 44, 43–62. doi:10.1002/jctb.280440106

CrossRef Full Text | Google Scholar

Crum, L. A. (1971). Acoustic force on a liquid droplet in an acoustic stationary wave. J. Acoust. Soc. Am. 50, 157–163. doi:10.1121/1.1912614

CrossRef Full Text | Google Scholar

Cushing, K., Undvall, E., Ceder, Y., Lilja, H., and Laurell, T. (2018). Reducing WBC background in cancer cell separation products by negative acoustic contrast particle immuno-acoustophoresis. Anal. Chim. Acta 1000, 256–264. doi:10.1016/j.aca.2017.11.064

PubMed Abstract | CrossRef Full Text | Google Scholar

Dyson, M., Woodward, B., and Pond, J. B. (1971). Flow of red blood cells stopped by ultrasound. Nature 232, 572–573. doi:10.1038/232572a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Eller, A. (1968). Force on a bubble in a standing acoustic wave. J. Acoust. Soc. Am. 43, 170–171. doi:10.1121/1.1910755

CrossRef Full Text | Google Scholar

Faraday, M. (1831). XVII. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 121, 299–340. doi:10.1098/rstl.1831.0018

CrossRef Full Text | Google Scholar

Foresti, D., Nabavi, M., Klingauf, M., Ferrari, A., and Poulikakos, D. (2013). Acoustophoretic contactless transport and handling of matter in air. Proc. Natl. Acad. Sci. U.S.A. 110, 12549–12554. doi:10.1073/pnas.1301860110

PubMed Abstract | CrossRef Full Text | Google Scholar

Gor’kov, L. P. (1962). On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys.-Doklady 6, 773–775.

Google Scholar

Gould, R., and Coakley, W. (1974). “The effects of acoustic forces on small particles in suspension,” in Proceedings of the 1973 symposium on finite amplitude wave effects in fluids bjorno (Pergamon, Guildford), 252–257.

Google Scholar

Gupta, S., Feke, D. L., and Manas-Zloczower, I. (1995). Fractionation of mixed particulate solids according to compressibility using ultrasonic standing wave fields. Chem. Eng. Sci. 50, 3275–3284. doi:10.1016/0009-2509(95)00154-w

CrossRef Full Text | Google Scholar

Hasegawa, T. (1979a). Acoustic radiation force on a sphere in a quasistationary wave field—experiment. J. Acoust. Soc. Am. 65, 41–44. doi:10.1121/1.382264

CrossRef Full Text | Google Scholar

Hasegawa, T. (1979b). Acoustic radiation force on a sphere in a quasistationary wave field—theory. J. Acoust. Soc. Am. 65, 32–40. doi:10.1121/1.382263

CrossRef Full Text | Google Scholar

Hemachandran, E., Karthick, S., Laurell, T., and Sen, A. (2019). Relocation of coflowing immiscible liquids under acoustic field in a microchannel. Europhys. Lett. 125, 54002. doi:10.1209/0295-5075/125/54002

CrossRef Full Text | Google Scholar

Karthick, S., Pradeep, P. N., Kanchana, P., and Sen, A. K. (2018). Acoustic impedance-based size-independent isolation of circulating tumour cells from blood using acoustophoresis. Lab. Chip 18, 3802–3813. doi:10.1039/C8LC00921J

PubMed Abstract | CrossRef Full Text | Google Scholar

King, K. L. (1934). On the acoustic radiation pressure on spheres. Proc. R. Soc. Lond. A - Math. Phys. Sci. 147, 212–240. doi:10.1098/rspa.1934.0215

CrossRef Full Text | Google Scholar

Kundt, A., and Lehmann, O. (1874). Ueber longitudinale Schwingungen und Klangfiguren in cylindrischen Flüssigkeitssäulen. Ann. Phys. 229, 1–12. doi:10.1002/andp.18742290902

CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1987). Fluid mechanics. Oxford, England, UK: Pergamon.

Google Scholar

Lenshof, A., Magnusson, C., and Laurell, T. (2012). Acoustofluidics 8: applications of acoustophoresis in continuous flow microsystems. Lab. Chip 12, 1210–1223. doi:10.1039/C2LC21256K

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P., Mao, Z., Peng, Z., Zhou, L., Chen, Y., Huang, P.-H., et al. (2015). Acoustic separation of circulating tumor cells. Proc. Natl. Acad. Sci. U.S.A. 112, 4970–4975. doi:10.1073/pnas.1504484112

PubMed Abstract | CrossRef Full Text | Google Scholar

Marston, P. L. (2017). Finite-size radiation force correction for inviscid spheres in standing waves. J. Acoust. Soc. Am. 142, 1167–1170. doi:10.1121/1.5000236

PubMed Abstract | CrossRef Full Text | Google Scholar

Nam, J., Lim, H., Kim, C., Kang, J. Y., and Shin, S. (2012). Density-dependent separation of encapsulated cells in a microfluidic channel by using a standing surface acoustic wave. Biomicrofluidics 6, 024120–2412010. doi:10.1063/1.4718719

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohlsson, P., Petersson, K., Augustsson, P., and Laurell, T. (2018). Acoustic impedance matched buffers enable separation of bacteria from blood cells at high cell concentrations. Sci. Rep. 8, 9156–9211. doi:10.1038/s41598-018-25551-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Pazos Ospina, J. F., Contreras, V., Estrada-Morales, J., Baresch, D., Ealo, J. L., and Volke-Sepúlveda, K. (2022). Particle-size effect in airborne standing-wave acoustic levitation: trapping particles at pressure antinodes. Phys. Rev. Appl. 18, 034026. doi:10.1103/PhysRevApplied.18.034026

CrossRef Full Text | Google Scholar

Petersson, F., Nilsson, A., Holm, C., Jonsson, H., and Laurell, T. (2004). Separation of lipids from blood utilizing ultrasonic standing waves in microfluidic channels. Analyst 129, 938–943. doi:10.1039/b409139f

PubMed Abstract | CrossRef Full Text | Google Scholar

Petersson, F., Nilsson, A., Jönsson, H., and Laurell, T. (2007). Free flow acoustophoresis: microfluidic-based mode of particle and cell separation. Anal. Chem. 79, 5117–5123. doi:10.1021/ac070444e

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajendran, V. K., Jayakumar, S., Azharudeen, M., and Subramani, K. (2022). Theory of nonlinear acoustic forces acting on inhomogeneous fluids. J. Fluid Mech. 940, A32. doi:10.1017/jfm.2022.257

CrossRef Full Text | Google Scholar

Rueckner, W., Peidle, J., Crockett, A., and Davis, D. (2023). Particle size effects on stable levitation positions in acoustic standing waves. J. Acoust. Soc. Am. 154, 1339–1346. doi:10.1121/10.0020730

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Huang, H., Stratton, Z., Huang, Y., and Huang, T. J. (2009). Continuous particle separation in a microfluidic channelvia standing surface acoustic waves (SSAW). Lab. Chip 9, 3354–3359. doi:10.1039/B915113C

PubMed Abstract | CrossRef Full Text | Google Scholar

Thévoz, P. J. D. A., Shea, H., Bruus, H., H, T. S., and Soh, H. T. (2010). Acoustophoretic synchronization of mammalian cells in microchannels. Anal. Chem. 82, 3094–3098. doi:10.1021/ac100357u

PubMed Abstract | CrossRef Full Text | Google Scholar

Thirisangu, J., Hemachandran, E., and Subramani, K. (2023). Suspending droplets beyond the Rayleigh limit: the interplay of acoustic and gravity forces. Phys. Fluids 35, 122012. doi:10.1063/5.0171492

CrossRef Full Text | Google Scholar

Thirisangu, J., Mahapatra, A., and Subramani, K. (2024a). Suspension dynamics of droplets in acoustic and gravitational fields. arXiv. doi:10.48550/arXiv.2412.06281

CrossRef Full Text | Google Scholar

Thirisangu, J., Rajendran, V. K., Selvakannan, S., Jayakumar, S., Hemachandran, E., and Subramani, K. (2024b). Droplets in acoustic fields: a unified theory from migration to splitting. arXiv. doi:10.48550/arXiv.2408.06092

CrossRef Full Text | Google Scholar

Weiser, M. A. H., and Apfel, R. E. (1982). Extension of acoustic levitation to include the study of micron-size particles in a more compressible host liquid. J. Acoust. Soc. Am. 71, 1261–1268. doi:10.1121/1.387776

CrossRef Full Text | Google Scholar

Wu, M., Ozcelik, A., Rufo, J., Wang, Z., Fang, R., and Jun Huang, T. (2019). Acoustofluidic separation of cells and particles. Microsyst. Nanoeng. 5, 32–18. doi:10.1038/s41378-019-0064-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Yosioka, K., and Kawasima, Y. (1955). Acoustic radiation pressure on a compressible sphere. Acta Acustica united Acustica 5, 167–173.

Google Scholar