Direct observation of small scale capillary wave turbulence using high speed digital holographic microscopy

Introduction: It is now known that capillary waves driven upon a fluid interface by high frequency ($>1$ MHz) ultrasound exhibit capillary wave turbulence: the appearance of waves with phase and wavelength far removed from the excitation signal that drives them. These waves are responsible in significant part for atomization, a useful application for ultrasound, though the physics responsible for their appearance is poorly understood.

Methods: We use high-speed digital holographic microscopy to observe these capillary waves, an important step towards understanding their generation and atomization phenomena.

Results: We observe Zakharov-Kolmogorov weak wave turbulence for a limited range of input power, and find broader turbulence phenomena outside this range. We see discrete thresholds as the input power is increased, where higher and higher frequency responses are driven in the capillary waves with sudden onset between regimes.

Discussion: We employed spatial analysis to find extensions of the capillary wave response to higher frequencies, suggesting there is additional information in the spatial distribution of the capillary wave that is rarely if ever measured. We verified via frequency modulation that nonlinear resonance broadening is present, which undermines the use of Faraday wave or parametric wave theories to characterize these waves, important in the context of atomization which is now, definitively, not a Faraday wave process.

Introduction

Weakly nonlinear interactions between a large number of waves with random phase result in wave turbulence that is typically modeled with the well developed statistical theory, “weak” wave turbulence (WWT) (Newell and Rumpf, 2011). Ample experimental work has been done on wave turbulent systems including liquid surface waves (Falcón et al., 2009; Brazhnikov et al., 2002), plasmas (Robinson, 1996; Yoon, 2000), and solid plates (Boudaoud et al., 2008). Studies in this area frequently provide evidence in support of WWT theory. A fundamental result of WWT is the Zakharov-Kolmogorov (ZK) spectrum, which shows the power spectral density (PSD) of the waves has a power-law dependence upon the frequency (or wavenumber) over a conservative regime of the wave response. For liquid surface waves dominated by surface tension (i.e., capillary waves), the ZK spectrum is represented by

$S\left(f\right)\propto {ϵ}^{1/2}{\left(\frac{\gamma }{\rho }\right)}^{1/6}{f}^{-\alpha },$

where $ϵ$ is the mean energy flux, $\gamma$ is the surface tension, $f$ is the frequency, $\rho$ is the liquid density, and $\alpha =17/6$ for capillary waves (Zakharov and Filonenko, 1971; Zakharov et al., 1992). In a log-log plot of the PSD, the power law produces a PSD that is linearly dependent upon $-\alpha$. In this model, energy is said to ‘cascade’ from low to high frequency in the system with the predicted scaling when certain conditions are met: i) the domain is infinite, ii) there is sufficient scale separation between energy injection and energy dissipation, iii) the cascade is driven by weakly nonlinear three-wave interactions, and iv) the wave interactions are local (i.e.,, they occur between waves with similar wavelengths).

Recent studies have attempted to reconcile discrepancies between the idealized conditions of WWT and the results of experiments where these idealizations are routinely violated. Connaughton et al. (2001) put forward a simple model that explains how quasi-resonances in finite domain capillary wave systems cause deviations from the predictions of WWT. At low levels of nonlinearity, discrete resonances are not broad enough to permit energy to traverse the eigengrid spacing imposed by the bounded domain, and so the energy cascade typical of WWT is stunted. Falcon et al. (2007) observed that the frequency scalings in a gravity-capillary wave turbulence system are dependent on the input power. Falcon and Laroche (2011) observed that the depth of the liquid also has an impact on the capillary wave spectrum, causing it to deviate from a power law, but the mechanism remains unknown. Deike et al. (2014) measured the wave height spectrum with varying viscosity and showed in real systems that dissipation, indicated by a deviation in the linear spectral slope, occurs in the (theoretically energy conservative) inertial region, between energy injection and the dissipation zone. They propose a new way to measure energy flux in the system and use it to account for non-ideal dissipation. We have previously investigated the effect of increasing nonlinearity beyond what can be considered weak and also showed experimental evidence of finite domain effects (Orosco and Friend, 2023). In the current work, we investigate how energy traverses length scales in a capillary wave system with a data-driven approach, taking into account much smaller scales than have been previously studied.

We are primarily interested in milli to micro-scale capillary waves because of their connection to ultrasonic atomization phenomena. Vibration of a surface in contact with liquid in the kHz or MHz range above a threshold amplitude produces many small droplets, on the order of microns, from the liquid surface (Kurosawa et al., 1995; Collignon et al., 2018; Lang, 1962). In the kHz range, the size of the resulting droplets can be related to Faraday wave theory. Michael Faraday discovered the appearance of capillary waves upon a pool of mercury in a pie tin on a chair (Xvii, 1831). As he tapped the chair at a set frequency with his hand, the “crispations”—capillary waves—appeared to oscillate at one-half the frequency of his tapping. Many studies have explored Faraday capillary waves, producing a rich tapestry of mathematical analysis (Bosch and van de Water, 1993; Goodridge et al., 1999; Wagner et al., 1999; Zhang and Viñals, 1996) upon an ostensibly simple phenomena. Lang (1962) showed experimentally that using this Faraday wave assumption along with Kelvin’s equation relating frequency to wavelength yields a good estimate of the median droplet diameter, $D=\kappa {((8\pi \gamma )/(\rho F^2))}^{1/3}$, where $\kappa =0.34$ is a fitting parameter, $\gamma$ is surface tension, $\rho$ is density, and $F$ is driving frequency. This relationship holds for low atomization rates ($\sim 0.01$ mL/s) and ultrasound frequencies between 10 and 800 kHz. Outside this frequency range, the value of $\kappa$ has been changed post hoc to $\kappa =3.8$ (Kurosawa et al., 1997) in an attempt to fit the equation to the results when the frequency was increased to 20 MHz. Post-hoc reasoning was used in that work even for the original definition of $\kappa =0.34$: a wave crest represents one-half of a wavelength and therefore it makes sense that $\kappa <0.5$. Lang photographically verified that the capillary waves appearing on the surface form a uniform lattice with wavelength that decreases with increasing ultrasound frequency. Subsequent studies have demonstrated that the droplet size also depends on viscosity, power input, and flow rate with more detailed empirical correlations (Ramisetty et al., 2013; Qi et al., 2008; Rajan and Pandit, 2001). Lang was not able to explain the measured variation in diameter about the median.

Many of these classical conceptions break down in the context of MHz-order, high power ultrasonic atomization. A fundamental assumption of Faraday wave theory—that the excitation frequency is on the same order as the principal capillary wave frequency—fails at frequencies beyond the 100 kHz range. In these small sessile droplet systems, the first oscillations that appear are on the order of 100 Hz, three orders of magnitude lower than the excitation frequency. Moreover, one would expect to see a capillary wave response at one-half the excitation frequency for it to be a Faraday wave. It has been shown experimentally that no peak in the spectrum exists at or near one-half the MHz-order driving frequency (Blamey et al., 2013). In fact, a broadband spectrum wave, indicating WWT, develops on the surface at powers far below the threshold for atomization. In this context, Lang’s simple approach of deducing droplets from wavelengths becomes untenable because there is no single frequency at which capillary waves occur—they no longer appear in a uniform lattice. The actual droplet size distributions measured from MHz-order ultrasound have two and sometimes three peaks and often disagree with Lang’s equation (Collins et al., 2012; Barreras et al., 2002; Kooij et al., 2019; Winkler et al., 2015).

Recent work claims to have solved the problem of determining the droplet size distribution (Kooij et al., 2019); a Gamma function is fit to droplet size distributions demonstrating that they obey well studied corrugation and ligamentation processes found in sprays. This helps to explain the variation about the median that Lang could not explain. However, the Gamma function takes two parameters, the width of the ligament distribution and the ligament corrugation, so that the method has no predictive power but simply exchanges one unknown, the distribution of capillary waves, for another. The authors suggest that, because they measure two droplet size peaks, then there must be a bi-modal distribution of capillary wavelengths on the surface of the liquid. This makes intuitive sense based on a paradigm of Faraday waves and, without measuring waves directly, it is difficult to validate this suggestion. The difficulty associated with gaining direct knowledge of the waves in this context originates in the time and space scales of the waves, which are much smaller and faster than most modern experimental equipment can reliably observe.

Methods

Overview

In the current work, we study capillary waves experimentally at micro-length and time scales. Our system is a millimeter length, microliter volume of water that completely insulates capillary wave phenomena from the effects of gravity while also clearly expressing finite domain effects. We drive the system using high frequency ($\sim$7 MHz), high power ($\sim$500 mW) ultrasound that pushes the wave interactions up to and beyond the weak nonlinearity assumption. We measure the surface displacement field at 115 kfps, representing a time period of 8.7 $\mu$s, using a bespoke high-speed digital holographic microscope (DHM) capable of producing full field of view measurements of the fluid interface’s displacement at up to 120 kfps (Emery et al., 2021).

We first apply standard, single-point time series analysis to this data to obtain standard amplitude spectra. We then analyze the broader spatial data using techniques that complement and improve upon the results of single-point time series analysis. Berhanu and Falcon (2013) were the first to use this type of data although they were limited to larger length and time scales. They showed that linear and nonlinear dispersion relations extracted from their data matched WWT theories using spatial and temporal Fourier methods. Another commonly used spatial technique is modal analysis using eigenfunction decomposition. The aim is to reveal coherent structures that may not be best represented by sinusoids or wavelets (Taira et al., 2017). Proper orthogonal decompositions (POD) produce independent spatial modes optimized by energy with no requirement set on time behavior and have been used extensively in turbulence studies (Berkooz et al., 1993; Rovira et al., 2021). We will show that standard modal analyses do not reveal coherent structures in our system. However, they successfully quantify energy shifts across length scales. It is well known that isotropic turbulent systems have POD modes that reduce to a Fourier basis (Taira et al., 2017; Schmidt and Colonius, 2020). As will be shown, the POD modes of our system are indeed closely related to 2D sinusoidal gratings. This detail allows us to attach a well-defined length scale to each mode. Using this approach, we track how energy flows across length scales as a function of power input.

Experimental setup

Our system consists of a sessile drop of water on a thickness-mode $25\times 25$ mm piezoelectric resonator (see Figure 1). The resonator has a 6-mm diameter circular window in the electrodes that allows light to pass through. The electrodes were formed by sputter depositing a 10-nm titanium bonding layer followed by 500 nm of gold on both sides of a transparent, double-side optically polished ($<0.1$ nm roughness), 0.5-mm thick, 127.68$°$ Y-rotated, X-propagating lithium niobate (LN) wafer. The 36$°$ Y-rotated cut is often used in thickness mode devices, but we have found the 127.68$°$ cut to be superior for operation at resonance (Collignon et al., 2018). A photoresist mask was used on both sides to coat the circular window region with AZ photoresist polymer. After titanium and gold deposition, the photoresist was dissolved, lifting off the metal films and leaving the transparent LN exposed (Mei et al., 2020). This procedure was repeated on the second side to produce a thickness-mode resonator with a fundamental resonance at 7 MHz.

Figure 1

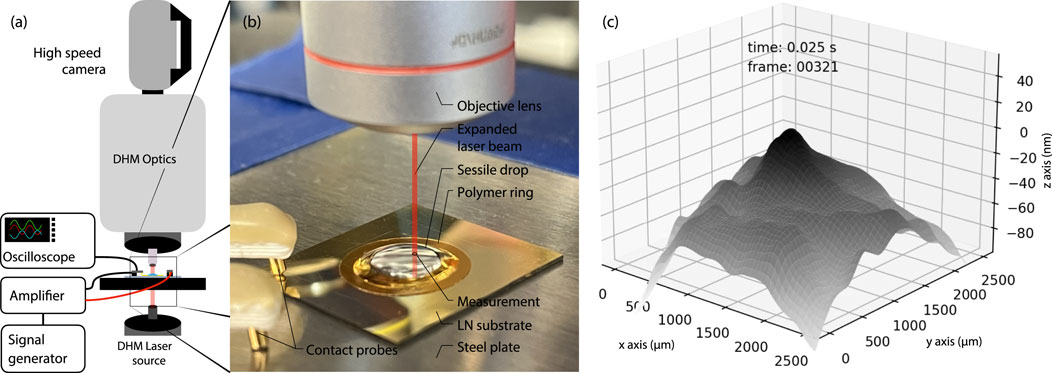
Figure 1. A schematic of our experimental setup incorporating a (A) high-speed digital holographic microscope (DHM) with a (B) sessile droplet placed upon a single-crystal lithium niobate thickness-mode ultrasound resonator. The droplet is placed directly over a transparent “window” in the lithium niobate substrate with a gold electrode on both sides everywhere else. An expanded laser propagates from below through the droplet and into the DHM to produce a holographic image captured by the high-speed camera to then produce a (C) height map over the measurement region (indicated in (b) as Measurement). For scale in (B), the lithium niobate resonator is a $25\times 25$ mm square and is 0.5 mm thick.

A 200 $\mu$m thick with a 9.5 mm inner diameter and a 12.7 mm outer diameter circular polyimide tape (Polyimide Film Electrical Tape 1,205, 3M, Maplewood, MN, United States) ring was cut and attached to the resonator around the window area in order to repeatably constrain the sessile droplet shape and location during experiments. We used a pipette to place 66 $\mu$L of distilled (ultrapure) water on the LN within the ring so that the drop was pinned around the entire perimeter. To reduce the effects of residual surfactants and contaminants—because these effects cannot be eliminated—the surface was carefully rinsed thrice before conducting each experiment with the ultrapure water. The fluid volume was chosen so that the surface of the drop would be relatively flat compared with the field of view while not deviating significantly from the inherent contact angle of water on LN. All this was sought to ensure the contact line with the ring remains pinned. This geometry also limits the system to deep water capillary waves for the frequencies and wavelengths in this study, so that we can avoid having to consider four-wave interactions in gravity capillary waves as gravity waves and the lateral fluid dynamics from shallow capillary waves (Newell and Rumpf, 2011). In fact, very few experiments solely consider capillary waves, as traditional methods for observing such waves require the reduction of gravity through spaceflight, parabolic aircraft flights, or special low-gravity experimental settings (Falcón et al., 2009). Reducing the apparent gravity, $g$, reduces the critical capillary frequency $f_c\propto g^{(3/4)}$, above which waves are dominated by surface tension. We instead limit the waves that can be generated by reducing the size of the sessile droplet “container”, thereby preventing most gravity waves and allowing us to focus on high frequency waves.

The resonator was driven directly with a signal generator (WF1946, NF Corporation, Yokohama, Japan), except for the highest power data set which used a linear 10 W amplifier (210L, E&I, Rochester, NY, United States). The signal passed to the resonator was a continuous, fixed amplitude, single frequency sine wave at the fundamental resonance frequency of the thickness mode device. The resonator was placed upon a 1 mm thick, $40\times 40$ mm steel plate with a 10 mm diameter hole aligned with the transparent window in the LN resonator. One spring probe was placed in contact with the top electrode, while another was placed in contact with the steel plate, forming an electrical contact with the bottom electrode. The current and voltage were measured with probes connected to an oscilloscope and their product was averaged over 1 million cycles to determine the true power entering the resonator. The signal was applied to the resonator 0.5 s after beginning measurement with the DHM and maintained until after the measurement was completed at 6 seconds of elapsed time. Experiments were performed over a range of power inputs with all other conditions controlled. We recorded eighteen data sets between 0 and 250 mW. The zero power data set was recorded for only 2 seconds.

Digital holographic microscopy

We measured the surface displacement in time using a customized digital transmission holographic microscope (DHM, LynceéTec, Lausanne, Switzerland) coupled to an ultra high speed camera (NOVA S12, Photron, San Diego, CA, United States). In this approach, laser light, with a wavelength of 660 nm, is split into a sample and a reference beam. The sample beam passes through the window in the resonator and the sessile drop and is then combined with the reference beam to form a phase image and an intensity image at the camera. The phase delay caused by passing through varying distances of water produces a two-dimensional map of the change in the height of the water surface. The measurable change is up to one wavelength of light without post-processing. However, if the height change is sufficiently smooth and gradual, the phase jumps caused by height changes greater than the wavelength of light can be unwrapped to still produce accurate measurements of the fluid interface’s deflection. The height resolution of the system is on the order of 10 nm. We refer the reader to Cuche et al. (1999) for details on the DHM technology. We used a ×10 objective lens and recorded at 115,200 frames per second with a $200\times 200$ pixel field of view, producing a pixel size at the fluid interface of 1.625 $\mu$m. Thus, we expected to observe behavior at frequencies up to 60 kHz and with reasonable amplitude accuracy up to approximately 30 kHz according to the Nyquist–Shannon sampling theorem (Shannon, 1949).

Time-series analysis

In order to obtain the power spectrum, we extracted the data describing the transverse displacement of the central pixel and performed Welch’s method (Welch, 1967) with blocks of $2^{15}$ time steps (see Figure 2) to minimize noise. Most studies of wave turbulence inject energy at a range of frequencies lower than the expected dissipation range in order to ensure nonlinear wave interactions and the observation of a turbulent cascade (Aubourg and Mordant, 2016; Falcon et al., 2007). When these systems are driven parametrically, at a single frequency, it is common to observe Faraday waves indicated by a dominant peak at one-half the driving frequency and well-ordered patterns in space at low power (Falcón et al., 2009). With sufficient power, however, Faraday wave systems do become turbulent (Wright et al., 1996). Our system is fundamentally different, because we drive the system at a frequency five orders of magnitude higher than the frequency of the capillary wave cascade’s starting frequency. It is important to note here that the driving signal of 7 MHz cannot be observed in Figure 2 because the frequency is beyond our high-speed DHM measurement range. However, Zhang et al. (2021) have proposed a mechanism by which large frequency excitation can stimulate much lower frequency wave behavior in a similar system, supported by past data captured by Blamey et al. (2013) where the spectral response at a single point was measured to 25 MHz. The mechanism occurs by the generation of an acoustic standing wave in the parent droplet as a cavity. This produces a spatially varying acoustic pressure upon the fluid interface that causes its deformation. If at low amplitude, the deformation is static (Manor et al., 2011), however, it quickly becomes dynamic beyond an excitation threshold dependent on the specific experimental setup. As the amplitude of the interface’s deformation grows larger, the standing acoustic wave in the fluid droplet changes shape, leading to a change in the acoustic pressure upon the interface, changing its shape, and so on to produce capillary wave motion at spatiotemporal scales associated with the 100 Hz range capillary wave resonances in this system. Those capillary wave resonances interact via a nonlinear three-wave mechanism to produce the cascade (Newell and Rumpf, 2011).

Figure 2

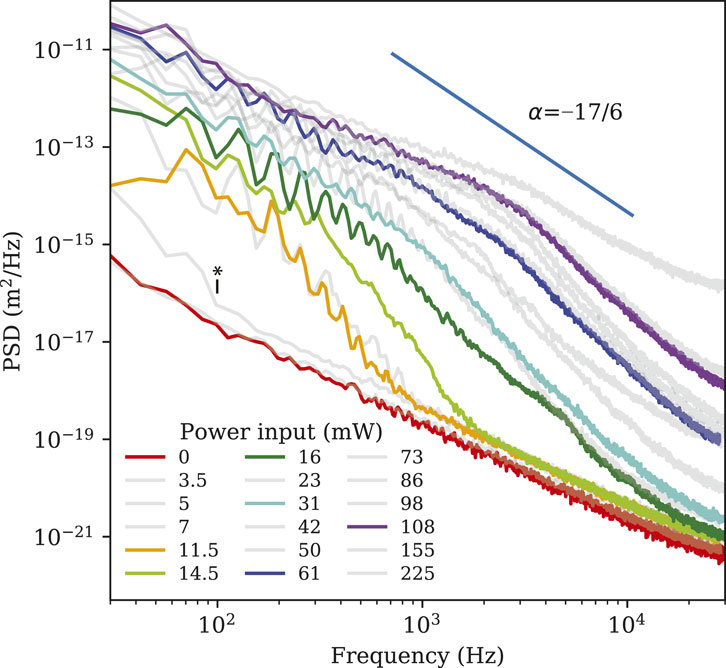
Figure 2. Power spectral density of the interfacial displacement plotted with respect to the frequency for a single point on the fluid interface at 7 MHz excitation. Note the red line indicates no input power, representing the noise floor with our measurement method. As the input power is increased, the appearance of capillary wave oscillations is apparent at about 5–7 mW, and progressive expansion of the cascade to higher frequencies is clear as the power is increased from 14.5 mW to 225 mW. The modal character of the capillary waves is lost from apparent frequency broadening at about 61 mW. The observed spectral slopes are generally lower than the theoretical value of $-17/6$. Colors indicate power input values where there were notable changes in the spectra.

Spatial mode analysis

Looking beyond the information that can be gleaned from observation of a single point on the fluid interface over time, we next consider the entire field of view and seek to determine how the fluid interface evolves over time and space as the input power is changed. We use the machinery of proper orthogonal decomposition (POD) to support this effort (Berkooz et al., 1993; Rovira et al., 2021).

When computing the POD modes and singular values, we selected $2^{13}$ frames from each data set. We transformed each frame into a 40,000 element column vector and collected all the frames together into a $\mathrm{40,000}\times \mathrm{8,192}$ matrix, $F$. The mean frame was subtracted from each frame to produce a matrix, $X$. We then performed a singular value decomposition (SVD) upon $X=US{V}^T$, which produced a $\mathrm{40,000}\times \mathrm{8,192}$ matrix $U$, a $\mathrm{8,192}\times \mathrm{8,192}$ matrix $S$, and a third matrix $V$. The matrix $U$ contains 8,192 modes, the diagonal matrix $S$ contains the singular values corresponding to those modes, and $V$ represents the corresponding eigenvectors. By virtue of SVD the singular values are automatically sorted in descending order and are equal to the square root of the eigenvalues, $\lambda$, of the classical eigenvalue problem: $R{\varphi }_i={\lambda }_i{\varphi }_i$, where $R$ is the auto-covariance matrix and $\varphi$ are the modes (Taira et al., 2017). When the measured data is velocity, the eigenvalues are proportional to the kinetic energy. In our case where the measurement field is displacement, the singular values are therefore proportional to the amplitude scaled by the number of time steps. This means that the most important spatial modes in terms of describing the amplitude of the water surface are the first columns of $U$: they represent the largest displacement components.

As has been seen in numerical simulations by Pushkarev and Zakharov, the finite domain in our system fails to produce a cascade at low power inputs where the nonlinearity is very weak (Pushkarev and Zakharov, 1996). Based on the model from Connaughton et al. (2001), there are multiple thresholds of resonance broadening and therefore of nonlinearity, all driven by power input. The definition of these thresholds in the context of capillary wave turbulence is considered at length in our previous work (Orosco and Friend, 2023). At each of these thresholds, the cascade increases in length towards larger wavenumbers, consistent with experimental observations of the cascade growing to higher frequencies with increases in input power (Blamey et al., 2013). It seems clear from their work that the specific thresholds for a given system depends on the spacing of the quasi-resonances and the relationship between forcing and broadening.

Results

Time-series analysis

The amplitude spectra in Figure 2 clearly show a consistent peak at around 30 Hz with harmonics except for the 0 and 5 mW results. The 0 mW data indicates the noise floor of our measurement system, a combination of shot noise in the measurement system and thermal excitation of the fluid interface. At 3.5, 5, and 7 mW, our system is highly intermittent, which explains why the 5 mW line is not separated from the 0 mW line. Up to 11.5 mW the capillary wave energy remains confined to frequencies below 100 Hz as indicated with the asterisk in the plot. As the power is increased to 14.5 mW there is a broadening of the harmonics and the beginning of a broadband response that extends the cascade to 200 Hz. At 16 mW the cascade abruptly extends to about 10 kHz, and continues to extend upward in frequency beyond our DHM’s measurement range from 31 mW and up. These characteristics seem to support Connaghton’s model of finite domain, “frozen” turbulence (Connaughton et al., 2001).

The predicted value of $\alpha =-17/6$ associated with the Zakharov-Kolmogorov (ZK) capillary wave cascade occurs only in a specific range of power inputs in a specific frequency range, 0.1–1 kHz at 15–35 mW (see Figure 3). The initial jump to large $\alpha$ above the slope of the noise floor at 0 mW in Figure 2 is a direct result of a finite domain. After the initial cascade extension is complete at around 20 mW, we observe the appearance of a corner frequency separating two regions of constant $\alpha$ at each power input. Below this frequency, the slope $\alpha$ is shallower than the predicted value, and above this frequency it is steeper. This spectral response is the opposite of what is typically observed in systems that contain both gravity and capillary forces driving the waves (Falcon et al., 2007). This would seem to indicate a transition to a stronger dissipation mechanism at the frequency where the shoulder occurs, 1 kHz at 23 mW and monotonically increasing to 4 kHz at 246 mW. Conversely, the low frequency range shifts from $\alpha =-17/6$ just after cascade completion in keeping with WWT towards smaller values of $\alpha$ as power increases. This may indicate a transition from weakly to strongly nonlinear wave interactions consistent with observations of this transition in related experiments (Orosco and Friend, 2023).

Figure 3

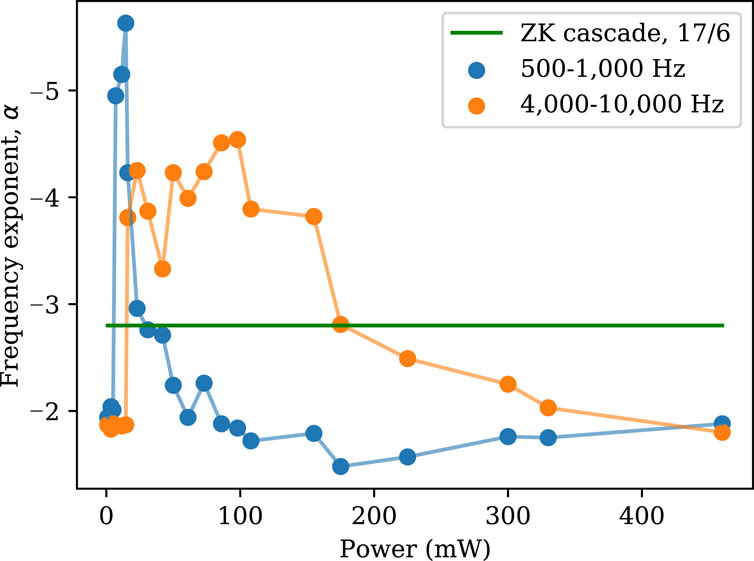
Figure 3. The frequency exponent of the wave height spectra, plotted here as average values determined from the slope of the spectra over the ranges 500–1,000 Hz and 4–10 kHz, rarely coincides with the ZK prediction of $\alpha =-17/6$. The low frequency component grows rapidly to more than $-5$ at low powers, a consequence of the appearance of the capillary wave, but shallows to $-2$ as the power increases beyond 50 mW. The change in the high frequency component from $-2$ to $-4$ occurs at the same time the low frequency component shallows from $-5$ to $-2$. As the input power increases from 100 mW, the high frequency component decreases through the ZK prediction to approach a value of $-2$.

We also observe frequency broadening of the low frequency modes as the power is increased from 16 to 108 mW, in concert with the growth of the high frequency portion of the cascade. The broadening of peaks with increased input power again supports Connaghton’s finite domain nonlinear resonance broadening model. Increased nonlinear interactions among discrete resonances allow energy to move down the cascade more easily and may explain faster growth at high frequency.Notably, we do not see any distinct resonance peaks above 100 Hz at the highest power. This power is well below the threshold of atomization onset for this system, so the presence of capillary waves at a certain frequency seems not to foreshadow the peaks of a droplet size distribution in this system as was suggested by Kooij et al. (2019).

To further explore this issue, we then sought to explicitly modulate the input signal at 5 kHz in an attempt to drive the appearance of a dominant capillary wave at this modulation frequency. At the relatively low power of 53 mW with the sinusoidal modulation of the input frequency, the modulation frequency does appear in the capillary wave with a corresponding strong response peak in Figure 4A, along with three harmonics up to about 20 kHz. As we increase the power to 100 mW, still well below the atomization threshold, the 5 kHz amplitude peak is still strong but broader while the harmonics are much less prominent. Increasing the power to 155 mW further broadens the 5 kHz peak with reduction in its maximum amplitude of about 50%; the harmonics are completely absent. Increasing the power beyond the measurement capabilities of the DHM to drive atomization at 500 mW, we found that there is no observable difference between the droplet size distribution for the atomized droplets whether or not the 5 kHz modulation is present, as determined using laser diffraction droplet sizing (Spraytec, Malvern Panalytical, Malvern, United Kingdom) and plotted in Figure 4B. This also implies that the input frequency of the excitation, whether 7 MHz or another frequency, is unlikely to affect the capillary wave distribution at the fluid interface—and consequently the droplets that may arise from it if atomization occurs.

Figure 4

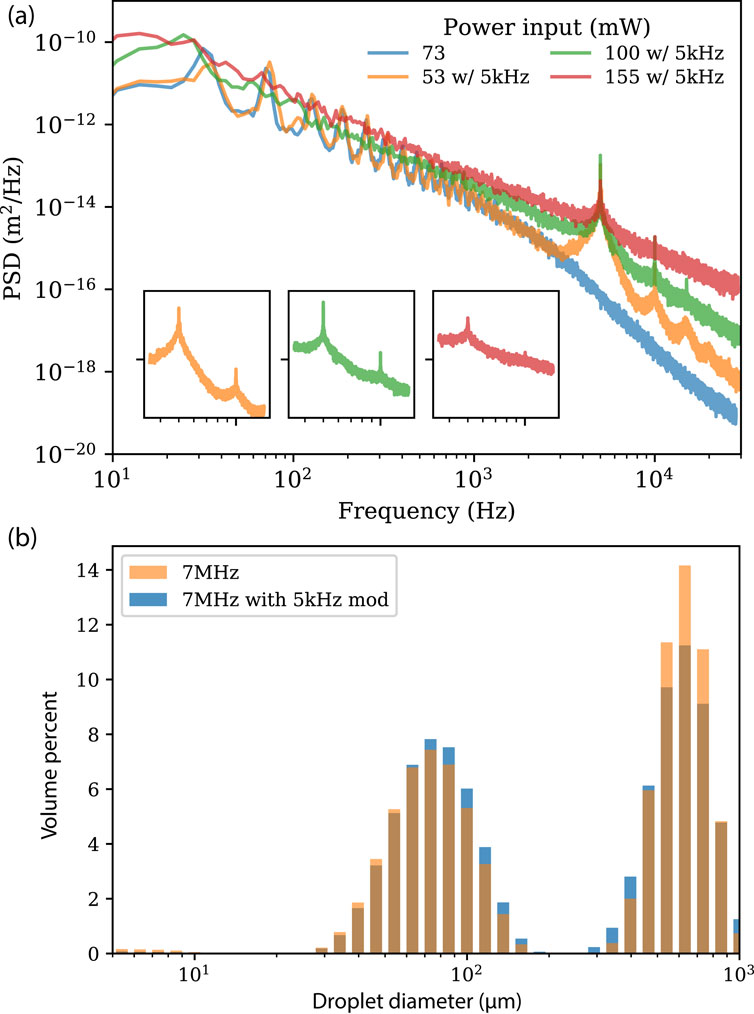
Figure 4. The effect of using 5 kHz modulation of the 7 MHz input signal upon the (A) capillary wave spectrum. At low amplitudes, the effect of the modulation is significant: compare 73 mW without modulation and 53 mW with modulation, and note how the response is significantly perturbed at 5 kHz. At greater amplitudes, the nonlinear resonance broadening appears to reduce the amplitude of the 5 kHz peak: compare 155 mW to the 100 mW data, both with the 5 kHz modulation. These input powers are well below what is required for atomization, and there is (B) no significant difference between the droplet sizes that are generated from atomization at 500 mW through the use of signal modulation at 5 kHz.

Spatial mode analysis

We now consider what information we may glean from the data by looking at the entire field of view of the fluid interface, seeking to determine how the interface spatiotemporally deforms as the input power is changed. Figure 5 provides the principal component analysis results for the surface deformation from a 16 mW data set; the interfacial data at other power levels were similar. The modes greater than 475 in each data set were discarded based on the appearance of a prominent corner in the singular value distribution at or below this mode number (see Figure 5), suggesting the modes above 475 play little to no role in defining the displacement of the fluid interface.

Figure 5

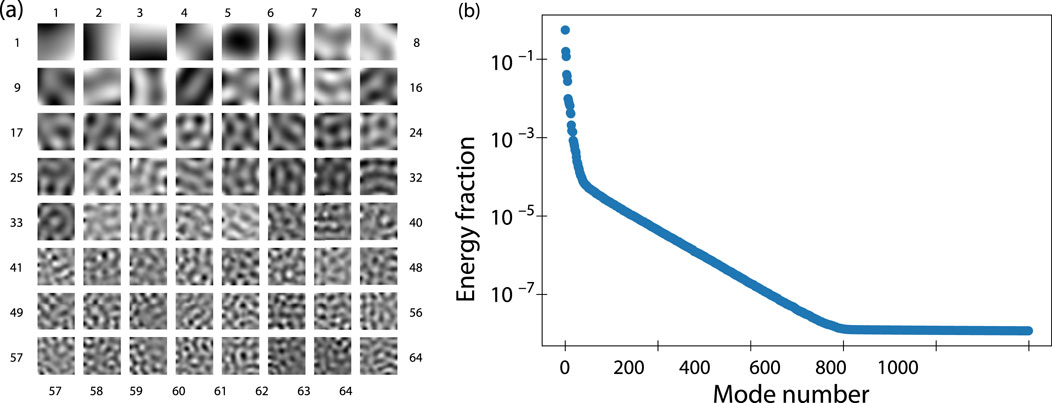
Figure 5. An example of the results from principal component analysis, showing (A) the first 64 modes for the interfacial displacement from the 16 mW data set. The distribution of the singular value amplitudes in terms of the fraction of the total energy each mode possesses is (B) plotted with respect to the mode number; in this case the vast majority of the response is in the first $\sim 40$ modes and modes beyond about 600 contribute negligibly to the response.

The first 64 POD modes are plotted in Figure 5. The characteristic length scale clearly decreases with increasing mode number as seen from Figure 5A. For the wavelength range where the field of view offers sufficient resolution ($<200\mu$m), it is evident from 2D FFT (see Supplementary Information) that only one length scale is present in each mode, and even for lower modes it is reasonable to assume by inspection that each mode is roughly composed of sinusoids of a single wavelength. In order to quantify the wavelength of the modes, we utilized a custom algorithm based on two-dimensional fast Fourier transforms (2DFFT). For each mode we reshaped its column vector into a $200\times 200$ image and performed 2DFFT, which produced another $200\times 200$ image. Each point in this new image is associated with a wavelength and a pixel value associated with the strength of that wavelength. For small wavelengths it is sufficient to define the wavelength as the pixel distance to the pixel with the largest value. However, for larger wavelengths, poor resolution in the wavelength space means we must take an average of some number of the pixels. Based on trial and error, we chose to average eight pixels with the largest values. Furthermore, in order to eliminate potential bias towards modes that are aligned with the square camera window we performed this procedure on 45 different rotations of the mode image and took the average of the wavelength values over these rotations.

In this way, we were able to obtain the relationship between wavelength and mode number in Figure 6 for the capillary waves in this system at each input power. This allows us to plot the singular values for each mode, which are equal to wave amplitudes as we described earlier, against their respective length scale in Figure 7. Energy is clearly restricted to length scales greater than 500 $\mu$m until the power reaches 7 mW. There is also a clear transition between 98 and 108 mW where energy shifts towards much smaller length scales. This second transition was not apparent from Fourier analysis alone (see Figure 2). Increasing power in this range abruptly extends the cascade, as we could not see in Figure 2 due to frequency resolution, similar to the cascade extension between 7 and 16 mW that is observable in Figure 2. Finally, notice that while the wave amplitude at scales greater than approximately 200 $\mu$m grow monotonically with an increase in input power, the wave amplitude at smaller length scales grows much more rapidly as the input power increases from 61 mW to 225 mW.

Figure 6

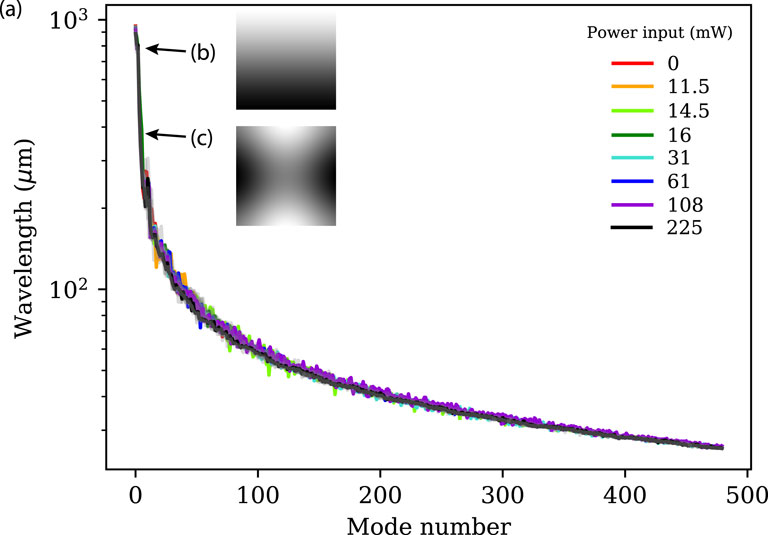
Figure 6. The computed wavelength for each mode found via 2DFFT of the principal component analysis results is plotted with respect to mode number. The largest measurable modes have a wavelength twice the field of view. (B) Mode 2, essentially a 800 $\mu$m sine grating and (C) mode 5, a 400 $\mu$m sine grating are indicated in the plot. Note how the distribution of wavelengths does not significantly change as the input power is increased from 0 to 460 mW. All powers are plotted, but only those with significant changes in the spectral response (see Figure 2) are noted in the legend for clarity.

Figure 7

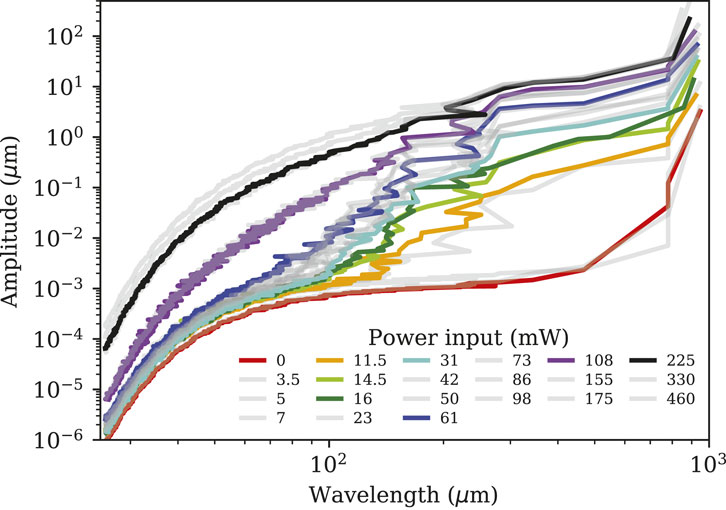
Figure 7. Singular values scaled by the number of frames from POD plotted against the wavelength obtained by performing a 2DFFT algorithm on each mode. This is the same plot as Figure 5C), but with the y-axis scaled to be amplitude and with the x-axis transformed from mode to wavelength.

In order to understand if modes of the same number between data sets are related, we took the covariance between the $U$ matrix for each data set and that of a compiled data set, $U_c$. The compiled data set, comprised of 1,024 frames, was constructed from frames taken randomly from each individual data set, upon which the same POD procedure was used to obtain $U_c$. The covariance reveals how similar each $U$ matrix is to a common basis, $U_c$. Figure 8 shows the covariance of $U_{61}$ for the 61 mW case with $U_c$. It also highlights cross-sections (vertical lines) that appear in Figure 8 where they reveal components of the given mode in terms of the basis modes (i.e.,, the dot product). For a given mode in an individual data set, the distribution of modal components tend to be centered near the corresponding mode in the basis. We can quantify the deviation of this distribution from the corresponding basis mode using the first and second moments, analogous to the expected value and variance, respectively. The first moment $({\mu }_1)$ is given by

${\mu }_1=\frac{1}{\mathrm{\Delta }}{\displaystyle \sum _{j=1}^n}jD\left(j\right),$

where $D(j)=U_{ci}\cdot U_{ij}$ is the distribution of the $i^{\text{th}}$ components of the $j^{\text{th}}$ mode of $U_{ij}$ across the $i$ modes of $U_c$ (e.g., the cross-section); and $\mathrm{\Delta }=\sum D(j)$ is the sum of these components over $j$. The deviation in the expected value is then the difference between ${\mu }_1$ and $a$. The second moment, variance ${\mu }_2$, is given by

${\mu }_2={\displaystyle \sum _{j=1}^n}D\left(j\right){\left({\mu }_1-j\right)}^2.$

Figure 8

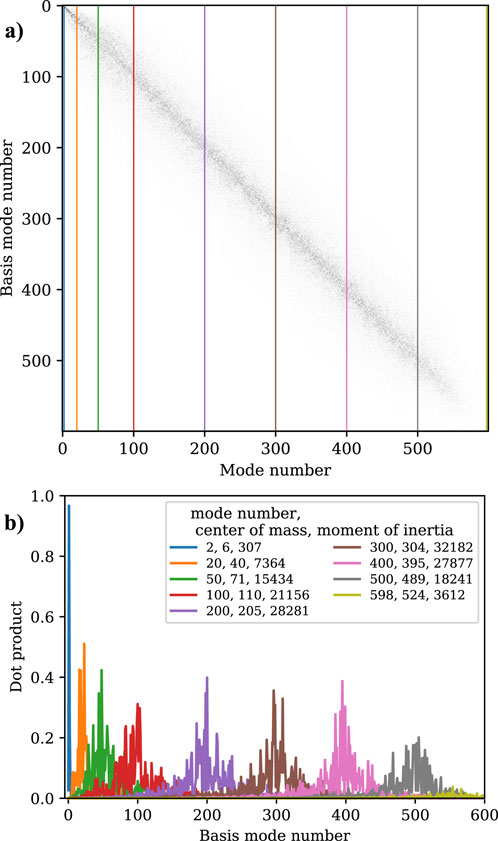
Figure 8. To determine the broadening of the capillary wave modes, we plot the (A) covariance of the 61-mW input power case with respect to the original mode numbers. If there were no broadening of the responses, this would be a diagonal line from upper left to lower right. Instead, it spreads laterally but remains locally distributed as nearly diagonal, indicating that broadening does indeed occur but there are no apparent sub- or super-harmonic parametric resonant cascades across significantly different wavelength scales. The (A) colored vertical lines in the plot are next (B) plotted showing the amplitude of the product of the chosen mode with the basis mode.

The variance is a convenient way to show that the modes identified by POD are essentially common between different data sets, not merely just their length scale. They also quantify how the modes themselves change with power input—setting aside the singular values, which rank the amplitudes of the modes within a data set at a single power. We plot the deviation of the first and second moments for each mode of every data set in Figure 9. The first three lines (in red) have a similar shape, but then suddenly the 7 mW line is different, which aligns with the sudden changes in both Figures 2, 7. The way this shape changes indicates that the modes around the 20th mode are interacting with a much larger number of adjacent modes than they were at only a slightly lower power.

Figure 9

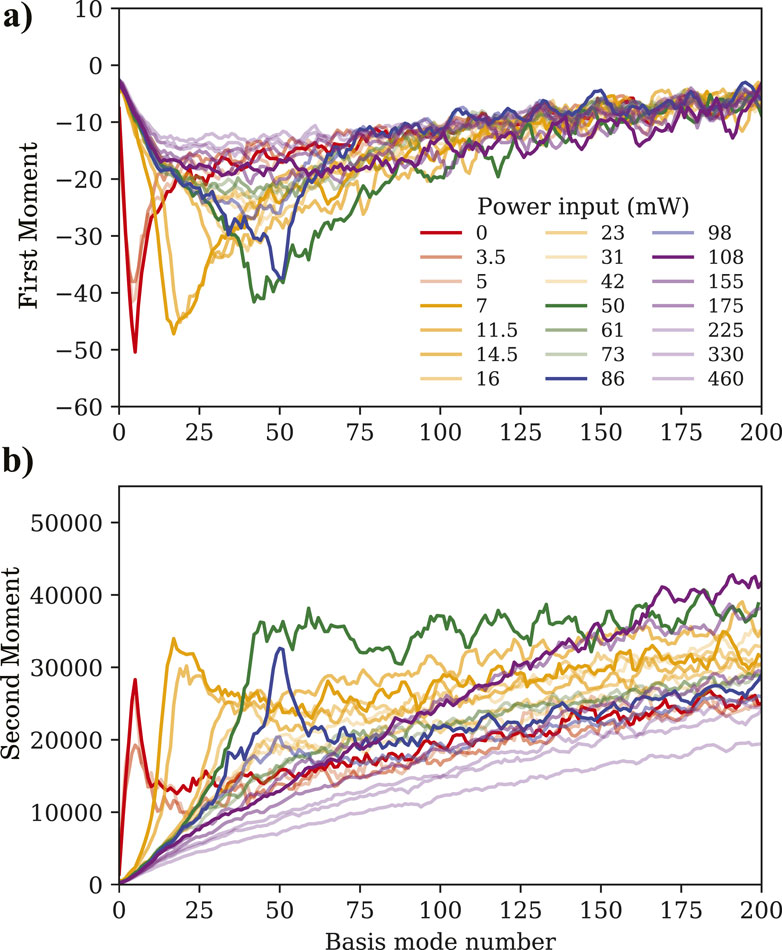
Figure 9. (A) First and (B) second moments versus basis mode number as a proxy for the wavelength. Recall that the modes are sequentially ordered from largest wavelength to smallest.

The fact that the cross-sections in Figure 8 are distributed generally around their corresponding basis mode is an expression of local wave interaction. When the power crosses some threshold near 6 mW, the modes near 20 suddenly become less localized and interact with modes possessing wavelength scales of greater difference. As power increases from 7 to 42 mW the moment lines gradually move towards the zero power line, indicating that the modes interact more locally and they are more closely described by the corresponding basis modes.

Once again, however, at 50 mW the modes beyond mode 45 become de-localized, but again move towards the zero power lines at slightly larger powers. This process repeats from 86 mW for modes near the 50th mode. The final de-localization apparent in the data is centered closer to the ${140}^{\text{th}}$ mode, indicating even smaller length scales. This de-localization coincides with the transition identified in Figure 7.

Conclusion

Fourier analysis often used in wave turbulence problems identifies the relationship between wave height and frequency for micro-scale capillary waves in a small sessile droplet. The effects of the finite sized droplet produce frozen turbulence and low frequency (relative to the high-speed DHM measurement capabilities) repeated and abrupt cascade extension at specific input powers. Immediately upon cascade completion we see a small region of capillary wave dynamics that correspond to the classic ZK theory of WWT where $\alpha =-17/6$. At greater powers, there is a corner frequency separating $\alpha$ into two frequency domains, a relatively shallow-sloped region at lower frequencies and a steeper-sloped region at higher frequencies. These observations suggest an increasingly strong nonlinear wave interaction at low frequencies and increasing dissipation at larger frequencies.

Spatial analysis with POD provides us with a direct link between amplitude and wavelength. Energy flowing towards smaller length scales exhibits a nonlinear dependence upon the input power, with discrete thresholds repeatedly appearing as the power is increased. These shifts are analogous to cascade extension, most of which are observable using standard Fourier analysis. However, spatial analysis allows us to identify a small scale, high frequency cascade extension that was not apparent with Fourier analysis. The covariance between each data set and the basis modes provides us with information about how coherent modes change with power input. We are able to identify de-localization events where waves interact with wavelengths of greater difference as the power is increased.

Uniform Faraday waves are a poor model for capillary wave dynamics in this system, and therefore are unlikely to be appropriate for predicting atomization which requires greater power. Resonant peaks in the capillary wave response are quickly broadened by the nonlinear coupling, even when the input signal is modulated to force the resonance into existence. This occurs at input power levels well below the atomization threshold, and it remains unclear how to predict which wavelengths will be preferentially amplified—if any—in order to form droplets at a larger power input. A theory of wave turbulence beyond the weak and infinite regimes dictated by WWT are therefore needed to predict which waves will produce droplets in high frequency ultrasound atomization systems. Such systems are potentially beneficial in a wide range of applications, from pulmonary vaccination (Rajapaksa et al., 2014) to hospital disinfection (Kumaraswamy et al., 2018), fuel (Brown et al., 2024) and paint (Dalili et al., 2020) sprays, and particle production (Alvarez et al., 2008). Crucially, the identification of droplet sizes and flow rates in the process of designing these devices hinges on an understanding of the underlying mechanism. Whatever that mechanism is, it is certainly a strongly nonlinear one, complicating the process of modeling it.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

WC: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–original draft, Writing–review and editing. JO: Conceptualization, Data curation, Investigation, Methodology, Software, Supervision, Validation, Writing–original draft, Writing–review and editing. OS: Investigation, Methodology, Validation, Writing–review and editing. JF: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. We are grateful to the Office of Naval Research, United States (grants 13423461 and 12368098) and the W. M. Keck Foundation, United States for funding provided to JF in support of this work. JO is grateful for support provided by the University of California’s Presidential Postdoctoral Fellowship program. We are also grateful to Yves Emery and team at LynceéTec for assistance with adapting the DHM to this project’s needs. Fabrication was performed in part at the San Diego Nanotechnology Infrastructure (SDNI) of UCSD, a member of the National Nanotechnology Coordinated Infrastructure, which is supported by the National Science Foundation (Grant ECCS–1542148).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alvarez, M., Yeo, L., and Friend, J. (2008). Rapid generation of protein aerosols and nanoparticles via surface acoustic wave atomization. Nanotechnology 19, 455103. doi:10.1088/0957-4484/19/45/455103

PubMed Abstract | CrossRef Full Text | Google Scholar

Aubourg, Q., and Mordant, N. (2016). Investigation of resonances in gravity-capillary wave turbulence. Phys. Rev. Fluids 1, 023701. doi:10.1103/PhysRevFluids.1.023701

CrossRef Full Text | Google Scholar

Barreras, F., Amaveda, H., and Lozano, A. (2002). Transient high-frequency ultrasonic water atomization. Exp. Fluids 33, 405–413. doi:10.1007/s00348-002-0456-1

CrossRef Full Text | Google Scholar

Berhanu, M., and Falcon, E. (2013). Space-time-resolved capillary wave turbulence. Phys. Rev. E 87, 033003. doi:10.1103/PhysRevE.87.033003

CrossRef Full Text | Google Scholar

Berkooz, G., Holmes, P., and Lumley, J. L. (1993). The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575. doi:10.1146/annurev.fluid.25.1.539

CrossRef Full Text | Google Scholar

Blamey, J., Yeo, L. Y., and Friend, J. R. (2013). Microscale capillary wave turbulence excited by high frequency vibration. Langmuir 29, 3835–3845. doi:10.1021/la304608a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bosch, E., and van de Water, W. (1993). Spatiotemporal intermittency in the faraday experiment. Phys. Rev. Lett. 70, 3420–3423. doi:10.1103/PhysRevLett.70.3420

PubMed Abstract | CrossRef Full Text | Google Scholar

Boudaoud, A., Cadot, O., Odille, B., and Touzé, C. (2008). Observation of wave turbulence in vibrating plates. Phys. Rev. Lett. 100, 234504. doi:10.1103/PhysRevLett.100.234504

PubMed Abstract | CrossRef Full Text | Google Scholar

Brazhnikov, M. Y., Kolmakov, G. V., Levchenko, A. A., and Mezhov-Deglin, L. P. (2002). Observation of capillary turbulence on the water surface in a wide range of frequencies. Europhys. Lett. (EPL) 58, 510–516. doi:10.1209/epl/i2002-00425-9

CrossRef Full Text | Google Scholar

Brown, T., Hytovick, R., Berson, J., Burke, R., Salauddin, S., and Ahmed, K. (2024). Dynamics of mono-size aerosolized liquid fuel detonations. Proc. Combust. Inst. 40, 105416. doi:10.1016/j.proci.2024.105416

CrossRef Full Text | Google Scholar

Collignon, S., Manor, O., and Friend, J. (2018). Improving and predicting fluid atomization via hysteresis-free thickness vibration of lithium niobate. Adv. Funct. Mater. 28, 1704359. doi:10.1002/adfm.201704359

CrossRef Full Text | Google Scholar

Collins, D. J., Manor, O., Winkler, A., Schmidt, H., Friend, J. R., and Yeo, L. Y. (2012). Atomization off thin water films generated by high-frequency substrate wave vibrations. Phys. Rev. E 86, 056312. doi:10.1103/PhysRevE.86.056312

PubMed Abstract | CrossRef Full Text | Google Scholar

Connaughton, C., Nazarenko, S., and Pushkarev, A. (2001). Discreteness and quasiresonances in weak turbulence of capillary waves. Phys. Rev. E 63, 046306. doi:10.1103/physreve.63.046306

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuche, E., Marquet, P., and Depeursinge, C. (1999). Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 38, 6994. doi:10.1364/AO.38.006994

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalili, A., Sidawi, K., and Chandra, S. (2020). Surface coverage by impact of droplets from a monodisperse spray. J. Coatings Technol. Res. 17, 207–217. doi:10.1007/s11998-019-00258-7

CrossRef Full Text | Google Scholar

Deike, L., Berhanu, M., and Falcon, E. (2014). Energy flux measurement from the dissipated energy in capillary wave turbulence. Phys. Rev. E 89, 023003. doi:10.1103/PhysRevE.89.023003

PubMed Abstract | CrossRef Full Text | Google Scholar

Emery, Y., Colomb, T., and Cuche, E. (2021). Metrology applications using off-axis digital holography microscopy. J. Phys. Photonics 3, 034016. doi:10.1088/2515-7647/ac0957

CrossRef Full Text | Google Scholar

Falcón, C., Falcon, E., Bortolozzo, U., and Fauve, S. (2009). Capillary wave turbulence on a spherical fluid surface in low gravity. Eur. Phys. Lett. 86, 14002. doi:10.1209/0295-5075/86/14002

CrossRef Full Text | Google Scholar

Falcon, E., and Laroche, C. (2011). Observation of depth-induced properties in wave turbulence on the surface of a fluid. EPL Europhys. Lett. 95, 34003. doi:10.1209/0295-5075/95/34003

CrossRef Full Text | Google Scholar

Falcon, É., Laroche, C., and Fauve, S. (2007). Observation of gravity-capillary wave turbulence. Phys. Rev. Lett. 98, 094503. doi:10.1103/physrevlett.98.094503

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodridge, C. L., Hentschel, H. G. E., and Lathrop, D. P. (1999). Breaking faraday waves: critical slowing of droplet ejection rates. Phys. Rev. Lett. 82, 3062–3065. doi:10.1103/PhysRevLett.82.3062

CrossRef Full Text | Google Scholar

Kooij, S., Astefanei, A., Corthals, G. L., and Bonn, D. (2019). Size distributions of droplets produced by ultrasonic nebulizers. Sci. Rep. 9, 6128. doi:10.1038/s41598-019-42599-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumaraswamy, M., Collignon, S., Do, C., Kim, J., Nizet, V., and Friend, J. (2018). Decontaminating surfaces with atomized disinfectants generated by a novel thickness-mode lithium niobate device. Appl. Microbiol. Biotechnol. 15, 6459–6467. doi:10.1007/s00253-018-9088-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurosawa, M., Futami, A., and Higuchi, T. (1997). Characteristics of liquids atomization using surface acoustic wave. Proc. Int. Solid State Sensors Actuators Conf. 2, 801–804. doi:10.1109/SENSOR.1997.635221

CrossRef Full Text | Google Scholar

Kurosawa, M., Watanabe, T., Futami, A., and Higuchi, T. (1995). Surface acoustic wave atomizer. Sensors Actuators A Phys. 50, 69–74. doi:10.1016/0924-4247(96)80086-0

CrossRef Full Text | Google Scholar

Lang, R. J. (1962). Ultrasonic atomization of liquids. J. Acoust. Soc. Am. 34, 6–8. doi:10.1121/1.1909020

CrossRef Full Text | Google Scholar

Manor, O., Dentry, M., Friend, J. R., and Yeo, L. Y. (2011). Substrate dependent drop deformation and wetting under high frequency vibration. Soft Matter 7, 7976–7979. doi:10.1039/c1sm06054f

CrossRef Full Text | Google Scholar

Mei, J., Zhang, N., and Friend, J. (2020). Fabrication of surface acoustic wave devices on lithium niobate. J. Vis. Exp. 160, e61013. doi:10.3791/61013

PubMed Abstract | CrossRef Full Text | Google Scholar

Newell, A. C., and Rumpf, B. (2011). Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78. doi:10.1146/annurev-fluid-122109-160807

CrossRef Full Text | Google Scholar

Orosco, J., and Friend, J. (2023). Identification of weakly to strongly-turbulent three-wave processes in a micro-scale system. Chaos. Solit. Fractals 172, 1–7.

Google Scholar

Pushkarev, A. N., and Zakharov, V. E. (1996). Turbulence of capillary waves. Phys. Rev. Lett. 76, 3320–3323. doi:10.1103/PhysRevLett.76.3320

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, A., Yeo, L. Y., and Friend, J. R. (2008). Interfacial destabilization and atomization driven by surface acoustic waves. Phys. Fluids 20, 074103. doi:10.1063/1.2953537

CrossRef Full Text | Google Scholar

Rajan, R., and Pandit, A. (2001). Correlations to predict droplet size in ultrasonic atomisation. Ultrasonics 39, 235–255. doi:10.1016/s0041-624x(01)00054-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajapaksa, A. E., Ho, J. J., Qi, A., Bischof, R., Nguyen, T. H., Tate, M., et al. (2014). Effective pulmonary delivery of an aerosolized plasmid DNA vaccine via surface acoustic wave nebulization. Respir. Res. 15, 60–12. doi:10.1186/1465-9921-15-60

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramisetty, K. A., Pandit, A. B., and Gogate, P. R. (2013). Investigations into ultrasound induced atomization. Ultrason. Sonochemistry 20, 254–264. doi:10.1016/j.ultsonch.2012.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, P. A. (1996). Scalings, spectra, and statistics of strong wave turbulence. Phys. Plasmas 3, 192–201. doi:10.1063/1.871845

CrossRef Full Text | Google Scholar

Rovira, M., Engvall, K., and Duwig, C. (2021). Proper orthogonal decomposition analysis of the large-scale dynamics of a round turbulent jet in counterflow. Phys. Rev. Fluids 6, 014701. doi:10.1103/PhysRevFluids.6.014701

CrossRef Full Text | Google Scholar

Schmidt, O. T., and Colonius, T. (2020). Guide to spectral proper orthogonal decomposition. AIAA J. 58, 1023–1033. doi:10.2514/1.J058809

CrossRef Full Text | Google Scholar

Shannon, C. (1949). Communication in the presence of noise. Proc. IRE 37, 10–21. doi:10.1109/JRPROC.1949.232969

CrossRef Full Text | Google Scholar

Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., McKeon, B. J., et al. (2017). Modal analysis of fluid flows: an overview. AIAA J. 55, 4013–4041. doi:10.2514/1.J056060

CrossRef Full Text | Google Scholar

Wagner, C., Müller, H. W., and Knorr, K. (1999). Faraday waves on a viscoelastic liquid. Phys. Rev. Lett. 83, 308–311. doi:10.1103/PhysRevLett.83.308

CrossRef Full Text | Google Scholar

Welch, P. (1967). The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoustics 15, 70–73. doi:10.1109/TAU.1967.1161901

CrossRef Full Text | Google Scholar

Winkler, A., Harazim, S. M., Menzel, S. B., and Schmidt, H. (2015). SAW-based fluid atomization using mass-producible chip devices. Lab a Chip 15, 3793–3799. doi:10.1039/C5LC00756A

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, W. B., Budakian, R., and Putterman, S. J. (1996). Diffusing light photography of fully developed isotropic ripple turbulence. Phys. Rev. Lett. 76, 4528–4531. doi:10.1103/physrevlett.76.4528

PubMed Abstract | CrossRef Full Text | Google Scholar

Xvii, F. M. (1831). On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philosophical Trans. R. Soc. Lond., 299–340.

Google Scholar

Yoon, P. H. (2000). Generalized weak turbulence theory. Phys. Plasmas 7, 4858–4871. doi:10.1063/1.1318358

CrossRef Full Text | Google Scholar

Zakharov, V. E., and Filonenko, N. N. (1971). Weak turbulence of capillary waves. J. Appl. Mech. Tech. Phys. 8, 37–40. doi:10.1007/BF00915178

CrossRef Full Text | Google Scholar

Zakharov, V. E., L’vov, V. S., and Falkovich, G. (1992). Kolmogorov spectra of turbulence I in Springer series in nonlinear dynamics. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-50052-7

CrossRef Full Text | Google Scholar

Zhang, S., Orosco, J., and Friend, J. (2021). Onset of low-frequency capillary waves driven by high-frequency ultrasound. ArXiv:2108.09579.

Google Scholar

Zhang, W., and Viñals, J. (1996). Square patterns and quasipatterns in weakly damped faraday waves. Phys. Rev. E 53, R4283–R4286. doi:10.1103/PhysRevE.53.R4283

PubMed Abstract | CrossRef Full Text | Google Scholar